Approximating Fixed Points of Bregman Generalized α-Nonexpansive Mappings

Abstract

In this paper, we introduce a new class of Bregman generalized $\alpha$-nonexpansive mappings in terms of the Bregman distance. We establish several weak and strong convergence theorems of the Ishikawa and Noor iterative schemes for Bregman generalized $\alpha$-nonexpansive mappings in Banach spaces. A numerical example is given to illustrate the main results of fixed point approximation using Halpern’s algorithm.

1. Introduction

In 1967, Bregman [1] discovered an effective technique using the so-called Bregman distance function $D_f$ in the process of designing and analyzing feasibility and optimization algorithms. This opened a growing area of research in which Bregman’s technique was applied in various ways in order to design and analyze some algorithms for solving not only feasibility and optimization problems, but also algorithms for solving variational inequality problems, equilibrium problems, and fixed point problems for nonlinear mappings (see [2,3,4]).

In recent years, several authors have been constructing algorithms for finding fixed points of nonlinear mappings by using the Bregman distance and the Bregman projection (see [5,6] and the reference therein). In 2003, Bauschke et al. [7,8] first introduced the class of Bregman firmly nonexpansive mappings which is a generalization of the classical firmly nonexpansive mappings. A few years ago, Reich [9] studied the class of Bregman strongly nonexpansive mappings and showed the existence of their common fixed points.

Motivated by the aforementioned results, we investigate the new class of Bregman generalized $\alpha$-nonexpansive mappings. We prove the existence of fixed points for such mappings under some conditions, and establish weak and strong convergence theorems regarding those fixed points. This is achieved by utilizing the Ishikawa and Noor iterative schemes, as well as Halpern’s algorithm to generate a convergent sequence with desired properties.

Throughout this paper, we assume that E is a real Banach space with the norm $\parallel ·\parallel$ and the dual space $E^{\ast }$. We denote the value of $x^{\ast }\in E^{\ast }$ at $x\in E$ by $⟨x,x^{\ast }⟩.$ If ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is a sequence in $E,$ we denote the strong convergence and the weak convergence of ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ to a point $x\in E$ by $x_n\to x$ and $x_n\rightharpoonup x,$ respectively.

Let C be a nonempty subset of E and $T:C\to C$ be a mapping. Then, a point $x\in C$ is called a fixed point of T if $Tx=x$ and the set of all fixed points of T is denoted by $F\left(T\right).$ A mapping $T:C\to C$ is said to be:

• nonexpansive if

  $$\parallel Tx-Ty\parallel \le \parallel x-y\parallel ,\forall x,y\in C;$$
• quasi-nonexpansive if $F\left(T\right)\ne \varnothing$ and

  $$\parallel Tx-y\parallel \le \parallel x-y\parallel ,\forall x\in C,y\in F\left(T\right);$$
• Suzuki-type generalized nonexpansive [10] if

  $${\displaystyle \frac{1}{2}}\parallel x-Tx\parallel \le \parallel x-y\parallel ⟹\parallel Tx-Ty\parallel \le \parallel x-y\parallel ,\forall x,y\in C;$$
• α-nonexpansive, where $\alpha <1$, if

  $${\parallel Tx-Ty\parallel }^2\le {\alpha \parallel Tx-y\parallel }^2{+\alpha \parallel x-Ty\parallel }^2+(1-2\alpha ){\parallel x-y\parallel }^2,\forall x,y\in C;$$
• generalized α-nonexpansive [11], where $\alpha \in [0,1)$, if

  $${\displaystyle \frac{1}{2}}\parallel x-Tx\parallel \le \parallel x-y\parallel$$

  $$⟹\parallel Tx-Ty\parallel \le \alpha \parallel Tx-y\parallel +\alpha \parallel x-Ty\parallel +(1-2\alpha )\parallel x-y\parallel ,\forall x,y\in C.$$

Let C be a nonempty subset of a Banach space E and $T:C\to C$ be a nonexpansive mapping. For any $x_1\in C$,

• The Ishikawa iteration [12] is given by

  $$\left\{\begin{array}{c}{y}_n={\beta }_{n}T{x}_n+(1-{\beta }_n)x_n,\hfill \\ x_{n+1}={\gamma }_{n}T{y}_n+(1-{\gamma }_n)x_n,\forall n\in \mathbb{N},\hfill \end{array}\right.$$

  (1)

  where ${\left\{{\beta }_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{{\gamma }_n\right\}}_{n\in \mathbb{N}}$ are sequences in $[0,1)$ with some appropriate conditions.
• The Noor iteration [13] is given by

  $$\left\{\begin{array}{c}{z}_n={\alpha }_{n}T{x}_n+(1-{\alpha }_n)x_n,\hfill \\ y_n={\beta }_{n}T{z}_n+(1-{\beta }_n)x_n,\hfill \\ x_{n+1}={\gamma }_{n}T{y}_n+(1-{\gamma }_n)x_n,\forall n\in \mathbb{N},\hfill \end{array}\right.$$

  (2)

  where ${\left\{{\alpha }_n\right\}}_{n\in \mathbb{N}}$, ${\left\{{\beta }_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{{\gamma }_n\right\}}_{n\in \mathbb{N}}$ are the sequences in $[0,1)$ with some appropriate conditions.

A Banach space E is said to satisfy Opial’s property if, for any sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ in E that converges weakly to $x\in E,$ we have

$$\underset{n\to \infty }{lim\; sup}\parallel x_n-x\parallel <\underset{n\to \infty }{lim\; sup}\parallel x_n-y\parallel ,\forall y\in E\setminus \left\{x\right\}.$$

Opial’s property is a powerful tool that can be utilized to derive a weak or strong convergence of some iterative sequences [14]. In fact, since every weakly convergent sequence is necessarily bounded, we have ${lim\; sup}_{n\to \infty }\parallel x_n-x\parallel$ and ${lim\; sup}_{n\to \infty }\parallel x_n-y\parallel$ are finite.

Note that Opial’s property is satisfied in Banach spaces $l^p$ for $1\le p<\infty$, but not in $L_p[0,2\pi ]$ spaces for $1\le p<\infty$ and $p\ne 2$.

Next, we recall the definition of a Bregman distance which is not a distance in the usual sense. Let E be a Banach space and $f:E\to \mathbb{R}$ be a strictly convex and Gâteaux differentiable function. Let $D_f:E\times E\to \mathbb{R}$ be defined by

$$D_f(x,y)=f\left(x\right)-f\left(y\right)-⟨x-y,\nabla f\left(y\right)⟩,\forall (x,y)\in E\times E.$$

(3)

Then, we define The Bregman distance [15] between x and y to be $D_f(x,y)$. In general, $D_f$ is not symmetric and does not satisfy the triangle inequality. Clearly, we have $D_f(x,x)=0$, but $D_f(x,y)=0$ may not imply $x=y$, for instance, when f is a linear function on $E.$ Moreover, since f is convex, it is clear that $D_f(x,y)\ge 0$ for all $x,y\in E.$

Let $f:E\to \mathbb{R}$ be a strictly convex and Gâteaux differentiable function and $C\subseteq E$ be nonempty. A mapping $T:C\to E$ is said to be:

• Bregman nonexpansive if

  $$D_f(Tx,Ty)\le D_f(x,y),\forall x,y\in C;$$
• Bregman quasi-nonexpansive if $F\left(T\right)\ne \varnothing$ and

  $$D_f(p,Tx)\le D_f(p,x),\forall x\in C,p\in F\left(T\right);$$
• Bregman skew quasi-nonexpansive if $F\left(T\right)\ne \varnothing$ and

  $$D_f(Tx,p)\le D_f(x,p),\forall x\in C,p\in F\left(T\right);$$
• Bregman nonspreading if

  $$D_f(Tx,Ty)+D_f(Ty,Tx)\le D_f(Tx,y)+D_f(Ty,x),\forall x,y\in C.$$

Working with a Bregman distance $D_f$ with respect to f, the following Opial-like inequality holds [16]: for any Banach space E and sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ in E, we have

$$\underset{n\to \infty }{lim\; sup}{D}_f(x_n,x)<\underset{n\to \infty }{lim\; sup}{D}_f(x_n,y),$$

(4)

whenever $x_n\rightharpoonup x\ne y$ (see Lemma 4 for details). This is called the Bregman–Opial property.

Inspired by the property, we propose a new class of Bregman generalized α-nonexpansive mappings by using the Bregman distance as follows:

For any $\alpha \in [0,1)$, a mapping $T:C\to C$ is said to be Bregman generalized α-nonexpansive if

$$D_f(Tx,Ty)\le \alpha D_f(Tx,y)+\alpha D_f(x,Ty)+(1-2\alpha )D_f(x,y),\forall x,y\in C.$$

(5)

Let us give an example of a Bregman generalized $\alpha$-nonexpansive mapping where $F\left(T\right)\ne \varnothing$.

Example 1.

Let $f:\mathbb{R}\to \mathbb{R}$ be a mapping defined by $f\left(x\right)=x^4.$ The associated Bregman distance is given by

$$\begin{array}{ll}{D}_f(x,y)& =x^4-y^4-(x-y)\left(4y^3\right)\\ & =x^4+3y^4-4x{y}^3,\forall x,y\in \mathbb{R}.\end{array}$$

Now, we define a mapping $T:[0,0.9]\to [0,0.9]$ by

$$Tx=x^2,\forall x\in [0,0.9].$$

It is easy to verify that $F\left(T\right)=\left\{0\right\}$. While T is not a generalized α-nonexpansive mapping, it is indeed a Bregman generalized α-nonexpansive mapping with respect to $D_f$ in the sense of the equation (5). Indeed, define a mapping $g:[0,0.9]\times [0,0.9]\to \mathbb{R}$ by

$$g(x,y)=\alpha D_f(Tx,y)+\alpha D_f(x,Ty)+(1-2\alpha )D_f(x,y)-D_f(Tx,Ty),\forall x,y\in [0,0.9],$$

where

$$\begin{gathered} D_f(Tx,y)=f\left(Tx\right)-f\left(y\right)-⟨Tx-y,\nabla f\left(y\right)⟩=x^8+3y^4-4x^2{y}^3, \\ {D}_f(x,Ty)=f\left(x\right)-f\left(Ty\right)-⟨x-Ty,\nabla f\left(Ty\right)⟩=x^4+3y^8-4x{y}^6, \\ {D}_f(x,y)=f\left(x\right)-f\left(y\right)-⟨x-y,\nabla f\left(y\right)⟩=x^4+3y^4-4x{y}^3, \\ {D}_f(Tx,Ty)=f\left(Tx\right)-f\left(Ty\right)-⟨Tx-Ty,\nabla f\left(Ty\right)⟩=x^8+3y^8-4x^2{y}^6. \end{gathered}$$

Then, we have

$$\begin{array}{cc}\hfill g(x,y)& =\alpha D_f(Tx,y)+\alpha D_f(x,Ty)+(1-2\alpha )D_f(x,y)-D_f(Tx,Ty)\hfill \\ & =\alpha (x^8+3y^4-4x^2{y}^3)+\alpha (x^4+3y^8-4x{y}^6)\hfill \\ & +(1-2\alpha )(x^4+3y^4-4x{y}^3)-(x^8+3y^8-4x^2{y}^6).\hfill \\ & =(1-\alpha )(x^4+3y^4-x^8-3y^8)+4x{y}^3\left(\alpha (2-y^3)+x{y}^3-x\right).\hfill \end{array}$$

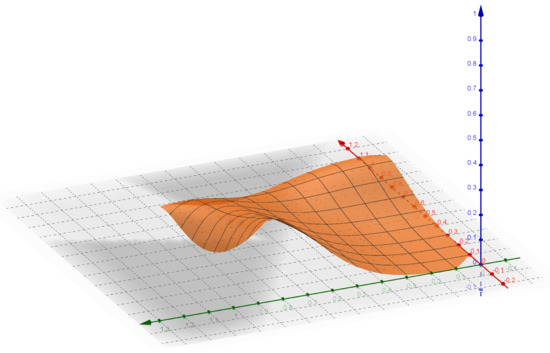
If we take $\alpha \in [\frac{1}{2},1)$, then we can verify that $g(x,y)\ge 0$ for all $x,y\in [0,0.9]$ as shown in Figure 1. Hence, T is a Bregman generalized α-nonexpansive mapping.

Figure 1. Plotting of $g(x,y)$ for all $x,y\in [0,0.9]$ and $\alpha =0.56$.

Our paper is organized as follows: in Section 2, we state several definitions and known results about Banach space and Bregman distance. In Section 3, we apply the Bregman–Opial property to present some fixed point theorems and we prove some weak and strong convergence theorems for Bregman generalized $\alpha$-nonexpansive mappings in Banach spaces. In Section 4, we give some numerical examples to illustrate the main results, which extend and generalize the results of Suzuki [10], Pant et al. [11] and Naraghirad et al. [17].

2. Preliminaries

In this section, we introduce necessary definitions and results to be used later on.

Let $S=\{x\in E:\parallel x\parallel =1\}$.

• A Banach space E is said to be strictly convex if $∥\frac{x+y}{2}∥<1$ whenever $x,y\in S$ and $x\ne y$.
• The space E is also said to be uniformly convex if, for all $ϵ\in (0,2],$ there exists $\delta >0$ such that $x,y\in S$ and $\parallel x-y\parallel \ge ϵ$ imply $∥\frac{x+y}{2}∥\le 1-\delta$.
• A Banach space E is said to be smooth if

  $${\displaystyle \underset{t\to 0}{lim}\frac{\parallel x+ty\parallel -\parallel x\parallel }{t}}$$

  (6)

  exists for all $x,y\in S$.
• The space E is also said to be uniformly smooth if the limit (6) is attained uniformly in $x,y\in S$.

Note that the following are well known:

(1)

Every uniformly convex Banach space is strictly convex and reflexive.

(2)

A Banach space E is uniformly convex if and only if $E^{\ast }$ is uniformly smooth.

(3)

If E is reflexive, then E is strictly convex if and only if $E^{\ast }$ is smooth (see, for instance, Takahashi [18] for more details).

Let E be a smooth Banach space and let $f\left(x\right)={\parallel x\parallel }^2$ for all $x\in E$. Then, it follows that $\nabla f\left(x\right)=2Jx$ for all $x\in E$, where J is the normalized duality mapping from E into $E^{\ast }.$ Hence, $D_f(x,y)=\varphi (x,y)$ ([19]), where $\varphi :E\times E\to \mathbb{R}$ is defined as follows:

$$\varphi (x,y):={\parallel x\parallel }^2-2⟨x,Jy⟩+{\parallel y\parallel }^2,\forall (x,y)\in E\times E.$$

(7)

If E is a Hilbert space, the Equation (7) reduces to $D_f(x,y)={\parallel x-y\parallel }^2.$

A function $f:E\to (-\infty ,+\infty ]$ is said to be proper if the $domf=\{x\in E:f(x)<\infty \}\ne \varnothing .$ It is also said to be lower semi-continuous if the set $\{x\in E:f(x)\le r\}$ is closed for all $r\in \mathbb{R}.$ The function f is said to be convex if

$$f(\alpha x+(1-\alpha \left)y\right)\le \alpha f\left(x\right)+(1-\alpha )f\left(y\right),\forall x,y\in E,\alpha \in (0,1).$$

(8)

It is also said to be strictly convex if the strict inequality holds in the inequality (8) for all $x,y\in domf$ with $x\ne y$ and $\alpha \in (0,1).$

In the sequel, we shall denote by $\Gamma \left(E\right)$ the class of proper lower semi-continuous convex functions on E.

For each $f\in \Gamma \left(E\right)$, the subdifferential$\partial f$ of f is defined by

$$\partial f\left(x\right)=\{x^{\ast }\in E^{\ast }:f\left(x\right)+⟨y-x,x^{\ast }⟩\le f\left(y\right),\forall y\in E\},\forall x\in E.$$

Rockafellar’s theorem [20,21] ensures that $\partial f\subset E\times E^{\ast }$ is maximal monotone. If $f\in \Gamma \left(E\right)$ and $g:E\to \mathbb{R}$ is a continuous convex function, then $\partial (f+g)=\partial f+\partial g.$ For each $f\in \Gamma \left(E\right)$, the (Fenchel) conjugate function$f^{\ast }$ of f is defined by

$$f^{\ast }\left(x^{\ast }\right)=\underset{x\in E}{sup}\{⟨x,x^{\ast }⟩-f\left(x\right)\},\forall x^{\ast }\in E^{\ast }.$$

It is well known that

$$f\left(x\right)+f^{\ast }\left(x^{\ast }\right)\ge ⟨x,x^{\ast }⟩,\forall (x,x^{\ast })\in E\times E^{\ast },$$

and $(x,x^{\ast })\in \partial f$ is equivalent to

$$f\left(x\right)+f^{\ast }\left(x^{\ast }\right)=⟨x,x^{\ast }⟩.$$

(9)

We also know that, if $f\in \Gamma \left(E\right)$, then $f^{\ast }:E^{\ast }\to (-\infty ,+\infty ]$ be a proper ${\mathrm{weak}}^{\ast }$ lower semi-continuous convex function (see Phelps [22] for more details on convex analysis).

In the sequel, we shall denote by ${\Gamma }^{\ast }\left(E^{\ast }\right)$ the class of proper ${\mathrm{weak}}^{\ast }$ lower semi-continuous convex function on $E^{\ast }$.

Let $f:E\to \mathbb{R}$ be a convex function.

• For any $x\in E,$ the gradient$\nabla f\left(x\right)$ of f is defined to be the linear functional in $E^{\ast }$ such that

  $$⟨y,\nabla f\left(x\right)⟩=\underset{t\to 0}{lim}\frac{f(x+ty)-f\left(x\right)}{t},\forall y\in E.$$
• The function f is said to be Gâteaux differentiable at x if $⟨-,\nabla f\left(x\right)⟩\in E^{\ast }$ for all $x\in E$. In this case, we denote $⟨-,\nabla f\left(x\right)⟩$ by $\nabla f\left(x\right)$.
• The function f is also said to be Fréchet differentiable at x if, for all $ϵ>0,$ there exists $\delta >0$ such that $\parallel y-x\parallel \le \delta$ implies (see [6])

  $$\left|f\right(y)-f(x)-⟨y-x,\nabla f(x)⟩|\le ϵ\parallel y-x\parallel .$$
• A convex function $f:E\to \mathbb{R}$ is said to be Gâteaux differentiable on E (Fréchet differentiable on E, respectively) if it is Gâteaux differentiable everywhere (Fréchet differentiable everywhere, respectively).

We know that, if a continuous convex function $f:E\to \mathbb{R}$ is Gâteaux differentiable on E, then $\nabla f$ is norm-to-${\mathrm{weak}}^{\ast }$ continuous on E. We also know that, if f is Fréchet differentiable on E, then $\nabla f$ is norm-to-norm continuous on E (see Butnariu and Iusem [15]).

Let $S_r\left(x_0\right)=\{x\in E:\parallel x-x_0\parallel =r\}$ be the closed unit sphere with the radius $r>0$ centered at $x_0\in E$ in a Banach space $E.$

• A function $f:E\to \mathbb{R}$ is said to be strongly coercive if, for any sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ such that $\parallel x_n\parallel$ converges to ∞, we have

  $${\displaystyle \underset{n\to \infty }{lim}\frac{f\left(x_n\right)}{\parallel x_n\parallel }=\infty .}$$
• It is also said to be bounded on bounded sets if $f\left(S_r\left(x_0\right)\right)$ is bounded for each $r>0.$ Let $S=\{x\in E:\parallel x\parallel =1\}$ be the unit sphere of $E.$
• A function $f:E\to \mathbb{R}$ is said to be uniformly convex on bounded sets [23] (pp. 203, 221) if ${\rho }_r\left(t\right)>0$ for all $r,t>0$, where ${\rho }_r:[0,+\infty )\to [0,+\infty ]$ is called the uniform convexity of f defined by

  $${\displaystyle {\rho }_r\left(t\right)=\underset{x,y\in S_r\left(0\right),\parallel x-y\parallel =t,\alpha \in (0,1)}{inf}{\displaystyle \frac{\alpha f\left(x\right)+(1-\alpha )f\left(y\right)-f(\alpha x+(1-\alpha \left)y\right)}{\alpha (1-\alpha )}},\forall t\ge 0.}$$

It is known that ${\rho }_r\left(t\right)$ is a nondecreasing function. The function f is also said to be locally uniformly smooth on bounded sets ([23], pp. 207, 221) if the function ${\sigma }_r:[0,+\infty )\to [0,+\infty ]$ defined by

$${\displaystyle {\sigma }_r\left(t\right)=\underset{x\in S_r\left(0\right),y\in S_E,\alpha \in (0,1)}{sup}{\displaystyle \frac{\alpha f(x+(1-\alpha \left)ty\right)+(1-\alpha )f(x-\alpha ty)-f\left(x\right)}{\alpha (1-\alpha )}}}$$

satisfies

$$\underset{t\downarrow 0}{lim}\frac{{\sigma }_r\left(t\right)}{t}=0,\forall r>0.$$

If $f:E\to \mathbb{R}$ is uniformly convex on bounded sets of E, then we have

$$f(\alpha x+(1-\alpha )y)\le \alpha f\left(x\right)+(1-\alpha )f\left(y\right)-\alpha (1-\alpha ){\rho }_r(\parallel x-y\parallel )$$

(10)

for all $x,y$ in $S_r\left(0\right)$ and $\alpha \in (0,1).$

Let E be a Banach space and $f:E\to \mathbb{R}$ be a strictly convex and G$\widehat{a}$teaux differentiable function. By the Equation (3), the Bregman distance $D_f$ satisfies [24]

$$D_f(x,z)=D_f(x,y)+D_f(y,z)+⟨x-y,\nabla f\left(y\right)-\nabla f\left(z\right)⟩,\forall x,y,z\in E.$$

(11)

In particular, we have

$$D_f(x,y)=-D_f(y,x)+⟨y-x,\nabla f\left(y\right)-\nabla f\left(x\right)⟩,\forall x,y\in E.$$

(12)

The following definition is slightly different from that in Butnariu and Iusem [15] (p. 65) and Koshsaka [6]:

Definition 1.

Let E be a Banach space. Then, a function $f:E\to \mathbb{R}$ is said to be a Bregman function if the following conditions are satisfied:

(a) 

f is continuous, strictly convex and Gâteaux differentiable;

(b) 

the set $\{y\in E:D_f(x,y)\le r\}$ is bounded for all $x\in E$ and $r>0.$

The following lemma follows from Butnariu and Iusem [15] and Zǎlinscu [23]:

Lemma 1.

Let E be a reflexive Banach space and let $f:E\to \mathbb{R}$ be a strongly coercive Bregman function. Then, we have the following:

1. 

$\nabla f:E\to E^{\ast }$ is one-to-one, onto and norm-to-${\mathrm{weak}}^{\ast }$ continuous.

2. 

$⟨x-y,\nabla f\left(x\right)-\nabla \left(y\right)⟩=0$ if and only if $x=y.$

3. 

$\{x\in E:D_f(x,y)\le r\}$ is bounded for all y in E and $r>0.$

4. 

dom $f^{\ast }=E^{\ast },f^{\ast }$ is Gâteaux differentiable function and $\nabla f^{\ast }={(\nabla f)}^{-1}.$

Let C be a nonempty closed convex subset of a reflexive Banach space $E.$ Let $f:E\to \mathbb{R}$ be a strictly convex and Gâteaux differentiable function. Then, it follows from [25] that, for any $x\in E$ and $x_0\in C,$ we have

$${\displaystyle D_f(x_0,x)=\underset{y\in C}{min}{D}_f(y,x).}$$

The Bregman projection $pro{j}_C^f$ from E onto C is defined by $pro{j}_C^f\left(x\right)=x_0$ for all $x\in E.$ It is well known that $x_0=pro{j}_C^f\left(x\right)$ if and only if

$$⟨y-x_0,\nabla f\left(x\right)-\nabla f\left(x_0\right)⟩\le 0,\forall y\in C.$$

(13)

It is also known that $pro{j}_C^f$ from E onto C has the following property:

$$D_f(y,pro{j}_C^f\left(x\right))+D_f(pro{j}_C^f\left(x\right),x)\le D_f(y,x),\forall y\in C,x\in E.$$

(14)

For more details on Bregman projection $pro{j}_C^f$, see Butnariu and Iusem [15].

Now, we have the following propositions (see Zǎlinscu [23] (pp. 222, 224)):

Proposition 1.

Let $f\in \Gamma \left(E\right)$ be convex. Consider the following statements:

1. 

f is bounded and uniformly smooth on bounded sets;

2. 

f is Fréchet differentiable on $E=$ dom f and $\nabla f$ is uniformly continuous on bounded sets;

3. 

$f^{\ast }$ is strongly coercive and uniformly convex on bounded sets.

Then, we have $1⟺2⟸3.$ Moreover, if f is strongly coercive, then we also have $1⟹3$. In this case, $E^{\ast }$ is reflexive (also E is reflexive if E is a Banach space).

Proposition 2.

Let $f\in \Gamma \left(E\right)$. Consider the following statements:

1. 

f is strongly coercive and uniformly convex on bounded sets;

2. 

$f^{\ast }$ is bounded and uniformly smooth on bounded sets;

3. 

$f^{\ast }$ is Fréchet differentiable on $E^{\ast }$ dom $f^{\ast }$ and $\nabla f^{\ast }$ is uniformly continuous on bounded sets.

Then, we have $1⟹2⟺3.$ Moreover, if f is bounded on bounded sets then $2⟹1$. In this case $E^{\ast }$ is reflexive (also E is reflexive if E is a Banach space).

The following result was first proved in Kohsaka and Takahashi [6] (see Lemma 3.1, p. 511):

Lemma 2.

Let E be a Banach space and let $f:E\to \mathbb{R}$ be a Gâteaux differentiable function, which is uniformly convex on bounded sets. Let ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{y_n\right\}}_{n\in \mathbb{N}}$ be bounded sequences in E and ${\displaystyle \underset{n\to \infty }{lim}{D}_f(x_n,y_n)=0,}$ then we have ${\displaystyle \underset{n\to \infty }{lim}\parallel x_n-y_n\Vert =0.}$

The following lemma is slightly different from that in Kohsaka and Takahashi [6] (see Lemmas 3.2 and 3.3, pp. 511, 512):

Lemma 3.

Let E be a reflexive Banach space, let $f:E\to \mathbb{R}$ be a strongly coercive Bregman function and V be the function defined by

$$V(x,x^{\ast })=f\left(x\right)-⟨x,x^{\ast }⟩+f^{\ast }\left(x^{\ast }\right),\forall x\in E,x^{\ast }\in E^{\ast }.$$

The following assertions hold:

1. 

$D_f\left(x,\nabla f^{\ast }\left(x^{\ast }\right)\right)=V(x,x^{\ast })$ for all $x\in E$ and $x^{\ast }\in E^{\ast }.$

2. 

$V(x,x^{\ast })+⟨\nabla f^{\ast }\left(x^{\ast }\right)-x,y^{\ast }⟩\le V(x,x^{\ast }+y^{\ast })$ for all $x\in E$ and $x^{\ast },y^{\ast }\in E^{\ast }.$

It also follows from the definition that V is convex in the second variable $x^{\ast }$ and

$$V\left(x,\nabla f\left(y\right)\right)=D_f(x,y).$$

The following result was proved by Huang [16]:

Lemma 4.

Let E be a Banach space and $f:E\to \mathbb{R}$ be a strictly convex and Gâteaux differentiable function. Suppose that ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is a sequence in E such that $x_n\rightharpoonup x$ for some $x\in E.$ Then,

$${\displaystyle \underset{n\to \infty }{lim\; sup}{D}_f(x_n,x)<\underset{n\to \infty }{lim\; sup}{D}_f(x_n,y)}$$

for all y in the interior of $domf$ with $y\ne x.$

Let C be a nonempty closed convex subset of a reflexive Banach space E. Let ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ be a bounded sequence in E and $f\in \Gamma \left(E\right)$ be Gâteaux differentiable function. For any $x\in E,$ we set

$${\displaystyle Br(x,\left\{x_n\right\})=\underset{n\to \infty }{lim\; sup}{D}_f(x_n,x).}$$

• The Bregman asymptotic radius of ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ relative to C is defined by

  $$Br(C,\left\{x_n\right\})=inf\{Br(x,\left\{x_n\right\}):x\in C\}.$$
• The Bregman asymptotic center of ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ relative to C is defined by

  $$BA(C,\left\{x_n\right\})=\{x\in C:Br(x,\left\{x_n\right\})=Br(C,\left\{x_n\right\})\}.$$

The following result was proved by Naraghirad [17]:

Proposition 3.

Let E be a reflexive Banach space and $f:E\to \mathbb{R}$ be strictly convex, Gâteaux differentiable function, bounded on bounded sets. Let C be a nonempty closed convex subset of $E.$ If ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is a bounded sequence of C, then $BA(C,{\left\{x_n\right\}}_{n\in \mathbb{N}})=\left\{z\right\}$ is a singleton.

Proof. 

In view of the definition of Bregman asymptotic radius, we may assume that ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ converges weakly to $z\in C.$ By Lemma 4, we conclude that $BA(C,{\left\{x_n\right\}}_{n\in \mathbb{N}})=\left\{z\right\}.$ □

Let S be a nonempty set and $B\left(S\right)$ be the Banach space of all bounded real-valued functions on S with the supremum norm. Let E be a subspace of $B\left(S\right)$ and $\mu$ be an element of $E^{\ast }.$ Then, we denote by $\mu \left(f\right)$ the value of $\mu$ at $f\in E.$ If $e\left(s\right)=1$ for all $s\in S,$ sometimes $\mu \left(e\right)$ will be denoted by $\mu \left(1\right).$ When E contains constants, a linear functional $\mu$ on E is called a mean on E if $\parallel \mu \parallel =\mu \left(1\right)=1$ (see, for instance, Takahashi [18] for more details).

Theorem 1.

Let E be a subspace of $B\left(S\right)$ containing constants and let μ be a linear functional on $E.$ Then, the following conditions are equivalent:

1. 

$\parallel \mu \parallel =\mu \left(1\right)=1,$ i.e., μ is a mean on $E.$

2. 

The inequalities

$${\displaystyle \underset{s\in S}{inf}f\left(s\right)\le \mu \left(f\right)\le \underset{s\in S}{sup}f\left(s\right)}$$

hold for each $f\in E.$

Let $l^{\infty }$ be the Banach lattice of bounded real sequences with the supremum norm and $\mu$ be a linear continuous functional on $l^{\infty }$. Let $x=(x_1,x_2,\cdots )$ be a sequence in $l^{\infty }.$ Then, sometimes we denote by ${\mu }_n\left(x_n\right)$ the value $\mu \left(x\right).$

Theorem 2.

(The existence of Banach limit) There exists a linear continuous functional μ on $l^{\infty }$ such that $\parallel \mu \parallel =\mu \left(1\right)=1$ and $\mu \left(x_n\right)=\mu \left(x_{n+1}\right)$ for each $x=(x_1,x_2,\cdots )\in l^{\infty }.$

Note that

• If ${\left\{x_n\right\}}_{n\in \mathbb{N}}\in l^{\infty }$ and $x_n\ge 0$ for each $n\in \mathbb{N},$ then $\mu \left(x_n\right)\ge 0.$
• If $x_n=1$ for each $n\in \mathbb{N}$, then $\mu \left(x_n\right)=1.$

Such a functional $\mu$ is called a Banach limit and the value of $\mu$ at ${\left\{x_n\right\}}_{n\in \mathbb{N}}\in l^{\infty }$ is denoted by ${\mu }_n{x}_n$ (see, for example [18].)

The following lemmas were proved by Reich and Sabach [26]:

Lemma 5.

Let E be a reflexive Banach space and let $f:E\to \mathbb{R}$ be strictly convex, continuous, strongly coercive, G$\widehat{a}$teaux differentiable function, and bounded on bounded sets. Let C be a nonempty, closed and convex subset of $E.$ Let $T:C\to E$ be a Bregman quasi-nonexpansive mapping. Then, $F\left(T\right)$ is closed and convex.

The following result was proved by Mainge [27]:

Lemma 6.

Let ${\left\{a_n\right\}}_{n\in \mathbb{N}}$ be a sequence in $\mathbb{R}$ with a subsequence ${\left\{a_{n_i}\right\}}_{i\in \mathbb{N}}$ such that $a_{n_i}<a_{n_i+1}$ for each $i\in \mathbb{N}.$ Then, there exists another subsequence ${\left\{a_{m_k}\right\}}_{k\in \mathbb{N}}$ such that, for all (sufficiently large) number k, we have

$$a_{m_k}<a_{m_k+1},a_k<a_{m_k+1}.$$

In fact, we can set $m_k=max\{j\le k:a_j<a_{j+1}\}.$

Lemma 7. ([28])

Let ${\left\{s_n\right\}}_{n\in \mathbb{N}}$ be a sequence of nonnegative real numbers satisfying

$$s_{n+1}\le (1-{\gamma }_n)s_n+{\gamma }_n{\delta }_n,\forall n\ge 1,$$

where ${\left\{{\gamma }_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{{\delta }_n\right\}}_{n\in \mathbb{N}}$ satisfy the following conditions:

(a) 

${\left\{{\gamma }_n\right\}}_{n\in \mathbb{N}}\subset [0,1]$ and ${\displaystyle {\Sigma }_{n=1}^{\infty }{\gamma }_n=+\infty }$ or, equivalently, ${\displaystyle {\Pi }_{n=1}^{\infty }(1-{\gamma }_n)=0;}$

(b) 

${\displaystyle \underset{n\to \infty }{lim\; sup}{\delta }_n<0}$ or ${\displaystyle {\Sigma }_{n=1}^{\infty }{\gamma }_n{\delta }_n<\infty .}$

Then, we have ${\displaystyle \underset{n\to \infty }{lim}{s}_n=0.}$

3. The Main Results

3.1. Approximating Fixed Points

In this section, we obtain some fixed point theorem for a generalized $\alpha$-nonexpansive mapping with respect to the Bregman–Opial property.

Lemma 8.

Let $f:E\to \mathbb{R}$ be a strictly convex and Gâteaux differentiable function. Let C be a nonempty closed convex subset of a reflexive Banach space $E.$ Let $T:C\to E$ be a Bregman generalized α-nonexpansive mapping. Then, we have

$$\begin{array}{ll}{D}_f(x,Ty)& \le D_f(x,Tx)+(1-\alpha )D_f(x,y)+\alpha D_f(Tx,Ty)\\ & +\alpha ⟨x-Tx,\nabla f\left(y\right)-\nabla f\left(Ty\right)⟩+⟨x-Tx,\nabla f\left(Tx\right)-\nabla f\left(Ty\right)⟩,\forall x,y\in C.\end{array}$$

Proof. 

Let $x,y\in C.$ In view of the equation (11), we have

$$\begin{array}{ll}{D}_f(Tx,Ty)& \le \alpha D_f(Tx,y)+\alpha D_f(x,Ty)+(1-2\alpha )D_f(x,y)\\ & =\alpha \left[D_f(Tx,x)+D_f(x,y)+⟨Tx-x,\nabla f\left(x\right)-\nabla f\left(y\right)⟩\right]\\ & +\alpha [D_f(x,Tx)+D_f(Tx,Ty)+⟨x-Tx,\nabla f\left(Tx\right)-\nabla f\left(Ty\right)⟩]\\ & +(1-2\alpha )D_f(x,y)\\ & =\alpha D_f(Tx,x)+\alpha D_f(x,y)+\alpha ⟨Tx-x,\nabla f\left(x\right)-\nabla f\left(y\right)⟩\\ & +\alpha D_f(x,Tx)+\alpha D_f(Tx,Ty)+\alpha ⟨x-Tx,\nabla f\left(Tx\right)-\nabla f\left(Ty\right)⟩\\ & +(1-2\alpha )D_f(x,y)\\ & =D_f(Tx,x)+(1-\alpha )D_f(x,y)+\alpha D_f(x,Tx)+\alpha D_f(Tx,Ty)\\ & +\alpha ⟨Tx-x,\nabla f\left(x\right)-\nabla f\left(y\right)⟩+\alpha ⟨x-Tx,\nabla f\left(Tx\right)-\nabla f\left(Ty\right)⟩\\ & =-\alpha D_f(x,Tx)+\alpha ⟨x-Tx,\nabla f\left(x\right)-\nabla f\left(Tx\right)⟩\\ & +(1-\alpha )D_f(x,y)+\alpha D_f(x,Tx)+\alpha D_f(Tx,Ty)\\ & +\alpha ⟨Tx-x,\nabla f\left(x\right)-\nabla f\left(y\right)⟩+\alpha ⟨x-Tx,\nabla f\left(Tx\right)-\nabla f\left(Ty\right)⟩\\ & =(1-\alpha )D_f(x,y)+\alpha D_f(Tx,Ty)\\ & +\alpha ⟨x-Tx,\nabla f\left(y\right)-\nabla f\left(Ty\right)⟩+\alpha ⟨x-Tx,\nabla f\left(Tx\right)-\nabla f\left(Ty\right)⟩\\ & =(1-\alpha )D_f(x,y)+\alpha D_f(Tx,Ty)+\alpha ⟨x-Tx,\nabla f\left(y\right)-\nabla f\left(Ty\right)⟩.\end{array}$$

This, together with the equation (11), implies that

$$\begin{array}{ll}{D}_f(x,Ty)& =D_f(x,Tx)+D_f(Tx,Ty)+⟨x-Tx,\nabla f\left(Tx\right)-\nabla f\left(Ty\right)⟩\\ & \le D_f(x,Tx)+(1-\alpha )D_f(x,y)+\alpha D_f(Tx,Ty)\\ & +\alpha ⟨x-Tx,\nabla f\left(y\right)-\nabla f\left(Ty\right)⟩+⟨x-Tx,\nabla f\left(Tx\right)-\nabla f\left(Ty\right)⟩.\end{array}$$

This completes the proof. □

Proposition 4.

(Demiclosedness Principle) Let $f:E\to \mathbb{R}$ be a strictly convex, Gâteaux differentiable function and bounded on bounded sets function. Let C be a nonempty subset of a reflexive Banach space E and $T:C\to E$ be a Bregman generalized α-nonexpansive mapping. If $x_n\rightharpoonup z$ in C and ${\displaystyle \underset{n\to \infty }{lim}\parallel T{x}_n-x_n\Vert =0}$, then we have Tz = z.

Proof. 

Since ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ converges weakly to z and ${lim}_{n\to \infty }\parallel T{x}_n-x_n\Vert =0,$ both the sequences ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{T{x}_n\right\}}_{n\in \mathbb{N}}$ are bounded. Since $\nabla f$ is uniformly norm-to-norm continuous on bounded subsets of E (see, for instance, [23]), we arrive at

$${\displaystyle \underset{n\to \infty }{lim}\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\Vert =0.}$$

In view of Lemma 2, we deduce that ${\displaystyle \underset{n\to \infty }{lim}{D}_f(x_n,T{x}_n)=0}$. Set

$$M_1=sup\{\parallel \nabla f\left(x_n\right)\parallel ,\parallel \nabla f\left(T{x}_n\right)\parallel ,\parallel \nabla f\left(z\right)\parallel ,\parallel \nabla f\left(Tz\right)\parallel :n\in \mathbb{N}\}<+\infty .$$

By Lemma 8, it follows that, for all $n\in \mathbb{N}$,

$$\begin{array}{ll}{D}_f(x_n,Tz)& \le D_f(x_n,T{x}_n)+(1-\alpha )D_f(x_n,z)+\alpha D_f(T{x}_n,Tz)\\ & +\alpha ⟨x_n-T{x}_n,\nabla f\left(z\right)-\nabla f\left(Tz\right)⟩+⟨x_n-T{x}_n,\nabla f\left(T{x}_n\right)-\nabla f\left(Tz\right)⟩\\ & =D_f(x_n,T{x}_n)+(1-\alpha )D_f(x_n,z)\\ & +\alpha [D_f(T{x}_n,x_n)+D_f(x_n,Tz)+⟨T{x}_n-x_n,\nabla f\left(x_n\right)-\nabla f\left(Tz\right)⟩]\\ & +\alpha ⟨x_n-T{x}_n,\nabla f\left(z\right)-\nabla f\left(Tz\right)⟩+⟨x_n-T{x}_n,\nabla f\left(T{x}_n\right)-\nabla f\left(Tz\right)⟩\\ & =D_f(x_n,T{x}_n)+(1-\alpha )D_f(x_n,z)\\ & +\alpha D_f(T{x}_n,x_n)+\alpha D_f(x_n,Tz)+\alpha ⟨T{x}_n-x_n,\nabla f\left(x_n\right)-\nabla f\left(Tz\right)⟩\\ & +\alpha ⟨x_n-T{x}_n,\nabla f\left(z\right)-\nabla f\left(Tz\right)⟩+⟨x_n-T{x}_n,\nabla f\left(T{x}_n\right)-\nabla f\left(Tz\right)⟩\\ & =D_f(x_n,T{x}_n)+(1-\alpha )D_f(x_n,z)\\ & -\alpha D_f(x_n,T{x}_n)+\alpha ⟨x_n-T{x}_n,\nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)⟩\\ & +\alpha D_f(x_n,Tz)+\alpha ⟨x_n-T{x}_n,\nabla f\left(Tz\right)-\nabla f\left(x_n\right)⟩\\ & +\alpha ⟨x_n-T{x}_n,\nabla f\left(z\right)-\nabla f\left(Tz\right)⟩+⟨x_n-T{x}_n,\nabla f\left(T{x}_n\right)-\nabla f\left(Tz\right)⟩\\ & =(1-\alpha )D_f(x_n,T{x}_n)+(1-\alpha )D_f(x_n,z)+\alpha D_f(x_n,T_z)\\ & +\alpha ⟨x_n-T{x}_n,\nabla f\left(z\right)-\nabla f\left(T{x}_n\right)⟩+⟨x_n-T{x}_n,\nabla f\left(T{x}_n\right)-\nabla f\left(Tz\right)⟩\\ & \le (1-\alpha )D_f(x_n,T{x}_n)+(1-\alpha )D_f(x_n,z)+\alpha D_f(x_n,T_z)\\ & +\alpha \parallel x_n-T{x}_n\parallel \parallel \nabla f\left(z\right)-\nabla f\left(T{x}_n\right)\parallel \\ & +\parallel x_n-T{x}_n\parallel \parallel \nabla f\left(T{x}_n\right)-\nabla f\left(Tz\right)\parallel \\ & \le (1-\alpha )D_f(x_n,T{x}_n)+(1-\alpha )D_f(x_n,z)+\alpha D_f(x_n,T_z)\\ & +2\alpha M_1\parallel x_n-T{x}_n\parallel +2M_1\parallel x_n-T{x}_n\parallel \\ & \le (1-\alpha )D_f(x_n,T{x}_n)+D_f(x_n,z)\\ & +2\alpha M_1\parallel x_n-T{x}_n\parallel +2M_1\parallel x_n-T{x}_n\parallel ,\end{array}$$

which implies that

$${\displaystyle \underset{n\to \infty }{lim\; sup}{D}_f(x_n,Tz)\le \underset{n\to \infty }{lim\; sup}{D}_f(x_n,z).}$$

Therefore, it follows from the Bregman–Opial-like property that $Tz=z.$ This completes the proof. □

By Theorem 2, we can derive the following result, in which examples of the mapping T satisfying all the conditions can be found in Hussain [5].

Theorem 3.

Let $f:E\to \mathbb{R}$ be a strictly convex, continuous, strongly coercive, Gâteaux differentiable function, bounded on bounded sets and uniformly convex on bounded sets of $E.$ Let C be a nonempty closed convex subset of a reflexive Banach space E and $T:C\to C$ be a mapping. Let ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ be a bounded sequence of C and μ be a mean on $l^{\infty }.$ Suppose that

$${\mu }_n{D}_f(x_n,Ty)\le {\mu }_n{D}_f(x_n,y),\forall y\in C.$$

Then, T has a fixed point in $C.$

Corollary 1.

Let $f,C$ and T be given as above. If C is also bounded and $T:C\to C$ is a Bregman generalized α-nonexpansive mapping, then T has a fixed point.

Proof. 

Let $\mu$ be a Banach limit on $l^{\infty }$ and $x\in C$ be such that ${\left\{T^{n}x\right\}}_{n\in \mathbb{N}}$ is bounded. For each $n\in \mathbb{N}$, we have

$$D_f(T^{n}x,Ty)\le \alpha D_f(T^{n}x,y)+\alpha D_f(T^{n-1}x,Ty)+(1-2\alpha )D_f(T^{n-1}x,y),\forall y\in C.$$

This implies that

$$\begin{array}{cc}{\mu }_n{D}_f(T^{n}x,Ty)& \le \alpha {\mu }_n{D}_f(T^{n}x,y)+\alpha {\mu }_n{D}_f(T^{n}x,Ty)+(1-2\alpha ){\mu }_n{D}_f(T^{n}x,y)\hfill \\ & \le (1-\alpha ){\mu }_n{D}_f(T^{n}x,y)+\alpha {\mu }_n{D}_f(T^{n}x,Ty).\hfill \end{array}$$

Thus, we have

$${\mu }_n{D}_f(T^{n}x,Ty)\le {\mu }_n{D}_f(T^{n}x,y),\forall y\in C.$$

Therefore, it follows from Theorem 3 that $F\left(T\right)\ne \varnothing$. This completes the proof. □

3.2. Weak and Strong Convergence Theorems for Bregman Generalized $\alpha$-Nonexpansive Mappings

In this section, we prove some weak and strong convergence theorems concerning Bregman generalized $\alpha$-nonexpansive mappings in a reflexive Banach space. Naraghirad [17] proves the following lemma.

Lemma 9.

Let $f:E\to \mathbb{R}$ be a strictly convex and Gâteaux differentiable function. Let C be a nonempty closed convex subset of a reflexive Banach space E and $T:C\to C$ be a Bregman skew quasi-nonexpansive mapping with $F\left(T\right)\ne \varnothing .$ Let ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{y_n\right\}}_{n\in \mathbb{N}}$ be the sequences defined by the Ishikawa iteration:

$$\left\{\begin{array}{l}{y}_n={\beta }_{n}T{x}_n+(1-{\beta }_n)x_n,\\ x_{n+1}={\gamma }_{n}T{y}_n+(1-{\gamma }_n)x_n,\forall n\in \mathbb{N},\end{array}\right.$$

(15)

where ${\left\{{\beta }_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{{\gamma }_n\right\}}_{n\in \mathbb{N}}$ satisfy the following control conditions:

(a) 

$0\le {\gamma }_n\le {\beta }_n<1$ for all $n\in \mathbb{N};$

(b) 

${\displaystyle \underset{n\to \infty }{lim}{\beta }_n=0;}$

(c) 

${\displaystyle {\Sigma }_{n=1}^{\infty }{\gamma }_n{\beta }_n=\infty .}$

Then, the following assertions hold:

1. 

$max\{D_f(x_{n+1},z),D_f(y_n,z)\}\le D_f(x_n,z)$ for all $z\in F\left(T\right)$ and $n\in \mathbb{N}.$

2. 

${\displaystyle \underset{n\to \infty }{lim}{D}_f(x_n,z)}$ exists for any $z\in F\left(T\right).$

Proof. 

1. Let $z\in F\left(T\right).$ In view of inequality (10), we have

$$\begin{array}{ll}{D}_f(y_n,z)& =D_f({\beta }_{n}T{x}_n+(1-{\beta }_n)x_n,z)\\ & \le {\beta }_n{D}_f(T{x}_n,z)+(1-{\beta }_n)D_f(x_n,z)-{\beta }_n(1-{\beta }_n){\rho }_r\left(\parallel T{x}_n,z)-(x_n,z)\parallel \right)\\ & \le {\beta }_n{D}_f(x_n,z)+(1-{\beta }_n)D_f(x_n,z)\\ & =D_f(x_n,z).\end{array}$$

Consequently, we get

$$\begin{array}{ll}{D}_f(x_{n+1},z)& =D_f({\gamma }_{n}T{y}_n+(1-{\gamma }_n)x_n,z)\\ & \le {\gamma }_n{D}_f(T{y}_n,z)+(1-{\gamma }_n)D_f(x_n,z)-{\gamma }_n(1-{\gamma }_n){\rho }_r\left(\parallel T{y}_n,z)-(x_n,z)\parallel \right)\\ & \le {\gamma }_n{D}_f(y_n,z)+(1-{\gamma }_n)D_f(x_n,z)\\ & \le {\gamma }_n{D}_f(x_n,z)+(1-{\gamma }_n)D_f(x_n,z)\\ & =D_f(x_n,z).\end{array}$$

Therefore, we have 1.

2. Since $D_f(x_{n+1},z)\le D_f(x_n,z)$ for each $n\in \mathbb{N},$${\left\{D_f(x_n,z)\right\}}_{n\in \mathbb{N}}$ is a bounded and nonincreasing sequence for all $z\in F\left(T\right).$ Thus, we have ${lim}_{n\to \infty }{D}_f(x_n,z)$ exists for any $z\in F\left(T\right).$ This completes the proof. □

Theorem 4.

Let $f:E\to \mathbb{R}$ be a strictly convex, Gâteaux differentiable function, bounded on bounded sets and uniformly convex on bounded sets of $E.$ Let C be a nonempty closed convex subset of a reflexive Banach space E and $T:C\to C$ be a Bregman generalized α-nonexpansive and Bregman skew quasi-nonexpansive mapping. Let ${\left\{{\beta }_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{{\gamma }_n\right\}}_{n\in \mathbb{N}}$ be the sequences in $[0,1)$ and ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ be the sequence defined by the Ishikawa iteration with $x_1\in C$. Assume that ${\displaystyle \underset{n\to \infty }{lim}\parallel x_n-T{x}_n\parallel =0.}$ Then, we have the following:

1. 

If ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is bounded and ${\displaystyle \underset{n\to \infty }{lim\; inf}\parallel T{x}_n-x_n\parallel =0,}$ then $F\left(T\right)\ne \varnothing .$

2. 

If $F\left(T\right)\ne \varnothing$, then ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is bounded.

Proof. 

1. By Corollary 1, we see that the fixed point set $F\left(T\right)$ of T is nonempty. Assume that ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is bounded and ${\displaystyle \underset{n\to \infty }{lim\; inf}\parallel T{x}_n-x_n\Vert =0.}$ Consequently, there is a bounded subsequence ${\left\{T{x}_{n_k}\right\}}_{k\in \mathbb{N}}$ of ${\left\{T{x}_n\right\}}_{n\in \mathbb{N}}$ such that ${\displaystyle \underset{k\to \infty }{lim}\parallel T{x}_{n_k}-x_{n_k}\parallel =0.}$ Since $\nabla g$ is uniformly norm-to-norm continuous on bounded sets of E (see, for example, [23]), we have

$${\displaystyle \underset{k\to \infty }{lim}\parallel \nabla f\left(T{x}_{n_k}\right)-\nabla f\left(x_{n_k}\right)\parallel =0.}$$

In view of Proposition 3, we conclude that $BA(C,\left\{x_{n_k}\right\})=\left\{z\right\}$ for some z in $C.$ Let

$$M_2=sup\{\parallel \nabla f\left(x_{n_k}\right)\parallel ,\parallel \nabla f\left(T{x}_{n_k}\right)\parallel ,\parallel \nabla f\left(z\right)\parallel ,\parallel \nabla f\left(Tz\right)\parallel :k\in \mathbb{N}\}<+\infty .$$

It follows from Lemma 4 that

$$\begin{array}{ll}{D}_f(x_{n_k},Tz)& \le D_f(x_{n_k},T{x}_{n_k})+(1-\alpha )D_f(x_{n_k},z)+\alpha D_f(T{x}_{n_k},Tz)\\ & +\alpha ⟨x_{n_k}-T{x}_{n_k},\nabla f\left(z\right)-\nabla f\left(Tz\right)⟩+⟨x_{n_k}-T{x}_{n_k},\nabla f\left(T{x}_{n_k}\right)-\nabla f\left(Tz\right)⟩\\ & =D_f(x_{n_k},T{x}_{n_k})+(1-\alpha )D_f(x_{n_k},z)\\ & +\alpha [D_f(T{x}_{n_k},x_{n_k})+D_f(x_{n_k},Tz)+⟨T{x}_{n_k}-x_{n_k},\nabla f\left(x_{n_k}\right)-\nabla f\left(Tz\right)⟩]\\ & +\alpha ⟨x_{n_k}-T{x}_{n_k},\nabla f\left(z\right)-\nabla f\left(Tz\right)⟩+⟨x_{n_k}-T{x}_{n_k},\nabla f\left(T{x}_{n_k}\right)-\nabla f\left(Tz\right)⟩\\ & =D_f(x_{n_k},T{x}_{n_k})+(1-\alpha )D_f(x_{n_k},z)\\ & +\alpha D_f(T{x}_{n_k},x_{n_k})+\alpha D_f(x_{n_k},Tz)+\alpha ⟨T{x}_{n_k}-x_{n_k},\nabla f\left(x_{n_k}\right)-\nabla f\left(Tz\right)⟩\\ & +\alpha ⟨x_{n_k}-T{x}_{n_k},\nabla f\left(z\right)-\nabla f\left(Tz\right)⟩+⟨x_{n_k}-T{x}_{n_k},\nabla f\left(T{x}_{n_k}\right)-\nabla f\left(Tz\right)⟩\\ & =D_f(x_{n_k},T{x}_{n_k})+(1-\alpha )D_f(x_{n_k},z)\\ & -\alpha D_f(x_{n_k},T{x}_{n_k})+\alpha ⟨x_{n_k}-T{x}_{n_k},\nabla f\left(x_{n_k}\right)-\nabla f\left(T{x}_{n_k}\right)⟩\\ & +\alpha D_f(x_{n_k},Tz)+\alpha ⟨x_{n_k}-T{x}_{n_k},\nabla f\left(Tz\right)-\nabla f\left(x_{n_k}\right)⟩\\ & +\alpha ⟨x_{n_k}-T{x}_{n_k},\nabla f\left(z\right)-\nabla f\left(Tz\right)⟩+⟨x_{n_k}-T{x}_{n_k},\nabla f\left(T{x}_{n_k}\right)-\nabla f\left(Tz\right)⟩\\ & =(1-\alpha )D_f(x_{n_k},T{x}_{n_k})+(1-\alpha )D_f(x_{n_k},z)+\alpha D_f(x_{n_k},T_z)\\ & +\alpha ⟨x_{n_k}-T{x}_{n_k},\nabla f\left(z\right)-\nabla f\left(T{x}_{n_k}\right)⟩+⟨x_{n_k}-T{x}_{n_k},\nabla f\left(T{x}_{n_k}\right)-\nabla f\left(Tz\right)⟩\\ & \le (1-\alpha )D_f(x_{n_k},T{x}_{n_k})+(1-\alpha )D_f(x_{n_k},z)+\alpha D_f(x_{n_k},T_z)\\ & +\alpha \parallel x_{n_k}-T{x}_{n_k}\parallel \parallel \nabla f\left(z\right)-\nabla f\left(T{x}_{n_k}\right)\parallel +\parallel x_{n_k}-T{x}_{n_k}\parallel \parallel \nabla f\left(T{x}_{n_k}\right)-\nabla f\left(Tz\right)\parallel \\ & \le (1-\alpha )D_f(x_{n_k},T{x}_{n_k})+(1-\alpha )D_f(x_{n_k},z)+\alpha D_f(x_{n_k},T_z)\\ & +2\alpha M_1\parallel x_{n_k}-T{x}_{n_k}\parallel +2M_1\parallel x_{n_k}-T{x}_{n_k}\parallel \\ & \le (1-\alpha )D_f(x_{n_k},T{x}_{n_k})+D_f(x_{n_k},z)\\ & +2\alpha M_1\parallel x_{n_k}-T{x}_{n_k}\parallel +2M_1\parallel x_{n_k}-T{x}_{n_k}\parallel \end{array}$$

for each $k\in \mathbb{N}.$ This implies

$${\displaystyle \underset{n\to \infty }{lim\; sup}{D}_f(x_{n_k},Tz)\le \underset{n\to \infty }{lim\; sup}{D}_f(x_{n_k},z).}$$

From the Bregman–Opial-like property, we obtain $Tz=z$.

2. Let $F\left(T\right)\ne \varnothing$ and let $z\in F\left(T\right)$. It follows from Lemma 9 that ${\displaystyle \underset{n\to \infty }{lim}\parallel x_n-z\Vert =0}$ exists and hence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is bounded. This implies that the sequence ${\left\{T{y}_n\right\}}_{n\in \mathbb{N}}$ is bounded too. This completes the proof. □

Theorem 5.

Let $f:E\to \mathbb{R}$ be a uniformly convex, Gâteaux differentiable function and bounded subset on bounded sets of $E.$ Let C be a nonempty closed convex subset of a reflexive Banach space $E.$ Let $T:C\to C$ be a Bregman generalized α-nonexpansive and Bregman skew quasi-nonexpansive mapping with $F\left(T\right)\ne \varnothing .$ Let ${\left\{{\beta }_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{{\gamma }_n\right\}}_{n\in \mathbb{N}}$ be the sequences in $[0,1)$ and ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ be the sequence with $x_1\in C$ defined by the Ishikawa iteration. Then, the sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ converges weakly to a fixed point of $T.$

Proof. 

By Corollary 1, we see that the fixed point set $F\left(T\right)$ of T is nonempty. It follows from Theorem 4 that ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is bounded and ${\displaystyle \underset{n\to \infty }{lim}\parallel T{y}_n-x_n\parallel =0.}$ Since E is reflexive, there exists a subsequence ${\left\{x_{n_i}\right\}}_{i\in \mathbb{N}}$ of ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ such that $x_{n_i}\rightharpoonup p\in C$ as $i\to \infty .$ By Proposition 4, we have $p\in F\left(T\right).$

Now, we claim that $x_n\rightharpoonup p$ as $n\to \infty .$ If not, then there exists a subsequence ${\left\{x_{n_i}\right\}}_{i\in \mathbb{N}}$ of ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ such that ${\left\{x_{n_j}\right\}}_{j\in \mathbb{N}}$ converges weakly to a point $q\in C$ with $p\ne q.$ In view of Proposition 4 again, we conclude that $q\in F\left(T\right).$ By Lemma 9, ${\displaystyle \underset{n\to \infty }{lim}{D}_f(x_n,z)}$ exists for all $z\in F\left(T\right).$ Thus, it follows from the Bregman–Opial-like property that

$$\begin{array}{cc}{\displaystyle \underset{n\to \infty }{lim}{D}_f(x_n,p)}& {\displaystyle =\underset{i\to \infty }{lim}{D}_f(x_{n_i},p)<\underset{i\to \infty }{lim}{D}_f(x_{n_i},q)}\hfill \\ & {\displaystyle =\underset{n\to \infty }{lim}{D}_f(x_n,q)=\underset{j\to \infty }{lim}{D}_f(x_{n_j},q)}\hfill \\ & {\displaystyle <\underset{j\to \infty }{lim}{D}_f(x_{n_j},p)=\underset{n\to \infty }{lim}{D}_f(x_n,p),}\hfill \end{array}$$

which is a contradiction. Thus, we have $p=q$ and the desired assertion follows. This completes the proof. □

Theorem 6.

Let $f:E\to \mathbb{R}$ be a uniformly convex, Gâteaux differentiable function bounded subset on bounded sets of $E.$ Let C be a nonempty closed convex subset of a reflexive Banach space $E.$ Let $T:C\to C$ the Bregman generalized α-nonexpansive and Bregman skew quasi-nonexpansive mapping. Let ${\left\{{\beta }_n\right\}}_{n\in \mathbb{N}}$, ${\left\{{\gamma }_n\right\}}_{n\in \mathbb{N}}$ be the sequences in $[0,1)$ and ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ be the sequence with $x_1\in C$ defined by the Ishikawa iteration. Then, the sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ converges strongly to a fixed point z of $T.$

Proof. 

By Corollary 1, we see that the fixed point set $F\left(T\right)$ of T is nonempty. In view of Theorem 4, it follows that ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is bounded and ${\displaystyle \underset{n\to \infty }{lim\; inf}\parallel T{x}_n-x_n\parallel =0.}$ By the compactness of C, there exists a subsequence ${\left\{x_{n_k}\right\}}_{k\in \mathbb{N}}$ of ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ such that ${\left\{x_{n_k}\right\}}_{k\in \mathbb{N}}$ converges strongly to a point $z\in C$. In view of Lemma 2, we deduce that ${\displaystyle \underset{k\to \infty }{lim}{D}_f(x_{n_k},z)=0}$.

Now, we assume that ${\displaystyle \underset{k\to \infty }{lim}\parallel T{x}_{n_k}-x_{n_k}\parallel =0}$ and, in particular, ${\left\{T{x}_{n_k}\right\}}_{k\in \mathbb{N}}$ is bounded. Since $\nabla f$ is uniformly norm-to-norm continuous on bounded sets of E (see, for example, [23]), we have

$${\displaystyle \underset{k\to \infty }{lim}\parallel \nabla f\left(T{x}_{n_k}\right)-\nabla f\left(x_{n_k}\right)\parallel =0.}$$

Let

$$M_3=sup\{\parallel \nabla f\left(x_{n_k}\right)\parallel ,\parallel T{x}_{n_k}\parallel ,\parallel \nabla f\left(z\right)\parallel ,\parallel \nabla f\left(Tz\right)\parallel :k\in \mathbb{N}\}<+\infty .$$

In view of Lemma 8, we obtain

$$\begin{array}{cc}{D}_f(x_{n_k},Tz)& \le D_f(x_{n_k},T{x}_{n_k})+(1-\alpha )D_f(x_{n_k},z)+\alpha D_f(T{x}_{n_k},Tz)\hfill \\ & +\alpha ⟨x_{n_k}-T{x}_{n_k},\nabla f\left(z\right)-\nabla f\left(Tz\right)⟩+⟨x_{n_k}-T{x}_{n_k},\nabla f\left(T{x}_{n_k}\right)-\nabla f\left(Tz\right)⟩\hfill \\ & =D_f(x_{n_k},T{x}_{n_k})+(1-\alpha )D_f(x_{n_k},z)\hfill \\ & +\alpha [D_f(T{x}_{n_k},x_{n_k})+D_f(x_{n_k},Tz)+⟨T{x}_{n_k}-x_{n_k},\nabla f\left(x_{n_k}\right)-\nabla f\left(Tz\right)⟩]\hfill \\ & +\alpha ⟨x_{n_k}-T{x}_{n_k},\nabla f\left(z\right)-\nabla f\left(Tz\right)⟩+⟨x_{n_k}-T{x}_{n_k},\nabla f\left(T{x}_{n_k}\right)-\nabla f\left(Tz\right)⟩\hfill \\ & =D_f(x_{n_k},T{x}_{n_k})+(1-\alpha )D_f(x_{n_k},z)\hfill \\ & +\alpha D_f(T{x}_{n_k},x_{n_k})+\alpha D_f(x_{n_k},Tz)+\alpha ⟨T{x}_{n_k}-x_{n_k},\nabla f\left(x_{n_k}\right)-\nabla f\left(Tz\right)⟩\hfill \\ & +\alpha ⟨x_{n_k}-T{x}_{n_k},\nabla f\left(z\right)-\nabla f\left(Tz\right)⟩+⟨x_{n_k}-T{x}_{n_k},\nabla f\left(T{x}_{n_k}\right)-\nabla f\left(Tz\right)⟩\hfill \\ & =D_f(x_{n_k},T{x}_{n_k})+(1-\alpha )D_f(x_{n_k},z)\hfill \\ & -\alpha D_f(x_{n_k},T{x}_{n_k})+\alpha ⟨x_{n_k}-T{x}_{n_k},\nabla f\left(x_{n_k}\right)-\nabla f\left(T{x}_{n_k}\right)⟩\hfill \\ & +\alpha D_f(x_{n_k},Tz)+\alpha ⟨x_{n_k}-T{x}_{n_k},\nabla f\left(Tz\right)-\nabla f\left(x_{n_k}\right)⟩\hfill \\ & +\alpha ⟨x_{n_k}-T{x}_{n_k},\nabla f\left(z\right)-\nabla f\left(Tz\right)⟩+⟨x_{n_k}-T{x}_{n_k},\nabla f\left(T{x}_{n_k}\right)-\nabla f\left(Tz\right)⟩\hfill \\ & =(1-\alpha )D_f(x_{n_k},T{x}_{n_k})+(1-\alpha )D_f(x_{n_k},z)+\alpha D_f(x_{n_k},T_z)\hfill \\ & +\alpha ⟨x_{n_k}-T{x}_{n_k},\nabla f\left(z\right)-\nabla f\left(T{x}_{n_k}\right)⟩+⟨x_{n_k}-T{x}_{n_k},\nabla f\left(T{x}_{n_k}\right)-\nabla f\left(Tz\right)⟩\hfill \\ & \le (1-\alpha )D_f(x_{n_k},T{x}_{n_k})+(1-\alpha )D_f(x_{n_k},z)+\alpha D_f(x_{n_k},T_z)\hfill \\ & +\alpha \parallel x_{n_k}-T{x}_{n_k}\parallel \parallel \nabla f\left(z\right)-\nabla f\left(T{x}_{n_k}\right)\parallel +\parallel x_{n_k}-T{x}_{n_k}\parallel \parallel \nabla f\left(T{x}_{n_k}\right)-\nabla f\left(Tz\right)\parallel \hfill \\ & \le (1-\alpha )D_f(x_{n_k},T{x}_{n_k})+(1-\alpha )D_f(x_{n_k},z)+\alpha D_f(x_{n_k},T_z)\hfill \\ & +2\alpha M_3\parallel x_{n_k}-T{x}_{n_k}\parallel +2M_3\parallel x_{n_k}-T{x}_{n_k}\parallel \hfill \\ & \le (1-\alpha )D_f(x_{n_k},T{x}_{n_k})+D_f(x_{n_k},z)\hfill \\ & +2\alpha M_3\parallel x_{n_k}-T{x}_{n_k}\parallel +2M_3\parallel x_{n_k}-T{x}_{n_k}\parallel \hfill \end{array}$$

for all $k\in \mathbb{N}$. It follows that ${\displaystyle \underset{k\to \infty }{lim}\parallel x_{n_k}-Tz\parallel =0}$, and thus we have $Tz=z.$ In view of Lemmas 2 and 9, we conclude that ${\displaystyle \underset{n\to \infty }{lim}\parallel x_n-z\parallel =0.}$ Therefore, z is the strong limit of the sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}.$ This completes the proof. □

3.3. Bregman Noor’s Type Iteration for Bregman Generalized $\alpha$-Nonexpansive Mappings

In this section, we propose the following Bregman Noor type iteration for Bregman generalized $\alpha$-nonexpansive mappings.

Let E be a reflexive Banach space and C be a nonempty closed convex subset of $E.$ Let $f:E\to \mathbb{R}$ be a strictly convex and Gâteaux differentiable function. Let $T:C\to C$ be a Bregman generalized $\alpha$-nonexpansive mapping with the fixed point set $F\left(T\right)\ne \varnothing$. Let ${\left\{x_n\right\}}_{n\in \mathbb{N}},$${\left\{y_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{z_n\right\}}_{n\in \mathbb{N}}$ be three sequences defined by

$$\left\{\begin{array}{c}{z}_n={\alpha }_n\nabla f\left(T{x}_n\right)+(1-{\alpha }_n)\nabla f\left(x_n\right),\hfill \\ y_n=\nabla f^{\ast }[{\beta }_n\nabla f\left(T{z}_n\right)+(1-{\beta }_n)\nabla f\left(x_n\right)],\hfill \\ x_{n+1}=pro{j}_C^f\left(\nabla f^{\ast }[{\gamma }_n\nabla f\left(T{y}_n\right)+(1-{\gamma }_n)\nabla f\left(x_n\right)]\right),\forall n\in \mathbb{N},\hfill \end{array}\right.$$

(16)

where ${\left\{{\alpha }_n\right\}}_{n\in \mathbb{N}}$, ${\left\{{\beta }_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{{\gamma }_n\right\}}_{n\in \mathbb{N}}$ are the sequences in $[0,1).$

Lemma 10.

Let $f:E\to \mathbb{R}$ be a strongly coercive Bregman function. Let C be a nonempty closed convex subset of a reflexive Banach space $E.$ Let $T:C\to C$ be the Bregman quasi-nonexpansive mapping. Let ${\left\{x_n\right\}}_{n\in \mathbb{N}}$, ${\left\{y_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{z_n\right\}}_{n\in \mathbb{N}}$ be the sequences defined by the equation (16) and ${\left\{{\alpha }_n\right\}}_{n\in \mathbb{N}}$, ${\left\{{\beta }_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{{\gamma }_n\right\}}_{n\in \mathbb{N}}$ be the sequences in $[0,1).$ Then, the following assertions hold:

1. 

$max\{D_f(w,x_{n+1}),D_f(w,y_n),D_f(w,z_n)\}\le D_f(w,x_n)$ for all $w\in F\left(T\right)$ and $n\in \mathbb{N}$.

2. 

${\displaystyle \underset{n\to \infty }{lim}{D}_f(w,x_n)}$ exists for any $w\in F\left(T\right).$

Proof. 

Let $w\in F\left(T\right).$ In view of Lemma 3 and the equation (16), we conclude that

$$\begin{array}{cc}{D}_f(w,z_n)& =D_f\left(w,{\alpha }_n\nabla f\left(T{x}_n\right)+(1-{\alpha }_n)\nabla f\left(x_n\right)\right)\hfill \\ & =V\left(w,{\alpha }_n\nabla f\left(T{x}_n\right)+(1-{\alpha }_n)\nabla f\left(x_n\right)\right)\hfill \\ & \le {\alpha }_{n}V\left(w,\nabla f\left(T{x}_n\right)\right)+(1-{\alpha }_n)V\left(w,\nabla f\left(x_n\right)\right)\hfill \\ & ={\alpha }_n{D}_f\left(w,T{x}_n\right)+(1-{\alpha }_n)D_f\left(w,x_n\right)\hfill \\ & \le {\alpha }_n{D}_f\left(w,x_n\right)+(1-{\alpha }_n)D_f\left(w,x_n\right)\hfill \\ & =D_f\left(w,x_n\right).\hfill \end{array}$$

In addition, we have

$$\begin{array}{cc}{D}_f(w,y_n)& =D_f\left(w,\nabla f^{\ast }[{\beta }_n\nabla f\left(T{z}_n\right)+(1-{\beta }_n)\nabla f\left(x_n\right)\right)\hfill \\ & =V\left(w,{\beta }_n\nabla f\left(T{z}_n\right)+(1-{\beta }_n)\nabla f\left(x_n\right)\right)\hfill \\ & \le {\beta }_{n}V\left(w,\nabla f\left(T{z}_n\right)\right)+(1-{\beta }_n)V\left(w,\nabla f\left(x_n\right)\right)\hfill \\ & ={\beta }_n{D}_f\left(w,T{z}_n\right)+(1-{\beta }_n)D_f\left(w,x_n\right)\hfill \\ & \le {\beta }_n{D}_f\left(w,z_n\right)+(1-{\beta }_n)D_f\left(w,x_n\right)\hfill \\ & ={\beta }_n{D}_f\left(w,x_n\right)+(1-{\beta }_n)D_f\left(w,x_n\right)\hfill \\ & =D_f\left(w,x_n\right).\hfill \end{array}$$

Consequently, using the inequality (14), we have

$$\begin{array}{cc}{D}_f(w,x_{n+1})& =D_f(w,pro{j}_C^f\left(\nabla f^{\ast }[{\gamma }_n\nabla f\left(T{y}_n\right)+(1-{\gamma }_n)\nabla f\left(x_n\right)])\right)\hfill \\ & \le D_f\left(w,\nabla f^{\ast }[{\gamma }_n\nabla f\left(T{y}_n\right)+(1-{\gamma }_n)\nabla f\left(x_n\right)]\right)\hfill \\ & =V\left(w,{\gamma }_n\nabla f\left(T{y}_n\right)+(1-{\gamma }_n)\nabla f\left(x_n\right)\right)\hfill \\ & \le {\gamma }_{n}V\left(w,\nabla f\left(T{y}_n\right)\right)+(1-{\gamma }_n)V\left(w,\nabla f\left(x_n\right)\right)\hfill \\ & ={\gamma }_n{D}_f\left(w,T{y}_n\right)+(1-{\gamma }_n)D_f\left(w,x_n\right)\hfill \\ & \le {\gamma }_n{D}_f\left(w,y_n\right)+(1-{\gamma }_n)D_f\left(w,x_n\right)\hfill \\ & ={\gamma }_n{D}_f\left(w,x_n\right)+(1-{\gamma }_n)D_f\left(w,x_n\right)\hfill \\ & =D_f\left(w,x_n\right).\hfill \end{array}$$

This implies that ${\left\{D_f(w,x_n)\right\}}_{n\in \mathbb{N}}$ is a bounded and nonincreasing sequence for all $w\in F\left(T\right).$ Thus, we have ${\displaystyle \underset{n\to \infty }{lim}{D}_f(w,x_n)}$ exists for any $w\in F\left(T\right).$ This completes the proof. □

Theorem 7.

Let $f:E\to \mathbb{R}$ be a strongly coercive Bregman function that is bounded on bounded sets and locally uniformly convex and locally uniformly smooth on $E.$ Let C be a nonempty, closed and convex subset of a reflexive Banach space $E.$ Let $T:C\to C$ be the Bregman generalized α-nonexpansive mapping. Let ${\left\{{\alpha }_n\right\}}_{n\in \mathbb{N}},$${\left\{{\beta }_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{{\gamma }_n\right\}}_{n\in \mathbb{N}}$ be the sequences in $[0,1)$ satisfying the following control condition:

$${\displaystyle \sum _{n=1}^{\infty }{\gamma }_n{\beta }_n{\alpha }_n(1-{\alpha }_n)=+\infty .}$$

(17)

Then, the following are equivalent:

1. 

There exists a bounded sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}\subset C$ generated by equations (16) such that

$${\displaystyle \underset{n\to \infty }{lim\; inf}\parallel T{x}_n-x_n\parallel =0.}$$

2. 

The fixed point set $F\left(T\right)\ne \varnothing .$

Proof. 

The implication $1⟹2$ follows similarly as in the first part of the proof of Theorem 4.

For the implication $2⟹1$, we assume that $F\left(T\right)\ne \varnothing$. The boundedness of the sequences ${\left\{x_n\right\}}_{n\in \mathbb{N}}$, ${\left\{y_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{z_n\right\}}_{n\in \mathbb{N}}$ follows from Lemma 10 and Definition 1. Since T is a Bregman quasi-nonexpansive mapping, it follows that, for any $q\in F\left(T\right)$, we have

$$D_f(q,T{x}_n)\le D_f(q,x_n),\forall n\in \mathbb{N}.$$

This, together with Definition 1 and the boundedness of ${\left\{x_n\right\}}_{n\in \mathbb{N}},$ implies that ${\left\{T{x}_n\right\}}_{n\in \mathbb{N}}$ is bounded. The function f is bounded on bounded sets of E and so $\nabla f$ is also bounded on bounded sets of $E^{\ast }$ (see, for example, [[15], Proposition 1.1.11] for more details). This implies that the sequences ${\{\nabla f\left(x_n\right)\}}_{n\in \mathbb{N}},$${\{\nabla f\left(y_n\right)\}}_{n\in \mathbb{N}},$${\{\nabla f\left(z_n\right)\}}_{n\in \mathbb{N}},$${\{\nabla f\left(T{z}_n\right)\}}_{n\in \mathbb{N}}$, ${\{\nabla f\left(T{y}_n\right)\}}_{n\in \mathbb{N}}$ and ${\{\nabla f\left(T{x}_n\right)\}}_{n\in \mathbb{N}}$ are bounded in $E^{\ast }.$ In view of Proposition 1, it follows that $dom{f}^{\ast }=E^{\ast }$ and $f^{\ast }$ is strongly coercive and uniformly convex on bounded sets of $E^{\ast }.$ Let $s_2=sup\{\parallel \nabla f\left(x_n\right)\parallel ,\parallel \nabla f\left(T{x}_n\right)\parallel :n\in \mathbb{N}\}<\infty$ and let ${\rho }_{s_2}^{\ast }:E^{\ast }\to \mathbb{R}$ be the gauge of uniform convexity of the (Fenchel) conjugate function $f^{\ast }.$

Claim. For any $p\in F\left(T\right)$ and $n\in \mathbb{N},$ we have

$$D_f(p,z_n)\le D_f(p,x_n)-{\alpha }_n(1-{\alpha }_n){\rho }_{s_2}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel ).$$

(18)

Let $p\in F\left(T\right).$ For each $n\in \mathbb{N},$ it follows from the definition of the Bregman distance (3), Lemma 3, the inequality (10) and the equation (16) that

$$\begin{array}{cc}{D}_f(p,z_n)& =f\left(p\right)-f\left(z_n\right)-⟨p-z_n,\nabla f\left(z_n\right)⟩\hfill \\ & =f\left(p\right)+f^{\ast }\left(\nabla f\left(z_n\right)\right)-⟨z_n,\nabla f\left(z_n\right)⟩-⟨p-z_n,\nabla f\left(z_n\right)⟩\hfill \\ & =f\left(p\right)+f^{\ast }\left(\nabla f\left(z_n\right)\right)-⟨z_n,\nabla f\left(z_n\right)⟩-⟨p,\nabla f\left(z_n\right)⟩+⟨z_n,\nabla f\left(z_n\right)⟩\hfill \\ & =f\left(p\right)+f^{\ast }\left((1-{\alpha }_n)\nabla f\left(x_n\right)+{\alpha }_n\nabla f\left(T{x}_n\right)\right)-⟨p,((1-{\alpha }_n)\nabla f\left(x_n\right)+{\alpha }_n\nabla f\left(T{x}_n\right)⟩\hfill \\ & \le (1-{\alpha }_n)f\left(p\right)+{\alpha }_{n}f\left(p\right)+(1-{\alpha }_n)f^{\ast }(\nabla f\left(x_n\right)+{\alpha }_n{f}^{\ast }(\nabla f\left(T{x}_n\right))\hfill \\ & -{\alpha }_n(1-{\alpha }_n){\rho }_{s_2}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )-(1-{\alpha }_n)⟨p,\nabla f\left(x_n\right)⟩-{\alpha }_n⟨p,\nabla f\left(T{x}_n\right)⟩\hfill \\ & =(1-{\alpha }_n)[f\left(p\right)+f^{\ast }(\nabla f\left(x_n\right))-⟨p,\nabla f\left(x_n\right)⟩]\hfill \\ & +{\alpha }_n[f\left(p\right)+f^{\ast }(\nabla f\left(T{x}_n\right))-⟨p,\nabla f\left(T{x}_n\right)⟩]-{\alpha }_n(1-{\alpha }_n){\rho }_{s_2}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )\hfill \\ & =(1-{\alpha }_n)[f\left(p\right)-f\left(x_n\right)+⟨x_n,\nabla f\left(x_n\right)⟩-⟨p,\nabla f\left(x_n\right)⟩]\hfill \\ & +{\alpha }_n[f\left(p\right)-f\left(T{x}_n\right)+⟨T{x}_n,\nabla f\left(T{x}_n\right)⟩-⟨p,\nabla f\left(T{x}_n\right)⟩]\hfill \\ & -{\alpha }_n(1-{\alpha }_n){\rho }_{s_2}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )\hfill \\ & =(1-{\alpha }_n)D_f(p,x_n)+{\alpha }_n{D}_f(p,T{x}_n)-{\alpha }_n(1-{\alpha }_n){\rho }_{s_2}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )\hfill \\ & \le (1-{\alpha }_n)D_f(p,x_n)+{\alpha }_n{D}_f(p,x_n)-{\alpha }_n(1-{\alpha }_n){\rho }_{s_2}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )\hfill \\ & =D_f(p,x_n)-{\alpha }_n(1-{\alpha }_n){\rho }_{s_2}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel ).\hfill \end{array}$$

In view of Lemma 3 and the inequality (18), we obtain

$$\begin{array}{cc}{D}_f(p,y_n)& =D_f\left(p,{\beta }_n\nabla f\left(T{z}_n\right)+(1-{\beta }_n)\nabla f\left(x_n\right)\right)\hfill \\ & =V\left(p,{\beta }_n\nabla f\left(T{z}_n\right)+(1-{\beta }_n)\nabla f\left(x_n\right)\right)\hfill \\ & \le {\beta }_{n}V\left(p,\nabla f\left(T{z}_n\right)\right)+(1-{\beta }_n)V\left(p,\nabla f\left(x_n\right)\right)\hfill \\ & ={\beta }_n{D}_f\left(p,T{z}_n\right)+(1-{\beta }_n)D_f\left(p,x_n\right)\hfill \\ & \le {\beta }_n{D}_f\left(p,z_n\right)+(1-{\beta }_n)D_f\left(p,x_n\right)\hfill \\ & ={\beta }_n{D}_f\left(p,x_n\right)-{\beta }_n{\alpha }_n(1-{\alpha }_n){\rho }_{s_2}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel ).\hfill \end{array}$$

Thus, it follows from Lemma 3 and the inequality (18) that

$$\begin{array}{cc}{D}_f(p,x_{n+1})& =D_f\left(p,\nabla f^{\ast }[{\gamma }_n\nabla f\left(T{y}_n\right)+(1-{\gamma }_n)\nabla f\left(x_n\right)])\right)\hfill \\ & =V\left(p,{\gamma }_n\nabla f\left(T{y}_n\right)+(1-{\gamma }_n)\nabla f\left(x_n\right)\right)\hfill \\ & \le {\gamma }_{n}V\left(p,\nabla f\left(T{y}_n\right)\right)+(1-{\gamma }_n)V\left(p,\nabla f\left(x_n\right)\right)\hfill \\ & ={\gamma }_n{D}_f\left(p,T{y}_n\right)+(1-{\gamma }_n)D_f\left(p,x_n\right)\hfill \\ & \le {\gamma }_n{D}_f\left(p,y_n\right)+(1-{\gamma }_n)D_f\left(p,x_n\right)\hfill \\ & ={\gamma }_n{D}_f\left(p,x_n\right)-{\gamma }_n{\alpha }_n{\beta }_n(1-{\alpha }_n){\rho }_{s_2}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )+(1-{\gamma }_n)D_f\left(p,x_n\right)\hfill \\ & \le D_f\left(p,x_n\right)-{\gamma }_n{\alpha }_n{\beta }_n(1-{\alpha }_n){\rho }_{s_2}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )\hfill \end{array}$$

and so

$${\gamma }_n{\alpha }_n{\beta }_n(1-{\alpha }_n){\rho }_{s_2}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )\le D_f(p,x_n)-D_f(p,x_{n+1}).$$

(19)

Since ${\left\{D_f(x_n,z)\right\}}_{n\in \mathbb{N}}$ converges, together with the control condition in equation (17), we have

$${\displaystyle \underset{n\to \infty }{lim}\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel =0.}$$

Since $\nabla f^{\ast }$ is uniformly norm-to-norm continuous on bounded sets of $E^{\ast }$ (see [23]), we arrive at

$${\displaystyle \underset{n\to \infty }{lim\; inf}\parallel x_n-T{x}_n\parallel =0.}$$

(20)

This completes the proof. □

Theorem 8.

Let $f:E\to \mathbb{R}$ be a strongly coercive Bregman function which is bounded on bounded sets, locally uniformly convex and locally uniformly smooth on $E.$ Let C be a nonempty closed convex subset of a reflexive Banach space $E.$ Let $T:C\to C$ be the Bregman generalized α-nonexpansive mapping with $F\left(T\right)\ne \varnothing .$ Let ${\left\{{\alpha }_n\right\}}_{n\in \mathbb{N}},$${\left\{{\beta }_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{{\gamma }_n\right\}}_{n\in \mathbb{N}}$ be the sequences in $[0,1)$ satisfying the following control condition:

$${\displaystyle {\Sigma }_{n=1}^{\infty }{\gamma }_n{\beta }_n{\alpha }_n(1-{\alpha }_n)=+\infty .}$$

Let ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ be iteratively generated by the Equation (16). Then, there exists a subsequence ${\left\{x_{n_i}\right\}}_{i\in \mathbb{N}}$ of ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ which converges weakly to a fixed point of T.

Proof. 

It follows from Theorem 7 that ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is bounded and ${\displaystyle \underset{n\to \infty }{lim\; inf}\parallel T{x}_n-x_n\parallel =0.}$ Since E is reflexive, then there exists a subsequence ${\left\{x_{n_i}\right\}}_{i\in \mathbb{N}}$ of ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ such that $x_{n_i}\rightharpoonup p\in C$ as $i\to \infty .$ Thus, in view of Proposition 4, we conclude that $p\in F\left(T\right)$ and the desired conclusion follows. This completes the proof. □

The construction of fixed points of nonexpansive mappings via Halpern’s algorithm [29] has been extensively investigated recently in the current literature (see, for example, [30] and the references therein). Numerous results have been proved on Halpern’s iterations for nonexpansive mappings in Hilbert and Banach spaces (see, for example, [10,31,32]).

Theorem 9.

Let $f:E\to \mathbb{R}$ be a strongly coercive Bregman function which is bounded on bounded sets, locally uniformly convex and locally uniformly smooth on $E.$ Let C be a nonempty closed convex subset of a reflexive Banach space $E.$ Let $T:C\to C$ be the Bregman generalized α-nonexpansive mapping with $F\left(T\right)\ne \varnothing .$ Let ${\left\{{\alpha }_n\right\}}_{n\in \mathbb{N}},$${\left\{{\beta }_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{{\gamma }_n\right\}}_{n\in \mathbb{N}}$ be the sequences in $[0,1)$ satisfying the following control conditions:

(a) 

${\displaystyle \underset{n\to \infty }{lim}{\gamma }_n=0;}$

(b) 

${\displaystyle {\Sigma }_{n=1}^{\infty }{\gamma }_n=+\infty ;}$

(c) 

${\displaystyle 0<\underset{n\to \infty }{lim\; inf}{\beta }_n\le \underset{n\to \infty }{lim\; sup}{\beta }_n<1.}$

Let $u,x_1\in C$ be chosen arbitrarily and let ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ be the sequence generated by

$$\left\{\begin{array}{c}{z}_n={\alpha }_n\nabla f\left(x_n\right)+(1-{\alpha }_n)\nabla f\left(T{x}_n\right),\hfill \\ y_n=\nabla f^{\ast }[{\beta }_n\nabla f\left(x_n\right)+(1-{\beta }_n)\nabla f\left(z_n\right)],\hfill \\ x_{n+1}=pro{j}_C^f\left(\nabla f^{\ast }[{\gamma }_n\nabla f\left(u\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)]\right),\forall n\in \mathbb{N}.\hfill \end{array}\right.$$

(21)

Then, $\left\{x_n\right\}$ converges strongly to $pro{j}_{F\left(T\right)}^{f}u$.

Proof. 

We divide the proof into three steps. In view of Lemma 5, we conclude that $F\left(T\right)$ is closed and convex. Set

$$w=pro{j}_{F\left(T\right)}^{f}u.$$

Step 1. Now, we prove that ${\left\{x_n\right\}}_{n\in \mathbb{N}}$, ${\left\{y_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{z_n\right\}}_{n\in \mathbb{N}}$ are the bounded sequences in $C.$ In fact, we first show that ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is bounded. Let $p\in F\left(T\right)$ be fixed. In view of Lemma 3 and the Equation (21), we have

$$\begin{array}{cc}{D}_f(p,z_n)& =D_f\left(p,{\alpha }_n\nabla f\left(x_n\right)+(1-{\alpha }_n)\nabla f\left(T{x}_n\right)\right)\hfill \\ & =V\left(p,{\alpha }_n\nabla f\left(x_n\right)+(1-{\alpha }_n)\nabla f\left(T{x}_n\right)\right)\hfill \\ & \le {\alpha }_{n}V\left(p,\nabla f\left(x_n\right)\right)+(1-{\alpha }_n)V\left(p,\nabla f\left(T{x}_n\right)\right)\hfill \\ & ={\alpha }_n{D}_f\left(p,x_n\right)+(1-{\alpha }_n)D_f\left(p,T{x}_n\right)\hfill \\ & \le {\alpha }_n{D}_f\left(p,x_n\right)+(1-{\alpha }_n)D_f\left(p,x_n\right)\hfill \\ & =D_f\left(p,x_n\right).\hfill \end{array}$$

In addition, we have

$$\begin{array}{cc}{D}_f(p,y_n)& =D_f\left(p,\nabla f^{\ast }[{\beta }_n\nabla f\left(x_n\right)+(1-{\beta }_n)\nabla f\left(z_n\right)]\right)\hfill \\ & =V\left(p,{\beta }_n\nabla f\left(x_n\right)+(1-{\beta }_n)\nabla f\left(z_n\right)\right)\hfill \\ & \le {\beta }_{n}V\left(p,\nabla f\left(x_n\right)\right)+(1-{\beta }_n)V\left(p,\nabla f\left(z_n\right)\right)\hfill \\ & ={\beta }_n{D}_f\left(p,x_n\right)+(1-{\beta }_n)D_f\left(p,z_n\right)\hfill \\ & \le {\beta }_n{D}_f\left(p,x_n\right)+(1-{\beta }_n)D_f\left(p,x_n\right)\hfill \\ & =D_f\left(p,x_n\right).\hfill \end{array}$$

This, together with the Equation (16), implies that

$$\begin{array}{cc}{D}_f(p,x_{n+1})& =D_f(p,pro{j}_C^f\left(\nabla f^{\ast }[{\gamma }_n\nabla f\left(u\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)]\right)\hfill \\ & =D_f\left(p,\nabla f^{\ast }[{\gamma }_n\nabla f\left(u\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)]\right)\hfill \\ & =V\left(p,{\gamma }_n\nabla f\left(u\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)\right)\hfill \\ & \le {\gamma }_{n}V\left(p,\nabla f\left(u\right)\right)+(1-{\gamma }_n)V\left(p,\nabla f\left(y_n\right)\right)\hfill \\ & ={\gamma }_n{D}_f\left(p,u\right)+(1-{\gamma }_n)D_f\left(p,y_n\right)\hfill \\ & \le {\gamma }_n{D}_f\left(p,u\right)+(1-{\gamma }_n)D_f\left(p,y_n\right)\hfill \\ & \le {\gamma }_n{D}_f\left(p,u\right)+(1-{\gamma }_n)D_f\left(p,x_n\right)\hfill \\ & \le max\{D_f\left(p,u\right),D_f\left(p,x_n\right)\}.\hfill \end{array}$$

Thus, by induction, we obtain

$$D_f\left(p,x_{n+1}\right)\le max\{D_f\left(p,u\right),D_f\left(p,x_1\right)\},\forall n\in \mathbb{N}.$$

(22)

This implies that the sequence ${\left\{D_f(p,x_n)\right\}}_{n\in \mathbb{N}}$ is bounded:

$$D_f\left(p,x_n\right)\le M_4,\forall n\in \mathbb{N}.$$

(23)

In view of Definition 1, we deduce that the sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is bounded. Since T is the Bregman quasi-nonexpansive mapping from C into itself, we conclude that

$$D_f\left(p,T{x}_n\right)\le D_f\left(p,x_n\right),\forall n\in \mathbb{N}.$$

(24)

This, together with Definition 1 and the boundedness of ${\left\{x_n\right\}}_{n\in \mathbb{N}}$, implies that ${\left\{T{x}_n\right\}}_{n\in \mathbb{N}}$ is bounded. The function f is bounded on bounded sets of E and so $\nabla f$ is also bounded on bounded sets of $E^{\ast }$ (see, for example, [[15], Proposition 1.1.11] for more details). This, together with Step 1, implies that the sequences ${\{\nabla f\left(x_n\right)\}}_{n\in \mathbb{N}}$, ${\{\nabla f\left(y_n\right)\}}_{n\in \mathbb{N}}$, ${\{\nabla f\left(z_n\right)\}}_{n\in \mathbb{N}}$ and ${\{\nabla f\left(T{x}_n\right)\}}_{n\in \mathbb{N}}$ are bounded in $E^{\ast }$. In view of Proposition 1, it follows that $dom{f}^{\ast }=E^{\ast }$ and $f^{\ast }$ is strongly coercive and uniformly convex on bounded sets of $E.$ Let $s_3=sup\{\parallel \nabla f\left(x_n\right)\parallel ,\parallel \nabla f\left(T{x}_n\right)\parallel :n\in \mathbb{N}\}$ and ${\rho }_{s_3}^{\ast }:E^{\ast }\to \mathbb{R}$ be the gauge of the uniform convexity of the (Fenchel) conjugate function $f^{\ast }.$

Step 2. Next, we prove that

$$D_f(w,z_n)\le D_f(w,x_n)-{\alpha }_n(1-{\alpha }_n)(1-{\beta }_n){\rho }_{s_3}^{\ast }\left(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel \right),\forall n\in \mathbb{N}.$$

(25)

For each $n\in \mathbb{N}$, in view of the definition of the Bregman distance (3), Lemma 3 and Lemma (10), we obtain

$$\begin{array}{cc}{D}_f(w,z_n)& =f\left(w\right)-f\left(z_n\right)-⟨w-z_n,\nabla f\left(z_n\right)⟩\hfill \\ & =f\left(w\right)+f^{\ast }\left(\nabla f\left(z_n\right)\right)-⟨z_n,\nabla f\left(z_n\right)⟩-⟨w-z_n,\nabla f\left(z_n\right)⟩\hfill \\ & =f\left(w\right)+f^{\ast }\left(\nabla f\left(z_n\right)\right)-⟨z_n,\nabla f\left(z_n\right)⟩-⟨w,\nabla f\left(z_n\right)⟩+⟨z_n,\nabla f\left(z_n\right)⟩\hfill \\ & =f\left(w\right)+f^{\ast }\left((1-{\alpha }_n)\nabla f\left(x_n\right)+{\alpha }_n\nabla f\left(T{x}_n\right)\right)-⟨w,((1-{\alpha }_n)\nabla f\left(x_n\right)+{\alpha }_n\nabla f\left(T{x}_n\right)⟩\hfill \\ & \le (1-{\alpha }_n)f\left(w\right)+{\alpha }_{n}f\left(w\right)+(1-{\alpha }_n)f^{\ast }(\nabla f\left(x_n\right)+{\alpha }_n{f}^{\ast }(\nabla f\left(T{x}_n\right))\hfill \\ & -{\alpha }_n(1-{\alpha }_n){\rho }_{s_3}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )\hfill \\ & -(1-{\alpha }_n)⟨w,\nabla f\left(x_n\right)⟩-{\alpha }_n⟨w,\nabla f\left(T{x}_n\right)⟩\hfill \\ & =(1-{\alpha }_n)[f\left(w\right)+f^{\ast }(\nabla f\left(x_n\right))-⟨w,\nabla f\left(x_n\right)⟩]\hfill \\ & +{\alpha }_n[f\left(w\right)+f^{\ast }(\nabla f\left(T{x}_n\right))-⟨w,\nabla f\left(T{x}_n\right)⟩]\hfill \\ & -{\alpha }_n(1-{\alpha }_n){\rho }_{s_3}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )\hfill \\ & =(1-{\alpha }_n)[f\left(w\right)-f\left(x_n\right)+⟨x_n,\nabla f\left(x_n\right)⟩-⟨w,\nabla f\left(x_n\right)⟩]\hfill \\ & +{\alpha }_n[f\left(w\right)-f\left(T{x}_n\right)+⟨T{x}_n,\nabla f\left(T{x}_n\right)⟩-⟨w,\nabla f\left(T{x}_n\right)⟩]\hfill \\ & -{\alpha }_n(1-{\alpha }_n){\rho }_{s_3}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )\hfill \\ & =(1-{\alpha }_n)D_f(w,x_n)+{\alpha }_n{D}_f(w,T{x}_n)-{\alpha }_n(1-{\alpha }_n){\rho }_{s_3}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )\hfill \\ & \le (1-{\alpha }_n)D_f(w,x_n)+{\alpha }_n{D}_f(w,x_n)-{\alpha }_n(1-{\alpha }_n){\rho }_{s_3}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )\hfill \\ & =D_f(w,x_n)-{\alpha }_n(1-{\alpha }_n){\rho }_{s_3}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel ).\hfill \end{array}$$

In addition, we have

$$\begin{array}{cc}{D}_f(w,y_n)& =D_f\left(w,{\beta }_n\nabla f\left(x_n\right)+(1-{\beta }_n)\nabla f\left(z_n\right)\right)\hfill \\ & =V\left(w,{\beta }_n\nabla f\left(x_n\right)+(1-{\beta }_n)\nabla f\left(z_n\right)\right)\hfill \\ & \le {\beta }_{n}V\left(w,\nabla f\left(x_n\right)\right)+(1-{\beta }_n)V\left(w,\nabla f\left(z_n\right)\right)\hfill \\ & ={\beta }_n{D}_f\left(w,x_n\right)+(1-{\beta }_n)D_f\left(w,z_n\right)\hfill \\ & \le {\beta }_n{D}_f\left(w,x_n\right)+(1-{\beta }_n)D_f\left(w,x_n\right)\hfill \\ & -{\alpha }_n(1-{\alpha }_n)(1-{\beta }_n){\rho }_{s_3}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )\hfill \\ & =D_f\left(w,x_n\right)-{\alpha }_n(1-{\alpha }_n)(1-{\beta }_n){\rho }_{s_3}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel ).\hfill \end{array}$$

In view of Lemma 3 and the inequality (25), we obtain

$$\begin{array}{ll}{D}_f(w,x_{n+1})& =D_f(w,pro{j}_C^f\left(\nabla f^{\ast }[{\gamma }_n\nabla f\left(u\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)]\right)\\ & =D_f\left(w,\nabla f^{\ast }[{\gamma }_n\nabla f\left(u\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)]\right)\\ & =V\left(w,{\gamma }_n\nabla f\left(u\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)\right)\\ & \le {\gamma }_{n}V\left(w,\nabla f\left(u\right)\right)+(1-{\gamma }_n)V\left(w,\nabla f\left(y_n\right)\right)\\ & ={\gamma }_n{D}_f\left(w,u\right)+(1-{\gamma }_n)D_f\left(w,y_n\right)\\ & \le {\gamma }_n{D}_f\left(w,u\right)+(1-{\gamma }_n)[D_f\left(w,x_n\right)\\ & -{\alpha }_n(1-{\alpha }_n)(1-{\beta }_n){\rho }_{s_3}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel \left)\right].\end{array}$$

(26)

Let

$$M_5=sup\left\{\right|D_f\left(w,u\right)-D_f\left(w,x_n\right)|+{\alpha }_n(1-{\alpha }_n)(1-{\beta }_n){\rho }_{s_3}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel ):n\in \mathbb{N}\}.$$

It follows from the inequality (26) that

$${\alpha }_n(1-{\alpha }_n)(1-{\beta }_n){\rho }_{s_3}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel )\le D_f(w,x_n)-D_f(w,x_{n+1})+{\gamma }_n{M}_5.$$

(27)

Let

$$w_n=\nabla f^{\ast }[{\gamma }_n\nabla f\left(u\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)].$$

Then, $x_{n+1}=pro{j}_C^f\left(w_n\right)$ for each $n\in \mathbb{N}.$ In view of Lemma 3 and the inequality (25), we obtain

$$\begin{array}{ll}{D}_f(w,x_{n+1})& =D_f(w,pro{j}_C^f\left(\nabla f^{\ast }[{\gamma }_n\nabla f\left(u\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)]\right)\\ & \le D_f\left(w,\nabla f^{\ast }[{\gamma }_n\nabla f\left(u\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)]\right)\\ & =V\left(w,{\gamma }_n\nabla f\left(u\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)\right)\\ & \le V\left(w,{\gamma }_n\nabla f\left(u\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)\right)-{\gamma }_n(\nabla f\left(u\right)-\nabla f\left(w\right))\\ & -⟨\nabla f^{\ast }[{\gamma }_n\nabla f\left(u\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)]-w,-{\gamma }_n(\nabla f\left(u\right)-\nabla f\left(w\right))⟩\\ & =V\left(w,{\gamma }_n\nabla f\left(w\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)\right)+{\gamma }_n⟨w_n-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩\\ & \le {\gamma }_{n}V\left(w,\nabla f\left(w\right)\right)+(1-{\gamma }_n)V\left(w,\nabla f\left(y_n\right)\right)+{\gamma }_n⟨w_n-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩\\ & ={\gamma }_n{D}_f\left(w,w\right)+(1-{\gamma }_n)D_f\left(w,y_n\right)+{\gamma }_n⟨w_n-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩\\ & =(1-{\gamma }_n)D_f\left(w,y_n\right)+{\gamma }_n⟨w_n-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩.\end{array}$$

(28)

Step 3. Next, we show that $x_n\to w$ as $n\to \infty .$

Case 1. If there exists $n_0\in \mathbb{N}$ such that ${\left\{D_f(w,x_n)\right\}}_{n=n_0}^{\infty }$ is nonincreasing, then ${\left\{D_f(w,x_n)\right\}}_{n\in \mathbb{N}}$ is convergent. Thus, we have $D_f(w,x_n)-D_f(w,x_{n+1})\to 0$ as $n\to \infty$. This, together with the inequality (27) and the conditions (a) and (c), implies that

$${\displaystyle \underset{n\to \infty }{lim}{\rho }_{s_3}^{\ast }(\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel =0.}$$

Therefore, from the property of ${\rho }_{s_3}^{\ast }$, it follows that

$${\displaystyle \underset{n\to \infty }{lim}\parallel \nabla f\left(x_n\right)-\nabla f\left(T{x}_n\right)\parallel =0.}$$

(29)

Since $\nabla f^{\ast }={(\nabla f)}^{-1}$ (Lemma 1) is uniformly norm-to-norm continuous on bounded sets of $E^{\ast }$ (see, for example, [23]), we arrive at

$${\displaystyle \underset{n\to \infty }{lim}\parallel x_n-T{x}_n\parallel =0.}$$

(30)

On the other hand, we have

$$\begin{array}{cc}{D}_f(T{x}_n,z_n)& =D_f\left(T{x}_n,{\gamma }_n\nabla f\left(x_n\right)+(1-{\gamma }_n)\nabla f\left(T{x}_n\right)\right)\hfill \\ & =V\left(T{x}_n,{\gamma }_n\nabla f\left(x_n\right)+(1-{\gamma }_n)\nabla f\left(T{x}_n\right)\right)\hfill \\ & \le {\gamma }_{n}V\left(T{x}_n,\nabla f\left(x_n\right)\right)+(1-{\gamma }_n)V\left(T{x}_n,\nabla f\left(T{x}_n\right)\right)\hfill \\ & ={\gamma }_n{D}_f\left(T{x}_n,x_n\right)+(1-{\gamma }_n)D_f\left(T{x}_n,T{x}_n\right)\hfill \\ & \le {\gamma }_n{D}_f\left(T{x}_n,x_n\right).\hfill \end{array}$$

This, together with Lemma 2 and the Equation (30), implies that

$${\displaystyle \underset{n\to \infty }{lim}{D}_f(T{x}_n,z_n)=0.}$$

Similarly, we have

$$D_f(z_n,w_n)\le {\gamma }_n{D}_f(z_n,u)+(1-{\gamma }_n)D_f(z_n,z_n)={\gamma }_n{D}_f(z_n,u)\to 0$$

as $n\to \infty$. In view of Lemma 2 and the Equation (30), we conclude that

$${\displaystyle \underset{n\to \infty }{lim}\parallel z_n-T{x}_n\parallel =0,\underset{n\to \infty }{lim}\parallel w_n-x_n\parallel =0.}$$

Since ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is bounded, together with the inequality (13), we can assume that there exists a subsequence ${\left\{x_{n_i}\right\}}_{i\in \mathbb{N}}$ of ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ such that $x_{n_i}\rightharpoonup z\in F\left(T\right)$ (Proposition 4) and

$$\begin{array}{cc}{\displaystyle \underset{n\to \infty }{lim\; sup}⟨x_n-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩}& {\displaystyle =\underset{i\to \infty }{lim}⟨x_{n_i}-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩}\hfill \\ & =⟨y-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩\hfill \\ & \le 0.\hfill \\ \end{array}$$

Thus, it follows that

$${\displaystyle \underset{n\to \infty }{lim\; sup}⟨z_n-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩=\underset{n\to \infty }{lim\; sup}⟨x_n-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩\le 0.}$$

The desired result follows from Lemmas 2 and 7 and the inequality (28).

Case 2. Suppose that there exists a subsequence ${\left\{n_i\right\}}_{i\in \mathbb{N}}$ of ${\left\{n\right\}}_{n\in \mathbb{N}}$ such that

$$D_f(w,x_{n_i})<D_f(w,x_{n_i+1}),\forall i\in \mathbb{N}.$$

By Lemma 6, there exists a non-decreasing sequence ${\left\{m_k\right\}}_{k\in \mathbb{N}}$ of positive integers with $m_k\to \infty$ such that

$$D_f(w,x_{m_k})<D_f(w,x_{m_k+1}),\mathrm{and}{D}_f(w,x_k)<D_f(w,x_{m_k+1}),\forall k\in \mathbb{N}.$$

This, together with the inequality (27), implies that

$$\begin{array}{cc}{\alpha }_{m_k}(1-{\alpha }_{m_k})(1-{\beta }_{m_k}){\rho }_{s_3}^{\ast }(\parallel \nabla f\left(x_{m_k}\right)-\nabla f\left(T{x}_{m_k}\right)\parallel )& \le D_f(w,x_{m_k})-D_f(w,x_{m_k+1})+{\gamma }_{m_k}{M}_5\hfill \\ & \le {\gamma }_{m_k}{M}_5,\forall k\in \mathbb{N}.\hfill \end{array}$$

Then, by the conditions (a) and (c), we get

$${\displaystyle \underset{k\to \infty }{lim}{\rho }_{s_3}^{\ast }(\parallel \nabla g\left(x_{m_k}\right)-\nabla f\left(T{x}_{m_k}\right)\parallel )=0.}$$

By the same argument as in Case 1, we arrive at

$${\displaystyle \underset{k\to \infty }{lim\; sup}⟨w_{m_k}-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩=\underset{k\to \infty }{lim\; sup}⟨x_{m_k}-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩\le 0.}$$

(31)

It follows from the inequality (28) that

$$D_f(w,x_{m_k+1})\le (1-{\gamma }_{m_k})D_f(w,x_{m_k})+{\gamma }_{m_k}{D}_f(w,x_{m_k})+{\gamma }_{m_k}⟨z_{m_k}-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩.$$

(32)

Since $D_f(w,x_{m_k})\le D_f(w,x_{m_k+1}),$ it follows that

$$\begin{array}{cc}{\gamma }_{m_k}{D}_f(w,x_{m_k})& \le D_f(w,x_{m_k})-D_f(w,x_{m_k+1})+{\gamma }_{m_k}⟨w_{m_k}-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩\hfill \\ & \le {\gamma }_{m_k}⟨w_{m_k}-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩.\hfill \end{array}$$

In particular, since ${\gamma }_{m_k}>0,$ we obtain

$$D_f(w,x_{m_k})\le ⟨w_{m_k}-w,\nabla f\left(u\right)-\nabla f\left(w\right)⟩.$$

In view of the inequality (31), we deduce that

$${\displaystyle \underset{k\to \infty }{lim}{D}_f(w,x_{m_k})=0.}$$

This, together with the inequality (32), implies

$${\displaystyle \underset{k\to \infty }{lim}{D}_f(w,x_{m_k+1})=0.}$$

On the other hand, we have

$$D_f(w,x_k)\le D_f(w,x_{m_k+1}),\forall k\in \mathbb{N}.$$

This ensures that $x_k\to w$ as $k\to \infty$ by Lemma 2. This completes the proof. □

4. Numerical Examples

In this section, we illustrate a direct application of Theorem 9 on a typical example on a real line.

Example 2.

Let the mappings f and T be given in Example 1 and set

$$\left\{{\alpha }_n\right\}=\left\{\frac{n+1}{4n}\right\},\{{\beta }_n\}=\left\{\frac{n+1}{5n}\right\},\left\{{\gamma }_n\right\}=\left\{\frac{1}{500n}\right\},\forall n\ge 1.$$

Consider the following:

$$\begin{array}{c}E=\mathbb{R},C=[0,0.9],Tx=x^2,f\left(x\right)=x^4,\nabla f\left(x\right)=4x^3,\hfill \\ f^{\ast }\left(x^{\ast }\right)=sup\{⟨x^{\ast },x⟩-f\left(x\right):x\in E\},f^{\ast }\left(z\right)=\frac{3z^{\frac{4}{3}}}{4^{\frac{4}{3}}},\nabla f^{\ast }\left(z\right)={\left(\frac{z}{4}\right)}^{\frac{1}{3}}.\hfill \end{array}$$

Let initial values $x_1=0$ and $u=0.1.$ Then, we use iteration from the Equation (21) to generate the sequences $\left\{x_n\right\},\left\{y_n\right\}$ and $\left\{z_n\right\}$ as follows:

$$\left\{\begin{array}{c}{\displaystyle z_n={\alpha }_n\nabla f\left(x_n\right)+(1-{\alpha }_n)\nabla f\left(T{x}_n\right)=\left(\frac{n+1}{n}\right)x_n^3+\left(\frac{3n+1}{n}\right)x_n^6,}\hfill \\ {\displaystyle y_n=\nabla f^{\ast }[{\beta }_n\nabla f\left(x_n\right)+(1-{\beta }_n)\nabla f\left(z_n\right)]={\left[\left(\frac{n+1}{5n}\right)x_n^3+\left(\frac{3n+1}{4n}\right)z_n^3\right]}^{\frac{1}{3}},}\hfill \\ {\displaystyle x_{n+1}=\nabla f^{\ast }[{\gamma }_n\nabla f\left(u\right)+(1-{\gamma }_n)\nabla f\left(y_n\right)]={\left[\frac{u^3}{500n}+\left(\frac{500n-1}{500n}\right)y_n^3\right]}^{\frac{1}{3}}.}\hfill \end{array}\right.$$

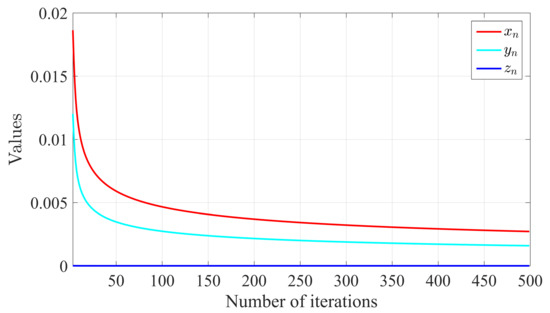
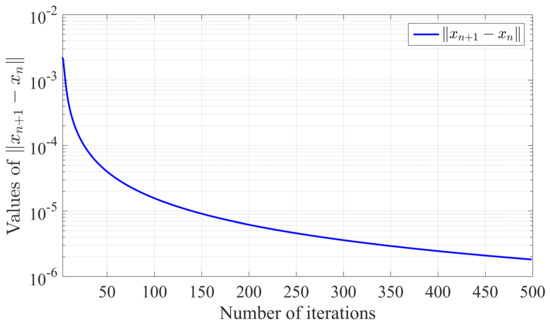
We have the following Table 1 and Figure 2 and Figure 3 which show that $\left\{x_n\right\},\left\{z_n\right\}$ and $\left\{y_n\right\}$ converge to $w=0$.

Table 1. Values of $z_n$, $y_n$ and $x_n$.

No. of Iterations	${\mathit{z}}_{\mathit{n}}$	${\mathit{y}}_{\mathit{n}}$	${\mathit{x}}_{\mathit{n}}$	$\parallel {\mathit{x}}_{\mathit{n}+1}-{\mathit{x}}_{\mathit{n}}\parallel$
1	0.0000000	0.0000000	0.0200000	0.0200000
2	0.0000120	0.0133887	0.0185640	0.0014360
3	0.0000085	0.0119489	0.0163510	0.0022130
4	0.0000055	0.0103005	0.0145690	0.0017821
5	0.0000037	0.0090538	0.0132797	0.0012893
6	0.0000027	0.0081755	0.0123411	0.0009386
7	0.0000021	0.0075456	0.0116283	0.0007128
8	0.0000018	0.0070726	0.0110622	0.0005662
9	0.0000015	0.0067004	0.0105959	0.0004662
10	0.0000013	0.0063966	0.0102015	0.0003944
⋮	⋮	⋮	⋮	⋮
100	0.0000001	0.0027372	0.0046494	0.0000157
200	0.0000001	0.0021635	0.0036871	0.0000062
300	0.0000000	0.0018873	0.0032201	0.0000036
400	0.0000000	0.0017135	0.0029252	0.0000024
⋮	⋮	⋮	⋮	⋮
491	0.0000000	0.0015998	0.0027318	0.0000019
492	0.0000000	0.0015987	0.0027300	0.0000019
493	0.0000000	0.0015976	0.0027281	0.0000018
494	0.0000000	0.0015965	0.0027263	0.0000018
495	0.0000000	0.0015954	0.0027244	0.0000018
496	0.0000000	0.0015943	0.0027226	0.0000018
497	0.0000000	0.0015933	0.0027208	0.0000018
498	0.0000000	0.0015922	0.0027190	0.0000018
499	0.0000000	0.0015911	0.0027171	0.0000018

Figure 2. Plotting of $\left\{x_n\right\},\left\{y_n\right\}$ and $\left\{z_n\right\}$ converging to 0 as $n\to \infty$.

Figure 3. Plotting of $\parallel x_{n+1}-x_n\parallel$.

5. Conclusions

First, we have established the new class of Bregman generalized $\alpha$-nonexpansive mappings. Second, we have obtained new theorems on fixed points and weak and strong convergence using multi-step iterations and Bregman generalized $\alpha$-nonexpansive mappings. Finally, we have analysed computational procedures based on Ishikawa and Noor iterations with a numerical simulation to support the results.