Methods for Assessing Human–Machine Performance under Fuzzy Conditions
Abstract
:1. Introduction
2. Fuzzy Sets and Generalizations
- The principle of identity
- The law of the excluded middle
- The law of contradiction
3. Types of Uncertainty in Fuzzy Systems
- G1 = {(A, ), (B, ), (C, ), (D, ), (F, 0) }; and
- G2 = {(A, ), (B, ), (C, ), (D, 0), (F, ) }.
4. The Center of Gravity Defuzzification Technique
- Choose the suitable universal set.
- Fuzzify the given data by defining suitable membership functions for the FSs involved in this procedure.
- Elaborate the fuzzy data with FL techniques for expressing the solution of the given problem in the form of a unique FS.
- Defuzzify the above FS by representing it with a real numerical value to “translate” the problem’s solution into the natural language.
4.1. The Rectangular Fuzzy Assessment Model
- The group with the greater value of xc demonstrates the better performance.
- In the case of the same value of xc, if xc ≥ 2.5, then the group with the greater value of yc performs better. On the contrary, if xc < 2.5, then the group with the lower value of yc demonstrates the better performance.
4.2. Comparison of the RFAM with the GPA Index
5. Triangular Fuzzy Numbers
5.1. Preliminaries
- A is normal, i.e., there exists x in R such that mA(x) = 1.
- A is convex, i.e., all its a-cuts Aa = {x ∈ R: mA (x) ≥ a}, with a in [0, 1], are closed real intervals.
- Its membership function y = m(x) is a piecewise continuous function.
- The sum A + B = (a+a1, b+b1, c+c1).
- The difference A – B = A + (–B) = (a – c1, b – b1, c – a1), where –B = (–c1, –b1, –a1) is defined to be the opposite of B.
- k + A = (k + a, k + b, k + c), k ∈ R.
- kA = (ka, kb, kc), if k > 0 and kA = (kc, kb, ka), if k < 0, k ∈ R.
5.2. The Assessment Method Using TFNs
- Define the mean value of a finite number of given TFNs A1, A2, …, n ≥ 2, to be the TFN A = (A1 + A2 + … + An).
- Assign a scale of numerical scores from 1 to 100 to the linguistic grades A = excellent, B = very good, C = good, D = fair and F = unsatisfactory as follows: A (85–100), B (75–84), C (60–74), D (50–59) and F (0–49).
- Use for simplicity the same letters to represent the above grades by the TFNs A = (85, 92.5, 100), B = (75, 79.5, 84), C (60, 67, 74), D (50, 54.5, 59) and F (0, 24.5, 49), respectively, where the middle entry of each of them is equal to the mean value of its other two entries.
- Assess the individual performance of the system components by the above five qualitative grades and assign one of the TFNs A, B, C, D, F to each of those components. Then, if n is the total number of the system’s components and nX denotes the number of the components corresponding to the TFN X, with X = A, B, C, D, F, the mean value M of all those TFNs is equal to the TFN
6. Grey System Theory
6.1. Grey Numbers
- Addition by A + B ∈ [a1 + b1, a2 + b2].
- Subtraction by A − B = A + (−B) ∈ [a1 − b2, a2 – b1], where −B ∈ [−b2, −b1] is defined to be the opposite of B.
- Multiplication by A × B [min{a1b1, a1b2, a2b1, a2b2}, max{a1b1, a1b2, a2b1, a2b2}].
- Division by A: B = A × B−1 ∈ [min{}, max{}]. with b1, b2 ≠ 0 and B−1 ∈ [] , which is defined to be the inverse of B.
- Scalar multiplication by kA ∈ [ka1, ka2], if k ≥ 0 and by kA ≥ [ka2, ka1], if k < 0.
6.2. The Assessment Method with GNs
- Attach the numerical scores A (100–85), B (84–75), C (74–60), D (59–50), and F (49–0) to the corresponding linguistic grades.
- Assign to each grade a GN as follows: A ∈ [85, 100], B ∈ [75, 84], C ∈ [60, 74], D ∈ [50, 59], and F ∈ [0, 49].
- Correspond to each of the system’s components one of the above GNs evaluating its performance.
- Using analogous notation with the case of TFNs, calculate the mean value
- Since nAA ∈ [85nA, 100nA], nBB ∈ [75nB, 84nB], nCC ∈ [60nC, 74nC], nDD ∈ [50nD, 59nD], and nFF ∈ [0nF, 49nF], one obtains that M* ∈ [m1, m2], where
- Since the distribution of M* is unknown, take
- (1)
- From Equations (15) and (18), one obtains that X(M) = W(M*). Therefore, one concludes that the assessment methods with the TFNs and the GNs are equivalent to each other, because they provide the same assessment outcomes.
- (2)
- It is straightforward to check that, if the maximal possible numerical score corresponds to each system’s component for each grade, then the mean value of those scores is equal to c or m2, respectively. In the same way, if the minimal possible score corresponds to each system’s component for each grade, then the mean value of all scores is equal to a or m1, respectively. Consequently, assessment methods with TFNs and GNs give a reliable approximation of the system’s mean performance.
6.3. Applications of the Assessment Methods with TFNs and GNs
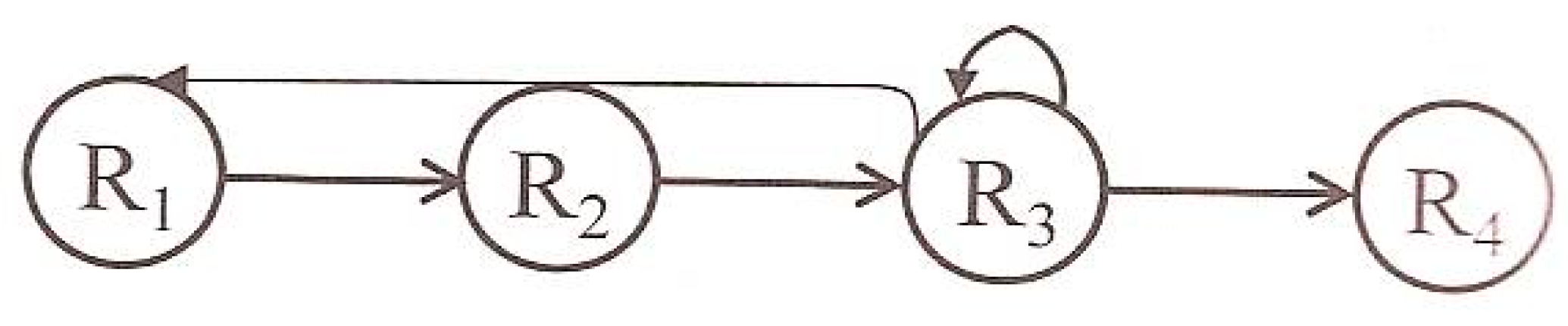
- R1: Retrieve the most suitable past case to the new problem.
- R2: Reuse the information of the retrieved case to solve the new problem.
- R3: Revise the solution.
- R4: Retain the part of the solution that could be useful for future problems.
- (i)
- As we show in the previous section, the use of GNs provides in general the same assessment outcomes with the use of TFNs. However, observe that, to obtain the mean value M* ∈ [m1, m2], one needs to calculate two components only, in contrast to the mean value M (a, b, c) where the calculation of three components is needed. Consequently, the method with GNs reduces the required computational burden.
- (ii)
- Another promising area for applying the above assessment methods is the fuzzy control systems (e.g., see [43], [44] (Paragraph 5.3), [45]). Traditional controllers, often implemented as PID (proportional–integral–derivative) controllers, are based on mathematical models in which the control system is described using one or more differential equations that define the system response to its inputs. They are the products of decades of development and theoretical analysis and are highly effective in general. However, in certain cases, the mathematical model of the control process may not exist, or may be too “expensive” in terms of computer processing power and memory. In such cases, a system based on empirical rules may be more effective.
7. Application of Fuzzy Relation Equations to Mathematical Modeling
7.1. Mathematical Modeling
- S1: Analyze the given problem (understanding the statement and recognizing the restrictions and requirements imposed by the corresponding real system).
- S2: Mathematize (formulation of the problem and construction of the mathematical model).
- S3: Solve the model.
- S4: Validate (control) the model, which is usually achieved by reproducing, through the model, the behavior of the real system under the conditions existing before the solution of the model and by comparing it to the existing from the previous “history” of the real system, i.e., data. In cases of systems having no past history, an extra simulation model could be used for the validation of the mathematical model.
- S5: Interpret the final mathematical results and implement them in the real system to give the “answer” to the real-world problem.
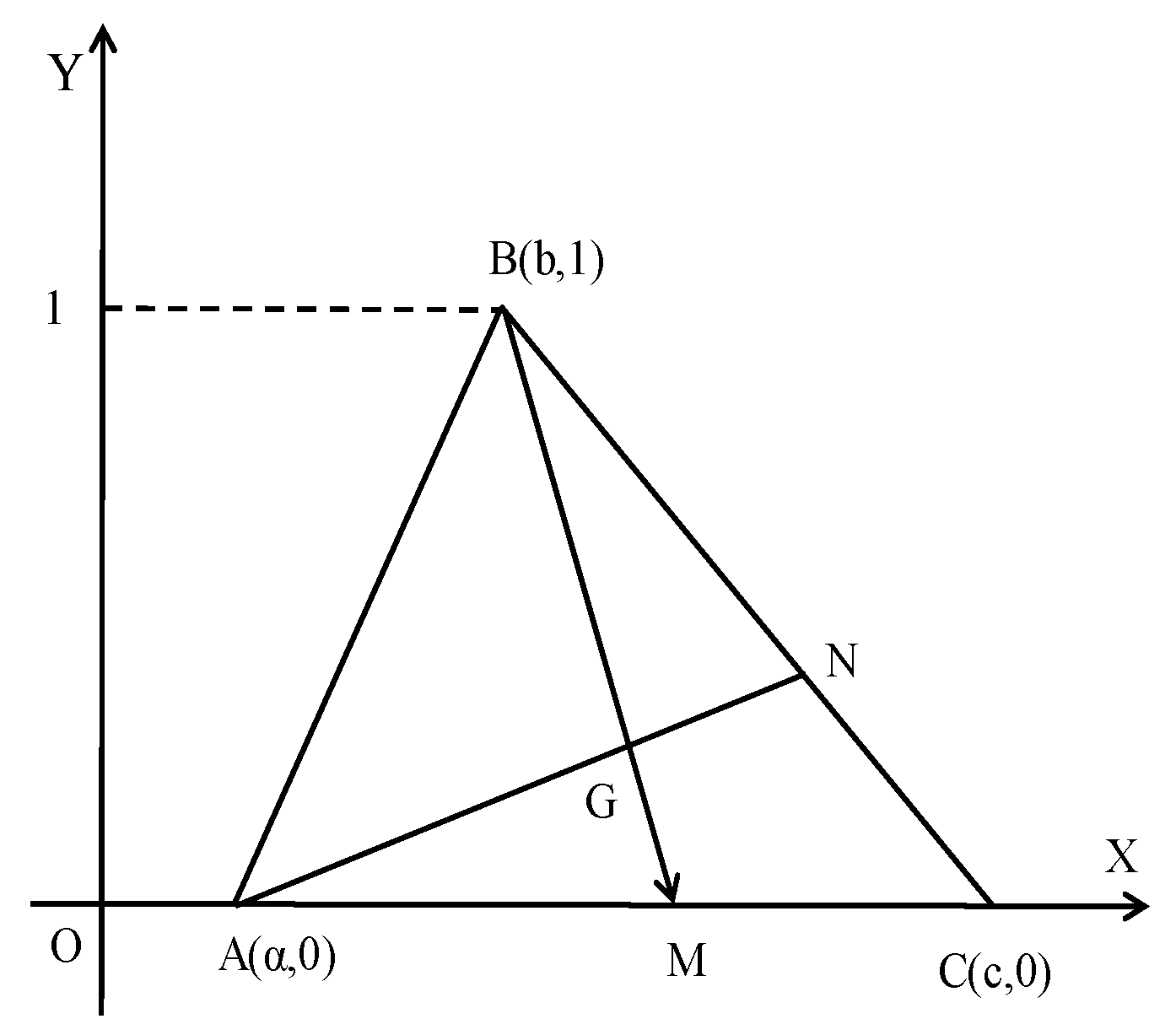
7.2. Fuzzy Relation Equations
7.3. A Study of MM Skills Using FRE
- Only of the students of the class were ready to use contents of their memory (background knowledge, etc.) to facilitate the solution of the given problems.
- All the above students were able to design the model and almost all of them were able to execute the solutions of the given problems.
- On the contrary, half of the above students could not check the correctness of the solutions found and therefore implement correctly the mathematical results to the real system.
- max {min (p1, 0.7), min (p2, 0.4), min (p3, 0.2), min (p4, 0.1), (p5, 0)}= 0.33
- max {min (p1, 0.5), min (p2, 0.6), min (p3, 0.7), min (p4, 0.5), min (p5, 0.1)}= 0.33
- max {min (p1, 0.3), min (p2, 0.3), min (p3, 0.6), min (p4, 0.7), (p5, 0.5)}= 0.3
- max {min (p1, 0), min (p2, 0.1), min (p3, 0.2), min (p4, 0.5), min (p5, 0.8)}= 0.17
8. Discussion and Conclusions
- The measurement of the corresponding fuzzy system’s probabilistic uncertainty (generalized Shannon’s entropy) or its total possibilistic uncertainty (the sum of strife and non-specificity) for evaluating its mean performance. However, this method can be applied for comparing the performance of two different systems with respect to a common activity only under the assumption that the uncertainty in those systems is the same before the activity (equivalent systems). Moreover, the method cannot provide an exact characterization of a system’s performance and it involves laborious calculations.
- The utilization of the COG defuzzification technique (rectangular fuzzy assessment model) for assessing a fuzzy system’s quality performance. This method, initiated by Subbotin et al. [31], is useful, due to its logical nature, when comparing the performance of two systems with equal values of the traditional GPA index. In this case, the GPA index could lead to conclusions that are not close to the reality. On the contrary, for different values of the GPA index, the two methods provide the same assessment outcomes.
- The use of TFNs as assessment tools, a method that is easy to apply in practice and gives an exact characterization of the system’s mean performance. That method is useful when qualitative grades and not numerical scores are used for the evaluation of the system’s performance, which makes impossible the calculation of the mean value of those grades in a traditional way. However, a disadvantage of the method is that its understanding requires knowledge of basic principles of FS theory, which is not always easy for non-specialists.
- The use of GNs, instead of TFNs, as assessment tools. These two methods are equivalent to each other, providing the same assessment outcomes. However, GNs can be easily defined with the help of closed real intervals, which makes the method more accessible to non-specialists. Moreover, the use of GNs reduces significantly the required computational burden.
- The application of FRE for assessing MM skills. This method enables the teacher to obtain useful conclusions about student progress and was applied by the author, with the proper modifications each time, to various other assessment situations (problem-solving, learning a subject matter, human and machine reasoning, etc.) [53,54,55].
Funding
Conflicts of Interest
References
- Balley, K.D. Sociology and the New Systems Theory: Toward a Theoretical Synthesis; State of New York Press: New York, NY, USA, 1994. [Google Scholar]
- Xu, K.; Tang, L.C.; Xie, M.; Ho, S.L.; Zhu, M.L. Fuzzy assessment of FMEA for engine systems. Reliab. Eng. Syst. Saf. 2002, 75, 17–29. [Google Scholar] [CrossRef]
- Liu, L.; Lee, H.-M. Fuzzy assessment method on sampling survey analysis. Expert Syst. Appl. 2009, 36, 5955–5961. [Google Scholar]
- Macwan, N.; Srinivas, S.P. A Linguistic Fuzzy Approach for Employee Evaluation. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2014, 1, 975–980. [Google Scholar]
- Liu, R.-T.; Huang, W.-C. Fuzzy Assessment on Reservoir Water Quality. J. Mar. Sci. Technol. 2015, 23, 231–239. [Google Scholar]
- Jevscek, M. Competencies assessment using fuzzy logic. J. Univers. Excell. 2016, 5, 187–202. [Google Scholar]
- Korner, S. Laws of Thought. In Encyclopaedia of Philosophy; Mac Millan: New York, NY, USA, 1967; Volume 4, pp. 414–417. [Google Scholar]
- Lejewski, C. Jan Lukasiewicz. Encycl. Philos. 1967, 5, 104–107. [Google Scholar]
- Tarski, A. Encyclopaedia Brittanica. 2018. Available online: www.britannica.com/biography/Alfred-Tarski (accessed on 20 December 2018).
- Zadeh, L.A. Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans. Syst. Man Cybern. 1973, 3, 28–44. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Klir, G.J.; Folger, T.A. Fuzzy Sets, Uncertainty and Information; Prentice-Hall: London, UK, 1988. [Google Scholar]
- Haack, S. Do we need fuzzy logic? Int. J. Man-Mach. Stud. 1979, 11, 437–445. [Google Scholar] [CrossRef]
- Fox, J. Towards a reconciliation of fuzzy logic and standard logic. Int. J. Man Mach. Stud. 1981, 15, 213–220. [Google Scholar] [CrossRef]
- Tah, J.H.M.; Carr, V. A proposal for construction project risk assessment using fuzzy logic. Constr. Manag. Econ. 2010, 18, 491–500. [Google Scholar] [CrossRef]
- Collatta, M.; Pau, G.; Solerno, V.M.; Scata, G. A novel trust based algorithm for carpooling transportation systems. In Proceedings of the IEEE International Energy Conference and Exhibition, Florence, Italy, 9–12 September 2012. [Google Scholar]
- Voskoglou, M.G. Finite Markov Chain and Fuzzy Logic Assessment Models: Emerging Research and Opportunities; Createspace.com–Amazon: Columbia, SC, USA, 2017. [Google Scholar]
- Wu, C.; Liu, G.; Huang, G.; Liu, Q.; Guan, X. Ecological Vulnerability Assessment Based on Fuzzy Analytical Method and Analytic Hierarchy Process in Yellow River Delta. Int. J. Environ. Res. Public Health 2018, 15, 855. [Google Scholar] [CrossRef] [PubMed]
- Nilashi, M.; Cavallaro, F.; Mardani, A.; Zavadskas, E.K.; Samad, S.; Ibrahim, O. Measuring Country Sustainability Performance Using Ensembles of Neuro-Fuzzy Technique. Sustainability 2018, 10, 2707. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy/Neutrosophic Probability, Set, and Logic; Proquest: Ann Arbor, MI, USA, 1998. [Google Scholar]
- Deng, J. Control Problems of Grey Systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Pawlak, Z. Rough Sets: Aspects of Reasoning about Data; Kluer Academic Publishers: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Molodtsov, D. Soft Set Theory–First Results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communications. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Klir, G.J. Principles of Uncertainty: What are they? Why do we need them? Fuzzy Sets Syst. 1995, 74, 15–31. [Google Scholar] [CrossRef]
- Shackle, G.L.S. Decision, Order and Time in Human Affairs; Cambridge University Press: Cambridge, UK, 1961. [Google Scholar]
- Van Broekhoven, E.; De Baets, B. Fast and accurate centre of gravity defuzzification of fuzzy systems outputs defined on trapezoidal fuzzy partitions. Fuzzy Sets Syst. 2006, 157, 904–918. [Google Scholar] [CrossRef]
- Voskoglou, M.G. An Application of Fuzzy Sets to the Process of Learning. Heuristics Didact. Exact Sci. 1999, 10, 9–13. [Google Scholar]
- Voskoglou, M.G. Transition across Levels in the Process of Learning. Int. J. Model. Appl. 2009, 1, 37–44. [Google Scholar]
- Subbotin, I.Y.; Badkoobehi, H.; Bilotckii, N.N. Application of fuzzy logic to learning assessment. Didact. Math. Probl. Investig. 2004, 22, 38–41. [Google Scholar]
- Subbotin, I.Y. Trapezoidal Fuzzy Logic Model for Learning Assessment. arXiv, 2014; arXiv:1407.0823. [Google Scholar]
- Zadeh, L.A. The Concept of a Linguistic Variable and its Application to Approximate Reasoning, Parts 1–3. Inf. Sci. 1975, 8, 9, 43–80, 199–249, and 301–357 . [Google Scholar] [CrossRef]
- Sakawa, M. Fuzzy Sets and Interactive Multiobjective Optimization; Plenum Press: London, UK, 1993. [Google Scholar]
- Kaufmann, A.; Gupta, M. Introduction to Fuzzy Arithmetic; Van Nostrand Reinhold Company: New York, NY, USA, 1991. [Google Scholar]
- Voskoglou, M.G. Use of the Triangular Fuzzy Numbers for Student Assessment. Am. J. Appl. Math. Stat. 2015, 3, 146–150. [Google Scholar]
- Voskoglou, M.G. Assessment of Human Skills Using Trapezoidal Fuzzy Numbers. Am. J. Appl. Math. Stat. 2015, 5, 111–116. [Google Scholar]
- Deng, J. Introduction to Grey System Theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Moore, R.A.; Kearfort, R.B.; Clood, M.J. Introduction to Interval Analysis, 2nd ed.; SIAM: Philadelphia, PA, USA, 1995. [Google Scholar]
- Liu, S.F.; Lin, Y. (Eds.) Advances in Grey System Research; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Voskoglou, M.G.; Theodorou, Y. Application of Grey Numbers to Assessment Processes. Int. J. Appl. Fuzzy Sets Artif. Intell. 2017, 7, 59–72. [Google Scholar]
- Voskoglou, M.G.; Salem, A.-B.M. Analogy-Based and Case-Based Reasoning: Two Sides of the Same Coin. Int. J. Appl. Fuzzy Sets Artif. Intell. 2014, 4, 7–18. [Google Scholar]
- Reznik, L. Fuzzy Controllers; Newnes: Oxford, UK, 1997. [Google Scholar]
- Theodorou, Y.A. Introduction to Fuzzy Logic; Tziolas Editions: Thessaloniki, Greece, 2010. (In Greek) [Google Scholar]
- Wikipedia. Fuzzy Control System. March 2012. Available online: http://en.wikipedia.org/wiki/Fuzzy_control_system (accessed on 20 December 2018).
- Voskoglou, M.G. Mathematical modelling as a teaching method of mathematics. J. Res. Innov. Teach. (Natl. Univ. CA) 2015, 8, 35–50. [Google Scholar]
- Zadeh, L.A. Similarity relations and fuzzy orderings. Inf. Sci. 1971, 3, 177–200. [Google Scholar] [CrossRef]
- Kaufmann, A. Introduction to the Theory of Fuzzy Subsets; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Sanchez, E. Resolution of Composite Fuzzy Relation Equations. Inf. Control 1976, 30, 38–43. [Google Scholar] [CrossRef]
- Prevot, M. Algorithm for the solution of fuzzy relations. Fuzzy Sets Syst. 1981, 5, 319–322. [Google Scholar] [CrossRef]
- Czogala, E.; Drewniak, J.; Pedryz, W. Fuzzy relation equations on a finite set. Fuzzy Sets Syst. 1982, 7, 89–101. [Google Scholar] [CrossRef]
- Higashi, M.; Klir, G.J. Resolution of finite fuzzy relation equations. Fuzzy Sets Syst. 1984, 13, 65–82. [Google Scholar] [CrossRef]
- Voskoglou, M.G. A Study of Student Learning Skills Using Fuzzy Relation Equations. Egypt. Comput. Sci. J. 2018, 42, 80–87. [Google Scholar]
- Voskoglou, M.G. Application of Fuzzy Relation Equations to Assessment of Analogical Problem Solving Skills. J. Phys. Math. Educ. 2018, 15, 122–127. [Google Scholar] [CrossRef]
- Voskoglou, M.G. Application of Fuzzy Relation Equations Student Assessment. Am. J. Appl. Math. Stat. 2018, 6, 167–171. [Google Scholar] [CrossRef]
- Voskoglou, M.G. Solving Systems of Equations with Grey Data. Int. J. Appl. Fuzzy Sets Artif. Intell. 2018, 8, 103–111. [Google Scholar]
- Voskoglou, M.G. Solving Linear Programming Problems with Grey Data. Orient. J. Phys. Sci. 2018, 3, 17–23. [Google Scholar]
- Voskoglou, M.G. Fuzzy Linear Programming. Egypt. J. Comput. Sci. 2018, 42, 1–14. [Google Scholar]
- Voskoglou, M.G. Systems of Equations with Fuzzy Coefficients. J. Phys. Sci. 2018, 23, 77–88. [Google Scholar]


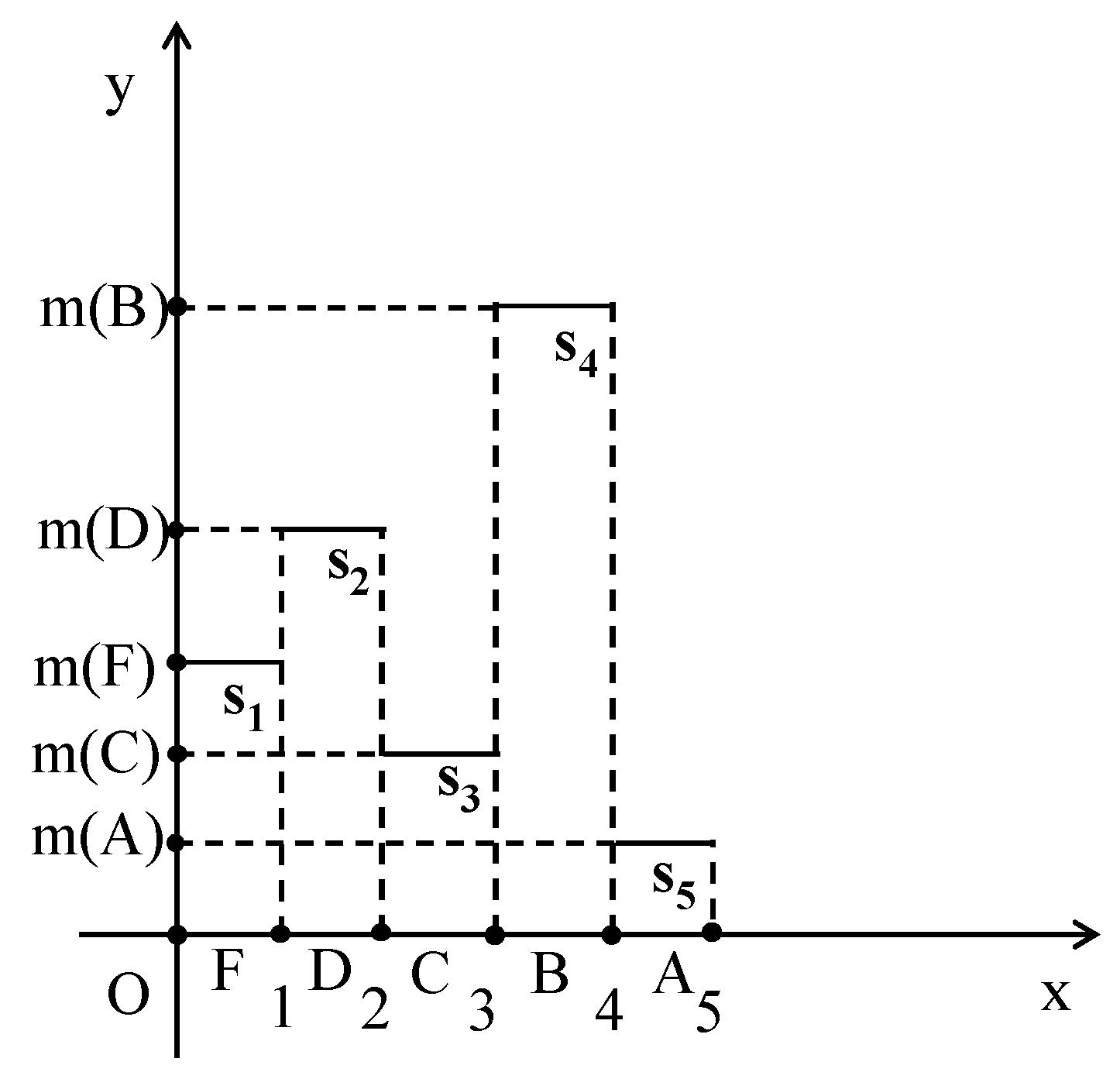

| Grade | G1 | G2 |
|---|---|---|
| A | 1 | 10 |
| B | 13 | 6 |
| C | 4 | 3 |
| D | 3 | 0 |
| F | 0 | 1 |
| Total | 21 | 20 |
| Grades | Class I | Class II |
|---|---|---|
| C | 10 | 0 |
| B | 0 | 20 |
| A | 50 | 40 |
| First system | |||||
| Steps | F | D | C | B | A |
| R1 | 0 | 0 | 51 | 24 | 30 |
| R2 | 18 | 18 | 48 | 21 | 0 |
| R3 | 36 | 30 | 39 | 0 | 0 |
| Second system | |||||
| Steps | F | D | C | B | A |
| R1 | 0 | 18 | 45 | 27 | 0 |
| R2 | 18 | 24 | 48 | 0 | 0 |
| R3 | 36 | 27 | 27 | 0 | 0 |
| Grade | No. of Students |
|---|---|
| A | 20 |
| B | 15 |
| C | 7 |
| D | 10 |
| F | 8 |
| Total | 60 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voskoglou, M.G. Methods for Assessing Human–Machine Performance under Fuzzy Conditions. Mathematics 2019, 7, 230. https://doi.org/10.3390/math7030230
Voskoglou MG. Methods for Assessing Human–Machine Performance under Fuzzy Conditions. Mathematics. 2019; 7(3):230. https://doi.org/10.3390/math7030230
Chicago/Turabian StyleVoskoglou, Michael Gr. 2019. "Methods for Assessing Human–Machine Performance under Fuzzy Conditions" Mathematics 7, no. 3: 230. https://doi.org/10.3390/math7030230
APA StyleVoskoglou, M. G. (2019). Methods for Assessing Human–Machine Performance under Fuzzy Conditions. Mathematics, 7(3), 230. https://doi.org/10.3390/math7030230




