Fractional Integrations of a Generalized Mittag-Leffler Type Function and Its Application
Abstract
1. Introduction
2. The Generalized Mittag-Leffler Type Function (GMLTF)
Special Cases
3. Fractional Integration of (13)
4. Generalized Fractional Kinetic Equations Involving GMLTF
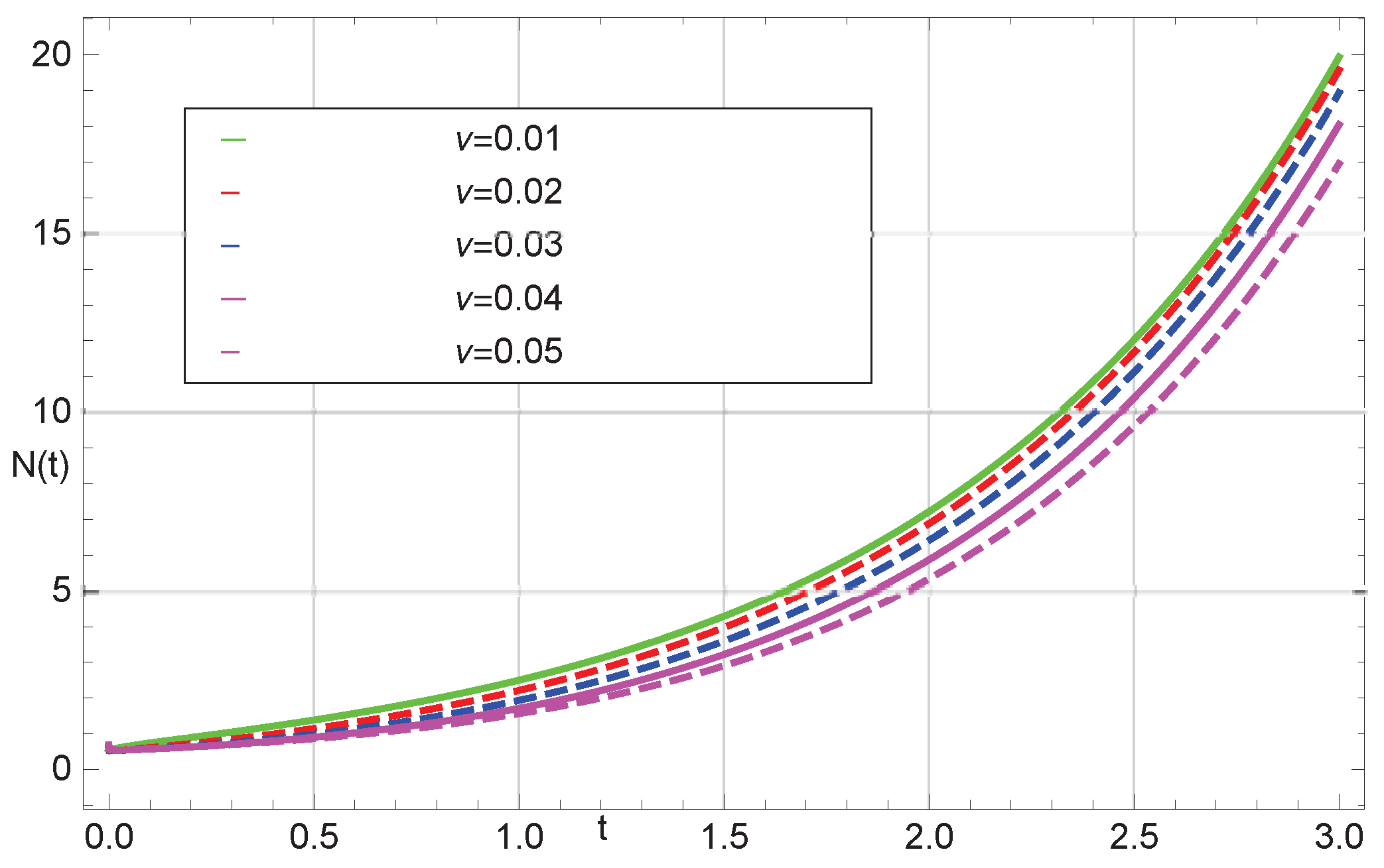
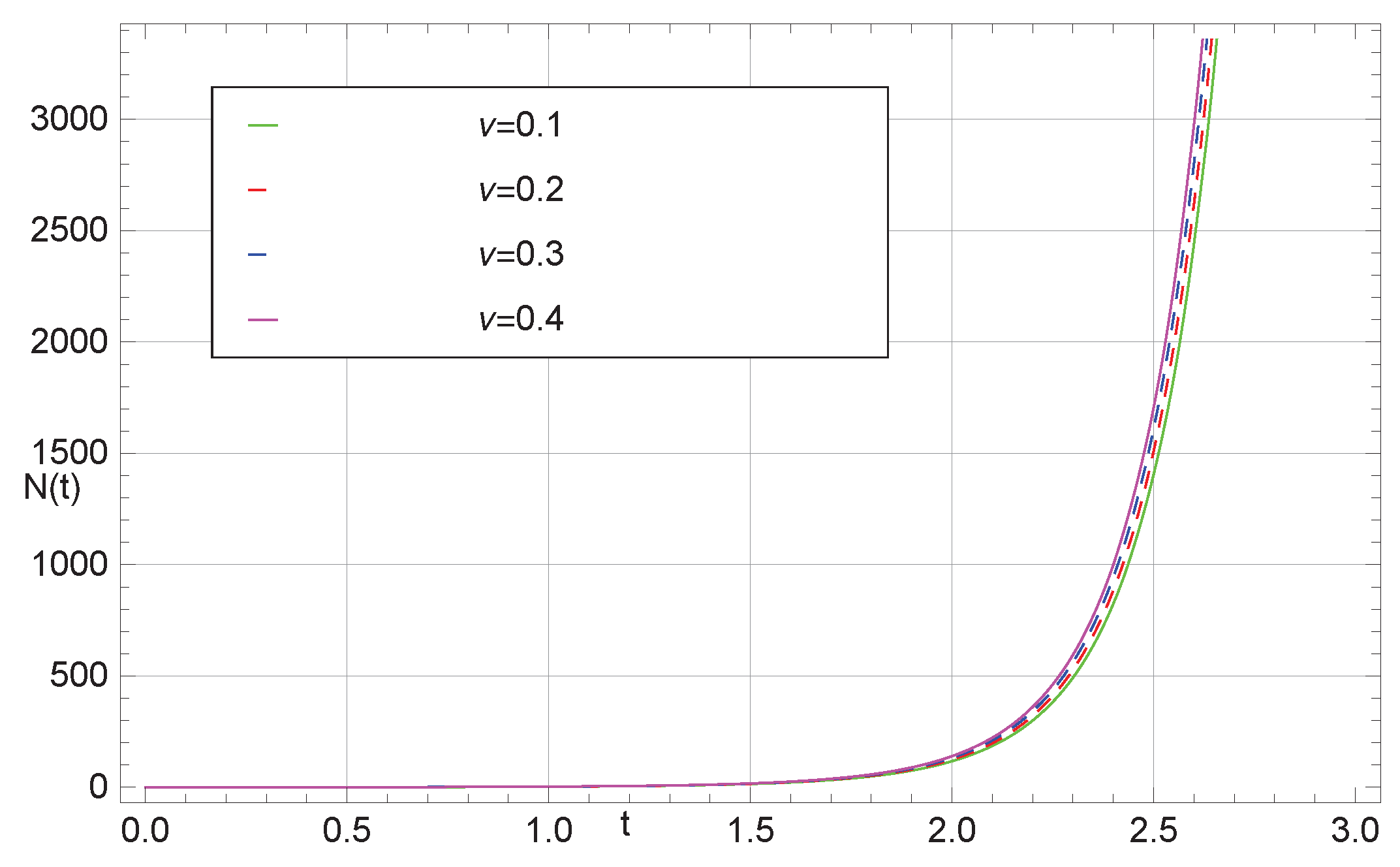
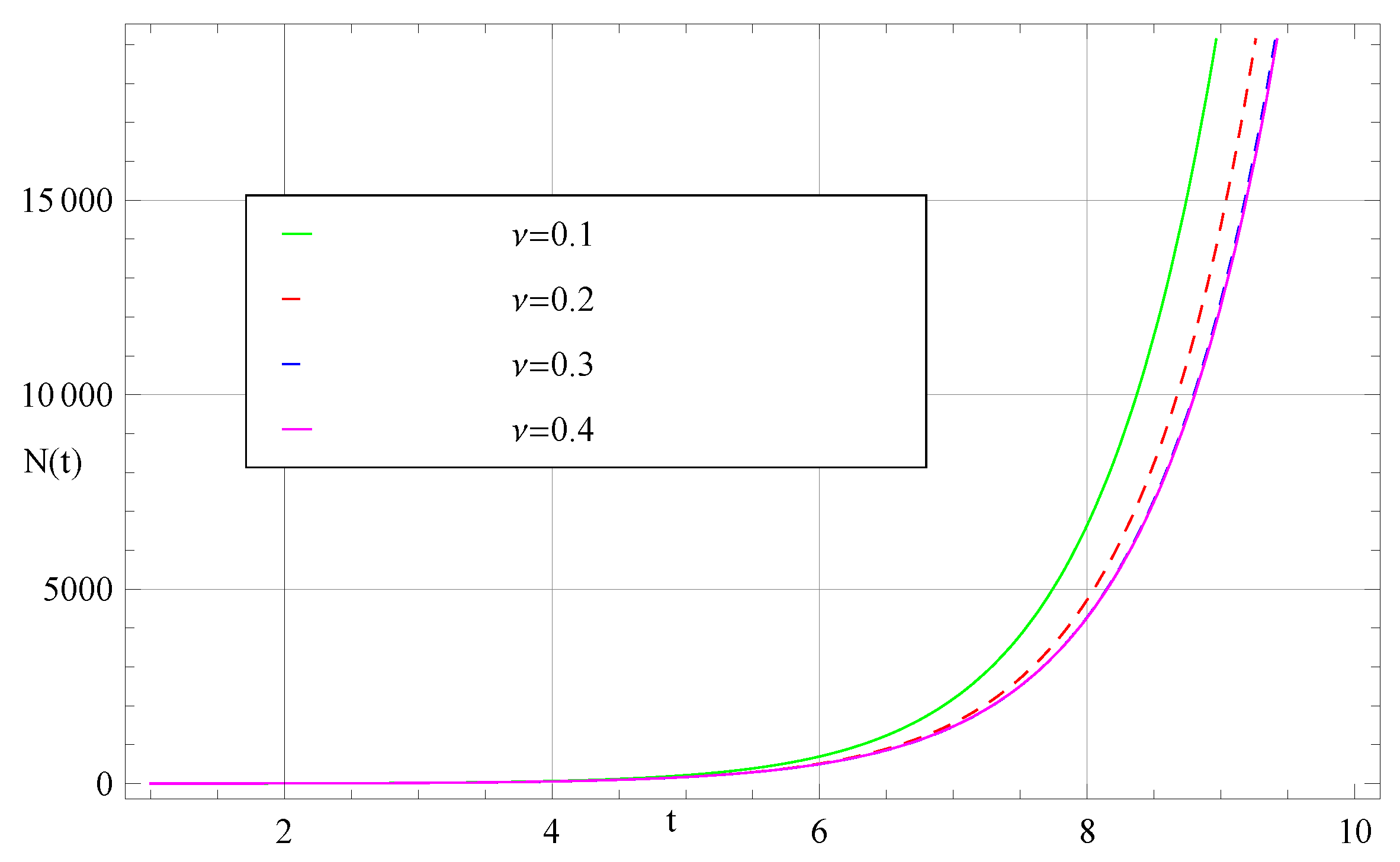
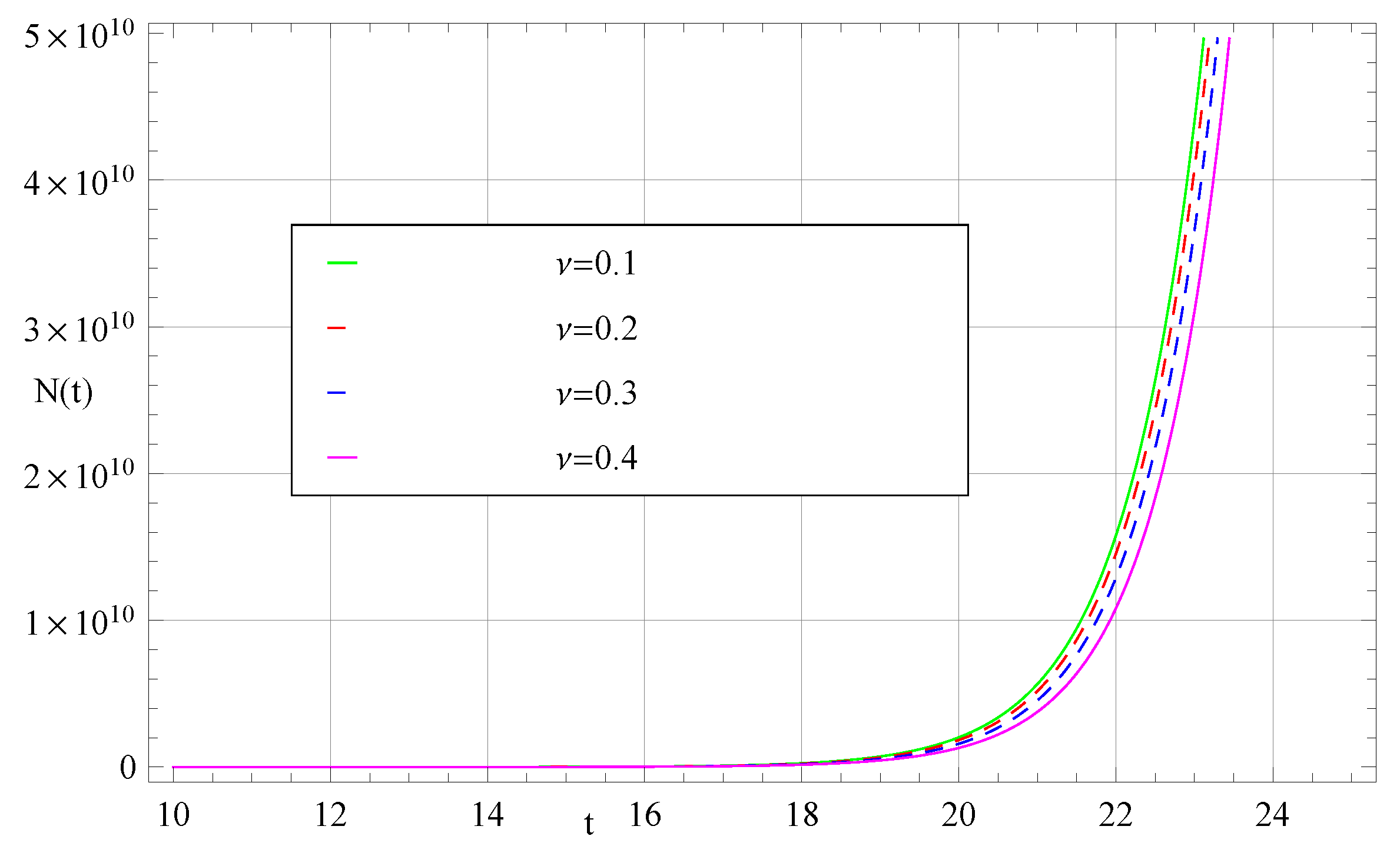
5. Graphical Results and Discussion
6. Conclusions
Funding
Conflicts of Interest
References
- Srivastava, H.M.; Choi, J. Zeta and q-Zeta Functions and Associated Series and Integrals; Elsevier Science Publishers: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 2012. [Google Scholar]
- Rainville, E.D. Special Functions; Macmillan: New York, NY, USA, 1960. [Google Scholar]
- Fox, C. The asymptotic expansion of generalized hypergeometric functions. Proc. Lond. Math. Soc. 1928, 27, 389–400. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Saigo, M.; Trujillo, J.J. On the generalized Wright function. Fract. Calc. Appl. Anal. 2002, 5, 437–460. [Google Scholar]
- Wright, E.M. The asymptotic expansion of integral functions defined by Taylor series. Philos. Trans. R. Soc. Lond. Ser. A 1940, 238, 423–451. [Google Scholar] [CrossRef]
- Wright, E.M. The asymptotic expansion of the generalized hypergeometric function. Proc. Lond. Math. Soc. 1940, 46, 389–408. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies 204; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Kilbas, A.A.; Sebastian, N. Generalized fractional integration of Bessel function of the first kind. Int. Transf. Spec. Funct. 2008, 19, 869–883. [Google Scholar] [CrossRef]
- Thakar, U.; Joshi, V.; Vyawahare, V.A. Composite non-linear feedback control using Mittag-Leffler function. Int. J. Dyn. Control 2019, 7, 785–794. [Google Scholar] [CrossRef]
- Zhou, H.C.; Lv, C.; Guo, B.Z.; Chen, Y. Mittag-Leffler stabilization for an unstable time-fractional anomalous diffusion equation with boundary control matched disturbance. Int. J. Robust Nonlinear Control 2019, 29. [Google Scholar] [CrossRef]
- Kumar, D.; Baleanu, D. Fractional Calculus and its Applications in Physics. Front. Phys. 2019, 7, 81. [Google Scholar] [CrossRef]
- Djida, J.D.; Mophou, G.; Area, I. Optimal control of diffusion equation with fractional time derivative with nonlocal and nonsingular Mittag-Leffler kernel. J. Optim. Theory Appl. 2019, 182, 540–557. [Google Scholar] [CrossRef]
- Saqib, M.; Khan, I.; Shafie, S. New direction of Atangana–Baleanu fractional derivative with Mittag-Leffler kernel for non-Newtonian channel flow. In Fractional Derivatives with Mittag-Leffler Kernel; Springer: Cham, Switzerland, 2019; pp. 253–268. [Google Scholar]
- Bhatter, S.; Mathur, A.; Kumar, D.; Nisar, K.S.; Singh, J. Fractional modified Kawahara equation with Mittag–Leffler law. Chaos Solitons Fractals 2019, 2019, 109508. [Google Scholar] [CrossRef]
- Mittag-Leffler, G.M. Sur la representation analytiqie d’une fonction monogene cinquieme note. Acta Math. 1905, 29, 101–181. [Google Scholar] [CrossRef]
- Wiman, A. Uber den fundamental satz in der theorie der funktionen Eα (z). Acta Math. 1905, 29, 191–201. [Google Scholar] [CrossRef]
- Prabhakar, T.R. A singular integral equation with a generalized Mittag-Leffler function in the Kernel. Yokohama Math. J. 1971, 19, 7–15. [Google Scholar]
- Shukla, A.K.; Prajapati, J.C. On a generalization of Mittag-Leffler function and its properties. J. Math. Anal. Appl. 2007, 336, 797–811. [Google Scholar] [CrossRef]
- Salim, T.O. Some properties relating to the generalized Mittag-Leffler function. Adv. Appl. Math. Anal. 2009, 4, 21–30. [Google Scholar]
- Salim, T.O.; Faraj, A.W. A generalization of Mittag-Leffler function and integral operator associated with fractional calculus. J. Fract. Calc. Appl. 2012, 3, 1–13. [Google Scholar]
- Khan, M.A.; Ahmed, S. On some properties of the generalized Mittag-Leffler function. SpringerPlus 2013, 2, 337. [Google Scholar] [CrossRef]
- Sharma, K. Application of fractional calculus operators to related Areas. Gen. Math. Notes 2011, 7, 33–40. [Google Scholar]
- Srivastava, H.M.; Tomovski, Z. Fractional calculus with an integral operator containing a generalized Mittag–Leffler function in the kernel. Appl. Math. Comput. 2009, 211, 198–210. [Google Scholar] [CrossRef]
- Araci, S.; Rahman, G.; Ghaffar, A.; Nisar, K.S. Fractional Calculus of Extended Mittag-Leffler Function and Its Applications to Statistical Distribution. Mathematics 2019, 7, 248. [Google Scholar] [CrossRef]
- Andrić, M.; Farid, G.; Pećarić, J. A further extension of Mittag-Leffler function. Fract. Calc. Appl. Anal. 2018, 21, 1377–1395. [Google Scholar] [CrossRef]
- Bansal, M.K.; Jolly, N.; Jain, R.; Kumar, D. An integral operator involving generalized Mittag-Leffler function and associated fractional calculus results. J. Anal. 2019, 27, 727–740. [Google Scholar] [CrossRef]
- Choi, J.; Parmar, R.K.; Chopra, P. Extended Mittag-Leffler function and associated fractional calculus operators. Georgian Math. J. 2017. [Google Scholar] [CrossRef]
- Choi, J.; Rahman, G.; Nisar, K.S.; Mubeen, S.; Arshad, M. Formulas for Saigo fractional integral operators with 2F1 generalized k -Struve functions. Far East J. Math. Sci. 2017, 102, 55–66. [Google Scholar]
- Kumar, D.; Singh, J.; Baleanu, D. A new analysis of the Fornberg-Whitham equation pertaining to a fractional derivative with Mittag-Leffler-type kernel. Eur. Phys. J. Plus. 2018, 133, 70. [Google Scholar] [CrossRef]
- Parmar, R. A Class of Extended Mittag–Leffler Functions and Their Properties Related to Integral Transforms and Fractional Calculus. Mathematics 2015, 3, 1069–1082. [Google Scholar] [CrossRef]
- Rahman, G.; Baleanu, D.; Qurashi, M.A.; Purohit, S.D.; Mubeen, S.; Arshad, M. The extended Mittag-Leffler function via fractional calculus. J. Nonlinear Sci. Appl. 2017, 10, 4244–4253. [Google Scholar] [CrossRef]
- Rahman, G.; Nisar, K.S.; Choi, J.; Mubeen, S.; Arshad, M. Pathway Fractional Integral Formulas Involving Extended Mittag-Leffler Functions in the Kernel. Kyungpook Math. J. 2019, 59, 125–134. [Google Scholar]
- Choi, J.; Rahman, G.; Mubeen, S.; Nisar, K.S. Certain extended special functions and fractional integral and derivative operators via an extended beta function. Nonlinear Funct. Anal. Appl. 2019, 24, 1–13. [Google Scholar]
- Shang, Y. Vulnerability of networks: Fractional percolation on random graphs. Phys. Rev. E 2014, 89, 012813. [Google Scholar] [CrossRef]
- Kiryakova, V. All the special functions are fractional differintegrals of elementary functions. J. Phys. A 1977, 30, 5085–5103. [Google Scholar] [CrossRef]
- Machado, J.T. Fractional derivatives and negative probabilities. Commun. Nonlinear Sci. Numer. Simul. 2019, 79, 104913. [Google Scholar] [CrossRef]
- Machado, J.T. Fractional calculus: Fundamentals and applications. In Acoustics and Vibration of Mechanical Structures—AVMS-2017, Proceedings of the 14th AVMS Conference, Timisoara, Romania, 25–26 May 2017; Springer: Cham, Switzerland, 2018; pp. 3–11. [Google Scholar]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Machado, J.T.; Galhano, A.M.; Trujillo, J.J. On development of fractional calculus during the last fifty years. Scientometrics 2014, 98, 577–582. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Srivastava, H.M.; Lin, S.-D.; Wang, P.-Y. Some fractional-calculus results for the H-function associated with a class of Feynman integrals. Russ. J. Math. Phys. 2006, 13, 94–100. [Google Scholar] [CrossRef]
- Haubold, H.J.; Mathai, A.M. The fractional kinetic equation and thermonuclear functions. Astrophys. Space Sci. 2000, 327, 53–63. [Google Scholar] [CrossRef]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. On Fractional kinetic equations. Astrophys. Space Sci. 2002, 282, 281–287. [Google Scholar] [CrossRef]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. On generalized fractional kinetic equations. Physica A 2004, 344, 657–664. [Google Scholar] [CrossRef]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. Solution of generalized fractional reaction-diffusion equations. Astrophys. Space Sci. 2006, 305, 305–313. [Google Scholar] [CrossRef]
- Saxena, R.K.; Kalla, S.L. On the solutions of certain fractional kinetic equations. Appl. Math. Comput. 2008, 199, 504–511. [Google Scholar] [CrossRef]
- Saichev, A.; Zaslavsky, M. Fractional kinetic equations: Solutions and applications. Chaos 1997, 7, 753–764. [Google Scholar] [CrossRef] [PubMed]
- Gupta, V.G.; Sharma, B.; Belgacem, F.B.M. On the solutions of generalized fractional kinetic equations. Appl. Math. Sci. 2011, 5, 899–910. [Google Scholar] [CrossRef]
- Gupta, A.; Parihar, C.L. On solutions of generalized kinetic equations of fractional order. Bol. Soc. Paran. Mat. 2014, 32, 181–189. [Google Scholar] [CrossRef]
- Nisar, K.S.; Purohit, S.D.; Mondal, S.R. Generalized fractional kinetic equations involving generalized Struve function of the first kind. J. King Saud Univ. -Sci. 2016, 28, 167–171. [Google Scholar] [CrossRef]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Tables of Integral Transforms; Based, in part, on notes left by Harry Bateman; McGraw-Hill Book Company, Inc.: New York, NY, USA; Toronto, ON, Canada; London, UK, 1954; Volume II. [Google Scholar]
- Srivastava, H.M.; Saxena, R.K. Operators of fractional integration and their applications. Appl. Math. Comput. 2001, 118, 1–52. [Google Scholar] [CrossRef]
- Shang, Y. Localized recovery of complex networks against failure. Sci. Rep. 2016, 6, 30521. [Google Scholar] [CrossRef]
- Shang, Y. Percolation on random networks with proliferation. Int. J. Mod. Phys. B 2018, 32, 1850359. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nisar, K.S. Fractional Integrations of a Generalized Mittag-Leffler Type Function and Its Application. Mathematics 2019, 7, 1230. https://doi.org/10.3390/math7121230
Nisar KS. Fractional Integrations of a Generalized Mittag-Leffler Type Function and Its Application. Mathematics. 2019; 7(12):1230. https://doi.org/10.3390/math7121230
Chicago/Turabian StyleNisar, Kottakkaran Sooppy. 2019. "Fractional Integrations of a Generalized Mittag-Leffler Type Function and Its Application" Mathematics 7, no. 12: 1230. https://doi.org/10.3390/math7121230
APA StyleNisar, K. S. (2019). Fractional Integrations of a Generalized Mittag-Leffler Type Function and Its Application. Mathematics, 7(12), 1230. https://doi.org/10.3390/math7121230




