A New Generalized Taylor-Like Explicit Method for Stiff Ordinary Differential Equations

Abstract

A new generalised Taylor-like explicit method for stiff ordinary differential equations (ODEs) is proposed. The algorithm is presented in its component and vector forms. The error and stability analysis of the method are developed showing that it has an arbitrary high order of convergence and the L-stability property. Moreover, it is verified that several integration schemes are special cases of the new general form. The method is applied on stiff problems and the numerical solutions are compared with those of the classical Taylor-like integration schemes. The results show that the proposed method is accurate and overcomes the shortcoming of the classical Taylor-like schemes in their component and vector forms.

1. Introduction

Most of the mathematical models describing real-world phenomena are often stiff ordinary differential equations (SODEs). Such problems involve a wide range of temporal scales and solving these SODEs requires careful treatment. Efficient numerical and semi-analytical numerical methods for solving stiff problems must have good accuracy, wide region of stability and low computational effort. It is well known that explicit linear multistep methods are not absolutely stable. In addition, most of the implicit methods are absolutely stable and work adequately with SODEs, but they involve a higher computational load per step than the explicit methods [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] Wu and Xia [9,10,11] presented a vector form for A-stable explicit one step Taylor-like method for solving stiff ODE systems. Wu and Xia [9] proposed a vector form for the two low accuracy methods [5] to be applied on stiff ODE systems. Wu and Xia [10] proposed a vector form for the sixth-order Taylor-like explicit method [7] to be applied on stiff ODE systems. Wu and Xia [9,10] showed the superiority of the Taylor-like methods when formulated in vector form compared to their component form. More recently, Wu and Xia [11] derived a general form of the Taylor-like explicit method and derived its corresponding vector form. One of the main advantages of using Taylor-like methods is that the approximate solution is given as an arbitrary order piecewise analytical function defended on the sub-intervals of the whole integration interval. This property offers different facility for adaptive error control [19,20]. Moreover, the Taylor-like method [11] is an arbitrary high order A-stable method that avoids extremely small stepsizes during the integration procedure. To avoid the analytical computation of the successive derivatives involved in the Taylor-like methods, numerical differentiation [21,22], automatic differentiation [23], differential transformation [24,25,26] and Infinity Computer with a new numeral system [27,28,29,30,31,32] can be used. In fact, Taylor-like explicit methods [5,7,9,10,11] have computational drawbacks with zero-component derivative or zero-vector norm in their component or vector forms, respectively. Moreover, the computational errors due to the round-off, particularly in the case of long time intervals or large time-step sizes, may lead to very small values of the derivatives or very large values of the derivatives’ ratio at some grid points. Consequently, poor results are obtained. To overcome these limitations a new generalised Taylor-like explicit method for SODEs and stiff ODE systems is present. The method is developed both in its component and vector forms. The error and stability analysis of the method are presented. It is shown that the new method has an arbitrary order of convergence and the L-stability property. Indeed, many other integration schemes are essentially special cases of the proposed general form method. The method is applied on stiff test problems and the numerical results are compared with those in the literature. The results show that the proposed method is accurate and avoids the shortcoming of the classical Taylor-like explicit methods both in their component and vector forms.

2. Generalised Taylor-Like Method

Consider the initial-value problem given by:

$$y^{\prime }\left(t\right)=f(t,y\left(t\right)),y\left(t_0\right)=y_0,$$

(1)

where $y\left(t\right),f(t,y(t\left)\right)\in \mathrm{R}$ and $t\in [t_0,T]\subset \mathrm{R}$. The interval $[t_0,T]$ is divided into sub-intervals $[t_j,t_{j+1}]$ with $t_j=t_0+jh$, such that h is the time-step size. Assume that the solution of (1) can be approximated by

$$\overline{y}\left(t\right)=a(e^{b(t-t_j)}-1)+\sum _{n=0}^m{c}_n\frac{{(t-t_j)}^n}{\mathit{n}!},a,b\ne 0,t\in [t_j,t_{j+1}],$$

(2)

where $a,b$ and $c_n$ are unknowns and determined later from the local truncation error and stability analysis of the method. By considering Taylor’s expansions of $y\left(t\right)$ and $\overline{y}\left(t\right)$ about $t_j$, we have:

$$y_{j+1}=y_j+\sum _{n=1}^{\infty }{y}_j^{\left(n\right)}\frac{h^n}{\mathit{n}!},$$

(3)

where $y_j^{\left(n\right)}=\frac{d^{n}y}{d{t}^n}\left(t_j\right)$ and

$${\overline{y}}_{j+1}=c_0+\sum _{n=1}^m(a{b}^n+c_n)\frac{h^n}{\mathit{n}!}+\sum _{n=m+1}^{\infty }a{b}^n\frac{h^n}{\mathit{n}!}.$$

(4)

The approximation in (2) is constructed so that $y_{j+1}$ and ${\overline{y}}_{j+1}$ agree and their derivatives up to order $m+1$, that is

$$\left(c_0+\sum _{n=1}^m(a{b}^n+c_n)\frac{h^n}{\mathit{n}!}+\sum _{n=m+1}^{\infty }a{b}^n\frac{h^n}{\mathit{n}!}\right)-\left(y_j+\sum _{n=1}^{\infty }{y}_j^{\left(n\right)}\frac{h^n}{\mathit{n}!}\right)=O\left(h^{m+2}\right).$$

(5)

Equating the coefficients of the same powers of $h^L$, $L=0,1,\cdots ,m+1$, in (5) by zero, results in the following system of nonlinear equations

$$\left.\begin{array}{c}{c}_0-y_j=0\hfill \\ a{b}^n+c_n-y_j^{\left(n\right)}=0,n=1,\cdots ,m\hfill \\ a{b}^{m+1}-y_j^{(m+1)}=0\hfill \end{array}\right\}.$$

(6)

Solving the first and last equations in (6) results in

$$c_0=y_j,a=\frac{y_j^{(m+1)}}{b^{m+1}}.$$

(7)

Consequently, solving the remaining equations in (6) results in

$$c_n=y_j^{\left(n\right)}-\frac{y_j^{(m+1)}}{b^{m+1-n}},n=1,\cdots ,m.$$

(8)

From (2), (7) and (8) we obtain the following integration algorithm:

$${\overline{y}}_{j+1}=y_j+\frac{y_j^{(m+1)}}{b^{m+1}}\left(e^{bh}-1\right)+\sum _{n=1}^m\left(y_j^{\left(n\right)}-\frac{y_j^{(m+1)}}{b^{m+1-n}}\right)\frac{h^n}{\mathit{n}!},\mathit{b}\ne 0.$$

(9)

2.1. Local Truncation Error

The local truncation error $T_{j+1}$ is readily obtained from subtracting (9) from the Taylor series expansion in (3) and collecting terms in h

$$T_{j+1}=\sum _{s=0}^{\infty }\left(y_j^{(m+1)}{b}^{s+1}-y_j^{(m+2+s)}\right)\frac{h^{m+2+s}}{(m+2+s)!}.$$

(10)

It is clear that relation (9) has at least $m+1$ order of accuracy.

2.2. Stability Analysis

In order to examine the integration scheme (9) for the stability, let us consider the differential equation,

$$y^{\prime }=\lambda y,$$

where $\lambda$ is a complex constant and $\mathit{Re}\left(\lambda \right)<0$. For this equation, Equation (9) results in

$$y_{j+1}=y_j+y_j\frac{{\lambda }^{m+1}}{b^{m+1}}\left(e^{bh}-1\right)+y_j\sum _{n=1}^m\left({\lambda }^n-\frac{{\lambda }^{m+1}}{b^{m+1-n}}\right)\frac{h^n}{\mathit{n}!},b\ne 0.$$

(11)

For $b=\frac{y_j^{\left(k\right)}}{y_j^{(k-1)}}=\lambda ,k=1,2,\cdots ,m+1$, Equation (11) results in

$$y_{j+1}=y_j{e}^{\lambda h}.$$

Setting $z=\lambda h$ in the above equation, the amplification factor is given by

$$R\left(z\right)=e^z$$

and thus we have obtained the following A-stable and L-stable method with at least $(m+1)$ order of accuracy

$$y_{j+1}=\sum _{n=0}^m{y}_j^{\left(n\right)}\frac{h^n}{\mathit{n}!}+y_j^{(m+1)}{\left(\frac{y_j^{(k-1)}}{y_j^{\left(k\right)}}\right)}^{m+1}\left(e^{\frac{y_j^{\left(k\right)}h}{y_j^{(k-1)}}}-\sum _{n=0}^m{\left(\frac{y_j^{\left(k\right)}h}{y_j^{(k-1)}}\right)}^n\frac{1}{\mathit{n}!}\right),y_j^{\left(k\right)}{y}_j^{(k-1)}\ne 0,$$

(12)

where $k=1,2,\cdots ,m+1$.

The local truncation error of (12) is given by

$$T_{j+1}=\sum _{s=0}^{\infty }\left(y_j^{(m+1)}{\left(\frac{y_j^{\left(k\right)}}{y_j^{(k-1)}}\right)}^{s+1}-y_j^{(m+2+s)}\right)\frac{h^{m+2+s}}{(m+2+s)!}.$$

(13)

2.3. Consistency

Subtracting $y_j$ from both sides of (12) and dividing the result by h leads to

$$\frac{y_{j+1}-y_j}{h}=y_j^{\left(1\right)}+\sum _{n=2}^m{y}_j^{\left(n\right)}\frac{h^{n-1}}{\mathit{n}!}+y_j^{(m+1)}{\left(\frac{y_j^{(k-1)}}{y_j^{\left(k\right)}}\right)}^{m+1}\left(\frac{e^{\frac{y_j^{\left(k\right)}h}{y_j^{(k-1)}}}-1}{h}-\left(\frac{y_j^{\left(k\right)}}{y_j^{(k-1)}}\right)-\sum _{n=2}^m{\left(\frac{y_j^{\left(k\right)}}{y_j^{(k-1)}}\right)}^n\frac{h^{n-1}}{\mathit{n}!}\right).$$

(14)

Taking the limit as h tends to zero, on both sides of (14), yields

$$\underset{h\to 0}{lim}\frac{y_{j+1}-y_j}{h}=y_j^{\left(1\right)}+y_j^{(m+1)}{\left(\frac{y_j^{(k-1)}}{y_j^{\left(k\right)}}\right)}^{m+1}\left(\underset{h\to 0}{lim}\frac{e^{\frac{y_j^{\left(k\right)}h}{y_j^{(k-1)}}}-1}{h}-\left(\frac{y_j^{\left(k\right)}}{y_j^{(k-1)}}\right)\right)=y_j^{\left(1\right)}=f(t_j,y_j),$$

(15)

showing that the method defined in (12) is consistent.

Thus we have the following theorem:

Theorem 1.

The generalised Taylor-like explicit method (12) is L-stable and convergent with at least $(m+1)$ order of accuracy.

For a fixed value of m and different values of k ($k=1,2,$ …, $m+1$) the method formulated in (12) results in $(m+1)$ L-stable different integration schemes with the same order of accuracy $O(m+1)$.

Remark 1.

For $m=0$ and $k=1$ the Equation (12) is reduced to

$$y_{j+1}=y_j{\mathrm{e}}^{y_{{}_j}^{\left(1\right)}/y_{j}h},y_j{y}_j^{\left(1\right)}\ne 0,$$

(16)

which is the first order L-stable method in [5,9].

Remark 2.

For $m=0$ and $k=2$ the Equation (12) is reduced to

$$y_{j+1}=y_j+\frac{{\left(y_{{}_j}^{\left(1\right)}\right)}^2}{y_{{}_j}^{\left(2\right)}}\left({\mathrm{e}}^{y_{{}_j}^{\left(2\right)}/y_{{}_j}^{\left(1\right)}h}-1\right),y_j^{\left(1\right)}{y}_j^{\left(2\right)}\ne 0,$$

(17)

which is the second order L-stable methods in [5,9].

Remark 3.

For $m=5$ and $k=6$ the Equation (12) is reduced to

$$y_{j+1}=\sum _{n=0}^5{y}_j^{\left(n\right)}\frac{h^n}{\mathit{n}!}+y_j^{\left(6\right)}{\left(\frac{y_j^{\left(5\right)}}{y_j^{\left(6\right)}}\right)}^6\left(e^{\frac{y_j^{\left(6\right)}h}{y_j^{\left(5\right)}}}-\sum _{n=0}^5{\left(\frac{y_j^{\left(6\right)}h}{y_j^{\left(5\right)}}\right)}^n\frac{1}{\mathit{n}!}\right),y_j^{\left(6\right)}{y}_j^{\left(5\right)}\ne 0,$$

(18)

which is the sixth-order L-stable method in [7].

Remark 4.

For $m=4$ and $k=6$ the Equation (12) is reduced to

$$y_{j+1}=\sum _{n=0}^4{y}_j^{\left(n\right)}\frac{h^n}{\mathit{n}!}+y_j^{\left(5\right)}{\left(\frac{y_j^{\left(5\right)}}{y_j^{\left(6\right)}}\right)}^6\left(e^{\frac{y_j^{\left(6\right)}h}{y_j^{\left(5\right)}}}-\sum _{n=0}^4{\left(\frac{y_j^{\left(6\right)}h}{y_j^{\left(5\right)}}\right)}^n\frac{1}{\mathit{n}!}\right),y_j^{\left(6\right)}{y}_j^{\left(5\right)}\ne 0,$$

(19)

which is the sixth-order L-stable method in [9].

Remark 5.

For $m=5$ and $k=7$ the Equation (12) is reduced to

$$y_{j+1}=\sum _{n=0}^5{y}_j^{\left(n\right)}\frac{h^n}{\mathit{n}!}+y_j^{\left(6\right)}{\left(\frac{y_j^{\left(6\right)}}{y_j^{\left(7\right)}}\right)}^6\left(e^{\frac{y_j^{\left(7\right)}h}{y_j^{\left(6\right)}}}-\sum _{n=0}^5{\left(\frac{y_j^{\left(7\right)}h}{y_j^{\left(6\right)}}\right)}^n\frac{1}{\mathit{n}!}\right),y_j^{\left(6\right)}{y}_j^{\left(7\right)}\ne 0,$$

(20)

which is the seventh-order L-stable method in [8].

Remark 6.

When k is set to $m+2$, Equation (12) is reduced to

$$y_{j+1}=\sum _{n=0}^m{y}_j^{\left(n\right)}\frac{h^n}{\mathit{n}!}+y_j^{(m+1)}{\left(\frac{y_j^{(m+1)}}{y_j^{(m+2)}}\right)}^{m+1}\left(e^{\frac{y_j^{(m+2)}h}{y_j^{(m+1)}}}-\sum _{n=0}^m{\left(\frac{y_j^{(m+2)}h}{y_j^{(m+1)}}\right)}^n\frac{1}{\mathit{n}!}\right),y_j^{(m+2)}{y}_j^{(m+1)}\ne 0,$$

(21)

and the local truncation error (13) is reduced to

$$T_{j+1}=\sum _{s=0}^{\infty }\left(y_j^{(m+1)}{\left(\frac{y_j^{(m+2)}}{y_j^{(m+1)}}\right)}^{s+2}-y_j^{(m+3+s)}\right)\frac{h^{m+3+s}}{(m+3+s)!},$$

(22)

that is the classical general form of Taylor-like $m+2$ order L-stable method in [11].

3. Extension to Vector Form

The method (12) can also be extended directly to systems of ODEs by using the new definitions of vector product and quotient defined in [9,12] as

$$b.{\left(\frac{a}{b}\right)}^n=\left\{\begin{array}{c}\frac{{\rho }^n-{\kappa }^n}{\rho -\kappa }a+\frac{\rho {\kappa }^n-\kappa {\rho }^n}{\rho -\kappa }b,\rho \ne \kappa \hfill \\ n{\rho }^{n-1}a-(n-1){\rho }^{n}b,\rho =\kappa \hfill \end{array}\right.,n=1,2,\cdots$$

(23)

$$b.e^{a/b}=\left\{\begin{array}{c}\frac{e^{\rho }-e^{\kappa }}{\rho -\kappa }a+\frac{\rho e^{\kappa }-\kappa e^{\rho }}{\rho -\kappa }b,\rho \ne \kappa \hfill \\ e^{\rho }a+(1-\rho )e^{\rho }b,\rho =\kappa \hfill \end{array},\right.$$

(24)

where $a,b\in C^m$ and $\rho =\frac{1}{2}\left(\beta +\sqrt{{\beta }^2+4\alpha }\right),\kappa =\frac{1}{2}\left(\beta -\sqrt{{\beta }^2+4\alpha }\right),\alpha =-\frac{(a,a)}{(b,b)},\beta =2\frac{Re(a,b)}{(b,b)}$.

The vector version of the proposed method is of the form

$$y_{j+1}=\sum _{n=0}^m{y}_j^{\left(n\right)}\frac{h^n}{n!}+y_j^{\left(k\right)}.{\left(\frac{y_j^{(k-1)}}{y_j^{\left(k\right)}}\right)}^m.\left(y_j^{(k-1)}.e^{\frac{y_j^{\left(k\right)}h}{y_j^{(k-1)}}}-\sum _{n=0}^m{y}_j^{(k-1)}.{\left(\frac{y_j^{\left(k\right)}h}{y_j^{(k-1)}}\right)}^n\frac{1}{n!}\right).\frac{y_j^{(m+1)}}{{\left(y_j^{\left(k\right)}\right)}^2},$$

(25)

where ${∥y_j^{\left(k\right)}∥}_2\times {∥y_j^{(k-1)}∥}_2\ne 0$.

The local truncation error of (25) is given by

$$T_{j+1}=\epsilon +\sum _{s=0}^{\infty }\left(y_j^{(m+1)}{\left(\frac{y_j^{\left(k\right)}}{y_j^{(k-1)}}\right)}^{s+1}-y_j^{(m+2+s)}\right)\frac{h^{m+2+s}}{(m+2+s)!},$$

(26)

where $\epsilon$ is a vector and ${∥\epsilon ∥}_2=O\left(h^{m+3}\right)$. The error in (26) is derived in a similar way as in [9,10]. The case $k=m+2$ can be found in [11]. It is clear that the new method can overcome the restrictions in the classical Taylor-like explicit method in its component applicable form (i.e., $y_j^{(m+2)}{y}_j^{(m+1)}\ne 0$) and in its vector applicable form (i.e., $∥y_j^{(m+2)}∥\times ∥y_j^{(m+1)}∥\ne 0$). With the proposed method, the value of k can be adapted automatically to use any arbitrary pairs $y_j^{\left(k\right)}{y}_j^{(k-1)}\ne 0$, or $∥y_j^{\left(k\right)}∥\times ∥y_j^{(k-1)}∥\ne 0$, $k=1,2,$ …, $m+1$, while maintaining the order of convergence and the L-stability property.

4. Numerical Results

In this section, we provide six numerical experiments to illustrate the theoretical results obtained in Section 2 and Section 3. All numerical experiments are carried out using Matlab 8.3. The test problems were collected from the literature and the results are compared in the follow-up.

Problem 1.

Consider the following SODE [8]:

$$y^{\prime }\left(t\right)=-100y\left(t\right)+99e^{2t},y\left(0\right)=0.$$

(27)

The theoretical solution of (27) is given by

$$y\left(t\right)=\frac{33}{34}\left(e^{2t}-e^{-100t}\right).$$

(28)

Problem 1 is solved numerically using the generalised Taylor-like method (GTL) in its component form. The results are shown in Table 1, Table 2 and Table 3. Table 1 compares the solution error presented in [8] using the seventh order Sin and Explicit Taylor-like methods (STL7 and ETL7) with one given by the new method of seventh order (GTL7) having $m=6$ and $k=7$. The results show that the GTL7 leads to a more accurate solution than the STL7 and ETL7. Table 2 lists the maximum solution error $E_{max}=\underset{0\le t_i\le 0.5}{max}\left|y\left(t_i\right)-y_i\right|$ using the time-step size $h=0.05$ at different values of m and k, $k\le m+1$. The results show that as the order $m+1$, or the value of k, increases, the solution error decreases. Moreover, increasing k is more effective than increasing m for improving the solution accuracy, and setting $k=m+1$ leads to more accurate results. Table 3 shows the computed order of convergence at different values of m and k using two different step sizes $h=\left\{0.1,0.05\right\}$. The results confirm that the order of convergence depends only on the value of m for all values of $k\le m+1$. Figure 1 shows the exact and numerical solutions of Problem 1 at $h=0.05$. Figure 2 shows the behaviour of the solution error of different-order GTL component form at $h=0.05$.

Table 1. Comparison of the solution error for the STL7, ETL7 and GTL7 in the solution of Problem 1.

	Error $\left|\mathit{y}\left({\mathit{t}}_{\mathit{i}}\right)-{\mathit{y}}_{\mathit{i}}\right|$
	$\mathit{h}=\mathbf{0.025}$			$\mathit{h}=\mathbf{0.05}$
${\mathit{t}}_{\mathit{i}}$	STL7 [8]	ETL7 [8]	GTL7	STL7 [8]	ETL7 [8]	GTL7
0.05	8.883 × 10−2	2.676 × 10−10	1.484 × 10−12	4.920 × 10−1	1.813 × 10−8	2.505 × 10−10
0.10	9.326 × 10−3	2.938 × 10−10	1.777 × 10−12	2.427 × 10−1	2.016 × 10−8	2.785 × 10−10
0.15	9.204 × 10−4	2.753 × 10−10	1.965 × 10−12	1.214 × 10−1	2.228 × 10−8	3.078 × 10−10
0.20	9.045 × 10−5	3.559 × 10−10	2.172 × 10−12	6.073 × 10−2	2.444 × 10−8	3.402 × 10−10
0.25	8.886 × 10−6	3.453 × 10−11	2.482 × 10−12	3.037 × 10−2	2.476 × 10−8	3.851 × 10−10
0.30	8.711 × 10−7	3.449 × 10−11	3.548 × 10−13	1.519 × 10−2	2.691 × 10−8	4.912 × 10−10
0.35	8.325 × 10−8	3.754 × 10−11	5.329 × 10−15	7.597 × 10−3	2.967 × 10−8	5.333 × 10−10
0.40	4.195 × 10−9	3.967 × 10−11	4.441 × 10−16	3.800 × 10−3	3.279 × 10−8	5.910 × 10−10
0.45	1.247 × 10−10	1.826 × 10−11	4.441 × 10−16	1.900 × 10−3	3.623 × 10−8	6.529 × 10−10
0.50	2.690 × 10−1	1.613 × 10−11	4.441 × 10−16	9.506 × 10−4	4.005 × 10−8	7.216 × 10−10

Table 2. Maximum solution error for different values of m and k, $k\le m+1$.

	Error ${\mathit{E}}_{max}$
$\mathit{k}$	$\mathit{m}=\mathbf{3}$	$\mathit{m}=\mathbf{4}$	$\mathit{m}=\mathbf{5}$	$\mathit{m}=\mathbf{6}$
2	3.1315 × 10−1	3.6102 × 10−1	2.4102 × 10−1	2.1939 × 10−1
3	6.2574 × 10−3	7.2204 × 10−3	4.8204 × 10−3	4.3878 × 10−3
4	1.3071 × 10−4	1.4431 × 10−4	9.6410 × 10−5	8.7756 × 10−5
5		2.9867 × 10−6	1.9267 × 10−6	1.7551 × 10−6
6			4.0047 × 10−8	3.5082 × 10−8
7				7.2161 × 10−10

Table 3. Computed order of convergence for different values of m and k, $k\le m+1$.

	Order of Convergence
$\mathit{k}$	$\mathit{m}=\mathbf{3}$	$\mathit{m}=\mathbf{4}$	$\mathit{m}=\mathbf{5}$	$\mathit{m}=\mathbf{6}$
2	3.7000	4.6003	5.9730	6.6588
3	3.6993	4.6003	5.9730	6.6588
4	3.7300	4.5997	5.9730	6.6588
5		4.6310	5.9727	6.6589
6			5.9898	6.6583
7				6.6845

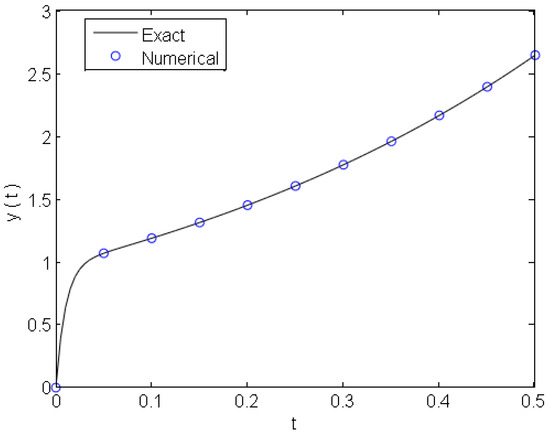
Figure 1. Exact and numerical solutions of Problem 1.

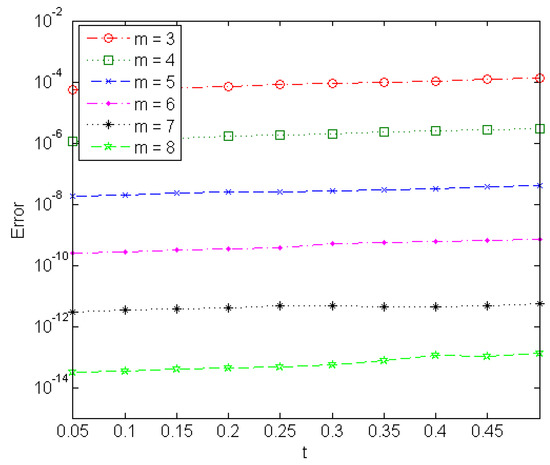
Figure 2. Solution error of different-order generalised Taylor-like method (GTL) in solving Problem 1 at $h=0.05$.

Problem 2.

Consider the oscillating SODE [17]:

$$y^{\prime }\left(t\right)=1-2\pi sin\left(2\pi t\right)-\frac{1}{\epsilon }\left(y-t-cos\left(2\pi t\right)\right),y\left(0\right)=1,t\in [0,0.5],$$

(29)

where ε is a parameter controlling the stiffness.

The theoretical solution is given by

$$y\left(t\right)=t+cos\left(2\pi t\right).$$

(30)

From the theoretical point of view, we have $y^{\left(k\right)}\left(0\right)=0,k=3,5,7,\cdots$, which results in the computational overflow when adopting the high order classical ETL method. Problem 2 is solved numerically at $\epsilon =1/200$ using the GTL component form with forth, fifth and sixth orders (i.e., the GTL4, GTL5, GTL6). The solution error, maximum solution error and the computed order of convergence are listed in Table 4. The results show that the GTL is not only stable and accurate but also overcomes the overflow in computation at $t=0$ by reducing the value of k from 6 to 2, without losing the convergence order and the L-stability property. Figure 3 shows the exact and numerical solutions at $h=0.05$. Figure 4 depicts the solution error of different-order GTL component form at $h=0.05$. In fact, since the GTL overcomes the overflow in computations by reducing the value of k, the accuracy may be little decreased while the order of convergence remains constant. Being that the effect occurs more in the component than in the vector form, we conclude that the component form GTL is more suitable for scalar stiff problems than for stiff ODE systems where the GTL vector form can be applied.

Table 4. Numerical results for problem 2 using the component form of GTL4, GTL5 and GTL6.

	Error $\left|\mathit{y}\left({\mathit{t}}_{\mathit{i}}\right)-{\mathit{y}}_{\mathit{i}}\right|$
	$\mathit{h}=\mathbf{0.05}$			$\mathit{h}=\mathbf{0.025}$
${\mathit{t}}_{\mathit{i}}$	GTL4	GTL5	GTL6	GTL4	GTL5	GTL6
0.05	1.1805 × 10−4	1.3329 × 10−6	2.9825 × 10−7	3.4591 × 10−5	2.2243 × 10−7	1.9292 × 10−8
0.10	1.2102 × 10−3	1.4098 × 10−4	4.2739 × 10−6	1.0607 × 10−4	5.0636 × 10−6	7.8031 × 10−8
0.15	1.9675 × 10−3	1.4222 × 10−4	7.0659 × 10−6	1.5377 × 10−4	4.6107 × 10−6	1.1578 × 10−7
0.20	2.5142 × 10−3	9.4632 × 10−5	9.1280 × 10−6	1.8598 × 10−4	2.6845 × 10−6	1.4094 × 10−7
0.25	2.8145 × 10−3	3.7845 × 10−5	1.0296 × 10−5	1.9994 × 10−4	5.0224 × 10−7	1.5220 × 10−7
0.30	2.8391 × 10−3	2.2603 × 10−5	1.0456 × 10−5	1.9429 × 10−4	1.8512 × 10−6	1.4851 × 10−7
0.35	2.5857 × 10−3	8.1111 × 10−5	9.5920 × 10−6	1.6959 × 10−4	3.8450 × 10−6	1.3023 × 10−7
0.40	2.0791 × 10−3	1.3136 × 10−4	7.7892 × 10−6	1.2825 × 10−4	5.5345 × 10−6	9.9157 × 10−8
0.45	1.3689 × 10−3	1.6884 × 10−4	5.2238 × 10−6	7.4287 × 10−5	6.6865 × 10−6	5.8272 × 10−8
0.50	5.2450 × 10−4	1.8981 × 10−4	2.1466 × 10−6	1.2760 × 10−5	7.1855 × 10−6	1.1294 × 10−8
$E_{max}$	2.8391 × 10−3	1.8981 × 10−4	1.0456 × 10−5	1.9994 × 10−4	7.1855 × 10−6	1.5220 × 10−7
Order	3.8278	4.7233	6.1019

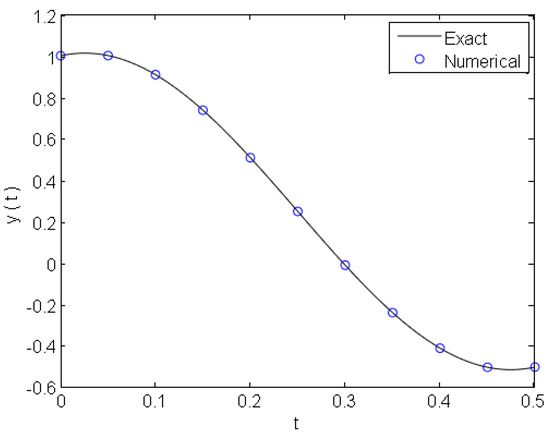
Figure 3. Exact and numerical solutions of Problem 2.

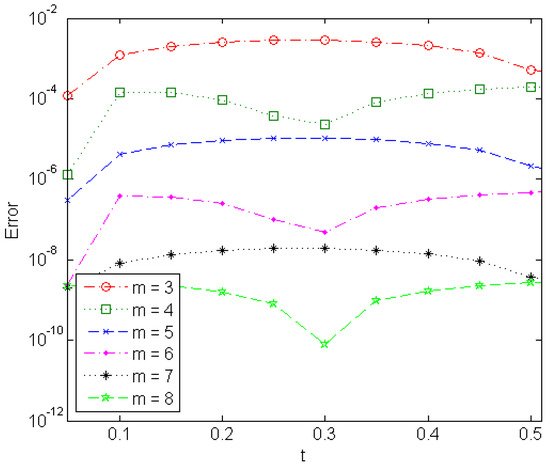
Figure 4. Solution error of different-order GTL in solving Problem 2 at $h=0.05$.

Problem 3.

Consider the following stiff ODE system [7,10,16]:

$$\begin{array}{c}{y}_1^{{}^{\prime }}=-20y_1-0.25y_2-19.75y_3,y_1\left(0\right)=1\hfill \\ y_2^{{}^{\prime }}=20y_1-20.25y_2-0.25y_3,y_2\left(0\right)=0\hfill \\ y_3^{{}^{\prime }}=20y_1-19.75y_2-0.25y_3,y_3\left(0\right)=-1.\hfill \end{array}$$

(31)

The theoretical solution is given by

$$\begin{array}{c}{y}_1=0.5\left[e^{-0.5t}+e^{-20t}(sin\left(20t\right)+cos\left(20t\right))\right]\hfill \\ y_2=0.5\left[e^{-0.5t}+e^{-20t}(sin\left(20t\right)-cos\left(20t\right))\right]\hfill \\ y_3=0.5\left[e^{-0.5t}-e^{-20t}(sin\left(20t\right)+cos\left(20t\right))\right].\hfill \end{array}$$

(32)

Due to the round-off error in computations, the ratio between $y_j^6$ and $y_j^5$, $j=2,3$ may be very large at some grid points and the classical component form of the ETL6 [7,10] results in low accuracy, or even in an overflow, as shown in Table 5. On the other hand, the present component form of the GTL6 can overcome this drawback easily by reducing the value of k from 6 to 5 for $h=\{0.01,0.1\}$ at $t=\{0.55,0.3\}$, respectively. Table 6 reveals that the vector forms of the ETL6 and GTL6 can overcome the overflow in computations with the component form of the ETL6 at $h=0.1$ and both of them have accurate results since there are no vectors with zero norms. Figure 5 depicts the exact and numerical solutions at $h=0.1$. Figure 6 and Figure 7 show the solution error of different-order vector form GTL at $h=0.1$ and $h=0.01$ respectively.

Table 5. Numerical results for Problem 3 using the component forms of the ETL6 and GTL6.

t	h	Y	Theoretical Results	Numerical Results
				ETL6 [7]		Present GTL6
				Solution	Error	Solution	Error
50	0.01	$y_1$	6.943971932482010 × 10−12	1.750801573149305 × 10−10	1.68 × 10−10	6.943971918388283 × 10−12	1.41 × 10−20
		$y_2$	6.943971932482010 × 10−12	1.750801573149305 × 10−10	1.68 × 10−10	6.943971918388283 × 10−12	1.41 × 10−20
		$y_3$	−6.943971932482010 × 10−12	−1.750801573149305 × 10−10	1.68 × 10−10	−6.943971918388284 × 10−12	1.41 × 10−20
100	0.1	$y_1$	9.643749239819589 × 10−23			9.643749274555274 × 10−23	3.47 × 10−31
		$y_2$	9.643749239819589 × 10−23	Overflow		9.643749274555277 × 10−23	3.47 × 10−31
		$y_3$	−9.643749239819589 × 10−23			−9.643749274555273 × 10−23	3.47 × 10−31

Table 6. Numerical results for Problem 3 using the vector forms of the ETL6 and GTL6 methods.

t	h	Y	Theoretical Results	Numerical Results
				ETL6 [10]		Present GTL6
				Solution	Error	Solution	Error
100	0.1	$y_1$	9.643749239819589 × 10−23	9.643749287321430 × 10−23	4.75 × 10−31	9.643749301944275 × 10−23	6.21 × 10−31
		$y_2$	9.643749239819589 × 10−23	9.643749287321430 × 10−23	4.75 × 10−31	9.643749301944272 × 10−23	6.21 × 10−31
		$y_3$	−9.643749239819589 × 10−23	−9.643749287321429 × 10−23	4.75 × 10−31	−9.643749301944270 × 10−23	6.21 × 10−31

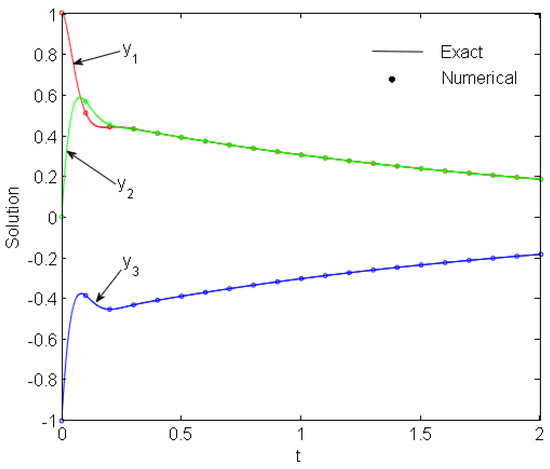
Figure 5. Exact and numerical solutions of Problem 3.

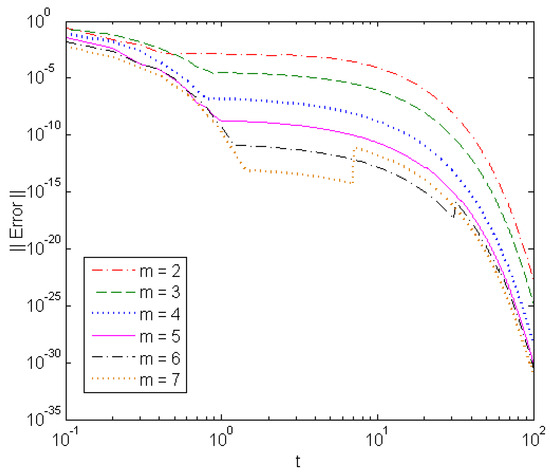
Figure 6. Solution error of different-order GTL in solving Problem 2 at $h=0.1$.

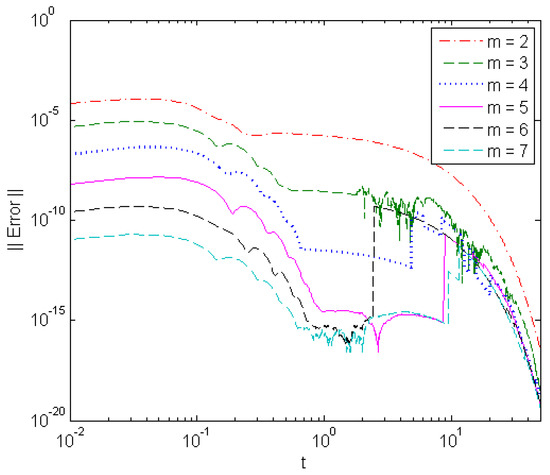
Figure 7. Solution error of different-order GTL in solving Problem 2 at $h=0.01$.

Problem 4.

Consider the following stiff ODE system [2,13,15].

$$\begin{array}{c}{y}_1^{{}^{\prime }}=2y_1+y_2+2sin\left(t\right),y_1\left(0\right)=2,\hfill \\ y_2^{{}^{\prime }}=998y_1-999y_2+999\left(cos\left(t\right)-sin\left(t\right)\right),y_2\left(0\right)=3.\hfill \end{array}$$

(33)

The theoretical solution is given by

$$\begin{array}{c}{y}_1=2e^{-t}+sin\left(t\right)\hfill \\ y_2=2e^{-t}+cos\left(t\right).\hfill \end{array}$$

(34)

Problem 4 is solved using both the component and vector forms of the ETL6 and GTL6. The numerical results are listed in Table 7 and Table 8. Table 7 shows that the component form GTL6 results in more accurate results than the ETL6 for $h=0.005$. Furthermore, the GTL6 can overcome the overflow in computations for $h=0.001$ by reducing the value of k from 6 to 5 at $t=0.283$. Table 8 shows that the vector form GTL6 leads to the same results as ETL6 for $h=0.01$ due to the absence of zero-vector norms. For $h=0.005$, ETL6 exhibits an overflow while GTL6 overcomes this overflow by reducing the value of k from 6 to 5 at $t=76.93$. Figure 8 shows the exact and numerical solutions at $h=0.1$. Figure 9, Figure 10 and Figure 11 illustrate the solution error of different-order vector form GTL at $h=0.001,0.005$ and $0.1$, respectively.

Table 7. Numerical results for Problem 4 using the component form of the ETL6 and GTL6.

t	h	Y	Theoretical Results	Numerical Results
				ETL6		GTL6
				Solution	Error	Solution	Error
4	0.005	$y_1$	−7.201712175304599 × 10−1	−7.285780200859474 × 10−1	8.41 × 10−3	−7.201712175725966 × 10−1	4.21 × 10−11
		$y_2$	−6.170123430861436 × 10−1	−6.254191456416346 × 10−1	8.41 × 10−3	−6.170123431282837 × 10−1	4.21 × 10−11
2	0.001	$y_1$	1.179967993298907	Overflow		1.179967993029105	2.70 × 10−10
		$y_3$	−1.454762700739170 × 10−1			−1.454762703437013 × 10−1	2.70 × 10−10

Table 8. Numerical results for Problem 4 using the vector form of the ETL6 and GTL6 methods.

t	h	Y	Theoretical Results	Numerical Results
				ETL6		GTL6
				Solution	Error	Solution	Error
10	0.01	$y_1$	−5.439303110298448 × 10−1	−5.439303110059717 × 10−1	2.39 × 10−11	−5.439303110059727 × 10−1	2.39 × 10−11
		$y_2$	−8.389807292169275 × 10−1	−8.389807291935291 × 10−1	2.34 × 10−11	−8.389807291935302 × 10−1	2.34 × 10−11
100	0.005	$y_1$	−5.063656411097588 × 10−1	Overflow		−5.063656411196315 × 10−1	9.87 × 10−12
		$y_3$	8.623188722876839 × 10−1			8.623188722778098 × 10−1	9.87 × 10−12

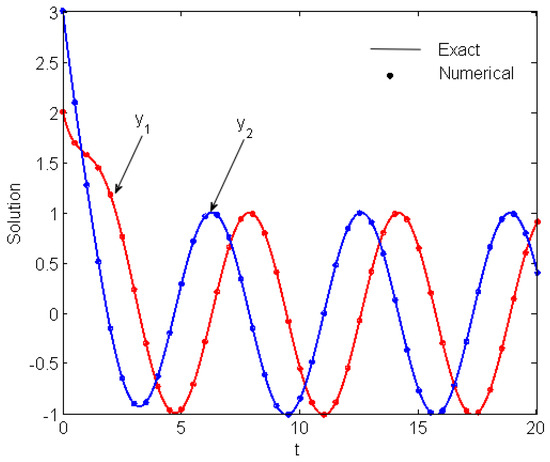
Figure 8. Exact and numerical solutions of Problem 4.

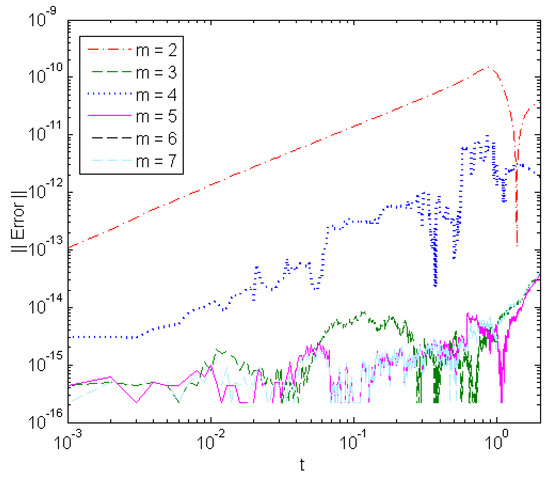
Figure 9. Solution error of different-order GTL in solving Problem 4 at $h=0.001$.

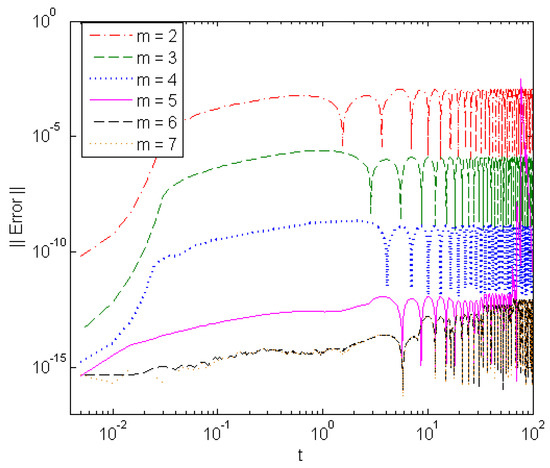
Figure 10. Solution error of different-order GTL in solving Problem 4 at $h=0.005$.

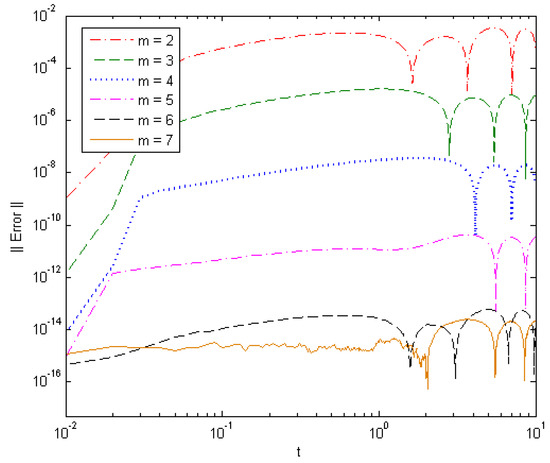
Figure 11. Solution error of different-order GTL method in solving Problem 4 at $h=0.1$.

Problem 5.

Consider the following nonlinear stiff ODE system [10]:

$$\begin{array}{c}{y}_1^{{}^{\prime }}=-1002y_1+1000y_2^2,y_1\left(0\right)=1,\hfill \\ y_2^{{}^{\prime }}=y_1-y_2(1+y_2),y_2\left(0\right)=1,\hfill \\ y_3^{{}^{\prime }}=y_2-2y_3,y_3\left(0\right)=1-\frac{e^{0.01}}{64}.\hfill \end{array}$$

(35)

The theoretical solution is given by

$$\begin{array}{c}{y}_1=e^{-2t},\hfill \\ y_2=e^{-t},\hfill \\ y_3=e^{-t}-\frac{e^{0.01-2t}}{64}.\hfill \end{array}$$

(36)

Table 9 and Table 10 compare the results achieved by ETL6 [7,10] with those obtained by GTL6. From the theoretical point of view, $y_3^{\left(6\right)}=0$ at $t=0.01$ and so, as shown in Table 9, the component form ETL6 results in computational overflow, while THE GTL6 overcomes the overflow in computations at zero derivative component by changing the value of k from 6 to 5 at $t=0.01$. Table 10 shows that both the ETL6 and GTL6 have the same accurate results in their vector forms due to the absence of zero-vector norms. Figure 12 shows the exact and numerical solutions at $h=0.01$. Figure 13 depicts the solution error of different-order vector form GTL at $h=0.01$.

Table 9. Numerical results for Problem 5 using the component forms of the ETL6 and GTL6 methods.

t	h	Y	Theoretical Results	Numerical Results
				ETL6 [7]		GTL6
				Solution	Error	Solution	Error
10	0.01	$y_1$	2.061153622438558 × 10−9			2.219610845565104 × 10−9	1.59 × 10−10
		$y_2$	4.539992976248485 × 10−5	Overflow		4.711274610485264 × 10−5	1.71 × 10−6
		$y_3$	4.539989723328859 × 10−5			4.711104436407183 × 10−5	1.71 × 10−6

Table 10. Numerical results for Problem 5 using the vector forms of the ETL6 and GTL6 methods.

t	h	Y	Theoretical Results	Numerical Results
				ETL6 [10]		GTL6
				Solution	Error	Solution	Error
10	0.01	$y_1$	2.061153622438558 × 10−9	2.061153624612472 × 10−9	2.17 × 10−18	2.061153624612640 × 10−9	2.17 × 10−18
		$y_2$	4.539992976248485 × 10−5	4.539992977820482 × 10−5	1.57 × 10−14	4.539992977820673 × 10−5	1.57 × 10−14
		$y_3$	4.539989723328859 × 10−5	4.539989724900820 × 10−5	1.57 × 10−14	4.539989724901008 × 10−5	1.57 × 10−14

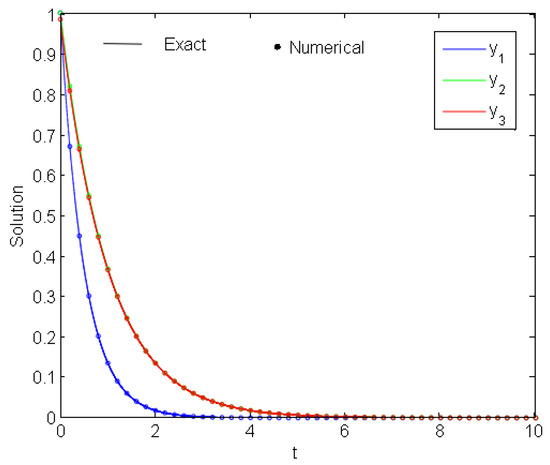
Figure 12. Exact and numerical solutions of Problem 5.

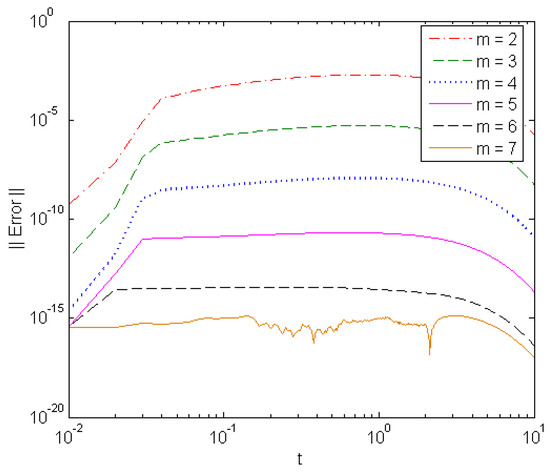
Figure 13. Solution error of different-order GTL in solving Problem 5 at $h=0.01$.

Problem 6.

Consider the following nonlinear chemical reaction system involving eight reactants [1]:

$$\begin{array}{c}{y}_1^{\prime }=-1.71y_1+0.43y_2+8.32y_3+0.0007,\hfill \\ y_2^{\prime }=1.71y_1-8.75y_2,\hfill \\ y_3^{\prime }=-10.03y_3+0.43y_4+0.035y_5,\hfill \\ y_4^{\prime }=8.32y_2+1.71y_3-1.12y_4,\hfill \\ y_5^{\prime }=-1.745y_5+0.43y_6+0.43y_7,\hfill \\ y_6^{\prime }=-280y_6{y}_8+0.69y_4+1.71y_5-0.43y_6+0.69y_7,\hfill \\ y_7^{\prime }=280y_6{y}_8-1.81y_7,\hfill \\ y_8^{\prime }=-y_7^{\prime },\hfill \end{array}$$

(37)

with initial conditions $y_1\left(0\right)=1,y_2\left(0\right)=y_3\left(0\right)=y_4\left(0\right)=y_5\left(0\right)=y_6\left(0\right)=y_7\left(0\right)=y_8\left(0\right)=0$.

This problem has no known analytical solution, and therefore, a numerical approximate solution using the built in BVP4C MATLAB solver [33,34,35] is taken as the reference solution for comparison. The problem is solved using different-order vector form GTL at $h=0.1$ and the solution error is represented in Figure 14 at $h=0.1$. The same results are obtained using the ETL due to the absence of zero derivatives or zero vectors. Moreover, the exact and numerical solutions are illustrated in Figure 15.

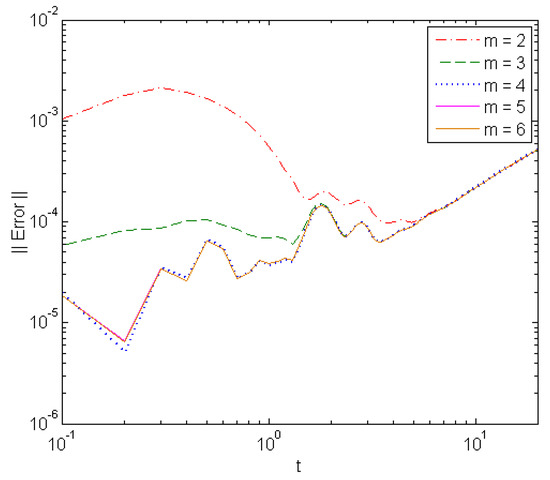
Figure 14. Solution error of different-order GTL in solving Problem 6 at $h=0.1$.

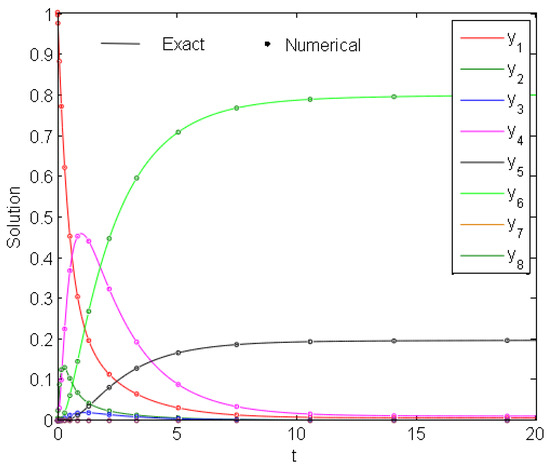
Figure 15. Exact and numerical solutions of Problem 6.

5. Conclusions

This paper presented a new generalised Taylor-like explicit method for SODEs and stiff ODE systems. The new method was formulated in its general component and vector applicable forms. The error and stability analysis of the method were discussed showing that it has at least ($m+1$) order of convergence and the L-stability property. It was shown that several other integration schemes are essentially special cases of the proposed method.The algorithm is applied to six stiff test problems and the results are analyzed in several figures and tables and compared with those obtained by means of the classical Taylor-like methods. The results show that the new method is not only stable and accurate but also overcomes the shortcomings of the classical Taylor-like explicit methods in their component and vector forms by adapting the value of k during the computations without losing the convergence order and the L-stability property.