The k-Rainbow Domination Number of Cn□Cm
Abstract
1. Introduction
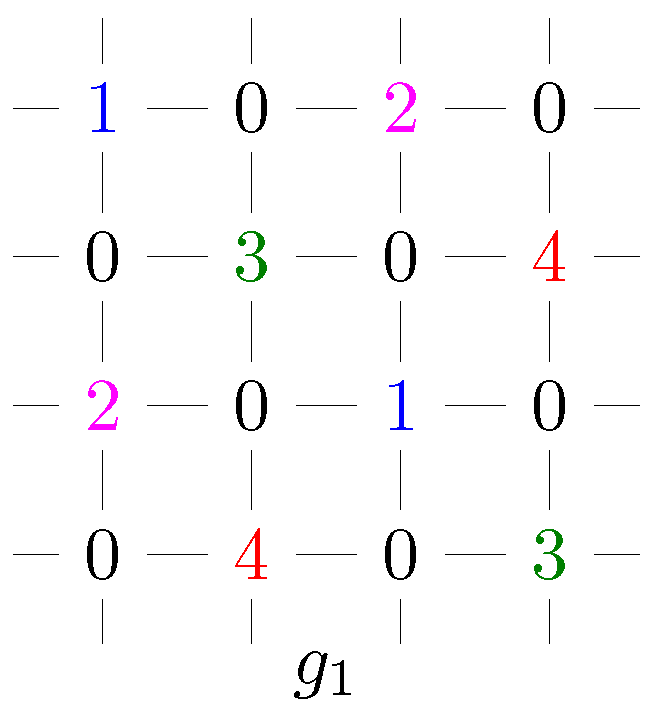
2. 4-Rainbow Domination Number of Graph
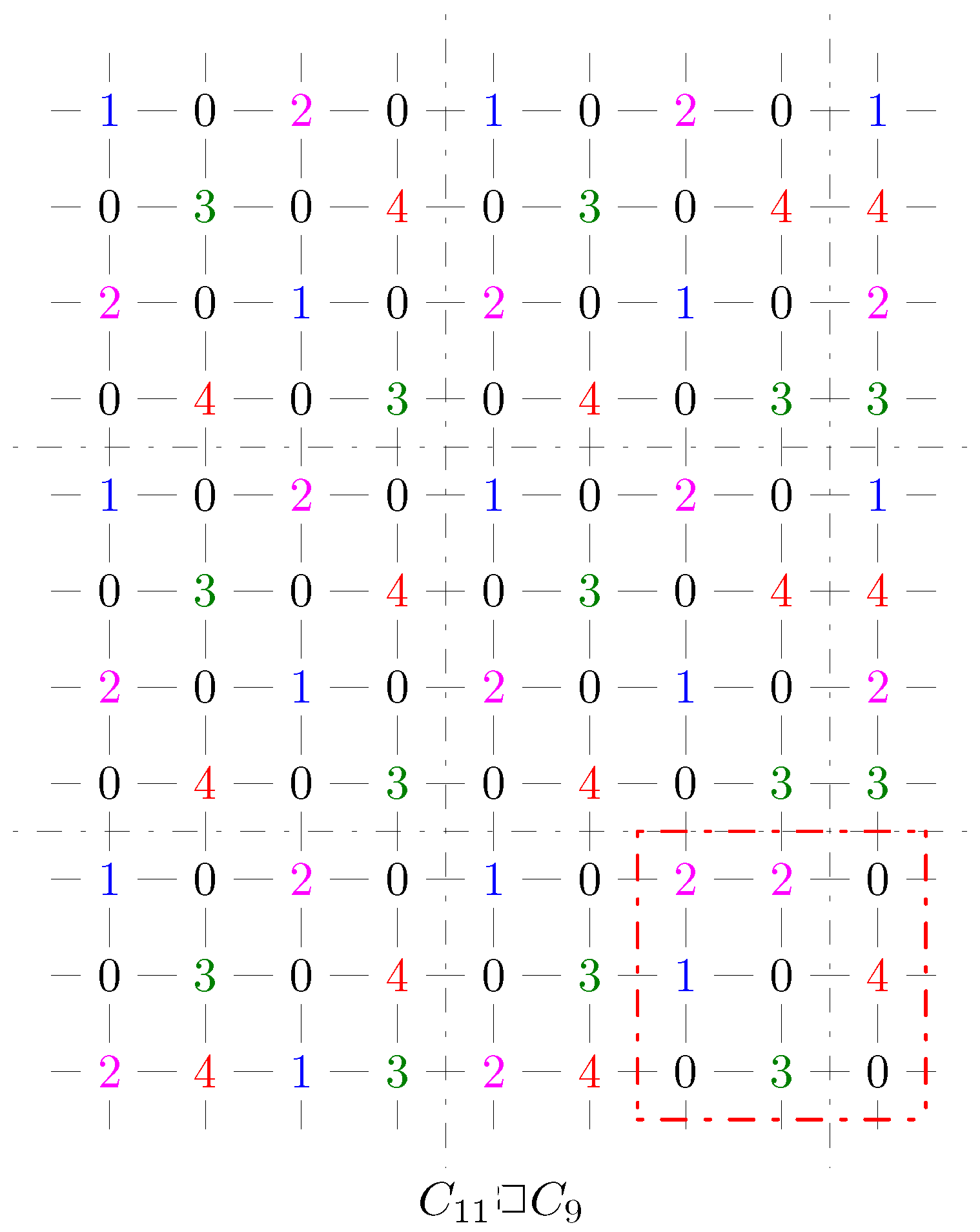
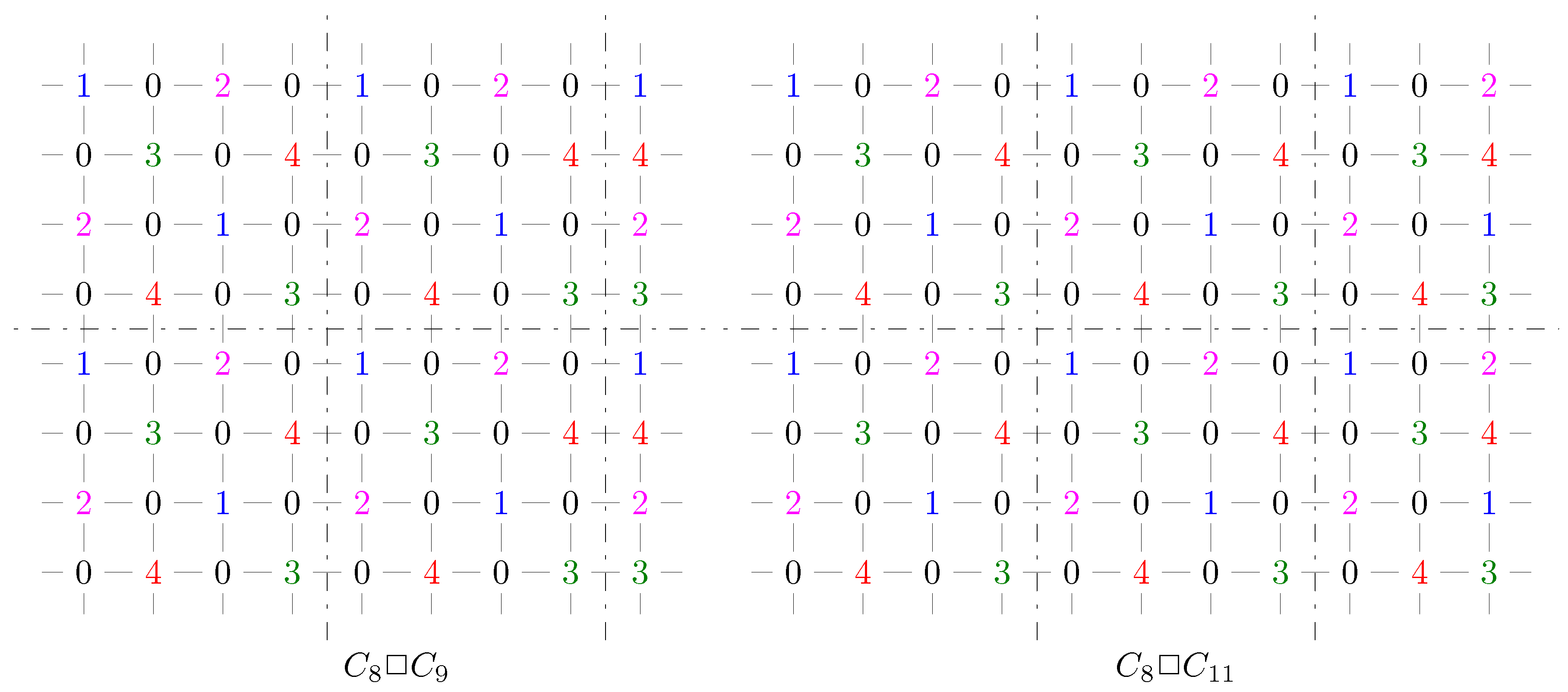
2.1. Lower Bounds on the 4-Rainbow Domination Number of Graph
- ; ; ;
- if , then ; ;
- if , then ; ;
- if , then ; ;
- if , then ; ;
- It follows . Let .
- ; ; ;
- if , then ; ;
- if , then ; .
- It has . Let .
- ; ; ;
- if , then ; .
- It follows . Let .
- ; ; .
- It has .
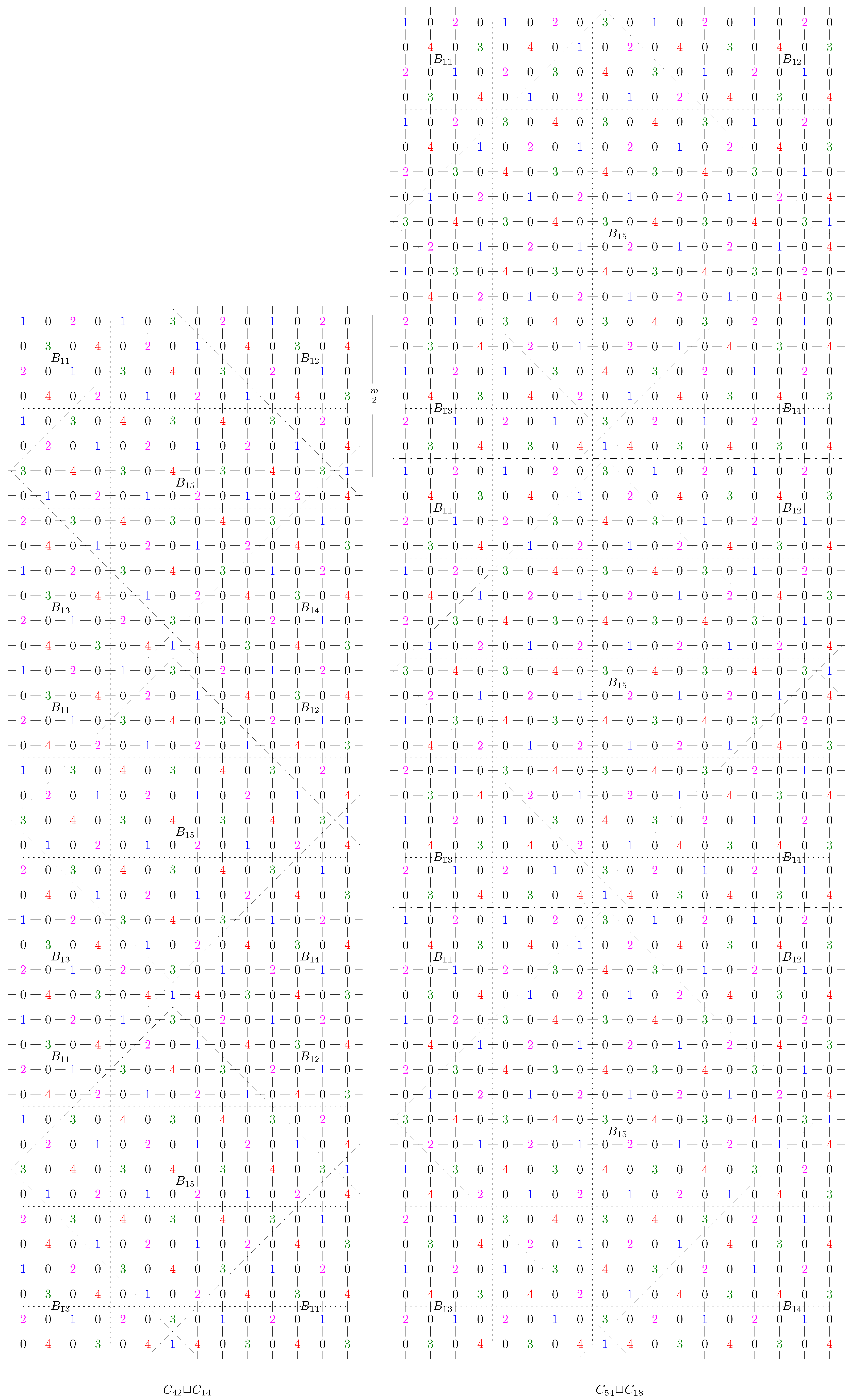
2.2. Upper Bounds on the 4-Rainbow Domination Number of Graph
- (1)
- m, n are evens and , (Lemma 6).
- (2)
- m, n are evens and , (Lemma 7).
- (3)
- m, n are evens and , (Lemma 8).
- (4)
- m, n are odds and , (Lemma 9).
- (5)
- m, n are odds and , (Lemma 10).
- (6)
- m, n are odds and , (Lemma 9).
- (7)
- m is odd, n is even and , (Lemma 11).
- (8)
- m is odd, n is even and , (Lemma 12).
2.3. The Values and Bounds of
3. The k-Rainbow Domination Number of Graph
4. Discussion on Vizing’s Conjecture
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brešar, B.; Henning, M.A.; Rall, D.F. Rainbow domination in graphs. Taiwan J. Math. 2008, 12, 213–225. [Google Scholar] [CrossRef]
- Dehgardi, N.; Sheikholeslami, S.M.; Volkmann, L. The k-rainbow bondage number of a graph. Discret. Appl. Math. 2014, 174, 133–139. [Google Scholar]
- Vizing, V.G. Some unsolved problems in graph theory. Uspehi Mater. Nauk. 1968, 23, 117–134. [Google Scholar]
- Chen, Q.; Zhao, C.Y.; Zhao, M. Dominator colorings of certain cartesian products of paths and cycles. Graph Combinator. 2017, 33, 73–83. [Google Scholar]
- Li, Z.P.; Shao, Z.H.; Xu, J. Weak {2}-domination number of Cartesian products of cycles. J. Comb. Optim. 2018, 35, 75–85. [Google Scholar]
- Ye, A.S.; Miao, F.; Shao, Z.H.; Liu, J.B.; Žerovnik, J.; Repolusk, P. More Results on the Domination Number of Cartesian Product of Two Directed Cycles. Mathematics 2019, 7, 210. [Google Scholar] [CrossRef]
- Brešar, B.; Šumenjak, T.K. On the 2-rainbow domination in graphs. Discret. Appl. Math. 2007, 155, 2397–2400. [Google Scholar]
- Stepień, Z.; Zwierzchowski, M. 2-rainbow domination number of cartesian products: Cn□C3 and Cn□C5. J. Comb. Optim. 2014, 28, 748–755. [Google Scholar] [CrossRef][Green Version]
- Stepień, Z.; Szymaszkiewicz, A.; Szymaszkiewicz, L.; Zwierzchowski, M. 2-Rainbow domination number of Cn□C5. Discret. Appl. Math. 2014, 170, 113–116. [Google Scholar] [CrossRef]
- Stepień, Z.; Szymaszkiewicz, L.; Zwierzchowski, M. The Cartesian product of cycles with small 2-rainbow domination number. J. Comb. Optim. 2015, 30, 668–674. [Google Scholar] [CrossRef]
- Shao, Z.H.; Li, Z.P.; Erveš, R.; Žerovnik, J. The 2-Rainbow domination numbers of C4□Cn and C8□Cn. Natl. Acad. Sci. Lett. 2019, 2, 1–8. [Google Scholar]
- Shao, Z.H.; Jiang, H.Q.; Wu, P.; Wang, S.H.; Žerovnik, J.; Zhang, X.S.; Liu, J.B. On 2-rainbow domination of generalized Petersen graphs. Discret. Appl. Math. 2019, 257, 370–384. [Google Scholar] [CrossRef]
- Wang, Y.L.; Wu, K.H. A tight upper bound for 2-rainbow domination in generalized Petersen graphs. Discret. Appl. Math. 2013, 161, 2178–2188. [Google Scholar] [CrossRef]
- Liu, J.J.; Chang, S.C.; Lin, C.J. The 2-rainbow domination of Sierpiński graphs and extended Sierpiński graphs. Theor. Comput. Syst. 2017, 61, 893–906. [Google Scholar] [CrossRef]
- Furuya, M.; Koyanagi, M.; Yokota, M. Upper bound on 3-rainbow domination in graphs with minimum degree 2. Discret. Optim. 2018, 29, 45–76. [Google Scholar] [CrossRef]
- Shao, Z.H.; Liang, M.L.; Yin, C.; Xu, X.D.; Pavlič, P.; Žerovnik, J. On rainbow domination numbers of graphs. Inform. Sci. 2014, 254, 225–234. [Google Scholar] [CrossRef]
- Chang, G.J.; Wu, J.J.; Zhu, X.D. Rainbow domination on trees. Discret. Appl. Math. 2010, 158, 8–12. [Google Scholar] [CrossRef]
- Hao, G.L.; Qian, J.G. On the rainbow domination number of digraphs. Graph Combinator. 2016, 32, 1903–1913. [Google Scholar] [CrossRef]
- Kang, Q.; Samodivkin, V.; Shao, Z.H.; Sheikholeslami, S.M.; Soroudi, M. Outer-independent k-rainbow domination. J. Taibah Univ. Sci. 2019, 1, 883–891. [Google Scholar] [CrossRef]
- Brezovnik, S.; Šumenjak, T.K. Complexity of k-rainbow independent domination and some results on the lexicographic product of graphs. Appl. Math. Comput. 2019, 349, 214–220. [Google Scholar] [CrossRef]
- Amjadi, J.; Dehgardi, N.; Furuya, M.; Sheikholeslam, S.M. A sufficient condition for large rainbow domination number. Int. J. Comput. Math. Comput. Syst. Theory 2017, 2, 53–65. [Google Scholar] [CrossRef]


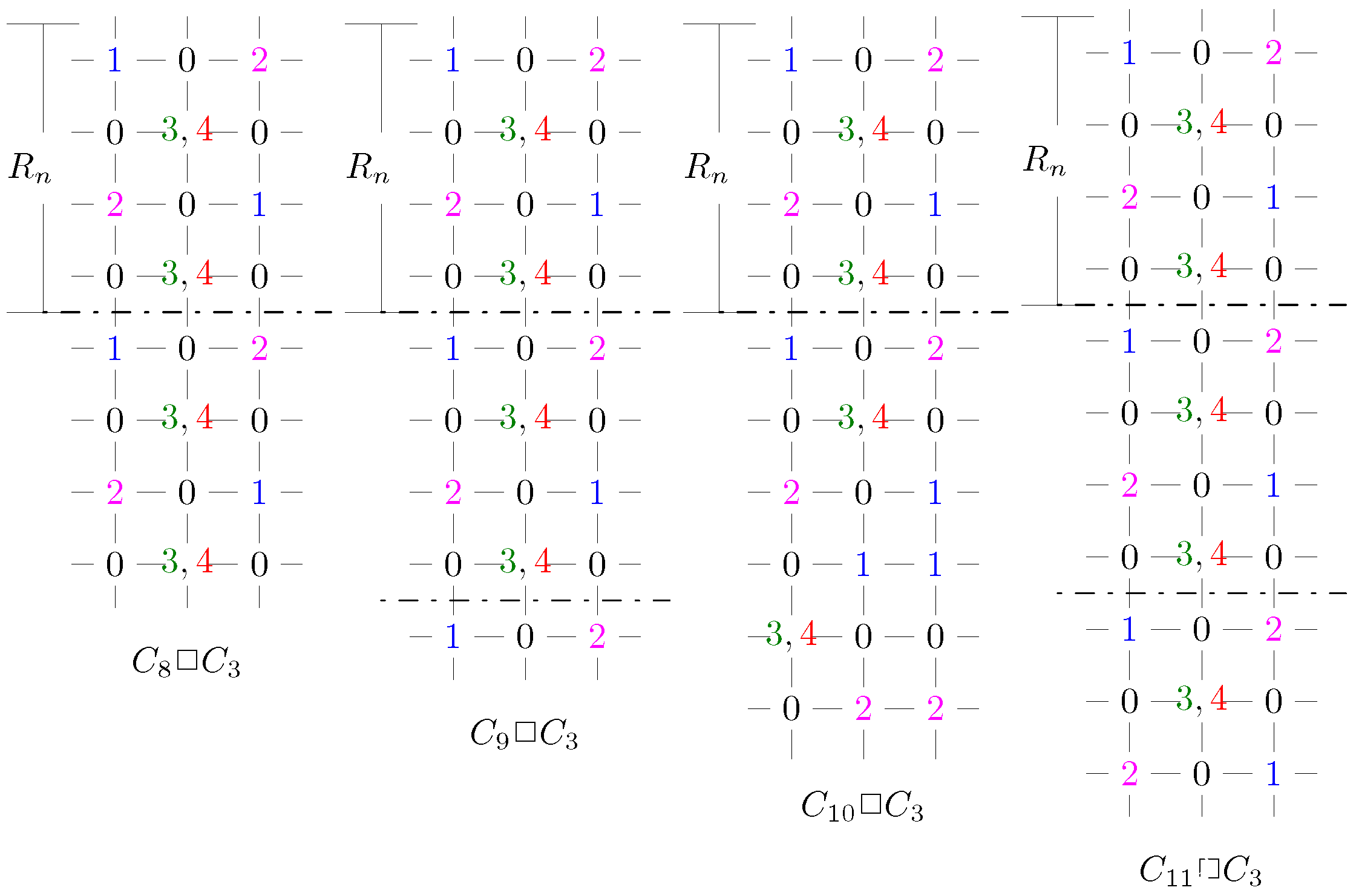
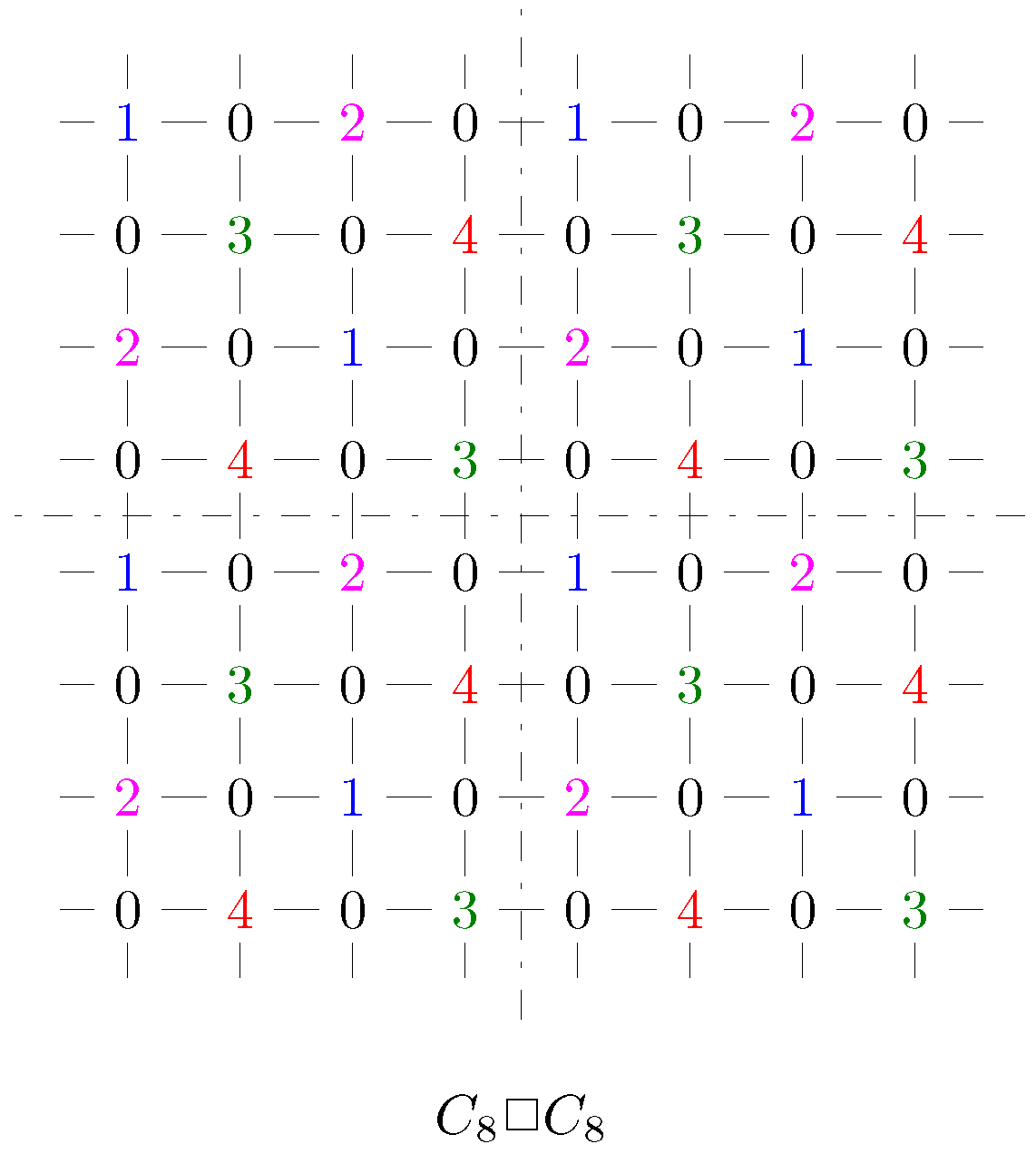


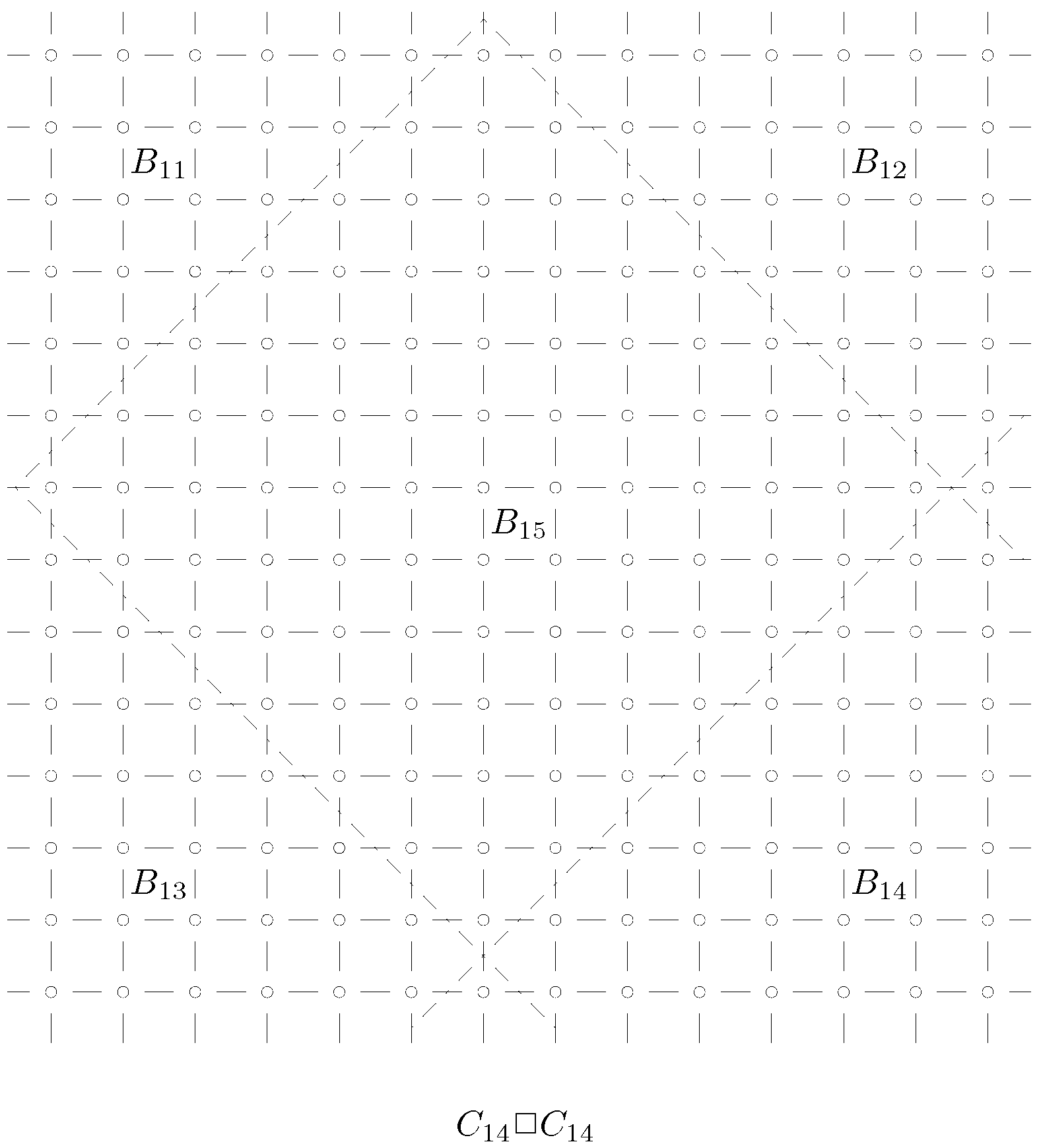
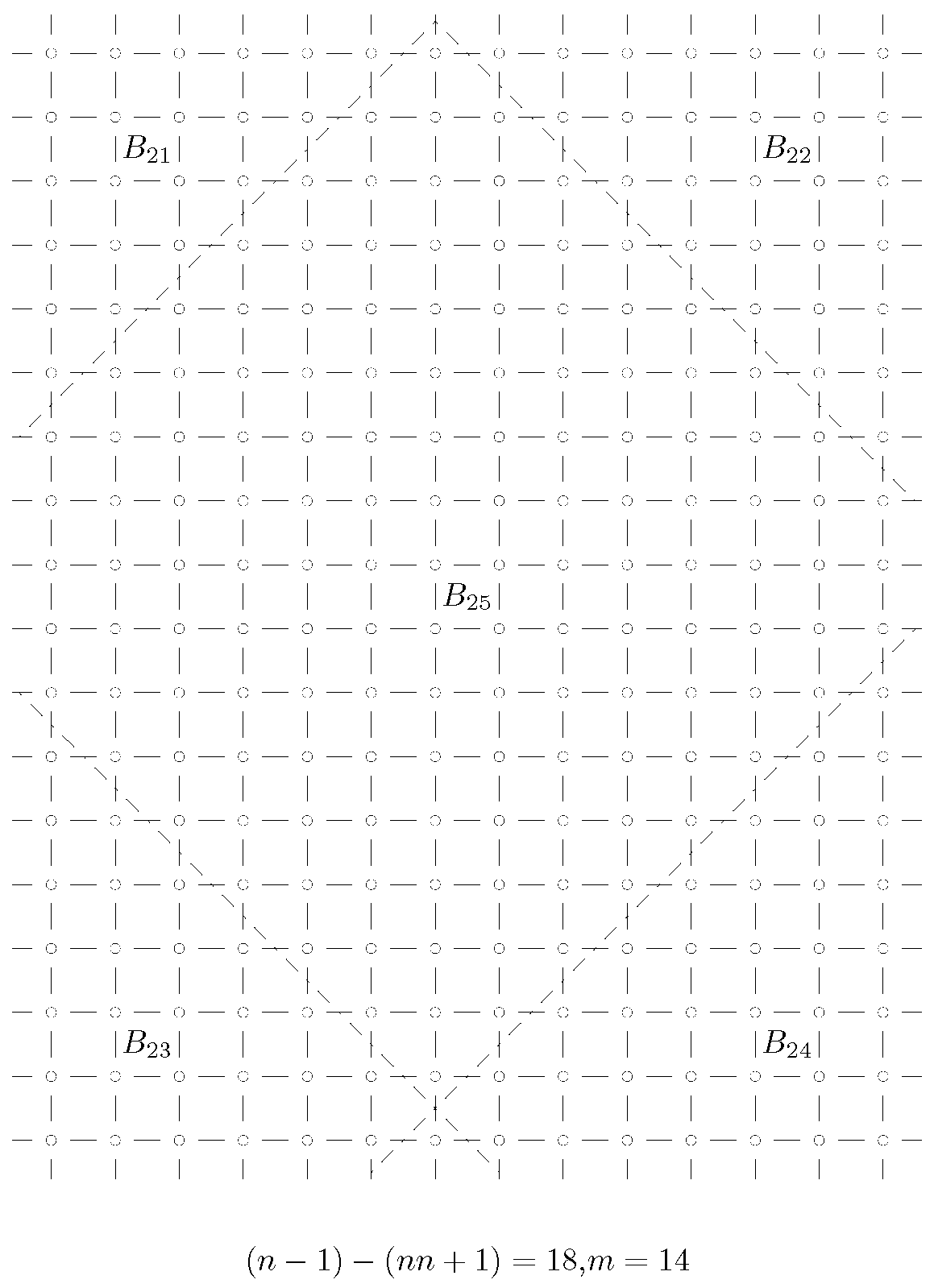


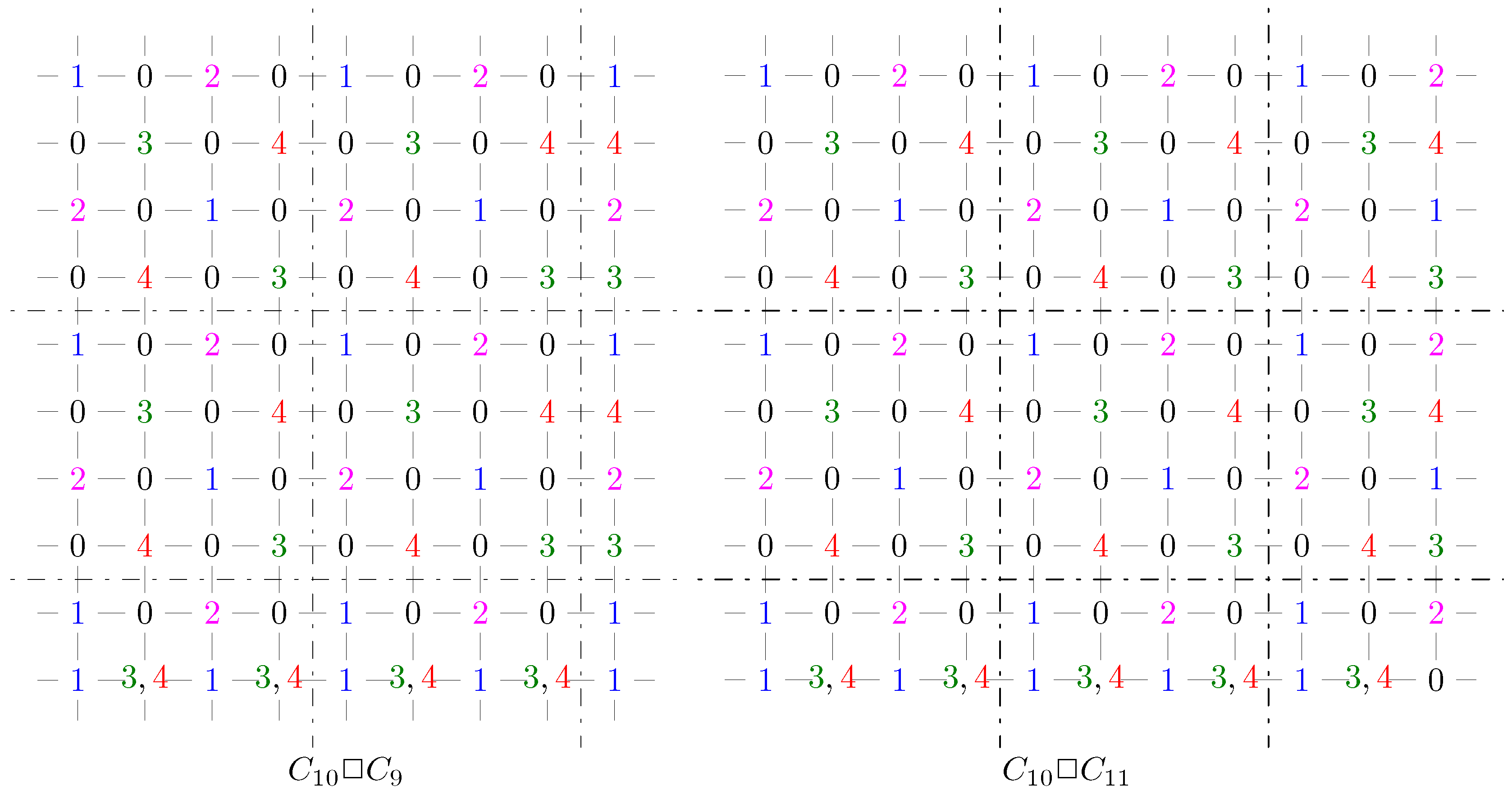
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Li, K.; Yang, Y. The k-Rainbow Domination Number of Cn□Cm. Mathematics 2019, 7, 1153. https://doi.org/10.3390/math7121153
Gao H, Li K, Yang Y. The k-Rainbow Domination Number of Cn□Cm. Mathematics. 2019; 7(12):1153. https://doi.org/10.3390/math7121153
Chicago/Turabian StyleGao, Hong, Kun Li, and Yuansheng Yang. 2019. "The k-Rainbow Domination Number of Cn□Cm" Mathematics 7, no. 12: 1153. https://doi.org/10.3390/math7121153
APA StyleGao, H., Li, K., & Yang, Y. (2019). The k-Rainbow Domination Number of Cn□Cm. Mathematics, 7(12), 1153. https://doi.org/10.3390/math7121153




