Enhancing Strong Neighbor-Based Optimization for Distributed Model Predictive Control Systems
Abstract
:1. Introduction
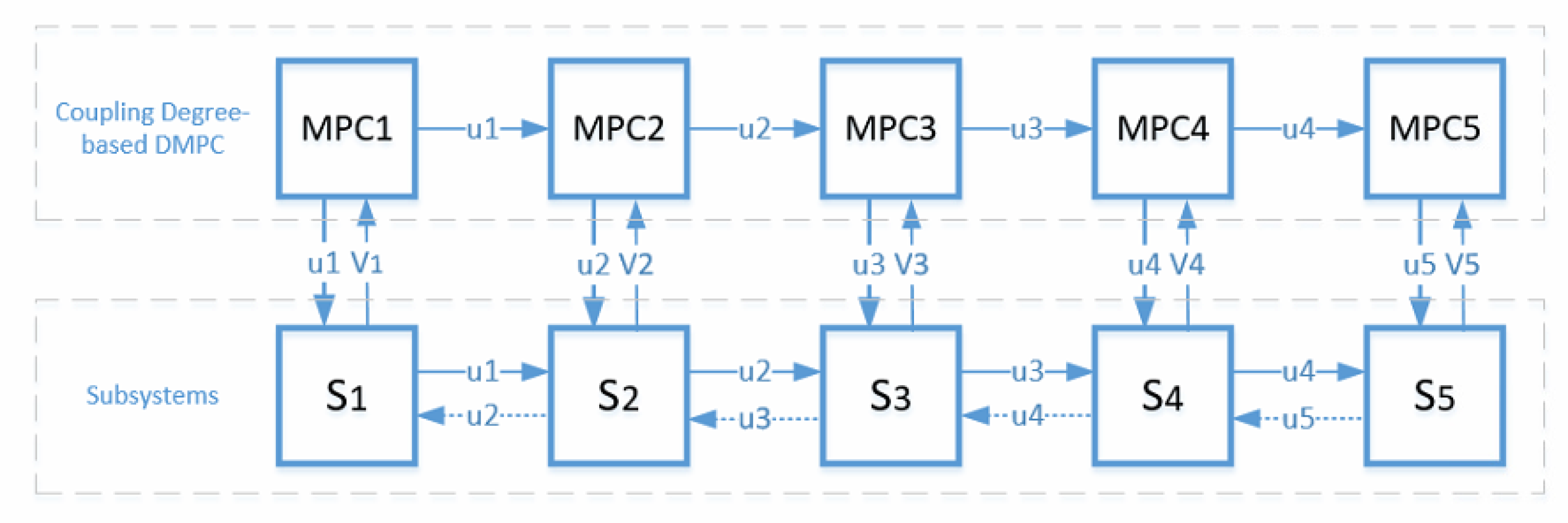
2. Problem Description
- to achieve a good optimization performance of the entire closed-loop system.
- to guarantee the feasibility of target tracking.
- to simplify the information connectivity among controllers to guarantee good structural flexibility and error-tolerance of the distributed control framework.
3. DMPC Design
3.1. Strong-Coupling Neighbor-Based Optimization for Tracking
| Algorithm 1 Enhancing Strong Neighbor-Based Optimization DMPC |
 |
3.2. Warm Start
| Algorithm 2 Warm Start for Iterative Algorithm |
 |
3.3. RPI Control Law and RPI Set
3.4. Determination of Strong Coupling
4. Stability and Convergence
5. Simulation
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
References
- Christofides, P.D.; Scattolini, R.; Muñoz de la Peña, D.; Liu, J. Distributed model predictive control: A tutorial review and future research directions. Comput. Chem. Eng. 2013, 51, 21–41. [Google Scholar] [CrossRef]
- Del Real, A.J.; Arce, A.; Bordons, C. Combined environmental and economic dispatch of smart grids using distributed model predictive control. Int. J. Electr. Power Energy Syst. 2014, 54, 65–76. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Tan, R. Distributed Model Predictive Control for On-Connected Microgrid Power Management. IEEE Trans. Control Syst. Technol. 2018, 26, 1028–1039. [Google Scholar] [CrossRef]
- Yu, W.; Liu, D.; Huang, Y. Operation optimization based on the power supply and storage capacity of an active distribution network. Energies 2013, 6, 6423–6438. [Google Scholar] [CrossRef]
- Scattolini, R. Architectures for distributed and hierarchical model predictive control-a review. J. Process Control 2009, 19, 723–731. [Google Scholar] [CrossRef]
- Du, X.; Xi, Y.; Li, S. Distributed model predictive control for large-scale systems. In Proceedings of the 2001 American Control Conference, Arlington, VA, USA, 25–27 June 2001; Volume 4, pp. 3142–3143. [Google Scholar]
- Li, S.; Yi, Z. Distributed Model Predictive Control for Plant-Wide Systems; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Mota, J.F.C.; Xavier, J.M.F.; Aguiar, P.M.Q.; Püschel, M. Distributed Optimization With Local Domains: Applications in MPC and Network Flows. IEEE Trans. Autom. Control 2015, 60, 2004–2009. [Google Scholar] [CrossRef]
- Qin, S.; Badgwell, T. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Maciejowski, J. Predictive Control: With Constraints; Pearson Education: London, UK, 2002. [Google Scholar]
- Vaccarini, M.; Longhi, S.; Katebi, M. Unconstrained networked decentralized model predictive control. J. Process Control 2009, 19, 328–339. [Google Scholar] [CrossRef]
- Leirens, S.; Zamora, C.; Negenborn, R.; De Schutter, B. Coordination in urban water supply networks using distributed model predictive control. In Proceedings of the American Control Conference (ACC), Baltimore, MD, USA, 30 June–2 July 2010; pp. 3957–3962. [Google Scholar]
- Wang, Z.; Ong, C.J. Distributed Model Predictive Control of linear discrete-time systems with local and global constraints. Automatica 2017, 81, 184–195. [Google Scholar] [CrossRef]
- Trodden, P.A.; Maestre, J. Distributed predictive control with minimization of mutual disturbances. Automatica 2017, 77, 31–43. [Google Scholar] [CrossRef]
- Al-Gherwi, W.; Budman, H.; Elkamel, A. A robust distributed model predictive control algorithm. J. Process Control 2011, 21, 1127–1137. [Google Scholar] [CrossRef]
- Kirubakaran, V.; Radhakrishnan, T.; Sivakumaran, N. Distributed multiparametric model predictive control design for a quadruple tank process. Measurement 2014, 47, 841–854. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.; Li, C. Distributed model predictive control for polytopic uncertain systems subject to actuator saturation. J. Process Control 2013, 23, 1075–1089. [Google Scholar] [CrossRef]
- Liu, J.; Muñoz de la Peña, D.; Christofides, P.D. Distributed model predictive control of nonlinear systems subject to asynchronous and delayed measurements. Automatica 2010, 46, 52–61. [Google Scholar] [CrossRef]
- Cheng, R.; Fraser Forbes, J.; Yip, W.S. Dantzig–Wolfe decomposition and plant-wide MPC coordination. Comput. Chem. Eng. 2008, 32, 1507–1522. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Qiu, H. Networked coordination-based distributed model predictive control for large-scale system. IEEE Trans. Control Syst. Technol. 2013, 21, 991–998. [Google Scholar] [CrossRef]
- Groß, D.; Stursberg, O. A Cooperative Distributed MPC Algorithm With Event-Based Communication and Parallel Optimization. IEEE Trans. Control Netw. Syst. 2016, 3, 275–285. [Google Scholar] [CrossRef]
- Walid Al-Gherwi, H.B.; Elkamel, A. Selection of control structure for distributed model predictive control in the presence of model errors. J. Process Control 2010, 20, 270–284. [Google Scholar] [CrossRef]
- Camponogara, E.; Jia, D.; Krogh, B.; Talukdar, S. Distributed model predictive control. IEEE Control Syst. Mag. 2002, 22, 44–52. [Google Scholar]
- Conte, C.; Jones, C.N.; Morari, M.; Zeilinger, M.N. Distributed synthesis and stability of cooperative distributed model predictive control for linear systems. Automatica 2016, 69, 117–125. [Google Scholar] [CrossRef]
- Tippett, M.J.; Bao, J. Reconfigurable distributed model predictive control. Chem. Eng. Sci. 2015, 136, 2–19. [Google Scholar] [CrossRef]
- Zheng, Y.; Wei, Y.; Li, S. Coupling Degree Clustering-Based Distributed Model Predictive Control Network Design. IEEE Trans. Autom. Sci. Eng. 2018, 1–10. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y.; Zhu, Q. Nash-optimization enhanced distributed model predictive control applied to the Shell benchmark problem. Inf. Sci. 2005, 170, 329–349. [Google Scholar] [CrossRef]
- Venkat, A.N.; Hiskens, I.A.; Rawlings, J.B.; Wright, S.J. Distributed MPC Strategies with Application to Power System Automatic Generation Control. IEEE Trans. Control Syst. Technol. 2008, 16, 1192–1206. [Google Scholar] [CrossRef]
- Stewart, B.T.; Wright, S.J.; Rawlings, J.B. Cooperative distributed model predictive control for nonlinear systems. J. Process Control 2011, 21, 698–704. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S. N-Step Impacted-Region Optimization based Distributed Model Predictive Control. IFAC-PapersOnLine 2015, 48, 831–836. [Google Scholar] [CrossRef]
- De Lima, M.L.; Camponogara, E.; Marruedo, D.L.; de la Peña, D.M. Distributed Satisficing MPC. IEEE Trans. Control Syst. Technol. 2015, 23, 305–312. [Google Scholar] [CrossRef]
- De Lima, M.L.; Limon, D.; de la Pena, D.M.; Camponogara, E. Distributed Satisficing MPC With Guarantee of Stability. IEEE Trans. Autom. Control 2016, 61, 532–537. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Wang, X. Distributed model predictive control for plant-wide hot-rolled strip laminar cooling process. J. Process Control 2009, 19, 1427–1437. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Li, N. Distributed model predictive control over network information exchange for large-scale systems. Control Eng. Pract. 2011, 19, 757–769. [Google Scholar] [CrossRef]
- Li, S.; Zheng, Y.; Lin, Z. Impacted-Region Optimization for Distributed Model Predictive Control Systems with Constraints. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1447–1460. [Google Scholar] [CrossRef]
- Riverso, S.; Ferrari-Trecate, G. Tube-based distributed control of linear constrained systems. Automatica 2012, 48, 2860–2865. [Google Scholar] [CrossRef]
- Riverso, S.; Boem, F.; Ferrari-Trecate, G.; Parisini, T. Plug-and-Play Fault Detection and Control-Reconfiguration for a Class of Nonlinear Large-Scale Constrained Systems. IEEE Trans. Autom. Control 2016, 61, 3963–3978. [Google Scholar] [CrossRef]
- Ferramosca, A.; Limon, D.; Alvarado, I.; Camacho, E. Cooperative distributed MPC for tracking. Automatica 2013, 49, 906–914. [Google Scholar] [CrossRef]
- Limon, D. MPC for tracking of piece-wise constant references for constrained linear systems. In Proceedings of the 16th IFAC World Congress, Prague, Czech Republic, 3–8 July 2005; p. 882. [Google Scholar]
- Limon, D.; Alvarado, I.; Alamo, T.; Camacho, E.F. Robust tube-based MPC for tracking of constrained linear systems with additive disturbances. J. Process Control 2010, 20, 248–260. [Google Scholar] [CrossRef]
- Shao, Q.M.; Cinar, A. Coordination scheme and target tracking for distributed model predictive control. Chem. Eng. Sci. 2015, 136, 20–26. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Mayne, D.Q. Model Predictive Control: Theory and Design; Nob Hill Publishing: Madison, WI, USA, 2009; pp. 3430–3433. [Google Scholar]
- Alvarado, I. On the Design of Robust Tube-Based MPC for Tracking. In Proceedings of the 17th World Congress The International Federation of Automatic Control, Seoul, Korea, 6–11 July 2008; pp. 15333–15338. [Google Scholar]
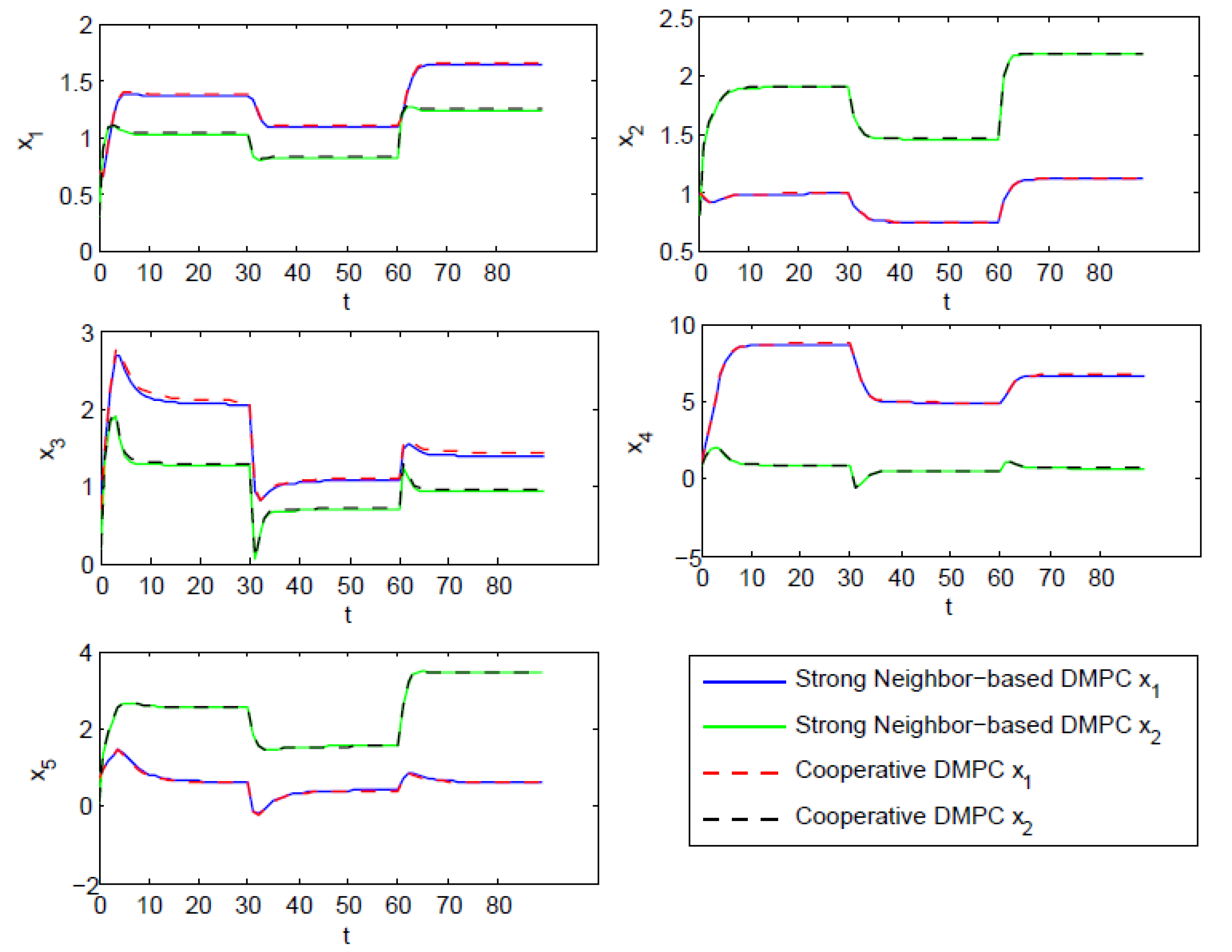
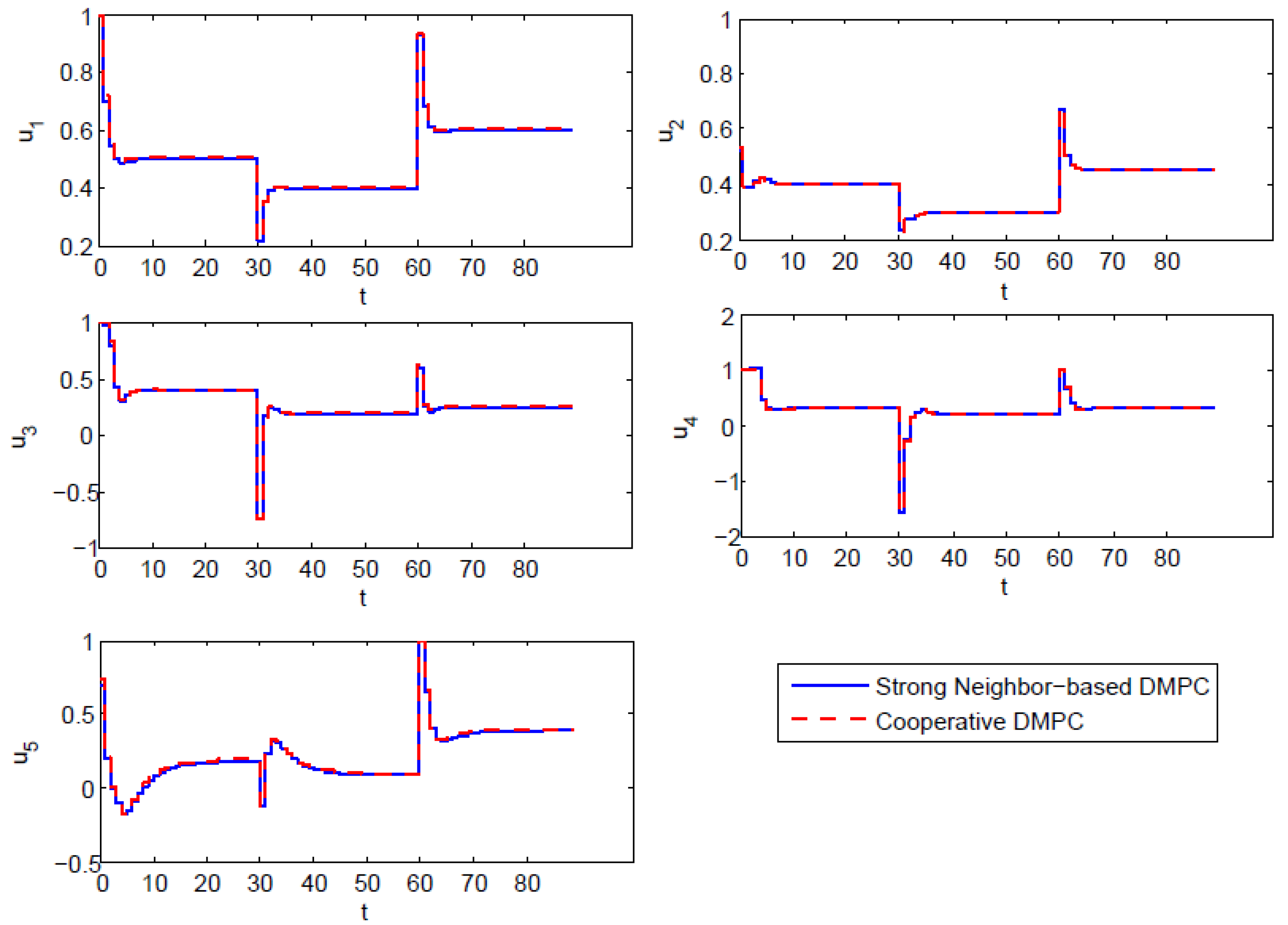
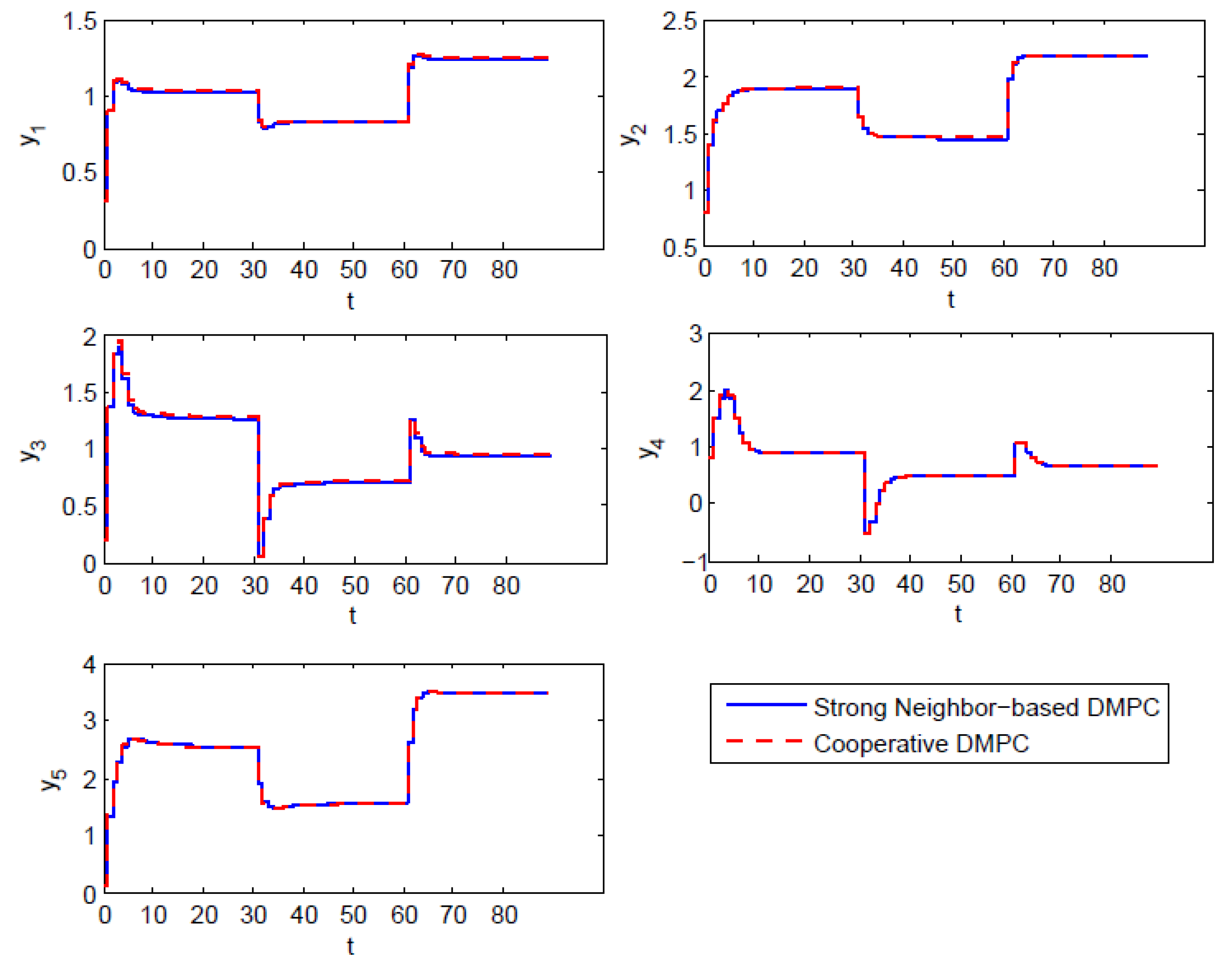
| Item | |||||
|---|---|---|---|---|---|
| MSE | 0.5771 | 1.1512 | 0.7111 | 0.1375 | 0.9162 |
| System | SCN-DMPC | Cooperative DMPC |
|---|---|---|
| 1 | 2 | |
| 2 | 3 | |
| 2 | 4 | |
| 2 | 3 | |
| 1 | 1 | |
| 8 | 13 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, S.; Zheng, Y.; Li, S. Enhancing Strong Neighbor-Based Optimization for Distributed Model Predictive Control Systems. Mathematics 2018, 6, 86. https://doi.org/10.3390/math6050086
Gao S, Zheng Y, Li S. Enhancing Strong Neighbor-Based Optimization for Distributed Model Predictive Control Systems. Mathematics. 2018; 6(5):86. https://doi.org/10.3390/math6050086
Chicago/Turabian StyleGao, Shan, Yi Zheng, and Shaoyuan Li. 2018. "Enhancing Strong Neighbor-Based Optimization for Distributed Model Predictive Control Systems" Mathematics 6, no. 5: 86. https://doi.org/10.3390/math6050086
APA StyleGao, S., Zheng, Y., & Li, S. (2018). Enhancing Strong Neighbor-Based Optimization for Distributed Model Predictive Control Systems. Mathematics, 6(5), 86. https://doi.org/10.3390/math6050086






