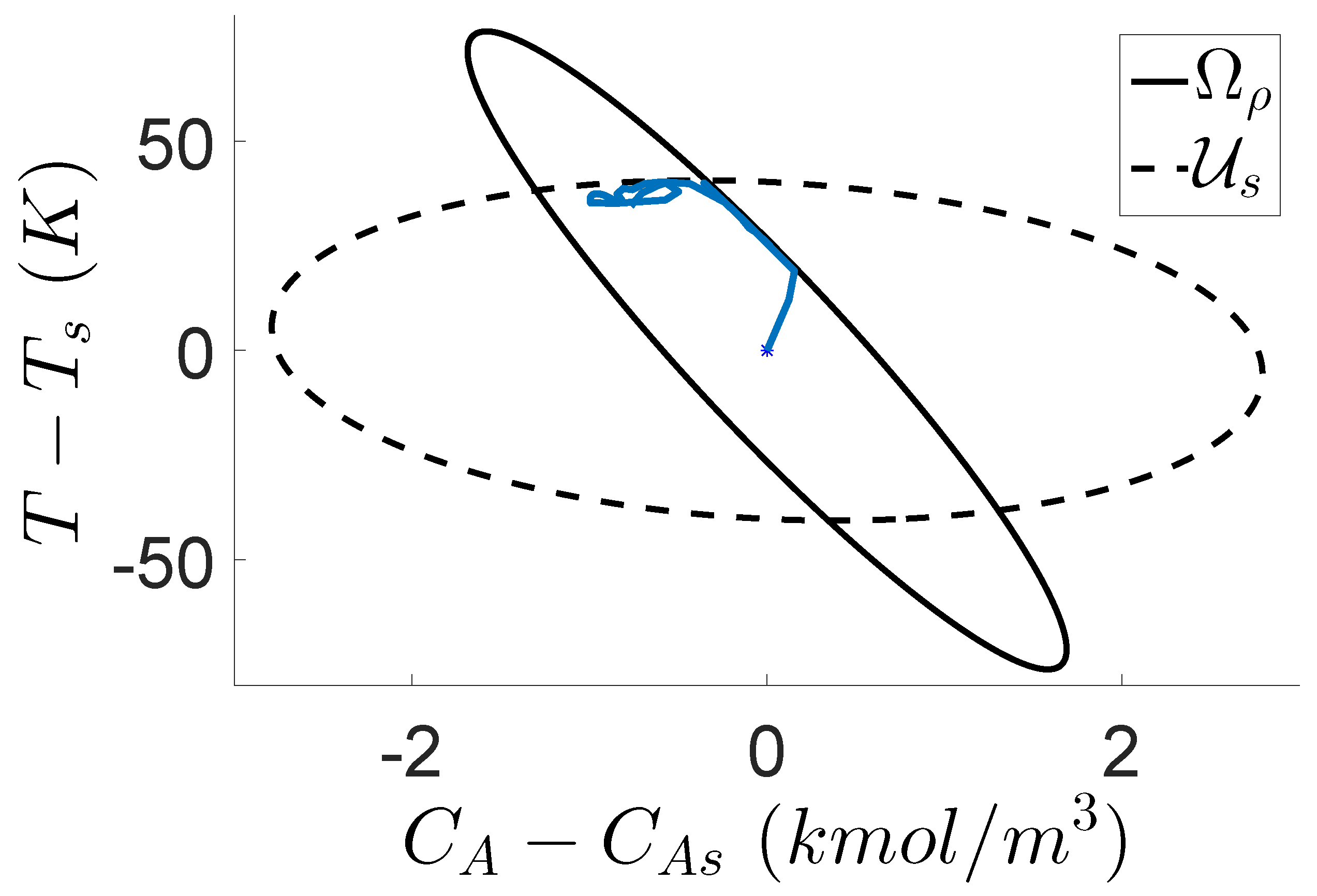Safeness Index-Based Economic Model Predictive Control of Stochastic Nonlinear Systems

Abstract

Process operational safety plays an important role in designing control systems for chemical processes. Motivated by this, in this work, we develop a process Safeness Index-based economic model predictive control system for a broad class of stochastic nonlinear systems with input constraints. A stochastic Lyapunov-based controller is first utilized to characterize a region of the state-space surrounding the origin, starting from which the origin is rendered asymptotically stable in probability. Using this stability region characterization and a process Safeness Index function that characterizes the region in state-space in which it is safe to operate the process, an economic model predictive control system is then developed using Lyapunov-based constraints to ensure economic optimality, as well as process operational safety and closed-loop stability in probability. A chemical process example is used to demonstrate the applicability and effectiveness of the proposed approach.

1. Introduction

Process operational safety has become crucially important in the chemical industry since the failure of process safety devices/human error often leads to disastrous incidents causing human and capital loss [1]. Motivated by this, recently, a new class of economic model predictive control systems (EMPC), in which the cost function penalizes process economics instead of the distances from the steady-state in a general quadratic form, was utilized to account for process operational safety and economic optimality based on a function called the Safeness Index [2,3]. These new EMPC methods complement previous efforts on economic model predictive control (e.g., [4,5,6,7]), which were not concerned explicitly with process operational safety. Specifically, in [2], a Safeness Index function that indicates the level of safety of a given state was utilized to characterize a safe operating region and used as a constraint in the EMPC design such that the closed-loop state of a nonlinear process is guaranteed to be driven into the safe operating region in finite time in the presence of sufficiently small bounded disturbances and, if the Safeness Index takes a special form related to a Lyapunov function used in the EMPC design, to never again exit that safe operating region while maximizing the economics of the process. However, in general, the Safeness Index does not have to take this special form and may therefore leave the safe operating region for finite periods of time (this may be acceptable depending on how the notion of a “safe” region of operation is selected; e.g., perhaps a “safe” region of operation means it is safe to operate in for all times, but that if the state is not in that region for short periods of time, there is not an immediate concern). Therefore, with a general form of the Safeness Index, the hard constraint on this function in the EMPC design of [2] with a Safeness Index-based constraint may not be feasible. Due to the potential infeasibility issue caused by the hard constraint, the potential for the state to leave the safe operating region unless the Safeness Index has a specific form and the fact that disturbances may not be sufficiently small to guarantee that the closed-loop state re-enters this safe operating region, the EMPC design with a Safeness Index-based constraint may be limited in terms of its applicability to stochastic nonlinear systems.

On the other hand, MPC and EMPC of stochastic nonlinear systems have received a lot of attention recently (e.g., [8,9]). Uncertainty in the process model may be considered to have a worst-case upper and lower bound, or it may be considered to have unbounded variation and therefore be treated in a probabilistic manner. Since the variation of disturbances is not bounded in a stochastic nonlinear system, the Lyapunov-based economic model predictive control (LEMPC) framework [4] developed for nonlinear systems with small bounded disturbances is unable to guarantee closed-loop stability (i.e., the state of the closed-loop system stays within a well-characterized region of the state-space); instead, probabilistic closed-loop stability results are expected in this case. To that end, in [10], the Markov-chain Monte Carlo technique was used to derive the probabilistic convergence to a near-optimal solution for a constrained stochastic optimization problem. In [9], a Lyapunov-based model predictive control (LMPC) method was proposed for stochastic nonlinear systems to drive the state to a steady-state within an explicitly characterized region of attraction in probability. Recently, the work [11] developed a Lyapunov-based EMPC method for stochastic nonlinear systems by utilizing the probability distribution of the disturbance term to derive closed-loop stability and recursive feasibility results in probability.

In the same direction, this work focuses on the design of Safeness Index-based economic model predictive control systems for a broad class of stochastic nonlinear systems with input constraints. Specifically, under the assumption of the stabilizability of the origin of the stochastic nonlinear system via a stochastic Lyapunov-based control law, a process Safeness Index function and the level sets of multiple Lyapunov functions are first utilized to characterize a safe operating region in state-space, starting from which recursive feasibility and process operational safety are derived in probability for the stochastic nonlinear system under an economic model predictive controller. This economic model predictive control method is then designed that utilizes stochastic Lyapunov-based constraints to achieve economic optimality, as well as feasibility and process operational safety in probability in the well-characterized safe operating region.

The rest of the manuscript is organized as follows: in the Preliminaries, the notation, the class of systems and the stabilizability assumptions are given. In the Main Results, the process Safeness Index and the Safeness Index-based LEMPC are introduced. Subsequently, the Safeness Index-based LEMPC using multiple level sets of Lyapunov functions (to broaden the state-space set for which it is recursively feasible) is developed for the nominal system. Based on this, the corresponding stochastic Safeness Index-based LEMPC and its probabilistic process operational safety and feasibility properties are developed for the nonlinear stochastic system. Finally, a nonlinear chemical process example is used to demonstrate the application of the proposed stochastic Safeness Index-based LEMPC.

2. Preliminaries

2.1. Notations

Throughout the paper, we use the notation $(\Omega ,\mathcal{F},\mathbf{P})$ to denote a probability space. The notation $\left|·\right|$ is used to denote the Euclidean norm of a vector, and the notation ${\left|·\right|}_Q$ denotes the weighted Euclidean norm of a vector (i.e., ${\left|x\right|}_Q=x^{T}Qx$ where Q is a positive definite matrix). $x^T$ denotes the transpose of x. ${\mathbf{R}}_{+}$ denotes the set $[0,\infty )$. The notation $L_{f}V(x)$ denotes the standard Lie derivative $L_{f}V(x):=\frac{\partial V(x)}{\partial x}f(x)$. Given a set $\mathcal{D}$, we denote the boundary of $\mathcal{D}$ by $\partial \mathcal{D}$, the closure of $\mathcal{D}$ by $\overline{\mathcal{D}}$ and the interior of $\mathcal{D}$ by ${\mathcal{D}}^{\mathrm{o}}$. Set subtraction is denoted by “\”, i.e., $A\backslash B:=\{x\in {\mathbf{R}}^n:x\in A,x\notin B\}$. A continuous function $\alpha :[0,a)\to [0,\infty )$ is said to be a class $\mathcal{K}$ function if $\alpha (0)=0$ and it is strictly increasing. The function $f(x)$ is said to be a class $C^k$ function if the i-th derivative of f exists and is continuous for all $i=1,2,\dots ,k$. Consider a stochastic process $x(t,w):[0,\infty )\times \Omega \to {\mathbf{R}}^n$ on $(\Omega ,\mathcal{F},\mathbf{P})$. For each $w\in \Omega$, $x(·,w)$ is a realization or trajectory of the stochastic process, and we abbreviate $x(t,w)$ as $x_w(t)$. $\mathbf{E}(A)$, $\mathbf{P}(A)$, $\mathbf{E}(A|·)$ and $\mathbf{P}(A|·)$ are the expectation, the probability, the conditional expectation and the conditional probability of the occurrence of the event A, respectively. The hitting time ${\tau }_X$ of a set X is the first time that the state trajectory hits the boundary of X. Additionally, we define ${\tau }_{X,T}(t)=\min \{{\tau }_X,T,t\}$, where T is the operation time.

2.2. Class of Systems

Consider a class of continuous-time stochastic nonlinear systems described by the following system of stochastic differential equations:

$$dx(t)=f(x(t))dt+g(x(t))u(t)dt+h(x(t))dw(t)$$

(1)

where $x\in {\mathbf{R}}^n$ is the stochastic state vector and $u\in {\mathbf{R}}^m$ is the input vector. The available control action is defined by $U:=\{u\in {\mathbf{R}}^m|u_i^{\min }\le u\le u_i^{\max },i=1,2,\dots ,m\}$. The disturbance $w(t)$ is a standard q-dimensional independent Wiener process defined on the probability space $(\Omega ,\mathcal{F},\mathbf{P})$. $f(·)$, $g(·)$, and $h(·)$ are sufficiently smooth vector and matrix functions of dimensions $n\times 1$, $n\times m$ and $n\times q$, respectively. It is assumed that the steady-state of the system with $w(t)\equiv 0$ is $(x_s^{\ast },u_s^{\ast })=(0,0)$. The initial time $t_0$ is defined as zero ($t_0=0$). We also assume that $h(0)=0$ such that the disturbance term $h(x(t))dw(t)$ of Equation (1) vanishes at the origin.

Definition 1.

Given a $C^2$ Lyapunov function $V:{\mathbf{R}}^n\to {\mathbf{R}}_{+}$, the infinitesimal generator ($\mathcal{L}V$) of the system of Equation (1) is defined as follows:

$$\begin{array}{cc}\hfill \mathcal{L}V(x)=& L_{f}V(x)+L_{g}V(x)u+\frac{1}{2}Tr\{h{(x)}^T\frac{{\partial }^{2}V}{\partial x^2}h(x)\}\hfill \end{array}$$

(2)

We assume that $L_{f}V(x)$, $L_{g}V(x)$ and $h{(x)}^T\frac{{\partial }^{2}V}{\partial x^2}h(x)$ are locally Lipschitz throughout the work.

Definition 2.

Assuming that the equilibrium of the uncontrolled system $dx(t)=f(x(t))dt+h(x(t))dw(t)$ is at the origin, then the origin is said to be asymptotically stable in probability, if for any $ϵ>0$, the following conditions hold ([12]):

$$\underset{x(0)\to 0}{lim}\mathbf{P}(\underset{t\to \infty }{lim}x(t)=0)=1$$

(3a)

$$\underset{x(0)\to 0}{lim}\mathbf{P}(\underset{t\ge 0}{\sup }\left|x(t)\right|>ϵ)=0$$

(3b)

Proposition 1.

Given the uncontrolled system $dx(t)=f(x(t))dt+h(x(t))dw(t)$, if for all $x\in D_0\subset {\mathbf{R}}^n$, where $D_0$ is an open neighborhood of the origin, $\mathcal{L}V<0$ holds $\forall t\in (0,\infty )$, then $\mathbf{E}(V(x(t)))<V(x(0))$, $\forall t\in (0,\infty )$, and the origin of the uncontrolled system is asymptotically stable in probability ([12]).

2.3. Stabilizability Assumptions

We assume there exists a stochastic stabilizing feedback control law $u={\Phi }_s(x)\in U$ (e.g., [13,14]) such that the origin of the system of Equation (1) can be rendered asymptotically stable in probability for all $x\in D\subset {\mathbf{R}}^n$, where D is an open neighborhood of the origin, in the sense that there exists a positive definite $C^2$ stochastic control Lyapunov function V that satisfies the following inequality:

$$\begin{array}{cc}\hfill \mathcal{L}V& =L_{f}V(x)+L_{g}V(x){\Phi }_s(x)+\frac{1}{2}Tr\{h^T\frac{{\partial }^{2}V}{\partial x^2}h\}\hfill \\ & \le -{\alpha }_1(|x|)\hfill \end{array}$$

(4)

where ${\alpha }_1(·)$ is a class $\mathcal{K}$ function.

Based on the controller ${\Phi }_s(x)$, we characterize the set ${\varphi }_d:=\{x\in {\mathbf{R}}^n|\mathcal{L}V+\kappa V(x)\le 0,u={\Phi }_s(x)\in U,\kappa >0\}$. We also choose a level set ${\Omega }_{\rho }:=\{x\in {\varphi }_d|V(x)\le \rho \}$ of $V(x)$ inside ${\varphi }_d$ as the stability region for the system of Equation (1). Therefore, the origin of the system of Equation (1) is rendered asymptotically stable via the controller ${\Phi }_s(x)$ in probability if $x(0)=x_0\in {\Omega }_{\rho }$.

In this work, we develop an economic MPC design that takes advantage of the Safeness Index function [2] in its design to achieve probabilistic process operational safety in the following sense:

Definition 3.

Consider the system of Equation (1) with input constraints $u\in U$. If there exists a control law $u=\Phi \in U$ such that the state trajectories of the system for any initial state $x(0)=x_0\in \mathcal{S}$ satisfy $x(t)\in \mathcal{S}$, $\forall t\ge 0$ with the probability p, where $\mathcal{S}$ is a safe operating region in state-space that excludes the unsafe region $\mathcal{D}$, we say that the control law $\Phi$ maintains the process state within a safe operating region $\mathcal{S}$ with probability p.

Remark 1.

In general, the safe operating region $\mathcal{S}$ is characterized as a subset of the stability region (because process operation is safe provided that the system is operated within a closed-loop stability region) for the closed-loop system of Equation (1) to account for the additional safety constraints. Therefore, if there exists a control law $u=\Phi (x)\in U$ that maintains the process state within $\mathcal{S}$ with the probability p, it also maintains the process state within the stability region at least with probability p. This implies that the probability of process operational safety of the system of Equation (1), which we will discuss in the following sections, also gives a lower bound on probabilistic closed-loop stability.

3. Main Results

In this section, the process Safeness Index and the optimization problem of Safeness Index-based LEMPC designed for the nominal system of Equation (1) with $w(t)\equiv 0$ are first presented. Based on that, the Safeness Index-based LEMPC using multiple level sets of Lyapunov functions is developed for the nominal system of Equation (1) to guarantee recursive feasibility and to guarantee that the closed-loop state does not enter an unsafe operating region $\mathcal{D}$. Subsequently, the stochastic Safeness Index-based LEMPC is developed for the system of Equation (1) to account for the disturbances $w(t)$ with unbounded variation. The stochastic safety and feasibility in probability of the closed-loop system of Equation (1) are finally investigated under the sample-and-hold implementation of the proposed stochastic Safeness Index-based LEMPC.

3.1. Process Safeness Index

In [2], the Safeness Index function $S(x)$ was developed to indicate the level of safety of a given state, through which process operational safety was integrated with process control system design to account for the process operational safety considerations resulting from multivariable interactions or interactions between units. There are various methods of determining the functional form of $S(x)$, for example by utilizing first-principles process models or using systematic safety analysis tools such as HAZOP and fault tree analysis.

Based on the functional form of $S(x)$, the closed-loop state predictions are required to be maintained within a safe region $\mathcal{S}$ (where $S(x)$ is below the threshold on the Safeness Index $S_{TH}$) by using the Safeness Index-based constraint within the process control design. Additionally, the safety systems (e.g., the alarm, emergency shut-down and relief systems) can be triggered if the threshold $S_{TH}$ is sufficiently exceeded, which implies that the process operation becomes unsafe and further actions are required.

3.2. Safeness Index-Based LEMPC

Safeness Index-based LEMPC optimizes an economic cost function $L_e(·,·)$ and maintains the closed-loop state of the nominal system of Equation (1) with $w(t)\equiv 0$ in a safe operating region by utilizing the Safeness Index function as a hard constraint within the LEMPC design. Specifically, the formulation of the Safeness Index-based LEMPC is as follows:

$$\begin{array}{cc}\hfill \underset{u(t)\in ST(\Delta )}{\max }& {\int }_{t_k}^{t_k+{\tau }_P\Delta }{L}_e(\tilde{x}(\tau ),u(\tau ))d\tau \hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \dot{\tilde{x}}(t)=f(\tilde{x}(t))+g(\tilde{x}(t))u(t)\hfill \end{array}$$

(5b)

$$\begin{array}{c}u(t)\in U,\forall t\in [t_k,t_k+{\tau }_P\Delta )\hfill \end{array}$$

(5c)

$$\begin{array}{c}\tilde{x}(t_k)=x(t_k)\hfill \\ V(\tilde{x}(t))<{\rho }_e^{\prime },\forall t\in [t_k,t_k+{\tau }_P\Delta )\hfill \end{array}$$

(5d)

$$\begin{array}{c}\mathrm{if}x(t_k)\in {\Omega }_{{\rho }_e^{\prime }}^{\mathrm{o}}\hfill \\ S(\tilde{x}(t))\le S_{TH},\forall t\in [t_k,t_k+{\tau }_P\Delta )\hfill \end{array}$$

(5e)

$$\begin{array}{c}\mathrm{if}S(x(t_k))\le S_{TH}\hfill \\ \dot{V}(x(t_k),u(t_k))\le \dot{V}(x(t_k),{\Phi }_n(x(t_k))),\hfill \end{array}$$

(5f)

$$\begin{array}{c}\mathrm{if}x(t_k)\in {\Omega }_{{\rho }^{\prime }}\backslash {\Omega }_{{\rho }_e^{\prime }}^{\mathrm{o}}\mathrm{or}S(x(t_k))>S_{TH}\hfill \end{array}$$

(5g)

where $\tilde{x}$ is the predicted state trajectory, $ST(\Delta )$ is the set of piecewise constant functions with sampling period $\Delta$, ${\tau }_P$ is the number of sampling periods of the prediction horizon and $\dot{V}=L_{f}V(x)+L_{g}V(x)u$. ${\Phi }_n(x)$ is the stabilizing feedback control law designed for the nominal system of Equation (1) with $w(t)\equiv 0$ such that the origin of the system of Equation (1) can be rendered asymptotically stable. Under the controller ${\Phi }_n(x)$, we first characterize the set ${\varphi }_n:=\{x\in {\mathbf{R}}^n|\dot{V}+\kappa V(x)\le 0,u={\Phi }_n(x)\in U,\kappa >0\}$ and choose the level set ${\Omega }_{{\rho }^{\prime }}:=\{x\in {\varphi }_n|V(x)\le {\rho }^{\prime }\}$ inside ${\varphi }_n$ as the stability region. ${\Omega }_{{\rho }_e^{\prime }}:=\{x\in {\mathbf{R}}^n|V(x)\le {\rho }_e^{\prime }\}$ where $0<{\rho }_e^{\prime }<{\rho }^{\prime }$ is further designed to make the region ${\Omega }_{{\rho }^{\prime }}$ a forward invariant set in the presence of sufficiently small bounded disturbances.

The constraint of Equation (5e) allows the cost function of Equation (5a) to be maximized while keeping the predicted closed-loop state within ${\Omega }_{{\rho }_e^{\prime }}^{\mathrm{o}}$ if $x(t_k)\in {\Omega }_{{\rho }_e^{\prime }}^{\mathrm{o}}$. The safety constraint of Equation (5f) is applied to maintain the predictions of the closed-loop state within the safe operating region $\mathcal{S}:=\{x\in {\mathbf{R}}^n|S(x)\le S_{TH}\}$ if $x(t_k)\in \mathcal{S}$. On the other hand, if $x(t_k)\in {\Omega }_{{\rho }^{\prime }}\backslash {\Omega }_{{\rho }_e^{\prime }}^{\mathrm{o}}$ or $x(t_k)$ is outside of $\mathcal{S}$, the constraint of Equation (5g) is activated to decrease $V(x)$ such that $x(t)$ will move towards the origin within the current sampling period.

Remark 2.

Since the safe operating region $\mathcal{S}$ is not necessarily a forward invariant set based on the formulation of the Safeness Index function, the threshold $S_{TH}$ set on the Safeness Index may define a region that is irregularly shaped, for example the grey region in Figure 1 [2] corresponding to a chemical reactor example similar to the one in the section “Application to a Chemical Process Example” of this manuscript. Therefore, the existence of feasible solutions (i.e., the satisfaction of the constraints of Equation (5)) of the Safeness Index-based LEMPC is not guaranteed in $\mathcal{S}$ due to the constraint of Equation (5f). Additionally, $S(x(t))$ may not even decrease under the constraint of Equation (5g) due to the same reason (that $\mathcal{S}$ is not an invariant set). Considering the above feasibility issue in the formulation of the Safeness Index-based LEMPC, a new Safeness Index-based LEMPC is developed in the following subsection by using multiple Lyapunov functions to characterize the safe operating region $\mathcal{S}$.

3.3. Safeness Index-Based LEMPC Using Multiple Level Sets

The improved Safeness Index-based LEMPC for the nominal system of Equation (1) with $w(t)\equiv 0$ is developed utilizing the level sets of two Lyapunov functions $V_1$ and $V_2$ to characterize the safe and unsafe operating regions. Throughout this work, we assume that the shape of the stability regions, $\mathcal{D}$, and their intersection are amenable to the treatment in this work, such as the use of only two Lyapunov functions in the LEMPC design and also the types of overlap of the stability regions described. Specifically, as shown in Figure 2, we define two level sets: ${\Omega }_{{\rho }^{\prime }}:=\{x\in {\varphi }_n^{\prime }|V_1(x)\le {\rho }^{\prime }\}$ and ${\mathcal{U}}_{s^{\prime }}:=\{x\in {\varphi }_n^{\prime }|V_2(x)\le s^{\prime }\}$ inside ${\varphi }_n^{\prime }:=\{x\in {\mathbf{R}}^n|{\dot{V}}_i+\kappa V_i(x)\le 0,i=1,2,u={\Phi }_n(x)\in U,\kappa >0\}$, from which the origin of the nominal system of Equation (1) is rendered asymptotically stable.

${\Omega }_{{\rho }^{\prime }}$ represents the stability region as it is in the Safeness Index-based LEMPC of Equation (5), and ${\mathcal{U}}_{s^{\prime }}$ is designed to exclude the unsafe region $\mathcal{D}$ where $S(x)>S_{TH}$. Therefore, the safe operating region $\mathcal{S}$ becomes the union of $S_1:={\Omega }_{{\rho }^{\prime }}\cap {\mathcal{U}}_{s^{\prime }}$ and $S_2:={\Omega }_{{\rho }^{\prime }}\backslash (S_1\cup \mathcal{D})$ in Figure 2. This new Safeness Index-based LEMPC design is formulated by the following optimization problem:

$$\begin{array}{c}\underset{u\in ST(\Delta )}{\max }{\int }_{t_k}^{t_k+{\tau }_P\Delta }{L}_e(\tilde{x}(t),u(t))dt\hfill \end{array}$$

(6a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \dot{\tilde{x}}(t)=f(\tilde{x}(t))+g(\tilde{x}(t))u(t)\hfill \end{array}$$

(6b)

$$\begin{array}{c}\tilde{x}(t_k)=x(t_k)\hfill \end{array}$$

(6c)

$$\begin{array}{c}u(t)\in U,\forall t\in [t_k,t_k+{\tau }_P\Delta )\hfill \\ V_1(\tilde{x}(t))<{\rho }_e^{\prime },\hfill \end{array}$$

(6d)

$$\begin{array}{c}\mathrm{if}x(t_k)\in {\Omega }_{{\rho }_e^{\prime }}^{\mathrm{o}},\forall t\in [t_k,t_k+{\tau }_P\Delta )\hfill \\ V_2(\tilde{x}(t))<s_e^{\prime },\hfill \end{array}$$

(6e)

$$\begin{array}{c}\mathrm{if}x(t_k)\in {\mathcal{U}}_{s_e^{\prime }}^{\mathrm{o}},\forall t\in [t_k,t_k+{\tau }_P\Delta )\hfill \\ {\dot{V}}_i(x(t_k),u(t_k))\le {\dot{V}}_i(x(t_k),{\Phi }_n(x(t_k))),i=1,2\hfill \end{array}$$

(6f)

$$\begin{array}{c}\mathrm{if}x(t_k)\in {\Omega }_{{\rho }^{\prime }}\backslash {\Omega }_{{\rho }_e^{\prime }}^{\mathrm{o}},\mathrm{or}x(t_k)\in {\mathcal{U}}_{s^{\prime }}\backslash {\mathcal{U}}_{s_e^{\prime }}^{\mathrm{o}}\hfill \end{array}$$

(6g)

where the notation follows that in Equation (5). ${\Omega }_{{\rho }_e^{\prime }}$ and ${\mathcal{U}}_{s_e^{\prime }}$ are again chosen as the level sets inside ${\varphi }_n^{\prime }$ to make ${\Omega }_{{\rho }^{\prime }}$ and ${\mathcal{U}}_{s^{\prime }}$ forward invariant sets, respectively. In the optimization problem of Equation (6), the objective function of Equation (6a) is the integral of $L_e(\tilde{x}(t),u(t))$ over the prediction horizon. The constraint of Equation (6b) is the nominal system of Equation (1) with $w(t)\equiv 0$ that is used to predict the states of the closed-loop system. Equation (6c) defines the initial condition $\tilde{x}(t_k)$ of the optimization problem determined from a state measurement $x(t_k)$ at $t=t_k$. Equation (6d) represents the input constraints applied over the entire prediction horizon. The constraint of Equation (6e) maintains the predicted states in ${\Omega }_{{\rho }_e^{\prime }}^{\mathrm{o}}$ when the current state $x(t_k)\in {\Omega }_{{\rho }_e^{\prime }}^{\mathrm{o}}$. Similarly, the constraint of Equation (6f) maintains the predicted states in ${\mathcal{U}}_{s_e^{\prime }}^{\mathrm{o}}$ when $x(t_k)\in {\mathcal{U}}_{s_e^{\prime }}^{\mathrm{o}}$. The contractive constraint of Equation (6g) is activated to decrease both $V_1$ and $V_2$ such that the closed-loop state enters the smaller level sets of $V_1$ and $V_2$ (i.e., towards the interior of ${\mathcal{S}}_1$). Therefore, under the Safeness Index-based LEMPC of Equation (6), if $x(t_k)\in {\mathcal{S}}_1$, the constraints of Equations (6e)–(6g) maintain the closed-loop state in ${\mathcal{S}}_1$. If $x(t_k)\in {\mathcal{S}}_2$, the constraints of Equations (6e) and (6g) are applied to maintain the closed-loop state in ${\Omega }_{{\rho }^{\prime }}$, under which $x(t)$ will stay in ${\mathcal{S}}_2$ or enter ${\mathcal{S}}_1$ in some time.

Remark 3.

Based on the Safeness Index function $S(x)$ and its threshold $S_{TH}$, the level set ${\mathcal{U}}_{s^{\prime }}$ of the Lyapunov function $V_2$ is chosen to exclude the unsafe region $\mathcal{D}$ that is originally in the level set ${\Omega }_{{\rho }^{\prime }}$ of the Lyapunov function $V_1$ as shown in Figure 2. Since ${\mathcal{U}}_{s^{\prime }}$ and ${\Omega }_{{\rho }^{\prime }}$ are both forward invariant sets for the nominal system (or the system with sufficiently small bounded disturbances) of Equation (1) under the controller ${\Phi }_n(x)\in U$ that satisfies ${\dot{V}}_i+\kappa V_i(x)\le 0,i=1,2,\kappa >0$, it follows that under the corresponding constraint of Equation (6g), the overlapping region ${\mathcal{S}}_1$ is also an invariant set. Therefore, the infeasibility problem caused by the Safeness Index constraint of Equation (5f) is solved by introducing the second level set ${\mathcal{U}}_{s^{\prime }}$ into the LEMPC design. For the remaining part of the safe operating region ${\mathcal{S}}_2$, the constraints of Equations (6e) and (6g) are utilized to ensure that the closed-loop state stays in ${\Omega }_{{\rho }^{\prime }}$ all the time, which is similar to closed-loop stability under the traditional LEMPC [4]. Since the sampling period $\Delta$ has to be sufficiently small in the sample-and-hold implementation of the Safeness Index-based LEMPC of Equation (6), we can utilize a sufficiently small $\Delta$ such that $x(t_{k+1})$ is unable to jump into $\mathcal{D}$ within one sampling period if $x(t_k)\in {\mathcal{S}}_2$. This implies that at the next sampling time, the state $x(t_{k+1})$ either stays in ${\mathcal{S}}_2$ or enters ${\mathcal{S}}_1$ via the boundary between ${\mathcal{S}}_1$ and ${\mathcal{S}}_2$. In both cases, it is considered that the state is maintained in the safe operating region according to Definition 3.

Remark 4.

Besides the above development of Safeness Index-based LEMPC using multiple Lyapunov functions, there are also other methods that can guarantee the feasibility of the Safeness Index-based constraint in the LEMPC design. For example, in the optimization problem of Equation (5), we can choose a more conservative level set of $V(x)$ (i.e., a small level set inside ${\Omega }_{{\rho }^{\prime }}$ that excludes $\mathcal{D}$) as the safe operating region. However, if the unsafe region characterized by the Safeness Index function is a set of points inside the stability region and is difficult to exclude by a single level set like ${\mathcal{U}}_{s^{\prime }}$, we may want to use control Lyapunov barrier functions to design the constraints that account for the unsafe region in state-space [15] and overcome the infeasibility problem.

3.4. Stochastic Safeness Index-Based LEMPC

Inspired by the Safeness Index-based LEMPC design of Equation (6), the stochastic Safeness Index-based LEMPC design is given by the following optimization problem:

$$\begin{array}{c}\underset{u\in ST(\Delta )}{\max }{\int }_{t_k}^{t_k+{\tau }_P\Delta }{L}_e(\tilde{x}(t),u(t))dt\hfill \end{array}$$

(7a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \dot{\tilde{x}}(t)=f(\tilde{x}(t))+g(\tilde{x}(t))u(t)\hfill \end{array}$$

(7b)

$$\begin{array}{c}\tilde{x}(t_k)=x(t_k)\hfill \end{array}$$

(7c)

$$\begin{array}{c}u(t)\in U,\forall t\in [t_k,t_k+{\tau }_P\Delta )\hfill \\ V_1(\tilde{x}(t))<{\rho }_e,\hfill \end{array}$$

(7d)

$$\begin{array}{c}\mathrm{if}x(t_k)\in {\Omega }_{{\rho }_e}^{\mathrm{o}},\forall t\in [t_k,t_k+{\tau }_P\Delta )\hfill \\ V_2(\tilde{x}(t))<s_e,\hfill \end{array}$$

(7e)

$$\begin{array}{c}\mathrm{if}x(t_k)\in {\mathcal{U}}_{s_e}^{\mathrm{o}},\forall t\in [t_k,t_k+{\tau }_P\Delta )\hfill \\ \mathcal{L}{V}_i(x(t_k),u(t_k))\le \mathcal{L}{V}_i(x(t_k),{\Phi }_s(x(t_k))),i=1,2\hfill \end{array}$$

(7f)

$$\begin{array}{c}\mathrm{if}x(t_k)\in {\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}},\mathrm{or}x(t_k)\in {\mathcal{U}}_s\backslash {\mathcal{U}}_{s_e}^{\mathrm{o}}\hfill \end{array}$$

(7g)

where the notation follows that in Equation (6) except using $\rho$, ${\rho }_e$, s, $s_e$, ${\Phi }_s(x)$ and $\mathcal{L}V$ to replace ${\rho }^{\prime }$, ${\rho }_e^{\prime }$, $s^{\prime }$, $s_e^{\prime }$, ${\Phi }_n(x)$ and $\dot{V}$, respectively. For the system of Equation (1) with multiple Lyapunov functions, ${\varphi }_d$ is characterized as: ${\varphi }_d=\{x\in {\mathbf{R}}^n|\mathcal{L}{V}_i+\kappa V_i(x)\le 0,i=1,2,u={\Phi }_s(x)\in U,\kappa >0\}$. ${\Omega }_{\rho }$, ${\Omega }_{{\rho }_e}$, ${\mathcal{U}}_s$ and ${\mathcal{U}}_{s_e}$ are level sets of $V_1$ and $V_2$ inside ${\varphi }_d$, where $0<{\rho }_e<\rho$ and $0<s_e<s$. Similar to the LEMPC designs of Equations (5) and (6), the optimal input trajectory determined by the optimization problem of the stochastic Safeness Index-based LEMPC is denoted by $u^{\ast }(t)$, which is calculated over the entire prediction horizon $t\in [t_k,t_k+{\tau }_P\Delta )$. The control action computed for the first sampling period of the prediction horizon $u^{\ast }(t_k)$ is sent to the actuators to be applied over the sampling period, and the optimization problem of Equation (7) is re-solved at the next sampling time.

The constraint of Equation (7e) maintains the predicted state in ${\Omega }_{{\rho }_e}^{\mathrm{o}}$ when the current state $x(t_k)\in {\Omega }_{{\rho }_e}^{\mathrm{o}}$ and the constraint of Equation (7f) maintains the predicted state in ${\mathcal{U}}_{s_e}^{\mathrm{o}}$ when the current state $x(t_k)\in {\mathcal{U}}_{s_e}^{\mathrm{o}}$. However, if $x(t_k)\in {\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}}$ or $x(t_k)\in {\mathcal{U}}_s\backslash {\mathcal{U}}_{s_e}^{\mathrm{o}}$, the constraint of Equation (7g) is activated to decrease $V_1(x)$ and $V_2(x)$ such that it is possible that $x(t)$ moves back to ${\Omega }_{{\rho }_e}^{\mathrm{o}}\cap {\mathcal{U}}_{s_e}^{\mathrm{o}}$.

Since there exists a disturbance $w(t)$ with unbounded variation $dw(t)$ in the system of Equation (1), process operational safety (i.e., the closed-loop state is bounded in the safe operating region $\mathcal{S}$) can only be ensured in probability. Therefore, in the following sections, we will establish the probabilities of process operational safety of the system of Equation (1) under the stochastic Safeness Index-based LEMPC of Equation (7).

3.5. Sample-And-Hold Implementation

We first investigate the impact of the sample-and-hold implementation of Equation (7) on the stability of the closed-loop system of Equation (1) following similar arguments to those in [9,11]. Specifically, the probabilities of the sets ${\Omega }_{\rho }$ and ${\mathcal{U}}_s$ remaining invariant under the sample-and-hold implementation of the Safeness Index-based LEMPC of Equation (7) with a sampling period $\Delta$ are given as follows.

Theorem 1.

Consider the system of Equation (1) with ${\Omega }_{\rho }$ and ${\mathcal{U}}_s$ inside ${\varphi }_d$ under the control actions u computed by the LEMPC of Equation (7). Let $u(t)=u(t_k),\forall t\in [t_k,t_k+\Delta )$. Then, given any probability $\lambda \in (0,1]$, there exist positive real numbers ${\rho }_s<{\rho }_e<\rho$ and ${\rho }_s<s_e<s$ where ${\Omega }_{{\rho }_s}$ and ${\mathcal{U}}_{{\rho }_s}$ are level sets of $V_1$ and $V_2$, respectively, around the origin where $\mathcal{L}{V}_i,i=1,2$ are not required to remain negative for the nominal system of Equation (1) under the sample-and-hold implementation of $u(t)$, and there also exists a sampling period ${\Delta }^{\ast }:={\Delta }^{\ast }(\lambda )$, such that if $\Delta \in (0,{\Delta }^{\ast }]$, then:

$$\mathbf{P}(\underset{t\in [0,\Delta ]}{\sup }{V}_1(x(t))<\rho )\ge 1-\lambda ,\forall x(0)\in {\Omega }_{{\rho }_e}^{\mathrm{o}}$$

(8)

$$\mathbf{P}(\underset{t\in [0,\Delta ]}{\sup }{V}_2(x(t))<s)\ge 1-\lambda ,\forall x(0)\in {\mathcal{U}}_{s_e}^{\mathrm{o}}$$

(9)

$$\begin{array}{c}\hfill \mathbf{P}(\underset{t\in [0,\Delta ]}{\sup }\mathcal{L}{V}_i(x(t))<-ϵ<0)\ge 1-\lambda ,i=1,2,\\ \forall x(0)\in ({\Omega }_{\rho }\cup {\mathcal{U}}_s)\backslash ({\Omega }_{{\rho }_s}^{\mathrm{o}}\cap {\mathcal{U}}_{{\rho }_s}^{\mathrm{o}})\hfill \end{array}$$

(10)

Proof. 

Let $A_B:=\{w:{\sup }_{t\in [0,{\Delta }^{\ast }]}\left|w(t)\right|\le B\}$. Using the results for standard Brownian motion [16], given any probability $\lambda \in (0,1]$, there exists a sufficiently small B, s.t. $P(A_B)=1-\lambda$. For each realization $x_w(t)$ with $x(0)\in {\Omega }_{\rho }\cup {\mathcal{U}}_s$ and $w\in A_B$, there almost surely exists a positive real number $k_1$, s.t. ${\sup }_{t\in [0,{\Delta }^{\ast }]}|x_w(t)-x(0)|\le k_1{({\Delta }^{\ast })}^r$, where $r<1/2$, according to the local Hölder continuity. Therefore, the probability of the event $A_W:=\{w:{\sup }_{t\in [0,{\Delta }^{\ast }]}|x(t)-x(0)|\le k_1{({\Delta }^{\ast })}^r\}$ is:

$$\mathbf{P}(A_W)\ge 1-\lambda$$

(11)

We first prove that the probabilities of Equations (8) and (9) hold for the first sampling period. It should be noted that the probabilities of Equations (8)–(10) can be generalized to any sampling period $t\in [t_k,t_k+\Delta ]$ with the measurement of $x(t_k)$ playing the role of $x(0)$ in Equations (8)–(10).

Since $V_i(x),i=1,2$ satisfies the local Lipschitz condition, there exist positive real numbers $k_{2i},i=1,2$, such that $|V_i(x(t))-V_i(x(0))|\le k_{2i}|x(t)-x(0)|$, $i=1,2$. Therefore, for all $w\in A_W$, if ${\Delta }^{\ast }<{\Delta }_1={(\frac{\rho -{\rho }_e}{k_{21}{k}_1})}^{(\frac{1}{r})}$, it follows that $|V_1(x_w(t))-V_1(x(0))|<\rho -{\rho }_e,\forall t\le {\Delta }^{\ast }$. Furthermore, $\forall x(0)\in {\Omega }_{{\rho }_e}^{\mathrm{o}}$, it is obtained that $V_1(x_w(t))<\rho$, $\forall t\le {\Delta }^{\ast }$ since $-(\rho -{\rho }_e)<V_1(x(t))-V_1(x(0))<\rho -{\rho }_e$ and ${\sup }_{x(0)\in {\Omega }_{{\rho }_e}^{\mathrm{o}}}{V}_1(x(0))={\rho }_e$. Therefore, if $x(0)\in {\Omega }_{{\rho }_e}^{\mathrm{o}}$, the probability of $x(t)$ staying inside ${\Omega }_{\rho }$ is $\mathbf{P}({\sup }_{t\in [0,{\Delta }^{\ast }]}{V}_1(x(t))<\rho )\ge 1-\lambda$. Similarly, if ${\Delta }^{\ast }<{\Delta }_2={(\frac{s-s_e}{k_{22}{k}_1})}^{(\frac{1}{r})}$, for any $x(0)\in {\mathcal{U}}_{s_e}^{\mathrm{o}}$, the probability of $x(t)$ staying inside ${\mathcal{U}}_s$ is $\mathbf{P}({\sup }_{t\in [0,{\Delta }^{\ast }]}{V}_2(x(t))<s)\ge 1-\lambda$.

We now prove the probability of Equation (10) by using the equation $\mathcal{L}{V}_i(x(t))=\mathcal{L}{V}_i(x(0))+(\mathcal{L}{V}_i(x(t))-\mathcal{L}{V}_i(x(0)))$, $\forall t\in [0,{\Delta }^{\ast }],i=1,2$. It is shown that there exists a positive real number $ϵ$ such that $\mathcal{L}{V}_i(x(t))<-ϵ$ holds $\forall x(0)\in ({\Omega }_{\rho }\cup {\mathcal{U}}_s)\backslash ({\Omega }_{{\rho }_s}^{\mathrm{o}}\cap {\mathcal{U}}_{{\rho }_s}^{\mathrm{o}})$ for the nominal system of Equation (1) based on the definition of the value of $\mathcal{L}{V}_i$ in ${\varphi }_d$. However, $\mathcal{L}{V}_i(x(t))<-ϵ$ only holds in probability for the system in the presence of the disturbances $w(t)$. Based on the local Lipschitz conditions of $L_f{V}_i(x)$, $L_g{V}_i(x)$ and $h{(x(t))}^T\frac{{\partial }^2{V}_i(x(t))}{\partial x^2}h(x(t))$, there exist positive real numbers $k_3$, $k_4$, $k_5$, such that $|L_f{V}_i(x(t))-L_f{V}_i(x(0))|$ $\le k_3|x(t)-x(0)|$, $|L_g{V}_i(x(t))-L_g{V}_i(x(0))|$ $\le k_4|x(t)-x(0)|$, $|\frac{1}{2}Tr\{h{(x(t))}^T\frac{{\partial }^2{V}_i(x(t))}{\partial x^2}h(x(t))\}-$ $\frac{1}{2}Tr$ $\{h{(x(0))}^T$ $\frac{{\partial }^2{V}_i(x(0))}{\partial x^2}h(x(0))\}|$ $\le k_5|x(t)-x(0)|$, $i=1,2$.

Let $0<ϵ<\kappa {\rho }_s$ and ${\Delta }^{\ast }<{\Delta }_3={(\frac{\kappa {\rho }_s-ϵ}{k_1(k_3+k_4+k_5)})}^{(\frac{1}{r})}$. It follows from $\mathcal{L}{V}_i(x(t))\le \mathcal{L}{V}_i(x(0))+|\mathcal{L}{V}_i(x(t))-\mathcal{L}{V}_i(x(0))|<\mathcal{L}{V}_i(x(0))+\kappa {\rho }_s-ϵ$ (which follows from the application of the Lipschitz properties of the components of $\mathcal{L}{V}_i$ with ${\Delta }^{\ast }<{\Delta }_3$) and the fact that $x(0)\in ({\Omega }_{\rho }\cup {\mathcal{U}}_s)\backslash ({\Omega }_{{\rho }_s}^{\mathrm{o}}\cap {\mathcal{U}}_{{\rho }_s}^{\mathrm{o}})$ and $\mathcal{L}{V}_i(x_0)<-\kappa V_i(x(0))$, that $\forall w\in A_W$, $\mathcal{L}{V}_i(x_w(t))<-ϵ<0$, $\forall t\le {\Delta }^{\ast },i=1,2$ holds. Therefore, by choosing the sampling period $\Delta \in (0,{\Delta }^{\ast }]$, given any initial condition $x(0)\in ({\Omega }_{\rho }\cup {\mathcal{U}}_s)\backslash ({\Omega }_{{\rho }_s}^{\mathrm{o}}\cap {\mathcal{U}}_{{\rho }_s}^{\mathrm{o}})$, the probability that $\mathcal{L}{V}_i(x(t))<-ϵ$ is as follows: $\mathbf{P}({\sup }_{t\in [0,{\Delta }^{\ast }]}\mathcal{L}{V}_i(x(t))<-ϵ,i=1,2)\ge 1-\lambda$. Finally, let ${\Delta }^{\ast }\le \min \{{\Delta }_1,{\Delta }_2,{\Delta }_3\}$, and the probabilities of Equations (8)–(10) are all satisfied for $\Delta \in (0,{\Delta }^{\ast }]$. ☐

3.6. Stability in Probability

Based on the results from the above section, the probabilistic process operational safety of the closed-loop system of Equation (1) under the Safeness Index-based LEMPC of Equation (7) applied in a sample-and-hold fashion is established by the following theorem.

Theorem 2.

Consider the system of Equation (1) under the stochastic Safeness Index-based LEMPC of Equation (7) applied in a sample-and-hold implementation (i.e., $u(t)=u(i\Delta )$, $\forall i\Delta \le t<(i+1)\Delta$, $i=0,1,2,\dots$). Then, given ${\rho }_e\in (0,\rho )$, $s_e\in (0,s)$ and probability $\lambda \in (0,1]$, there exist a sampling time $\Delta \in (0,{\Delta }^{\ast }(\lambda )]$ and probabilities $\beta ,{\beta }^{\prime },\gamma ,{\gamma }^{\prime }\in [0,1]$:

$$\frac{{\sup }_{x\in \partial {\Omega }_{{\rho }_e}}{V}_1(x)}{{\inf }_{x\in {\mathbf{R}}^n\backslash {\Omega }_{\rho }}{V}_1(x)}\le \beta$$

(12a)

$$\frac{{\sup }_{x\in \partial {\mathcal{U}}_{s_e}}{V}_2(x)}{{\inf }_{x\in {\mathbf{R}}^n\backslash {\mathcal{U}}_s}{V}_2(x)}\le {\beta }^{\prime }$$

(12b)

$$\max \{\frac{V_1(x(0))}{\rho },\beta \}\le \gamma$$

(12c)

$$\max \{\frac{V_2(x(0))}{s},{\beta }^{\prime }\}\le {\gamma }^{\prime }$$

(12d)

such that the following probabilities hold:

$$\begin{array}{c}\mathbf{P}(\underset{t\in [0,\Delta )}{\sup }{V}_1(x(t))<\rho ,\underset{t\in [0,\Delta )}{\sup }{V}_2(x(t))<s)\\ \ge (1-\beta )(1-{\beta }^{\prime })(1-\lambda ),\forall x(0)\in {\mathcal{S}}_{1e}\hfill \end{array}$$

(13)

$$\begin{array}{c}\mathbf{P}(\underset{t\in [0,\Delta )}{\sup }{V}_1(x(t))<\rho )\hfill \\ \ge (1-\beta )(1-\lambda ),\forall x(0)\in {\mathcal{S}}_{2e}\hfill \end{array}$$

(14)

$$\begin{array}{c}\mathbf{P}({\tau }_{{\mathbf{R}}^n\backslash {\mathcal{S}}_{1e}}(\Delta )\le {\tau }_{{\mathcal{S}}_1}(\Delta ))\hfill \\ \ge (1-\gamma )(1-{\gamma }^{\prime })(1-\lambda ),\forall x(0)\in {\mathcal{S}}_1\backslash {\mathcal{S}}_{1e}^{\mathrm{o}}\hfill \end{array}$$

(15)

where ${\mathcal{S}}_e:={\mathcal{S}}_{1e}\cup {\mathcal{S}}_{2e}$ is a subset of $\mathcal{S}$ that subtracts the risk margins $\rho -{\rho }_e$ and $s-s_e$. The relationship among the sets ${\mathcal{S}}_{1e}:={\Omega }_{{\rho }_e}\cap {\mathcal{U}}_{s_e}$ and ${\mathcal{S}}_{2e}:={\mathcal{S}}_e\backslash {\mathcal{S}}_{1e}$ and the unsafe region $\mathcal{D}$ are shown in Figure 3.

Proof. 

The proof consists of three parts. We first show that under the Safeness Index-based LEMPC of Equation (7), any state trajectory initiated from $x(0)\in {\mathcal{S}}_{1e}$ has the probability defined by Equation (13) of staying in ${\mathcal{S}}_1:={\Omega }_{\rho }\cap {\mathcal{U}}_s$. However, if $x(0)\in {\mathcal{S}}_{2e}$, we prove that under the Safeness Index-based LEMPC of Equation (7), there exists the probability of Equation (14) for the state of the closed-loop system to stay in ${\Omega }_{\rho }$ and with a sufficiently small $\Delta$ to stay in the part of ${\Omega }_{\rho }$ that excludes $\mathcal{D}$. Finally, if $x(0)$ is inside ${\mathcal{S}}_1\backslash {\mathcal{S}}_{1e}^{\mathrm{o}}$, we can show that the closed-loop state trajectory reaches the boundary of ${\mathcal{S}}_{1e}$ first before it leaves ${\mathcal{S}}_1$ (implying it does not enter $\mathcal{D}$) with the probability of Equation (15). However, if $x(0)\in {\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^o$ and $x(0)\notin ({\mathcal{U}}_s\cup \mathcal{D})$ (i.e., the white risk margin around ${\mathcal{S}}_{2e}$ in Figure 3), we show that it does not enter $\mathcal{D}$, $\forall t\in [0,\Delta )$ in probability, as well. Additionally, for the sake of simplicity, we denote the probabilities and expectations conditional on the event of $A_W$ given in the section “Sample-And-Hold Implementation” as ${\mathbf{P}}^{\ast }(·)$ and ${\mathbf{E}}^{\ast }(·)$.

$Part1$: To show that Equation (13) holds for all $x(0)\in {\mathcal{S}}_{1e}$, we consider both the case that $x(0)\in S_{1e}^o$ and that $x(0)\in \partial S_{1e}$. The former case is handled by Equations (8) and (9). Specifically, if $x(0)\in S_{1e}^o$, then both $x(0)\in {\Omega }_{{\rho }_e}^o$ and also $x(0)\in {\mathcal{U}}_{s_e}^o$. Then, $\mathbf{P}({\sup }_{t\in [0,\Delta )}{V}_1(x(t))<\rho$, ${\sup }_{t\in [0,\Delta )}{V}_2(x(t))<s)\ge 1-\lambda$ (Equations (8) and (9) for ${\Delta }^{\ast }\le \min \{{\Delta }_1,{\Delta }_2\}$). Since $(1-\lambda )\ge (1-\beta )(1-{\beta }^{\prime })(1-\lambda )$ for $\beta \in [0,1]$, ${\beta }^{\prime }\in [0,1]$, Equation (13) holds when $x(0)\in S_{1e}^o$. When $x(0)\in \partial {\mathcal{S}}_{1e}$, Equation (13) is also satisfied. To show this, we first assume $x(0)\in \partial {\Omega }_{{\rho }_e}$ and prove that the probability of $x(t)$ staying in ${\Omega }_{\rho }$ within one sampling period conditioned on the event of $A_W$ is $(1-\beta )$. When $x(0)\in \partial {\Omega }_{{\rho }_e}$, Equation (7g) will be utilized in the LEMPC of Equation (7). Under the constraint of Equation (7g), the optimization problem of Equation (7) is solved such that $\mathcal{L}{V}_1$ is forced to be negative for any $x(t_k)\in {\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}}$, which implies that Equation (10) holds (i.e., $\mathcal{L}{V}_1<-ϵ$ for $t\in [0,\Delta ]$ with the probability of the event $A_W$). Using Dynkin’s formula [17], the following equation can be derived:

$$\begin{array}{c}{\mathbf{E}}^{\ast }(V_1(x({\tau }_{{\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}}}(t))))\hfill \\ =V_1(x(0))+{\mathbf{E}}^{\ast }({\int }_0^{{\tau }_{{\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}}}(t)}\mathcal{L}{V}_1(x(s))ds)\hfill \end{array}$$

(16)

The following probability is derived using similar arguments as in [11], for all $x(0)\in \partial {\Omega }_{{\rho }_e}$:

$$\begin{array}{c}{\mathbf{P}}^{\ast }(V_1(x(t))\ge \rho ,\mathrm{for}\mathrm{some}t\in [0,\Delta ))\\ \le \frac{V_1(x(0))}{{\inf }_{x\in {\mathbf{R}}^n\backslash {\Omega }_{\rho }}{V}_1(x)}\hfill \end{array}$$

(17)

Bounding Equation (17) with Equation (12a) and taking the complementary events, the following probability is obtained:

$$\underset{x(0)\in \partial {\Omega }_{{\rho }_e}}{\inf }{\mathbf{P}}^{\ast }(V_1(x(t))<\rho ,\forall t\in [0,\Delta ))\ge (1-\beta )$$

(18)

Using the same steps as performed above, we can prove that $\forall x(0)\in \partial {\mathcal{U}}_{s_e}$, the probability of $x(t)$ staying in ${\mathcal{U}}_s$ within one sampling period conditioned on the event of $A_W$ is as follows:

$$\underset{x(0)\in \partial {\mathcal{U}}_{s_e}}{\inf }{\mathbf{P}}^{\ast }(V_2(x(t))<s,\forall t\in [0,\Delta ))\ge (1-{\beta }^{\prime })$$

(19)

Since the set of initial conditions $x(0)\in {\mathcal{S}}_{1e}$ is the intersection of ${\Omega }_{{\rho }_e}$ and ${\mathcal{U}}_{s_e}$, by combining the probabilities of Equations (18) and (19) together and using Equation (10), the probability of Equation (13) is obtained via the definition of conditional probability.

$Part2$: If $x(0)\in S_{2e}\subset {\Omega }_{{\rho }_e}$, then either $x(0)\in {\Omega }_{{\rho }_e}^o$ or $x(0)\in \partial {\Omega }_{{\rho }_e}$. If $x(0)\in S_{2e}$ and ${\Omega }_{{\rho }_e}^o$, then Equation (8) holds and $\mathbf{P}({\sup }_{t\in [0,\Delta )}{V}_1(x(t))<\rho )\ge 1-\lambda \ge (1-\beta )(1-\lambda )$ for $\beta \in [0,1]$, and Equation (14) therefore holds. If instead $x(0)\in S_{2e}$ and $\partial {\Omega }_{{\rho }_e}$, then the results of Part 1 indicate that Equation (18) holds. Applying the definition of conditional probability, this also gives that Equation (14) holds. Moreover, we show that $x(t)$ is maintained inside the safe operating region $\mathcal{S}$ within one sampling period with the probability of Equation (14) (i.e., $\forall t\in [0,\Delta )$, $x(t)$ will not jump into $\mathcal{D}$ in probability). It is shown in the section “Sample-And-Hold Implementation” that $\forall t\in [0,\Delta )$, the change of $V_i(x)$ is limited (i.e., $|V_1(x(t))-V_1(x(0))|<k_1{k}_{21}{\Delta }^{\ast },\forall t\le {\Delta }^{\ast }$ and $|V_2(x(t))-V_2(x(0))|<k_1{k}_{22}{\Delta }^{\ast },\forall t\le {\Delta }^{\ast }$) with a sufficiently small sampling period ${\Delta }^{\ast }$ (maybe smaller than the one derived by ${\Delta }^{\ast }\le \min \{{\Delta }_1,{\Delta }_2,{\Delta }_3\}$). Therefore, if $x(0)\in {\mathcal{S}}_{2e}\subset {\Omega }_{{\rho }_e}$, $x(t)$ cannot move across the entire level set ${\mathcal{U}}_s$ and jump into $\mathcal{D}$ within a sufficiently small $\Delta$ with the probability $(1-\lambda )$. Instead, the closed-loop state at the next sampling time either stays in ${\mathcal{S}}_{2e}$ or moves into ${\mathcal{S}}_{1e}$ in probability. If $x(t)$ enters ${\mathcal{S}}_{1e}$, the probability of Equation (13) will be used to estimate the probability of closed-loop process operational safety thereafter. Because $(1-\lambda )\ge (1-\beta )(1-\lambda )$, for $\beta ,\lambda \in (0,1]$, Equation (14) establishes the probability of $x(t)$ staying in the safe operating region $\mathcal{S}$ within one sampling period $\forall x(0)\in {\mathcal{S}}_{2e}$.

$Part3$: If $x(0)\in {\mathcal{S}}_1\backslash {\mathcal{S}}_{1e}^{\mathrm{o}}$, we show that it is possible that the closed-loop state trajectory hits the boundary of ${\mathcal{S}}_{1e}^{\mathrm{o}}$ before it hits the boundary of ${\mathcal{S}}_1$. If both hitting times ${\tau }_{{\mathbf{R}}^n\backslash {\mathcal{S}}_{1e}}(\Delta )$ and ${\tau }_{{\mathcal{S}}_1}(\Delta )$ are longer than a sampling period $\Delta$, Equation (15) is trivially satisfied. However, if one of them or both occur within one sampling period, we show that the probability of Equation (15) holds by first showing that the extreme case that $x(0)\in ({\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}})\cap ({\mathcal{U}}_s\backslash {\mathcal{U}}_{s_e}^{\mathrm{o}})$ (which are the corners where the risk margins $\rho -{\rho }_e$ and $s-s_e$ overlap in Figure 3) satisfies Equation (15). We first show that the probability of the event $A_T:=\{{\tau }_{{\mathbf{R}}^n\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}}}>{\tau }_{{\Omega }_{\rho }}\}$ can be given as follows $\forall x(0)\in {\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}}$:

$${\mathbf{P}}^{\ast }({\tau }_{{\mathbf{R}}^n\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}}}>{\tau }_{{\Omega }_{\rho }})\le {\mathbf{P}}^{\ast }(\frac{V_1(x({\tau }_{{\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}}}))}{\rho }\ge 1)\le \frac{V_1(x(0))}{\rho }$$

(20)

The event $A_T$ indicates that the state of the closed-loop system of Equation (1) reaches the boundary of ${\Omega }_{\rho }$ before it reaches the boundary of ${\Omega }_{{\rho }_e}$. The probability of Equation (20) is determined via Equation (17) and the fact that the event $\{{\tau }_{{\mathbf{R}}^n\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}}}>{\tau }_{{\Omega }_{\rho }}\}$ belongs to the event $\{\frac{V_1(x({\tau }_{{\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}}}))}{\rho }\ge 1\}$. Assuming $x(0)\in \partial {\Omega }_{{\rho }_c}$, where ${\Omega }_{{\rho }_c}:=\{x\in {\varphi }_d|V_1(x)\le {\rho }_c\}$ and ${\rho }_c\in [{\rho }_e,\rho ]$, the following probability is derived by bounding Equation (20) by Equation (12c):

$$\underset{x(0)\in {\Omega }_{{\rho }_c}\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}}}{\sup }{\mathbf{P}}^{\ast }({\tau }_{{\mathbf{R}}^n\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}}}>{\tau }_{{\Omega }_{\rho }})\le \gamma$$

(21)

Using the same steps as performed above, we can prove that $\forall x(0)\in {\mathcal{U}}_s\backslash {\mathcal{U}}_{s_e}^{\mathrm{o}}$, the probabilities similar to Equations (20) and (21) are derived as follows:

$$\begin{array}{c}{\mathbf{P}}^{\ast }({\tau }_{{\mathbf{R}}^n\backslash {\mathcal{U}}_s^{\mathrm{o}}}>{\tau }_{{\mathcal{U}}_s})\le \frac{V_2(x(0))}{s}\hfill \end{array}$$

(22a)

$$\begin{array}{cc}\hfill \underset{x(0)\in {\mathcal{U}}_{s_c}\backslash {\mathcal{U}}_{s_e}^{\mathrm{o}}}{\sup }& {\mathbf{P}}^{\ast }({\tau }_{{\mathbf{R}}^n\backslash {\mathcal{U}}_{s_e}^{\mathrm{o}}}>{\tau }_{{\mathcal{U}}_s})\le {\gamma }^{\prime }\hfill \end{array}$$

(22b)

where ${\mathcal{U}}_{s_c}:=\{x\in {\varphi }_d|V_2(x)\le s_c\}$ and $s_c\in [s_e,s]$. Hence, the probability $\mathbf{P}({\tau }_{{\mathbf{R}}^n\backslash {\mathcal{S}}_{1e}}(\Delta )\le {\tau }_{{\mathcal{S}}_1}(\Delta ))$ (i.e., Equation (15)) for the case where $x(0)\in ({\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}})\cap ({\mathcal{U}}_s\backslash {\mathcal{U}}_{s_e}^{\mathrm{o}})\subset {\mathcal{S}}_1\backslash {\mathcal{S}}_{1e}^{\mathrm{o}}$ is obtained by taking the complementary event of Equations (21) and (22b) and using the definition of conditional probability. We now address the other two possibilities for $x(0)\in {\mathcal{S}}_1\backslash {\mathcal{S}}_{1e}^o$ besides $x(0)\in ({\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^o)\cap ({\mathcal{U}}_s\backslash {\mathcal{U}}_{s_e}^o)$, which are: (1) $x(0)\in ({\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^o)\cap {\mathcal{U}}_{s_e}^o$ and (2) $x(0)\in ({\mathcal{U}}_s\backslash {\mathcal{U}}_{s_e}^o)\cap {\Omega }_{{\rho }_e}^o$. Consider the case where $x(0)\in ({\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^o)\cap {\mathcal{U}}_{s_e}^o$. If $x(t)\in {\mathcal{U}}_{s_e}^o$, $\forall t\in [0,\Delta )$, then ${\mathbf{P}}^{\ast }({\tau }_{{\mathbf{R}}^n\backslash {\mathcal{S}}_{1e}}(\Delta )\le {\tau }_{{\mathcal{S}}_1}(\Delta ))$ = ${\mathbf{P}}^{\ast }({\tau }_{{\mathbf{R}}^n\backslash {\Omega }_{{\rho }_e}^{\mathrm{o}}}(\Delta )\le {\tau }_{{\Omega }_{\rho }}(\Delta ))$. If $x(t)$ enters ${\mathcal{U}}_s\backslash {\mathcal{U}}_{s_e}^o$ before it leaves ${\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^o$, for some $t\in [0,\Delta )$, then for sure it holds that ${\tau }_{{\mathbf{R}}^n\backslash {\mathcal{S}}_{1e}}(\Delta )<{\tau }_{{\mathcal{S}}_1}(\Delta )$ because the closed-loop state trajectory crosses the boundary of ${\mathcal{S}}_{1e}$ first. Therefore, Equation (15) holds for both cases. The same analysis can be performed for the case where $x(0)\in ({\mathcal{U}}_s\backslash {\mathcal{U}}_{s_e}^o)\cap {\Omega }_{{\rho }_e}^o$. However, if $x(0)\in {\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^o$ and $x(0)\notin ({\mathcal{U}}_s\cup \mathcal{D})$, it is readily shown that Equation (21) holds due to the fact that $x(0)\in {\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^o$. Additionally, since it is demonstrated in $Part2$ that the change of $V_i(x)$ within one sampling period is limited in probability, it follows that $\forall x(0)\in {\Omega }_{\rho }\backslash {\Omega }_{{\rho }_e}^o$ and $x(0)\notin ({\mathcal{U}}_s\cup \mathcal{D})$, $x(t)$ does not enter $\mathcal{D}$ in one sampling period with the probability of $1-\lambda$, which implies that the closed-loop state either stays in ${\mathcal{S}}_2$ or moves into ${\mathcal{S}}_1$ in probability. ☐

Remark 5.

The Safeness Index-based LEMPC of Equation (7) is unable to ensure process operational safety for the closed-loop system of Equation (1) because of stochastic disturbances with unbounded variation. Additionally, in order to achieve process operational safety with higher probability, we should characterize the safe operating region $\mathcal{S}$ well and design large enough risk margins (i.e., $\rho -{\rho }_e$ and $s-s_e$) to avoid frequent activations of backup safety systems. Specifically, in Theorem 2, it is shown that as ${\rho }_e$ and $s_e$ decrease, the probabilities of Equations (13)–(15) become larger, which implies that if we want to improve process operational safety, the Safeness Index-based LEMPC design of Equation (7) should be designed with more conservatism (i.e., choosing smaller ${\rho }_e$ and $s_e$). However, an operating region with smaller ${\rho }_e$ and $s_e$ in turn leads to less economic benefits, which is undesired for the Safeness Index-based LEMPC of Equation (7). Therefore, the uncertain process operational safety caused by stochastic disturbances with unbounded variation is essentially a trade-off between economic benefits and probabilistic process operational safety (i.e., in practice, we will choose a conservative operating region to make the process sufficiently safe with respect to the unbounded disturbances, especially considering the other safety systems online and the risks involved, while also optimizing process economics).

3.7. Feasibility in Probability

Recursive feasibility for the nominal system of Equation (1) with $w(t)\equiv 0$ under the Safeness Index-based LEMPC of Equation (6) is guaranteed since there always exists a solution (e.g., the Lyapunov-based controller ${\Phi }_n(x)$ in sample-and-hold) that satisfies all the constraints of Equation (6). Now, consider the system of Equation (1) that has disturbance $w(t)$ with unbounded variation. Recursive feasibility under the stochastic Safeness Index-based LEMPC of Equation (7) can only be guaranteed in probability over the operation period $t\in [0,{\tau }_N\Delta )$. The probability is established as follows, from which it is shown that the probabilistic bounds on recursive feasibility for the remainder of the entire time of operation decrease as the operation period becomes longer (however, this does not necessarily mean the closed-loop system will not remain recursively feasible because at every sampling time, the remaining time of operation decreases and therefore the probability that the LEMPC will remain recursively feasible for the remaining time of operation increases at the next sampling time if the closed-loop state was maintained within $\mathcal{S}$ throughout the prior sampling period).

Theorem 3.

Consider the system of Equation (1) under the stochastic Safeness Index-based LEMPC of Equation (7) applied in a sample-and-hold fashion. Then, if $x(0)\in \mathcal{S}$, let $V_1(x(t+i\Delta ))={\rho }_i<\rho ,V_2(x(t+i\Delta ))=s_i<s,i=0,1,\dots ,{\tau }_N-1$, and let $A_F$ represent the event that the optimization problem of Equation (7) is solved with the satisfaction of recursive feasibility for time $t\in [0,{\tau }_N\Delta )$. The probability of $A_F$ can be calculated as follows:

$$\mathbf{P}(A_F)\ge {(1-\lambda )}^{{\tau }_N}\prod _{i=0,1,...,{\tau }_N-1}(1-{\beta }_i)(1-{\beta }_i^{\prime })$$

(23)

where ${\beta }_i$ and ${\beta }_i^{\prime }$ are given as follows:

$$\begin{array}{c}\hfill {\beta }_i=\max \{\beta ,\frac{{\sup }_{x\in \partial {\Omega }_{{\rho }_i}}{V}_1(x)}{{\inf }_{x\in {\mathbf{R}}^n\backslash {\Omega }_{\rho }}{V}_1(x)}\}\end{array}$$

(24a)

$$\begin{array}{c}\hfill {\beta }_i^{\prime }=\max \{{\beta }^{\prime },\frac{{\sup }_{x\in \partial {\mathcal{U}}_{s_i}}{V}_2(x)}{{\inf }_{x\in {\mathbf{R}}^n\backslash {\mathcal{U}}_s}{V}_2(x)}\}\end{array}$$

(24b)

Proof. 

We can derive the probability of Equation (23) following similar arguments to those in [11]. Since the deterministic prediction model of Equation (7b) is used in the stochastic Safeness Index-based LEMPC of Equation (7), it follows that there always exists a solution $u(t)={\Phi }_s(\tilde{x}(t_q))\in U$, $\forall t\in [t_q,t_{q+1})$, $q=k,\dots ,k+{\tau }_P-1$ that satisfies the constraints of Equation (7d–g) over the prediction horizon provided that $x(t_k),t_k\ge 0$ is inside the safe operating region $\mathcal{S}$. Therefore, this implies that the probability of recursive feasibility (i.e., Equation (23)) is equal to the probability of closed-loop process operational safety over $t\in [0,{\tau }_N\Delta )$, which can be obtained via the recursive application of Equation (13) with ${\beta }_i$ and ${\beta }_i^{\prime }$ of Equation (24) and the definition of conditional probability. Additionally, it should be noted that if $x(0)\in {\mathcal{S}}_{2e}$, the state is not in $\partial {\mathcal{U}}_{s_i}$ in Equation (24). In this case, ${\beta }_i^{\prime }$ simply takes the value of ${\beta }^{\prime }$, and the probability of Equation (23) still holds since it is shown in the proof of Theorem 2 that the state either stays in ${\mathcal{S}}_2$ or moves into ${\mathcal{S}}_1$ with the probability of $1-\lambda$ (i.e., Equation (23) gives a conservative result in this case). ☐

Remark 6.

In Theorem 3, probabilistic process operational safety and probabilistic recursive feasibility over the operation period $t\in [0,{\tau }_N\Delta )$ are established for the closed-loop system of Equation (1) under the Safeness Index-based LEMPC of Equation (7). Due to the disturbance $w(t)$ with unbounded variation, the closed-loop state $x(t)$ may leave $\mathcal{S}$ at any sampling step, and thus, closed-loop process operational safety and recursive feasibility of the Safeness Index-based LEMPC of Equation (7) can only be derived in a probabilistic manner (i.e., $\forall t\in [0,{\tau }_N\Delta )$, these properties hold with the probability of Equation (23)). Since the existence of a feasible control action is only guaranteed in the safe operating region $\mathcal{S}$, backup safety systems should be designed to handle the process if the state exits the safe operating region. Additionally, since the probabilities of Equations (13)–(15) are less than one if ${\rho }_e<\rho$ and $s_e<s$, the probabilities of recursive feasibility and process operational safety for $t\in [0,{\tau }_N\Delta )$ decrease as the operation period ${\tau }_N\Delta$ becomes longer. However, it should be noted that this dependence is not unique to the MPC, but to all control designs that try to keep the process state within a specific region in state-space in the presence of stochastic disturbances with unbounded variation (i.e., the probability to keep the closed-loop state in $\mathcal{S}$ for all the remaining time of operation goes to zero at $t_0$ as the process operation time ${\tau }_N\to \infty$).

4. Application to a Chemical Process Example

A chemical process example is used to illustrate the application of the stochastic Safeness Index-based LEMPC of Equation (7) to maintain the closed-loop state within a safe operating region in state-space in probability. Specifically, a well-mixed, non-isothermal continuous stirred tank reactor (CSTR) where an irreversible second-order exothermic reaction takes place is considered. The reaction transforms a reactant A to a product B ($A\to B$). The inlet concentration of A, the inlet temperature and the feed volumetric flow rate of the reactor are $C_{A0}$, $T_0$ and F, respectively. The CSTR is equipped with a heating jacket that supplies/removes heat at a rate Q. The CSTR dynamic model is described by the following material and energy balance equations:

$$\begin{array}{cc}\hfill d{C}_A=& {\displaystyle \frac{F}{V_L}}(C_{A0}-C_A)dt-k_0{e}^{-E/RT}{C}_A^{2}dt\hfill \\ & +{\sigma }_1(C_A-C_{As})d{w}_1(t)\hfill \end{array}$$

(25a)

$$\begin{array}{cc}\hfill dT=& {\displaystyle \frac{F}{V_L}}(T_0-T)dt-{\displaystyle \frac{\Delta H{k}_0}{{\rho }_L{C}_p}}{e}^{-E/RT}{C}_A^{2}dt+{\displaystyle \frac{Q}{{\rho }_L{C}_p{V}_L}}dt\hfill \\ & +{\sigma }_2(T-T_s)d{w}_2(t)\hfill \end{array}$$

(25b)

where $C_A$ is the concentration of reactant A in the reactor, $V_L$ is the volume of the reacting liquid in the reactor, T is the temperature of the reactor and Q denotes the heat input rate. The concentration of reactant A in the feed is $C_{A0}$. The feed temperature and the volumetric flow rate are $T_0$ and F, respectively. The reacting liquid has a constant density of ${\rho }_L$ and a heat capacity of $C_p$. $\Delta H$, $k_0$, E and R represent the enthalpy of reaction, pre-exponential constant, activation energy and ideal gas constant, respectively. Process parameter values are given in

Table 1. Parameter values of the continuous stirred tank reactor (CSTR).

$T_0=300$ K	$F=5$ m${}^3$/h
$V_L=1$ m${}^3$	$E=5\times {10}^4$ kJ/kmol
$k_0=8.46\times {10}^6$ m${}^3$/kmol h	$\Delta H=-1.15\times {10}^4$ kJ/kmol
$C_p=0.231$ kJ/kg K	$R=8.314$ kJ/kmol K
$\rho =1000$ kg/m${}^3$	$C_{A{0}_s}=4$ kmol/m${}^3$
$Q_s=0.0$ kJ/h	$C_{A_s}=1.22$ kmol/m${}^3$
$T_s=438$ K

. The disturbance terms $d{w}_1$ and $d{w}_2$ in Equation (25) are independent standard Gaussian white noise with the standard deviations ${\sigma }_1=2.5\times {10}^{-3}$ and ${\sigma }_2=0.15$, respectively. It is noted that the disturbance terms of Equation (25) vanish at the steady state.

The initial steady-state of the CSTR is at $(C_{As},T_s)=(1.22{\mathrm{kmol}/\mathrm{m}}^3,438\mathrm{K})$, and $(C_{A{0}_s}{Q}_s)$ $=(4{\mathrm{kmol}/\mathrm{m}}^3,$ $0\mathrm{kJ}/\mathrm{h})$. The manipulated inputs are the inlet concentration of species A and the heat input rate, which are represented by the deviation variables $u_1=\Delta C_{A0}=C_{A0}-C_{A{0}_s}$ and $u_2=\Delta Q=Q-Q_s$, respectively. The manipulated inputs are bounded as follows: $|\Delta C_{A0}|\le 3.5{\mathrm{kmol}/\mathrm{m}}^3$ and $|\Delta Q|\le 5\times {10}^5\mathrm{kJ}/\mathrm{h}$. Therefore, the states and the inputs of the closed-loop system are represented by $x^T=[C_A-C_{As}T-T_s]$ and $u^T=[\Delta C_{A0}\Delta Q]$, respectively.

The control objective of the stochastic Safeness Index-based LEMPC of Equation (7) is to maximize the production rate of B, while maintaining the closed-loop state trajectories in the safe operating region $\mathcal{S}$ in probability. The objective function of Equation (7a) is the production rate of B: $L_e(\tilde{x},u)=k_0{e}^{-E/RT}{C}_A^2$. The Lyapunov functions are designed using the standard quadratic form $V_i(x)=x^T{P}_{i}x,i=1,2$, where the positive definite matrices $P_1=\left[\begin{array}{cc}1060& 22\\ 22& 0.52\end{array}\right]$ and $P_2=\left[\begin{array}{cc}1060& 10\\ 10& 5\end{array}\right]$ are chosen to characterize the set ${\varphi }_d$ for the stochastic system of Equation (25). The nonlinear feedback controllers in [13,18] are utilized as ${\Phi }_n(x)$ and ${\Phi }_s(x)$, respectively. The level sets of the Lyapunov functions $V_1(x)$ and $V_2(x)$ are chosen as $\rho =368$ and $s=8100$ to create a safe operating region $\mathcal{S}$. The explicit Euler method with an integration time step of $h_c={10}^{-4}$ h is applied to numerically simulate the dynamic model of Equation (25). The nonlinear optimization problem of the stochastic Safeness Index-based LEMPC of Equation (7) is solved using the IPOPT software package [19] with the sampling period $\Delta ={10}^{-2}$ h. With the fixed sampling period $\Delta ={10}^{-2}$ h, $\rho =368$ and $s=8100$, we focus on the impact of ${\rho }_e$ and $s_e$ on probabilistic process operational safety in the following simulations.

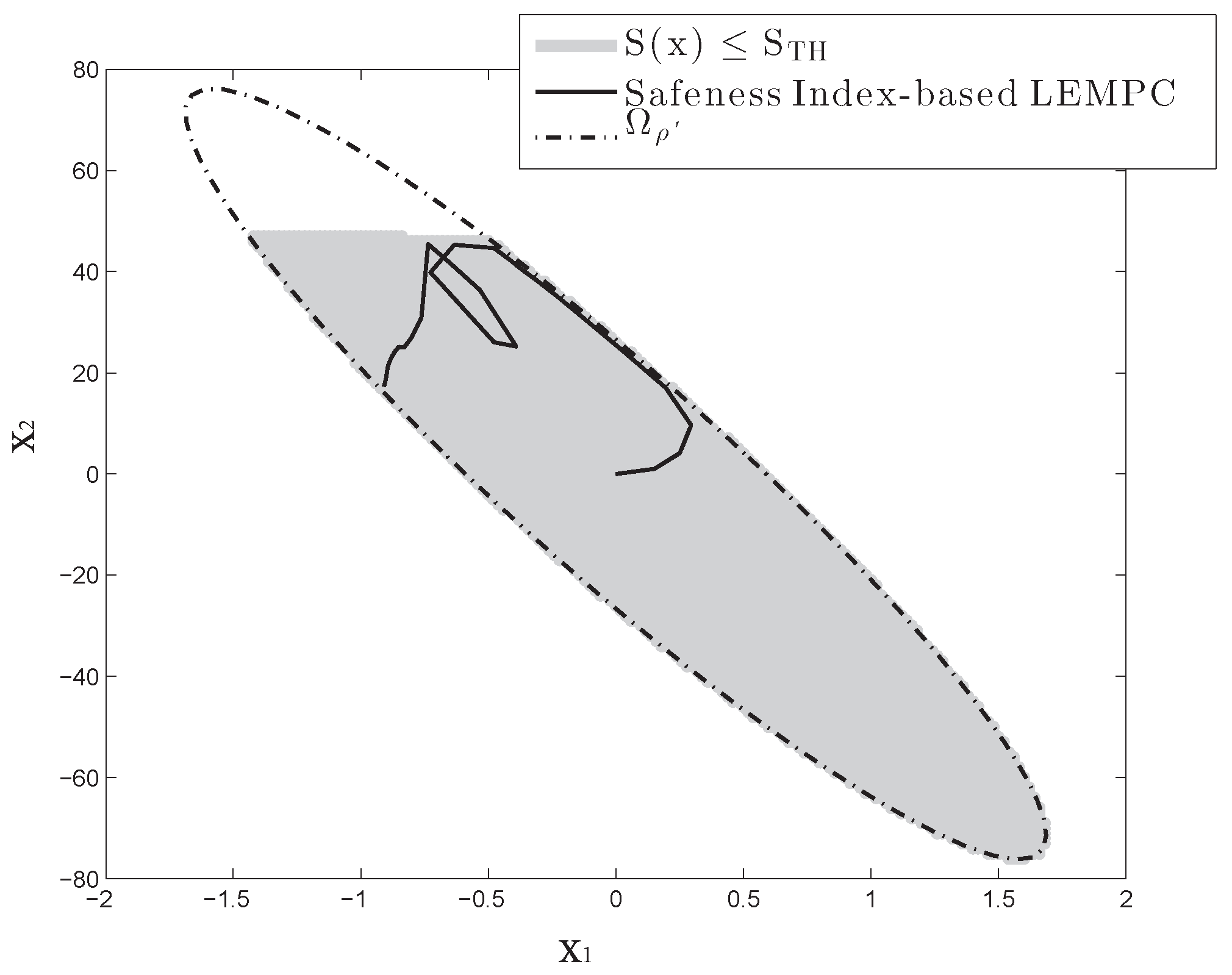
It is first shown in Figure 4 that under the Safeness Index-based LEMPC of Equation (6) designed for the nominal system of Equation (25), the closed-loop state of the nominal system of Equation (25) stays in the safe operating region $\mathcal{S}$ within the entire operation period $t_s=1$ h. Additionally, the Safeness Index-based LEMPC of Equation (6) is solved successfully in each iteration to obtain a feasible control action $u(t)$ that is applied in the next sampling period.

It follows that under the stochastic Safeness Index-based LEMPC of Equation (7), the state of the closed-loop system of Equation (25) stays in $\mathcal{S}$ with different probabilities for different ${\rho }_e$ and $s_e$. To better understand the relationship between probabilistic process operational safety and the choices of ${\rho }_e$ and $s_e$, we derived the experimental probabilities via 500 simulation runs for the same initial condition $(\Delta C_{As},\Delta T_s)=(0\mathrm{kmol}/{\mathrm{m}}^3,0\mathrm{K})$ and different choices of ${\rho }_e$ and $s_e$ (without the material constraint applied for the nominal system). Let $A_V$ denote the event that the closed-loop state stays in $\mathcal{S}$ over the operation period $t_s=1$ h. The results are reported in

Table 2. Experimental probability for different values of ${\rho }_e$ and $s_e$.

${\mathit{\rho }}_{\mathit{e}}/\mathit{\rho }$	${\mathit{s}}_{\mathit{e}}/\mathit{s}$	$\mathit{P}({\mathit{A}}_{\mathit{V}})$
$0.98$	$0.99$	$14.0\%$
$0.95$	$0.99$	$63.1\%$
$0.92$	$0.99$	$82.0\%$
$0.92$	$0.97$	$82.8\%$
$0.92$	$0.95$	$83.6\%$
$0.92$	$0.92$	$85.8\%$

.

From Table 2, it is observed that with fixed $s_e$, $\mathbf{P}(A_V)$ becomes larger as ${\rho }_e$ decreases. Likewise, with fixed ${\rho }_e$, $\mathbf{P}(A_V)$ increases as $s_e$ decreases. It is demonstrated that a higher probability of closed-loop process operational safety of the system of Equation (25) is achieved when ${\rho }_e$ and $s_e$ are more conservative. Let ${\rho }_e=320$ and $s_e=6800$. It is obtained that the probability of the states of the closed-loop system of Equation (25) remaining in the safe operating region $\mathcal{S}$ reaches $97.4\%$. Additionally, the averaged total economic benefit (i.e., the time integral of the stage cost $L_e$ over the operation period $t_s=1$ h) is $24.3$ under the Safeness Index-based LEMPC of Equation (7), which has an improvement of $81\%$ compared to $13.4$ under steady-state operation. Therefore, in this example, the closed-loop system of Equation (25) under the Safeness Index-based LEMPC achieves a relatively high probability of process safety and a satisfactory process economic performance simultaneously with ${\rho }_e=320$ and $s_e=6800$. For an actual process, additional work should likely be performed, which can use techniques like those demonstrated here, to increase the probability of the states of the closed-loop system remaining within the safe operating region to higher values considered acceptable for the process at hand given its design, hazards and the backup measures (alarms/operators, safety systems, relief systems) in place.

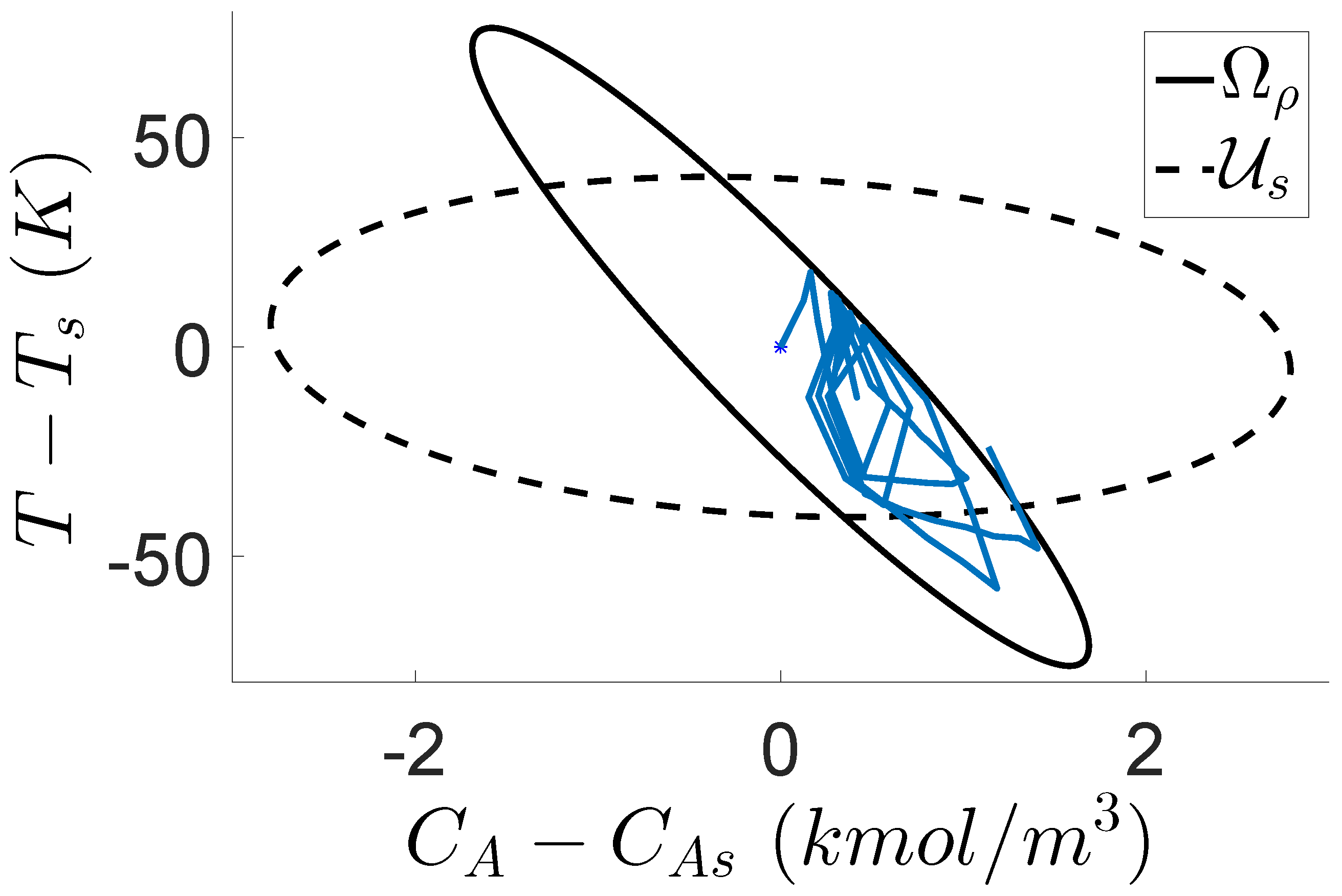
On the other hand, it is observed from Table 2 that decreasing ${\rho }_e$ increases the probability $\mathbf{P}(A_V)$. By looking at unsafe closed-loop trajectories (i.e., trajectories that leave the safe operating region $\mathcal{S}$ under the Safeness Index-based LEMPC of Equation (7) during the operation period $t_s$) in 500 simulation runs (one of them is shown in Figure 5), it is observed that almost all of the unsafe trajectories leave $\mathcal{S}$ through the boundary of ${\Omega }_{\rho }$ (i.e., the right edge of ${\Omega }_{\rho }$ in 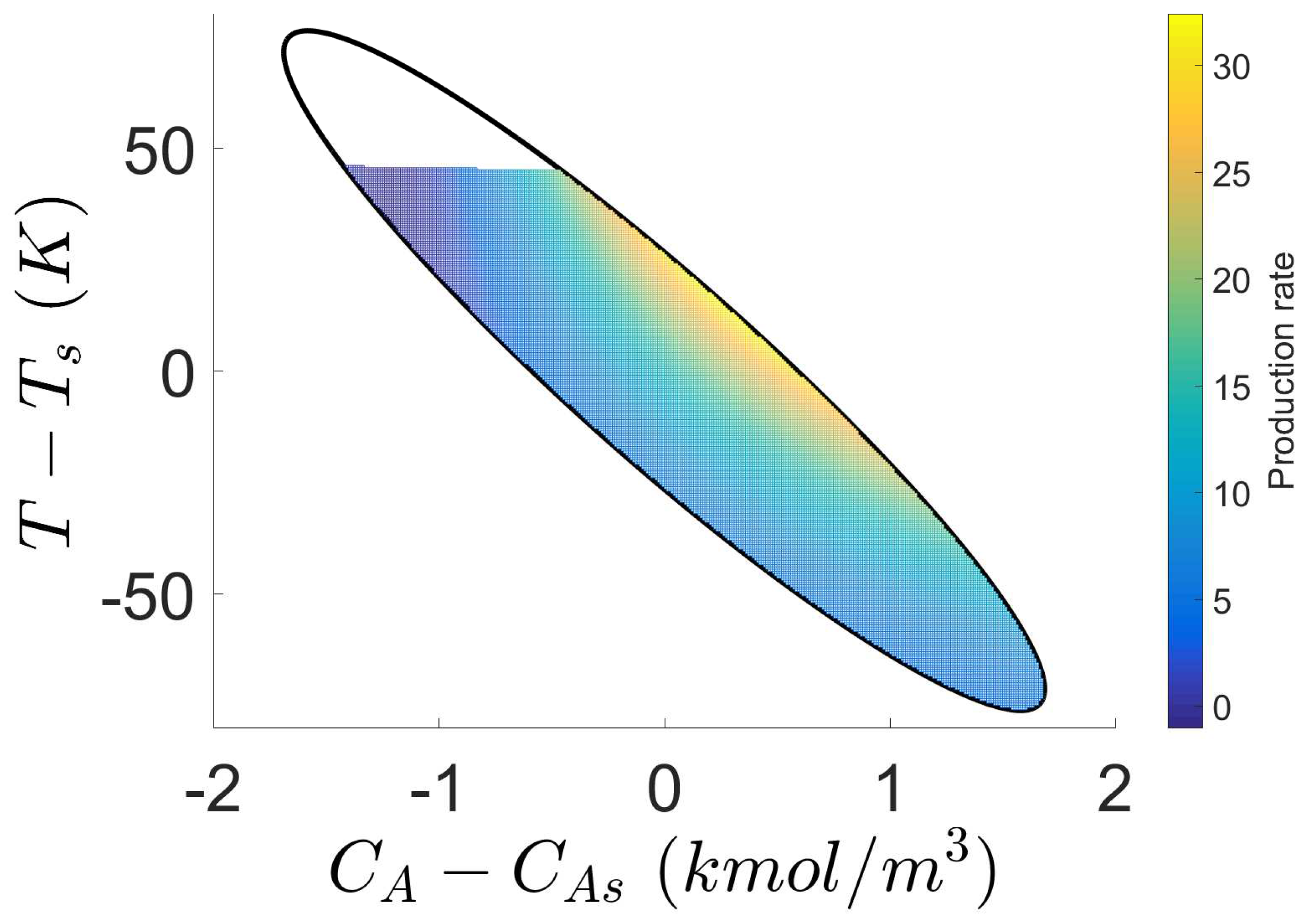Figure 5). The reason for this behavior is that the local optimum value of $L_e$ is calculated to be at the right edge of ${\Omega }_{\rho }$, which is shown as the yellow region in Figure 6. Therefore, under the Safeness Index-based LEMPC of Equation (7), the closed-loop trajectory is optimized to approach this high production rate region and begin circling back due to the disturbances, which leads to a higher probability of leaving the safe operating region $\mathcal{S}$ from ${\Omega }_{\rho }$. Additionally, it is observed in Figure 6 that the production rate decreases as the safe operating region shrinks (i.e., the color becomes darker), which is consistent with the fact that smaller ${\rho }_e$ and $s_e$ lead to safer process operation, at the cost of lower economic performance.

5. Conclusions

In this work, a Safeness Index-based LEMPC design was developed for stochastic nonlinear systems. Under the assumption of stabilizability of the origin of the stochastic nonlinear system via a stochastic Lyapunov-based control law, an economic model predictive controller was developed to account for process operational safety by utilizing Lyapunov-based constraints to maintain the closed-loop state in a safe operating region defined by a Safeness Index function. Under the stochastic Safeness Index-based LEMPC, economic optimality may be achieved with respect to the objective function and sampling period. Additionally, recursive feasibility and process operational safety of the closed-loop stochastic nonlinear system were derived in probability for a well-characterized safe operating region. A chemical reactor example was used to demonstrate the effectiveness of the proposed control method.