Abstract
This paper considers a class of large-scale systems which is composed of many interacting subsystems, and each of them is controlled by an individual controller. For this type of system, to improve the optimization performance of the entire closed-loop system in a distributed framework without the entire system’s information or too-complicated network information, connectivity is always an important topic. To achieve this purpose, a distributed model predictive control (DMPC) design method is proposed in this paper, where each local model predictive control (MPC) considers the optimization performance of its strong coupling subsystems and communicates with them. A method to determine the strength of the coupling relationship based on the closed-loop system’s performance and subsystem network connectivity is proposed for the selection of each subsystem’s neighbors. Finally, through integrating the steady-state calculation, the designed DMPC is able to guarantee the recursive feasibility and asymptotic stability of the closed-loop system in the cases of both tracking set point and stabilizing system to zeroes. Simulation results show the efficiency of the proposed DMPC.
1. Introduction
There is a class of complex large-scale industrial control systems which are composed of many interacting and spatially distributed subsystems, and each subsystem is controlled by an individual controller (e.g., large-scale chemical process [1], smart micro-grid [2,3] systems, distributed generation systems [4]), where the controllers exchange information with each other through a communication network. The objective is to achieve a good global performance of the entire closed-loop system or a common goal of all subsystems by the controller network. This objective is usually to track setpoints with minimized total error or to stabilize the entire system to zeroes in the dynamic control layer.
Distributed model predictive control (DMPC) controls each subsystem by an individual local model predictive control (MPC), and is one of the most important distributed control or optimization algorithms [1,5,6,7,8], since it not only inherits MPC’s ability to get good optimization performance and explicitly accommodate constraints [9,10], but also has the advantages of a distributed framework of fault-tolerance, less computation, and being flexible to system structure [7,11,12,13,14]. However, compared with the centralized control scheme, its performance is still not as good as that of centralized MPC for coupling systems in a peer-to-peer distributed control framework.
Many algorithms and design methods have appeared in the literature for different types of systems and for different problems in the design of DMPCs. For example, the design of DMPC for nonlinear systems [15,16], DMPC for uncertain systems [15,17], DMPC for networked systems with time delay [18], a decentralized optimization algorithm for solving DMPC [19], the design of cooperative strategies for improving the performance of DMPC [20], the design of an event-based communication DMPC for reducing the load on the communication network [21], as well as the design of a DPMC control structure [22]. Among these algorithms, several DMPC algorithms relate to the purpose of improving the closed-loop optimization performance while considering the information connectivity [5,21,23,24,25,26]. Information connectivity is considered because it directly affects the structural flexibility and error tolerance ability. Reference [27] proposed a DMPC where each subsystem-based MPC only communicates with its directly-impacted neighbors and uses an iterative algorithm to obtain the “Nash optimality”. References [20,28,29] proposed cooperative DMPC, where each MPC considers the cost of the entire system and communicates with all the other MPCs to obtain “Pareto optimality”. To reduce the information connectivity and increase the structural flexibility, Reference [30] proposed that each subsystem optimize all the subsystems impacted by it over the optimization horizon. The solution of this method is equal to the cooperative DMPC, while its communication efforts are less than the cooperative DMPC, especially for sparse systems. References [31,32] gave a strategy to dynamically adjust the weighting of performance index in cooperative MPC to avoid bad performance occurring in some subsystems. In an effort to achieve a trade-off between the optimization performance of the entire system and the information connectivity, an intuitively appealing strategy, called impacted-region cost optimization-based DMPC, is proposed in [33,34,35], where each subsystem-based MPC only considers the cost of its own subsystem and those of the subsystems directly impacted by it. Consequently, each MPC only communicates with its neighboring MPCs. In addition, in some papers, the control flexibility and information connectivity are paid more attention by researchers. References [14,36] provide a tube-based DMPC where all interactions are considered as disturbances and each subsystem-based MPC is solved independently. It does not exchange the state and input trajectory, but the interaction constraints, to avoid the interaction consistency problem. This method is able to improve the flexibility and fault tolerance ability of the control network [37]. References [25,37] proposed reconfigurable DMPC and plug-and-play DMPC based on dissipative theory, which focus on the problem of how to design a DMPC which allows the addition or deletion of subsystems without any change in existing controllers. It can be seen that the optimization performance of the entire system and structural flexibility are two conflicting key points in DMPC design. The selection of the range of each subsystem’s neighbors to be optimized in each subsystem-based MPC is important in the design of DMPC in order to obtain good optimization performance without unnecessary information connections. Thus, the aim of this paper is to design an algorithm to determine the range of each subsystem optimized from the point of view of enlarging each subsystem MPC’s feasible region, then to improve the entire system’s optimization performance without too-complicated network connectivity. Then, based on the result of this algorithm, we aim to design a stabilized neighborhood optimization-based DMPC that handles state constraints and is able to be used in target tracking.
As for target tracking, the difficulty in DMPC is to guarantee the recursive feasibility. References [38,39,40] provide a tracking algorithm for a series of MPC systems, where a steady-state target optimizer (SSTO) is integrated in the design of the cost function. The proposed controller is able to drive the whole system to any admissible setpoint in an admissible way, ensuring feasibility under any change of setpoint. As for distributed systems, [38] gives a DMPC for tracking based on the method introduced in [39] and a cooperative DMPC strategy. Reference [41] proposes another method based on global calculations of targeting tracking. It does not require a feasible starting point of each distributed predictive controller. These methods provide good references and possible methods for designing a tracking DMPC that considers optimization performance improvement and network connectivity.
In this paper, strong coupling neighbor-based optimization DMPC is proposed. With this method, each local MPC coordinates and communicates with its strong coupling neighbors. It takes its strongly-coupling downstream subsystems cost function into account in its cost function to improve the performance of the entire closed-loop system. To reduce the unnecessary network connectivity, the interaction terms of weak coupling upstream neighbors are ignored in its predictive model and are considered as bounded disturbances. In addition, the closed-loop optimization performance is used to determine which interaction should be regarded as strong coupling and be considered in DMPC. The strategy proposed in [38] is used to guarantee the recursive feasibility and stability in the target tracking problem. An asymptotically-stable closed-loop system with state constraints is guaranteed.
The remainder of this paper is organized as follows. Section 2 describes the problem to be solved. Section 3 describes the design of the proposed DMPC. Section 4 analyzes the stability of the closed-loop system. Section 5 presents the simulation results to demonstrate the effectiveness of the proposed algorithm. Finally, a brief conclusion to the paper is drawn in Section 6.
2. Problem Description
Considering a large-scale discrete-time linear system which is composed of many interacting subsystems, the overall system model is:
where is the system state, is the system current control input, is the controlled output, and is the successor state. The state of the system and control input applied at sample time t are denoted as ,, respectively. Moreover, there are hard constraints in the system state and control input. That is, for :
where and are compact convex polyhedra containing the origin in their interior.
Given Model (1), without loss of generality, the overall system is divided in to m subsystems, denoted as . Thus, and , then the subsystem model for is:
where is the set of subsystems that send inputs to the current subsystem . For subsystem , couples with by sending control input to . In particular, if . Given the overall system constraints set , fit hard constraints .
In this paper, for ease of analysis, here the definitions of neighbor (upstream-neighbor) and downstream neighbor are given.
Definition 1.
Given subsystem with state evolution Equation (3), define , which send input information to as the neighbor (upstream neighbor) of . Moreover, for arbitrary , since receives input information from , is defined as a downstream neighbor of .
Denote the tracking target as . Assume that is stabilizable and the state is measurable. The aim of a tracking problem given a target is to design a controller which enables in an admissible way when . Hence, the origin control objective function of the overall system is:
where , , and is the weighting coefficients matrix, and is steady input corresponding to .
The problem considered here is to design a DMPC algorithm to control a physical network, which coordinate with each other considering the following performance indicators:
- to achieve a good optimization performance of the entire closed-loop system.
- to guarantee the feasibility of target tracking.
- to simplify the information connectivity among controllers to guarantee good structural flexibility and error-tolerance of the distributed control framework.
To solve this problem, in this paper, an enhanced strong neighbor-based optimization DMPC is designed, and is detailed in the next section.
3. DMPC Design
In an interacting distributed system, the state evolution of each subsystem is affected by the optimal control decisions of its upstream neighbors. Each subsystem considers if these effects will help to improve the performance of entire closed-loop system. On the other hand, these impacts have different strengths for different downstream subsystems. Some of the effects are too small and can be ignored. If these weakly-coupling downstream subsystems’ cost functions are involved in each subsystem’s optimization problem, additional information connections arise with little improvement of the performance of the closed-loop system. The increase of information connections will hinder the error tolerance and flexibility of the distributed control system. Thus, each subsystem-based MPC takes the cost functions of its strongly-interacting downstream subsystems into account to improve the closed-loop performance of the entire system and receive information from its strong-coupling neighbors.
3.1. Strong-Coupling Neighbor-Based Optimization for Tracking
Given that the coupling degrees between different subsystems differ substantially, here we enable the subsystem to cooperate with strong-coupling neighbors while treating the weak-coupling ones as disturbance. Define as a set of strong-coupling neighboring subsystems and as set of weak-coupling neighbors. The rule for deciding strong-coupling systems is detailed in Section 3.4.
Then, for , we have:
where
The deviation represents the influence collection of weak-coupling upstream neighbors in . is contained in a convex and compact set which contains the origin.
If the weak coupling influence is neglected, a simplified model based on is acquired. That is:
Here , , and represent the state and input of a simplified subsystem model which neglects weak-coupling upstream neighbors’ influence .
The simplified overall system model with new coupling relation matrix is:
where and represent states and inputs in this simplified model.
Considering the target-tracking problem of the simplified model, in order to ensure the output track, given target , constraints are given for terminal state prediction. If the current target is set as the tracking target through the controller optimization, when changes, the terminal constraints need to change immediately. The optimal solution at a previous time may not fit the terminal constraints brought by the changed . This violates the recursive feasibility of the system. Thus, here a steady state optimization is integrated in the MPC for tracking where an artificial feasible tracking goal is proposed as a medium variable. This variable works as an optimized variable. With setting tracking point equal to the previous target, the recursive feasibility will not be violated by the target change.
The medium target and its state and input should satisfy the simplified system’s steady state equations. It has
Here is a suitable matrix. That is, target ’s corresponding inputs and states in the simplified model can be expressed by . The equation is based on the premise of Lemma 1.14 in [42]. If Lemma 1.14 does not hold, a and which fits can be found, which can replace the as a variable to be solved.
For the manual tracking target for the overall system, we have . That is, given , arbitrary subsystem gets a subtracking target . Similar to (9), are solved.
With the simplified model and artificial tracking target , according to (9), in the strong-coupling neighbor-based optimization MPC algorithm, the objective function optimized in subsystem is set as as follows:
where is the given initial state and target, are input predictions in sample time ahead. is the admissible target. and
Here, ’s controller design takes the strong-coupling downstream neighbors’ performances as part of its optimized objective. That is, the current subsystem ’s optimal solution is decided by its own and downstream neighbors in set , which is strongly impacted by .
Next, we will use the simplified model in (6) with only strong couplings to solve the tracking problem (10) for each subsystem. To guarantee control feasibility and stability, the following definitions and assumptions are given.
One important issue is to deal with the deviation caused by neglecting weak-coupling neighbor inputs. Here robust positively invariantt sets are adopted to enable the deviation of states to be bounded and the real system’s states to be controlled in .
Definition 2.
(Robust positively invariant set control law) Given which represents the dynamics of the error between the origin plant and the simplified model:
with . A set ϕ is called a robust positively invariant set for system (12) if , and the control law is called a robust positively invariant set control law.
The definition of a robust positively invariant set illustrates that for system if and robust positively invariant set control law K exist, then for , the trajectories of the original system at arbitrary time t denoted as can be controlled in .
Based on this definition, in this paper the dynamics of deviation introduced by neglecting weak-coupling neighbors can be solved. For subsystem proposed as (5), the deviation is written as:
where is the deviation from the simplified model to the original model and is the control law. There exists the set as a robust positively invariant set for if for all and all . Here is a feedback control input and we denote as the robust positively invariant set control law for . Then, it is easy to obtain for time t. Let , where , the origin system state and input satisfy . Thus, with the help of a robust positively invariant set, the original system optimization is transferred to a simplified model. For the overall system, we have .
With Definition 2, if the deviation brought by omitting weak-coupling neighbors is controlled in a robust positively invariant (RPI) set with control law and simplified model in (7) has control law and state confined in , respectively, the local subsystem will have a feasible solution for the optimization.
As for the manually-selected tracking target , based on the overall simplified model in (7), the following definition is given:
Definition 3.
(Tracking invariant set control law). Consider that overall system (7) is controlled by the following control law:
Let be Hurwitz, then this control law steers system (7) to the steady state and input . is denoted as the tracking invariant set control law.
Denote the set of initial state and steady output that can be stabilized by control law (13) while fulfilling the system constraints throughout its evolution as an invariant set for tracking . For any , the trajectory of the system controlled by is confined in and tends to .
Under Definitions 2 and 3, before introducing the enhancing strong neighbor-based optimization DMPC, some assumptions for the closed-loop system feasibility and stability are given as follows. The concrete theorem and an analysis of stability and feasibility are given in Section 4.
Assumption 1.
The eigenvalues of are in the interior of the unitary circle. is an admissible robust positively invariant set for ’s deviation subject to constraints , and the corresponding feedback control law is .
Assumption 2.
Let be a tracking invariant set for the simplified system (7) subject to constraints , and the corresponding feedback gain matrix is .
Assumption 3.
For , and , it has:
Assumption 1 ensures that with the feedback control law , , the state estimated by the simplified model (7) is near to the real system’s trajectory before the system reaches the target. In Assumption 2, is set as a terminal constraint of DMPC. Assumption 3 is used in the proof of the convergence of system presented in the Appendix A.
So far, the strong-coupling neighbor-based optimization DMPC algorithm, which is solved iteratively, can be defined as follows:
Firstly, denote the optimal objective of subsystem as . According to (10), at iterating step p, fits:
Compute the optimization solution
Subject to constraints:
with , and defined in Assumptions 2 and 3, respectively. The optimization function (16) updates ’s initial state, inputs in N steps and current tracking target based on the information from subsystems in .
Secondly, set
, is to guarantee the consistency of the optimization problem. That is, at the end of the current sample time, all shared variables converge.
After that, we take
to iterate until the solutions convergence. Then, we have , .
Finally, when the solution converges, according to Assumption 1, take the control law of as
where is the robust positively invariant set control law. is the first element of . For better understanding, the algorithm is also presented in Algorithm 1.
| Algorithm 1 Enhancing Strong Neighbor-Based Optimization DMPC |
 |
In this algorithm, we use an iterative strategy to guarantee the distributed control solution is consistent. Next, the selection of warm start, the given solution for each subsystem at initial iterative step 0, is proposed in the next section.
3.2. Warm Start
Considering a new sample time, with updated system states, the choice of a warm start is based on the principle that it fits the simplified system’s constraints in (17), so that real subsystem solution’s feasibility is guaranteed. The warm start is designed as the following algorithm:
| Algorithm 2 Warm Start for Iterative Algorithm |
 |
The algorithm illustrates that two choices are provided for the warm start. One is acquiring a solution from the tracking invariant set control law , with the simplified model prediction as initial state and tracking target, respectively. The other is taking a solution from the simplified model prediction at time t. Both of them fit the constraints of (17). Note that the second option will only be considered when the subsystem enters the tracking invariant set.
3.3. RPI Control Law and RPI Set
Here one constraint coupling subsystem is considered. Given that for we have and , express the constraints in inequalities: and . The robust positively invariant set is denoted as .
With the definition a of robust positively invariant set in Definition 2, should ensure that , . That is:
Based on definitions of and , is decided according to the constraints of . For deviation caused by neglecting the subsystem in , a minimization of robust positive invariant set by introducing a parameter can be obtained.
The parameter controls the size of the robust positive invariant set by further minimizing in . That is:
We should also consider the input constraint :
and the constraint brought by the property of robust positive invariant set itself should be considered.
Based on the above analysis, referring to [43], we can obtain and by solving the following linear matrix inequality optimization problem:
and . Thus, we get RPI control law and , which illustrates the size of . To get , we use the procedure in Reference [43].
3.4. Determination of Strong Coupling
There are many measurements to measure the strength of interactions among subsystems. Different measurements lead to different optimization performance. This paper focuses on the performance and connectivity of subsystems. Thus, the determination of strong-coupling neighbors is based on the influence on the size of current subsystem’s robust positively invariant (RPI) set and subsystem connectivity.
On the one hand, as defined in Definition 2, is a robust positively invariant set for subsystem described as when is set to zero. Given that deals with deviation caused by neglecting some of the inputs , the size of is expected to be sufficiently small. The benefit is that the solution in (15) can get a larger feasible domain. Here we consider that a sufficiently large domain means the solution has more degrees of freedom and brings better subsystem performance. Based on the idea above, to decide to omit the weak-coupling neighbor set , we choose a neighbor collection which results in a small size of robust positively invariant set . The basis of measuring the robust positively invariant set by introducing is mentioned in the previous section. On the other hand, connectivity, as the measurement of subsystem topology complexity, is easy to obtain. Next, we give the numerical analysis.
Denote an arbitrary option for deciding the strong-, weak-coupling neighbors as . is the label set of ways of ’s neighbors’ distribution. represents the size of feasible distribution methods which fits . For better understanding of , here we take an arbitrary neighbor set as an example. If we treat as a strong-coupling neighbor and as weak, we have , , satisfying:
Option results in a specified connectivity amount (normalized) and an RPI set denoted as . Here are defined as:
To find the optimal distribution of strong- and weak-coupling neighbors, here we take:
where for ,
In this equation, is a weight coefficient for the optimization. represent the under distribution . Moreover, is the optimal solution.
This optimization means that in order to make the optimal decision on strong-coupling neighbors and weak-coupling neighbors while taking both connectivity and performance into account, the optimization that minimizes the combination of subsystem connectivity and size of should be solved. To decide whether a neighbor is a strong-coupling neighbor or a weak one, the size of is expected to be small so that the solution in (15) can get a larger feasible domain. At the same time, the connectivity is expected to be small to reduce the system’s topological complexity.
The optimization achieves the goal of choosing neighbors which result in smaller size of robust positively invariant set and connectivity. Solution reflects the consideration of influence on RPI set and connectivity. With this method, even though “weak-coupling” neighbors are omitted and deviation is brought, the simplified model has a large degree of freedom to design the control law of tracking and reduces the connectivity at the same time. Thus, a good system performance and error tolerance can be obtained.
4. Stability and Convergence
In this section, the feasibility and stability theorem of strong-coupling neighbor-based DMPC are given. Denote
represents the current time’s state prediction after k sample time. is the feasible tracking set based on hard constraints of x and u.
Theorem 1.
Assume that Assumptions 1–3 hold. Then, for all initial state with tracking target if , the closed-loop system based on a strong-coupling neighbor-based DMPC algorithm is feasible and asymptotically stable and converges to , where , among feasible targets.
Proof.
Feasibility is proved by Lemmas A1, A2. Stability’s proofs are in Lemmas A3, A4 in the Appendix A. ☐
5. Simulation
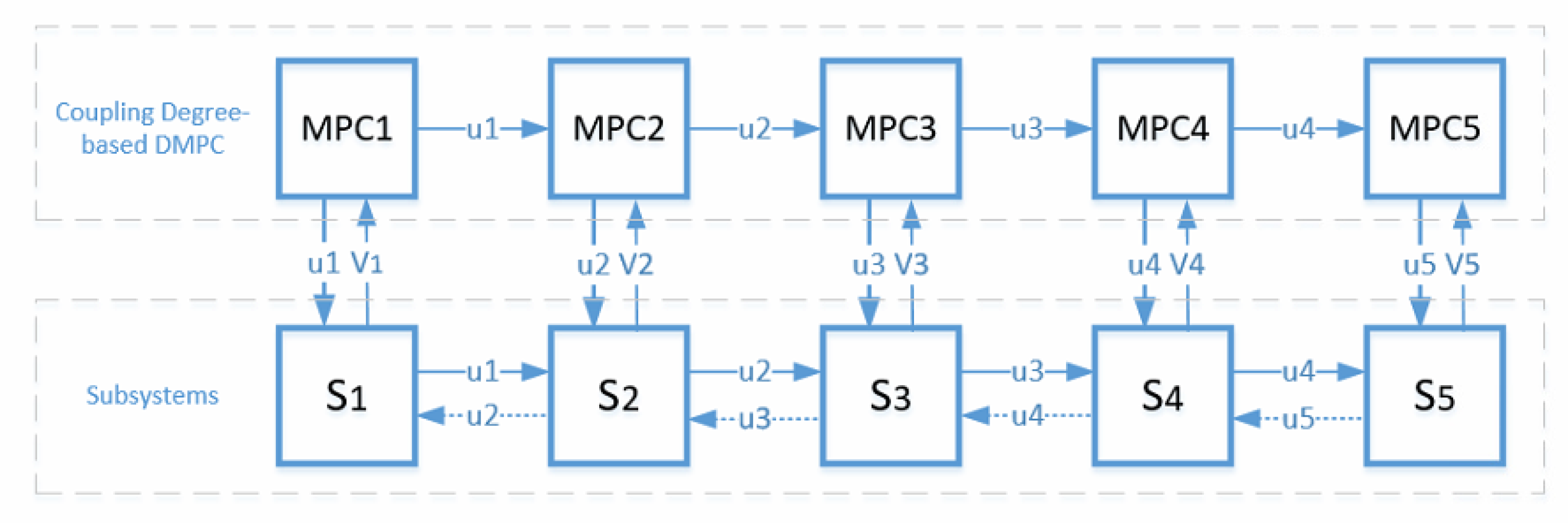
The simulation takes an industrial system model with five subsystems interacting with each other as an example. Between different subsystems, the coupling degrees vary substantially. The relationships of subsystems and the designed MPC are shown in Figure 1.
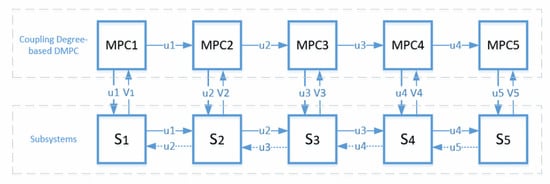
Figure 1.
An illustration of the structure of a distributed system and its distributed control framework. MPC: model predictive control; DMPC: distributed MPC.
In Figure 1, dotted lines are used to represent weak coupling, while solid lines are used to represent strong coupling. With the strategy we have defined in our paper, weak couplings are neglected. As a result, it can be seen in Figure 1 that only parts of the subsystems are joint in cooperation. Subsystem models are also given as follows:
By the strong-coupling neighbor-based DMPC, connections including , , , are neglected. For the five subsystems in the given model, , and , which evaluate the system performance, are obtained by optimization in Section 3.4, they are:
Among them, illustrates that subsystem has no weak-coupling upstream neighbors. Additionally, the robust positively invariant set feedback control laws are
The optimization horizon N is 10 sample time. Take and . To accelerate the iterative process, in both of these iterative algorithms, the terminal conditions of iteration are or . If either of these two conditions is satisfied, iteration terminates.
The following shows the system performance when the strong-coupling neighbor-based DMPC algorithm is applied. Here we chose different set-points to detect the system stability. Three groups of setpoints were given to verify the system’s feasibility and stability. For a better understanding, cooperative DMPC strategy control results which cooperate with all neighbors are also introduced to make a comparison. The simulation took a total of seconds for 90 sampling times. The performance comparison of strong-coupling neighbor-based DMPC (SCN-DMPC) with cooperative DMPC where each subsystem used the full system’s information in their controller is shown in Figure 2, Figure 3 and Figure 4.
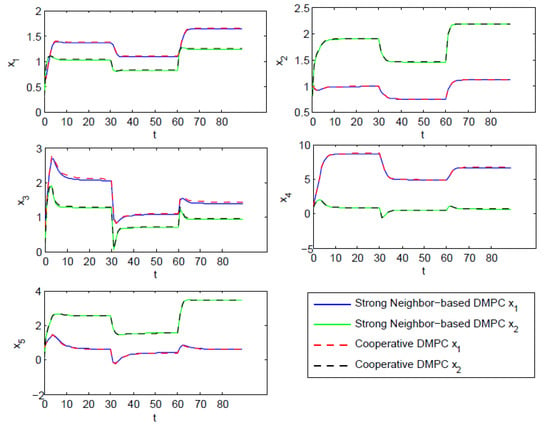
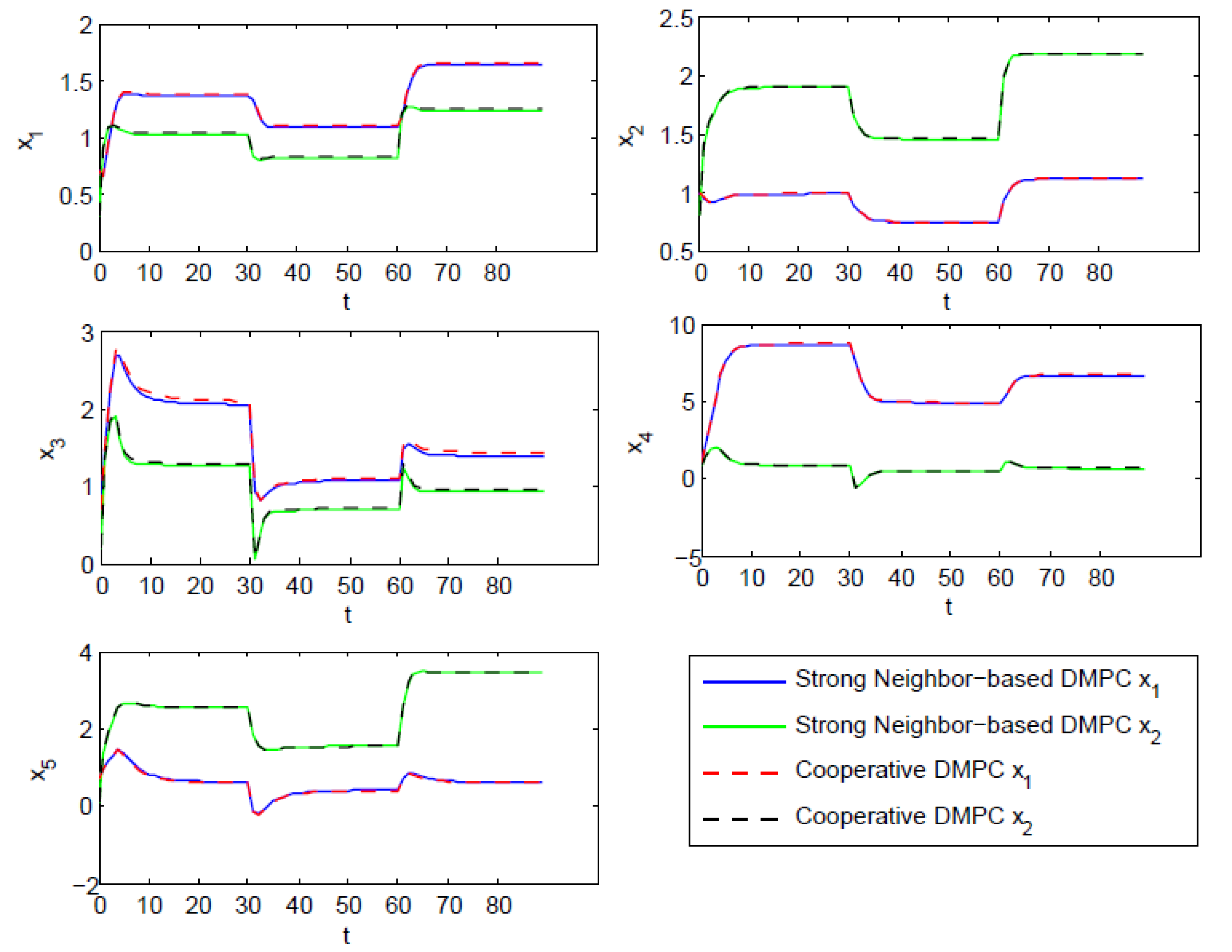
Figure 2.
States of each subsystem under the control of strong-coupling neighbor-based DMPC (SCN-DMPC) and cooperative DMPC.
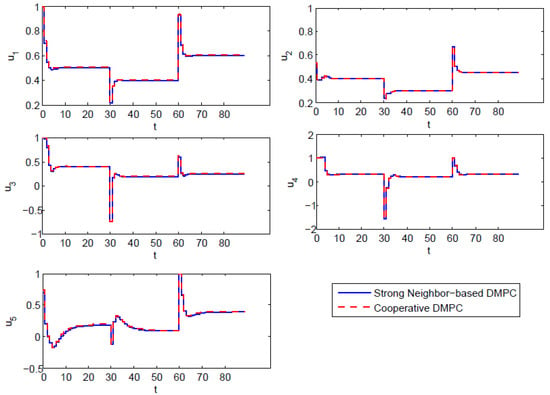
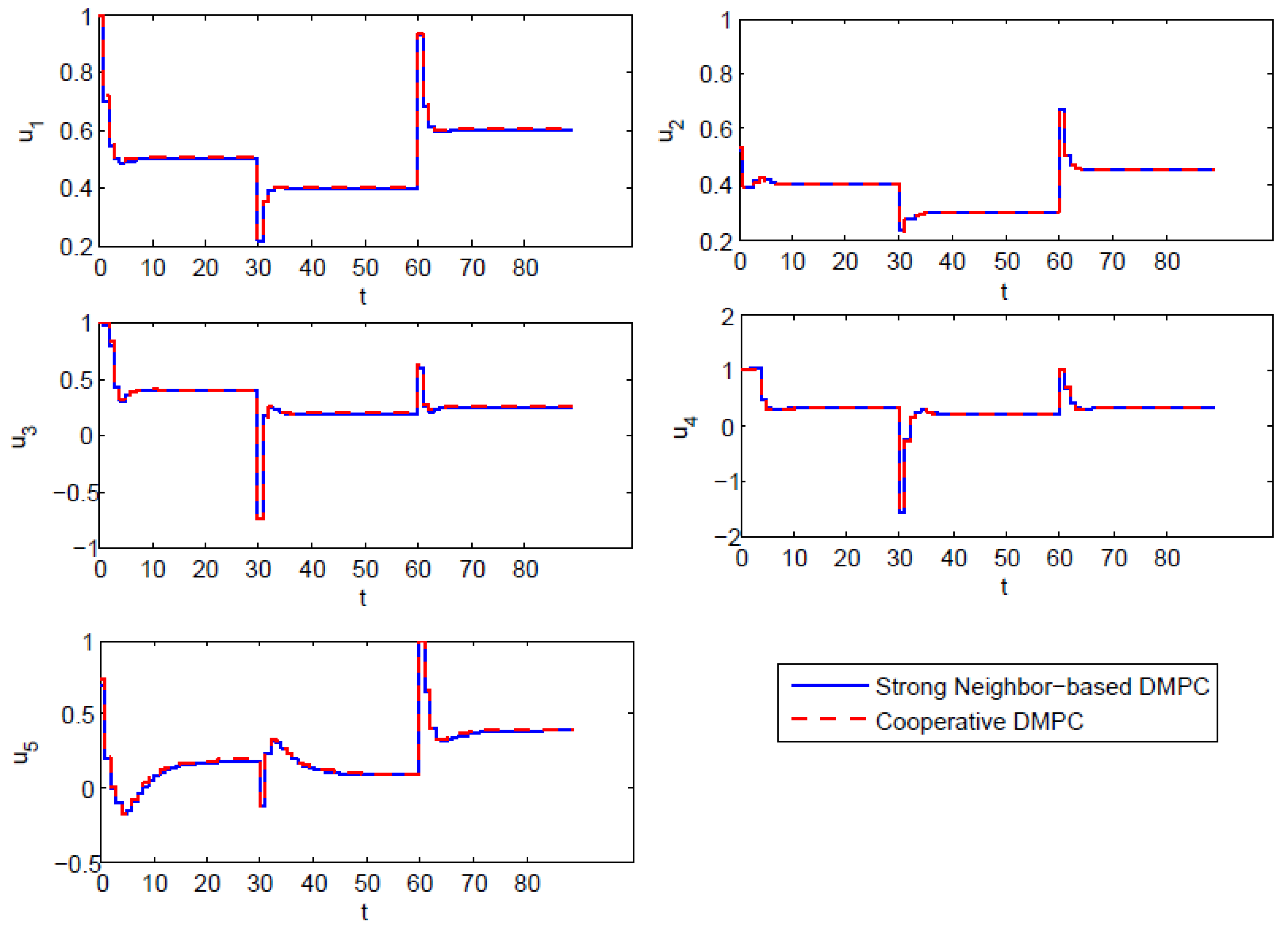
Figure 3.
Inputs of each subsystem under the control of SCN-DMPC and cooperative DMPC.
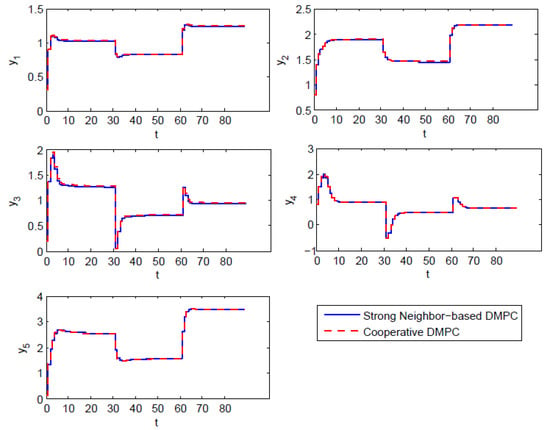
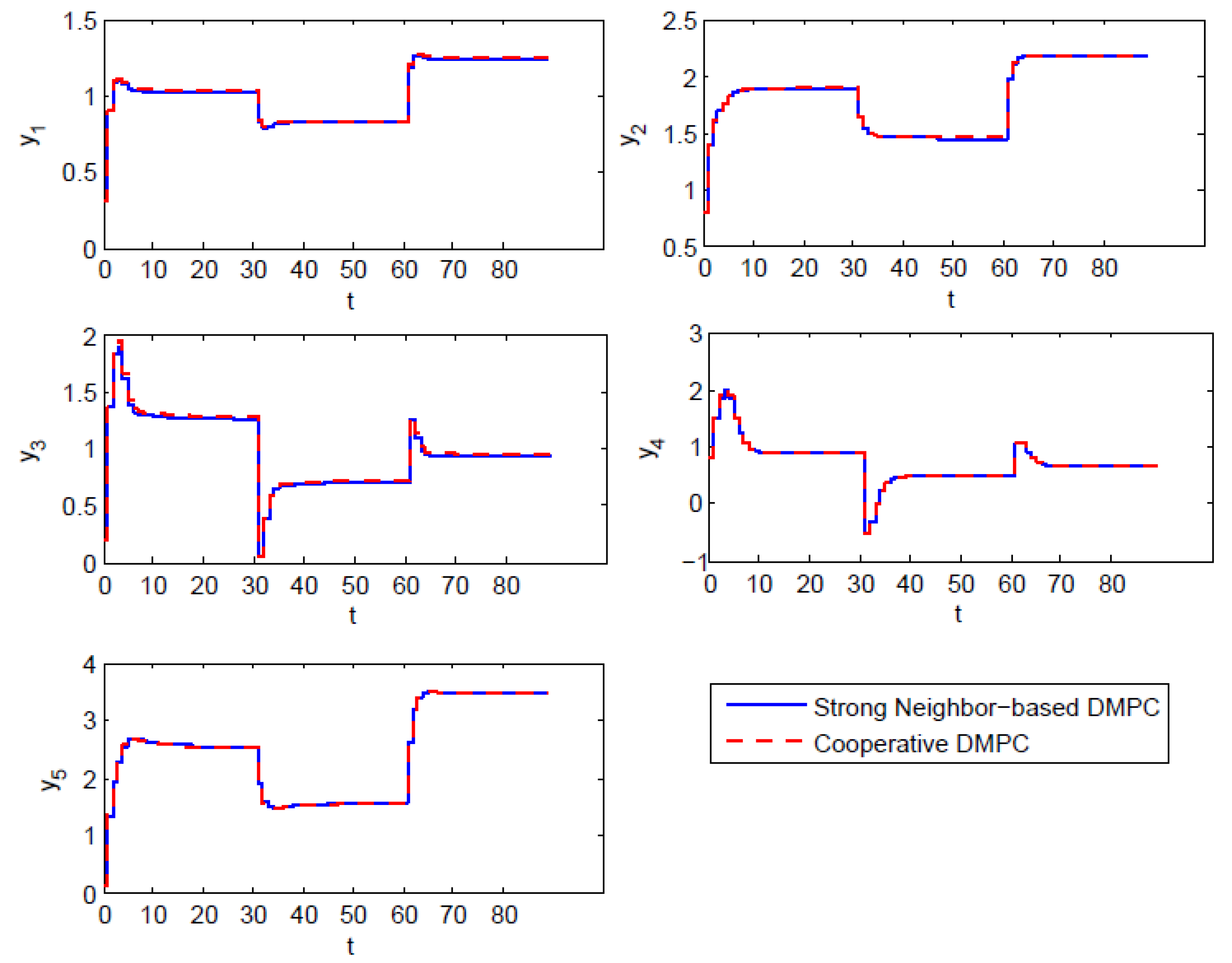
Figure 4.
Output of each subsystem under the control of SCN-DMPC and cooperative DMPC.
Figure 2 shows the state evolution of each subsystem. The two curves of SCN-DMPC and cooperative are close to each other. This is because the weak couplings in the given example are tiny compared with the strong couplings and thus do not have much of an impact on system dynamics. Besides, SCN-DMPC optimization algorithm was always feasible and was able to keep stable with a changing tracking target. Figure 3 shows the input difference between these two algorithms. The control laws of these two algorithms are almost the same. Tracking results are shown in Figure 4. There was a small off-set in subsystem , which could be eliminated by adding an observer. All other subsystems could track the steady-state target without steady-state off-set. From the simulation results of Figure 2, Figure 3 and Figure 4, the stability and good optimization performance of the closed-loop system using SCN-DMPC is verified.
In Figure 2, Figure 3 and Figure 4, the curves of SCN-DMPC and cooperative DMPC are close to each other. The reason is that the weak couplings in the given example were tiny compared with the strong couplings, and thus they did not have much of an impact on system dynamics, even though a small difference existed. Specifically, given the state equation input weight coefficients in each subsystem, the deviations of the five subsystems fit . The effects of these disturbances were very small compared with those of each subsystem’s inputs. Under robust feedback control law, they do not have much of an influence on system dynamics. Besides, the performance of the simplified model under SCN-DMPC equals to that under the control law optimizing the global performance of simplified system. As a result, the system performance under SCN-DMPC was close to that in cooperative DMPC. Under circumstances where the weak interactions are close to the impact of each subsystem’s inputs (which sacrifices part of the performance to achieve less network connectivity), omitting weak couplings may result in a greater influence on system dynamics, and the simulation results can differ.
Moreover, mean square errors between the closed-loop systems with strong-coupling neighbor-based optimization DMPC and cooperative DMPC outputs are listed in Table 1. The total error of five subsystems was only 3.5, which illustrates the good optimization performance of SCN-DMPC.

Table 1.
Mean square error (MSE) of outputs between SCN-DMPC and cooperative DMPC.
Connectivities are compared in the following table.
Table 2 shows that when strong-coupling neighbor-based DMPC was applied, the total information connections reduced to eight, which means that five connections were avoided compared with cooperative DMPC.

Table 2.
Comparison of system connectivity with different control methods.
Above all, the simulation results show that the proposed SCN-DMPC achieved a good performance close to the cooperative DMPC with a significant reduction of information connectivity.
6. Conclusions
In this paper, a strong-coupling neighbor-based optimization DMPC method is proposed to decide the cooperation among subsystems, where each subsystem’s MPC considers the optimization performance and evolution of its strong-coupling downstream subsystems and communicates with them. For strongly-coupled subsystems, the influence on state and objective function are considered. For weakly-coupled subsystems, influence is neglected in the cooperative design. A closed-loop system’s performance and network connectivity-based method is proposed to determine the strength of coupling relationships among subsystems. The feasibility and stability of the closed-loop system in the case of target-tracking are analyzed. Simulation results show that the proposed SCN-DMPC was able to achieve similar performance in comparison to the DMPC which did not neglect the information or influence of weakly coupling subsystems. At the same time, connectivity was significantly decreased.
Author Contributions
Shan Gao developed the main algorithm, contributed to the stability analysis, designed the simulation and prepared the draft of the paper. Yi Zheng and Shaoyuan Li proposed the idea of Enhancing Strong Neighbor-based coordination strategy. They contributed to the main theory of the work and gave the inspiration and guidance of the strong-coupling neighbors’ determination, the algorithm design and stability analysis.
Acknowledgments
This work is supported by the National Nature Science Foundation of China (61673273, 61590924).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In the strong-coupling neighbor-based optimization DMPC algorithm proposed in this paper, the optimal solution of each subsystem equals to the solution of optimizing the overall system objective function. That is:
where
Thus, for easy analysis, here we take the overall objective function to prove the feasibility and stability, and define:
Denote as
Lemma A1.
Feasibility. Feasibility can be proved by assuming . Then, we get .
Proof.
The feasibility of the model is proved by analyzing the simplified model.
Refer to the warm start algorithm. At time , the warm start for arbitrary : . With the warm start, all constraints in (17) are satisfied.
From to iterations, given that
are feasible, obviously their convex sum is feasible. As a result, the converged simplified solution is feasible. Based on this, the real system solution is around the invariant set of , and fits the system constraints. That is, . ☐
Lemma A2.
Convergence. Here we have
Proof.
Since it has
convergence is proved. ☐
According to the Lemma above, we have:
Lemma A3.
Local Bounded. When , then
Proof.
Firstly,
will be proved.
According to the definition of warm start and Assumption 3, here we have:
Thus, we have:
☐
Lemma A4.
Convergence. Let Assumption 3 hold, for any feasible solution , the system converges to equilibrium point . That is,
The final tracking points of the simplified system (the optimal solution of ) are , which are the centralized optimal solution.
Proof.
For simplified system optimization, we have
and also
According to (A11) and (A12), we have
Since the robust positively invariant set feedback control law ensures the real states in the invariant set of the simplified model, the real system’s stability is proved. ☐
References
- Christofides, P.D.; Scattolini, R.; Muñoz de la Peña, D.; Liu, J. Distributed model predictive control: A tutorial review and future research directions. Comput. Chem. Eng. 2013, 51, 21–41. [Google Scholar] [CrossRef]
- Del Real, A.J.; Arce, A.; Bordons, C. Combined environmental and economic dispatch of smart grids using distributed model predictive control. Int. J. Electr. Power Energy Syst. 2014, 54, 65–76. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Tan, R. Distributed Model Predictive Control for On-Connected Microgrid Power Management. IEEE Trans. Control Syst. Technol. 2018, 26, 1028–1039. [Google Scholar] [CrossRef]
- Yu, W.; Liu, D.; Huang, Y. Operation optimization based on the power supply and storage capacity of an active distribution network. Energies 2013, 6, 6423–6438. [Google Scholar] [CrossRef]
- Scattolini, R. Architectures for distributed and hierarchical model predictive control-a review. J. Process Control 2009, 19, 723–731. [Google Scholar] [CrossRef]
- Du, X.; Xi, Y.; Li, S. Distributed model predictive control for large-scale systems. In Proceedings of the 2001 American Control Conference, Arlington, VA, USA, 25–27 June 2001; Volume 4, pp. 3142–3143. [Google Scholar]
- Li, S.; Yi, Z. Distributed Model Predictive Control for Plant-Wide Systems; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Mota, J.F.C.; Xavier, J.M.F.; Aguiar, P.M.Q.; Püschel, M. Distributed Optimization With Local Domains: Applications in MPC and Network Flows. IEEE Trans. Autom. Control 2015, 60, 2004–2009. [Google Scholar] [CrossRef]
- Qin, S.; Badgwell, T. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Maciejowski, J. Predictive Control: With Constraints; Pearson Education: London, UK, 2002. [Google Scholar]
- Vaccarini, M.; Longhi, S.; Katebi, M. Unconstrained networked decentralized model predictive control. J. Process Control 2009, 19, 328–339. [Google Scholar] [CrossRef]
- Leirens, S.; Zamora, C.; Negenborn, R.; De Schutter, B. Coordination in urban water supply networks using distributed model predictive control. In Proceedings of the American Control Conference (ACC), Baltimore, MD, USA, 30 June–2 July 2010; pp. 3957–3962. [Google Scholar]
- Wang, Z.; Ong, C.J. Distributed Model Predictive Control of linear discrete-time systems with local and global constraints. Automatica 2017, 81, 184–195. [Google Scholar] [CrossRef]
- Trodden, P.A.; Maestre, J. Distributed predictive control with minimization of mutual disturbances. Automatica 2017, 77, 31–43. [Google Scholar] [CrossRef]
- Al-Gherwi, W.; Budman, H.; Elkamel, A. A robust distributed model predictive control algorithm. J. Process Control 2011, 21, 1127–1137. [Google Scholar] [CrossRef]
- Kirubakaran, V.; Radhakrishnan, T.; Sivakumaran, N. Distributed multiparametric model predictive control design for a quadruple tank process. Measurement 2014, 47, 841–854. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.; Li, C. Distributed model predictive control for polytopic uncertain systems subject to actuator saturation. J. Process Control 2013, 23, 1075–1089. [Google Scholar] [CrossRef]
- Liu, J.; Muñoz de la Peña, D.; Christofides, P.D. Distributed model predictive control of nonlinear systems subject to asynchronous and delayed measurements. Automatica 2010, 46, 52–61. [Google Scholar] [CrossRef]
- Cheng, R.; Fraser Forbes, J.; Yip, W.S. Dantzig–Wolfe decomposition and plant-wide MPC coordination. Comput. Chem. Eng. 2008, 32, 1507–1522. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Qiu, H. Networked coordination-based distributed model predictive control for large-scale system. IEEE Trans. Control Syst. Technol. 2013, 21, 991–998. [Google Scholar] [CrossRef]
- Groß, D.; Stursberg, O. A Cooperative Distributed MPC Algorithm With Event-Based Communication and Parallel Optimization. IEEE Trans. Control Netw. Syst. 2016, 3, 275–285. [Google Scholar] [CrossRef]
- Walid Al-Gherwi, H.B.; Elkamel, A. Selection of control structure for distributed model predictive control in the presence of model errors. J. Process Control 2010, 20, 270–284. [Google Scholar] [CrossRef]
- Camponogara, E.; Jia, D.; Krogh, B.; Talukdar, S. Distributed model predictive control. IEEE Control Syst. Mag. 2002, 22, 44–52. [Google Scholar]
- Conte, C.; Jones, C.N.; Morari, M.; Zeilinger, M.N. Distributed synthesis and stability of cooperative distributed model predictive control for linear systems. Automatica 2016, 69, 117–125. [Google Scholar] [CrossRef]
- Tippett, M.J.; Bao, J. Reconfigurable distributed model predictive control. Chem. Eng. Sci. 2015, 136, 2–19. [Google Scholar] [CrossRef]
- Zheng, Y.; Wei, Y.; Li, S. Coupling Degree Clustering-Based Distributed Model Predictive Control Network Design. IEEE Trans. Autom. Sci. Eng. 2018, 1–10. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y.; Zhu, Q. Nash-optimization enhanced distributed model predictive control applied to the Shell benchmark problem. Inf. Sci. 2005, 170, 329–349. [Google Scholar] [CrossRef]
- Venkat, A.N.; Hiskens, I.A.; Rawlings, J.B.; Wright, S.J. Distributed MPC Strategies with Application to Power System Automatic Generation Control. IEEE Trans. Control Syst. Technol. 2008, 16, 1192–1206. [Google Scholar] [CrossRef]
- Stewart, B.T.; Wright, S.J.; Rawlings, J.B. Cooperative distributed model predictive control for nonlinear systems. J. Process Control 2011, 21, 698–704. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S. N-Step Impacted-Region Optimization based Distributed Model Predictive Control. IFAC-PapersOnLine 2015, 48, 831–836. [Google Scholar] [CrossRef]
- De Lima, M.L.; Camponogara, E.; Marruedo, D.L.; de la Peña, D.M. Distributed Satisficing MPC. IEEE Trans. Control Syst. Technol. 2015, 23, 305–312. [Google Scholar] [CrossRef]
- De Lima, M.L.; Limon, D.; de la Pena, D.M.; Camponogara, E. Distributed Satisficing MPC With Guarantee of Stability. IEEE Trans. Autom. Control 2016, 61, 532–537. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Wang, X. Distributed model predictive control for plant-wide hot-rolled strip laminar cooling process. J. Process Control 2009, 19, 1427–1437. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Li, N. Distributed model predictive control over network information exchange for large-scale systems. Control Eng. Pract. 2011, 19, 757–769. [Google Scholar] [CrossRef]
- Li, S.; Zheng, Y.; Lin, Z. Impacted-Region Optimization for Distributed Model Predictive Control Systems with Constraints. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1447–1460. [Google Scholar] [CrossRef]
- Riverso, S.; Ferrari-Trecate, G. Tube-based distributed control of linear constrained systems. Automatica 2012, 48, 2860–2865. [Google Scholar] [CrossRef]
- Riverso, S.; Boem, F.; Ferrari-Trecate, G.; Parisini, T. Plug-and-Play Fault Detection and Control-Reconfiguration for a Class of Nonlinear Large-Scale Constrained Systems. IEEE Trans. Autom. Control 2016, 61, 3963–3978. [Google Scholar] [CrossRef]
- Ferramosca, A.; Limon, D.; Alvarado, I.; Camacho, E. Cooperative distributed MPC for tracking. Automatica 2013, 49, 906–914. [Google Scholar] [CrossRef]
- Limon, D. MPC for tracking of piece-wise constant references for constrained linear systems. In Proceedings of the 16th IFAC World Congress, Prague, Czech Republic, 3–8 July 2005; p. 882. [Google Scholar]
- Limon, D.; Alvarado, I.; Alamo, T.; Camacho, E.F. Robust tube-based MPC for tracking of constrained linear systems with additive disturbances. J. Process Control 2010, 20, 248–260. [Google Scholar] [CrossRef]
- Shao, Q.M.; Cinar, A. Coordination scheme and target tracking for distributed model predictive control. Chem. Eng. Sci. 2015, 136, 20–26. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Mayne, D.Q. Model Predictive Control: Theory and Design; Nob Hill Publishing: Madison, WI, USA, 2009; pp. 3430–3433. [Google Scholar]
- Alvarado, I. On the Design of Robust Tube-Based MPC for Tracking. In Proceedings of the 17th World Congress The International Federation of Automatic Control, Seoul, Korea, 6–11 July 2008; pp. 15333–15338. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).