Abstract
So far, most of the semi-supervised clustering algorithms focus on finding a suitable partition that well satisfies the given constraints. However, insufficient supervisory information may lead to over-fitting results and unstable performance, especially on complicated data. To address this challenge, this paper attempts to solve the semi-supervised clustering problem by self-learning sufficient constraints. The essential motivation is that constraints can be learned from the local neighbor structures within appropriate feature spaces, and sufficient constraints can directly divide the data into clusters. Hence, we first present a constraint self-learning framework. It performs an expectation–maximization procedure iteratively between exploring a discriminant space and learning new constraints. Then, a constraint-based clustering algorithm is proposed by taking advantage of sufficient constraints. Experimental studies on various real-world benchmark datasets show that the proposed algorithm achieves promising performance and outperforms the state-of-the-art semi-supervised clustering algorithms.
MSC:
68T30; 68Q04; 68P30
1. Introduction
In most real-world applications, the ground truth is expensive to generate for the whole dataset. Consequently, semi-supervised learning with partial background information has drawn more and more attention in the machine learning and data mining communities [1,2,3]. Recently, semi-supervised clustering has become a significant research topic due to the emergence of unlabeled big data of which only a few instances can be labeled by experts. The typical partial background information is formed as must-links, which specify the pairs of instances assigned to the same cluster, and cannot-links, which specify the pairs assigned to different clusters.
In the recent decade, many popular unsupervised clustering methods have been reformed into a semi-supervised way by adapting constraints as prior supervised knowledge, such as K-means [2,4,5,6]. The aim of a semi-supervised clustering algorithm is to find clusters satisfying as many constraints as possible. Its advantages have been validated and reported by many real-world applications [7,8]. However, most of the current methods focus on finding a suitable partition that can well enforce the given constraints, without paying attention to the intrinsic data structure itself. Meanwhile, insufficient constraints cannot yet well handle the non-Gaussian data [9], especially the manifold structure data. For the complex manifold data, the common way is to find a good distance metric, which is equivalent to finding a good feature space transformation [10]. The spectral clustering methods can be treated as a kind of space transformation way for cluster finding. Spectral clustering has been extended to the semi-supervised way by enforcing the constraints [11,12,13]. However, their performance becomes unstable when the prior supervised knowledge is scarce [14,15]. To address this challenge, this paper attempts to solve the semi-supervised clustering problem by self-learning sufficient constraints. We first present a constraint self-learning framework to iteratively explore more pairwise constraints from the local structure of various discriminant feature spaces. Technically speaking, the iterative framework of constraints self-learning and discriminant feature spaces exploring is a general expectation–maximization (EM) procedure. Its iteration alternates between performing the expectation (E) step, which exploits a discriminant feature space well enforcing the current constraints, and a maximization (M) step, which learns more constraints from the local structure of the data, i.e., nearest neighbors in the space explored in the E step. To take advantage of the augmented pairwise constraints, we then propose a two-step constraint-based clustering algorithm, i.e., greedy searching pure must-link sub-clusters and merging sub-clusters. It tries to find a near-optimal partition of the data by minimizing the cost of violating the constraints. The proposed method has the following advantages:
- The proposed method can learn partial discriminant feature spaces with the partial pairwise constraints, i.e., discriminant spaces for the labeled point. And, an approximately optimal discriminant feature space can be finally explored by constraints self-learning iteratively.
- This method allows self-learning more constraints by local neighbors in the Euclidean distance from the partial discriminant spaces. Even for complicated data, promising must-link and cannot-link constraints can be self-learned.
- The proposed constraint-based clustering algorithm is effective, which only uses the constraint information to conduct clustering. As prior knowledge of the number of clusters is unnecessary, it can be further used for detecting the outliers in a large dataset.
2. Related Works
As partial prior information existed in most of the real-world datasets [16], semi-supervised clustering has drawn a lot of attention in the past decade [17]. The semi-supervised clustering algorithms partition the data into groups enforcing the given constraints. The earlier algorithms tried to strictly satisfy all the constraints, such as semi-supervised variants of K-means [4,5,18]. Usually, domain knowledge is heuristic rather than exact [4], so it would be better to explore a soft partition way to satisfy most of the constraints [19,20].
Distance metric learning algorithms have also been incorporated into semi-supervised clustering, such as relevant component analysis [21], and Information Theoretic Metric Learning [22]. Currently, the dividing line between the constraint-based and metric-based algorithms is rather fuzzy. Bilenko et al. [6] proposed the MPCK-Means, incorporating both metric learning and the use of pairwise constraints in a uniform framework via an expectation–maximization process. Finding a good distance metric for clustering is equivalent to finding a good feature space transformation [10], such as spectral clustering. The most direct way is to manipulate the affinity matrix with the given pairwise constraints. For example, Lu et al. [11] proposed to update the affinity matrix by propagating the pairwise constraints information over the original affinity matrix.
Like unsupervised clustering, constrained algorithms suffer a lot when the intrinsic clusters have very different scales and densities [23]. Especially, the performance becomes unstable when the prior supervised knowledge is scarce [14]. To address this issue, a few works try to augment the constraints from existing knowledge. Yi et al. [24] casted the pairwise similarity matrix reconstruction into a matrix completion problem, which results in a convex optimization problem. Wang et al. [14] proposed a Self-Taught Spectral Clustering method by augmenting the given constraint set. And, their constraint augmentation procedure is realized by exploiting the low-rank property for matrix completion. However, these matrix completion-based methods do not explore the problem from the structure of data distribution itself and are very time-consuming [25]. So, it is not suitable for non-Gaussian data and high-dimensional manifold data. Klein et al. [26] proposed a constraints propagating algorithm by updating the proximity matrix with the shortest path searching. Its disadvantage is that the distance metric is learned in the original feature space and the process can be treated as somehow a density searching problem. Here, we will address the semi-supervised clustering problem by self-learning sufficient constraints from various explored discriminant spaces. Each discriminant space will be optimal for the current must-link and cannot-link constraints.
3. Materials and Methods
Assume we have N data instances, , , which can be mapped into K ground truth clusters. Let M be the must-link matrix where implies and should be in the same cluster, and C be the cannot-link matrix where implies and should be in different clusters. And, and are the ground truth constraint matrices; then, the sum of and should be an all-ones matrix. Assume the algorithm assigns each instance a label . So, the goal of clustering can be formulated as minimizing an objective function, defined as the sum of costs incurred by violating any constraint entries of and .
where is the indicator function and , and w is the penalty cost.
The perfect result of clustering is to encode every instance to a cluster enforcing and , i.e., . In the context of semi-supervised clustering, the constraint matrices M and C can be viewed as incomplete and a sparse observation of the ground truth. One possible way for better semi-supervised clustering is to achieve complete or approximately complete constraint matrices and .
Following this, we first propose a framework (CS-PDS) to achieve approximately complete constraint matrices and . Then, objective function (1) can be rewritten for semi-supervised clustering as follows:
Last, a two-step constraint-based clustering algorithm (FC2) is introduced to find a near-optimal partition of the data that minimizes the objective function (3). And the key symbols used in this paper are listed in Table 1.

Table 1.
Summarization of the key symbols.
3.1. Constraints Self-Learning from Partial Discriminant Spaces (CS-PDS)
Commonly, the discriminant space can provide a good view of the clusters, which makes distinct clusters as far from each other as possible. However, with partial constraint information, we cannot explore a space to have a perfect view of the intrinsic local structure for the whole data instances. Fortunately, a first-step discriminant space can be found to satisfy the partial constraints and be used to learn new constraints from the local structures. Together with the fresh constraints, we can further find another discriminant space to learn more constraints. The discriminant space should enforce constraints better in the structure, i.e., must-linked instances should be drawn much closer; meanwhile, cannot-linked instances should be much sparser. The local neighbors for each constrained instance can be exploited to form new constraints.
The key questions are as follows:
- How do we learn a discriminant space that can well illustrate the intrinsic structure of data in the Euclidean distance with the partial constraint information, i.e., must-links and cannot-links?
- Which kind of local neighborhoods can be used as new constraints?
- How do we tackle the conflict problem between must-link and cannot-link when we augment the constraints?
3.1.1. Solution for the 1st Question: Partial Discriminant Space Exploring
Let be the mapping of x from the original space to the new space, i.e., . For the must-link constraints, the optimal y should be satisfied by minimizing Formula (4), which means the must-link points should be close to each other.
For the cannot-link constraints, the optimal y should be satisfied by maximizing Formula (5), which means the cannot-link points should be far away from each other.
We firstly define the Laplacian matrix and diagonal matrix of the two constraint matrices as follows, respectively.
Then, the optimization problem can be formalized as maximizing Formula (8).
Assuming is the projection vector, the new representations of x can be obtained by . Formula (8) can be rewritten as exploring the optimal projection vector.
Let be a bonus matrix, which means cannot-link instances will be favored more if they are separated farther in the new space. Let and constraint be a constant c. Then, we can rewrite Equation (9) in Lagrangian form as Equation (10).
The solution can be obtained by solving the generalized eigenvalue decomposition problem as follows.
Note that it can suffer from a small sample size problem caused by limited must-link constraints, which makes the matrix singular. Therefore, in the first several iterations, we have to use another definition of P with Tikhonov regularization as follows.
where I is the identity matrix. For regularization , we can simply set in case of a non-positive definition of P.
3.1.2. Solution for the 2nd Question: Self-Learning
Here, we start the augmentation process from the given constrained instances. The unconstrained instances will be passively linked step by step.
- (1)
- Constraints learning for each must-link instance. u
Let be a set in which each instance must-link to instance u, and is the average distance between each linked instance pair with u. Then, we define , where and , as the at most k nearest neighbors set of u with . Finally, we will augment the must-links by making connections between u and the nodes in , and update the must-link matrix M as the following equation.
- (2)
- Constraints learning for each cannot-link instance. v
Define as the average distance between each must-link instance pair. And, is a set in which each instance is restricted to cannot-link to instance v. Then, let be the at most k nearest neighbors set of constraint instance v with , and . At last, we will augment the cannot-links by making connections between and , and update the cannot-link matrix C as the following equation.
3.1.3. Solution for the 3rd Question: Soft Regularization
We augment constraints within different spaces that may cause conflicts, i.e., two instances are labeled as must-link and cannot-link from different spaces. Such situations commonly occur on the points distributed on the edges between different clusters. Here, we introduce a soft regular solution as follows.
It can be drawn from the above formulas, in case of conflict, that constraint affiliation of the instance is a weight and the sum equals one (i.e., ).
Few constraints cannot project the data in a perfect space, but just a space satisfying the current constraints. However, the imperfect space is enough for learning local neighbor structures. The local structure in the projected space can be used to form new constraints. And, more self-learned constraints can make the projection more perfect step by step. As shown in the first line of Figure 1, we illustrate the must-link constraints self-learned step by step. It can be seen that, in only a few steps, all the iris points in one category are connected by must-links. The first algorithm (CS-PDS) provides a practical way to find a set of reasonable must-link and cannot-link constraints.

Figure 1.
Illustration of must-link constraints evolution by self-learning for the IRIS dataset. The first row shows the must-link connection graph of the points by visualization software Gephi (https://gephi.org/, accessed on 29 April 2025) with the Fruchterman Reingold layout algorithm, and the second row shows the corresponding matrices. Points in the same ground truth category are printed in the same color.
3.1.4. The Algorithm
Given a set of data points X, a given must-link constraint matrix M, and a given cannot-link constraint matrix C, the algorithm performs a moderate number of EM iterations between (E) partial discriminant space exploiting and (M) constraints self-learning. Pseudo-code for the algorithm is presented in Algorithm 1. The outputs are two approximately complete constraint matrices, which can be further used for clustering.
Parameter settings and convergence. The parameter k is the number of neighbors to construct the neighbor set , and is the experiential security setting for various datasets, which is based on the empirical performance or dataset characteristics. For the loop in the algorithm, we use the percentage of non-zero values in the matrix () and a maximum iteration time, Loops. For the experiments, we first set and .
Illustration. As shown in Figure 1, we take the IRIS data as a toy example to show the effectiveness of CS-PDS by visualizing the must-link matrix and its connection graph step by step. We can see that with the initial constraints, CS-PDS can explore an almost perfect constraint matrix within sixteen steps. As shown by the connection graph of the last iteration, the must-link matrix leads to a significantly good partition.
| Algorithm 1 Constraints Self-learning from Partial Discriminant Spaces (CS-PDS) |
|
3.2. Finding Clusters on Constraints
To take advantage of the augmented constraints, we propose an effective two-step algorithm for finding clusters that only relies on constraint matrices. For convenience, we first illustrate some definitions used in the algorithm. For each point , a must-link degree is defined as the number of must-links of point . is defined as the point set in which each point has at least one cannot-link constraint to a sub-cluster . (or ) is the point set in which each point must-link (or cannot-link) to point . denotes the number of elements of the point set. And, and denote the number of must-links and cannot-links between sub-clusters and , respectively. Pseudo-code for the algorithm is presented in Algorithm 2.
Step one. The first step is a straightforward greedy searching procedure that forms a set of pure must-link sub-clusters without any cannot-links itself. It begins the greedy searching from the point with the largest must-link degree every time. Step 5 initializes a new sub-cluster with the must-link points of and forms the cannot-link point set with its cannot-link points. Each iteration (Steps 7 to 15) will greedily search new points that only exist must-links to the current points of sub-cluster ; meanwhile, we make sure does not contain any cannot-links among its members. Moreover, Steps 10–11 eliminate the point from in case most of its must-link points have cannot-link constraints to . Each iteration, from Steps 3 to 17, will form a pure must-link sub-cluster.
Step two. The second step is to merge these subsets into k clusters. The repulsion r between two sub-clusters is defined as the ratio of the number of cannot-links and must-links between the two sub-clusters. We first calculate the repulsion r between each pair of sub-clusters, and then merge the sub-clusters into k clusters one by one from the lowest repulsion. In case of an isolated point, we assign it to the nearest cluster.
Proof.
The algorithm (FC2) gives a near-optimal solution for minimizing the objective function (3). It can be proved in a straightforward way. In the first step, the formed pure must-link sub-clusters guarantee that . According to the definition of repulsion r, the merging step minimizes the penalty cost of with the lowest cost of . □
| Algorithm 2 Finding Clusters on Constraints (FC2) |
|
4. Experiments
In this section, we empirically validate the effectiveness of the proposed algorithm with a comparison to various state-of-the-art algorithms.
4.1. Datasets and Experiments Setup
We chose three commonly used datasets from the UCI Archive including Iris, Wine, and Segmentation, the Protein dataset from the literature [27], and randomly sampled subsets from Digits {3, 8, 9} and Letters {I, J, L} handwritten character recognition datasets as suggested by Basu et al. [6]. These datasets come from different domains with various numbers of instances. The statistics of these datasets are listed in Table 2.

Table 2.
Statistics of datasets used in the experimental evaluation.
We compared the proposed semi-supervised clustering algorithm to the following eight algorithms, including three label-constrained algorithms, four pairwise-constrained algorithms, and the unsupervised spectral clustering as the baseline. The three label-constrained algorithms are (a) Flexible Constrained Spectral Clustering (FCSC) [12], (b) Constrained Spectral Clustering, and (c) Group with Bias (GrBias) [28,29]. The four pairwise-constrained algorithms include (d) Constrained K-Means clustering with background knowledge (C-K-Means) [4], (e) the Metric Pairwise-Constrained K-Means algorithm (MPCK-Means) [6], (f) the Information Theoretic Metric Learning algorithm (ITML) [22], and (g) Self-Taught Spectral Clustering (STSC) [14]. As mentioned earlier, both label and pairwise constraints can be formed as must-links and cannot-links. However, pairwise-constrained clustering poses more of a challenge for finding clusters from data. So, we conducted separate comparison studies on these state-of-the-art semi-supervised clustering algorithms with different types of constraints.
4.2. Results
As mentioned earlier, both label and pairwise constraints can be formed as must-links and cannot-links. However, pairwise-constrained clustering poses more of a challenge for finding clusters from data. So, we conducted separate comparison studies on these state-of-the-art semi-supervised clustering algorithms with different types of constraints. In order to examine the effectiveness of constraints for clustering, spectral clustering is applied as the baseline method without any constraints. In our experiments, we will report the Rand Index (RI) of all algorithms against the number of pairwise constraints and the percentage of known labels.
We first conducted comparison experiments with the label-constrained semi-supervised clustering algorithms. For each dataset, we randomly generated a set of labeled instances and then applied all algorithms to the dataset with the same label constraints. The process was repeated ten times with different label constraints. The average ARI and standard deviation are reported in Figure 2. Pairwise-constrained clustering is a much more difficult problem than the former one because the categories are uncleared. The number of must-link and cannot-link constraints are randomly generated and applied to all the algorithms at the same time. By executing the procedure ten times, we reported the average ARI and standard deviation in Figure 3.
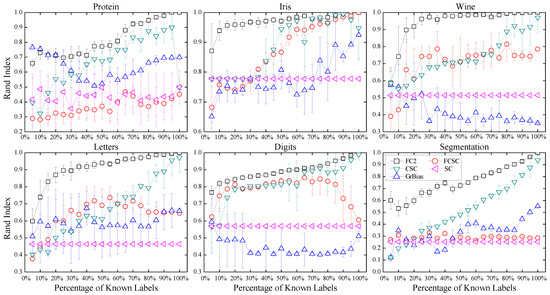
Figure 2.
Average clustering performance RI achieved by the proposed FC2 and the competing algorithms, i.e., FCSC, CSC, and GrBias.
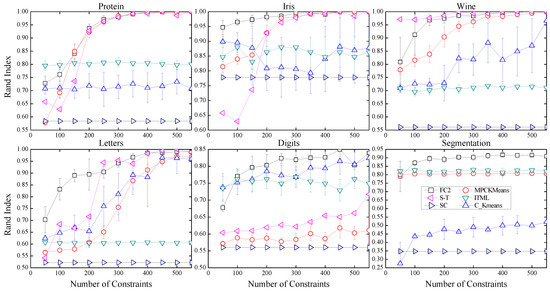
Figure 3.
Average performance achieved by our FC2 and competing algorithms, i.e., MPCK-Means, S-T, ITML, and C-K-Means.
As expected, pairwise constraints enhance the clustering performance in an effective way. We can observe from Figure 3 that the performance of a traditional method (i.e., C-K-Means) does not keep increasing when the number of constraints becomes larger. The reason is that inappropriate constraints may confuse the K-Means method. Combined with the metric learning method, the MPCK-Means and ITML methods perform more stably. However, the performance of these methods is still very low with insufficient constraints. The results indicate our method achieves steadily increasing performance against the number of constraints and outperforms the competing algorithms in most cases.
We can see that the Self-Taught (S-T) method also produces good performance, especially on the Wind dataset. In contrast, it employs a matrix completion approach to augment the given constraints. However, the matrix completion approach is very time-consuming and unstable. Table 3 summarizes the average running time for the six datasets of recovering a different number of constraints. The running time reported for our FC2 algorithm includes the CS-PDS algorithm. And, N/A means that the clustering task cannot be completed by the corresponding algorithm within 24 h. The Self-Taught (S-T) method takes more time than ours to obtain comparable performance. It is impractical for large data, such as the Segmentation dataset. We can draw a conclusion from Table 3 that the proposed algorithm is practical for large data and efficient.

Table 3.
Average running time (in seconds).
The algorithm of self-learning sufficient constraints is effective. Figure 4 shows the graph distance matrices of the original space and the space of the last iteration for three example datasets. The number of initial constraints are 50, 100, and 100, respectively. If the self-learned constraints are effective and correct, they can help to find a discriminant space to separate the points. It can be seen that obvious blocks can be found from the last explored discriminant space, which indirectly indicates that the self-learned constraints are effective. All the above results demonstrate that our algorithm can yield good performance with an insufficient number of constraints.
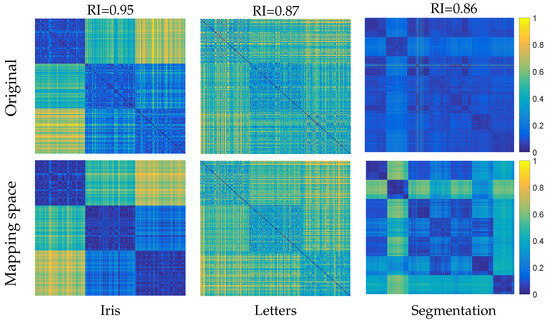
Figure 4.
Graph distance matrices of three example datasets.
5. Conclusions
Insufficient supervisory information sometimes confuses the semi-supervised clustering and misleads to unstable performance. In this paper, we solved the semi-supervised clustering problem from a new point of view that perfects the supervisory information in order to cluster the data. We first designed a self-learning framework to iteratively explore two approximately perfect constraint matrices. Then, a constraint-based clustering algorithm was presented to find a near-optimal partition for the data. Experimental results justified the effectiveness of our algorithm. Extending the algorithm to outliers detection is the primary avenue for future research work. One drawback of our algorithm is the efficiency of large datasets. In the case of a large dataset, it may take a long time to handle the clustering procedure. This is also one of our further research issues. The possible way is parallel performing the clustering procedure and employing it on GPU devices.
Funding
This research was funded by the Science and Technology Development Fund, Macao SAR, No.0006/2024/RIA1.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ye, W.; Tian, H.; Tang, S.; Sun, X. Enhancing Shortest-Path Graph Kernels via Graph Augmentation. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Vilnius, Lithuania, 9–13 September 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 180–198. [Google Scholar]
- Qian, L.; Plant, C.; Qin, Y.; Qian, J.; Böhm, C. DynoGraph: Dynamic Graph Construction for Nonlinear Dimensionality Reduction. In Proceedings of the 2024 IEEE International Conference on Data Mining (ICDM), Abu Dhabi, United Arab Emirates, 9–12 December 2024; pp. 827–832. [Google Scholar]
- Guo, W.; Ye, W.; Chen, C.; Sun, X.; Böhm, C.; Plant, C.; Rahardjy, S. Bootstrap Deep Spectral Clustering with Optimal Transport. IEEE Trans. Multimed. 2025. [Google Scholar]
- Wagstaff, K.; Cardie, C.; Rogers, S.; Schrödl, S. Constrained k-means clustering with background knowledge. In Proceedings of the ICML, Williamstown, MA, USA, 28 June–1 July 2001; Volume 1, pp. 577–584. [Google Scholar]
- Basu, S.; Banerjee, A.; Mooney, R. Semi-supervised clustering by seeding. In Proceedings of the 19th International Conference on Machine Learning (ICML-2002), San Francisco, CA, USA, 8–12 July 2002. [Google Scholar]
- Bilenko, M.; Basu, S.; Mooney, R.J. Integrating constraints and metric learning in semi-supervised clustering. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; ACM: New York, NY, USA, 2004; p. 11. [Google Scholar]
- Zhang, Z.Y. Community structure detection in complex networks with partial background information. EPL (Europhys. Lett.) 2013, 101, 48005. [Google Scholar] [CrossRef]
- Qian, L.; Plant, C.; Böhm, C. Density-Based Clustering for Adaptive Density Variation. In Proceedings of the 2021 IEEE International Conference on Data Mining (ICDM), Auckland, New Zealand, 7–10 December 2021; pp. 1282–1287. [Google Scholar]
- Mautz, D.; Ye, W.; Plant, C.; Böhm, C. Non-redundant subspace clusterings with nr-kmeans and nr-dipmeans. ACM Trans. Knowl. Discov. Data (TKDD) 2020, 14, 1–24. [Google Scholar] [CrossRef]
- Hoi, S.C.; Liu, W.; Lyu, M.R.; Ma, W.Y. Learning distance metrics with contextual constraints for image retrieval. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; Volume 2, pp. 2072–2078. [Google Scholar]
- Lu, Z.; Carreira-Perpinan, M.A. Constrained spectral clustering through affinity propagation. In Proceedings of the Computer Vision and Pattern Recognition, CVPR 2008, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Wang, X.; Davidson, I. Flexible constrained spectral clustering. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–28 July 2010; ACM: New York, NY, USA, 2010; pp. 563–572. [Google Scholar]
- Kawale, J.; Boley, D. Constrained Spectral Clustering using L1 Regularization. In Proceedings of the SDM, Austin, TX, USA, 2–4 May 2013; pp. 103–111. [Google Scholar]
- Wang, X.; Wang, J.; Qian, B.; Wang, F.; Davidson, I. Self-Taught Spectral Clustering via Constraint Augmentation. In Proceedings of the SDM, Philadelphia, PA, USA, 24–26 April 2014; pp. 416–424. [Google Scholar]
- Tang, S.; Tian, H.; Cao, X.; Ye, W. Deep hierarchical graph alignment kernels. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence, Jeju, Republic of Korea, 3–9 August 2024; pp. 4964–4972. [Google Scholar]
- Yi, J.; Zhang, L.; Yang, T.; Liu, W.; Wang, J. An Efficient Semi-Supervised Clustering Algorithm with Sequential Constraints. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, 10–13 August 2015; ACM: New York, NY, USA, 2015; pp. 1405–1414. [Google Scholar]
- Sun, X.; Song, Z.; Yu, Y.; Dong, J.; Plant, C.; Böhm, C. Network Embedding via Deep Prediction Model. IEEE Trans. Big Data 2023, 9, 455–470. [Google Scholar] [CrossRef]
- Shental, N.; Bar-Hillel, A.; Hertz, T.; Weinshall, D. Computing Gaussian mixture models with EM using equivalence constraints. Adv. Neural Inf. Process. Syst. 2004, 16, 465–472. [Google Scholar]
- Basu, S.; Bilenko, M.; Mooney, R.J. A probabilistic framework for semi-supervised clustering. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; ACM: New York, NY, USA, 2004; pp. 59–68. [Google Scholar]
- Bansal, N.; Blum, A.; Chawla, S. Correlation clustering. Mach. Learn. 2004, 56, 89–113. [Google Scholar] [CrossRef]
- Bar-Hillel, A.; Hertz, T.; Shental, N.; Weinshall, D. Learning a mahalanobis metric from equivalence constraints. J. Mach. Learn. Res. 2005, 6, 937–965. [Google Scholar]
- Davis, J.V.; Kulis, B.; Jain, P.; Sra, S.; Dhillon, I.S. Information-theoretic metric learning. In Proceedings of the 24th International Conference on Machine Learning, Corvalis, ON, USA, 20–24 June 2007; ACM: New York, NY, USA, 2007; pp. 209–216. [Google Scholar]
- Nadler, B.; Galun, M. Fundamental limitations of spectral clustering. Adv. Neural Inf. Process. Syst. 2006, 19, 1017–1024. [Google Scholar]
- Yi, J.; Zhang, L.; Jin, R.; Qian, Q.; Jain, A. Semi-supervised clustering by input pattern assisted pairwise similarity matrix completion. In Proceedings of the 30th International Conference on Machine Learning (ICML-13), Atlanta, GA, USA, 16–21 June 2013; pp. 1400–1408. [Google Scholar]
- Sun, X.; Zhang, Y.; Chen, C.; Xie, S.; Dong, J. High-order paired-ASPP for deep semantic segmentation networks. Inf. Sci. 2023, 646, 119364. [Google Scholar] [CrossRef]
- Klein, D.; Kamvar, S.D.; Manning, C.D. From Instance-level Constraints to Space-Level Constraints: Making the Most of Prior Knowledge in Data Clustering. In Proceedings of the Nineteenth International Conference on Machine Learning, Sydney, Australia, 8–12 July 2002; Volume 655989, pp. 307–314. [Google Scholar]
- Xing, E.P.; Ng, A.Y.; Jordan, M.I.; Russell, S. Distance metric learning with application to clustering with side-information. Adv. Neural Inf. Process. Syst. 2003, 15, 505–512. [Google Scholar]
- Yu, S.X.; Shi, J. Segmentation given partial grouping constraints. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 173–183. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.X.; Shi, J. Grouping with bias. In Proceedings of the NIPS, Vancouver, BC, Canada, 3–8 December 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).