Multiscale Fuzzy Temporal Pattern Mining: A Block-Decomposition Algorithm for Partial Periodic Associations in Event Data
Abstract
1. Introduction
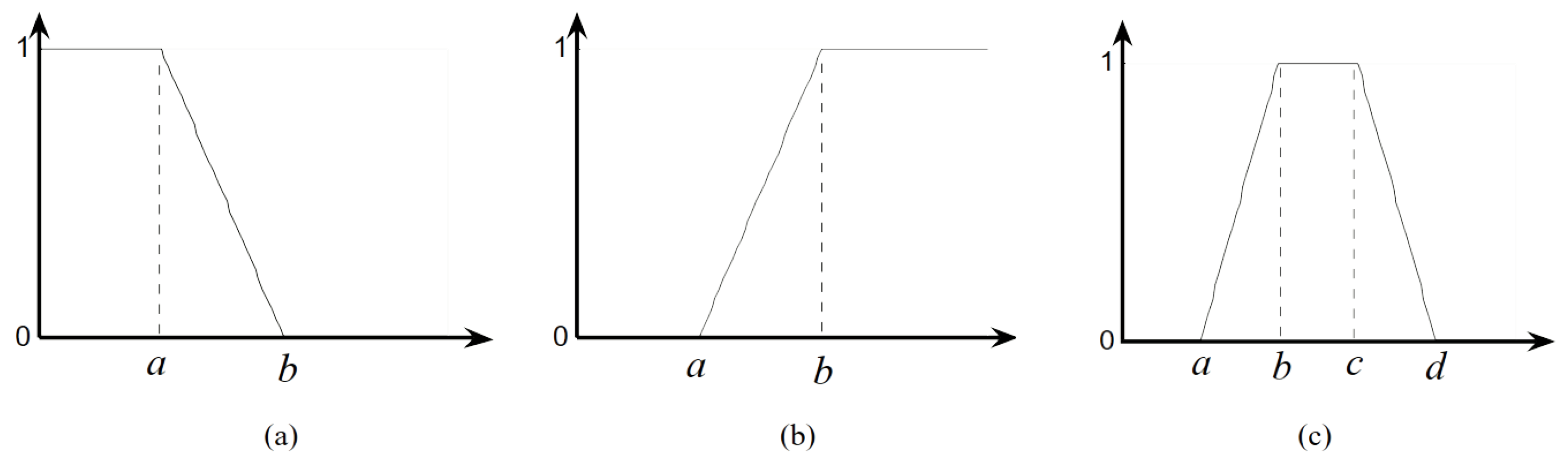
2. Partial Periodic Patterns in Fuzzy Temporal Events
- (1)
- Periodic Cycle Frequency (PCF): Characterizes the occurrence frequency of the rule throughout its entire lifecycle, calculated as:where is the periodic temporal type, and represents the maximum number of repetitions with as the period within the time interval .
- (2)
- Rule Frequency (RF): Reflects the repetition frequency of the rule within specific periods, calculated as:where is the base temporal type.
3. Mining Algorithm for Periodic Patterns of Fuzzy Temporal Events
3.1. Algorithm Design Approach
3.2. Core Algorithm Description
3.2.1. Fuzzy Temporal Event Preprocessing at the Base Time Unit Layer
3.2.2. Candidate Periodic Association Rules at the Occurrence Period Layer
3.2.3. Partial Periodic Pattern Validation at the Combined Period Layer
| Algorithm 1 Main Algorithm: Fuzzy Temporal Partial Periodic Mining Algorithm (3P-TFT) |
| Require: Fuzzy temporal event list , parameters r, , , Ensure: Fuzzy periodic rule list
|
4. Algorithm Testing and Result Analysis
4.1. Data Preparation
4.2. Results Analysis
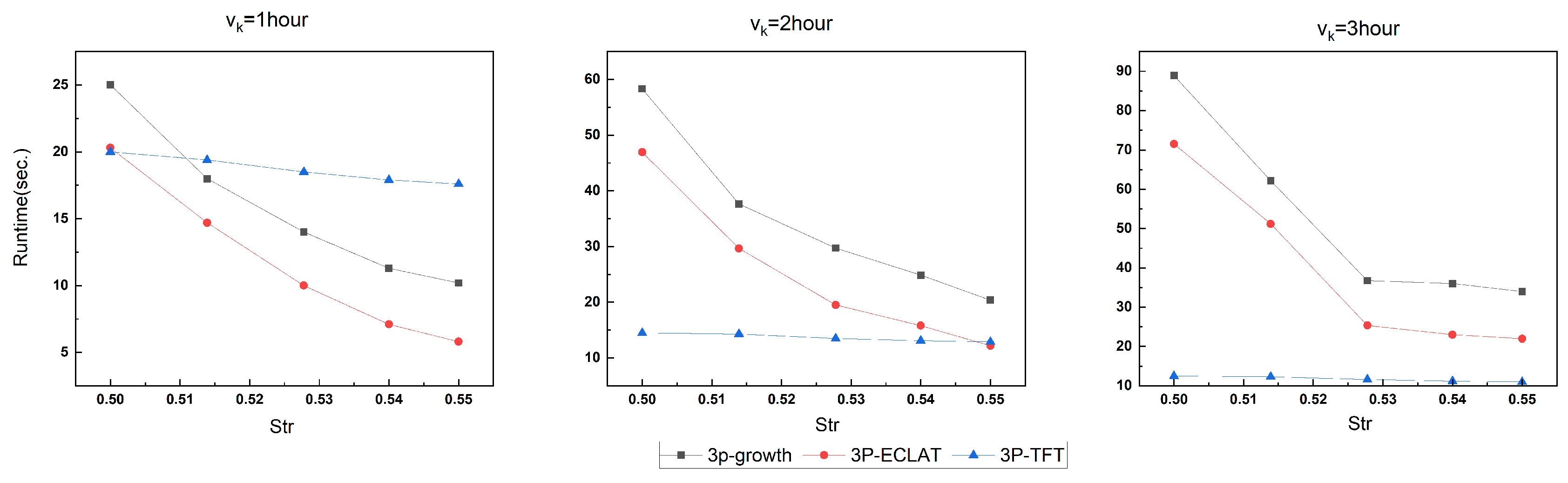
4.3. Algorithm Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kiran, R.U.; Venkatesh, J.; Toyoda, M.; Kitsuregawa, M.; Reddy, P.K. Discovering partial periodic-frequent patterns in a transactional database. J. Syst. Softw. 2017, 125, 170–182. [Google Scholar] [CrossRef]
- Kiran, R.U.; Kitsuregawa, M. Finding periodic patterns in big data. In Proceedings of the Big Data Analytics: 4th International Conference, BDA 2015, Hyderabad, India, 15–18 December 2015; pp. 121–133. [Google Scholar]
- Datta, S.; Mali, K.; Das, S.; Kundu, S.; Harh, S. Rhythmus periodic frequent pattern mining without periodicity threshold. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 8551–8563. [Google Scholar] [CrossRef]
- Upadhya, K.J.; Paleja, A.; Geetha, M.; Rao, B.D.; Chhabra, M.S. Finding Partial Periodic and Rare Periodic Patterns in Temporal Databases. IEEE Access 2023, 11, 92242–92257. [Google Scholar] [CrossRef]
- Kiran, R.U.; Chhabra, V.; Chennupati, S.; Reddy, P.K.; Dao, M.S.; Zettsu, K. A novel null-invariant temporal measure to discover partial periodic patterns in non-uniform temporal databases. In Proceedings of the International Conference on Database Systems for Advanced Applications, Online, 11–14 April 2022; pp. 569–577. [Google Scholar]
- Rage, U.K.; Chhabra, V.; Chennupati, S.; Polipalli, K.R.; Dao, M.S.; Zettsu, K. Periodic-confidence: A null-invariant measure to discover partial periodic patterns in non-uniform temporal databases. Int. J. Data Sci. Anal. 2023, 1–23. [Google Scholar] [CrossRef]
- Ale, J.M.; Rossi, G.H. An approach to discovering temporal association rules. In Proceedings of the 2000 ACM Symposium on Applied computing, Como, Italy, 19–21 March 2000; pp. 294–300. [Google Scholar]
- Mahanta, A.K.; Mazarbhuiya, F.A.; Baruah, H.K. Finding locally and periodically frequent sets and periodic association rules. In Proceedings of the Pattern Recognition and Machine Intelligence: First International Conference, PReMI 2005, Kolkata, India, 20–22 December 2005; pp. 576–582. [Google Scholar]
- Kiran, R.U.; Saideep, C.; Zettsu, K.; Toyoda, M.; Kitsuregawa, M.; Reddy, P.K. Discovering partial periodic spatial patterns in spatiotemporal databases. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 233–238. [Google Scholar]
- Pamalla, V.; Rage, U.K.; Penugonda, R.; Palla, L.; Watanobe, Y.; Ito, S.; Zettsu, K.; Toyoda, M.; Bathala, V.v.r. 3P-ECLAT: Mining partial periodic patterns in columnar temporal databases. Appl. Intell. 2024, 54, 657–679. [Google Scholar] [CrossRef]
- Likhitha, P.; Ravikumar, P.; Kiran, R.U.; Watanobe, Y. Discovering top-k periodic-frequent patterns in very large temporal databases. In Proceedings of the International Conference on Big Data Analytics, Hyderabad, India, 19–22 December 2022; pp. 200–210. [Google Scholar]
- Likhitha, P.; Ravikumar, P.; Saxena, D.; Kiran, R.U.; Watanobe, Y. k-PFPMiner: Top-k Periodic Frequent Patterns in Big Temporal Databases. IEEE Access 2023, 11, 119033–119044. [Google Scholar] [CrossRef]
- Kiran, R.U.; Saideep, C.; Ravikumar, P.; Zettsu, K.; Toyoda, M.; Kitsuregawa, M.; Reddy, P.K. Discovering fuzzy periodic-frequent patterns in quantitative temporal databases. In Proceedings of the 2020 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Saideep, C.; Uday Kiran, R.; Zettsu, K.; Wu, C.W.; Krishna Reddy, P.; Toyoda, M.; Kitsuregawa, M. Parallel mining of partial periodic itemsets in big data. In Proceedings of the Trends in Artificial Intelligence Theory and Applications. Artificial Intelligence Practices: 33rd International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, IEA/AIE 2020, Kitakyushu, Japan, 22–25 September 2020; pp. 807–819. [Google Scholar]
- Nofong, V.M. Discovering productive periodic frequent patterns in transactional databases. Ann. Data Sci. 2016, 3, 235–249. [Google Scholar] [CrossRef]
- Wang, S.; Chen, X.; Ma, D.; Wang, C.; Wang, Y.; Qi, H.; Zhou, G.; Li, Q.; Liu, M. MIANet: Multi-level temporal information aggregation in mixed-periodicity time series forecasting tasks. Eng. Appl. Artif. Intell. 2023, 121, 106175. [Google Scholar] [CrossRef]
- Sridevi, S.; Rajaram, S.; Swadhikar, C. An intelligent prediction system for time series data using periodic pattern mining in temporal databases. In Proceedings of the First International Conference on Intelligent Interactive Technologies and Multimedia, Allahabad, India, 27–30 December 2010; pp. 163–171. [Google Scholar]
- Meng, Z.; Jiang, H.; Jiang, M.; Liu, Y. An Algorithm of Discovering Approximate Periodicity Based on Self-Organizing Map for Temporal Data. In Proceedings of the Fourth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2007), Haikou, China, 24–27 August 2007; Volume 3, pp. 293–297. [Google Scholar]
- Zhang, X.; Qi, Y.; Chen, G.; Gan, W.; Fournier-Viger, P. Fuzzy-driven periodic frequent pattern mining. Inf. Sci. 2022, 618, 253–269. [Google Scholar] [CrossRef]
- Hong, T.P.; Chen, C.H.; Lin, J.C.W. A survey of fuzzy data mining techniques. In Fuzzy Statistical Decision-Making: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2016; pp. 329–354. [Google Scholar]
- Wu, T.Y.; Lin, J.C.W.; Yun, U.; Chen, C.H.; Srivastava, G.; Lv, X. An efficient algorithm for fuzzy frequent itemset mining. J. Intell. Fuzzy Syst. 2020, 38, 5787–5797. [Google Scholar] [CrossRef]
- Chen, C.H.; Chou, H.; Hong, T.P.; Nojima, Y. Cluster-based membership function acquisition approaches for mining fuzzy temporal association rules. IEEE Access 2020, 8, 123996–124006. [Google Scholar] [CrossRef]
- Hong, T.P.; Lan, G.C.; Su, J.H.; Wu, P.S.; Wang, S.L. Discovery of temporal association rules with hierarchical granular framework. Appl. Comput. Inform. 2016, 12, 134–141. [Google Scholar] [CrossRef][Green Version]
- Li, Y.; Ning, P.; Wang, X.S.; Jajodia, S. Discovering calendar-based temporal association rules. Data Knowl. Eng. 2003, 44, 193–218. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.S.; Jajodia, S. Discovering temporal patterns in multiple granularities. In Proceedings of the Temporal, Spatial, and Spatio-Temporal Data Mining: First International Workshop, TSDM 2000, Lyon, France, 12 September 2000; pp. 5–19. [Google Scholar]
- Mahanta, A.K.; Mazarbhuiya, F.A.; Baruah, H.K. Finding calendar-based periodic patterns. Pattern Recognit. Lett. 2008, 29, 1274–1284. [Google Scholar] [CrossRef]
- Mazarbhuiya, F.A.; Kichu, L.; AlZahrani, M. Fuzzy Periodic Patterns from Super-Market Datasets. In Proceedings of the International Conference on Intelligent and Fuzzy Systems, Izmir, Turkey, 19–21 July 2022; pp. 208–218. [Google Scholar]
- Lee, W.J.; Jiang, J.Y.; Lee, S.J. Mining fuzzy periodic association rules. Data Knowl. Eng. 2008, 65, 442–462. [Google Scholar] [CrossRef]
- Zhuo, C.; Jiahui, L.; Chen, L. A fuzzy calendar-based algorithm for mining temporal association rules and its application. In Proceedings of the 2009 Sixth International Conference on Fuzzy Systems and Knowledge Discovery, Tianjin, China, 14–16 August 2009; Volume 2, pp. 28–33. [Google Scholar]
- Zhu, A.; Meng, Z.; Shen, R. Research on Fuzzy Temporal Event Association Mining Model and Algorithm. Axioms 2023, 12, 117. [Google Scholar] [CrossRef]
- Kiran, R.U.; Veena, P.; Ravikumar, P.; Saideep, C.; Zettsu, K.; Shang, H.; Toyoda, M.; Kitsuregawa, M.; Reddy, P.K. Efficient discovery of partial periodic patterns in large temporal databases. Electronics 2022, 11, 1523. [Google Scholar] [CrossRef]
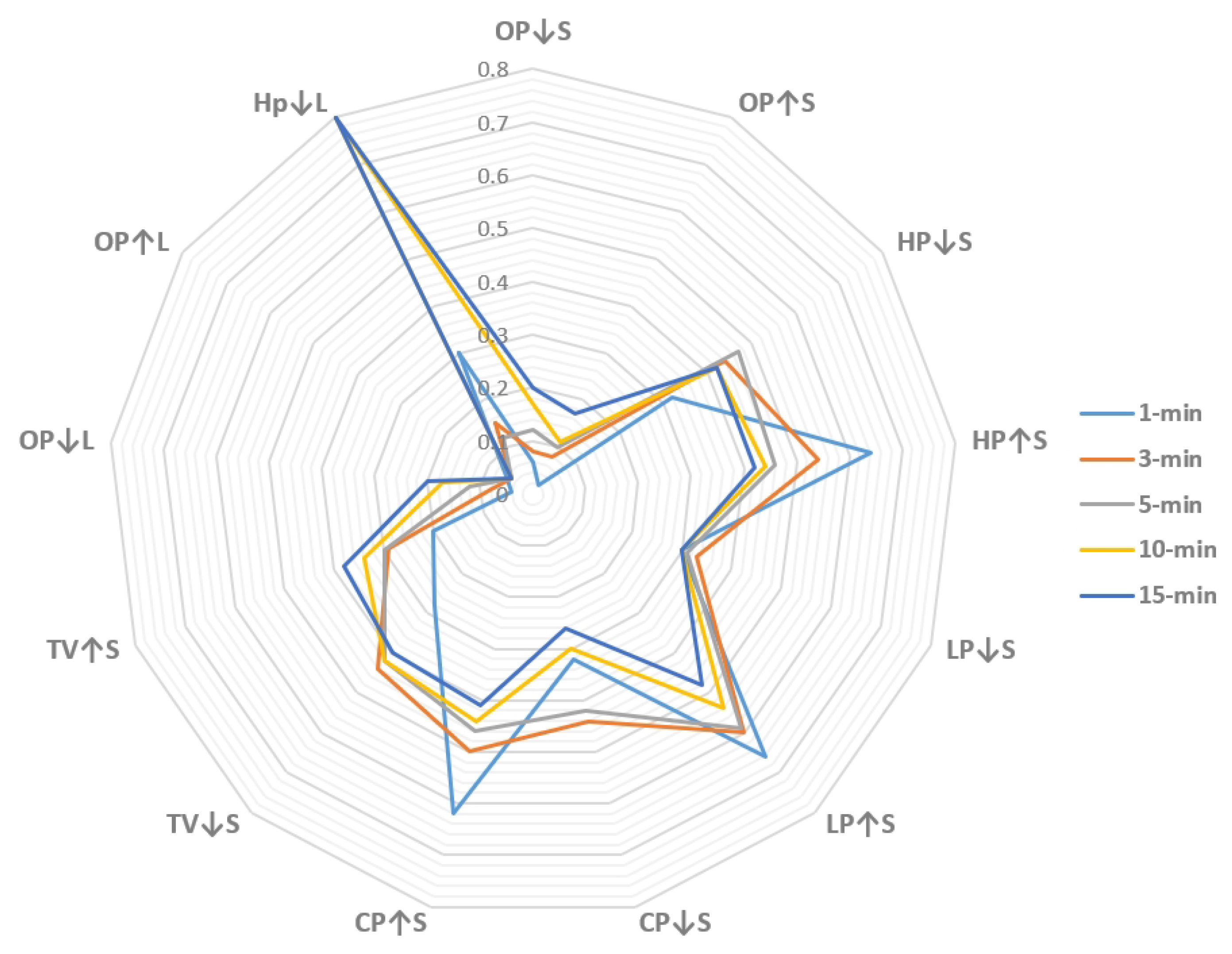

| 1-min | 3-min | 5-min | 10-min | 15-min | |
|---|---|---|---|---|---|
| Conventional | 13 | 27 | 24 | 14 | 9 |
| Fuzzy | 20 | 69 | 100 | 147 | 225 |
| Index | Rule Antecedent | Rule Consequent | Period (M) | Periodic Strength | Establishment Time |
|---|---|---|---|---|---|
| 1 | [CP↑S & CP↑L] | OP↑L | 1 | 0.7121 | [‘2010’, ‘2011’, ‘2012’, |
| ‘2013’, ‘2014’, ‘2015’, ‘2018’] | |||||
| 2 | [CP↑S & CP↑L] | LP↑S | 1 | 0.6524 | [‘2010’, ‘2013’, ‘2014’, |
| ‘2015’, ‘2016’, ‘2018’] | |||||
| 3 | [CP↑S & CP↑L] | LP↑S | 5 | 0.7114 | [‘2011’, ‘2012’, ‘2013’, |
| ‘2014’, ‘2016’, ‘2018’, ‘2019’] | |||||
| 4 | [CP↑S & CP↑L] | OP↑S | 2 | 0.6478 | [‘2012’, ‘2014’, ‘2016’, |
| ‘2017’, ‘2018’, ‘2019’] | |||||
| 5 | [CP↑S & TV↓S] | OP↑S | 6 | 0.6638 | [‘2010’, ‘2011’, ‘2012’, |
| ‘2014’, ‘2017’, ‘2018’] | |||||
| 6 | OP↑S | OP↓S | 3 | 0.6828 | [‘2010’, ‘2011’, ‘2012’, |
| ‘2013’, ‘2015’, ‘2017’, ‘2018’] | |||||
| 7 | [CP↓L & CP↓S] | [OP↓S & HP↓S] | 7 | 0.7050 | [‘2011’, ‘2012’, ‘2013’, |
| ‘2014’, ‘2016’, ‘2017’, ’2018’] | |||||
| 8 | CP↓L | [OP↓L & HP↓S] | 7 | 0.6982 | [‘2012’, ‘2013’, ‘2014’, |
| ‘2016’, ‘2017’, ‘2018’, ‘2019’] | |||||
| 9 | CP↓L | [OP↓L & HP↓L] | 7 | 0.7056 | [‘2012’, ‘2013’, ‘2014’, |
| ‘2015’, ‘2016’, ‘2018’, ‘2019’] | |||||
| 10 | CP↑L | TV↓S | 11 | 0.6855 | [‘2010’, ‘2011’, ‘2012’, |
| ‘2013’, ‘2014’, ‘2015’, ‘2018’] | |||||
| 11 | [HP↓S & CP↓L] | [OP↓L & OP↓S] | 12 | 0.7104 | [‘2011’, ‘2012’, ‘2013’, |
| ‘2015’, ‘2016’, ‘2017’, ‘2019’] |
| Dataset | Nature | Temper Type | lransaction Length (in Count) | Database Size (in Count) | ||
|---|---|---|---|---|---|---|
| Min. | Avg. | Max. | ||||
| Pollution | Dense | 1 h | 11 | 460 | 971 | 720 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, A.; Zhang, H.; Chen, X.; Zhu, D. Multiscale Fuzzy Temporal Pattern Mining: A Block-Decomposition Algorithm for Partial Periodic Associations in Event Data. Mathematics 2025, 13, 1349. https://doi.org/10.3390/math13081349
Zhu A, Zhang H, Chen X, Zhu D. Multiscale Fuzzy Temporal Pattern Mining: A Block-Decomposition Algorithm for Partial Periodic Associations in Event Data. Mathematics. 2025; 13(8):1349. https://doi.org/10.3390/math13081349
Chicago/Turabian StyleZhu, Aihua, Haote Zhang, Xingqian Chen, and Dingkun Zhu. 2025. "Multiscale Fuzzy Temporal Pattern Mining: A Block-Decomposition Algorithm for Partial Periodic Associations in Event Data" Mathematics 13, no. 8: 1349. https://doi.org/10.3390/math13081349
APA StyleZhu, A., Zhang, H., Chen, X., & Zhu, D. (2025). Multiscale Fuzzy Temporal Pattern Mining: A Block-Decomposition Algorithm for Partial Periodic Associations in Event Data. Mathematics, 13(8), 1349. https://doi.org/10.3390/math13081349






