Transient Post-Buckling of Microfluid-Conveying FG-CNTs Cylindrical Microshells Embedded in Kerr Foundation and Exposed to a 2D Magnetic Field
Abstract
1. Introduction
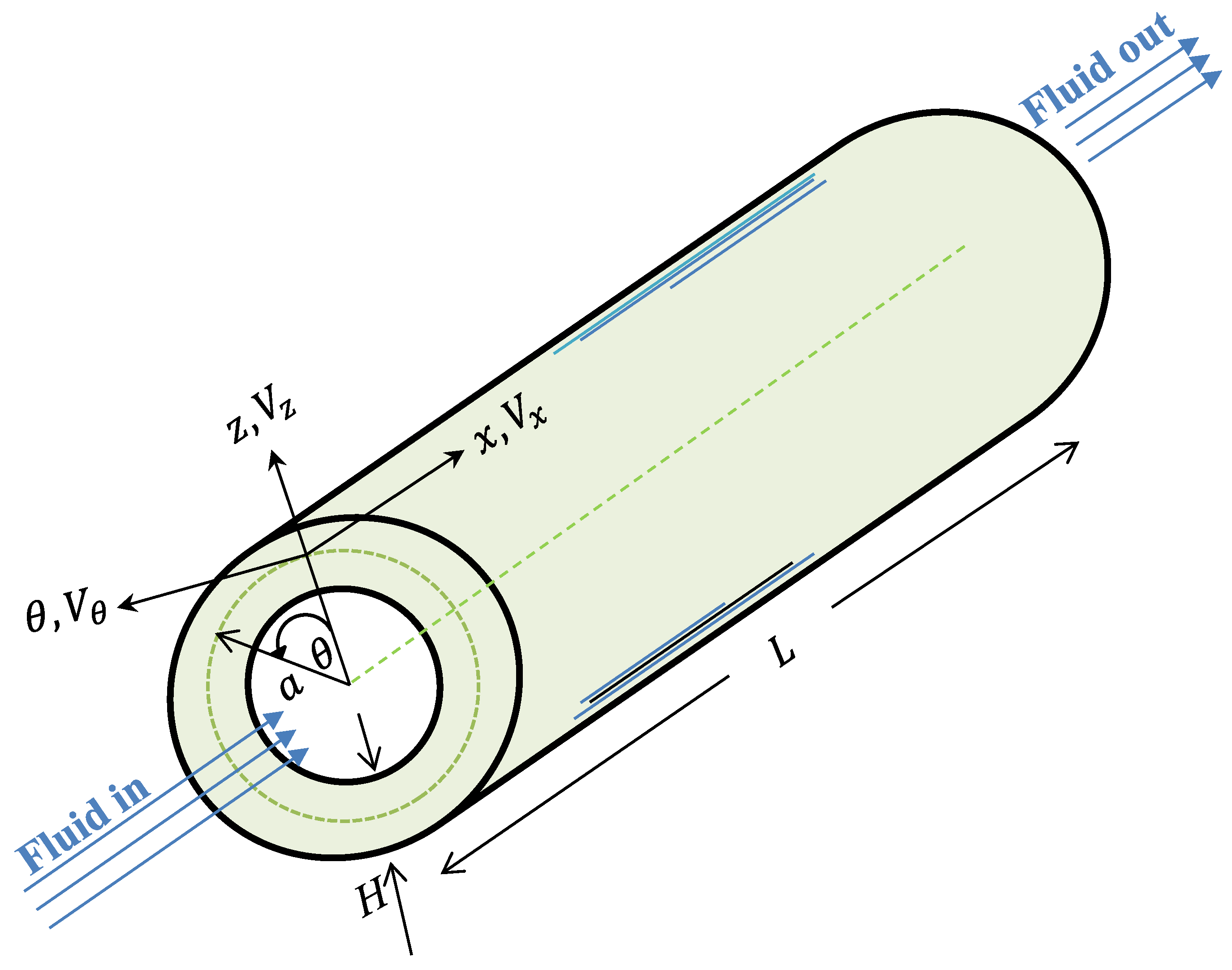
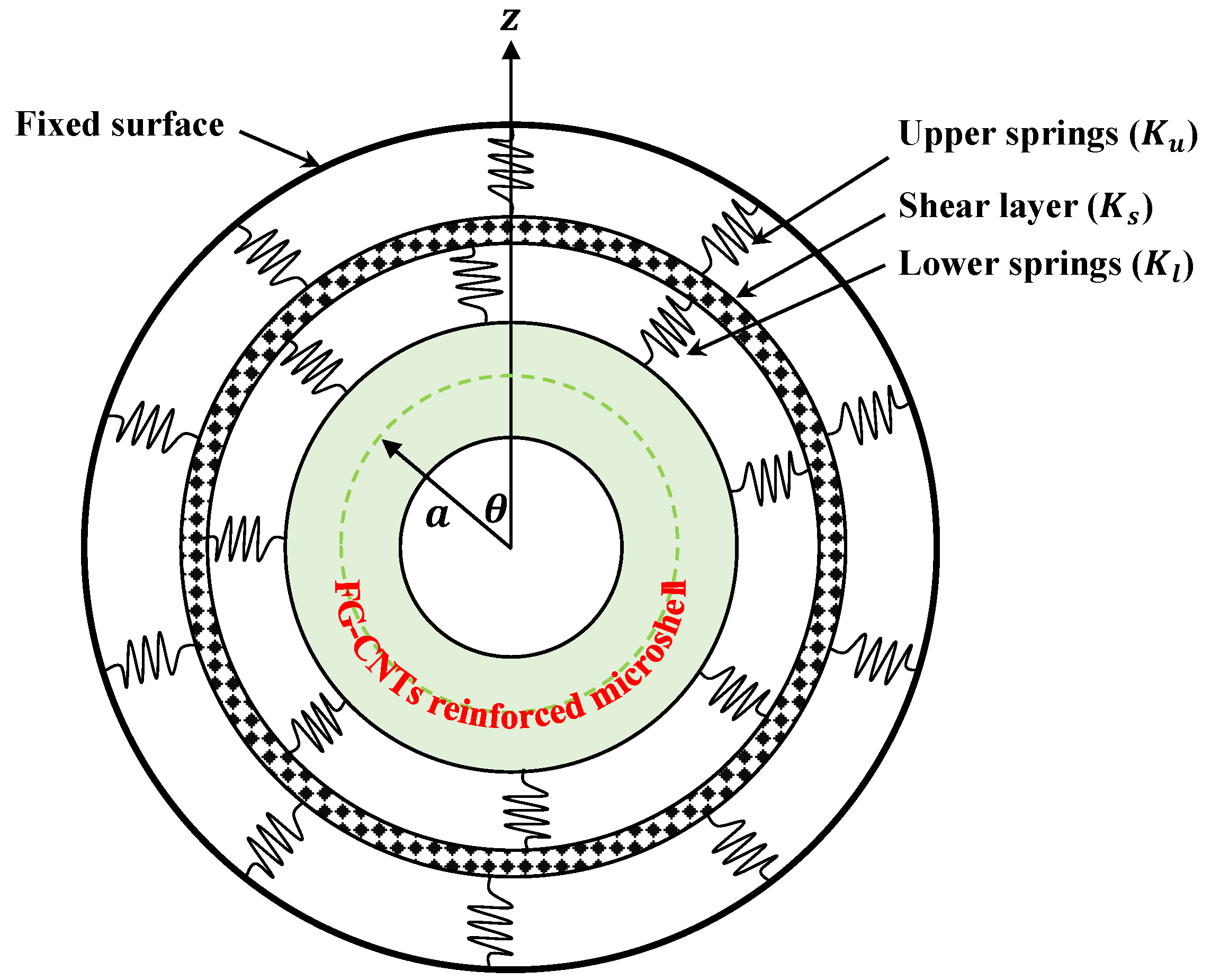
2. Formulation
2.1. Displacement Field
2.2. Strain-Displacement Relations
2.3. Rotation and Curvature Tensors
2.4. Modified Couple Stress Model
3. Equations of Motion
3.1. Lorentz Force Applied to the Microshell
3.2. Force Due to the Magnetic Fluid
3.3. Hamilton’s Principle
4. Solution Procedure
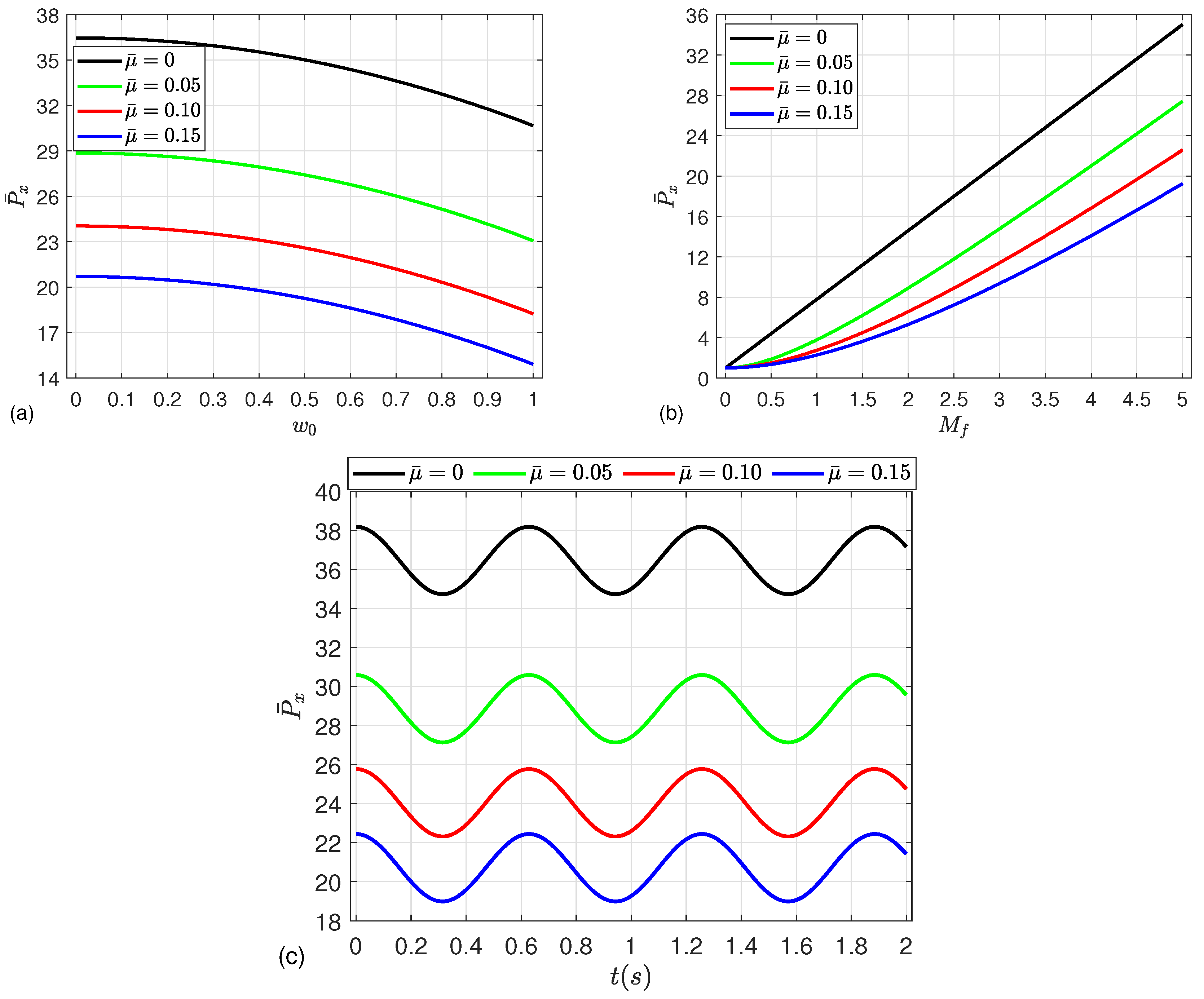
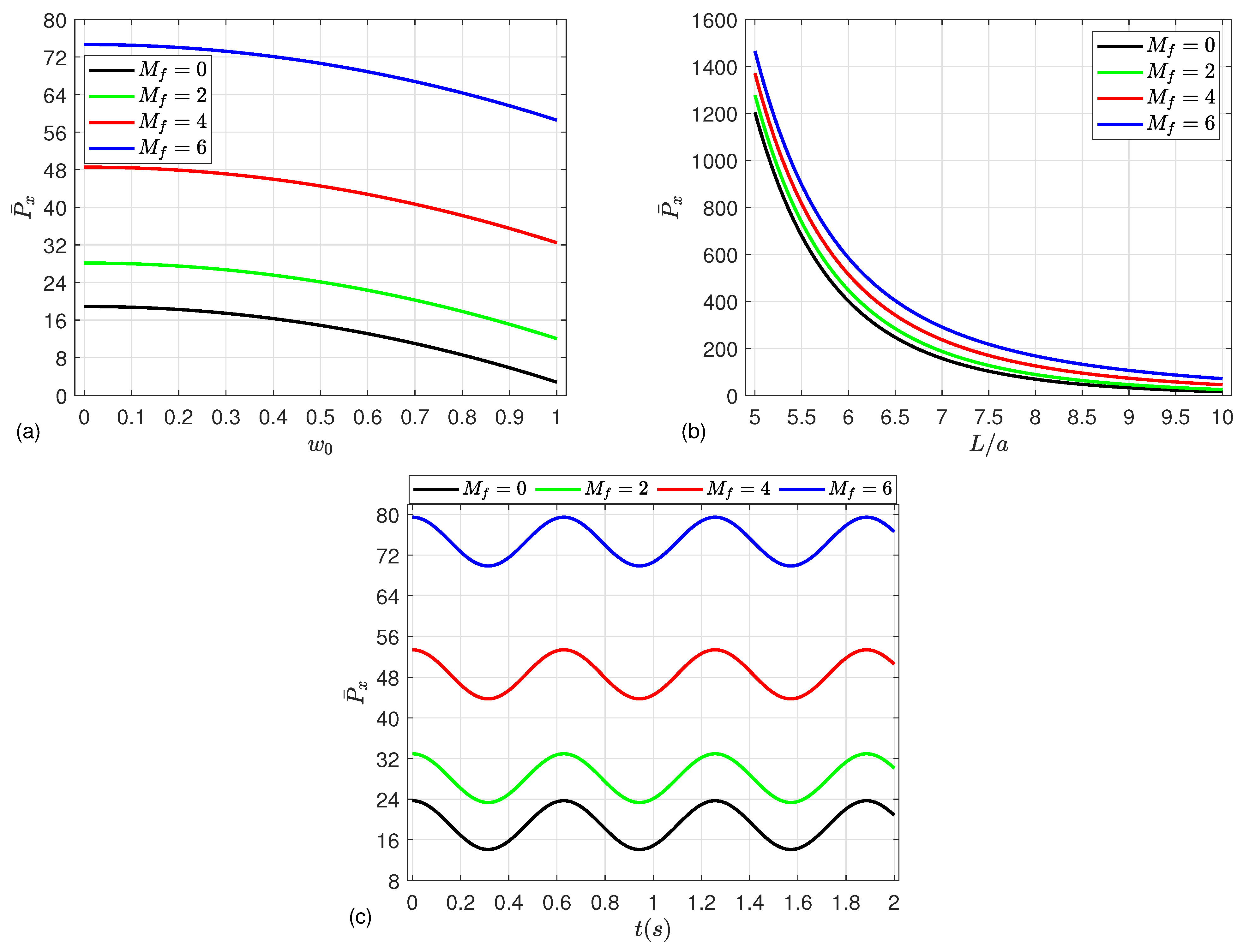
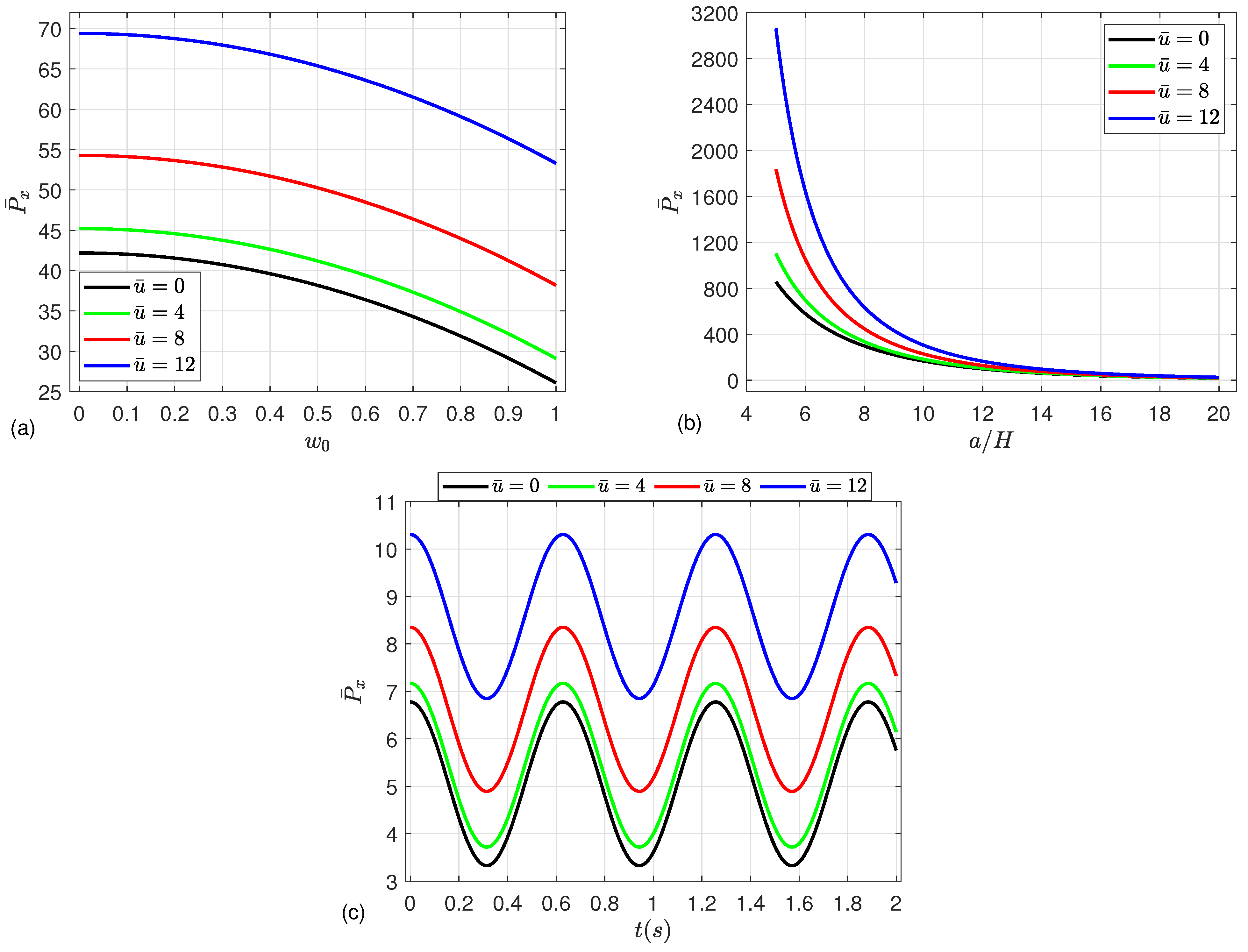
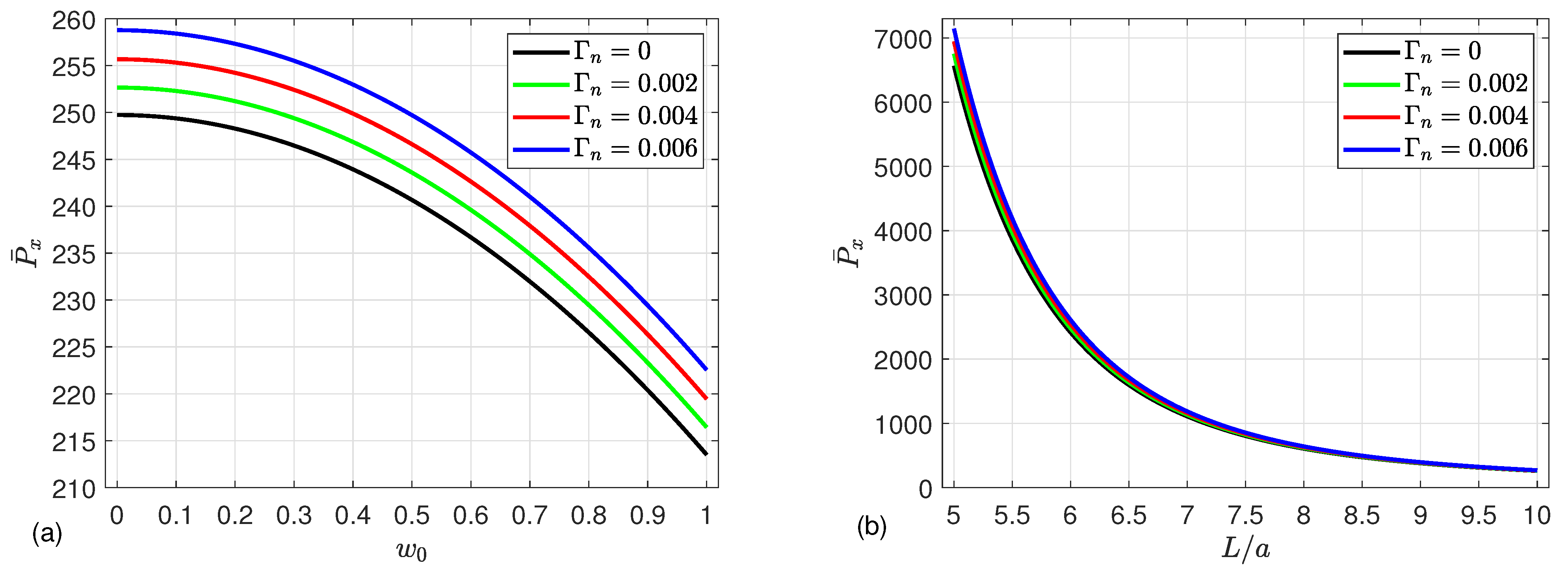
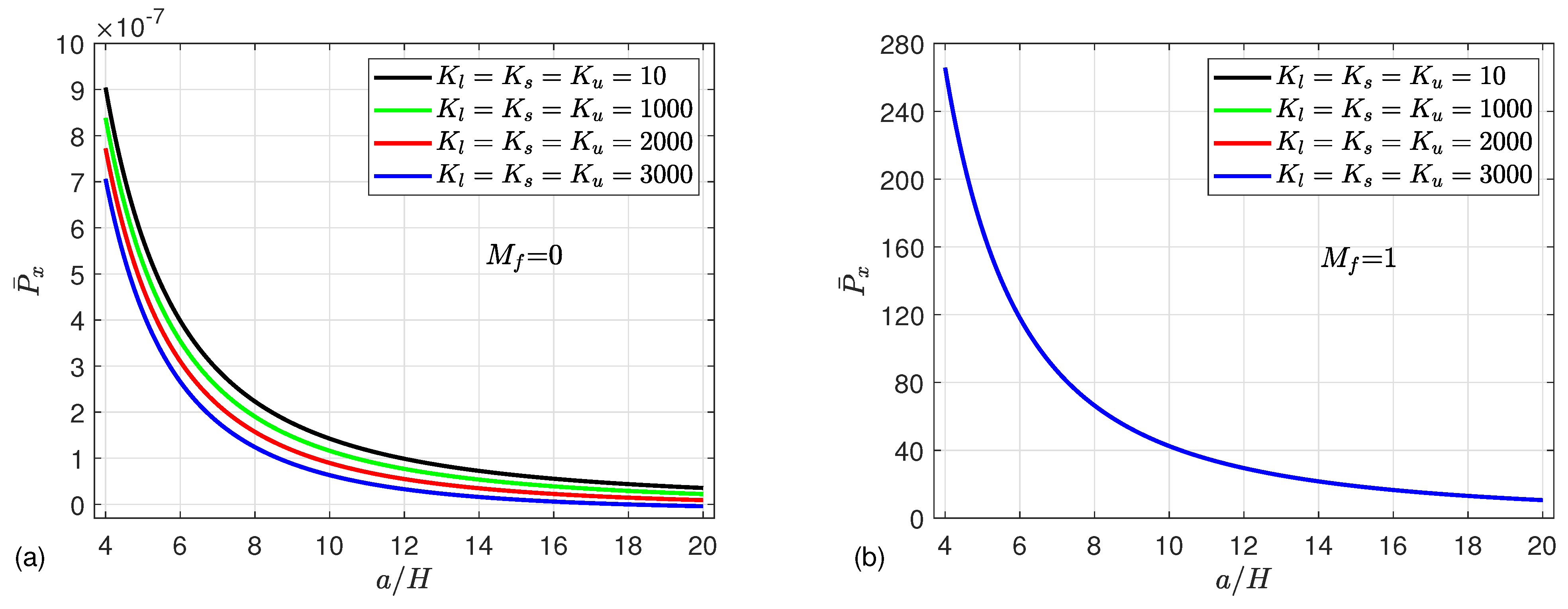
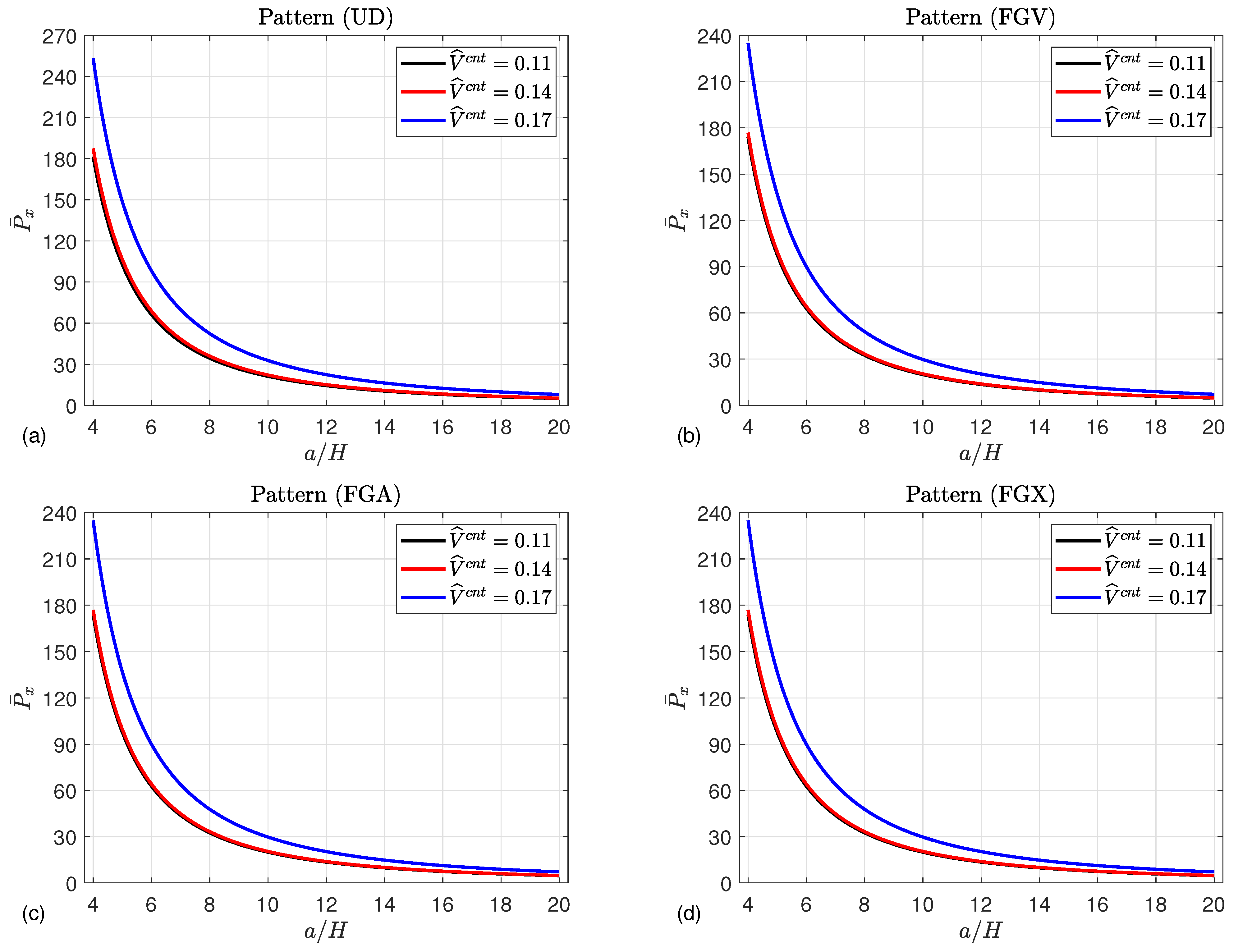
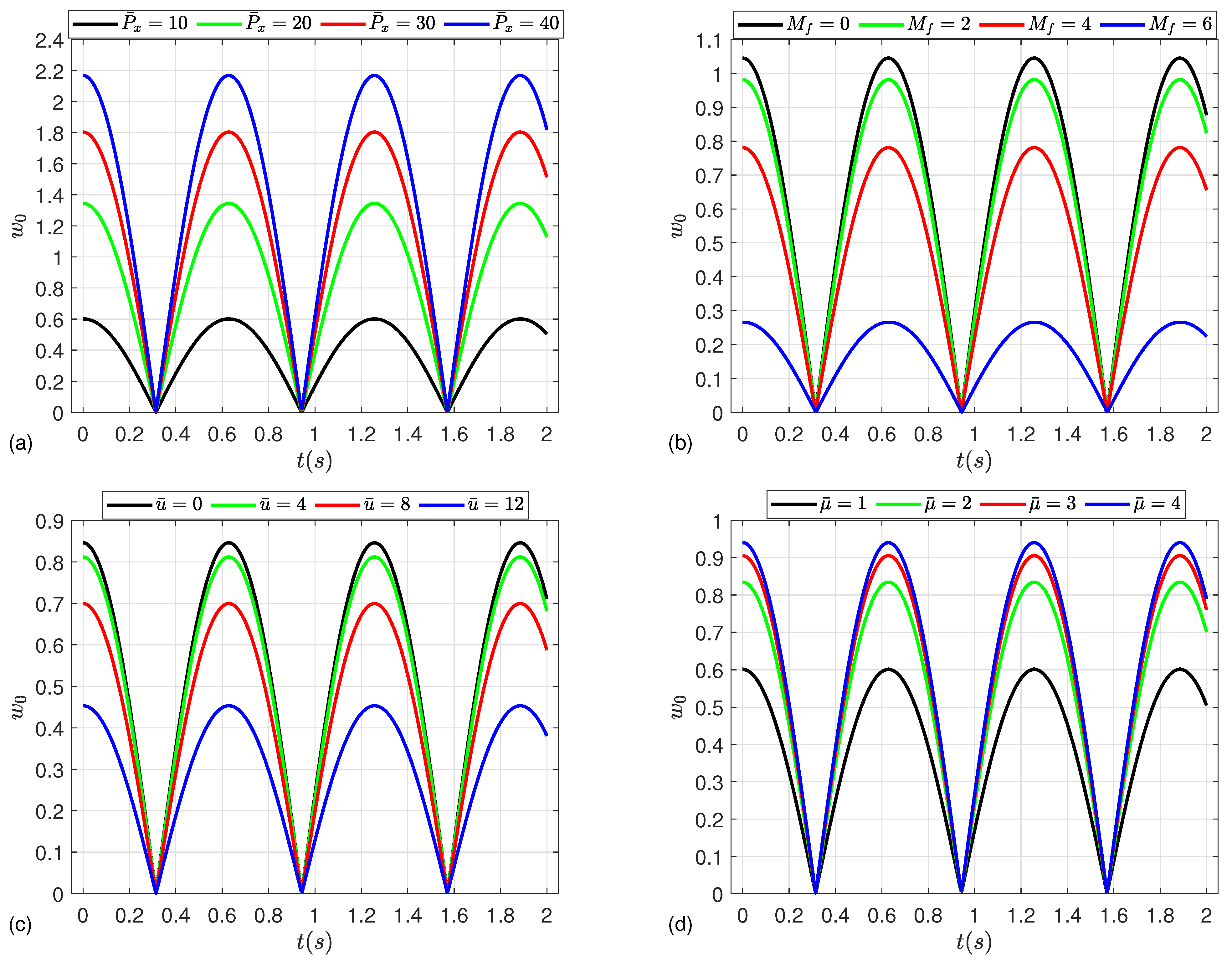
5. Numerical Results
6. Conclusions
- The strength of the microshells may be enhanced by increasing the mean flow velocity, magnetic field parameter, Knudsen number, and CNT volume fraction, leading to an increment in the post-buckling paths.
- In contrast, an increase in the radius-to-thickness ratio, length-to-radius ratio, deflection, material length scale parameter, and Kerr foundation parameters results in a reduction in post-buckling strength.
- Moreover, the nonlinear dynamic deflection increases as the compressive load and material parameter increase, while a severe reduction in the deflection occurs by increasing the magnetic parameter and mean flow velocity.
- In the absence of the magnetic field, the material length scale parameter and Kerr foundation have no influence on the post-buckling behavior.
- The theoretical insights developed here have potential applications in the design of microscale systems, including MEMS/NEMS devices, flexible microfluidic pipelines, and biomedical microtubes, where understanding the combined effects of mechanical, fluidic, and magnetic loading is critical for optimizing performance and ensuring structural stability.
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Hoseinzadeh, M.; Pilafkan, R.; Maleki, V.A. Size-dependent linear and nonlinear vibration of functionally graded CNT reinforced imperfect microplates submerged in fluid medium. Ocean. Eng. 2023, 268, 113257. [Google Scholar] [CrossRef]
- Coleman, J.N.; Khan, U.; Blau, W.J.; Gun’ko, Y.K. Small but strong: A review of the mechanical properties of carbon nanotube–polymer composites. Carbon 2006, 44, 1624–1652. [Google Scholar] [CrossRef]
- Sun, Y.; Sun, J.; Liu, M.; Chen, Q. Mechanical strength of carbon nanotube–nickel nanocomposites. Nanotechnology 2007, 18, 505704. [Google Scholar] [CrossRef]
- Zhu, P.; Lei, Z.; Liew, K.M. Static and free vibration analyses of carbon nanotube-reinforced composite plates using finite element method with first order shear deformation plate theory. Compos. Struct. 2012, 94, 1450–1460. [Google Scholar] [CrossRef]
- Alibeigloo, A. Three-dimensional thermoelasticity solution of functionally graded carbon nanotube reinforced composite plate embedded in piezoelectric sensor and actuator layers. Compos. Struct. 2014, 118, 482–495. [Google Scholar] [CrossRef]
- Sobhy, M.; Radwan, A.F. Influence of a 2D magnetic field on hygrothermal bending of sandwich CNTs-reinforced microplates with viscoelastic core embedded in a viscoelastic medium. Acta Mech. 2020, 231, 71–99. [Google Scholar] [CrossRef]
- Radwan, A.F.; Sobhy, M. Transient instability analysis of viscoelastic sandwich CNTs-reinforced microplates exposed to 2D magnetic field and hygrothermal conditions. Compos. Struct. 2020, 245, 112349. [Google Scholar] [CrossRef]
- Sobhy, M.; Zenkour, A.M. Magnetic field effect on thermomechanical buckling and vibration of viscoelastic sandwich nanobeams with CNT reinforced face sheets on a viscoelastic substrate. Compos. Part B Eng. 2018, 154, 492–506. [Google Scholar] [CrossRef]
- Ghasemi, H.; Mohammadi, Y.; Ebrahimi, F. Free vibration analysis of FG-GPL and FG-CNT hybrid laminated nano composite truncated conical shells using systematic differential quadrature method. Zamm-J. Appl. Math. Mech. 2023, 103, e202300280. [Google Scholar] [CrossRef]
- Zhao, L.C.; Xu, L.; Zeng, H.t. Thermal buckling of temperature-dependent FG-CNT reinforced composite conical-conical joined shell using GDQ. Thin-Walled Struct. 2024, 205, 112320. [Google Scholar] [CrossRef]
- You, Q.; Hua, F.; Huang, Q.; Zhou, X. Efficient analysis on buckling of FG-CNT reinforced composite joined conical–cylindrical laminated shells based on GDQ method under multiple loading conditions. Mech. Adv. Mater. Struct. 2024, 31, 11173–11190. [Google Scholar] [CrossRef]
- Sobhani, E.; Safaei, B. Vibrational characteristics of attached hemispherical-cylindrical ocean shell-structure reinforced by CNT nanocomposite with graded pores on two-parameter elastic foundations applicable in offshore components. Ocean. Eng. 2023, 285, 115413. [Google Scholar] [CrossRef]
- Avey, M.; Fantuzzi, N.; Sofiyev, A. Mathematical modeling and analytical solution of thermoelastic stability problem of functionally graded nanocomposite cylinders within different theories. Mathematics 2022, 10, 1081. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Dang, L.M.; Lee, J.; Nguyen, P.V. Load-carrying capacity of ultra-thin shells with and without CNTs reinforcement. Mathematics 2022, 10, 1481. [Google Scholar] [CrossRef]
- Chang, X.; Hong, X.; Qu, C.; Li, Y. Stability and nonlinear vibration of carbon nanotubes-reinforced composite pipes conveying fluid. Ocean. Eng. 2023, 281, 114960. [Google Scholar] [CrossRef]
- Mahesh, V.; Harursampath, D. Nonlinear vibration of functionally graded magneto-electro-elastic higher order plates reinforced by CNTs using FEM. Eng. Comput. 2022, 38, 1029–1051. [Google Scholar] [CrossRef]
- Sheng, G.; Han, Y.; Zhang, Z.; Zhao, L. Nonlinear dynamic response of functionally graded cylindrical microshells conveying steady viscous fluid. Compos. Struct. 2021, 274, 114318. [Google Scholar] [CrossRef]
- Kerschan-Schindl, K.; Grampp, S.; Henk, C.; Resch, H.; Preisinger, E.; Fialka-Moser, V.; Imhof, H. Whole-body vibration exercise leads to alterations in muscle blood volume. Clin. Physiol. 2001, 21, 377–382. [Google Scholar] [CrossRef]
- Ashley, H.; Haviland, G. Bending vibrations of a pipe line containing flowing fluid. J. Appl. Mech. 1950, 17, 229–232. [Google Scholar] [CrossRef]
- Weaver, D.; Ziada, S.; Au-Yang, M.; Chen, S.; Paı, M. Flow-induced vibrations in power and process plant components-progress and prospects. J. Press. Vessel. Technol. 2000, 122, 339–348. [Google Scholar] [CrossRef]
- Webster, P.M.; Sawatzky, R.P.; Hoffstein, V.; Leblanc, R.; Hinchey, M.J.; Sullivan, P.A. Wall motion in expiratory flow limitation: Choke and flutter. J. Appl. Physiol. 1985, 59, 1304–1312. [Google Scholar] [CrossRef] [PubMed]
- Firouz-Abadi, R.; Noorian, M.; Haddadpour, H. A fluid–structure interaction model for stability analysis of shells conveying fluid. J. Fluids Struct. 2010, 26, 747–763. [Google Scholar] [CrossRef]
- Zhang, D.; Li, P.; Lu, J.; Zhang, C.; Yang, Y. Stability analysis of cylindrical shell in axial flow: A DQ-based approach and an instability prediction formula. Ocean. Eng. 2023, 267, 113198. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, Z.M. Vibration Characteristics of a Functionally Graded Viscoelastic Fluid-Conveying Pipe with Initial Geometric Defects under Thermal–Magnetic Coupling Fields. Mathematics 2024, 12, 840. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Reese, J.M.; Gorman, D.G. Finite element analysis of the vibratory characteristics of cylindrical shells conveying fluid. Comput. Methods Appl. Mech. Eng. 2002, 191, 5207–5231. [Google Scholar] [CrossRef]
- Paak, M.; Païdoussis, M.; Misra, A. Nonlinear dynamics and stability of cantilevered circular cylindrical shells conveying fluid. J. Sound Vib. 2013, 332, 3474–3498. [Google Scholar] [CrossRef]
- Mohammadimehr, M.; Mehrabi, M. Stability and free vibration analyses of double-bonded micro composite sandwich cylindrical shells conveying fluid flow. Appl. Math. Model. 2017, 47, 685–709. [Google Scholar] [CrossRef]
- Rashvand, K.; Alibeigloo, A.; Safarpour, M. Free vibration and instability analysis of a viscoelastic micro-shell conveying viscous fluid based on modified couple stress theory in thermal environment. Mech. Based Des. Struct. Mach. 2022, 50, 1198–1236. [Google Scholar] [CrossRef]
- Ebrahimi, Z. Free vibration and stability analysis of a functionally graded cylindrical shell embedded in piezoelectric layers conveying fluid flow. J. Vib. Control. 2023, 29, 2515–2527. [Google Scholar] [CrossRef]
- Abdollahi, R.; Firouz-Abadi, R.; Rahmanian, M. Nonlinear vibrations and stability of rotating cylindrical shells conveying annular fluid medium. Thin-Walled Struct. 2022, 171, 108714. [Google Scholar] [CrossRef]
- Al-Furjan, M.S.H.; Bolandi, S.Y.; Habibi, M.; Ebrahimi, F.; Chen, G.; Safarpour, H. Enhancing vibration performance of a spinning smart nanocomposite reinforced microstructure conveying fluid flow. Eng. Comput. 2022, 38, 4097–4112. [Google Scholar] [CrossRef]
- Hoang, V.N.V.; Thanh, P.T.; Toledo, L. Impact of non-homogeneous Winkler–Pasternak foundation on nonlinear dynamic characteristics of fluid-conveying functionally graded cylindrical shells. Ocean. Eng. 2024, 307, 118123. [Google Scholar] [CrossRef]
- Sobhy, M. Nonlinear deflection and traveling wave solution for FG-GPLs reinforced microtubes embedded in Kerr foundation and conveying magnetic fluid. Ocean. Eng. 2024, 296, 117026. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, W.; Zhang, Y. Nonlinear resonant analyses of graphene oxide powder reinforced hyperelastic cylindrical shells containing flowing-fluid. Thin-Walled Struct. 2024, 203, 112248. [Google Scholar] [CrossRef]
- Johari, V.; Hassani, A.; Talebitooti, R.; Kazemian, M. Free vibration analysis of a circular cylindrical shell using a new four-variable refined shell theory. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2022, 236, 7079–7094. [Google Scholar] [CrossRef]
- Sobhy, M.; Radwan, A.F. Porosity and size effects on electro-hygrothermal bending of FG sandwich piezoelectric cylindrical shells with porous core via a four-variable shell theory. Case Stud. Therm. Eng. 2023, 45, 102934. [Google Scholar] [CrossRef]
- Ma, H.; Gao, X.L.; Reddy, J. A microstructure-dependent Timoshenko beam model based on a modified couple stress theory. J. Mech. Phys. Solids 2008, 56, 3379–3391. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Esawi, A.M.; Farag, M.M. Carbon nanotube reinforced composites: Potential and current challenges. Mater. Des. 2007, 28, 2394–2401. [Google Scholar] [CrossRef]
- Fidelus, J.; Wiesel, E.; Gojny, F.; Schulte, K.; Wagner, H. Thermo-mechanical properties of randomly oriented carbon/epoxy nanocomposites. Compos. Part Appl. Sci. Manuf. 2005, 36, 1555–1561. [Google Scholar] [CrossRef]
- Shen, H.S. Nonlinear bending of functionally graded carbon nanotube-reinforced composite plates in thermal environments. Compos. Struct. 2009, 91, 9–19. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, L.; Liew, K. Vibration analysis of CNT-reinforced functionally graded composite cylindrical shells in thermal environments. Int. J. Mech. Sci. 2016, 115, 339–347. [Google Scholar] [CrossRef]
- Sobhy, M. Levy solution for bending response of FG carbon nanotube reinforced plates under uniform, linear, sinusoidal and exponential distributed loadings. Eng. Struct. 2019, 182, 198–212. [Google Scholar] [CrossRef]
- John, K. Electromagnetics; McGraw-Hill: New York, NY, USA, 1984. [Google Scholar]
- Sobhy, M.; Al Mukahal, F.H. Magnetic control of vibrational behavior of smart FG sandwich plates with honeycomb core via a quasi-3D plate theory. Adv. Eng. Mater. 2023, 25, 2300096. [Google Scholar] [CrossRef]
- Sobhy, M. 3-D elasticity numerical solution for magneto-hygrothermal bending of FG graphene/metal circular and annular plates on an elastic medium. Eur. J.-Mech.-A/Solids 2021, 88, 104265. [Google Scholar] [CrossRef]
- Sadeghi-Goughari, M.; Jeon, S.; Kwon, H.J. Effects of magnetic-fluid flow on structural instability of a carbon nanotube conveying nanoflow under a longitudinal magnetic field. Phys. Lett. A 2017, 381, 2898–2905. [Google Scholar] [CrossRef]
- Andersson, H. An exact solution of the Navier-Stokes equations for magnetohydrodynamic flow. Acta Mech. 1995, 113, 241–244. [Google Scholar] [CrossRef]
- Wang, L.; Ni, Q. A reappraisal of the computational modelling of carbon nanotubes conveying viscous fluid. Mech. Res. Commun. 2009, 36, 833–837. [Google Scholar] [CrossRef]
- Rashidi, V.; Mirdamadi, H.R.; Shirani, E. A novel model for vibrations of nanotubes conveying nanoflow. Comput. Mater. Sci. 2012, 51, 347–352. [Google Scholar] [CrossRef]
- Mirramezani, M.; Mirdamadi, H.R. Effects of nonlocal elasticity and Knudsen number on fluid–structure interaction in carbon nanotube conveying fluid. Phys.-Low-Dimens. Syst. Nanostruct. 2012, 44, 2005–2015. [Google Scholar] [CrossRef]
- Sobhy, M.; Radwan, A.F. Levy solution and state-space approach for hygro-thermo-magnetic bending of a cross-ply laminated plate on Kerr foundation under various loadings. J. Compos. Mater. 2025, 59, 3–28. [Google Scholar] [CrossRef]
- Han, Y.; Elliott, J. Molecular dynamics simulations of the elastic properties of polymer/carbon nanotube composites. Comput. Mater. Sci. 2007, 39, 315–323. [Google Scholar] [CrossRef]
- Khdeir, A.; Reddy, J.; Frederick, D. A study of bending, vibration and buckling of cross-ply circular cylindrical shells with various shell theories. Int. J. Eng. Sci. 1989, 27, 1337–1351. [Google Scholar] [CrossRef]

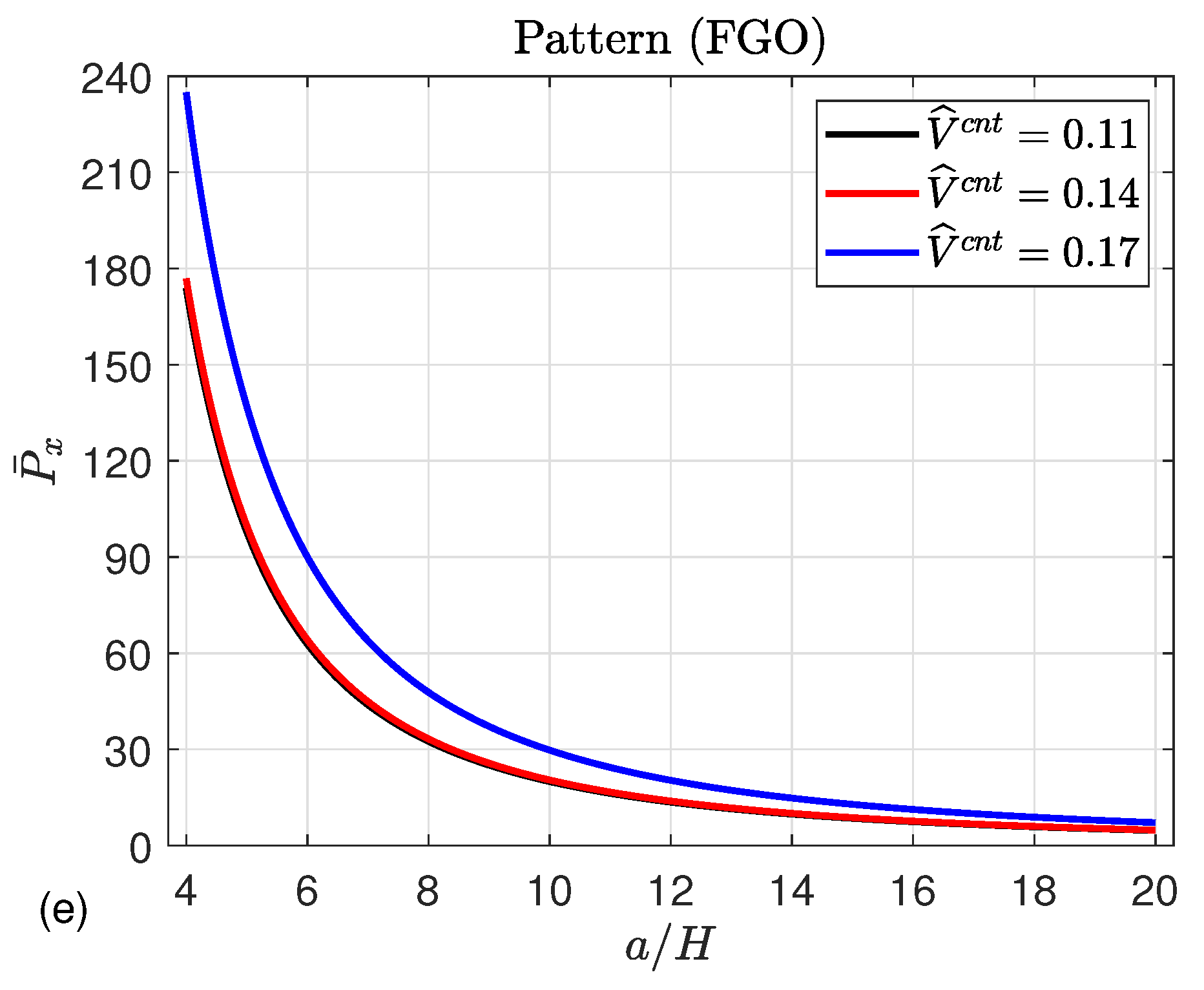
| 0.11 | 0.149 | 0.934 | 0.934 |
| 0.14 | 0.150 | 0.941 | 0.941 |
| 0.17 | 0.149 | 1.381 | 1.381 |
| Khdeir et al. [54] | Present | ||||
|---|---|---|---|---|---|
| Lamination | HST | FST | CST | ||
| 1 | 0.0804 | 0.0791 | 0.0866 | 0.0918 | |
| 2 | 0.1566 | 0.1552 | 0.1630 | 0.1692 | |
| 1 | 0.1097 | 0.1004 | 0.1479 | 0.1078 | |
| 2 | 0.1717 | 0.1779 | 0.2073 | 0.1960 | |
| 1 | 0.0984 | 0.0982 | 0.1235 | 0.1024 | |
| 10 layers | 2 | 0.1900 | 0.1899 | 0.1958 | 0.1856 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobhy, M. Transient Post-Buckling of Microfluid-Conveying FG-CNTs Cylindrical Microshells Embedded in Kerr Foundation and Exposed to a 2D Magnetic Field. Mathematics 2025, 13, 1518. https://doi.org/10.3390/math13091518
Sobhy M. Transient Post-Buckling of Microfluid-Conveying FG-CNTs Cylindrical Microshells Embedded in Kerr Foundation and Exposed to a 2D Magnetic Field. Mathematics. 2025; 13(9):1518. https://doi.org/10.3390/math13091518
Chicago/Turabian StyleSobhy, Mohammed. 2025. "Transient Post-Buckling of Microfluid-Conveying FG-CNTs Cylindrical Microshells Embedded in Kerr Foundation and Exposed to a 2D Magnetic Field" Mathematics 13, no. 9: 1518. https://doi.org/10.3390/math13091518
APA StyleSobhy, M. (2025). Transient Post-Buckling of Microfluid-Conveying FG-CNTs Cylindrical Microshells Embedded in Kerr Foundation and Exposed to a 2D Magnetic Field. Mathematics, 13(9), 1518. https://doi.org/10.3390/math13091518





