Efficient Numerical Methods for Reaction–Diffusion Problems Governed by Singularly Perturbed Fredholm Integro-Differential Equations
Abstract
1. Introduction
2. Analytical Results
- (i)
- (ii)
- (i)
- .
- (ii)
- .
- (iii)
3. Discretization Grid Points
3.1. The Shishkin Mesh (S-Mesh)
3.2. The Bakhvalov–Shishkin Mesh (BS-Mesh)
3.3. Numerical Experiments: Methods and Analysis
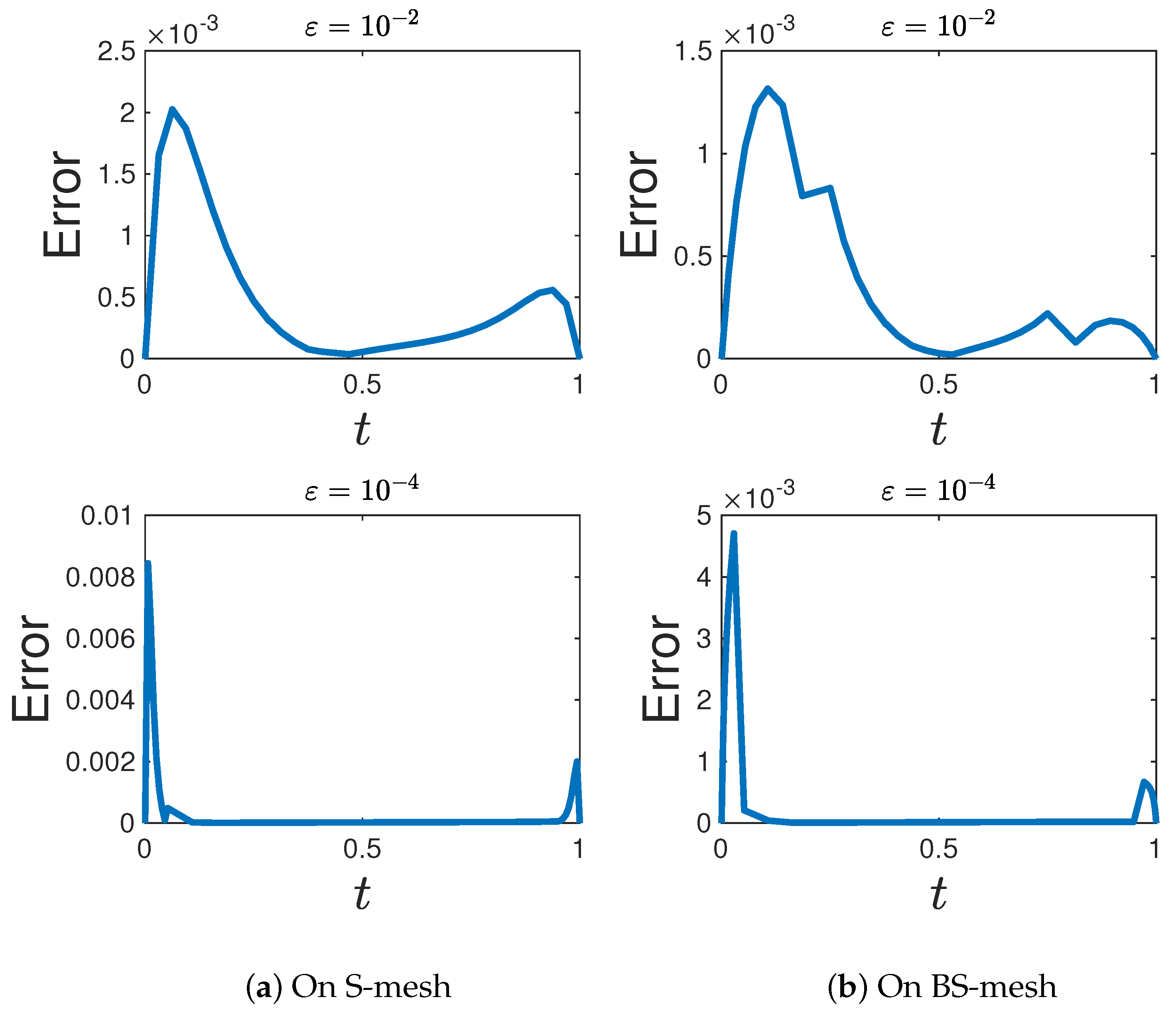
3.4. Error Estimation Techniques for Difference Schemes in Numerical Methods
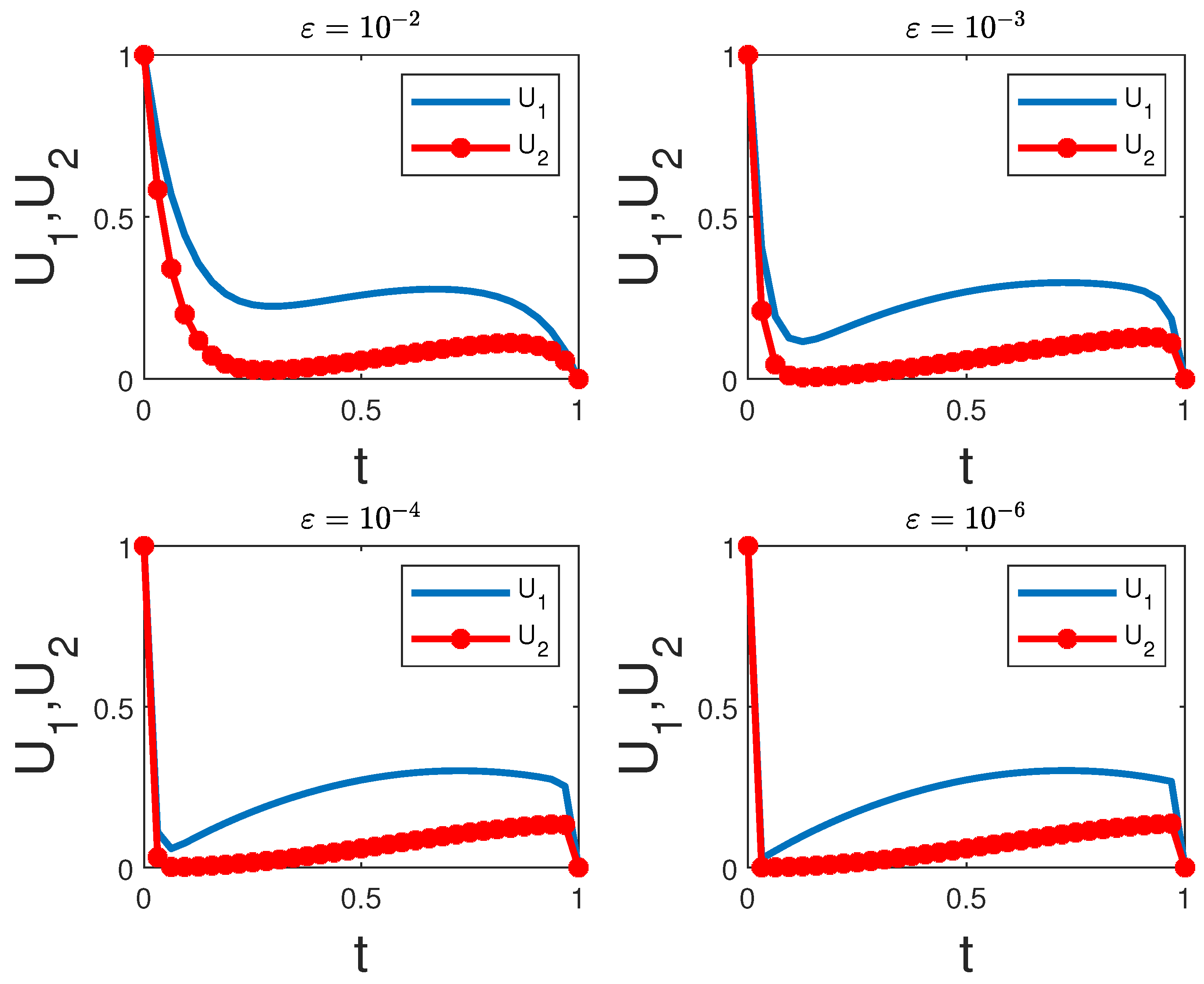
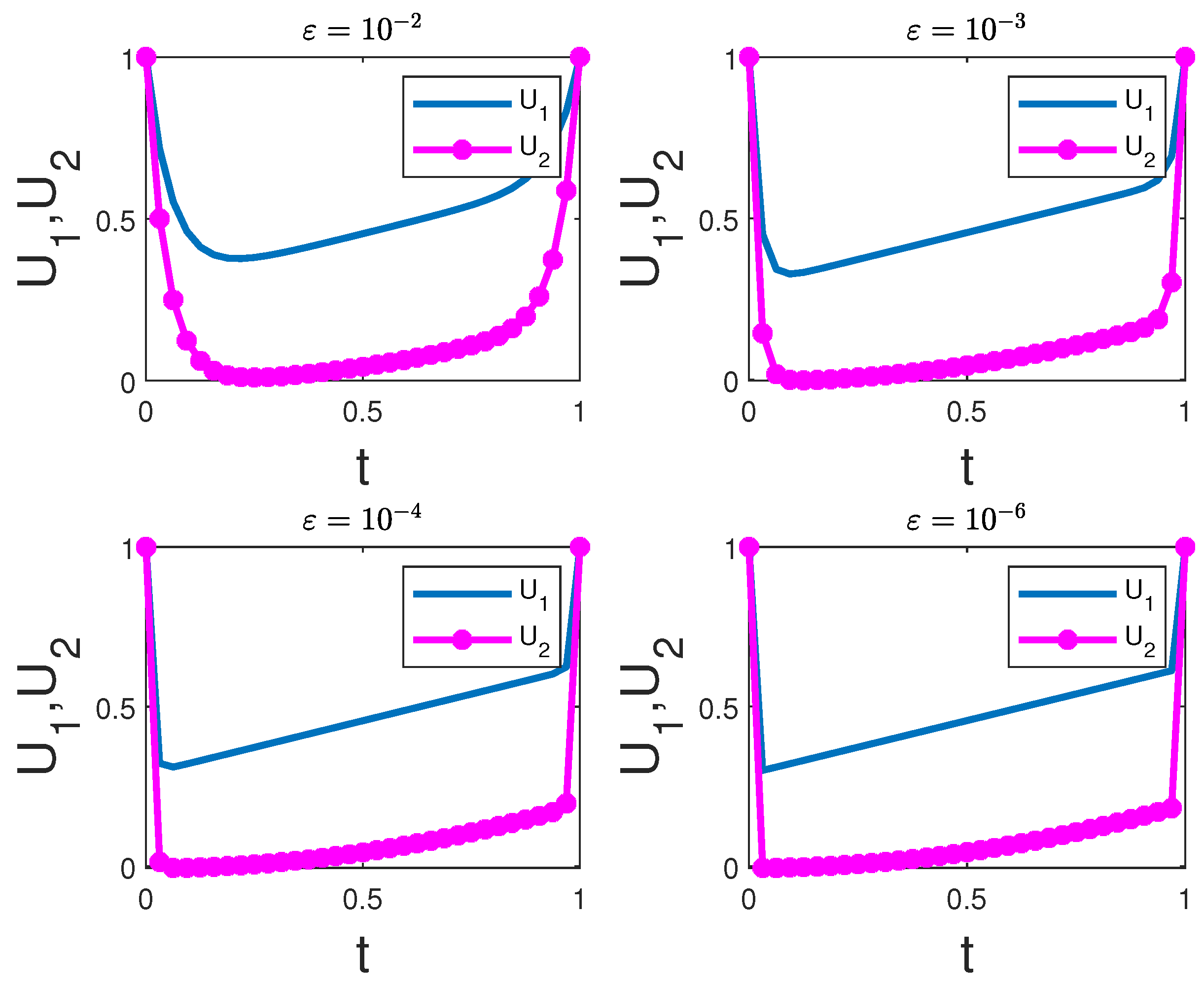
4. Computational Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rahman, M. Integral Equations and Their Applications; WIT Press: Southampton, UK, 2007. [Google Scholar]
- Wazwaz, A.M. Linear and Nonlinear Integral Equations; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Chen, J.; Huang, Y.; Rong, H.; Wu, T.; Zeng, T. A multiscale Galerkin method for second-order boundary value problems of Fredholm integro-differential equation. J. Comput. Appl. Math. 2015, 290, 633–640. [Google Scholar] [CrossRef]
- Akyüz-Daşcioğlu, A.; Sezer, M. A Taylor polynomial approach for solving the most general linear Fredholm integrao-differential-difference equations. Math. Methods Appl. Sci. 2012, 35, 839–844. [Google Scholar] [CrossRef]
- Raja, V.; Sekar, E.; Priya, S.S.; Unyong, B. Fitted mesh method for singularly perturbed fourth order differential equation of convection diffusion type with integral boundary condition. AIMS Math. 2023, 8, 16691–16707. [Google Scholar] [CrossRef]
- Raja, V.; Tamilselvan, A.; Jayalakshmi, G.J.; Sekar, E. Fitted finite difference technique for singularly perturbed reaction diffusion equations of third order with integral boundary condition. Int. J. Numer. Methods Fluids. 2023, 95, 1487–1501. [Google Scholar] [CrossRef]
- Sekar, E. Second order singularly perturbed delay differential equations with non-local boundary condition. J. Comput. Appl. Math. 2023, 417, 114498. [Google Scholar]
- Sekar, E.; Tamilselvan, A. Singularly perturbed delay differential equations of convection–diffusion type with integral boundary condition. J. Appl. Math. Comput. 2019, 59, 701–722. [Google Scholar] [CrossRef]
- Sekar, E.; Tamilselvan, A.; Vadivel, R.; Gunasekaran, N.; Zhu, H.; Cao, J.; Li, X. Finite difference scheme for singularly perturbed reaction diffusion problem of partial delay differential equation with non local boundary condition. Adv. Differ. Equ. 2021, 2021, 151. [Google Scholar]
- Sekar, E.; Tamilselvan, A. Parameter uniform method for a singularly perturbed system of delay differential equations of reaction–diffusion type with integral boundary conditions. Int. J. Appl. Math. 2019, 5, 85. [Google Scholar] [CrossRef]
- Sekar, E.; Unyong, B. Numerical Scheme for Singularly Perturbed Mixed Delay Differential Equation on Shishkin Type Meshes. Fractal. Fract. 2023, 7, 43. [Google Scholar]
- Cimen, E.; Cakir, M. A uniform numerical method for solving singularly perturbed Fredholm integro-differential problem. Comput. Appl. Math. 2021, 40, 42. [Google Scholar] [CrossRef]
- Şevgin, S. Numerical solution of a singularly perturbed Volterra integro-differential equation. Adv. Differ. Equ. 2014, 2014, 171. [Google Scholar] [CrossRef]
- Amiraliyev, G.M.; Durmaz, M.E.; Kudu, M. Uniform convergence results in singularly perturbed Fredholm integro-differential equations. J. Math. Anal. 2018, 9, 55–64. [Google Scholar]
- Amiraliyev, G.M.; Durmaz, M.E.; Kudu, M. Fitted second order numerical method for a singularly perturbed Fredholm integro-differential equation. Bull. Belgian Math. Soc. Simon Stevin 2020, 27, 71–88. [Google Scholar] [CrossRef]
- Durmaz, M.E.; Amiraliyev, G.M. A robust numerical method for a singularly perturbed Fredholm integro-differential equation. Mediterr. J. Math. 2021, 18, 24. [Google Scholar] [CrossRef]
- Sekar, E.; Govindarao, L.; Mohapatra, J.; Vadivel, R.; Hu, N. Numerical analysis for second order differential equation of reaction-diffusion problems in viscoelasticity. Alex. Eng. J. 2024, 92, 92–101. [Google Scholar]
- Govindarao, L.; Ramos, H.; Elango, S. Numerical scheme for singularly perturbed Fredholm integro-differential equations with non-local boundary conditions. Comp. Appl. Math. 2024, 43, 126. [Google Scholar] [CrossRef]
- Miller, J.J.H.; O’Riordan, E.; Shishkin, I.G. Fitted Numerical Methods for Singular Perturbation Problems; World Scientific: Singapore, 2012. [Google Scholar]
- Shishkin, G.I.; Shishkina, L.P. Difference Methods for Singular Perturbation Problems; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Liu, X.; Yang, M. Error estimations in the balanced norm of finite element method on Bakhvalov–Shishkin triangular mesh for reaction–diffusion problems. Appl. Math. Lett. 2022, 123, 107523. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, X.; Chen, Y.; Wei, L. A compact finite difference scheme for solving fractional Black-Scholes option pricing model. J. Inequalities Appl. 2025, 2025, 35. [Google Scholar] [CrossRef]
- Wei, L.; Yang, Y. Optimal order finite difference/local discontinuous Galerkin method for variable-order time-fractional diffusion equation. J. Comput. Appl. Math. 2021, 383, 113129. [Google Scholar] [CrossRef]
- Li, W.; Wei, L. Analysis of Local Discontinuous Galerkin Method for the Variable-order Subdiffusion Equation with the Caputo–Hadamard Derivative. Taiwan J. Math. 2024, 28, 1095–1110. [Google Scholar] [CrossRef]
- Chu, C.; Liu, H. Existence of positive solutions for a quasilinear Schrödinger equation. Nonlinear Anal. Real World Appl. 2018, 44, 118–127. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, L. Existence results for quasilinear Schrödinger equations with a general nonlinearity. Commun. Pure Appl. Anal. 2020, 19, 3429–3444. [Google Scholar] [CrossRef]
- Dong, H.; Krylov, N.V. Fully nonlinear elliptic and parabolic equations in weighted and mixed-norm Sobolev spaces. Calc. Var. 2019, 58, 145. [Google Scholar] [CrossRef]

| Number of Intervals N | ||||||
|---|---|---|---|---|---|---|
| 32 | 64 | 128 | 256 | 512 | ||
| S-mesh | 2.8991e-4 | 7.2784e-5 | 1.8207e-5 | 4.5536e-6 | 1.1385e-6 | |
| 1.9939 | 1.9991 | 1.9994 | 1.9999 | 2.0032 | ||
| 3.1597e-3 | 8.0857e-4 | 2.0377e-4 | 5.1082e-5 | 1.2775e-5 | ||
| 1.9664 | 1.9885 | 1.9960 | 1.9995 | 1.9997 | ||
| 1.2628e-2 | 4.7229e-3 | 1.7147e-3 | 5.1814e-4 | 1.3024e-4 | ||
| 1.4189 | 1.4617 | 1.7266 | 1.9922 | 1.9978 | ||
| 1.2692e-2 | 4.7495e-3 | 1.7244e-3 | 5.7464e-4 | 1.8352e-4 | ||
| 1.4180 | 1.4617 | 1.5853 | 1.6467 | 1.6942 | ||
| 1.2711e-2 | 4.7574e-3 | 1.7273e-3 | 5.7560e-4 | 1.8383e-4 | ||
| 1.4178 | 1.4617 | 1.5853 | 1.6467 | 1.6942 | ||
| 1.2717e-2 | 4.7574e-3 | 1.7273e-3 | 5.7560e-4 | 1.8383e-4 | ||
| 1.4177 | 1.4617 | 1.5853 | 1.6467 | 1.6942 | ||
| 1.2711e-2 | 4.7574e-3 | 1.7273e-3 | 5.7560e-4 | 1.8383e-4 | ||
| 1.4178 | 1.4617 | 1.5853 | 1.6467 | 1.6942 | ||
| 1.2711e-2 | 4.7574e-3 | 1.7273e-3 | 5.7560e-4 | 1.8383e-4 | ||
| 1.4178 | 1.4617 | 1.5853 | 1.6467 | 1.6942 | ||
| BS-mesh | 2.5218e-4 | 6.3134e-5 | 1.5789e-5 | 3.9477e-6 | 9.8694e-7 | |
| 1.9980 | 1.9995 | 1.9999 | 2.0000 | 1.9994 | ||
| 5.9839e-4 | 1.5376e-4 | 3.8722e-5 | 9.6987e-6 | 2.4258e-6 | ||
| 1.9604 | 1.9894 | 1.9973 | 1.9993 | 1.9998 | ||
| 1.8841e-3 | 4.6083e-4 | 1.1441e-4 | 2.8558e-5 | 7.1366e-6 | ||
| 2.0316 | 2.0100 | 2.0022 | 2.0006 | 2.0001 | ||
| 1.9838e-3 | 4.9614e-4 | 1.2470e-4 | 3.1313e-5 | 7.7980e-6 | ||
| 1.9995 | 1.9922 | 1.9937 | 2.0056 | 1.6393 | ||
| 2.0044e-3 | 4.9941e-4 | 1.2557e-4 | 3.1564e-5 | 7.9166e-6 | ||
| 2.0049 | 1.9917 | 1.9922 | 1.9953 | 1.9978 | ||
| 2.0117e-3 | 5.0056e-4 | 1.2586e-4 | 3.1629e-5 | 7.9342e-6 | ||
| 2.0068 | 1.9917 | 1.9925 | 1.9951 | 1.9974 | ||
| 2.0140e-3 | 5.0095e-4 | 1.2595e-4 | 3.1651e-5 | 7.9399e-6 | ||
| 2.0074 | 1.9918 | 1.9926 | 1.9950 | 1.9974 | ||
| 2.0140e-3 | 5.0095e-4 | 1.2595e-4 | 3.1651e-5 | 7.9399e-6 | ||
| 2.0074 | 1.9918 | 1.9926 | 1.9950 | 1.9974 | ||
| Number of Intervals N | ||||||
|---|---|---|---|---|---|---|
| 32 | 64 | 128 | 256 | 512 | ||
| S-mesh | 5.4048e-4 | 1.3640e-4 | 3.4136e-5 | 8.5361e-6 | 2.1344e-6 | |
| 1.9864 | 1.9985 | 1.9996 | 1.9998 | 1.9976 | ||
| 4.9656e-3 | 1.3671e-3 | 3.4531e-4 | 8.6660e-5 | 2.1686e-5 | ||
| 1.8608 | 1.9852 | 1.9945 | 1.9986 | 1.9996 | ||
| 1.1577e-2 | 4.3537e-3 | 1.5639e-3 | 5.1834e-4 | 1.6483e-4 | ||
| 1.4110 | 1.4771 | 1.5932 | 1.6529 | 1.6933 | ||
| 1.1613e-2 | 4.3696e-3 | 1.5690e-3 | 5.2000e-4 | 1.6532e-4 | ||
| 1.4102 | 1.4776 | 1.5933 | 1.6532 | 1.6931 | ||
| 1.1624e-2 | 4.3744e-3 | 1.5706e-3 | 5.2050e-4 | 1.6547e-4 | ||
| 1.4099 | 1.4778 | 1.5933 | 1.6533 | 1.6931 | ||
| 1.1627e-2 | 4.3759e-3 | 1.5711e-3 | 5.2066e-4 | 1.6552e-4 | ||
| 1.4098 | 1.4778 | 1.5933 | 1.6533 | 1.6930 | ||
| 1.1628e-2 | 4.3764e-3 | 1.5712e-3 | 5.2071e-4 | 1.6553e-4 | ||
| 1.4098 | 1.4779 | 1.5933 | 1.6533 | 1.6930 | ||
| 1.1628e-2 | 4.3765e-3 | 1.5713e-3 | 5.2072e-4 | 1.6554e-4 | ||
| 1.4098 | 1.4779 | 1.5933 | 1.6533 | 1.6930 | ||
| BS-mesh | 4.1438e-4 | 1.0381e-4 | 2.5965e-5 | 6.4921e-6 | 1.6229e-6 | |
| 1.9970 | 1.9993 | 1.9998 | 2.0001 | 1.9929 | ||
| 7.6187e-4 | 1.9758e-4 | 4.9562e-5 | 1.2401e-5 | 3.1008e-6 | ||
| 1.9471 | 1.9952 | 1.9988 | 1.9997 | 1.9999 | ||
| 1.7239e-3 | 4.4728e-4 | 1.1361e-4 | 2.8444e-5 | 7.1159e-6 | ||
| 1.9464 | 1.9771 | 1.9978 | 1.9990 | 1.9998 | ||
| 1.7702e-3 | 4.7562e-4 | 1.2232e-4 | 3.0724e-5 | 7.5141e-6 | ||
| 1.8960 | 1.9592 | 1.9932 | 2.0317 | 2.1596 | ||
| 1.7760e-3 | 4.7700e-4 | 1.2289e-4 | 3.1053e-5 | 7.7940e-6 | ||
| 1.8965 | 1.9566 | 1.9845 | 1.9943 | 2.0014 | ||
| 1.7775e-3 | 4.7731e-4 | 1.2297e-4 | 3.1077e-5 | 7.8059e-6 | ||
| 1.8969 | 1.9566 | 1.9844 | 1.9932 | 1.9969 | ||
| 1.7780e-3 | 4.7741e-4 | 1.2300e-4 | 3.1082e-5 | 7.8071e-6 | ||
| 1.8970 | 1.9566 | 1.9845 | 1.9932 | 1.9968 | ||
| 1.7782e-3 | 4.7743e-4 | 1.2300e-4 | 3.1084e-5 | 7.8074e-6 | ||
| 1.8970 | 1.9566 | 1.9845 | 1.9932 | 1.9968 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elango, S.; Govindarao, L.; Awadalla, M.; Zaway, H. Efficient Numerical Methods for Reaction–Diffusion Problems Governed by Singularly Perturbed Fredholm Integro-Differential Equations. Mathematics 2025, 13, 1511. https://doi.org/10.3390/math13091511
Elango S, Govindarao L, Awadalla M, Zaway H. Efficient Numerical Methods for Reaction–Diffusion Problems Governed by Singularly Perturbed Fredholm Integro-Differential Equations. Mathematics. 2025; 13(9):1511. https://doi.org/10.3390/math13091511
Chicago/Turabian StyleElango, Sekar, Lolugu Govindarao, Muath Awadalla, and Hajer Zaway. 2025. "Efficient Numerical Methods for Reaction–Diffusion Problems Governed by Singularly Perturbed Fredholm Integro-Differential Equations" Mathematics 13, no. 9: 1511. https://doi.org/10.3390/math13091511
APA StyleElango, S., Govindarao, L., Awadalla, M., & Zaway, H. (2025). Efficient Numerical Methods for Reaction–Diffusion Problems Governed by Singularly Perturbed Fredholm Integro-Differential Equations. Mathematics, 13(9), 1511. https://doi.org/10.3390/math13091511





