Abstract
Conventional deep learning models rely heavily on the McCulloch–Pitts (MCP) neuron, limiting their interpretability and biological plausibility. The Dendritic Neuron Model (DNM) offers a more realistic alternative by simulating nonlinear and compartmentalized processing within dendritic branches, enabling efficient and transparent learning. While DNMs have shown strong performance in various tasks, their learning capacity at the single-neuron level remains underexplored. This paper proposes a Reinforced Dynamic-grouping Differential Evolution (RDE) algorithm to enhance synaptic plasticity within the DNM framework. RDE introduces a biologically inspired mutation-selection strategy and an adaptive grouping mechanism that promotes effective exploration and convergence. Experimental evaluations on benchmark classification tasks demonstrate that the proposed method outperforms conventional differential evolution and other evolutionary learning approaches in terms of accuracy, generalization, and convergence speed. Specifically, the RDE-DNM achieves up to 92.9% accuracy on the BreastEW dataset and 98.08% on the Moons dataset, with consistently low standard deviations across 30 trials, indicating strong robustness and generalization. Beyond technical performance, the proposed model supports societal applications requiring trustworthy AI, such as interpretable medical diagnostics, financial screening, and low-energy embedded systems. The results highlight the potential of RDE-driven DNMs as a compact and interpretable alternative to traditional deep models, offering new insights into biologically plausible single-neuron computation for next-generation AI.
MSC:
68T07; 34A34
1. Introduction
In the past decade, deep learning has revolutionized the field of artificial intelligence, demonstrating extraordinary capabilities in a wide range of domains such as image recognition, speech processing, natural language understanding, and biomedical diagnostics [1,2]. Powerful architectures like convolutional neural networks and transformer-based models have set new benchmarks in performance, enabling machines to match or even surpass human-level accuracy in many tasks [3,4]. These models have fueled the development of intelligent systems in autonomous driving, medical imaging, financial forecasting, and robotics. The availability of large-scale datasets and computing resources has further propelled the success of deep learning applications, leading to widespread deployment in both academic research and industry practice.
Despite these impressive advances, most current deep learning systems are fundamentally built upon a simplistic neural abstraction—the McCulloch–Pitts (MCP) neuron [5]. This model, which processes input signals through linear summation followed by a fixed activation function, fails to capture the complex, nonlinear, and spatially distributed processing that characterizes real biological neurons. As a result, deep neural networks often suffer from poor interpretability and limited biological plausibility, which are critical issues in domains requiring high transparency and trustworthiness [6,7]. Moreover, the overreliance on large parameter sets and end-to-end black-box learning further contributes to inefficiencies in training and decision-making [8].
These limitations have sparked growing interest in more biologically grounded alternatives that can provide interpretable and efficient learning mechanisms. Among such efforts, the Dendritic Neuron Model (DNM) offers a promising direction by simulating the localized integration and nonlinear processing found in dendritic branches of biological neurons [9,10]. By revisiting the single-neuron level with enhanced realism, DNMs open new possibilities for designing compact, transparent, and cognitively inspired learning systems [11,12,13,14,15].
DNM represents a significant shift from traditional artificial neurons by incorporating biological mechanisms observed in real cortical neurons. Unlike the McCulloch–Pitts model, which performs only a global summation of weighted inputs, DNMs simulate compartmentalized processing across dendritic branches [16]. This architectural distinction is grounded in neurophysiological evidence showing that dendrites are not merely passive conduits; they also actively shape synaptic integration through nonlinear interactions [17,18]. Experimental studies have demonstrated that individual dendritic subunits can act as independent computational modules, capable of performing local logical operations such as AND, OR, and XOR [19]. These findings imply that even a single biological neuron can perform highly complex functions through nonlinear dendritic processing, supporting the foundation of DNMs. In DNMs, the soma integrates the outcomes of dendritic branches, each of which applies a nonlinear function to its synaptic inputs, closely mirroring the real synaptic–dendritic interplay observed in cortical pyramidal cells [20]. Todo et al. proposed a learnable neuron model that captures unsupervised learning capabilities by utilizing dendritic subunits and competitive learning mechanisms, enabling the extraction of localized features without supervision [21]. Later, they extended the model to incorporate multiplicative synaptic interactions, further enhancing the representational power of individual neurons and enabling higher-order nonlinear mappings [22]. These multiplicative mechanisms are consistent with known biological phenomena, such as NMDA receptor-dependent nonlinearities and shunting inhibition [23]. Such a biologically inspired structure grants DNMs superior interpretability and data efficiency, as fewer units are required to approximate complex functions. Compared to conventional deep networks that require thousands of neurons and parameters, a DNM with fewer computational units can achieve competitive performance due to its richer local computation. Moreover, DNMs allow fine-grained control of synaptic plasticity and dendritic structure, paving the way for more adaptive and energy-efficient architectures [24,25].
From a computational neuroscience perspective, DNMs align well with recent theories that emphasize the role of dendritic computations in hierarchical processing and sequence memory [26]. Models inspired by these principles have shown potential in learning temporal and spatial patterns more effectively than traditional neuron models. Furthermore, the local learning rules employed by DNMs offer a plausible alternative to backpropagation, which is often considered biologically implausible [27]. The flexibility to combine additive and multiplicative synaptic mechanisms also positions DNMs as a bridge between conventional neural networks and spiking neuron models. As a result, DNMs are increasingly viewed as a foundational unit for constructing more interpretable, biologically realistic, and cognitively capable learning systems. Their structure supports both supervised and unsupervised learning, enabling a wide range of applications in symbolic reasoning, pattern recognition, and sensorimotor control. In summary, DNMs provide a compelling alternative to traditional artificial neurons, offering biologically grounded mechanisms that enhance computational expressiveness, interpretability, and learning efficiency. This neuron model not only draws inspiration from the complex dynamics of real dendrites but also brings us closer to building next-generation AI systems that emulate the learning principles of the human brain [28,29].
Grounded in solid principles of biological neuroscience, DNM offers a biologically inspired computational framework that emulates the nonlinear and compartmentalized processing observed in real cortical neurons. In contrast to traditional MCP neurons, DNMs integrate both additive and multiplicative synaptic operations on dendritic subbranches, enabling richer and more interpretable internal representations [22]. Early studies have demonstrated that such structures can approximate complex decision boundaries using fewer neurons, significantly enhancing model compactness and computational efficiency [30]. For instance, Gao et al. developed a DNM with effective learning algorithms for classification and prediction, showing competitive performance against deep learning models on benchmark datasets [9]. Recent extensions of the DNM have explored a wide range of applications. In image processing, a dendritic architecture-empowered EfficientNet has shown high accuracy in diabetic retinopathy diagnosis, demonstrating DNM’s potential in enhancing existing deep networks [31]. Meanwhile, Zhang et al. introduced a lightweight pyramidal DNM with neural plasticity for image recognition, emphasizing biological plausibility and real-time adaptability [5]. In the medical domain, DNMs have been successfully applied to multi-scale segmentation tasks and tumor detection, offering precise region localization with fewer parameters [32,33]. Moreover, DNMs have been incorporated into vision transformers to improve interpretability while maintaining accuracy in image classification tasks [13]. Beyond visual tasks, DNMs have proven effective in time series modeling and prediction. Li et al. proposed a seasonal-trend decomposition-based DNM for greenhouse data analysis, achieving robust results in dynamic environments [34]. Similarly, dendritic models have been used for PM2.5 prediction and energy load forecasting, often outperforming conventional machine learning models in stability and generalization [35]. The integration of differential evolution and adaptive synapses further enhances the learning dynamics of DNMs, enabling rapid convergence and escape from local optima in nonconvex problems [36]. These advancements underline DNM’s advantages in interpretability, adaptability, and data efficiency. Compared with black-box deep models, DNMs offer neuron-level insights into decision processes, which is crucial in medical diagnostics, finance, and safety-critical systems. The biologically plausible plasticity mechanisms, including local learning, dendritic pruning, and structure expansion, make DNMs ideal for lifelong learning scenarios [37]. The continued evolution of DNMs—from shallow architectures to hybrid deep structures—reveals their broad potential as a core component in next-generation artificial intelligence systems [38,39,40].
Although DNM has achieved remarkable performance across various tasks—particularly when organized into network structures that exhibit lightweight yet powerful capabilities in regression and classification—its capacity as a single-neuron model still has limitations. Specifically, the information processing ability of DNM, especially during the evolution process where synaptic plasticity dynamically changes, remains an open issue with significant room for improvement. Therefore, enhancing the performance of DNM at the single-neuron level remains a challenging and important research question.
To address this, we propose a novel Reinforced Dynamic-grouping Differential Evolution (RDE) algorithm to learn synaptic plasticity within the DNM framework. The goal is to further boost the model’s classification performance across various complex machine learning tasks. RDE dynamically organizes the population into adaptive subgroups based on individual similarity during the evolutionary process, enabling more effective exploration and local exploitation. Moreover, a reinforced selection mechanism is incorporated to guide the evolution of synaptic weights more efficiently, accelerating convergence while maintaining diversity.
The main contributions of this study are as follows:
(1) A synaptic plasticity-oriented evolutionary strategy: We design a mutation and selection mechanism that aligns with the biological characteristics of synaptic plasticity, making the evolutionary learning process more adaptive and biologically plausible.
(2) A dynamic grouping mechanism for population management: The proposed approach adaptively clusters individuals during evolution, enhancing diversity preservation and local search efficiency, particularly in high-dimensional and complex scenarios.
(3) Comprehensive evaluation across benchmark tasks: We conduct extensive experiments on several standard classification datasets taken from UCI repository to validate the effectiveness of RDE. The results demonstrate that the proposed method outperforms conventional differential evolution algorithms and other state-of-the-art evolutionary learning-based approaches, highlighting its capability to enhance synaptic learning and generalization in DNMs.
This paper introduces a biologically plausible single-neuron model enhanced by the RDE algorithm, featuring dynamic population grouping, synaptic pruning, and logic-level interpretability. The remainder of this paper is organized as follows. In Section 2, we present the detailed architecture of DNM, highlighting its biologically inspired components and information processing mechanisms. We emphasize how dendritic branches and nonlinear synaptic interactions contribute to the model’s interpretability and representational power. In Section 3, we introduce the proposed RDE algorithm, focusing on its biologically plausible mutation strategies, dynamic population grouping scheme, and reinforced selection mechanism designed to optimize synaptic plasticity within DNMs. Section 4 reports experimental results across several benchmark classification tasks. We compare the performance of the proposed RDE-based learning framework with that of traditional differential evolution algorithms and other state-of-the-art evolutionary algorithms, providing a comprehensive analysis in terms of accuracy, convergence speed, and model complexity. Finally, Section 5 summarizes the main contributions of this study and outlines potential future directions for advancing synaptic learning and expanding the applicability of DNMs in more diverse learning scenarios.
2. Architecture of Dendritic Neuron Model (DNM)
To address the limitations of conventional neuron models in deep learning, such as poor biological plausibility and lack of interpretability, DNM has been proposed as a more realistic alternative inspired by neurophysiological findings. DNMs aim to bridge the gap between biological neurons and artificial models by simulating the spatial and nonlinear integration mechanisms observed in real dendritic structures [11,38]. Before delving into the mathematical formulation of the DNM, it is essential to first understand its architectural design and how it differs fundamentally from traditional neuron models.
Figure 1 illustrates the structural and computational distinctions between biological neurons, the classical MCP neuron model, and the DNM. As shown in Figure 1a, a biological single neuron consists of multiple dendritic branches and synaptic connections, each receiving signals from different input sources. In this example, the neuron comprises six dendrites and nine synapses. The synaptic inputs are distributed across dendrites, forming spatially distinct pathways that process local information before being integrated at the soma. Experimental evidence from neuroscience has confirmed that dendrites are not passive conduits but active computational subunits capable of performing nonlinear operations. This spatial arrangement enables biological neurons to carry out complex feature integration even at the single-cell level. In contrast, Figure 1b shows the conventional MCP model, where all input signals are directly connected to the neuron through weighted summation. The MCP neuron aggregates inputs globally using a linear summation followed by a threshold activation function. While simple and computationally efficient, this abstraction ignores the spatial structure and localized processing inherent in real neurons. All synaptic inputs are treated equally, eliminating the possibility of modeling spatial hierarchies or localized nonlinearity. Figure 1c presents the structure of the Dendritic Neuron Model, which more faithfully replicates the organization of a biological neuron. Inputs are connected to multiple dendritic branches, and each dendrite receives a subset of the input signals. These branches perform localized computations using nonlinear functions such as additive or multiplicative interactions, reflecting the functional subunits observed in biological dendrites. The outputs of each dendrite are then aggregated at the soma, where a final decision is made through a threshold function. This compartmentalized design enables DNMs to model spatial connectivity and heterogeneous synaptic integration, which are essential for building biologically plausible and interpretable learning systems. In summary, the DNM provides a middle ground between biological realism and computational efficiency. By introducing structured input partitioning and localized processing, it offers enhanced representational power compared to the MCP model while maintaining tractable complexity. The dendritic architecture in DNM serves as the foundation for more expressive single-neuron models capable of capturing rich input patterns with fewer computational units.
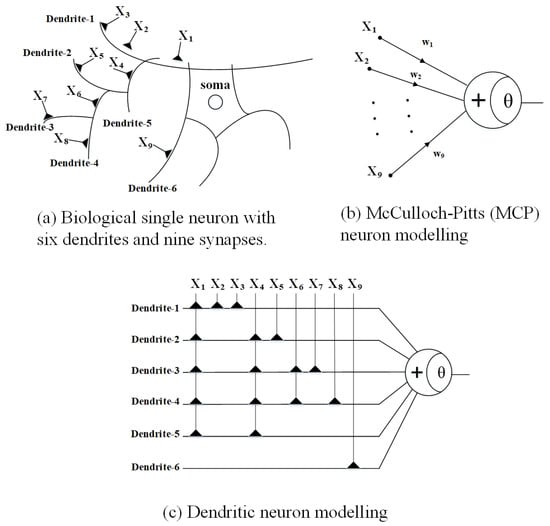
Figure 1.
Architecture of neuron models: (a) biological neuron, (b) MCP, and (c) DNM.
Mathematically, DNM comprises four functional layers: the synaptic interface, dendritic integration, membrane summation, and soma activation. Given a set of presynaptic inputs , the synaptic layer modulates each input through parameterized connections to the jth dendrite. Each connection is associated with a gain coefficient and a bias shift , and the synaptic transmission function is formulated as
where denotes the postsynaptic response transmitted to the jth dendritic segment from input and controls the steepness of the activation. The signs and magnitudes of and determine whether the synapse is excitatory, inhibitory, or functionally silent, and they are updated through learning algorithms to reflect synaptic plasticity.
In the dendritic layer, each branch functions as an independent nonlinear processing unit, integrating all its received inputs multiplicatively. The output of the jth dendrite is given by
where denotes the total signal propagated through dendrite j. This multiplicative operation enables complex interactions and gate-like behavior, enhancing selectivity to specific input patterns.
The outputs from all dendritic branches are aggregated in the membrane layer using a summation operator, yielding the total membrane potential:
where m is the total number of dendrites. The soma then applies a sigmoid activation to determine whether the neuron fires:
where is a firing threshold at the soma level and y is the final output of the neuron.
The hierarchical computation in DNM not only enhances its expressive power but also supports morphological adaptation. Dendritic branches or synaptic links that contribute negligibly—such as those resulting in constant outputs—can be pruned. This structural optimization leads to a task-specific morphology, reducing redundancy and improving interpretability. Furthermore, DNM’s architecture lends itself to efficient hardware implementation. Each computational component—comparators, multipliers, summators, and nonlinearity—can be mapped to logical circuits using standard gates (e.g., AND, OR, NOT). This makes DNM a promising model for neuromorphic applications where energy efficiency and model compactness are critical.
3. Proposed Evolutionary Learning-Based DNM
To efficiently learn the synaptic plasticity parameters (i.e., the gain coefficient and the bias shift ) in DNMs, we propose an evolutionary optimization framework based on a novel algorithm called Reinforced Dynamic-grouping Differential Evolution (RDE). This section first provides a comprehensive introduction to the classical Differential Evolution (DE) algorithm, followed by a detailed explanation of RDE’s architecture, motivation, and computational mechanism. Finally, we highlight the key innovations and advantages of the proposed approach.
3.1. Overview of Differential Evolution (DE)
DE is a robust and efficient population-based metaheuristic introduced by Storn and Price [41], widely used for continuous, nonlinear, and multimodal optimization problems. It maintains a population of candidate solutions that evolve over generations through mutation, crossover, and selection operations [42]. DE was selected as the base due to its strong global search capability, simple structure, and successful application in neuron-level optimization problems. Its population-based nature aligns well with the distributed computation in DNMs. Compared to other metaheuristics or gradient-based methods, DE avoids gradient computation and easily accommodates structural adaptations like pruning, making it especially suitable for sparse, interpretable neuron models.
Given a population of N individuals, each represented as a D-dimensional vector , the evolution process in DE proceeds as follows:
- Mutation: For each target vector , a mutant vector is generated by combining three randomly selected and distinct individuals from the population:where is the scaling factor that controls the magnitude of the differential variation.
- Crossover: A trial vector is generated by mixing the target vector and the mutant vector using a crossover probability :where is a uniform random number in and ensures that at least one parameter is inherited from .
- Selection: The trial vector competes with the original vector , and the one with the better fitness is selected for the next generation:
Although DE is effective, it may suffer from issues such as premature convergence and stagnation [43], particularly in high-dimensional and complex optimization landscapes such as those presented by DNM synaptic learning [9]. Therefore, we introduce a new variant of DE that adapts dynamically to population quality and search progress.
3.2. Reinforced Dynamic-Grouping Differential Evolution (RDE)
The proposed RDE algorithm enhances the standard DE in three fundamental ways: population division with dynamic adjustment, reinforced mutation by integrating poor individuals, and adaptive tuning of the mutation scaling factor. These innovations are particularly suited for dendritic neural systems, which require both global exploration and precise local refinement to learn biologically meaningful and structurally sparse models.
- (a)
- Dynamic Population Partitioning
In RDE, the entire population is sorted based on fitness at each generation. Then it is divided into two groups: a good population (higher fitness) and a bad population (lower fitness). The division ratio is not fixed but controlled by a dynamically changing parameter p, which is updated according to the optimization progress:
where nFES is the number of function evaluations conducted so far and FES is the total evaluation budget.
An index value is then computed to determine the split point:
Using this index, the population is divided:
Further, both groups are divided into two subgroups for variation and crossover:
The two new groups for variation and crossover are
- (b)
- Reinforced Mutation with Poor Individual Interference
Unlike traditional DE that selects vectors from random individuals or elites, RDE reinforces mutation with both good and poor individuals to maintain diversity and prevent premature convergence. The mutation operator is defined as
where
- is a randomly selected top individual.
- is a randomly chosen individual from the variation group.
- is a randomly chosen individual from the crossover group.
This formula incorporates constructive noise from low-performing individuals and encourages the algorithm to explore underrepresented regions of the search space.
- (c)
- Adaptive Scaling Factor Control
To further balance the search dynamics over time, the scaling factor F is also dynamically adjusted as follows:
This enables aggressive global search at early stages and fine-tuned local search near convergence.
3.3. Learning Process of RDE for DNM
The learning process of the DNM under the proposed RDE algorithm offers both structural interpretability and functional adaptability. Unlike conventional deep learning models that rely heavily on parameter tuning through backpropagation, DNMs adopt a more biologically plausible route: synaptic adaptation, dendritic pruning, and structural self-organization—all optimized via an evolutionary process. Figure 2 illustrates the overall learning procedure and post-training structural evolution of the DNM.
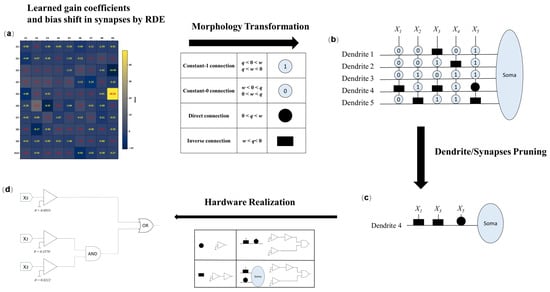
Figure 2.
Learning process and structural evolution of DNM using RDE. (a) Post-learning synaptic weight visualization; (b) classification of connection types; (c) neuron structure after pruning; (d) equivalent logic circuit representation.
3.3.1. Synaptic State Classification
One of the most distinctive features of DNM is the classification of synaptic connections based on the relationship between synaptic weight w and threshold q. After learning through RDE, each connection can be classified into one of four functional states, as shown in the central table of Figure 2:
- Constant-1 connection (①): Occurs when or . This means the synapse always outputs approximately one regardless of the input, essentially acting as a neutral multiplier in the dendritic product.
- Constant-0 connection (⓪): Defined by or . In this case, the synapse always transmits zero, making the entire dendrite inactive since any multiplication involving zero yields zero.
- Direct connection (●): Represented by . The synaptic output is positively correlated with the input signal, indicating excitatory influence.
- Inverse connection (▬): Defined by , producing an output inversely proportional to the input, emulating inhibitory synaptic behavior.
These states are learned through RDE by evolving parameters w and q toward functional optima, guided by the classification performance on the target dataset.
3.3.2. Dendrite and Synapse Pruning
Following synaptic state classification, RDE enables a biologically inspired pruning mechanism. As shown in the heatmap of Figure 2, connections classified as constant-0 (⓪) result in the inactivation of the entire dendritic branch. Consequently, such dendrites can be safely removed from the model without performance degradation. For instance, Dendrites 1 to 3 and 5 are completely pruned due to being composed only of constant-0 synapses.
Similarly, constant-1 connections (①) can be eliminated at the synaptic level since they do not influence the multiplicative outcome of a dendrite. For example, synapses and on Dendrite 4 are dropped due to being always active (i.e., equal to one). Such simplification leads to a more compact and interpretable model.
3.3.3. Neural Morphology Adaptation
The RDE-guided learning process enables the DNM to exhibit a form of neural morphology detection—a capability to infer the number, location, and type of dendritic and synaptic connections needed for a specific task. This property enhances biological plausibility and model efficiency. By analyzing the final structure, one can determine
- The minimum number of dendrites required.
- Which inputs are relevant and where they connect.
- Whether each synapse is excitatory, inhibitory, or functionally neutral.
Such localized structural adaptation is critical in tasks such as visual pattern recognition, auditory spatial processing, or motor control, where neurons operate with specialized and sparse input patterns.
3.3.4. Hardware Implementation Perspective
One of the significant advantages of DNM is its direct mapping to simple digital logic components, making it highly suitable for neuromorphic hardware. As shown at the bottom of Figure 2,
- A direct (excitatory) connection can be implemented using a comparator.
- An inverse (inhibitory) connection can be modeled using a comparator followed by a NOT gate.
- The multiplicative behavior of dendrites maps naturally to AND gates.
- The summation at the membrane level corresponds to an OR gate.
- The final soma output requires only a nonlinear activation, which can be approximated by a voltage threshold or even a wire in binary logic.
This logic-level abstraction implies that DNMs can be implemented efficiently on field-programmable gate arrays (FPGAs) or other edge-computing platforms with minimal energy consumption and circuit complexity [44]. This contrasts sharply with traditional deep neural networks that require large matrix multiplications and floating-point operations.
In summary, the RDE-driven learning process in DNM facilitates both functional optimization and structural compression. The model not only learns to solve classification problems effectively but also simplifies its internal configuration based on biological principles. This makes DNM a promising candidate for interpretable, efficient, and hardware-friendly AI systems. The combination of local synaptic evolution, structural pruning, and logic-based implementation brings DNMs closer to mimicking real neuronal behavior and practical deployment in resource-constrained environments.
3.4. Advantages of RDE for DNM Learning
The design of RDE is particularly aligned with the learning characteristics of DNMs. DNMs require flexible local adaptation (e.g., adjusting individual synaptic weights) as well as global structural refinement (e.g., pruning dendritic branches). The population grouping in RDE mimics neural competition, where only the fittest units survive and propagate, while others provide diversity. Poor individual interference corresponds to weak synaptic signals which may still influence neural learning.
The dynamic control of F and p helps allocate computational resources more effectively as the search progresses. Moreover, RDE naturally supports parallel implementation, allowing faster execution on high-dimensional DNM optimization tasks.
In summary, the proposed RDE algorithm enhances traditional DE with biologically inspired mechanisms of population structuring, variation reinforcement, and learning adaptivity, making it well suited for synaptic learning in DNMs. The next section presents empirical experiments to validate the effectiveness of RDE on real-world benchmark datasets.
4. Experiments and Results
This section presents the experimental evaluation of the proposed RDE algorithm applied to DNMs. The goal is to assess the classification performance, convergence behavior, and generalization ability of RDE-DNM on a diverse set of benchmark datasets.
4.1. Datasets Description
To comprehensively assess the robustness and generalization capability of the proposed RDE-DNM model, we selected 12 benchmark datasets from a wide range of application domains including medical diagnosis, financial decision-making, and synthetic logic tasks. These datasets were chosen to reflect diversity in data type (numerical, categorical, binary), instance count, feature dimensionality, and problem complexity. This cross-domain selection ensures a well-rounded evaluation of the model’s adaptability and stability across real-world and theoretical classification problems.
Below is a brief description of each dataset:
- Australia: A binary classification dataset used for credit card approval, containing 690 instances and 14 features with a mixture of numerical and categorical attributes.
- BUPA: A medical dataset with 345 samples and 6 continuous features. The task is to classify liver disorder patients based on blood test results.
- BreastEW: A cleaned and encoded version of the Breast Cancer Wisconsin dataset with 699 instances and 9 numerical attributes for benign/malignant tumor detection.
- Exactly: A synthetic dataset with 1000 samples and 13 binary features based on a known logical target function. It is often used to evaluate logic-oriented models.
- German: Comprising 1000 instances and 20 mixed-type attributes, this dataset is used for assessing credit risk levels of loan applicants.
- Heart: A medical dataset with 270 instances and 13 numerical attributes used for classifying patients with or without heart disease.
- Ionosphere: Contains 351 radar signal samples with 34 continuous attributes, representing the classification of ionospheric return signals as either good or bad.
- KrVsKpEW: A reduced version of the KR-vs-KP chess endgame dataset, including 3196 samples and 6 extracted features for classifying winning board positions.
- Moons: A well-known non-linearly separable synthetic dataset consisting of two interleaved half circles with 1000 samples and 2 numerical features.
- SpectEW: A binary classification dataset from the SPECT heart dataset with 267 instances and 22 binary features for heart abnormality detection.
- Tic-tac-toe: Contains 958 game board states described by 9 categorical features, where the task is to predict whether player "X” has won.
- Gaussians: A two-class synthetic dataset where the data points are drawn from overlapping Gaussian distributions in 2D space.
Although explicit correlation analysis between features and instances was not conducted for each dataset, the RDE-DNM learning framework implicitly addresses feature relevance through its built-in synapse and dendrite pruning mechanisms. As a result, low-impact or redundant features are automatically filtered out, and only task-relevant inputs are retained in the final dendritic structure, as illustrated in Figures 9 and 13. This indirect handling of correlation contributes to the model’s interpretability and functional sparsity. For consistency, all datasets were preprocessed: categorical features were encoded using one-hot representation; numerical values were normalized to the range. Each dataset was split randomly into 70% training and 30% testing sets, and experiments were repeated 30 times to report the average performance and standard deviation (Table 1).

Table 1.
Summary of Benchmark Datasets Used for Evaluation.
4.2. Experimental Settings
The training set was employed for learning the synaptic parameters of the DNM using the proposed RDE strategy, while the testing set was used to evaluate generalization performance. The number of dendrites for each neuron was initially set to 10, and the number of synapses was initialized based on the total number of input features. The population size N for the evolutionary algorithm was fixed at 50, and the maximum number of generations was set to 300. The mutation scaling factor F and grouping parameter p were dynamically adjusted using the equations defined in Section 3. The crossover rate was set to , and the fitness function used in all experiments was the classification accuracy on the training set. No regularization or dropout techniques were used in DNM, as the pruning mechanism of the model inherently controls redundancy.
4.3. Evaluation Metrics
To quantitatively compare the models, the following performance metrics were used:
- Classification Accuracy (acc): The percentage of correctly classified test samples. It is the primary metric for model comparison.
- Standard Deviation (std): The standard deviation of the test accuracy across 30 independent runs, reflecting the model’s stability.
4.4. Comparison Algorithms
To validate the effectiveness of RDE-DNM, we compare it against several state-of-the-art learning algorithms from both evolutionary and traditional machine learning paradigms:
- BBO [9]: The Biogeography-Based Optimization (BBO) algorithm is employed to optimize the synaptic parameters of the DNM. BBO simulates the migration and mutation of species across habitats to explore the solution space effectively. It balances global exploration and local exploitation by adjusting the immigration and emigration rates based on habitat suitability. This approach enables the DNM to achieve high accuracy and stability in classification, function approximation, and time-series prediction tasks.
- CJADE [45]: CJADE uses chaotic maps to perturb individuals during the evolutionary process, improving the balance between exploration and exploitation. This chaotic mechanism helps escape local optima and accelerates convergence. Experimental results show that CJADE outperforms several state-of-the-art DE variants on a wide range of benchmark functions.
- DPDE [36]: DPDE is an enhanced differential evolution algorithm that incorporates an information feedback mechanism to train the DNM. This mechanism adaptively adjusts evolutionary parameters based on feedback from previous generations, improving convergence speed and search efficiency. By dynamically guiding the search process, the algorithm effectively avoids premature convergence. The proposed approach demonstrates superior classification performance compared to conventional DE and other evolutionary learning methods.
- SASS [46]: SASS is a novel population-based metaheuristic inspired by spherical geometry. SASS generates new candidate solutions on hyperspheres centered around elite individuals, enabling balanced exploration and exploitation in the search space. The algorithm adapts the search radius dynamically based on convergence behavior to improve global optimization performance. Experimental results demonstrate that SASS achieves competitive accuracy and robustness compared to state-of-the-art algorithms on benchmark functions.
- SCJADE [47]: SCJADE combines the adaptive parameter control of JADE with stochastic perturbations from chaotic maps to improve search diversity and convergence. This hybrid strategy allows the algorithm to escape local optima more effectively while maintaining stability. Experimental results show that SCJADE achieves superior performance across various benchmark optimization problems.
- SEDE [48]: SEDE integrates multiple mutation strategies and adaptively selects among them based on their historical performance. It also adjusts control parameters dynamically to enhance robustness and convergence speed. The algorithm demonstrates high accuracy and stability in estimating photovoltaic model parameters across different environmental conditions.
- SHADE [49]: SHADE is an advanced DE variant that adaptively adjusts its control parameters based on historical success. It maintains a memory of successful mutation factors and crossover rates, updating them using a weighted learning strategy. This allows the algorithm to dynamically adapt to the optimization landscape and improve convergence performance. Experimental results show that SHADE consistently outperforms traditional DE variants on a wide range of benchmark problems.
- SMS [50]: The States of Matter Search (SMS) algorithm is used to optimize the parameters of an approximate logic DNM. SMS simulates the physical behavior of matter transitioning through gas, liquid, and solid states to balance exploration and exploitation. This staged search strategy enables efficient convergence while maintaining diversity in the population. The proposed SMS-based training method achieves competitive performance in solving classification and approximation problems.
- BP [30]: The backpropagation (BP) learning algorithm is used to train a logic-based DNM that incorporates dendritic processing. The BP algorithm is adapted to handle the non-linear, multiplicative interactions within dendritic branches by computing gradients through a customized error function. This enables efficient supervised learning while preserving the model’s interpretability and logic-like behavior. Experimental results show that the BP-trained Dendritic Neuron Model achieves high accuracy on classification tasks.
To better contextualize the novelty of RDE, we expand on the design philosophy of compared methods. For instance, BBO simulates migration patterns for balanced exploration, while CJADE and SCJADE integrate chaotic perturbations to avoid stagnation. DPDE uses information feedback for guided evolution, and SHADE adapts parameters from successful trials. In contrast, RDE emphasizes synaptic-level adaptation, dynamic grouping, and reinforced mutation—all specifically tailored to DNM learning. All baseline methods were implemented using the same training/testing splits and preprocessed datasets to ensure comparability. The experimental setup was carefully designed to evaluate the learning capacity, structural efficiency, and generalization ability of RDE-based DNM. By comparing against a diverse set of classical and evolutionary learning methods, we aim to demonstrate that the proposed approach is not only accurate but also interpretable, stable, and biologically plausible. The next section reports the detailed results of each method across the twelve benchmark datasets.
4.5. Experimental Results and Analysis
Table 2 summarizes the performance comparison between the proposed RDE-DNM and nine representative baseline algorithms across twelve benchmark datasets. For each dataset, we report the mean test classification accuracy and its standard deviation over 30 independent runs. The best-performing results are bolded, and the second-best results are underlined.

Table 2.
Performance comparison with RDE and its peers in terms of mean and standard deviation of test classification accuracy.
Overall, the proposed RDE-DNM achieves the highest classification accuracy on 5 out of 12 datasets, including Australia, BUPA, BreastEW, KrVsKpEW, and Tic-tac-toe. Additionally, RDE ranks as the second-best method on two datasets—German and Heart. On the remaining datasets, RDE consistently ranks within the top three. This demonstrates the robustness, reliability, and generalization capability of the proposed method across various types of data.
The proposed RDE-DNM demonstrates strong and consistent performance across a wide variety of benchmark datasets. On real-world medical and financial datasets, it ranks first on BUPA (0.6371) and BreastEW (0.9290), and second on the Heart (0.9158) and German credit datasets (0.7528), performing comparably or better than other competitive evolutionary algorithms such as SASS and DPDE. These results highlight the model’s ability to effectively learn from noisy and high-dimensional real-world data.
For structured and logic-oriented datasets, RDE-DNM achieves the highest classification accuracy on Tic-tac-toe (0.8056) and KrVsKpEW (0.8075), outperforming several ensemble-based and chaos-enhanced differential evolution variants. However, on the Exactly dataset, which involves strict logic-rule-based structure, RDE does not achieve a top ranking, indicating potential limitations when dealing with highly discrete or symbolic patterns.
On synthetic and nonlinear datasets such as Moons and Gaussians, RDE-DNM also achieves high accuracy (0.9808 and 0.8467, respectively), ranking among the top three methods. Although slightly outperformed by SHADE and BBO in these cases, RDE maintains competitive performance with low variance. On the Ionosphere dataset, RDE achieves 0.9415 accuracy, closely following the best-performing method DPDE (0.9426). These results further confirm the stability and generalization capacity of the proposed method in both structured and non-structured classification tasks.
In terms of stability and robustness, RDE-DNM consistently exhibits low standard deviations across most datasets, such as 0.0100 on Ionosphere and 0.0085 on BreastEW, indicating reliable convergence behavior and resistance to random initialization effects. In contrast, the BP method shows significant instability and poor classification performance, failing to generalize on nearly all datasets. Similarly, the SMS algorithm underperforms in most scenarios, with the exception of an anomalously high accuracy (1.000) on the Moons dataset, which likely reflects overfitting or a mismatch with the dataset’s properties rather than true generalization.
Overall, the results demonstrate that RDE-DNM is among the most accurate and robust evolutionary learning frameworks evaluated in this study. Its consistent top-tier performance across both real-world and synthetic benchmarks validates the efficacy of the reinforced dynamic grouping strategy in guiding DNM learning, achieving a desirable balance between structural interpretability, classification accuracy, and convergence stability.
4.6. Convergence Analysis
To further evaluate the optimization dynamics of the proposed RDE algorithm, we conducted a convergence analysis based on the mean squared error (MSE) over iterations on two representative datasets: KrVsKpEW and Tic-tac-toe. The results are depicted in Figure 3 and Figure 4.
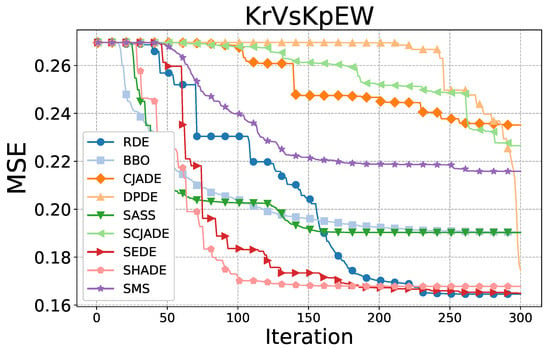
Figure 3.
Convergence comparison among all compared algorithms on the KrVsKpEW dataset.
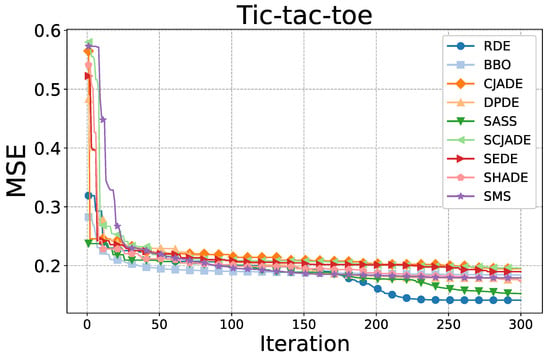
Figure 4.
Convergence comparison among all compared algorithms on the Tic-tac-toe dataset.
As shown in Figure 3, on the KrVsKpEW dataset, RDE demonstrates a rapid and stable decline in MSE throughout the evolutionary process. It converges faster and reaches a significantly lower final MSE compared to most other algorithms. While algorithms such as SEDE and SHADE show competitive early-stage performance, their convergence slows down considerably in later stages. Notably, methods like CJADE and SMS remain trapped in higher-error regions, suggesting insufficient exploitation capabilities. RDE’s performance indicates superior global-to-local search transition, owing to its dynamic grouping and reinforced selection mechanism.
Figure 4 presents the convergence behavior on the Tic-tac-toe dataset. Here, all algorithms experience a sharp initial error drop within the first 20 iterations. However, the differences become apparent in later stages. RDE continues to reduce the MSE beyond iteration 200, ultimately achieving the lowest final error. In contrast, algorithms such as CJADE, DPDE, and SEDE plateau early and fail to make significant improvements. The relatively flat curves of BBO and SMS also confirm their limited local search refinement abilities.
Overall, these convergence profiles reveal that RDE not only achieves high classification accuracy but also provides faster and more reliable convergence. This efficiency is particularly important in practical scenarios where training time and algorithmic stability are critical.
4.7. Robustness Analysis
To complement the convergence analysis, we further evaluate the robustness and stability of the compared algorithms using box-whisker plots, as shown in Figure 5 and Figure 6. These plots visualize the distribution of test classification accuracy over 30 independent runs on the KrVsKpEW and Tic-tac-toe datasets.
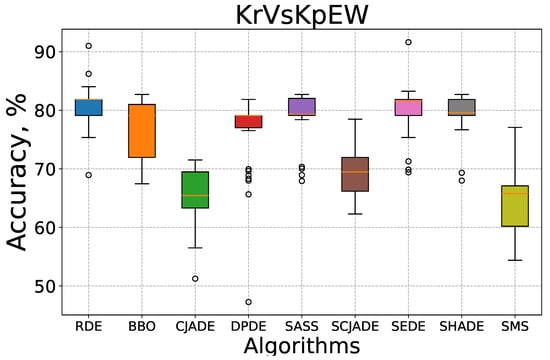
Figure 5.
Box-whisker plot for all compared algorithms on the KrVsKpEW dataset.
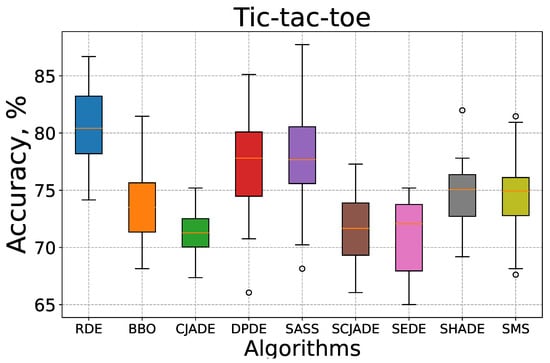
Figure 6.
Box-whisker plot for all compared algorithms on the Tic-tac-toe dataset.
In Figure 5, which presents the results on the KrVsKpEW dataset, the proposed RDE algorithm exhibits a compact interquartile range (IQR) and a high median accuracy above 80%. The presence of only a few outliers and relatively short whiskers indicates excellent stability across multiple runs. In contrast, algorithms such as CJADE, SCJADE, and SMS show larger IQRs and lower medians, reflecting higher performance fluctuations. SMS in particular displays a wide spread with a notably low lower bound, suggesting frequent poor convergence. While some methods like SEDE and SHADE achieve competitive medians, their variability is significantly greater than that of RDE.
Figure 6 illustrates the accuracy distributions on the Tic-tac-toe dataset. Once again, RDE outperforms other algorithms in both median accuracy and variance control. The interquartile box is narrow and located at the upper end of the accuracy scale, indicating that most RDE runs yield consistently high performance. Other methods, including BBO, SEDE, and SCJADE, demonstrate broader distributions with more outliers and lower medians. Notably, SCJADE and SEDE have both wide IQRs and multiple extreme values, further underscoring their limited robustness.
These results reinforce the conclusion that RDE is not only capable of achieving superior classification accuracy, but also does so with high consistency across independent trials. The low variance and tight accuracy distribution are indicative of strong optimization stability—a critical attribute in real-world applications where deterministic behavior is highly desirable.
4.8. Morphology and Hardware-Interpretable Logic on Tic-Tac-Toe and Australia Datasets
To demonstrate the interpretability and morphological learning capacity of the proposed RDE-DNM framework, we present a detailed analysis of two representative datasets: Tic-tac-toe and Australia. Figure 7, Figure 8, Figure 9 and Figure 10 and Figure 11, Figure 12, Figure 13 and Figure 14 illustrate the complete morphology evolution process and corresponding logic circuit realizations for both datasets.
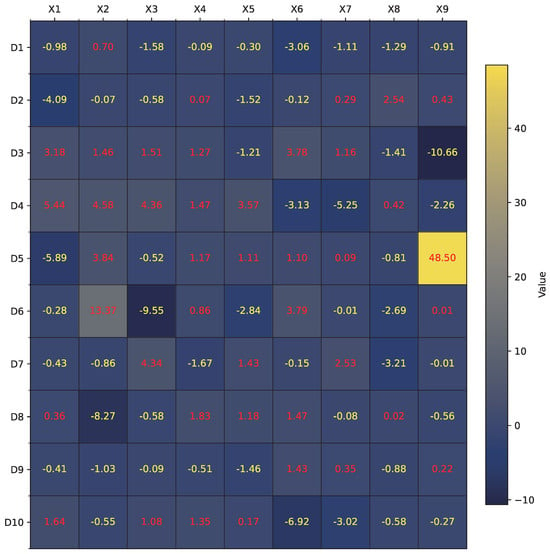
Figure 7.
Illustration of (q/w) learned by RDE for Tic-tac-toe dataset.
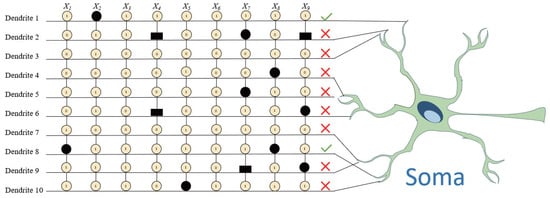
Figure 8.
The morphology of DNM learned by RDE on Tic-tac-toe dataset.
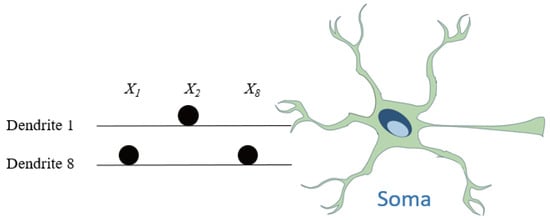
Figure 9.
The pruned morphology of DNM learned by RDE on Tic-tac-toe dataset.
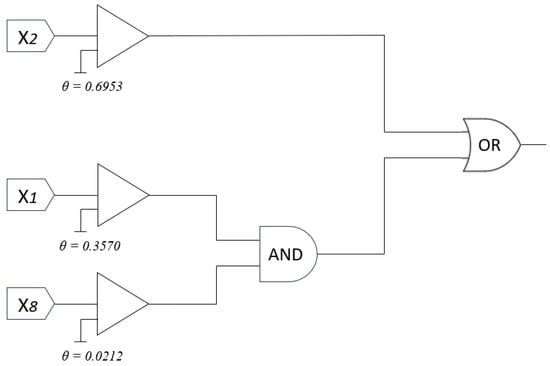
Figure 10.
Logical circle of DNM learned by RDE on Tic-tac-toe dataset.
For the Tic-tac-toe dataset, Figure 7 shows the learned synaptic ratios across 10 dendrites and 9 input features. After translating these values into their corresponding synaptic states (constant-1, constant-0, excitatory, inhibitory), the resulting full dendritic morphology is illustrated in Figure 8. As observed, only Dendrite 1 and Dendrite 8 contribute meaningful outputs, while the rest are pruned due to constant-0 or redundant synaptic connections. The pruned model, shown in Figure 9, retains only three informative features (, , and ) connected through two dendrites. These remaining connections are translated into a logic circuit in Figure 10, where one dendrite corresponds to an AND gate combining and , and the other dendrite passes directly to an OR gate. Each connection includes a learned comparator threshold, forming a circuit of only simple gates and three comparators.
For the Australia dataset, a similar analysis is conducted. Figure 11 visualizes the values across 5 dendrites and 14 features. Following the morphology transformation process, Figure 12 displays the complete neuron structure, which is then pruned down to a single effective dendrite, as shown in Figure 13. This dendrite integrates five active synaptic connections: , , , , and . The final hardware-friendly structure is translated into the logic circuit in Figure 14, composed of an AND-tree combining all five inputs after threshold filtering.
These two cases highlight the key advantages of the proposed RDE-DNM approach. First, the learning process enables automatic extraction of interpretable structures by identifying and retaining only task-relevant synapses and dendrites. Second, the resulting logic operations (e.g., AND, OR) match closely with biological neuron models, where dendrites act as nonlinear local processors. Finally, the final model can be directly mapped to hardware using only comparators and logic gates, making it highly suitable for low-resource embedded systems.
In terms of logic cost, the final model for Tic-tac-toe requires only three comparators and a two-level logic gate structure (one AND, one OR), while the model for Australia uses five comparators and a multi-level AND-tree. Despite the difference in feature space dimensionality, both learned DNMs maintain extremely compact and interpretable architectures.
To support the hardware-friendliness claim, we refer to prior studies such as [44,51] where logic-based DNMs and comparator circuits were implemented on FPGAs and edge devices. These implementations demonstrated compact logic design, low power consumption, and real-time processing capabilities, validating the deployability of DNM-based models. These results affirm the capability of RDE-DNM to perform morphology-aware learning, sparsify network structure, and produce logic-level representations that are directly implementable. Compared to traditional deep learning models that require high-dimensional floating-point computation or complex analog circuitry, the DNM architecture offers a promising alternative with low hardware overhead and high cognitive interpretability.
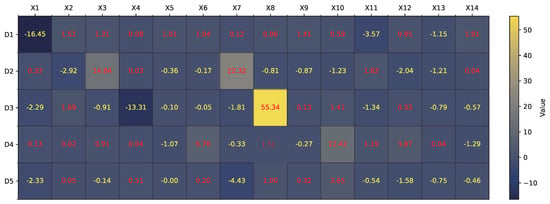
Figure 11.
Illustration of (q/w) learned by RDE for the Australia dataset.
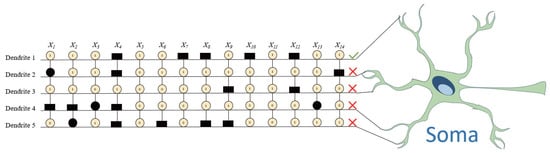
Figure 12.
The morphology of DNM learned by RDE on the Australia dataset.
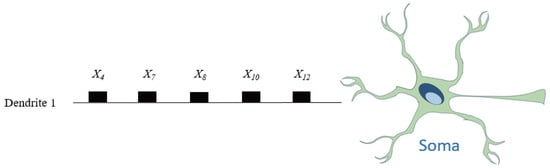
Figure 13.
The pruned morphology of DNM learned by RDE on the Australia dataset.
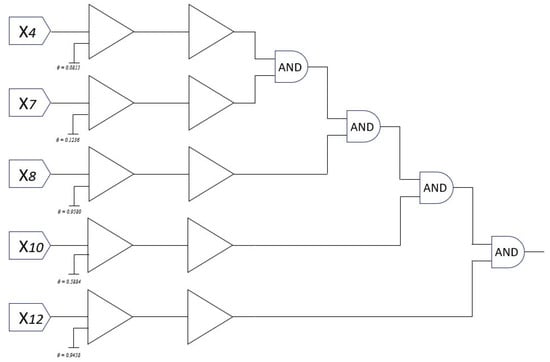
Figure 14.
Logical circle of DNM learned by RDE on the Australia dataset.
4.9. Comparative Analysis of Morphological Complexity and Hardware Cost
To further assess the interpretability and implementation efficiency of the RDE-trained dendritic neuron model, we compare the structural sparsity and hardware resource usage of the learned DNMs on the Tic-tac-toe and Australia datasets. Table 3 summarizes the pruning statistics, including the original and final number of dendrites, remaining synapses, and effective input features involved.

Table 3.
Pruning and logic gate stats of DNM after RDE learning.
As observed, both datasets undergo significant morphological simplification after learning. On the Tic-tac-toe dataset, the model retains only two out of ten dendrites and three informative features. The corresponding logic circuit consists of two comparators followed by a simple AND-OR cascade, as shown in Figure 10. The synaptic pruning rate exceeds 84%, indicating a highly sparse yet functional structure.
On the Australia dataset, a more compact model emerges: only one dendrite remains, connected to five inputs. This leads to a deep AND-tree composed of four logic gates and five threshold comparators, as visualized in Figure 14. Despite the increased number of active inputs, the circuit complexity remains minimal and interpretable.
These results show that the DNM trained via RDE not only learns accurate models but also automatically prunes redundant synapses and dendrites, producing compact and logical structures that can be directly implemented in hardware. Compared with traditional neural network architectures that rely on floating-point multipliers and nonlinear activations [52,53,54], the DNM requires only a small set of discrete logic operations and thresholds. This makes it suitable for edge AI applications with strict memory, energy, or silicon constraints.
In conclusion, the RDE-trained DNM achieves a unique balance between biological plausibility, model sparsity, logical interpretability, and practical deployability. Its built-in structure regularization and local morphological encoding open up new possibilities for hardware-friendly, brain-inspired learning systems.
5. Conclusions
This paper proposed a biologically inspired, interpretable, and hardware-friendly single-neuron learning framework, termed RDE-DNM, which combines the Dendritic Neuron Model (DNM) with a novel Reinforced Dynamic-grouping Differential Evolution (RDE) algorithm. Unlike conventional black-box deep learning systems based on simplistic McCulloch–Pitts neurons, DNM introduces biologically plausible compartmentalized dendritic processing that enhances interpretability and functional richness at the single-neuron level.
To effectively train the synaptic and dendritic parameters of DNM, we designed the RDE algorithm which incorporates a dynamic population grouping strategy and a reinforced mutation mechanism. RDE not only enhances global exploration and local exploitation during evolution but also improves convergence speed and robustness. Extensive experimental evaluations on twelve benchmark datasets confirmed that RDE-DNM consistently outperforms existing evolutionary and gradient-based learning approaches in terms of classification accuracy, stability, and generalization. For instance, RDE-DNM achieved up to 92.9% accuracy on the BreastEW dataset and 98.08% on the Moons dataset, with minimal performance variance across 30 independent runs.
Beyond predictive performance, the proposed method offers structural sparsity and logic-level interpretability. Through dendrite and synapse pruning, RDE-DNM is capable of reducing network complexity while preserving functionality. The pruned dendritic structures are compact and interpretable, and they can be directly translated into logical circuits composed of comparators and simple Boolean gates. Case studies on Tic-tac-toe and Australia datasets demonstrate that the learned DNMs can be mapped into minimal, hardware-friendly architectures suitable for real-world deployment in embedded or neuromorphic systems. Such low-overhead and interpretable structures are particularly beneficial for deployment in domains demanding transparency and energy efficiency, including medical diagnostics, financial screening, and IoT edge computing.
Although the proposed RDE-DNM performs well across various domains, its lower accuracy on the Exactly dataset (logic-intensive) highlights a limitation in handling highly discrete or symbolic structures. This suggests future work may require hybrid strategies or symbolic reasoning modules to improve performance in such scenarios.
In summary, this work takes a step toward next-generation biologically plausible learning by unifying efficient evolutionary learning and interpretable single-neuron modeling. In future work, we plan to explore multi-neuron extensions of DNM, integrate temporal coding for sequential tasks, and deploy RDE-DNM on FPGA and neuromorphic hardware for real-time decision-making applications.
Author Contributions
Conceptualization, C.W. and H.L.; methodology, C.W. and H.L.; software, C.W. and H.L.; validation, C.W. and H.L.; formal analysis, C.W. and H.L.; investigation, C.W. and H.L.; resources, H.L.; data curation, C.W. and H.L.; writing—original draft preparation, C.W.; writing—review and editing, H.L.; visualization, C.W. and H.L.; supervision, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used in the experiments are available upon request by contacting the corresponding author via email. Additionally, the dataset can be accessed at the following URL: https://archive.ics.uci.edu/.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; Long and Short Papers. Volume 1, pp. 4171–4186. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Montavon, G.; Samek, W.; Müller, K.R. Methods for interpreting and understanding deep neural networks. Digit. Signal Process. 2018, 73, 1–15. [Google Scholar] [CrossRef]
- Tjoa, E.; Guan, C. A survey on explainable artificial intelligence (XAI): Toward medical XAI. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4793–4813. [Google Scholar] [CrossRef]
- Hassija, V.; Chamola, V.; Mahapatra, A.; Singal, A.; Goel, D.; Huang, K.; Scardapane, S.; Spinelli, I.; Mahmud, M.; Hussain, A. Interpreting black-box models: A review on explainable artificial intelligence. Cogn. Comput. 2024, 16, 45–74. [Google Scholar] [CrossRef]
- Gao, S.; Zhou, M.; Wang, Y.; Cheng, J.; Yachi, H.; Wang, J. Dendritic neuron model with effective learning algorithms for classification, approximation, and prediction. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 601–614. [Google Scholar] [CrossRef]
- Gao, S.; Zhou, M.; Wang, Z.; Sugiyama, D.; Cheng, J.; Wang, J.; Todo, Y. Fully Complex-valued Dendritic Neuron Model. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 2105–2118. [Google Scholar] [CrossRef]
- Chavlis, S.; Poirazi, P. Dendrites endow artificial neural networks with accurate, robust and parameter-efficient learning. Nat. Commun. 2025, 16, 943. [Google Scholar] [CrossRef]
- Yu, Y.; Lei, Z.; Wang, Y.; Zhang, T.; Peng, C.; Gao, S. Improving Dendritic Neuron Model with Dynamic Scale-free Network-based Differential Evolution. IEEE/CAA J. Autom. Sin. 2022, 9, 99–110. [Google Scholar] [CrossRef]
- Zhang, Z.; Lei, Z.; Omura, M.; Hasegawa, H.; Gao, S. Dendritic learning-incorporated vision transformer for image recognition. IEEE/CAA J. Autom. Sin. 2024, 11, 539–541. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.; Lei, Z.; Omura, M.; Wang, R.L.; Gao, S. Dendritic deep learning for medical segmentation. IEEE/CAA J. Autom. Sin. 2024, 11, 803–805. [Google Scholar] [CrossRef]
- Li, J.; Lei, Z.; Zhang, Z.; Li, H.; Todo, Y.; Gao, S. Alternating Excitation-Inhibition Dendritic Computing for Classification. IEEE Trans. Artif. Intell. 2024, 5, 5431–5441. [Google Scholar] [CrossRef]
- Xu, W.; Song, Y.; Gupta, S.; Jia, D.; Tang, J.; Lei, Z.; Gao, S. Dmixnet: A dendritic multi-layered perceptron architecture for image recognition. Artif. Intell. Rev. 2025, 58, 129. [Google Scholar] [CrossRef]
- Stuart, G.; Spruston, N.; Häusser, M. Dendrites; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- London, M.; Häusser, M. Dendritic computation. Annu. Rev. Neurosci. 2005, 28, 503–532. [Google Scholar] [CrossRef]
- Poirazi, P.; Brannon, T.; Mel, B.W. Pyramidal neuron as two-layer neural network. Neuron 2003, 37, 989–999. [Google Scholar] [CrossRef]
- Hausser, M.; Major, G.; Stuart, G.J. Differential shunting of EPSPs by action potentials. Science 2001, 291, 138–141. [Google Scholar] [CrossRef]
- Todo, Y.; Tamura, H.; Yamashita, K.; Tang, Z. Unsupervised learnable neuron model with nonlinear interaction on dendrites. Neural Netw. 2014, 60, 96–103. [Google Scholar] [CrossRef]
- Todo, Y.; Tang, Z.; Todo, H.; Ji, J.; Yamashita, K. Neurons with multiplicative interactions of nonlinear synapses. Int. J. Neural Syst. 2019, 29, 1950012. [Google Scholar] [CrossRef]
- Polsky, A.; Mel, B.W.; Schiller, J. Computational subunits in thin dendrites of pyramidal cells. Nat. Neurosci. 2004, 7, 621–627. [Google Scholar] [CrossRef] [PubMed]
- Ji, J.; Tang, C.; Zhao, J.; Tang, Z.; Todo, Y. A survey on dendritic neuron model: Mechanisms, algorithms and practical applications. Neurocomputing 2022, 489, 390–406. [Google Scholar] [CrossRef]
- Pagkalos, M.; Makarov, R.; Poirazi, P. Leveraging dendritic properties to advance machine learning and neuro-inspired computing. Curr. Opin. Neurobiol. 2024, 85, 102853. [Google Scholar] [CrossRef]
- Hawkins, J.; Ahmad, S. Why neurons have thousands of synapses, a theory of sequence memory in neocortex. Front. Neural Circuits 2016, 10, 23. [Google Scholar] [CrossRef]
- Bengio, Y.; Lee, D.H.; Bornschein, J.; Mesnard, T.; Lin, Z. Towards biologically plausible deep learning. arXiv 2015, arXiv:1502.04156. [Google Scholar]
- Pagkalos, M.; Chavlis, S.; Poirazi, P. Introducing the Dendrify framework for incorporating dendrites to spiking neural networks. Nat. Commun. 2023, 14, 131. [Google Scholar] [CrossRef]
- Saxe, A.; Nelli, S.; Summerfield, C. If deep learning is the answer, what is the question? Nat. Rev. Neurosci. 2021, 22, 55–67. [Google Scholar] [CrossRef]
- Ji, J.; Gao, S.; Cheng, J.; Tang, Z.; Todo, Y. An approximate logic neuron model with a dendritic structure. Neurocomputing 2016, 173, 1775–1783. [Google Scholar] [CrossRef]
- Ju, Z.; Liu, Z.; Gao, Y.; Li, H.; Du, Q.; Yoshikawa, K.; Gao, S. EfficientNet Empowered by Dendritic Learning for Diabetic Retinopathy. IEICE Trans. Inf. Syst. 2024, 107, 1281–1284. [Google Scholar] [CrossRef]
- Zhong, L.; Liu, Z.; He, H.; Lei, Z.; Gao, S. Dendritic learning and miss region detection-based deep network for multi-scale medical segmentation. J. Bionic Eng. 2024, 21, 2073–2085. [Google Scholar] [CrossRef]
- Dong, S.; Liu, Z.; Li, H.; Lei, Z.; Gao, S. A Dendritic Architecture-Based Deep Learning for Tumor Detection. IEEJ Trans. Electr. Electron. Eng. 2024, 19, 1091–1093. [Google Scholar] [CrossRef]
- Li, Q.; He, H.; Xue, C.; Liu, T.; Gao, S. A Seasonal-Trend Decomposition and Single Dendrite Neuron-Based Predicting Model for Greenhouse Time Series. Environ. Model. Assess. 2024, 29, 427–440. [Google Scholar] [CrossRef]
- Yuan, Z.; Gao, S.; Wang, Y.; Li, J.; Hou, C.; Guo, L. Prediction of PM2. 5 time series by seasonal trend decomposition-based dendritic neuron model. Neural Comput. Appl. 2023, 35, 15397–15413. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Wang, Z.; Li, J.; Jin, T.; Meng, X.; Gao, S. Dendritic neuron model trained by information feedback-enhanced differential evolution algorithm for classification. Knowl.-Based Syst. 2021, 233, 107536. [Google Scholar] [CrossRef]
- Dohare, S.; Hernandez-Garcia, J.F.; Lan, Q.; Rahman, P.; Mahmood, A.R.; Sutton, R.S. Loss of plasticity in deep continual learning. Nature 2024, 632, 768–774. [Google Scholar] [CrossRef]
- Poirazi, P.; Papoutsi, A. Illuminating dendritic function with computational models. Nat. Rev. Neurosci. 2020, 21, 303–321. [Google Scholar] [CrossRef]
- Egrioglu, E.; Bas, E. A new deep neural network for forecasting: Deep dendritic artificial neural network. Artif. Intell. Rev. 2024, 57, 171. [Google Scholar] [CrossRef]
- Yang, Y.; Li, X.; Li, H.; Zhang, C.; Todo, Y.; Yang, H. Yet another effective dendritic neuron model based on the activity of excitation and inhibition. Mathematics 2023, 11, 1701. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar]
- Opara, K.R.; Arabas, J. Differential Evolution: A survey of theoretical analyses. Swarm Evol. Comput. 2019, 44, 546–558. [Google Scholar] [CrossRef]
- Li, X.; Tang, J.; Zhang, Q.; Gao, B.; Yang, J.J.; Song, S.; Wu, W.; Zhang, W.; Yao, P.; Deng, N.; et al. Power-efficient neural network with artificial dendrites. Nat. Nanotechnol. 2020, 15, 776–782. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Yu, Y.; Wang, Y.; Wang, J.; Cheng, J.; Zhou, M. Chaotic Local Search-based Differential Evolution Algorithms for Optimization. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3954–3967. [Google Scholar] [CrossRef]
- Kumar, A.; Misra, R.K.; Singh, D.; Mishra, S.; Das, S. The spherical search algorithm for bound-constrained global optimization problems. Appl. Soft Comput. 2019, 85, 105734. [Google Scholar] [CrossRef]
- Xu, Z.; Gao, S.; Yang, H.; Lei, Z. SCJADE: Yet Another State-of-the-Art Differential Evolution Algorithm. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 644–646. [Google Scholar] [CrossRef]
- Liang, J.; Qiao, K.; Yu, K.; Ge, S.; Qu, B.; Xu, R.; Li, K. Parameters estimation of solar photovoltaic models via a self-adaptive ensemble-based differential evolution. Sol. Energy 2020, 207, 336–346. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Success-history based parameter adaptation for differential evolution. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 71–78. [Google Scholar]
- Ji, J.; Song, S.; Tang, Y.; Gao, S.; Tang, Z.; Todo, Y. Approximate logic neuron model trained by states of matter search algorithm. Knowl.-Based Syst. 2018, 163, 120–130. [Google Scholar] [CrossRef]
- Baek, E.; Song, S.; Baek, C.K.; Rong, Z.; Shi, L.; Cannistraci, C.V. Neuromorphic dendritic network computation with silent synapses for visual motion perception. Nat. Electron. 2024, 7, 454–465. [Google Scholar] [CrossRef]
- Misra, J.; Saha, I. Artificial neural networks in hardware: A survey of two decades of progress. Neurocomputing 2010, 74, 239–255. [Google Scholar] [CrossRef]
- Mittal, S. A survey of FPGA-based accelerators for convolutional neural networks. Neural Comput. Appl. 2020, 32, 1109–1139. [Google Scholar] [CrossRef]
- Zhang, H.; Gu, M.; Jiang, X.; Thompson, J.; Cai, H.; Paesani, S.; Santagati, R.; Laing, A.; Zhang, Y.; Yung, M.H.; et al. An optical neural chip for implementing complex-valued neural network. Nat. Commun. 2021, 12, 457. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).