A Refined Spectral Galerkin Approach Leveraging Romanovski–Jacobi Polynomials for Differential Equations
Abstract
1. Introduction
2. A Short Overview of RJPs Is Outlined
3. Initial Value Problems of Higher Order
3.1. Initial Homogeneous Conditions Type
- For , is a banded matrix, capturing localized interactions between the basis functions caused by lower-order differential terms.
- For , the matrix becomes upper triangular, due to the dominance of higher-order derivatives and the hierarchical recurrence structure of the RJPs.In many practical problems, particularly those involving higher-order derivatives, both and are upper triangular, and hence the entire system matrix inherits this triangular structure.This feature yields several computational benefits:
- The assembly of the linear system requires at most operations, leveraging the sparsity and triangular structure.
- The solution of the system is efficiently carried out via backward substitution, with an overall computational cost less than that of dense system solvers [20].Such a structured formulation, combined with the spectral convergence of the Romanovski–Jacobi basis and the precision of Gauss-type quadrature, ensures that the proposed method is both highly accurate and computationally efficient for solving DEs on finite intervals with ICs.
3.2. Initial Conditions of Nonhomogeneous Type
4. Numerical Approach for Solving a System of IVPs
5. Partial Differential Equations
5.1. First-Order Hyperbolic PDEs
- If and are lower (or upper) triangular matrices, then their Kronecker product, , is also lower (or upper) triangular.
- If and are band matrices, then their Kronecker product, , is a band matrix. The bandwidth of depends on the bandwidths of and .Ultimately, the differential equation, along with the specified initial and boundary conditions, is transformed into a system of linear algebraic equations containing the unknown expansion coefficients. This system is then efficiently solved using the Gaussian elimination method.
5.2. Second-Order PDEs
6. Handling of Nonhomogeneous Conditions
7. Convergence and Error Analysis
7.1. The Convergence and Error Analysis for IVPs (5), (6), (18), and (19)
- (i)
- Establishing the corresponding hypotheses and assumptions in Theorem 3 to obtain the bound expression of the coefficients in the expansions:
- (ii)
- Deriving the error-bound expressions for , similar to in Theorem 5.
- (iii)
- Getting the bound expression of defined in (42):
7.2. The Convergence and Error Analysis for PDEs (23)–(25) and (31)–(32)
8. Numerical Results
| Algorithms 1 RJGM Algorithm for Example 1 | |
| Step 1. | Given , and . |
| Step 2. | Define the polynomials , the basis , and the vector and compute |
| the elements of the matrices , and . | |
| Step 3. | List the equation system as defined in (11). |
| Step 4. | Use Mathematica’s built-in numerical solver to solve the system |
| obtained in [Output 3]. | |
| Step 5. | Evaluate defined in (9). (In the case of homogeneous ICs.) |
| Step 6. | Evaluate using Equation (17). (In the case of nonhomogeneous ICs.) |
| Step 7. | Evaluate defined in (41). |
| Algorithms 2 RJGM Algorithm for Example 4 | |
| Step 1. | Given , and . |
| Step 2. | Define the polynomials , the basis , and the vector and compute |
| the elements of the matrices , and . | |
| Step 3. | Define defined in Equation (1). |
| Step 3. | List , defined in (16). |
| Step 4. | Use Mathematica’s built-in numerical solver to solve the system |
| obtained in [Output 3]. | |
| Step 5. | Evaluate defined in (9). (In the case of homogeneous ICs.) |
| Step 6. | Evaluate using Equation (17). (In the case of nonhomogeneous ICs.) |
| Step 7. | Evaluate defined in (41). |
| Algorithms 3 RJGM Algorithm for Example 5 | |
| Step 1. | Given . |
| Step 2. | Define the polynomials , the basis , and the vector and compute |
| the elements of matrices . | |
| Step 3. | Compute , and . |
| Step 4. | List the equations system as defined in (28). |
| Step 5. | Use Mathematica’s built-in numerical solver to solve the system |
| obtained in [Output 4]. | |
| Step 6. | Evaluate defined in (26). |
| Step 7. | Evaluate and defined in (51) and (52), respectively. |
| Algorithms 4 RJGM Algorithm for Example 6 | |
| Step 1. | Given , and . |
| Step 2. | Define the polynomials , the basis , and the vector and compute |
| the elements of matrices . | |
| Step 3. | Compute , , , , , and . |
| Step 4. | List the equation system as defined in (35). |
| Step 5. | Use Mathematica’s built-in numerical solver to solve the system |
| obtained in [Output 4]. | |
| Step 6. | Evaluate defined in (33). (In the case of homogeneous ICs.) |
| Step 7. | Evaluate using Equation (36). (In the case of nonhomogeneous ICs.) |
| Step 8. | Evaluate and defined in (51) and (52), respectively. |
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Antonov, D.V.; Shchepakina, E.A.; Sobolev, V.A.; Starinskaya, E.M.; Terekhov, V.V.; Strizhak, P.A.; Sazhin, S.S. A new solution to a weakly non-linear heat conduction equation in a spherical droplet: Basic idea and applications. Int. J. Heat Mass Transf. 2024, 219, 124880. [Google Scholar] [CrossRef]
- Beybalaev, V.D.; Aliverdiev, A.A.; Hristov, J. Transient Heat Conduction in a Semi-Infinite Domain with a Memory Effect: Analytical Solutions with a Robin Boundary Condition. Fractal Fract. 2023, 7, 770. [Google Scholar] [CrossRef]
- Ali, K.K.; Sucu, D.Y.; Karakoc, S.B.G. Two effective methods for solution of the Gardner–Kawahara equation arising in wave propagation. Math. Comput. Simul. 2024, 220, 192–203. [Google Scholar] [CrossRef]
- Gao, Q.; Yan, B.; Zhang, Y. An accurate method for dispersion characteristics of surface waves in layered anisotropic semi-infinite spaces. Comput. Struct. 2023, 276, 106956. [Google Scholar] [CrossRef]
- Daum, S.; Werner, R. A novel feasible discretization method for linear semi-infinite programming applied to basket option pricing. Optimization 2011, 60, 1379–1398. [Google Scholar] [CrossRef]
- Fazio, R. Free Boundary Formulation for Boundary Value Problems on Semi-Infinite Intervals: An up to Date Review. arXiv 2020, arXiv:2011.07723. [Google Scholar]
- Fazio, R.; Jannelli, A. Finite difference schemes on quasi-uniform grids for BVPs on infinite intervals. J. Comput. Appl. Math. 2014, 269, 14–23. [Google Scholar] [CrossRef]
- Givoli, D.; Neta, B.; Patlashenko, I. Finite element analysis of time-dependent semi-infinite wave-guides with high-order boundary treatment. Int. J. Numer. Methods Eng. 2003, 58, 1955–1983. [Google Scholar] [CrossRef]
- Huang, W.; Yang, J.; Sladek, J.; Sladek, V.; Wen, P. Semi-infinite structure analysis with bimodular materials with infinite element. Materials 2022, 15, 641. [Google Scholar] [CrossRef]
- Abo-Gabal, H.; Zaky, M.A.; Hafez, R.M.; Doha, E.H. On Romanovski–Jacobi polynomials and their related approximation results. Numer. Methods Partial Differ. Equ. 2020, 36, 1982–2017. [Google Scholar] [CrossRef]
- Youssri, Y.H.; Zaky, M.A.; Hafez, R.M. Romanovski-Jacobi spectral schemes for high-order differential equations. Appl. Numer. Math. 2024, 198, 148–159. [Google Scholar] [CrossRef]
- Hafez, R.; Haiour, M.; Tantawy, S.; Alburaikan, A.; Khalifa, H. A Comprehensive Study on Solving Multitype Differential Equations Using Romanovski-Jacobi Matrix Methods. Fractals 2025. [Google Scholar] [CrossRef]
- Nataj, S.; He, Y. Anderson acceleration for nonlinear PDEs discretized by space–time spectral methods. Comput. Math. Appl. 2024, 167, 199–206. [Google Scholar] [CrossRef]
- Yan, Q.; Jiang, S.W.; Harlim, J. Spectral methods for solving elliptic PDEs on unknown manifolds. J. Comput. Phys. 2023, 486, 112132. [Google Scholar] [CrossRef]
- Ahmed, H.M. Enhanced shifted Jacobi operational matrices of integrals: Spectral algorithm for solving some types of ordinary and fractional differential equations. Bound. Value Probl. 2024, 2024, 75. [Google Scholar] [CrossRef]
- Ahmed, H.M. Solutions of 2nd-order linear differential equations subject to Dirichlet boundary conditions in a Bernstein polynomial basis. J. Egypt. Math. Soc. 2014, 22, 227–237. [Google Scholar] [CrossRef]
- Masjedjamei, M. Three finite classes of hypergeometric orthogonal polynomials and their application in functions approximation. Integr. Transf. Spec. Funct. 2002, 13, 169–190. [Google Scholar] [CrossRef]
- Izadi, M.; Veeresha, P.; Adel, W. The fractional-order marriage–divorce mathematical model: Numerical investigations and dynamical analysis. Eur. Phys. J. Plus 2024, 139, 205. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Izadi, M.; Adel, W. Robust and accurate numerical framework for multi-dimensional fractional-order telegraph equations using Jacobi/Jacobi-Romanovski spectral technique. Bound. Value Probl. 2024, 2024, 131. [Google Scholar] [CrossRef]
- Lakshmikantham, V.; Sen, S.K. Computational Error and Complexity in Science and Engineering; Elsevier: Melbourne, FL, USA, 2005. [Google Scholar]
- Toutounian, F.; Tohidi, E. A new Bernoulli matrix method for solving second order linear partial differential equations with the convergence analysis. Appl. Math. Comput. 2013, 223, 298–310. [Google Scholar] [CrossRef]
- Jeffrey, A.; Dai, H.H. Handbook of Mathematical Formulas and Integrals; Elsevier: London, UK, 2008. [Google Scholar]
- Hassan, I.H.A.H. Differential transformation technique for solving higher-order initial value problems. Appl. Math. Comput. 2004, 154, 299–311. [Google Scholar]
- Yuzbasi, S. An efficient algorithm for solving multi-pantograph equation systems. Comput.Math. Appl. 2012, 64, 589–603. [Google Scholar] [CrossRef]
- Hassan, I.H.A.H. Application to differential transformation method for solving systems of differential equations. Appl. Math. Model 2008, 32, 2552–2559. [Google Scholar] [CrossRef]
- Gireesha, B.J.; Gowtham, K.J. Efficient hypergeometric wavelet approach for solving lane-emden equations. J. Comput. Sci. 2024, 82, 102392. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, X. Numerical solutions for the linear and nonlinear singular boundary value problems using Laguerre wavelets. Adv. Differ. Equ. 2016, 2016, 17. [Google Scholar] [CrossRef]
- Shiralashetti, S.C.; Kumbinarasaiah, S. Hermite wavelets operational matrix of integration for the numerical solution of nonlinear singular initial value problems. Alex. Eng. J. 2018, 57, 2591–2600. [Google Scholar] [CrossRef]
- Tohidi, E.; Toutounian, F. Convergence analysis of bernoulli matrix approach for onedimensional matrix hyperbolic equations of the first order. Comput. Math. Appl. 2014, 68, 1–12. [Google Scholar] [CrossRef]
- Singh, S.; Patel, V.K.; Singh, V.K. Application of wavelet collocation method for hyperbolic partial differential equations via matrices. Appl. Math. Comput. 2018, 320, 407–424. [Google Scholar] [CrossRef]
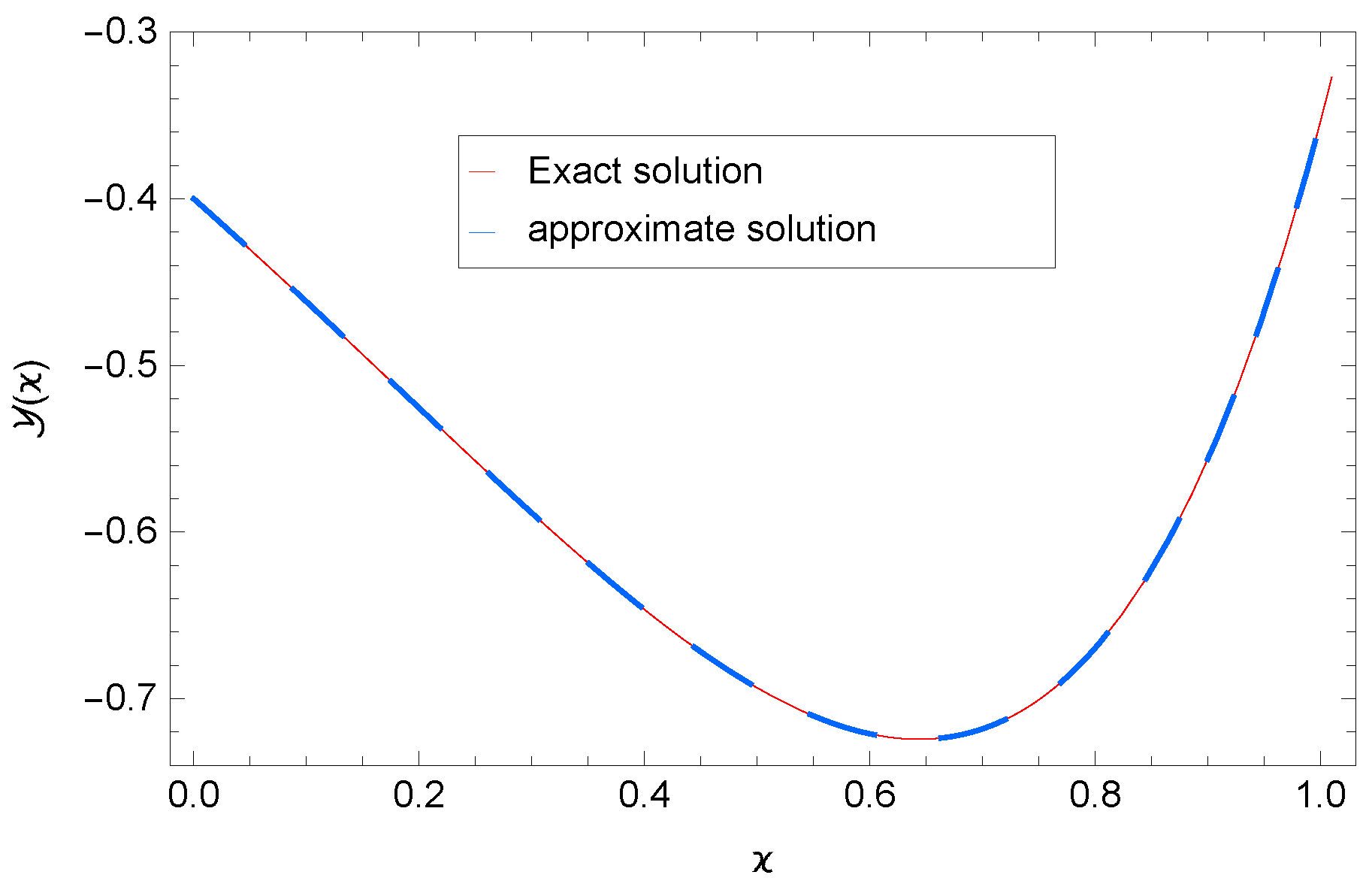
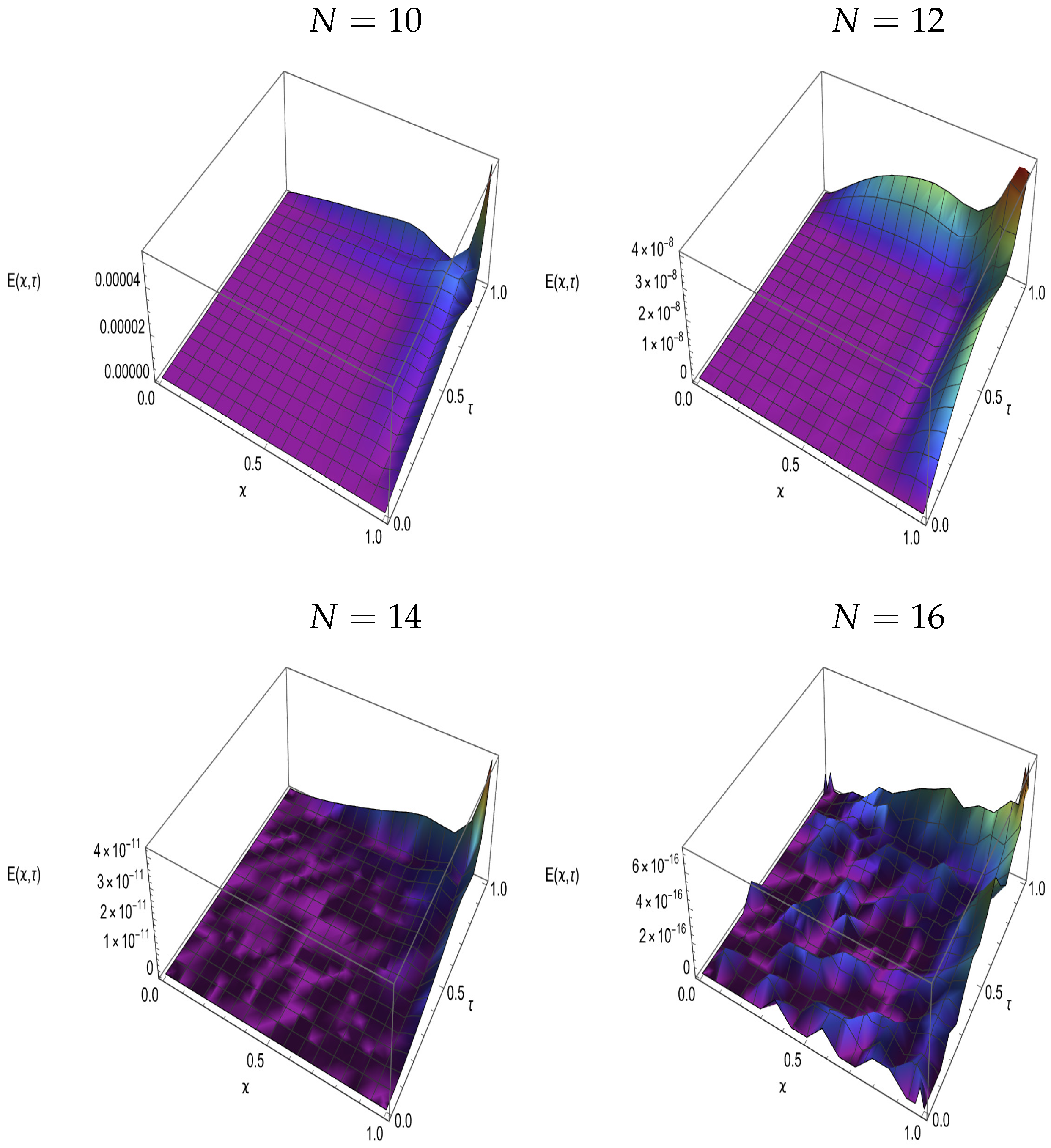


| DTM | RJGM at () | |||
|---|---|---|---|---|
| [23] | ||||
| N | ||||||
|---|---|---|---|---|---|---|
| RJTM [11] | RJGM | RJTM [11] | RJGM | RJTM [11] | RJGM | |
| 8 | ||||||
| 12 | ||||||
| 16 | ||||||
| 20 | ||||||
| N | ||||||
|---|---|---|---|---|---|---|
| RJTM [11] | RJGM | RJTM [11] | RJGM | RJTM [11] | RJGM | |
| 8 | ||||||
| 12 | ||||||
| 16 | ||||||
| 20 | ||||||
| DTM [25] | BCM [24] | Present Method | |
|---|---|---|---|
| 0.2 | |||
| 0.4 | |||
| 0.6 | |||
| 0.8 | |||
| 1.0 |
| DTM [25] | BCM [24] | Present Method | |
|---|---|---|---|
| 0.2 | |||
| 0.4 | |||
| 0.6 | |||
| 0.8 | |||
| 1.0 |
| N | |||
|---|---|---|---|
| 11 | |||
| 14 | |||
| 17 | |||
| 20 |
| BMM | RJGM at () | |||
|---|---|---|---|---|
| [21] | ||||
| 0 | 0 | 0 | ||
| 0 | ||||
| 0 | 0 | 0 | ||
| 0 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hafez, R.M.; Abdelkawy, M.A.; Ahmed, H.M. A Refined Spectral Galerkin Approach Leveraging Romanovski–Jacobi Polynomials for Differential Equations. Mathematics 2025, 13, 1461. https://doi.org/10.3390/math13091461
Hafez RM, Abdelkawy MA, Ahmed HM. A Refined Spectral Galerkin Approach Leveraging Romanovski–Jacobi Polynomials for Differential Equations. Mathematics. 2025; 13(9):1461. https://doi.org/10.3390/math13091461
Chicago/Turabian StyleHafez, Ramy M., Mohamed A. Abdelkawy, and Hany M. Ahmed. 2025. "A Refined Spectral Galerkin Approach Leveraging Romanovski–Jacobi Polynomials for Differential Equations" Mathematics 13, no. 9: 1461. https://doi.org/10.3390/math13091461
APA StyleHafez, R. M., Abdelkawy, M. A., & Ahmed, H. M. (2025). A Refined Spectral Galerkin Approach Leveraging Romanovski–Jacobi Polynomials for Differential Equations. Mathematics, 13(9), 1461. https://doi.org/10.3390/math13091461







