Fairness in Healthcare Services for Italian Older People: A Convolution-Based Evaluation to Support Policy Decision Makers
Abstract
1. Introduction
- It uses advanced artificial intelligence methods to automate how healthcare services are distributed in Italy for people over 65, tackling the issue of thoroughly assessing healthcare resources and checking the fairness of services in different regions.
- It provides a new way to evaluate the unfair distribution of health services by combining an image processing technique with geographic analysis, using weighted convolution matrices as statistical units instead of administrative boundaries, which improve the accuracy of estimating health resources in the area.
- It uses a measure of inequality called Gini Index to assess the fairness of health services distribution, taking into account both how many from the aged population live in an area and how the wealth is spread out in that area.
- It could aid in the future practical development of support systems by incorporating the proposed methodological model into decision support systems improved through dashboards with more accessible information for policymakers.
- All the software and scripts used for this analysis are available on GitHub in their first release at the following link: https://github.com/daviderusso/FairnessForHealthServices.git (accessed on 8 April 2025), promoting reproducibility and open science.
2. Methodology
2.1. Data
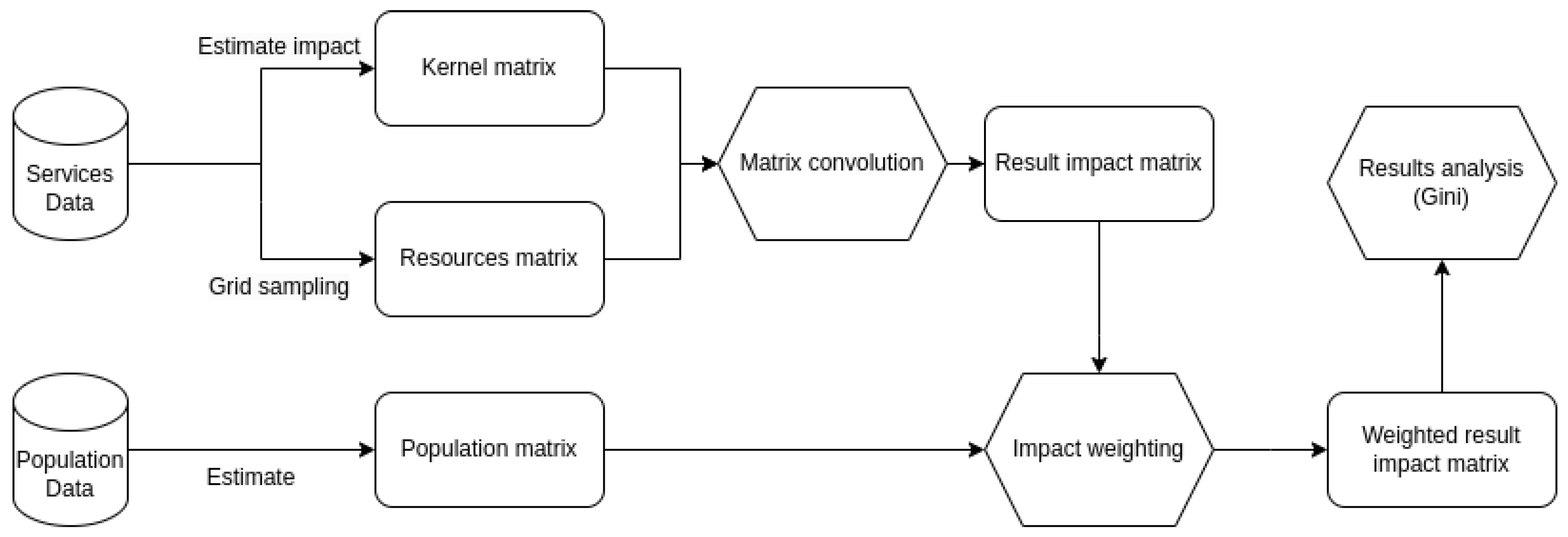
2.2. Method
2.2.1. Data Matrix Generation
2.2.2. Kernel Design Rationale
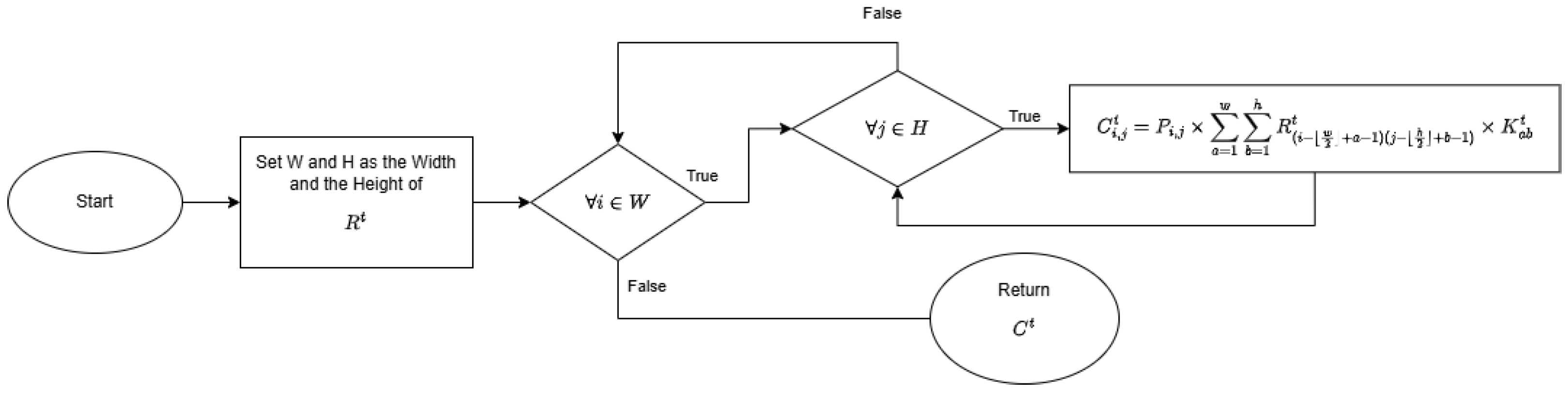
2.2.3. Convolution Implementation
2.2.4. Gini Coefficient Calculation
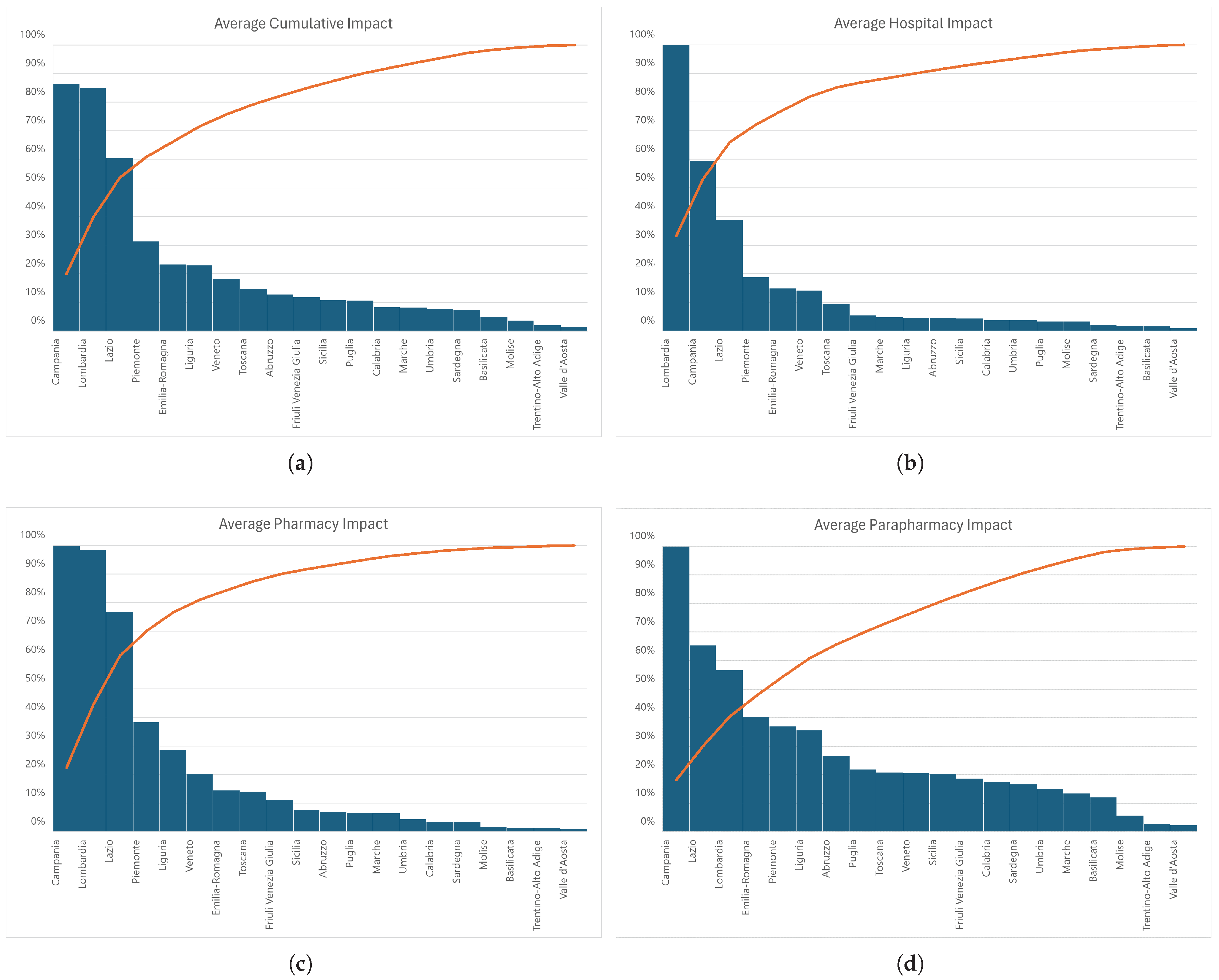
3. Results
4. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, L.; Yang, M.; De Vos, J.; Witlox, F. Examining geographical accessibility to multi-tier hospital care services for the elderly: A focus on spatial equity. J. Transp. Health 2020, 19, 100926. [Google Scholar] [CrossRef]
- Wang, F.; Luo, W. Assessing spatial and nonspatial factors for healthcare access: Towards an integrated approach to defining health professional shortage areas. Health Place 2005, 11, 131–146. [Google Scholar] [CrossRef] [PubMed]
- Carroll, C.; Sworn, K.; Booth, A.; Tsuchiya, A.; Maden, M.; Rosenberg, M. Equity in healthcare access and service coverage for older people: A scoping review of the conceptual literature. Integr. Healthc. J. 2022, 4, e000092. [Google Scholar] [CrossRef]
- Levesque, J.F.; Harris, M.F.; Russell, G. Patient-centred access to health care: Conceptualising access at the interface of health systems and populations. Int. J. Equity Health 2013, 12, 18. [Google Scholar] [CrossRef]
- Wu, H.C.; Tseng, M.H. Evaluating disparities in elderly community care resources: Using a geographic accessibility and inequality index. Int. J. Environ. Res. Public Health 2018, 15, 1353. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, J.; Rosenberg, M.W. Spatial access to residential care resources in Beijing, China. Int. J. Health Geogr. 2012, 11, 32. [Google Scholar] [CrossRef]
- Iyer, H.S.; Flanigan, J.; Wolf, N.G.; Schroeder, L.F.; Horton, S.; Castro, M.C.; Rebbeck, T.R. Geospatial evaluation of trade-offs between equity in physical access to healthcare and health systems efficiency. BMJ Glob. Health 2020, 5, e003493. [Google Scholar] [CrossRef]
- Peters, D.H.; Garg, A.; Bloom, G.; Walker, D.G.; Brieger, W.R.; Hafizur Rahman, M. Poverty and access to health care in developing countries. Ann. N. Y. Acad. Sci. 2008, 1136, 161–171. [Google Scholar] [CrossRef]
- Calovi, M.; Seghieri, C. Using a GIS to support the spatial reorganization of outpatient care services delivery in Italy. BMC Health Serv. Res. 2018, 18, 883. [Google Scholar] [CrossRef]
- Han, J.; Jiang, W.; Shi, J.; Xin, S.; Peng, J.; Liu, H. A method for assessing the fairness of health resource allocation based on geographical grid. Comput. Mater. Contin. 2020, 64, 1171–1184. [Google Scholar] [CrossRef]
- Pinto, D.M.; Russo, D.D.; Sudoso, A.M. Optimal Placement of Nature-Based Solutions for Urban Challenges. arXiv 2025, arXiv:2502.11065. [Google Scholar]
- Zhang, W.; Chen, G.; Zhuang, P.; Zhao, W.; Zhou, L. CATNet: Cascaded attention transformer network for marine species image classification. Expert Syst. Appl. 2024, 256, 124932. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Z.; Li, G.; Zhuang, P.; Hou, G.; Zhang, Q.; Li, C. GACNet: Generate adversarial-driven cross-aware network for hyperspectral wheat variety identification. IEEE Trans. Geosci. Remote Sens. 2023, 62, 5503314. [Google Scholar] [CrossRef]
- Capobianco, G.; Cerrone, C.; Di Placido, A.; Durand, D.; Pavone, L.; Russo, D.D.; Sebastiano, F. Image convolution: A linear programming approach for filters design. Soft Comput. 2021, 25, 8941–8956. [Google Scholar] [CrossRef]
- Erdenee, O.; Paramita, S.A.; Yamazaki, C.; Koyama, H. Distribution of health care resources in Mongolia using the Gini coefficient. Hum. Resour. Health 2017, 15, 56. [Google Scholar] [CrossRef]
- Pu, L. Fairness of the distribution of public medical and health resources. Front. Public Health 2021, 9, 768728. [Google Scholar] [CrossRef]
- Lee, J.K.; Alshehri, S.; Kutbi, H.I.; Martin, J.R. Optimizing pharmacotherapy in elderly patients: The role of pharmacists. Integr. Pharm. Res. Pract. 2015, 4, 101–111. [Google Scholar] [CrossRef]
- della Salute, M. Open Data per la Salute Pubblica. 2024. Available online: https://www.dati.salute.gov.it/dati/homeDataset.jsp (accessed on 1 October 2024).
- Contributors, O. Open Street Map. 2017. Available online: https://www.openstreetmap.org/#map=6/42.09/12.56 (accessed on 1 October 2024).
- ISTAT. Banca Dati Istat. 2024. Available online: http://dati.istat.it/Index.aspx (accessed on 1 October 2024).
- Khan, S.; Mohiuddin, K. Evaluating the parameters of ArcGIS and QGIS for GIS Applications. Int. J. Adv. Res. Sci. Eng. 2018, 7, 582–594. [Google Scholar]
- QGIS. QGIS Geographic Information System; QGIS Association: Grüt, Switzerland.
- Guagliardo, M.F. Spatial accessibility of primary care: Concepts, methods and challenges. Int. J. Health Geogr. 2004, 3, 3. [Google Scholar] [CrossRef]
- Hui, E.C.; Chau, C.K.; Pun, L.; Law, M. Measuring the neighboring and environmental effects on residential property value: Using spatial weighting matrix. Build. Environ. 2007, 42, 2333–2343. [Google Scholar] [CrossRef]
- NUVAP. Aggiornamento 2020 della Mappa delle Aree Interne; Nota Tecnica NUVAP: Rome, Italy, 2022. [Google Scholar]
- Castell, M.V.; Sánchez, M.; Julián, R.; Queipo, R.; Martín, S.; Otero, Á. Frailty prevalence and slow walking speed in persons age 65 and older: Implications for primary care. BMC Fam. Pract. 2013, 14, 86. [Google Scholar] [CrossRef] [PubMed]
- Belcore, E.; Colucci, E.; Aicardi, I.; Angeli, S. Analisi, classificazione e visualizzazione di dati UAV ad alta risoluzione spaziale e spettrale con l’utilizzo di FOSS. In FOSS4G Italia 2020 Raccolta Abstract; FOSS4G IT: Portland, OR, USA, 2020; pp. 31–32. [Google Scholar]
- Amaduzzi, S.; Pascolini, M. GIS e metodi di analisi territoriale. Una proposta per la caratterizzazione del paesaggio italiano. Dalla Mappa Al GIS 2011, 1, 13–32. [Google Scholar]
- QGis. Rasterize (Vector to Raster). Available online: https://download.qgis.org/qgisdata/QGIS-Documentation-2.6/live/html/it/docs/user_manual/processing_algs/gdalogr/gdal_conversion/rasterize.html (accessed on 1 October 2024).
- ArcGis. ArcGIS—Rasterize Features Function. Available online: https://pro.arcgis.com/en/pro-app/latest/help/analysis/raster-functions/rasterize-features-function.htm (accessed on 1 October 2024).
- GDAL. GDAL—Rasterize. Available online: https://gdal.org/en/stable/programs/gdal_rasterize.html (accessed on 1 October 2024).
- Lujak, M.; Salvatore, A.; Fernández, A.; Giordani, S.; Cousy, K. How to fairly and efficiently assign tasks in individually rational agents’ coalitions? Models and fairness measures. Comput. Sci. Inf. Syst. 2024, 21, 269–289. [Google Scholar] [CrossRef]
- Dorfman, R. A formula for the Gini coefficient. Rev. Econ. Stat. 1979, 61, 146–149. [Google Scholar] [CrossRef]
- Chen, Y.; Ge, Y.; Yang, G.; Wu, Z.; Du, Y.; Mao, F.; Liu, S.; Xu, R.; Qu, Z.; Xu, B.; et al. Inequalities of urban green space area and ecosystem services along urban center-edge gradients. Landsc. Urban Plan. 2022, 217, 104266. [Google Scholar] [CrossRef]
- Dixon, P.M.; Weiner, J.; Mitchell-Olds, T.; Woodley, R. Bootstrapping the Gini coefficient of inequality. Ecology 1987, 68, 1548–1551. [Google Scholar] [CrossRef]
- Benassi, F.; Tomassini, C.; Di Felice, G. Spatial Heterogeneities or Inequalities? Health Care Supply and Demand of the Older Population in Italy. Appl. Spat. Anal. Policy 2025, 18, 44. [Google Scholar] [CrossRef]
- Luo, W.; Qi, Y. An enhanced two-step floating catchment area (E2SFCA) method for measuring spatial accessibility to primary care physicians. Health Place 2009, 15, 1100–1107. [Google Scholar] [CrossRef]
- Higgs, G. A literature review of the use of GIS-based measures of access to health care services. Health Serv. Outcomes Res. Methodol. 2004, 5, 119–139. [Google Scholar] [CrossRef]
- ISTAT. Indicatori Demografici: Regione Liguria, Friuli Venezia Giulia, Campania. 2024. Available online: http://dati.istat.it/Index.aspx?QueryId=18563# (accessed on 28 January 2025).
- Mucciardi, M.; Benassi, F. Measuring the spatial concentration of population: A new approach based on the graphical representation of the Gini index. Qual. Quant. 2023, 57, 5193–5211. [Google Scholar] [CrossRef]
- Rey, S.J.; Smith, R.J. A spatial decomposition of the Gini coefficient. Lett. Spat. Resour. Sci. 2013, 6, 55–70. [Google Scholar] [CrossRef]
- Mussard, S.; Seyte, F.; Terraza, M. Decomposition of Gini and the generalized entropy inequality measures. Econ. Bull. 2003, 4, 1–6. [Google Scholar]
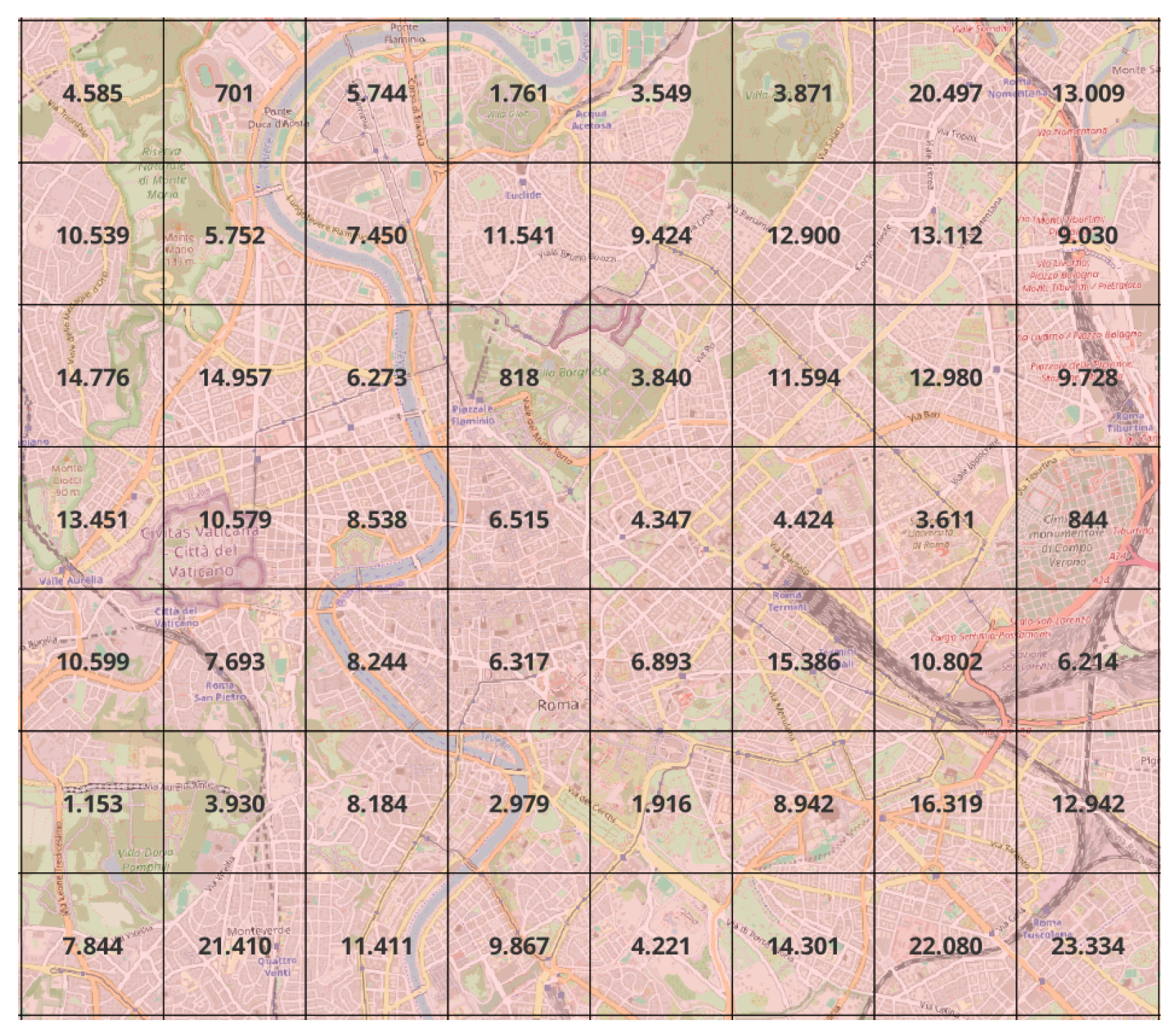



| Type | Name | Address | Municipality | Latitude | Longitude |
|---|---|---|---|---|---|
| Hospital | ospedale ca’ granda-niguarda—milano | Piazza Ospedale Maggiore 3 | Milano | 45.5091226 | 9.1890984 |
| fondaz.irccs ca’ granda—ospedale maggi | Via Francesco Sforza, 28 | Milano | 45.4604789 | 9.1957932 | |
| Pharmacy | comunale ponte vittorio | Corso Vittorio Emanuele, 343 | Roma | 41.7203878 | 12.713078 |
| farmacia durazzano srl | Viale XXI Aprile, 42-42a | Roma | 41.9236809 | 12.571148 | |
| Parapharmacy | parafarmacia dott.ssa valeria di pinto | Via Torino, 12 | Termoli | 41.9926745 | 14.969991 |
| parafarmacia di lombardi antonia | Viale Trieste N.9 | Termoli | 42.0015076 | 14.990566 |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| 0.1 | 0.55 | 0.55 | 0.55 | 0.1 |
| 0.1 | 0.55 | 1.0 | 0.55 | 0.1 |
| 0.1 | 0.55 | 0.55 | 0.55 | 0.1 |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Region | Pharmacy | Parapharmacy | Hospital | Cumlative Effect | |||||
|---|---|---|---|---|---|---|---|---|---|
| Total | Average | Total | Average | Total | Average | Total | Average | ||
| North | Valle d’Aosta | 0.001 | 0.011 | 0.004 | 0.023 | 0.001 | 0.009 | 0.002 | 0.014 |
| Veneto | 0.167 | 0.201 | 0.278 | 0.206 | 0.116 | 0.142 | 0.187 | 0.183 | |
| Piemonte | 0.421 | 0.383 | 0.660 | 0.370 | 0.204 | 0.188 | 0.428 | 0.314 | |
| Liguria | 0.119 | 0.287 | 0.239 | 0.356 | 0.019 | 0.046 | 0.126 | 0.230 | |
| Lombardia | 1.000 | 0.984 | 0.934 | 0.567 | 1.000 | 1.000 | 0.978 | 0.850 | |
| Trentino-Alto Adige | 0.007 | 0.014 | 0.024 | 0.029 | 0.010 | 0.019 | 0.014 | 0.020 | |
| Friuli Venezia Giulia | 0.034 | 0.112 | 0.093 | 0.187 | 0.017 | 0.055 | 0.048 | 0.118 | |
| Emilia-Romagna | 0.128 | 0.145 | 0.579 | 0.403 | 0.130 | 0.149 | 0.279 | 0.232 | |
| Centre | Toscana | 0.150 | 0.142 | 0.358 | 0.208 | 0.100 | 0.095 | 0.203 | 0.148 |
| Umbria | 0.014 | 0.044 | 0.074 | 0.150 | 0.011 | 0.037 | 0.033 | 0.077 | |
| Lazio | 0.725 | 0.768 | 1.000 | 0.654 | 0.361 | 0.388 | 0.695 | 0.603 | |
| Marche | 0.026 | 0.065 | 0.086 | 0.135 | 0.019 | 0.048 | 0.043 | 0.083 | |
| Abruzzo | 0.027 | 0.070 | 0.165 | 0.267 | 0.017 | 0.046 | 0.070 | 0.128 | |
| South | Basilicata | 0.005 | 0.014 | 0.067 | 0.121 | 0.006 | 0.017 | 0.026 | 0.051 |
| Calabria | 0.023 | 0.037 | 0.177 | 0.175 | 0.024 | 0.038 | 0.074 | 0.083 | |
| Campania | 0.552 | 1.000 | 0.895 | 1.000 | 0.323 | 0.595 | 0.590 | 0.865 | |
| Molise | 0.003 | 0.018 | 0.014 | 0.057 | 0.005 | 0.034 | 0.007 | 0.036 | |
| Puglia | 0.103 | 0.066 | 0.551 | 0.219 | 0.052 | 0.034 | 0.235 | 0.107 | |
| Sardegna | 0.026 | 0.035 | 0.200 | 0.167 | 0.015 | 0.021 | 0.080 | 0.074 | |
| Sicilia | 0.168 | 0.077 | 0.715 | 0.202 | 0.093 | 0.043 | 0.325 | 0.107 | |
| Region | Gini Index | ||||
|---|---|---|---|---|---|
| Pharmacy | Parapharmacy | Hospital | Cumulated | ||
| North | Valle d’Aosta | 0.921 | 0.986 | 0.878 | 0.908 |
| Veneto | 0.844 | 0.964 | 0.775 | 0.812 | |
| Piemonte | 0.973 | 0.988 | 0.903 | 0.937 | |
| Liguria | 0.970 | 0.986 | 0.899 | 0.954 | |
| Lombardia | 0.931 | 0.966 | 0.863 | 0.881 | |
| Trentino-Alto Adige | 0.957 | 0.992 | 0.934 | 0.945 | |
| Friuli Venezia Giulia | 0.901 | 0.980 | 0.837 | 0.888 | |
| Emilia-Romagna | 0.926 | 0.986 | 0.860 | 0.899 | |
| Centre | Toscana | 0.942 | 0.984 | 0.876 | 0.909 |
| Umbria | 0.918 | 0.986 | 0.854 | 0.904 | |
| Lazio | 0.966 | 0.974 | 0.898 | 0.927 | |
| Marche | 0.879 | 0.975 | 0.833 | 0.871 | |
| Abruzzo | 0.895 | 0.980 | 0.825 | 0.896 | |
| South | Basilicata | 0.950 | 0.988 | 0.908 | 0.953 |
| Calabria | 0.892 | 0.970 | 0.857 | 0.897 | |
| Campania | 0.952 | 0.970 | 0.885 | 0.913 | |
| Molise | 0.912 | 0.991 | 0.883 | 0.907 | |
| Puglia | 0.930 | 0.967 | 0.898 | 0.928 | |
| Sardegna | 0.964 | 0.983 | 0.925 | 0.956 | |
| Sicilia | 0.944 | 0.973 | 0.898 | 0.929 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Russo, D.D.; Milella, F.; Di Felice, G. Fairness in Healthcare Services for Italian Older People: A Convolution-Based Evaluation to Support Policy Decision Makers. Mathematics 2025, 13, 1448. https://doi.org/10.3390/math13091448
Russo DD, Milella F, Di Felice G. Fairness in Healthcare Services for Italian Older People: A Convolution-Based Evaluation to Support Policy Decision Makers. Mathematics. 2025; 13(9):1448. https://doi.org/10.3390/math13091448
Chicago/Turabian StyleRusso, Davide Donato, Frida Milella, and Giuseppe Di Felice. 2025. "Fairness in Healthcare Services for Italian Older People: A Convolution-Based Evaluation to Support Policy Decision Makers" Mathematics 13, no. 9: 1448. https://doi.org/10.3390/math13091448
APA StyleRusso, D. D., Milella, F., & Di Felice, G. (2025). Fairness in Healthcare Services for Italian Older People: A Convolution-Based Evaluation to Support Policy Decision Makers. Mathematics, 13(9), 1448. https://doi.org/10.3390/math13091448






