Numerical Solution of Nonlinear Quadratic Integral Equation of Hammerstein Type Based on Fixed-Point Scheme

Abstract

Existence of the solution for the nonlinear quadratic integral equation of the Hammerstein type in the Banach space BC(${\mathbb{R}}_{+}$) has been proved by using the technique of measure of noncompactness and fixed-point theorem. In this article, we obtain an approximate solution for the quadratic integral equation by using the Sinc method and the fixed-point technique. Moreover, the convergence of the numerical scheme for the solution of the integral equation is demonstrated by a theorem, and numerical experiments are presented to show the accuracy of the numerical scheme and guarantee the analytical results.

1. Introduction

In this paper, we illustrate a numerical method for solving the Hammerstein integral equation on the half-line in Banach space $BC\left({\mathbb{R}}_{+}\right).$

$$x\left(t\right)=g\left(t\right)+f(t,x\left(t\right)){\int }_0^{\infty }\phi (t,s)\rho (s,x\left(s\right))ds$$

(1)

where $g, f, \phi ,$ and $\rho$ are the known functions and x is the unknown function to be found in $BC\left({\mathbb{R}}_{+}\right)$, a space of all bounded continuous functions on ${\mathbb{R}}_{+}$.

Nonlinear quadratic integral equation of Hammerstein type (1) arises in many physical applications [1] and appears in solutions of initial and boundary value problems for ordinary differential equations. In semiconductor devices, wherein Poisson’s equation has to be solved in two adjacent domains, where one is bounded and the another is unbounded, integral Equation (1) plays a significant role. Several applications, for instance in vehicular traffic theory, queuing and biology theory [2], use nonlinear integral equations on the half-line. Moreover, in the Wiener-Hopf equation and radiative transfer theory [3], and neutron transport theory and kinetic theory of gases [4,5,6,7,8], this type of integral equations appears.

In the case of a bounded interval, this equation has the form

$$x\left(t\right)=g\left(t\right)+f(t,x\left(t\right)){\int }_a^b\phi (t,s)\rho (s,x\left(s\right))dst\in [a,b]$$

(2)

and if $f(t,x(t\left)\right)=1$, Equation (2) is as follows:

$$x\left(t\right)=g\left(t\right)+{\int }_a^b\phi (t,s)\rho (s,x\left(s\right))dst\in [a,b].$$

(3)

This equation arises as a reformulation of two-point boundary value problems with a certain nonlinear boundary condition [9,10]. Also, multidimensional analogues of Equation (3) appear as various reformulations of an elliptic partial differential equation with nonlinear boundary conditions [11,12].

Based on our knowledge, for integral Equation (2), there is no numerical investigation, but for some simplified models, there are some numerical approaches presented in some research papers, which we review here very briefly. The existence and approximation of solutions of (3) have been studied in [1]. In this paper, the solution of an integral equation on $[0,\infty )$ is approximated by finite approximation, which reduces to an integral equation on a bounded interval $[0,\beta ]$. In the case where solutions are unique, the solutions $x_{\beta }$ to the finite-section approximations converge uniformly to the solution x of the integral equation on $[0,\infty )$, under natural hypotheses on its kernel. Numerical discretization and linearization processes to approximate the solution of (3) are developed in [13].

In [14], projection methods are developed to approximate the solution of the nonlinear Hammerstein-type integral equation on the half-line by using the space of piecewise polynomials. In this research, the authors proved that the approximate and iterated approximate solutions in the Galerkin and collocation methods converge with the orders $\mathcal{O}\left(n^{-r}\right)$ and $\mathcal{O}\left(n^{-2r}\right)$, respectively, in the infinity norm, where $n^{-1}$ is the maximum norm of the partition and r denotes the order of the piecewise polynomial employed in the approximation. The discrete Galerkin method in [15] is employed to solve Fredholm–Hammerstein integral equations of the second kind. The method utilizes the radial basis functions to estimate the solution of integral equations.

There are several numerical methods for solving Hammerstein integral equations in finite intervals. In [16], a new collocation-type method is presented for the numerical solution of nonlinear integral equations of the Hammerstein type. In this research, the function $\rho$ is assumed to be nonlinear in x. Appropriate smoothness assumptions to be made on $g, \phi$ and $\rho$ will ensure that, in a suitable Banach space, the right-hand side of (3) defines a completely continuous operator acting on x. The collocation-type method combined with a degenerate kernel based on Daubechies wavelets is presented to develop a numerical solution to the nonlinear integral equations of the Hammerstein type in [17].

The Petrov–Galerkin method and the iterated Petrov–Galerkin method are used to approximate a solution for a class of Hammerstein equations in [18]. Also, they applied the sparsity advantage of wavelets to extend the proposed numerical method to the nonlinear Hammerstein equations. Nyström and degenerate kernel methods for approximating the solution of Fredholm integral equations of the second kind with a smooth kernel were introduced in [19]. By using interpolation at Gauss points, they showed that the solution derived by the proposed methods converges.

In [20], the solvability of a nonlinear quadratic integral equation of Hammerstein type (1) was discussed. Using the technique of measures of noncompactness, they proved that this equation has solutions on an unbounded interval, and also an asymptotic property of these solutions was derived. In this paper, our main goal is to develop a numerical technique to approximate a solution for Equation (1). For this, we apply the fixed-point iteration method to generate successive approximations, and in each iteration, we introduce and use Sinc quadrature, which has exponential error of convergence, to approximate the integral term.

The remainder of the paper is organized as follows. Section 2 outlines the theoretical background of the solution of integral Equation (1). Then, Sinc approximation is introduced in Section 3. The numerical strategy based on fixed-point iteration and its convergence are discussed in Section 4, and finally some numerical illustrations are presented in Section 5 to show the efficiency and applicability of the proposed numerical method.

2. Theoretical Background

In this section, we give a collection of Definitions and Theorems which will be used to verify the solvability of a nonlinear quadratic integral equation of Hammerstein type (1).

Let E be an infinite dimensional Banach space with norm $\parallel .\parallel$ and zero element $\theta$. Also, let $B(x,r)$ be the closed ball centered at x with radius r. The symbol $B_r$ stands for the ball $B(\theta ,r)$. If X is a subset of E, we write $\overline{X}$, conv X in order to denote the closure and convex closure of X, respectively. Finally, let us denote by $M_E$ the family of nonempty and bounded subsets of E and by $N_E$ its subfamily consisting of all relatively compact sets.

Definition 1.

A mapping $\mu :M_E⟶{\mathbb{R}}_{+}=[0,\infty )$ will be called a measure of noncompactness in the space E if it satisfies the following conditions:

(i) 

The family ker $\mu =\{X\in M_E:\mu \left(X\right)=0\}$ is nonempty and ker $\mu \subset N_E$;

(ii) 

$X\subseteq Y⟹\mu \left(X\right)\le \mu \left(Y\right)$;

(iii) 

$\mu \left(\overline{X}\right)=\mu \left(convX\right)=\mu \left(X\right)$;

(iv) 

$\mu (\lambda X+(1-\lambda \left)Y\right)⩽\lambda \mu \left(X\right)+(1-\lambda )\mu \left(Y\right)$ for $\lambda \in [0,1)$;

(v) 

If $\left(X_n\right)$ is a sequence of sets from $M_E$ such that $X_{n+1}\subset X_n$, ${\overline{X}}_n=X_n(n=1,2,3,\dots )$ and if ${\displaystyle \underset{n\to \infty }{lim}\mu \left(X_n\right)=0}$, then the intersection $X_{\infty }={\bigcap }_{n=1}^{\infty }{X}_n$ is nonempty;

(vi) 

$\mu (X\cup Y)=max\left\{\mu \right(X),\mu (Y\left)\right\}$.

The family ker μ described in $\left(1\right)$ is called the kernel of the measures of noncompactness μ.

A measure $\mu$ is said to be sublinear if it satisfies the following two conditions:

(vii) 

$\mu \left(\lambda X\right)=\left|\lambda \right|\mu \left(X\right)$ for $\lambda \in R$;

(viii) 

$\mu (X+Y)\le \mu \left(X\right)+\mu \left(Y\right)$.

Other facts concerning measures of noncompactness and their properties may be found in [21]. We will use the following fixed-point theorem due to Darbo [21,22].

Theorem 1.

Let Q be a nonempty bounded closed convex subset of the space E and let $G:Q\to Q$ be continuous such that $\mu \left(GX\right)\le k\mu \left(X\right)$ for any nonempty subset X of Q, where k is a constant, $k\in [0,\infty )$. Then, G has a fixed point in the set Q.

In what follows, we will work in the Banach space $BC\left({\mathbb{R}}_{+}\right)$ consisting of all real functions defined as continuous and bounded on ${\mathbb{R}}_{+}$. The space $BC\left({\mathbb{R}}_{+}\right)$ is equipped with the standard norm $\Vert x\Vert =sup\left\{\right|x\left(t\right)|:t\ge 0\}$.

Theorem 2.

Under the following conditions, Equation (1) has at least one solution $x=x\left(t\right)$ in the space $BC\left({\mathbb{R}}_{+}\right).$ Moreover, all solutions of Equation (1) belonging to the ball $B_{r_0}$ tend to zero at infinity uniformly with respect to the ball $B_{r_0}.$

Proof. 

Ref. [20]

The existence conditions of the solution are as follows:

(1)

Function $g:{\mathbb{R}}_{+}\to \mathbb{R}$ is continuous and $g\left(t\right)\to 0$ as $t\to \infty$.

(2)

Function $f:{\mathbb{R}}_{+}\times \mathbb{R}\to \mathbb{R}$ is continuous and the function $t\to f(t,0)$ belongs to the space $BC\left({\mathbb{R}}_{+}\right)$.

(3)

There exists a continuous function $m:{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ such that

$$\left|f\right(t,x)-f(t,y\left)\right|\le m\left(t\right)|x-y|$$

$t\in {\mathbb{R}}_{+}$ and $x,y\in \mathbb{R}$.

(4)

The function $\rho :{\mathbb{R}}_{+}\times \mathbb{R}\to \mathbb{R}$ is uniformly continuous on every rectangle of the form ${\mathbb{R}}_{+}\times [-\nu ,\nu ]$; moreover, there exists a continuous function $a:{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ and a continuous and nondecreasing function $b:{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ such that

$$\left|\rho \right(t,x\left)\right|\le a\left(t\right)b\left(\right|x\left|\right)$$

for $t\in {\mathbb{R}}_{+}$ and $x\in \mathbb{R}.$

(5)

The function $\phi :{\mathbb{R}}_{+}\times {\mathbb{R}}_{+}\to \mathbb{R}$ is continuous and there exist continuous functions $p,q:{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ such that functions $q\left(t\right)$ and $a\left(t\right)p\left(t\right)$ are integrable over ${\mathbb{R}}_{+}$ and the following inequality

$$\left|\phi \right(t,s\left)\right|\le p\left(t\right)q\left(s\right)$$

is satisfied for $t,s\in {\mathbb{R}}_{+}$. Moreover, we assume that $li{m}_{t\to \infty }p\left(t\right)=0$ and function $m\left(t\right)p\left(t\right)$ is bounded on the interval $R_{+}.$

(6)

The constants $F,M,P,Q$ are defined as follows:

$F=\sup \left[\right|f(t,0)|:t\ge 0]$;

$M=\sup \left[m\right(t\left)p\right(t):t\ge 0]$;

$P=\sup \left[p\right(t):t\ge 0]$;

$Q={\int }_0^{\infty }a\left(s\right)q\left(s\right)ds$.

These constants are finite.

(7)

The inequality $\Vert g\Vert +b\left(r\right)(MQr+FPQ)\le r$ has a positive solution $r_0$.

□

3. Sinc Method

The Sinc method is a powerful numerical technique often used in signal processing, interpolation, and approximation problems. In this section, we introduce the Sinc approximation and fixed-point method that have been used for approximating the solution of the nonlinear integral Equation (1). The Sinc function is defined on the real line $\mathbb{R}$ by

$$Sinc\left(x\right)=\left\{\begin{array}{cc}{\displaystyle \frac{sin\left(\pi x\right)}{\pi x}},\hfill & \hfill \mathrm{if}x\ne 0\\ 1,\hfill & \hfill \mathrm{if}x=0\end{array}\right.$$

(4)

The Sinc approximation for a function f defined on the real line $\mathbb{R}$ is given by

$$f\left(x\right)\approx \sum _{j=-M}^{N}f\left(jh\right)S(j,h)\left(x\right)$$

(5)

where $S(j,h)\left(x\right)$ is the jth Sinc function defined by

$$S(j,h)\left(x\right)={\displaystyle \frac{\sin \left[\left({\displaystyle \frac{\pi }{h}}\right)(x-jh)\right]}{{\displaystyle \frac{\pi }{h}}(x-jh)}}$$

with $h>0$.

Let ${\mathcal{D}}_d$ be a strip domain defined by ${\mathcal{D}}_d=\left\{\omega \in C\mid \left|Im\right(\omega \left)\right|<d\right\}$ for $d>0$. For a variable transformation $\psi \left(\xi \right)=e^{\xi }$, $\psi \left({\mathcal{D}}_d\right)=\left\{z=\psi \left(z\right),\xi \in {\mathcal{D}}_d\right\}$ denotes the image of ${\mathcal{D}}_d$ by the map $\psi$.

Theorem 3.

Assume that f is analytic in $\psi \left({\mathcal{D}}_d\right)$, and there exist positive constants K, α, and β such that

$$\left|f\left(z\right)\right|\le K{\displaystyle \frac{z^{\alpha -1}}{{(1+z^2)}^{(\alpha +\beta )/2}}}$$

for all $z\in \psi \left({\mathcal{D}}_d\right)$. Let $\mu =min\left\{\alpha ,\beta \right\}$, $h=\sqrt{{\displaystyle \frac{2\pi d}{\mu n}}}$ and let M and N be defined as

$$\left\{\begin{array}{cc}M=n,N=\lceil {\displaystyle \frac{\alpha n}{\beta }}\rceil ,\hfill & \mu =\alpha ;\hfill \\ N=n,M=\lceil {\displaystyle \frac{\beta n}{\alpha }}\rceil ,\hfill & \mu =\beta ;\hfill \end{array}\right.$$

Then, there exists a constant C, independent of n, such that

$$\left|{\int }_0^{\infty }f\left(t\right)dt-h\sum _{k=-M}^{N}f\left(\psi \left(kh\right)\right){\psi }^{\prime }\left(kh\right)\right|\le C{e}^{-\sqrt{2\pi d\mu n}}$$

where

$$C={\displaystyle \frac{2K}{\mu }}\left\{{\displaystyle \frac{2}{(1-e^{\sqrt{2\pi d\mu }}){\left(\cos \left(d\right)\right)}^{(\alpha +\beta )/2}}}+1\right\}.$$

Proof. 

[23]

To construct numerical quadrature on the interval $[0,\infty )$, which is used in this paper, we consider the conformal map $\varphi \left(z\right)=\log \left(z\right).$ This map carries the interval $(0,\infty )$ onto the interval $(-\infty ,+\infty )$. The function $z=\psi \left(\xi \right)={\varphi }^{-1}\left(\xi \right)=e^{\xi }$ is the inverse map of $\xi =\varphi \left(z\right).$

For $h>0$, the Sinc points $z_k\in [0,\infty )$ are defined by $z_k=e^{kh},$$k=0,\pm 1,\pm 2,\pm 3,\dots$ Then, the explicit formula for quadrature on $\Gamma =[0,\infty )$ will be

$${\int }_0^{\infty }G\left(x\right)dx\approx h\sum _{k=-M}^N{e}^{kh}G\left(e^{kh}\right)$$

(6)

which has been discussed thoroughly in [24,25]. If we replace the Sinc quadrature (6) in Equation (1), then

$$x\left(t\right)\simeq g\left(t\right)+f(t,x\left(t\right))\left[h\sum _{k=-M}^N{e}^{kh}\phi (t,e^{kh})\rho (e^{kh},x\left(e^{kh}\right))\right].$$

(7)

In order to approximate solution $x\left(t\right)$ in (7), we apply the fixed-point iteration method, which yields the sequence of successive approximations

$$x_i\left(t\right)\simeq g\left(t\right)+f(t,x_{i-1}\left(t\right))\left[h\sum _{k=-M}^N{e}^{kh}\phi (t,e^{kh})\rho (e^{kh},x_{i-1}\left(e^{kh}\right))\right],\mathrm{for}i=1,2,\dots$$

(8)

for the solution of integral Equation (1), and to start the successive iterations, we select $x_0\left(t\right)=g\left(t\right)$ as the initial function. □

4. Convergence Analysis

To discuss the convergence of the fixed-point scheme (8), define an integral operator H on the space $BC\left(R_{+}\right)$ by

$$\left(Hx\right)\left(t\right)=g\left(t\right)+f(t,x\left(t\right)){\int }_0^{\infty }\phi (t,s)\rho (s,x\left(s\right))ds$$

where $t⩾0.$ In view of the conditions (1), (2), and (4)–(6) from Theorem 2, the operator H is continuous in the interval $R_{+}$, and also this is continuous on the ball $B_{r_0}$; see [20].

Theorem 4.

Under the assumptions of Theorem 2, the iterative numerical technique (8) is convergent provided $x_0\left(t\right)$ is close enough to the fixed point of the operator H and $MQb\left(r_0\right)<1.$

Proof. 

Fix $\epsilon >0$ and take $x,x_0\in B_{r_0}$ such that x is a fixed point of the operator H and $x_0$ is an initial function of the successive technique based on the fixed-point method, and also $\parallel x_0-x\parallel \le \epsilon$. Then, for arbitrarily fixed $t\in R_{+}$, we get

$$\begin{array}{ccc}\hfill \parallel x_{i+1}-x\parallel & =& \underset{t\in R_{+}}{sup}|\left(H{x}_i\right)\left(t\right)-\left(Hx\right)\left(t\right)|\hfill \\ & \le & \left|f(t,x_i\left(t\right)){\int }_0^{\infty }\phi (t,s)\rho (s,x_i\left(s\right))ds-f(t,x\left(t\right)){\int }_0^{\infty }\phi (t,s)\rho (s,x_i\left(s\right))ds\right|\hfill \\ & +& \left|f(t,x\left(t\right)){\int }_0^{\infty }\phi (t,s)\rho (s,x_i\left(s\right))ds-f(t,x\left(t\right)){\int }_0^{\infty }\phi (t,s)\rho (s,x\left(s\right))ds\right|\hfill \\ & \le & \left|f(t,x_i\left(t\right))-f(t,x\left(t\right))\right|{\int }_0^{\infty }\left|\phi (t,s)\right||\rho (s,x_i\left(s\right))|ds\hfill \\ & +& \left|f(t,x(t\left)\right)\right|{\int }_0^{\infty }\left|\phi (t,s)\right||\rho (s,x_i\left(s\right))-\rho (s,x\left(s\right))|ds\hfill \end{array}$$

regarding the assumptions of Theorem 2, we have

$$\begin{array}{ccc}\hfill \parallel x_{i+1}-x\parallel & \le & m\left(t\right)|x_i\left(t\right)-x\left(t\right)|{\int }_0^{\infty }p\left(t\right)q\left(s\right)a\left(s\right)b\left(\right|x\left(s\right)\left|\right)ds\hfill \\ & +& \left[\left|f\right(t,x\left(t\right))-f(t,0\left)\right|+\left|f\right(t,0\left)\right|\right]{\int }_0^{\infty }p\left(t\right)q\left(s\right)|\rho (s,x_i)\left(s\right)-\rho (s,x\left(s\right))|ds\hfill \\ & \le & MQb\left(r_0\right)|x_i\left(t\right)-x\left(t\right)|+[M{r}_0+F]P{\omega }_{r_0}\left(\epsilon \right){\int }_0^{\infty }q\left(s\right)ds\hfill \end{array}$$

where

$${\omega }_{r_0}\left(\epsilon \right)=sup\left[\right|\rho (s,x_i)-\rho (s,x)|:s\ge 0,|x_i-x|\le \epsilon ].$$

Condition $\left(4\right)$ from Theorem 2 implies that ${\omega }_{r_0}\left(\epsilon \right)\to 0$ as $\epsilon \to 0$; then,

$$\parallel x_{i+1}-x\parallel \le MQb\left(r_0\right)\parallel x_i-x\parallel \le \dots \le {\left(MQb\left(r_0\right)\right)}^i\parallel x_0-x\parallel$$

and this completes the proof. □

5. Numerical Examples

In this section, we employ the proposed numerical method to obtain an approximate solution of some Hammerstein integral equations. Before proposing some examples, we define a relative error as $E\left(t\right)=\left|{\displaystyle \frac{x\left(t\right)-x_i\left(t\right)}{x\left(t\right)}}\right|$ where $x\left(t\right)$ and $x_i\left(t\right)$ are the exact and ith approximate solution, respectively. If the exact solution is not available, we set a very large number for i to compute the ith solution and use it as the reference solution and exact solution. We used MATLAB (https://www.mathworks.com/products/matlab.html, accessed on 21 April 2025) with an 11th Gen Intel Core i7 processor and 16 GB RAM to perform all computations.

Example 1.

Consider the nonlinear integral equation

$$x\left(t\right)=t{e}^{-4t}+(tx\left(t\right)+{\displaystyle \frac{t}{16+t^2}}){\int }_0^{\infty }{\displaystyle \frac{t^2{e}^{-s}}{1+t^2}}\sqrt{\left|x\right(s\left)\right|}ds.$$

Regarding Equation (1), we have $g\left(t\right)=t{e}^{-4t}$, $f(t,x)=tx+{\displaystyle \frac{t}{16+t^2}}$, $\phi (t,s)={\displaystyle \frac{t{e}^{-s}}{1+t^2}}$ and $\rho (t,x)=t\sqrt{\left|x\right|}.$

In [20], the authors showed that all assumptions of Theorem 2.3 are satisfied, and Assumption (7) from Theorem 2 leads to the inequality

$${\displaystyle \frac{1}{4e}}+\sqrt{r}(r+{\displaystyle \frac{1}{16}})\le r$$

where $r_0={\displaystyle \frac{1}{4}}$ is a solution of it.

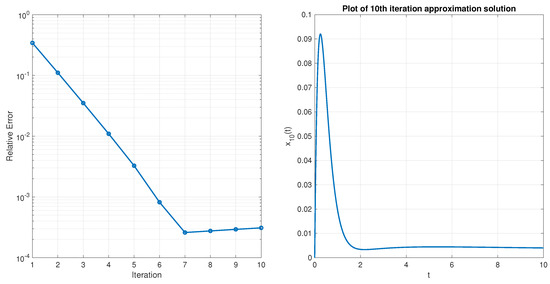
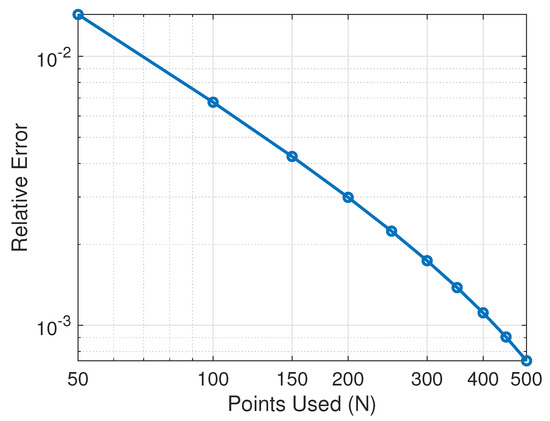
In this example, since the exact solution is not available, we set $N=1000$, $h={\displaystyle \frac{\pi }{\sqrt{N}}}$ and $i=100$ iterations to evaluate the reference solution. Relative errors for Example 1 in different iterations for $N=500$, $h={\displaystyle \frac{\pi }{\sqrt{N}}}$ are depicted on the left in Figure 1, and the approximate solution after ten iterations is presented on the right in Figure 1. It is easy to verify that the solution of the equation belongs to the ball $B_{\frac{1}{4}}$ and tends to zero at infinity uniformly with respect to the ball $B_{\frac{1}{4}}.$ It is easy to derive that by increasing the number of iterations, the relative errors decrease. To show how the number of used points (N) affects accuracy, relative errors are depicted for the 10th iteration for different values of N in Figure 2. From this, it is obvious that, by increasing used points, relative errors decrease.

Figure 1. Relative errors for Example 1 in different iterations (Left) and approximate solution after ten iterations (Right).

Figure 2. Relative errors for Example 1 in 10th iteration for different values of N.

Example 2.

Consider the following nonlinear integral equation:

$$x\left(t\right)={\displaystyle \frac{e^{-\frac{3}{4}t}}{1+t}}+(2\sqrt{t}x\left(t\right)+{\displaystyle \frac{12t}{5+t^3}}){\int }_0^{\infty }{\displaystyle \frac{st{e}^{-2s}}{1+t^2}}sin\left(s\right)\sqrt{\left|x\right(s\left)\right|}ds$$

where $g\left(t\right)={\displaystyle \frac{e^{-\frac{3}{4}t}}{1+t}}$, $f(t,x)=(2\sqrt{t}x\left(t\right)+{\displaystyle \frac{12t}{5+t^3}})$, $\phi (t,s)={\displaystyle \frac{st}{1+t^2}}{e}^{-2s}sin\left(s\right)$ and $\rho (t,x)=\sqrt{\left|x\right(s\left)\right|}$.

This equation satisfies the conditions of Theorem 2, because $g\left(t\right)$ is a continuous function, $li{m}_{t\to \infty }g\left(t\right)=0$, f is a continuous function, the function $t⟶f(t,0)={\displaystyle \frac{12t}{5+t^3}}$ belongs to the space $BC\left({\mathbb{R}}_{+}\right)$, and f satisfies the condition

$$\left|f\right(t,x)-f(t,y\left)\right|⩽m\left(t\right)|x-y|$$

by $m\left(t\right)=2\sqrt{t}$ for $t\in {\mathbb{R}}_{+}$ and $x\in \mathbb{R}.$

Function $\rho :{\mathbb{R}}_{+}\times \mathbb{R}⟶\mathbb{R}$ is continuous such that

$$\left|\rho \right(t,x\left)\right|\le a\left(t\right)b\left(\right|x\left|\right)$$

where $a\left(t\right)=1$ is a continuous and positive function and $b\left(\right|x\left|\right)=\sqrt{\left|x\right|}$ is a continuous and nondecreasing function for $t\in {\mathbb{R}}_{+}$ and $x\in \mathbb{R}.$

Function φ is continuous and there exist continuous functions $p\left(t\right)={\displaystyle \frac{t}{1+t^2}}$ and $q\left(s\right)=e^{-2s}s\sin \left(s\right)$ such that

$$\left|\phi \right(t,s\left)\right|\le p\left(t\right)q\left(s\right)$$

for $t,s\in {\mathbb{R}}_{+}.$ Moreover $li{m}_{t\to \infty }p\left(t\right)=0$ and the function $m\left(t\right)p\left(t\right)$ is bounded on the interval ${\mathbb{R}}_{+}$ and functions $q\left(t\right)$ and $a\left(t\right)q\left(t\right)$ are integrable over ${\mathbb{R}}_{+}.$

Assumption (6) from Theorem 2 leads to $F=2.2$, $M=1.15$, $P=0.5$, $\parallel g\parallel \hspace{0.17em}=1$ and $Q=0.16$; so, we have the inequality

$$1+\sqrt{r}(0.184r+0.176)\le r$$

where $r_0=1.6$ is a positive solution of the above inequality.

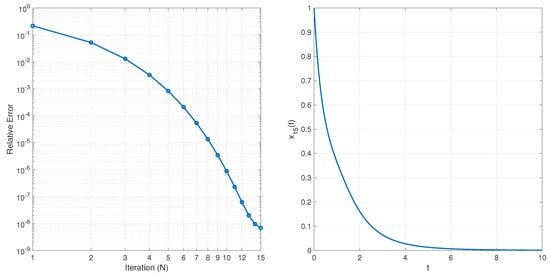
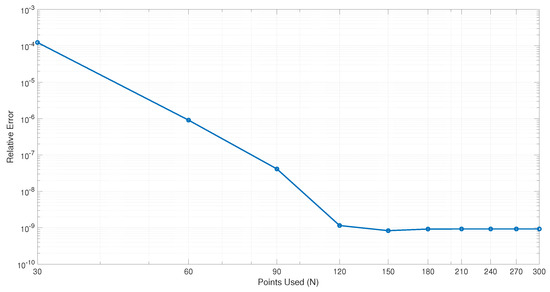
In this example, since the exact solution is not available, we set $N=1000$, $h={\displaystyle \frac{\pi }{\sqrt{N}}}$, and $i=100$ iterations to evaluate the reference solution. Relative errors for Example 2 in different iterations for $N=100$ and $h={\displaystyle \frac{\pi }{\sqrt{N}}}$ are depicted on the left of Figure 3, and the approximate solution after fifteen iterations is presented on the right of Figure 3. It is easy to verify that the solution of the equation belongs to the ball $B_{1.6}$ and tends to zero at infinity uniformly with respect to the ball $B_{1.6}.$ It is easy to derive that by increasing the number of iterations, relative errors decrease. To show how the number of used points (N) affects accuracy, relative errors are depicted for the 15th iteration for different values of N in Figure 4. From this, it is obvious that by increasing used points, the relative errors decease.

Figure 3. Relative errors for Example 2 in different iterations (Left) and approximate solution after fifteen iterations (Right).

Figure 4. Relative errors for Example 2 in 15th iteration for different values of N.

Example 3.

In this example, we apply the fixed-point iterative method for the nonlinear Hammerstein integral equation

$$x\left(t\right)=g\left(t\right)+(4x\left(t\right)+{\displaystyle \frac{\sqrt{t}}{1+t}}){\int }_0^{\infty }{\displaystyle \frac{t{s}^4{e}^{-5s}}{1+t^2}}\left|x\left(s\right)\right|ds.$$

The above integral equation has the exact solution $x\left(t\right)={\displaystyle \frac{1}{30t+35}}$. In this case, we obtain $g\left(t\right)$ by substituting the exact solution in the above integral equation and it is easy to show that $g\left(t\right)$ is a continuous function such that $li{m}_{t\to \infty }g\left(t\right)=0$. Also, $f(t,x)=(4x\left(t\right)+{\displaystyle \frac{\sqrt{t}}{1+t}})$ is a continuous function and the function $t⟶f(t,0)={\displaystyle \frac{\sqrt{t}}{1+t}}$ belongs to the space $BC\left({\mathbb{R}}_{+}\right)$ and satisfies the condition

$$\left|f\right(t,x)-f(t,y\left)\right|⩽m\left(t\right)|x-y|$$

where $m\left(t\right)=4$ for $t\in {\mathbb{R}}_{+}$ and $x,y\in \mathbb{R}$. The function $\rho :{\mathbb{R}}_{+}\times \mathbb{R}⟶\mathbb{R}$ is a continuous function such that

$$\left|\rho \right(t,x\left)\right|\le a\left(t\right)b\left(\right|x\left|\right),$$

where $a\left(t\right)=1$ is a continuous and positive function and $b\left(\right|x\left|\right)=\left|x\right|$ is a continuous and nondecreasing function for $t\in {\mathbb{R}}_{+}$ and $x\in \mathbb{R}.$ $\phi (t,s)={\displaystyle \frac{t}{1+t^2}}{e}^{-5s}{s}^4$ is a continuous function and there exist continuous functions $p,q:{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$ such that

$$\left|\phi \right(t,s\left)\right|\le p\left(t\right)q\left(s\right)$$

for $t,s\in {\mathbb{R}}_{+}$ where $p\left(t\right)={\displaystyle \frac{t}{1+t^2}}$ and $q\left(s\right)=e^{-5s}{s}^4$. Moreover, $li{m}_{t\to \infty }p\left(t\right)=0$ and the function $m\left(t\right)p\left(t\right)$ is bounded on the interval ${\mathbb{R}}_{+}$ and functions $q\left(t\right)$ and $a\left(t\right)q\left(t\right)$ are integrable over ${\mathbb{R}}_{+}$.

It is easy to check that $F=0.5$, $M=2$, $P=0.5$, $\Vert g\Vert =0.03$ and $Q={\int }_0^{\infty }{s}^4{e}^{-5s}ds=0.00768$. Now, in view of the inequality $\Vert g\Vert +b\left(r\right)(MQr+FPQ)\le r$, we obtain

$$0.03+r(0.01536r+0.00192)\le r,$$

where $r_0=0.03$ is a positive solution of the above inequality.

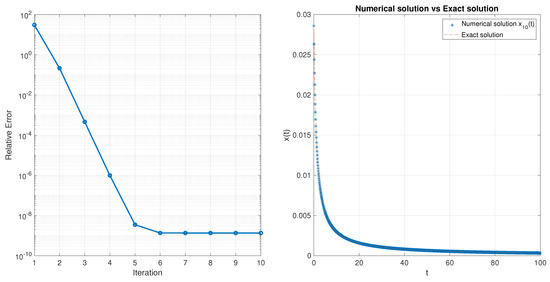
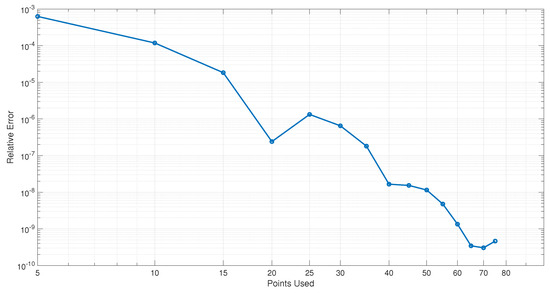
Relative errors for Example 3 in different iterations for $N=60$, $h={\displaystyle \frac{\pi }{\sqrt{N}}}$ are depicted on the left of Figure 5, and the approximate solution after ten iterations vs. the exact solution are presented on the right of Figure 5. It is easy to verify that the solution of the equation belongs to the ball $B_{0.03}$ and tends to zero at infinity uniformly with respect to the ball $B_{0.03}.$ It is easy to derive that by increasing the number of iterations, relative errors decrease. To show how the number of used points (N) affects accuracy, relative errors are depicted for the 10th iteration for different values of N in Figure 6. From this, it is obvious that by increasing used points, relative errors decease.

Figure 5. Relative errors for Example 3 in different iterations (Left) and approximate solution after ten iterations vs. exact solution (Right).

Figure 6. Relative errors for Example 3 in 10th iteration for different values of N.

Example 4.

We consider the following nonlinear Hammerstein integral equation

$$x\left(t\right)=g\left(t\right)+(x\left(t\right)+{\displaystyle \frac{t^{\frac{2}{3}}}{8+t^3}}){\int }_0^{\infty }{\displaystyle \frac{t^2}{\sqrt{s}(1+t^3)(1+s)}}\left|x\left(s\right)\right|ds$$

where $f(t,x)=x\left(t\right)+{\displaystyle \frac{t^{\frac{2}{3}}}{8+t^3}}$, $\phi (t,s)={\displaystyle \frac{t}{\sqrt{s}(1+t^3)(1+s)}}$ and $\rho (t,x)=t\left|x\right(t\left)\right|.$

In this example, the exact solution is $x\left(t\right)={\displaystyle \frac{t}{(90t^3+75)}}$. $g\left(t\right)$ is obtained by substituting the exact solution in the above integral equation, and we can deduce that g is continuous and $g\left(t\right)⟶0$ as $t⟶\infty$. Function f is continuous and satisfies the following condition

$$\left|f\right(t,x)-f(t,y\left)\right|\le m\left(t\right)|x-y|$$

for $x,y\in \mathbb{R}$ and $t\in {\mathbb{R}}_{+}$, where $m\left(t\right)=1$ is a continuous and non-negative function and moreover function $t⟶f(t,0)={\displaystyle \frac{t^{\frac{2}{3}}}{8+t^3}}$ belongs to the space $BC\left({\mathbb{R}}_{+}\right)$. The function $\rho (t,x)$ is uniformly continuous and also

$$\left|\rho \right(t,x\left)\right|\le a\left(t\right)b\left(\right|x\left|\right),$$

where $a\left(t\right)=t$ is a continuous function and $b\left(\right|x\left|\right)=\left|x\right|$ is a continuous and nondecreasing function for $t\in {\mathbb{R}}_{+},x\in \mathbb{R}.$

Also, φ is a continuous function and there exist continuous and positive functions $p,q$; moreover, functions $q\left(t\right)$ and $a\left(t\right)q\left(t\right)$ are integrable over ${\mathbb{R}}_{+}$ such that

$$\left|\phi \right(t,s\left)\right|\le p\left(t\right)q\left(s\right)$$

with $p\left(t\right)={\displaystyle \frac{t}{1+t^3}}$ and $q\left(s\right)={\displaystyle \frac{1}{\sqrt{s}(1+s)}}$ and $t,s\in {\mathbb{R}}_{+}$.

Moreover, $li{m}_{t\to \infty }p\left(t\right)=0$ and the function $m\left(t\right)p\left(t\right)={\displaystyle \frac{t}{1+t^3}}$ is bounded on the interval ${\mathbb{R}}_{+}$, and also, $F=0.12$, $M=0.52$, $P=0.52$, and $Q={\int }_0^{\infty }a\left(s\right)q\left(s\right)ds={\int }_0^{\infty }{\displaystyle \frac{1}{\sqrt{s}(1+s)}}ds=\pi$. According to condition (7) from Theorem 2, we have

$$0.0064+r(1.6328r+0.195936)⩽r$$

where $r_0=0.008$ is a solution from the above inequality.

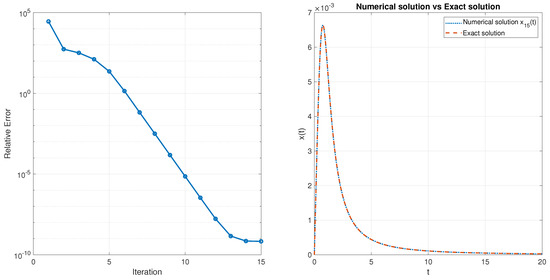
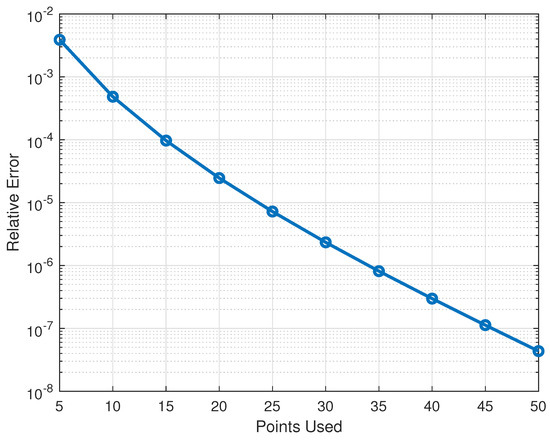
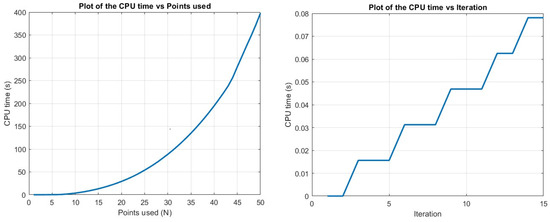
Relative errors for Example 4 in different iterations for $N=70$, $h={\displaystyle \frac{\pi }{\sqrt{N}}}$ are depicted on the of left Figure 7, and the approximate solution after fifteen iterations vs. the exact solution is presented on the right of Figure 7. It is easy to verify that the solution of the equation belongs to the ball $B_{0.008}$ and tends to zero at infinity uniformly with respect to the ball $B_{0.008}.$ It is easy to derive that by increasing the number of iterations, relative errors decrease. To show how the number of used points (N) affects accuracy, relative errors are depicted for the 10th iteration for different values of N in Figure 8. From this, it is obvious that by increasing used points, relative errors decease. Also, to show the computational complexity of the proposed algorithm, the CPU times are depicted in Figure 9 for different numbers of iterations and Sinc points used.

Figure 7. Relative errors for Example 4 in different iterations (Left) and approximate solution after fifteen iterations vs. exact solution (Right).

Figure 8. Relative errors for Example 4 in 10th iteration for different values of N.

Figure 9. CPU times in seconds for Example 4 for different numbers of iterations (Right) and Sinc points used (Left).

Example 5.

The conductor-like screening model for real solvents is an important method for thermodynamic equilibria investigation in fluid and liquid mixtures. The molecular interactions in solvent are described by $P_S\left(\sigma \right)$ and the chemical potential of the surface segments ${\mu }_S\left(\sigma \right)$ is evaluated by

$$\begin{array}{c}\hfill {\mu }_S\left(\sigma \right)=-RTln\left[{\int }_a^b{P}_S\left(\tilde{\sigma }\right)\exp \left({\displaystyle \frac{-ϵ(\sigma ,\tilde{\sigma })+{\mu }_S\left(\tilde{\sigma }\right)}{RT}}\right)d\tilde{\sigma }\right],\end{array}$$

(9)

where R is the gas constant, T the temperature, and the term $ϵ(\sigma ,\tilde{\sigma })$ in Equation (9) denotes the interaction energy expression for the segments with screening charge density σ and $\tilde{\sigma }$, respectively, where σ and $\tilde{\sigma }$ are the polarization charges of two interacting surface segments.

We can rewrite Equation (9) as

$$-{\displaystyle \frac{{\mu }_S\left(\sigma \right)}{RT}}=ln\left[{\int }_a^b{P}_S\left(\tilde{\sigma }\right)\Omega (\sigma ,\tilde{\sigma })\exp \left({\displaystyle \frac{{\mu }_S\left(\tilde{\sigma }\right)}{RT}}\right)d\tilde{\sigma }\right]$$

where

$$\Omega (\sigma ,\tilde{\sigma })=\exp \left(-{\displaystyle \frac{ϵ(\sigma ,\tilde{\sigma })}{RT}}\right).$$

Now, by substituting

$$f\left(\sigma \right)=\exp \left(-{\displaystyle \frac{{\mu }_S\left(\sigma \right)}{RT}}\right)$$

we have

$$f\left(\sigma \right)={\int }_a^b{\displaystyle \frac{P_S\left(\tilde{\sigma }\right)\Omega (\sigma ,\tilde{\sigma })}{f\left(\tilde{\sigma }\right)}}d\tilde{\sigma },$$

(10)

which is a nonlinear Hammerstein integral equation. Since there is no analytical method to compute the exact solution of this equation, we apply the proposed numerical method in this paper to evaluate an approximate solution.

We let

$$P_S\left(\sigma \right)=e^{-{(5\sigma +2.5)}^2}+{\displaystyle \frac{1}{25{\sigma }^2+1}}+{\displaystyle \frac{{\left(\sin (5\sigma +2.5)\right)}^2}{{(5\sigma -2.5)}^4+1}}+q\left(5\sigma \right),$$

(11)

for $\sigma \in [-2,2)$ as a synthetic σ-profile and

$$q\left(\sigma \right)=\left\{\begin{array}{cc}-(\sigma -7)(\sigma -9),\hfill & 7\le \sigma <9;\hfill \\ 0,\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

In this example, since the exact solution is not available, we set $N=200$, $h={\displaystyle \frac{\pi }{\sqrt{N}}}$, and $i=200$ iterations to evaluate the reference solution. To improve the convergence rate of the fixed-point iteration method, in this example we employ the following iteration formula:

$$f_{n+1}\left(\sigma \right)={\displaystyle \frac{1}{2}}{f}_n\left(\sigma \right)+{\displaystyle \frac{h}{2}}\sum _{k=-N}^N{\displaystyle \frac{P_S\left(\widetilde{{\sigma }_k}\right)\exp (-{(\sigma +\widetilde{{\sigma }_k})}^2)}{{\varphi }^{\prime }\left(\widetilde{{\sigma }_k}\right)f_n\left(\widetilde{{\sigma }_k}\right)}}$$

where $\varphi \left(x\right)=ln\left({\displaystyle \frac{x+3}{3-x}}\right)$ and we select the initial function as any positive function.

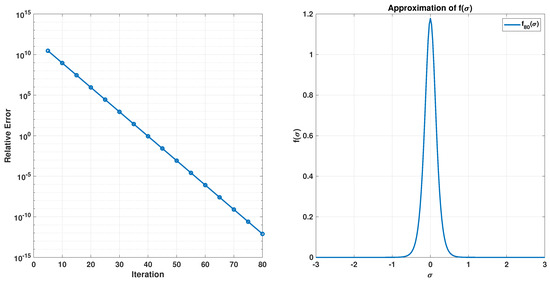
Relative errors for Example 5 in different iterations for $N=100$, $h={\displaystyle \frac{\pi }{\sqrt{N}}}$ are depicted on the left of Figure 10, and the approximate solution after eighty iterations is presented on the right of Figure 10.

Figure 10. Relative errors for Example 5 in different iterations (Left) and approximate solution (Right).

6. Conclusions

In this work, we investigate a numerical method for solving Hammerstein integral equations on the half-line. A numerical method for finding an approximate solution is constructed by using the Sinc method and the successive approximation method based on a fixed point. Moreover, the convergence of the numerical scheme for the solution of the integral equation is demonstrated by a theorem, and numerical experiments are presented to show the accuracy of the numerical scheme and guarantee the analytical results. Also, we evaluate convergence based on the number of iterations and the number of used Sinc points separately. In both cases, the figures confirm that by increasing number of iterations or number of used Sinc points, a very fast decrease in relative errors occurs.