A Characterization of Three-Dimensional Convex Polytopes with Five Pairwise Antipodal Vertices

Abstract

Concerning the antipodality properties of finite sets, we focus on convex polytopes in ${\mathbb{R}}^3$ with less than $2^3$ vertices and characterize convex polytopes with 5 vertices that are pairwise antipodal.

1. Introduction

Let A be a subset of ${\mathbb{R}}^n$ and $a,b\in A$. If there are distinct parallel hyperplanes $H_a$ and $H_b$ passing through a and b, respectively, such that A lies on the slab between $H_a$ and $H_b$, then a and b are said to be (affinely) antipodal. A classical result in Convex and Discrete Geometry states that the maximum cardinality of a subset A of ${\mathbb{R}}^n$, whose points are pairwise antipodal, is $2^n$, and that a subset A of ${\mathbb{R}}^n$ consisting of $2^n$ points that are pairwise antipodal is the set of vertices of an n-dimensional parallelotope; see [1,2]. It is clear that the vertices of an n-dimensional parallelotope in ${\mathbb{R}}^n$ are pairwise antipodal. Thus, the result mentioned above provides a characterization of n-dimensional convex polytopes with $2^n$ vertices that are pairwise antipodal. Since an n-dimensional convex polytope has at least $n+1$ vertices, it is natural to ask for characterizations of n-dimensional convex polytopes with m ($n+1\le m<2^n$) vertices that are pairwise antipodal. We refer to [3,4,5] for estimations of the cardinality of antipodal pairs of points in a finite subset in ${\mathbb{R}}^n$.

Note that antipodality has many applications in Convex and Discrete Geometry. For example, this notion is closely related to the study of Hadwiger’s covering conjecture, a long-standing open problem in Convex and Discrete Geometry.

Let K be a convex compact set whose affine dimension is at least 1. The closure, interior, relative interior, boundary, and relative boundary of K are denoted by $clK$, $intK$, $relintK$, $bdK$, and $relbdK$, respectively. Let $x\in relbdK$ and $u\in {\mathbb{R}}^n$ be a direction (i.e., a nonzero vector). The point x is said to be illuminated by u if there exists a positive number $\lambda$ such that

$$x+\lambda u\in relintK.$$

If each point of $relbdK$ can be illuminated by at least one of the directions $u_1,u_2,\dots ,u_m$, then we say that $relbdK$ is illuminated by $u_1,u_2,\dots ,u_m$.

Hadwiger’s covering conjecture asserts that each n-dimensional convex body (compact convex set whose affine dimension is n) that is not affinely equivalent to ${[0,1]}^n$ can be illuminated by at most $2^n-1$ directions. While the case for $n=2$ has been fully resolved (cf. [6]), this conjecture remains open for $n\ge 3$. For a deeper dive into this fascinating conjecture, we recommend the monographs cited in [7,8] and the survey articles in [9,10,11,12].

It is clear that two points in the boundary of a convex body K are antipodal if and only if they cannot be illuminated by the same direction (cf. Lemma 1 below). Therefore, the least number of directions needed to illuminate $bdK$ is not less than the maximum number of points in $bdK$ that are pairwise antipodal. Moreover, it is not difficult to verify that each n-dimensional convex polytope having at most $2^n$ vertices can be illuminated by at most $2^n$ directions, and $2^n$ directions are necessary only if such a convex polytope is an n-dimensional parallelotope (cf. [13]). To study the illumination of an n-dimensional convex polytope K with $2^n+m$ vertices when m is not too large, one can distinguish several cases based on the maximum number of vertices of such a polytope that are pairwise antipodal. Let $V_1$ be the set of vertices of K that is maximally pairwise antipodal and let $V_2$ be the set of the rest vertices. Then $K=conv(conv{V}_1\cup conv{V}_2)$, where $conv{V}_1$ is an n-dimensional convex polytope whose vertices are pairwise antipodal. For this purpose, it is also important to develop characterizations of n-dimensional convex polytopes with m vertices that are pairwise antipodal.

In this paper, we present a characterization of three-dimensional convex polytopes with five pairwise antipodal vertices. Such polytopes are special cases of n-dimensional polytopes with $n+2$ vertices. Combinatorial properties of this type of polytopes can be found in Section 6.1 of [14].

For each convex body K and each $(n-1)$-dimensional subspace H of ${\mathbb{R}}^n$, there exists a pair of distinct parallel supporting hyperplanes $H_1$ and $H_2$ of K that are parallel to H. The closed subset of ${\mathbb{R}}^n$ bounded by $H_1$ and $H_2$ is called a supporting slab of K.

For each positive integer m, set

$$\left[m\right]=\left\{i\in {\mathbb{Z}}^{+}|1\le i\le m\right\}.$$

Let $x,y\in {\mathbb{R}}^n$. The inner product of x and y is denoted as $⟨x|y⟩$. The line segment connecting x and y is denoted by $[x,y]$. I.e.,

$$[x,y]=\{\lambda x+(1-\lambda \left)y\right|\lambda \in [0,1]\}.$$

When $x\ne y$, set

$$\begin{array}{c}\hfill [x,y)=\left\{\lambda x+(1-\lambda )y|0<\lambda \le 1\right\},\\ \hfill (x,y]=\left\{\lambda x+(1-\lambda )y|0\le \lambda <1\right\},\\ \hfill (x,y)=\left\{\lambda x+(1-\lambda )y|0<\lambda <1\right\}.\end{array}$$

The following two results follow directly from the classical result in [1].

Corollary 1.

Let $Y\subseteq {\mathbb{R}}^n$ be an m-dimensional affine subset and $X\subseteq Y$. Then there are at most $2^m$ points in X that are pairwise antipodal.

Corollary 2.

If X is an m-dimensional convex polytope with $2^m$ vertices, then the $2^m$ vertices are pairwise antipodal in X if and only if X is an m-dimensional parallelotope.

Lemma 1.

Let $K\subseteq {\mathbb{R}}^n$ be a convex body. Two points $x,y\in bdK$ are not antipodal if and only if there is a direction that illuminates both x and y.

Proof. 

Lemma 5 in [15] shows that if x and y are not antipodal, then they can be illuminated by a direction.

Conversely, suppose that x and y are illuminated by a direction u. Then there exist ${\lambda }_1,{\lambda }_2>0$ such that $x+{\lambda }_{1}u,y+{\lambda }_{2}u\in intK$. Let $\lambda =min\{{\lambda }_1,{\lambda }_2\}$. Then $x+\lambda u,y+\lambda u\in intK$. Hence, $[x,y]$ is not a longest chord of K that is parallel to the line passing through x and y. By 3.1 in [16], x and y are not antipodal. □

The proof of the following result demonstrates the usage of antipodality in the study of Hadwiger’s covering conjecture.

Lemma 2.

Let K be an n-dimensional convex polytope in ${\mathbb{R}}^n$ having $2^n+1$ vertices. Then K can be illuminated by at most $2^n$ directions.

Proof. 

Since there are at most $2^n$ points in ${\mathbb{R}}^n$ that are pairwise antipodal (see [1] again), there exists a pair x and y of vertices of K that are not antipodal. By Lemma 1, x and y can be illuminated by a single direction, and the rest of the vertices can be illuminated by at most $2^n-1$ directions. □

The upper bound in Lemma 2 is not optimal if Hadwiger’s covering conjecture has an affirmative answer in ${\mathbb{R}}^n$: the boundary of such a polytope can be illuminated by at most $2^n-1$ directions. To improve the estimation in Lemma 2, one needs characterizations of convex polytopes in ${\mathbb{R}}^n$ having $2^n-1$ pairwise antipodal vertices.

Let K be a compact convex set whose affine dimension is at least 1 and $x\in relbdK$. Let

$$I(K,x)=\left\{u\in {\mathbb{R}}^n\setminus \left\{o\right\}|\exists \lambda >0\mathrm{s}.\mathrm{t}.x+\lambda u\in relintK\right\}.$$

I.e., $I(K,x)$ is the set of directions that can illuminate x as a relative boundary point of K. If K is a convex body in ${\mathbb{R}}^n$, then $I(K,x)$ is an open subset of ${\mathbb{R}}^n$; see [17].

Let $A\subseteq {\mathbb{R}}^n$ be a nonempty closed convex set and $x\in A$. The tangent cone of A at x is the closure of the cone generated by $A-\left\{x\right\}$—i.e.,

$$T_A\left(x\right)=cl\left\{d\in {\mathbb{R}}^n|\exists u\in A,\alpha \ge 0\mathrm{s}.\mathrm{t}.d=\alpha (u-x)\right\}.$$

As a closed convex set, $T_A\left(x\right)$ can also be described as an intersection of closed halfspaces (cf. page 65 in [18]).

Lemma 3.

Let K be a convex body in ${\mathbb{R}}^n$ and $x\in bdK$. Then

$$I(K,x)=int{T}_K\left(x\right)\hspace{1em}and\hspace{1em}clI(K,x)=T_K\left(x\right).$$

Proof. 

For any $d\in I(K,x)$, there exists $\lambda >0$ such that $x+\lambda d\in intK$. Let $u=x+\lambda d$. Then $u\in K$ and

$$d={\displaystyle \frac{1}{\lambda }}(u-x)\in T_K\left(x\right).$$

Thus, $I(K,x)\subseteq T_K\left(x\right)$ and therefore $clI(K,x)\subseteq T_K\left(x\right)$.

Suppose that $d=\alpha (u-x)$ where $u\in K$ and $\alpha \ge 0$. We claim that $d\in clI(K,x)$. If d is the origin o, then, for any $v\in I(K,x)$ and any positive integer k, $(1/k)v$ is also a direction in $I(K,x)$ and $(1/k)v\to o$ as $k\to \infty$. Thus, $d\in clI(K,x)$. Now, assume that $d\ne o$. If $u\in intK$, then obviously $d\in I(K,x)$. Otherwise, $u\in bdK$. For any positive integer k, there exists $u_k\in B(u,1/k)\cap intK$, where $B(u,1/k)$ is the closed Euclidean ball centered at u having radius $1/k$. Thus, $d_k=\alpha (u_k-x)\in I(K,x)$ and $d_k\to d$ as $k\to \infty$. Hence, $d\in clI(K,x)$. It follows that

$$\left\{d\in {\mathbb{R}}^n|\exists u\in K,\alpha \ge 0\mathrm{s}.\mathrm{t}.d=\alpha (u-x)\right\}\subseteq clI(K,x).$$

Therefore, $T_K\left(x\right)\subseteq clI(K,x)$. Thus, $clI(K,x)=T_K\left(x\right)$. Since $I(K,x)$ is open, we have (cf. Theorem 2.38 in [19])

$$int{T}_K\left(x\right)=int(clI(K,x))=intI(K,x)=I(K,x).$$

The proof is complete. □

We end this section with the following lemma.

Lemma 4.

Let $K\subseteq {\mathbb{R}}^n$ be a convex body and $x_1,x_2\in bdK$. Then $x_2$ can be illuminated by a direction in $I(K,x_1)$ if and only if $(I(K,x_1)+x_2)\cap K\ne \varnothing$.

Proof. 

If there exists a direction $u\in I(K,x_1)$ such that u illuminates $x_2$, then there exists $\lambda >0$ such that $x_2+\lambda u\in intK$. Clearly, $\lambda u\in I(K,x_1)$. Thus, $(I(K,x_1)+x_2)\cap K\ne \varnothing$.

Conversely, assume that $(I(K,x_1)+x_2)\cap K\ne \varnothing$. Let c be a fixed point in $intK$. There exists $u\in I(K,x_1)$ such that $u+x_2\in K$. Since $I(K,x_1)$ is open, there exists $\gamma >0$ such that the closed Euclidean ball $B(u,\gamma )$ centered at u having radius $\gamma$ is contained in $I(K,x_1)$. Let v be a point in $[u+x_2,c]\cap intK$ such that $\left|\right|v-(u+x_2)\left|\right|<\gamma$. Then,

$$v-x_2=u+(v-(u+x_2))\in I(K,x_1)\hspace{1em}\mathrm{and}\hspace{1em}v=x_2+(v-x_2)\in intK.$$

I.e., $x_2$ is illuminated by a direction in $I(K,x_1)$. □

2. The Convex Hull of the Union of a Simplex and a Singleton

Throughout this section, $S\subseteq {\mathbb{R}}^n$ is an n-simplex with $x_0,x_1,\cdots ,x_n$ as vertices and

$$C=conv\left\{x_i|i\in \left[n\right]\right\}.$$

For each $j\in \left[n\right]\cup \left\{0\right\}$, let

$$H_j=aff(\left\{x_i|i\in \left[n\right]\cup \left\{0\right\}\right\}\setminus \left\{x_j\right\})$$

and $e_j$ be the unit vector in ${(H_j-H_j)}^{\perp }$ such that $⟨x_j|e_j⟩>⟨x|e_j⟩,\forall x\in H_j$. Clearly, $⟨·|e_j⟩$ is constant on $H_j$. Let $H_j^{+}$ be the open halfspace bounded by $H_j$ that contains $x_j$ and let $H_j^{-}$ be the other open halfspace bounded by $H_j$. Obviously,

$$H_i^{+}=\left\{x\in {\mathbb{R}}^n|⟨x|e_i⟩>⟨x_0|e_i⟩\right\},\forall i\in \left[n\right].$$

Let y be a point in $H_0^{-}$ and $K_y=conv(\left\{y\right\}\cup S)$. One can easily verify that both $x_0$ and y are vertices of $K_y$.

We have the following characterizations of $I(S,x_0)$ and its closure.

Lemma 5.

We have

$$I(S,x_0)=\left\{x\in {\mathbb{R}}^n|⟨x|e_i⟩>0,\forall i\in \left[n\right]\right\}$$

and

$$clI(S,x_0)=\left\{x\in {\mathbb{R}}^n|⟨x|e_i⟩\ge 0,\forall i\in \left[n\right]\right\}.$$

Proof. 

Note that

$$S=\left\{x\in {\mathbb{R}}^n|⟨x|e_0⟩\ge ⟨x_1|e_0⟩,⟨x|e_i⟩\ge ⟨x_0|e_i⟩,\forall i\in \left[n\right]\right\}.$$

By Example 5.2.6(b) in [18],

$$T_S\left(x_0\right)=\left\{x\in {\mathbb{R}}^n|⟨x|e_i⟩\ge 0,\forall i\in \left[n\right]\right\}.$$

From Lemma 3, the desired equalities follow. □

We shall also use the following representation of $I(S,x)$.

Lemma 6.

We have

$$u\in I(S,x_0)\iff u+x_0\in \bigcap _{i\in \left[n\right]}{H}_i^{+}.$$

Proof. 

By Lemma 5, we have

$$\begin{array}{cc}\hfill u\in I(S,x_0)& \iff ⟨u|e_i⟩>0,\forall i\in \left[n\right]\hfill \\ \hfill & \iff ⟨u+x_0|e_i⟩>⟨x_0|e_i⟩,\forall i\in \left[n\right]\hfill \\ \hfill & \iff u+x_0\in \bigcap _{i\in \left[n\right]}{H}_i^{+}.\hfill \end{array}$$

The proof is complete. □

Lemma 7.

The following statements are equivalent:

1. 

$[x_0,y]\cap C\ne \varnothing$,

2. 

$I(S,x_0)=I(K_y,x_0)$.

Proof. 

1⇒2. Since $S\subseteq K_y$, we have $I(S,x_0)\subseteq I(K_y,x_0)$. If $I(K_y,x_0)⊈I(S,x_0)$, then there exists $u\in I(K_y,x_0)\setminus I(S,x_0)$. Since $I(K_y,x_0)$ is open, we may require further that $u\in I(K_y,x_0)\setminus clI(S,x_0)$. There exists $\lambda >0$ such that

$$x^{\prime }:=x_0+\lambda u\in int{K}_y.$$

Then

$$x_0+\gamma u\in int{K}_y,\forall \gamma \in (0,\lambda ).$$

Therefore we may assume, without loss of generality, that $x^{\prime }\in H_0^{+}$.

Since $u\notin clI(S,x_0)$, by Lemma 5, there exists $i\in \left[n\right]$ such that $⟨x_0+\lambda u|e_i⟩<⟨x_0|e_i⟩$. I.e., $x^{\prime }\notin H_i^{+}$. Without loss of generality, we may assume that $x^{\prime }\notin H_n^{+}$. By Theorem 3.13 in [19], there exist $x^{″}\in S$ and $\gamma \in [0,1]$ such that $x^{\prime }=\gamma y+(1-\gamma )x^{″}$. Since $x^{\prime }\notin S$ and $y\notin int{K}_y$, $\gamma \in (0,1)$. Then

$$\begin{array}{cc}\hfill ⟨x^{\prime }|e_n⟩& =\lambda ⟨y|e_n⟩+(1-\lambda )⟨x^{″}|e_n⟩\hfill \\ \hfill & \ge \lambda ⟨y|e_n⟩+(1-\lambda )⟨x_1|e_n⟩\hfill \\ \hfill & >\lambda ⟨y|e_n⟩+(1-\lambda )⟨x^{\prime }|e_n⟩.\hfill \end{array}$$

Thus, $⟨x_1|e_n⟩>⟨x^{\prime }|e_n⟩>⟨y|e_n⟩$. Since $y\in H_0^{-}$ and $[x_0,y]\cap C\ne \varnothing$, there exist $z\in C$ and $\eta >0$ such that $y=z+\eta (z-x_0)$. Since z is a convex combination of $x_1,\dots ,x_n$, we have

$$⟨z|e_n⟩\ge ⟨x_0|e_n⟩=⟨x_1|e_n⟩.$$

It follows that $⟨y|e_n⟩\ge ⟨x_1|e_n⟩$, a contradiction.

2⇒1. Clearly, $[x_0,y]\cap H_0$ is a singleton, namely, $\left\{h\right\}$. If $h\notin C$, then there exists $i\in \left[n\right]$ such that h is not in $H_i^{+}$. Assume, without loss of generality, that $i=1$. Since $h\in (x_0,y)$, there exists $\gamma \in (0,1)$ such that $h=\gamma y+(1-\gamma )x_0$. We have

$$⟨h|e_1⟩=\gamma ⟨y|e_1⟩+(1-\gamma )⟨x_0|e_1⟩<⟨x_0|e_1⟩.$$

Thus, $⟨y|e_1⟩<⟨x_0|e_1⟩$. Let $x^{″}$ be the point of intersection of $H_1$ and $[y,\left({\displaystyle \sum _{i=0}^n}{x}_i\right)/(n+1)]$. Then

$$x^{″}=x_0+x^{″}-x_0\in (int{K}_y)\setminus intS,$$

a contradiction to the assumption that $I(S,x_0)=I(K_y,x_0)$. □

Lemma 8.

Suppose that $relintC\cap [x_0,y]=\left\{c_0\right\}$ and $i\in \left[n\right]$. The following statements are equivalent:

1. 

The points $x_0$ and $x_i$ are antipodal in $K_y$.

2. 

$y\notin I(S,x_0)+x_i$.

Proof. 

It is clear that $c_0\in int{K}_y$. By Lemma 7, $I(S,x_0)=I(K_y,x_0)$. Take the case when $i=1$, for example.

1⇒2. Suppose the contrary that $y\in I(S,x_0)+x_1$. Since $I(S,x_0)+x_1$ is open (cf. [17]), there exists $\alpha >0$ such that

$$B(y,\alpha )\subset I(S,x_0)+x_1,$$

where $B(y,\alpha )$ is the closed ball centered at y having radius $\alpha$. Let $y^{\prime }$ be a point in $[c_0,y)\cap B(y,\alpha )$. Then $y^{\prime }\in int{K}_y$. Since

$$y^{\prime }\in I(S,x_0)+x_1=I(K_y,x_0)+x_1,$$

there exists a direction that illuminates $x_0$ and $x_1$ as boundary points of $K_y$ simultaneously, a contradiction to the fact that $x_0$ and $x_1$ are antipodal.

2⇒1. Since $c_0\in int{K}_y$, we have

$$y\in I(K_y,x_0)+x_0=I(S,x_0)+x_0.$$

Thus, $⟨y|e_i⟩>⟨x_0|e_i⟩$, $\forall i\in \left[n\right]$. By Lemma 4, it suffices to show that

$$(I(K_y,x_0)+x_1)\cap K_y=(I(S,x_0)+x_1)\cap K_y=\varnothing .$$

For any $z\in K_y$, there exist $s\in S$ and $\lambda \in [0,1]$ such that $z=\lambda s+(1-\lambda )y$. From $y\notin I(S,x_0)+x_1$, it follows that $⟨y|e_1⟩\le ⟨x_1|e_1⟩$. Actually, if $⟨y|e_1⟩>⟨x_1|e_1⟩$, then $⟨y|e_i⟩>⟨x_1|e_i⟩$ holds for all $i\in \left[n\right]$ because $⟨y|e_j⟩>⟨x_0|e_j⟩=⟨x_1|e_j⟩$, $j=2,\cdots ,n$. This implies that $y-x_1\in int{T}_S\left(x_0\right)=I(S,x_0)$, a contradiction. Hence,

$$⟨z|e_1⟩=\lambda ⟨s|e_1⟩+(1-\lambda )⟨y|e_1⟩\le \lambda ⟨x_1|e_1⟩+(1-\lambda )⟨x_1|e_1⟩=⟨x_1|e_1⟩.$$

By Lemmas 5 and 7,

$$I(K_y,x_0)+x_1=I(S,x_0)+x_1=\left\{x\in {\mathbb{R}}^n|⟨x|e_i⟩>⟨x_1|e_i⟩,\forall i\in \left[n\right]\right\}.$$

Thus, $(I(K_y,x_0)+x_1)\cap K_y=\varnothing$. □

Corollary 3.

If $relintC\cap [x_0,y]\ne \varnothing$, then, for each $i\in \left[n\right]$, $x_0$ and $x_i$ are antipodal in $K_y$ if and only if

$$y\notin \bigcup _{i\in \left[n\right]}\left(I(S,x_0)+x_i\right).$$

Results in this section have potential applications for characterizing antipodality of vertices of convex polytopes in high-dimensional spaces and can be directly applied to the three-dimensional case in the next section.

3. Main Results

Set

$$\begin{array}{cc}\hfill P=\{({\beta }_1,{\beta }_2,{\beta }_3)\mid & 0<{\beta }_1\le 1,0<{\beta }_2\le 1,{\beta }_1+{\beta }_2\ge 1,\hfill \\ \hfill & {\beta }_1+{\beta }_3\le 0,{\beta }_2+{\beta }_3\le 0,0\le {\beta }_1+{\beta }_2+{\beta }_3<1\},\hfill \end{array}$$

$$y_0=(0,1,0),y_1=(0,0,1),y_3=(0,0,0),\mathrm{and}{y}_4=(1,0,0).$$

Put

$$\mathcal{P}=\left\{conv\{y_0,y_1,y_2,y_3,y_4\}|y_2\in P\right\}.$$

For each $K\in \mathcal{P}$, let

$$I=\{1,2\},J=\{0,3,4\},C_1^{\prime }=conv\left\{y_i|i\in I\right\},\mathrm{and}{C}_2^{\prime }=conv\left\{y_j|j\in J\right\}.$$

Proposition 1.

Each member of $\mathcal{P}$ is a convex polytope with five pairwise antipodal vertices.

Proof. 

Suppose that $K=conv\left\{y_i|i\in \left[4\right]\cup \left\{0\right\}\right\}\in \mathcal{P}$. Note that

$$\begin{array}{c}{H}_0^{\prime }:=aff\{y_1,y_3,y_4\}=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_2=0\right\},\\ H_1^{\prime }:=aff\{y_0,y_3,y_4\}=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_3=0\right\},\\ H_3^{\prime }:=aff\{y_0,y_1,y_4\}=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1+{\beta }_2+{\beta }_3=0\right\},\end{array}$$

and

$$H_4^{\prime }:=aff\{y_0,y_1,y_3\}=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1=0\right\}.$$

Since ${\beta }_3\le -{\beta }_1<0$, $H_1^{\prime }+y_1$ and $H_1^{\prime }+y_2$ are parallel supporting hyperplanes of K passing through $y_1$ and $y_2$, respectively. Thus $y_1$ and $y_2$ are antipodal. From $0<{\beta }_1\le 1$ and $0<{\beta }_2\le 1$, it follows that $H_0^{\prime }$ and $H_0^{\prime }+y_0$, and $H_4^{\prime }$ and $H_4^{\prime }+y_4$ are two pairs of parallel supporting hyperplanes of K. Thus $y_0$, $y_3$, and $y_4$ are pairwise antipodal.

Let $y_2=({\alpha }_1,{\alpha }_2,{\alpha }_3)$ and $\left\{c\right\}=C_1^{\prime }\cap aff{C}_2^{\prime }$. There exists $\lambda \in (0,1)$ such that

$$c=(1-\lambda )y_1+\lambda y_2=(\lambda {\alpha }_1,\lambda {\alpha }_2,(1-\lambda )+\lambda {\alpha }_3).$$

Note that

$$relint{C}_2^{\prime }=\left\{({\beta }_1,{\beta }_2,0)|0<{\beta }_1<1,0<{\beta }_2<1,0<{\beta }_1+{\beta }_2<1\right\}.$$

Since $y_2\in P$, we have $0<\lambda {\alpha }_1<1$, $0<\lambda {\alpha }_2<1$, and

$$\lambda {\alpha }_1+\lambda {\alpha }_2+(1-\lambda )+\lambda {\alpha }_3=(1-\lambda )+\lambda ({\alpha }_1+{\alpha }_2+{\alpha }_3)<(1-\lambda )+\lambda =1.$$

From $c\in aff{C}_2^{\prime }=H_1^{\prime }$, it follows that $(1-\lambda )+\lambda {\alpha }_3=0$. Therefore, $\lambda {\alpha }_1+\lambda {\alpha }_2<1$, which shows that $c\in relint{C}_2^{\prime }$. Hence, $C_1^{\prime }\cap relint{C}_2^{\prime }\ne \varnothing$, which implies that

$$y_2\in P_1:=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1>0,{\beta }_2>0,{\beta }_3<0,{\beta }_1+{\beta }_2+{\beta }_3<1\right\}.$$

Consider the three-simplex $conv\{y_0,y_1,y_3,y_4\}$ in ${\mathbb{R}}^3$. Since

$$\begin{array}{c}aff\{y_1,y_0,y_3\}=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1=0\right\},\\ aff\{y_1,y_0,y_4\}=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1+{\beta }_2+{\beta }_3=1\right\},\\ aff\{y_1,y_3,y_4\}=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_2=0\right\},\end{array}$$

by viewing $y_1$ and $y_2$ as $x_0$ and y in Section 2, respectively, from Lemmas 6 and 7, it follows that

$$I(K,y_1)+y_1=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1>0,{\beta }_2>0,{\beta }_1+{\beta }_2+{\beta }_3<1\right\}.$$

Thus,

$$\begin{array}{c}I(K,y_1)+y_3=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1>0,{\beta }_2>0,{\beta }_1+{\beta }_2+{\beta }_3<0\right\},\\ I(K,y_1)+y_4=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1>1,{\beta }_2>0,{\beta }_1+{\beta }_2+{\beta }_3<1\right\},\\ I(K,y_1)+y_0=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1>0,{\beta }_2>1,{\beta }_1+{\beta }_2+{\beta }_3<1\right\}.\end{array}$$

Let

$$\begin{array}{c}{D}_1=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_2\le 0\right\},D_2=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1+{\beta }_2+{\beta }_3\ge 0\right\},\\ D_3=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1\le 0\right\},D_4=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_2\le 1\right\},\\ D_5=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1+{\beta }_2+{\beta }_3\ge 1\right\},\mathrm{and}{D}_6=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1\le 1\right\}.\end{array}$$

Then

$$\begin{array}{cc}\hfill {(I(K,y_1)+y_3)}^c& =D_1\cup D_2\cup D_3,\hfill \\ \hfill {(I(K,y_1)+y_4)}^c& =D_1\cup D_5\cup D_6,\hfill \\ \hfill {(I(K,y_1)+y_0)}^c& =D_3\cup D_4\cup D_5.\hfill \end{array}$$

It follows that

$$\begin{array}{cc}\hfill P_2:=& P_1\cap \bigcap _{j\in J}{(I(K,y_1)+y_j)}^c\hfill \\ \hfill =& P_1\cap (D_1\cup D_2\cup D_3)\cap (D_1\cup D_5\cup D_6)\cap (D_3\cup D_4\cup D_5)\hfill \\ \hfill =& (P_1\cap D_2)\cap (P_1\cap D_6)\cap (P_1\cap D_4)\hfill \\ \hfill =& \left\{({\beta }_1,{\beta }_2,{\beta }_3)|0<{\beta }_1\le 1,0<{\beta }_2\le 1,{\beta }_3<0,0\le {\beta }_1+{\beta }_2+{\beta }_3<1\right\}.\hfill \end{array}$$

Similarly, $conv\{y_0,y_2,y_3,y_4\}$ is a three-simplex in ${\mathbb{R}}^3$. View $y_2$ and $y_1$ as $x_0$ and y in Section 2, respectively. Since

$$\begin{array}{c}aff\{y_2,y_3,y_4\}=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\alpha }_3{\beta }_1-{\alpha }_1{\beta }_3=0\right\},\\ aff\{y_2,y_0,y_3\}=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\alpha }_3{\beta }_2-{\alpha }_2{\beta }_3=0\right\},\\ aff\{y_2,y_0,y_4\}=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\alpha }_3{\beta }_1+{\alpha }_3{\beta }_2+(1-{\alpha }_1-{\alpha }_2){\beta }_3={\alpha }_3\right\},\end{array}$$

by Lemmas 6 and 7, we have

$$\begin{array}{cc}\hfill I(K,y_2)+y_2=\left\{({\beta }_1,{\beta }_2,{\beta }_3)\right|& {\alpha }_3{\beta }_1-{\alpha }_1{\beta }_3<0,{\alpha }_3{\beta }_2-{\alpha }_2{\beta }_3<0,\hfill \\ \hfill & {\alpha }_3{\beta }_1+{\alpha }_3{\beta }_2+(1-{\alpha }_1-{\alpha }_2){\beta }_3>{\alpha }_3\}.\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill I(K,y_2)+y_3=\left\{({\beta }_1,{\beta }_2,{\beta }_3)\right|& {\alpha }_3{\beta }_1-{\alpha }_1{\beta }_3<0,{\alpha }_3{\beta }_2-{\alpha }_2{\beta }_3<0,\hfill \\ \hfill & {\alpha }_3{\beta }_1+{\alpha }_3{\beta }_2+(1-{\alpha }_1-{\alpha }_2){\beta }_3>0\},\hfill \\ \hfill I(K,y_2)+y_4=\left\{({\beta }_1,{\beta }_2,{\beta }_3)\right|& {\alpha }_3{\beta }_1-{\alpha }_1{\beta }_3<{\alpha }_3,{\alpha }_3{\beta }_2-{\alpha }_2{\beta }_3<0,\hfill \\ \hfill & {\alpha }_3{\beta }_1+{\alpha }_3{\beta }_2+(1-{\alpha }_1-{\alpha }_2){\beta }_3>{\alpha }_3\},\hfill \\ \hfill I(K,y_2)+y_0=\left\{({\beta }_1,{\beta }_2,{\beta }_3)\right|& {\alpha }_3{\beta }_1-{\alpha }_1{\beta }_3<0,{\alpha }_3{\beta }_2-{\alpha }_2{\beta }_3<{\alpha }_3,\hfill \\ \hfill & {\alpha }_3{\beta }_1+{\alpha }_3{\beta }_2+(1-{\alpha }_1-{\alpha }_2){\beta }_3>{\alpha }_3\}.\hfill \end{array}$$

Let

$$\begin{array}{cc}\hfill D_1^{\prime }& =\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\alpha }_3{\beta }_2-{\alpha }_2{\beta }_3\ge 0\right\},\hfill \\ \hfill D_2^{\prime }& =\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\alpha }_3{\beta }_1+{\alpha }_3{\beta }_2+(1-{\alpha }_1-{\alpha }_2){\beta }_3\le 0\right\},\hfill \\ \hfill D_3^{\prime }& =\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\alpha }_3{\beta }_1-{\alpha }_1{\beta }_3\ge 0\right\},\hfill \\ \hfill D_4^{\prime }& =\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\alpha }_3{\beta }_2-{\alpha }_2{\beta }_3\ge {\alpha }_3\right\},\hfill \\ \hfill D_5^{\prime }& =\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\alpha }_3{\beta }_1+{\alpha }_3{\beta }_2+(1-{\alpha }_1-{\alpha }_2){\beta }_3\le {\alpha }_3\right\},\hfill \\ \hfill D_6^{\prime }& =\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\alpha }_3{\beta }_1-{\alpha }_1{\beta }_3\ge {\alpha }_3\right\}.\hfill \end{array}$$

Then

$$\begin{array}{cc}\hfill {(I(K,y_2)+y_3)}^c& =D_1^{\prime }\cup D_2^{\prime }\cup D_3^{\prime },\hfill \\ \hfill {(I(K,y_2)+y_4)}^c& =D_1^{\prime }\cup D_5^{\prime }\cup D_6^{\prime },\hfill \\ \hfill {(I(K,y_2)+y_0)}^c& =D_3^{\prime }\cup D_4^{\prime }\cup D_5^{\prime }.\hfill \end{array}$$

Thus, $y_1\in {(I(K,y_2)+y_3)}^c$ if and only if

$$y_2\in P_3:=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1\le 0\mathrm{or}{\beta }_2\le 0\mathrm{or}{\beta }_1+{\beta }_2\ge 1\right\}.$$

Similarly, $y_1\in {(I(K,y_2)+y_4)}^c$ and $y_1\in {(I(K,y_2)+y_0)}^c$ are equivalent to

$$y_2\in P_4:=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_2\le 0\mathrm{or}{\beta }_1+{\beta }_2+{\beta }_3\ge 1\mathrm{or}{\beta }_1+{\beta }_3\le 0\right\}$$

and

$$y_2\in P_5:=\left\{({\beta }_1,{\beta }_2,{\beta }_3)|{\beta }_1\le 0\mathrm{or}{\beta }_2+{\beta }_3\le 0\mathrm{or}{\beta }_1+{\beta }_2+{\beta }_3\ge 1\right\},$$

respectively.

Since

$$\begin{array}{cccc}\hfill {\displaystyle \bigcap _{i\in \left[5\right]}}{P}_i& =& \left\{({\beta }_1,{\beta }_2,{\beta }_3)\right|\hfill & 0<{\beta }_1\le 1,0<{\beta }_2\le 1,{\beta }_3<0,{\beta }_1+{\beta }_2\ge 1,\hfill \\ & & & 0\le {\beta }_1+{\beta }_2+{\beta }_3<1\}\cap P_4\cap P_5\hfill \\ & =& \left\{({\beta }_1,{\beta }_2,{\beta }_3)\right|\hfill & 0<{\beta }_1\le 1,0<{\beta }_2\le 1,{\beta }_3<0,{\beta }_1+{\beta }_2\ge 1,\hfill \\ & & & {\beta }_1+{\beta }_3\le 0,0\le {\beta }_1+{\beta }_2+{\beta }_3<1\}\cap P_5\hfill \\ & =& \left\{({\beta }_1,{\beta }_2,{\beta }_3)\right|\hfill & 0<{\beta }_1\le 1,0<{\beta }_2\le 1,{\beta }_3<0,{\beta }_1+{\beta }_2\ge 1,\hfill \\ & & & {\beta }_1+{\beta }_3\le 0,{\beta }_2+{\beta }_3\le 0,0\le {\beta }_1+{\beta }_2+{\beta }_3<1\}\hfill \\ & =& P,\hfill \end{array}$$

from $y_2\in P$ it follows that

$$y_2\in \bigcap _{j\in J}{(I(K,y_1)+y_j)}^c\mathrm{and}{y}_1\in \bigcap _{j\in J}{(I(K,y_2)+y_j)}^c.$$

By Lemma 7 and Corollary 3, for each $i\in I$, $y_i$ and each point in $\left\{y_j|j\in J\right\}$ are antipodal. Hence, the vertices of K are pairwise antipodal. □

Remark 1.

In fact, $P=conv\left\{a_i\right|i\in \left[5\right]\}\setminus \{a_2,a_3,a_4\}$, where

$$a_1=({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}},-{\displaystyle \frac{1}{2}}),a_2=(1,0,-1),a_3=(1,1,-1),a_4=(0,1,-1),a_5=(1,1,-2),$$

see Figure 1.

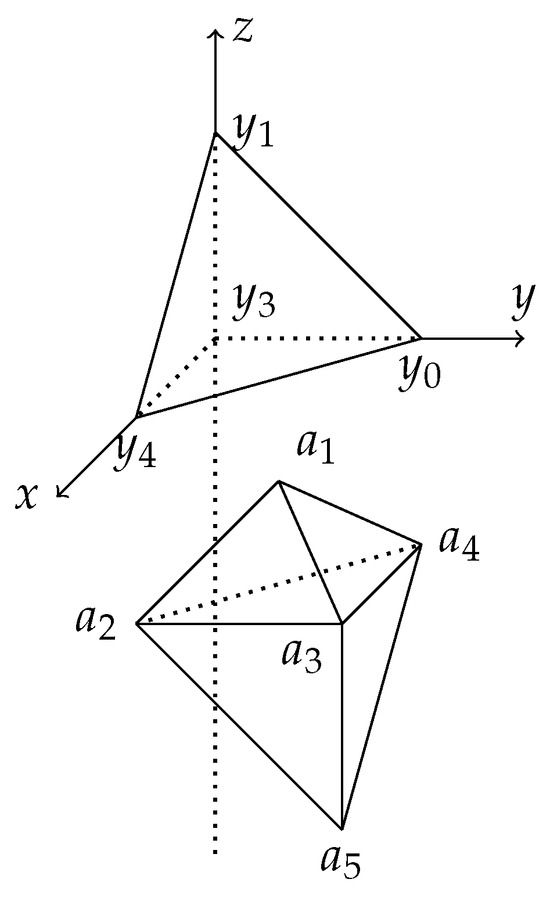
Figure 1. The range of $y_2$.

Theorem 1.

Let $K\subseteq {\mathbb{R}}^3$ be a three-dimensional convex polytope with five vertices. Then the vertices of K are pairwise antipodal if and only if one of the following conditions holds:

1. 

K is the convex hull of the union of a singleton and a parallelogram.

2. 

K is affinely equivalent to a member of $\mathcal{P}$.

Proof. 

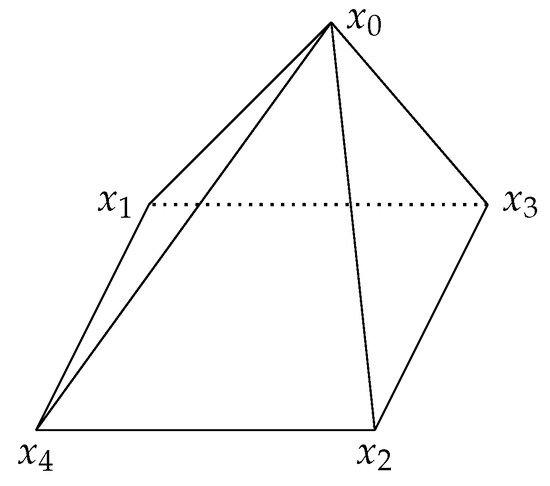
Suppose that $\left\{x_i|i\in \left[4\right]\cup \left\{0\right\}\right\}$ is the set of vertices of K. By Radon’s Lemma (cf. [20]), there are two possible cases.

Case 1. There exist two disjoint two-subsets I and J of $\left[4\right]\cup \left\{0\right\}$ such that

$$conv\left\{x_i|i\in I\right\}\cap conv\left\{x_j|j\in J\right\}\ne \varnothing .$$

Without loss of generality, we may assume that

$$\left[x_1,x_2\right]\cap \left[x_3,x_4\right]\ne \varnothing .$$

It follows that

$$relint\left[x_1,x_2\right]\cap relint\left[x_3,x_4\right]\ne \varnothing .$$

Let $C_0=conv\left\{x_i\right|i\in \left[4\right]\}$.

First, suppose that the vertices of K are pairwise antipodal. From Corollaries 1 and 2, it follows that $x_0\notin aff{C}_0$ and that $C_0$ is a parallelogram. Therefore, K is a convex hull of the union of a singleton and a parallelogram.

Conversely, suppose that K is the convex hull of the union of a singleton and a parallelogram. If $\left\{x_0\right\}$ is not the singleton, then $x_0$ is coplanar with three points from $\left\{x_i|i\in \left[4\right]\right\}$, which would show that $\left\{x_i|i\in \left[4\right]\cup \left\{0\right\}\right\}$ is contained in a plane, a contradiction. Thus, $K=conv\{x_0,C_0\}$, where $C_0$ is a parallelogram (see Figure 2). Note that

$$conv\left\{x_i|i\in \left[3\right]\cup \left\{0\right\}\right\}$$

is a three-simplex with vertices $x_0,x_1,x_2,x_3$. Let C, $H_j$, and $e_j$ be defined as in Section 2 for each $j\in \left[3\right]\cup \left\{0\right\}$. Since $C_0$ is a parallelogram and $x_0\notin aff{C}_0$, we have

$$C\subseteq C_0\mathrm{and}aff{C}_0=H_0.$$

Figure 2. K is the convex hull of the union of a singleton and a parallelogram.

Thus, $⟨x_0|e_0⟩>⟨u|e_0⟩$, $\forall u\in H_0$. For any $x\in K$, there exist ${\lambda }_0,{\lambda }_1,\cdots ,{\lambda }_4\ge 0$ such that

$$\sum _{i\in \left[4\right]\cup \left\{0\right\}}{\lambda }_i=1\mathrm{and}x=\sum _{i\in \left[4\right]\cup \left\{0\right\}}{\lambda }_i{x}_i.$$

Therefore,

$$⟨u|e_0⟩\le ⟨x|e_0⟩={\lambda }_0⟨x_0|e_0⟩+\sum _{i\in \left[4\right]}{\lambda }_i⟨x_i|e_0⟩\le ⟨x_0|e_0⟩,\forall u\in H_0.$$

This means that K lies in the supporting slab between parallel hyperplanes $H_0$ and

$$\left\{x\in {\mathbb{R}}^3|⟨x|e_0⟩=⟨x_0|e_0⟩\right\}.$$

Thus, $x_0$ and each point in $C_0$ are antipodal in K.

Since $C_0$ is parallelogram and $\left[x_1,x_2\right]\cap \left[x_3,x_4\right]\ne \varnothing$, we have

$$⟨x_4|e_2⟩=⟨x_1|e_2⟩+⟨x_4-x_1|e_2⟩=⟨x_3|e_2⟩+⟨x_2-x_3|e_2⟩=⟨x_2|e_2⟩.$$

For any $x\in K$, we have

$$⟨u|e_2⟩\le ⟨x|e_2⟩=\sum _{i\in \{2,4\}}{\lambda }_i⟨x_i|e_2⟩+\sum _{j\in \{0,1,3\}}{\lambda }_j⟨x_j|e_2⟩\le ⟨x_2|e_2⟩,\forall u\in H_2.$$

Hence, K lies in the supporting slab between parallel hyperplanes $H_2$ and

$$\left\{x\in {\mathbb{R}}^3|⟨x|e_2⟩=⟨x_2|e_2⟩\right\}.$$

Similarly,

$$⟨x_4|e_1⟩=⟨x_2|e_1⟩+⟨x_4-x_2|e_1⟩=⟨x_3|e_1⟩+⟨x_1-x_3|e_1⟩=⟨x_1|e_1⟩.$$

For any $x\in K$, we have

$$⟨u|e_1⟩\le ⟨x|e_1⟩=\sum _{i\in \{1,4\}}{\lambda }_i⟨x_i|e_1⟩+\sum _{j\in \{0,2,3\}}{\lambda }_j⟨x_j|e_1⟩\le ⟨x_1|e_1⟩,\forall u\in H_1.$$

Hence, K lies in the supporting slab between parallel hyperplanes $H_1$ and

$$\left\{x\in {\mathbb{R}}^3|⟨x|e_1⟩=⟨x_1|e_1⟩\right\}.$$

It follows that $x_1,x_2,x_3$, and $x_4$ are pairwise antipodal in K.

Case 2. There exists a two-subset I of $\left[4\right]\cup \left\{0\right\}$ such that $conv\left\{x_i|i\in I\right\}$ intersects

$$conv\left\{x_j|j\in (\left[4\right]\cup \left\{0\right\})\setminus I\right\}$$

in its relative interior. Without loss of generality, we may assume that

$$I=\{1,2\}\hspace{1em}\mathrm{and}\hspace{1em}J=\{0,3,4\}.$$

Set $C_1=conv\left\{x_i|i\in I\right\}$ and $C_2=conv\left\{x_j|j\in J\right\}$. Then $C_1\cap relint{C}_2\ne \varnothing$.

If K is affinely equivalent to a member of $\mathcal{P}$, then, by Proposition 1, K has pairwise antipodal vertices.

Suppose now that the vertices of K are pairwise antipodal. Let $\left\{c\right\}=C_1\cap relint{C}_2$. It is clear that $c\in intK$. Since $x_1,x_2\notin aff{C}_2$, $x_1$ and $x_2$ are strictly separated by the hyperplane determined by $aff{C}_2$. Then $x_1-x_3,x_4-x_3,x_0-x_3$ form a basis of ${\mathbb{R}}^3$. There exists a linear mapping $L:{\mathbb{R}}^3\to {\mathbb{R}}^3$ such that

$$L(x_1-x_3)=(0,0,1),L(x_4-x_3)=(1,0,0),L(x_0-x_3)=(0,1,0).$$

Clearly,

$$\begin{array}{cc}\hfill T:{\mathbb{R}}^3& \to {\mathbb{R}}^3\hfill \\ \hfill x& \mapsto L(x-x_3)=L\left(x\right)-L\left(x_3\right)\hfill \end{array}$$

is a non-singular affine transformation. Let $K^{\prime }$ be the convex polytope in ${\mathbb{R}}^3$ with the set of vertices

$$\left\{y_i\in {\mathbb{R}}^3|y_i=T\left(x_i\right),i\in \left[4\right]\cup \left\{0\right\}\right\},$$

where

$$y_0=(0,1,0),y_1=(0,0,1),y_3=(0,0,0),\hspace{1em}\mathrm{and}\hspace{1em}{y}_4=(1,0,0).$$

Let $C_1^{\prime }=conv\{y_1,y_2\}$ and $C_2^{\prime }=conv\{y_0,y_3,y_4\}$.

First, we claim that $K^{\prime }=T\left(K\right)$. For each $x\in K$, there exist ${\lambda }_0,{\lambda }_1,\cdots ,{\lambda }_4\ge 0$ such that

$$\sum _{i\in \left[4\right]\cup \left\{0\right\}}{\lambda }_i=1\hspace{1em}\mathrm{and}\hspace{1em}x=\sum _{i\in \left[4\right]\cup \left\{0\right\}}{\lambda }_i{x}_i.$$

Then,

$$T\left(x\right)=T\left(\sum _{i\in \left[4\right]\cup \left\{0\right\}}{\lambda }_i{x}_i\right)=\sum _{i\in \left[4\right]\cup \left\{0\right\}}{\lambda }_{i}T\left(x_i\right)=\sum _{i\in \left[4\right]\cup \left\{0\right\}}{\lambda }_i{y}_i\in K^{\prime }.$$

Thus, $T\left(K\right)\subseteq K^{\prime }$. Conversely, for any $y\in K^{\prime }$, there exist ${\mu }_0,{\mu }_1,\cdots ,{\mu }_4\ge 0$ such that

$$\sum _{j\in \left[4\right]\cup \left\{0\right\}}{\mu }_j=1\mathrm{and}y=\sum _{j\in \left[4\right]\cup \left\{0\right\}}{\mu }_j{y}_j.$$

Then

$$y=\sum _{j\in \left[4\right]\cup \left\{0\right\}}{\mu }_j{y}_j=\sum _{j\in \left[4\right]\cup \left\{0\right\}}{\mu }_{j}T\left(x_j\right)=T\left(\sum _{j\in \left[4\right]\cup \left\{0\right\}}{\mu }_j{x}_j\right)\in T\left(K\right),$$

which shows that $K^{\prime }\subseteq T\left(K\right)$. Hence, $K^{\prime }=T\left(K\right)$—i.e., K and $K^{\prime }$ are affinely equivalent.

In a similar way, we have

$$C_1^{\prime }=T\left(C_1\right)\hspace{1em}\mathrm{and}\hspace{1em}relint{C}_2^{\prime }=T(relint{C}_2).$$

Since $c\in C_1\cap relint{C}_2$, we have

$$T\left(c\right)\in T\left(C_1\right)\cap T(relint{C}_2)=C_1^{\prime }\cap relint{C}_2^{\prime },$$

which implies that $C_1^{\prime }\cap relint{C}_2^{\prime }\ne \varnothing$.

Let $P_1,P_2,\cdots ,P_5$ be defined as in the proof of Proposition 1. From $C_1^{\prime }\cap relint{C}_2^{\prime }\ne \varnothing$, it follows that $y_2\in P_1$. Since K is affinely equivalent to $K^{\prime }$ and the vertices of K are pairwise antipodal, the vertices $y_0,y_1,y_2,y_3,y_4$ of $K^{\prime }$ are also pairwise antipodal. By Corollary 3, we have

$$y_1\in \bigcap _{j\in J}{(I(K^{\prime },y_2)+y_j)}^c\hspace{1em}\mathrm{and}\hspace{1em}{y}_2\in \bigcap _{j\in J}{(I(K^{\prime },y_1)+y_j)}^c.$$

Hence

$$y_2\in \bigcap _{i\in \left[5\right]}{P}_i=P.$$

Therefore, $K^{\prime }$ is a member of $\mathcal{P}$. □