Elite Evolutionary Discrete Particle Swarm Optimization for Recommendation Systems
Abstract
1. Introduction
- This paper proposes EEDPSO, a novel RS optimization algorithm. We redesign velocity and position updates through discretization, integrate neighborhood search, and implement an elite evolution strategy to address PSO’s limitations while retaining its computational efficiency and global search capability. EEDPSO is specifically tailored for high-dimensional combinatorial optimization, enabling more effective solution space exploration.
- We enhance PSO by incorporating neighborhood search to mitigate premature convergence and integrate roulette-wheel selection to maintain exploration diversity. These improvements not only demonstrate strong experimental performance but also offer insights into hybrid metaheuristic optimization strategies.
- Comparative experiments on two datasets show that EEDPSO outperforms five metaheuristic algorithms in efficiency and accuracy. Ablation and controlled experiments further analyze its exploration–exploitation balance. Finally, we summarize its applications and potential optimizations, providing new research directions for future studies.
2. Literature Review
3. Recommendation Systems and Particle Swarm Optimization
3.1. Recommendation Systems
3.2. Particle Swarm Optimization in Recommendation Systems
- Position : The position information is defined as a list, where each element represents an item, and the length of the list corresponds to the length of the target recommendation list. This list serves as a recommendation list generated by the recommendation system.
- Velocity : Controls the update direction.
- Personal best (): Historically best recommendation list.
- Global best (): Best recommendation list among all particles.
4. Elite Evolutionary Discrete Particle Swarm Optimization
4.1. Motivation
4.2. Improvements
4.2.1. Neighborhood Search
4.2.2. Velocity Update Mechanism
| Algorithm 1: Update velocity. |
Input: Current velocity v; weight w; cognitive coefficient ; social coefficient ; Current solution ; personal best ; global best Output: Updated velocity
|
4.2.3. Position Update Mechanism
4.2.4. Exploration Maintenance Mechanism
| Algorithm 2: Roulette-wheel selection for position update. |
 |
| Algorithm 3: Elite evolutionary discrete particle swarm optimization. |
 |
5. Experiments and Analysis
- Genetic algorithm (GA) evolves a population of candidate solutions through selection, crossover, and mutation. It employs tournament selection (size = 3) to choose parents, followed by two-point crossover, where a random segment is swapped between parents. Random replacement mutation is applied, replacing each gene with a new item with a small probability.
- Differential evolution (DE) generates new solutions through differential mutation, where a base solution is perturbed using the difference between two other randomly selected solutions. The resulting trial solution undergoes binomial crossover, where each gene is replaced with a probability . The better solution between the trial and original is selected for the next generation.
- Simulated annealing (SA) explores the solution space by applying random perturbations to the current solution. If the new solution improves fitness, it is accepted. Otherwise, it is accepted probabilistically based on the Boltzmann function , allowing temporary acceptance of worse solutions to escape local optima. The temperature T decreases exponentially over iterations.
- Sine–cosine algorithm (SCA) updates solutions using a balance of exploitation (moving towards the best solution) and exploration (searching new areas). The update mechanism is guided by sine and cosine functions, ensuring smooth transitions between local and global search. Position correction mechanisms maintain valid solutions.
- Particle swarm optimization (PSO) models candidate solutions as particles that update positions based on velocity, which is influenced by inertia, personal best, and global best components. The updated position ensures uniqueness by removing duplicates.
- 6.
- FairGo (fair-graph-based recommendation) mitigates recommendation bias by learning fair user/item embeddings. It applies adversarial training to remove sensitive attribute signals (e.g., gender or age) from both user embeddings and their ego-centric graph structures. This ensures the recommendation process is fair while maintaining accuracy.
- 7.
- The PRM (personalized re-ranking model) refines initial recommendation lists using a transformer-based encoder with user-specific embeddings. By modeling mutual item interactions and user intent via self-attention, the PRM reorders the list to better match user preferences. It operates efficiently and supports large-scale deployment in real-time systems.
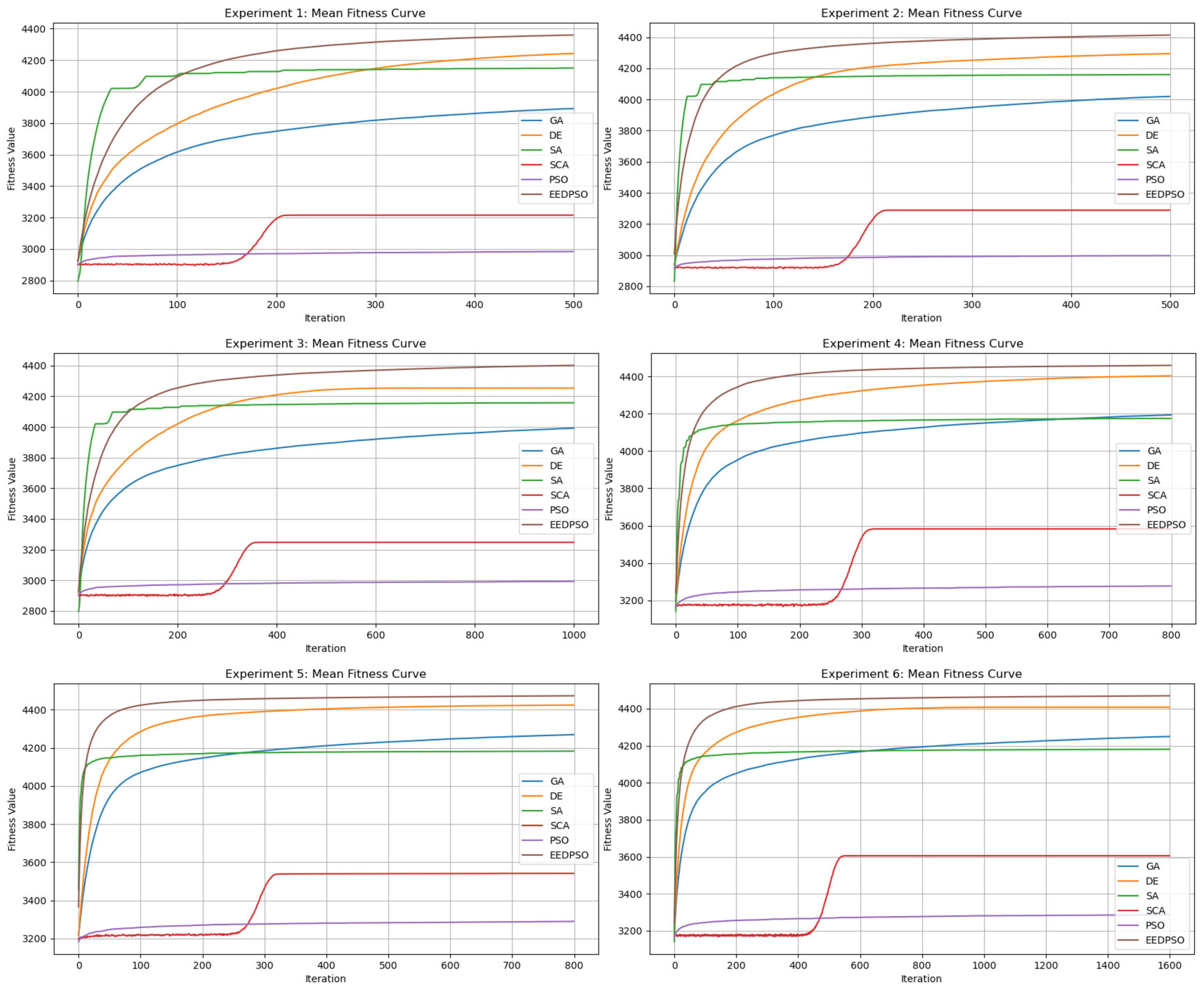
- Average Fitness Curve: This plot shows the evolution of the algorithm’s average fitness over time or generations, illustrating its convergence speed and improvement during later stages.
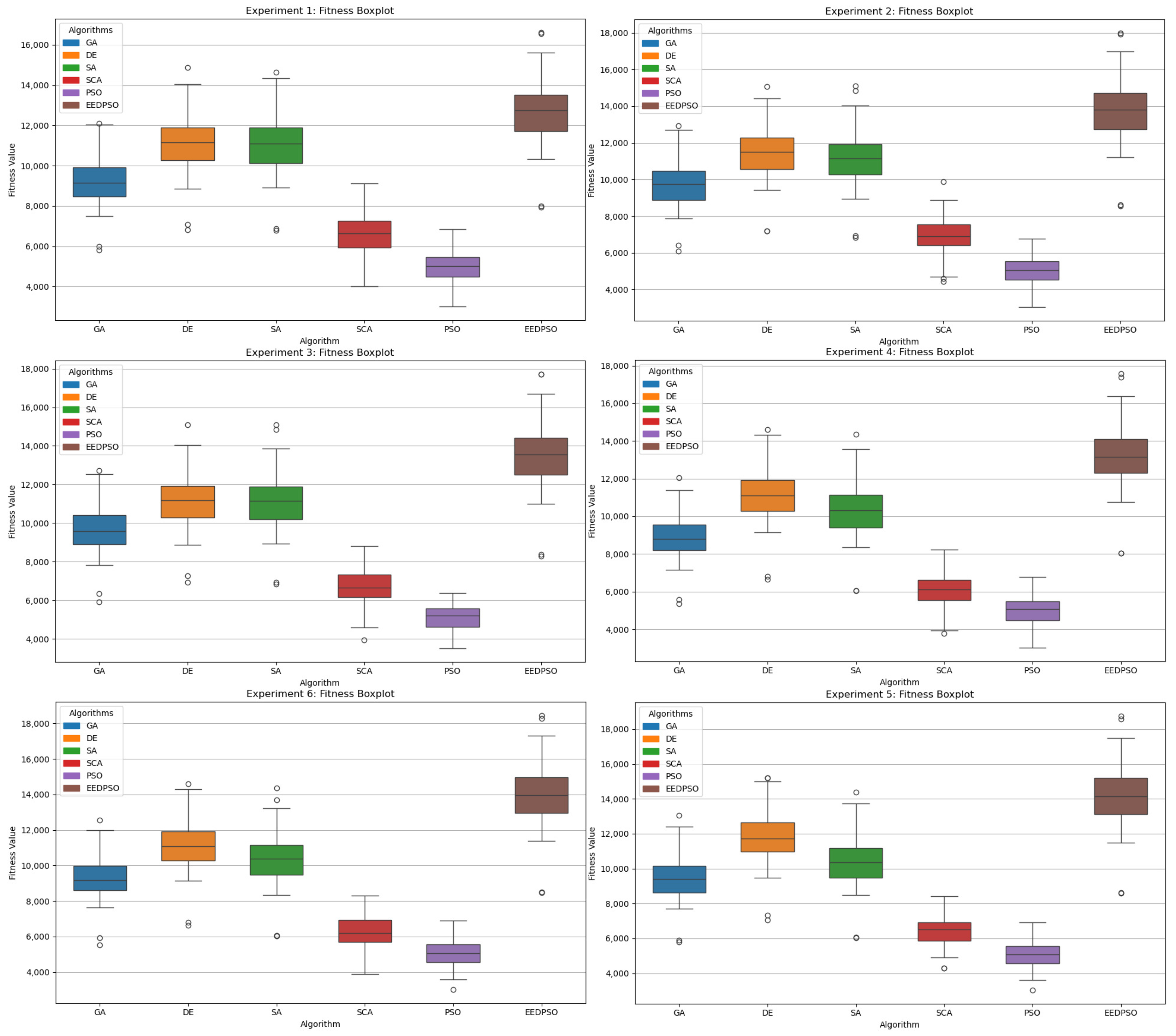
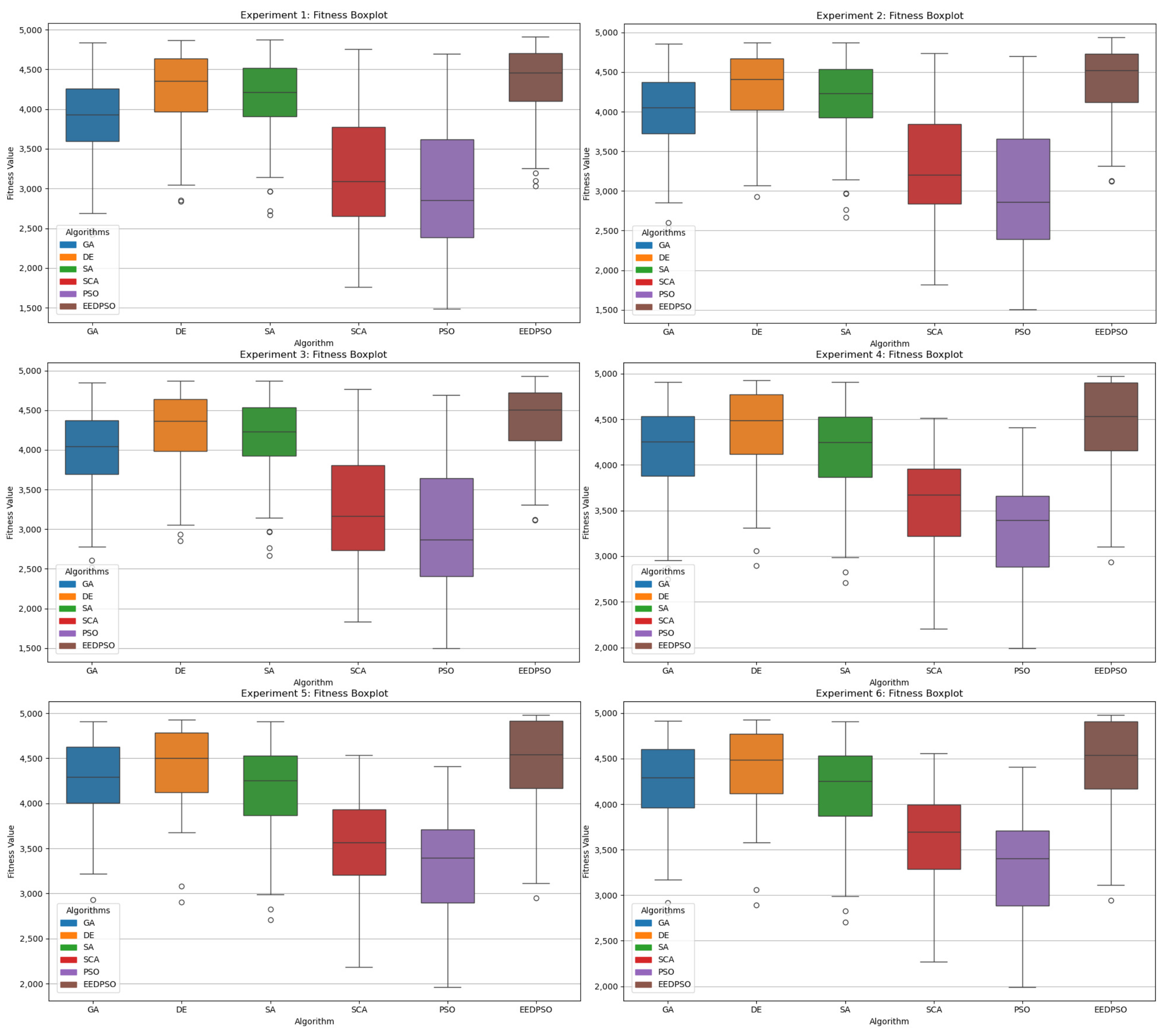
- Box Plot: The box plot displays the median, quartiles, and outliers of the final fitness distribution, reflecting the algorithm’s robustness across multiple runs and highlighting the best and worst solutions.
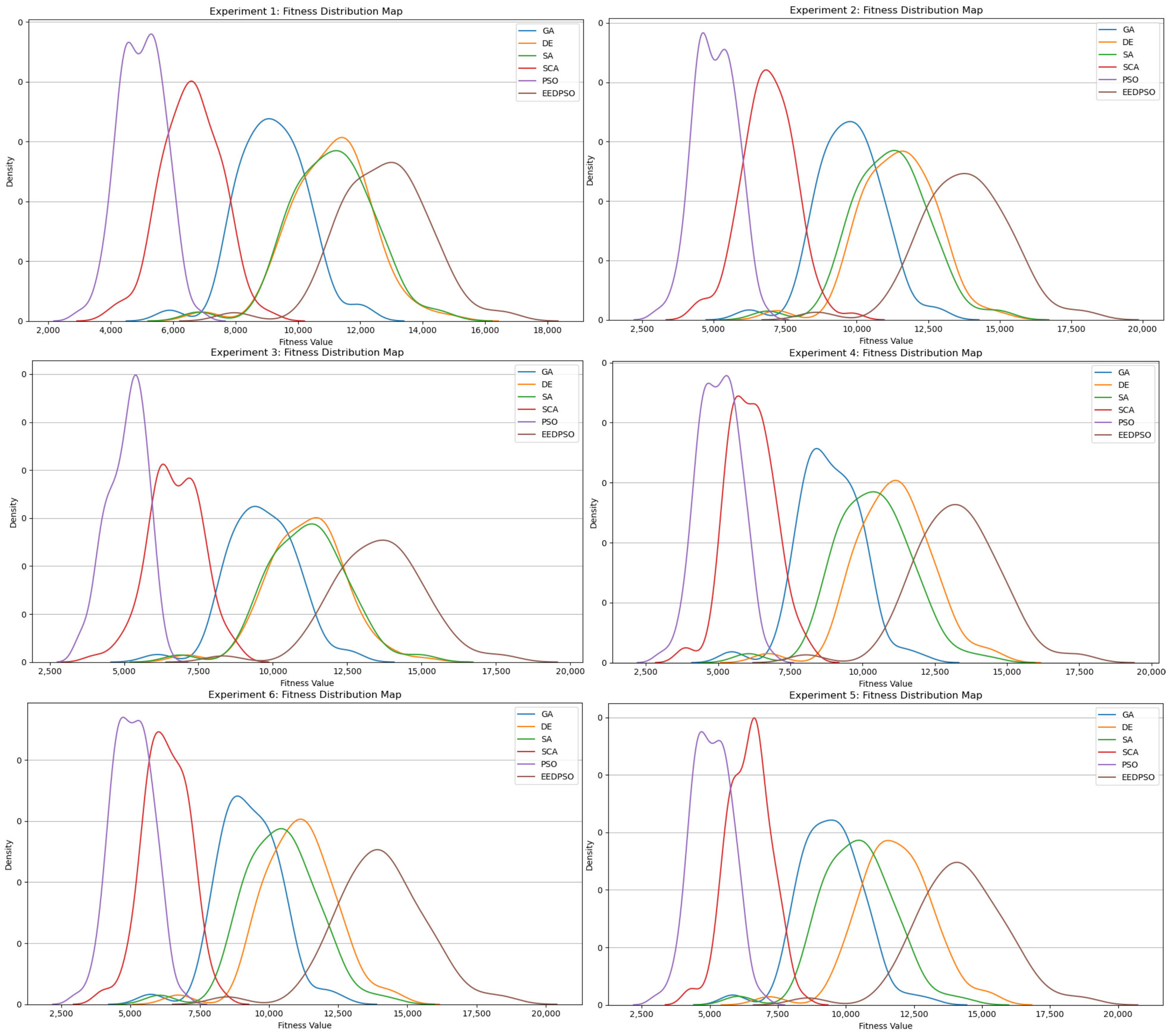
- Fitness Distribution Plot: Using kernel density estimation or smoothed histograms, this plot presents the probability distribution of final fitness values from multiple trials, revealing the concentration and tail behavior of the algorithm’s solutions.
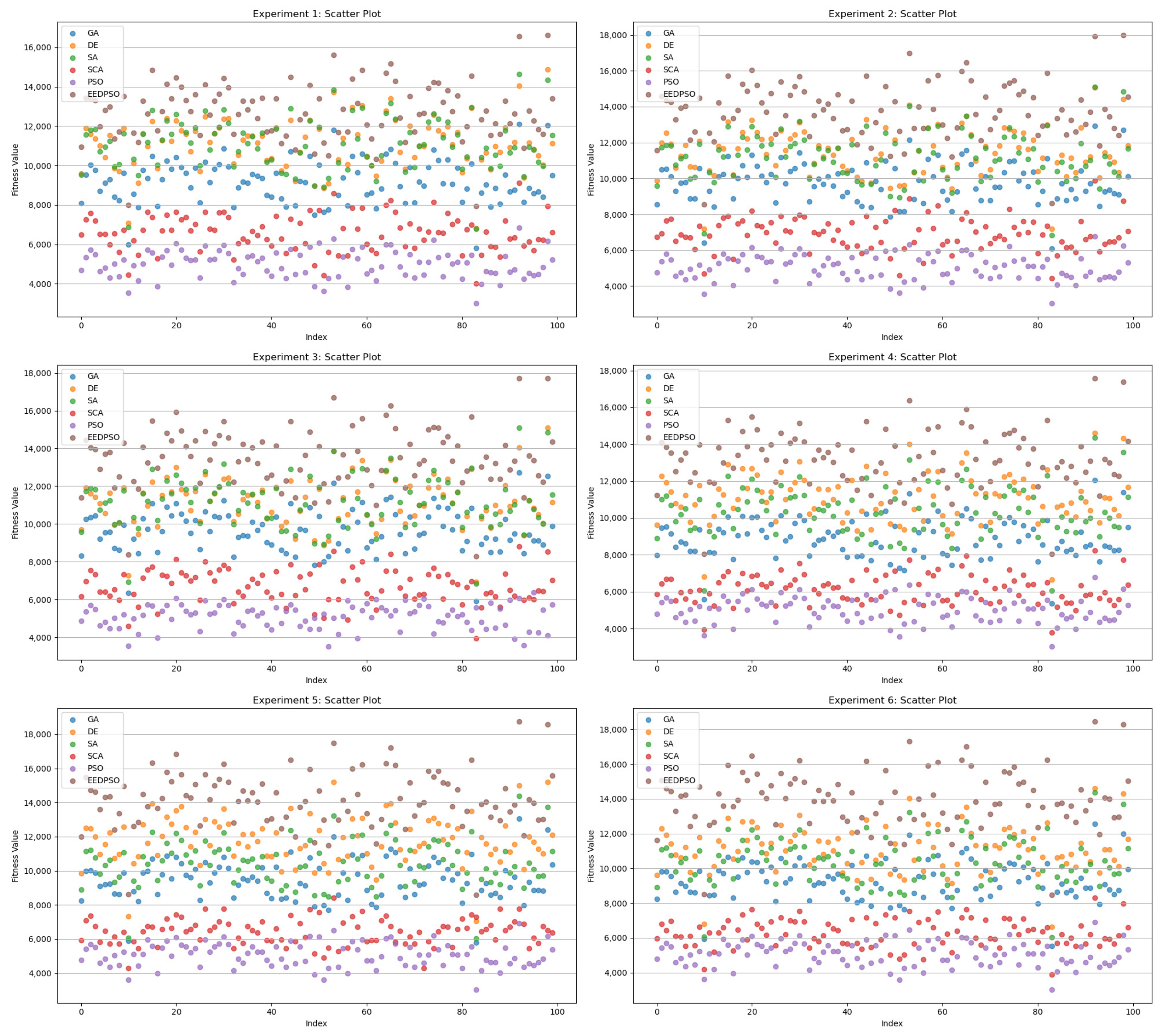
- Scatter Plot: This plot sets the trial index on the horizontal axis and the final fitness value on the vertical axis, allowing for assessment of solution quality and consistency across independent runs.
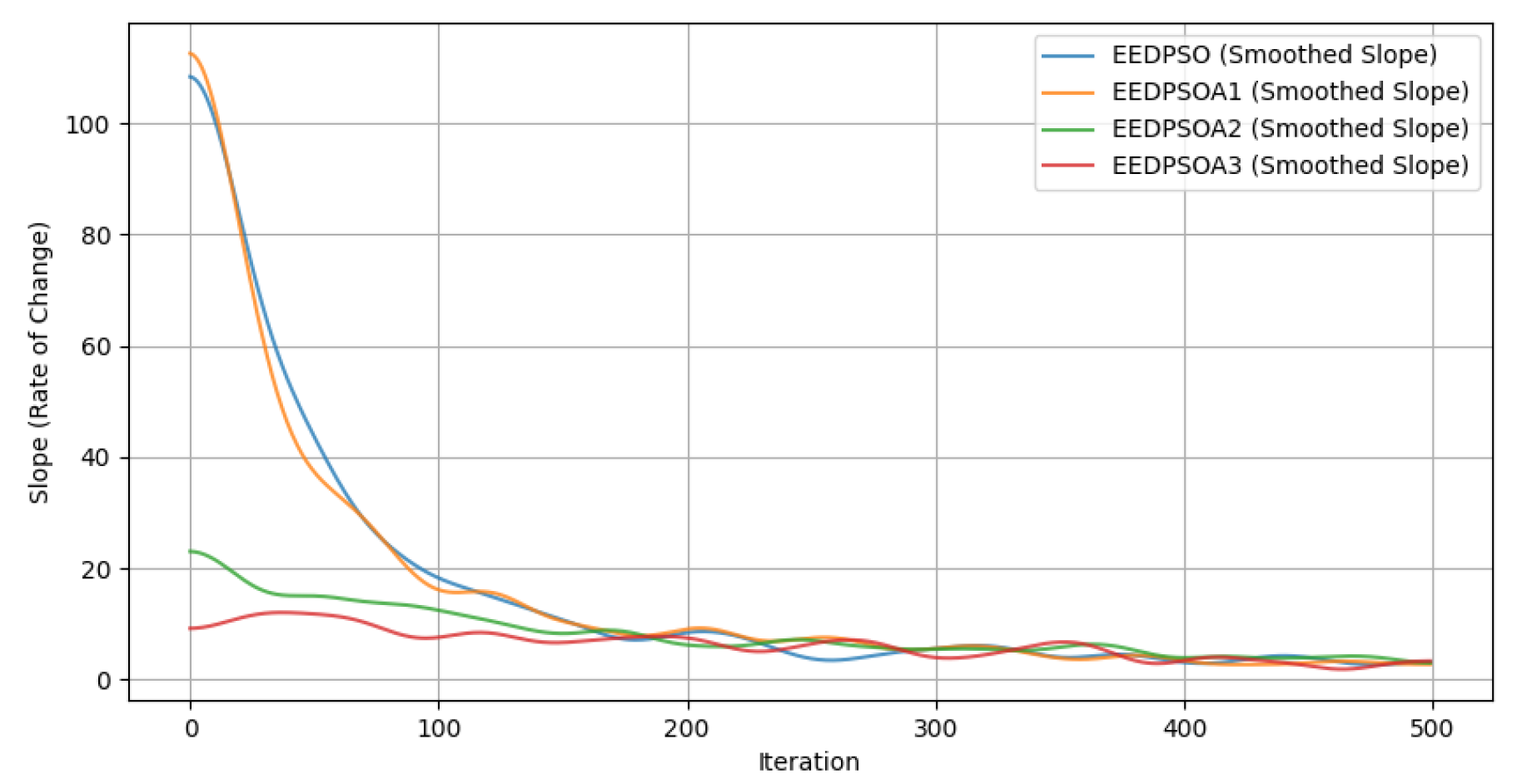
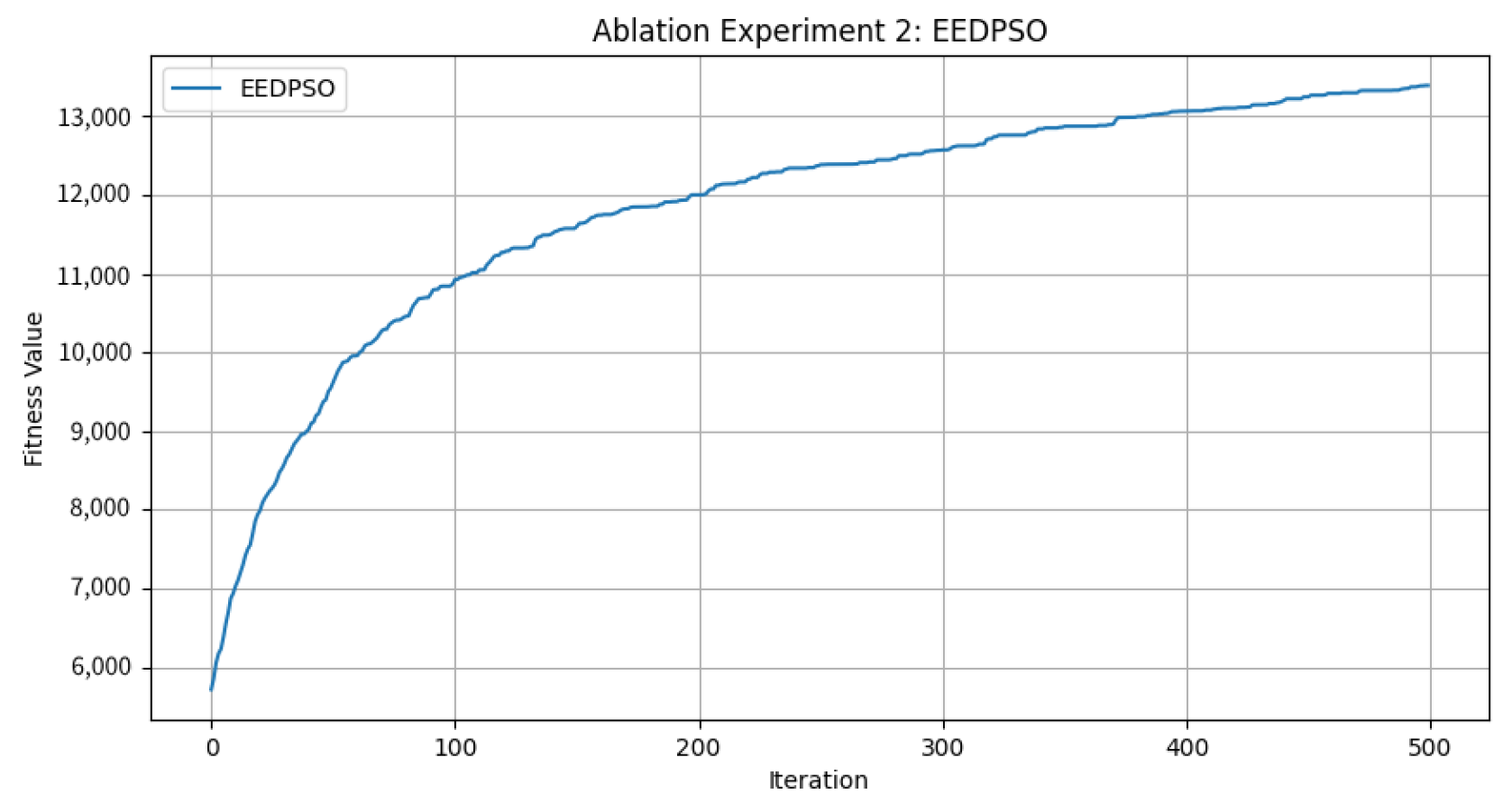
- The EEDPSO curve in the fitness graph is the highest and shows significant improvement in later stages, demonstrating strong global search and local fine-tuning capabilities. As iterations progress, its late-stage advantages become more evident. DE and SA perform at a mid-to-high level, with SA excelling in early-stage speed. GAs show moderate performance but exhibit continuous growth.
- In the box plot, EEDPSO has the highest median and maximum values, indicating stable solution quality and occasional optimal solutions. DE and SA rank second, with DE slightly outperforming SA in extreme values. GAs show substantial fluctuations but generally remain moderate.
- In the distribution plot, the EEDPSO curve is right-shifted and has the longest tail, indicating superior initial performance and optimization ability. Its low peak suggests the algorithm avoids stagnation in specific regions, showcasing strong exploration. EEDPSO offers higher solution diversity and a broader search range than other algorithms.
- In the scatter plot, EEDPSO achieves the highest mean and a broad distribution range, indicating consistent convergence to high-quality solutions rather than occasional outliers.
6. Discussion
- The elite evolution strategy consists of two modules. How does each module contribute to improving algorithm performance?
- The experimental results indicate that the new velocity update strategy performs well in solving optimization problems. How is its effectiveness reflected in the results?
- The new position update strategy guides particles toward more targeted random exploration. What are its actual effects?
- Under the combined influence of multiple strategies, how should parameters and be proportionally allocated in EEDPSO? Does this allocation help to balance exploration and exploitation?
6.1. Elite Evolution Strategy
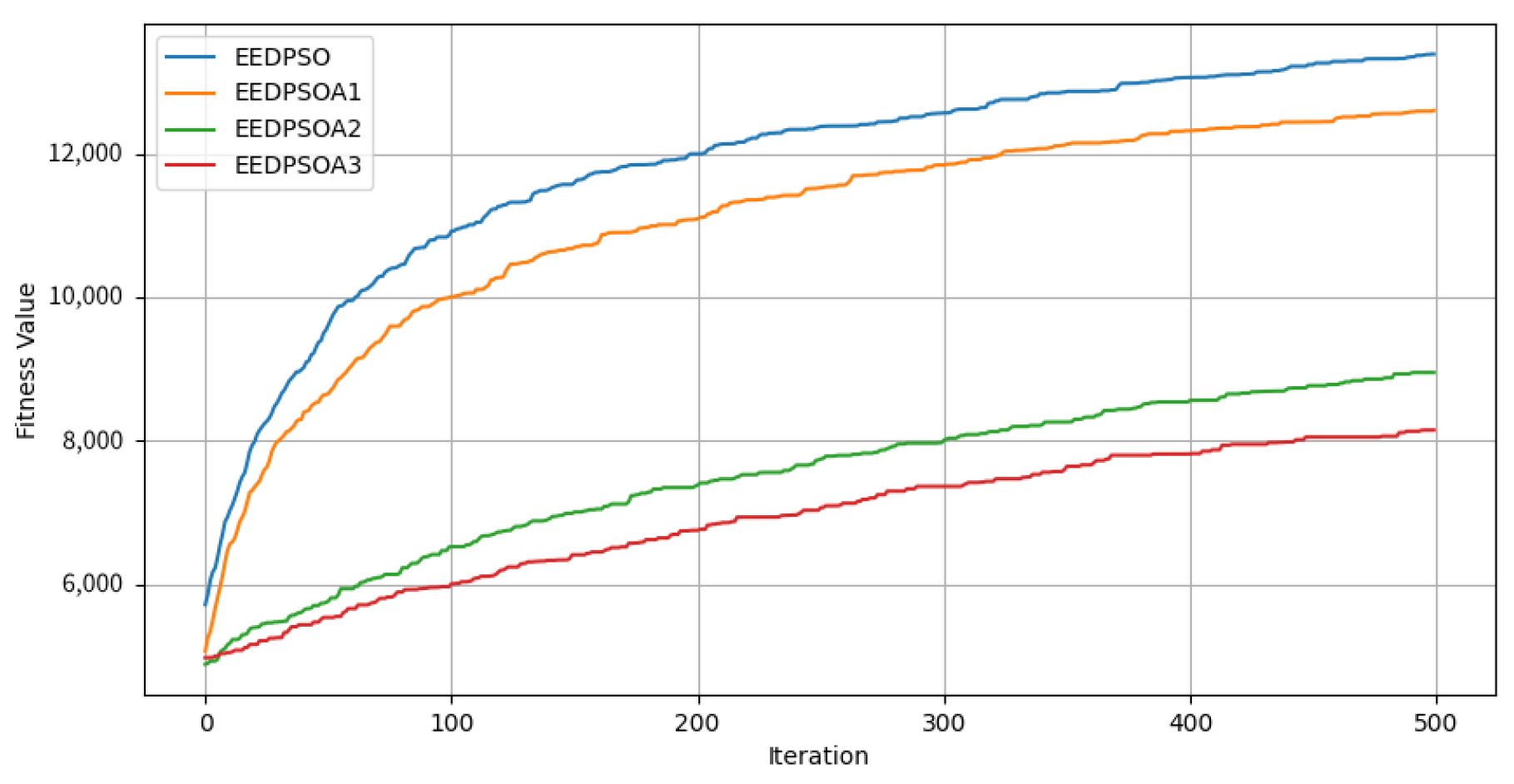
- Final Fitness Distribution (a). This subplot illustrates the final fitness distributions of the four experimental variants: the full algorithm (EEDPSO) and three ablation versions (EEDPSOA1, EEDPSOA2, and EEDPSOA3). The full algorithm achieves the highest performance overall, with a clearly higher median and upper quartile. In contrast, EEDPSOA3—which removes both components—demonstrates a significant drop in performance, as indicated by the leftward shift in distribution. This result suggests that the absence of both strategies substantially impairs the algorithm’s global search ability and convergence effectiveness.
- Performance Scatter Comparison (b). This subplot compares the final fitness results of each ablated version with those of the full algorithm. The dense and separated clusters, especially for EEDPSOA3, reveal that jointly removing both personal and global components significantly degrades performance. The other two ablation variants show milder performance degradation, indicating that either component alone contributes positively to optimization, but the joint presence is crucial.
- Interaction Effect Analysis (c). This subplot presents the interaction effect between the two components, visualized through a point plot derived from a linear regression model with an interaction term (Fitness Personal + Global + Personal × Global). The two lines (Global = 0 and Global = 1) are clearly non-parallel and intersect, indicating the presence of an interaction effect. Although the interaction term is not statistically significant (p = 0.176), the trend suggests that the combined removal of both components causes a synergistic deterioration in fitness, beyond the sum of their individual effects.
- Correlation Matrix of Experimental Results (d). The final subplot shows the Pearson correlation matrix among the four experiment groups. EEDPSO and EEDPSOA1 exhibit the highest correlation (r = 0.99), suggesting that removing only the personal component does not substantially change the search behavior. On the other hand, EEDPSOA3 shows the lowest correlation with the full algorithm (r = 0.96), implying that removing both components significantly alters not just the performance but the behavior and search dynamics of the algorithm.
6.2. Changes in Update Mechanisms
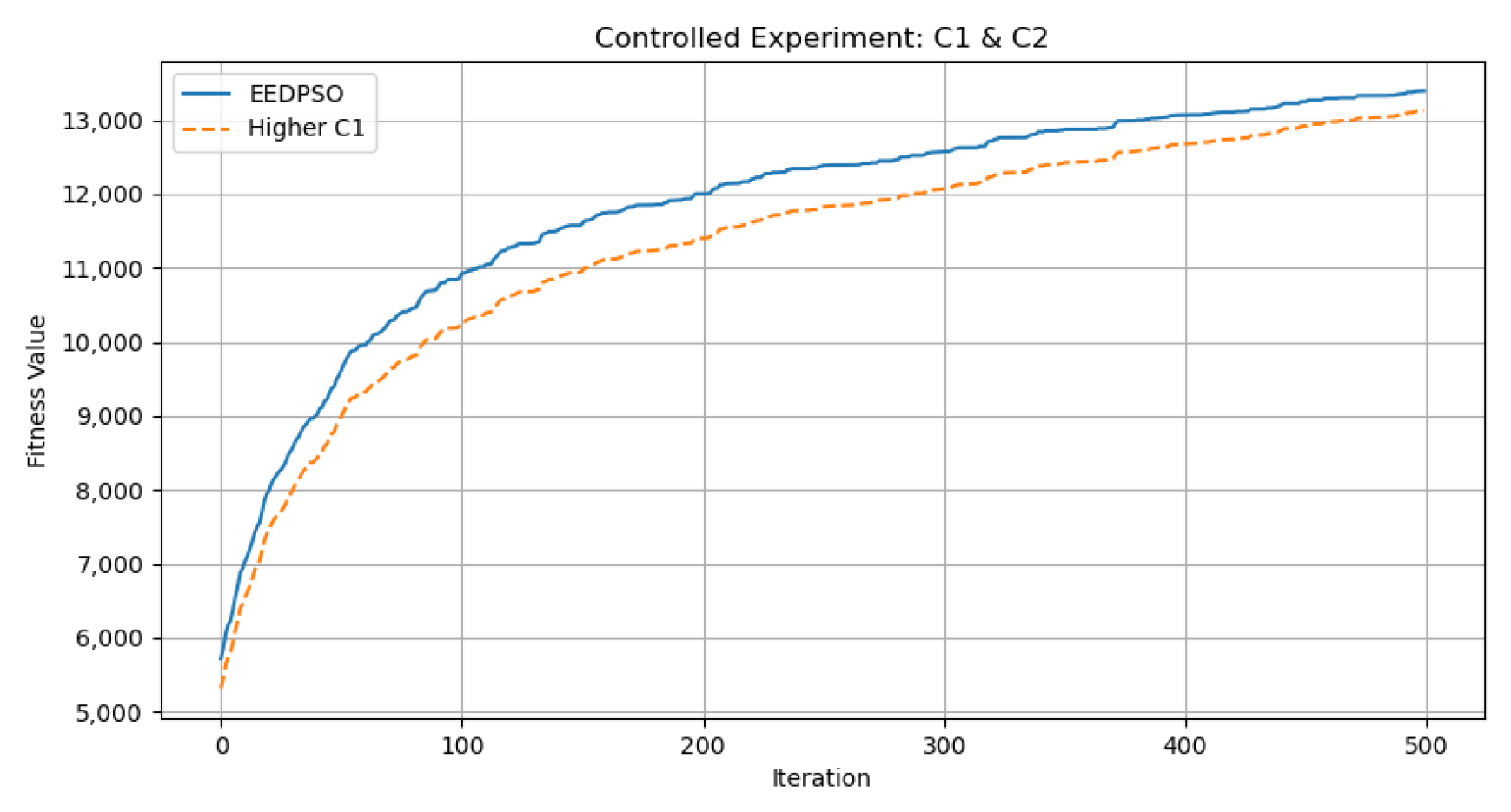
6.3. Distribution of Individual Learning Term (c1) and Global Learning Term (c2)
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Park, D.H.; Kim, H.K.; Choi, I.Y.; Kim, J.K. A literature review and classification of recommender systems research. Expert Syst. Appl. 2012, 39, 10059–10072. [Google Scholar] [CrossRef]
- Lyu, Y. Recommender Systems in e-Commerce. In Proceedings of the 2021 International Conference on Intelligent Computing, Automation and Applications (ICAA), Nanjing, China, 25–27 June 2021; pp. 209–212. [Google Scholar] [CrossRef]
- Lops, P.; de Gemmis, M.; Semeraro, G. Content-based Recommender Systems: State of the Art and Trends. In Recommender Systems Handbook; Springer: Boston, MA, USA, 2011; pp. 73–105. [Google Scholar] [CrossRef]
- Wu, L.; Chen, L.; Shao, P.; Hong, R.; Wang, X.; Wang, M. Learning Fair Representations for Recommendation: A Graph-based Perspective. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; WWW ’21. ACM: New York, NY, USA, 2021; pp. 2198–2208. [Google Scholar] [CrossRef]
- Pei, C.; Zhang, Y.; Zhang, Y.; Sun, F.; Lin, X.; Sun, H.; Wu, J.; Jiang, P.; Ge, J.; Ou, W.; et al. Personalized re-ranking for recommendation. In Proceedings of the 13th ACM Conference on Recommender Systems, Copenhagen, Denmark, 16–20 September 2019; RecSys ’19. ACM: New York, NY, USA, 2019; pp. 3–11. [Google Scholar] [CrossRef]
- Bruun, S.B.; Leśniak, K.K.; Biasini, M.; Carmignani, V.; Filianos, P.; Lioma, C.; Maistro, M. Graph-Based Recommendation for Sparse and Heterogeneous User Interactions. In Proceedings of the Advances in Information Retrieval; Kamps, J., Goeuriot, L., Crestani, F., Maistro, M., Joho, H., Davis, B., Gurrin, C., Kruschwitz, U., Caputo, A., Eds.; Springer: Cham, Switzerland, 2023; pp. 182–199. [Google Scholar] [CrossRef]
- Su, X.; Khoshgoftaar, T.M. A survey of collaborative filtering techniques. Adv. in Artif. Intell. 2009, 2009, 421425. [Google Scholar] [CrossRef]
- Sengupta, S.; Basak, S.; Peters, R.A. Particle Swarm Optimization: A Survey of Historical and Recent Developments with Hybridization Perspectives. Mach. Learn. Knowl. Extr. 2019, 1, 157–191. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Jain, M.; Saihjpal, V.; Singh, N.; Singh, S.B. An Overview of Variants and Advancements of PSO Algorithm. Appl. Sci. 2022, 12, 8392. [Google Scholar] [CrossRef]
- Eberhart; Shi, Y. Particle swarm optimization: Developments, applications and resources. In Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No.01TH8546), Seoul, Republic of Korea, 27–30 May 2001; Volume 1, pp. 81–86. [Google Scholar] [CrossRef]
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Yang, H.; Yu, Y.; Cheng, J.; Lei, Z.; Cai, Z.; Zhang, Z.; Gao, S. An intelligent metaphor-free spatial information sampling algorithm for balancing exploitation and exploration. Knowl.-Based Syst. 2022, 250, 109081. [Google Scholar] [CrossRef]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Gad, A.G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Hao, Z.F.; Guo, G.H.; Huang, H. A Particle Swarm Optimization Algorithm with Differential Evolution. In Proceedings of the 2007 International Conference on Machine Learning and Cybernetics, Hong Kong, China, 19–22 August 2007; Volume 2, pp. 1031–1035. [Google Scholar] [CrossRef]
- Peng, Z.; Al Chami, Z.; Manier, H.; Manier, M.A. A hybrid particle swarm optimization for the selective pickup and delivery problem with transfers. Eng. Appl. Artif. Intell. 2019, 85, 99–111. [Google Scholar] [CrossRef]
- Bag, S.; Kumar, S.K.; Tiwari, M.K. An efficient recommendation generation using relevant Jaccard similarity. Inf. Sci. 2019, 483, 53–64. [Google Scholar] [CrossRef]
- Črepinšek, M.; Liu, S.H.; Mernik, M. Exploration and exploitation in evolutionary algorithms: A survey. ACM Comput. Surv. 2013, 45, 1–33. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications. Math. Probl. Eng. 2015, 2015, 931256. [Google Scholar] [CrossRef]
- Tomar, V.; Bansal, M.; Singh, P. Metaheuristic Algorithms for Optimization: A Brief Review. Eng. Proc. 2023, 59, 238. [Google Scholar] [CrossRef]
- Cui, J.s.; Shang, T.z.; Yang, F.; Yu, J.w. Ranking recommendation to implement meta-heuristic algorithm based on multi-label k-nearest neighbor method. Control. Decis. 2022, 37, 1289–1298. [Google Scholar] [CrossRef]
- Li, G.; Zhang, T.; Tsai, C.Y.; Yao, L.; Lu, Y.; Tang, J. Review of the metaheuristic algorithms in applications: Visual analysis based on bibliometrics. Expert Syst. Appl. 2024, 255, 124857. [Google Scholar] [CrossRef]
- Petroski Such, F.; Madhavan, V.; Conti, E.; Lehman, J.; Stanley, K.O.; Clune, J. Deep Neuroevolution: Genetic Algorithms Are a Competitive Alternative for Training Deep Neural Networks for Reinforcement Learning. arXiv 2017. [Google Scholar] [CrossRef]
- Young, S.R.; Rose, D.C.; Karnowski, T.P.; Lim, S.H.; Patton, R.M. Optimizing deep learning hyper-parameters through an evolutionary algorithm. In Proceedings of the Workshop on Machine Learning in High-Performance Computing Environments, Austin, TX, USA, 15 November 2015; MLHPC ’15. ACM: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Cinar, A.C. A comprehensive comparison of accuracy-based fitness functions of metaheuristics for feature selection. Soft Comput. 2023, 27, 8931–8958. [Google Scholar] [CrossRef]
- Alhijawi, B.; Kilani, Y. A collaborative filtering recommender system using genetic algorithm. Inf. Process. Manag. 2020, 57, 102310. [Google Scholar] [CrossRef]
- Alhijawi, B.; Kilani, Y.; Alsarhan, A. Improving recommendation quality and performance of genetic-based recommender system. Int. J. Adv. Intell. Paradig. 2020, 15, 77–88. [Google Scholar] [CrossRef]
- Boryczka, U.; Bałchanowski, M. Differential Evolution in a Recommendation System Based on Collaborative Filtering. In Proceedings of the Computational Collective Intelligence; Nguyen, N.T., Iliadis, L., Manolopoulos, Y., Trawiński, B., Eds.; Springer: Cham, Switzerland, 2016; pp. 113–122. [Google Scholar] [CrossRef]
- Boryczka, U.; Bałchanowski, M. Speed up Differential Evolution for ranking of items in recommendation systems. Procedia Comput. Sci. 2021, 192, 2229–2238. [Google Scholar] [CrossRef]
- Tlili, T.; Krichen, S. A simulated annealing-based recommender system for solving the tourist trip design problem. Expert Syst. Appl. 2021, 186, 115723. [Google Scholar] [CrossRef]
- Ye, Z.; Xiao, K.; Ge, Y.; Deng, Y. Applying Simulated Annealing and Parallel Computing to the Mobile Sequential Recommendation. IEEE Trans. Knowl. Data Eng. 2019, 31, 243–256. [Google Scholar] [CrossRef]
- Yang, S.; Wang, H.; Xu, Y.; Guo, Y.; Pan, L.; Zhang, J.; Guo, X.; Meng, D.; Wang, J. A Coupled Simulated Annealing and Particle Swarm Optimization Reliability-Based Design Optimization Strategy under Hybrid Uncertainties. Mathematics 2023, 11, 4790. [Google Scholar] [CrossRef]
- Katarya, R.; Verma, O.P. A collaborative recommender system enhanced with particle swarm optimization technique. Multimed. Tools Appl. 2016, 75, 9225–9239. [Google Scholar] [CrossRef]
- Kuo, R.; Li, S.S. Applying particle swarm optimization algorithm-based collaborative filtering recommender system considering rating and review. Appl. Soft Comput. 2023, 135, 110038. [Google Scholar] [CrossRef]
- Gu, X.L.; Huang, M.; Liang, X. A Discrete Particle Swarm Optimization Algorithm with Adaptive Inertia Weight for Solving Multiobjective Flexible Job-shop Scheduling Problem. IEEE Access 2020, 8, 33125–33136. [Google Scholar] [CrossRef]
- Zhou, T.; Su, R.Q.; Liu, R.R.; Jiang, L.L.; Wang, B.H.; Zhang, Y.C. Accurate and diverse recommendations via eliminating redundant correlations. New J. Phys. 2009, 11, 123008. [Google Scholar] [CrossRef]
- Zhang, S.; Yao, L.; Sun, A.; Tay, Y. Deep Learning Based Recommender System: A Survey and New Perspectives. ACM Comput. Surv. 2019, 52, 1–38. [Google Scholar] [CrossRef]
- Jannach, D.; Zanker, M.; Felfernig, A.; Friedrich, G. Recommender Systems: An Introduction, 1st ed.; Cambridge University Press: Cambridge, UK, 2010; Available online: https://dl.acm.org/doi/book/10.5555/1941904 (accessed on 21 December 2024).
- Herlocker, J.L.; Konstan, J.A.; Terveen, L.G.; Riedl, J.T. Evaluating collaborative filtering recommender systems. ACM Trans. Inf. Syst. 2004, 22, 5–53. [Google Scholar] [CrossRef]
- Lim, Y.J.; Teh, Y.W. Variational Bayesian approach to movie rating prediction. In Proceedings of the KDD Cup and Workshop, San Jose, CA, USA, 12–15 August 2007; Volume 7, pp. 15–21. Available online: https://www.cs.uic.edu/~liub/KDD-cup-2007/proceedings/variational-Lim.pdf (accessed on 4 January 2025).
- Ning, X.; Karypis, G. SLIM: Sparse Linear Methods for Top-N Recommender Systems. In Proceedings of the 2011 IEEE 11th International Conference on Data Mining, Vancouver, BC, Canada, 11–14 December 2011; pp. 497–506. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H.; Lei, Z.; Yang, H.; Wang, J. A Nonlinear Dimensionality Reduction Search Improved Differential Evolution for large-scale optimization. Swarm Evol. Comput. 2025, 92, 101832. [Google Scholar] [CrossRef]
- AlRashidi, M.R.; El-Hawary, M.E. A Survey of Particle Swarm Optimization Applications in Electric Power Systems. IEEE Trans. Evol. Comput. 2009, 13, 913–918. [Google Scholar] [CrossRef]
- Raß, A.; Schmitt, M.; Wanka, R. Explanation of Stagnation at Points that are not Local Optima in Particle Swarm Optimization by Potential Analysis. In Proceedings of the Companion Publication of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; GECCO Companion ’15. ACM: New York, NY, USA, 2015; pp. 1463–1464. [Google Scholar] [CrossRef]
- Ceschia, S.; Di Gaspero, L.; Rosati, R.M.; Schaerf, A. Reinforcement Learning for Multi-Neighborhood Local Search in Combinatorial Optimization. In Proceedings of the Machine Learning, Optimization, and Data Science; Nicosia, G., Ojha, V., La Malfa, E., La Malfa, G., Pardalos, P.M., Umeton, R., Eds.; Springer: Cham, Switzerland, 2024; pp. 206–221. [Google Scholar]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Lipowski, A.; Lipowska, D. Roulette-wheel selection via stochastic acceptance. Phys. A Stat. Mech. Its Appl. 2012, 391, 2193–2196. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1945–1950. [Google Scholar] [CrossRef]
- movielens. movielens-20m. Available online: https://files.grouplens.org/datasets/movielens/ml-20m-README.html (accessed on 3 December 2019).
- movielens. movielens-32m. Available online: https://files.grouplens.org/datasets/movielens/ml-32m-README.html (accessed on 13 October 2023).
- Jianmo Ni, U. Amazon Review Data (2018). Available online: https://nijianmo.github.io/amazon/index.html (accessed on 8 August 2020).
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning, 1st ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989; Available online: https://dl.acm.org/doi/book/10.5555/534133 (accessed on 9 December 2024).
- Assad, A.; Deep, K. A Hybrid Harmony search and Simulated Annealing algorithm for continuous optimization. Inf. Sci. 2018, 450, 246–266. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Success-history based parameter adaptation for Differential Evolution. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 71–78. [Google Scholar] [CrossRef]
- Bilal; Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Suman, B.; Kumar, P. A survey of simulated annealing as a tool for single and multiobjective optimization. J. Oper. Res. Soc. 2006, 57, 1143–1160. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; KDD ’19. ACM: New York, NY, USA, 2019; pp. 2623–2631. [Google Scholar] [CrossRef]
- Wang, M.; Zheng, S.; Li, X.; Qin, X. A new image denoising method based on Gaussian filter. In Proceedings of the 2014 International Conference on Information Science, Electronics and Electrical Engineering, Sapporo, Japan, 26–28 April 2014; Volume 1, pp. 163–167. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, F.; An, J. Review on Similarity Calculation of Recommendation Algorithms. Oper. Res. Fuzziol. 2022, 12, 119–124. [Google Scholar] [CrossRef]
- Xu, H.; Deng, Q.; Zhang, Z.; Lin, S. A hybrid differential evolution particle swarm optimization algorithm based on dynamic strategies. Sci. Rep. 2025, 15, 4518. [Google Scholar] [CrossRef]
- Clerc, M.; Kennedy, J. The particle swarm - explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Ko, H.; Lee, S.; Park, Y.; Choi, A. A survey of recommendation systems: Recommendation models, techniques, and application fields. Electronics 2022, 11, 141. [Google Scholar] [CrossRef]
- Yang, H.; Gao, S.; Lei, Z.; Li, J.; Yu, Y.; Wang, Y. An improved spherical evolution with enhanced exploration capabilities to address wind farm layout optimization problem. Eng. Appl. Artif. Intell. 2023, 123, 106198. [Google Scholar] [CrossRef]
- Yang, Y.; Tao, S.; Li, H.; Yang, H.; Tang, Z. A Multi-Local Search-Based SHADE for Wind Farm Layout Optimization. Electronics 2024, 13, 3196. [Google Scholar] [CrossRef]
- Nagata, Y. High-Order Entropy-Based Population Diversity Measures in the Traveling Salesman Problem. Evol. Comput. 2020, 28, 595–619. [Google Scholar] [CrossRef] [PubMed]
- Nagata, Y.; Imahori, S. Creation of Dihedral Escher-like Tilings Based on As-Rigid-As-Possible Deformation. ACM Trans. Graph. 2024, 43, 1–18. [Google Scholar] [CrossRef]
- Konstantakopoulos, G.D.; Gayialis, S.P.; Kechagias, E.P. Vehicle routing problem and related algorithms for logistics distribution: A literature review and classification. Oper. Res. 2022, 22, 2033–2062. [Google Scholar] [CrossRef]
- Yang, H.; Yang, Y.; Zhang, Y.; Tang, C.; Hashimoto, K.; Nagata, Y. Chaotic Map-Coded Evolutionary Algorithms for Dendritic Neuron Model Optimization. In Proceedings of the 2024 IEEE Congress on Evolutionary Computation (CEC), Yokohama, Japan, 30 June–5 July 2024; pp. 1–8. [Google Scholar] [CrossRef]
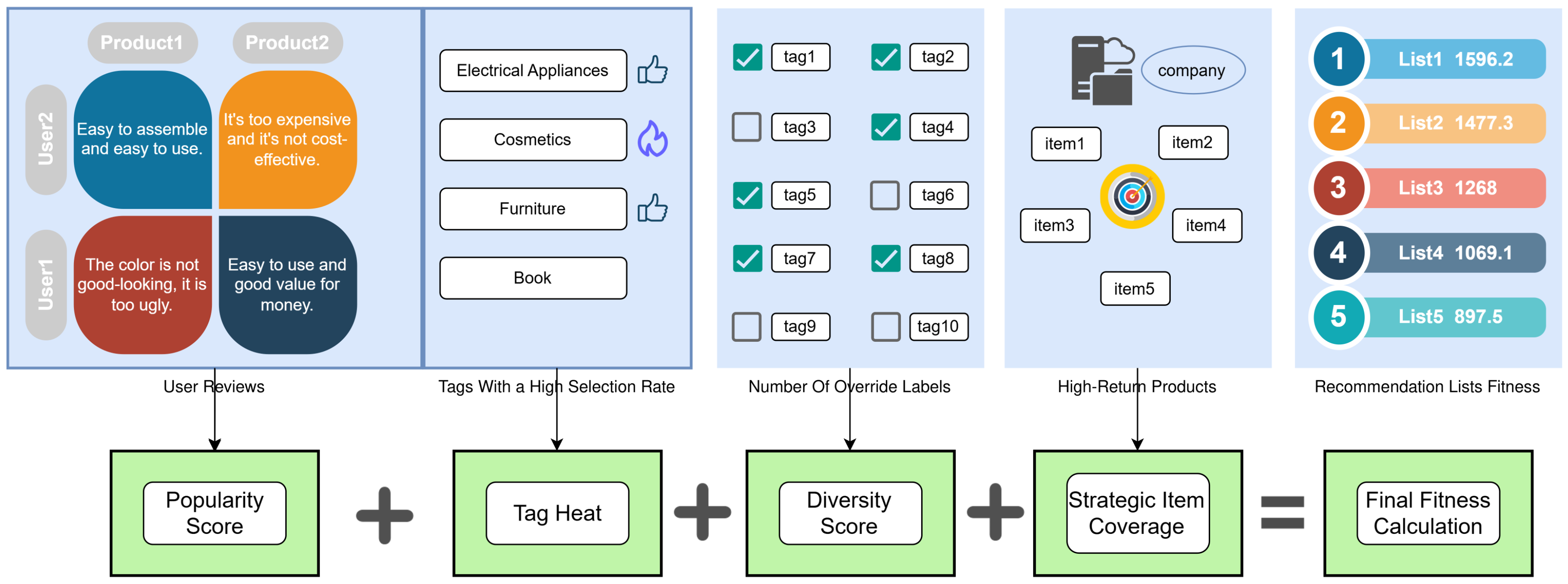










| (Diversity) | (Strategy) | Tag Coverage | Strategic Coverage | Meets Tag Coverage Goal | Meets Strategy Goal |
|---|---|---|---|---|---|
| 1 | 50 | 0.52 | 0.04 | ✗ | ✗ |
| 1 | 100 | 0.51 | 0.12 | ✗ | ✓ |
| 3 | 100 | 0.72 | 0.11 | ✓ | ✓ |
| 5 | 100 | 0.81 | 0.10 | ✓ | ✓ |
| 3 | 150 | 0.69 | 0.17 | ✗ | ✓ |
| MovieLens-20m | MovieLens-32m | AmazonReviewData-sm | AmazonReviewData-lg | |||||
|---|---|---|---|---|---|---|---|---|
| GA | cxpb | 0.58 | cxpb | 0.73 | cxpb | 0.94 | cxpb | 0.79 |
| mutpb | 0.16 | mutpb | 0.13 | mutpb | 0.2 | mutpb | 0.2 | |
| DE | F | 0.3 | F | 0.33 | F | 0.37 | F | 0.27 |
| CR | 0.84 | CR | 0.69 | CR | 0.71 | CR | 0.92 | |
| SA | initial_temperature | 258.77 | initial_temperature | 124.23 | initial_temperature | 133.86 | initial_temperature | 207.62 |
| cooling_rate | 0.99 | cooling_rate | 0.87 | cooling_rate | 0.99 | cooling_rate | 0.95 | |
| alpha | 0.84 | alpha | 0.94 | alpha | 0.89 | alpha | 0.90 | |
| perturbation_size | 1.00 | perturbation_size | 1.00 | perturbation_size | 1.00 | perturbation_size | 1.00 | |
| PSO | w | 0.53 | w | 1.03 | w | 0.8 | w | 1.17 |
| c1 | 1.67 | c1 | 1.40 | c1 | 2.12 | c1 | 1.98 | |
| c2 | 1.19 | c2 | 1.16 | c2 | 2.12 | c2 | 1.27 | |
| EEDPSO | w | 0.55 | w | 0.67 | w | 0.52 | w | 0.69 |
| c1 | 1.26 | c1 | 1.23 | c1 | 1.13 | c1 | 1.11 | |
| c2 | 0.74 | c2 | 0.64 | c2 | 0.91 | c2 | 0.89 | |
| Fitness | Worst Fitness | Standard Deviation | Convergence Generation | p-Value | Significant | Time (s) | |||
|---|---|---|---|---|---|---|---|---|---|
| Experiment 1 | GA | ngen = 500 pop = 80 particles = 30 | 9184.99 | 5431.11 | 809.34 | 481 | 0 | **** | 17.93 |
| DE | 11,068.45 | 5439.99 | 1180.69 | 472 | **** | 16.04 | |||
| SA | 11,079.88 | 5047.36 | 798.39 | 305 | **** | 4.33 | |||
| SCA | 6584.37 | 5183.51 | 555.91 | 202 | 0 | **** | 32.58 | ||
| PSO | 4989.12 | 4670.35 | 51.07 | 246 | 0 | **** | 7.57 | ||
| EEDPSO | 12,741.04 | 5496.08 | 1450.12 | 496 | * | * | 7.9 | ||
| Experiment 2 | GA | ngen = 500 pop = 200 particles = 75 | 9766.18 | 5463.31 | 873.35 | 481 | 0 | **** | 44.37 |
| DE | 11,452.14 | 5501.96 | 1164.35 | 486 | 0 | **** | 53.81 | ||
| SA | 11,175.88 | 5257.64 | 525.21 | 294 | 0 | **** | 10.2 | ||
| SCA | 6915.61 | 5266.28 | 688.09 | 207 | 0 | **** | 79.95 | ||
| PSO | 5042.56 | 4733.8 | 51.08 | 216 | **** | 19.13 | |||
| EEDPSO | 13,777.85 | 5816.11 | 1360.3 | 497 | * | * | 18.6 | ||
| Experiment 3 | GA | ngen = 1000 pop = 80 particles = 30 | 9652.39 | 5431.11 | 781.65 | 960 | 0 | **** | 35.24 |
| DE | 11,141.38 | 5439.99 | 1098.75 | 497 | 0 | **** | 25.62 | ||
| SA | 11,145.64 | 5047.36 | 599.52 | 558 | 0 | **** | 8.14 | ||
| SCA | 6716.21 | 5175.46 | 597.81 | 346 | 0 | **** | 62.88 | ||
| PSO | 5086.81 | 4739.93 | 48.69 | 516 | 0 | **** | 15.39 | ||
| EEDPSO | 13,542.45 | 5478.1 | 1407.47 | 993 | * | * | 14.97 | ||
| DRS Experiment 1 | FairGo | ngen = 200 | 11,076.8 | 3931.66 | 1295.16 | 197 | |||
| PRM | 4722.95 | 4304.71 | 132.26 | 82 (early stopping) |
| Fitness | Worst Fitness | Standard Deviation | Convergence Generation | p-Value | Significant | Time (s) | |||
|---|---|---|---|---|---|---|---|---|---|
| Experiment 4 | GA | ngen = 800 pop = 120 particles = 45 | 8872.67 | 4780.43 | 739.47 | 764 | 0 | **** | 43.52 |
| DE | 11,088.85 | 4792.31 | 1253.44 | 591 | **** | 35.22 | |||
| SA | 10,359.6 | 4975.74 | 538.38 | 461 | 0 | **** | 9.92 | ||
| SCA | 6123.51 | 4549.07 | 636.21 | 298 | 0 | **** | 77.21 | ||
| PSO | 5022.42 | 4696.83 | 46.72 | 404 | 0 | **** | 24.64 | ||
| EEDPSO | 13,241 | 4903.1 | 1453.34 | 795 | 18.92 | ||||
| Experiment 5 | GA | ngen = 800 pop = 300 particles = 110 | 9458.04 | 4848.85 | 776.01 | 768 | 0 | **** | 110.37 |
| DE | 11,792.77 | 4855.48 | 1216.69 | 786 | 0 | **** | 125.27 | ||
| SA | 10,426.62 | 5770.2 | 354.33 | 403 | 0 | **** | 25.27 | ||
| SCA | 6436.12 | 4689.2 | 728.37 | 304 | 0 | **** | 196.82 | ||
| PSO | 5067.66 | 4764.2 | 42.5 | 428 | 0.00 | **** | 60.96 | ||
| EEDPSO | 14,209.51 | 5341.78 | 1333.98 | 795 | * | * | 46.12 | ||
| Experiment 6 | GA | ngen = 1600 pop = 120 particles = 45 | 9278.33 | 4780.43 | 691.79 | 1550 | 0 | **** | 90.61 |
| DE | 11,089.61 | 4792.31 | 1042.8 | 592 | 0 | **** | 59.08 | ||
| SA | 10,415.96 | 4975.74 | 406.81 | 847 | 0 | **** | 20.43 | ||
| SCA | 6285.38 | 4541.12 | 690.43 | 521 | 0 | **** | 151.66 | ||
| PSO | 5054.24 | 4696.83 | 44.51 | 831 | 0 | **** | 50.47 | ||
| EEDPSO | 14,007.29 | 4917.78 | 1374.89 | 1591 | * | 37.93 | |||
| DRS Experiment 2 | FairGo | ngen = 320 | 12,188.82 | 3546.43 | 1474.85 | 315 | |||
| PRM | 4642.94 | 4256.76 | 182.54 | 117 (early stopping) |
| Fitness | Worst Fitness | Standard Deviation | Convergence Generation | p-Value | Significant | Time (s) | |||
|---|---|---|---|---|---|---|---|---|---|
| Experiment 7 | GA | ngen = 500 pop = 80 particles = 30 | 3892.64 | 2920.16 | 190.08 | 483 | **** | 18.77 | |
| DE | 4242.21 | 2923.55 | 272.28 | 466 | 0.0181852 | * | 13.54 | ||
| SA | 4149.65 | 4975.74 | 173.52 | 292 | **** | 4.63 | |||
| SCA | 3215.52 | 2849.87 | 145.3 | 209 | 0 | **** | 36.37 | ||
| PSO | 2984.39 | 2899.95 | 13.17 | 255 | 0 | **** | 8.84 | ||
| EEDPSO | 4359.57 | 2924.65 | 266.02 | 496 | * | * | 7.98 | ||
| Experiment 8 | GA | ngen = 500 pop = 200 particles = 75 | 4019.59 | 2939.12 | 200.15 | 487 | **** | 47.2 | |
| DE | 4294.45 | 2940.93 | 256 | 485 | 0.0097806 | ** | 48.64 | ||
| SA | 4160.08 | 2833.14 | 109.67 | 264 | **** | 11.53 | |||
| SCA | 3288.77 | 2871.74 | 172.92 | 214 | 0 | **** | 82.54 | ||
| PSO | 2996.51 | 2916.77 | 13.74 | 242 | 0.00 | **** | 21.78 | ||
| EEDPSO | 4414.12 | 3009.19 | 191.6 | 496 | * | * | 19.48 | ||
| Experiment 9 | GA | ngen = 1000 pop = 80 particles = 30 | 3992.14 | 2920.16 | 177.98 | 969 | **** | 37.42 | |
| DE | 4253.65 | 2923.55 | 232.91 | 488 | 0.00316204 | * | 19.96 | ||
| SA | 4157.76 | 2796.79 | 127 | 530 | **** | 9.23 | |||
| SCA | 3247.24 | 2847.69 | 155.14 | 355 | 0 | **** | 69.45 | ||
| PSO | 2992.83 | 2899.95 | 13.11 | 488 | 0 | **** | 19.46 | ||
| EEDPSO | 4401.49 | 2929.27 | 212.26 | 994 | * | * | 15.83 | ||
| DRS Experiment 3 | FairGo | ngen = 200 | 4319.91 | 1432.51 | 733.94 | 192 | |||
| PRM | 2287.48 | 2175.73 | 24.65 | 79 (early stopping) |
| Fitness | Worst Fitness | Standard Deviation | Convergence Generation | p-Value | Significant | time(s) | |||
|---|---|---|---|---|---|---|---|---|---|
| Experiment 10 | GA | ngen = 800 pop = 120 particles = 45 | 4193.66 | 3194.59 | 153.88 | 783 | **** | 39.25 | |
| DE | 4403.42 | 3197.31 | 174.41 | 684 | 0.0369414 | * | 27.82 | ||
| SA | 4174.95 | 3140.4 | 65.24 | 417 | **** | 9.81 | |||
| SCA | 3582.69 | 3112.19 | 189.58 | 315 | 0 | **** | 72.9 | ||
| PSO | 3277.02 | 3164.8 | 16.4 | 401 | 0 | **** | 27.76 | ||
| EEDPSO | 4459.33 | 3241.8 | 134.69 | 794 | * | * | 24.59 | ||
| Experiment 11 | GA | ngen = 800 pop = 300 particles = 110 | 4269.09 | 3214.48 | 150.43 | 785 | 0.00010553 | ** | 98.4 |
| DE | 4424.1 | 3216.91 | 160.26 | 782 | 0.0315705 | * | 97.09 | ||
| SA | 4182.63 | 3457.91 | 37.3 | 407 | **** | 24.42 | |||
| SCA | 3541.79 | 3161.69 | 151.13 | 341 | 0 | **** | 188.81 | ||
| PSO | 3290.26 | 3183.18 | 16.06 | 404 | 0.00 | **** | 58.73 | ||
| EEDPSO | 4472.8 | 3366.29 | 89.53 | 795 | * | * | 45.64 | ||
| Experiment 12 | GA | ngen = 1600 pop = 120 particles = 45 | 4249.83 | 3194.59 | 132.54 | 1569 | **** | 78.34 | |
| DE | 4408.43 | 3197.31 | 136.56 | 699 | 0.0310538 | * | 40.76 | ||
| SA | 4181.02 | 3140.4 | 47.84 | 864 | **** | 19.45 | |||
| SCA | 3605.47 | 3109.71 | 194.08 | 546 | 0 | **** | 143.75 | ||
| PSO | 3286.44 | 3164.8 | 15.96 | 805 | 0 | **** | 46.01 | ||
| EEDPSO | 4470.09 | 3242.12 | 100.91 | 1591 | * | * | 34.3 | ||
| DRS Experiment 3 | FairGo | ngen = 320 | 4650.32 | 1416.29 | 816.2 | 316 | |||
| PRM | 2445.43 | 2198.55 | 37.05 | 87 (early stopping) |
| Experiment | Fitness | Time (s) | Fitness Change (%) | Time Change (%) |
|---|---|---|---|---|
| EEDPSO | 13,394.04 | 7.94 | 0.00 | 0.00 |
| EEDPSOA1 | 12,608.43 | 5.86 | −5.72 | −26.26 |
| EEDPSOA2 | 8953.20 | 6.00 | −33.17 | −24.56 |
| EEDPSOA3 | 8150.71 | 4.32 | −39.17 | −45.60 |
| Setting | Dimension | w | Fitness | |||
|---|---|---|---|---|---|---|
| Baseline (EEDPSO) | 200 | 0.55 | 1.26 | 0.74 | 2.00 | 13,394.04 |
| C2↑, C1↓ | 200 | 0.55 | 0.74 | 1.26 | 2.00 | 12,858.28 |
| C1↑, C2↓ | 200 | 0.55 | 1.46 | 0.54 | 2.00 | 13,126.16 |
| C1↓, C2↔ | 200 | 0.55 | 0.40 | 0.80 | 1.20 | 11,742.51 |
| C2↓, C1↔ | 200 | 0.55 | 0.80 | 0.40 | 1.20 | 11,875.97 |
| Baseline (EEDPSO) | 100 | 0.55 | 1.38 | 0.62 | 2.00 | 6560.22 |
| C2↑, C1↓ | 100 | 0.55 | 0.98 | 1.02 | 2.00 | 6284.10 |
| C1↑, C2↓ | 100 | 0.55 | 1.68 | 0.32 | 2.00 | 6622.71 |
| C1↓, C2↔ | 100 | 0.55 | 0.40 | 0.80 | 1.20 | 5503.51 |
| C2↓, C1↔ | 100 | 0.55 | 0.80 | 0.40 | 1.20 | 5620.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.; Yang, Y.; Nagata, Y.; Yang, H. Elite Evolutionary Discrete Particle Swarm Optimization for Recommendation Systems. Mathematics 2025, 13, 1398. https://doi.org/10.3390/math13091398
Lin S, Yang Y, Nagata Y, Yang H. Elite Evolutionary Discrete Particle Swarm Optimization for Recommendation Systems. Mathematics. 2025; 13(9):1398. https://doi.org/10.3390/math13091398
Chicago/Turabian StyleLin, Shanxian, Yifei Yang, Yuichi Nagata, and Haichuan Yang. 2025. "Elite Evolutionary Discrete Particle Swarm Optimization for Recommendation Systems" Mathematics 13, no. 9: 1398. https://doi.org/10.3390/math13091398
APA StyleLin, S., Yang, Y., Nagata, Y., & Yang, H. (2025). Elite Evolutionary Discrete Particle Swarm Optimization for Recommendation Systems. Mathematics, 13(9), 1398. https://doi.org/10.3390/math13091398







