BERT Mutation: Deep Transformer Model for Masked Uniform Mutation in Genetic Programming

Abstract

We introduce BERT mutation, a novel, domain-independent mutation operator for Genetic Programming (GP) that leverages advanced Natural Language Processing (NLP) techniques to improve convergence, particularly using the Masked Language Modeling approach. By combining the capabilities of deep reinforcement learning and the BERT transformer architecture, BERT mutation intelligently suggests node replacements within GP trees to enhance their fitness. Unlike traditional stochastic mutation methods, BERT mutation adapts dynamically by using historical fitness data to optimize mutation decisions, resulting in more effective evolutionary improvements. Through comprehensive evaluations across three benchmark domains, we demonstrate that BERT mutation significantly outperforms conventional and state-of-the-art mutation operators in terms of convergence speed and solution quality. This work represents a pivotal step toward integrating state-of-the-art deep learning into evolutionary algorithms, pushing the boundaries of adaptive optimization in GP.

1. Introduction

Genetic Programming (GP) is a specialized form of Evolutionary Algorithm (EA) that evolves programs or expressions, typically represented as tree structures. Similar to other EAs, GP is a population-based meta-heuristic optimization algorithm that operates on a population of candidate solutions, referred to as individuals, iteratively improving the quality of solutions over generations. GP employs a selection operator to choose fit individuals and crossover and mutation operators to generate new individuals based on their fitness values, which are computed by means of a fitness function [1]. Algorithm 1 outlines the pseudo-code of canonical GP, comprising the main fitness selection–crossover–mutation loop.

In conventional GP, the mutation operator may assume a dominant role and can even be used as the sole genetic operator, with no crossover whatsoever. A widely used mutation operator for GP is point mutation, wherein a random tree node is replaced with an appropriate random node, i.e., a random function with the same arity or a random terminal, depending on the replaced node type [2].

Algorithm 1 Canonical genetic programming pseudo code

1: generate an initial population of candidate solutions (a.k.a. individuals) to the problem 2: while termination condition not satisfied do 3:     compute fitness value of each individual 4:     perform crossover between parents 5:     perform mutation on the resultant offspring 6: end while

Continuing the recent advancements in combining EAs with deep learning approaches [3,4,5,6], BERT mutation—introduced herein—takes point mutation a step further. It masks multiple tree nodes (rather than a single node) and then tries to replace these masks with tree nodes that will most likely improve the individual’s fitness. The operator draws inspiration from natural language processing (NLP) techniques, particularly the Masked Language Modeling (MLM) approach used to train models like BERT (Bidirectional Encoder Representations from Transformers) [7].

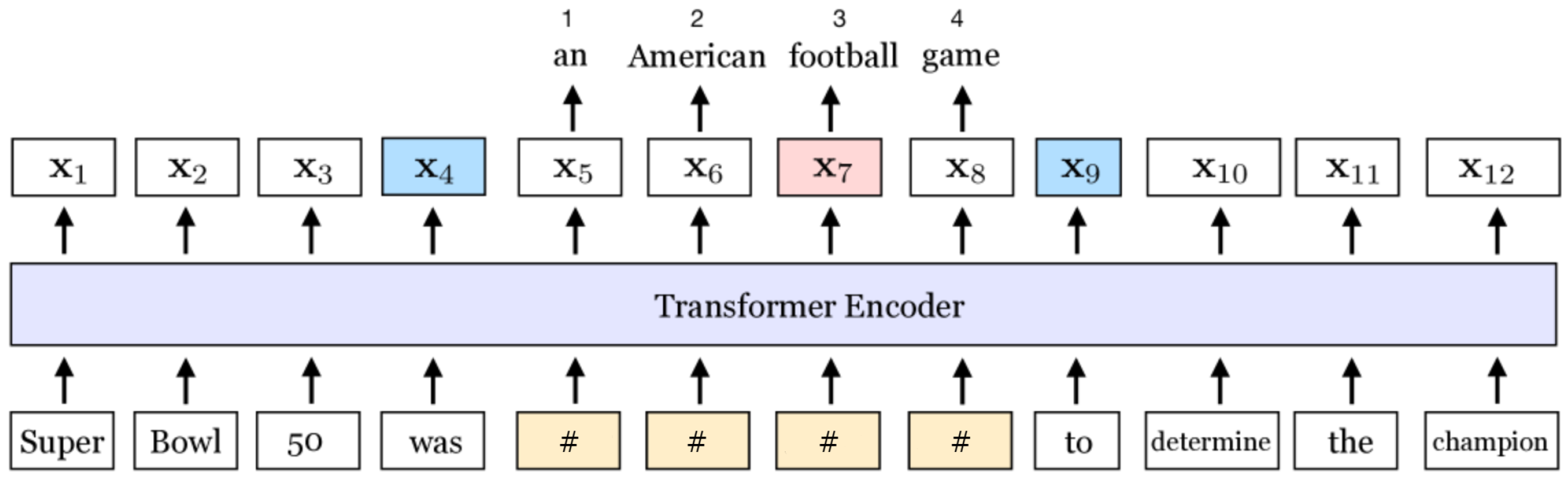
MLM involves masking a certain percentage of tokens in input sentences and tasking the model to predict these masked tokens based on contextual information, which processes all tokens simultaneously (thus called bidirectional) (see Figure 1). MLM enables the model to learn rich contextual representations of language by optimizing the model to predict masked words. This approach revolutionized NLP, offering state-of-the-art performance across various downstream tasks and setting a new benchmark for contextualized embeddings.

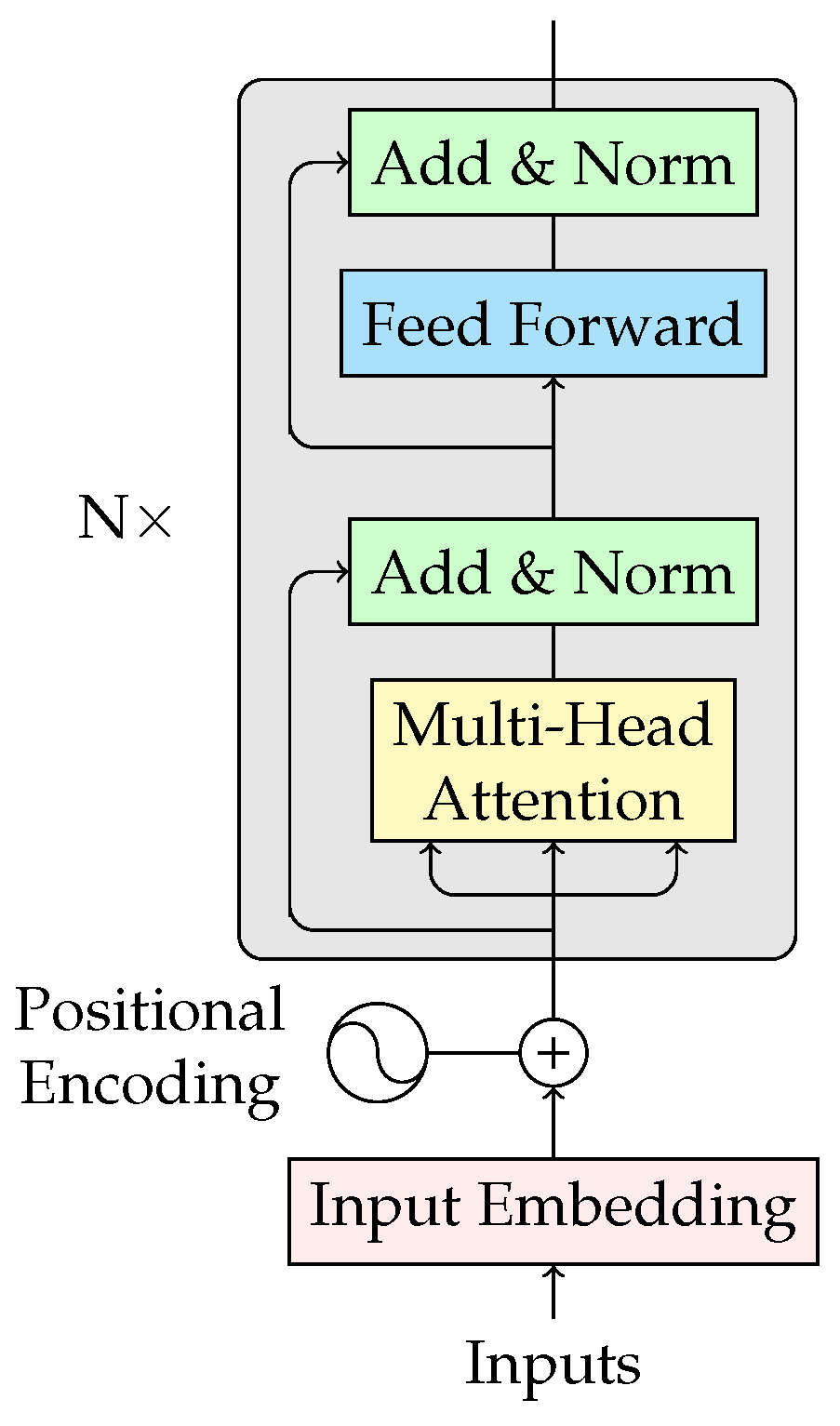
BERT [7] is composed of multiple layers of self-attention mechanisms and feedforward neural networks. Each encoder layer (depicted in Figure 2) processes the input by computing attention scores, allowing the model to focus on different parts of the sequence, regardless of their position. The self-attention mechanism enables BERT to capture contextual relationships between words, while the feedforward network further refines the representations. Layer normalization and residual connections are applied to maintain gradient flow and improve training stability. This architecture allows BERT to generate deep, bidirectional contextual embeddings for natural language understanding.

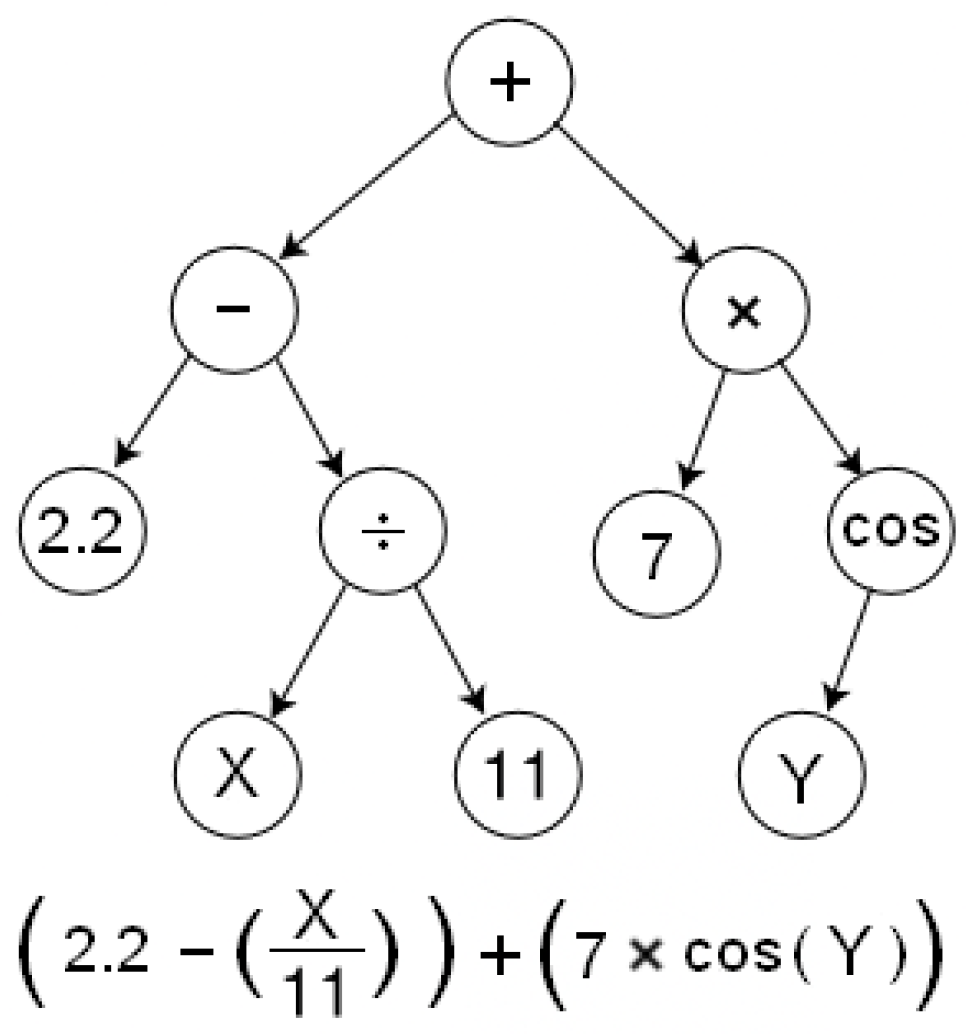
GP offers an intriguing case for integrating the MLM approach. Each individual within the population can be represented as a string drawn from a predefined language containing functions and terminals. Consider the GP tree depicted in Figure 3, which can be represented as a string: $(2.2-(x/11\left)\right)+(7\ast cos(y\left)\right)$. We can obtain the following string from the masking procedure: $(\#-(x/\#\left)\right)+(7\#cos(y\left)\right)$.

Inspired by the training process of BERT, we propose applying MLM to the string representation of GP trees along with the mutation masks. However, instead of optimizing the network to predict masked nodes, we use reinforcement learning to select new nodes that optimize the population’s fitness scores, where fitness improvement serves as the reward signal. In other words, we model a probability distribution for each masked node, aiming to assign higher probabilities to functions and terminals that are expected to enhance the fitness of the mutated individual. This optimization process ensures that the mutations introduced by evolution are more likely to lead to improved solutions.

Throughout the years, numerous mutation operators have been proposed to enhance population convergence. Often, these operators are tailored to specific problem domains, such as job scheduling [9], classification [10,11,12], robotics [13], genetic analysis [14], and more. This paper introduces a novel domain-independent mutation operator that harnesses the capabilities of deep reinforcement learning (DRL) and transformer models for gene selection. Our aim is to create an operator that can adapt to different problem domains seamlessly, without requiring hand-crafted adjustments to each problem. Instead, BERT mutation uses an online learning algorithm to dynamically optimize the mutation procedure to the domain at hand without relying on predefined problem-specific settings. Specifically, it utilizes deep learning to learn a stochastic policy that—given a masked individual—returns a distribution for all mutated individuals over all possible trees that can be generated using a uniform mutation.

The development of domain-independent mutation operators for GP remains an underexplored area. Commonly used operators include hoist, point, and subtree mutations, which we discuss and compare against our BERT-based operator in Section 4. These traditional operators are simplistic and function by applying stochastic transformations to the genome. The most relevant works identified in the literature that deviate from purely stochastic methods are semantic mutation [15] and LLM mutation [16]. LLM mutation generates a new mutated individual by leveraging prompting with a language model. The current individual is provided to the LLM as context, along with a request to perform a mutation. While the result is a domain-independent individual, it does not utilize the fitness values for improving the mutation. In addition, combining LLMs with GP introduces significant computational costs, and the output generated by LLMs can often be incorrect. Semantic mutation prioritizes genome modifications that yield semantically similar individuals. However, semantic mutation is not domain-independent, as it necessitates defining a similarity function tailored to each domain. Despite this limitation, certain domains may share similarity definitions, broadening its applicability. We expand on LLM and semantic mutations in the next section and compare them with BERT in Section 4.

EAs naturally aim to discover the optimal arrangement of genes and determine which genes are beneficial or detrimental to the population. However, the information accumulated across generations is often underutilized in this process. Some efforts, such as the hall-of-fame (HoF) approach [17], have attempted to address this limitation by allowing high-quality genes to persist across generations, thus preserving some of the knowledge and experience gained during evolution. However, the scope of such preserved information remains quite limited. Evolution may use the HoF method for maintaining a list of high-quality individuals, but it does not gain any insights on how to combine and utilize the accumulated knowledge from all generations. This is where our proposed mutation operator stands out. By leveraging the experience accumulated over generations, our operator uses BERT to learn and optimize the gene mutation based on this historical data. The operator continuously gathers insights throughout the evolutionary process, enabling it to identify superior gene arrangements and more effective genes. This adaptive learning approach ensures that the mutation operator evolves in tandem with the population, resulting in a more informed and efficient optimization process compared to traditional methods.

Using deep learning algorithms for mutation may raise concerns about increased time and computational resources compared to standard mutation methods, e.g., point mutation. It is important to note that the training of the BERT mutation operator does not necessitate additional fitness evaluations. Instead, it uses online learning, wherein the fitness values calculated during the evolutionary process are utilized for training the operator. Nevertheless, to address the time-related concerns, we perform a time analysis, showing that the time cost is negligible, considering the much better solution obtained.

The key contributions of this work are as follows:

• We present a novel, domain-independent, generic mutation operator for GP. This seems to be an underdeveloped area, with only a few operators found in the literature.
• Our proposed mutation operator leverages information accumulated across generations by optimizing BERT to learn which gene arrangements and genes are most effective. Unlike traditional approaches that use limited mechanisms, our operator dynamically adapts and improves throughout the evolutionary process, enabling more efficient and informed optimization.

This paper represents a significant extension of [5]. Key additions include the following: more in-depth experiments, more baselines, more domains, and revisions to the text resulting from constructive feedback.

2. Previous Work

Moraglio et al. [15] introduced Geometric Semantic Mutation (GSM) operators for GP trees as a method to control mutation effects on the semantics of the evolved programs. This operator was used in many works (e.g., [18,19,20]). Unlike random mutations, GSM introduces changes that are intended to alter program behavior in smooth and incremental ways, reducing abrupt disruptions. Instead of merely manipulating syntax, GSM modifies functions in ways that affect their output (or “semantics”) while maintaining a controlled level of similarity to the original function. For example, in symbolic regression, a semantic mutation operator may be defined as $TM=T+\alpha ·(T_{R_1}-T_{R_2})$, where $\alpha$ is the step size, T is the premutated individual, and $T_{R_1},T_{R_2}$ are randomly generated GP trees. This ensures that the semantics of the premutated individual remain close to the mutated individual. However, it is important to note that GSM is not fully domain-independent; it requires specific adjustments per domain to specify how the mutations remain semantically close to the mutated individual. For example, the above-mentioned operator will also work for symbolic classification, though it will not work for the evolution of computer programs. In contrast, our approach is entirely domain-independent and does not require modifications when applied across different domains. Nevertheless, since the authors for GSM defined the operator for symbolic regression and classification, we compare our approach against GSM in Section 4.

Blanchard et al. [21] proposed a method that uses mask prediction to create new molecule sequences during the mutation process. This approach eliminates the need for hand-crafted mutation rules and allows for incorporating larger subsequence rearrangements beyond single-point changes. In the proposed approach, a masked language model is trained on tokenized data of molecules to produce possible mutations for the evolutionary algorithm. While their approach shares similar concepts to our proposed operator (i.e., using a masked language model), it relies on a large dataset of unique individuals from the domain, such as specific molecular arrangements, which limits its transferability to other domains. In contrast, our approach is domain-independent and does not require a large dataset of individual strings in order to produce mutations, but rather learns online during evolution via reinforcement learning what mutations might lead to improved fitness scores.

Recently, many papers employed large language models (LLMs) to improve the performance of evolutionary algorithms [22]. A recent study by Lehman et al. [23] investigated the potential synergy between LLMs and evolutionary computation, particularly focusing on the Evolution through Large Models (ELM) approach. ELM leverages LLMs trained on code to suggest intelligent mutations, enhancing the effectiveness of mutation operators in GP. They employed a diff model, which is an LLM that is optimized to predict the differences between code files based on their commit messages from GitHub data. The mutation process involves maintaining a set of commit messages, which are then randomly selected during evolution, and the model’s predicted diff is applied as a mutation to the code. In this way, they make small tweaks to specific functions and segments of the code by choosing the appropriate commit message. In contrast to their approach, which relies on a fixed set of commit messages, our method learns online and is not restricted to a predefined set of changes that can be made to the program.

Other recent works utilize LLMs in evolutionary computation through a system that introduces LLM-based operators, including mutation, crossover, and replacement [16,24]. Their approach leverages the generative capabilities of LLMs to randomly produce new individuals through prompting based on a premutated individual or a batch of parents. While this method benefits from the creativity and diversity provided by the LLM, it does not incorporate explicit fitness evaluations or policies to guide the mutation process. In contrast, by utilizing fitness scores as a feedback mechanism, our system learns a policy to generate increasingly optimized mutated individuals across generations. This ensures that the evolutionary process is not only guided by randomness but also by an adaptive understanding of what improves population fitness. Moreover, unlike prompting-based methods that may suffer from inconsistencies in the generated outputs, our approach guarantees the correctness of the generated solutions by maintaining domain-specific constraints during mutation. We compare our operator with an LLM mutation operator in Section 4.

3. BERT Mutation

The idea of our BERT-mutation operator is simple in nature: we provide the BERT model with a masked version of a GP tree and “ask” it to predict the masked nodes in such a way that a possibly better individual is formed. We first explain how we use the BERT model and then explain how we train it.

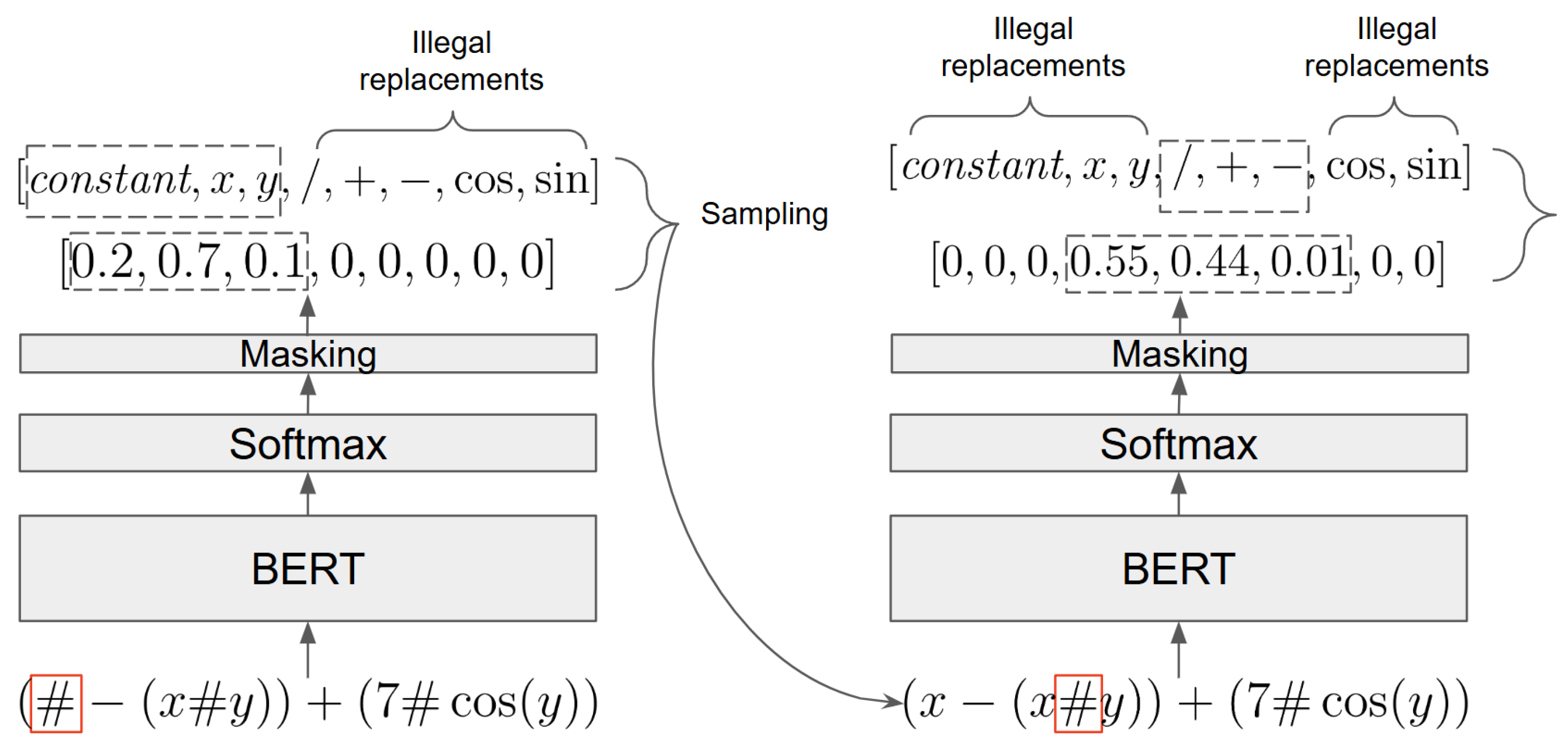
When applied to an individual, the BERT mutation operator randomly masks the individual’s string representation with a masking probability constant. It then uses the BERT model to replace the masks one at a time, taking into account the previous replacements. The replacement process for a given mask is depicted in Figure 4. The trained BERT model produces a distribution over the possible replacements for the given mask. Next, the softmax activation of BERT chooses a replacement by sampling the distribution. The sampling is constrained to include only valid options: When replacing terminals, only terminal tokens are considered; similarly, when replacing functions, only functions with the corresponding arity are allowed. This method ensures that replacements are contextually appropriate. Since the proposed mutation operator does not change the size of the existing GP trees in the population, we introduce more variability to the population by using hoist and subtree mutations with a small probability.

We tokenize each GP tree string representation by assigning an integer to all operators and terminals. Constant terminals are represented using the same tokenized integer representation. Additionally, when the model replaces a masked node with a constant, we draw a random float between predefined boundaries.

More formally, we represent the probability of an individual $i_m$ to be generated by a masked node mutation from individual i as $p(i_m\mid i)$. We use the following chain rule to compute the probability of a mutated individual as a trajectory:

$$p(i_m\mid i)=\prod _{j\in M}p(i_m\left[j\right]\mid i_m[<j],i).$$

(1)

Here, M represents the ordered list of indexes corresponding to the mutated nodes. The probability $p(i_m\left[j\right]\mid i_m[<j],i)$ determines which valid node replacement should occur at index j. In modeling the probability distribution over a gene at index j, it is essential to account for the previously selected mutations as well as the remaining parts of the premutated individual. The term $i_m[<j]=(c_k\in M|k<j)$, along with i, captures this context within the policy by considering the previously selected masked node replacements. Consequently, the probability of an offspring is decomposed into an iterative decision-making process (trajectory), where mutations at each masked index are chosen sequentially. The complete algorithm is given in Algorithm 2.

Algorithm 2 BERT mutation

Require:  i (masked premutated individual), M (ordered list of masked indices), ${\pi }_{\theta }$ (policy distribution parameterized by BERT’s parameters $\theta$), $ϵ$ (exploration probability) Ensure:  $i_m$ (mutated individual), probability of getting the mutated individual given the policy ${\pi }_{\theta }$ and i   1: $i_m\leftarrow i$   2: $P_{trajectory}\leftarrow \left\{\right\}$   3: for each index $j\in M$ do   4:     $p\left(j\right)\leftarrow {\pi }_{\theta }\left(i_m\right)$   5:     Mask illegal replacements in $p\left(j\right)$ by setting their probabilities to 0   6:     Renormalize $p\left(j\right)$   7:     if random() $<ϵ$ then   8:         Choose a random valid replacement r   9:     else 10:         Sample replacement $r\sim p\left(j\right)$ 11:     end if 12:     $P_{trajectory}\leftarrow P_{trajectory}\cup \left\{p\left(j\right)\left[r\right]\right\}$ 13:     $i_m\left[j\right]\leftarrow r$ 14: end for 15: $p_{i_m}\leftarrow {\prod }_{p\in P_{trajectory}}p$ 16: return $i_m$, $p_{i_m}$

Although BERT primarily consists of an encoder transformer block and is not traditionally used as a language model, we draw upon the work of Wang and Cho [25], which demonstrates that BERT functions as a Markov random field language model. This implies that sentences can be generated from it in an MLM trajectory, following a defined sequence.

Since we lack a ground truth solution for the masking, we employ reinforcement learning to train the model. We define the reward signal R as the total fitness improvement achieved over the premutated individual i, which is expressed as follows:

$$R(i_m,i)=fitness\left(i_m\right)-fitness\left(i\right).$$

(2)

We treat the MLM as a Markov decision process, where a trajectory is defined by the sequence of masked node replacements. The process consists of the following components:

• States:

  –

  The current state of the GP tree, including both the masked and unmasked nodes.

  –

  The sequence of previous mutations applied to the tree.

• Actions:

  –

  Selecting a replacement for a masked node within the GP tree.

  –

  The action corresponds to the choice of a legal replacement from a masked node.

• Reward:

  –

  The fitness improvement achieved by the mutated individual compared with the original, premutated individual.

• Transition probability function (depicted in Figure 4):

  –

  The probability of performing action a in state s is modeled by the deep transformer model BERT.

  –

  We sample from this probability distribution to determine the replacement and then move on to the next step in the trajectory.

To balance between exploration and exploitation for the generated mutated individual, we introduce $ϵ$-greedy exploration: with probability $ϵ$, a random action is performed by selecting a single random mask replacement for the mutated individual.

We aim to improve the expected fitness improvement score of the mutated individual $i_m$ that is sampled from the policy distribution ${\pi }_{\theta }$. The policy distribution ${\pi }_{\theta }$ receives an individual genome i and returns an epsilon-greedy-induced masked node mutation distribution generated by our architecture. Thus, our objective function is

$$J(\theta \mid i)={\mathbb{E}}_{i_m\sim {\pi }_{\theta }\left(i\right)}-R(i_m,i).$$

(3)

To optimize the mutation process, we utilize policy-based reinforcement learning with the REINFORCE policy gradient method [26], employing stochastic gradient descent:

$${\Delta }_{\theta }J(\theta \mid i)={\mathbb{E}}_{i_m\sim {\pi }_{\theta }\left(i\right)}[-R(i_m\mid i){\Delta }_{\theta }log{\pi }_{\theta }(i_m\mid i)].$$

(4)

We approximate the gradient in Equation (4) using a Monte Carlo sampling by drawing offspring from the policy distribution. Training the BERT model requires a dataset of individuals and their fitness. To train it without affecting the overall evolutionary computation time, we cache the individuals and their fitness values during the evolutionary process. Once the cache reaches a specified batch size, we use it to train the BERT model. As we demonstrate in the results, the overall evolutionary speed is hardly affected.

4. Evaluation

We used EC-KitY [27] and gplearn [28] for GP and implemented our architecture using PyTorch 2.0.1 [29] and the Transformers [30] Python 3.11.0 packages. Our code and datasets can be accessed at https://github.com/EC-KitY/BERT-Mutation (accessed on 20 February 2025).

4.1. Problem Domains and Datasets

To assess the performance of the proposed operator, we carried out extensive experiments on various domains and datasets.

4.1.1. Symbolic Regression

• The Airfoil Self-Noise regression dataset, containing five features and 1503 instances [31].
• The Concrete Compressive Strength regression dataset, containing eight features and 1030 instances [32].
• The Friedman 1–3 regression problems [33]. We generated 5000 instances using scikit-learn. The problems are defined as follows:

  (a)

  $\mathit{Friedman}\text{-}\mathit{1}:y=10·sin(\pi ·x_0·x_1)+20{(x_2-0.5)}^2+10x_3+5x_4+\mathit{noise}·N(0,1)$.

  (b)

  $\mathit{Friedman}\text{-}\mathit{2}:y={(x_0^2+{(x_1·x_2-({\displaystyle \frac{1}{x_2·x_4}}))}^2)}^{0.5}+\mathit{noise}·N(0,1)$.

  (c)

  $\mathit{Friedman}\text{-}\mathit{3}:y=arctan({\displaystyle \frac{(x_1·x_2-(\frac{1}{x1·x_3}))}{x_0}})+\mathit{noise}·N(0,1)$.

• We generated 5000 instances in the ranges of $\left[-10,10\right]$ for the following equations:

  (a)

  $\mathit{f}\mathit{2}:y={(x_0-3)}^4+{(x_1-2)}^3$.

  (b)

  $\mathit{non}\text{-}\mathit{analytic}:y={(x+1)}^2 \mathit{if} x>0 \mathit{else} sin\left(x\right)$.

4.1.2. Symbolic Binary Classification

• The Tic-Tac-Toe Endgame dataset, containing nine features and 958 instances [34].
• The Breast Cancer Wisconsin dataset, containing 30 features and 569 instances [35].
• The Occupancy Detection dataset, containing six features and 20560 instances [36].
• The Diabetic Retinopathy Debrecen dataset, containing 19 features and 1151 instances [37].
• The QSAR Androgen Receptor dataset, containing 1024 features and 1687 instances [38].
• The Census Income dataset, containing 14 features and 48842 instances [39].

4.1.3. Artificial Ant Problem

The Artificial Ant problem is a well-known benchmark commonly used in GP. The task involves designing a strategy to control an agent—referred to as the artificial ant—within a predefined grid environment, as shown in Figure 5. Certain cells in the grid contain “food” pellets distributed along a specific trail. The objective is to maximize the number of food cells the agent can collect within a limited number of moves.

The Artificial Ant domain differs substantially from the previous domains due to two key reasons. First, evaluation is based on a simulation rather than a dataset of examples, introducing a dynamic and interactive component to the evaluation process. Second—unlike regression and classification—there is no semantic mutation definition for the Artificial Ant domain in the literature (and we have been unable to devise one).

We used the following primitive set for the construction of the GP trees:

• is_food_ahead is a primitive that executes its first argument if there is food in front of the ant; otherwise, it executes its second argument.
• prog2 and prog3 execute their children in order, from the first to the last. For instance, prog2 will first execute its first argument, then its second.
• move_front makes the artificial ant move one cell forward. This is a terminal.
• turn_right and turn_left make the artificial ant turn clockwise and counter-clockwise without changing its position. Those are also terminals.

We used five benchmark environments from [40]. For fitness evaluation, we used the total number of food cells visited over a maximum of 300 moves. To support 300 moves, the tree size must be considerably larger than the tree sizes of the previous benchmarks. As we will show, the tree size dramatically affects the average generation time.

4.2. Baselines

We compared against the following baseline mutation operators.

Hoist mutation. This is a bloat-preventing mutation operation [41]. The purpose of this mutation is to remove genetic material from individuals. In hoist mutation, an individual from the population is selected, and a random subtree within this individual is identified. From this selected subtree, a further random subtree is chosen. This second subtree, which is a subset of the first, is then “hoisted”, or elevated, to replace the original subtree of which it was a part. The result is that the individual’s overall structure is simplified, typically resulting in a more compact and potentially more efficient solution.

Subtree mutation. This operator involves taking an individual and altering it by focusing on a specific segment of its structure [42]. In this process, a random subtree within an individual is chosen to be replaced. To do this, a new subtree—often referred to as a donor subtree—is generated randomly. This donor subtree is then inserted into the original tree at the point of the removed subtree. The resulting modified tree, which integrates the new subtree, becomes an offspring in the next generation.

Point mutation. This operator modifies an individual by selecting random nodes within it for replacement [43]. In this process, terminals are substituted with other terminals, and functions are replaced with other functions that require the same number of arguments as the original node. This selective alteration ensures that the structural integrity and functionality of the tree are maintained while introducing genetic diversity. The modified tree, now sporting these changes, becomes an offspring in the subsequent generation. This mechanism is crucial for exploring the solution space and enhancing diversity within the population, potentially leading to improved solutions over successive generations.

Mixed mutation. This operator uses all the previous operators with equal probability to be chosen.

Semantic mutation. Semantic mutation [15] aims to produce offspring functions that differ slightly from their parent functions in a smooth, controlled manner. The suggested operator in the paper applies small perturbations to the premutated individual, thus ensuring that the new offspring is semantically close. For regression and classification problems, the mutation is defined as follows: $TM=T+\alpha ·(T_{R_1}-T_{R_2})$. Therein, $\alpha$ is the step size, T is the premutated individual, and $T_{R_1},T_{R_2}$ are randomly generated GP trees. We used a constant step size of $0.1$ across all experiments. Notably, semantic mutation is not defined for the Artificial Ant problem, further highlighting the strength of BERT mutation, which is fully domain-independent and adaptable to a wide range of tasks.

LLM mutation [16] generates a new mutated individual by leveraging prompting with a language model. The individual is provided to the LLM as context, along with a prompt to perform a mutation constrained by a predefined list of legal functions and terminals. We adhered to the implementation details outlined in [16] and utilized gpt-4o-mini as the LLM for this approach. It is worth noting that this baseline is significantly more computationally expensive; furthermore, LLM access often involves paid, token-based API requests, adding further to the cost.

5. Results

We used a population size of 128 individuals run for 500 generations for the regression problems and 50 generations for the Artificial Ant problem. We initialized the population using the ramped half-and-half technique, where the depth of grown trees was in the range of $\left[2,10\right]$. We used a crossover probability of 0.6 with a subtree crossover probability and a mutation probability of 0.1 for the BERT mutation and 0.05 for the subtree and hoist mutation. The fitness measures we used were RMSE for the regression problems and AUC-ROC for the classification problems. We repeated each experiment 10 times and reported on the average best fitness value of the last generation. We performed a train-test split with 10% of the data left to the test set. We used NVIDIA RTX-6000 GPUs to run our suggested mutation.

We utilized a batch size of 16, a word embedding dimension of 32, an internal embedding dimension of 128, four attention heads, and three transformer layers. For the epsilon-greedy approach, we set $ϵ=0.1$. The maximum context length was configured as 2048 tokens for the regression and classification tasks, while for the Artificial Ant problem, a larger context length of 32,768 tokens was employed to accommodate the construction of larger trees. For efficiency, we allowed a maximum of 200 nodes to be selected for mutation.

Table 1. Comparison of mutation operators across various datasets for symbolic regression test set fitness. The reported numbers represent the RMSE of the best individual on the test set. The numbers are averaged over 10 experiments. Lower values indicate better performance. Standard deviations are given in parentheses. Best results are boldfaced.

Dataset	BERT Mutation	Mixed	Subtree	Point	Hoist	Semantic	LLM Mutation
AirfoilSelfNoise	$\mathbf{6}.\mathbf{76}$  $\left(0.98\right)$	$8.85$  $\left(4.80\right)$	$9.30$  $\left(4.31\right)$	$16.35$  $\left(10.93\right)$	$24.80$  $\left(14.30\right)$	$7.11$  $\left(2.83\right)$	$15.08$  $\left(3.15\right)$
concrete_data	$\mathbf{8}.\mathbf{86}$  $\left(1.22\right)$	$12.89$  $\left(3.80\right)$	$12.12$  $\left(2.70\right)$	$14.75$  $\left(4.98\right)$	$18.90$  $\left(5.75\right)$	$9.38$  $\left(1.71\right)$	$10.58$  $\left(4.45\right)$
friedman1	$\mathbf{2}.\mathbf{08}$  $\left(0.12\right)$	$2.97$  $\left(1.07\right)$	$2.75$  $\left(0.88\right)$	$2.90$  $\left(1.07\right)$	$4.22$  $\left(0.78\right)$	$3.78$  $\left(0.93\right)$	$3.17$  $\left(1.37\right)$
friedman2	$\mathbf{5}.\mathbf{13}$  $\left(1.29\right)$	$11.29$  $\left(4.71\right)$	$8.64$  $\left(3.79\right)$	$11.17$  $\left(4.50\right)$	$57.90$  $\left(129.15\right)$	$9.72$  $\left(2.98\right)$	$12.28$  $\left(4.49\right)$
friedman3	$\mathbf{0}.\mathbf{30}$  $\left(0.06\right)$	$0.39$  $\left(0.03\right)$	$0.39$  $\left(0.03\right)$	$0.40$  $\left(0.01\right)$	$0.39$  $\left(0.04\right)$	$0.33$  $\left(0.03\right)$	$0.36$  $\left(0.01\right)$
f2	$\mathbf{5}.\mathbf{42}$  $\left(0.83\right)$	$8.82$  $\left(6.79\right)$	$6.16$  $\left(2.00\right)$	$12.86$  $\left(7.06\right)$	$17.02$  $\left(7.06\right)$	$8.31$  $\left(2.86\right)$	$9.34$  $\left(5.83\right)$
non_analytic	$\mathbf{0}.\mathbf{19}$  $\left(0.27\right)$	$2.60$  $\left(3.51\right)$	$2.03$  $\left(1.97\right)$	$1.32$  $\left(1.22\right)$	$5.67$  $\left(4.35\right)$	$3.63$  $\left(3.24\right)$	$3.04$  $\left(3.54\right)$

shows the regression results,

Table 2. Comparison of mutation operators across various datasets for symbolic classification test set fitness. The reported numbers represent the AUC-ROC of the best individual. The numbers are averaged over 10 experiments. Higher values indicate better performance. Standard deviations are given in parentheses. Best results are boldfaced.

Dataset	BERT Mutation	Mixed	Subtree	Point	Hoist	Semantic	LLM Mutation
adult_income	$\mathbf{0}.\mathbf{778}$  $\left(0.026\right)$	$0.590$  $\left(0.103\right)$	$0.686$  $\left(0.111\right)$	$0.658$  $\left(0.120\right)$	$0.647$  $\left(0.112\right)$	$0.649$  $\left(0.111\right)$	$0.716$  $\left(0.111\right)$
cancer	$\mathbf{0}.\mathbf{987}$  $\left(0.013\right)$	$0.939$  $\left(0.040\right)$	$0.958$  $\left(0.029\right)$	$0.874$  $\left(0.137\right)$	$0.865$  $\left(0.145\right)$	$0.968$  $\left(0.015\right)$	$0.916$  $\left(0.036\right)$
diabetic	$\mathbf{0}.\mathbf{730}$  $\left(0.032\right)$	$0.691$  $\left(0.026\right)$	$0.707$  $\left(0.040\right)$	$0.683$  $\left(0.000\right)$	$0.677$  $\left(0.010\right)$	$0.668$  $\left(0.024\right)$	$0.710$  $\left(0.040\right)$
occupancy	$\mathbf{0}.\mathbf{989}$  $\left(0.008\right)$	$0.931$  $\left(0.087\right)$	$0.971$  $\left(0.059\right)$	$0.873$  $\left(0.147\right)$	$0.826$  $\left(0.183\right)$	$0.913$  $\left(0.059\right)$	$0.956$  $\left(0.083\right)$
tic-tac-toe	$\mathbf{0}.\mathbf{644}$  $\left(0.04\right)$	$0.592$  $\left(0.069\right)$	$0.609$  $\left(0.063\right)$	$0.522$  $\left(0.047\right)$	$0.533$  $\left(0.047\right)$	$0.558$  $\left(0.041\right)$	$0.548$  $\left(0.083\right)$
qsar	$\mathbf{0}.\mathbf{728}$  $\left(0.052\right)$	$0.637$  $\left(0.105\right)$	$0.621$  $\left(0.094\right)$	$0.660$  $\left(0.082\right)$	$0.524$  $\left(0.039\right)$	$0.520$  $\left(0.021\right)$	$0.614$  $\left(0.071\right)$

shows the classification results, and

Table 3. Comparison of mutation operators across different Artificial Ant trail instances. The reported numbers represent performance scores. Higher values indicate better performance. Standard deviations are given in parentheses. Best results are boldfaced.

Instance	BERT Mutation	Hoist	Mixed	Point	Subtree
Auxiliary 1	$\mathbf{43}.\mathbf{1}$  $\left(6.22\right)$	$36.7$  $\left(6.53\right)$	$37.2$  $\left(1.54\right)$	$37.7$  $\left(2.54\right)$	$38.8$  $\left(4.56\right)$
Auxiliary 2	$\mathbf{35}.\mathbf{2}$  $\left(5.22\right)$	$31.6$  $\left(4.69\right)$	$32.2$  $\left(3.01\right)$	$33.1$  $\left(4.35\right)$	$30.9$  $\left(4.33\right)$
John Muir	$\mathbf{48}.\mathbf{3}$  $\left(6.56\right)$	$35.7$  $\left(6.16\right)$	$37.2$  $\left(6.14\right)$	$34.9$  $\left(4.25\right)$	$34.4$  $\left(6.83\right)$
Santa Fe	$\mathbf{31}.\mathbf{5}$  $\left(4.76\right)$	$24.0$  $\left(5.71\right)$	$26.1$  $\left(2.81\right)$	$27.0$  $\left(2.49\right)$	$23.0$  $\left(2.05\right)$
Los Altos	$\mathbf{32}.\mathbf{3}$  $\left(7.31\right)$	$19.4$  $\left(3.77\right)$	$25.2$  $\left(6.25\right)$	$22.0$  $\left(3.55\right)$	$20.6$  $\left(2.98\right)$

shows the Artificial Ant results. Notably, our BERT operator outperformed all other operators for all domains and datasets. In the regression and classification domains, where semantic mutation is specifically defined and designed for these domains, our operator also outperformed semantic mutation. The LLM mutation was not applicable for the Artificial Ant domain due to the trees’ size.

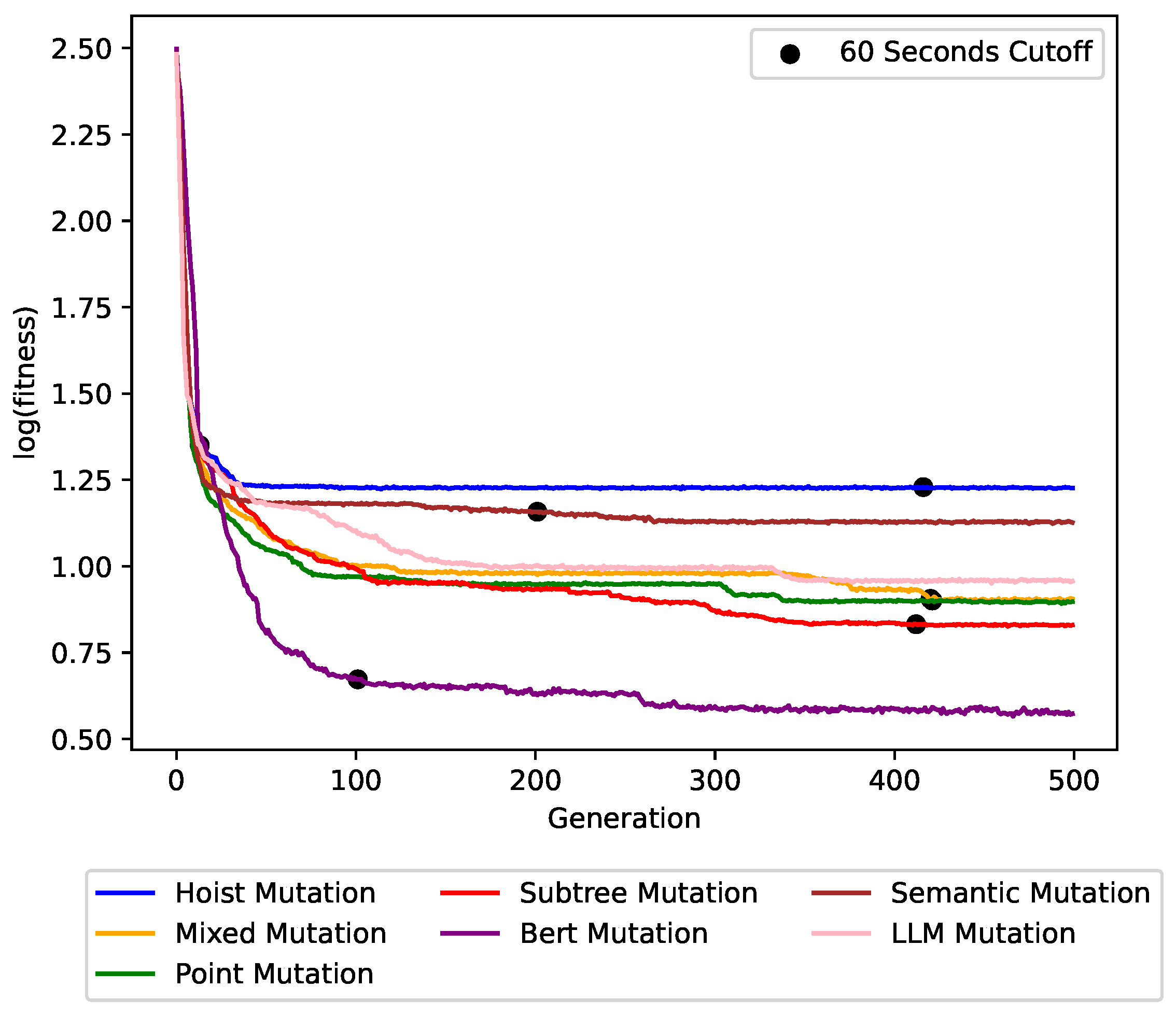
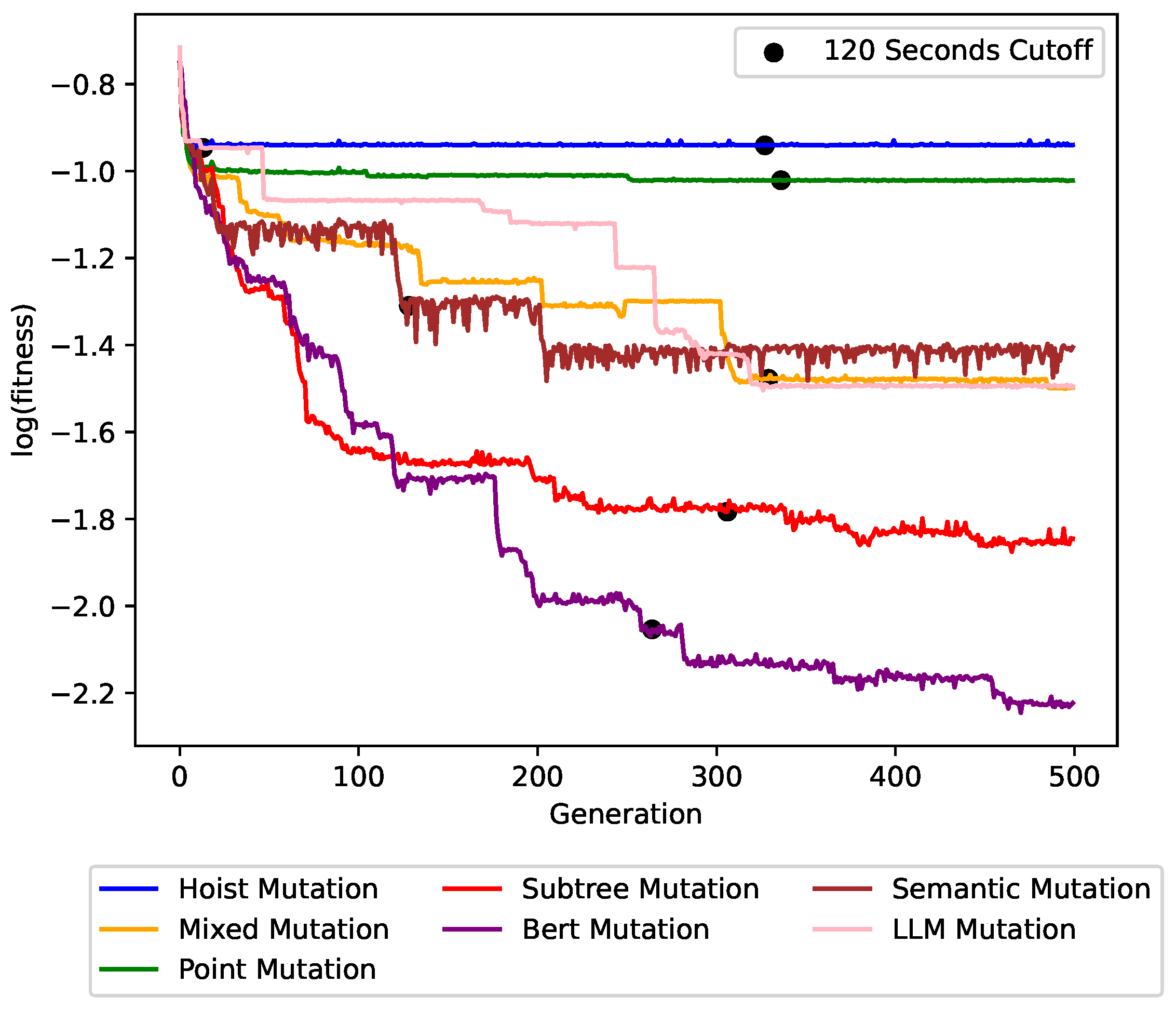
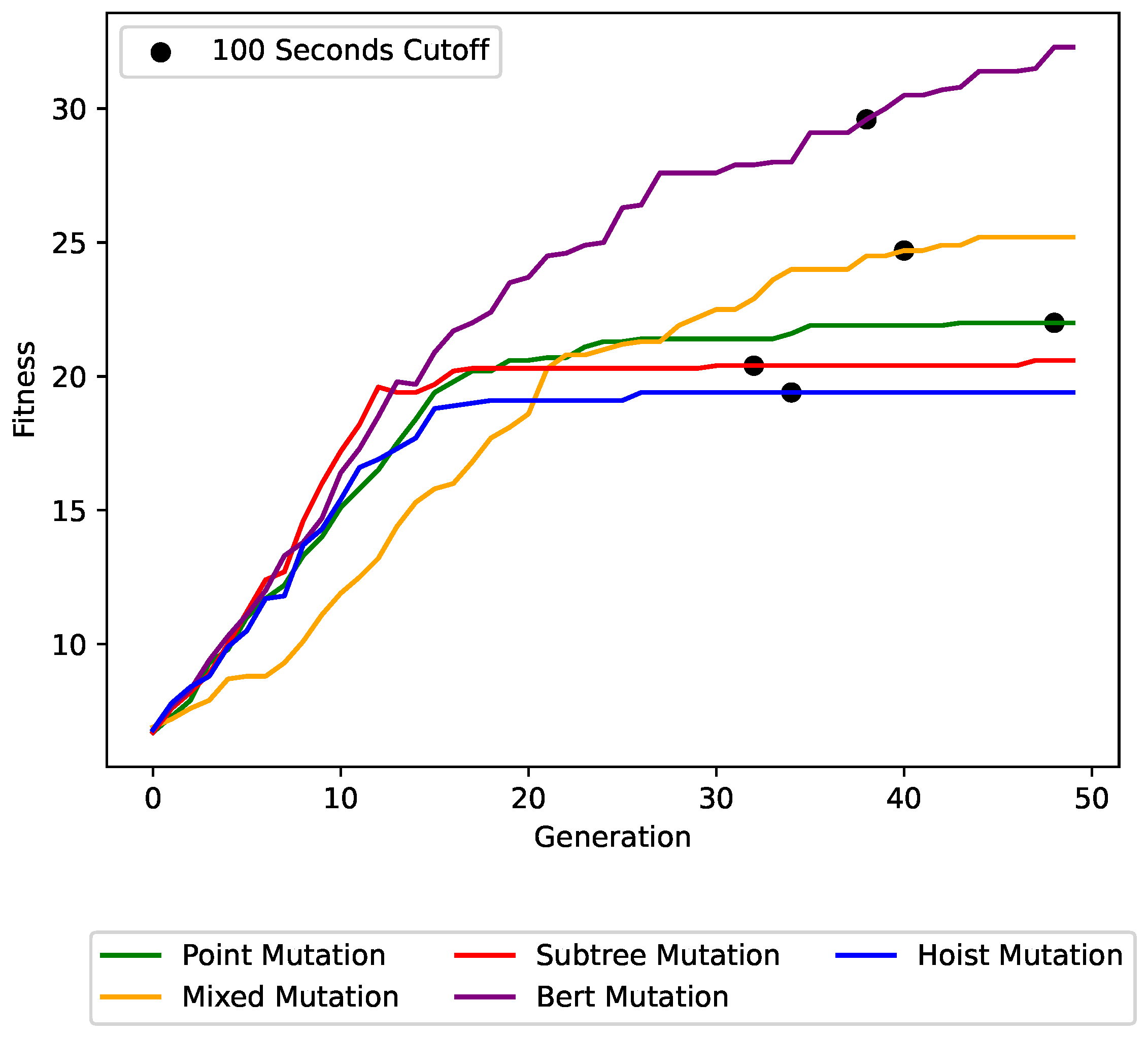
Figure 6, Figure 7 and Figure 8 show the impact of the different mutation operators on the maximum fitness value per generation for the concrete symbolic regression dataset, the cancer symbolic classification dataset, and the Artificial Ant Los Altos trail instance, respectively. Each plot line represents a different mutation operator, allowing for a direct comparison of their performance over successive generations. BERT mutation outperformed all other mutation operators with a clear improvement in solution quality and convergence speed. This trend persisted across other problem instances.

The figures also show the trade-off between the runtime and the achieved solution quality. The cutoff times are denoted in the graphs. After 20–120 s only, our BERT mutation was far better than the baselines.

In

Table 4. Mean generation times (in seconds) of each operator.

	Regression & Classification			Ant Colony
Operator	Mean	Std	Max	Mean	Std	Max
BERT Mutation	$0.328$	$0.145$	$0.672$	$2.991$	$2.858$	$10.923$
Hoist Mutation	$0.145$	$0.061$	$0.307$	$4.528$	$4.120$	$14.578$
Mixed Mutation	$0.146$	$0.062$	$0.325$	$2.55$	$1.920$	$7.495$
Point Mutation	$0.145$	$0.062$	$0.310$	$3.441$	$3.166$	$11.997$
Subtree Mutation	$0.139$	$0.066$	$0.329$	$6.936$	$7.473$	$28.178$
Semantic Mutation	$0.280$	$0.077$	$0.634$	-	-	-
LLM Mutation	$6.450$	$7.018$	$33.116$	-	-	-

, we compare the time per generation for each operator. For symbolic regression and classification tasks, our operator was slightly slower than the baseline operators, excluding LLM mutation, with a run time increase of approximately 0.2 s per generation. However, the trade-off between run-time and solution quality is evident. Notably, the running times for LLM mutation were significantly higher than all other operators. This is due to the substantial computational resources required by the model, as well as the overhead introduced by its reliance on API requests.

The run times for the Artificial Ant Problem present a more intriguing scenario. For this domain, the fitness evaluations for all baselines were more computationally expensive due to the much larger individual size (see Figure 9). Certain operators generated larger trees early on in the evolutionary process, further inflating the cost of fitness evaluations. In contrast, our operator maintained relatively small tree sizes, yet it was efficient. This is achieved by optimizing fitness scores during earlier generations, when the trees are still smaller, effectively reducing computational costs in this challenging domain.

6. Limitations

The above sections have highlighted the advantages of BERT mutation. However, in its current form, certain limitations may arise in practical applications.

One limitation of our model lies in BERT’s fixed context window, which restricts the mutation operator from processing individuals longer than the supported context length. In the ant colony experiments, we increased the context size to accommodate larger trees. However, expanding the context window increased the model’s run time and computational complexity, as longer inputs require more processing power and memory. Future research could address this limitation by exploring alternative tokenization techniques for GP trees. These techniques could aim to create more efficient representations of GP individuals, potentially enabling support for larger context windows without a proportional increase in computational overhead. This approach could make BERT mutation more scalable and applicable to a broader range of problem domains.

Additionally, the underlying BERT model does not fully leverage the structural properties of the input space, which is inherently graph-based. This presents an opportunity for future work to investigate the use of Graph Neural Networks (GNNs) [44] as the basis for policy probability models. GNNs could better capture the relational and hierarchical nature of GP trees, potentially improving performance and efficiency.

7. Concluding Remarks

In this paper, we introduced BERT mutation, a novel mutation operator for Genetic Programming that leverages advanced Natural Language Processing techniques, specifically the Masked Language Modeling approach, to intelligently suggest fitness-improving node replacements within GP trees. By integrating deep reinforcement learning and the BERT transformer architecture, BERT mutation dynamically adapts to the evolutionary process, significantly enhancing convergence and solution quality across various classification and regression problems.

Our findings demonstrate the potential of combining state-of-the-art deep learning models with evolutionary algorithms to create adaptive, domain-independent operators that outperform traditional approaches. By harnessing the information accumulated across generations, BERT mutation represents a new paradigm in mutation design, offering a powerful tool for optimizing gene arrangements in GP.

While this work focuses on the application of BERT mutation in GP, its design as a string-based mutation operator allows it to be extended to Genetic Algorithms (GAs). This opens up exciting opportunities to test its effectiveness in GA settings, where candidate solutions are represented as strings of bits, integers, or real numbers. We plan to explore this avenue in future studies, assessing how BERT mutation influences convergence and performance in GA frameworks.

Additionally, we believe that BERT models—especially those pretrained on code datasets—hold significant promise for advancing code evolution tasks. By leveraging the contextual understanding of programming constructs offered by such pretrained models, BERT mutation could further improve the optimization of program structures in GP.

Through these explorations, we aim to extend the applicability of BERT mutation and contribute to the growing synergy between evolutionary computation and deep learning. By doing so, we hope to unlock new possibilities in adaptive optimization, bridging the gap between modern machine learning and classical evolutionary algorithms.