Ninth-Order Two-Step Methods with Varying Step Lengths

Abstract

This study investigates a widely recognized ninth-order numerical technique within the explicit two-step family of methods (a.k.a. hybrid Numerov-type methods). To boost its performance, we incorporate an economical step-size control algorithm that, after each iteration, either preserves the current step length, reduces it by half, or doubles it. Any additional off-grid points needed by this strategy are computed using a local interpolation routine. Indicative numerical experiments confirm the substantial efficiency gains realized by this method. It is particularly adept at resolving differential equations with oscillatory dynamics, delivering high precision with fewer function evaluations. Furthermore, a detailed Mathematica implementation is supplied, enhancing usability and fostering further research in the field. By simultaneously improving computational efficiency and accuracy, this work offers a significant contribution to the numerical analysis community.

1. Introduction

Our research delves into a specific type of second-order initial value problem (IVP), characterized by the following equation:

$${\psi }^{″}=f(x,\psi ),\psi \left(x_0\right)={\psi }_0,{\psi }^{\prime }\left(x_0\right)={\psi }_0^{\prime },$$

(1)

where

$$f:\mathbb{R}\times {\mathbb{R}}^{\nu }⟶{\mathbb{R}}^{\nu }\mathrm{and}{\psi }_0,{\psi }_0^{\prime }\in {\mathbb{R}}^{\nu }.$$

Notably, ${\psi }^{\prime }$ does not appear explicitly in (1).

The Numerov method is a well-established numerical technique for advancing the solution from $x_{\kappa }$ to $x_{\kappa +1}=x_{\kappa }+h$. Its formula is given by the following:

$${\psi }_{\kappa +1}=2{\psi }_{\kappa }-{\psi }_{\kappa -1}+\frac{h^2}{12}\left(f_{\kappa +1}+10f_{\kappa }+f_{\kappa -1}\right),$$

where

$${\psi }_{\kappa }\approx \psi \left(x_{\kappa }\right)\mathrm{and}{f}_{\kappa }\approx {\psi }^{″}\left(x_{\kappa }\right)=f(x_{\kappa },{\psi }_{\kappa }),$$

with $f_{\kappa },{\psi }_{\kappa }\in {\mathbb{R}}^{\nu }$.

Pioneers such as Hairer [1], Cash [2], and Chawla [3] introduced hybrid implicit Numerov-type methods approximately 40–45 years ago. These methods utilized off-grid points and addressed the challenge of P-stability, which is crucial for stiff oscillatory problems. Later, Chawla [4] proposed a modified explicit Numerov scheme:

$$\begin{array}{c}{v}_1={\psi }_{\kappa -1},\\ v_2={\psi }_{\kappa },\\ v_3=2{\psi }_{\kappa }-{\psi }_{\kappa -1}+h^{2}f(x_{\kappa },v_2),\\ {\psi }_{\kappa +1}-2{\psi }_{\kappa }+{\psi }_{\kappa -1}=\frac{1}{12}{h}^2\left(f(x_{\kappa +1},v_3)+10f(x_{\kappa },v_2)+f(x_{\kappa -1},v_1)\right),\end{array}$$

(2)

where h is the constant step size:

$$h=x_{\kappa }-x_{\kappa -1}=x_{\kappa +1}-x_{\kappa }=\cdots =x_1-x_0.$$

The vectors ${\psi }_{\kappa +1},{\psi }_{\kappa },{\psi }_{\kappa -1}$ approximate $\psi (x_{\kappa }+h),\psi \left(x_{\kappa }\right),\psi (x_{\kappa }-h)$, respectively, while the stages $v_1,v_2,v_3\in {\mathbb{R}}^{\nu }$ represent the function evaluations used by the method. We leverage the information at the grid:

$$v_1={\psi }_{\kappa -1},v_2={\psi }_{\kappa }.$$

Given that $f(x_{\kappa -1},v_1)$ is calculated in the previous step, only $f(x_{\kappa +1},v_3)$ and $f(x_{\kappa },v_2)$ need to be evaluated at each step, resulting in just two function evaluations per step.

Following this, Tsitouras developed a technique drawing inspiration from Runge–Kutta–Nyström (RKN) methods [5], which significantly reduced computational overhead. As a result, only four steps are required to construct a sixth-order method, whereas earlier approaches necessitated six function evaluations (see [6]). Building upon this progress, our research group has extensively explored this topic. Tsitouras developed eighth-order methods that require nine steps per iteration in [7], and concurrently, a team of Spanish researchers conducted notable studies on similar problems [8,9,10].

A distinction must be made between the term “second-order initial value problem”, which signifies the presence of ${\psi }^{″}$, and the algebraic order of a numerical scheme, which defines its degree of precision.

Despite these advancements, current numerical methods often struggle with efficiency when applied to differential equations with oscillatory behavior. Our work addresses this limitation by optimizing the step-length adjustment in a ninth-order Numerov-type method, thereby considerably enhancing computational performance.

Here, we present a ninth-order Numerov-type approach that uniquely integrates a variable step-length algorithm, substantially improving computational efficiency for solving second-order IVPs with oscillatory behavior. This study aims to introduce a novel method specifically designed to better handle problems with periodic solutions. Traditionally, various characteristics of a basic test equation are utilized for this purpose; our innovation involves fine-tuning the free parameters across a broad range of relevant problems. Differential evolution is employed for this optimization, and we anticipate that this strategy will yield a method exceptionally well-suited for oscillatory challenges.

The main contributions of this work are as follows:

• The construction of a ninth-order two-step method with variable step lengths, tailored for second-order oscillatory problems;
• The development of an embedded error estimation mechanism enabling efficient step-size control through symbolic interpolation;
• A detailed Mathematica implementation that facilitates symbolic order verification and adaptive logic; and (iv) numerical evidence demonstrating the method’s practical advantages in terms of accuracy and computational efficiency on classical orbital problems such as the Kepler and Arenstorf systems.

2. Derivation of Hybrid Numerov Methods

To address the given problem via advanced algebraic methodologies, we first express the independent parameter t as a component of $\psi$. Consequently, without any loss of generality, we concentrate on the autonomous formulation:

$${\psi }^{″}=f\left(\psi \right).$$

A blended Numerov algorithm utilizing s stages (as delineated in [7]) is formulated as follows:

$$\begin{array}{c}{\psi }_{\kappa +1}=2{\psi }_{\kappa }-{\psi }_{\kappa -1}+h^2·\left(b\otimes I_s\right)·f\left(v\right)\\ v=\left(\mathbf{1}+c\right)\otimes {\psi }_{\kappa }-c\otimes {\psi }_{\kappa -1}+h^2·\left(A\otimes I_s\right)·f\left(v\right)\end{array}$$

(3)

where $I_s\in {\mathbb{R}}^{s \times s}$ denotes the identity matrix, and $A\in {\mathbb{R}}^{s \times s}$, $b^T\in {\mathbb{R}}^s$, and $c\in {\mathbb{R}}^s$ signify the coefficient matrices of the approach, with the following:

$$\mathbf{1}={[11\cdots 1]}^T\in {\mathbb{R}}^s.$$

To delineate these coefficients, we employ the Butcher tableau [11,12]:

$$\begin{array}{cc}\hfill c\hfill & A\\ & b\end{array}.$$

Since the function assessments are conducted in a sequential manner, these techniques are explicit, implying that A is a strictly lower triangular matrix. For the scenario where $s=9$, the matrices assume the following configuration:

$$\begin{array}{ccc}\hfill f_{\kappa -1}& =& f\left(x_{\kappa -1},{\psi }_{\kappa -1}\right)={\psi }_{\kappa -1}^{″},\hfill \\ \hfill f_{\kappa }& =& f\left(x_{\kappa },{\psi }_{\kappa }\right)={\psi }_{\kappa }^{″},\hfill \\ \hfill {\psi }_{\alpha }& =& c_3{\psi }_{\kappa -1}+\left(1-c_3\right){\psi }_{\kappa }+h^2\left(a_{31}{f}_{\kappa -1}+a_{d2}{f}_{\kappa }\right),\hfill \\ \hfill f_{\alpha }& =& f\left(x_{\kappa }+c_{3}h,{\psi }_{\alpha }\right),\hfill \\ \hfill {\psi }_{\beta }& =& c_4{\psi }_{\kappa -1}+\left(1-c_4\right){\psi }_{\kappa }+h^2\left(a_{41}{f}_{\kappa -1}+a_{42}{f}_{\kappa }+a_{43}{f}_{\alpha }\right),\hfill \\ \hfill f_{\beta }& =& f\left(x_{\kappa }+c_{4}h,{\psi }_{\beta }\right),\hfill \\ \hfill {\psi }_{\gamma }& =& c_5{\psi }_{\kappa -1}+\left(1-c_5\right){\psi }_{\kappa }+h^2\left(a_{51}{f}_{\kappa -1}+a_{52}{f}_{\kappa }+a_{53}{f}_{\alpha }+a_{54}{f}_{\beta }\right),\hfill \\ \hfill f_{\gamma }& =& f\left(x_{\kappa }+c_{5}h,{\psi }_{\gamma }\right),\hfill \\ \hfill {\psi }_{\delta }& =& c_6{\psi }_{\kappa -1}+\left(1-c_6\right){\psi }_{\kappa }+h^2\left(a_{61}{f}_{\kappa -1}+a_{62}{f}_{\kappa }+a_{63}{f}_{\alpha }+a_{64}{f}_{\beta }+a_{65}{f}_{\gamma }\right),\hfill \\ \hfill f_{\delta }& =& f\left(x_{\kappa }+c_{6}h,{\psi }_{\delta }\right),\hfill \\ \hfill {\psi }_{ϵ}& =& c_7{\psi }_{\kappa -1}+\left(1-c_7\right){\psi }_{\kappa }+h^2\left(a_{71}{f}_{\kappa -1}+a_{72}{f}_{\kappa }+a_{73}{f}_{\alpha }+a_{74}{f}_{\beta }+a_{75}{f}_{\gamma }+a_{76}{f}_{\delta }\right),\hfill \\ \hfill f_{ϵ}& =& f\left(x_{\kappa }+c_{7}h,{\psi }_{ϵ}\right),\hfill \\ \hfill {\psi }_{\zeta }& =& c_8{\psi }_{\kappa -1}+\left(1-c_8\right){\psi }_{\kappa }+h^2\left(\begin{array}{c}{a}_{81}{f}_{\kappa -1}+a_{82}{f}_{\kappa }+a_{83}{f}_{\alpha }\\ +a_{84}{f}_{\beta }+a_{85}{f}_{\gamma }+a_{86}{f}_{\delta }+a_{87}{f}_{ϵ}\end{array}\right),\hfill \\ \hfill f_{\zeta }& =& f\left(x_{\kappa }+c_{8}h,{\psi }_{\zeta }\right),\hfill \\ \hfill {\psi }_{\eta }& =& c_9{\psi }_{\kappa -1}+\left(1-c_9\right){\psi }_{\kappa }+h^2\left(\begin{array}{c}{a}_{91}{f}_{\kappa -1}+a_{92}{f}_{\kappa }+a_{93}{f}_{\alpha }+a_{94}{f}_{\beta }\\ +a_{95}{f}_{\gamma }+a_{96}{f}_{\delta }+a_{97}{f}_{ϵ}+a_{98}{f}_{\zeta }\end{array}\right),\hfill \\ \hfill f_{\eta }& =& f\left(x_{\kappa }+c_{9}h,{\psi }_{\eta }\right),\hfill \\ \hfill {\psi }_{\kappa +1}& =& 2{\psi }_{\kappa }-{\psi }_{\kappa -1}+h^2\left(\begin{array}{c}{b}_1{f}_{\kappa -1}+b_2{f}_{\kappa }+b_3{f}_{\alpha }+b_4{f}_{\beta }\\ +b_4{f}_{\gamma }+b_6{f}_{\delta }+b_6{f}_{ϵ}+b_1{f}_{\zeta }+b_1{f}_{\eta }\end{array}\right).\hfill \end{array}$$

Since we assumed the following above:

$$b_3=0,b_5=b_4,b_7=b_6,b_8=b_1,c_5=-c_4,c_7=-c_6,c_8=0,c_9=1,$$

the associated matrices take the following form:

$$A=\left[\begin{array}{ccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ a_{31}& a_{32}& 0& 0& 0& 0& 0& 0& 0\\ a_{41}& a_{42}& a_{43}& 0& 0& 0& 0& 0& 0\\ a_{51}& a_{52}& a_{53}& a_{54}& 0& 0& 0& 0& 0\\ a_{61}& a_{62}& a_{63}& a_{64}& a_{65}& 0& 0& 0& 0\\ a_{71}& a_{72}& a_{73}& a_{74}& a_{75}& a_{76}& 0& 0& 0\\ a_{81}& a_{82}& a_{83}& a_{84}& a_{85}& a_{86}& a_{87}& 0& 0\\ a_{91}& a_{92}& a_{93}& a_{94}& a_{95}& a_{96}& a_{97}& a_{98}& 0\end{array}\right],$$

$$b=\left[\begin{array}{ccccccccc}{b}_1& b_2& 0& b_4& b_4& b_6& b_6& b_1& b_1\end{array}\right]$$

and

$$c={\left[\begin{array}{ccccccccc}-1& 0& c_3& c_4& -c_4& c_6& -c_6& 0& 1\end{array}\right]}^T.$$

Since $f_{\kappa -1}$ is derived from the preceding iteration, only seven function evaluations are required per step. To attain an algebraic order of eight, it is crucial to eliminate the corresponding truncation error components (refer to [13]).

The proposed technique comprises a total of 34 parameters. As previously highlighted, there exist 27 coefficients associated with the matrix A, explicitly:

$$a_{31},a_{32},a_{41},a_{42},a_{43},\cdots ,a_{87}.$$

Furthermore, 4 coefficients correspond to the vector b, while 3 components belong to the vector c. The total number of order conditions at different accuracy levels aligns with those of Runge–Kutta–Nyström techniques, as illustrated in

Table 1. Number of order constraints.

Order p	1	2	3	4	5	6	7	8	9	10	11
No of conditions	1	1	2	3	6	10	20	36	72	137	275

. To obtain ninth-order precision, a total of

$$1+1+2+3+6+10+20+36+72=151$$

equations must be fulfilled. Conditions extending to the ninth order can be found in several tables within [13].

Since the number of available parameters is insufficient to match the number of governing equations—a difficulty similar to that encountered in the formulation of Runge–Kutta (RK) schemes—specific simplifying assumptions must be imposed. These reductions decrease the number of constraints, thereby minimizing the number of coefficients. Frequently employed simplifications include the following:

$$\begin{array}{c}{(A·\mathbf{1})}_{(3-8)}=\frac{1}{2}{\left(c^2+c\right)}_{(3-9)},\\ {(A·c)}_{(3-8)}=\frac{1}{6}{\left(c^3-c\right)}_{(3-9)},\\ {(A·c^2)}_{(4-8)}=\frac{1}{12}{\left(c^4+c\right)}_{(4-9)},\end{array}$$

(4)

where

$$c^i={\left[\begin{array}{cccccccc}{(-1)}^i\hfill & 0\hfill & c_3^i\hfill & c_4^i\hfill & {(-c_4)}^i\hfill & {(-c_5)}^i\hfill & c_5^i\hfill & 1\hfill \end{array}\right]}^T,$$

and

$$c^0={\left[\begin{array}{cccccccc}1\hfill & 1\hfill & 1\hfill & 1\hfill & 1\hfill & 1\hfill & 1\hfill & 1\hfill \end{array}\right]}^T=\mathbf{1}.$$

For indices satisfying ${\mu }_1<{\mu }_2$, the notation

$${\left(v\right)}_{({\mu }_1-{\mu }_2)}={[v_{{\mu }_1}{v}_{{\mu }_1+1}\cdots v_{{\mu }_2}]}^T$$

is employed.

The additional order constraints are compiled in

Table 2. Equations of conditions up to the ninth order, under assumption (4).

$T_1^{\left(1\right)}=b·\mathbf{1}=1,$$T_2^{\left(3\right)}=b·c^2=\frac{1}{6},$	$T_6^{\left(5\right)}=b·c^4=\frac{1}{15},$
$b·c^6=\frac{1}{28},$	$b·A^2·c=0,$
$b·A^3·\mathbf{1}=\frac{1}{20160},$	$b·A·\left(c\ast Ac\right)=-\frac{11}{15120},$
$b·c^8=\frac{1}{45},$	$b·A·\left(c\ast A^2·\mathbf{1}\right)=\frac{1}{7560},$
$b·\left(c\ast A^{2}c\right)=\frac{17}{10080},$	$b·\left(c\ast A·\left(c\ast A·c\right)\right)=-\frac{1}{720},$
$b·\left(c\ast A^3·\mathbf{1}\right)=\frac{23}{60480},$	$b·\left(A·\mathbf{1}\ast A^2·c\right)=\frac{17}{20160},$
$b·A·\left(A·\mathbf{1}\ast A^2\mathbf{1}\right)=-\frac{1}{17280},$	$b·\left(c\ast A·(c\ast A^2·\mathbf{1})\right)=-\frac{47}{181440},$
$b·\left(A·\mathbf{1}\ast A^3·\mathbf{1}\right)=\frac{373}{1814400},$	$-\frac{799}{907200}=b·(A·\mathbf{1}\ast A·(c\ast A·c)),$
$-\frac{1}{16200}=\frac{1}{36}b·(c^3\ast A·c^3),$	$-\frac{31}{181440}=b·(c\ast A^3·c)$
$\frac{1}{1814400}=b·A^4·\mathbf{1},$	$\frac{1}{1814400}=\frac{1}{2}b·A^3·c^2,$
$b·A^2·(c\ast A·c)=-\frac{13}{907200},$	$T_7^{\left(9\right)}=-\frac{71}{907200}+b·A·(c\ast A^2·c)=0.$

. Within this table, the notation “*” represents element-wise multiplication:

$${[v_1{v}_2\cdots v_n]}^T\ast {[u_1{u}_2\cdots u_n]}^T={[v_1{u}_1{v}_2{u}_2\cdots v_n{u}_n]}^T.$$

This operation has lower precedence, meaning that parentheses, exponentiation, and dot products are always evaluated before applying “*”.

Thus, we arrive at a nonlinear system consisting of 23 equations involving 23 unknown coefficients. For an in-depth discussion on deriving truncation error coefficients, the extensive review in [13] provides valuable insights. Coleman [14] highlighted the significance of the B2 series framework in analyzing the local truncation error, establishing links with T2 rooted tree structures.

To tackle this challenge, we adopt the differential evolution algorithm [15,16]. Differential evolution operates as an iterative optimization strategy where, at each iteration—termed generation $\lambda$—a “population” of candidate solutions is maintained, denoted as ${\left(a_3^{\left(\lambda \right)},a_4^{\left(\lambda \right)},a_6^{\left(\lambda \right)},w_1^{\left(\lambda \right)},w_2^{\left(\lambda \right)},\cdots ,d_{98}^{\left(\lambda \right)}\right)}_i$, for $i=1,2,\cdots ,N$, with N representing the population size. Initially, a starting population ${\left(a_3^{\left(0\right)},a_4^{\left(0\right)},a_6^{\left(0\right)},w_1^{\left(0\right)},w_2^{\left(0\right)},\cdots ,d_{98}^{\left(0\right)}\right)}_i$, for $i=1,2,\cdots ,N$, is randomly generated. The fitness function used for evaluation is defined as follows:

$$s=\sqrt{{\left(T_1^{\left(1\right)}\right)}^2+{\left(T_2^{\left(3\right)}\right)}^2+{\left(T_6^{\left(5\right)}\right)}^2+\cdots +{\left(T_7^{\left(9\right)}\right)}^2}$$

which quantifies the residuals for the 23 governing equations listed in Table 2. Each candidate in the initial population is assessed based on this function, with the objective of minimizing its value.

Every iteration g involves a structured three-step process to refine each candidate solution. These phases include the following:

• Mutation (Differentiation): Generating a new potential candidate based on variations within the existing population.
• Crossover: Recombining individuals to introduce diversity.
• Selection: Retaining the fittest individuals for the subsequent generation.

For implementation, we employed the DeMat software [17] within the MATLAB environment [18], which incorporates this evolutionary strategy. Since a single execution does not guarantee optimal results, we conducted several hundred runs of the optimization process to ensure convergence to a viable solution. The obtained result was then further refined to greater accuracy using multi-precision arithmetic, employing the NMinimize function in Mathematica [19].

The specific parameters that yield an optimal ninth-order scheme Num9s8 are documented in [20] and can be found implemented in http://users.uoa.gr/~tsitourasc/NumerovSol9.m (accessed on 5 March 2025).

3. Variable Step Implementation

To establish a variable step-size algorithm, it is necessary to devise an error estimator. A similar strategy was used for 8th-order methods [21]. Here, we introduce an auxiliary vector

$$\tilde{b}=\left[{\tilde{b}}_1{\tilde{b}}_2{\tilde{b}}_3{\tilde{b}}_4{\tilde{b}}_5{\tilde{b}}_6{\tilde{b}}_7{\tilde{b}}_8{\tilde{b}}_9\right],$$

with the aim of determining its coefficients so that the solution is approximated locally with sixth-order accuracy, i.e., with an error of $O\left(h^8\right)$. Consequently, the following order conditions must be satisfied:

$$\begin{array}{cc}\tilde{b}e=1,& \tilde{b}c=0,\\ \tilde{b}{c}^3=0,& \tilde{b}{c}^2=\frac{1}{6},\\ \tilde{b}{c}^4=\frac{1}{15},& \tilde{b}{c}^5=0,\\ \frac{1}{120}\tilde{b}c+\frac{1}{120}\tilde{b}Ac+\tilde{b}{A}^{2}c=0.\end{array}$$

We have obtained a solution for these coefficients, which is provided in the method’s implementation in Appendix A. Notably, no additional order conditions are required since the row-simplifying assumption (4) allows the other conditions to be eliminated.

The resulting, cost-free sixth-order approximation is given by the following:

$${\tilde{\psi }}_{\kappa +1}-2{\psi }_{\kappa }+{\psi }_{\kappa -1}=h_{\kappa }^2·\left(\begin{array}{c}{\tilde{b}}_1{f}_{\kappa -1}+{\tilde{b}}_2{f}_{\kappa }+{\tilde{b}}_3{f}_{\alpha }+{\tilde{b}}_4{f}_{\beta }\\ +{\tilde{b}}_5{f}_{\gamma }+{\tilde{b}}_6{f}_{\delta }+{\tilde{b}}_7{f}_{ϵ}+{\tilde{b}}_8{f}_{\zeta }+{\tilde{b}}_9{f}_{\eta }\end{array}\right).$$

Thus, we obtain two approximations—one of order nine and one of order six—without any extra cost. By subtracting these approximations, we derive an $O\left(h^8\right)$ estimate of the local error:

$$E=\parallel {\psi }_{\kappa +1}-{\tilde{\psi }}_{\kappa +1}\parallel =h_{\kappa }^2·∥\left(\begin{array}{c}(b_1-{\tilde{b}}_1)f_{\kappa -1}+(b_2-{\tilde{b}}_2)f_{\kappa }+(b_3-{\tilde{b}}_3)f_{\alpha }\\ +(b_4-{\tilde{b}}_4)f_{\beta }+(b_5-{\tilde{b}}_5)f_{\gamma }+(b_6-{\tilde{b}}_6)f_{\delta }\\ +(b_7-{\tilde{b}}_7)f_{ϵ}+(b_8-{\tilde{b}}_8)f_{\zeta }+(b_9-{\tilde{b}}_9)f_{\eta }\end{array}\right)∥.$$

We set a tolerance $\tau$ and keep the step unchanged if $32\tau >E>\tau /32$. If $E<\tau /32$, we double the step for the next interval. In this way, using the available data ${\psi }_{\kappa -1},{\psi }_{\kappa -1}^{″}$ and ${\psi }_{\kappa +1},{\psi }_{\kappa +1}^{″}$, we can compute the subsequent approximation as follows:

$${\psi }_{\kappa +2}=\psi \left(x_{\kappa +1}+2h_{\kappa }\right)+O\left(h^8\right)=\psi \left(x_{\kappa +1}+h_{\kappa +1}\right)+O\left(h^8\right)\left(\mathrm{locally}\right).$$

Proper adjustments in the indices are applied; see Figure 1 for a graphical illustration.

If instead $E>32\tau$, we reject the trial step ${\tilde{h}}_{\kappa }=h_{\kappa -1}$ and instead compute the solution at $x_{\kappa }+\frac{1}{2}{\tilde{h}}_{\kappa }=x_{\kappa }+h_{\kappa }$, where $h_{\kappa }$ is the halved step used for advancing the solution. We then use ${\psi }_{\kappa },{\psi }_{\kappa }^{″}$ and suitable approximations for ${\psi }_{\kappa -\frac{1}{2}},{\psi }_{\kappa -\frac{1}{2}}^{″}$ to apply methods of the form (3), after adjusting indices appropriately (see Figure 2 for details).

A local $O\left(h^{11}\right)$ approximation for ${\psi }_{\kappa -\frac{1}{2}}$ and $h^2{\psi }_{\kappa -\frac{1}{2}}^{″}$ is necessary to prevent order reduction due to error propagation. Such approximations can be obtained by applying the interpolation theory as introduced in [22]. Specifically, we add four additional stages $f_1,f_2,f_3$ and $f_4$:

$$\begin{array}{ccc}\hfill {\psi }_{1^{\ast }}& =& c_{10}{\psi }_{\kappa -1}+\left(1-c_{10}\right){\psi }_{\kappa }+h_{\kappa }^2(a_{10,1}{f}_{\kappa -1}+a_{10,2}{f}_{\kappa }+a_{10,3}{f}_{\alpha }+a_{10,4}{f}_{\beta }\hfill \\ & & +a_{10,5}{f}_{\gamma }+a_{10,6}{f}_{\delta }+a_{10,7}{f}_{ϵ}+a_{10,8}{f}_{\zeta }+a_{10,9}{f}_{\eta }),\hfill \\ \hfill f_{1^{\ast }}& =& f\left(x_{\kappa }+c_{10}{h}_{\kappa },{\psi }_{1^{\ast }}\right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\psi }_{2^{\ast }}& =& c_{11}{\psi }_{\kappa -1}+\left(1-c_{11}\right){\psi }_{\kappa }+h_{\kappa }^2(a_{11,1}{f}_{\kappa -1}+a_{11,2}{f}_{\kappa }+a_{11,3}{f}_{\alpha }+a_{11,4}{f}_{\beta }\hfill \\ & & +a_{11,5}{f}_{\gamma }+a_{11,6}{f}_{\delta }+a_{11,7}{f}_{ϵ}+a_{11,8}{f}_{\zeta }+a_{11,9}{f}_{\eta }+a_{11,10}{f}_{1^{\ast }}),\hfill \\ \hfill f_{2^{\ast }}& =& f\left(x_{\kappa }+c_{11}{h}_{\kappa },{\psi }_{2^{\ast }}\right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\psi }_{3^{\ast }}& =& c_{12}{\psi }_{\kappa -1}+\left(1-c_{12}\right){\psi }_{\kappa }+h_{\kappa }^2(a_{12,1}{f}_{\kappa -1}+a_{12,2}{f}_{\kappa }+a_{12,3}{f}_{\alpha }+a_{12,4}{f}_{\beta }\hfill \\ & & +a_{12,5}{f}_{\gamma }+a_{12,6}{f}_{\delta }+a_{12,7}{f}_{ϵ}+a_{12,8}{f}_{\zeta }+a_{12,9}{f}_{\eta }+a_{12,10}{f}_{1^{\ast }}+a_{12,11}{f}_{2^{\ast }}),\hfill \\ \hfill f_{3^{\ast }}& =& f\left(x_{\kappa }+c_{12}{h}_{\kappa },{\psi }_{3^{\ast }}\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\psi }_{4^{\ast }}& =& c_{13}{\psi }_{\kappa -1}+\left(1-c_{13}\right){\psi }_{\kappa }+h_{\kappa }^2(a_{13,1}{f}_{\kappa -1}+a_{13,2}{f}_{\kappa }+a_{13,3}{f}_{\alpha }+a_{13,4}{f}_{\beta }+a_{13,5}{f}_{\gamma }\hfill \\ & & +a_{13,6}{f}_{\delta }+a_{13,7}{f}_{ϵ}+a_{13,8}{f}_{\zeta }+a_{13,9}{f}_{\eta }+a_{13,10}{f}_{1^{\ast }}+a_{13,11}{f}_{2^{\ast }}+a_{13,12}{f}_{3^{\ast }}),\hfill \\ \hfill f_{4^{\ast }}& =& f\left(x_{\kappa }+c_{12}{h}_{\kappa },{\psi }_{4^{\ast }}\right).\hfill \end{array}$$

This yields the following:

$$\begin{array}{c}\hfill {\psi }_{\kappa -\frac{1}{2}}=\frac{1}{2}{\psi }_{\kappa }+\frac{1}{2}{\psi }_{\kappa -1}+h_{\kappa }^2\left(\begin{array}{c}{\widehat{b}}_1{f}_{\kappa -1}+{\widehat{b}}_2{f}_{\kappa }+{\widehat{b}}_3{f}_{\alpha }+{\widehat{b}}_4{f}_{\beta }\\ +{\widehat{b}}_5{f}_{\gamma }+{\widehat{b}}_6{f}_{\delta }+{\widehat{b}}_7{f}_{ϵ}+{\widehat{b}}_8{f}_{\zeta }\\ +{\widehat{b}}_9{f}_{\eta }+{\widehat{b}}_{10}{f}_{1^{\ast }}+{\widehat{b}}_{11}{f}_{2^{\ast }}+{\widehat{b}}_{12}{f}_{3^{\ast }}+{\widehat{b}}_{13}{f}_{4^{\ast }}\end{array}\right)\\ \hfill =\psi \left(x_{\kappa }-\frac{1}{2}{h}_{\kappa }\right)+O\left(h^{11}\right),\end{array}$$

where the approximations (i.e., big O notation) are considered locally.

Accordingly,

$${\psi }^{″}\left(x_{\kappa }-\frac{1}{2}{h}_{\kappa }\right)\approx f\left(x_{\kappa }-\frac{1}{2}{h}_{\kappa },{\psi }_{\kappa -\frac{1}{2}}\right)={\psi }_{\kappa -\frac{1}{2}}^{″}.$$

It is evident that rejecting a step incurs a cost of 12 function evaluations compared to the 8 evaluations used in a conventional step—namely, the usual seven stages $f_{\alpha },f_{\beta },f_{\gamma },f_{\delta }$, $f_{ϵ}$, $f_{\zeta },f_{\eta }$ plus the extra stages $f_{1^{\ast }},f_{2^{\ast }}{f}_{3^{\ast }}{f}_{4^{\ast }}$ and the evaluation of $f\left(x_{\kappa }-\frac{1}{2}{h}_{\kappa },{\psi }_{\kappa -\frac{1}{2}}\right)$. Stage $f_k$ remains unchanged and is reused.

The set of new coefficients, i.e., $\widehat{b}$, and the enhanced matrix, $\widehat{A}$, containing original matrix A and $\widehat{c}={[-1,0,c_3,c_4,-c_4,c_6,-c_6,0,1,c_{10},c_{11},c_{12},c_{13}]}^T$, have to fulfill a modified set of 151 order conditions. This set has the form shown in

Table 3. Error conditions for the sixth-order interpolant.

$\frac{1}{2}·(-\rho -{\rho }^2)+\widehat{b}e,$

$-\frac{1}{6}\rho +\frac{1}{6}{\rho }^3-\widehat{b}\widehat{c},$

$-\frac{1}{24}\rho -\frac{1}{24}{\rho }^4-\frac{1}{2}\widehat{b}\widehat{c}+\widehat{b}{A}^{\ast }e,$

$-\frac{1}{24}\rho -\frac{1}{24}{\rho }^4+\frac{1}{2}\widehat{b}{c}^{\ast 2},$

$\frac{1}{120}\rho -\frac{1}{120}{\rho }^5+\frac{1}{6}\widehat{b}\widehat{c}+\widehat{b}{A}^{\ast }\widehat{c},$

$\frac{1}{40}\rho -\frac{1}{40}{\rho }^5-\frac{1}{2}\widehat{b}{c}^{\ast 2}+\widehat{b}(\widehat{c}\ast A^{\ast }e),$

$-\frac{1}{120}\rho +\frac{1}{120}{\rho }^5-\frac{1}{6}\widehat{b}{\widehat{c}}^3,$

$-\frac{1}{720}\rho -\frac{1}{720}{\rho }^6-\frac{1}{24}\widehat{b}c-\frac{1}{2}\widehat{b}A\widehat{c}+\widehat{b}{A}^{2}e,$

$-\frac{1}{720}\rho -\frac{1}{720}{\rho }^6-\frac{1}{24}\widehat{b}\widehat{c}+\frac{1}{2}\widehat{b}A{\widehat{c}}^2,$

$-\frac{1}{180}\rho -\frac{1}{180}{\rho }^6+\frac{1}{6}\widehat{b}{\widehat{c}}^2+\widehat{b}(\widehat{c}\ast A\widehat{c}),$

$-\frac{1}{240}\rho -\frac{1}{240}{\rho }^6+\frac{1}{8}\widehat{b}{c}^2-\frac{1}{2}\widehat{b}(\widehat{c}\ast Ae)+\frac{1}{2}\widehat{b}{\left(Ae\right)}^2,$

$-\frac{1}{120}\rho -\frac{1}{120}{\rho }^6-\frac{1}{4}\widehat{b}{\widehat{c}}^3+\frac{1}{2}\widehat{b}({\widehat{c}}^2\ast Ae),$

$-\frac{1}{720}\rho -\frac{1}{720}{\rho }^6+\frac{1}{24}\widehat{b}{\widehat{c}}^4$.

(see [22]). Here, we set $\rho =-\frac{1}{2}$ to properly approximate ${\psi }_{\kappa -\frac{1}{2}}$.

All coefficients are provided in the Mathematica listing in the appendix. It can also be retrieved from http://users.uoa.gr/~tsitourasc/NumerovSol9var.m (accessed on 5 March 2025), where we have implemented the method in Mathematica format. In that file, we also include, in a separate section, the verification of the given coefficients over the 151 equations of the condition for the interpolatory approximation of ${\psi }_{\kappa -\frac{1}{2}}$ described above.

4. Numerical Tests

The innovative variable step method is designated as NumerovSol9var, reflecting its connection to Numerov, its 9th-order accuracy, and its variable step capability. It is compared with a method labeled as Num8s9 in [20] which is the underlying method here when the step is kept constant. This comparison is justified because Num8s9 has demonstrated superior performance over other methods of similar or lower orders, as evidenced in [20].

Initially, we implement the new method with various tolerance settings, documenting the number of stages used alongside the precision achieved for approximations of $\psi$ at the endpoint. Subsequently, at a comparable computational cost (i.e., the total number of stages utilized in the variable step implementation), we execute the constant step method Num9s8 and also record the precision at the endpoint. The results are presented in efficiency curves. All tests were conducted using Mathematica.

The problems on which the methods were evaluated are as follows.

4.1. The Two-Body Problem

At the outset, we select the well-known two-body problem (a.k.a., Kepler problem), characterized by eccentricity e:

$$\begin{array}{c}\hfill {\psi }_1^{″}=-\frac{y_1}{{({\psi }_1^2+{\psi }_2^2)}^{3/2}},{\psi }_2^{″}=-\frac{{\psi }_2}{{({\psi }_1^2+{\psi }_2^2)}^{3/2}},\\ \hfill {\psi }_1\left(0\right)=1-e,{\psi }_1^{\prime }=0,{\psi }_2\left(0\right)=0,{\psi }_2^{\prime }=\sqrt{\frac{1+e}{1-e}}.\end{array}$$

The Kepler problem, a fundamental issue in celestial mechanics, entails determining the trajectory of a planet or another celestial object influenced by a central gravitational force. Within the framework of this paper, the Kepler problem acts as a crucial test case for assessing the efficacy of the variable step-size implementation of the ninth-order hybrid Numerov-type method. Its significance in this research stems from its oscillatory characteristics and well-established periodic solutions, which offer a stringent evaluation of the new numerical technique’s effectiveness. By applying this method to such a classical problem, we can showcase its robustness and potential for wider applications in both theoretical and practical contexts involving differential equations with oscillatory dynamics.

Refer to [23] for the theoretical solution. It is important to note that in this problem’s definition, the indices correspond to the coordinates of $\psi$. We solved the aforementioned equation over the interval $\left[0,6\pi \right]$.

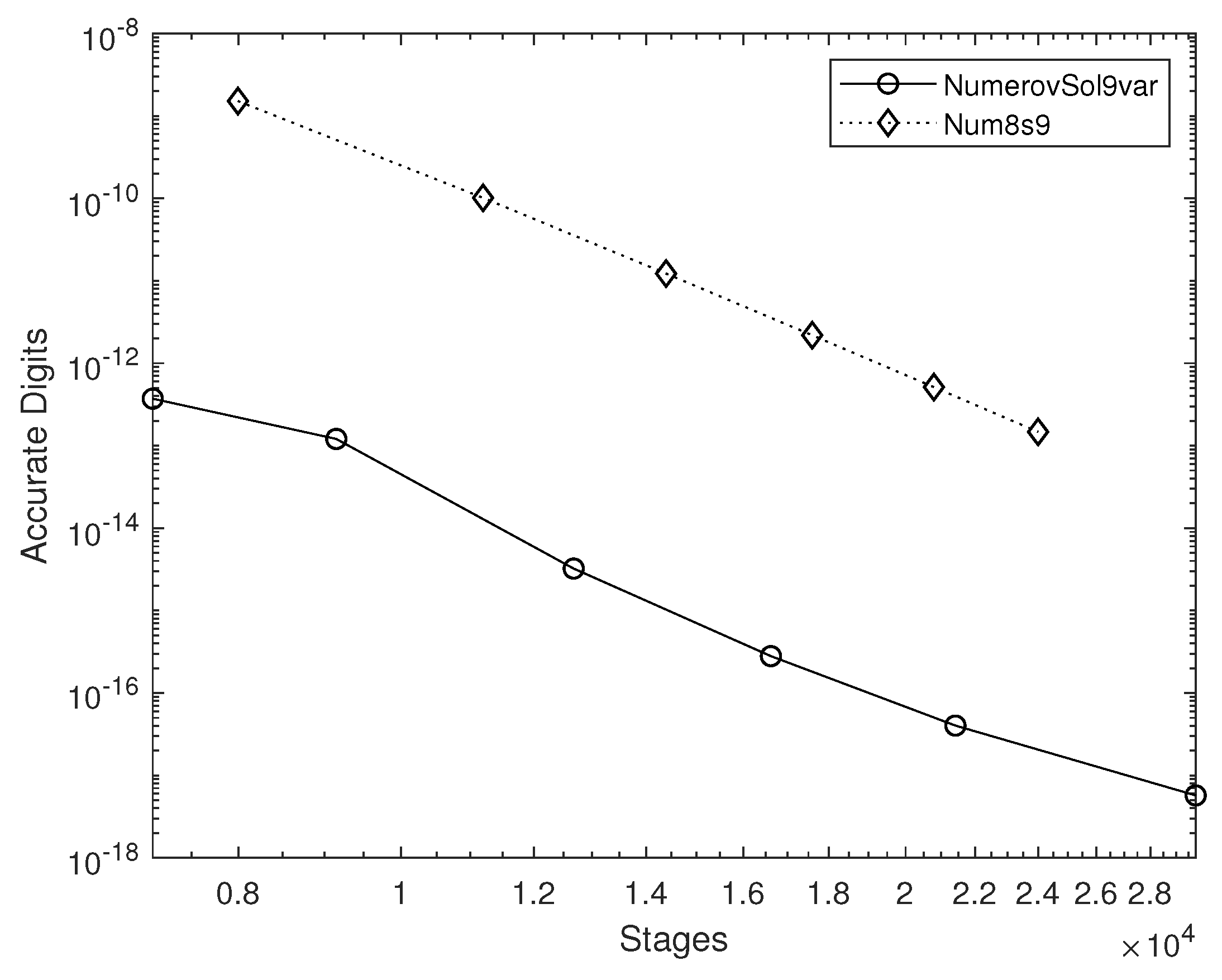
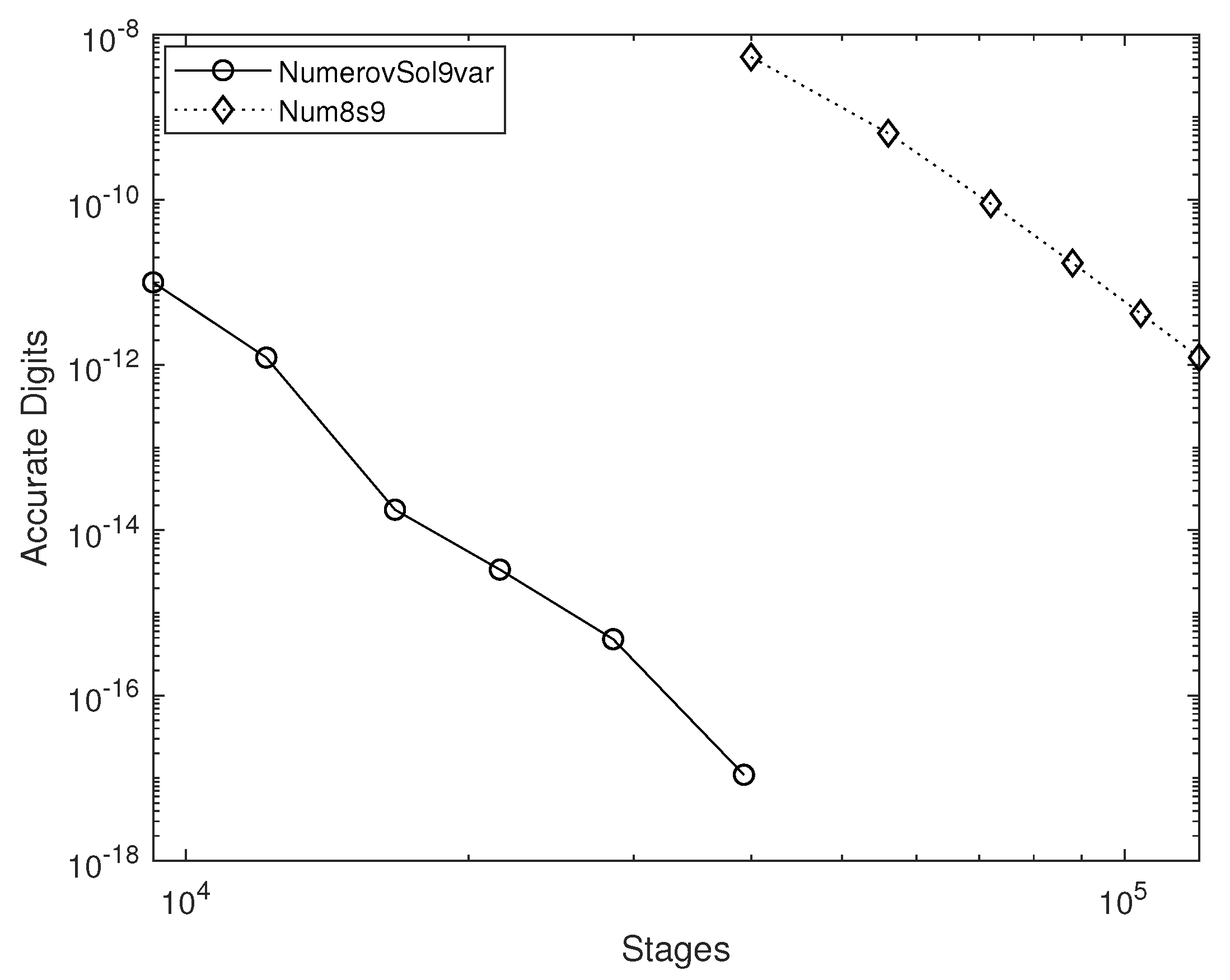
We examined three scenarios for eccentricities $e=0.5$ (problem D3 of DETEST as outlined in [23]), $e=0.7$ (problem D4 of DETEST), and $e=0.9$ (problem D5 of DETEST), with results documented in Figure 3, Figure 4, and Figure 5, respectively. These findings demonstrate that utilizing the variable step algorithm provides a distinct advantage.

In the context of an elliptical solution (i.e., when $e>>0$), the significant gain in precision is evident for NumerovSol9var across all scenarios. However, when applying an eccentricity of $e=0.9$, the difference becomes pronounced. Although the proposed ninth-order Numerov-type method with variable step lengths offers considerable efficiency enhancements, its benefits may be less pronounced for problems that do not necessitate frequent step adjustments, such as the Kepler problem with zero eccentricity. Conversely, when rapidly changing dynamics are present (e.g., Kepler with high eccentricity), the ability to adjust the step size is of paramount importance.

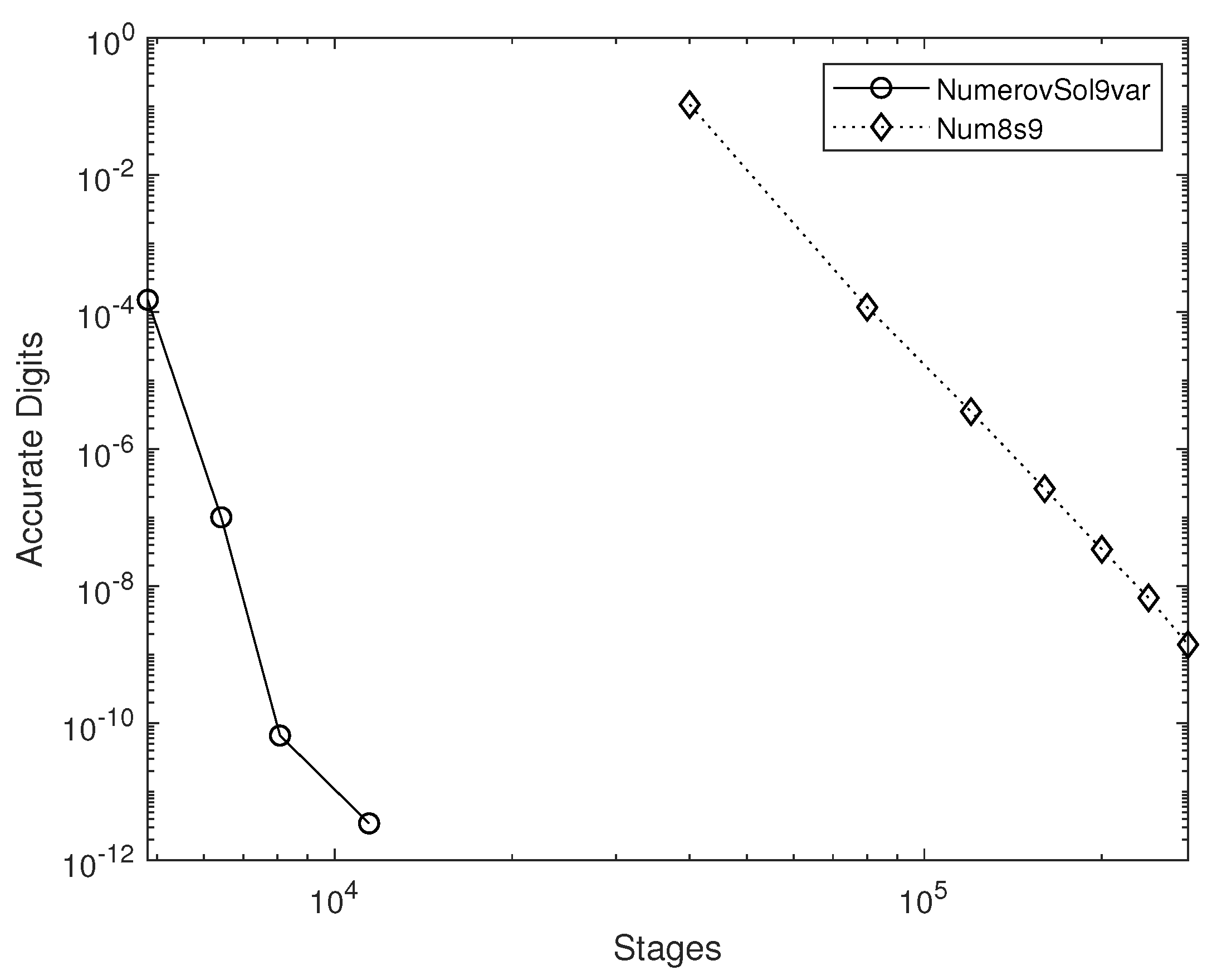
4.2. The Arenstorf Problem

The Arenstorf orbit is a stable orbit between Earth and Moon [24]. In form (1), it reads [25], (p. 296).

$$\begin{array}{ccc}\hfill {\psi }_1^{″}& =& \left(1-\mu \right)\frac{-\mu cosx-{\psi }_1}{\left({\left({\psi }_1+\mu cosx\right)}^2+{\left({\psi }_2+\mu sinx\right)}^2\right)}\hfill \\ & +& \mu \frac{\left(1-\mu \right)cosx-{\psi }_1}{\left({\left({\psi }_1-\left(1-\mu \right)cosx\right)}^2+{\left({\psi }_2-\left(1-\mu \right)sinx\right)}^2\right)},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\psi }_2^{″}& =& \left(1-\mu \right)\frac{-\mu sinx-{\psi }_2}{\left({\left({\psi }_1+\mu cosx\right)}^2+{\left({\psi }_2+\mu sinx\right)}^2\right)}\hfill \\ & +& \mu \frac{\left(1-\mu \right)sinx-{\psi }_2}{\left({\left({\psi }_1-\left(1-\mu \right)cosx\right)}^2+{\left({\psi }_2-\left(1-\mu \right)sinx\right)}^2\right)},\hfill \end{array}$$

with initial values:

$${\psi }_1\left(0\right)=0.994,{\psi }_1^{\prime }\left(0\right)=0,{\psi }_2\left(0\right)=0,{\psi }_2^{\prime }\left(0\right)=-1.00758510637908252,$$

$\mu =0.012277471$ and end point $x_{\mathrm{end}}=17.0652165601579625589$.

The solution at end–point is as follows:

$${\psi }_1\left(x_{\mathrm{end}}\right)=0.994cos\left(x_{\mathrm{end}}\right),{\psi }_2\left(x_{\mathrm{end}}\right)=0.994sin\left(x_{\mathrm{end}}\right),$$

and the corresponding efficiency curves are shown in Figure 6.

Here, the results are really astonishing in favor of NumerovSol9var since the behavior of the solution requires many rapid and significant changes in the step size.

5. Conclusions

In this work, we introduced a novel ninth-order explicit two-step method equipped with a variable step-size mechanism specifically tailored for second-order initial value problems with oscillatory characteristics. The main contribution lies in the combination of high-order accuracy with a computationally efficient step-size control strategy, which employs error estimation through embedded methods and local interpolation to manage step doubling and halving.

We demonstrated the method’s performance across several challenging test problems, including the Kepler and Arenstorf orbits, where the proposed approach showed significant improvements in both accuracy and efficiency compared to fixed-step counterparts. The robustness of the method in handling stiff and rapidly varying dynamics underscores its potential for a wide range of scientific and engineering applications.

Moreover, the implementation in Mathematica, including symbolic verification of order conditions and adaptive control logic, enhances reproducibility and encourages further exploration by the research community.

Future work could investigate more flexible step-size control policies beyond binary step changes (doubling or halving), potentially guided by continuous error estimators. Additionally, extending the method to systems with variable coefficients, discontinuities, or multiphysics coupling would broaden its scope. The optimization of method parameters for specific subclasses of differential equations remains a promising direction for ongoing research.