Control of Vehicle Lateral Handling Stability Considering Time-Varying Full-State Constraints
Abstract
1. Introduction
- 1.
- Adaptability to dynamically changing state constraints for enhanced vehicle safety.
- 2.
- Simultaneous consideration of constraint satisfaction and control performance for enhanced adaptability under complex driving conditions.
2. Vehicle Lateral Handling Stability Control Process
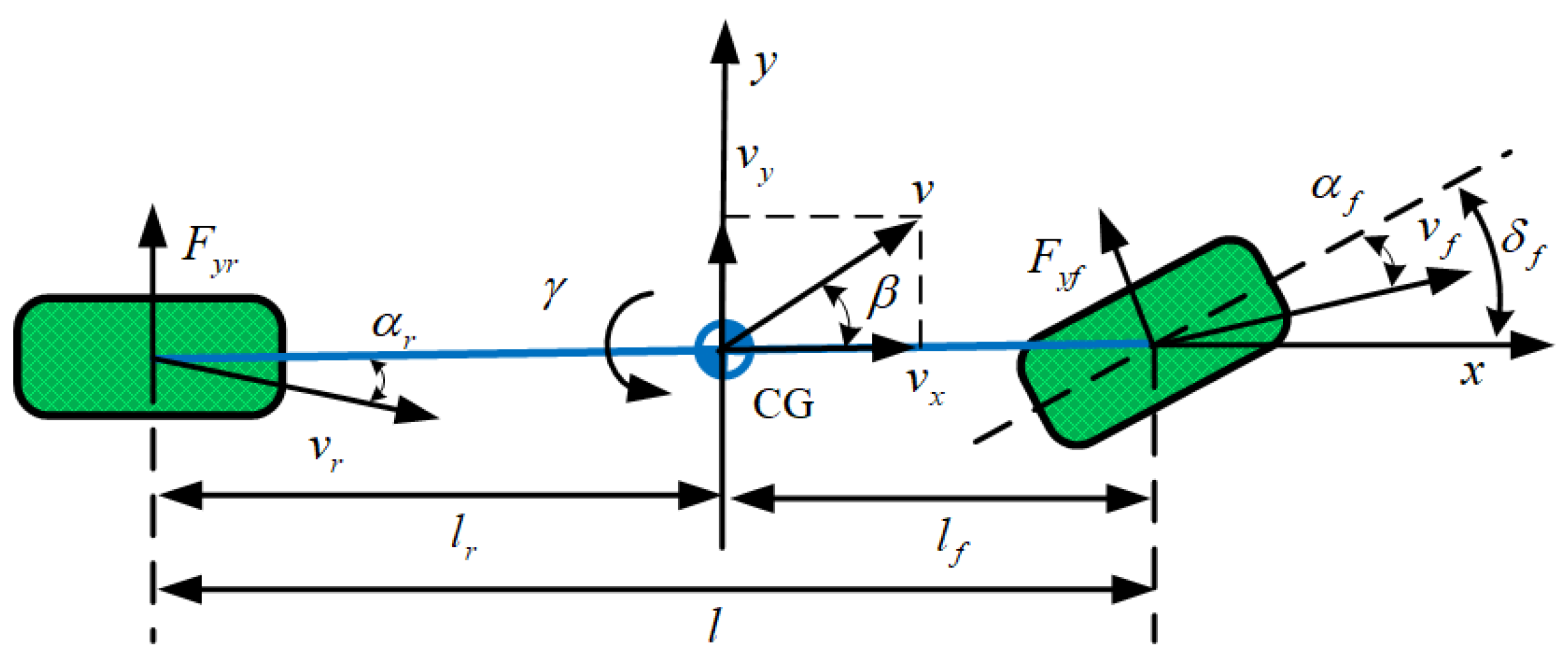
3. Simplification and Problem Formulation of the Coupled Vehicle Dynamics Model
Simplification of the Coupled Vehicle Dynamics Model
- ①
- When , .
- ②
- .
4. Design and Stability Analysis of Vehicle Lateral Handling Stability Controller with Time-Varying Full-State Constraints
4.1. Controller Design
4.2. Stability Analysis
5. Simulation Verification and Result Analysis
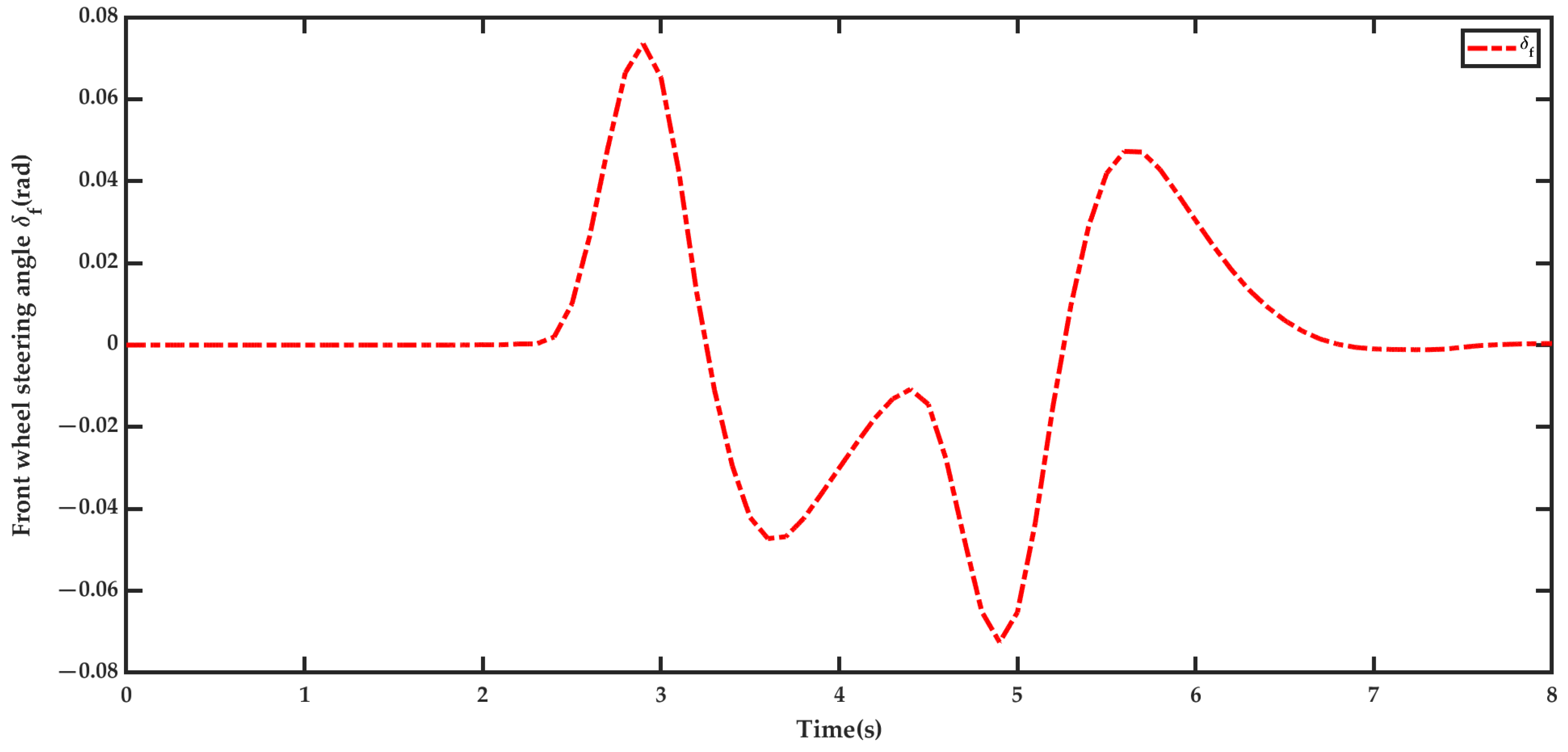
5.1. Parameter Settings
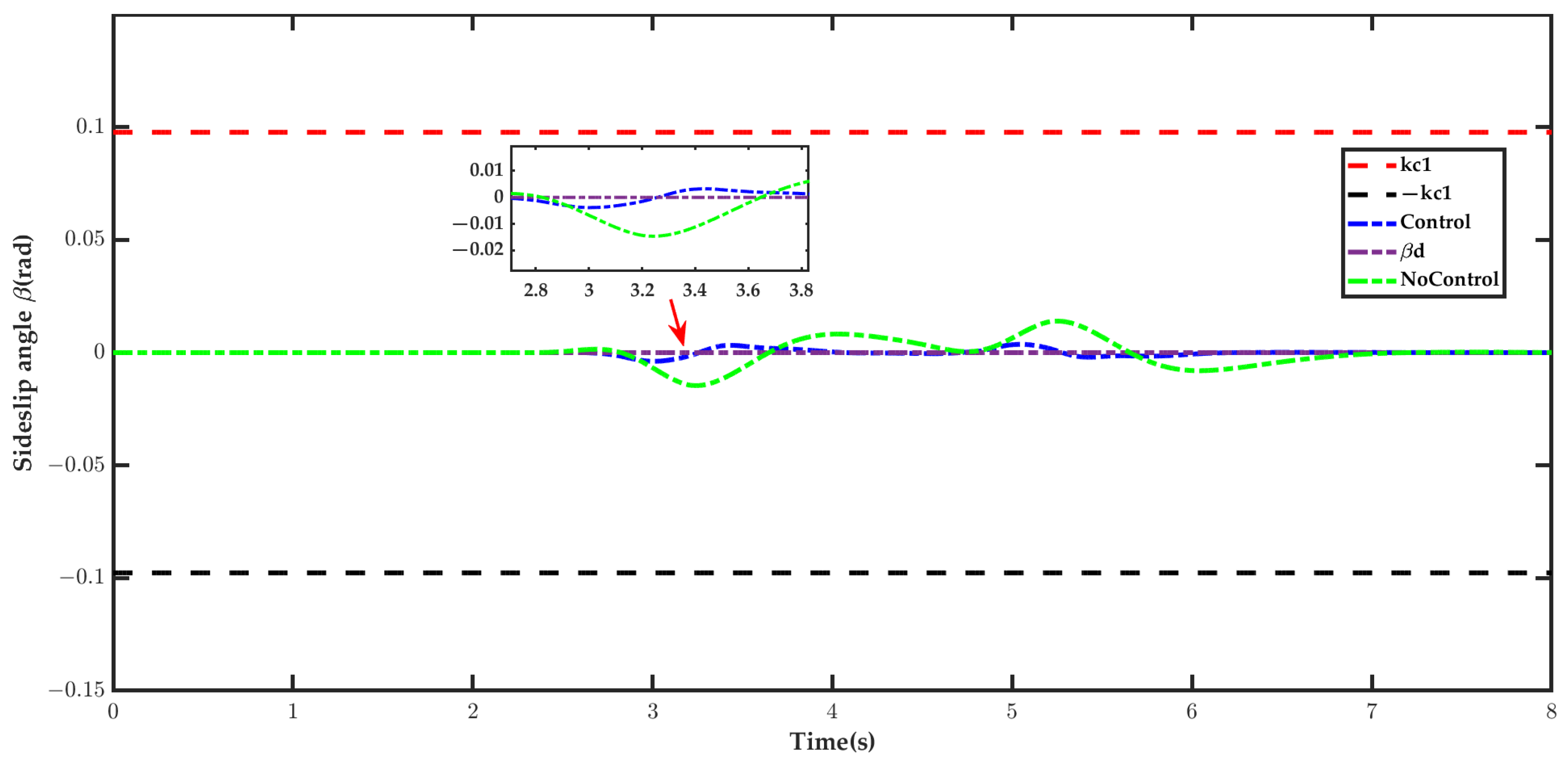
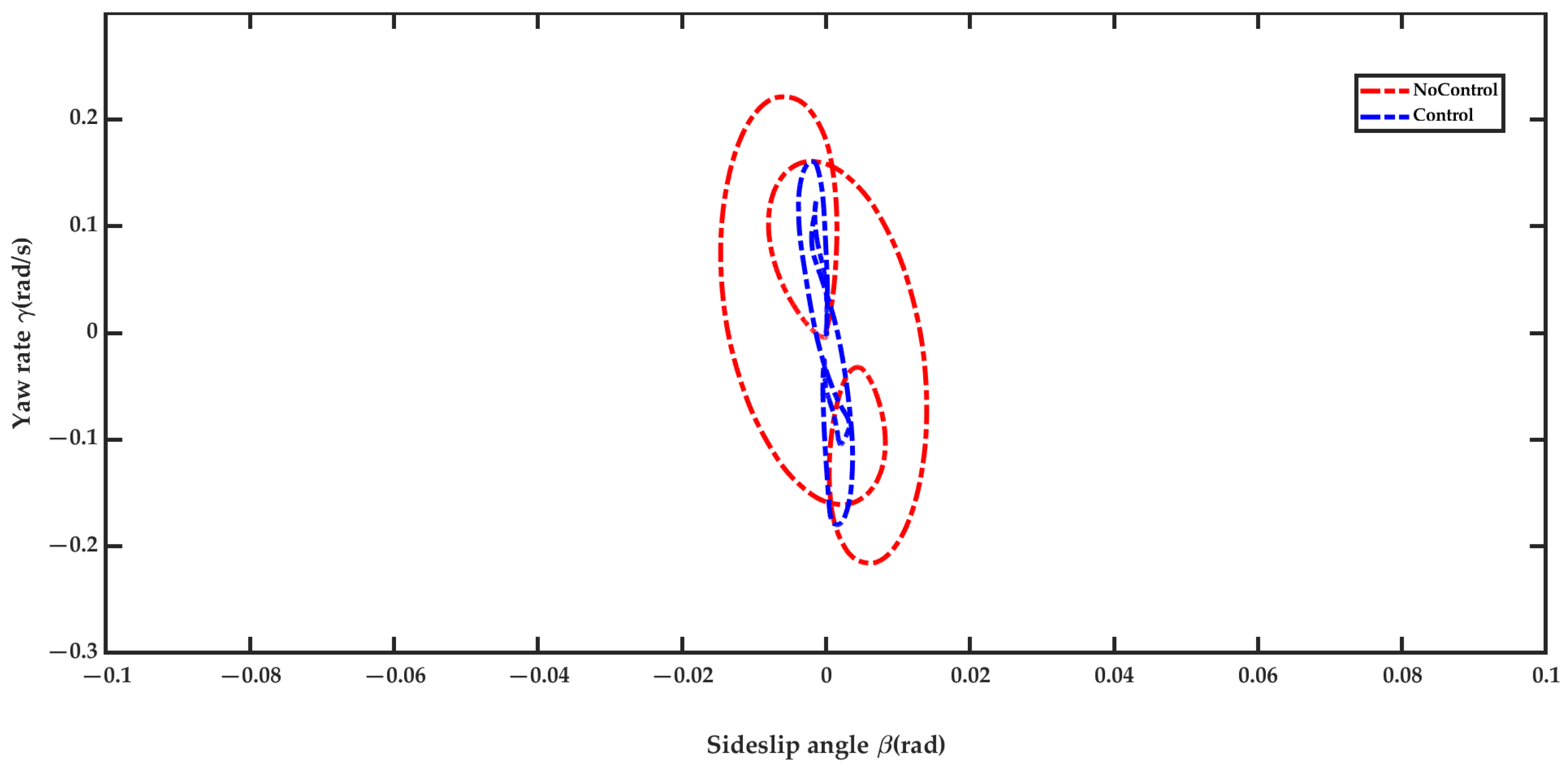
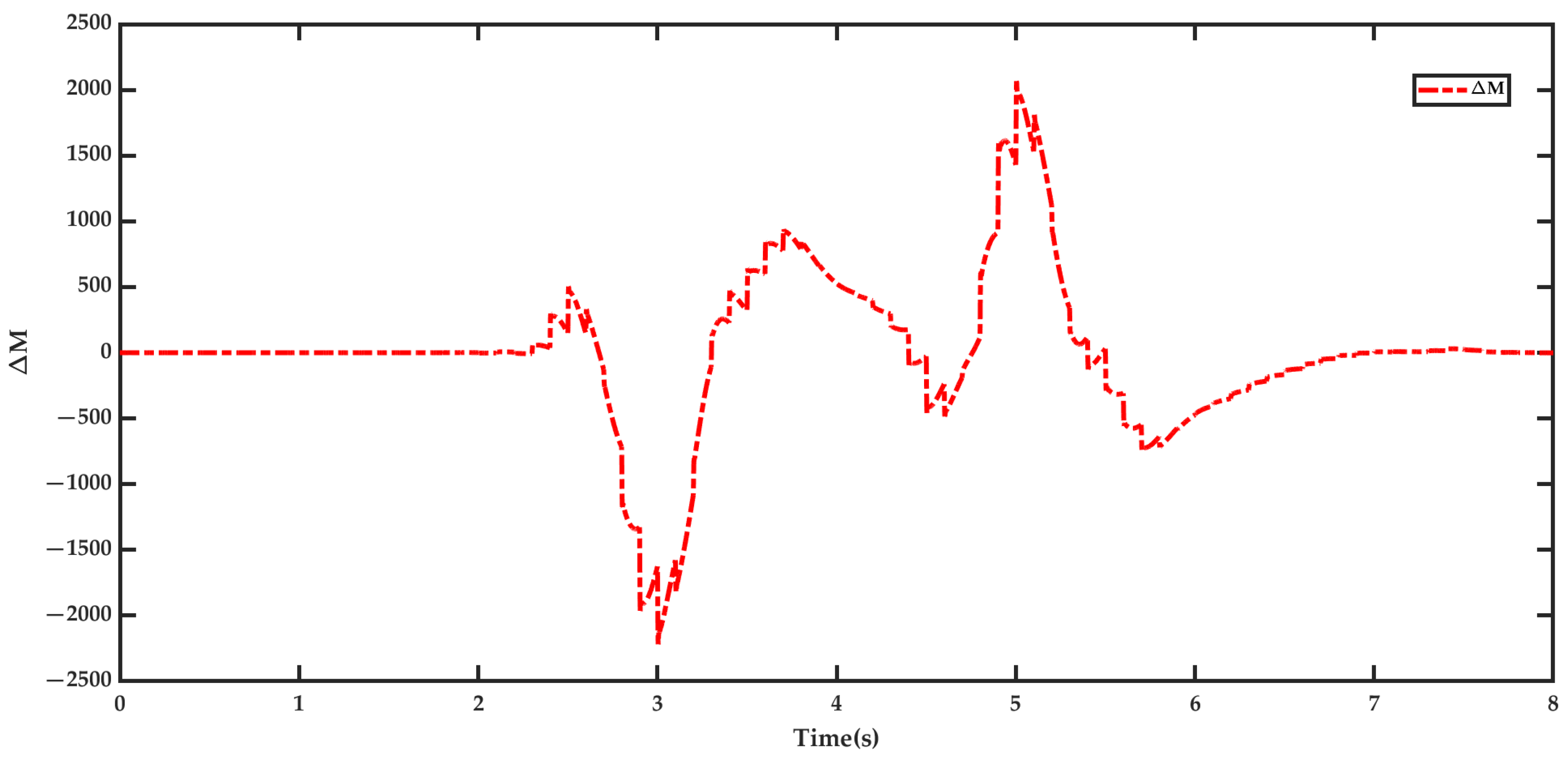
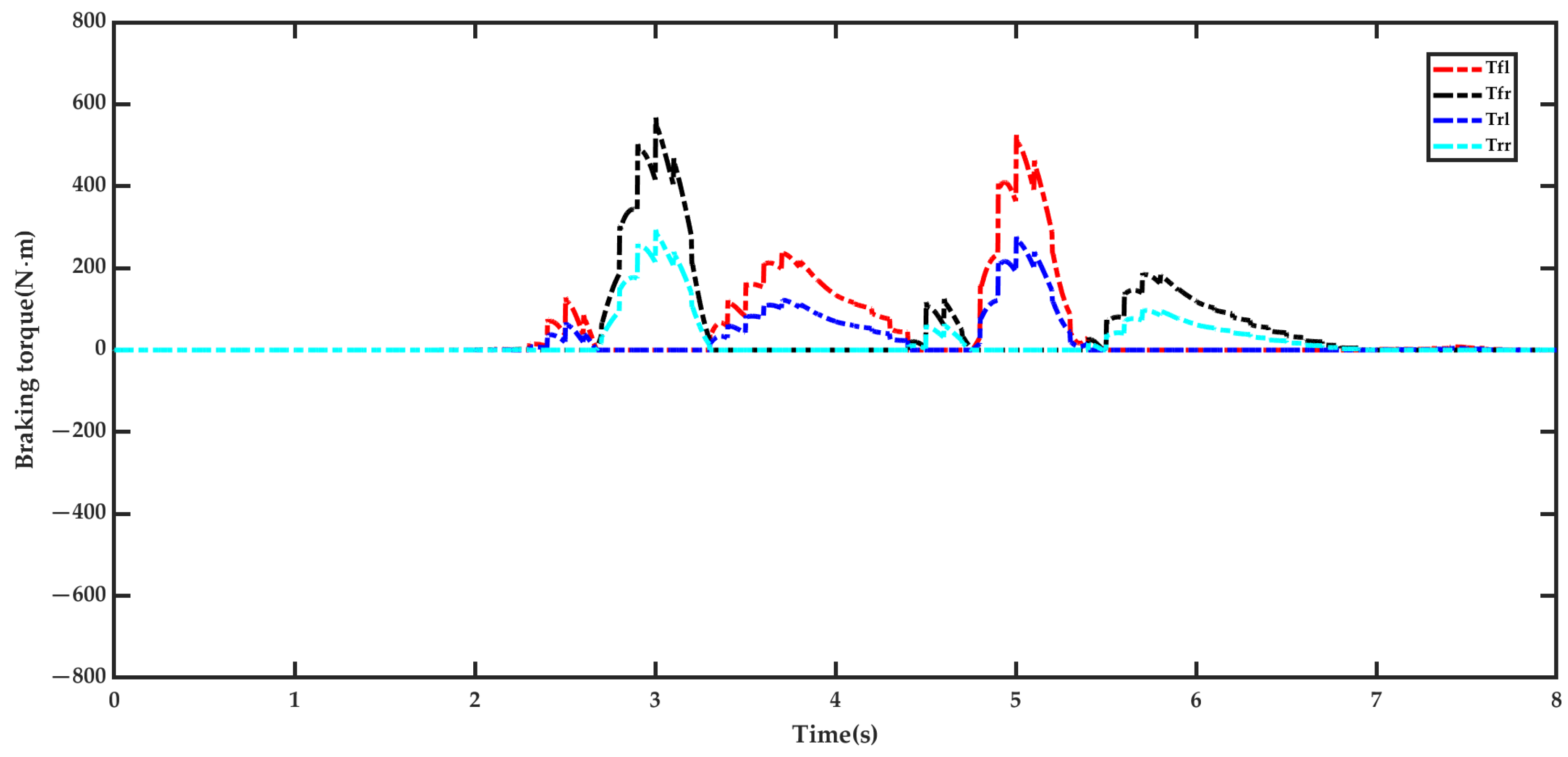
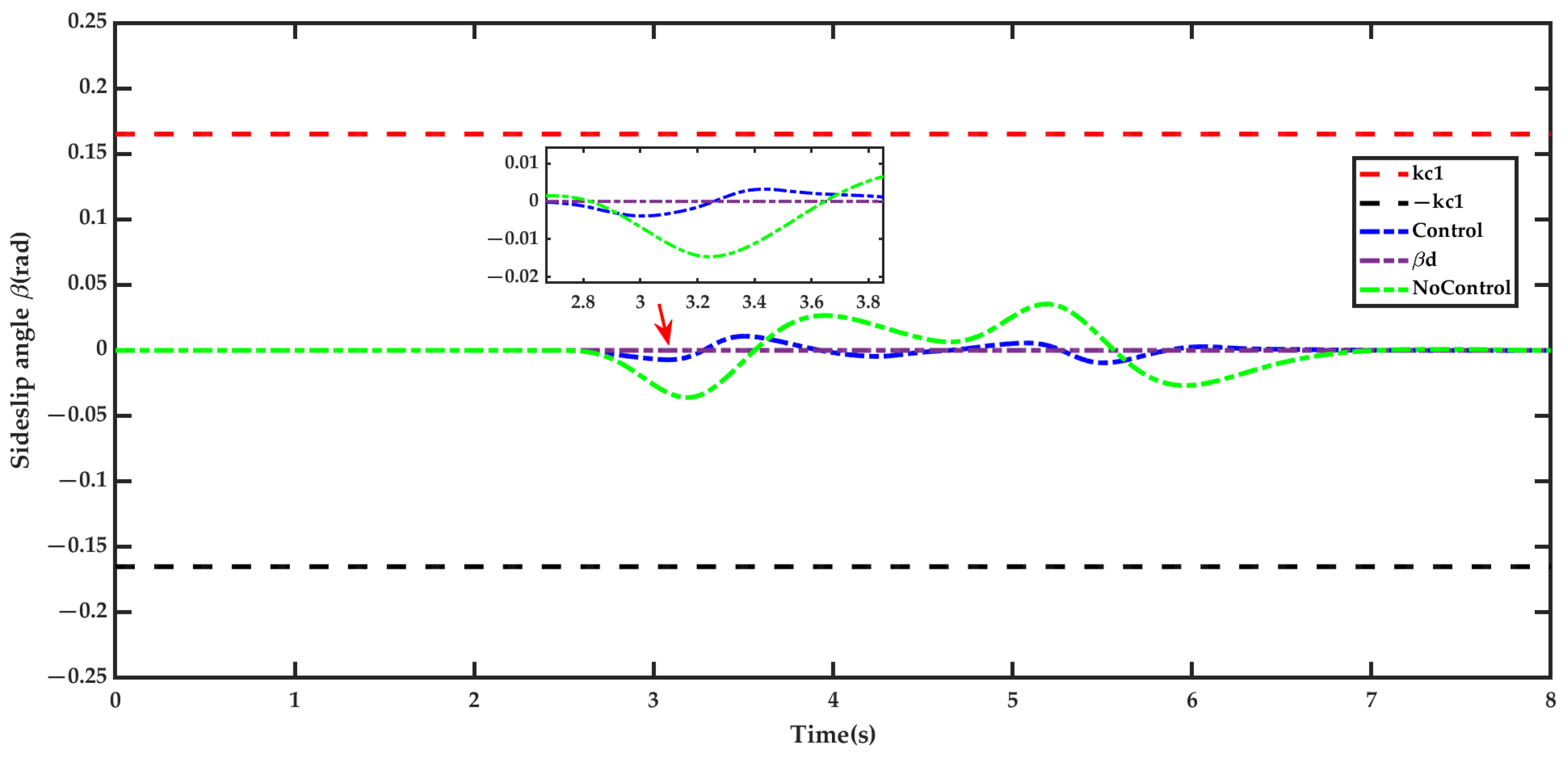
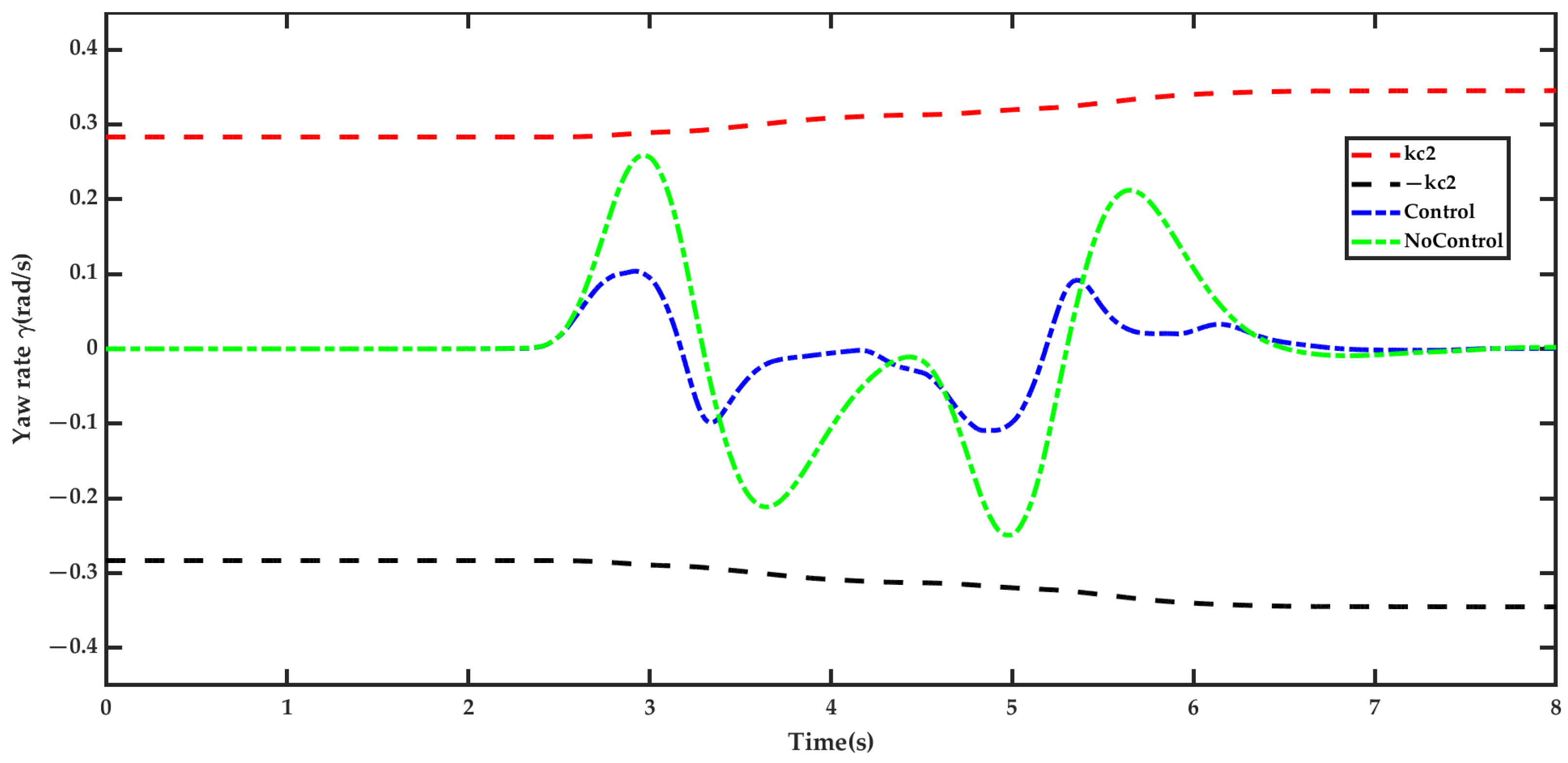
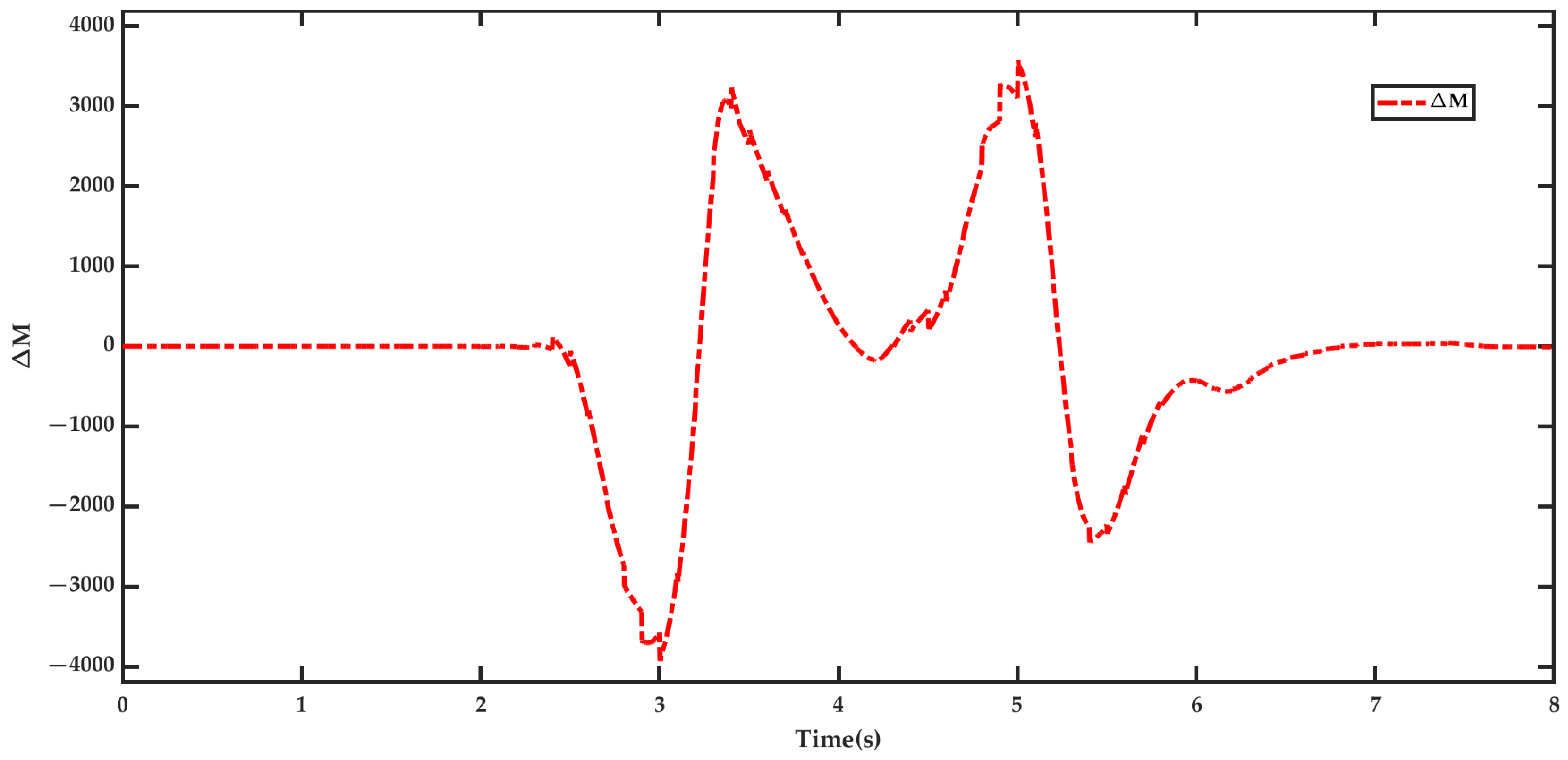
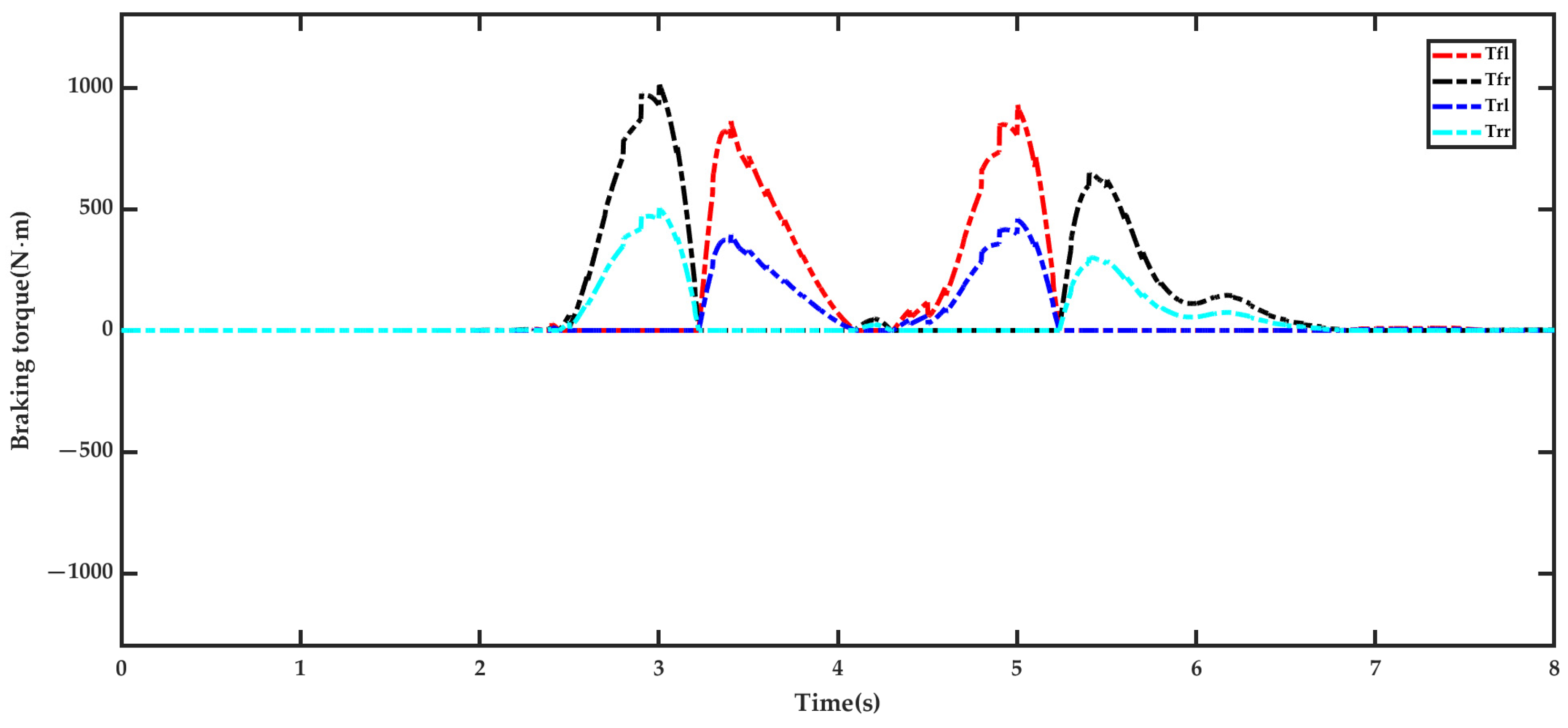
5.2. Result Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jeong, E.; Cheol, O. Evaluating the effectiveness of active vehicle safety systems. Accid. Anal. Prev. 2017, 100, 85–96. [Google Scholar] [PubMed]
- Song, C.; Xuan, S.; Li, J.; Jin, L. Research on Vehicle Electronic Stability Control Method. In Proceedings of the 2010 2nd International Workshop on Intelligent Systems and Applications, Wuhan, China, 22–23 May 2010. [Google Scholar]
- Hu, J.; Wang, Y.; Fujimoto, H.; Hori, Y. Robust yaw stability control for in-wheel motor electric vehicles. IEEE/ASME Trans. Mechatron. 2017, 22, 1360–1370. [Google Scholar] [CrossRef]
- Hang, P.; Xia, X.; Chen, X. Handling stability advancement with 4WS and DYC coordinated control: A gain-scheduled robust control approach. IEEE Trans. Veh. Technol. 2021, 70, 3164–3174. [Google Scholar]
- Li, Z.; Jiao, X.; Zhang, T. Robust H∞ Output Feedback Trajectory Tracking Control for Steer-by-Wire Four-Wheel Independent Actuated Electric Vehicles. World Electr. Veh. J. 2023, 14, 147. [Google Scholar] [CrossRef]
- Ge, P.; Guo, L.; Feng, J.; Zhou, X. Adaptive Stability Control Based on Sliding Model Control for BEVs Driven by In-Wheel Motors. Sustainability 2023, 15, 8660. [Google Scholar] [CrossRef]
- Chen, L.; Tang, L. Yaw stability control for steer-by-wire vehicle based on radial basis network and terminal sliding mode theory. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 237, 2036–2048. [Google Scholar]
- Chen, Y.; Cheng, Q.; Gan, H.; Hao, X. Lateral Stability Control of a Distributed Electric Vehicle Using a New Sliding Mode Controler. Int. J. Automot. Technol. 2023, 24, 1089–1100. [Google Scholar] [CrossRef]
- Silva, F.; Silva, L.; Eckert, J.; Yamashita, R.; Lourenço, M. Parameter influence analysis in an optimized fuzzy stability control for a four-wheel independent-drive electric vehicle. Control Eng. Pract. 2022, 120, 105000. [Google Scholar] [CrossRef]
- Geng, G.; Cheng, P.; Sun, L.; Xu, X.; Shen, F. A Study on Lateral Stability Control of Distributed Drive Electric Vehicle Based on Fuzzy Adaptive Sliding Mode Control. Int. J. Automot. Technol. 2024, 25, 1415–1429. [Google Scholar] [CrossRef]
- Cao, Y.; Xie, Z.; Li, W.; Wang, X.; Wong, P.; Zhao, J. Combined Path Following and Direct Yaw-Moment Control for Unmanned Electric Vehicles Based on Event-Triggered T–S Fuzzy Method. Int. J. Fuzzy Syst. 2024, 26, 2433–2448. [Google Scholar] [CrossRef]
- Ileš, Š.; Švec, M.; Makarun, P.; Hromatko, J. Predictive direct yaw moment control with active steering based on polytopic linear parameter-varying model. In Proceedings of the 2022 8th International Conference on Control, Decision and Information Technologies (CoDIT), Istanbul, Turkey, 17–20 May 2022. [Google Scholar]
- Rini, G.; Mazzilli, V.; Bottiglione, F.; Gruber, P.; Dhaens, M.; Sorniotti, A. On Nonlinear Model Predictive Vehicle Dynamics Control for Multi-Actuated Car-Semitrailer Configurations. IEEE Access 2024, 12, 165928–165947. [Google Scholar] [CrossRef]
- Guo, N.; Lenzo, B.; Zhang, X.; Zou, Y.; Zhai, R.; Zhang, T. A Real-Time Nonlinear Model Predictive Controller for Yaw Motion Optimization of Distributed Drive Electric Vehicles. IEEE Trans. Veh. Technol. 2020, 69, 4935–4946. [Google Scholar] [CrossRef]
- Tee, K.; Ge, S.; Tay, E. Barrier Lyapunov functions for the control of output-constrained nonlinear systems. Automatica 2009, 45, 918–927. [Google Scholar] [CrossRef]
- Li, H.; Luo, P.; Li, Z.; Zhu, G.; Zhang, X. Finite Time-Adaptive Full-State Quantitative Control of Quadrotor Aircraft and QDrone Experimental Platform Verification. Drones 2024, 8, 351. [Google Scholar] [CrossRef]
- Kim, S.; Kim, M.; Kim, Y. Fault-Tolerant Adaptive Control for Trajectory Tracking of a Quadrotor Considering State Constraints and Input Saturation. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 3148–3159. [Google Scholar] [CrossRef]
- Wang, C.; Yang, N.; Li, W.; Liang, M. Event-Triggered Finite-Time Fuzzy Tracking Control for a Time-Varying State Constrained Quadrotor System based on Disturbance Observer. Aerosp. Sci. Technol. 2024, 151, 109329. [Google Scholar] [CrossRef]
- Xu, F.; Tang, L.; Liu, Y. Tangent barrier Lyapunov function-based constrained control of flexible manipulator system with actuator failure. Int. J. Robust Nonlinear Control 2021, 31, 8523–8536. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y. Adaptive neural boundary control for state constrained flexible manipulators. Int. J. Adapt. Control Signal Process. 2023, 37, 2184–2203. [Google Scholar] [CrossRef]
- Li, Q.; Mei, K. A state-constrained second-order sliding mode control for permanent magnet synchronous motor drives. Nonlinear Dyn. 2024, 112, 12269–12282. [Google Scholar] [CrossRef]
- Jiang, Q.; Ma, Y.; Liu, J.; Yu, J. Full state constraints-based adaptive fuzzy finite-time command filtered control for permanent magnet synchronous motor stochastic systems. Int. J. Control Autom. Syst. 2022, 20, 2543–2553. [Google Scholar] [CrossRef]
- Dai, B.; Wang, Z. Disturbance observer-based sliding mode control using barrier function for output speed fluctuation constraints of PMSM. IEEE Trans. Energy Convers. 2024, 39, 1192–1201. [Google Scholar] [CrossRef]
- Cao, Z.; Mao, J.; Zhang, C.; Cui, C.; Yang, J. Safety-Critical Generalized Predictive Control for Speed Regulation of PMSM Drives Based on Dynamic Robust Control Barrier Function. IEEE Trans. Ind. Electron. 2024, 72, 1881–1891. [Google Scholar] [CrossRef]
- Farrell, J.; Polycarpou, M.; Sharma, M.; Dong, W. Command filtered backstepping. IEEE Trans. Autom. 2009, 54, 1391–1395. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, X.; Xu, R. Command-filter-based adaptive neural tracking control for a class of nonlinear MIMO state-constrained systems with input delay and saturation. Neural Netw. 2022, 147, 152–162. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Chen, F.; Fang, J. Command filter-based adaptive finite-time control of fractional-order nonlinear constrained systems with input saturation. Asian J. Control, 2024; online version of record. [Google Scholar] [CrossRef]
- Zhang, Y.; Lei, Y.; Zhang, T.; Song, R.; Li, Y.; Du, F. Robust Command-Filtered Control With Prescribed Performance for Flexible-Joint Robots. IEEE Trans. Instrum. Meas. 2023, 72, 7506013. [Google Scholar] [CrossRef]
- Wu, L.; Liu, Z.; Zhao, D. Command-Filtered Yaw Stability Control of Vehicles with State Constraints. Actuators 2025, 14, 148. [Google Scholar] [CrossRef]
- Gao, M.; Li, J.; Hu, T.; Luo, J.; Feng, B. Intelligent vehicle trajectory tracking with an adaptive robust nonsingular fast terminal sliding mode control in complex scenarios. Sci. Rep. 2024, 14, 31085. [Google Scholar] [CrossRef]
- Dugoff, H.; Fancher, P.; Segel, L. An analysis of tire traction properties and their influence on vehicle dynamic performance. SAE Trans. 1970, 79, 1219–1243. [Google Scholar] [CrossRef]
- Zhang, L.; Yan, T.; Pan, F.; Ge, W.; Kong, W. Research on direct yaw moment control of electric vehicles based on Electrohydraulic Joint Action. Sustainability 2022, 14, 11072. [Google Scholar] [CrossRef]
- Li, H.; Wang, K.; Hao, H.; Wu, Z. Yaw Moment Control Based on Brake-by-Wire for Vehicle Stbility. World Electr. Veh. J. 2023, 14, 256. [Google Scholar] [CrossRef]
- Masato, A. Vehicle Handling Dynamics: Theory and Application; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Ren, B.; Ge, S.; Tee, K.; Lee, T. Adaptive Neural Control for Output Feedback Nonlinear Systems Using a Barrier Lyapunov Function. IEEE Trans. Neural Netw. 2010, 21, 1339–1345. [Google Scholar] [PubMed]
- Yu, J.; Zhao, L.; Yu, H.; Lin, C. Barrier Lyapunov functions-based command filtered output feedback control for full-state constrained nonlinear systems. Automatica 2019, 105, 71–79. [Google Scholar]
- Cui, G.; Xu, S.; Zhang, B.; Lu, J.; Li, Z.; Zhang, Z. Adaptive tracking control for uncertain switched stochastic nonlinear pure-feedback systems with unknown backlash-like hysteresis. J. Frankl. Inst. 2017, 354, 1801–1818. [Google Scholar] [CrossRef]
- Yu, J.; Shi, P.; Zhao, L. Finite-time command filtered backstepping control for a class of nonlinear systems. Automatica 2018, 92, 173–180. [Google Scholar]
- Liang, J.; Feng, J.; Lu, Y.; Yin, G.; Zhuang, W.; Mao, X. A direct yaw moment control framework through robust TS fuzzy approach considering vehicle stability margin. IEEE/ASME Trans. Mechatron. 2023, 29, 166–178. [Google Scholar]
- Chen, J.; Liu, Y.; Liu, R.; Xiao, F.; Huang, J. Integrated control of braking-yaw-roll stability under steering-braking conditions. Sci. Rep. 2023, 13, 21110. [Google Scholar]
- Muhammad, E.; Vali, A.; Kashaninia, A.; Behnamgol, V. Coordination of Active Front Steering and Direct Yaw Control Systems Using MIMO Sliding Mode Control. Int. J. Control Autom. Syst. 2024, 22, 1–15. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Zhao, D. Control of Vehicle Lateral Handling Stability Considering Time-Varying Full-State Constraints. Mathematics 2025, 13, 1217. https://doi.org/10.3390/math13081217
Wu L, Zhao D. Control of Vehicle Lateral Handling Stability Considering Time-Varying Full-State Constraints. Mathematics. 2025; 13(8):1217. https://doi.org/10.3390/math13081217
Chicago/Turabian StyleWu, Lizhe, and Dingxuan Zhao. 2025. "Control of Vehicle Lateral Handling Stability Considering Time-Varying Full-State Constraints" Mathematics 13, no. 8: 1217. https://doi.org/10.3390/math13081217
APA StyleWu, L., & Zhao, D. (2025). Control of Vehicle Lateral Handling Stability Considering Time-Varying Full-State Constraints. Mathematics, 13(8), 1217. https://doi.org/10.3390/math13081217






