Abstract
Consider the collection of analytic functions f defined within the open unit disk , subject to the conditions and . For the parameter , define the subclass as follows: In this paper, we derive sharp bounds on for f in the class and compute the boundary length of . Additionally, we investigate the inclusion properties of the sequences of partial sums for functions . Our results extend and refine several classical results in the theory of univalent functions.
Keywords:
univalent functions; starlike and convex functions; extremal problems; subordination; arc length; partial sums MSC:
33C45
1. Introduction
The study of analytic functions and their geometric properties forms the cornerstone of geometric function theory (GFT). A central object of study in GFT is the class of univalent functions, which are analytic functions that map the open unit disk onto domains without self-intersections. These functions have profound applications in various areas of mathematics and physics, including fluid dynamics, conformal mappings, and potential theory.
1.1. Univalent Functions
Let denote the collection of all analytic functions f defined on that satisfy the normalization conditions and . A function is said to be univalent in if it maps distinct points in to distinct points in its image, i.e., implies for . The class of all such univalent functions is denoted by . One of the trivial examples of is . The other example can be as
One of the most celebrated examples of a univalent function is the Koebe function, defined as
The Koebe function maps onto the slit domain . The function and its rotations play a pivotal role in the theory of univalent functions. In particular, serves as an extremal function for many classical problems, including growth, distortion, and rotation. Figure 1 illustrates the rate of growth of the region as r moves from 0 to 1 and shows that blasts out to cover the whole of with removed as .
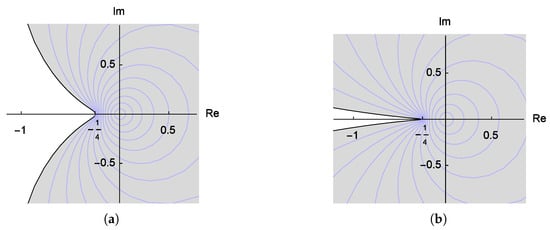
Figure 1.
(a) Image of . (b) Image of .
For the foundational principles and core results in the theory of univalent functions, the works of Duren [1], Pommerenke [2] and Goodman [3] serve as essential references. Additionally, for a comprehensive overview of recent advancements and developments in univalent function theory, the monograph by Thomas et al. [4] provides an up-to-date and thorough exploration of the subject.
For , we define two important subclasses of the family of univalent functions in , namely the families of starlike functions of order λ and convex functions of order λ, denoted by and , respectively. These classes are characterized analytically by the conditions
and
These conditions reflect the geometric properties of the respective function classes: the former ensures that the image of f remains starlike with respect to the origin, while the latter guarantees convexity. Notably, when the order parameter is set to , these classes reduce to their classical counterparts, namely the families of starlike functions and convex functions , which have been extensively studied in geometric function theory; see [1,2,3].
Another fundamental subclass of is the family of close-to-convex functions of order λ and argument μ, denoted by . A function belongs to (see [5,6]) if there exists a function and a real parameter , such that
This definition extends the notion of closeness to convexity by permitting controlled deviations from strict convexity, governed by the parameters and the reference function g. Notably, when , we retrieve the classical family of close-to-convex functions, originally introduced by Kaplan [7].
Geometrically, a function f belongs to if and only if none of the image curves for exhibit a reverse hairpin turn, meaning that the image domain remains free from inward-pointing loops that could obstruct its univalence. This criterion provides an intuitive geometric interpretation of closeness to convexity, distinguishing it from the stricter notion of convexity while preserving essential structural properties.
1.2. Functions Whose Derivatives Lie in a Half-Plane
For , we introduce as
This class, originally introduced by MacGregor [8], consists of analytic functions whose derivatives have real parts bounded below by , ensuring controlled geometric behaviour in the unit disk.
A fundamental property of this family follows from the Noshiro–Warschawski theorem (see [1]), which guarantees that every function in is univalent. Moreover, this class exhibits strong structural properties: it forms a convex and compact subfamily within the class of univalent functions . A key observation is that when choosing the reference function and setting in (2), the family coincides precisely with the subclass , further reinforcing its geometric significance.
MacGregor [8] conducted a comprehensive analysis of the family , obtaining key results on distortion estimates, the radius of convexity, and the univalence of partial sums. Further contributions were made by Hallenbeck [9], who explored characteristic results for , establishing connections between this class and other well-known subclasses of univalent functions. Moreover, some radius problems of this nature have been recently discussed by Todorov [10].
In this paper, we focus on three fundamental problems related to the family :
- Sharp estimates for the functional , where and .
- Computation of the length of the boundary curve of for .
- Inclusion properties of the sequences of partial sums for functions .
Our results extend and refine several classical results in the theory of univalent functions, providing new insights into the geometric and analytic properties of .
2. Extremizing the Functional
In this section, we derive sharp estimates for the quantity for functions in the family . These estimates extend and refine earlier results for the family , which were partially addressed by [11,12] and later fully resolved by Gray and Ruscheweyh [13]. Our results provide a complete solution for the family and establish sharp bounds for the ratio .
The problem of estimating is of fundamental importance in the theory of univalent functions. For the family , Gray and Ruscheweyh [13] proved the following sharp result:
Theorem 1
([13]). For and , we have
The bounds are sharp for the function
with equality achieved at (lower bound) and (upper bound).
Our goal is to generalize this result to the family . To achieve this, we first establish several key lemmas and corollaries that will be instrumental in proving our main theorem.
Lemma 1
([14]). A function is analytic in with and if and only if
where is analytic and satisfies in .
Using this lemma, we derive the following estimates for functions with positive real parts.
Theorem 2.
Let be analytic in and satisfy and for all . Then,
- i .
- for all .
- ii .
- DefineThen,
Proof.
- According to Lemma 1, there exists a function analytic in such that andTaking absolute values, we obtainSince , the result follows.
- Substituting and using part i., we getEvaluating the integral gives
This completes the proof. □
Corollary 1.
For all , we have
Proof.
Consider the function , which satisfies and for all (see [1]). Define
According to Theorem 2(ii), we have
Taking the negative of both sides provides the desired result. □
Definition 1
(Subordination [1]). ” Let f and g be analytic functions in the open unit disk . We say that f is subordinate to g in , denoted by , if there exists an analytic function such that and for all , satisfying
In particular, if g is univalent in , then subordination is equivalent to
This characterization highlights that under univalence, subordination implies that f preserves both the initial value and the image inclusion structure dictated by g.
Lemma 2.
Let . For all , we have
Proof.
Since , it follows from [9] (Theorem 6) that
The function is univalent in since is univalent in . According to the subordination principle, (see [1] (Chapter 6)), we obtain
Applying Corollary 1 to the right-hand side completes the proof. □
We now present our main theorem, which establishes sharp bounds for where .
Theorem 3.
For and , we have
where
and
The bounds are sharp for the function
with equality achieved at (lower bound) and (upper bound).
Proof.
We note that the family is compact and rotationally invariant (see [9]), i.e., if , then for all x with . Therefore, in view of [15] (Theorem 1.1, Corollary 1.1, Theorem 1.6), it is sufficient to prove the inequality (6) for the extremal function We will first establish the lower bound by making use of the following mixed form of the triangle inequalities:
Since is analytic and , we can express using the Fundamental Theorem of Calculus as
Applying the chain rule, this simplifies to
Since , we obtain
Substituting and , we arrive at
For and , we have . Taking the modulus on (8) and applying the right-hand side of inequality (7), we obtain
Over , we apply the Maximum Modulus Principle to obtain
where z is chosen such that is maximized and is minimized. The integral in (9) is evaluated as , leading to
Taking the reciprocal of (10), we obtain the desired lower bound of (6).Now, for the upper bound of (6), using , for , we get
Using (11) and (4), we obtain
This establishes the upper bound in (6).
The bounds are sharp, since the extremal function achieves equality at (lower bound) and (upper bound).
Thus, the proof of the theorem is complete. □
Remark 1.
If we set in Theorem 3, the class reduces to (where ), and the bounds in Theorem 3 reduce to the bounds in Theorem 1.
Corollary 2.
For and , we have
The bound is sharp for the extremal function .
Proof.
To prove this corollary, we apply Theorem 3 to the function . Since , it follows that satisfies
Thus, belongs to a class of functions similar to , and we can apply the bounds from Theorem 3 to .
From Theorem 3, we have
Substituting and , we obtain the following result:
Simplifying the left-hand side, we get
Rearranging terms, we isolate
Simplifying further, we obtain the desired bound
The bound is sharp for the extremal function , as it achieves equality in the distortion estimates used in the proof. □
Remark 2.
This corollary provides a distortion estimate for the second derivative of functions in . It generalizes similar results for the class (where ) and demonstrates how the parameter λ influences the growth of . The sharpness of the bound highlights the role of the extremal function in solving extremal problems for this class.
3. Arc Length of Image Curve
In this section, we investigate the arc length of the image curve for functions . The arc length problem is a classical topic in geometric function theory, with significant contributions from MacGregor [8], who established sharp bounds for the family . Our goal is to extend these results to the family and derive sharp estimates for the arc length of the boundary curve .
The arc length of the image curve is defined as the length of the boundary of the region . For any member f of , MacGregor [8] established that
where . This result is sharp, and the extremal function plays a crucial role in understanding the geometric properties of .
In this section, we generalize MacGregor’s result to the family . Specifically, we derive sharp upper bounds for when , and we establish the sharpness of these bounds.
To prove our main result, we rely on the following lemma, which provides a key inequality for subordinated functions.
Lemma 3
([1]). Let F and G be analytic in the unit disk , and suppose . Then, for ,
This lemma allows us to compare the integrals of subordinated functions, which is essential for deriving bounds on the arc length.
We now state and prove our main theorem, which provides sharp upper bounds for the arc length when .
Theorem 4.
Let , and let denote the length of the image curve for . Then,
The result is sharp.
Proof.
Let . By definition, , which implies the subordination
Setting and applying Lemma 3 with , we obtain
Since , it follows that
Expressing the integrand in terms of its real and imaginary parts, we have
Using the properties of the Poisson kernel (see [16] (Chapter 11)) and the fact that
and
we conclude that
The sharpness of the bound follows from the extremal functions
This establishes the result completely. □
Remark 3.
When , the family reduces to , and we recover the following classical result as a corollary.
Corollary 3.
For , the arc-length satisfies
This result aligns with MacGregor’s original theorem and demonstrates the consistency of our generalized bounds with prior work.
4. Sequence of Partial Sums
In this section, we investigate the properties of the partial sums (or sections) of functions in the family . Specifically, we determine the radius of univalence for the nth partial sum of a function and establish conditions under which preserves the properties of the original function f.
The study of partial sums of univalent functions has a rich history in geometric function theory. A fundamental result due to Szegő [17] states that every partial sum of a function is univalent in the disk , and this radius cannot be improved. This is demonstrated by the second partial sum of the Koebe function , which fails to be univalent outside this disk.
For functions in , the situation is more nuanced. While the partial sums of may not preserve univalence in the entire unit disk , we can determine a radius such that remains in for . This section establishes such a result and provides explicit bounds for .
We begin by defining the nth partial sum of a function .
Definition 2.
Let be given by
The nth partial sum (or nth section) of f, denoted by , is the polynomial defined as
For a given analytic function with its partial sum , the partial sum radius is the largest radius, such that retains a desired geometric property (e.g., univalence, starlikeness or convexity) within the disk . Beyond this radius, the truncated series may fail to maintain these properties, emphasizing the significance of in geometric function theory. Our main result establishes the radius of univalence for the partial sums of functions in .
Theorem 5.
Let , and let be its nth partial sum. Then, inside the disk , where
Proof.
Since , we have . Define the function as
It is straightforward to verify that is analytic in , satisfies for all , and attains the value . Consequently, is a function with a positive real part (such functions are called Carathéodory functions) and, according to a classical result (see [3] (Chapter 7, pp. 77–81)), it admits the series representation
where the coefficients satisfy
Furthermore, the function satisfies the following bound on its real part (see Herglotz’s representation theorem [1] (p. 22) and [3] (Chapter 7, Theorem 4)),
Let denote the nth partial sum of , given by
Now, consider the difference , where
satisfies
Therefore,
To simplify this, we have
This expression is non-negative, as shown below:
Let . Then, if
Expanding , we find
For , the right-hand side of the above inequality is positive for . Thus, for . Since is harmonic, we conclude via the maximum modulus principle that in the disk . Consequently, it follows from (12) that in the disk . Thus, in where . □
Remark 4.
The result demonstrates that the partial sums of functions in retain the property in a disk of radius . This radius decreases as n increases, reflecting the fact that higher-order partial sums are less likely to preserve the properties of the original function. The result aligns with Szegő’s [17] classical theorem for and extends it to the family .
5. Conclusions
In this paper, we have investigated several extremal problems for the family , consisting of analytic functions with derivatives which have positive real parts bounded by , as shown below. For , we determine the estimates for the quantity , compute the length of the boundary curve of the image domain , and find the radius of univalence for the partial sums . These results not only generalize and refine existing theorems but also provide new insights into the geometric and analytic properties of . Future work could explore similar problems for other subclasses of univalent functions or investigate the behaviour of higher-order partial sums and their geometric implications.
Author Contributions
Conceptualization, L.A.W. and S.R.M.; Formal analysis, L.A.W. and S.R.M.; Funding acquisition, S.R.M.; Methodology, L.A.W. and S.R.M.; Writing—original draft, L.A.W.; Writing—review and editing, L.A.W. and S.R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Grant No. KFU251212].
Data Availability Statement
The original data contributions presented in this study are included in the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Duren, P.L. Univalent Functions; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Pommerenke, C. Univalent Functions; Vandenhoeck & Ruprecht: Göttingen, Germany, 1975. [Google Scholar]
- Goodman, A.W. Univalent Functions. Vol. I; Mariner Publishing Co., Inc.: Boston, MA, USA, 1983. [Google Scholar]
- Thomas, D.K.; Tuneski, N.; Vasudevarao, A. Univalent Functions; De Gruyter: Berlin, Germany, 2018. [Google Scholar]
- Kapoor, G.; Mishra, A. Closed convex hulls and extreme points of some subclasses of close-to-convex functions. Period. Math. Hung. 1983, 14, 197–208. [Google Scholar] [CrossRef]
- Ali, M.F.; Vasudevarao, A. On logarithmic coefficients of some close-to-convex functions. Proc. Am. Math. Soc. 2018, 146, 1131–1142. [Google Scholar] [CrossRef]
- Kaplan, W. Close-to-convex schlicht functions. Mich. Math. J. 1952, 1, 169–185. [Google Scholar]
- MacGregor, T.H. Functions whose derivative has a positive real part. Trans. Am. Math. Soc. 1962, 104, 532–537. [Google Scholar]
- Hallenbeck, D.J. Convex hulls and extreme points of some families of univalent functions. Trans. Am. Math. Soc. 1974, 192, 285–292. [Google Scholar]
- Todorov, P.G. On the radius of convexity of functions whose derivative has a positive real part. J. Dyn. Syst. Geom. Theor. 2004, 2, 35–41. [Google Scholar] [CrossRef]
- Thomas, D.K. On functions whose derivative has positive real part. Proc. Am. Math. Soc. 1986, 98, 68–70. [Google Scholar] [CrossRef]
- London, R.R. Functions whose derivative has positive real part. Proc. Am. Math. Soc. 1988, 103, 521–524. [Google Scholar] [CrossRef]
- Gray, F.; Ruscheweyh, S. Functions whose derivatives take values in a half-plane. Proc. Am. Math. Soc. 1988, 104, 215–218. [Google Scholar] [CrossRef]
- MacGregor, T.H. The radius of convexity for starlike functions of order 12. Proc. Am. Math. Soc. 1963, 14, 71–76. [Google Scholar]
- Ruscheweyh, S. Convolutions in Geometric Function Theory; Presses de l’Université de Montréal: Montréal, Canada, 1982. [Google Scholar]
- Rudin, W. Real and Complex Analysis; McGraw-Hill, Inc.: New York, NY, USA, 1987. [Google Scholar]
- Szegő, G. Zur Theorie der schlichten Abbildungen. Math. Ann. 1928, 100, 188–211. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).