Dynamic Event-Triggered Sliding Mode Control of Markov Jump Delayed System with Partially Known Transition Probabilities

Abstract

This paper investigates the dynamic event-triggered (ET) sliding mode control (SMC) of Markov jump delayed systems (MJDSs) with partially known transition probabilities. Firstly, a dynamic ET scheme is introduced for the Markov SMC system, and the effect of time delays is considered. In addition, the Razumikhin condition is used to deal with the time delay. Moreover, in the case of a Markov jump system with partially known transition probabilities, using the vertex method, weak infinitesimal generator, and Dynkin’s formula, the finite-time boundness (FTB) problem of a class of ET SMC systems with stochastic delay is studied. Finally, a numerical example is given to illustrate the viability of our results.

1. Introduction

SMC is a robust control method. It exhibits remarkable robustness against parameter uncertainties and external disturbances, a feature that is highly congruent with the demands of MJDSs. In MJDSs, system parameters fluctuate with state transitions, and time delays introduce additional uncertainties. SMC copes with these issues by crafting a suitable sliding mode surface. It compels the system state to reach this surface within a finite time frame and sustain stable sliding thereon, thereby efficiently surmounting these uncertainties. When juxtaposed with other closed-loop control techniques, SMC’s advantages become apparent. Adaptive control, for example, may struggle to adjust its parameters promptly when confronted with rapidly changing system states during jumps. This delay in parameter adjustment can lead to subpar control performance. Model predictive control, on the other hand, faces the challenge of high computational complexity when dealing with complex systems featuring time delays. This complexity makes it arduous to satisfy the real-time control requirements. Consequently, SMC holds unique advantages in the control of MJDSs [1,2,3,4]. The basic idea of SMC is to force the system state trajectory to the pre-designed sliding mode surface, after which the system state will remain on the sliding mode surface [5,6,7]. With the development of science and technology, SMC has been developed rapidly in life, especially in industrial control. Compared with the traditional control system, there is a lot of information to be shared and transmitted in daily communication. How to save communication resources has become the focus of current research [8,9,10,11,12]. Recently, to reduce the transmission frequency, some researchers have proposed a more optimized ET strategy for the ET mechanism. The important feature of the ET strategy is that information is only passed when certain conditions are met [13]. Based on the above design ideas, there have been studies and reports on ET policy rules, such as static ET strategy, dynamic ET strategy, and adaptive event-triggering strategy, in the literature, for example, in [14]. It is worth mentioning that the dynamic ET strategy contains an internal dynamic variable, which effectively increases the minimum event interval time, and is widely used in both continuous time and discrete time systems [15,16]. In recent years, some researchers have focused on ET SMC, and have made some achievements in the study of ET SMC [17]. In the literature, authors mostly use average resident time technology to study the design scheme of ET SMC and put forward the identification condition of the exponential stability of closed-loop systems.

Most existing studies assume that the transition probability is completely known. However, in practical applications, such as in the aerospace and power systems fields, the transition probabilities of Markov jump systems can usually only be partially obtained. This poses a challenge to the effectiveness of existing control strategies [18]. Meanwhile, the presence of time delays can degrade system performance and even lead to system instability. Nevertheless, the existing methods have limitations in dealing with time delay problems. Therefore, conducting research on MJDSs with partially unknown transition probabilities is of great theoretical and practical significance, which is precisely the motivation for this study.

On the other hand, the problem of FTB has wide practical significance, especially in the field of aerospace. So far, there has been some excellent research on SMC problems of Markov jump systems with unknown transition probabilities which solve the FTB SMC problem [19]. For example, the paper [20,21,22] proposed a partitioning strategy for finite time which divided the entire finite-time interval into two parts: before and after reaching the sliding mode surface. After reaching the sliding mode surface, the system state would always be on the sliding mode surface under certain constraints [23,24,25]. In addition, this work has been extended to some more complex systems, such as the switching system and Markov jump system. However, it should be noted that although some important research has solved the FTB SMC problem, the dynamic ET control problem of time-delayed Markov jump systems with unknown transition probabilities has not been studied, which directly inspires the related work in this paper. Compared with the existing research [26,27,28], this paper not only takes into account the scenario where the transition probabilities are partially unknown but also adopts a dynamic ET mechanism. This mechanism effectively reduces the data transmission volume and enhances the resource utilization efficiency of the system. In terms of dealing with time delays, this paper applies the Razumikhin condition and proposes a more accurate analysis method for FTB, which provides a more reliable theoretical basis for controller design. Meanwhile, in [26] studied a similar control problem of Markov jump systems. However, that study assumed that the transition probabilities were completely known and did not consider the influence of time delays. In contrast, this paper conducts research on MJDSs with partially unknown transition probabilities, thus expanding the application scope of relevant theories. In this paper, we discuss the finite-time SMC of a class of time-delayed Markov jump linear systems (MJLSs) with unknown transition probabilities for partially unknown and completely unknown cases, respectively.

In this paper, the issue of dynamic ET finite-time sliding mode control for a class of delayed MJLSs with unknown transition probabilities is studied. First, the integral sliding mode surface is constructed based on the state observer method, and the equivalent control law is derived using SMC theory. Second, a partitioning strategy is adopted to analyze the reachability of the sliding mode motion. The vertex method is utilized to address the uncertainties introduced by the partially unknown transition probabilities. Through the analysis of vertex cases, the crucial properties of the system can be derived. Meanwhile, the weak infinitesimal generator and Dynkin’s formula offer potent mathematical means for investigating the FTB of the system. They are capable of characterizing the dynamic evolutions of the system across different states, thereby facilitating the derivation of the system’s stability conditions. Additionally, the Lyapunov function, Razumikhin method, and Alamo vertex method are used to derive the FTB sufficient conditions for delayed Markov continuous systems with partially/completely unknown transition probabilities. Third, based on the FTB discriminant condition of the system, and comprehensively using Schur’s complementary lemma as well as the linear matrix inequality and binary diagonal matrix inequality methods, a dynamic ET finite-time sliding mode control law is designed for delayed MJLSs with unknown transition probabilities. Finally, using YALMIP toolbox and MATLAB simulation, a numerical simulation of the considered system is conducted to demonstrate the feasibility and effectiveness of the sliding mode control design scheme proposed in this paper.

Notations: Let $\mathbb{N}=\{1,2,3,\cdots \}$ be the set of positive integers. Let $\mathbb{S}=\{0,1,2,\cdots \}$ be the set of positive integers except 0. ${\mathbb{R}}^n$ is n-dimensional of the Euclidean space. $\mathbb{E}$ is the denoted mathematical expectation. ${\mathbb{S}}_{+}^n$ is the set of $n\times n$ real symmetric positive definite matrices. The superscript “T” denotes the transpose for vectors or matrices. The symbol “∗” stands for the symmetry element of a matrix. $a_{ij}$ is the $(i,j)$-th component of a matrix A. For a square matrix A, $He\left\{A\right\}=A+A^{\mathrm{T}}$. $\parallel ·\parallel$ refers to the Euclidean norm for vectors. $\underline{\lambda }={\lambda }_{min}\left(Q\right)$ and $\overline{\lambda }={\lambda }_{max}\left(Q\right)$ are the minimum and maximum eigenvalues of matrix Q, respectively. Define $x_t\left(\theta \right)=x(t+\theta )$. Given a matrix $\Theta \in {\mathbb{R}}^{n\times m}$ with non-negative entries, define $I\left(\Theta \right)=\left\{A:\left|a_{ij}\right|\le {\theta }_{ij},\forall i,j\right\}$. Let ${\Delta }_n$ be the set of $n\times n$ binary diagonal matrices (BDMs), with each entry being 1 or $-1$. The left limit of the function $x\left(t\right)$ is denoted as $x\left(t^{-}\right)={lim}_{t\to t^{-}}x\left(t\right)$. ${\sum }_{j\in I_u^i/i}$ is expressed as ${\sum }_{j\in I_u^i,j\ne i}$, and set $\{a_1,\cdots ,a_n\}/\left\{a_i\right\}=\{a_1,\cdots ,a_{i-1},a_{i+1},\cdots ,a_n\}(1\le i\le n)$. Let ${\mathbf{1}}_D\left(x\right)$ be the indicator function of a set D. $\mathrm{sgn}\left(f\right(x\left)\right)$ is the sign function of $f\left(x\right)$.

2. Preliminaries

2.1. System Description

Consider the Markov jump system with norm-bounded uncertainties as follows:

$$\left\{\begin{array}{c}\dot{x}\left(t\right)=A_{r\left(t\right)}x\left(t\right)+B_{r\left(t\right)}^{\omega }\omega \left(t\right)+B_{r\left(t\right)}u\left(t\right)+A_{r\left(t\right)}^{\tau }x(t-\tau ),\hfill \\ y\left(t\right)=C_{r\left(t\right)}x\left(t\right),\hfill \\ x\left(t\right)=\varphi \left(t\right),t\in [-\tau ,0],\hfill \end{array}\right.$$

(1)

where $x\left(t\right)\in {\mathbb{R}}^n$ is the system state. $y\left(t\right)\in {\mathbb{R}}^m$ is the measurement output. $A_{r\left(t\right)}$ is a set of system matrices. $A_{r\left(t\right)}^{\tau }$ is the time-delayed system matrix. $\varphi \left(t\right)$ is the initial condition with $t\in [-\tau ,0]$ and $\tau >0$ denotes the constant time delay. $\omega \left(t\right)$ is the external disturbance and there exists a known scalar value $\parallel \omega \left(t\right)\parallel \le \overline{\omega }$. $r\left(t\right)\in 𝒮=\{1,2,3,\cdots N\}$ and $N\in \mathbb{N}$. For simplicity, when $r\left(t\right)=i$, we denote $A_{r\left(t\right)}=A_i,A_{r\left(t\right)}^{\tau }=A_i^{\tau }{B}_{r\left(t\right)}^{\omega }=B_i^{\omega },B_{r\left(t\right)}=B_i,C_{r\left(t\right)}=C_i$. Then, the system (1) becomes

$$\left\{\begin{array}{c}\dot{x}\left(t\right)=A_{i}x\left(t\right)+B_i^{\omega }\omega \left(t\right)+B_{i}u\left(t\right)+A_i^{\tau }x(t-\tau ),\hfill \\ y\left(t\right)=C_{i}x\left(t\right),\hfill \\ x\left(t\right)=\varphi \left(t\right),t\in [-\tau ,0]\hfill \end{array}\right.$$

(2)

As [29], the transition rate matrix $\Gamma =\left({\gamma }_{ij}\right)$, and the transition probabilty is given by

$$\mathbb{P}\{r(t+\Delta )=j\mid r\left(t\right)=i\}=\left\{\begin{array}{cc}{\gamma }_{ij}\Delta +o(\Delta ),\hfill & i\ne j\hfill \\ 1+{\gamma }_{ii}\Delta +o(\Delta ),\hfill & i=j\hfill \end{array}\right.$$

(3)

where $\Delta t>0$, ${lim}_{\Delta t\to 0}{\displaystyle \frac{o(\Delta t)}{\Delta t}}=0$ and ${\gamma }_{ij}\ge 0(i,j\in 𝒮,j\ne i)$ are the transition rates (TRs) from state i at time t to j at time $t+\Delta$, and ${\gamma }_{ii}=-{\sum }_{j\ne i}{\gamma }_{ij}(i\in 𝒮)$. In this article, we discuss the following two cases, where some elements in $\Gamma$ are unknown, but not all of them. All of the elements in $\Gamma$ are unknown.

• For the case where the TRs are partially unknown, we define the following two sets $I_k^i=\left\{j\right|{\gamma }_{ij}\mathrm{is}\mathrm{known}\},I_u^i=\left\{j\right|{\gamma }_{ij}\mathrm{is}\mathrm{unknown}\},i\in 𝒮,$ where $I_k^i\left(I_u^i\right)$ denotes the set of known (unknown) elements of the i-th row of $\Gamma$, and $I_k^i\ne Ø$ [29]. Assume the number of elements in $I_k^i$ is $q_i$, then $q_i$ may take the value of $1,2,\cdots ,N-2.$ Let

  $$\begin{array}{c}\hfill I_k^i=\left\{l_i^1,l_i^2,\cdots ,l_i^{q_i}\right\}\end{array}$$

  (4)

  where $l_i^{q_l},1\le q_l\le q_i$ represents the $q_l$-th element of $I_k^i$. It should be noted that the sum of elements in every row is zero, so there is no such situation where only one element is unknown in the given row, i.e., $q_i<N-1$.
• For the case of completely unknown TRs, it is assumed that the lower bound and upper bound of the TRs ${\gamma }_{ij}$ are available, i.e., there exist non-negative constants ${\underline{\gamma }}_{ij}$ and ${\overline{\gamma }}_{ij}$ such that ${\underline{\gamma }}_{ij}\le {\gamma }_{ij}\le {\overline{\gamma }}_{ij}$. Then, ${\gamma }_{ij}$ can be represented by

  $${\gamma }_{ij}={\gamma }_{ij}^0+\Delta {\gamma }_{ij},$$

  (5)

  where ${\gamma }_{ij}^0={\displaystyle \frac{1}{2}}\left({\underline{\gamma }}_{ij}+{\overline{\gamma }}_{ij}\right)$ and $\left|\Delta {\gamma }_{ij}\right|\le {\theta }_{ij}$ with ${\theta }_{ij}={\displaystyle \frac{1}{2}}\left({\overline{\gamma }}_{ij}-{\underline{\gamma }}_{ij}\right)$.

In this work, only the measurement output $y\left(t\right)$ is assumed to be available. In order to save the network resources, the model-dependent dynamic ET mechanism is utilized between the sensor/controller network. The ET instant $t_k$ is determined by the following rule [30]:

$$\begin{array}{c}\hfill t_{k+1}=inf\left\{t\in R^{+}|t\ge t_k,{\displaystyle \frac{{\theta }_{r\left(t\right)}\left(t\right)}{{\lambda }_0}}+{\lambda }_1{y}^T\left(t\right)M_{r\left(t\right)}y\left(t\right)-e_y^T\left(t\right)N_{r\left(t\right)}{e}_y\left(t\right)\le 0\right\}\end{array}$$

(6)

where $e_y\left(t\right)=y\left(t_k\right)-y\left(t\right)$ is the event-triggering error. $M_{r\left(t\right)},N_{r\left(t\right)}$ are known matrices. ${\lambda }_0$ and ${\lambda }_1$ represent two parameters of the trigger condition. The internal dynamical variable ${\theta }_{r\left(t\right)}\left(t\right)$ is a bounded non-negative function and satisfies

$${\dot{\theta }}_{r\left(t\right)}\left(t\right)=-c{\theta }_{r\left(t\right)}\left(t\right)+{\lambda }_1{y}^T\left(t\right)M_{r\left(t\right)}y\left(t\right)-e_y^T\left(t\right)N_{r\left(t\right)}{e}_y\left(t\right)$$

(7)

where $c>0$ and ${\theta }_{r\left(0\right)}\left(0\right)=0$.

Next, utilizing the transmitted signal $y\left(t_k\right)$ at triggering instant $t_k$, the following state observer is constructed:

$$\left\{\begin{array}{c}\dot{\widehat{x}}\left(t\right)=A_i\widehat{x}\left(t\right)+A_i^{\tau }\widehat{x}(t-\tau )+B_{i}u\left(t\right)+L_i(y\left(t_k\right)-\widehat{y}\left(t\right))\hfill \\ \widehat{y}\left(t\right)=C_i\widehat{x}\left(t\right)\hfill \end{array}\right.$$

(8)

where $\widehat{x}\left(t\right)$ is the state estimate and L is the observer gain. Let the estimation error be $e\left(t\right)=x\left(t\right)-\widehat{x}\left(t\right)$; then, from (2) and (8), we obtain

$$\begin{array}{cc}\hfill \dot{e}\left(t\right)=& (A_i-L_i{C}_i)e\left(t\right)+A_i^{\tau }e(t-\tau )-L_i{e}_y\left(t\right)+B_i^{\omega }\omega \left(t\right)\hfill \end{array}$$

(9)

Remark 1.

From (6), in the interval $[t_k,t_{k+1})$ and ${\lambda }_0>0$, we have ${\lambda }_1{y}^T\left(t\right)N_{r\left(t\right)}y\left(t\right)-e_x^T\left(t\right)N_{r\left(t\right)}{e}_x\left(t\right)\ge -{\displaystyle \frac{{\theta }_{r\left(t\right)}\left(t\right)}{{\lambda }_0}}.$ By (7), we have ${\theta }_{r\left(t\right)}\left(t\right)\ge e^{-(c+{\displaystyle \frac{1}{{\lambda }_0}})(t-t_0)}{\theta }_{r\left(t_0\right)}\left(t_0\right)$, so ${\theta }_{r\left(t\right)}\left(t\right)\ge 0$. By (7), we again obtain ${\theta }_{r\left(t\right)}\left(t\right)={\theta }_{r\left(t_0\right)}\left(t_0\right)e^{-c(t-t_0)}+{\int }_{t_0}^t{e}^{c(s-t)}\left[{\lambda }_1{y}^T\left(s\right)N_{r\left(s\right)}y\left(s\right)-e_x^T\left(s\right)N_{r\left(s\right)}{e}_x\left(s\right)\right]$$ds,$ so the dynamic event-trigger variable is a continuous function. Then, ${\theta }_{r\left(t\right)}\left(t\right)$ is a non-negative continuous function.

2.2. Slide Mode

Consider the ITSM as follows [31]:

$$s\left(t\right)=G_i\widehat{x}\left(t\right)-{\int }_0^t{G}_i[A_i+B_i{K}_i]\widehat{x}\left(\psi \right)d\psi$$

(10)

where $G_i\in {\mathbb{R}}^{m\times n}$ is to be designed to ensure that the matrix $G_i{B}_i$ is a non-singularity. It can be easily shown that the non-singularity of $G_i{B}_i$ can be ensured by choosing $G_i=B_i^T{X}_i$ with the matrix $X_i>0$.

Then, it follows from (8) that

$$\begin{array}{c}\hfill \dot{s}\left(t\right)=G_i{A}_i^{\tau }\widehat{x}(t-\tau )+G_i{B}_{i}u\left(t\right)+G_i{L}_i(y\left(t_k\right)-C_i\widehat{x}\left(t\right))-G_i{B}_i{K}_i\widehat{x}\left(t\right)\end{array}$$

(11)

According to SMC theory, when the state trajectories are driven to the sliding surface, i.e., $s\left(t\right)=\dot{s}\left(t\right)=0$, we can obtain the equivalent control law:

$$\begin{array}{cc}\hfill u_{eq}=& K_i\widehat{x}\left(t\right)-{\left(G_i{B}_i\right)}^{-1}{G}_i{A}_i^{\tau }\widehat{x}(t-\tau )-{\left(G_i{B}_i\right)}^{-1}{G}_i{L}_i\left(y\left(t_k\right)-C_i\widehat{x}\left(t\right)\right)\hfill \end{array}$$

(12)

Then, consider the SMC as

$$u\left(t\right)=u_{eq}-\overline{\delta }\left(t\right)$$

(13)

where $\overline{\delta }\left(t\right)=\delta ·\mathrm{sgn}\left(s\left(t\right)\right)$ is the switching control term, and the parameter $\delta$ will be designed later.

Remark 2.

When the system state reaches the sliding surface in finite time, we can obviously obtain $s\left(t\right)=0$ and $\dot{s}\left(t\right)=0$. Then, with the controller, it moves along the sliding surface. Thus, in (11), let $\dot{s}\left(t\right)=0$; we can obtain $u_{eq}$ in (12).

Let ${\widehat{G}}_i=I-B_i{\left(G_i{B}_i\right)}^{-1}{G}_i$. By (12), the augmented closed-loop system of (8) can be described as

$$\begin{array}{cc}\hfill \dot{\widehat{x}}\left(t\right)=& \left[A_i+B_i{K}_i\right]\widehat{x}\left(t\right)+{\widehat{G}}_i{A}_i^{\tau }\widehat{x}(t-\tau )+{\widehat{G}}_i{L}_i{e}_y\left(t\right)+{\widehat{G}}_i{L}_i{C}_{i}e\left(t\right)-B_i\overline{\delta }\left(t\right)\hfill \end{array}$$

(14)

Then, from (14) and (9), we have the closed-loop system

$$\dot{\eta }\left(t\right)={\mathcal{A}}_i\eta \left(t\right)+{\mathcal{A}}_i^{\tau }\eta (t-\tau )+{\mathcal{L}}_i{e}_y\left(t\right)+{\mathcal{B}}_i^{\omega }\omega \left(t\right)+{\mathcal{B}}_i\overline{\delta }\left(t\right)$$

(15)

where

$$\begin{array}{cc}\hfill & \eta \left(t\right)={\left[{\widehat{x}}^T\left(t\right)e^T\left(t\right)\right]}^T;\hfill \\ \hfill & {\mathcal{A}}_i=\left[\begin{array}{cc}{A}_i+B_i{K}_i& {\widehat{G}}_i{L}_i{C}_i\\ 0& A_i-L_i{C}_i\end{array}\right],{\mathcal{A}}_i^{\tau }=\left[\begin{array}{cc}{\widehat{G}}_i{A}_i^{\tau }& 0\\ 0& A_i^{\tau }\end{array}\right];\hfill & \\ \hfill & {\mathcal{L}}_i=\left[\begin{array}{c}{\widehat{G}}_i{L}_i\\ -L_i\end{array}\right],{\mathcal{B}}_i^{\omega }=\left[\begin{array}{c}0\\ B_i^{\omega }\end{array}\right],{\mathcal{B}}_i=\left[\begin{array}{c}-B_i\\ 0\end{array}\right].\hfill \end{array}$$

Definition 1

([32]). Scalars $c_1$ and $c_2$ are positive, $Q>0$, and $t_1\le t_2$. Then, within $u\left(t\right)=0$, the argument system (15) is FTB with $(c_1,c_2,[t_1,t_2],Q,\overline{\omega })$. If

$$\mathbb{E}\left\{{\eta }^T\left(t_1\right)Q\eta \left(t_1\right)\right\}\le c_1⟹\mathbb{E}\left\{{\eta }^T\left(t\right)Q\eta \left(t\right)\right\}\le c_2,t\in [t_1,t_2].$$

Lemma 1

([33]). Given the matrices $F\in {\mathbb{R}}^{n\times n}$ and $Q\in {\mathbb{R}}^{m\times n}$, consider the robust constraint

$$F+\mathrm{He}\left\{HQ\right\}<0,\forall H\in I\left(\Theta \right),$$

where $\Theta \in {\mathbb{R}}^{n\times m}$ with non-negative entries. Then, the following inequality holds if and only if

$$F+He\left\{{\Delta }_0\Theta {\Delta }_{1}Q\right\}<0,\forall {\Delta }_0\in {\Delta }_n,{\Delta }_1\in {\Delta }_m.$$

(16)

3. Main Results

This section analyzes the FTB, both with some elements in $\Gamma$ being unknown and all elements being unknown. For any given $T\in [0,T]$, there are two intervals $[0,T^{*}]$ and $[T^{*},T]$. The FTB for both the reach ability phase in $[0,T^{*}]$ and the sliding phase in $[T^{*},T]$ are analyzed, respectively.

Lemma 2

([2]). The closed-loop system (15) can be driven to the specified sliding surface $s\left(t\right)=0$ with the SMC law $u\left(t\right)=-{\left(G_i{B}_i\right)}^{-1}\left(G_i{A}_i^{\tau }\widehat{x}(t-\tau )+G_i{L}_i(y\left(t_k\right)-C_i\widehat{x}\left(t\right))-G_i{B}_i{K}_i\widehat{x}\left(t\right)\right)-\delta ·\mathrm{sgn}\left(s\left(t\right)\right)$, in a finite time $T^{*}$ with $T^{*}<T$ for any given $T>0$, if the adjustable parameter δ satisfies

$$\delta \ge {\displaystyle \frac{1}{T-ϵ}}{\lambda }_{max}{\left(G_i{B}_i\right)}^{-1}\parallel G_i\widehat{x}\left(0\right)\parallel$$

with a small constant $0<ϵ<T$.

Proof. 

In the following, an adequate SMC law is considered by ITMS to enable the state to reach SMC in a finite-time interval $[0,T^{*}].$ Consider the following Lyapunov function

$$V_s\left(t\right)={\displaystyle \frac{1}{2}}{s}^T\left(t\right){\left(G_i{B}_i\right)}^{-1}s\left(t\right)$$

(17)

From (11), we have

$$\begin{array}{cc}\hfill {\dot{V}}_s\left(t\right)=& s^T\left(t\right){\left(G_i{B}_i\right)}^{-1}(G_i{A}_i^{\tau }\widehat{x}(t-\tau )+G_i{L}_i(y\left(t_k\right)\hfill \\ \hfill & -C_i\widehat{x}\left(t\right))-G_i{B}_i{K}_i\widehat{x}\left(t\right))+s^T\left(t\right)u\left(t\right)\hfill \\ \hfill \le & -s^T\left(t\right)\delta ·\mathrm{sgn}\left(s\left(t\right)\right)\hfill \\ \hfill \le & -\delta \left|s\right(t\left)\right|\le -\delta \parallel s\left(t\right)\parallel \hfill \end{array}$$

(18)

Due to

$${\displaystyle \frac{1}{2}}{\lambda }_{min}{\left(G_i{B}_i\right)}^{-1}\parallel s\left(t\right){\parallel }^2\le V_S\left(t\right)\le {\displaystyle \frac{1}{2}}{\lambda }_{max}{\left(G_i{B}_i\right)}^{-1}{\parallel s\left(t\right)\parallel }^2$$

(19)

it follows from (18) that

$$\begin{array}{c}\hfill {\displaystyle \frac{{\dot{V}}_s\left(t\right)}{\sqrt{V_s\left(t\right)}}}\le -\delta \sqrt{{\displaystyle \frac{2}{{\lambda }_{max}{\left(G_i{B}_i\right)}^{-1}}}}\end{array}$$

(20)

Integrating 0 to $T^{*}$, and noting $s\left(T^{*}\right)=0$, we obtain

$$\begin{array}{cc}\hfill T^{*}\le & {\displaystyle \frac{\sqrt{{\lambda }_{max}{\left(G_i{B}_i\right)}^{-1}}}{\delta }}\sqrt{{\lambda }_{max}{\left(G_i{B}_i\right)}^{-1}{\parallel s\left(0\right)\parallel }^2}\hfill \\ \hfill \le & {\displaystyle \frac{{\lambda }_{max}{\left(G_i{B}_i\right)}^{-1}}{\delta }}\parallel s\left(0\right)\parallel \hfill \\ \hfill =& {\displaystyle \frac{{\lambda }_{max}{\left(G_i{B}_i\right)}^{-1}}{\delta }}\parallel G_i\widehat{x}\left(0\right)\parallel \hfill \end{array}$$

(21)

so there exist a small positive scalar $ϵ$ and $T^{*}\le T-ϵ<T$

$$\delta \ge {\displaystyle \frac{1}{T-ϵ}}{\lambda }_{max}{\left(G_i{B}_i\right)}^{-1}\parallel G_i\widehat{x}\left(0\right)\parallel$$

then, there exists a finite time $T^{*}\in [0,T]$ which enables the state trajectories to slide into the surface. This completes the proof. □

3.1. FTB over Reaching Phase Within $[0,T^{*}]$

Theorem 1.

Consider the system (15) with partially known TRs. Given $(c_1,c^{*},[0,T^{*}],Q,\overline{\omega })$ and scalars $\beta >0,{\mu }_i>0$, if there exist scalars ${\rho }_i>0$ and positive matrices ${\overline{P}}_i$ with appropriate dimensions satisfying

$$\begin{array}{cc}\hfill {\Omega }^i\left(r\right)=& \left[\begin{array}{ccccc}{\Omega }_{11}^i\left(r\right)& {\Omega }_{12}^i& {\Omega }_{13}^i& {\Omega }_{14}^i& 0\\ *& {\Omega }_{22}^i& 0& 0& 0\\ *& *& {\Omega }_{33}^i& 0& 0\\ *& *& *& {\Omega }_{44}^i& 0\\ *& *& *& *& {\Omega }_{55}^i\end{array}\right]<0\hfill \end{array}$$

(22)

$$P_i\le {\rho }_{i}I$$

(23)

$$\begin{array}{c}\hfill e^{\beta T^{*}}(\overline{\lambda }{c}_1+{\theta }_{r\left(0\right)}\left(0\right)+\beta {\overline{\omega }}^2{T}^{*}+\beta m{\delta }^2{T}^{*})\le c^{*}\underline{\lambda }\end{array}$$

(24)

where

$$\begin{array}{cc}{P}_i=diag\left({\overline{P}}_i,{\overline{P}}_i\right),\widetilde{C_i}=[C_i,C_i],\hfill & \hfill \\ {\Omega }_{11}^i\left(r\right)=P_i{\mathcal{A}}_i+{\left(P_i{\mathcal{A}}_i\right)}^T+S_i\left(r\right)+({\mu }_i-\beta )P_i+{\displaystyle \frac{{\rho }_i}{{\mu }_i}}{\lambda }_{max}\left({\left(A_i^{\tau }\right)}^T{A}_i^{\tau }\right)I+\lambda (1+h){\tilde{C}}_i^T{M}_i{\tilde{C}}_i,\hfill & \hfill \\ {\Omega }_{12}^i=P_i{\mathcal{L}}_i,{\Omega }_{13}^i=P_i{\mathcal{B}}_i^{\omega },{\Omega }_{14}^i=P_i{\mathcal{B}}_i,\hfill & \hfill \\ {\Omega }_{22}^i=-(1+h)N_i,{\Omega }_{33}^i=-\beta I,{\Omega }_{44}^i=-\beta I,{\Omega }_{55}^i=-c-\beta +{\displaystyle \frac{h}{{\lambda }_0}},\hfill & \hfill \\ \underline{\lambda }={\displaystyle \underset{i\in \mathbb{S}}{min}}\{{\lambda }_{min}(Q^{-{\displaystyle \frac{1}{2}}}{P}_i{Q}^{-{\displaystyle \frac{1}{2}}})\},\overline{\lambda }={\displaystyle \underset{i\in \mathbb{S}}{max}}\{{\lambda }_{max}(Q^{-{\displaystyle \frac{1}{2}}}{P}_i{Q}^{-{\displaystyle \frac{1}{2}}})\},\hfill & \hfill \\ S_i\left(r\right)=\left\{\begin{array}{cc}\sum _{j=1,j\in I_k^i}^N{\gamma }_{ij}\left(P_j-P_r\right),\hfill & i\in I_k^i,r\in I_u^i,\hfill \\ \sum _{j=1,j\in I_k^i/i}^N{\gamma }_{ij}(P_j-P_r-P_i)-{\alpha }_i{P}_r,\hfill & i\in I_u^i,r\in I_u^i/i.\hfill \end{array}\right.\hfill \end{array}$$

then the closed-loop system (15) is FTP.

Proof. 

Note that the dynamic ET condition (6) implies thatfor any $t\in \left[t_k,t_{k+1}\right),r\left(t\right)=i$,

$${\displaystyle \frac{{\theta }_i\left(t\right)}{{\lambda }_0}}+{\lambda }_1{y}^T\left(t\right)M_{i}y\left(t\right)-e_y^T\left(t\right)N_i{e}_y\left(t\right)>0$$

From (7) and (8) have

$$\begin{array}{cc}\hfill {\dot{\theta }}_i\left(t\right)=& -c{\theta }_i\left(t\right)-e_y^T\left(t\right)N_i{e}_y\left(t\right)+{\lambda }_1{\left({\tilde{C}}_i\eta \left(t\right)\right)}^T{M}_i\left({\tilde{C}}_i\eta \left(t\right)\right)\hfill \end{array}$$

(25)

By the dynamic Equation (25), we have ${\dot{\theta }}_i\left(t\right)>-\left(c+{\displaystyle \frac{1}{{\lambda }_0}}\right){\theta }_i\left(t\right).$ Then, integrating from 0 to t, yields ${\theta }_i\left(t\right)>{\theta }_{r\left(0\right)}\left(0\right)e^{-\left(c+{\displaystyle \frac{1}{{\lambda }_0}}\right)t}.$ For ${\theta }_{r\left(0\right)}\left(0\right)>0$, one obtains ${\theta }_i\left(t\right)>0$ for $t\in [0,\infty )$.

Choose the Lyapunov function as

$$\begin{array}{c}\hfill 𝒱(\eta \left(t\right),i,t)={\eta }^T\left(t\right)P_i\eta \left(t\right)+{\theta }_i\left(t\right)\end{array}$$

(26)

By the Razumikhin condition $\parallel \eta (t-\tau )\parallel \le \parallel \eta \left(t\right)\parallel$ and (23), we obtain

$$\begin{array}{cc}\hfill \mathcal{L}\left({\eta }^T\left(t\right)P_i\eta \left(t\right)\right)\le & {\eta }^T\left(t\right)\left(2P_i{\mathcal{A}}_i+\sum _{j=1}^s{\gamma }_{ij}{P}_j\right)\eta \left(t\right)+2{\eta }^T\left(t\right)P_i{\mathcal{L}}_i{e}_y\left(t\right)+2{\eta }^T\left(t\right)P_i{\mathcal{B}}_i^{\omega }\omega \left(t\right)\hfill \\ \hfill & +2{\eta }^T\left(t\right)P_i{\mathcal{B}}_i\overline{\delta }\left(t\right)+{\mu }_i{\eta }^T\left(t\right)P_i\eta \left(t\right)+{\displaystyle \frac{{\rho }_i}{{\mu }_i}}{\lambda }_{max}\left({\left(A_i^{\tau }\right)}^T{A}_i^{\tau }\right){\parallel \eta \left(t\right)\parallel }^2\hfill \end{array}$$

(27)

It follows from (27) that

$$\begin{array}{cc}\hfill \mathcal{L}𝒱\le & {\eta }^T\left(t\right)\left(2P_i{\mathcal{A}}_i+\sum _{j=1}^s{\gamma }_{ij}{P}_j\right)\eta \left(t\right)+2{\eta }^T\left(t\right)P_i{\mathcal{L}}_i{e}_y\left(t\right)+2{\eta }^T\left(t\right)P_i{\mathcal{B}}_i^{\omega }\omega \left(t\right)\hfill \\ \hfill & +2{\eta }^T\left(t\right)P_i{\mathcal{B}}_i\overline{\delta }\left(t\right)+{\alpha }_i{\eta }^T\left(t\right)P_i\eta \left(t\right)+{\displaystyle \frac{{\rho }_i}{{\mu }_i}}{\lambda }_{max}\left({\left(A_i^{\tau }\right)}^T{A}_i^{\tau }\right){\parallel \eta \left(t\right)\parallel }^2\hfill \\ \hfill & -c{\theta }_i\left(t\right)-e_y^T\left(t\right)N_i{e}_y\left(t\right)+{\lambda }_1{\left({\tilde{C}}_i\eta \left(t\right)\right)}^T{M}_i\left({\tilde{C}}_i\eta \left(t\right)\right)\hfill \end{array}$$

(28)

Define the auxiliary function

$$J_1:=\mathcal{L}𝒱\left(t\right)-\beta 𝒱\left(t\right)-\beta {\omega }^T\left(t\right)\omega \left(t\right)-\beta {\overline{\delta }}^T\left(t\right)\overline{\delta }\left(t\right)$$

(29)

If the dynamic event triggering condition (6) is violated, for any $h>0$, we can obtain from (28) that

$$\begin{array}{cc}\hfill J_1\le & J_1+h\left({\displaystyle \frac{{\theta }_i\left(t\right)}{{\lambda }_0}}+{\lambda }_1{y}^T\left(t\right)M_{i}y\left(t\right)-e_y^T\left(t\right)N_i{e}_y\left(t\right)\right)\hfill \\ \hfill =& \mathcal{L}𝒱\left(t\right)-\beta \left({\eta }^T\left(t\right)P_i\eta \left(t\right)+{\theta }_i\left(t\right)\right)\hfill \\ \hfill & -\beta {\omega }^T\left(t\right)\omega \left(t\right)-\beta {\overline{\delta }}^T\left(t\right)\overline{\delta }\left(t\right)+h_1\left({\displaystyle \frac{{\theta }_i\left(t\right)}{{\lambda }_0}}+{\lambda }_1{y}^T\left(t\right)M_{i}y\left(t\right)-e_y^T\left(t\right)N_i{e}_y\left(t\right)\right)\hfill \end{array}$$

(30)

In the above inequality (30), only the term ${\eta }^T\left(t\right){\sum }_{j=1}^s{\gamma }_{ij}{P}_j\eta \left(t\right)$ is affected by the uncertainty of the probability. For case (i), ${\gamma }_{ii}\in I_k^i$, we have ${\sum }_{j=1,j\in I_k^i}^N{\gamma }_{ij}=-{\sum }_{j=1,j\in I_u^i}^N{\gamma }_{ij}$, and let ${\rho }_{ij}^1={\displaystyle \frac{{\gamma }_{ij}}{{\sum }_{j=1,j\in I_u^i}^N{\gamma }_{ij}}},j\in I_u^i$; then, ${\sum }_{j=1,j\in I_u^i}^N{\rho }_{ij}^1=1$, and we have

$$\begin{array}{cc}\hfill \sum _{j=1}^N{\gamma }_{ij}{P}_j& =\sum _{j\in I_k^i}{\gamma }_{ij}{P}_j+\sum _{j\in I_u^i}{\gamma }_{ij}{P}_j\hfill \\ \hfill & =\sum _{r\in I_u^i}{\rho }_{ir}^1\left[\sum _{j\in I_k^i}{\gamma }_{ij}\left(P_j-P_r\right)\right]\hfill \end{array}$$

(31)

For case (2), ${\gamma }_{ii}\in I_u^i$. Let ${\rho }_{ij}^2={\displaystyle \frac{{\gamma }_{ij}}{{\sum }_{j=1,j\in I_u^i/i}^N{\gamma }_{ij}}}\ge 0,j\in I_u^i/i$, then ${\sum }_{j=1,j\in I_u^i/i}{\rho }_{ij}^2=1$. We have ${\sum }_{j\in I_u^i/i}{\gamma }_{ij}=-{\sum }_{j\in I_k^i/i}{\gamma }_{ij}-{\gamma }_{ii}$. From those, we have

$$\begin{array}{cc}\hfill \sum _{j=1}^N{\gamma }_{ij}{P}_j& =\sum _{j\in I_k^i/i}{\gamma }_{ij}{P}_j+\sum _{j\in I_u^i/i}{\gamma }_{ij}{P}_j+{\gamma }_{ii}{P}_i\hfill \\ \hfill & =\sum _{r\in I_u^i/i}{\rho }_{ir}^2\left[\sum _{j\in I_k^i/i}{\gamma }_{ij}(P_j-P_r)+{\gamma }_{ii}(P_i-P_r)\right]\hfill \end{array}$$

(32)

Noting ${\sum }_{j=1}^N{\gamma }_{ij}=0$ and ${\alpha }_i\le {\gamma }_{ii}\le -{\sum }_{j=1,j\in I_k^i/i}^N{\gamma }_{ij}$, we have

$$\begin{array}{ccc}\hfill \sum _{j=1}^N{\gamma }_{ij}{P}_j& \le \hfill & \hfill \sum _{r\in I_u^i/i}{\rho }_{ij}^2\left[\sum _{j\in I_k^i/i}{\gamma }_{ij}(P_j-P_r-P_i)-{\alpha }_i{P}_r\right]\end{array}$$

(33)

Therefore, by (31) and (33), we can obtain from (30) that

$$J_1\le \sum _{r\in I_u^i}{\rho }_{ij}^q{\mathcal{M}}^T\left(t\right){\Omega }^i\left(r\right)\mathcal{M}\left(t\right),q=1,2.$$

where $\mathcal{M}\left(t\right)={\left[{\eta }^T\left(t\right),e_y^T\left(t\right),{\omega }^T\left(t\right),{\overline{\delta }}^T\left(t\right),{\sqrt{{\theta }_i}}^T\right]}^T.$

Thus, if the condition (22) holds, we have $J_1<0$. Combined with Equation (49), we have

$$\mathcal{L}𝒱\left(t\right)<\beta 𝒱\left(t\right)+\beta {\omega }^T\left(t\right)\omega \left(t\right)+\beta {\overline{\delta }}^T\left(t\right)\overline{\delta }\left(t\right).$$

(34)

Multiplying $e^{-\beta t}$ for both sides of (34), integrating from 0 to t with $t\in \left[0,T^{*}\right]$, and taking the expectation, one has

$$\begin{array}{cc}\hfill & E{\int }_0^t\mathcal{L}(e^{-\beta s}𝒱\left(s\right))ds<\beta E{\int }_0^t{e}^{-\beta s}{\omega }^T\left(s\right)\omega \left(s\right)ds+\beta E{\int }_0^t{e}^{-\beta s}{\overline{\delta }}^T\left(s\right)\overline{\delta }\left(t\right)ds\hfill \end{array}$$

then, we have

$$e^{-\beta t}E𝒱\left(t\right)\le 𝒱\left(0\right)+\beta {\overline{\omega }}^2{\int }_0^t{e}^{-\beta s}ds+\beta m{\delta }^2{\int }_0^t{e}^{-\beta s}ds,$$

so

$$\begin{array}{cc}\hfill & e^{-\beta t}\mathbb{E}\left\{{\eta }^T\left(t\right)P_i\eta \left(t\right)\right\}\hfill \\ \hfill \le & 𝒱\left(0\right)+\beta {\overline{\omega }}^2{T}^{*}+\beta m{\delta }^2{T}^{*}-e^{-\beta t}{\theta }_i\left(t\right)\hfill \\ \hfill \le & 𝒱\left(0\right)+\beta {\overline{\omega }}^2{T}^{*}+\beta m{\delta }^2{T}^{*}\le {\eta }^T\left(0\right)P_i\eta \left(0\right)+{\theta }_i\left(0\right)+\beta {\overline{\omega }}^2{T}^{*}+\beta m{\delta }^2{T}^{*}\hfill \end{array}$$

(35)

At the same time, we have

$$\begin{array}{c}\hfill \underline{\lambda }\mathbb{E}\left\{{\eta }^T\left(t\right)Q\eta \left(t\right)\right\}\le \mathbb{E}\left\{{\eta }^T\left(t\right)P_i\eta \left(t\right)\right\}\le \overline{\lambda }\mathbb{E}\left\{{\eta }^T\left(t\right)Q\eta \left(t\right)\right\}\end{array}$$

(36)

Hence, we have

$$\begin{array}{cc}\hfill & {\eta }^T\left(0\right)P_i\eta \left(0\right)+{\theta }_i\left(0\right)\le \overline{\lambda }{\eta }^T\left(0\right)Q\eta \left(0\right)+{\theta }_i\left(0\right)\le \overline{\lambda }{c}_1+{\theta }_i\left(0\right)\hfill \end{array}$$

(37)

Then, from (35) and (36), we have

$$\begin{array}{cc}\hfill \mathbb{E}\left\{{\eta }^T\left(t\right)Q\eta \left(t\right)\right\}\le & {\displaystyle \frac{e^{\beta T^{*}}(\overline{\lambda }{c}_1+{\theta }_i\left(0\right)+\beta {\overline{\omega }}^2{T}^{*}+\beta m{\delta }^2{T}^{*})}{\underline{\lambda }}}\le c^{*}\hfill \end{array}$$

obviously, we have

$$c^{*}\ge c_1$$

Then, $t\in [0,T^{*}]$ and the system (15) is FTB about Definition 1. This completes the proof. □

In what follows, we will consider that the TRs are completely unknown. For ${\underline{\gamma }}_{ij}\le {\gamma }_{ij}\le {\overline{\gamma }}_{ij}$, let ${\gamma }_{ij}^0={\displaystyle \frac{1}{2}}({\underline{\gamma }}_{ij}+{\overline{\gamma }}_{ij})$, ${\theta }_{ij}={\displaystyle \frac{1}{2}}({\overline{\gamma }}_{ij}-{\underline{\gamma }}_{ij})$; then, ${\gamma }_{ij}={\gamma }_{ij}^0+\Delta {\gamma }_{ij}$, where $|\Delta {\gamma }_{ij}|\le {\theta }_{ij}$. Since ${\sum }_{j=1,i\ne j}^N{\gamma }_{ij}=-{\gamma }_{ii}$, we have ${\sum }_{j=1}^N{\gamma }_{ij}{P}_j={\sum }_{j=1,j\ne i}^N{\gamma }_{ij}{P}_j-{\sum }_{j=1,i\ne j}^N{\gamma }_{ij}{P}_i={\sum }_{j=1,j\ne i}^N{\gamma }_{ij}(P_j-P_i)$. Therefore,

$$\sum _{j=1,j\ne i}^N{\gamma }_{ij}(P_j-P_i)=\sum _{j=1,j\ne i}^N({\gamma }_{ij}^0+\Delta {\gamma }_{ij})(P_j-P_i)$$

Then, by Lemma 1, we obtain

$$\begin{array}{cc}\hfill \sum _{j=1}^N{\gamma }_{ij}{P}_j=& \sum _{j=1,j\ne i}^N{\gamma }_{ij}^0(P_j-P_i)+{\displaystyle \frac{1}{2}}\mathrm{He}\left(\sum _{j=1,j\ne i}^N{\Delta }_0^j{\theta }_{ij}{\Delta }_1^j(P_j-P_i)\right)\hfill \end{array}$$

(38)

where ${\Delta }_0^j,{\Delta }_1^j\in {\Delta }_n$.

Theorem 2.

Consider the system (15) with completely unknown TRs (5). Given $(c_1,c^{*},[0,T^{*}],$$Q,\overline{\omega })$ and scalars $\beta >0,{\mu }_i>0$, if there exist scalars ${\rho }_i>0$ and positive matrices ${\overline{P}}_i$ with appropriate dimensions satisfying

$$\begin{array}{cc}\hfill {\tilde{\Omega }}^i\left(r\right)=& \left[\begin{array}{ccccc}{\tilde{\Omega }}_{11}^i\left(r\right)& {\tilde{\Omega }}_{12}^i& {\tilde{\Omega }}_{13}^i& {\tilde{\Omega }}_{14}^i& 0\\ *& {\tilde{\Omega }}_{22}^i& 0& 0& 0\\ *& *& {\tilde{\Omega }}_{33}^i& 0& 0\\ *& *& *& {\tilde{\Omega }}_{44}^i& 0\\ *& *& *& *& {\tilde{\Omega }}_{55}^i\end{array}\right]<0\hfill \end{array}$$

(39)

$$P_i\le {\rho }_{i}I$$

(40)

$$\begin{array}{c}\hfill e^{\beta T^{*}}(\overline{\lambda }{c}_1+{\theta }_{r\left(0\right)}\left(0\right)+\beta {\overline{\omega }}^2{T}^{*}+\beta m{\delta }^2{T}^{*}+c_0)\le c^{*}\underline{\lambda }\end{array}$$

(41)

where

$$\begin{array}{cc}& {\tilde{\Omega }}_{11}^i\left(r\right)=P_i{\mathcal{A}}_i+{\left(P_i{\mathcal{A}}_i\right)}^T+\sum _{j=1,j\ne i}^N{\gamma }_{ij}^0\left(P_j-P_i\right)+{\displaystyle \frac{1}{2}}He\left(\sum _{j=1,j\ne i}^N{\Delta }_0^j{\theta }_{ij}{\Delta }_1^j\left(P_j-P_i\right)\right)\hfill \\ & +\left({\mu }_i-\beta \right)P_i+{\displaystyle \frac{{\rho }_i}{{\mu }_i}}{\lambda }_{max}\left({\left(A_i^{\tau }\right)}^T{A}_i^{\tau }\right)I+\lambda (1+h){\tilde{C}}_i^T{M}_i{\tilde{C}}_i,{\Delta }_0^j,{\Delta }_1^j\in {\Delta }_n,\hfill \end{array}$$

$${\tilde{\Omega }}_{12}^i=P_i{\mathcal{L}}_i,{\tilde{\Omega }}_{13}^i=P_i{\mathcal{B}}_i^{\omega },{\tilde{\Omega }}_{14}^i=P_i{\mathcal{B}}_i,{\tilde{\Omega }}_{22}^i=-(1+h)N_i$$

$${\tilde{\Omega }}_{33}^i=-\beta I,{\tilde{\Omega }}_{44}^i=-\beta I,{\tilde{\Omega }}_{55}^i=-c-\beta +{\displaystyle \frac{h}{{\lambda }_0}},P_i=diag\left({\overline{P}}_i,{\overline{P}}_i\right),{\tilde{C}}_i=\left[C_i,C_i\right]$$

$$\underline{\lambda }=\underset{i\in \mathbb{S}}{min}\{{\lambda }_{min}(Q^{-{\displaystyle \frac{1}{2}}}{P}_i{Q}^{-{\displaystyle \frac{1}{2}}})\},\overline{\lambda }=\underset{i\in \mathbb{S}}{max}\{{\lambda }_{max}(Q^{-{\displaystyle \frac{1}{2}}}{P}_i{Q}^{-{\displaystyle \frac{1}{2}}})\}$$

then the closed-loop system (15) is FTP.

Proof. 

Noting (38), the proof of Theorem 2 is similar to the proof of Theorem 1, so it is omitted here. □

3.2. FTB over Sliding Motion Within $[T^{*},T]$

Next, we shall analyze the $\mathrm{FTB}$ of the sliding motion during the interval $\left[T^{*},T\right]$, where the state trajectories maintain in the sliding surface $s\left(t\right)=0$. Substituting the equivalent control law (12) into (8) and (9), we yield the following sliding mode dynamics:

$$\dot{\eta }\left(t\right)={\mathcal{A}}_i\eta \left(t\right)+{\mathcal{A}}_i^{\tau }\eta (t-\tau )+{\mathcal{L}}_i{e}_y\left(t\right)+{\mathcal{B}}_i^{\omega }\omega \left(t\right).$$

(42)

Theorem 3.

Consider the system (15) with partially known TRs. Given $(c^{*},c_2,[T^{*},T],Q,\overline{\omega })$ and scalars $\beta >0,{\mu }_i>0$, if there exist scalars ${\rho }_i>0$ and positive matrices ${\overline{P}}_i$ with appropriate dimensions satisfying

$$\begin{array}{cc}\hfill {\widehat{\Omega }}^i\left(r\right)=& \left[\begin{array}{cccc}{\widehat{\Omega }}_{11}^i\left(r\right)& {\widehat{\Omega }}_{12}^i& {\widehat{\Omega }}_{13}^i& 0\\ *& {\widehat{\Omega }}_{22}^i& 0& 0\\ *& *& {\widehat{\Omega }}_{33}^i& 0\\ *& *& *& {\widehat{\Omega }}_{44}^i\end{array}\right]<0\hfill \end{array}$$

(43)

$$P_i\le {\rho }_{i}I$$

(44)

$$\begin{array}{c}\hfill \overline{\lambda }{c}^{*}+{\theta }_{r\left(0\right)}\left(0\right)e^{-\left(c+{\displaystyle \frac{1}{{\lambda }_0}}\right)T^{*}}+\beta {\overline{\omega }}^2(T-T^{*})\le e^{-\beta T}\underline{\lambda }{c}_2\end{array}$$

(45)

where

$$\begin{array}{cc}\hfill & P_i=diag{\overline{P}}_i,{\overline{P}}_i,\widetilde{C_i}=[C_i,C_i],\hfill \\ \hfill & {\widehat{\Omega }}_{11}^i\left(r\right)=P_i{\mathcal{A}}_i+{\left(P_i{\mathcal{A}}_i\right)}^T+S_i\left(r\right)+({\mu }_i-\beta )P_i+{\displaystyle \frac{{\rho }_i}{{\mu }_i}}{\lambda }_{max}\left({\left(A_i^{\tau }\right)}^T{A}_i^{\tau }\right)I+\lambda (1+h){\tilde{C}}_i^T{M}_i{\tilde{C}}_i,\hfill \\ \hfill & {\widehat{\Omega }}_{12}^i=P_i{\mathcal{L}}_i,{\widehat{\Omega }}_{13}^i=P_i{\mathcal{B}}_i^{\omega },{\widehat{\Omega }}_{22}^i=-(1+h)N_i,\hfill \\ \hfill & {\widehat{\Omega }}_{33}^i=-\beta I,{\Omega }_{44}^i=-\beta I,{\widehat{\Omega }}_{44}^i=-c-\beta +{\displaystyle \frac{h}{{\lambda }_0}},\hfill \\ \hfill & \underline{\lambda }=\underset{i\in \mathbb{S}}{min}\{{\lambda }_{min}(Q^{-{\displaystyle \frac{1}{2}}}{P}_i{Q}^{-{\displaystyle \frac{1}{2}}})\},\overline{\lambda }=\underset{i\in \mathbb{S}}{max}\{{\lambda }_{max}(Q^{-{\displaystyle \frac{1}{2}}}{P}_i{Q}^{-{\displaystyle \frac{1}{2}}})\}\hfill \\ \hfill & S_i\left(r\right)=\left\{\begin{array}{cc}\sum _{j=1,j\in I_k^i}^N{\gamma }_{ij}\left(P_j-P_r\right),\hfill & i\in I_k^i,r\in I_u^i\hfill \\ \sum _{j=1,j\in I_k^i/i}^N{\gamma }_{ij}(P_j-P_r-P_i)-{\alpha }_i{P}_r,\hfill & i\in I_u^i,r\in I_u^i/i\hfill \end{array}\right.\hfill \end{array}$$

then the closed-loop system (15) is FTP.

Proof. 

Choose the Lyapunov function as

$$\begin{array}{c}\hfill \widehat{𝒱}(\eta \left(t\right),i,t)={\eta }^T\left(t\right)P_i\eta \left(t\right)+{\theta }_i\left(t\right)\end{array}$$

(46)

By the Razumikhin condition $\parallel \eta (t-\tau )\parallel \le \parallel \eta \left(t\right)\parallel$ and (42), we obtain

$$\begin{array}{cc}\hfill \mathcal{L}\left[{\eta }^T\left(t\right)P_i\eta \left(t\right)\right]=& {\eta }^T\left(t\right)\left(2P_i{\mathcal{A}}_i+\sum _{j=1}^s{\gamma }_{ij}{P}_j\right)\eta \left(t\right)+2{\eta }^T\left(t\right)P_i{\mathcal{A}}_i^{\tau }\eta (t-\tau )\hfill \\ \hfill & +2{\eta }^T\left(t\right)P_i{\mathcal{L}}_i{e}_y\left(t\right)+2{\eta }^T\left(t\right)P_i{\mathcal{B}}_i^{\omega }\omega \left(t\right)\hfill \\ \hfill \le & {\eta }^T\left(t\right)\left(2P_i{\mathcal{A}}_i+\sum _{j=1}^s{\gamma }_{ij}{P}_j\right)\eta \left(t\right)+2{\eta }^T\left(t\right)P_i{\mathcal{L}}_i{e}_y\left(t\right)\hfill \\ \hfill & +2{\eta }^T\left(t\right)P_i{\mathcal{B}}_i^{\omega }\omega \left(t\right)+{\mu }_i{\eta }^T\left(t\right)P_i\eta \left(t\right)+{\displaystyle \frac{{\rho }_i}{{\mu }_i}}{\lambda }_{max}\left({\left(A_i^{\tau }\right)}^T{A}_i^{\tau }\right){\parallel \eta \left(t\right)\parallel }^2\hfill \end{array}$$

(47)

then

$$\begin{array}{cc}\hfill \mathcal{L}\widehat{𝒱}\le & {\eta }^T\left(t\right)\left(2P_i{\mathcal{A}}_i+\sum _{j=1}^s{\gamma }_{ij}{P}_j\right)\eta \left(t\right)+2{\eta }^T\left(t\right)P_i{\mathcal{L}}_i{e}_y\left(t\right)\hfill \\ \hfill & +2{\eta }^T\left(t\right)P_i{\mathcal{B}}_i^{\omega }\omega \left(t\right)+{\mu }_i{\eta }^T\left(t\right)P_i\eta \left(t\right)+{\displaystyle \frac{{\rho }_i}{{\mu }_i}}{\lambda }_{max}\left({\left(A_i^{\tau }\right)}^T{A}_i^{\tau }\right){\parallel \eta \left(t\right)\parallel }^2\hfill \\ \hfill & -c{\theta }_i\left(t\right)-e_y^T\left(t\right)N_i{e}_y\left(t\right)+{\lambda }_1{\left({\tilde{C}}_i\eta \left(t\right)\right)}^T{M}_i\left({\tilde{C}}_i\eta \left(t\right)\right)\hfill \end{array}$$

(48)

Define the auxiliary function

$$J_2:=\mathcal{L}\widehat{𝒱}\left(t\right)-\beta \widehat{𝒱}\left(t\right)-\beta {\omega }^T\left(t\right)\omega \left(t\right).$$

(49)

For any scale $h_2>0$, we have

$$\begin{array}{cc}\hfill J_2\le & \mathcal{L}\widehat{𝒱}\left(t\right)-\beta \left({\eta }^T\left(t\right)P_i\eta \left(t\right)+{\theta }_i\left(t\right)\right)-\beta {\omega }^T\left(t\right)\omega \left(t\right)\hfill \\ \hfill & +h_1\left({\displaystyle \frac{{\theta }_i\left(t\right)}{{\lambda }_0}}+{\lambda }_1{y}^T\left(t\right)M_{i}y\left(t\right)-e_y^T\left(t\right)N_i{e}_y\left(t\right)\right)\hfill \end{array}$$

similarly, by (31) and (33), we can obtain from (30) that

$$J_2\le \sum _{r\in I_u^i}{\rho }_{ij}^q{\widehat{\mathcal{M}}}^T\left(t\right){\widehat{\Omega }}^i\left(r\right)\widehat{\mathcal{M}}\left(t\right),q=1,2.$$

where $\widehat{\mathcal{M}}\left(t\right)={\left[{\eta }^T\left(t\right),e_y^T\left(t\right),{\omega }^T\left(t\right),{\overline{\delta }}^T\left(t\right),{\sqrt{{\theta }_i}}^T\right]}^T.$

It can be shown that expression (39) can promise $J_2<0$, from which we obtain

$$\mathcal{L}\widehat{𝒱}\left(t\right)<\beta \widehat{𝒱}\left(t\right)+\beta {\omega }^T\left(t\right)\omega \left(t\right)$$

(50)

Multiplying $e^{-\beta t}$ for both sides of (50), integrating from $T^{*}$ to t with $t\in \left[T^{*},T\right]$, and taking the expectation, one has

$$\begin{array}{cc}\hfill & E{\int }_{T^{*}}^T\mathcal{L}\left(e^{-\beta s}\widehat{𝒱}\left(s\right)\right)ds<\beta E{\int }_{T^{*}}^T{e}^{-\beta s}{\omega }^T\left(s\right)\omega \left(s\right)ds\hfill \end{array}$$

then we have

$$e^{-\beta t}E𝒱\left(t\right)\le e^{-\beta T^{*}}\widehat{𝒱}\left(T^{*}\right)+\beta {\overline{\omega }}^2{\int }_{T^{*}}^t{e}^{-\beta s}ds.$$

(51)

Based on inequality (25), it can be deduced that ${\theta }_i\left(t\right)>{\theta }_{r\left(0\right)}\left(0\right)e^{-\left(c+{\displaystyle \frac{1}{{\lambda }_0}}\right)t}.$ Subsequently, the following inequality can be obtained

$$\widehat{𝒱}\left(T^{*}\right)<\overline{\lambda }{c}^{*}+{\theta }_{r\left(0\right)}\left(0\right)e^{-\left(c+{\displaystyle \frac{1}{{\lambda }_0}}\right)T^{*}}.$$

(52)

Resulting from (51) and (52), we have

$$e^{-\gamma t}\underline{\lambda }\mathbb{E}\left\{{\eta }^T\left(t\right)Q\eta \left(t\right)\right\}+e^{-\beta t}{\theta }_i\left(t\right)<\overline{\lambda }{c}^{*}+{\theta }_{r\left(0\right)}\left(0\right)e^{-\left(c+{\displaystyle \frac{1}{{\lambda }_0}}\right)T^{*}}+\beta {\overline{\omega }}^2(T-T^{*})$$

For ${\theta }_i\left(t\right)>0$, the condition (41) can promise $\mathbb{E}\left\{{\eta }^T\left(t\right)Q\eta \left(t\right)\right\}<c_2$ for all $t\in \left[T^{*},T\right]$, which implies the sliding motion FTB within $\left[T^{*},T\right]$. This completes the proof. □

Theorem 4.

Consider the system (15) with completely unknown TRs (5). Given $(c^{*},c_2,[T^{*},T],$$Q,\overline{\omega })$ and scalars $\beta >0,{\mu }_i>0$, if there exist scalars ${\rho }_i>0$ and positive matrices ${\overline{P}}_i$ with appropriate dimensions satisfying

$$\begin{array}{cc}\hfill {\breve{\Omega }}^i\left(r\right)=& \left[\begin{array}{cccc}{\breve{\Omega }}_{11}^i\left(r\right)& {\breve{\Omega }}_{12}^i& {\breve{\Omega }}_{13}^i& 0\\ *& {\breve{\Omega }}_{22}^i& 0& 0\\ *& *& {\breve{\Omega }}_{33}^i& 0\\ *& *& *& {\breve{\Omega }}_{44}^i\end{array}\right]<0\hfill \end{array}$$

(53)

$$P_i\le {\rho }_{i}I$$

(54)

$$\begin{array}{c}\hfill \overline{\lambda }{c}^{*}+{\theta }_{r\left(0\right)}\left(0\right)e^{-\left(c+{\displaystyle \frac{1}{{\lambda }_0}}\right)T^{*}}+\beta {\overline{\omega }}^2(T-T^{*})\le e^{-\beta T}\underline{\lambda }{c}_2\end{array}$$

(55)

where

$$\begin{array}{cc}\hfill & P_i=diag{\overline{P}}_i,{\overline{P}}_i,\widetilde{C_i}=[C_i,C_i],\hfill \\ \hfill & {\breve{\Omega }}_{11}^i\left(r\right)=P_i{\mathcal{A}}_i+{\left(P_i{\mathcal{A}}_i\right)}^T+\sum _{j=1,j\ne i}^N{\gamma }_{ij}^0(P_j-P_i)+{\displaystyle \frac{1}{2}}\mathrm{He}\left(\sum _{j=1,j\ne i}^N{\Delta }_0^j{\theta }_{ij}{\Delta }_1^j(P_j-P_i)\right)\hfill \\ \hfill & +({\mu }_i-\beta )P_i+{\displaystyle \frac{{\rho }_i}{{\mu }_i}}{\lambda }_{max}\left({\left(A_i^{\tau }\right)}^T{A}_i^{\tau }\right)I+\lambda (1+h){\tilde{C}}_i^T{M}_i{\tilde{C}}_i,{\Delta }_0^j,{\Delta }_1^j\in {\Delta }_n,\hfill \\ \hfill & {\breve{\Omega }}_{12}^i=P_i{\mathcal{L}}_i,{\breve{\Omega }}_{13}^i=P_i{\mathcal{B}}_i^{\omega },{\breve{\Omega }}_{22}^i=-(1+h)N_i,{\breve{\Omega }}_{33}^i=-\beta I,{\Omega }_{44}^i=-\beta I,\hfill \\ \hfill & {\breve{\Omega }}_{44}^i=-c-\beta +{\displaystyle \frac{h}{{\lambda }_0}},\underline{\lambda }=\underset{i\in \mathbb{S}}{min}\{{\lambda }_{min}(Q^{-{\displaystyle \frac{1}{2}}}{P}_i{Q}^{-{\displaystyle \frac{1}{2}}})\},\overline{\lambda }=\underset{i\in \mathbb{S}}{max}\{{\lambda }_{max}(Q^{-{\displaystyle \frac{1}{2}}}{P}_i{Q}^{-{\displaystyle \frac{1}{2}}})\}\hfill \end{array}$$

then the closed-loop system (15) is FTP.

Proof. 

Noting (38), the proof of Theorem 4 is similar to the proof of Theorem 3, so it is omitted here. □

3.3. Zeno Phenomena

The following Theorem ensures that the lower bound of the inter-event time is a positive value, which effectively avoids the Zeno phenomena. Theorem 4. Let $t_k(k=1,\dots ,\infty )$ be the triggering sequences generated by the event-trigger rule (2) and the inter-event time as $T_{in}\triangleq t_{k+1}-t_k$; one has

Theorem 5.

Let $t_k(k=1,\dots ,\infty )$ be the triggering sequences generated by the event-trigger rule $\left(2\right)$ and the inter-event time as $T_{in}\triangleq t_{k+1}-t_k$; one has

$$T_{in}\ge {\displaystyle \frac{1}{{\zeta }_1}}ln\left(1+{\displaystyle \frac{{\zeta }_1\left({\theta }_{r\left(t_{k+1}\right)}\left(t_{k+1}\right)+{\lambda }_0\left({\lambda }_1\mathbb{E}{y}^T\left(t_{k+1}\right)M_{i}y\left(t_{k+1}\right)\right)\right)}{{\lambda }_0{\lambda }_{max}\left(N_i\right)\left({\zeta }_2\mathbb{E}{∥y\left(t_k\right)∥}^2+{\zeta }_0\right)}}\right)$$

where

$$\begin{array}{ccc}\hfill & {\zeta }_0=\parallel C_i{B}_i^{\omega }\parallel \parallel \overline{\omega }{\parallel }^2+\delta m\parallel C_i{B}_i\parallel +(\parallel \mathcal{G}\parallel +\parallel {\mathcal{G}}^{\tau }\parallel ){\displaystyle \frac{c_2}{{\lambda }_{min}\left(Q\right)}},\hfill & \\ \hfill & {\zeta }_1=\parallel {\mathcal{G}}_1\parallel +\parallel {\mathcal{G}}^{\tau }\parallel +\parallel C_i{B}_i^{\omega }\parallel +\delta \parallel C_i{B}_i\parallel +\parallel C_i{B}_i{\left(G_i{B}_i\right)}^{-1}{G}_i{L}_i\parallel ,\hfill & \\ \hfill & {\zeta }_2=\parallel C_i{B}_i{\left(G_i{B}_i\right)}^{-1}{G}_i{L}_i\parallel ,\hfill & \\ \hfill & \mathcal{G}=[C_i\left(A_i+B_i{K}_i+B_i{\left(G_i{B}_i\right)}^{-1}{G}_i{L}_i{C}_i,C_i{A}_i\right],\hfill & \\ \hfill & {\mathcal{G}}^{\tau }=\left[C_i(A_i^{\tau }-B_i{\left(G_i{B}_i\right)}^{-1}{G}_i{A}_i^{\tau }),C_i{A}_i^{\tau }\right].\hfill \end{array}$$

Proof. 

For $t\in [t_k,t_{k+1}]$, we have the event-trigger error

$$\begin{array}{cc}\hfill {\dot{e}}_y\left(t\right)=& -C_i\dot{x}\left(t\right)\hfill \\ \hfill =& -C_i(\dot{e}\left(t\right)+\dot{\widehat{x}}\left(t\right))\hfill \\ \hfill =& -\mathcal{G}\eta \left(t\right)-{\mathcal{G}}^{\tau }\eta (t-\tau )-C_i{B}_i^{\omega }\omega \left(t\right)\hfill \\ & +C_i{B}_i{\left(G_i{B}_i\right)}^{-1}{G}_i{L}_{i}y\left(t_k\right)+\delta C_i{B}_i\mathrm{sgn}\left(s\left(t\right)\right).\hfill \end{array}$$

(56)

Then, by the Razumikhin condition $\parallel \eta (t-\tau )\parallel \le \parallel \eta \left(t\right)\parallel$, we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{\parallel e_y\left(t\right)\parallel }^2\le & 2\parallel e_y\left(t\right)\parallel \parallel {\dot{e}}_y\left(t\right)\parallel \hfill \\ \hfill \le & (\parallel \mathcal{G}\parallel +\parallel {\mathcal{G}}^{\tau }{\parallel )\parallel \eta \left(t\right)\parallel }^2\hfill \\ \hfill & +(\parallel \mathcal{G}\parallel +\parallel {\mathcal{G}}^{\tau }\parallel +\parallel C_i{B}_i^{\omega }\parallel \hfill \\ \hfill & +\parallel C_i{B}_i{\left(G_i{B}_i\right)}^{-1}{G}_i{L}_i\parallel )\parallel e_y\left(t\right){\parallel }^2+\parallel C_i{B}_i^{\omega }\parallel \parallel \overline{\omega }{\parallel }^2\hfill \\ \hfill & +\delta \parallel C_i{B}_i\parallel +\parallel C_i{B}_i{\left(G_i{B}_i\right)}^{-1}{G}_i{L}_i\parallel \parallel y\left(t_k\right){\parallel }^2\hfill \\ \hfill & +\delta m\parallel C_i{B}_i\parallel \hfill \end{array}$$

(57)

Due to $\mathbb{E}\left\{{\eta }^T\left(t\right)Q\eta \left(t\right)\right\}\le c_2$, then

$${\mathbb{E}\parallel \eta \left(t\right)\parallel }^2\le {\displaystyle \frac{c_2}{{\lambda }_{min}\left(Q\right)}}$$

(58)

Then

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathbb{E}{\parallel e_y\left(t\right)\parallel }^2\le & {\zeta }_1\mathbb{E}\parallel e_y{\left(t\right)\parallel }^2+{\zeta }_2\mathbb{E}{\parallel y\left(t_k\right)\parallel }^2+{\zeta }_0\hfill \end{array}.$$

(59)

Integrating (59) from $t_k$ to $t_{k+1}$ and noting at the trigger moment that we have $e_y\left(t_k\right)=0$, then

$$\begin{array}{c}\hfill \mathbb{E}\parallel e_y\left(t_{k+1}\right){\parallel }^2\le {\displaystyle \frac{{\zeta }_2\mathbb{E}{\parallel y\left(t_k\right)\parallel }^2+{\zeta }_0}{{\zeta }_1}}(e^{{\zeta }_1{T}_{in}}-1)\end{array}$$

(60)

In addition, by the event-trigger rule (6), we have

$$\begin{array}{c}\hfill \mathbb{E}\parallel e_y^T\left(t_{k+1}\right){\parallel }^2\ge {\displaystyle \frac{{\theta }_{r\left(t_{k+1}\right)}\left(t_{k+1}\right)+{\lambda }_0\left({\lambda }_1\mathbb{E}{y}^T\left(t_{k+1}\right)M_{i}y\left(t_{k+1}\right)\right)}{{\lambda }_0{\lambda }_{max}\left(N_i\right)}}\end{array}$$

(61)

Combining (60) and (61), we can achieve the lower bound of the inter-event time, which avoids the Zeno phenomena. □

3.4. Controller Design

In this section, Schur’s complementary lemma, linear matrix inequalities (LMIs), and binary diagonal matrix inequalities are adopted based on the sufficient conditions of the finite-time bound for the above systems. In this section, we used the dynamic ET finite-time SMC scheme for time-delayed Markov continuous systems with unknown transition probabilities. Two cases of partial unknown and complete unknown transition probability are classified and discussed, respectively.

Theorem 6.

Consider the system (15) with partially known TRs, for ${\lambda }_{ii}\in I_k^i,i\in 𝒮$. Given the parameters $\left(c_1,c_2,T,Q,\overline{\omega }\right)$ and the adjustable parameters ${\mu }_i>0,\beta$, $h_1,{\lambda }_1$ and ${\kappa }_i$, if there exist a positive matrix $R_i>0$, real matrices ${\mathcal{K}}_i,{\mathcal{L}}_i,{\mathcal{U}}_i$ with appropriate dimensions, and scalars $c^{*}>0,\overline{\kappa }>0,\underline{\kappa }>0,{\rho }_i>0$ and ${ϵ}_i>0$ satisfying the following LMIs:

$$\left[\begin{array}{cc}-{ϵ}_{i}I& *\\ C_i{R}_i-{\mathcal{U}}_i{C}_i& -I\end{array}\right]<0$$

(62)

$$\underline{\kappa }{Q}^{-1}<\widetilde{R_i}<\overline{\kappa }{Q}^{-1}$$

(63)

$$\left[\begin{array}{cc}{\theta }_{r\left(0\right)}\left(0\right)+\beta {\overline{\omega }}^{2}T+\beta m{\delta }^{2}T-{\displaystyle \frac{1}{\overline{\kappa }}}{e}^{-\beta T}{c}^{*}& \sqrt{c_1}\\ *& -\underline{\kappa }\end{array}\right]<0$$

(64)

$$c^{*}+\underline{\kappa }{\theta }_{r\left(0\right)}\left(0\right)+\underline{\kappa }\beta {\overline{\omega }}^{2}T-{\displaystyle \frac{1}{\overline{\kappa }}}{e}^{-\beta T}\underline{\kappa }{c}_2<0$$

(65)

$$c_1<c^{*}<c_2$$

(66)

$$\left[\begin{array}{cc}-R_i& I\\ *& -{\rho }_{i}I\end{array}\right]\le 0$$

(67)

case (1) for $i\in I_k^i,r\in I_u^i$

$${\Theta }^i\left(r\right)\triangleq \left[\begin{array}{ccccc}{\Theta }_{11}^i& {\Theta }_{12}^i& {\Theta }_{13}^i& {\Theta }_{14}^i& {\Theta }_{15}^i\\ *& {\Theta }_{22}^i& 0& 0& 0\\ *& *& {\Theta }_{33}^i& 0& 0\\ *& *& *& {\Theta }_{44}^i\left(r\right)& 0\\ *& *& *& *& {\Theta }_{55}^i\end{array}\right]<0$$

(68)

where

$$\begin{array}{cc}\hfill & {\Theta }_{11}^i=\left[\begin{array}{cc}\mathrm{He}(A_i{R}_i+B_i{\mathcal{K}}_i)+({\mu }_i-\beta +{\gamma }_{ii})R_i& {\widehat{G}}_i{\mathcal{L}}_i{C}_i\\ *& He(A_i{R}_i-{\mathcal{L}}_i{C}_i)+({\mu }_i-\beta +{\gamma }_{ii})R_i\end{array}\right]\hfill \\ \hfill & {\Theta }_{12}^i=\left[\begin{array}{cccc}{\widehat{G}}_i{\mathcal{L}}_i{C}_i{C}_i^T& 0& -B_i& 0\\ -{\mathcal{L}}_i{C}_i{C}_i^T& B_i^{\omega }& 0& 0\end{array}\right],{\Theta }_{13}^i=\left[\begin{array}{ccc}\lambda (1+h)R_i{C}_i^T& {\tilde{\rho }}_i{R}_i& 0\\ \lambda (1+h)R_i{C}_i^T& 0& {\tilde{\rho }}_i{R}_i\end{array}\right],\hfill & \\ \hfill & {\Theta }_{14}^i=\left[\begin{array}{cc}\left[\{\sqrt{{\gamma }_{i,l_i^1}},\cdots ,\sqrt{{\gamma }_{i,l_i^{q_i}}}\}/\left\{\sqrt{{\gamma }_{i,i}}\right\}\right]R_i& R_i\\ 0& 0\end{array}\right],\hfill \\ \hfill & {\Theta }_{15}^i=\left[\begin{array}{cc}0& 0\\ \left[\{\sqrt{{\gamma }_{i,l_i^1}},\cdots ,\sqrt{{\gamma }_{i,l_i^{q_i}}}\}/\left\{\sqrt{{\gamma }_{i,i}}\right\}\right]R_i& R_i\end{array}\right],\hfill \\ \hfill & {\Theta }_{22}^i=diag\left\{{\displaystyle \frac{{\kappa }_i^2}{1+h}}{N}_i^{-1}-2{\kappa }_i{C}_i{R}_i{C}_i^T,-\beta I,-\beta I,-c-\beta +{\displaystyle \frac{h}{{\lambda }_0}}\right\},\hfill & \\ \hfill & {\Theta }_{33}^i=diag\left\{-\lambda (1+h)M_i^{-1},-{\tilde{\rho }}_{i}I,-{\tilde{\rho }}_{i}I\right\},\hfill & \\ \hfill & {\Theta }_{44}^i\left(r\right)=diag\left\{\{-R_{l_i^1},\cdots ,-R_{l_i^{q_i}}\}/\{-R_i\},{\displaystyle \frac{R_r}{{\sum }_{j=1,j\in I_k^i}^N{\gamma }_{ij}}}\right\},\hfill & \\ \hfill & {\Theta }_{55}^i={\Theta }_{44}^i,\widetilde{R_i}\triangleq diag\{R_i,R_i\},\widetilde{{\rho }_i}={\displaystyle \frac{{\rho }_i}{{\mu }_i}}{\lambda }_{max}\left({\left(A_i^{\tau }\right)}^T{A}_i^{\tau }\right),\hfill \end{array}$$

where $\left\{a_1,\cdots ,a_n\right\}/\left\{a_i\right\}$ is $\left\{a_1,\cdots ,a_{i-1},a_{i+1},\cdots ,a_n\right\}(1\le i\le n)$, and the same below.

case (2) for $i\in I_u^i,r\in I_u^i/i$

$${\tilde{\Theta }}^i\left(r\right)=\left[\begin{array}{ccccc}{\tilde{\Theta }}_{11}^i\left(r\right)& {\tilde{\Theta }}_{12}^i& {\tilde{\Theta }}_{13}^i& {\tilde{\Theta }}_{14}^i& 0\\ *& {\tilde{\Theta }}_{22}^i& 0& 0& {\tilde{\Theta }}_{25}^i\\ *& *& {\tilde{\Theta }}_{33}^i& 0& 0\\ *& *& *& {\tilde{\Theta }}_{44}^i& 0\\ *& *& *& *& {\tilde{\Theta }}_{55}^i\end{array}\right]<0,$$

(69)

where

$$\begin{array}{cc}\hfill & {\tilde{\Theta }}_{11}^i\left(r\right)=\left[\begin{array}{cc}{\tilde{\Theta }}_{11}^{i\left(1\right)}\left(r\right)& {\widehat{G}}_i{\mathcal{L}}_i{C}_i\\ *& {\tilde{\Theta }}_{11}^{i\left(2\right)}\left(r\right)\end{array}\right],{\tilde{\Theta }}_{11}^{i\left(1\right)}\left(r\right)=\left[\begin{array}{c}\mathrm{He}(A_i{R}_i+B_i{\mathcal{K}}_i)\\ +({\mu }_i-\beta -\sum _{j=1,j\in I_k^i/i}^N{\gamma }_{ij})R_i\\ +(\sum _{j=1,j\in I_k^i/i}^N{\gamma }_{ij}+{\alpha }_i)(R_r-2R_i)\end{array}\right],\hfill \\ \hfill & {\tilde{\Theta }}_{11}^{i\left(2\right)}\left(r\right)=\left[\begin{array}{c}He(A_i{R}_i-{\mathcal{L}}_i{C}_i)\\ +({\mu }_i-\beta -\sum _{j=1,j\in I_k^i/i}^N{\gamma }_{ij})R_i\\ +(\sum _{j=1,j\in I_k^i/i}^N{\gamma }_{ij}+{\alpha }_i)(R_r-2R_i)\end{array}\right],\hfill \\ \hfill & {\tilde{\Theta }}_{12}^i={\Theta }_{12}^i,{\tilde{\Theta }}_{13}^i={\Theta }_{13}^i,{\tilde{\Theta }}_{22}^i={\Theta }_{22}^i,{\tilde{\Theta }}_{33}^i={\Theta }_{33}^i,\hfill \\ \hfill & {\tilde{\Theta }}_{14}^i=\left[\begin{array}{c}\left[\sqrt{{\gamma }_{i,l_i^1}}{R}_i,\cdots ,\sqrt{{\gamma }_{i,l_i^{q_i}}}{R}_i\right]\\ 0\end{array}\right],{\tilde{\Theta }}_{25}^i=\left[\begin{array}{c}0\\ \left[\sqrt{{\gamma }_{i,l_i^1}}{R}_i,\cdots ,\sqrt{{\gamma }_{i,l_i^{q_i}}}{R}_i\right]\end{array}\right],\hfill \\ \hfill & {\tilde{\Theta }}_{44}^i\triangleq diag\left\{-R_{l_i^1},\cdots ,-R_{l_i^{q_i}}\right\},{\tilde{\Theta }}_{55}^i={\tilde{\Theta }}_{44}^i.\hfill \end{array}$$

With the controller gain $K_i={\mathcal{K}}_i{R}_i^{-1}$ and observer gain $L_i={\mathcal{L}}_i{\mathcal{U}}_i^{-1}$, the closed-loop system (15) is FTB with $\left(c_1,c_2,[0,T],Q,\overline{\omega }\right)$

Proof. 

For case (1), let $R_i\triangleq {\overline{P}}_i^{-1}$. Let us multiply both sides of (22), (43) by $diag\{R_i,R_i,C_i{R}_i{C}_i^T,$$I,I,I\},diag\left\{R_i,R_i,C_i{R}_i{C}_i^T,I,I\right\},$ Then, use Schur’s complementary lemma and $-Y{X}^{-1}Y\le {\kappa }^{2}X-2\kappa Y$, let $K_i{R}_i={\mathcal{K}}_i,L_i{\mathcal{U}}_i={\mathcal{L}}_i$, and consider the linear equality constraint $C_i{R}_i={\mathcal{U}}_i{C}_i$; it is easy to verify that (68) makes both (22) and (43) true. □

Meanwhile, the linear equality constraint $C_i{R}_i={\mathcal{U}}_i{C}_i$ can be approximately solved by the inequality (62).

On the other hand, by the condition (63), there is $\underline{\kappa }I<Q^{{\displaystyle \frac{1}{2}}}{\tilde{R}}_i{Q}^{{\displaystyle \frac{1}{2}}}<\overline{\kappa }I.$ Combine that with the equation ${\lambda }_{max}\left(Q^{{\displaystyle \frac{1}{2}}}{\tilde{R}}_i{Q}^{{\displaystyle \frac{1}{2}}}\right)={\displaystyle \frac{1}{\underline{\lambda }}},{\lambda }_{min}\left(Q^{{\displaystyle \frac{1}{2}}}{\tilde{R}}_i{Q}^{{\displaystyle \frac{1}{2}}}\right)={\displaystyle \frac{1}{\overline{\lambda }}}.$ so there exist $\underline{\lambda }>{\displaystyle \frac{1}{\overline{\kappa }}},\overline{\lambda }<{\displaystyle \frac{1}{\underline{\kappa }}}.$ Therefore, the conditions (64) and (65) ensure that expressions (24) and (41) are valid.

In addition, inequality (67) guarantees that inequality (23) and (40) hold.

The proof in case (2) is similar to that in case (1) and is omitted.

According to the above analysis, the condition of Theorem 7 can ensure that the condition of Theorems 1 and 3 holds simultaneously. This means that in the controller gain $K_i={\mathcal{K}}_i{R}_i^{-1}$ and observer gain $L_i={\mathcal{L}}_i{\mathcal{U}}_i^{-1}$, the closed-loop system (15) is FTP with respect to $\left(c_1,c_2,[0,T],Q,\overline{\omega }\right)$. □

Theorem 7.

Consider a time-delayed Markov jump system (15) with completely unknown transition probability. Given parameter $(c_1,c_2,$$T,Q,\overline{\omega })$ and adjustable parameter {${\mu }_i>0,\beta$, $\overline{\kappa }>0,h>0,\lambda ,{\kappa }_i>0$}, if there exists a positive matrix $R_i>0$, matrix ${\mathcal{K}}_i,{\mathcal{L}}_i,{\mathcal{U}}_i$, and scalar {$c^{*}>0,\underline{\kappa }>0,{\rho }_i>0,{\beta }_i>0,{ϵ}_i>0$}, the following linear matrix inequality is true:

$${\breve{\Theta }}^i\triangleq \left[\begin{array}{ccccc}{\breve{\Theta }}_{11}^i& {\breve{\Theta }}_{12}^i& {\breve{\Theta }}_{13}^i& {\breve{\Theta }}_{14}^i& 0\\ *& {\breve{\Theta }}_{22}^i& 0& 0& {\breve{\Theta }}_{25}^i\\ *& *& {\breve{\Theta }}_{33}^i& 0& 0\\ *& *& *& {\breve{\Theta }}_{44}^i& 0\\ *& *& *& *& {\breve{\Theta }}_{55}^i\end{array}\right]<0$$

(70)

$$R_i{\Delta }_0^{\left(j\right)}{\Delta }_1^{\left(j\right)}\le {\beta }_j{R}_i,{\Delta }_0^j,{\Delta }_1^j\in {\Delta }_n,j\ne i,$$

(71)

$$\left[\begin{array}{cc}-{ϵ}_{i}I& *\\ C_i{R}_i-{\mathcal{U}}_i{C}_i& -I\end{array}\right]<0$$

(72)

$$\underline{\kappa }{Q}^{-1}<\widetilde{R_i}<\overline{\kappa }{Q}^{-1}$$

(73)

$$\left[\begin{array}{cc}{\theta }_{r\left(0\right)}\left(0\right)+\beta {\overline{\omega }}^{2}T+\beta m{\delta }^{2}T-{\displaystyle \frac{1}{\overline{\kappa }}}{e}^{-\beta T}{c}^{*}& \sqrt{c_1}\\ *& -\underline{\kappa }\end{array}\right]<0$$

(74)

$$c^{*}+\underline{\kappa }{\theta }_{r\left(0\right)}\left(0\right)+\underline{\kappa }\beta {\overline{\omega }}^{2}T-{\displaystyle \frac{1}{\overline{\kappa }}}{e}^{-\beta T}\underline{\kappa }{c}_2<0$$

(75)

$$c_1<c^{*}<c_2$$

(76)

$$\left[\begin{array}{cc}-R_i& I\\ *& -{\rho }_{i}I\end{array}\right]\le 0$$

(77)

where

$$\begin{array}{cc}\hfill & {\breve{\Theta }}_{11}^i\triangleq \left[\begin{array}{cc}{\breve{\Theta }}_{11}^{i\left(1\right)}& {\widehat{G}}_i{\mathcal{L}}_i{C}_i\\ *& {\breve{\Theta }}_{11}^{i\left(2\right)}\end{array}\right],{\breve{\Theta }}_{11}^{i\left(1\right)}=\left[\begin{array}{c}\mathrm{He}(A_i{R}_i+B_i{\mathcal{K}}_i)+({\mu }_i-\beta )R_i\\ -\sum _{j=1,j\ne i}^N{\gamma }_{ij}^0\left(R_i+{\displaystyle \frac{1}{2}}He\left({\theta }_{ij}{R}_i{\Delta }_0^{\left(j\right)}{\Delta }_1^{\left(j\right)}\right)\right)\end{array}\right],\hfill \\ \hfill & {\breve{\Theta }}_{11}^{i\left(2\right)}=\left[\begin{array}{c}He(A_i{R}_i-{\mathcal{L}}_i{C}_i)+({\mu }_i-\beta )R_i\\ -\sum _{j=1,j\ne i}^N{\gamma }_{ij}^0\left(R_i+{\displaystyle \frac{1}{2}}He\left({\theta }_{ij}{R}_i{\Delta }_0^{\left(j\right)}{\Delta }_1^{\left(j\right)}\right)\right)\end{array}\right],\hfill \\ \hfill & {\breve{\Theta }}_{12}^i\triangleq \left[\begin{array}{cccc}{\widehat{G}}_i{\mathcal{L}}_i{C}_i{C}_i^T& 0& -B_i& 0\\ -{\mathcal{L}}_i{C}_i{C}_i^T& B_i^{\omega }& 0& 0\end{array}\right],{\breve{\Theta }}_{13}^i\triangleq \left[\begin{array}{ccc}\lambda (1+h)R_i{C}_i^T& {\tilde{\rho }}_i{R}_i& 0\\ \lambda (1+h)R_i{C}_i^T& 0& {\tilde{\rho }}_i{R}_i\end{array}\right],\hfill \\ \hfill & {\breve{\Theta }}_{14}^i\triangleq \left[\begin{array}{c}\left[\sqrt{{\overline{\gamma }}_{i,1}^0}{R}_i,\cdots ,\sqrt{{\overline{\gamma }}_{i,i-1}^0}{R}_i,\sqrt{{\overline{\gamma }}_{i,i+1}^0}{R}_i,\cdots ,\sqrt{{\overline{\gamma }}_{i,N}^0}{R}_i\right]\\ 0\end{array}\right],\hfill \\ \hfill & {\breve{\Theta }}_{25}^i\triangleq \left[\begin{array}{c}0\\ \left[\sqrt{{\overline{\gamma }}_{i,1}^0}{R}_i,\cdots ,\sqrt{{\overline{\gamma }}_{i,i-1}^0}{R}_i,\sqrt{{\overline{\gamma }}_{i,i+1}^0}{R}_i,\cdots ,\sqrt{{\overline{\gamma }}_{i,N}^0}{R}_i\right]\end{array}\right],\hfill & \\ \hfill & {\breve{\Theta }}_{22}^i\triangleq diag\left\{{\displaystyle \frac{{\kappa }_i^2}{1+h}}{N}_i^{-1}-2{\kappa }_i{C}_i{R}_i{C}_i^T,-\beta I,-\beta I,-c-\beta +{\displaystyle \frac{h}{{\lambda }_0}}\right\},\hfill \\ \hfill & {\breve{\Theta }}_{33}^i\triangleq diag\left\{-\lambda (1+h)M_i^{-1},-{\tilde{\rho }}_{i}I,-{\tilde{\rho }}_{i}I\right\},{\breve{\Theta }}_{44}^i\triangleq -diag\left\{R_1,\cdots ,R_{i-1},R_{i+1},\cdots ,R_N\right\},\hfill \\ \hfill & {\breve{\Theta }}_{55}^i={\breve{\Theta }}_{44}^i,\widetilde{R_i}\triangleq diag\{R_i,R_i\},\widetilde{{\rho }_i}={\displaystyle \frac{{\rho }_i}{{\mu }_i}}{\lambda }_{max}\left({\left(A_i^{\tau }\right)}^T{A}_i^{\tau }\right),{\overline{\gamma }}_{i,j}^0={\gamma }_{ij}^0+{\beta }_j{\theta }_{ij}.\hfill \end{array}$$

Then, with the action of $K_i={\mathcal{K}}_i{R}_i^{-1}$ and $L_i={\mathcal{L}}_i{\mathcal{U}}_i^{-1}$, and $\left(c_1,c_2,[0,T],Q,\overline{\omega }\right)$, a time-delayed Markov jump system (15) with completely unknown transition probability is FTB.

Proof. 

Let $R_i\triangleq {\overline{P}}_i^{-1}$, multiply both sides of the condition (39) and (53) by

$$diag\left\{R_i,R_i,C_i{R}_i{C}_i^T,I,I,I\right\}\left(diag\left\{R_i,R_i,C_i{R}_i{C}_i^T,I,I\right\}\right),$$

and, using inequality (71), Schur’s complementary, and $-Y{X}^{-1}Y\le {\kappa }^{2}X-2\kappa Y$, let $K_i{R}_i={\mathcal{K}}_i,L_i{\mathcal{U}}_i={\mathcal{L}}_i$, and consider the constraints $C_i{R}_i={\mathcal{U}}_i{C}_i$; an easy verification condition (70) guarantees that inequalities (39) and (53) are both true.

In addition, $C_i{R}_i={\mathcal{U}}_i{C}_i$ can be solved by (72).

By (73), we have $\underline{\kappa }I<Q^{{\displaystyle \frac{1}{2}}}{\tilde{R}}_i{Q}^{{\displaystyle \frac{1}{2}}}<\overline{\kappa }I.$ Combined with the inequalities ${\lambda }_{max}\left(Q^{{\displaystyle \frac{1}{2}}}{\tilde{R}}_i{Q}^{{\displaystyle \frac{1}{2}}}\right)={\displaystyle \frac{1}{\underline{\lambda }}},{\lambda }_{min}\left(Q^{{\displaystyle \frac{1}{2}}}{\tilde{R}}_i{Q}^{{\displaystyle \frac{1}{2}}}\right)={\displaystyle \frac{1}{\overline{\lambda }}},$ we have $\underline{\lambda }>{\displaystyle \frac{1}{\overline{\kappa }}},\overline{\lambda }<{\displaystyle \frac{1}{\underline{\kappa }}}.$ Therefore, the conditions (74) and (75) ensure that expressions (41) and (55) are valid.

In addition, inequality (77) guarantees that inequality (40) and (54) hold.

According to the above analysis, the condition of Theorem 7 can ensure that the condition of Theorems 2 and 4 holds simultaneously. This means that in the controller gain $K_i={\mathcal{K}}_i{R}_i^{-1}$ and observer gain $L_i={\mathcal{L}}_i{\mathcal{U}}_i^{-1}$, the closed-loop system (15) is FTP with respect to $\left(c_1,c_2,[0,T],Q,\overline{\omega }\right)$. □

4. Numerical Example

In this section, we use a numerical simulation example to verify the feasibility and effectiveness of the dynamic ET SMC for time-delayed Markov systems with unknown transition probabilities.

Example 1.

Consider a class of time-delayed Markov jump systems (1) with unknown transition probabilities; the system matrices are as follows:

$$\begin{array}{cc}\hfill A_1=& \left[\begin{array}{cc}-2.6& 2\\ 1& -2\end{array}\right],A_2=\left[\begin{array}{cc}-2.62& 1.8\\ 0.9& -2.3\end{array}\right],A_3=\left[\begin{array}{cc}-2.58& 2.1\\ 1.05& -1.9\end{array}\right],\hfill \\ \hfill A_4=& \left[\begin{array}{cc}-2.64& 2.2\\ 0.85& -2.2\end{array}\right],A_4^{\tau }=\left[\begin{array}{cc}0.43& 0.38\\ -0.26& 0.64\end{array}\right],\tau =0.1,\hfill \\ \hfill A_1^{\tau }=& \left[\begin{array}{cc}0.4& 0.8\\ -0.3& 0.6\end{array}\right],A_2^{\tau }=\left[\begin{array}{cc}0.3& -0.4\\ 0.20.5\end{array}\right],A_3^{\tau }=\left[\begin{array}{cc}0.5& -0.36\\ 0.22& -0.4\end{array}\right],\hfill \\ \hfill B_1=& \left[\begin{array}{c}-0.5\\ 1\end{array}\right],B_2=\left[\begin{array}{c}-0.55\\ 0.95\end{array}\right],B_3=\left[\begin{array}{c}-0.48\\ 1.1\end{array}\right],B_4=\left[\begin{array}{c}-0.56\\ 1.08\end{array}\right],\hfill \\ \hfill B_1^{\omega }=& \left[\begin{array}{c}0.1\\ 0.2\end{array}\right],B_2^{\omega }=\left[\begin{array}{c}0.55\\ 0.95\end{array}\right],B_3^{\omega }=\left[\begin{array}{c}0.09\\ 0.18\end{array}\right],B_4^{\omega }=\left[\begin{array}{c}0.1\\ 0.2\end{array}\right],\hfill \\ \hfill C_1=& \left[\begin{array}{cc}4& 6\end{array}\right],C_2=\left[\begin{array}{cc}3.9& 6.1\end{array}\right],C_3=\left[\begin{array}{cc}4.1& 5.9\end{array}\right],C_4=\left[\begin{array}{cc}3.92& 5.86\end{array}\right].\hfill \end{array}$$

Consider a partially unknown transition rate matrix as

$$\Gamma =\left[\begin{array}{cccc}-2.6& 0.9& ?& ?\\ ?& -2.3& 0.76& ?\\ 0.84& ?& -2.5& ?\\ ?& 0.8& ?& -2.1\end{array}\right]$$

where “?” represents the unknown element in the transition rate matrix.

The parameters involved in dynamic ET rules (6) and (7) and control design are set as follows: $\left(c_1,c_2,T,Q,\overline{\omega }\right)=(0.43,0.25,5,I_4,0.5)$, ${\mu }_i=0.2,\beta =0.1,{\kappa }_i=0.5,\overline{\kappa }=1,\lambda =0.4,h=1$, $\lambda =0.4,{\lambda }_0=0.8,{\theta }_0=0.1$, $M_1=6,M_2=6.2,M_3=6.5,M_4=5.8$, $N_1=30,$ $N_2=19,N_3=31,N_4=28.5$.

Using MATLAB YALMIP toolbox to solve the linear matrix inequality (62)–(68) of Theorem 6, the controller gain can be obtained as follows: $K_1=\left[\begin{array}{cc}19.16& -47.32\end{array}\right],K_2=\left[\begin{array}{cc}18.6& -46.55\end{array}\right],K_3=\left[\begin{array}{cc}19.34& -47.61\end{array}\right],K_4=\left[\begin{array}{cc}18.42& -46.82\end{array}\right].$ The observer gain is $L_1=\left[\begin{array}{c}-0.0457\\ -0.0176\end{array}\right],L_2=\left[\begin{array}{c}-0.0462\\ -0.0164\end{array}\right],L_3=\left[\begin{array}{c}-0.038\\ -0.0182\end{array}\right],L_4=\left[\begin{array}{c}-0.0496\\ -0.0186\end{array}\right].$ For the convenience of simulation, the initial value is $x_0={[1,-1]}^{\mathrm{T}},r_0=1$. 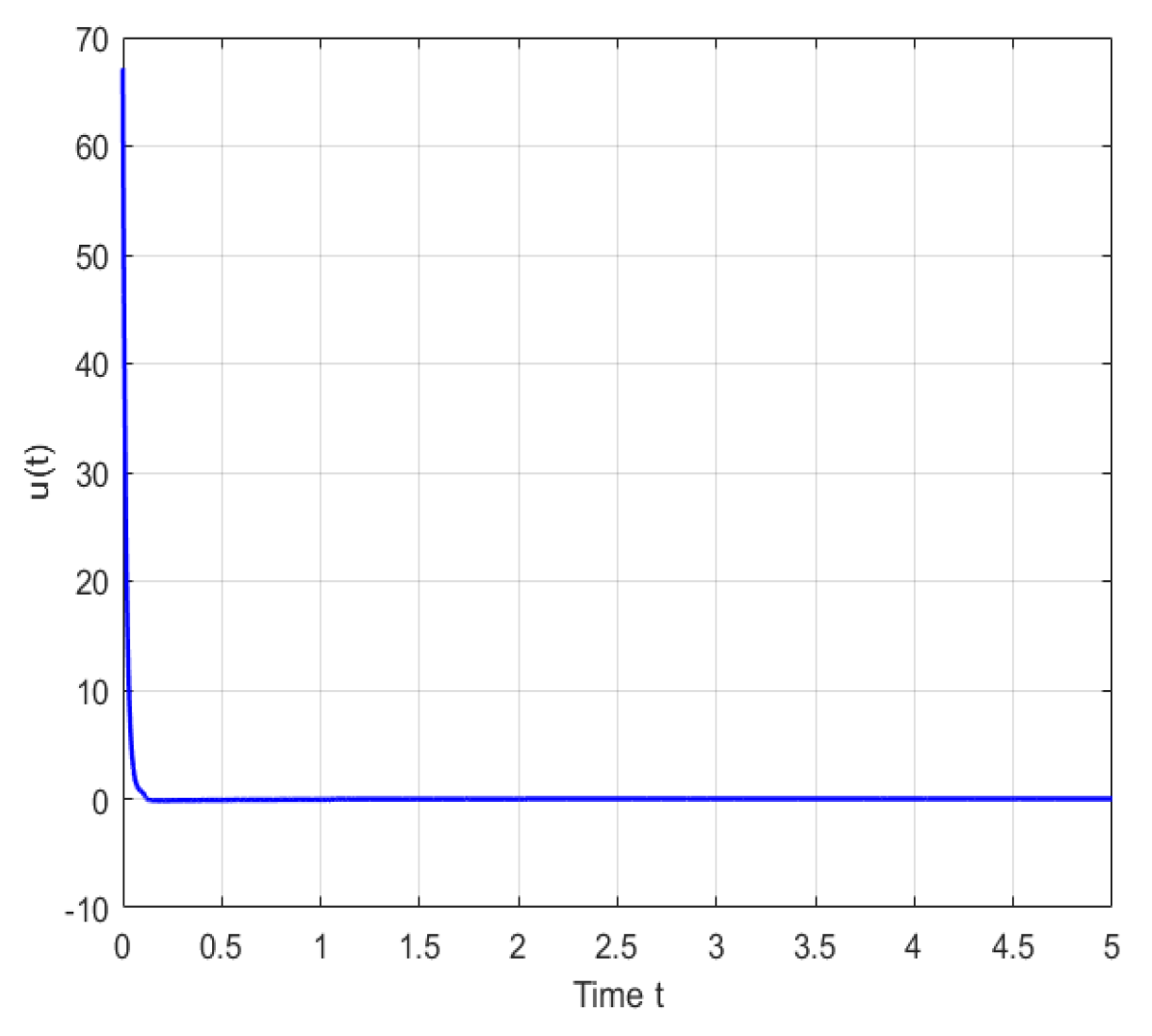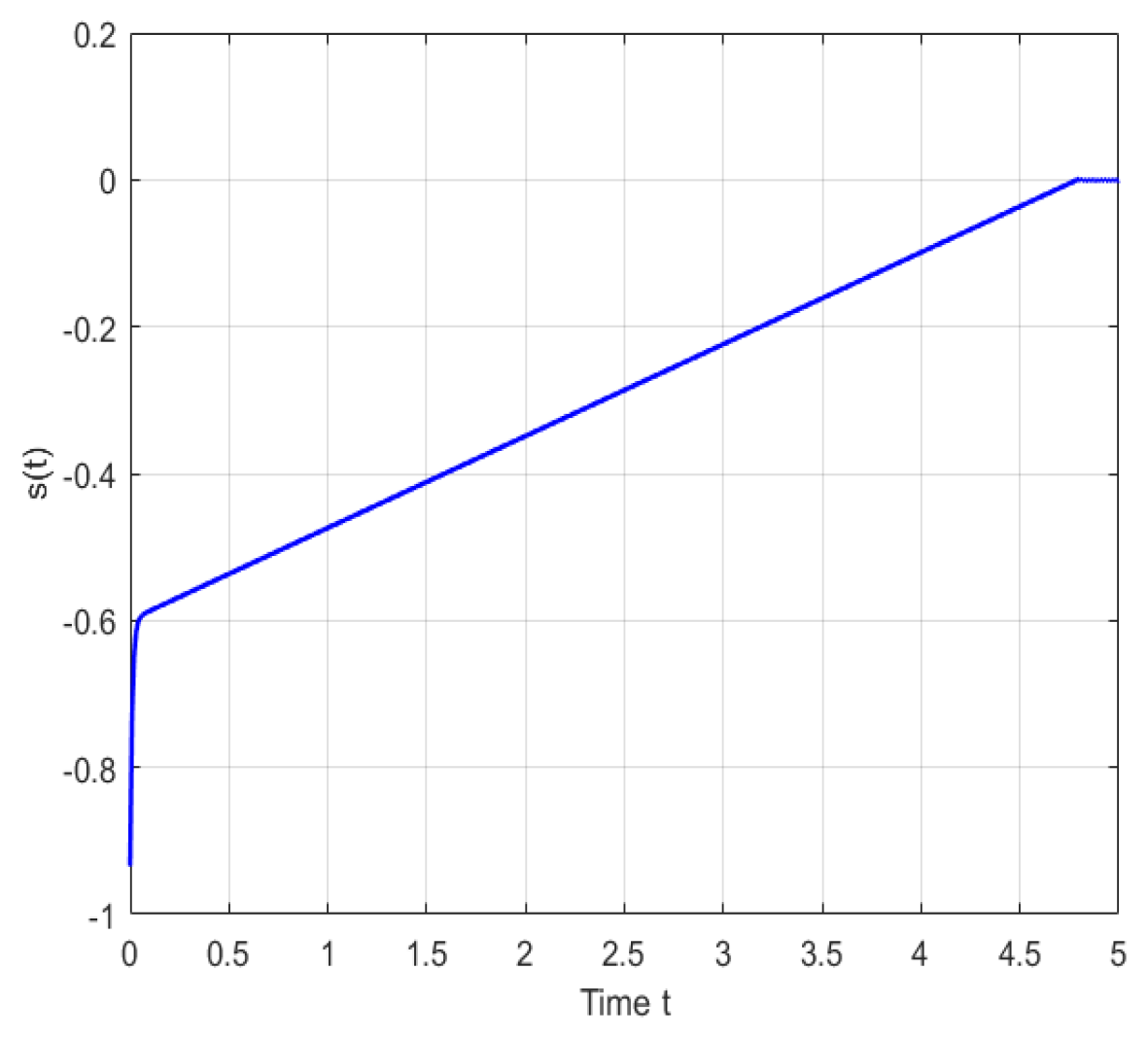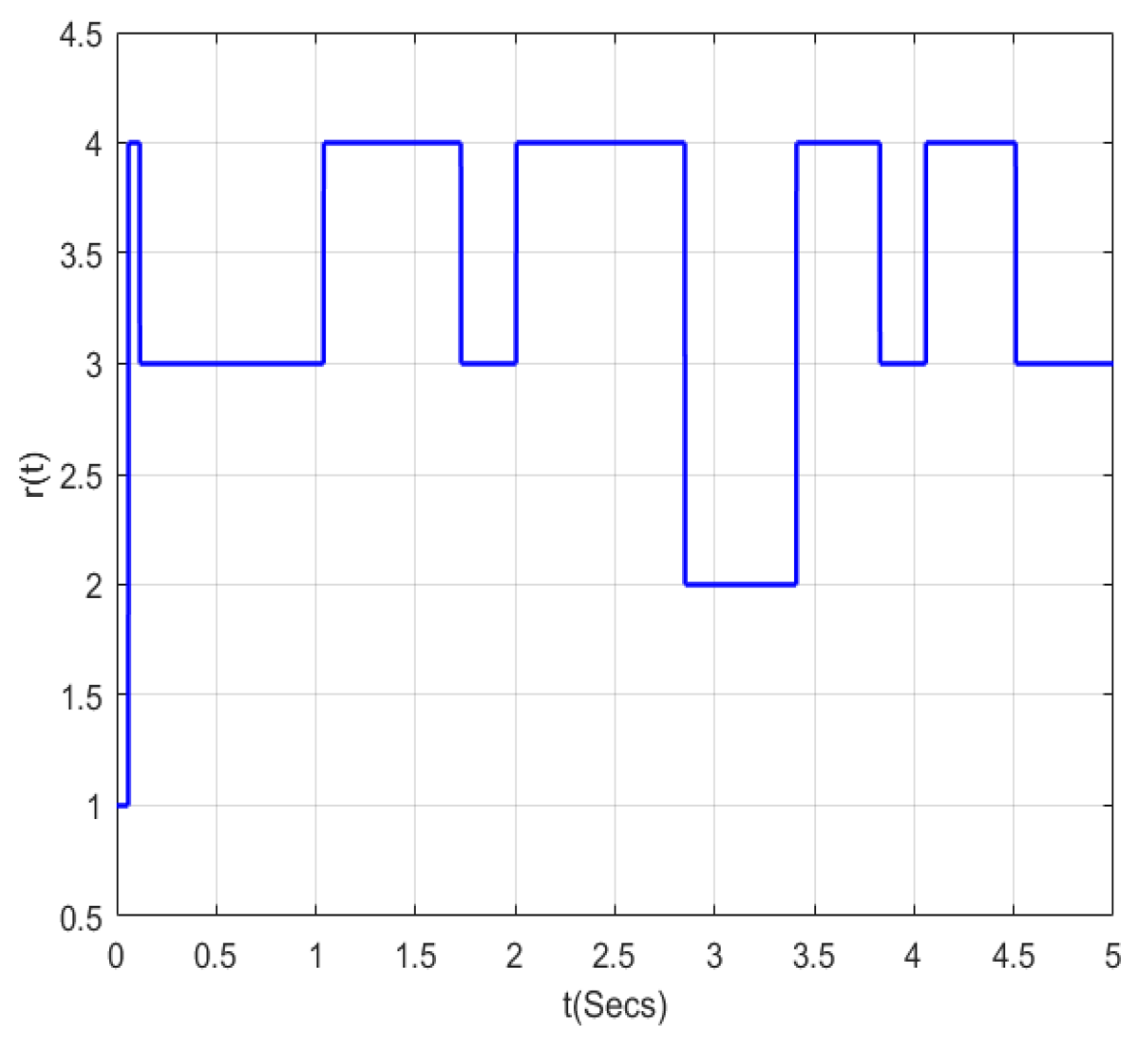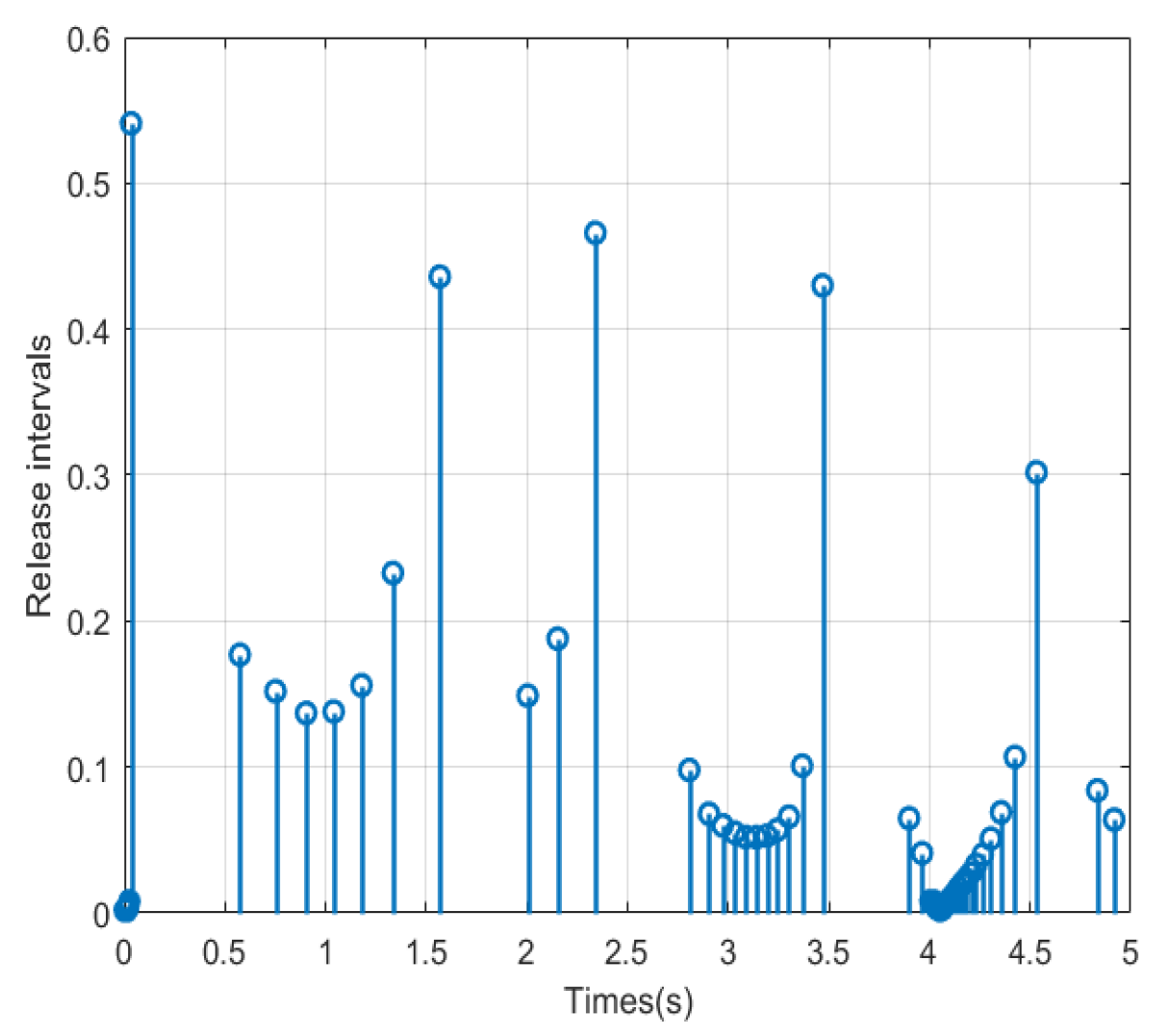Figure 1, Figure 2, Figure 3 and Figure 4 show the simulation results, where Figure 1 is the control input, Figure 2 represents the integral sliding mode variable, Figure 3 represents the switching signal, and Figure 4 indicates the ET release time and trigger interval.

Figure 1. Control input.

Figure 2. Sliding mode variable.

Figure 3. Switching signal.

Figure 4. Release moments and intervals.

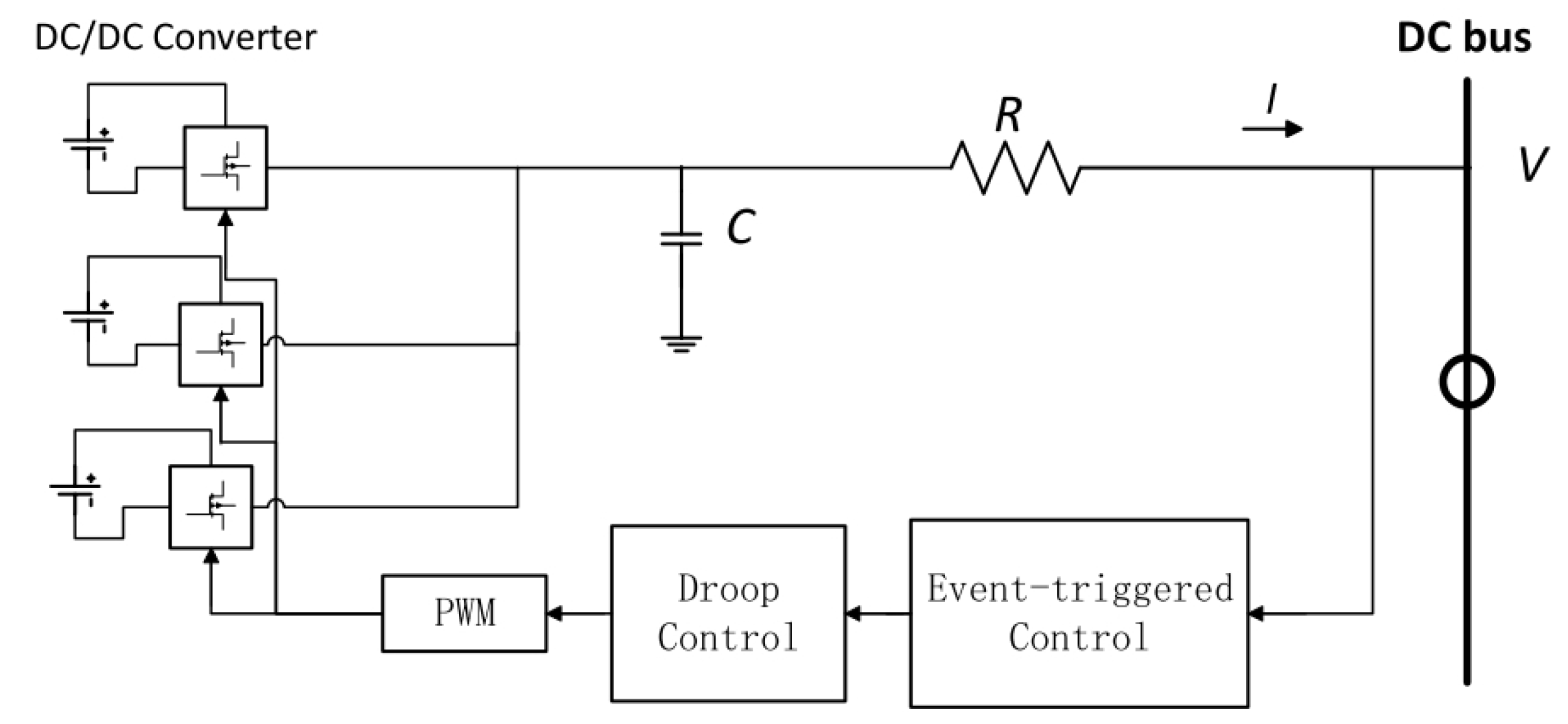
Example 2.

Figure 5 illustrates the construction of a microgrid system comprising three BOOST circuits. Within this system, we have implemented a microgrid droop control strategy, aimed at achieving optimal energy distribution and precise control. To address the issue of heavy communication burden inherent in traditional control methods, we have further introduced an event-triggered mechanism. This mechanism, by setting specific trigger conditions, initiates control actions only when the system state meets these conditions, thereby effectively reducing unnecessary communication data exchange and significantly alleviating the communication burden. Where the input voltage V_in = 100 V, the output given voltage V_out, L = 1e-2H, C = 1e-2F, R = 5 $\Omega ,$ and the IGBT and diode adopt the default values. The event trigger signal is simplified to the absolute value of the difference between the given value and the sampled value.

Figure 5. Microgrid system composed of three BOOST circuits.

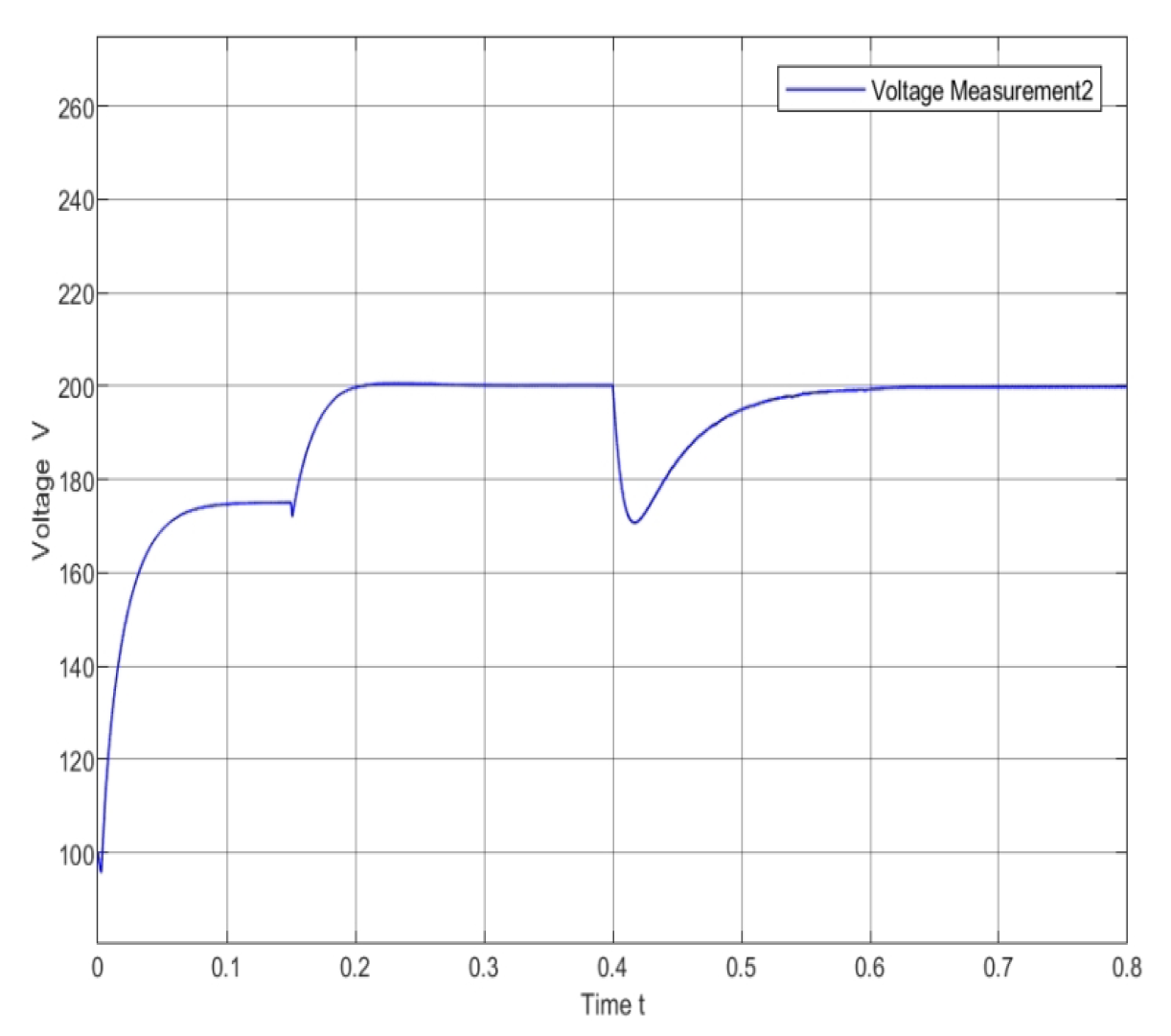
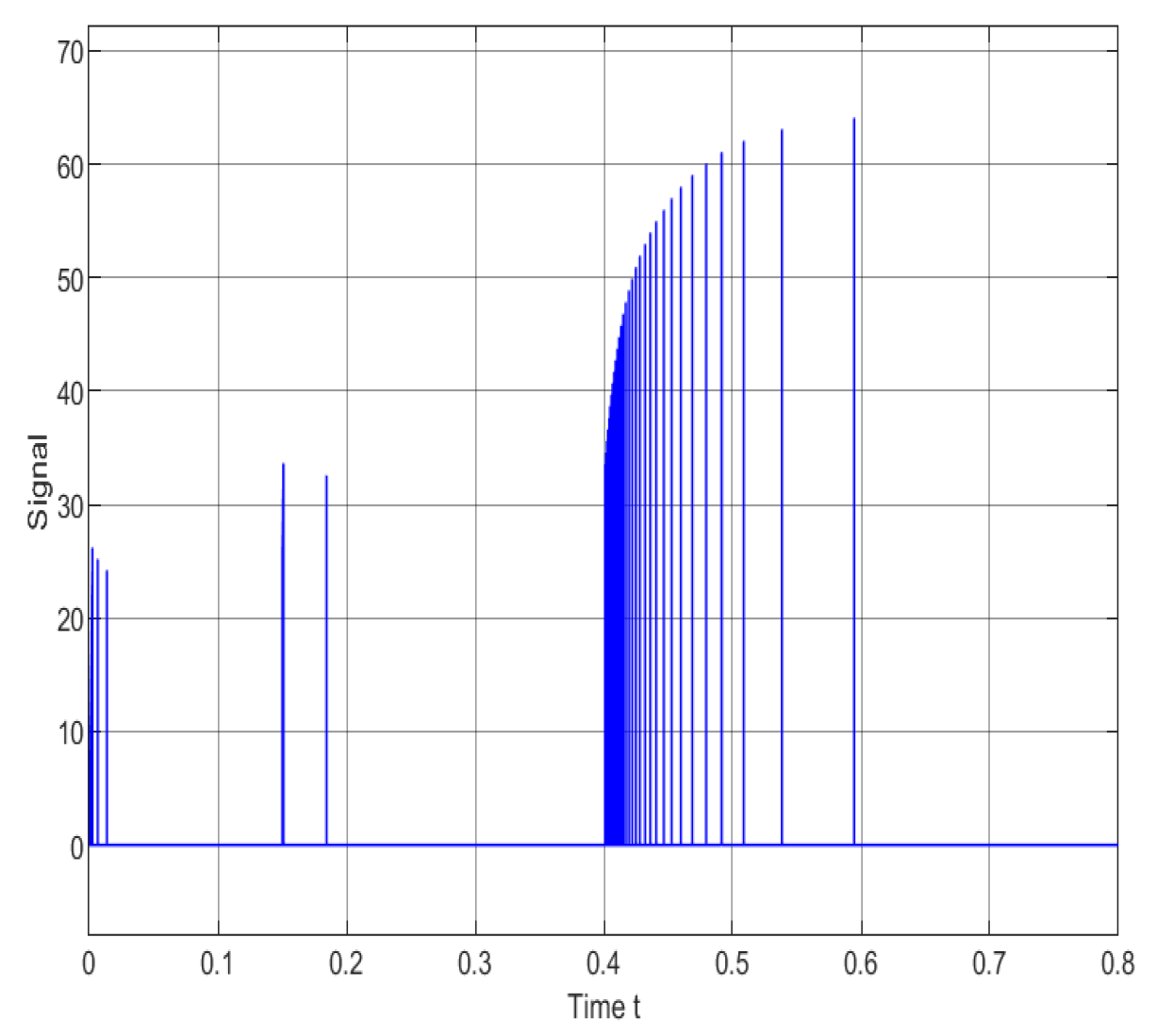
As depicted in Figure 6, the system output voltage, under the control of the event-triggered signal (refer to Figure 7, exhibits distinct phase characteristics. During the initial unstable phase, the system continuously engages in signal acquisition and trigger control to ensure a rapid response. As the system gradually stabilizes, the event-triggered control mechanism demonstrates its superiority by effectively avoiding signal redundancy and substantially reducing the communication burden. Specifically, comparative analysis reveals a marked decrease in signal transmission frequency post-stabilization, with no compromise in control precision. Upon entering the second load variation phase, the event-triggered mechanism responds swiftly, executing precise trigger control to ensure the system output voltage quickly returns to a stable value. This process further validates the effectiveness and stability of the event-triggered control mechanism in responding to load variations.

Figure 6. Output voltage.

Figure 7. Event-triggered signal.

Through the above simulation results, we can see that the dynamic ET SMC design scheme proposed in this chapter is feasible and effective for time-delayed Markov systems with unknown transition probabilities.

5. Conclusions

In this paper, we study the dynamic ET finite-time SMC for a class of delayed Markov jump systems with unknown transition probabilities. The main contributions of this paper are as follows: First, the integral sliding mode surface is constructed, and the equivalent control law can be obtained. Second, various control methods derive sufficient conditions for finite-time boundedness in delayed Markov continuous systems with partially/completely unknown transition probabilities; Third, a dynamic ET finite-time SMC law for delayed Markov jump systems with unknown transition probabilities is designed. Finally, numerical simulations are carried out for the considered system.

In this study, while certain achievements have been made, several limitations exist. The dynamic ET finite-time SMC scheme for time-delayed semi-Markov jump continuous systems has been investigated, and the results are expected to be extended to semi-Markov jump systems in the future with the aid of the Alamo vertex method, the binary diagonal matrix inequality method, and the Razumikhin method. The conclusions can also be applied to cyber-control systems considering spoofing or DOS attacks to enhance depth and applicability. However, the control strategy may degrade in the face of extremely high-frequency Markov jumps or long-term time delays due to the inefficiency of current algorithms in handling rapid state changes and long-term accumulative effects. Additionally, since the research assumes bounded external disturbances, the control strategy’s efficacy needs further exploration under more complex non-Gaussian or time-varying disturbance scenarios. For future research, optimizing the control strategy by developing advanced algorithms that are adaptable to a wider range of system parameters and exploring the extension of the findings to other stochastic systems, such as Lévy-driven or mixed-type random process systems, are promising directions. These efforts can expand the theoretical scope and enhance practical applicability.