Distributed Observer-Based Adaptive Formation-Containment Tracking for Multi-Agent Systems on Directed Graphs
Abstract
1. Introduction
- (i)
- (ii)
- In contrast to the adaptive control algorithm developed in [18,19,20] under undirected graphs, in this paper we design the observer-based adaptive TVFCT control algorithm in the topology of directed communication, considering the case of directed communication topology and the fact that the state of most agents in real life is unknown.
- (iii)
2. Preliminaries
2.1. Graph Theory
2.2. Description of the Problem
3. Main Results
3.1. The Case with Multiple Tracking Leaders
- (i)
- The compensation for the input signal is provided by the formula
- (ii)
- The unequal relationship is fulfilled by selecting τ and κ so as to ensure thatwhere , and , with ε being a given arbitrarily small positive number.
- (iii)
- For any given matrices the matrices H and Q are solutions to the algebraic Riccati inequalities listed below:
3.2. The Case with One Tracking Leader
- (i)
- The compensation for the input signal is provided by the formula
- (ii)
- The inequality relation is fulfilled by choosing and κ such thatwhere and , with ε being a given arbitrarily small positive number.
- (iii)
- For any given matrices the matrices H and Q are solutions of the following algebraic Riccati inequalities:
4. Simulations
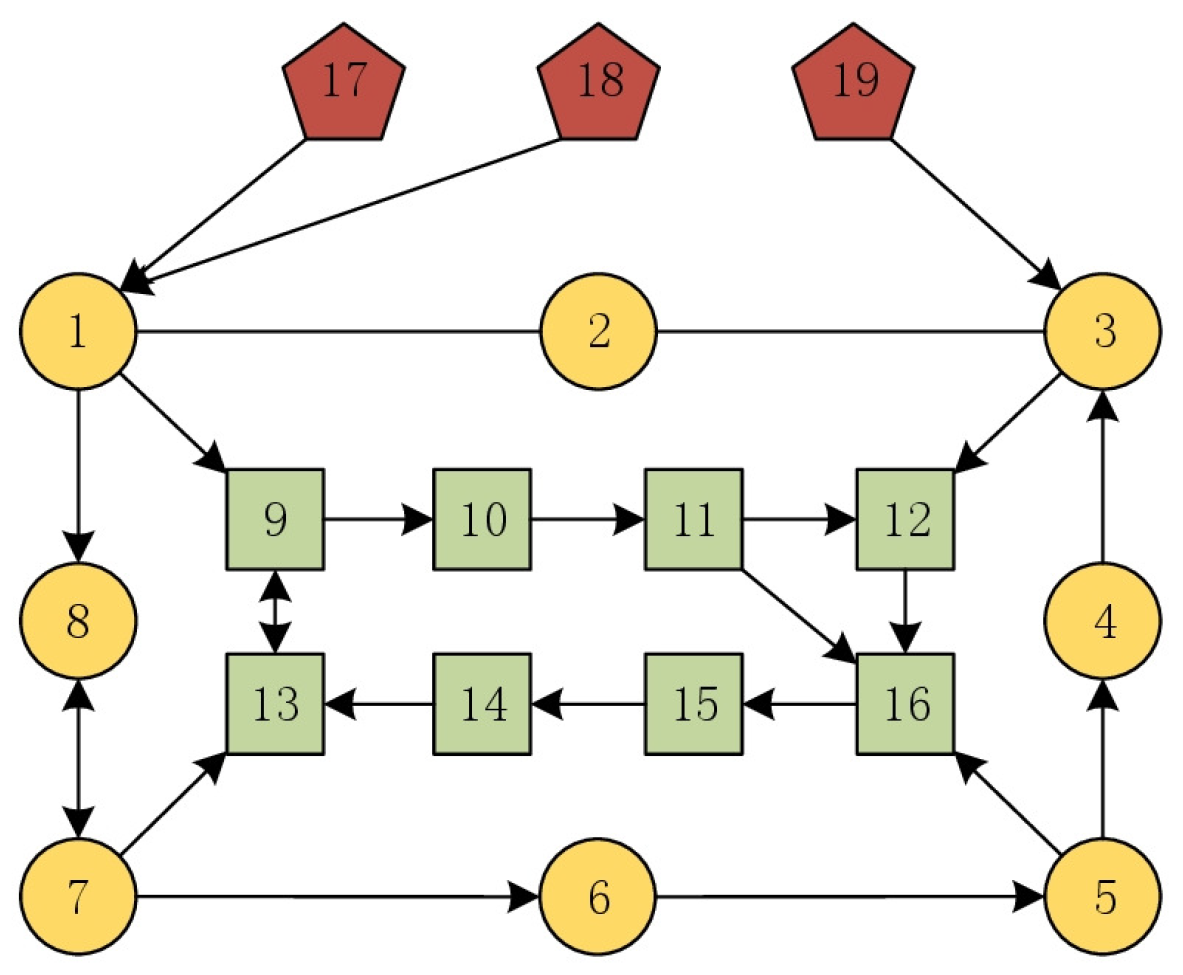
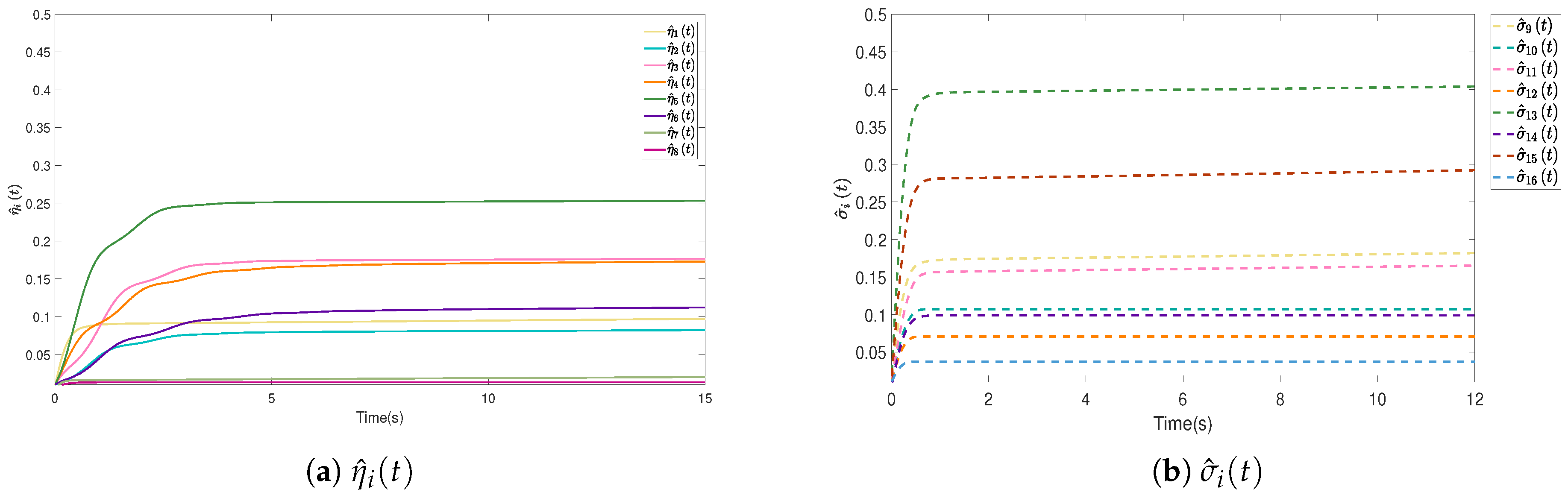
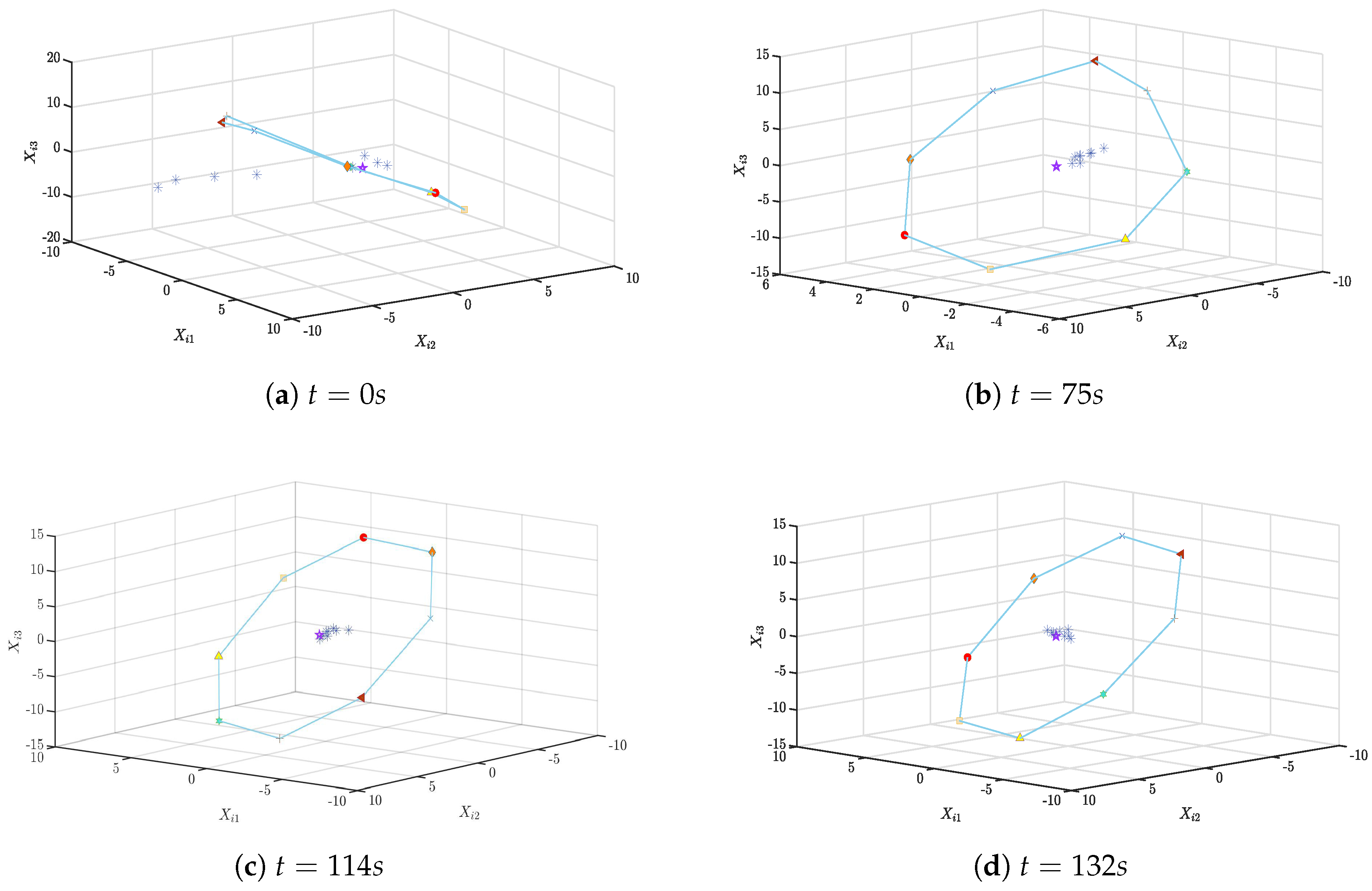
4.1. The Case with Multiple Tracking Leaders
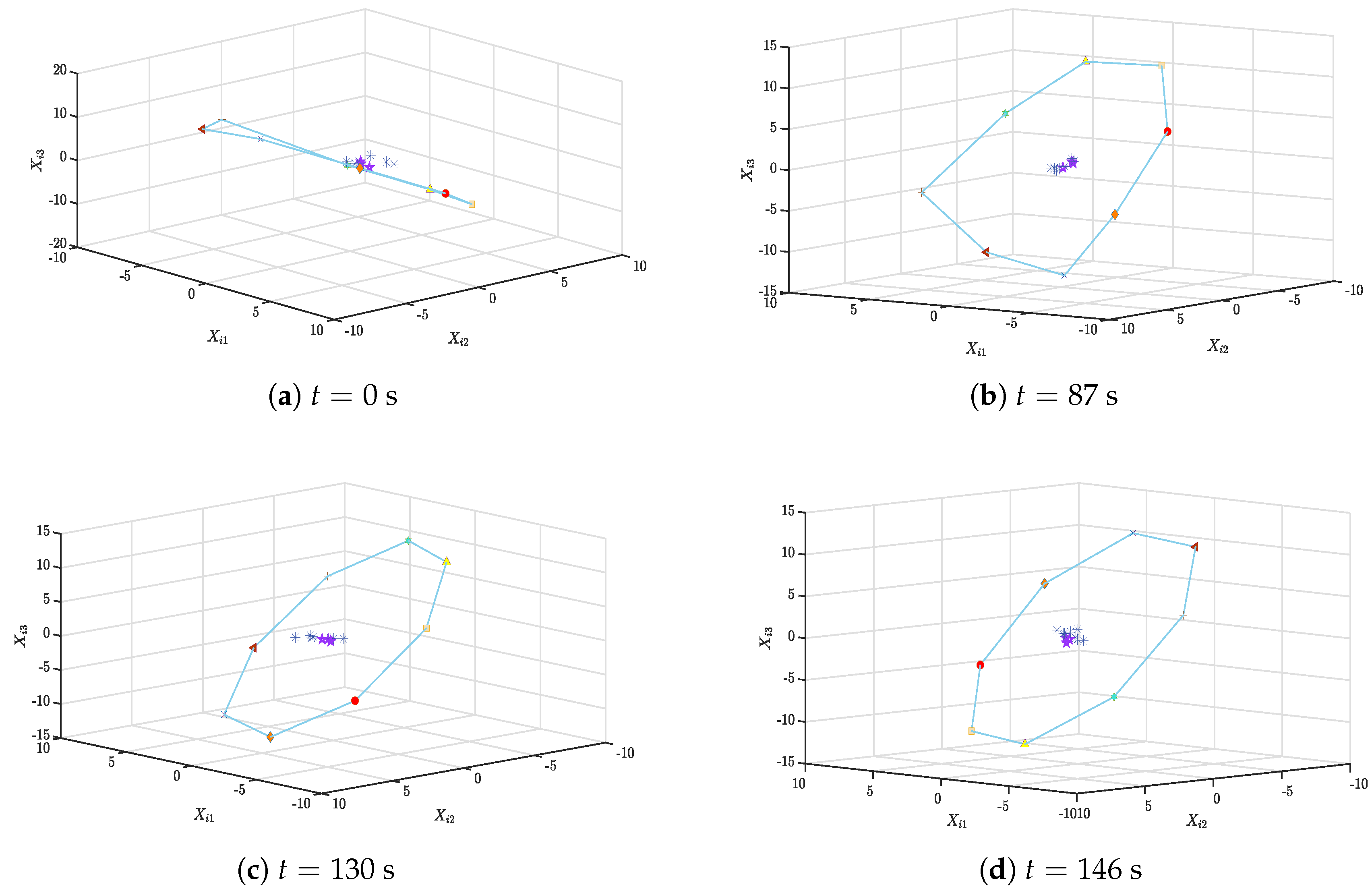
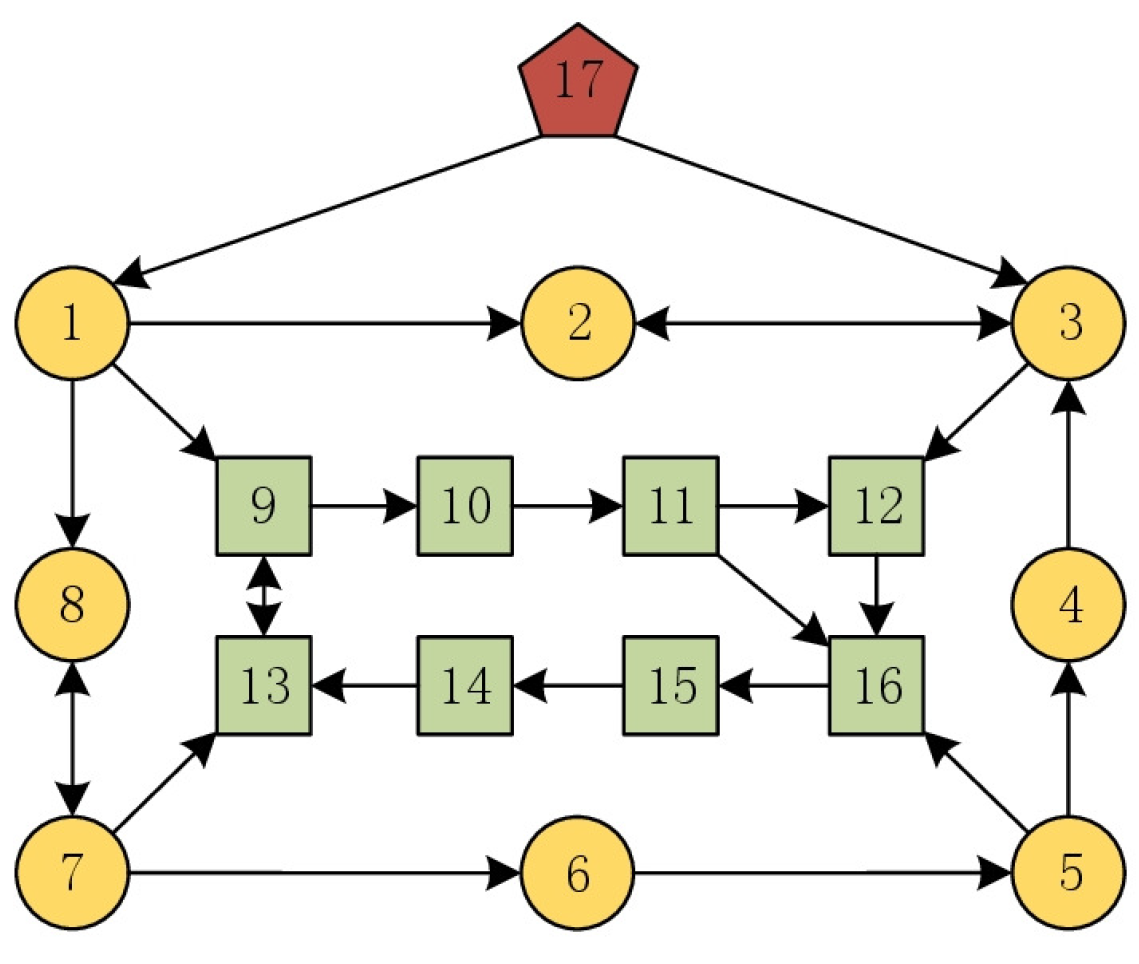
4.2. The Case with One Tracking Leader
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TVFCT | Time-Varying Formation-Containment Tracking |
| MASs | Multi-Agent Systems |
| FLs | Formation Leaders |
References
- He, S.; Dong, C.; Dai, S.-L.; Zou, T. Cooperative deterministic learning and formation control for underactuated USVs with prescribed performance. Int. J. Robust Nonlinear Control 2022, 32, 2902–2924. [Google Scholar] [CrossRef]
- Han, T.; Guan, Z.-H.; Zhan, X.-S.; Yan, H.; Chen, J. Observer-based bipartite consensus of descriptor multi-agent systems. Control Theory Appl. 2023, 40, 32–38. [Google Scholar]
- Han, T.; Zheng, W.X. Bipartite output consensus for heterogeneous multi-agent systems via output regulation approach. IEEE Trans. Circuits Syst. II Exp. Briefs 2021, 68, 281–285. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, G. Cooperative adaptive fault-tolerant control for multi-agent systems with deception attacks. J. Frankl. Inst. 2020, 357, 3419–3433. [Google Scholar] [CrossRef]
- Cui, J.; Pan, Y.; Tan, L. Simplified optimized finite-time containment control for a class of multi-agent systems with actuator faults. Nonlinear Dyn. 2022, 109, 2799–2816. [Google Scholar] [CrossRef]
- Zhang, L.; Xia, Y.; Shen, G.; Cui, B. Fixed-time attitude tracking control for spacecraft based on a fixed-time extended state observer. Sci. China Inf. Sci. 2021, 64, 212201. [Google Scholar] [CrossRef]
- Han, T.; Guan, Z.-H.; Xiao, B.; Yan, H. Bipartite average tracking for multi-agent systems with disturbances: Finite-time and fixed-time convergence. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 4393–4402. [Google Scholar] [CrossRef]
- Yan, K.-X.; Han, T.; Xiao, B.; Yan, H. Adaptive guaranteed-performance consensus for high-order nonlinear multi-agent systems with switching topologies. Int. J. Adapt. Control Signal Process. 2023, 37, 1135–1150. [Google Scholar] [CrossRef]
- Zhao, X.-F.; Han, T.; Xiao, B.; Yan, H.; Ge, M.-F.; Liang, C.-D. Task-space time-varying formation tracking for heterogeneous Euler-Lagrange systems via hierarchical predefined-time control approach. Nonlinear Dyn. 2022, 109, 2675–2692. [Google Scholar] [CrossRef]
- Xi, J.; Wang, X.; Li, H.; Zhang, Q.; Han, X. Energy-constraint output formation for swarm systems with dynamic output feedback control protocols. ISA Trans. 2022, 120, 235–246. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Q.; Zheng, Y.; Zhu, Y. Containment control of hybridmulti-agent systems. Int. J. Robust Nonlinear Control 2022, 32, 1355–1373. [Google Scholar] [CrossRef]
- Gu, N.; Wang, D.; Peng, Z.; Li, T.; Tong, S. Model-free containment control of underactuated surface vessels under switching topologies based on guiding vector fields and data-driven neural predictors. IEEE Trans. Cybern. 2022, 52, 10843–10854. [Google Scholar] [CrossRef]
- Liu, C.; Wan, X.; Lu¨, J. Time-varying output formation tracking of heterogeneous linear multi-agent systems with dynamical controllers. Neurocomputing 2021, 441, 36–43. [Google Scholar] [CrossRef]
- Yang, S.; Bai, W.; Li, T.; Shi, Q.; Yang, Y.; Wu, Y.; Philip Chen, C.L. Neural-network-based formation control with collision, obstacle avoidance and connectivity maintenance for a class of second-order nonlinear multi-agent systems. Neurocomputing 2021, 439, 243–255. [Google Scholar] [CrossRef]
- Zheng, C.-B.; Peng, Z.-H.; Sun, J.; Liu, G.-P.; Han, Q.-L. Time-varying formation predictive control of second-order networked multi-agent systems with three-channel random communication constraints. IEEE Trans. Circuits Syst. II Exp. Briefs 2023, 71, 2119–2123. [Google Scholar] [CrossRef]
- Wang, L.; Xi, J.; He, M.; Liu, G. Robust time-varying formation design for multiagent systems with disturbances: Extended-state-observer method. Int. J. Robust Nonlinear Control 2020, 30, 2796–2808. [Google Scholar] [CrossRef]
- Yang, H.; Ye, D. Time-varying formation tracking control for high-order nonlinear multi-agent systems in fixed-time framework. Appl. Math. Comput. 2020, 377, 125119. [Google Scholar] [CrossRef]
- Li, Q.; Wei, Q.; Guo, Q.; Niu, Z. Distributed adaptive fixed-time formation control for second-order multi-agent systems with collision avoidance. Inf. Sci. 2021, 564, 27–44. [Google Scholar] [CrossRef]
- Yu, J.; Dong, X.; Li, Q.; Lü, J.; Ren, Z. Adaptive Practical optimal time-varying formation tracking control for disturbed high-order multi-agent systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 2567–2578. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Z. Distributed adaptive formation control of multi-agent systems with measurement noises. Automatica 2023, 150, 110857. [Google Scholar] [CrossRef]
- Xiong, T.; Gu, Z. Observer-based adaptive fixed-time formation control for multi-agent systems with unknown uncertainties. Neurocomputing 2021, 423, 506–517. [Google Scholar] [CrossRef]
- Lu, Y.; Dong, X.; Li, Q.; Lü, J.; Ren, Z. Time-varying group formation-containment tracking control for general linear multiagent systems with unknown inputs. IEEE Trans. Cybern. 2022, 52, 11055–11067. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Wang, Z.; Ding, D.; Ghinea, G.; Liu, H. Distributed formation-containment control for discrete-time multiagent systems under dynamic event-triggered transmission scheme. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 1308–1319. [Google Scholar] [CrossRef]
- Zhou, S.; Dong, Y.; Hua, Y.; Yu, J.; Ren, Z. Predefined formation-containment control of high-order multi-agent systems under communication delays and switching topologies. IET Control Theory Appl. 2021, 15, 1661–1672. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Meng, Z.Y.; Ren, W.; You, Z. Distributed finite-time attitude containment control for multiple rigid bodies. Automatica 2010, 46, 2092–2099. [Google Scholar] [CrossRef]
- Dong, X.; Tan, Q.; Li, Q.; Ren, Z. Necessary and sufficient conditions for average formation tracking of second-order multi-agent systems with multiple leaders. J. Frankl. Inst. 2017, 354, 611–626. [Google Scholar] [CrossRef]
- Zhang, H.; Lewis, F.L.; Qu, Z. Lyapunov, adaptive, and optimal design techniques for cooperative systems on directed communication graphs. IEEE Trans. Ind. Electron. 2012, 59, 3026–3041. [Google Scholar] [CrossRef]
- Sain, M.K. Matrix mathematics: Theory, facts, and formulas with application to linear systems theory [Book review; D.S. Berstein]. IEEE Trans. Autom. Control 2007, 52, 1539–1540. [Google Scholar] [CrossRef]
- Sorine, M.; Winternitz, P. Superposition laws for solutions of differential matrix Riccati equations arising in control theory. IEEE Trans. Autom. Control 1985, 30, 266–272. [Google Scholar] [CrossRef]
- Lang, Z.Q.; Billings, S.A. Output frequency characteristics of nonlinear systems. Int. J. Control 1995, 64, 1049–1067. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Yan, K.-X.; Xiao, B.; Han, T. Distributed Observer-Based Adaptive Formation-Containment Tracking for Multi-Agent Systems on Directed Graphs. Mathematics 2025, 13, 558. https://doi.org/10.3390/math13040558
Zhang Q, Yan K-X, Xiao B, Han T. Distributed Observer-Based Adaptive Formation-Containment Tracking for Multi-Agent Systems on Directed Graphs. Mathematics. 2025; 13(4):558. https://doi.org/10.3390/math13040558
Chicago/Turabian StyleZhang, Qi, Ke-Xing Yan, Bo Xiao, and Tao Han. 2025. "Distributed Observer-Based Adaptive Formation-Containment Tracking for Multi-Agent Systems on Directed Graphs" Mathematics 13, no. 4: 558. https://doi.org/10.3390/math13040558
APA StyleZhang, Q., Yan, K.-X., Xiao, B., & Han, T. (2025). Distributed Observer-Based Adaptive Formation-Containment Tracking for Multi-Agent Systems on Directed Graphs. Mathematics, 13(4), 558. https://doi.org/10.3390/math13040558





