Abstract
Task offloading in satellite networks, which involves distributing computational tasks among heterogeneous satellite nodes, is crucial for optimizing resource utilization and minimizing system latency. However, existing approaches such as static offloading strategies and heuristic-based offloading methods neglect dynamic topologies and uncertain conditions that hinder adaptability to sudden changes. Furthermore, current collaborative computing strategies inadequately address satellite platform heterogeneity and often overlook resource fluctuations, resulting in inefficient resource sharing and inflexible task scheduling. To address these issues, we propose a dynamic gradient descent-based task offloading method. This method proposes a collaborative optimization framework based on dynamic programming. By constructing delay optimization and resource efficiency models and integrating dynamic programming with value iteration techniques, the framework achieves real-time updates of system states and decision variables. Then, a distributed gradient descent algorithm combined with Gradient Surgery techniques is employed to optimize task offloading decisions and resource allocation schemes, ensuring a precise balance between delay minimization and resource utilization maximization in dynamic network environments. Experimental results demonstrate that the proposed method enhances the global optimizing result by at least 1.97%, enhances resource utilization rates by at least 3.91%, and also reduces the solution time by at least 191.91% in large-scale networks.
Keywords:
dynamic satellite networks; resource allocation; task offloading; collaborative optimization; gradient descent MSC:
37N40; 68U35; 68U35
1. Introduction
Space information networks consist of satellite platforms, ground stations, and other communication nodes that provide global coverage and real-time data transmission services. These networks play an important role in disaster response, emergency communications, and military operations by decreasing transmission delays and expanding coverage, ensuring seamless data exchange and thus significantly improving communication efficiency [1,2]. In contrast to traditional terrestrial networks and localized communication systems, space information networks utilize space platforms to provide continuous communication support across geographic regions [3], and their multi-level resource management and task scheduling capabilities satisfy communication needs in complex environments [4,5], thereby improving information transmission efficiency and system reliability [6].
Despite the advantages of space information networks in providing global coverage and real-time data transmission, it is still a significant challenge to efficiently and optimally allocate network resources under limited conditions [7]. Several specific challenges arise from the heterogeneity among LEO satellite constellations and ground stations. The differences in computational capabilities, bandwidth, and storage resources among various satellite platforms result in load imbalances during task offloading. Additionally, the hardware configurations, network connectivity, and geographical locations of ground stations further complicate resource allocation and task scheduling. In dynamic topologies and under resource fluctuations, these heterogeneities make it difficult for existing task offloading strategies to adapt to rapidly changing environments [8].
In particular, the space–terrestrial integrated network (STIN) faces specific challenges such as seamless connectivity between satellites and ground stations, cross-domain resource management, and load balancing in dynamic environments [9,10]. Variations in satellite and ground station delays, bandwidth, and computational capabilities, coupled with external factors like orbital changes and weather disruptions, increase the complexity of task offloading decisions. Moreover, the inherent security challenges of STIN arise from its system heterogeneity, which expands potential attack surfaces and complicates privacy protection during data transmission.
To cope with these challenges, existing research has mainly addressed the complexity of node heterogeneity and inter-node collaboration by introducing distributed optimization algorithms and collaborative computing strategies [11]. Researchers have proposed optimization frameworks based on Lagrangian duality and gradient descent methods to improve the efficiency of task offloading decisions and address the resource imbalance between platforms, achieving good local optimization results in static environments [12,13]. However, these methods usually focus on a single optimization objective or local problem, which fail to consider inter-task dependencies and coordination globally and lack a systematic and holistic solution, resulting in poor performance when dealing with heterogeneous platforms and real-time scheduling in large-scale dynamic environments, and failing to adequately solve these multi-level, multi-objective and complex problems.
This paper proposes a dynamic gradient descent-based task offloading method (D-GTOM), a distributed framework designed to address dynamic resource allocation and task offloading issues in STIN. This method introduces delay optimization models, resource efficiency models, and collaborative task scheduling optimization to tackle the challenges in dynamic environments. To address dynamic optimization challenges such as resource conflicts and task delays in satellite networks, our approach integrates delay optimization and resource efficiency models into a unified framework. The method effectively improves resource utilization and reduces task latency, ultimately achieving stable resource scheduling and task offloading in dynamic environments by employing multi-objective optimization and gradient correction techniques, combined with gradient descent and distributed optimization.
In this paper, our main contributions are as follows:
- To address the dynamic resource scheduling and task offloading optimization problem in satellite networks, we propose a dynamic resource scheduling framework based on distributed optimization, incorporating delay optimization and resource efficiency models. This method achieves the goal of effectively optimizing resource allocation and task scheduling in dynamic environments.
- To address the task offloading and resource management problem in satellite time–space information networks, we propose a task offloading and resource allocation optimization method using a distributed optimization framework and Lagrange multipliers. By combining gradient descent and gradient correction techniques, the framework effectively solves the resource conflict and delay optimization issues.
- To validate the effectiveness of the proposed method, we conducted experiments on multiple satellite network simulation datasets using a CSTK simulation platform and selected five baseline algorithms for comparison across four datasets. The experimental results demonstrate that our method outperforms existing methods in resource utilization and running time.
2. Related Work
In recent years, research on resource management, task offloading, and collaborative computing in satellite networks and STIN has made significant progress. Existing studies can mainly be categorized into three areas: resource scheduling optimization, collaborative computing strategies, and task offloading methods. Although resource scheduling optimization focuses on the efficiency and flexibility of resource allocation, it still faces challenges when dealing with dynamic network environments and complex task demands. Collaborative computing strategies enhance computing performance through cooperation between different nodes, but optimization issues remain when addressing the heterogeneity between satellite platforms. Task offloading methods alleviate terminal load by offloading tasks to satellites or ground stations, but challenges in optimizing offloading decisions and task distribution mechanisms remain. Overall, existing research has yet to fully consider the cross-optimization of these methods, and there is considerable potential for further exploration.
2.1. Resource Scheduling Optimization Methods
As satellite networks increasingly play a key role in providing global coverage and efficient communication, optimizing resource scheduling has become a central research issue. To address the varying needs of different users and tasks, researchers have proposed a range of resource scheduling optimization methods. These approaches mainly focus on enhancing resource allocation efficiency, reducing delays, and improving the adaptability of networks. Various studies have introduced optimization algorithms that leverage machine learning and deep learning techniques, which can predict network states and optimize resource allocation, thereby improving resource utilization and minimizing delays. For example, Song et al. [14] proposes a mixed-integer programming model for the EDSSP problem and a Genetic Algorithm based on reinforcement learning (RL-GA).
Other researchers have also explored data-driven scheduling methods, particularly in satellite network environments, where these methods predict future network states and optimize resource scheduling through historical data analysis [15,16,17,18]. For instance, Du et al. [15] introduced a data-driven parallel scheduling approach to predict the probabilities that a task will be fulfilled by different satellites. Similarly, Boulila et al. [19] proposed a new approach to predict spatiotemporal changes in satellite image databases. The proposed method exploits fuzzy sets and data mining concepts to build predictions and decisions for several remote sensing fields.
Despite the significant progress made by these optimization algorithms and machine learning methods, challenges still exist when dealing with complex dynamic network environments. While these approaches improve resource utilization efficiency, they lack effective strategies to address unexpected changes, such as network topology variations and transmission conditions in high-dynamic environments.
2.2. Collaborative Computing Strategies
Collaborative computing strategies, built upon optimized resource scheduling, aim to enhance network computing capabilities and service quality in satellite networks and STIN. With the growth of the computational power of satellite platforms, efficient resource sharing through collaboration among different satellite nodes becomes essential. Approaches have been employed to address challenges related to task processing and resource sharing, such as edge computing, distributed computing, and cloud computing. Studies demonstrate that satellite collaboration can significantly boost computing capacity and task processing efficiency without adding system load. For example, Liu et al. [20] introduced the SATCECN architecture, which facilitates cloud–edge–device collaboration for effective computing resource allocation. Similarly, Jia et al. [21] designed a collaborative satellite–terrestrial network architecture with a central-edge multi-agent collaboration model, enhancing task offloading efficiency.
To further enhance flexibility and scalability, distributed computing models have been developed [22,23,24]. Particularly, Sun et al. [22] presented a distributed optimization model using the alternating direction method of multipliers (ADMMs), which alleviates computational burdens through collaborative calculations among multiple satellites. In a similar vein, Kai et al. [23] explored a collaborative computation offloading and resource allocation framework, enabling tasks from mobile devices (MDs) to be partially processed at terminals, edge nodes (ENs), and cloud centers (CCs).
However, current collaborative computing strategies primarily focus on static environments, frequently overlooking dynamic changes such as node mobility and network topology variations. This limitation underscores the need for more robust and adaptable strategies, which will be further addressed in the following section on task offloading methods.
2.3. Task Offloading Methods
Task offloading is a pivotal method for enhancing terminal computing capabilities and reducing load in satellite networks by transferring tasks from resource-limited devices to satellites or ground cloud platforms. This approach aims to achieve a balanced distribution of computational load and maximize resource utilization. Recent studies have explored various offloading strategies, including dynamic offloading based on network conditions, task allocation based on user demands, and intelligent scheduling based on computational requirements. These strategies seek to improve task processing efficiency, reduce delays, and ensure quality of service for users.
For example, Deng et al. [25] developed an autonomous partial offloading system for delay-sensitive computation tasks in multiuser IIoT MEC systems, aiming to minimize delay and enhance quality of service (QoS). Similarly, Li et al. [26] introduced a scheduling optimization method that incorporates an atomic task offloading model based on maximum flow theory alongside a dynamic caching model. Addressing varying task demands, Aghapour et al. [27] proposed a deep reinforcement learning-based approach that divides the offloading and resource allocation problem into two subproblems, optimizing resource allocation using the Salp Swarm Algorithm (SSA). Liu et al. [28] propose an optimized distributed computation offloading scheme with dependency guarantees in vehicular edge networks, leveraging deep reinforcement learning to improve task scheduling, minimize system latency, and enhance privacy while outperforming existing offloading methods.
Furthermore, multi-level task offloading schemes have been developed to integrate different resource management strategies, thereby enhancing flexibility and efficiency [29,30,31]. For instance, Yang [29] formulated a collaborative task offloading and resource scheduling framework as a Markov Decision Process (MDP) and deployed deep reinforcement learning (DRL) agents for decision-making. Similarly, Yan et al. [30] presented an optimal task offloading and resource allocation strategy that minimizes the weighted sum of the energy consumption and task execution time of wireless devices (WDs).
Despite these improvements, current task offloading methods often assume stable network environments and consistent computational demands, neglecting the impact of resource fluctuations and topology changes.
2.4. Integrated Methods and Cross-Domain Collaboration
Individual advancements in resource scheduling optimization, collaborative computing, task offloading, integrated methods, and cross-domain collaboration are emerging as promising avenues to enhance overall satellite network performance. These approaches typically address multiple optimization goals simultaneously, such as reducing delays, improving resource utilization, and enhancing system robustness by merging various computing resources, network topologies, and task characteristics.
For example, Xie et al. [32] developed a delay-based deep reinforcement learning (DRL) framework for computation offloading decisions, effectively reducing energy consumption. Similarly, Zhao et al. [33] introduced an asynchronous adaptive collaborative aggregation algorithm (AFLS) for satellite–ground architectures, enabling federated members to update model parameters during dynamic aggregation promptly. Additionally, Yang et al. [34] proposed a deep supervised learning-based computational offloading (DSLO) algorithm tailored for dynamic tasks in MEC networks.
Moreover, the collaborative optimization of task scheduling further enhances system efficiency [35,36,37]. For instance, Wang et al. [35] designed a three-layer network architecture integrated with a software-defined networking (SDN) model to manage inter-satellite link (ISL) connections and ECS resource scheduling. Similarly, Lyu et al. [36] developed a hybrid cloud and satellite multi-layer multi-access edge computing (MEC) network architecture that provides heterogeneous computing resources to terrestrial users.
In conclusion, existing research often falls short in addressing the combined challenges of dynamic network environments and multi-objective optimization within satellite networks and STIN. Specifically, there is a lack of comprehensive frameworks that ensure both fairness and efficiency in resource allocation while managing high temporal variability and complex constraints. To bridge these gaps, this paper proposes a novel collaborative optimization framework grounded in cooperative game theory and dynamic programming, enhanced by multi-objective optimization models and Gradient Surgery techniques. This approach aims to optimize resource utilization and minimize system latency, enhancing the performance and robustness of satellite network systems.
3. Problem Definition and Formulation
This study focuses on the task scheduling and resource management problem in STIN, specifically on dynamic resource optimization and task offloading based on a collaborative computation framework. In this system, satellite nodes, ground stations, user terminals, and satellite intercommunication links together form the basic architecture of the network. Satellite nodes have varying computational, storage, bandwidth, and task-processing capabilities, all of which are dynamically adjusted in response to changes in network topology, node failures, and fluctuations in task load. Thus, how to minimize system delay and at the same time maximize resource utilization becomes a critical problem.
3.1. System Architecture Analysis
STIN system comprises multiple heterogeneous satellite nodes, each with unique resource configurations. These nodes are interconnected via satellite intercommunication links, which form a dynamically changing network. Ground stations function as control centers for coordinating and scheduling the satellite nodes, while user terminals interact with the network by initiating task requests and receiving processing results. Due to the inherent characteristics of satellite networks, task scheduling and resource management must account for uncertainties such as dynamic topology, varying channel quality, and potential node failures.
Each satellite node i is characterized by a resource vector as
where denotes the computational capacity, measured in Flops; represents the storage capacity, measured in GB; indicates the bandwidth, measured in Gbps; and signifies the processing capability coefficient, reflecting the node’s parallel computing ability, typically within the range [0,1].
These resources are influenced by network states, topology changes, and other factors, and they evolve dynamically as the network operates. Precise modeling of each satellite node’s resources is crucial for effective task offloading and resource allocation.
Tasks in the network are characterized by their computational, storage, and bandwidth requirements. Each task j is represented by the vector as
where denotes the computational requirement, measured in Flops; represents the storage requirement, measured in GB; and indicates the bandwidth requirement, measured in Gbps.
To effectively schedule and offload tasks, a task assignment matrix is defined, where indicates whether task j is offloaded to satellite node i. The task assignment must satisfy
ensuring that each task is assigned to exactly one satellite node for processing.
During task offloading, data are transmitted and processed through satellite nodes. Let represent the amount of data transmitted from satellite node i to user terminal k for task j, and denote the transmission latency. The data flow and transmission latency are modeled as
where are the data transmitted from node i to terminal k for task j, and indicates the task assignment. The transmission latency is calculated based on the allocated bandwidth and the transmitted data amount as follows:
Network congestion, route choices, and channel quality also affect transmission delays, which are necessary to account for these changing factors in practical models. The combined effect of resource allocation, task assignment, and data transmission dynamics defines the overall performance and efficiency of the STIN system. Accurate modeling ensures optimal use of resources, efficient task execution, and minimized system delays, while facing network uncertainties and changing operational conditions.
To facilitate a comprehensive understanding of the system model, we summarize the key variables and parameters in Table 1. This table provides detailed definitions and units for each variable, ensuring clarity and consistency throughout the analysis.

Table 1.
List of variables and descriptions.
3.2. Constraints
In the task scheduling and resource optimization problem of STIN, a set of constraints must be introduced to ensure the efficient operation of the system and the successful completion of tasks. These constraints ensure the proper utilization of computational, storage, and bandwidth resources, while also ensuring the timely completion of tasks and the stability of the system. The following are the main constraints involved in the problem model, along with their necessity and explanations.
3.2.1. Computational Resource Constraint
Each node’s computational resources cannot exceed its maximum capacity. For node i, the computational resource constraint is given as
This constraint ensures that the total computational resource usage at node i for task j does not exceed the computational capacity of node i, where represents the computational resource requirement of task j, and represents the computational capacity of node i.
3.2.2. Storage Resource Constraint
Each node’s storage resources are also subject to constraints.
Assumption 1.
Storage resources are limited and dynamically influenced by the total number of tasks being processed.
The storage resource constraint for node i is given as
This constraint ensures that the total storage resource usage at node i for task j does not exceed the storage capacity of node i, where is the storage resource requirement of task j, and is the storage capacity of node i.
3.2.3. Bandwidth Resource Constraint
Bandwidths ensure that each node is not overloaded, so they are critical for efficient task scheduling.
Assumption 2.
The bandwidth availability is finite and may vary dynamically based on network conditions.
The bandwidth resource constraint is given as
This constraint ensures that the total bandwidth usage at node i for task j does not exceed the bandwidth capacity of node i, where represents the bandwidth resource requirement of task j, and is the bandwidth capacity of node i.
3.2.4. Task Assignment Constraint
Each task must be assigned to exactly one node for processing. This constraint ensures that tasks are clearly assigned for processing, avoiding resource waste and task incompletion. The constraint is given as
This constraint ensures that each task j is assigned to exactly one node i, meaning that each task is processed by a single node and cannot be assigned to multiple nodes.
3.2.5. Delay Constraint
The delay constraint is critical in preventing excessive delays that could affect user experience and system reliability.
Assumption 3.
Network and processing delays may vary depending on the availability of resources such as bandwidth and storage at the selected node.
The delay constraint is given as
This constraint requires that the total delay for tasks received by each user terminal k does not exceed the maximum allowable delay . Here, represents the delay for task j from satellite node i to user terminal k; indicates whether task j is assigned to satellite node i; and is the maximum delay acceptable for user terminal k.
3.3. Objective Function
To optimize task offloading and resource management, the following objective function is designed to balance system delay minimization and resource utilization maximization within the distributed optimization framework. The objective function can be decomposed into local objective functions for each node, which are ultimately summed up into a global objective function. To better distinguish these two functions, corresponding constraint conditions are matched to each of them.
The local objective function for each node i is based on the delay and resource consumption of the task assignments at that node. It is defined as follows:
The first term represents the transmission delay for tasks from node i to user terminal k, where represents the transmission delay for task j from node i to user terminal k, and is a binary variable indicating whether task j is assigned to node i. The second term represents the total resources (computational, storage, and bandwidth) used during task offloading, aiming to maximize resource utilization. The local objective function is primarily influenced by these node-level constraints as constraints (6), (7), and (8).
The global objective function is the sum of the local objective functions across all nodes, representing the total system delay and resource consumption. It is defined as follows:
The global objective function includes the delays and resource consumptions for each node, aiming to optimize the overall performance of the system, which is primarily influenced by these global constraints as constraints in Equations (9) and (10), which ensure that the task scheduling and resource allocation meet the overall performance requirements of the system.
Proof.
We reduce the 3-dimensional matching (3DM) problem to the task scheduling and resource allocation problem. Given three sets , , and , and a collection , the 3DM problem asks to find a subset such that each element in X, Y, and Z appears exactly once in M.
To reduce 3DM to the task scheduling problem, for each triple , we define a task with resource demands . These tasks must be assigned to satellite nodes, where each node represents an element from X, Y, or Z. The task assignment is represented by a binary matrix , where indicates that task is assigned to satellite node i, and otherwise.
The objective function in the task scheduling problem is
We also enforce resource constraints:
The task assignment matrix must ensure that each task is assigned exactly once, implying a matching in T and that each element in X, Y, and Z is covered by exactly one triple.
This task scheduling problem corresponds to solving the 3DM problem, where the task assignment directly mirrors the matching required in 3DM. As 3DM is NP-hard, the task scheduling and resource allocation problem is also NP-hard.
Note: The NP-hardness of the task scheduling problem is due to the combinatorial nature of the problem. Specifically, the task assignment must ensure that every task is assigned to exactly one node, similar to the matching requirement in the 3DM problem. Additionally, the resource constraints (such as computational, storage, and bandwidth requirements) further increase the complexity of the problem, making it intractable to solve in polynomial time for large instances. As a result, the problem exhibits NP-hard characteristics, meaning that no polynomial time algorithm is likely to exist for solving it optimally. □
4. Methodology
To cope with the issues of low resource utilization and high system latency in satellite networks, this study proposes a collaborative optimization framework based on cooperative dynamic programming. It aims to ensure fairness and efficiency in resource allocation within dynamic network environments. To address the network’s significant temporal variability and intricate constraints, we have proposed a multi-objective optimization model and introduced Gradient Surgery methods to manage the interactions between various objectives. This approach helps to ensure the successful convergence of the optimization process.
Figure 1 illustrates the overall framework of the method proposed in this paper. This framework comprises several key modules that work collaboratively to achieve the optimization of objectives and the handling of constraints. Firstly, the input to the model consists of raw data from the data collection module. The data preprocessing module normalizes the raw data to ensure data quality and accuracy. Subsequently, the data are transferred to the optimization module, which employs multi-objective optimization methods to solve for the optimal decision and then introduces distributed gradient descent and Gradient Surgery techniques to enhance optimization efficiency and solution precision. The optimization results generate the Pareto frontier, showcasing trade-off solutions among multiple objectives.
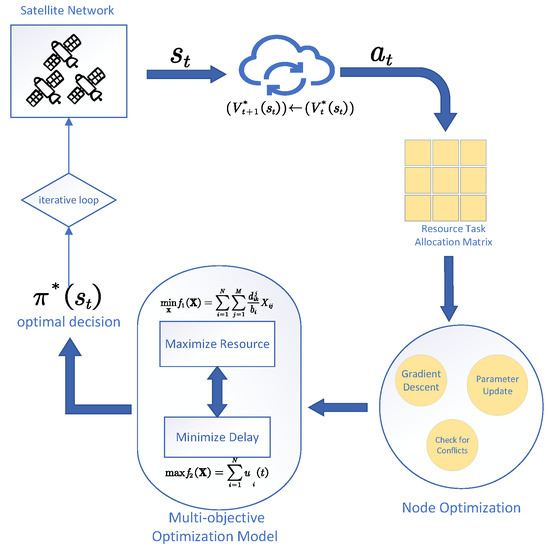
Figure 1.
Schematic basic idea D-GTOM framework.
4.1. Dynamic Resource Scheduling and Task Offloading Based on Value Iteration
To effectively address the issues of low resource utilization and high system latency in satellite networks, this paper proposes a collaborative optimization framework based on cooperative dynamic programming. This framework constructs delay optimization models and resource efficiency models, combining dynamic programming and value iteration techniques to achieve real-time updates of system states and decision variables. Specifically, task offloading decisions are represented by discrete matrices, which not only consider the priority and deadline of tasks but also evaluate each node’s computational, storage, and bandwidth resources. By iteratively updating the value function based on the Bellman equation, this method optimizes resource allocation and task scheduling strategies at each time step until convergence to the optimal decision strategy.
4.1.1. System State and Decision Variables
Let the system state at time t be denoted by , where represents the state space. The system state encompasses each task’s computational demand, each node’s resource status, and link delays.The decision variables for resource allocation are represented by , where is the set of all possible resource allocation actions. The task offloading decision aims to minimize maximum delay and maximize resource utilization efficiency. Therefore, we define an appropriate objective function and constraints for optimization.
Specifically, the decision variable includes the task j assignment to node i represented by the offloading matrix :
4.1.2. Mathematical Formulation for Task Offloading and Resource Scheduling
To optimize task offloading and resource scheduling in dynamic environments, we introduce a more comprehensive model that considers task dependencies, resource utilization efficiency, and task priorities.
The latency model is extended to account for task dependencies and parallel processing capabilities. In this extended model, the start time of task j depends on the completion time of task k. Therefore, the latency incurred during task offloading is influenced by both the transmission delay and the task dependency structure. The modified latency function is given by
The first part of the equation represents the latency during task offloading, where and represent the computational and storage times for task j. denotes the processing capability of node i at time t. represents the transmission delay for task j from node i to user terminal k at time t. The second part accounts for the additional delay due to task dependencies, where represents the additional delay between task j and task k.
A dynamic resource utilization rate is introduced to model resource efficiency more accurately. The resource utilization rate for node i at time t is defined as the weighted sum of the resource usages across computational, storage, and bandwidth dimensions. This resource utilization rate is used to define the resource efficiency function as follows:
where indicates whether task j is assigned to node i at time t. , , and represent the computational, storage, and bandwidth capacities of node i, respectively.
This formula considers the resource demand of each task on node i and calculates the node’s resource utilization rate as the weighted sum of the total resource usage. By optimizing this resource utilization rate, we can ensure the proper allocation of resources, avoiding both over-utilization and under-utilization.
The resource efficiency function is then given by
where N is the total number of nodes. represents the resource utilization rate of node i at time t. The term ensures that the efficiency is maximized when the resource utilization is close to its capacity.
This function quantifies the system’s resource efficiency by measuring the deviation of the resource utilization rate from the node’s maximum resource capacity. When approaches 1, the efficiency reaches its maximum, indicating that the resources are being fully utilized. This efficiency function can guide the system to optimize towards higher resource utilization.
To further optimize task scheduling, we incorporate task priorities and deadlines into the objective function. The priority and deadline of task j are considered to adjust the scheduling strategy. The extended objective function is
where represents the priority of task j. , , and are weighting parameters that control the trade-offs between resource efficiency, computational time, and transmission delay.
This objective function considers the impact of task priorities on scheduling, balancing the resources between computational, storage, and bandwidth needs. By adjusting the weights , , and , we can control the trade-off between resource efficiency, computational time, and transmission delay.
Incorporating task priorities ensures that higher-priority tasks are allocated resources first, which improves the overall system performance by minimizing the latency for critical tasks while maintaining resource efficiency.
4.1.3. Optimization Strategy
To effectively address the issues of low resource utilization and high system latency in satellite networks, this study proposes a collaborative optimization framework based on cooperative dynamic programming. This framework constructs latency optimization and resource efficiency models, employing dynamic programming and value iteration techniques to enable real-time updates of system states and decision variables. Specifically, task offloading decisions are represented by a discrete matrix , which considers not only task priorities and deadlines but also the computational, storage, and bandwidth resources of each node.
The state transition is influenced by the current task processing status, node resource availability, and link delays. The state transition probability is defined as , where is the system state at the next time step. The state transition is governed by
During state transitions, the system must adhere to the following constraint:
where represents the state change of node i at time t.
The optimal decision problem for dynamic resource scheduling and task offloading is formulated as a constrained optimization problem. By incorporating the state transition equations and reward function, the problem is expressed as
where is the optimal value function for state , and is the discount factor representing the importance of future rewards.
We iteratively update the value function until convergence:
where is the value function at iteration t.
The optimal policy is a mapping from each possible state to an optimal action . Its goal is to maximize the long-term cumulative reward, typically achieved by solving the Bellman equation. Specifically, the optimal policy is defined as
where is the immediate reward obtained by taking action in state . is the discount factor controlling the weight of future rewards. is the probability of transitioning from state to state after taking action . is the optimal value function at state .
We design an iterative algorithm based on value function updates. Initially, the value function is set to zero or an initial estimate, and the learning rate , discount factor , and maximum number of iterations T are specified. During each iteration, the Bellman update is computed using the current value function and the reward associated with each action. This update provides an estimation of the optimal value for the next time step. The value function is then updated using the difference between the estimated and current values, adjusted by the learning rate:
The iteration continues until the value function converges, i.e., the change in the value function falls below a predefined threshold . Once convergence is achieved, the optimal policy is extracted by selecting the action that maximizes the following expression:
This policy represents the optimal strategy for task offloading and resource allocation in the dynamic environment, ensuring maximum long-term resource utilization and minimized task delays. Finally, we design Algorithm 1 to clear the expression of the main idea above.
| Algorithm 1 Dynamic resource scheduling and task offloading algorithm (RSTO) | |
| Input: Initial state , learning rate , discount factor , maximum number of iterations T, reward function parameters , state transition probabilities . | |
| Output: Optimal task offloading and resource scheduling policy . | |
| 1: | Initialize value function to zero or initial estimate. |
| 2: | for each iteration do |
| 3: | for each time step t do |
| 4: | Perceive current state ; |
| 5: | Select optimal action using Equation (24); |
| 6: | Execute action , update system state using Equation (18); |
| 7: | Observe reward ; |
| 8: | Update value function using Equation (23); |
| 9: | end for |
| 10: | end for |
| 11: | if then |
| 12: | terminate |
| 13: | for each state do |
| 14: | Compute optimal policy using Equation (22); |
| 15: | end for |
| 16: | return |
| 17: | end if |
The input parameters include the initial state , learning rate , discount factor , maximum number of iterations T, reward function parameters and , and state transition probabilities . The output is the optimal task offloading and resource scheduling policy . The algorithm begins by initializing the value function to zero or another initial estimate (line 1), which serves as the baseline for iteration. The iterative process runs from iteration 0 to , traversing all time steps t (lines 2–3). At each time step, the current system state is perceived for decision-making (line 4), representing the system’s understanding of its current situation, including resource availability and task statuses. The optimal action is selected based on the optimal policy equation (line 5), ensuring long-term performance optimization by balancing immediate rewards with future rewards. The action is executed, and the system state is updated to (line 6), with the transition governed by . The immediate reward is observed (line 7), reflecting the feedback from the action taken. The value function is adjusted using the value function update formula (line 8), incorporating both immediate rewards and expected future rewards to iteratively improve the system’s decision-making process.
After completing all time steps, the change in the value function is checked to determine if it is less than the preset threshold (lines 11 and 12). This check ensures convergence, meaning that further iterations will not significantly improve the value estimates. If the convergence condition is met, the iteration terminates. The optimal policy is computed for each state using the optimal policy equation (lines 13–16), representing the best strategy for task offloading and resource scheduling to achieve maximum resource utilization and minimal latency. This policy is output to guide the system’s decision-making process, ensuring that the system optimizes its operations based on the learned strategy.
4.2. Multi-Objective Task Scheduling Based on Gradient Descent
Due to bottleneck problems, traditional centralized computing methods struggle to solve resource scheduling issues in multi-node distributed environments due to bottleneck problems. To tackle this issue, we propose a task scheduling and resource management framework based on distributed optimization, integrating multi-objective optimization (MOML) and Gradient Surgery techniques. This framework leverages collaborative computing and edge computing to effectively enhance system performance, resolving resource conflicts and latency issues. Specifically, the framework employs a distributed gradient descent algorithm to optimize task offloading decisions and resource allocation schemes, utilizes multi-objective optimization methods to balance the objectives of minimizing latency and maximizing resource utilization, and coordinates the relationships between different optimization goals through Gradient Surgery techniques to ensure the convergence of the multi-objective optimization process. This approach not only improves resource utilization efficiency but also significantly reduces task processing latency.
The resource scheduling and latency minimization problem in STIN can be modeled as a multi-objective optimization problem with the following objective function:
Here, represents the transmission latency of task on satellite node , while , , and denote the computational, storage, and bandwidth resources of node , respectively.
The optimization problem can be decomposed into two separate objectives: minimizing latency and minimizing resource consumption. These are expressed as
We introduce weighting coefficients and , combining them into a single objective function:
We employ the Lagrangian function, as follows:
The Lagrange multipliers enforce the constraint that the sum of the offloading decisions for each task equals 1. This formulation leads to the dual problem:
To solve this dual problem, distributed optimization techniques such as gradient descent are employed, iteratively solving for the optimal offloading decision matrix and Lagrange multipliers .
Given the multi-objective nature of the task offloading and resource allocation problem, we employ a distributed gradient descent algorithm enhanced with Gradient Surgery to ensure convergence to a Pareto optimal solution. The gradients of the objective functions concerning the decision variables are defined as follows:
The combined gradient for the task offloading matrix is
The update rule for is given by
where is the learning rate. This iterative process drives the task offloading matrix towards an optimal solution by moving in the direction of the gradient of the objective function.
However, since the two objectives and may conflict, directly applying gradient descent could lead to suboptimal solutions. To mitigate this, Gradient Surgery is employed to adjust the gradient directions, ensuring that the updates balance both the latency minimization and resource utilization maximization. The adjusted gradients are defined as
where is the gradient related to resource allocation. These adjusted gradients ensure that the optimization process moves towards a Pareto optimal solution, where no objective can be improved without worsening another.
The framework optimizes task offloading decisions and resource allocation plans through iterative adjustments using distributed gradient descent and Gradient Surgery. This approach ensures that the system converges to an optimal policy, which maximizes long-term resource utilization while minimizing task delays and thereby enhancing the overall performance and robustness of the satellite network.
Additionally, the interdependence between task offloading and computational resource allocation plays a crucial role in optimizing both system latency and resource utilization. The task offloading matrix determines the allocation of tasks to nodes, while the resource allocation matrix defines the computational resources allocated to each task at each node. Specifically, for task offloaded to node , the computational demand must be satisfied by the allocated resources , i.e.,
This interdependence leads to a coupled multi-objective optimization problem:
s.t.
In the presence of multiple objectives, Gradient Surgery is employed to adjust the gradients for task offloading and resource allocation, ensuring that the update direction balances latency and resource utilization. The combined gradient for the task offloading matrix is
The adjusted gradients ensure that the optimization process proceeds towards a Pareto optimal solution, where both latency and resource consumption are optimized without conflicting gradients. The task offloading and resource allocation matrices are then updated as follows:
where is the step size. This iterative process ensures that the optimization converges to a balanced solution that minimizes latency and maximizes resource utilization, thereby achieving optimal system scheduling.
Overall, the proposed distributed optimization-based framework, enhanced with multi-objective optimization and Gradient Surgery, provides an effective solution for task scheduling and resource management in dynamic and distributed satellite networks. Based on the conceptions, we propose Algorithm 2.
| Algorithm 2 Distributed optimization-based resource management (DORM) | |
| Input: Number of satellite nodes N with resources , , ; Number of tasks M with Latency , Data volume ; Computational demand ; Max resources ; Maximum number of iterations . | |
| Output: Task offloading matrix ; Resource allocation matrix . | |
| 1: | Initialize randomly, based on initial resource allocation. |
| 2: | Set learning rate ; Set weights , for latency and resource functions. |
| 3: | for to K do |
| 4: | Compute , using Equations (31) and (32); |
| 5: | Compute using Equation (33); |
| 6: | Adjust , using Equations (36) and (37); |
| 7: | ← with Equation (41); |
| 8: | ← with Equation (42); |
| 9: | if or then |
| 10: | terminate. |
| 11: | end if |
| 12: | end for |
| 13: | return , |
The input includes the number of satellite nodes N and their resources , , ; the number of tasks M and their latency ; data volume ; computational demand ; maximum resources of nodes ; and the maximum number of iterations . The output consists of the optimal task offloading matrix and resource allocation matrix . The matrices and are initialized randomly, with the resource allocation matrix set based on initial distribution (line 1). The learning rate , and weight parameters and for latency and resource functions are set (line 2). The iterative process runs from to K (line 3), with a maximum of iterations to prevent infinite loops. This limits the time for optimization while allowing convergence. In each iteration, the gradients of the task offloading objective function and the resource consumption objective function with respect to are computed (line 4). These gradients guide the adjustment of task offloading decisions to optimize the objective function. The gradient of with respect to the resource allocation matrix is computed (line 5). The gradients for task offloading and resource allocation are adjusted using Gradient Surgery (line 6), ensuring a balanced optimization process by orthogonalizing conflicting gradients. This step mitigates trade-off issues between minimizing latency and maximizing resource usage.
The matrices and are updated using the adjusted gradients (lines 7 and 8). This update step allows the optimization process to move towards a Pareto optimal solution by dynamically adjusting resource allocation based on the task offloading decisions. The iterative adjustment ensures that both the task offloading matrix and the resource allocation matrix evolve towards an optimal configuration that balances system performance. The change in the objective function is checked to determine if it meets the convergence threshold or if the iteration limit is reached (line 9). If so, the process terminates (line 10). This check prevents unnecessary computations once convergence is achieved. The loop ends (line 11), and the final matrices and are returned (line 12).
4.3. Overall Time Complexity Analysis of Algorithm
The proposed method integrates dynamic programming, multi-objective optimization, as well as distributed gradient descent and Gradient Surgery techniques, aiming to optimize resource scheduling and task offloading in satellite networks. To comprehensively evaluate the time complexity of this approach, it is essential to analyze the complexity of each component module.
In the dynamic resource scheduling and task offloading framework, dynamic programming (DP) and value iteration techniques are employed to update system states and decision variables in real time, thereby optimizing resource allocation and task scheduling strategies. Assuming the size of the system state space is , and the size of the action space is , the value iteration process requires T iterations, with each iteration having a time complexity of . Therefore, the total time complexity of dynamic programming and value iteration is . Additionally, task offloading decisions are represented by a discrete matrix . Considering the number of tasks M and the number of nodes N, the time complexity for updating at each time step is .
In the distributed optimization segment, this study employs multi-objective optimization and distributed gradient descent algorithms to balance the minimization of latency and maximization of resource utilization. Assuming the number of objective functions is K (typically a constant, such as 2), gradient descent requires I iterations, with each iteration necessitating the computation of gradients for each task and node, resulting in a time complexity of . Gradient Surgery is utilized to adjust the gradient directions to ensure that the gradients do not conflict during the multi-objective optimization process, with a time complexity of . Since Gradient Surgery is performed during each gradient update, its overall time complexity is proportional to the number of gradient descent iterations I. Thus, the total time complexity of distributed gradient descent and Gradient Surgery is .
The overall time complexity of the proposed method, which combines the complexities of the aforementioned components, can be approximated as
Considering this, in practical applications, the state space and action space are typically related to the number of nodes N and tasks M (e.g., and ); the above time complexity can be further simplified to
where T is the number of value iterations, N is the number of nodes, M is the number of tasks, K is the number of objective functions, and I is the number of gradient descent iterations.
Moreover, although distributed optimization techniques theoretically allow for the distribution of time complexity across multiple computing nodes, thereby reducing the computational burden on individual nodes, in practice, communication overhead and synchronization delays are significant factors that must be considered. These factors typically introduce additional time complexity, specifically for communication overhead. Therefore, while distributed optimization offers substantial advantages in parallel computation, the actual time performance requires balancing computational and communication overheads.
4.4. Computational Overhead Analysis
In task offloading and resource allocation problems, computational overhead is an important indicator for evaluating the practical feasibility of an algorithm. The dynamic gradient descent-based task offloading method (D-GTOM) proposed in this paper has a lower computational complexity compared to traditional algorithms. The algorithm mainly updates the offloading decisions in real time based on network states and resource variations, thus avoiding the high computational overhead required by large-scale parallel computation. Specifically, in each iteration, D-GTOM only involves updating local network information and computing gradients, making its computational burden relatively light.
To quantify the computational overhead of D-GTOM, we have conducted a theoretical analysis. Let the complexity of each gradient computation in one iteration be , where n is the number of variables in the task offloading decision, which is typically related to the number of satellites and the task scale. Let the total number of iterations be T, then the total computational overhead can be expressed as . Furthermore, since communication between satellites is required, the communication cost cannot be ignored. Assuming the communication complexity is , where N is the number of satellites and K is the complexity of the network topology, the overall computational overhead becomes
Although computational overhead increases with the network scale and task complexity, compared to traditional global optimization methods, D-GTOM achieves optimal offloading decisions with relatively low computational overhead by utilizing local information updates and gradient descent optimization strategies. To further reduce computational overhead, future research may explore adaptive computation strategies and hierarchical optimization methods to improve the algorithm’s efficiency in practical applications.
5. Experiment Results
To address the research problem of dynamic resource allocation and task offloading in STIN, we constructed multiple experimental scenarios on our self-developed Common Satellite Tool Kit (CSTK) platform. These experimental scenarios simulate the dynamic changes of satellite nodes, ground stations, user terminals, and inter-satellite communication links, aiming to validate the effectiveness of the proposed task scheduling and resource optimization model in minimizing system latency and maximizing resource utilization. Figure 2 illustrates the satellite network topology used in our simulations, showing the distribution of satellites, ground stations, and their communication links. The yellow coverage areas represent the effective communication regions of different satellites, while the red and blue lines depict inter-satellite and ground communication links, respectively. The CSTK platform provides comprehensive orbital simulation and mission planning functionalities, enabling precise simulation of satellite trajectories and their communication contact windows. This ensures that accurate satellite trajectory and communication delay information are provided for the experiments, thereby supporting the implementation and validation of the model.
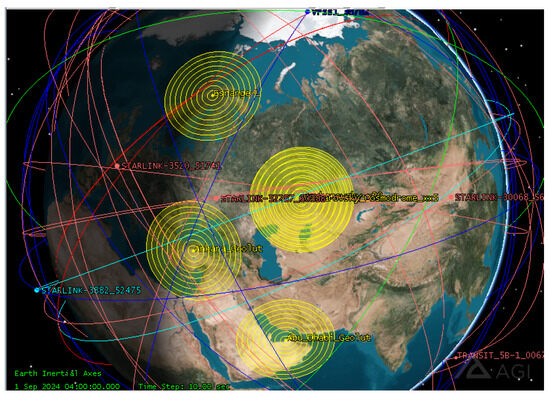
Figure 2.
Main simulation interface of the CSTK platform.
5.1. Dataset Detail and Scenario Description
To ensure the feasibility and scalability of the proposed task offloading and resource management framework, we make the following assumptions regarding the satellite nodes and datasets.
Assumption 4.
The computational, storage, and bandwidth resources of satellite nodes are assumed to be sufficient to handle the tasks assigned to them. Specifically, for each satellite node , the total available resources are denoted as , , and . These resources are assumed to be fixed and limited.
Assumption 5.
All satellites operate normally throughout the duration of the scenario without any failures. The network communication is stable, and there will be no interruptions in visibility periods.
The dataset used in the experiments encompasses satellite orbital parameters, resource configurations, and task demand data, which are crucial for multi-satellite collaborative computing in remote sensing missions. The satellite orbital parameters include semi_major_axis, eccentricity, inclination, argument_of_perigee, longitude_of_ascending_node, and mean_anomaly. These parameters are sourced from the CelesTrak database (CelesTrak, “Two-Line Element Set (TLE) Satellite Catalog”, https://www.celestrak.com/NORAD/elements/, accessed on 4 December 2024), and are used to accurately simulate satellite trajectories and the communication contact windows between satellites.
The CSTK platform provides robust orbital simulation and mission planning functionalities, enabling the simulation of satellite movement trajectories and inter-satellite communication links over different time periods. The platform also provides precise position and velocity information for each satellite during the simulation period, which allows for the calculation of communication delays and available bandwidth between satellites. This information is essential for implementing the task scheduling and resource optimization model.
The resource configurations of satellite nodes include computational_capacity (Flops), storage_capacity (GB), bandwidth (Gbps), and processing_capability coefficient. These resource parameters are set based on the specifications of the European Space Agency’s Sentinel satellites (European Space Agency, “Sentinel Missions”, https://www.esa.int/Applications/Observing_the_Earth/Copernicus/Sentinel-1, accessed on 6 December 2024), where computational_capacity ranges from 100 to 1000 MIPS, storage_capacity spans from 4 to 64 GB, bandwidth ranges from 1 to 500 Mbps, and the processing_capability coefficient lies between 0 and 1. These parameters reflect each satellite node’s computational, storage, and communication capabilities during task execution.
Task demand parameters include task_priority (priority level, from 1 to 10), data_size (data size, from 10 MB to 2000 MB), and execution_time (execution time, from 1 to 120 min). These parameters are manually selected based on actual remote sensing mission areas, with task size estimated according to the target area and task priority set according to user-specific criteria.
The simulation scenario’s time span is defined by scenario_start_time and scenario_end_time. For instance, the simulation time is from 00:00 UTC on 3 September 2023, to 23:59 UTC on 15 September 2023. Based on this simulation scenario, task demand parameters are defined, and 12 datasets with varying numbers of satellites are constructed. Each dataset corresponds to a different number of tasks, with 20 experiments conducted for each dataset to evaluate system performance under diverse satellite configurations and task loads.
5.2. Comparative Algorithms
To address the multi-satellite collaboration and network resource optimization problem, this study selects five comparative algorithms for performance evaluation. These algorithms include Adaptive Batch Inductive Optimization (ABIO) [38], Mutation Quantum Particle Swarm Optimization (QPSO) [39], Differential Evolution with Local Search (DE) [40], Adaptive Genetic Algorithm (AGA-ES) [41], and Adaptive Temperature Simulated Annealing (TSA) [42]. Specifically, ABIO has a time complexity of , QPSO has a time complexity of , DE has a time complexity of , AGA-ES has a time complexity of , and TSA has a time complexity of when the number of iterations per time scale is approximately equal, and when the batch size increases exponentially with the time scale. These algorithms demonstrate excellent convergence and adaptability in solving network optimization problems, effectively balancing global and local searches in dynamic environments.
Specifically, ABIO [38] was selected for its efficient handling of batch processing and inductive reasoning capabilities, enabling effective resource allocation under fluctuating network conditions with a time complexity of , where T is the number of iterations, B is the adaptive batch size, and D is the problem dimension (i.e., the number of variables in the optimization problem). QPSO [39] was chosen due to its enhanced exploration capabilities through quantum mutation strategies, which help to avoid premature convergence in complex optimization landscapes, with a time complexity of , where T is the number of iterations, M is the number of particles, and D is the problem dimension. DE [40] employs a hybrid approach that combines Differential Evolution with local search, ensuring a balanced exploration and exploitation of the solution space, and has a time complexity of , where T is the number of iterations, N is the population size, and D is the problem dimension. AGA-ES [41] exhibits high adaptability by dynamically adjusting mutation and crossover rates, maintaining high performance in heterogeneous satellite environments, with a time complexity of , where P is the population size, G is the number of generations, and N is the population size. Finally, TSA [42] improves the balance between exploration and exploitation through an adaptive temperature schedule, enhancing task offloading decisions in dynamic network scenarios. Its time complexity is when the number of iterations per time scale is approximately equal, and when the batch size increases exponentially with the time scale, where K is the number of time scales, is the initial batch size, m is the batch size growth factor, and T is the total number of external time scales.
5.3. Evaluation Metrics
In this study, to comprehensively evaluate the performance of the proposed algorithm for task scheduling and resource management in STIN, we have selected the following four evaluation metrics: global objective function value, resource utilization rate, algorithm running time, and average task delay. The rationale and calculation methods for each evaluation metric are detailed below, referencing the variables defined in the Problem Definition and Formulation section.
The global objective function value is the primary metric for assessing the overall performance of the system. It is defined in Equation (12), which integrates both task transmission delay and resource consumption, aiming to minimize the overall system delay while maximizing the effective utilization of resources. Optimizing ensures efficient task scheduling and optimal resource management, thereby enhancing system performance in dynamic network environments.
Resource utilization rate R measures the efficiency of computational, storage, and bandwidth resource usage within the system. It is calculated as follows:
where , , and represent the computational, storage, and bandwidth requirements of task j, while , , and are the respective resource capacities of node i.
The resource utilization rate quantifies the proportion of allocated resources relative to the available resources. A high resource utilization rate indicates that the system effectively leverages its existing resources, minimizing waste and enhancing overall operational efficiency. This metric is particularly crucial in the resource-constrained and dynamically changing environment of satellite networks, where optimal resource allocation is essential for maintaining system performance.
Algorithm running time is a critical metric for assessing the efficiency of the proposed task scheduling and resource management algorithm. This metric directly reflects the computational time required by the algorithm to solve the scheduling and resource allocation problem. In the context of STIN, where the network is dynamic and potentially large-scale, the running time of the algorithm significantly impacts the responsiveness and overall performance of task scheduling. Therefore, minimizing the algorithm running time is a key objective to ensure timely task processing and maintain system efficiency.
Average task delay D evaluates the mean time required to complete all tasks within the system. It is calculated using the following formula:
where denotes the delay associated with transmitting task j from node i, is the task assignment matrix, and M is the total number of tasks.
The average task delay provides insight into the system’s responsiveness and efficiency in handling task processing. Lower average delays indicate that tasks are being processed and completed more swiftly, which enhance user experience and ensure the reliability of the system. In STIN, timely task completion is vital for maintaining service quality and system dependability, making the optimization of average task delay a significant evaluation objective.
5.4. Numerical Analysis
To evaluate the performance of the proposed task offloading and resource scheduling algorithms, we utilized a set of representative datasets with varying scales. These datasets, denoted as D1, D2, D3, and D4, vary in the number of satellite nodes, tasks, and user terminals, providing a comprehensive evaluation of the algorithm’s robustness and scalability. The configuration of these datasets is summarized in Table 2.

Table 2.
Configuration of selected datasets.
As shown in Figure 3 and Table 3, the proposed D-GTOM algorithm consistently outperforms the five comparative optimization algorithms (TSA, AGA-ES, QPSO, DE, and ABIO) across all four satellite counts (5, 10, 100, and 200 satellites). Specifically, the D-GTOM algorithm achieves a target function value of 6251.00 for five satellites, representing an average reduction of 22.56% compared to the comparative algorithms. For 10 satellites, the value is 12,777.23, a decrease of 18.92%; for 100 satellites, it significantly lowers to 124,328.53, marking a reduction of 56.56%; and for 200 satellites, the value stands at 396,287.42, reflecting a 13.42% decrease relative to the comparative algorithms. These results indicate that the D-GTOM algorithm, through its cooperative optimization framework based on dynamic programming, effectively achieves fairness and efficiency in resource allocation within dynamic network environments. Specifically, the application of dynamic programming and value iteration techniques enables real-time updates of system states and decision variables. By incorporating Gradient Surgery techniques, the D-GTOM algorithm successfully coordinates the relationships between different optimization objectives, avoiding gradient conflicts. This innovative architecture demonstrates exceptional performance in handling high-dimensional and large-scale problems. In contrast, other algorithms struggle to achieve the same level of optimization effectiveness under identical conditions due to limitations in computational complexity and optimization efficiency, further validating the significant advantages and superiority of the proposed method in satellite network resource scheduling.
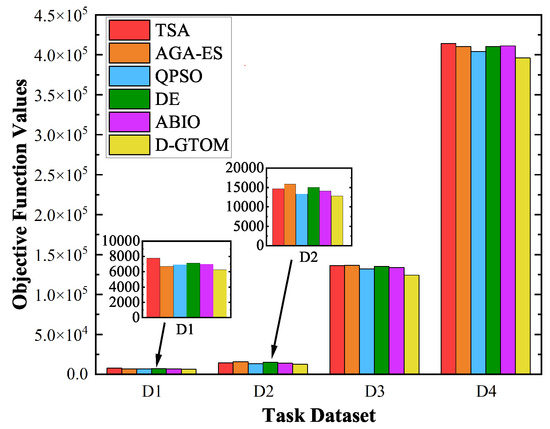
Figure 3.
Comparison of objective function values for different algorithms across 4 datasets.

Table 3.
Objective function values and reduction ratios across four datasets.
The proposed D-GTOM algorithm consistently achieves significantly higher resource utilization rates across all four satellite datasets compared to the five comparative algorithms, as illustrated in Figure 4. Based on the specific result presented in Table 4, the D-GTOM algorithm attains resource utilization rates of 0.391 for 5 satellites, 0.407 for 10 satellites, 0.486 for 100 satellites, and 0.606 for 200 satellites. These results indicate that the D-GTOM algorithm effectively balances fairness and efficiency in resource allocation through its multi-objective optimization model, while Gradient Surgery techniques ensure the coordination between different optimization objectives, preventing conflicts and imbalances in resource distribution. Additionally, the application of dynamic programming and value iteration techniques allows the D-GTOM algorithm to update system states and decision variables in real time, swiftly responding to the high temporal variability and complex constraints of the network, thereby enhancing overall resource utilization efficiency. In contrast, other algorithms are limited in their ability to fully exploit resource potential due to constraints in handling multi-objective optimization and dynamic resource scheduling, resulting in lower resource utilization rates compared to the D-GTOM algorithm. This further validates the superior performance and significant advantages of the D-GTOM algorithm in satellite network resource management.
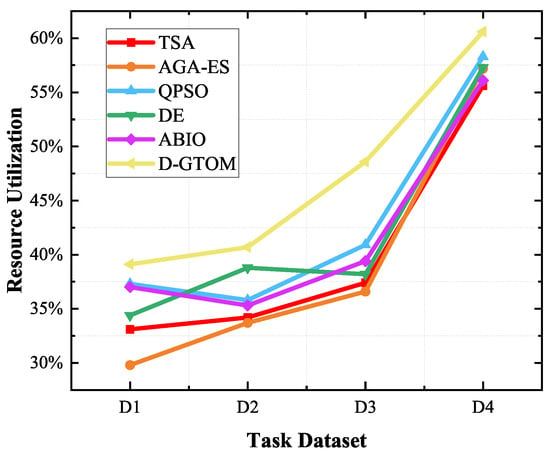
Figure 4.
Comparison of resource utilization rates for different algorithms across 4 datasets.

Table 4.
Resource utilization rate and reduction ratios across 4 datasets.
In Figure 5a and Table 5 and Table 6, the proposed D-GTOM algorithm exhibits notably lower running times across all datasets, with values of 0.050 s for 5 satellites, 0.090 s for 10 satellites, 0.027 s for 100 satellites, and 0.266 s for 200 satellites. These running times are significantly reduced compared to the other comparative algorithms, highlighting the computational efficiency advantage of the D-GTOM algorithm. Although in some smaller-scale datasets, the running time of D-GTOM is slightly higher than that of Simulated Annealing and ABIO algorithms, its performance remains highly efficient in large-scale and high-dimensional problems. This high efficiency is primarily due to the D-GTOM algorithm’s construction of latency optimization and resource efficiency models, which effectively balance fairness and efficiency in resource allocation. Additionally, the use of dynamic programming and value iteration techniques allows the D-GTOM algorithm to update system states and decision variables in real time, swiftly responding to the high temporal variability and complex constraints of the network. These characteristics not only enhance the convergence speed of the algorithm but also optimize the utilization of computational resources, ensuring scalability and robustness in large-scale satellite networks.
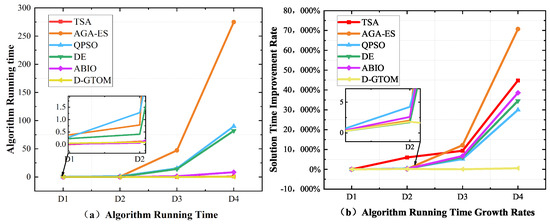
Figure 5.
Running time and improvement rates of algorithms across 4 datasets.

Table 5.
Algorithm running time (in seconds) and reduction ratios across 4 datasets.

Table 6.
Algorithm running time improvement rates compared to D1 across 3 datasets.
This outstanding performance is primarily attributed to the collaborative optimization framework based on dynamic programming employed by the MSGT algorithm. By constructing latency optimization and resource efficiency models, and integrating multi-objective optimization with Gradient Surgery techniques, the MSGT algorithm ensures high resource utilization and low system latency in dynamic network environments. Furthermore, the application of dynamic programming and value iteration techniques enables the MSGT algorithm to swiftly respond to the high temporal variability and complex constraints of the network, thereby enhancing the algorithm’s convergence speed and optimization accuracy. In contrast, other benchmark algorithms struggle to achieve comparable running efficiency and optimization effectiveness when confronted with large-scale and highly complex problems, due to their higher computational complexities and limitations in optimization strategies.
As shown in Figure 6, the proposed D-GTOM algorithm demonstrates competitive performance in terms of average task delay across four satellite datasets with varying scales. Specifically, while D-GTOM achieves a task delay of 0.185 s for 5 satellites and 0.176 s for 10 satellites, it is slightly outperformed by the Simulated Annealing algorithm, which records delays of 0.180 s and 0.169 s, respectively. In larger-scale scenarios, D-GTOM maintains commendable performance with delays of 0.191 s for 100 satellites and 0.192 s for 200 satellites, although Particle Swarm Optimization achieves marginally lower delays of 0.186 s and 0.189 s in these cases. These observations indicate that while D-GTOM does not consistently yield the lowest task delays across all datasets, it balances delay with other critical performance metrics effectively. The underlying collaborative optimization framework based on dynamic programming enables D-GTOM to achieve high resource utilization and robust performance under dynamic network conditions. Additionally, the integration of multi-objective optimization and Gradient Surgery techniques facilitates efficient resource allocation and minimizes latency where possible. Consequently, D-GTOM offers a well-rounded solution that prioritizes both efficiency and fairness in resource distribution, making it a reliable choice for complex and large-scale satellite network environments despite not always being the top performer in task delay alone.
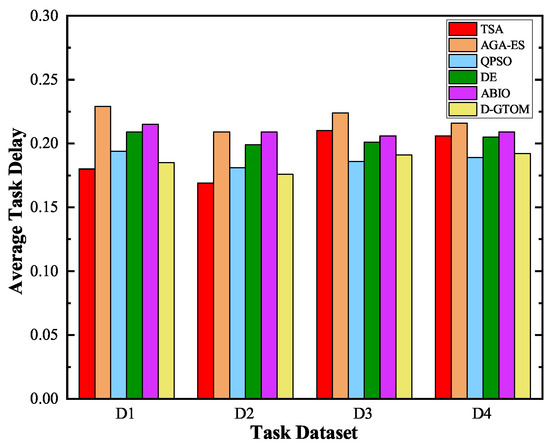
Figure 6.
Comparison of average task delay for different algorithms across 4 datasets.
Additionally, the experiments were conducted on a large-scale dataset comprising 300 satellites, with task numbers corresponding to 600, 900, 1500, 2400, and 3600. The numerical results from large-scale satellite network experiments highlight the performance of different algorithms under increasing task sizes, as shown in Figure 7 and Table 7. Figure 7a demonstrates that D-GTOM achieves superior resource utilization across varying task scales. Specifically, for 600 tasks, D-GTOM attains a utilization rate of approximately 0.48, surpassing TSA and AGA-ES, which fall in the 0.35–0.45 range. For larger-scale scenarios, such as 3600 tasks, D-GTOM achieves a utilization rate nearing 0.9, outperforming other algorithms capped at around 0.85. These results highlight D-GTOM’s robust scalability and capability in maintaining high resource utilization under diverse and large-scale workloads, underscoring its effectiveness in dynamic satellite network environments. Figure 7b provides the average task delays, showing that D-GTOM maintains competitive delays, such as 0.165 s for smaller datasets and 0.185 s for larger datasets, demonstrating a clear advantage over TSA and AGA-ES in minimizing delay. As shown in Figure 7c, D-GTOM consistently achieves the shortest runtime, ranging from 0.406 s for 600 tasks to 2.621 s for 3600 tasks, significantly outperforming TSA (1.663 to 9.601 s) and AGA-ES (507.411 to 3078.633 s). Meanwhile, Table 7 highlights the execution time of scheduling schemes, where D-GTOM achieves substantial reductions, requiring 1534 h for 600 tasks and 12,019 h for 3600 tasks, compared to TSA’s 2577 to 13,709 h. These results collectively validate the superior scalability, computational efficiency, and adaptability of D-GTOM in handling large-scale satellite network scheduling scenarios.
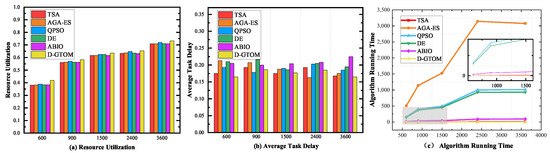
Figure 7.
Comparison of evaluation metrics in large-scale satellite dataset with growing task quantity.

Table 7.
Scheduling scheme execution time in large-scale satellite dataset with growing task quantity.
5.5. Experimental Conclusion
In this section, we constructed experimental scenarios on our self-developed Common Satellite Tool Kit (CSTK) platform to simulate the dynamic changes of satellite nodes, ground stations, user terminals, and inter-satellite communication links. This was performed to validate the effectiveness of the proposed task scheduling and resource optimization model in minimizing system latency and maximizing resource utilization. The experimental results demonstrate that the D-GTOM algorithm exhibits outstanding performance across satellite networks of varying scales, significantly outperforming five traditional comparative optimization algorithms (Differential Evolution, Genetic Algorithm, Particle Swarm Optimization, ABIO, and Simulated Annealing). Specifically, the D-GTOM algorithm achieved notable improvements in objective function values, resource utilization rates, and algorithm running times, particularly showcasing greater scalability and computational efficiency in large-scale and high-dimensional problems. These achievements are attributed to the collaborative optimization framework based on dynamic programming employed by the D-GTOM algorithm, as well as the effective integration of a multi-objective optimization model with Gradient Surgery techniques. This combination enables fair and efficient resource allocation in complex and dynamic network environments. Overall, the experiments validate the superiority and practicality of the D-GTOM algorithm in satellite network resource scheduling and task offloading, providing robust support for the efficient management of future large-scale satellite networks.
In satellite networks, implementing D-GTOM requires the careful consideration of communication and integration with existing infrastructure. The algorithm relies on real-time communication between satellites and ground stations to share resource information and offloading decisions. This communication overhead grows with the number of satellites and the frequency of updates. To manage this, lightweight protocols like gossip or low-latency message-passing can be adopted to reduce global synchronization delays and ensure scalability. As for integration with existing satellite network infrastructure, particularly in heterogeneous LEO constellations, D-GTOM must adapt to the varying computational, storage, and communication capabilities of each satellite. This requires compatibility with satellite communication protocols, considering dynamic orbital movements, varying link capacities, and latency fluctuations. Additionally, integration with existing network management systems must ensure that task offloading decisions are harmonized with resource allocation models, enabling smooth scalability without disrupting legacy systems. By addressing these communication and integration challenges, D-GTOM can effectively be deployed within existing satellite network frameworks.
6. Conclusions
This paper addresses the problem of low resource utilization and high system latency in dynamic satellite networks concerning resource allocation and task offloading. The innovation lies in proposing a collaborative optimization framework based on dynamic programming, combined with a multi-objective optimization model and Gradient Surgery techniques, ensuring fairness and efficiency in resource distribution. Experimental results demonstrate that the proposed D-GTOM algorithm outperforms existing comparative algorithms in terms of objective function value and resource utilization while also exhibiting high computational efficiency. Specifically, D-GTOM achieves an average reduction of 22.56% to 56.56% in objective function values across varying satellite configurations. The algorithm also demonstrates a significant improvement in resource utilization, ranging from 5.21% to 54.68%, and exhibits lower running times, with reductions up to 96% compared to other algorithms. Although the task delay is slightly higher than some comparative algorithms in smaller-scale datasets, D-GTOM maintains competitive delays of 0.185 s for 5 satellites and 0.192 s for 200 satellites, ensuring efficiency and fairness in larger-scale and high-dimensional problems.
For future research, we will focus on the following aspects: further optimizing the D-GTOM algorithm to significantly reduce task delays in small-scale datasets; expanding the algorithm to adapt to more complex and heterogeneous satellite network environments, including multiple types of satellite nodes and diverse task requirements; and exploring the scalability and performance optimization of the algorithm in larger satellite constellations, ensuring its widespread applicability and practicality in future large-scale satellite networks.
Author Contributions
Conceptualization, Y.L.; methodology, Y.W. and Y.L.; software, Y.W.; validation, Y.W. and S.W.; formal analysis, Y.L.; investigation, Y.W.; resources, Y.L. and S.W.; data curation, Y.W.; writing—original draft preparation, Y.L. and Y.W.; writing—review and editing, Y.L. and S.W.; visualization, Y.W. and S.W.; supervision, S.W.; project administration, Y.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant U1911401 and the National Natural Science Foundation of China under Grant U1435215.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yan, S.; Cao, X.; Liu, Z.; Liu, X. Interference management in 6G space and terrestrial integrated networks: Challenges and approaches. Intell. Converg. Netw. 2020, 1, 271–280. [Google Scholar] [CrossRef]
- Chen, L.; Tang, F.; Li, Z.; Yang, L.T.; Yu, J.; Yao, B. Time-Varying Resource Graph Based Resource Model for Space-Terrestrial Integrated Networks. In Proceedings of the IEEE INFOCOM 2021—IEEE Conference on Computer Communications, Virtual, 14–23 June 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Jiang, W.; Zhan, Y.; Xiao, X.; Sha, G. Network Simulators for Satellite-Terrestrial Integrated Networks: A Survey. IEEE Access 2023, 11, 98269–98292. [Google Scholar] [CrossRef]
- Chen, Q.; Guo, Z.; Meng, W.; Han, S.; Li, C.; Quek, T.Q.S. A Survey on Resource Management in Joint Communication and Computing-Embedded SAGIN. IEEE Commun. Surv. & Tutor. 2024; Early Access. [Google Scholar] [CrossRef]
- Fan, H.; Yang, Z.; Zhang, X.; Wu, S.; Long, J.; Liu, L. A novel multi-satellite and multi-task scheduling method based on task network graph aggregation. Expert Syst. Appl. 2022, 205, 117565. [Google Scholar] [CrossRef]
- Wang, B.; Feng, T.; Huang, D. A Joint Computation Offloading and Resource Allocation Strategy for LEO Satellite Edge Computing System. In Proceedings of the 2020 IEEE 20th International Conference on Communication Technology (ICCT), Nanning, China, 28–31 October 2020; pp. 649–655. [Google Scholar] [CrossRef]
- Shi, Y.; Xia, Y.; Gao, Y. Joint Gateway Selection and Resource Allocation for Cross-Tier Communication in Space-Air-Ground Integrated IoT Networks. IEEE Access 2021, 9, 4303–4314. [Google Scholar] [CrossRef]
- Wang, C.; Ren, Z.; Cheng, W.; Zhang, H. CDMR: Effective Computing-Dependent Multi-Path Routing Strategies in Satellite and Terrestrial Integrated Networks. IEEE Trans. Netw. Sci. Eng. 2022, 9, 3715–3730. [Google Scholar] [CrossRef]
- Yao, S.; Guan, J.; Yan, Z.; Xu, K. SI-STIN: A Smart Identifier Framework for Space and Terrestrial Integrated Network. IEEE Netw. 2019, 33, 8–14. [Google Scholar] [CrossRef]
- Cai, H.; Yang, X.; Wu, H.; Bu, Z. Freshness-Aware Task Offloading and Resource Scheduling for Satellite Edge Computing. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Q.; Zhang, Y.; Li, X. Game Theory Based Power Allocation Method for Inter-satellite Links in LEO/MEO Two-layered Satellite Networks. In Proceedings of the 2021 IEEE/CIC International Conference on Communications in China (ICCC), Xiamen, China, 28–30 July 2021; pp. 398–403. [Google Scholar] [CrossRef]
- Wei, X.; Fan, L.; Guo, Y.; Han, Z.; Wang, Y. Entanglement From Sky: Optimizing Satellite-Based Entanglement Distribution for Quantum Networks. IEEE/ACM Trans. Netw. 2024, 32, 529–5309. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, L. A Deep Learning Approach for Downlink Sum Rate Maximization in Satellite-Terrestrial Integrated Network. In Proceedings of the 2022 International Symposium on Networks, Computers and Communications (ISNCC), Shenzhen, China, 19–22 July 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Song, Y.; Wei, L.; Yang, Q.; Wu, J.; Xing, L.; Chen, Y. RL-GA: A Reinforcement Learning-based Genetic Algorithm for Electromagnetic Detection Satellite Scheduling Problem. Swarm Evol. Comput. 2023, 77, 101236. [Google Scholar] [CrossRef]
- Du, Y.; Wang, T.; Xin, B.; Wang, L.; Chen, Y.; Xing, L. A Data-Driven Parallel Scheduling Approach for Multiple Agile Earth Observation Satellites. IEEE Trans. Evol. Comput. 2020, 24, 679–693. [Google Scholar] [CrossRef]
- Meng, H.; Li, C.; Lu, W.; Dong, Y.; Zhao, Z.; Wu, B. Multi-satellite resource scheduling based on deep neural network. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Meng, Q.Q.; Li, X.; Shao, L.; Zhao, S. An onboard periodic rescheduling algorithm for satellite observation scheduling problem with common dynamic tasks. Adv. Space Res. 2024, 73, 5242–5253. [Google Scholar] [CrossRef]
- Liu, J.; Xing, L.; Wang, L.; Du, Y.; Yan, J.; Chen, Y. A data-driven parallel adaptive large neighborhood search algorithm for a large-scale inter-satellite link scheduling problem. Swarm Evol. Comput. 2022, 74, 101124. [Google Scholar] [CrossRef]
- Boulila, W.; Farah, I.; Ettabaa, K.S.; Solaiman, B.; Ghézala, H.B. A data mining based approach to predict spatiotemporal changes in satellite images. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 386–395. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Z.; Han, G.; Shen, B. Satellite-Air-Terrestrial Cloud Edge Collaborative Networks: Architecture, Multi-Node Task Processing and Computation. Intell. Autom. Soft Comput. 2023, 37. [Google Scholar] [CrossRef]
- Jia, M.; Zhang, L.; Wu, J.; Meng, S.; Guo, Q. Collaborative Satellite-Terrestrial Edge Computing Network for Everyone-Centric Customized Services. IEEE Netw. 2023, 37, 197–205. [Google Scholar] [CrossRef]
- Sun, J.; Chen, X.; Li, Z.; Wang, J.; Chen, Y. Joint Optimization of Multiple Resources for Distributed Service Deployment in Satellite Edge Computing Networks. IEEE Internet Things J. 2024, 12, 2359–2372. [Google Scholar] [CrossRef]
- Kai, C.; Zhou, H.; Yi, Y.; Huang, W. Collaborative Cloud-Edge-End Task Offloading in Mobile-Edge Computing Networks with Limited Communication Capability. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 624–634. [Google Scholar] [CrossRef]
- Shuai, J.; Cui, H.; He, Y.; Guizani, M. Dynamic Satellite Edge Computing Offloading Algorithm Based on Distributed Deep Learning. IEEE Internet Things J. 2024, 11, 27790–27802. [Google Scholar] [CrossRef]
- Deng, X.; Yin, J.; Guan, P.; Xiong, N.N.; Zhang, L.; Mumtaz, S. Intelligent Delay-Aware Partial Computing Task Offloading for Multiuser Industrial Internet of Things Through Edge Computing. IEEE Internet Things J. 2023, 10, 2954–2966. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, W.; Fan, H. Offloading of Atomic Tasks in Satellite Networks: A Fast Adaptive Resource Collaboration Method. Appl. Sci. 2022, 12, 3319. [Google Scholar] [CrossRef]
- Aghapour, Z.; Sharifian, S.; Taheri, H. Task offloading and resource allocation algorithm based on deep reinforcement learning for distributed AI execution tasks in IoT edge computing environments. Comput. Netw. 2023, 223, 109577. [Google Scholar] [CrossRef]
- Liu, H.; Huang, W.; Kim, D.I.; Sun, S.; Zeng, Y.; Feng, S. Towards Efficient Task Offloading with Dependency Guarantees in Vehicular Edge Networks Through Distributed Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2024, 73, 13665–13681. [Google Scholar] [CrossRef]
- Yang, S. A joint optimization scheme for task offloading and resource allocation based on edge computing in 5G communication networks. Comput. Commun. 2020, 160, 759–768. [Google Scholar] [CrossRef]
- Yan, J.; Bi, S.; Zhang, Y.J.; Tao, M. Optimal Task Offloading and Resource Allocation in Mobile-Edge Computing with Inter-User Task Dependency. IEEE Trans. Wirel. Commun. 2020, 19, 235–250. [Google Scholar] [CrossRef]
- Acheampong, A.; Zhang, Y.; Xu, X.; Kumah, D.A. A review of the current task offloading algorithms, strategies and approach in edge computing systems. Comput. Model. Eng. Sci. 2023, 134, 35–88. [Google Scholar] [CrossRef]
- Xie, B.; Cui, H.; Ho, I.W.H.; He, Y.; Guizani, M. Computation Offloading and Resource Allocation in LEO Satellite-Terrestrial Integrated Networks with System State Delay. IEEE Trans. Mob. Comput. 2024; Early Access. [Google Scholar] [CrossRef]
- Zhao, M.; Chen, C.; Liu, L.; Lan, D.; Wan, S. Orbital collaborative learning in 6G space-air-ground integrated networks. Neurocomputing 2022, 497, 94–109. [Google Scholar] [CrossRef]
- Yang, S.; Lee, G.; Huang, L. Deep learning-based dynamic computation task offloading for mobile edge computing networks. Sensors 2022, 22, 4088. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Jiang, D.; Qi, S.; Qiao, C.; Shi, L. A dynamic resource scheduling scheme in edge computing satellite networks. Mob. Netw. Appl. 2021, 26, 597–608. [Google Scholar] [CrossRef]
- Lyu, T.; Xu, Y.; Liu, F.; Xu, H.; Han, Z. Task Offloading and Resource Allocation for Satellite-Terrestrial Integrated Networks. IEEE Internet Things J. 2025, 12, 262–275. [Google Scholar] [CrossRef]
- Chai, F.; Zhang, Q.; Yao, H.; Xin, X.; Gao, R.; Guizani, M. Joint multi-task offloading and resource allocation for mobile edge computing systems in satellite IoT. IEEE Trans. Veh. Technol. 2023, 72, 7783–7795. [Google Scholar] [CrossRef]
- Xiao, Y.; Ning, J.; Xiong, Z.; Qin, H. Batch sequential adaptive designs for global optimization. J. Korean Stat. Soc. 2022, 51, 780–802. [Google Scholar] [CrossRef]
- Kaiqiao Yang, K.M.; Nomura, H. Parameters identification of chaotic systems by quantum-behaved particle swarm optimization. Int. J. Comput. Math. 2009, 86, 2225–2235. [Google Scholar] [CrossRef]
- Noman, N.; Iba, H. Accelerating Differential Evolution Using an Adaptive Local Search. IEEE Trans. Evol. Comput. 2008, 12, 107–125. [Google Scholar] [CrossRef]
- Li, J.; Liu, R.; Wang, R. Handling dynamic capacitated vehicle routing problems based on adaptive genetic algorithm with elastic strategy. Swarm Evol. Comput. 2024, 86, 101529. [Google Scholar] [CrossRef]
- Gao, Z.; Koppel, A.; Ribeiro, A. Balancing Rates and Variance via Adaptive Batch-Size for Stochastic Optimization Problems. IEEE Trans. Signal Process. 2022, 70, 3693–3708. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).