Distributed Observer-Based Adaptive Formation-Containment Tracking for Multi-Agent Systems on Directed Graphs

Abstract

This article investigates the issue of observer-based adaptive time-varying formation-containment tracking (TVFCT) for multi-agent systems (MASs) with bounded unknown input in directed graphs. By applying estimated statuses of neighboring agents, two observer-based adaptive TVFCT control algorithms are deployed for MASs with multiple tracking leaders and one tracking leader, respectively. Notably, the proposed control algorithms remain independent and do not rely on the comprehensive global information of the entire communication network. Furthermore, the algebraic Riccati inequalities and the Lyapunov theorem provide the bases for assessing the achievement of TVFCT in MASs within directed graphs. Lastly, simulation results are provided to validate the theoretical conclusions.

1. Introduction

Over the preceding two decades, the topic of coordinated control strategies has attracted widespread attention from scholars in such various fields as mathematics, engineering, and science [1,2,3]. This research topic finds applications in many fields, for instance collaborative sensor networks [4], distributed optimization [5], and spacecraft formation [6], among others. Presently, there are many academic works dealing with coordination control problems of multi-agent systems (MASs), including consensus control [7,8], formation control [9,10], and containment control [11,12], among others.

Formation control is one of the most vital issues within the subject of cooperative control, and there exist a number of correlation results that have seen discussion [13,14,15,16,17]. A dynamic protocol was developed in [13] which reduces the communication consumption while solving the time-varying formation tracking control (TVFTC) problem. To address the formation tracking challenge in nonlinear multi-agent systems (MASs) subject to disturbances, a distributed control approach incorporating obstacle avoidance was introduced in [14]. The stability of the considered system was then demonstrated using Lyapunov stability theory. To tackle the TVFTC problem for second-order MASs, a distributed predictive method was devised in [15]. The problem of TVFTC for second-order MASs with external disturbances was analyzed in [16], and the effect of perturbation compensation on the formation center function was considered as well, while [17] suggested a novel fixed-time control algorithm and focused on the TVFTC problem with contact-uncertain nonlinear MASs.

Furthermore, as agents form the desired formation, it is natural for them to join or leave the group, leading to alterations in the associated Laplacian matrix. At this stage, developing more resilient and dependable control algorithms to guarantee the achievement of the intended formation is a pivotal research issue. Adaptive control strategies can be taken into account to allow for the acquisition of control parameters, thereby enhancing the stability of the protocol. In [18], a protocol incorporating adaptive formation was devised to ensure the achievement of collision avoidance while minimizing the state error. Additionally, Ref. [19] introduced an adaptive optimal control protocol to solve the optimal TVFTC problem in the presence of unknown leader control and external disturbances. The problem of formation control under multiple factors of noise influence was addressed in [20] by introducing a distributed adaptive TVFTC. In [21], a novel adaptive observer was introduced to evaluate the state, which then was used to supply conditions to secure fixed-time convergence of the tracking error by analyzing the Lyapunov stability. However, the adaptive control protocols mentioned above are all appropriate only for the case of undirected communications topologies. To establish the TVFTC with coupled gain in a directed graph is challenging, as the Laplace matrix which matches the structure of the directed graph is often asymmetric.

In light of the foregoing discussion regarding previous formation control works, the research on containment control provokes further consideration. Consequently, a more interesting and complicated topic is introduced for exploration, namely, the analysis of time-varying formation-containment tracking (TVFCT) control, in which formation leaders (FLs) need to achieve the desired formation shape while followers need to converge into the convex hull enclosed by the FLs. In [22], the authors devised a category of algorithms for determining the parameters of control algorithms that provides for the implementation of the group TVFCT problem via the Laplacian matrix properties. With the aim of improved availability of communication resources, a class of time-triggered mechanisms was deployed in [23] to enable the handling of the TVFCT problem under dynamic event-triggered schemes. The control algorithm with edge-state observers was suggested in [24], and the sufficient requirements for the realization of TVFCT were formulated on the basis of Lyapunov’s theorem. Despite the results of the above mentioned studies [22,23,24] dedicated to the study of formation containment problems, all of them focused on one or no target/tracking leader scenarios. However, in numerous practical industrial operations the formation shape for MASs varies with the situation, and is not applicable to cooperative transport or interaction problems for a single target; therefore, further focus on TVFCT problems with multiple tracking leaders has meaningful research value.

Inspired by the aforementioned contributions, this article addresses the observer-based adaptive TVFCT issue for MASs with tracking leaders and directed graphs. The contributions of this research are summarized as follows.

(i)

In comparison with the formation topics in [13,14,15,16,17], which focused on time-varying formation control, this paper analyzes the more complex case, namely, the problem of TVFCT with bounded unknown input.

(ii)

In contrast to the adaptive control algorithm developed in [18,19,20] under undirected graphs, in this paper we design the observer-based adaptive TVFCT control algorithm in the topology of directed communication, considering the case of directed communication topology and the fact that the state of most agents in real life is unknown.

(iii)

Unlike [22,23,24], which only considered the case of one tracking leader, we separately discuss the TVFCT problem for cases with multiple tracking leaders and with only one tracking leader.

2. Preliminaries

2.1. Graph Theory

Consider a communication network comprising N FLs, L followers and M tracking leaders, where $N,L,M$ are positive integers. This network is represented by a digraph $\mathcal{G}=\{\mathcal{V},\mathcal{E},\mathcal{A}\}$ which delineates the relationships among the $N+L+M$ agents. Here, $\mathcal{V}=\left\{1,2,\dots ,M+N+L\right\}$ denotes the set of nodes, $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ represents the set of edges, and $\mathcal{A}=\left[w_{ij}\right]\in {\mathcal{R}}^{\left(M+N+L\right)\times \left(M+N+L\right)}$ stands for the adjacency matrix. An edge $\left(i,j\right)\in \mathcal{E}$ exists if the i-th agent can acquire information from the j-th one, in which case $w_{ij}>0$; otherwise, $w_{ij}=0$. The Laplacian matrix $\mathcal{L}$ associated with the graph $\mathcal{G}$ can be partitioned as follows:

$$\mathcal{L}=\left[\begin{array}{ccc}{0}_{M\times M}& 0_{M\times N}& 0_{M\times L}\\ L_{N\times M}^T& L_{N\times N}^F& 0_{N\times L}\\ 0_{L\times M}& L_C& L_{L\times L}^f\end{array}\right]$$

where $L_C\in {\mathcal{R}}^{L\times N}$.

2.2. Description of the Problem

The dynamics of each follower and formation leader are defined as

$$\left\{\begin{array}{c}{\dot{x}}_i\left(t\right)=A{x}_i\left(t\right)+B{u}_i\left(t\right),\hfill \\ y_i\left(t\right)=C{x}_i\left(t\right),i\in \mathcal{F}\cup \mathcal{E}=\left\{1,\dots ,N+L\right\},\hfill \end{array}\right.$$

(1)

where $\mathcal{F}=\left\{1,\dots ,N\right\}$, $\mathcal{E}=\left\{N+1,\dots ,N+L\right\}$, $u_i\left(t\right)\in {\mathcal{R}}^p,x_i\left(t\right)\in {\mathcal{R}}^q$ and $y_i\left(t\right)\in {\mathcal{R}}^n$ correspondingly denote the control input, state, and output of the i-th agent.

The closed-loop dynamics of each tracking leader are provided by

$$\left\{\begin{array}{c}{\dot{x}}_k\left(t\right)=A{x}_k\left(t\right)+B{u}_k\left(t\right),\hfill \\ y_k\left(t\right)=C{x}_k\left(t\right),k\in \mathcal{T}=\left\{1+N+L,\dots ,M+N+L\right\},\hfill \end{array}\right.$$

(2)

where $u_k\left(t\right)\in {\mathcal{R}}^p,x_k\left(t\right)\in {\mathcal{R}}^q$ and $y_k\left(t\right)\in {\mathcal{R}}^n$ respectively stand for the control input, state, and output of the k-th tracking leader.

The formation leaders need to achieve the desired formation shape, while the followers need to converge into the convex hull enclosed by the formation leaders. The problems to be solved are described by the two definitions below.

Definition 1.

It is said that dynamic systems (1) and (2) implement time-varying formation tracking (TVFT) if and only if the following equation is respected:

$$\underset{t\to \infty }{lim}\left(x_i\left(t\right)-f_i\left(t\right)-\left(\sum _{k=N+1}^{N+M}{\displaystyle \frac{w_{ik}}{w_{i,N+1}+\dots +w_{i,N+M}}}{x}_{0k}\left(t\right)\right)\right)=0,i\in \mathcal{F}$$

(3)

where $f_i\left(t\right)$ is the formation offset for the i-th agent and $x_{0k}\left(t\right)$ denotes the k-th tracking leader.

Definition 2.

If there exist non-negative constants ${\beta }_{ki}$ satisfying ${\displaystyle \sum _{k=1}^N}{\beta }_{ki}$ $=1$ such that

$$\underset{t\to \infty }{lim}\left(x_i\left(t\right)-\sum _{k=1}^N{\beta }_{ki}{x}_k\left(t\right)\right)=0,i\in \mathcal{E},$$

(4)

 then systems (1) and (2) are said to accomplish containment.

We define a variable ${\delta }_i\left(t\right)$ to indicate the formation tracking local error for the i-th formation leader:

$${\delta }_i\left(t\right)=\sum _{j=1}^N{w}_{ij}\left[x_i\left(t\right)-f_i\left(t\right)-x_j\left(t\right)+f_j\left(t\right)\right]+\sum _{k=N+1}^{N+M}{w}_{ik}\left(x_i\left(t\right)-f_i\left(t\right)-x_k\left(t\right)\right).$$

(5)

As affected by the FLs and their neighboring followers, the expression for the local error of the containment can be expanded and written in the following form:

$${\xi }_i\left(t\right)=\sum _{j=1}^{N+L}{w}_{ij}\left(x_i\left(t\right)-x_j\left(t\right)\right).$$

(6)

To comply with the calculations, the corresponding sets are defined as $x_{\mathcal{T}}\left(t\right)={\left[x_{1+N+L}^T\left(t\right),\dots ,x_{M+N+L}^T\left(t\right)\right]}^T$ for the tracking leaders, $x_{\mathcal{F}}\left(t\right)={\left[x_1^T\left(t\right),\dots ,x_N^T\left(t\right)\right]}^T$ for the FLs, and $x_f\left(t\right)={\left[x_{N+1}^T\left(t\right),\dots ,x_{N+L}^T\left(t\right)\right]}^T$ for the followers. This allows us to analyze the compact form indicated below:

$$\delta \left(t\right)=\left(L^F\otimes I_q\right)\left(x_{\mathcal{F}}\left(t\right)-f_{\mathcal{F}}\left(t\right)\right)+\left(L^T\otimes I_q\right)x_{\mathcal{T}}\left(t\right),$$

(7)

$$\xi \left(t\right)=\left(L^f\otimes I_q\right)x_f\left(t\right)+\left(L_C\otimes I_q\right)x_{\mathcal{F}}\left(t\right),$$

(8)

where $I_q\in R^{q\times q}$ is the identity matrix, $f_{\mathcal{F}}\left(t\right)={\left[f_1^T\left(t\right),\dots ,f_N^T\left(t\right)\right]}^T$, $\delta \left(t\right)={\left[{\delta }_1^T\left(t\right),\dots ,{\delta }_N^T\left(t\right)\right]}^T$, and $\xi \left(t\right)={\left[{\xi }_1^T\left(t\right),\dots ,{\xi }_L^T\left(t\right)\right]}^T$. In order to implement the TVFCT with unknown control inputs for multiple tracking leaders, the following control algorithms are presented:

$$\left\{\begin{array}{c}{u}_i\left(t\right)=\left({\eta }_i\left(t\right)+{\omega }_i\left(t\right)\right)K_u{\delta }_i\left(t\right)+r_i\left(t\right)-{\rho }_{1}g\left({\delta }_i\left(t\right)\right),\hfill \\ {\dot{\eta }}_i\left(t\right)={\delta }_i^T\left(t\right)\widehat{\mathsf{\Gamma }}{\delta }_i\left(t\right),i\in \mathcal{F},\hfill \end{array}\right.$$

(9)

$$\left\{\begin{array}{c}{u}_i\left(t\right)=\left({\sigma }_i\left(t\right)+{\upsilon }_i\left(t\right)\right)K_u{\xi }_i\left(t\right)-{\rho }_{2}g\left({\xi }_i\left(t\right)\right),\hfill \\ {\dot{\sigma }}_i\left(t\right)={\xi }_i^T\left(t\right)\widehat{\mathsf{\Gamma }}{\xi }_i\left(t\right),i\in \mathcal{E},\hfill \end{array}\right.$$

(10)

where ${\omega }_i\left(t\right)$ and ${\upsilon }_i\left(t\right)$ stand for the time-varying coupling gain with ${\omega }_i\left(t\right)>0$ and ${\upsilon }_i\left(t\right)>0$, ${\rho }_1$ and ${\rho }_2$ are the constants of the subsequent design, $\widehat{\mathsf{\Gamma }}\in R^{q\times q}$ is a positive matrix, and $r_i\left(t\right)\in R^p$ is introduced to compensate the input signal. The nonlinear function $g\left(·\right)$ is defined as

$$g\left(\chi \left(t\right)\right)=\left\{\begin{array}{c}{\displaystyle \frac{B^{T}P\chi \left(t\right)}{∥B^{T}P\chi \left(t\right)∥}},∥B^{T}P\chi \left(t\right)∥\ne 0\hfill \\ 0,∥B^{T}P\chi \left(t\right)∥=0,\hfill \end{array}\right.$$

(11)

where ‖‖ is the Euclidean norm. We define $\eta \stackrel{\mathsf{\Delta }}{=}diag\left\{{\eta }_1,{\eta }_2,\dots ,{\eta }_N\right\},$ $\omega \stackrel{\mathsf{\Delta }}{=}diag\left\{{\omega }_1,{\omega }_2,\dots ,{\omega }_N\right\},$ $r\left(t\right)={\left[r_1^T,r_2^T,\dots ,r_N^T\right]}^T,$ $\sigma \stackrel{\mathsf{\Delta }}{=}diag\left\{{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_L\right\},$ $G\left(\delta \left(t\right)\right)={\left[g^T\left({\delta }_1\left(t\right)\right),\dots ,g^T\left({\delta }_N\left(t\right)\right)\right]}^T$, $G\left(\xi \left(t\right)\right)=\left[g^T\left({\xi }_1\left(t\right)\right),\dots ,\right.$ ${\left.g^T\left({\xi }_L\left(t\right)\right)\right]}^T$; further, $\upsilon \stackrel{\mathsf{\Delta }}{=}diag\left\{{\upsilon }_1,{\upsilon }_2,\dots ,{\upsilon }_L\right\}$ represent some shorthand. Substituting Equations (9) and (10) into (1) and (2), respectively, the compact form of the time derivative is generated as follows:

$$\begin{array}{cc}\hfill {\dot{x}}_{\mathcal{F}}\left(t\right)=& \left(I_N\otimes A\right)x_{\mathcal{F}}\left(t\right)+\left(\left(\eta +\omega \right)\otimes B{K}_u\right)\delta \left(t\right)\hfill \\ \hfill & +\left(I_N\otimes B\right)r\left(t\right)-{\rho }_1\left(I_N\otimes B\right)G\left(\delta \left(t\right)\right)\hfill \\ \hfill =& \left(\left(I_N\otimes A\right)+\left(L^F\left(\eta +\omega \right)\otimes B{K}_u\right)\right)x_{\mathcal{F}}\left(t\right)\hfill \\ \hfill & -\left(L^F\left(\eta +\omega \right)\otimes B{K}_u\right)f_{\mathcal{F}}\left(t\right)\hfill \\ \hfill & +\left(L^T\left(\eta +\omega \right)\otimes B{K}_u\right)x_{\mathcal{T}}\left(t\right)\hfill \\ \hfill & +\left(I_N\otimes B\right)r\left(t\right)-{\rho }_1\left(I_N\otimes B\right)G\left(\delta \left(t\right)\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\dot{x}}_f\left(t\right)=& \left(I_L\otimes A\right)x_f\left(t\right)+\left(\left(\sigma +\upsilon \right)\otimes B{K}_u\right)\xi \left(t\right)-{\rho }_2\left(I_L\otimes B\right)G\left(\xi \left(t\right)\right)\hfill \\ \hfill =& \left(\left(I_L\otimes A\right)+\left(L^f\left(\sigma +\upsilon \right)\otimes B{K}_u\right)\right)x_f\left(t\right)+\left(L_C\left(\sigma +\upsilon \right)\otimes B{K}_u\right)x_{\mathcal{F}}\left(t\right)\hfill \\ \hfill & - {\rho }_2\left(I_L\otimes B\right)G\left(\xi \left(t\right)\right).\hfill \end{array}$$

Defining ${\theta }_i=x_i\left(t\right)-f_i\left(t\right),i\in \mathcal{F}$ and correspondingly substituting the above control algorithms (9) and (10) into the closed-loop systems in (1) and (2), the following compact formal formulas are yielded:

$$\begin{array}{cc}\hfill \dot{\theta }\left(t\right)=& \left(I_N\otimes A\right)\theta \left(t\right)+\left(I_N\otimes A\right)f\left(t\right)+\left(\left(\eta +\omega \right)\otimes B{K}_u\right)\delta \left(t\right)\hfill \\ \hfill & -\left(I_N\otimes I_q\right)\dot{f}\left(t\right)-{\rho }_1\left(I_N\otimes B\right)G\left(\delta \left(t\right)\right)+\left(I_N\otimes B\right)r\left(t\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill \dot{\delta }\left(t\right)=& \left(L^F\otimes I_q\right){\dot{\theta }}_{\mathcal{F}}\left(t\right)+\left(L^T\otimes I_q\right){\dot{x}}_{\mathcal{T}}\left(t\right)\hfill \\ \hfill =& \left(L^F\otimes A\right){\theta }_{\mathcal{F}}\left(t\right)+\left(L^F\otimes A\right)f_{\mathcal{F}}\left(t\right)\hfill \\ \hfill & +\left(L^F\left(\eta +\omega \right)\otimes B{K}_u\right)\delta \left(t\right)-{\rho }_1\left(L^F\otimes B\right)G\left(\delta \left(t\right)\right)\hfill \\ \hfill & +\left(L^F\otimes B\right)r\left(t\right)+\left(L^T\otimes A\right)x_{\mathcal{T}}\left(t\right)+\left(L^T\otimes B\right)S\left(t\right)\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \dot{\xi }\left(t\right)=& \left(L^f\otimes I_q\right){\dot{x}}_f\left(t\right)+\left(L_C\otimes I_q\right){\dot{x}}_f\left(t\right)\hfill \\ \hfill =& \left(L^f\otimes A\right)x_f\left(t\right)-{\rho }_2\left(L^f\otimes B\right)G\left(\delta \left(t\right)\right)+\left(L^f\left(\sigma \left(t\right)+\upsilon \left(t\right)\right)\otimes B{K}_w\right)\xi \left(t\right)\hfill \\ \hfill & +\left(L_C\otimes A\right)x_{\mathcal{F}}\left(t\right)+\left(L_C\left(\eta +\omega \right)\otimes B{K}_u\right)\delta \left(t\right)-{\rho }_1\left(L_C\otimes B\right)G\left(\delta \left(t\right)\right)+\left(L_C\otimes B\right)S\left(t\right)\hfill \\ \hfill =& \left[\left(I_L\otimes A\right)+L^f\left(\sigma \left(t\right)+\upsilon \left(t\right)\right)\otimes B{K}_w\right]\xi \left(t\right)+\left(L_C\left(\eta +\omega \right)\otimes B{K}_u\right)\delta \left(t\right)+\left(L_C\otimes B\right)S\left(t\right)\hfill \\ \hfill & -{\rho }_2\left(L^f\otimes B\right)G\left(\delta \left(t\right)\right)-{\rho }_1\left(L_C\otimes B\right)G\left(\delta \left(t\right)\right),\hfill \end{array}$$

(13)

where $S\left(t\right)={\left[u_1^T\left(t\right),\dots ,u_M^T\left(t\right)\right]}^T\in {\mathcal{R}}^{Mp}.$

The following assumptions and lemmas are provided for the demonstration in the next section.

Assumption 1.

There is at least one formation leader for every follower, along with a directed path.

Assumption 2.

The directed graph ${\mathcal{G}}^L$ among the tracking leader and formation leader has a spanning tree with the tracking leader as the root node.

Assumption 3.

The pair $\left(A,B\right)$ is stabilizable, and $\left(A,C\right)$ is observable.

Lemma 1

([25]). With regard to Assumptions 1∼2, all eigenvalues of $L^F$ and $L^f$ process positive real parts.

Lemma 2

([26]). According to Assumption 1, each element of $-L^f{L}_C$ is non-negative; additionally, the sum of each row in $-L^f{L}_C$ equals one.

Lemma 3

([27]). Under on Assumption 2, for $-{\left(L^F\right)}^{-1}{L}^T$, each row is equal to

$$1_N\otimes \left[b_{N+1},b_{N+2},\dots ,b_{N+M}\right]\phantom{1_N\otimes \left[b_{N+1},b_{N+2},\dots ,b_{N+M}\right]\sum _{k=N+1}^{N+M}{b}_k}/\sum _{k=N+1}^{N+M}{b}_k,$$

where $1_N$ is the N-dimensional vector with all elements being 1, $b_k=w_{ik}.$

Lemma 4

([28]). There are real diagonal matrices ${\mathsf{\Delta }}_F$, ${\mathsf{\Delta }}_L$, Θ, and Ξ that may be employed to demonstrate ${\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F+{\left(L^F\right)}^T{\mathsf{\Delta }}_F\mathsf{\Theta }>0$ and ${\mathsf{\Delta }}_f\mathsf{\Xi }{L}^f+{\left(L^f\right)}^T{\mathsf{\Delta }}_f\mathsf{\Xi }>0$.

Lemma 5

([29]). If c and d are non-negative real numbers and both m and n are positive real numbers that result in ${\displaystyle \frac{1}{m}}+{\displaystyle \frac{1}{n}}=1$, then $cd\le {\displaystyle \frac{c^m}{m}}+{\displaystyle \frac{d^n}{n}}$ holds if and only if $c^m=d^n$.

Lemma 6

([30]). For any $k,y\in {\mathcal{R}}^q$ and $M,Z\in {\mathcal{R}}^{q\times q}$, the following inequality holds:

$$2k^{T}MZy\le k^{T}Z{Z}^{T}k+y^{T}M{M}^{T}y.$$

3. Main Results

This section addresses the TVFCT issue with directed graphs and proposes two observer-based adaptive TVFCT control algorithms for the cases with multiple tracking leaders and one tracking leader.

3.1. The Case with Multiple Tracking Leaders

As the state of most agents in the real environment is inaccessible to measure, a novel distributed observer that estimates the state of each agent is introduced, as illustrated below:

$$\left\{\begin{array}{c}{\dot{\widehat{x}}}_i\left(t\right)=A{\widehat{x}}_i\left(t\right)-F\left(y_i\left(t\right)-C{\widehat{x}}_i\left(t\right)\right)+B{u}_i\left(t\right),i\in \mathcal{F}\cup \mathcal{E}\hfill \\ {\dot{\widehat{x}}}_k\left(t\right)=A{\widehat{x}}_k\left(t\right)-F\left(y_k\left(t\right)-C{\widehat{x}}_k\left(t\right)\right)+B{u}_k\left(t\right),k\in \mathcal{T}.\hfill \end{array}\right.$$

(14)

The TVFTC law with observer-based adaptive designed for each formation leader is shown below:

$$\left\{\begin{array}{c}{u}_i\left(t\right)=\left({\widehat{\eta }}_i\left(t\right)+{\omega }_i\left(t\right)\right)K_u{\widehat{\delta }}_i\left(t\right)+r_i\left(t\right)-{\rho }_{1}g\left({\widehat{\delta }}_i\left(t\right)\right),\hfill \\ {\dot{\widehat{\eta }}}_i\left(t\right)={\widehat{\delta }}_i^T\left(t\right)\widehat{\mathsf{\Gamma }}{\widehat{\delta }}_i\left(t\right),\hfill \\ {\widehat{\delta }}_i\left(0\right)={\widehat{\delta }}_{i0},i\in \mathcal{F}\hfill \end{array}\right.$$

(15)

where ${\widehat{\delta }}_i\left(t\right)={\displaystyle \sum _{j=1}^N}{w}_{ij}\left[{\widehat{x}}_i\left(t\right)-f_i\left(t\right)-{\widehat{x}}_j\left(t\right)+f_j\left(t\right)\right]+{\displaystyle \sum _{k=N+1}^{N+M}}{w}_{ik}\left({\widehat{x}}_i\left(t\right)-f_i\left(t\right)-{\widehat{x}}_k\left(t\right)\right)$ with ${\widehat{x}}_i\left(t\right)$ and ${\widehat{x}}_k\left(t\right)$, which are respectively employed to estimate the state of each formation leader and each tracking leader. The time-varying coupling gain is expressed by the ${\widehat{\eta }}_i\left(t\right)$ symbol.

Assumption 4.

The tracking leaders’ control inputs are bounded, i.e., ${∥u_k\left(t\right)∥}_{\infty }\le \tau$, where τ is a positive constant.

For each follower, the adaptive observer-based TVFCT control law is devised with

$$\left\{\begin{array}{c}{u}_i\left(t\right)=\left({\widehat{\sigma }}_i\left(t\right)+{\upsilon }_i\left(t\right)\right)K_w{\widehat{\xi }}_i\left(t\right)-{\rho }_{2}g\left({\widehat{\xi }}_i\left(t\right)\right),\hfill \\ {\dot{\widehat{\sigma }}}_i\left(t\right)={\widehat{\xi }}_i^T\left(t\right)\widehat{\mathsf{\Gamma }}{\widehat{\xi }}_i\left(t\right),\hfill \\ {\widehat{\sigma }}_i\left(0\right)={\widehat{\sigma }}_{i0},i\in \mathcal{E},\hfill \end{array}\right.$$

(16)

where ${\widehat{\xi }}_i\left(t\right)={\displaystyle \sum _{j=1}^{N+L}}{w}_{ij}\left({\widehat{x}}_i\left(t\right)-{\widehat{x}}_j\left(t\right)\right).$

Let ${\psi }_i\left(t\right)={\delta }_i\left(t\right)-{\widehat{\delta }}_i\left(t\right)$; then, the following compact form arises:

$$\begin{array}{c}\psi \left(t\right)=\delta \left(t\right)-\widehat{\delta }\left(t\right)\hfill \\ =\left(L^F\otimes I_q\right)\left(x_{\mathcal{F}}\left(t\right)-{\widehat{x}}_{\mathcal{F}}\left(t\right)\right)+\left(L^T\otimes I_q\right)\left(x_{\mathcal{T}}\left(t\right)-{\widehat{x}}_{\mathcal{T}}\left(t\right)\right)\hfill \end{array}$$

(17)

where $I_q\in R^{q\times q}$ is the identity matrix.

Based on Equations (14)–(17), the time derivative of $\widehat{\delta }\left(t\right)$ can be derived as follows:

$$\begin{array}{cc}\hfill \dot{\widehat{\delta }}\left(t\right)=& \left(I_N\otimes A\right)\widehat{\delta }\left(t\right)+\left(L^F\otimes A\right)f\left(t\right)-\left(I_N\otimes FC\right)\psi \left(t\right)-\left(L^F\otimes I_q\right)\dot{f}\left(t\right)\left(L^F\left(\widehat{\eta }\left(t\right)\right.\right.\hfill \\ \hfill & +\left.\left.\omega \left(t\right)\right)\otimes B{K}_u\right)\widehat{\delta }\left(t\right)+\left(L^F\otimes B\right)r\left(t\right)+\left(L^T\otimes B\right)S\left(t\right)-{\rho }_1\left(L^F\otimes B\right)G\left(\widehat{\delta }\left(t\right)\right)\hfill \\ \hfill =& \left[\left(I_N\otimes A\right)+L^F\left(\widehat{\eta }\left(t\right)+\omega \left(t\right)\right)\otimes B{K}_u\right]\widehat{\delta }\left(t\right)-\left(I_N\otimes FC\right)\psi \left(t\right)+\left(L^F\otimes A\right)f\left(t\right)\hfill \\ \hfill & +\left(L^F\otimes B\right)r\left(t\right)+\left(L^T\otimes B\right)S\left(t\right)-\left(L^F\otimes I_q\right)\dot{f}\left(t\right)-{\rho }_1\left(L^F\otimes B\right)G\left(\widehat{\delta }\left(t\right)\right),\hfill \end{array}$$

(18)

$$\begin{array}{c}\dot{\psi }\left(t\right)=\dot{\delta }\left(t\right)-\dot{\widehat{\delta }}\left(t\right)\hfill \\ =\left(I_N\otimes \left(A+FC\right)\right)\psi \left(t\right),\hfill \end{array}$$

(19)

where $G\left(\widehat{\delta }\left(t\right)\right)={\left[g^T\left({\widehat{\delta }}_1\left(t\right)\right),g^T\left({\widehat{\delta }}_2\left(t\right)\right)\dots ,g^T\left({\widehat{\delta }}_N\left(t\right)\right)\right]}^T.$

Theorem 1.

Under Assumptions 1–4, the systems in (1) and (2) with unknown inputs of multiple tracking leaders can achieve observer-based adaptive TVFCT under directed graphs by employing the nonlinear and fully distributed control protocols in (15) and (16) with parameters $K_u=-B^{T}H,$ $\mathsf{\Gamma }=HB{B}^{T}H$, ${\omega }_i\left(t\right)={\widehat{\delta }}_i^T\left(t\right)H{\widehat{\delta }}_i\left(t\right)$, and ${\upsilon }_i\left(t\right)={\widehat{\xi }}_i^T\left(t\right)H{\widehat{\xi }}_i\left(t\right)$ for the given design if the viability requirements listed below are met:

(i) 

The compensation for the input signal $r_i\left(t\right)$ is provided by the formula

$$\underset{t\to \infty }{lim}\left(A{f}_i\left(t\right)-{\dot{f}}_i\left(t\right)+B{r}_i\left(t\right)\right)=0,i=1,\dots ,N.$$

(20)

(ii) 

The unequal relationship is fulfilled by selecting τ and κ so as to ensure that

$$\begin{array}{c}{\rho }_1\ge \tau ,\hfill \\ \kappa \ge \sout{\lambda }+\epsilon ,\hfill \end{array}$$

where $\sout{\lambda }\stackrel{\mathsf{\Delta }}{=}max\left\{∥r_i\left(t\right)∥\right\},i\in \mathcal{F}$, and ${\rho }_1=\tau +\epsilon$, with ε being a given arbitrarily small positive number.

(iii) 

For any given matrices $H,Q>0,$ the matrices H and Q are solutions to the algebraic Riccati inequalities listed below:

$$HA+A^{T}H-2HB{B}^{T}H+I_q\le 0,$$

(21)

$$Q\left(A+FC\right)+{\left(A+FC\right)}^{T}Q+I_q\le 0.$$

(22)

Proof of Theorem 1.

In accordance with the aforementioned preparations, the Lyapunov function is taken into regard as follows: $V_1\left(t\right)=V_{ob}\left(t\right)+V_{e1}\left(t\right)$, with

$$V_{ob}\left(t\right)=\sum _{i=1}^N{\displaystyle \frac{1}{2}}{\phi }_i\left(2{\widehat{\eta }}_i+{\omega }_i\right){\omega }_i+{\displaystyle \frac{1}{2}}\sum _{i=1}^N{\phi }_i{\left({\widehat{\eta }}_i-\alpha \right)}^2$$

(23)

and

$$V_{e1}\left(t\right)={\iota }_1{\psi }^T\left(t\right)\left(I_N\otimes Q\right)\psi \left(t\right),$$

(24)

where ${\phi }_i>0$ is a positive number, ${\mathsf{\Delta }}_F\mathsf{\Theta }=diag\left\{{\phi }_1,{\phi }_2,\dots ,{\phi }_N\right\}$ is a postive definite matrix such that ${\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F+{\left(L^F\right)}^T{\mathsf{\Delta }}_F\mathsf{\Theta }>0$, $\alpha$ is a positive constant of a subsequent design, and ${\iota }_1$ is the normal number discussed below. The time derivative of $V_{ob}\left(t\right)$ defined in (23) along the trajectory of (18) is derived as follows:

$$\begin{array}{cc}\hfill {\dot{V}}_{ob}\left(t\right)=& \sum _{i=1}^N\left({\phi }_i\left({\widehat{\eta }}_i+{\displaystyle \frac{1}{2}}{\dot{\omega }}_i\right){\omega }_i\right)+\sum _{i=1}^N{\displaystyle \frac{1}{2}}{\phi }_i\left(2{\widehat{\eta }}_i+{\omega }_i\right){\dot{\omega }}_i+\sum _{i=1}^N{\phi }_i\left({\widehat{\eta }}_i-\alpha \right){\dot{\widehat{\eta }}}_i\hfill \\ \hfill =& 2\sum _{i=1}^N{\phi }_i\left({\widehat{\eta }}_i+{\omega }_i\right){\widehat{\delta }}_i^T\left(t\right)P{\dot{\widehat{\delta }}}_i\left(t\right)+\sum _{i=1}^N{\phi }_i\left({\widehat{\eta }}_i+{\omega }_i-\alpha \right){\dot{\widehat{\eta }}}_i.\hfill \end{array}$$

(25)

Then, (15) and (18) yield the following equations:

$$\begin{array}{cc}\hfill & \sum _{i=1}^N{\phi }_i\left({\widehat{\eta }}_i+{\omega }_i-\alpha \right){\dot{\widehat{\eta }}}_i\left(t\right)\hfill \\ \hfill =& {\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega -\alpha I\right){\mathsf{\Delta }}_F\mathsf{\Theta }\otimes \mathsf{\Gamma }\right]\widehat{\delta }\left(t\right),\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & \sum _{i=1}^{N}2{\phi }_i\left({\widehat{\eta }}_i+{\omega }_i\right){\widehat{\delta }}_i^T\left(t\right)H^{-1}{\dot{\widehat{\delta }}}_i\left(t\right)\hfill \\ \hfill =& \sum _{i=1}^{N}2{\widehat{\delta }}_i^T\left(t\right)\left[{\mathsf{\Delta }}_F\mathsf{\Theta }\left({\widehat{\eta }}_i+{\omega }_i\right)\otimes H\right]{\dot{\widehat{\delta }}}_i\left(t\right)\hfill \\ \hfill =& {\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }\otimes \left(HA+A^{T}H\right)+{\left(\widehat{\eta }+\omega \right)}^2\left({\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F+{\left(L^F\right)}^T{\mathsf{\Delta }}_F\mathsf{\Theta }\right)\otimes HBK\right]\widehat{\delta }\left(t\right)\hfill \\ \hfill & +2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes HA\right]f_{\mathcal{F}}\left(t\right)-2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes H\right]{\dot{f}}_{\mathcal{F}}\left(t\right)\hfill \\ \hfill & -2{\rho }_1{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes HB\right]G\left(\widehat{\delta }\left(t\right)\right)+2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes HB\right]r\left(t\right)\hfill \\ \hfill & -2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }\otimes HFC\right]\psi \left(t\right)+2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^T\otimes HB\right]S\left(t\right).\hfill \end{array}$$

(27)

By applying the set of nonlinear function from (11), we obtain

$$\begin{array}{cc}\hfill & -2{\rho }_1{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes HB\right]G\left(\widehat{\delta }\left(t\right)\right)\hfill \\ \hfill =& -2{\rho }_1\sum _{i=1}^N\left({\widehat{\eta }}_i+{\omega }_i\right){\phi }_i{\widehat{\delta }}_i^T\left(t\right)HB\left[\sum _{j=1}^N{w}_{ij}\left(g\left({\widehat{\delta }}_i\left(t\right)-{\widehat{\delta }}_j\left(t\right)\right)\right)+\sum _{k=1}^M{w}_{ik}g\left({\widehat{\delta }}_i\left(t\right)\right)\right]\hfill \\ \hfill \le & -2\left(\tau +\epsilon \right)\sum _{i=1}^N\left({\widehat{\eta }}_i+{\omega }_i\right){\phi }_i\sum _{k=1}^M{w}_{ik}∥B^{T}H{\widehat{\delta }}_i\left(t\right)∥,\hfill \end{array}$$

(28)

where ${\rho }_1$ is designed as ${\rho }_1=\tau +\epsilon$, with $\epsilon$ selected to be an arbitrarily small positive constant. As a result of Assumption 4, it follows that

$$\begin{array}{cc}\hfill & 2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^T\otimes HB\right]S\left(t\right)\hfill \\ \hfill =& 2\sum _{i=1}^N\left({\widehat{\eta }}_i+{\omega }_i\right){\phi }_i\sum _{k=1}^M{w}_{ik}∥B^{T}H{\widehat{\delta }}_i\left(t\right)∥∥u_k\left(t\right)∥\hfill \\ \hfill \le & 2\tau \sum _{i=1}^N\left({\widehat{\eta }}_i+{\omega }_i\right){\phi }_i\sum _{k=1}^M{w}_{ik}∥B^{T}H{\widehat{\delta }}_i\left(t\right)∥.\hfill \end{array}$$

(29)

Equations (26)–(29) are reorganized and substituted into (26) to arrive at the following:

$$\begin{array}{cc}\hfill {\dot{V}}_{ob}\left(t\right)\le & {\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }\otimes \left(HA+A^{T}H+\mathsf{\Gamma }\right)+{\left(\widehat{\eta }+\omega \right)}^2\left({\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F+{\left(L^F\right)}^T{\mathsf{\Delta }}_F\mathsf{\Theta }\right)\right.\hfill \\ \hfill & \left.\otimes HB{K}_u\right]\widehat{\delta }\left(t\right)\hfill \\ \hfill & +2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes HA\right]f_{\mathcal{F}}\left(t\right)-2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes H\right]{\dot{f}}_{\mathcal{F}}\left(t\right)\hfill \\ \hfill & +2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes HB\right]r\left(t\right)-2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }\otimes HFC\right]\psi \left(t\right)\hfill \\ \hfill & -{\widehat{\delta }}^T\left(t\right)\left[\alpha {\mathsf{\Delta }}_F\mathsf{\Theta }\otimes \mathsf{\Gamma }\right]\widehat{\delta }\left(t\right).\hfill \end{array}$$

(30)

The minimal eigenvalue of ${\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F+{\left(L^F\right)}^T{\mathsf{\Delta }}_F\mathsf{\Theta }>0$ is expressed as ${\lambda }_1^f$. Then, Equation (30) is represented as

$$\begin{array}{cc}\hfill {\dot{V}}_{ob}\left(t\right)\le & {\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }\otimes \left(HA+A^{T}H+\mathsf{\Gamma }\right)-\left({\lambda }_1^f{\left(\widehat{\eta }+\omega \right)}^2+\alpha {\mathsf{\Delta }}_F\mathsf{\Theta }\right)\otimes \mathsf{\Gamma }\right]\widehat{\delta }\left(t\right)\hfill \\ \hfill & +2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes HA\right]f_{\mathcal{F}}\left(t\right)-2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes H\right]{\dot{f}}_{\mathcal{F}}\left(t\right)\hfill \\ \hfill & +2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes HB\right]r\left(t\right)-2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }\otimes HFC\right]\psi \left(t\right).\hfill \end{array}$$

(31)

With respect to Lemma 6, it can be inferred that the following inequality exists:

$$\begin{array}{cc}\hfill & -2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }\otimes HFC\right]\psi \left(t\right)\hfill \\ \hfill \le & {\displaystyle \frac{{\lambda }_1^f}{2}}{\widehat{\delta }}^T\left(t\right)\left[{\left(\widehat{\eta }+\omega \right)}^2\otimes HB{B}^{T}H\right]\widehat{\delta }\left(t\right)+{\psi }^T\left(t\right){\displaystyle \frac{2{\mathsf{\Pi }}^2{\lambda }_{max}\left(HFC{C}^T{F}^{T}H\right)}{{\lambda }_1^f{\lambda }_{min}\left(\mathsf{\Gamma }\right)}}\psi \left(t\right),\hfill \end{array}$$

(32)

where $\mathsf{\Pi }=max\left\{{\phi }_1,\dots ,{\phi }_N\right\}$ is a constant and where ${\lambda }_{min}(·)$ and ${\lambda }_{max}(·)$ respectively denote the minimum and the maximum eigenvalues of a matrix. According to Lemma 6 and the above Equation (32), substitution into (31) leads to

$$\begin{array}{cc}\hfill {\dot{V}}_{ob}\left(t\right)\le & {\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }\otimes \left(HA+A^{T}H+\mathsf{\Gamma }\right)-\left({\displaystyle \frac{{\lambda }_1^f}{2}}{\left(\widehat{\eta }+\omega \right)}^2+\alpha {\mathsf{\Delta }}_F\mathsf{\Theta }\right)\otimes \mathsf{\Gamma }\right]\widehat{\delta }\left(t\right)\hfill \\ \hfill & +2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes HA\right]f_{\mathcal{F}}\left(t\right)-2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes H\right]{\dot{f}}_{\mathcal{F}}\left(t\right)\hfill \\ \hfill & +2{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes HB\right]r\left(t\right)+{\psi }^T\left(t\right){\displaystyle \frac{2{\mathsf{\Pi }}^2{\lambda }_{max}\left(HFC{C}^T{F}^{T}H\right)}{{\lambda }_1^f{\lambda }_{min}\left(\mathsf{\Gamma }\right)}}\psi \left(t\right),\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & {\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes HA\right]f_{\mathcal{F}}\left(t\right)-{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes H\right]{\dot{f}}_{\mathcal{F}}\left(t\right)\hfill \\ \hfill & +{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes HB\right]r\left(t\right)\hfill \\ \hfill =& {\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes H\right]\left[\left(I_N\otimes A\right)f_{\mathcal{F}}\left(t\right)-\left(I_N\otimes I_q\right){\dot{f}}_{\mathcal{F}}\left(t\right)+\left(I_N\otimes B\right)r\left(t\right)\right].\hfill \end{array}$$

Letting $h\left(t\right)={\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }{L}^F\otimes H\right]\left[\left(I_N\otimes A\right)f_{\mathcal{F}}\left(t\right)\right]-\left(I_N\otimes I_q\right){\dot{f}}_{\mathcal{F}}\left(t\right)+\left(I_N\otimes B\right)r\left(t\right)$, per the feasible condition that Equation (20) is satisfied, we acquire $\underset{t\to \infty }{lim}h\left(t\right)=0$. It is evident from Lemma 5 that

$$\begin{array}{cc}\hfill & -{\widehat{\delta }}^T\left(t\right)\left[\left({\displaystyle \frac{{\lambda }_1^f}{2}}{\left(\widehat{\eta }+\omega \right)}^2+\alpha {\mathsf{\Delta }}_F\mathsf{\Theta }\right)\otimes \mathsf{\Gamma }\right]\widehat{\delta }\left(t\right)\hfill \\ \hfill \le & -2{\widehat{\delta }}^T\left(t\right)\left[\sqrt{{\displaystyle \frac{{\lambda }_1^f}{2}}\alpha {\mathsf{\Delta }}_F\mathsf{\Theta }}\left(\widehat{\eta }+\omega \right)\otimes \mathsf{\Gamma }\right]\widehat{\delta }\left(t\right).\hfill \end{array}$$

(34)

By choosing $\alpha \ge {\displaystyle \frac{9\mathsf{\Pi }}{2{\lambda }_1^f}}$ and substituting Equation (34) into Equation (33), we obtain

$$\begin{array}{c}{\dot{V}}_{ob}\left(t\right)\le -{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }\otimes \mathrm{M}\right]\widehat{\delta }\left(t\right)+{\displaystyle \frac{2{\mathsf{\Pi }}^2{\lambda }_{max}\left(HFC{C}^T{F}^{T}H\right)}{{\lambda }_1^f{\lambda }_{min}\left(\mathsf{\Gamma }\right)}}{\psi }^T\left(t\right)\psi \left(t\right),\hfill \end{array}$$

(35)

where $\mathrm{M}\stackrel{\mathsf{\Delta }}{=}-\left(HA+A^{T}H-2\mathsf{\Gamma }\right).$ The derivative of $V_{e1}\left(t\right)$ defined in (24) along with (19) is listed as

$$\begin{array}{c}{\dot{V}}_{e1}\left(t\right)=2{\iota }_1{\psi }^T\left(t\right)\left(I_N\otimes Q\right)\dot{\psi }\left(t\right)\hfill \\ \le -{\psi }^T\left(t\right)\left[I_N\otimes \mathrm{Z}\right]\psi \left(t\right)-{\displaystyle \frac{2{\mathsf{\Pi }}^2{\lambda }_{max}\left(HFC{C}^T{F}^{T}H\right)}{{\lambda }_1^f{\lambda }_{min}\left(\mathsf{\Gamma }\right)}}{\psi }^T\left(t\right)\psi \left(t\right),\hfill \end{array}$$

(36)

where ${\iota }_1=1+{\displaystyle \frac{2{\mathsf{\Pi }}^2{\lambda }_{max}\left(HFC{C}^T{F}^{T}H\right)}{{\lambda }_1^f{\lambda }_{min}\left(\mathsf{\Gamma }\right)}}$ and $\mathrm{Z}\stackrel{\mathsf{\Delta }}{=}-\left(Q\left(A+FC\right)+{\left(A+FC\right)}^{T}Q\right).$

The derivative of the Lyapunov function $V_1\left(t\right)$ can be derived from Formulas (35) and (36) as follows:

$$\begin{array}{c}{\dot{V}}_1\left(t\right)={\dot{V}}_{ob}\left(t\right)+{\dot{V}}_{e1}\left(t\right)\hfill \\ \le -{\psi }^T\left(t\right)\left[I_N\otimes \mathrm{Z}\right]\psi \left(t\right)-{\widehat{\delta }}^T\left(t\right)\left[\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }\otimes \mathrm{M}\right]\widehat{\delta }\left(t\right).\hfill \end{array}$$

(37)

Defining a variable $\mathsf{\Omega }\left(t\right)$ such that $\mathsf{\Omega }\left(t\right)=\left(\sqrt{\left(\widehat{\eta }+\omega \right){\mathsf{\Delta }}_F\mathsf{\Theta }}\otimes I\right)\widehat{\delta }\left(t\right),$ Equation (37) can then be simplified to

$$\begin{array}{c}{\dot{V}}_1\left(t\right)={\dot{V}}_{ob}\left(t\right)+{\dot{V}}_{e1}\left(t\right)\hfill \\ \le -{\psi }^T\left(t\right)\left(I_N\otimes \mathrm{Z}\right)\psi \left(t\right)-{\mathsf{\Omega }}^T\left(t\right)\left(I_N\otimes \mathrm{M}\right)\mathsf{\Omega }\left(t\right).\hfill \end{array}$$

(38)

In light of the algebraic Riccati inequalities in (21) and (22), this means that $V_1\le 0$. From the above inequality (38), it can be proved that the closed-loop system as applied to the control law in (15) is asymptotically stable. As a result of LaSalle’s invariance principle [31], it is inferred that both $V_1\left(t\right)$ and ${\widehat{\eta }}_i\left(t\right)$ are bounded. Thus, it is clear that $\underset{t\to \infty }{lim}\left[{\widehat{x}}_{\mathcal{F}}\left(t\right)-f_{\mathcal{F}}\left(t\right)-\left(-{\left(L^F\right)}^{-1}{L}^T\otimes I_q\right){\widehat{x}}_{\mathcal{T}}\left(t\right)\right]=0.$ Consequently, the FLs can both realize the expected TVFT designated by $f\left(t\right)$ and simultaneously trace the state trajectory of the tracking leaders. Letting ${\varsigma }_i\left(t\right)={\xi }_i\left(t\right)-{\widehat{\xi }}_i\left(t\right),$ its compact form can be written as

$$\begin{array}{c}\varsigma \left(t\right)=\xi \left(t\right)-\widehat{\xi }\left(t\right)\hfill \\ =\left(L^f\otimes I_q\right)\left(x_f\left(t\right)-{\widehat{x}}_f\left(t\right)\right)+\left(L_C\otimes I_q\right)\left(x_{\mathcal{F}}\left(t\right)-{\widehat{x}}_{\mathcal{F}}\left(t\right)\right).\hfill \end{array}$$

(39)

Employing (14), (15), (16), and (39), the ensuing time derivation of the equations can be calculated as follows:

$$\dot{\varsigma }\left(t\right)=\left(I_N\otimes \left(A+FC\right)\right)\varsigma \left(t\right),$$

(40)

$$\begin{array}{cc}\hfill \dot{\widehat{\xi }}\left(t\right)=& \left(L^f\otimes I_q\right){\dot{\widehat{x}}}_f\left(t\right)+\left(L_C\otimes I_q\right){\dot{\widehat{x}}}_{\mathcal{F}}\left(t\right)\hfill \\ \hfill =& \left[\left(I_L\otimes A\right)+L^f\left(\widehat{\sigma }+\upsilon \right)\otimes B{K}_u\right]\widehat{\xi }\left(t\right)-{\rho }_2\left(L^f\otimes B\right)G\left(\widehat{\xi }\left(t\right)\right)+\left[L_C\left(\widehat{\eta }+\omega \right)\otimes B{K}_u\right]\widehat{\delta }\left(t\right)\hfill \\ \hfill & +\left(L_C\otimes B\right)\left[r\left(t\right)-{\rho }_{1}G\left(\widehat{\delta }\left(t\right)\right)\right]-\left(I_N\otimes FC\right)\left(\xi \left(t\right)-\widehat{\xi }\left(t\right)\right),\hfill \end{array}$$

(41)

where $G\left(\widehat{\xi }\left(t\right)\right)={\left[g^T\left({\widehat{\xi }}_1\left(t\right)\right),g^T\left({\widehat{\xi }}_2\left(t\right)\right)\dots ,g^T\left({\widehat{\xi }}_L\left(t\right)\right)\right]}^T$ and ${\rho }_2=\tau +\kappa .$ To prove that followers can converge into a convex hull composed of FLs, the following candidate Lyapunov function is designed for analysis: $V_2\left(t\right)=V_{ob1}\left(t\right)+V_{e2}\left(t\right)$, with

$$V_{ob1}\left(t\right)=\sum _{i=1}^L{\displaystyle \frac{1}{2}}{q}_i\left(2{\widehat{\sigma }}_i+{\upsilon }_i\right){\upsilon }_i+{\displaystyle \frac{1}{2}}\sum _{i=1}^L{q}_i{\left({\widehat{\sigma }}_i-\beta \right)}^2$$

(42)

and

$$V_{e2}\left(t\right)={\iota }_2{\varsigma }^T\left(t\right)\left(I_N\otimes Q\right)\varsigma \left(t\right),$$

(43)

where ${\iota }_2$ is the is the constant of the subsequent design and ${\mathsf{\Delta }}_f\mathsf{\Xi }=diag\left\{q_1,q_2,\dots ,q_L\right\}$. Then, the time derivative of $V_{ob1}\left(t\right)$ along the trajectory of (41) is yielded as

$$\begin{array}{c}{V}_{ob1}\left(t\right)={\displaystyle \sum _{i=1}^L}\left[q_i\left({\dot{\widehat{\sigma }}}_i+{\displaystyle \frac{1}{2}}{\dot{\upsilon }}_i\right){\upsilon }_i\right]+{\displaystyle \sum _{i=1}^L}{\displaystyle \frac{1}{2}}{q}_i\left(2{\widehat{\sigma }}_i+{\upsilon }_i\right){\dot{\upsilon }}_i+{\displaystyle \sum _{i=1}^L}{q}_i\left({\widehat{\sigma }}_i-\beta \right){\dot{\widehat{\sigma }}}_i\hfill \\ ={\displaystyle \sum _{i=1}^L}{q}_i\left({\widehat{\sigma }}_i+{\upsilon }_i\right){\dot{\upsilon }}_i+{\displaystyle \sum _{i=1}^L}{q}_i\left({\upsilon }_i+{\widehat{\sigma }}_i-\beta \right){\dot{\widehat{\sigma }}}_i.\hfill \end{array}$$

(44)

Based on (14) and (41), this results in

$$\sum _{i=1}^L{g}_i\left({\upsilon }_i+{\widehat{\sigma }}_i-\beta \right){\dot{\widehat{\sigma }}}_i={\widehat{\xi }}^T\left(t\right)\left[\left(\upsilon +\widehat{\sigma }-\beta I\right){\mathsf{\Delta }}_f\mathsf{\Xi }\otimes \mathsf{\Gamma }\right]\widehat{\xi }\left(t\right),$$

(45)

$$\begin{array}{cc}\hfill & \sum _{i=1}^L{q}_i\left({\widehat{\sigma }}_i+{\upsilon }_i\right){\dot{\upsilon }}_i\hfill \\ \hfill =& 2\sum _{i=1}^L{q}_i\left({\widehat{\sigma }}_i+{\upsilon }_i\right){\widehat{\xi }}_i^T\left(t\right)H{\dot{\widehat{\xi }}}_i\left(t\right)\hfill \\ \hfill =& {\widehat{\xi }}^T\left(t\right)\left({\mathsf{\Delta }}_f\mathsf{\Xi }\left(\widehat{\sigma }+\upsilon \right)\otimes \left(HA+A^{T}H\right)\right)\widehat{\xi }\left(t\right)\hfill \\ \hfill & +{\widehat{\xi }}^T\left(t\right)\left[\left(\widehat{\sigma }+\upsilon \right)\left({\mathsf{\Delta }}_f\mathsf{\Xi }{L}^f+{\left(L^f\right)}^T{\mathsf{\Delta }}_f\mathsf{\Xi }\right)\left(\widehat{\sigma }+\upsilon \right)\otimes HB{K}_u\right]\widehat{\xi }\left(t\right)\hfill \\ \hfill & -2{\widehat{\xi }}^T\left(t\right)\left[\left(\widehat{\sigma }+\upsilon \right){\mathsf{\Delta }}_f\mathsf{\Xi }\otimes HFC\right]\varsigma \left(t\right)\hfill \\ \hfill & +2{\widehat{\xi }}^T\left(t\right)\left[\left(\widehat{\sigma }+\upsilon \right){\mathsf{\Delta }}_f\mathsf{\Xi }{L}_C\otimes HB\right]\left[r\left(t\right)-{\rho }_{1}G\left(\widehat{\delta }\left(t\right)\right)\right]\hfill \\ \hfill & +2{\widehat{\xi }}^T\left(t\right)\left[\left(\widehat{\sigma }+\upsilon \right){\mathsf{\Delta }}_f\mathsf{\Xi }{L}_C\otimes HB{K}_u\right]\widehat{\delta }\left(t\right)\hfill \\ \hfill & -2{\widehat{\xi }}^T\left(t\right)\left[\left(\widehat{\sigma }+\upsilon \right){\mathsf{\Delta }}_f\mathsf{\Xi }{L}^f\otimes HB\right]{\rho }_{2}G\left(\widehat{\xi }\left(t\right)\right).\hfill \end{array}$$

(46)

To facilitate the representation, we define ${\varpi }_i\left(t\right)=r_i\left(t\right)-\left(\tau +\epsilon \right)g\left({\widehat{\delta }}_i\left(t\right)\right)$. According to Equation (11), it can be deduced that $\sout{\lambda }\stackrel{\mathsf{\Delta }}{=}max\left\{∥r_i\left(t\right)∥\right\}$ with $\sout{\lambda }\stackrel{\mathsf{\Delta }}{=}max\left\{∥r_i\left(t\right)∥\right\}.$ By similar steps as the foregoing, the following inequalities can be derived:

$$\begin{array}{cc}\hfill & 2{\widehat{\xi }}^T\left(t\right)\left[\left(\widehat{\sigma }+\upsilon \right){\mathsf{\Delta }}_f\mathsf{\Xi }{L}_C\otimes HB\right]\left[r\left(t\right)-{\rho }_{1}G\left(\widehat{\delta }\left(t\right)\right)\right]\hfill \\ \hfill \le & 2\sum _{i=1}^L{q}_i{\widehat{\xi }}^T\left(t\right)HB\left({\widehat{\sigma }}_i+{\upsilon }_i\right)\sum _{i=1}^N{w}_{ij}\left(r\left(t\right)+\left(\tau +\epsilon \right)G\left(\widehat{\delta }\left(t\right)\right)\right)\hfill \\ \hfill \le & 2\left(\sout{\lambda }+\tau +\epsilon \right)\sum _{i=1}^L{q}_i{\widehat{\xi }}^T\left(t\right)HB\left({\widehat{\sigma }}_i+{\upsilon }_i\right)\sum _{i=1}^N{w}_{ij}\hfill \\ \hfill \le & 2\varpi \sum _{i=1}^L\left({\widehat{\sigma }}_i+{\upsilon }_i\right)g_i∥B^{T}H{\widehat{\xi }}_i^T\left(t\right)∥\sum _{k=1}^N{w}_{ik}.\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill & -2{\rho }_2{\widehat{\xi }}^T\left(t\right)\left(\widehat{\sigma }+\upsilon \right){\mathsf{\Delta }}_f\mathsf{\Xi }{L}^f\otimes HBG\left(\widehat{\delta }\left(t\right)\right)\hfill \\ \hfill =& -2{\rho }_2\sum _{i=1}^L{\widehat{\xi }}_i^T\left(t\right)HB\left[\left(\sum _{j=1}^L{w}_{ij}\left(g\left({\widehat{\xi }}_i\left(t\right)\right)-g\left({\widehat{\xi }}_j\left(t\right)\right)\right.\right)+\sum _{k=1}^N{w}_{ik}g\left({\widehat{\xi }}_i\left(t\right)\right)\right]\hfill \\ \hfill \le & -2\left(\tau +\kappa \right)\sum _{i=1}^L∥B^{T}H{\widehat{\xi }}_i\left(t\right)∥\sum _{k=1}^N{w}_{ik}.\hfill \end{array}$$

(48)

Lemma 6 leads to the result that

$$\begin{array}{cc}\hfill & -2{\widehat{\xi }}^T\left(t\right)\left[\left(\widehat{\sigma }+\upsilon \right){\mathsf{\Delta }}_f\mathsf{\Xi }\otimes HFC\right]\varsigma \left(t\right)\hfill \\ \hfill \le & {\displaystyle \frac{{\lambda }_1^c}{2}}{\widehat{\xi }}^T\left(t\right)\left[{\left(\widehat{\sigma }+\upsilon \right)}^2\otimes HFC\right]\widehat{\xi }\left(t\right)+{\displaystyle \frac{2{\widehat{\mathsf{\Pi }}}^2{\lambda }_{max}\left[{\left(HFC\right)}^{T}HFC\right]}{{\lambda }_1^c{\lambda }_{min}\left(\mathsf{\Gamma }\right)}}{\varsigma }^T\left(t\right)\varsigma \left(t\right),\hfill \end{array}$$

where ${\lambda }_1^c$ is the minimum eigenvalue of ${\mathsf{\Delta }}_f\mathsf{\Xi }{L}^f+{\left(L^f\right)}^T{\mathsf{\Delta }}_f\mathsf{\Xi }$ and $\widehat{\mathsf{\Pi }}=max\left\{q_1,q_2,\dots ,q_L\right\}.$ By relying on the previous part of the proof, the expected TVFT problem is realized, which leads to the conclusion that $\underset{t\to \infty }{lim}\widehat{\delta }\left(t\right)=0$. Substituting (45)–(48) into (44) yields

$$\begin{array}{c}{V}_{ob1}\left(t\right)\le {\widehat{\xi }}^T\left(t\right)\left({\mathsf{\Delta }}_f\mathsf{\Xi }\left(\widehat{\sigma }+\upsilon \right)\otimes \left(HA+A^{T}H+\mathsf{\Gamma }\right)\right)\widehat{\xi }\left(t\right)\hfill \\ -{\widehat{\xi }}^T\left(t\right)\left[\left({\displaystyle \frac{{\lambda }_1^c}{2}}{\left(\widehat{\sigma }+\upsilon \right)}^2+\beta I{\mathsf{\Delta }}_f\mathsf{\Xi }\right)\otimes \mathsf{\Gamma }\right]\widehat{\xi }\left(t\right)+{\displaystyle \frac{2{\widehat{\mathsf{\Pi }}}^2{\lambda }_{max}\left[{\left(HFC\right)}^{T}HFC\right]}{{\lambda }_1^c{\lambda }_{min}\left(\mathsf{\Gamma }\right)}}{\varsigma }^T\left(t\right)\varsigma \left(t\right)\hfill \\ -2\left(\tau +\epsilon +\kappa \right){\displaystyle \sum _{i=1}^L}∥B^{T}H{\widehat{\xi }}^T\left(t\right)∥{\displaystyle \sum _{k=1}^N}{w}_{ik},\hfill \end{array}$$

(49)

where $\kappa$ is chosen to satisfy $\kappa \ge \sout{\lambda }+\epsilon .$ From Lemma 5, we obtain

$$\begin{array}{cc}\hfill & -{\widehat{\xi }}^T\left(t\right)\left[\left({\displaystyle \frac{{\lambda }_1^c}{2}}{\left(\widehat{\sigma }+\upsilon \right)}^2+\beta I{\mathsf{\Delta }}_f\mathsf{\Xi }\right)\otimes \mathsf{\Gamma }\right]\widehat{\xi }\left(t\right)\hfill \\ \hfill \le & -2{\widehat{\xi }}^T\left(t\right)\left[\left(\sqrt{{\displaystyle \frac{{\lambda }_1^c}{2}}\beta I{\mathsf{\Delta }}_f\mathsf{\Xi }}\left(\widehat{\sigma }+\upsilon \right)\right)\otimes \mathsf{\Gamma }\right]\widehat{\xi }\left(t\right).\hfill \end{array}$$

(50)

Then, placing the inequality in (50) into (49) provides

$$\begin{array}{c}{V}_{ob1}\left(t\right)\le {\widehat{\xi }}^T\left(t\right)\left({\mathsf{\Delta }}_f\mathsf{\Xi }\left(\widehat{\sigma }+\upsilon \right)\otimes \left(HA+A^{T}H-2\mathsf{\Gamma }\right)\right)\widehat{\xi }\left(t\right)+{\displaystyle \frac{2{\widehat{\mathsf{\Pi }}}^2{\lambda }_{max}\left[{\left(HFC\right)}^{T}HFC\right]}{{\lambda }_1^c{\lambda }_{min}\left(\mathsf{\Gamma }\right)}}{\varsigma }^T\left(t\right)\varsigma \left(t\right).\hfill \end{array}$$

(51)

The time derivative of $V_{e2}$ can be obtained from the trajectory of Equation (40) as follows:

$$\begin{array}{c}{\dot{V}}_{e2}\left(t\right)=2{\iota }_2{\varsigma }^T\left(t\right)\left(I_N\otimes Q\right)\dot{\varsigma }\left(t\right)\hfill \\ \le -{\iota }_2{\varsigma }^T\left(t\right)\mathrm{Z}\varsigma \left(t\right).\hfill \end{array}$$

(52)

Let $\mathsf{\Phi }\left(t\right)=\left(\sqrt{{\mathsf{\Delta }}_f\mathsf{\Xi }\left(\widehat{\sigma }+\upsilon \right)}\otimes I\right)\widehat{\xi }\left(t\right)$; then, the time derivative from Equations (51) and (52) is provided as follows:

$$\begin{array}{c}{\dot{V}}_2\left(t\right)\le V_{ob1}\left(t\right)+V_{e2}\left(t\right)\hfill \\ \le -{\iota }_2{\varsigma }^T\left(t\right)\left(I_L\otimes \mathrm{Z}\right)\varsigma \left(t\right)+{\displaystyle \frac{2{\widehat{\mathsf{\Pi }}}^2{\lambda }_{max}\left[{\left(HFC\right)}^{T}HFC\right]}{{\lambda }_1^c{\lambda }_{min}\left(\mathsf{\Gamma }\right)}}{\varsigma }^T\left(t\right)\varsigma \left(t\right)-{\mathsf{\Phi }}^T\left(t\right)\left(I_L\otimes \mathrm{M}\right)\mathsf{\Phi }\left(t\right)\hfill \\ \le -{\varsigma }^T\left(t\right)\left(I_L\otimes \mathrm{Z}\right)\varsigma \left(t\right)-{\mathsf{\Phi }}^T\left(t\right)\left(I_L\otimes \mathrm{M}\right)\mathsf{\Phi }\left(t\right),\hfill \end{array}$$

(53)

where ${\iota }_2\ge 1+{\displaystyle \frac{2{\widehat{\mathsf{\Pi }}}^2{\lambda }_{max}\left[{\left(HFC\right)}^{T}HFC\right]}{{\lambda }_1^c{\lambda }_{min}\left(\mathsf{\Gamma }\right)}}.$ Using (53) and Lemma 2, it can be inferred that $\underset{t\to \infty }{lim}\varsigma \left(t\right)=0$ and $\underset{t\to \infty }{lim}\widehat{\xi }\left(t\right)=0$; hence, the closed-loop system is implemented under the control protocols (15) and (16) for the TVFCT problem. The demonstration of Theorem 1 is currently complete. □

3.2. The Case with One Tracking Leader

This part deals with the TVFCT issue for MASs with a tracking leader and bounded unknown input in directed graphs.

With the above analysis, the case of a tracking leader is further considered. Then, the Laplace matrix which matches the topology of the system can be presented as follows:

$${\mathcal{L}}^1=\left[\begin{array}{ccc}0& 0_{1\times N}& 0_{1\times L}\\ L_{N\times 1}^T& L_{N\times N}^F& 0_{N\times L}\\ 0_{L\times 1}& L_C& L_{L\times L}^f\end{array}\right].$$

We consider the dynamics of the tracking leader as

$$\left\{\begin{array}{c}{\dot{x}}_0\left(t\right)=A{x}_0\left(t\right)+B{u}_0\left(t\right),\hfill \\ y_0\left(t\right)=C{x}_0\left(t\right),\hfill \end{array}\right.$$

(54)

where $x_0\left(t\right)\in {\mathcal{R}}^q,$ $y_0\left(t\right)\in {\mathcal{R}}^n$ and $u_0\left(t\right)\in {\mathcal{R}}^p$ respectively denote the state, output, and control input of the tracking leader.

Assumption 5.

One tracking leader’s control input is variable in time and bounded, i.e., ${∥u_0\left(t\right)∥}_{\infty }\le \overline{\tau }$ and $\overline{\tau }$ is a positive constant.

For the estimate of each agent state, the observer is portrayed as

$$\left\{\begin{array}{c}{\dot{\widehat{x}}}_i\left(t\right)=A{\widehat{x}}_i\left(t\right)-F\left(y_i\left(t\right)-C{\widehat{x}}_i\left(t\right)\right)+B{u}_i\left(t\right),i\in \mathcal{F}\cup \mathcal{E}\hfill \\ {\dot{\widehat{x}}}_0\left(t\right)=A{\widehat{x}}_0\left(t\right)-F\left(y_0\left(t\right)-C{\widehat{x}}_0\left(t\right)\right)+B{u}_0\left(t\right),\hfill \end{array}\right.$$

where ${\widehat{x}}_0\left(t\right)\in {\mathcal{R}}^q$. The formation leader’s control law is then envisioned as

$$\left\{\begin{array}{c}{u}_i\left(t\right)=\left({{\widehat{\eta }}^1}_i\left(t\right)+{\overline{\omega }}_i\left(t\right)\right)K_u{\widehat{\varphi }}_i\left(t\right)+r_i\left(t\right)-{\rho }_{3}g\left({\widehat{\varphi }}_i\left(t\right)\right),\hfill \\ {{\dot{\widehat{\eta }}}^1}_i\left(t\right)={\widehat{\varphi }}_i^T\left(t\right)\widehat{\mathsf{\Gamma }}{\widehat{\varphi }}_i\left(t\right),\hfill \\ {{\widehat{\eta }}^1}_i\left(0\right)={{\widehat{\eta }}^1}_{i0},i\in \mathcal{F}\hfill \end{array}\right.$$

(55)

where $\widehat{\varphi }\left(t\right)={\displaystyle \sum _{j=1}^N}{w}_{ij}\left[{\widehat{x}}_i\left(t\right)-f_i\left(t\right)-{\widehat{x}}_j\left(t\right)+f_j\left(t\right)\right]+w_{i0}\left({\widehat{x}}_i\left(t\right)-f_i\left(t\right)-{\widehat{x}}_0\left(t\right)\right).$ Then, the compact form of the time derivative of $\widehat{\varphi }\left(t\right)$ is described as

$$\begin{array}{c}\dot{\widehat{\varphi }}\left(t\right)=\left(L^F\otimes I_q\right)\left({\dot{\widehat{x}}}_{\mathcal{F}}\left(t\right)-1_N\otimes \left({\dot{\widehat{x}}}_0\left(t\right)+{\dot{f}}_{\mathcal{F}}\left(t\right)\right)\right)\hfill \\ =\left[\left(I_N\otimes A\right)+\left({\widehat{\eta }}^1+\overline{\omega }\right)\otimes B{K}_u\right]\widehat{\varphi }\left(t\right)+\left(L^F\otimes A\right)f_{\mathcal{F}}\left(t\right)\hfill \\ +\left(L^F\otimes B\right)r\left(t\right)-{\rho }_1\left(L^F\left({\widehat{\eta }}^1+\overline{\omega }\right)\otimes B\right)G\left(\widehat{\varphi }\left(t\right)\right)\hfill \\ -\left(L^F\otimes B\right)\left(1_N\otimes u_0\left(t\right)\right)-\left(L^F\otimes I_q\right){\dot{f}}_{\mathcal{F}}\left(t\right)-\left(I_N\otimes FC\right)\left(\varphi \left(t\right)-\widehat{\varphi }\left(t\right)\right),\hfill \end{array}$$

(56)

where $\widehat{\varphi }\left(t\right)={\left[{\widehat{\varphi }}_1^T\left(t\right),{\widehat{\varphi }}_2^T\left(t\right),\dots ,{\widehat{\varphi }}_N^T\left(t\right)\right]}^T.$

For each follower, the control law with the adaptive observer is organized as follows:

$$\left\{\begin{array}{c}{u}_i\left(t\right)=\left({{\widehat{\sigma }}^1}_i\left(t\right)+{\overline{\upsilon }}_i\left(t\right)\right)K_w{\widehat{\zeta }}_i\left(t\right)-{\rho }_{2}g\left({\widehat{\zeta }}_i\left(t\right)\right),\hfill \\ {{\dot{\widehat{\sigma }}}^1}_i\left(t\right)={\widehat{\zeta }}_i^T\left(t\right)\widehat{\mathsf{\Gamma }}{\widehat{\zeta }}_i\left(t\right),\hfill \\ {{\widehat{\sigma }}^1}_i\left(0\right)={{\widehat{\sigma }}^1}_{i0},i\in \mathcal{E},\hfill \end{array}\right.$$

(57)

where ${\widehat{\zeta }}_i\left(t\right)={\displaystyle \sum _{j=1}^{N+L}}{w}_{ij}\left({\widehat{x}}_i\left(t\right)-{\widehat{x}}_j\left(t\right)\right)$ and $K_w\in R^{q\times q}$ is a positive matrix.

Theorem 2.

Under Assumptions 1, 2, 3, and 5, the systems in (1) and (2) with unknown input of one tracking leader can achieve observer-based adaptive TVFCT under directed graphs by adopting the nonlinear and fully distributed control protocols in (15) and (16) with parameters $K_u=-B^{T}H,$ $\mathsf{\Gamma }=HB{B}^{T}H,$ ${\overline{\omega }}_i\left(t\right)={\widehat{\varphi }}_i^T\left(t\right)H{\widehat{\varphi }}_i\left(t\right)$ and ${\overline{\upsilon }}_i\left(t\right)={\widehat{\zeta }}_i^T\left(t\right)H{\widehat{\zeta }}_i\left(t\right)$ for the given design if the viability requirements listed below are met:

(i) 

The compensation for the input signal $r_i\left(t\right)$ is provided by the formula

$$\underset{t\to \infty }{lim}\left(A{f}_i\left(t\right)-{\dot{f}}_i\left(t\right)+B{r}_i\left(t\right)\right)=0,i=1,\dots ,N.$$

(ii) 

The inequality relation is fulfilled by choosing ${\tau }_1$ and κ such that

$${\rho }_3\ge {\tau }_1,$$

$$\kappa \ge \sout{\lambda }+\epsilon ,$$

where $\sout{\lambda }\stackrel{\mathsf{\Delta }}{=}max\left\{∥r_i\left(t\right)∥\right\},i\in \mathcal{F}$ and ${\rho }_3={\tau }_1+\epsilon$, with ε being a given arbitrarily small positive number.

(iii) 

For any given matrices $H,Q>0,$ the matrices H and Q are solutions of the following algebraic Riccati inequalities:

$$\begin{array}{c}HA+A^{T}H-2HB{B}^{T}H+I_q\le 0,\hfill \\ Q\left(A+FC\right)+{\left(A+FC\right)}^{T}Q+I_q\le 0.\hfill \end{array}$$

Proof of Theorem 2.

Let $\varphi \left(t\right)={\displaystyle \sum _{j=1}^N}{w}_{ij}\left[x_i\left(t\right)-f_i\left(t\right)-x_j\left(t\right)+f_j\left(t\right)\right]+w_{i0}\left(x_i\left(t\right)-f_i\left(t\right)\right.$ $\left.- x_0\left(t\right)\right)$ and ${\overline{\psi }}_i\left(t\right)={\varphi }_i\left(t\right)-{\widehat{\varphi }}_i\left(t\right)$; then, the compact form of their time derivative can be expressed as

$$\begin{array}{c}\dot{\varphi }\left(t\right)=\left[\left(I_N\otimes A\right)+\left(\left({\widehat{\eta }}^1+\overline{\omega }\right)\otimes B{K}_u\right)\right]\varphi \left(t\right)+\left(L^F\otimes B\right)r\left(t\right)-{\rho }_1\left(L^F\otimes B\right)G\left(\varphi \left(t\right)\right)\hfill \\ +\left(L^F\otimes A\right)f_{\mathcal{F}}\left(t\right)-\left(L^F\otimes B\right)u_0\left(t\right)-\left(L^F\otimes I_q\right){\dot{f}}_{\mathcal{F}}\left(t\right),\hfill \end{array}$$

(58)

$${\dot{\overline{\psi }}}_i\left(t\right)=\left(I_N\otimes \left(A+FC\right)\right)\overline{\psi }\left(t\right).$$

(59)

The Lyapunov function is established by the same principle as in Theorem 1, as follows:

$$V_3\left(t\right)=\sum _{i=1}^N{\displaystyle \frac{1}{2}}{\widehat{\varphi }}_i\left(t\right)\left(2{{\widehat{\eta }}^1}_i+{\overline{\omega }}_i\right){\overline{\omega }}_i+{\displaystyle \frac{1}{2}}\sum _{i=1}^N{\widehat{\varphi }}_i\left(t\right){\left({{\widehat{\eta }}^1}_i-\alpha \right)}^2+{\iota }_3{\overline{\psi }}^T\left(t\right)\left(I_N\otimes Q\right)\overline{\psi }\left(t\right).$$

Then, according to (55), (56), and (59), similar to the proof process of Theorem 1, the time derivative of $V_3\left(t\right)$ can be deduced as follows:

$$\begin{array}{c}{\dot{V}}_3\left(t\right)\le {\widehat{\varphi }}^T\left(t\right)\left[\left({\widehat{\eta }}^1+\overline{\omega }\right){\mathsf{\Delta }}_F\mathsf{\Theta }\otimes \left(HA+A^{T}H-2\mathsf{\Gamma }\right)\right]\widehat{\varphi }\left(t\right)\hfill \\ -2\left({\rho }_3-{\tau }_1\right){\displaystyle \sum _{i=1}^N}\left({{\widehat{\eta }}^1}_i+{\overline{\omega }}_i\right){\phi }_i{w}_{i0}∥B^{T}H{\widehat{\varphi }}_i∥\hfill \\ -{\overline{\psi }}^T\left(t\right)\left(I_N\otimes \left(Q\left(A+FC\right)+{\left(A+FC\right)}^{T}Q\right)\right)\overline{\psi }\left(t\right),\hfill \end{array}$$

where we choose ${\rho }_3\ge {\tau }_1.$ It can be inferred that the system enables solving the TVFT problem such that ${\dot{V}}_3\left(t\right)<0$, with $V_3$, ${\widehat{\eta }}_i,$ $\varphi$ and $\overline{\mathsf{\Psi }}$ all being bounded. To further consider the containment problem, we construct the Lyapunov function $V_4\left(t\right)$ such that $V_4\left(t\right)={\displaystyle \sum _{i=1}^L}{\displaystyle \frac{1}{2}}{q}_i\left(2{{\widehat{\sigma }}^1}_i+{\overline{\upsilon }}_i\right){\overline{\upsilon }}_i+{\displaystyle \frac{1}{2}}{\displaystyle \sum _{i=1}^L}{q}_i{\left({{\widehat{\sigma }}^1}_i-\beta \right)}^2+{\iota }_2{\varsigma }^T\left(t\right)\left(I_N\otimes Q\right)\varsigma \left(t\right).$ The subsequent proof procedure is identical to the steps in Theorem 1, and as such is omitted. Finally, it is not difficult to conclude that the system realizes the TVFCT problem with a tracking leader under the control protocols in (55) and (57). □

Remark 1.

This subsection investigates the TVFCT problem with one tracking leader. Compared to the control protocols designed in [14,15,16,17], which are based on the case where the states of the agents are measurable, in practical scenarios some of the states of the agents will be unknown because the state of each agent cannot be completely measurable. Therefore, this paper introduces an observer to observe the state of each agent as means of solving the above problem.

4. Simulations

With the help of Matlab 2020b software, this section aims to deal with the formation containment issue in three dimensions. To confirm the feasibility of the theoretical results, two numerical simulation samples for MASs are provided: one dealing with multiple tracking leaders, and another dealing with a single tracking leader.

4.1. The Case with Multiple Tracking Leaders

In this case, a network topology composed of eight formation leaders, eight followers, and three tracking leaders is considered in sequence, labeled 1 to 19, as shown in Figure 1. Here, $w_{ij}$ is equal to 1 if $(i,j)\in \mathcal{E}$. The dynamics of each agent are provided by (14), where $x_i\left(t\right)={\left[x_{i1}\left(t\right),x_{i2}\left(t\right),x_{i3}\left(t\right)\right]}^T\left(i=1,2,\dots ,19\right)$, $A=\left[\begin{array}{ccc}0& 1& 1\\ 1& 2& 1\\ -2& 1& -2\end{array}\right],$ $B=\left[\begin{array}{cc}0& 1\\ 1& 0\\ 0& 0\end{array}\right],$ $C=\left[\begin{array}{ccc}0& 1& 0\end{array}\right]$, and $F=\left[\begin{array}{c}0\\ -2\\ 0\end{array}\right].$ The desired formation vector $f_i\left(t\right)={\left[f_1\left(t\right),f_2\left(t\right),f_3\left(t\right)\right]}^T$ is provided as follows: $f_i\left(t\right)=\left[\begin{array}{c}h\ast sin\left(t+\left(i-1\right)\pi /\phantom{\left(i-1\right)\pi 4}4\right)\\ -h\ast cos\left(t+\left(i-1\right)\pi /\phantom{\left(i-1\right)\pi 4}4\right)\\ 2h\ast cos\left(t+\left(i-1\right)\pi /\phantom{\left(i-1\right)\pi 4}4\right)\end{array}\right],i=1,2,\dots ,8$, with $h=6.$ It can be seen from Figure 2 that the time-varying coupling gains ${\widehat{\eta }}_i\left(t\right)$ and ${\widehat{\sigma }}_i\left(t\right)$ eventually converge to finite values with the devised control laws in (15) and (16).

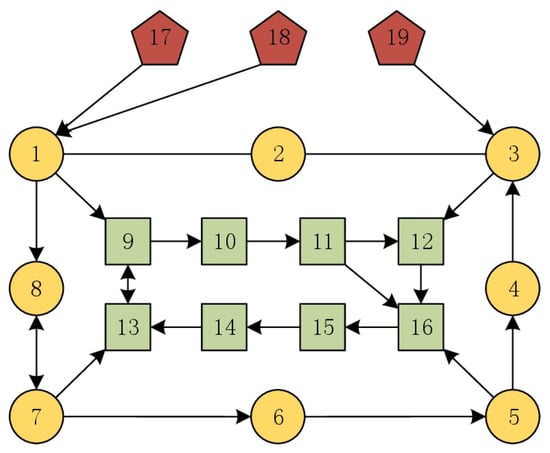
Figure 1. The directed network topology for the case with multiple tracking leaders.

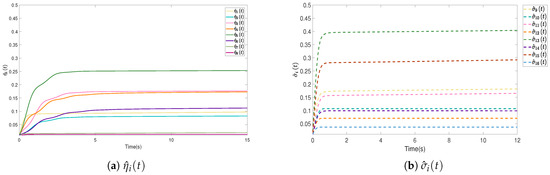
Figure 2. The values of the coupling gains ${\widehat{\eta }}_i\left(t\right)$ and ${\widehat{\sigma }}_i\left(t\right)$.

The state observer error for each agent is defined as $e\left(t\right)={\left[e_{i1}^T\left(t\right),e_{i2}^T\left(t\right),e_{i3}^T\left(t\right)\right]}^T$, where $e_i\left(t\right)=\left|x_i\left(t\right)-{\widehat{x}}_i\left(t\right)\right|,i=1,2,\dots ,19.$ Based on the desired formation vector $f_i\left(t\right)$ above, if the desired TVFCT is attained, then the states of the eight FLs will form a parallel octagon, with eight followers entering into the convex hull formed by the FLs and rotating continuously around the states of the three tracking leaders. Figure 3 shows snapshots of the state trajectories of each agent at $t=0$ s, $t=87$ s, $t=130$ s, and $t=146$ s, where the symbol ∗ denotes the follower, the pentagram denotes the tracking leader, and the remaining symbols in the figure represent each formation leader. Depending on the state observer error variable of the agent defined above, the trajectory curve of its error can be observed from Figure 4.

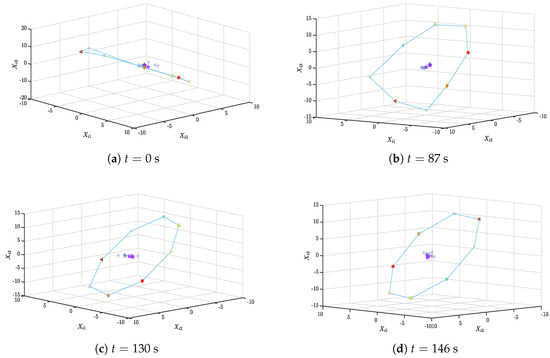
Figure 3. Snapshots of the state trajectories of the nineteen agents at various moments.

Figure 4. TErrors of the state observer for the nineteen agents.

In accordance with the formation tracking error variable and containment error variable defined in Theorem 1, we let ${\widehat{\delta }}_i\left(t\right)={\left[{\widehat{\delta }}_{i1}\left(t\right),{\widehat{\delta }}_{i2}\left(t\right),{\widehat{\delta }}_{i3}\left(t\right)\right]}^T$ and ${\widehat{\xi }}_i\left(t\right)={\left[{\widehat{\xi }}_{i1}\left(t\right),{\widehat{\xi }}_{i2}\left(t\right),{\widehat{\xi }}_{i3}\left(t\right)\right]}^T$. The formation tracking errors and containment errors eventually converge to zero over time, as illustrated in Figure 5 and Figure 6, respectively. Figure 3, Figure 4, Figure 5 and Figure 6 establish that the formation tracking and containment errors are eventually bounded throughout time. Thus, utilizing the developed control laws in (15) and (16), the TVFCT is achieved for MASs with multiple tracking leaders under directed graphs.

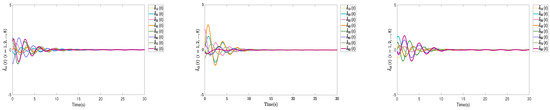
Figure 5. Curves of the containment errors for the case with multiple tracking leaders.

Figure 6. Curves of the containment errors for the case with multiple tracking leaders.

4.2. The Case with One Tracking Leader

In this case, a network topology of seventeen agents is considered, in which there are eight FLs, eight followers and one tracking leader, sequentially labeled 1–17 as presented in Figure 7. Here, $w_{ij}$ is equal to 1 if $(i,j)\in \mathcal{E}$. If TVFCT is implemented for MASs with the tracking leader, all FLs will form an octagon with the given time-varying regulation and trace the tracking leader’s state trajectory; simultaneously, the state trajectories of the eight followers will converge to the convex hull formed by the FLs. It is clear from Figure 8 that the coupling weight gains ${\widehat{\eta }}_i^1\left(t\right)$ and ${\widehat{\sigma }}_i^1\left(t\right)$ are eventually uniformly bounded throughout time. Figure 9 depicts snapshots of each agent’s state trajectories at various points in time.

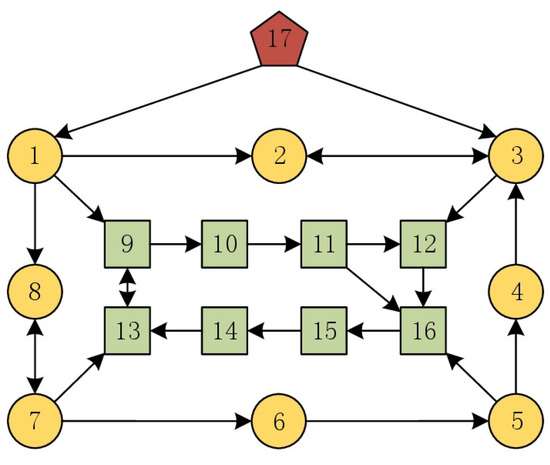
Figure 7. The directed network topology for the case with one tracking leader.

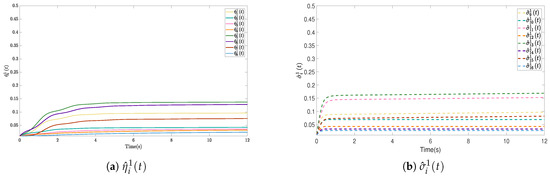
Figure 8. The values of the coupling gains ${\widehat{\eta }}_i^1\left(t\right)$ and ${\widehat{\sigma }}_i^1\left(t\right)$.

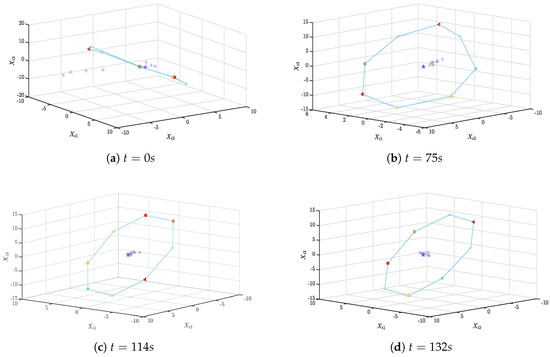
Figure 9. Snapshots of the state trajectories of the seventeen agents at various moments.

It can be inferred from Figure 10 and Figure 11 that the containment errors and formation tracking errors eventually tend to be zero. Establishing the state of the observer error variable as ${\overline{e}}_i\left(t\right)=\left|x_i\left(t\right)-{\widehat{x}}_i\left(t\right)\right|,\left(i=1,2,\dots ,17\right)$, we let ${\overline{e}}_i\left(t\right)={\left[{\overline{e}}_{i1}\left(t\right),{\overline{e}}_{i2}\left(t\right),{\overline{e}}_{i3}\left(t\right)\right]}^T.$ As can be seen from the Figure 12, the errors of the state observer for the seventeen agents tend to 0. Consequently, the TVFCT of a tracking leader under a directed graph is achieved with the developed control protocols in (55) and (57).

Figure 10. Curves of the formation tracking errors for the case with one tracking leader.

Figure 11. Curves of the formation tracking errors for the case with one tracking leader.

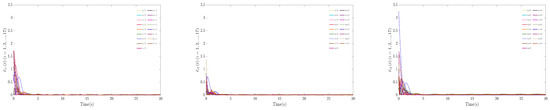
Figure 12. Errors of the state observer for the seventeen agents.

5. Conclusions

This research tackles the problem of observer-based adaptive TVFCT on directed graphs. Two novel observer-based adaptive TVFCT control laws have been designed and applied to two different cases, namely, multiple tracking leaders and a single tracking leader. In addition, the stability analysis of the established algorithm is justified with the help of the Lyapunov theorem and algebraic Riccati inequalities. Finally, simulations are employed to confirm the theoretical results. In future research, the finite-time control method will be combined with the control algorithm proposed in this paper to increase its application range.