DOA Estimation Based on Golden Ratio-Inspired Coprime Array

Abstract

To address the challenges of limited degrees of freedom (DOF) and mutual coupling effects in sparse array-based Direction-of-arrival (DOA) estimation, this paper proposes a novel array configuration termed the Golden ratio Inspired Coprime Array (GICA). This design integrates the golden ratio ($\varphi \approx 1.618$) into the geometric arrangement of three hierarchically structured subarrays to achieve enhanced difference coarray properties. Theoretical analysis demonstrates that the proposed configuration, through strategic sensor placement and virtual domain processing, significantly increases the achievable DOF. Comprehensive simulations show that this design exhibits competitive estimation performance, achieving reduced root mean square error (RMSE) across most signal-to-noise ratio (SNR) regimes and snapshot conditions when compared with contemporary coprime array configurations. Additionally, quantitative mutual coupling analysis reveals that the proposed structure achieves superior electromagnetic compatibility, demonstrating the lowest coupling leakage coefficient among tested configurations. Experimental validation under varying coupling strengths shows that this array design maintains stable estimation performance with minimal degradation. These results confirm the proposed configuration as an effective sparse array solution that simultaneously enhances DOA estimation accuracy and mutual coupling robustness.

1. Introduction

Direction-of-arrival (DOA) estimation is fundamental in array signal processing with applications in radar, wireless communications, sonar, and radio astronomy [1,2,3,4]. Array structure critically influences DOA estimation performance, directly impacting degrees of freedom (DOF), resolution, hardware cost, and algorithmic complexity [5]. Traditional uniform linear arrays (ULA) require numerous physical sensors for high resolution, with estimated sources limited by array elements, imposing substantial costs and computational complexity.

Sparse arrays significantly enhance DOF and resolution through non-uniform element distribution with the same number of physical sensors. Earlier proposed sparse arrays include Minimum Redundancy Arrays (MRA) [6,7] and Minimum Hole Arrays (MHA) [8], which lack closed-form expressions for sensor positions, limiting their practical engineering applications. To address this, nested arrays [9,10] and coprime arrays [11,12] with closed-form expressions were subsequently introduced. Among various sparse array designs, coprime arrays stand out due to their unique structural design and performance advantages.

However, traditional coprime arrays face two significant challenges in practical applications. First, the holes (missing elements) in their difference coarrays limit the effective DOF and potentially reduce estimation accuracy [5]. Second, mutual coupling effects between closely spaced sensors can severely degrade DOA estimation performance [13,14]. To address these fundamental limitations, the research community has developed various modified coprime array architectures. In what follows, we review the major advancement directions in coprime array design, which can be organized into four complementary research streams.

Strategic subarray modification: Pal and Vaidyanathan [12] developed the Augmented Coprime Array (ACA) by doubling one subarray’s sensors, expanding the continuous difference coarray segment from N + M − 1 to MN + M − 1. Qin et al. [15] introduced Coprime Arrays With Displaced Subarrays (CADIS), achieving MN + 2M + N−1 continuous lags with only M + N − 1 physical sensors through calculated subarray displacement.

Sensor position optimization: Ahsan et al. [16] proposed Thinning Coprime Arrays (TCA), which produce 2M(N + 1) − 1 consecutive lags using only M + N + [M/2] − 1 physical sensors. Importantly, the structure’s sparser configuration substantially reduces the number of sensor pairs with small separation, significantly improving its robustness against mutual coupling effects. Zheng et al. [17] developed Relocating Extended Coprime Arrays (RECA). This approach achieves 4MN + 4M − 2N[M/2] − 1 consecutive lags with 2M + N − 1 physical sensors.

Advanced displacement methodologies: Alamoudi et al. [18] introduced Shifted Coprime Arrays (SCA) utilizing displacement Ls = [N/2]M to maximize continuous virtual aperture. Shaalan and Yu [19] further refined displacement strategies with their Optimized Coprime Array (OpCA) configuration. Unlike previous techniques using fixed displacement values, OpCA adaptively selects the optimal displacement Ls based on the particular coprime pair, ensuring maximum virtual array continuity. The structure maintains the same physical sensor count as ACA (N + 2M − 1) while substantially extending the continuous difference coarray segment from MN + M − 1 to MN + M − 1 + Ls + M. This enhancement effectively incorporates the displacement value itself into the DOF equation.

Difference-sum coarray techniques: Recent research has expanded beyond difference coarrays to incorporate difference-sum coarrays. Wang et al. [20] introduced Prototype Coprime Arrays (PCA) achieving 2MN + 2M + 2N − 1 continuous DOF by leveraging both difference and sum operations. Ye et al. [21] introduced Novel Shifted Coprime Arrays (NSCA), achieving remarkable DOF enhancement: for odd configurations, 3MN + 2M + 2N − 1 consecutive DOF, and for even configurations, 3MN + 2M + 2N + (M − 1) consecutive DOF, while demonstrating superior mutual coupling resistance through optimized sensor displacement strategy. Ye et al. [22] presented Interpolated Coprime Arrays (ICA), replacing conventional subarrays with sparse sub-uniform linear arrays. This configuration generates at least 2MN + 1 continuous DOF with only M + N physical sensors for difference coarrays, and 4MN − 1 continuous DOF for difference-sum coarrays, while maintaining favorable mutual coupling characteristics.

The aforementioned studies have made significant strides in addressing either DOF limitations or mutual coupling challenges through various structural modifications and displacement strategies. However, opportunities remain for exploring alternative mathematical frameworks that can simultaneously optimize both aspects. Motivated by the unique equidistribution and aperiodic properties of the golden ratio, this paper proposes a novel approach that integrates mathematical principles into the geometric design of coprime arrays.

This paper proposes the Golden ratio Inspired Coprime Array (GICA). GICA consists of three strategically designed subarrays with positions determined by golden ratio ($\varphi \approx 1.618$) principles, creating optimal spacing patterns that naturally minimize mutual coupling while preserving critical spatial information. We employ Toeplitz matrix reconstruction [23] and TLS-ESPRIT [24] for all array configurations to ensure fair comparative evaluation. The main contributions of this paper are summarized as follows:

1. A unique three-subarray configuration based on golden ratio, where the design incorporates a uniform baseline subarray, a golden ratio progression subarray for optimized distribution, and a strategic compensation subarray targeting critical positions for enhanced virtual coverage.

2. A balanced “physical domain optimization + virtual domain processing” methodology that achieves superior mutual coupling resistance through strategic sensor placement while maintaining effective DOA estimation capability through enhanced virtual array synthesis.

3. Comprehensive analysis and validation demonstrating simultaneous enhancement of DOA accuracy and mutual coupling robustness across varying conditions.

The remainder of this paper is organized as follows: Section 2 introduces the preliminaries, including the signal model and mutual coupling model. Section 3 presents the proposed GICA structure, detailing its design principles, virtual array characteristics, and degrees of freedom analysis. Section 4 evaluates GICA’s performance through comprehensive simulations, examining DOA estimation accuracy and mutual coupling resistance. Section 5 concludes the paper with a summary of key findings.

2. Preliminaries

2.1. Signal Model

As shown in Figure 1, the coprime array consists of two linear sub-arrays with a specific spacing relationship. The spatial distribution of the physical array can be expressed as

$$\mathcal{S}={\left\{Mnd\right\}}_{n=0}^{N-1}\cup {\left\{Nmd\right\}}_{m=0}^{M-1}={\mathcal{S}}_1\cup {\mathcal{S}}_2$$

(1)

where M and N are coprime integers, $d=\lambda /2$ represents the half-wavelength spacing. The two subarrays are integrated, resulting in a coprime array with a total of $M+N-1$ sensor nodes.

When K uncorrelated narrowband signals impinge on the sparse array from directions $\{{\theta }_1,{\theta }_2,\dots ,{\theta }_K\}$, the kth signal source can be expressed as

$$s_k\left(t\right)=a_k\left(t\right)e^{j{\omega }_{0}t}$$

(2)

where $a_k\left(t\right)$ represents the signal amplitude, and ${\omega }_0=2\pi f_0$ is the carrier angular frequency.

The composite signal received by the coprime array at time t can be represented as

$$\mathbf{x}\left(t\right)=\sum _{k=1}^K\mathbf{a}\left({\theta }_k\right)s_k\left(t\right)+\mathbf{n}\left(t\right)=\mathbf{A}\mathbf{s}\left(t\right)+\mathbf{n}\left(t\right)$$

(3)

where $\mathbf{A}=[\mathbf{a}\left({\theta }_1\right),\mathbf{a}\left({\theta }_2\right),\dots ,\mathbf{a}\left({\theta }_K\right)]$ is the array steering matrix. $\mathbf{a}\left({\theta }_k\right)={[1,e^{-j{\displaystyle \frac{2\pi }{\lambda }}{d}_2\sin \left({\theta }_k\right)},\dots ,e^{-j{\displaystyle \frac{2\pi }{\lambda }}{d}_{M+N-1}\sin \left({\theta }_k\right)}]}^T$ is the steering vector for the kth signal source. $\mathbf{s}\left(t\right)={[s_1\left(t\right),s_2\left(t\right),\dots ,s_K\left(t\right)]}^T$ represents the signal source vector. $\mathbf{n}\left(t\right)$ is the zero-mean Gaussian white noise vector.

The covariance matrix of the received signal $\mathbf{x}\left(t\right)$ is defined as

$$\begin{array}{cc}\hfill {\mathbf{R}}_x& =\mathbb{E}\left[\mathbf{x}\left(t\right){\mathbf{x}}^H\left(t\right)\right]\hfill \\ \hfill & =\sum _{k=1}^K{p}_k\mathbf{a}\left({\theta }_k\right){\mathbf{a}}^H\left({\theta }_k\right)+{\sigma }_n^2\mathbf{I}\hfill \end{array}$$

(4)

where $p_k$ is the power of the kth signal source. In practical systems, this covariance matrix is typically estimated using finite samples:

$${\widehat{\mathbf{R}}}_x={\displaystyle \frac{1}{T}}\sum _{t=1}^T\mathbf{x}\left(t\right){\mathbf{x}}^H\left(t\right),$$

(5)

where T represents the number of sampling snapshots.

Based on the physical array positions, the additional DOF are exploited by constructing a differential co-array. The virtual sensor positions constructed by the difference coarray are

$${\mathcal{L}}_{diff}=\{d_i-d_j\mid d_i,d_j\in \mathcal{S}\}$$

(6)

For simplification, we represent the difference set as

$${\mathcal{L}}_{diff}=\{l_d\mid l_d\in {\mathcal{L}}_{diff}^{\prime }\}$$

(7)

2.2. Mutual Coupling Model

Mutual coupling is a significant practical issue in array signal processing that affects the accuracy of direction estimation and array performance. When electromagnetic waves impinge on an array, each element receives not only the incident signal but also signals radiated or scattered by other elements, a phenomenon known as mutual coupling.

From a mathematical perspective, mutual coupling can be modeled through a coupling matrix. The array manifold matrix without coupling is $\mathbf{A}$, then the actual array manifold matrix ${\mathbf{A}}_c$ with coupling can be represented as

$${\mathbf{A}}_c=\mathbf{C}\mathbf{A}$$

(8)

According to Equations (3) and (8), we can derive the data vector received by the sensors under mutual coupling effect as

$${\mathbf{x}}_c\left(t\right)=\mathbf{C}\mathbf{A}\mathbf{s}\left(t\right)+\mathbf{n}\left(t\right)={\mathbf{A}}_c\mathbf{s}\left(t\right)+\mathbf{n}\left(t\right)$$

(9)

where $\mathbf{C}$ is the mutual coupling matrix, ${\mathbf{A}}_c$ represents the array manifold matrix considering mutual coupling effects, and ${\mathbf{x}}_c\left(t\right)$ denotes the actual received signal vector under coupling conditions. According to [21], $\mathbf{C}$ is defined as

$${\left(C\right)}_{w_1,w_2}=\left\{\begin{array}{cc}{c}_{|w_1-w_2|},\hfill & |w_1-w_2|\le B,\hfill \\ 0,\hfill & |w_1-w_2|>B,\hfill \end{array}\right.$$

(10)

In this formulation, $w_1$ and $w_2$ represent element positions within the array domain, while the sequence of coupling coefficients $c_0,c_1,\dots ,c_B$ demonstrates a monotonically decreasing magnitude relationship such that $1=c_0>|c_1|>|c_2|>\dots >|c_B|$. The parameter B defines the cut-off threshold beyond which mutual coupling effects become negligible.

To quantify the spatial correlation structure of arrays and its impact on mutual coupling effects, the weight function $w\left(m\right)$ is introduced [21]:

$$w\left(m\right)={\displaystyle \frac{1}{2}}\sum _{i=1}^H\sum _{j=1,j\ne i}^{H}I\left(\right|d_i-d_j\left|\right)=m·d_{min}$$

(11)

where $I(·)$ denotes the indicator function, $d_{min}$ represents the minimum element spacing in the array, and H is the total number of array elements. The function $w\left(m\right)$ characterizes the frequency distribution of element pairs separated by $m·d_{min}$, directly reflecting spatial sampling characteristics and potential coupling patterns.

The contribution of the weight function to mutual coupling analysis is manifested in two critical aspects: first, since coupling intensity decreases exponentially with distance, the low-order $w\left(m\right)$ values directly correlate with the number of element pairs subjected to the strongest coupling effects, serving as deterministic parameters for predicting overall coupling intensity; second, the uniformity and peak characteristics of the $w\left(m\right)$ distribution determine the spatial distribution pattern of coupling effects, where a more uniform distribution typically corresponds to more dispersed coupling structures.

3. Proposed Special Coprime Array Structure

3.1. Array Structure and Design Principles

The golden ratio $\varphi ={\displaystyle \frac{1+\sqrt{5}}{2}}\approx 1.618$ represents an irrational number characterized by unique mathematical properties, satisfying the fundamental relation ${\varphi }^2=\varphi +1$. This constant exhibits superior equidistribution properties and minimal periodicity, thereby offering a distinctive mathematical framework for array design applications.

The suitability of golden ratio-based spacing stems from its exceptional low-discrepancy properties [25]. While Weyl’s equidistribution [26] theorem formally applies to linear sequences such as ${\left\{n\varphi \right\}}_{n=1}^{\infty }$, the exponential form ${\varphi }^i$ employed in ${\mathcal{H}}_2$ inherits analogous distribution characteristics [25,26] that ensure optimal spatial coverage without periodic clustering. As a quadratic irrational, $\varphi$ ensures that sequences based on ${\varphi }^i$ exhibit strong aperiodicity [25], minimizing redundant spatial samples in the difference coarray while avoiding regular patterns that generate grating lobes in array processing. The exponential growth ${\varphi }^i$ generates spacings following Fibonacci-like ratios [27], creating a hierarchical structure that naturally distributes sensors across multiple spatial scales. These mathematical properties yield direct performance benefits. The quasi-random positioning reduces closely spaced sensor pairs (primary contributors to mutual coupling) while maintaining sufficient sampling density for DOA resolution. Unlike random arrays lacking structure or uniform arrays suffering periodic ambiguities, golden ratio-based placement balances spatial diversity with structural predictability, enabling both analytical tractability and superior performance. While practical implementation requires rounding to integer sensor positions, the underlying $\varphi$-based design principle ensures that the resulting discrete array preserves the favorable spatial distribution characteristics inherent to golden ratio sequences.

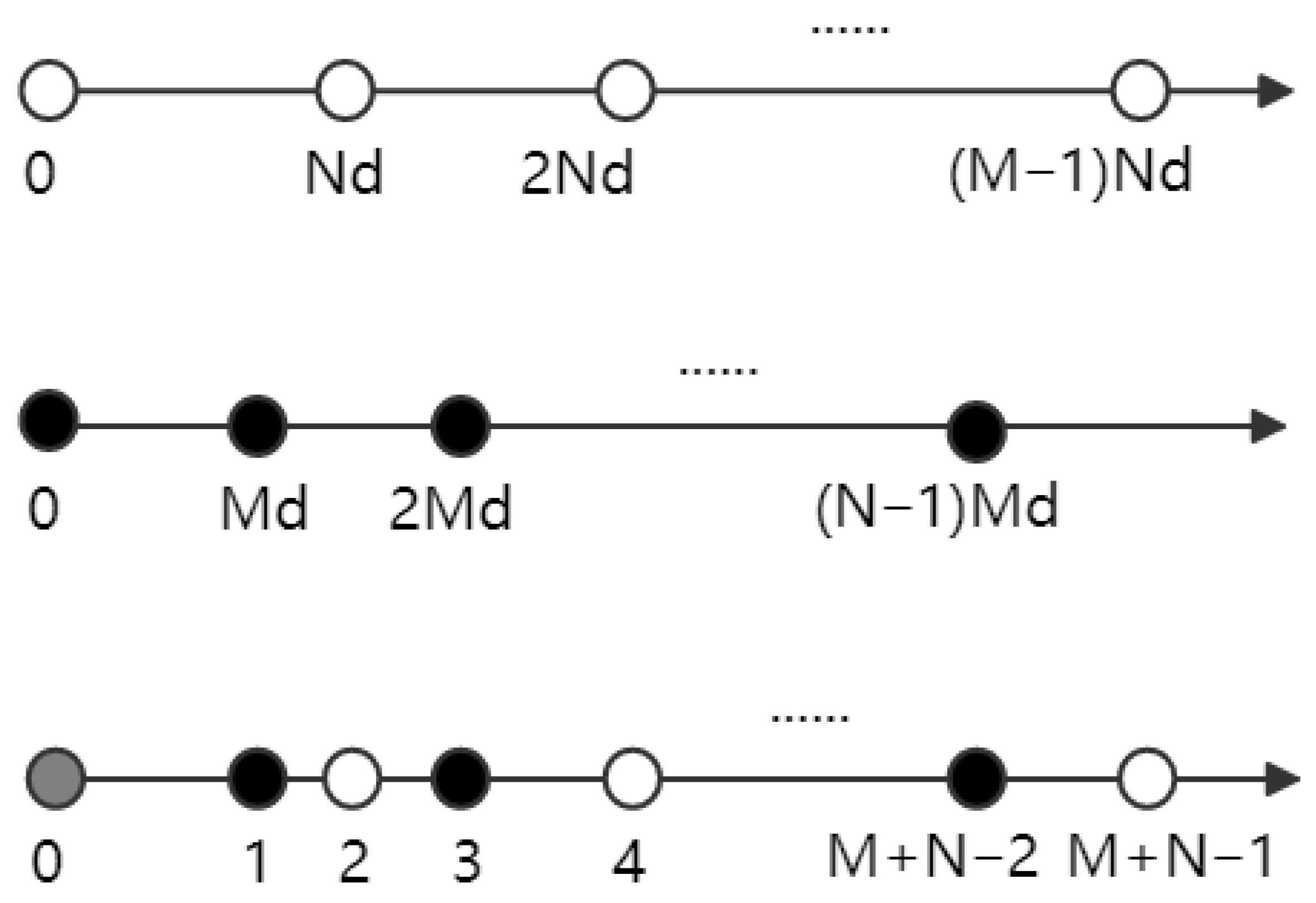
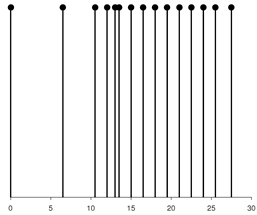
To construct a high-performance array structure with optimized mutual coupling characteristics, this paper proposes GICA based on golden ratio mathematical properties. The structure employs a three-layer hierarchical design that enhances performance and suppresses mutual coupling in traditional coprime arrays through golden ratio parameter incorporation. GICA’s physical element distribution consists of three functionally complementary subarrays, each undertaking specific optimization functions to synergistically maximize overall performance. The GICA physical array structure is shown in Figure 2, with mathematical formulation defined as

$$\left\{\begin{array}{c}{\mathcal{H}}_1={\left\{nN\right\}}_{n=0}^M\hfill \\ {\mathcal{H}}_2={\left\{\mathrm{round}(MN+M({\varphi }^i+i))\right\}}_{i=1}^N\hfill \\ {\mathcal{H}}_3=\{\mathrm{round}\left(M\varphi \right),\mathrm{round}\left(N\varphi \right),\mathrm{round}(MN/\varphi )\}\hfill \\ \mathcal{S}={\mathcal{H}}_1\cup {\mathcal{H}}_2\cup {\mathcal{H}}_3\hfill \end{array}\right.$$

(12)

where $\varphi ={\displaystyle \frac{1+\sqrt{5}}{2}}$ is the golden ratio, M and N are coprime positive integers. GICA employs a three-layer hierarchical architecture, with each layer undertaking distinct functional roles and synergistic optimization:

Foundation Layer (${\mathcal{H}}_1$): Linear distribution with uniform spacing N, providing the stable core structure of traditional coprime arrays for direction estimation.

Optimization Layer (${\mathcal{H}}_2$): Utilizes golden ratio recurrence ${\varphi }^i+i$ for non-uniform distribution. The ${\varphi }^i$ term provides quasi-randomness avoiding periodic repetition, while linear term i ensures monotonic increase maintaining density gradients, achieving optimized spatial sampling.

Filling Layer (${\mathcal{H}}_3$): Strategically selects three critical positions $M\varphi$, $N\varphi$, and $MN/\varphi$ based on difference coarray theory for hole compensation, optimizing virtual array continuity.

3.2. Virtual Array Characteristic Analysis

For the proposed GICA structure ${\mathcal{S}}_{GICA}={\mathcal{H}}_1\cup {\mathcal{H}}_2\cup {\mathcal{H}}_3$, the difference coarray is constructed by computing pairwise differences between physical elements. The virtual covariance matrix reconstruction employs the Toeplitz matrix approach [23]. Given GICA’s position set $\mathcal{P}={\left\{p_i\right\}}_{i=1}^{M+N+4}$ and following (6), the difference coarray is constructed through

$$\mathcal{D}=\{d_{ij}=p_i-p_j:i,j\in [1,M+N+4]\}$$

(13)

To obtain discretized lag representation, we introduce the quantization operator:

$$\mathcal{Q}:\mathbb{R}\to \mathbb{Z},\mathcal{Q}\left(x\right)=\mathrm{round}(x/d)$$

(14)

where d denotes the unit element spacing. Applying this operator yields the normalized lag matrix:

$$\mathbf{L}=\mathcal{Q}\left(\mathbf{D}\right)={\left[\mathcal{Q}\left(D_{ij}\right)\right]}_{i,j=1}^{M+N+4}$$

(15)

Extracting unique lag values forms the difference lag set:

$${\mathcal{L}}_{diff}=\mathrm{unique}\left(\mathrm{vec}\left(\mathbf{L}\right)\right)$$

(16)

GICA’s three-layer architecture produces a uniquely structured difference coarray. The contribution from each layer exhibits distinct characteristics:

Layer ${\mathcal{H}}_1$ Contribution: The uniform subarray ${\mathcal{H}}_1$ with positions $\{0,N,2N,\dots ,MN\}$ generates a foundational lag structure:

$${\mathcal{L}}_{{\mathcal{H}}_1}=\{k·N:k\in \mathbb{Z},|k|\le M\}$$

(17)

This creates a periodic sampling pattern with spacing N, forming the backbone of the difference coarray.

Layer ${\mathcal{H}}_2$ Contribution: The golden ratio-based positions ${\{p_i^{\left({\mathcal{H}}_2\right)}=\mathrm{round}(MN+M({\varphi }^i+i))\}}_{i=1}^N$ introduce a revolutionary non-uniform sampling:

$${\mathcal{L}}_{{\mathcal{H}}_2}\supset \{p_i^{\left({\mathcal{H}}_2\right)}-p_j^{\left({\mathcal{H}}_2\right)}:i\ne j\}$$

(18)

The exponential growth rate ${\varphi }^i$ ensures that ${\mathcal{H}}_2$ generates increasingly sparse lags at larger distances, balancing local density with global coverage.

Layer ${\mathcal{H}}_3$ Contribution: The strategic positions $\left\{\mathrm{round}\right(M\varphi ),\mathrm{round}(N\varphi ),\mathrm{round}(MN/\varphi \left)\right\}$ serve as compensators:

$${\mathcal{L}}_{{\mathcal{H}}_3}=\bigcup _{p\in {\mathcal{H}}_3}\{p-q:q\in \mathcal{P}\}$$

(19)

These chosen values fill some of the critical gaps in the combined ${\mathcal{H}}_1$-${\mathcal{H}}_2$ lag distribution.

For the processing of differential arrays, GICA adopts a virtual domain completion strategy to expand the sparse differential lag set to the continuous domain. Define the virtual domain boundaries:

$$L_{min}=\min \left({\mathcal{L}}_{diff}\right),L_{max}=\max \left({\mathcal{L}}_{diff}\right)$$

(20)

Construct the complete virtual lag domain:

$${\mathcal{L}}_{virtual}=\{l\in \mathbb{Z}:L_{min}\le l\le L_{max}\}$$

(21)

This construction process can be formalized as an embedding map:

$$\iota :{\mathcal{L}}_{diff}\hookrightarrow {\mathcal{L}}_{virtual}$$

(22)

Having determined the virtual domain extent $L_{virtual}$, the next step establishes mapping from physical covariance measurements to virtual array responses. Following (5), GICA’s covariance matrix is

$${\widehat{\mathbf{R}}}_x={\displaystyle \frac{1}{T}}\sum _{t=1}^T\mathbf{x}\left(t\right){\mathbf{x}}^H\left(t\right)$$

(23)

For each virtual lag $\mathcal{\ell }\in {\mathcal{L}}_{virtual}$, define its pre-image set in the physical array:

$${\mathcal{I}}_{\mathcal{\ell }}=\{(i,j):L_{ij}=\mathcal{\ell },1\le i,j\le M+N+4\}$$

(24)

The virtual array response is constructed through the following piecewise function:

$$z_{\mathcal{\ell }}=\left\{\begin{array}{cc}{\displaystyle \frac{1}{|{\mathcal{I}}_{\mathcal{\ell }}|}\sum _{(i,j)\in {\mathcal{I}}_{\mathcal{\ell }}}{\left[{\mathbf{R}}_{xx}\right]}_{ij},}\hfill & {\mathcal{I}}_{\mathcal{\ell }}\ne Ø\hfill \\ 0,\hfill & {\mathcal{I}}_{\mathcal{\ell }}=Ø\hfill \end{array}\right.$$

(25)

When ${\mathcal{I}}_{\mathcal{\ell }}\ne Ø$, redundancy is exploited by averaging contributing elements; when ${\mathcal{I}}_{\mathcal{\ell }}=Ø$, zero assignment maintains covariance matrix positive semi-definiteness. The virtual array response preserves original signal second-order statistics. For K uncorrelated far-field sources with powers ${\left\{{\sigma }_k^2\right\}}_{k=1}^K$ and angles ${\left\{{\theta }_k\right\}}_{k=1}^K$, the expected virtual response is

$$\mathbb{E}\left[z_{\mathcal{\ell }}\right]=\sum _{k=1}^K{\sigma }_k^2\exp \left(j{\displaystyle \frac{2\pi d}{\lambda }}\mathcal{\ell }\sin {\theta }_k\right)+{\sigma }_n^2{\delta }_{\mathcal{\ell },0}$$

(26)

where ${\sigma }_n^2$ denotes noise power and ${\delta }_{\mathcal{\ell },0}$ represents the Kronecker delta. This demonstrates the virtual array response is statistically equivalent to a uniform linear array with $(L_{max}-L_{min}+1)$ elements.

Equation (25) completes virtual response construction. The next step constructs these discrete values ${\left\{z_{\mathcal{\ell }}\right\}}_{\mathcal{\ell }\in {\mathcal{L}}_{virtual}}$ into a structured covariance matrix.

First, locate the zero-lag position:

$${\mathcal{\ell }}_0=\mathrm{find}(\mathrm{virtual}\_\mathrm{lags}=0)$$

(27)

Starting from the zero-lag position, extract all non-negative lag responses:

$${\mathbf{z}}_{+}={[z_0,z_1,z_2,\dots ,z_{L_{max}}]}^T$$

(28)

The virtual covariance matrix is constructed via the Toeplitz operation [23]:

$${\mathbf{R}}_T=\mathrm{Toeplitz}({\mathbf{z}}_{+},{\mathbf{z}}_{+}^{\ast })$$

(29)

Its elements satisfy

$${\left[R_T\right]}_{ij}=z_{|i-j|}$$

(30)

This completes GICA’s virtual array construction and the resulting matrix ${\mathbf{R}}_T$ can be directly used for subspace-based DOA estimation.

3.3. Degrees of Freedom Analysis

Building upon Section 3.2’s virtual array construction, GICA’s DOF are determined by the difference coarray’s continuous range. The virtual lag set ${\mathcal{L}}_{virtual}=\{L_{min},L_{min}+1,\dots ,L_{max}\}$ constructed through hole-filling directly translates to available DOF for DOA estimation. GICA’s single-sided DOF can be derived from the virtual array construction process in Section 3.2.

$${\mathrm{DOF}}_{single}=L_{max}+1$$

(31)

For GICA structure, the maximum difference lag is determined by the H2 layer’s furthest element:

$$L_{max}=\mathrm{round}(MN+M({\varphi }^N+N))$$

(32)

Therefore, the single-sided DOF of GICA is

$$\mathrm{DOF}=\mathrm{round}(MN+M({\varphi }^N+N))+1$$

(33)

To quantitatively demonstrate GICA’s performance advantages and verify its innovative value,

Table 1. Comparison of physical sensors and one-sided DOF for various coprime array configurations.

Array Configuration	Physical Sensors	One-Sided DOF
ACA	$N+2M-1$	$MN+M-1$
TCA	$M+N+\lfloor M/2\rfloor -1$	$2M(N+1)-1$
OpCA	$N+2M-1$	$MN+M-1+L_s+M$
NSCA (odd)	$M+N$	$3MN+2M+2N-1$
NSCA (even)	$M+N$	$3MN+2M+2N+(M-1)$
ICA (difference)	$M+N$	$2MN-1$
ICA (difference-sum)	$M+N$	$4MN-1$
GICA	$\mathit{M}+\mathit{N}+4$	$\mathrm{round}(\mathit{MN}+\mathit{M}({\mathit{\varphi }}^{\mathit{N}}+\mathit{N}))+1$

systematically compares physical elements and single-sided DOF of various coprime array configurations. This comparison illustrates how different array design strategies impact DOF performance and how GICA’s unique exponential growth characteristic yields significant advantages for large N values.

4. Simulation Results

4.1. Methodology and Simulation Setup

To evaluate the proposed GICA performance, we employ root mean square error (RMSE) as the primary metric. RMSE is a widely used statistical measure for assessing predictive model accuracy, particularly suitable for regression and estimation tasks. It quantifies deviation between estimated and true values, providing comprehensive algorithm performance evaluation. The RMSE for DOA estimation is defined as

$$\mathrm{RMSE}={\displaystyle \frac{1}{L}}\sum _{j=1}^L\sqrt{{\displaystyle \frac{1}{K}}\sum _{i=1}^K{({\widehat{\theta }}_{i,j}-{\theta }_i)}^2}$$

(34)

where L represents the number of Monte Carlo simulation trials, ensuring statistical reliability, K denotes the number of signal sources, ${\widehat{\theta }}_{i,j}$ is the DOA estimate of the ith source in the jth trial, and ${\theta }_i$ is the true direction angle of the ith source.

All simulations use a unit element spacing of $d=\lambda /2$ (half-wavelength spacing), which is the standard practice in sparse array design to avoid spatial aliasing while maximizing aperture. To evaluate the performance of different array structures, this study compares GICA, ICA, SCA, and OpCA. All DOA estimations use the ESPRIT algorithm after Toeplitz matrix reconstruction, with physical array elements fixed at 15 for fair comparison. Each estimation is based on 500 independent Monte Carlo trials for statistical reliability. The Cramér–Rao Bound (CRB) [28] is also introduced as a theoretical reference curve to assess the estimation efficiency. Performance evaluation is conducted under two signal source scenarios: three sources (angles at [11.5°, 22.8°, 30°]) and five sources (angles at [10°, 20°, 30°, 40°, 50°]).

For mutual coupling analysis, coupling leakage $L_{CL}$ serves as the primary evaluation metric [13,21] and is calculated as

$$L_{CL}={\displaystyle \frac{{\parallel C-\mathrm{diag}\left(C\right)\parallel }_F}{{\parallel C\parallel }_F}}$$

(35)

where C is the mutual coupling matrix, and ${\parallel ·\parallel }_F$ denotes the Frobenius norm. This indicator effectively reflects the relative intensity of non-diagonal coupling elements to the overall coupling matrix in the array, with smaller values indicating weaker mutual coupling effects.

The following experiments are designed to comprehensively evaluate GICA’s performance:

Experiment 1—SNR Variation: With a fixed snapshot count of 256, DOA estimation RMSE curves are plotted as a function of SNR. SNR varies from $-10$ dB to 20 dB with 5 dB steps to examine performance under different noise conditions.

Experiment 2—Snapshot Variation: With SNR maintained at 20 dB and utilizing the same array configuration as the previous experiment, RMSE performance is systematically examined as a function of varying snapshot numbers. Snapshot count increases from 8 to 298 with 36 steps to assess how estimation accuracy is affected by the quantity of available measurement samples.

Experiment 3—Mutual Coupling Analysis: This experiment comprehensively evaluates the mutual coupling resistance performance of different array structures by calculating the coupling leakage indicator $L_{CL}$, analyzing mutual coupling matrix heatmaps, and examining weight function distributions. To ensure fair comparison, the number of physical array elements is consistently maintained at 15 for all array structures. The primary coupling coefficient is characterized by $c_1=0.3e^{j\pi /3}$, with a distance threshold of $B=10$.

Experiment 4—Coupling Strength Variation: Three signal sources are configured with identical angles as Experiment 1’s three-source scenario. SNR is set to −5 dB and 10 dB with 256 snapshots. Mutual coupling effects are introduced with coupling strength varying from 0.1 to 0.9 across 500 Monte Carlo simulations. DOA estimation uses the same method as Experiment 1.

4.2. Results and Analysis

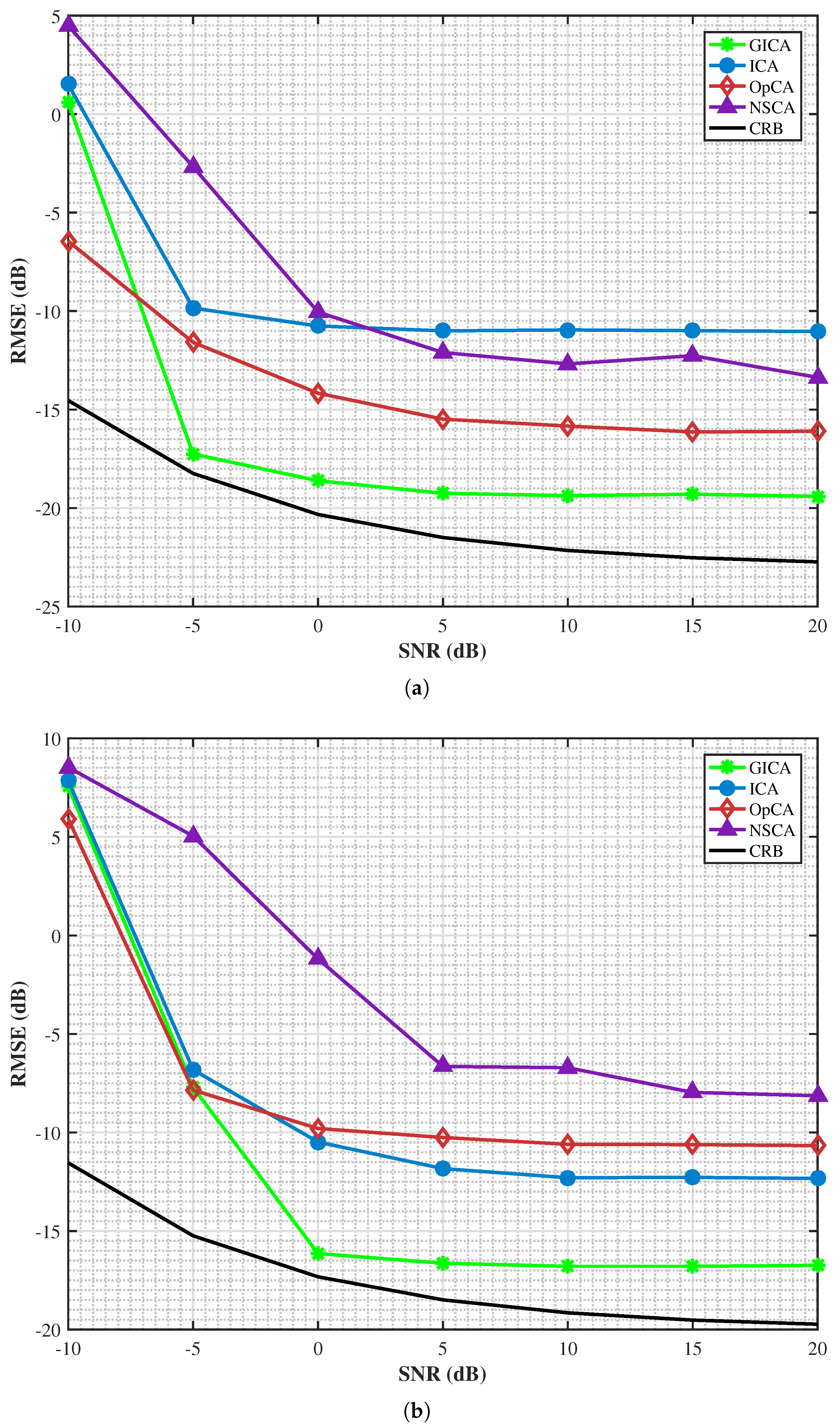
Figure 3 illustrates RMSE performance for both scenarios as a function of SNR. As shown in Figure 3a,b, estimation performance of all array structures improves as SNR increases from $-10$ dB to 20 dB. The proposed GICA generally exhibits the best performance across the entire SNR range in both scenarios (though slightly inferior to OpCA in very few ranges), with particularly significant advantages in the higher SNR region (≥−5 dB), demonstrating substantially lower RMSE values compared to other structures.

Figure 4 illustrates the RMSE performance for both the 3-source and 5-source scenarios as a function of snapshot number. As shown in Figure 4a,b, the estimation performance of all array structures improves as the snapshot number increases from 8 to 298. The proposed GICA structure generally exhibits the best performance across the entire snapshot range in both testing scenarios (though slightly inferior to OpCA and ICA in very few ranges), with particularly significant advantages in the higher snapshot region (≥100), demonstrating substantially lower RMSE values compared to other structures.

The preceding results of experiments (1–2) have validated GICA’s DOA estimation performance, which benefits from virtual domain optimization where the difference coarray construction through ${\mathcal{H}}_2$’s exponential growth and ${\mathcal{H}}_3$’s strategic positioning expands the effective aperture via Toeplitz reconstruction. The following experiments (3–4) examine GICA’s physical domain optimization, where golden ratio-based sensor placement in ${\mathcal{H}}_2$ creates naturally dispersed spacings that reduce closely spaced element pairs, thereby suppressing electromagnetic mutual coupling. This physical arrangement directly influences the weight function $w\left(m\right)$ and coupling leakage metric $L_{CL}$. These dual-domain mechanisms work synergistically: virtual processing enhances DOA estimation capability while physical design ensures robust hardware implementation with reduced coupling.

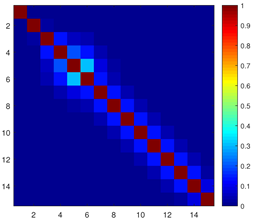
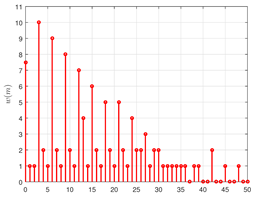
To systematically evaluate mutual coupling resistance performance across different array structures, this study compares GICA, ICA, OpCA, and NSCA using key metrics: weight function $w\left(m\right)$, mutual coupling matrix C, and coupling leakage $L_{CL}$. The analysis examines how these structures mitigate mutual coupling effects, which are critical for accurate DOA estimation. The experimental results are presented in

Table 2. Comparison of mutual coupling characteristics of different array structures.

	${\mathit{L}}_{\mathbf{CL}}$	C	$\mathit{w}\left(\mathit{m}\right)$	Physical_pos
GICA	0.1526
ICA	0.2261
OpCA	0.2054
NSCA	0.2103

.

As shown in Table 2, GICA exhibits an $L_{CL}$ value of 0.1526, significantly lower than those of ICA (0.2261), OpCA (0.2054), and NSCA (0.2103). This demonstrates that GICA has the minimum coupling leakage value, indicating its superior mutual coupling resistance capability compared to the other three array structures.

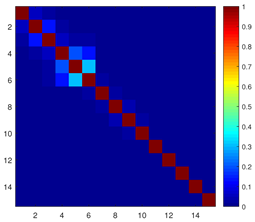
From the mutual coupling matrix heatmaps (C) in Table 2, it can be observed that GICA’s coupling matrix displays deeper blue tones in the non-diagonal regions, indicating generally lower coupling intensity. In contrast, the coupling matrices of ICA, OpCA, and NSCA exhibit brighter cyan to yellow transition tones in multiple non-diagonal regions, revealing higher degrees of mutual coupling at these positions, which further confirms the comparative results of the $L_{CL}$ values.

Examining the weight function distributions of the four array structures in Table 2, GICA demonstrates relatively uniform spatial distribution, with first three weight values of (1, 1, 2) and maximum weight not exceeding 7.5. This balanced distribution effectively reduces spatial correlation concentration, suppressing mutual coupling effects. In comparison, ICA, OpCA, and NSCA exhibit significant non-uniformity with multiple high peaks (maximums of 8, 9, and 10, respectively), increasing spatial correlation and leading to stronger mutual coupling effects, consistent with $L_{CL}$ value trends.

Based on the above analysis, GICA demonstrates superior mutual coupling resistance across multiple dimensions, including weight function distribution, coupling matrix characteristics, and coupling leakage indicators. This feature holds significant importance in practical DOA estimation applications, where GICA’s mutual coupling resistance advantage translates into more robust and accurate direction angle estimation performance.

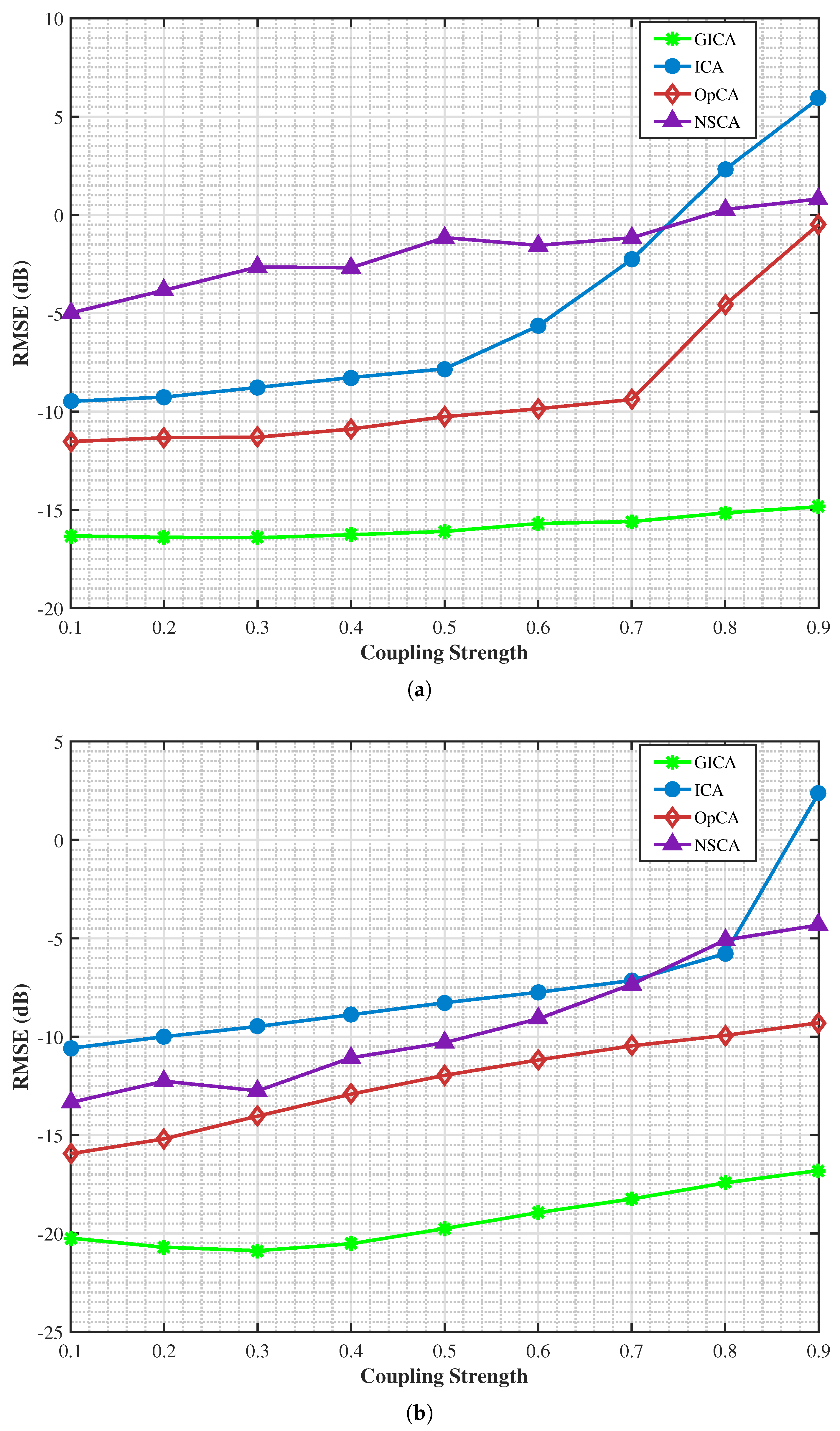
Figure 5a,b show RMSE trends with increasing coupling strength under SNR = −5 dB and SNR = 10 dB, respectively. Under both SNR conditions, all array structures show increasing RMSE as coupling strength rises from 0.1 to 0.9, indicating mutual coupling significantly degrades DOA estimation accuracy. However, GICA maintains the lowest RMSE values across the entire coupling strength range with the smallest performance degradation slope, demonstrating superior mutual coupling resistance. These results align with previous mutual coupling resistance analysis.

5. Conclusions

This paper introduces the GICA, a novel coprime array structure that enhances DOA estimation capabilities. The GICA design uniquely incorporates the golden ratio ($\varphi \approx 1.618$) to optimize sensor distribution across three strategically designed subarrays, resulting in significantly improved difference coarray properties. The theoretical analysis demonstrates that the proposed GICA structure, which combines with efficient virtual domain processing, effectively increases the available DOF in the virtual array domain. GICA leverages an optimized geometric configuration that improves effective aperture while reducing mutual coupling effects. Through comprehensive simulations, GICA structure demonstrates superior DOA estimation performance compared to existing array structures (ICA, OpCA, and NSCA), particularly in moderate-to-high SNR environments and with sufficient snapshot numbers. The analysis of mutual coupling effects reveals that GICA structure achieves the lowest coupling leakage coefficient among tested configurations, enabling it to maintain stable estimation accuracy even under strong electromagnetic interference conditions. Its enhanced DOA estimation capability and excellent immunity to mutual coupling are demonstrated, proving its value as a robust solution for practical direction finding applications.