Reinforcement Learning Enhanced Multi-Objective Social Network Search Algorithm for Engineering Design Problems
Abstract
1. Introduction
- The proposed QMOSNS enhances population diversity through Halton sequence initialization and maintains a multi-objective archive for storing Pareto-optimal solutions and selecting parent individuals. Moreover, Q-learning is integrated to dynamically adjust user behavior modes within the SNS framework, improving the balance between exploration and exploitation;
- The performance of QMOSNS was rigorously evaluated on a suite of test problems, including constrained and unconstrained benchmarks as well as engineering design problems. The algorithm was compared against state-of-the-art MOO methods using two performance metrics, with the results validated by statistical tests, robustness analysis, and Pareto front visualizations;
- Analysis shows that QMOSNS successfully handles MOPs, achieving well-balanced Pareto fronts across diverse benchmarks and engineering applications. Comparative results confirm its highly competitive performance, outperforming other algorithms in most cases.
2. Background
2.1. Multi-Objective Optimization
2.1.1. Pareto Dominance
2.1.2. Pareto Optimality
2.1.3. Pareto Optimal Set
2.1.4. Pareto Optimal Front
2.2. Multi-Objective Performance Metrics
2.2.1. Inverted Generational Distance
2.2.2. Hypervolume
3. Social Network Search Algorithm
3.1. Imitation Mood
3.2. Conversation Mood
3.3. Disputation Mood
3.4. Innovation Mood
3.5. Network Rules
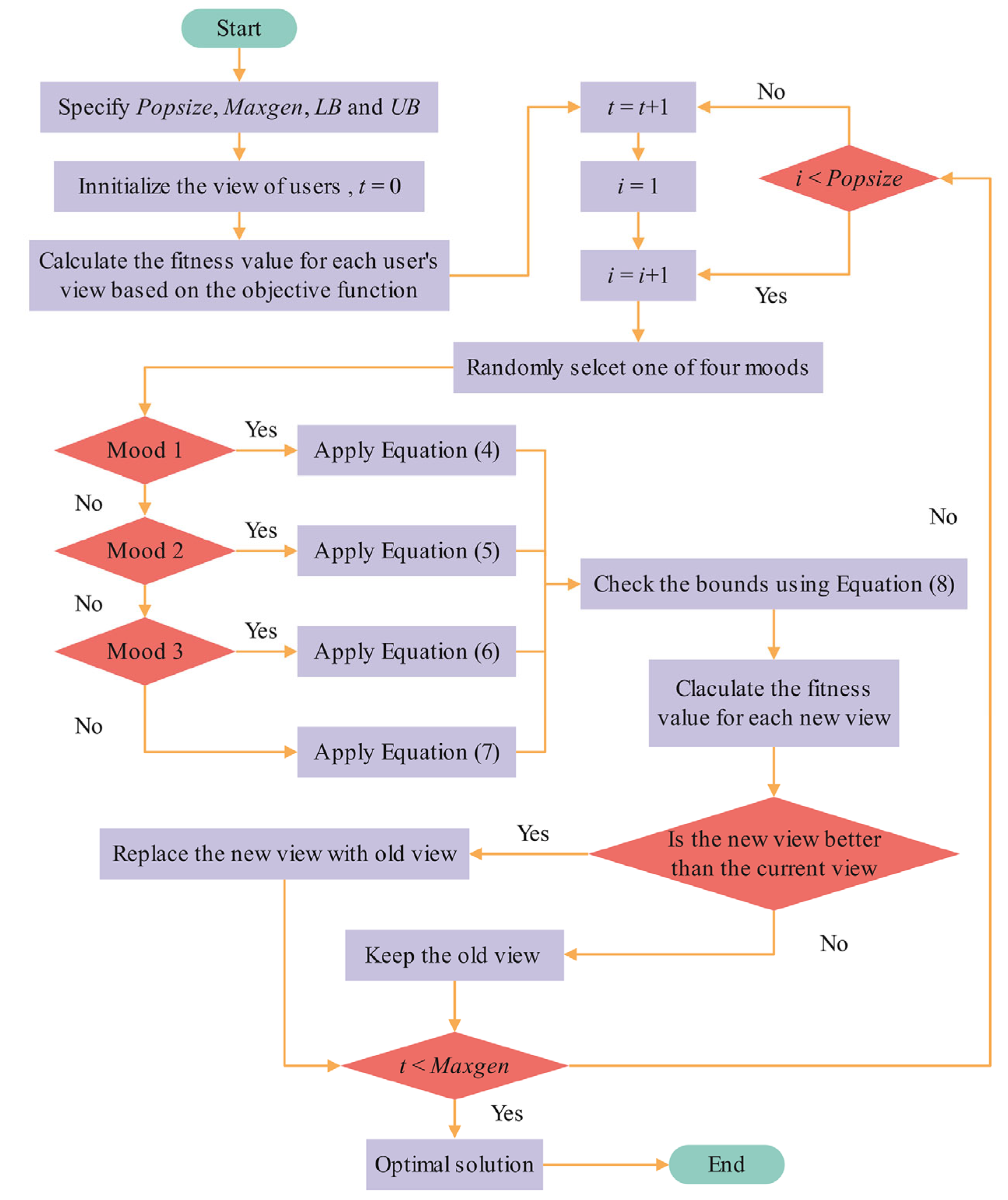
4. The Proposed QMOSNS
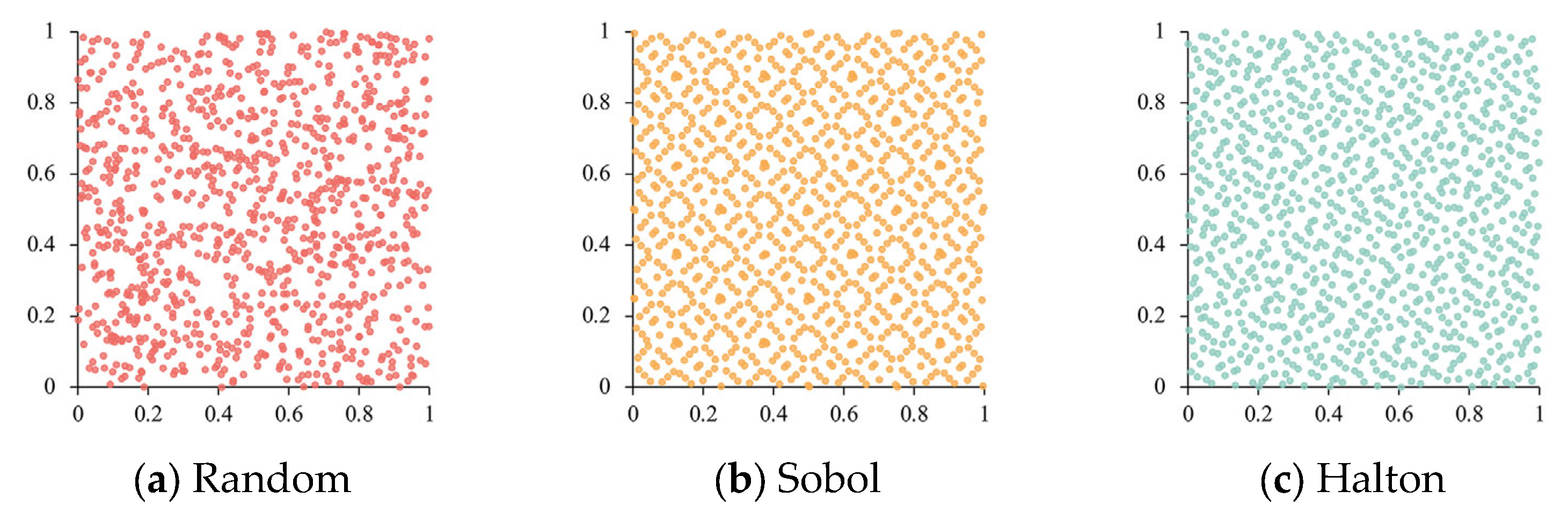
4.1. Population Initialization Based on Halton Sequence
4.2. Multi-Objective Archive
- If the number of solutions satisfying < 1 is precisely equal to N, these solutions are stored in the A;
- If the number of solutions satisfying < 1 exceeds N, the top N solutions are selected based on and stored in the A;
- If the number of solutions satisfying < 1 is less than N, then the k compliant solutions are stored in the A, and the remaining (N – k) solutions are selected from the top-ranked candidates based on and stored in the A.
4.3. Q-Learning-Based Mood Selection Strategy
- State 1 (): Both HV and CV improve simultaneously;
- State 2 (): Only the HV improves;
- State 3 (): Only the CV improves;
- State 4 (): There is no improvement in either HV or CV.
| Algorithm 1 QMOSNS Algorithm |
| Input: Popsize: Number of population, Maxgen: Maximum iterations, D: Dimension size, UB: Upper bound of a variable, LB: Lower bound of a variable. |
| Output: Return the archive. |
| Initialize the Q-table. |
| Initialize the population using Halton sequence. |
| Calculate the fitness value of each individual in the population. |
| Update the archive. |
| for t = 1: Maxgen |
| if t = 1 |
| Randomly select a mood. |
| else |
| Select a mood using the Q-table. |
| End if |
| Generate offspring using the selected mood. |
| Calculate the fitness value of each individual in the offspring. |
| Update the archive and select parent solutions. |
| Update the Q-table. |
| end for |
4.4. Computational Complexity
5. Numerical Examples and Results
5.1. Experimental Setup
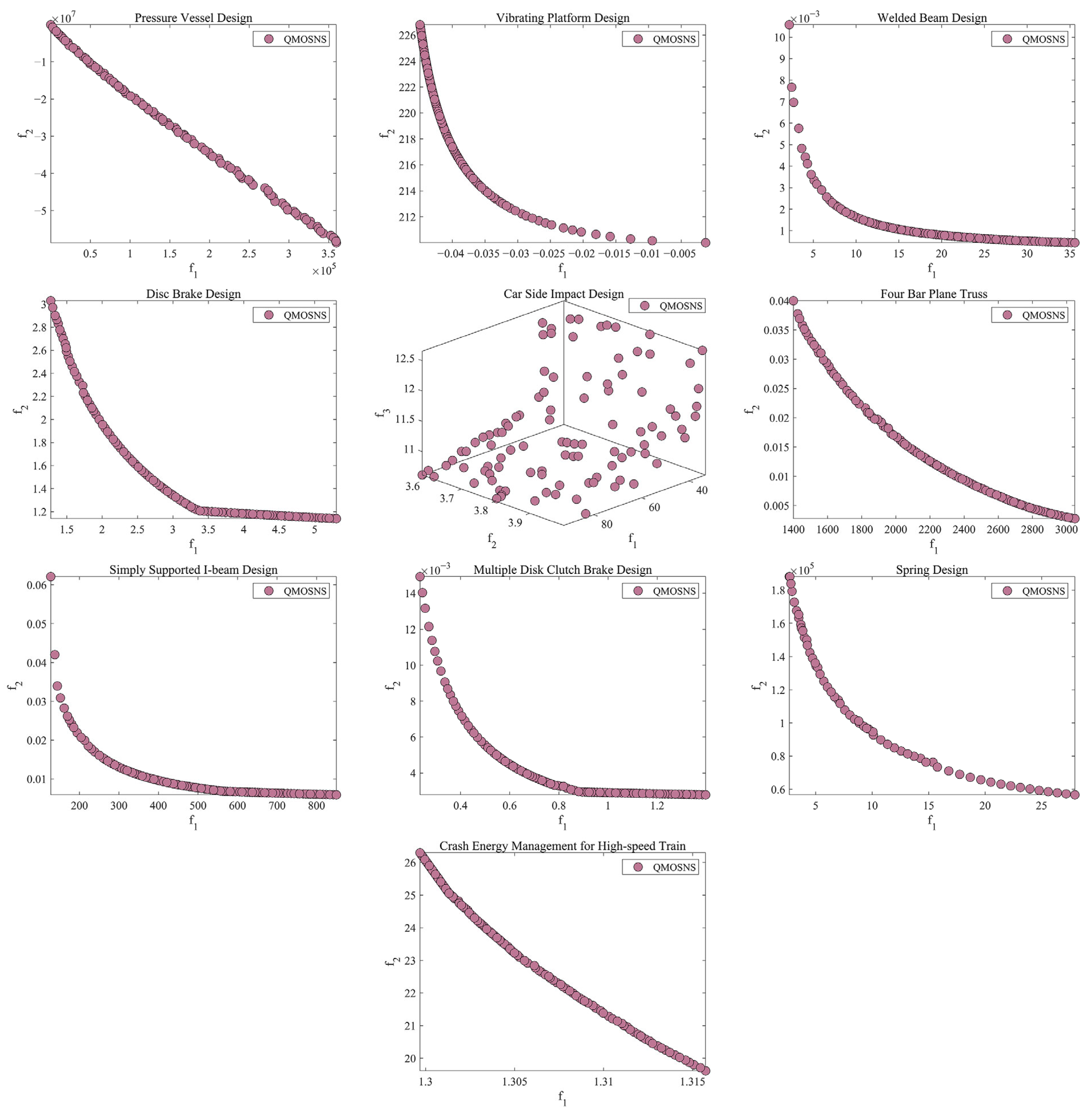
- Multi-objective engineering design problems: Pressure Vessel Design [52], Vibrating Platform Design [53], Welded Beam Design [54], Disc Brake Design [55], Car Side Impact Design [50], Four Bar Plane Truss [56], Multiple Disk Clutch Brake Design [57], Spring Design [52], Multi-product Batch Plant [58], Crash Energy Management for High-speed Train [59].
5.2. Multi-Objective Benchmark Problems
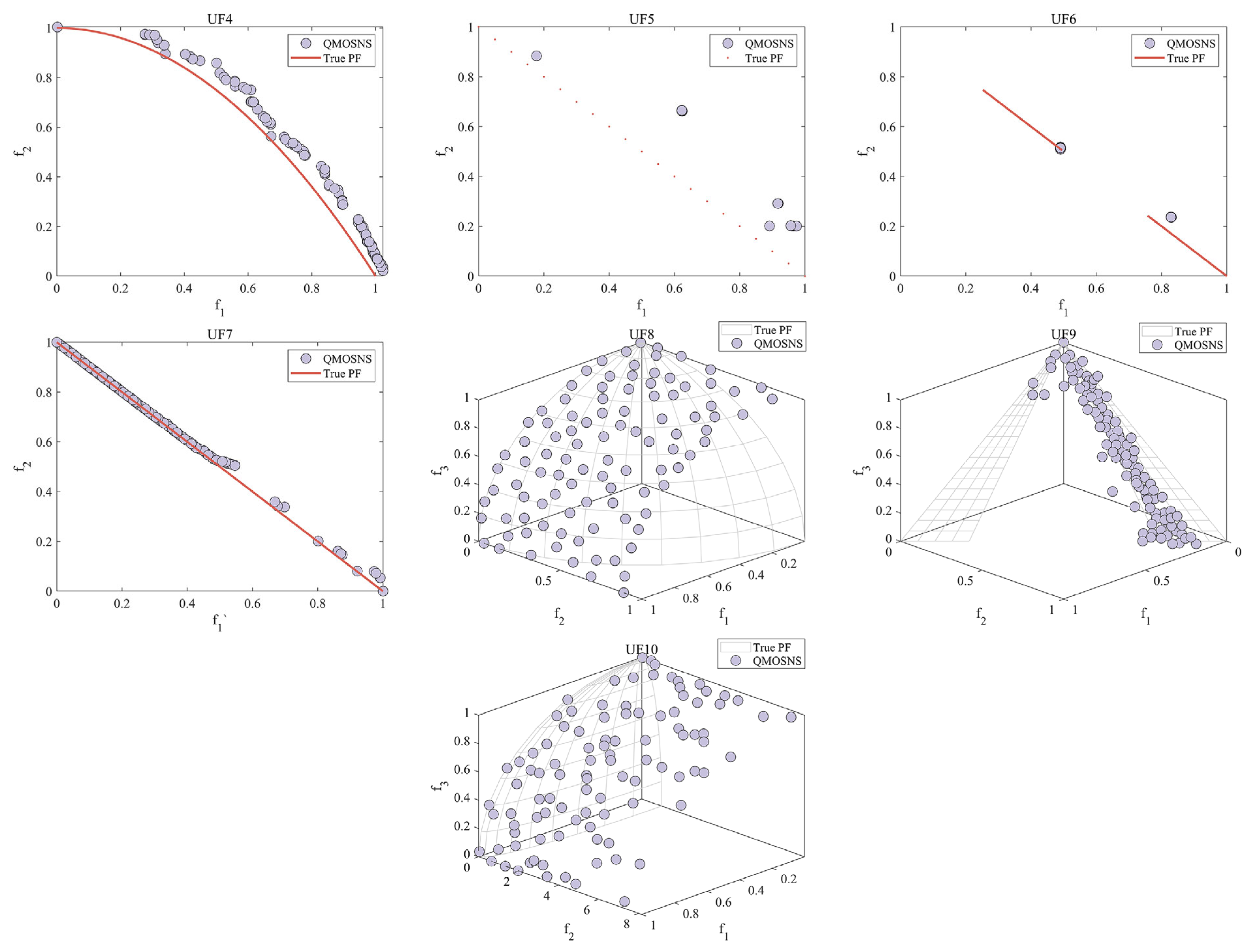
5.2.1. Unconstrained Multi-Objective Problems
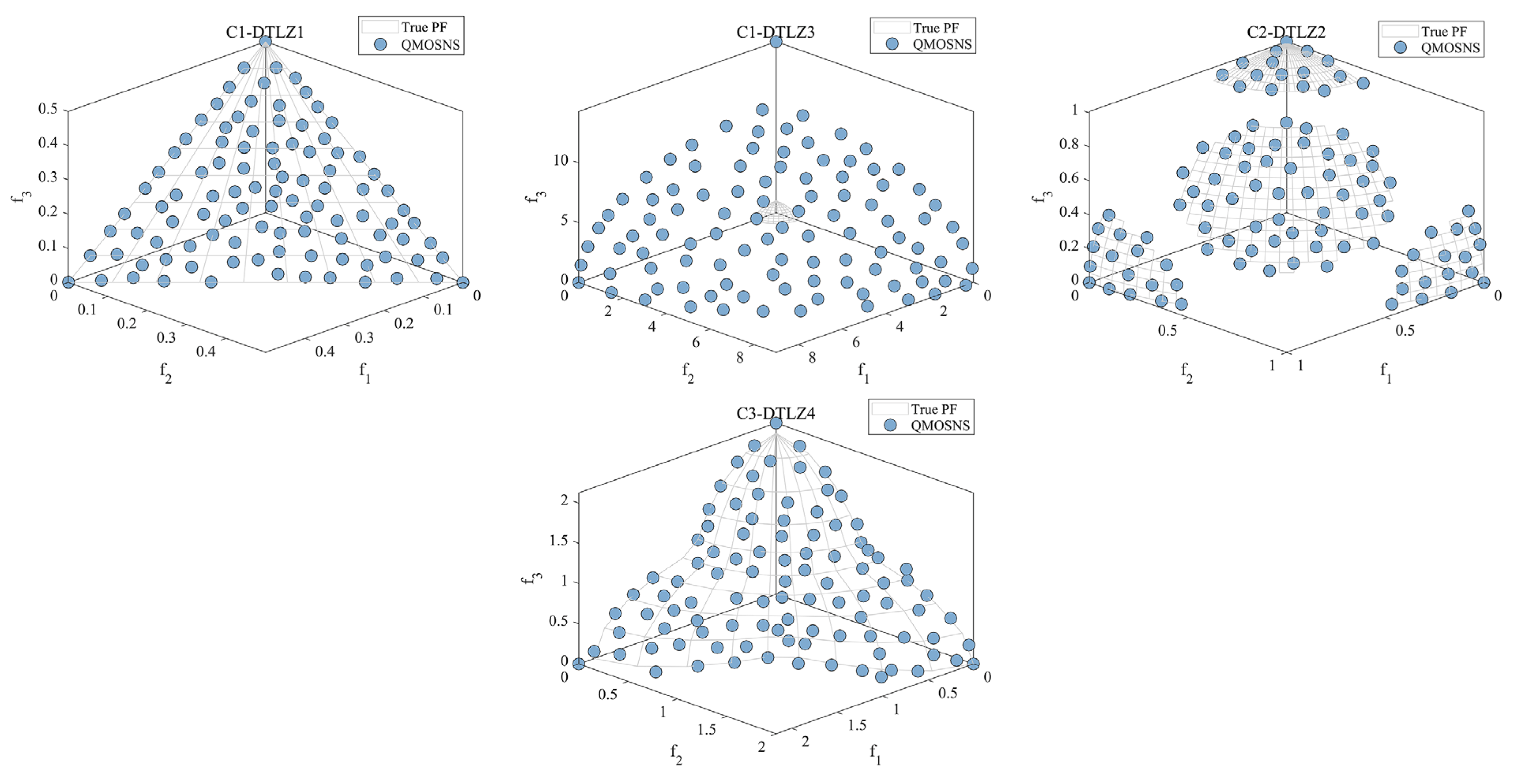
5.2.2. Constrained Multi-Objective Problems
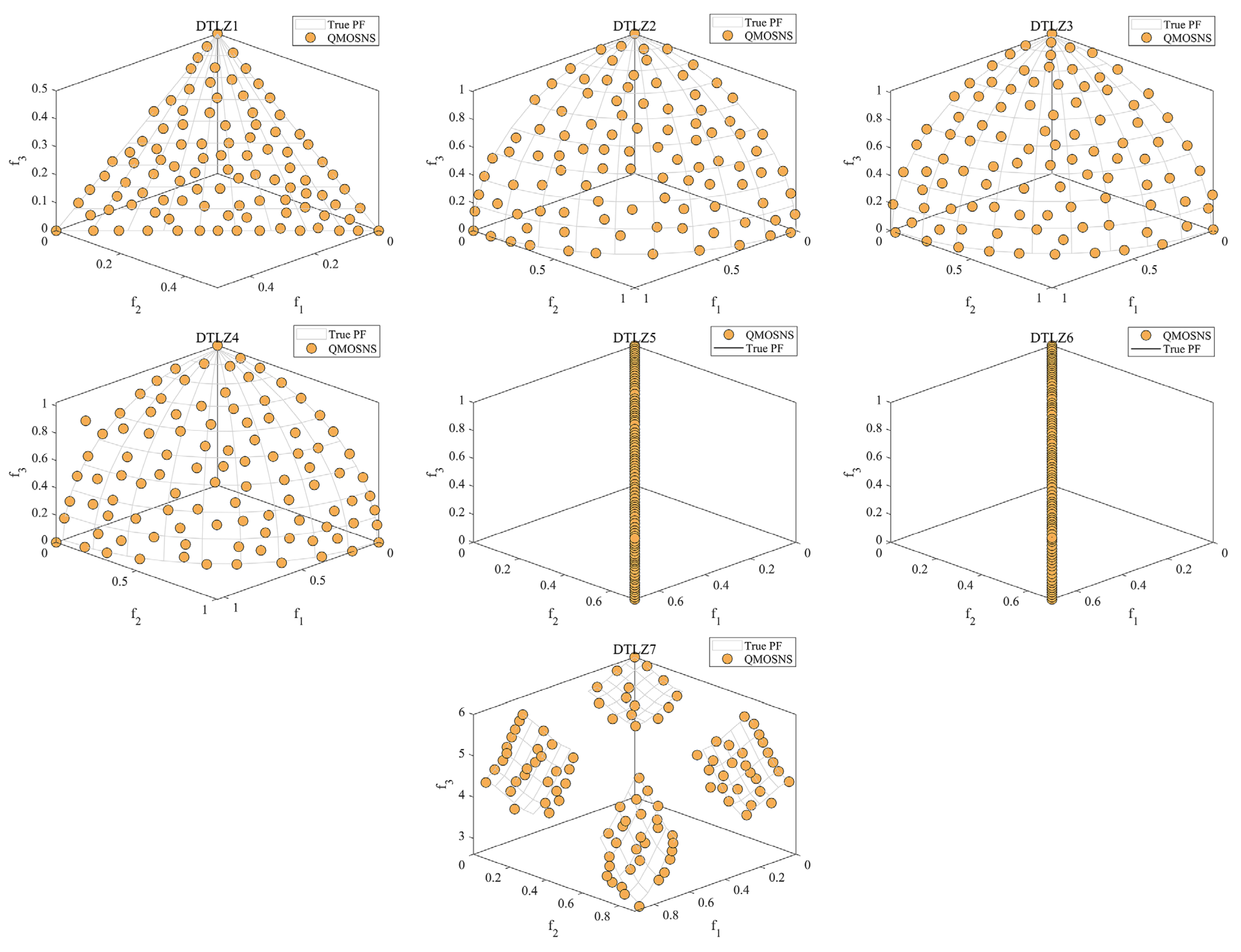
5.3. Multi-Objective Engineering Design Problems
5.4. Ablation Study on Initialization Strategy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, M.; Wang, Z.; Chen, H.; Cao, Y.; Ma, L. Multi-Objective Evolutionary Algorithm Based on Decomposition with Orthogonal Experimental Design. Expert Syst. 2025, 42, e13802. [Google Scholar] [CrossRef]
- Yin, L.; Sun, Z. Distributed Multi-Objective Grey Wolf Optimizer for Distributed Multi-Objective Economic Dispatch of Multi-Area Interconnected Power Systems. Appl. Soft Comput. 2022, 117, 108345. [Google Scholar] [CrossRef]
- Tang, J.; Dou, T.; Wu, F.; Hu, L.; Yu, T. Scheduling Optimization of a Vehicle Power Battery Workshop Based on an Improved Multi-Objective Particle Swarm Optimization Method. Mathematics 2025, 13, 2790. [Google Scholar] [CrossRef]
- Méndez, M.; Rossit, D.A.; González, B.; Frutos, M. Proposal and Comparative Study of Evolutionary Algorithms for Optimum Design of a Gear System. IEEE Access 2020, 8, 3482–3497. [Google Scholar] [CrossRef]
- Zhou, X.; Cai, X.; Zhang, H.; Zhang, Z.; Jin, T.; Chen, H.; Deng, W. Multi-Strategy Competitive-Cooperative Co-Evolutionary Algorithm and Its Application. Inf. Sci. 2023, 635, 328–344. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. The Weighted Sum Method for Multi-Objective Optimization: New Insights. Struct. Multidiscip. Optim. 2010, 41, 853–862. [Google Scholar] [CrossRef]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-Objective Optimization Using Genetic Algorithms: A Tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A Bio-Inspired Optimizer for Engineering Design Problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Mirjalili, S.; Jangir, P.; Saremi, S. Multi-Objective Ant Lion Optimizer: A Multi-Objective Optimization Algorithm for Solving Engineering Problems. Appl. Intell. 2017, 46, 79–95. [Google Scholar] [CrossRef]
- Premkumar, M.; Jangir, P.; Sowmya, R.; Alhelou, H.H.; Heidari, A.A.; Chen, H. MOSMA: Multi-Objective Slime Mould Algorithm Based on Elitist Non-Dominated Sorting. IEEE Access 2021, 9, 3229–3248. [Google Scholar] [CrossRef]
- Kalita, K.; Jangir, P.; Pandya, S.B.; Cep, R.; Abualigah, L.; Migdady, H.; Daoud, M.S. Many-Objective Artificial Hummingbird Algorithm: An Effective Many-Objective Algorithm for Engineering Design Problems. J. Comput. Des. Eng. 2024, 11, 16–39. [Google Scholar] [CrossRef]
- Schaffer, J.D. Multiple Objective Optimization with Vector Evaluated Genetic Algorithms. In Proceedings of the First International Conference on Genetic Algorithms and Their Applications, Pittsburgh, PA, USA, 24–26 July 1985; Lawrence Erlbaum: Hillsdale, NJ, USA, 1985; pp. 93–100. [Google Scholar]
- Srinivas, N.; Deb, K. Multiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling Multiple Objectives with Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Fu, S.; Li, K.; Huang, H.; Ma, C.; Fan, Q.; Zhu, Y. Red-Billed Blue Magpie Optimizer: A Novel Metaheuristic Algorithm for 2D/3D UAV Path Planning and Engineering Design Problems. Artif. Intell. Rev. 2024, 57, 134. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.d.S. Multi-Objective Grey Wolf Optimizer: A Novel Algorithm for Multi-Criterion Optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Sadollah, A.; Eskandar, H.; Kim, J. Water Cycle Algorithm for Solving Constrained Multi-Objective Optimization Problems. Appl. Soft Comput. 2015, 27, 279–298. [Google Scholar] [CrossRef]
- Ganesh, N.; Shankar, R.; Kalita, K.; Jangir, P.; Oliva, D.; Perez-Cisneros, M. A Novel Decomposition-Based Multi-Objective Symbiotic Organism Search Optimization Algorithm. Mathematics 2023, 11, 1898. [Google Scholar] [CrossRef]
- Khodadadi, N.; Soleimanian Gharehchopogh, F.; Mirjalili, S. MOAVOA: A New Multi-Objective Artificial Vultures Optimization Algorithm. Neural Comput. Appl. 2022, 34, 20791–20829. [Google Scholar] [CrossRef]
- Rahman, C.M.; Mohammed, H.M.; Abdul, Z.K. Multi-Objective Group Learning Algorithm with a Multi-Objective Real-World Engineering Problem. Appl. Soft Comput. 2024, 166, 112145. [Google Scholar] [CrossRef]
- Khodadadi, N.; Abualigah, L.; Mirjalili, S. Multi-Objective Stochastic Paint Optimizer (MOSPO). Neural Comput. Appl. 2022, 34, 18035–18058. [Google Scholar] [CrossRef]
- Lin, W.; Yu, D.Y.; Zhang, C.; Liu, X.; Zhang, S.; Tian, Y.; Liu, S.; Xie, Z. A Multi-Objective Teaching−learning-Based Optimization Algorithm to Scheduling in Turning Processes for Minimizing Makespan and Carbon Footprint. J. Clean. Prod. 2015, 101, 337–347. [Google Scholar] [CrossRef]
- Tawhid, M.A.; Savsani, V. Multi-Objective Sine-Cosine Algorithm (MO-SCA) for Multi-Objective Engineering Design Problems. Neural Comput. Appl. 2019, 31, 915–929. [Google Scholar] [CrossRef]
- Yang, Z.; Hu, X.; Li, Y.; Liang, M.; Wang, K.; Wang, L.; Tang, H.; Guo, S. A Q-Learning-Based Improved Multi-Objective Genetic Algorithm for Solving Distributed Heterogeneous Assembly Flexible Job Shop Scheduling Problems with Transfers. J. Manuf. Syst. 2025, 79, 398–418. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, Q.; Zhang, L.; Li, Z.; Cheng, L. A Q-Learning-Based Multi-Population Algorithm for Multi-Objective Distributed Heterogeneous Assembly No-Idle Flowshop Scheduling with Batch Delivery. Expert Syst. Appl. 2025, 263, 125690. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, S. A Q-Learning Multi-Objective Grey Wolf Optimizer for the Distributed Hybrid Flowshop Scheduling Problem. Eng. Optim. 2024, 57, 2609–2628. [Google Scholar] [CrossRef]
- Zhang, Z.; Shao, Z.; Shao, W.; Chen, J.; Pi, D. MRLM: A Meta-Reinforcement Learning-Based Metaheuristic for Hybrid Flow-Shop Scheduling Problem with Learning and Forgetting Effects. Swarm Evol. Comput. 2024, 85, 101479. [Google Scholar] [CrossRef]
- Huang, Y.; Guo, Y.; Chen, G.; Wei, H.; Zhao, X.; Yang, S.; Ge, S. Q-Learning Assisted Multi-Objective Evolutionary Optimization for Low-Carbon Scheduling of Open-Pit Mine Trucks. Swarm Evol. Comput. 2025, 92, 101778. [Google Scholar] [CrossRef]
- Ebrie, A.S.; Kim, Y.J. Reinforcement Learning-Based Multi-Objective Optimization for Generation Scheduling in Power Systems. Systems 2024, 12, 106. [Google Scholar] [CrossRef]
- Zheng, R.; Zhang, Y.; Sun, X.; Yang, L.; Song, X. A Reinforcement Learning-Assisted Multi-Objective Evolutionary Algorithm for Generating Green Change Plans of Complex Products. Appl. Soft Comput. 2025, 170, 112660. [Google Scholar] [CrossRef]
- Qi, R.; Li, J.; Wang, J.; Jin, H.; Han, Y. QMOEA: A Q-Learning-Based Multiobjective Evolutionary Algorithm for Solving Time-Dependent Green Vehicle Routing Problems with Time Windows. Inf. Sci. 2022, 608, 178–201. [Google Scholar] [CrossRef]
- Huy, T.H.B.; Nallagownden, P.; Truong, K.H.; Kannan, R.; Vo, D.N.; Ho, N. Multi-Objective Search Group Algorithm for Engineering Design Problems. Appl. Soft Comput. 2022, 126, 109287. [Google Scholar] [CrossRef]
- Adam, S.P.; Alexandropoulos, S.-A.N.; Pardalos, P.M.; Vrahatis, M.N. No Free Lunch Theorem: A Review. In Approximation and Optimization: Algorithms, Complexity and Applications; Demetriou, I.C., Pardalos, P.M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 57–82. ISBN 978-3-030-12767-1. [Google Scholar]
- Talatahari, S.; Bayzidi, H.; Saraee, M. Social Network Search for Global Optimization. IEEE Access 2021, 9, 92815–92863. [Google Scholar] [CrossRef]
- Zamli, K.Z.; Alhadawi, H.S.; Din, F. Utilizing the Roulette Wheel Based Social Network Search Algorithm for Substitution Box Construction and Optimization. Neural Comput. Appl. 2023, 35, 4051–4071. [Google Scholar] [CrossRef]
- M. Shaheen, A.; El-Sehiemy, R.A.; Hasanien, H.M.; Ginidi, A. An Enhanced Optimizer of Social Network Search for Multi-Dimension Optimal Power Flow in Electrical Power Grids. Int. J. Electr. Power Energy Syst. 2024, 155, 109572. [Google Scholar] [CrossRef]
- Han, H.; Zhang, L.; Yinga, A.; Qiao, J. Adaptive Multiple Selection Strategy for Multi-Objective Particle Swarm Optimization. Inf. Sci. 2023, 624, 235–251. [Google Scholar] [CrossRef]
- Sierra, M.R.; Coello Coello, C.A. Improving PSO-Based Multi-Objective Optimization Using Crowding, Mutation and ε-Dominance. In Evolutionary Multi-Criterion Optimization; Coello Coello, C.A., Hernández Aguirre, A., Zitzler, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 505–519. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective Evolutionary Algorithms: A Comparative Case Study and the Strength Pareto Approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Li, Q.; Liu, S.-Y.; Yang, X.-S. Influence of Initialization on the Performance of Metaheuristic Optimizers. Appl. Soft Comput. 2020, 91, 106193. [Google Scholar] [CrossRef]
- Tharwat, A.; Schenck, W. Population Initialization Techniques for Evolutionary Algorithms for Single-Objective Constrained Optimization Problems: Deterministic vs. Stochastic Techniques. Swarm Evol. Comput. 2021, 67, 100952. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; ETH Zurich, Computer Engineering and Networks Laboratory: Zurich, Switzerland, 2001. [Google Scholar]
- Xia, M.; Dong, M. A Novel Two-Archive Evolutionary Algorithm for Constrained Multi-Objective Optimization with Small Feasible Regions. Knowl.-Based Syst. 2022, 237, 107693. [Google Scholar] [CrossRef]
- Gao, M.; Gao, K.; Ma, Z.; Tang, W. Ensemble Meta-Heuristics and Q-Learning for Solving Unmanned Surface Vessels Scheduling Problems. Swarm Evol. Comput. 2023, 82, 101358. [Google Scholar] [CrossRef]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of Multiobjective Evolutionary Algorithms: Empirical Results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable Test Problems for Evolutionary Multiobjective Optimization. In Evolutionary Multiobjective Optimization: Theoretical Advances and Applications; Abraham, A., Jain, L., Goldberg, R., Eds.; Springer: London, UK, 2005; pp. 105–145. ISBN 978-1-84628-137-2. [Google Scholar]
- Zhang, Q.; Zhou, A.; Zhao, S.; Suganthan, P.N.; Liu, W.; Tiwari, S. Multiobjective Optimization Test Instances for the CEC 2009 Special Session and Competition. In Special Session on Performance Assessment of Multi-Objective Optimization Algorithms, Technical Report; University of Essex: Colchester, UK; Nanyang Technological University: Singapore, 2008. [Google Scholar]
- Jain, H.; Deb, K. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. IEEE Trans. Evol. Comput. 2014, 18, 602–622. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Y. Evolutionary Constrained Multiobjective Optimization: Test Suite Construction and Performance Comparisons. IEEE Trans. Evol. Comput. 2019, 23, 972–986. [Google Scholar] [CrossRef]
- Narayanan, S.; Azarm, S. On Improving Multiobjective Genetic Algorithms for Design Optimization. Struct. Optim. 1999, 18, 146–155. [Google Scholar] [CrossRef]
- Chiandussi, G.; Codegone, M.; Ferrero, S.; Varesio, F.E. Comparison of Multi-Objective Optimization Methodologies for Engineering Applications. Comput. Math. Appl. 2012, 63, 912–942. [Google Scholar] [CrossRef]
- Deb, K. Evolutionary Algorithms for Multi-Criterion Optimization in Engineering Design. Evol. Algorithms Eng. Comput. Sci. 1999, 2, 135–161. [Google Scholar]
- Kumar, A.; Wu, G.; Ali, M.; Luo, Q.; Mallipeddi, R.; Suganthan, P.; Das, S. A Benchmark-Suite of Real-World Constrained Multi-Objective Optimization Problems and Some Baseline Results. Swarm Evol. Comput. 2021, 67, 100961. [Google Scholar] [CrossRef]
- Cheng, F.Y.; Li, X.S. Generalized Center Method for Multiobjective Engineering Optimization. Eng. Optim. 1999, 31, 641–661. [Google Scholar] [CrossRef]
- Steven, G. Evolutionary Algorithms for Single and Multicriteria Design Optimization. Struct. Multidisc. Optim. 2002, 24, 88–89. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Multi-Objective Spotted Hyena Optimizer: A Multi-Objective Optimization Algorithm for Engineering Problems. Knowl.-Based Syst. 2018, 150, 175–197. [Google Scholar] [CrossRef]
- Zhang, H.; Peng, Y.; Hou, L.; Tian, G.; Li, Z. A Hybrid Multi-Objective Optimization Approach for Energy-Absorbing Structures in Train Collisions. Inf. Sci. 2019, 481, 491–506. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Cheng, F.; Jin, Y. An Indicator-Based Multiobjective Evolutionary Algorithm with Reference Point Adaptation for Better Versatility. IEEE Trans. Evol. Comput. 2018, 22, 609–622. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, Q.; Lin, Q. A Constrained Multiobjective Evolutionary Algorithm with Detect-and-Escape Strategy. IEEE Trans. Evol. Comput. 2020, 24, 938–947. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, Z.; Yen, G.G.; Zhang, L. Two-Stage Multiobjective Evolution Strategy for Constrained Multiobjective Optimization. IEEE Trans. Evol. Comput. 2024, 28, 17–31. [Google Scholar] [CrossRef]
- Fan, Z.; Li, W.; Cai, X.; Li, H.; Wei, C.; Zhang, Q.; Deb, K.; Goodman, E. Push and Pull Search for Solving Constrained Multi-Objective Optimization Problems. Swarm Evol. Comput. 2019, 44, 665–679. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB Platform for Evolutionary Multi-Objective Optimization [Educational Forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]




| Function | NSGA-II | MOEA/D | ARMOEA | MOEADDAE | CMOES | PPS | QMOSNS |
|---|---|---|---|---|---|---|---|
| Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | |
| ZDT1 | 4.8007 × 10−3 (1.47 × 10−4) − | 7.0791 × 10−3 (1.06 × 10−3) − | 3.9528 × 10−3 (2.41 × 10−5) − | 4.8121 × 10−3 (2.25 × 10−4) − | 4.7270 × 10−3 (2.15 × 10−4) − | 2.0890 × 10−2 (7.40 × 10−3) − | 3.9049 × 10−3 (3.89 × 10−5) |
| ZDT2 | 5.0362 × 10−3 (2.23 × 10−4) − | 8.4050 × 10−3 (9.83 × 10−4) − | 4.0055 × 10−3 (4.51 × 10−4) = | 4.7507 × 10−3 (1.51 × 10−4) − | 4.7763 × 10−3 (2.66 × 10−4) − | 1.4206 × 10−2 (3.44 × 10−3) − | 3.9016 × 10−3 (2.58 × 10−5) |
| ZDT3 | 5.4060 × 10−3 (1.88 × 10−4) − | 1.5031 × 10−2 (6.45 × 10−3) − | 6.4548 × 10−3 (3.82 × 10−5) − | 6.3604 × 10−3 (5.34 × 10−3) − | 5.1903 × 10−3 (1.37 × 10−4) − | 3.6501 × 10−2 (1.99 × 10−2) − | 4.8132 × 10−3 (1.01 × 10−4) |
| ZDT4 | 6.5004 × 10−3 (1.71 × 10−3) + | 3.3404 × 10−2 (3.83 × 10−2) − | 1.0461 × 10−2 (9.27 × 10−3) − | 6.8525 × 10−3 (1.93 × 10−3) + | 8.1588 × 10−3 (3.02 × 10−3) − | 3.9894 × 10−1 (2.59 × 10−1) − | 7.8272 × 10−3 (1.50 × 10−2) |
| ZDT6 | 3.7976 × 10−3 (1.42 × 10−4) − | 1.6414 × 10−2 (3.69 × 10−3) − | 3.3904 × 10−3 (3.56 × 10−4) − | 4.1197 × 10−3 (3.53 × 10−4) − | 4.3082 × 10−3 (1.41 × 10−3) − | 5.0399 × 10−3 (4.64 × 10−4) − | 3.1914 × 10−3 (1.05 × 10−4) |
| +/−/= | 1/4/0 | 0/5/0 | 0/4/1 | 1/4/0 | 0/5/0 | 0/5/0 |
| Function | NSGA-II | MOEA/D | ARMOEA | MOEADDAE | CMOES | PPS | QMOSNS |
|---|---|---|---|---|---|---|---|
| Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | |
| ZDT1 | 7.1890 × 10−1 (2.35 × 10−4) − | 7.1401 × 10−1 (1.55 × 10−3) − | 7.1990 × 10−1 (1.08 × 10−4) − | 7.1898 × 10−1 (2.79 × 10−4) − | 7.1799 × 10−1 (4.48 × 10−4) − | 6.9475 × 10−1 (9.54 × 10−3) − | 7.2028 × 10−1 (1.24 × 10−4) |
| ZDT2 | 4.4341 × 10−1 (2.61 × 10−4) − | 4.3492 × 10−1 (1.83 × 10−3) − | 4.4421 × 10−1 (1.66 × 10−3) − | 4.4361 × 10−1 (2.79 × 10−4) − | 4.4219 × 10−1 (5.75 × 10−4) − | 4.2465 × 10−1 (6.44 × 10−3) − | 4.4497 × 10−1 (9.26 × 10−5) |
| ZDT3 | 5.9922 × 10−1 (1.20 × 10−4) − | 5.9586 × 10−1 (1.74 × 10−2) − | 5.9847 × 10−1 (1.66 × 10−4) − | 6.0238 × 10−1 (1.62 × 10−2) + | 5.9856 × 10−1 (3.01 × 10−4) − | 5.8569 × 10−1 (1.49 × 10−2) − | 5.9964 × 10−1 (1.52 × 10−4) |
| ZDT4 | 7.1515 × 10−1 (2.76 × 10−3) + | 6.7703 × 10−1 (5.13 × 10−2) − | 7.1151 × 10−1 (8.12 × 10−3) − | 7.1448 × 10−1 (3.06 × 10−3) − | 7.1270 × 10−1 (4.00 × 10−3) − | 3.0545 × 10−1 (1.75 × 10−1) − | 7.1499 × 10−1 (2.05 × 10−2) |
| ZDT6 | 3.8762 × 10−1 (4.61 × 10−4) − | 3.6811 × 10−1 (5.25 × 10−3) − | 3.8764 × 10−1 (7.94 × 10−4) − | 3.8669 × 10−1 (7.49 × 10−4) − | 3.8618 × 10−1 (2.37 × 10−3) − | 3.8675 × 10−1 (5.50 × 10−4) − | 3.8881 × 10−1 (1.00 × 10−4) |
| +/−/= | 1/4/0 | 0/5/0 | 0/5/0 | 1/4/0 | 0/5/0 | 0/5/0 |
| Function | NSGA-II | MOEA/D | ARMOEA | MOEADDAE | CMOES | PPS | QMOSNS |
|---|---|---|---|---|---|---|---|
| Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | |
| DTLZ1 | 2.7010 × 10−2 (1.04 × 10−3) − | 2.0563 × 10−2 (1.32 × 10−5) − | 2.0568 × 10−2 (2.21 × 10−5) − | 2.1404 × 10−2 (5.45 × 10−4) − | 2.0403 × 10−2 (1.99 × 10−4) = | 2.8786 × 10−2 (9.66 × 10−4) − | 2.0382 × 10−2 (1.70 × 10−4) |
| DTLZ2 | 6.8903 × 10−2 (2.80 × 10−3) − | 5.4464 × 10−2 (1.99 × 10−7) − | 5.4464 × 10−2 (6.50 × 10−6) − | 5.6688 × 10−2 (3.96 × 10−4) − | 5.5572 × 10−2 (6.70 × 10−4) − | 7.5507 × 10−2 (2.58 × 10−3) − | 5.3918 × 10−2 (4.79 × 10−4) |
| DTLZ3 | 6.9464 × 10−2 (2.82 × 10−3) − | 5.4598 × 10−2 (1.57 × 10−4) − | 5.4733 × 10−2 (3.85 × 10−4) − | 6.6398 × 10−2 (4.96 × 10−3) − | 5.4374 × 10−2 (8.44 × 10−4) = | 1.2166 × 10−1 (2.45 × 10−1) − | 5.4170 × 10−2 (5.96 × 10−4) |
| DTLZ4 | 9.6545 × 10−2 (1.60 × 10−1) − | 5.4464 × 10−2 (2.16 × 10−6) + | 3.0845 × 10−1 (2.93 × 10−1) = | 2.6884 × 10−1 (2.82 × 10−1) − | 5.5979 × 10−2 (9.59 × 10−4) − | 1.2650 × 10−1 (7.54 × 10−2) − | 5.5368 × 10−2 (9.92 × 10−4) |
| DTLZ5 | 5.7453 × 10−3 (2.68 × 10−4) − | 3.3923 × 10−2 (3.72 × 10−6) − | 5.4262 × 10−3 (9.78 × 10−5) − | 4.9348 × 10−3 (1.32 × 10−4) − | 4.9725 × 10−3 (2.05 × 10−4) − | 1.0745 × 10−2 (7.82 × 10−4) − | 4.1164 × 10−3 (3.74 × 10−5) |
| DTLZ6 | 5.9844 × 10−3 (4.38 × 10−4) − | 3.3929 × 10−2 (1.23 × 10−6) − | 5.0046 × 10−3 (6.22 × 10−5) − | 4.6426 × 10−3 (9.85 × 10−5) − | 4.1375 × 10−3 (3.12 × 10−5) = | 6.4126 × 10−3 (3.31 × 10−4) − | 4.1217 × 10−3 (2.98 × 10−5) |
| DTLZ7 | 8.5734 × 10−2 (5.06 × 10−2) − | 1.5470 × 10−1 (1.80 × 10−3) − | 2.0421 × 10−1 (1.78 × 10−1) − | 7.0888 × 10−2 (5.31 × 10−2) − | 6.2679 × 10−2 (1.62 × 10−3) − | 1.6311 × 10−1 (8.57 × 10−2) − | 6.0120 × 10−2 (1.83 × 10−3) |
| +/−/= | 0/7/0 | 1/6/0 | 0/6/1 | 0/7/0 | 0/4/3 | 0/7/0 |
| Function | NSGA-II | MOEA/D | ARMOEA | MOEADDAE | CMOES | PPS | QMOSNS |
|---|---|---|---|---|---|---|---|
| Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | |
| DTLZ1 | 8.2451 × 10−1 (3.56 × 10−3) − | 8.4165 × 10−1 (1.71 × 10−4) = | 8.4158 × 10−1 (2.71 × 10−4) = | 8.4032 × 10−1 (1.67 × 10−3) − | 8.4151 × 10−1 (7.38 × 10−4) = | 8.0270 × 10−1 (5.47 × 10−3) − | 8.4163 × 10−1 (5.88 × 10−4) |
| DTLZ2 | 5.3254 × 10−1 (3.28 × 10−3) − | 5.5962 × 10−1 (2.16 × 10−6) = | 5.5960 × 10−1 (3.07 × 10−5) = | 5.5540 × 10−1 (1.23 × 10−3) − | 5.5119 × 10−1 (1.58 × 10−3) − | 5.1945 × 10−1 (4.19 × 10−3) − | 5.5963 × 10−1 (1.73 × 10−3) |
| DTLZ3 | 5.3014 × 10−1 (7.32 × 10−3) − | 5.5696 × 10−1 (1.93 × 10−3) = | 5.5573 × 10−1 (3.02 × 10−3) = | 5.5408 × 10−1 (2.39 × 10−3) − | 5.5584 × 10−1 (3.22 × 10−3) = | 4.9416 × 10−1 (9.38 × 10−2) − | 5.5673 × 10−1 (3.19 × 10−3) |
| DTLZ4 | 5.2057 × 10−1 (8.12 × 10−2) − | 5.5961 × 10−1 (5.47 × 10−5) + | 4.4322 × 10−1 (1.41 × 10−1) = | 4.5384 × 10−1 (1.39 × 10−1) − | 5.4909 × 10−1 (2.74 × 10−3) − | 5.0963 × 10−1 (2.09 × 10−2) − | 5.5565 × 10−1 (1.88 × 10−3) |
| DTLZ5 | 1.9918 × 10−1 (1.90 × 10−4) − | 1.8185 × 10−1 (2.28 × 10−6) − | 1.9909 × 10−1 (1.32 × 10−4) − | 1.9949 × 10−1 (1.50 × 10−4) − | 1.9905 × 10−1 (1.60 × 10−4) − | 1.9603 × 10−1 (2.45 × 10−4) − | 2.0003 × 10−1 (5.60 × 10−5) |
| DTLZ6 | 1.9947 × 10−1 (1.61 × 10−4) − | 1.8185 × 10−1 (1.04 × 10−6) − | 1.9951 × 10−1 (5.88 × 10−5) − | 1.9994 × 10−1 (7.23 × 10−5) − | 2.0003 × 10−1 (4.69 × 10−5) = | 1.9930 × 10−1 (1.47 × 10−4) − | 2.0005 × 10−1 (5.32 × 10−5) |
| DTLZ7 | 2.6686 × 10−1 (5.28 × 10−3) − | 2.5729 × 10−1 (5.57 × 10−4) − | 2.6002 × 10−1 (1.97 × 10−2) − | 2.7680 × 10−1 (6.80 × 10−3) = | 2.7520 × 10−1 (1.05 × 10−3) − | 2.4195 × 10−1 (6.62 × 10−3) − | 2.7806 × 10−1 (9.45 × 10−4) |
| +/−/= | 0/7/0 | 1/3/3 | 0/3/4 | 0/6/1 | 0/4/3 | 0/7/0 |
| Function | NSGA-II | MOEA/D | ARMOEA | MOEADDAE | CMOES | PPS | QMOSNS |
|---|---|---|---|---|---|---|---|
| Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | |
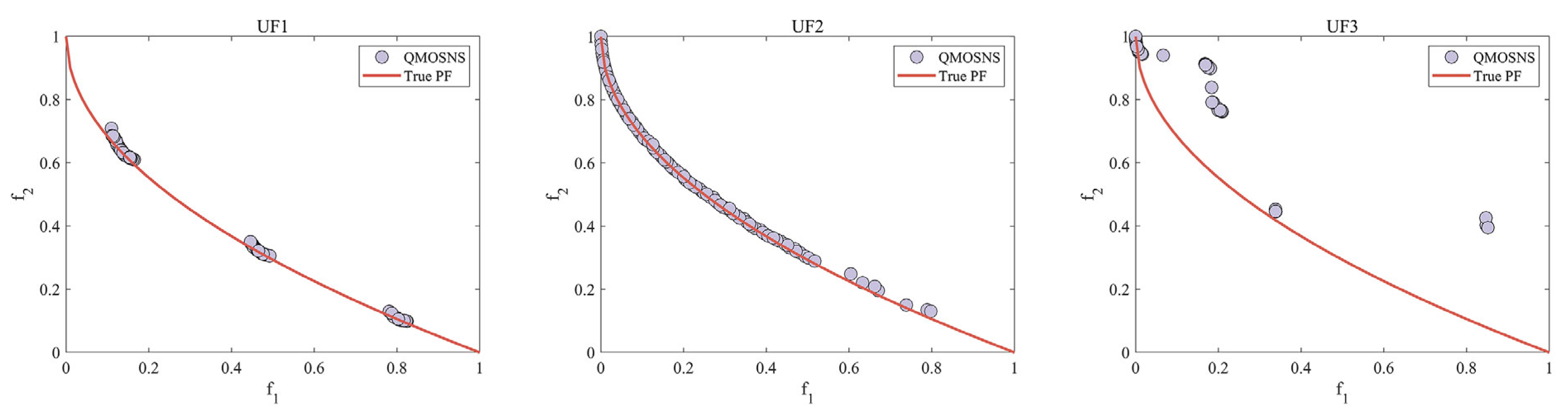
| UF1 | 1.0436 × 10−1 (2.06 × 10−2) − | 1.3958 × 10−1 (5.00 × 10−2) − | 1.1366 × 10−1 (2.55 × 10−2) − | 1.2412 × 10−1 (6.88 × 10−2) − | 9.9917 × 10−2 (2.04 × 10−2) − | 2.5277 × 10−2 (2.46 × 10−2) + | 8.1566 × 10−2 (2.49 × 10−3) |
| UF2 | 3.7636 × 10−2 (1.35 × 10−2) − | 9.2915 × 10−2 (4.85 × 10−2) − | 4.7011 × 10−2 (1.55 × 10−2) − | 4.9463 × 10−2 (3.75 × 10−2) − | 3.4721 × 10−2 (1.01 × 10−2) − | 3.3001 × 10−2 (2.69 × 10−2) − | 2.9344 × 10−2 (6.98 × 10−3) |
| UF3 | 2.2090 × 10−1 (6.33 × 10−2) = | 2.5427 × 10−1 (3.45 × 10−2) = | 2.9052 × 10−1 (3.39 × 10−2) − | 2.6687 × 10−1 (4.38 × 10−2) − | 1.8408 × 10−1 (4.54 × 10−2) + | 1.2160 × 10−1 (5.52 × 10−2) + | 2.3783 × 10−1 (3.95 × 10−2) |
| UF4 | 4.6240 × 10−2 (1.18 × 10−3) = | 5.5563 × 10−2 (2.96 × 10−3) − | 4.6259 × 10−2 (1.60 × 10−3) = | 5.2656 × 10−2 (4.99 × 10−3) − | 4.4842 × 10−2 (7.00 × 10−4) = | 7.9341 × 10−2 (7.25 × 10−3) − | 4.8162 × 10−2 (5.50 × 10−3) |
| UF5 | 3.0432 × 10−1 (7.93 × 10−2) − | 4.3658 × 10−1 (1.18 × 10−1) − | 3.3533 × 10−1 (1.15 × 10−1) − | 3.9002 × 10−1 (1.38 × 10−1) − | 3.1027 × 10−1 (1.07 × 10−1) − | 4.9008 × 10−1 (1.08 × 10−1) − | 2.7604 × 10−1 (1.28 × 10−1) |
| UF6 | 1.9411 × 10−1 (9.74 × 10−2) = | 2.7970 × 10−1 (1.58 × 10−1) − | 2.1489 × 10−1 (1.29 × 10−1) = | 2.8230 × 10−1 (1.24 × 10−1) − | 1.5863 × 10−1 (9.66 × 10−2) − | 3.3513 × 10−1 (1.61 × 10−1) − | 1.5848 × 10−1 (7.48 × 10−2) |
| UF7 | 1.5186 × 10−1 (1.52 × 10−1) = | 2.1207 × 10−1 (1.64 × 10−1) − | 2.0253 × 10−1 (1.49 × 10−1) − | 2.9699 × 10−1 (1.92 × 10−1) − | 9.4093 × 10−2 (1.07 × 10−1) = | 3.3251 × 10−2 (1.00 × 10−1) + | 1.4691 × 10−1 (1.28 × 10−1) |
| UF8 | 2.7834 × 10−1 (6.53 × 10−2) − | 2.9534 × 10−1 (4.76 × 10−2) − | 2.5379 × 10−1 (2.50 × 10−2) − | 1.8529 × 10−1 (1.16 × 10−1) + | 2.6765 × 10−1 (6.46 × 10−2) − | 2.4754 × 10−1 (6.58 × 10−2) − | 2.1906 × 10−1 (5.01 × 10−2) |
| UF9 | 3.7086 × 10−1 (1.13 × 10−1) − | 3.3210 × 10−1 (5.02 × 10−2) − | 2.6802 × 10−1 (8.26 × 10−2) = | 2.5230 × 10−1 (6.55 × 10−2) = | 2.9483 × 10−1 (9.63 × 10−2) = | 3.0348 × 10−1 (8.14 × 10−2) = | 2.8510 × 10−1 (3.74 × 10−2) |
| UF10 | 4.4203 × 10−1 (9.14 × 10−2) = | 6.3308 × 10−1 (2.43 × 10−1) − | 4.2346 × 10−1 (1.46 × 10−1) = | 4.9013 × 10−1 (1.02 × 10−1) − | 3.6983 × 10−1 (5.24 × 10−2) = | 7.0851 × 10−1 (1.07 × 10−1) − | 3.9883 × 10−1 (1.23 × 10−1) |
| +/−/= | 0/5/5 | 0/9/1 | 0/6/4 | 1/8/1 | 1/5/4 | 3/6/1 |
| Function | NSGA-II | MOEA/D | ARMOEA | MOEADDAE | CMOES | PPS | QMOSNS |
|---|---|---|---|---|---|---|---|
| Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | |
| UF1 | 5.9375 × 10−1 (2.46 × 10−2) − | 5.6023 × 10−1 (4.72 × 10−2) − | 5.8039 × 10−1 (2.32 × 10−2) − | 5.7774 × 10−1 (4.54 × 10−2) − | 6.0197 × 10−1 (2.17 × 10−2) − | 6.9003 × 10−1 (3.21 × 10−2) + | 6.2120 × 10−1 (3.92 × 10−3) |
| UF2 | 6.8125 × 10−1 (8.17 × 10−3) − | 6.5392 × 10−1 (2.23 × 10−2) − | 6.7160 × 10−1 (9.89 × 10−3) − | 6.7670 × 10−1 (1.95 × 10−2) − | 6.8453 × 10−1 (6.11 × 10−3) − | 6.8895 × 10−1 (2.04 × 10−2) = | 6.9277 × 10−1 (4.14 × 10−3) |
| UF3 | 4.6623 × 10−1 (5.40 × 10−2) = | 4.4097 × 10−1 (3.10 × 10−2) − | 4.0582 × 10−1 (2.90 × 10−2) − | 4.0569 × 10−1 (3.53 × 10−2) − | 5.0818 × 10−1 (5.12 × 10−2) + | 5.3844 × 10−1 (7.89 × 10−2) + | 4.7645 × 10−1 (2.50 × 10−2) |
| UF4 | 3.8307 × 10−1 (1.43 × 10−3) − | 3.6728 × 10−1 (5.20 × 10−3) − | 3.8356 × 10−1 (1.95 × 10−3) − | 3.7410 × 10−1 (7.25 × 10−3) − | 3.8632 × 10−1 (8.47 × 10−4) − | 3.3559 × 10−1 (8.86 × 10−3) − | 3.9195 × 10−1 (4.71 × 10−3) |
| UF5 | 2.2367 × 10−1 (7.89 × 10−2) − | 1.6565 × 10−1 (6.24 × 10−2) − | 2.2215 × 10−1 (6.74 × 10−2) − | 1.9810 × 10−1 (7.67 × 10−2) − | 2.2981 × 10−1 (7.94 × 10−2) − | 1.2029 × 10−1 (8.22 × 10−2) − | 2.7202 × 10−1 (8.26 × 10−2) |
| UF6 | 3.1154 × 10−1 (6.15 × 10−2) − | 2.8049 × 10−1 (6.81 × 10−2) − | 3.1103 × 10−1 (5.79 × 10−2) − | 2.7102 × 10−1 (7.11 × 10−2) − | 3.3925 × 10−1 (3.41 × 10−2) − | 2.1913 × 10−1 (9.83 × 10−2) − | 3.5475 × 10−1 (3.07 × 10−2) |
| UF7 | 4.4883 × 10−1 (1.06 × 10−1) = | 3.9918 × 10−1 (1.10 × 10−1) − | 4.0966 × 10−1 (1.05 × 10−1) − | 3.4553 × 10−1 (1.32 × 10−1) − | 4.8942 × 10−1 (7.79 × 10−2) = | 5.4923 × 10−1 (7.42 × 10−2) + | 4.5492 × 10−1 (1.02 × 10−1) |
| UF8 | 2.6536 × 10−1 (4.80 × 10−2) − | 3.1474 × 10−1 (2.36 × 10−2) − | 3.3145 × 10−1 (1.48 × 10−2) − | 3.9744 × 10−1 (7.11 × 10−2) + | 2.8342 × 10−1 (4.08 × 10−2) − | 2.9743 × 10−1 (4.79 × 10−2) − | 3.5811 × 10−1 (3.54 × 10−2) |
| UF9 | 3.7830 × 10−1 (9.85 × 10−2) − | 4.4321 × 10−1 (4.34 × 10−2) − | 4.9272 × 10−1 (7.11 × 10−2) − | 5.4239 × 10−1 (6.47 × 10−2) − | 4.5524 × 10−1 (9.24 × 10−2) − | 4.8820 × 10−1 (9.64 × 10−2) − | 5.9433 × 10−1 (3.51 × 10−2) |
| UF10 | 1.0160 × 10−1 (4.50 × 10−2) − | 1.5012 × 10−1 (7.41 × 10−2) − | 1.6860 × 10−1 (7.13 × 10−2) = | 1.2644 × 10−1 (6.87 × 10−2) − | 1.4521 × 10−1 (2.65 × 10−2) = | 3.0092 × 10−2 (2.45 × 10−2) − | 2.0826 × 10−1 (1.02 × 10−1) |
| +/−/= | 0/8/2 | 0/10/0 | 0/9/1 | 1/9/0 | 1/7/2 | 3/6/1 |
| Function | NSGA-II | MOEA/D | ARMOEA | MOEADDAE | CMOES | PPS | QMOSNS |
|---|---|---|---|---|---|---|---|
| Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | |
| C1_DTLZ1 | 2.6661 × 10−2 (1.11 × 10−3) − | 2.0490 × 10−2 (5.91 × 10−5) − | 2.0443 × 10−2 (8.87 × 10−5) − | 2.1013 × 10−2 (1.25 × 10−4) − | 2.0163 × 10−2 (1.84 × 10−4) = | 2.5783 × 10−2 (6.41 × 10−4) − | 2.0190 × 10−2 (1.43 × 10−4) |
| C1_DTLZ3 | 4.5775 × 100 (4.01 × 100) = | 4.4759 × 100 (3.90 × 100) + | 6.4188 × 100 (3.23 × 100) + | 6.2912 × 10−2 (4.69 × 10−3) + | 5.4429 × 10−2 (7.75 × 10−4) + | 2.4606 × 100 (3.70 × 100) + | 8.0120 × 100 (3.77 × 10−3) |
| C2_DTLZ2 | 5.6989 × 10−2 (3.13 × 10−3) − | 4.9314 × 10−2 (3.04 × 10−5) − | 4.3653 × 10−2 (2.09 × 10−4) − | 4.4162 × 10−2 (4.91 × 10−4) − | 4.2947 × 10−2 (7.13 × 10−4) − | 5.5358 × 10−2 (1.71 × 10−3) − | 4.2112 × 10−2 (5.25 × 10−4) |
| C3_DTLZ4 | 1.2813 × 10−1 (5.22 × 10−3) − | 1.1649 × 10−1 (1.37 × 10−1) − | 2.4717 × 10−1 (3.84 × 10−1) − | 8.9333 × 10−1 (4.07 × 10−1) − | 9.7132 × 10−2 (1.54 × 10−3) − | 1.7135 × 10−1 (9.25 × 10−2) − | 9.4932 × 10−2 (1.71 × 10−3) |
| +/−/= | 0/3/1 | 1/3/0 | 1/3/0 | 1/3/0 | 1/2/1 | 1/3/0 |
| Function | NSGA-II | MOEA/D | ARMOEA | MOEADDAE | CMOES | PPS | QMOSNS |
|---|---|---|---|---|---|---|---|
| Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | |
| C1_DTLZ1 | 8.2413 × 10−1 (4.20 × 10−3) − | 8.4050 × 10−1 (1.22 × 10−3) = | 8.3981 × 10−1 (2.04 × 10−3) − | 8.4032 × 10−1 (1.00 × 10−3) − | 8.3986 × 10−1 (2.55 × 10−3) = | 8.1900 × 10−1 (4.06 × 10−3) − | 8.4101 × 10−1 (6.92 × 10−4) |
| C1_DTLZ3 | 2.2957 × 10−1 (2.67 × 10−1) + | 2.1690 × 10−1 (2.72 × 10−1) + | 1.0804 × 10−1 (2.21 × 10−1) + | 5.5702 × 10−1 (1.70 × 10−3) + | 5.5816 × 10−1 (1.59 × 10−3) + | 3.5964 × 10−1 (2.40 × 10−1) + | 0.0000 × 100 (0.00 × 100) |
| C2_DTLZ2 | 4.8983 × 10−1 (4.02 × 10−3) − | 5.1524 × 10−1 (9.47 × 10−5) − | 5.1410 × 10−1 (1.74 × 10−3) − | 5.1497 × 10−1 (1.79 × 10−3) − | 5.1247 × 10−1 (2.26 × 10−3) − | 4.9937 × 10−1 (3.75 × 10−3) − | 5.1746 × 10−1 (1.17 × 10−3) |
| C3_DTLZ4 | 7.6465 × 10−1 (4.48 × 10−3) − | 7.8688 × 10−1 (4.87 × 10−2) − | 7.3721 × 10−1 (1.51 × 10−1) − | 4.0066 × 10−1 (1.83 × 10−1) − | 7.8811 × 10−1 (1.43 × 10−3) − | 7.5983 × 10−1 (2.65 × 10−2) − | 7.9090 × 10−1 (1.71 × 10−3) |
| +/−/= | 1/3/0 | 1/2/1 | 1/3/0 | 1/2/1 | 1/2/1 | 1/3/0 |
| Function | NSGA-II | MOEA/D | ARMOEA | MOEADDAE | CMOES | PPS | QMOSNS |
|---|---|---|---|---|---|---|---|
| Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | |
| MW1 | 5.0439 × 10−3 (2.92 × 10−3) − | 8.6758 × 10−3 (3.45 × 10−3) − | 1.1113 × 10−2 (1.55 × 10−2) − | 8.2137 × 10−3 (1.85 × 10−2) − | 1.6647 × 10−3 (4.00 × 10−5) − | 7.6059 × 10−3 (4.53 × 10−3) − | 1.6484 × 10−3 (5.13 × 10−5) |
| MW2 | 2.5613 × 10−2 (1.03 × 10−2) − | 2.3825 × 10−2 (8.72 × 10−3) − | 2.8420 × 10−2 (1.40 × 10−2) − | 3.9482 × 10−2 (1.23 × 10−2) − | 1.3023 × 10−2 (8.64 × 10−3) − | 1.5179 × 10−1 (1.27 × 10−1) − | 3.7268 × 10−3 (1.89 × 10−5) |
| MW3 | 6.0586 × 10−3 (2.61 × 10−4) = | 1.7567 × 10−2 (3.35 × 10−2) − | 1.3161 × 10−2 (2.39 × 10−2) = | 5.7479 × 10−3 (5.07 × 10−4) = | 5.1306 × 10−3 (3.03 × 10−4) + | 6.0695 × 10−3 (5.26 × 10−4) = | 5.6287 × 10−3 (5.54 × 10−4) |
| MW4 | 5.6744 × 10−2 (2.20 × 10−3) − | 4.4540 × 10−2 (2.55 × 10−3) − | 4.1562 × 10−2 (1.10 × 10−4) − | 4.3055 × 10−2 (1.22 × 10−3) − | 4.2187 × 10−2 (6.53 × 10−4) − | 8.9115 × 10−2 (7.52 × 10−2) − | 4.1135 × 10−2 (3.62 × 10−4) |
| MW5 | 4.7616 × 10−1 (3.45 × 10−1) − | 3.6708 × 10−3 (2.25 × 10−3) = | 3.3312 × 10−1 (3.57 × 10−1) − | 1.4872 × 10−2 (1.30 × 10−2) − | 8.3645 × 10−4 (1.36 × 10−4) + | 2.4809 × 10−1 (2.98 × 10−1) − | 3.6696 × 10−3 (1.14 × 10−3) |
| MW6 | 1.0426 × 10−1 (1.69 × 10−1) − | 1.7326 × 10−2 (9.05 × 10−3) − | 6.6015 × 10−2 (1.36 × 10−1) − | 7.0572 × 10−2 (4.29 × 10−2) − | 1.2291 × 10−2 (8.44 × 10−3) − | 5.2652 × 10−1 (3.31 × 10−1) − | 3.2689 × 10−3 (1.57 × 10−3) |
| MW7 | 1.0394 × 10−1 (1.84 × 10−1) = | 4.8889 × 10−3 (2.11 × 10−4) + | 1.4826 × 10−2 (1.98 × 10−2) = | 5.1604 × 10−3 (7.30 × 10−4) + | 4.9246 × 10−3 (3.83 × 10−4) + | 5.5890 × 10−3 (5.08 × 10−4) + | 6.8865 × 10−3 (1.09 × 10−3) |
| MW8 | 6.5049 × 10−2 (8.69 × 10−3) − | 5.0555 × 10−2 (1.18 × 10−3) − | 4.9557 × 10−2 (5.82 × 10−3) − | 7.7832 × 10−2 (4.26 × 10−2) − | 4.3733 × 10−2 (1.18 × 10−3) − | 1.5878 × 10−1 (1.02 × 10−1) − | 4.2075 × 10−2 (6.58 × 10−4) |
| MW9 | 1.5317 × 10−1 (2.86 × 10−1) = | 2.8690 × 10−2 (2.89 × 10−2) = | 1.5522 × 10−2 (8.52 × 10−3) = | 7.7868 × 10−2 (2.22 × 10−1) − | 4.7448 × 10−3 (2.06 × 10−4) + | 2.1343 × 10−1 (3.05 × 10−1) − | 1.4595 × 10−2 (4.58 × 10−3) |
| MW10 | 1.3243 × 10−1 (6.33 × 10−2) − | 5.6674 × 10−2 (2.03 × 10−2) − | 1.6107 × 10−1 (1.72 × 10−1) − | 2.4756 × 10−1 (2.18 × 10−1) − | 1.6548 × 10−2 (2.04 × 10−2) − | 3.9786 × 10−1 (2.64 × 10−1) − | 3.5036 × 10−3 (6.87 × 10−5) |
| MW11 | 5.5903 × 10−1 (2.90 × 10−1) − | 3.5536 × 10−1 (3.61 × 10−1) − | 4.2591 × 10−1 (3.50 × 10−1) − | 7.7566 × 10−3 (5.96 × 10−4) = | 6.1930 × 10−3 (1.95 × 10−4) + | 7.1952 × 10−3 (2.41 × 10−4) = | 7.9184 × 10−3 (1.85 × 10−3) |
| MW12 | 1.5406 × 10−1 (3.01 × 10−1) − | 5.0312 × 10−3 (1.55 × 10−4) = | 7.6721 × 10−2 (1.74 × 10−1) − | 8.2274 × 10−2 (2.43 × 10−1) − | 7.2094 × 10−2 (2.12 × 10−1) = | 1.5019 × 10−1 (2.51 × 10−1) − | 5.0175 × 10−3 (1.77 × 10−4) |
| MW13 | 1.1926 × 10−1 (8.21 × 10−2) − | 7.2207 × 10−2 (3.29 × 10−2) − | 4.1184 × 10−1 (4.19 × 10−1) − | 1.0196 × 10−1 (3.71 × 10−2) − | 3.6053 × 10−2 (2.90 × 10−2) − | 4.5019 × 10−1 (3.62 × 10−1) − | 1.1450 × 10−2 (1.02 × 10−3) |
| MW14 | 1.2762 × 10−1 (8.93 × 10−3) = | 2.1166 × 10−1 (2.53 × 10−3) = | 1.0980 × 10−1 (2.44 × 10−3) = | 1.0405 × 10−1 (3.87 × 10−3) = | 1.0135 × 10−1 (1.49 × 10−3) = | 1.7169 × 10−1 (4.30 × 10−2) = | 1.6694 × 10−1 (1.08 × 10−1) |
| +/−/= | 0/10/4 | 1/9/4 | 0/10/4 | 1/10/3 | 5/7/2 | 1/10/3 |
| Function | NSGA-II | MOEA/D | ARMOEA | MOEADDAE | CMOES | PPS | QMOSNS |
|---|---|---|---|---|---|---|---|
| Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | |
| MW1 | 4.8335 × 10−1 (6.12 × 10−3) − | 4.7744 × 10−1 (7.10 × 10−3) − | 4.7571 × 10−1 (1.67 × 10−2) − | 4.8100 × 10−1 (2.43 × 10−2) = | 4.8970 × 10−1 (1.54 × 10−4) = | 4.7675 × 10−1 (9.19 × 10−3) − | 4.8975 × 10−1 (2.63 × 10−4) |
| MW2 | 5.4575 × 10−1 (1.55 × 10−2) − | 5.4763 × 10−1 (1.29 × 10−2) − | 5.4218 × 10−1 (2.19 × 10−2) − | 5.2548 × 10−1 (1.71 × 10−2) − | 5.6644 × 10−1 (1.47 × 10−2) − | 3.9623 × 10−1 (1.33 × 10−1) − | 5.8242 × 10−1 (2.24 × 10−5) |
| MW3 | 5.4287 × 10−1 (4.00 × 10−4) − | 5.3498 × 10−1 (2.29 × 10−2) − | 5.3708 × 10−1 (2.16 × 10−2) = | 5.4328 × 10−1 (4.94 × 10−4) = | 5.4377 × 10−1 (7.16 × 10−4) = | 5.4277 × 10−1 (8.79 × 10−4) = | 5.4361 × 10−1 (1.02 × 10−3) |
| MW4 | 8.2383 × 10−1 (2.81 × 10−3) − | 8.3859 × 10−1 (2.21 × 10−3) − | 8.4127 × 10−1 (1.37 × 10−4) = | 8.3964 × 10−1 (1.49 × 10−3) − | 8.3994 × 10−1 (6.07 × 10−4) − | 7.7147 × 10−1 (8.04 × 10−2) − | 8.4142 × 10−1 (2.69 × 10−4) |
| MW5 | 1.6046 × 10−1 (9.06 × 10−2) − | 3.2280 × 10−1 (1.08 × 10−3) = | 2.0545 × 10−1 (1.07 × 10−1) − | 3.1550 × 10−1 (9.29 × 10−3) = | 3.2410 × 10−1 (1.22 × 10−4) + | 2.2144 × 10−1 (1.04 × 10−1) − | 3.2206 × 10−1 (8.09 × 10−4) |
| MW6 | 2.7885 × 10−1 (4.08 × 10−2) − | 3.0718 × 10−1 (1.16 × 10−2) − | 2.8563 × 10−1 (4.31 × 10−2) − | 2.5336 × 10−1 (3.65 × 10−2) − | 3.1386 × 10−1 (1.24 × 10−2) − | 1.0847 × 10−1 (9.03 × 10−2) − | 3.2764 × 10−1 (2.60 × 10−3) |
| MW7 | 3.7545 × 10−1 (6.97 × 10−2) = | 4.1097 × 10−1 (2.78 × 10−4) + | 4.0907 × 10−1 (3.56 × 10−3) = | 4.1207 × 10−1 (3.71 × 10−4) + | 4.1144 × 10−1 (7.45 × 10−4) + | 4.1146 × 10−1 (3.37 × 10−4) + | 4.0883 × 10−1 (1.82 × 10−3) |
| MW8 | 4.7937 × 10−1 (2.39 × 10−2) − | 5.3247 × 10−1 (6.10 × 10−3) − | 5.2155 × 10−1 (1.77 × 10−2) − | 4.6104 × 10−1 (7.82 × 10−2) − | 5.4346 × 10−1 (7.60 × 10−3) − | 3.3354 × 10−1 (1.32 × 10−1) − | 5.5278 × 10−1 (6.68 × 10−4) |
| MW9 | 3.0354 × 10−1 (1.60 × 10−1) = | 3.6331 × 10−1 (3.07 × 10−2) = | 3.7990 × 10−1 (8.09 × 10−3) = | 3.5461 × 10−1 (1.25 × 10−1) − | 3.9749 × 10−1 (1.63 × 10−3) + | 2.5766 × 10−1 (1.74 × 10−1) − | 3.8034 × 10−1 (4.66 × 10−3) |
| MW10 | 3.5692 × 10−1 (4.08 × 10−2) − | 4.0208 × 10−1 (1.45 × 10−2) − | 3.4582 × 10−1 (8.59 × 10−2) − | 3.0205 × 10−1 (1.09 × 10−1) − | 4.3812 × 10−1 (1.82 × 10−2) − | 2.2690 × 10−1 (1.23 × 10−1) − | 4.5434 × 10−1 (2.14 × 10−4) |
| MW11 | 3.0737 × 10−1 (7.33 × 10−2) − | 3.5860 × 10−1 (9.10 × 10−2) − | 3.4045 × 10−1 (8.79 × 10−2) − | 4.4413 × 10−1 (1.08 × 10−3) − | 4.4728 × 10−1 (1.64 × 10−4) + | 4.4730 × 10−1 (1.21 × 10−4) + | 4.4638 × 10−1 (7.78 × 10−4) |
| MW12 | 4.7973 × 10−1 (2.48 × 10−1) − | 6.0436 × 10−1 (3.16 × 10−4) + | 5.3769 × 10−1 (1.64 × 10−1) = | 5.4315 × 10−1 (1.91 × 10−1) = | 5.4577 × 10−1 (1.86 × 10−1) − | 4.6451 × 10−1 (2.24 × 10−1) − | 6.0402 × 10−1 (3.06 × 10−4) |
| MW13 | 4.1837 × 10−1 (4.53 × 10−2) − | 4.4437 × 10−1 (1.93 × 10−2) − | 3.6279 × 10−1 (7.88 × 10−2) − | 4.2589 × 10−1 (2.17 × 10−2) − | 4.6150 × 10−1 (1.28 × 10−2) − | 2.8453 × 10−1 (1.13 × 10−1) − | 4.7643 × 10−1 (5.69 × 10−4) |
| MW14 | 4.5107 × 10−1 (1.93 × 10−3) = | 4.3980 × 10−1 (3.66 × 10−3) = | 4.7076 × 10−1 (2.92 × 10−3) + | 4.7392 × 10−1 (1.70 × 10−3) + | 4.6970 × 10−1 (1.70 × 10−3) = | 4.3802 × 10−1 (9.40 × 10−3) = | 4.4873 × 10−1 (3.67 × 10−2) |
| +/−/= | 0/11/3 | 2/9/3 | 1/8/5 | 2/8/4 | 4/7/3 | 2/10/2 |
| Problem | Name | m | d | ng | nh |
|---|---|---|---|---|---|
| RWMOP1 | Pressure Vessel Design | 2 | 2 | 2 | 0 |
| RWMOP2 | Vibrating Platform Design | 2 | 5 | 5 | 0 |
| RWMOP3 | Welded Beam Design | 2 | 4 | 4 | 0 |
| RWMOP4 | Disc Brake Design | 2 | 4 | 4 | 0 |
| RWMOP5 | Car Side Impact Design | 3 | 7 | 9 | 0 |
| RWMOP6 | Four Bar Plane Truss | 2 | 4 | 1 | 0 |
| RWMOP7 | Multiple Disk Clutch Brake Design | 2 | 5 | 8 | 0 |
| RWMOP8 | Spring Design | 2 | 3 | 8 | 0 |
| RWMOP9 | Multi-product Batch Plant | 3 | 10 | 10 | 0 |
| RWMOP10 | Crash Energy Management for High-speed Train | 2 | 6 | 4 | 0 |
| Function | NSGA-II | MOEA/D | ARMOEA | MOEADDAE | CMOES | PPS | QMOSNS |
|---|---|---|---|---|---|---|---|
| Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | |
| RWMOP1 | 6.0530 × 10−1 (5.84 × 10−4) − | 1.0776 × 10−1 (5.79 × 10−4) − | 6.0749 × 10−1 (6.23 × 10−4) + | 5.5592 × 10−1 (2.36 × 10−2) − | 6.0590 × 10−1 (5.74 × 10−4) − | 4.7622 × 10−1 (5.18 × 10−2) − | 6.0670 × 10−1 (5.63 × 10−4) |
| RWMOP2 | 2.4666 × 10−1 (1.27 × 10−1) − | 2.9075 × 10−1 (1.08 × 10−1) − | 2.1771 × 10−1 (1.31 × 10−1) − | 5.6270 × 10−3 (2.57 × 10−2) − | 3.1711 × 10−1 (8.92 × 10−2) − | 3.9133 × 10−1 (8.94 × 10−4) − | 3.9286 × 10−1 (6.52 × 10−5) |
| RWMOP3 | 8.5762 × 10−1 (6.20 × 10−3) + | 1.6127 × 10−2 (3.04 × 10−2) − | 8.5250 × 10−1 (9.13 × 10−3) = | 8.5470 × 10−1 (2.28 × 10−3) − | 8.5671 × 10−1 (4.08 × 10−3) = | 8.4743 × 10−1 (3.32 × 10−3) − | 8.5620 × 10−1 (2.84 × 10−3) |
| RWMOP4 | 4.3373 × 10−1 (9.72 × 10−4) − | 4.1892 × 10−1 (8.92 × 10−3) − | 4.3348 × 10−1 (1.53 × 10−3) − | 4.2924 × 10−1 (3.33 × 10−3) − | 4.3388 × 10−1 (8.57 × 10−4) − | 4.3296 × 10−1 (4.76 × 10−4) − | 4.3477 × 10−1 (1.82 × 10−4) |
| RWMOP5 | 2.5911 × 10−2 (5.60 × 10−5) − | 9.7880 × 10−3 (6.84 × 10−4) − | 2.6094 × 10−2 (5.91 × 10−5) + | 2.5747 × 10−2 (1.14 × 10−4) − | 2.5990 × 10−2 (5.96 × 10−5) − | 2.4220 × 10−2 (9.09 × 10−4) − | 2.6040 × 10−2 (5.00 × 10−5) |
| RWMOP6 | 4.0908 × 10−1 (1.47 × 10−4) − | 5.3063 × 10−2 (3.74 × 10−5) − | 4.1008 × 10−1 (7.14 × 10−5) + | 3.8484 × 10−1 (4.90 × 10−3) − | 4.0936 × 10−1 (1.14 × 10−4) − | 3.8505 × 10−1 (6.51 × 10−3) − | 4.0945 × 10−1 (1.25 × 10−4) |
| RWMOP7 | 6.1757 × 10−1 (1.02 × 10−3) = | 1.1983 × 10−1 (2.61 × 10−2) − | 6.1727 × 10−1 (1.41 × 10−3) = | 6.0043 × 10−1 (1.77 × 10−2) − | 6.1585 × 10−1 (1.31 × 10−3) − | 5.7821 × 10−1 (1.68 × 10−2) − | 6.1801 × 10−1 (2.73 × 10−4) |
| RWMOP8 | 5.4172 × 10−1 (9.93 × 10−4) − | 6.6012 × 10−2 (7.77 × 10−6) − | 5.4127 × 10−1 (1.85 × 10−3) − | 4.1054 × 10−1 (6.20 × 10−2) − | 5.3602 × 10−1 (4.67 × 10−3) − | 5.3369 × 10−1 (2.23 × 10−3) − | 5.4288 × 10−1 (8.25 × 10−4) |
| RWMOP9 | 3.3496 × 10−1 (1.03 × 10−2) = | 1.9624 × 10−1 (4.20 × 10−2) − | 3.1811 × 10−1 (1.49 × 10−2) − | 2.2856 × 10−1 (5.31 × 10−2) − | 3.3105 × 10−1 (1.17 × 10−2) − | 3.1082 × 10−1 (2.08 × 10−2) − | 3.3861 × 10−1 (1.75 × 10−2) |
| RWMOP10 | 3.1711 × 10−2 (1.49 × 10−4) − | 2.9320 × 10−2 (2.81 × 10−6) − | 3.1658 × 10−2 (2.34 × 10−4) − | 3.1485 × 10−2 (1.12 × 10−4) − | 3.1741 × 10−2 (4.08 × 10−5) − | 3.1627 × 10−2 (2.60 × 10−5) − | 3.1760 × 10−2 (8.15 × 10−7) |
| +/−/= | 1/7/2 | 0/10/0 | 3/5/2 | 0/10/0 | 0/9/1 | 0/10/0 |
| Problem | QMOSNS-1 | QMOSNS-2 | QMOSNS-1 | QMOSNS-2 |
|---|---|---|---|---|
| Mean (Std) | Mean (Std) | Mean (Std) | Mean (Std) | |
| IGD | HV | |||
| ZDT1 | 3.9705 × 10−3 (6.68 × 10−5) − | 3.9049 × 10−3 (3.89 × 10−5) | 7.1997 × 10−1 (2.24 × 10−4) − | 7.2028 × 10−1 (1.24 × 10−4) |
| ZDT6 | 6.7421 × 10−3 (1.74 × 10−2) − | 3.1914 × 10−3 (1.05 × 10−4) | 3.8432 × 10−1 (2.18 × 10−2) − | 3.8881 × 10−1 (1.00 × 10−4) |
| DTLZ1 | 2.0464 × 10−2 (1.92 × 10−4) = | 2.0382 × 10−2 (1.70 × 10−4) | 8.4135 × 10−1 (7.37 × 10−4) = | 8.4163 × 10−1 (5.88 × 10−4) |
| DTLZ2 | 5.3883 × 10−2 (6.02 × 10−4) = | 5.3918 × 10−2 (4.79 × 10−4) | 5.5960 × 10−1 (1.25 × 10−3) = | 5.5963 × 10−1 (1.73 × 10−3) |
| UF6 | 2.1746 × 10−1 (1.37 × 10−1) = | 1.5848 × 10−1 (7.48 × 10−2) | 3.2183 × 10−1 (5.77 × 10−2) − | 3.5475 × 10−1 (3.07 × 10−2) |
| UF8 | 2.4906 × 10−1 (4.16 × 10−3) = | 2.1906 × 10−1 (5.01 × 10−2) | 3.3624 × 10−1 (3.86 × 10−3) − | 3.5811 × 10−1 (3.54 × 10−2) |
| C1_DTLZ1 | 2.0196 × 10−2 (2.24 × 10−4) = | 2.0190 × 10−2 (1.43 × 10−4) | 8.4041 × 10−1 (1.10 × 10−3) − | 8.4101 × 10−1 (6.92 × 10−4) |
| C2_DTLZ2 | 4.2039 × 10−2 (3.31 × 10−4) = | 4.2112 × 10−2 (5.25 × 10−4) | 5.1651 × 10−1 (1.75 × 10−3) | 5.1746 × 10−1 (1.17 × 10−3) |
| MW3 | 5.8982 × 10−3 (4.08 × 10−4) = | 5.6287 × 10−3 (5.54 × 10−4) | 5.4295 × 10−1 (8.32 × 10−4) = | 5.4361 × 10−1 (1.02 × 10−3) |
| MW10 | 5.5396 × 10−3 (3.06 × 10−3) − | 3.5036 × 10−3 (6.87 × 10−5) | 4.5037 × 10−1 (5.86 × 10−3) = | 4.5434 × 10−1 (2.14 × 10−4) |
| +/−/= | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, W.; Li, Z.; Li, J.; Hu, G. Reinforcement Learning Enhanced Multi-Objective Social Network Search Algorithm for Engineering Design Problems. Mathematics 2025, 13, 3613. https://doi.org/10.3390/math13223613
Peng W, Li Z, Li J, Hu G. Reinforcement Learning Enhanced Multi-Objective Social Network Search Algorithm for Engineering Design Problems. Mathematics. 2025; 13(22):3613. https://doi.org/10.3390/math13223613
Chicago/Turabian StylePeng, Wei, Zihan Li, Ji Li, and Guoqing Hu. 2025. "Reinforcement Learning Enhanced Multi-Objective Social Network Search Algorithm for Engineering Design Problems" Mathematics 13, no. 22: 3613. https://doi.org/10.3390/math13223613
APA StylePeng, W., Li, Z., Li, J., & Hu, G. (2025). Reinforcement Learning Enhanced Multi-Objective Social Network Search Algorithm for Engineering Design Problems. Mathematics, 13(22), 3613. https://doi.org/10.3390/math13223613





