Mono-ViM: A Self-Supervised Mamba Framework for Monocular Depth Estimation in Endoscopic Scenes

Abstract

Self-supervised depth estimation methods enable the recovery of scene depth information from monocular endoscopic images, thereby assisting endoscopic navigation. However, existing monocular endoscopic depth estimation methods generally fail to capture the inherent continuity of depth in intestinal structures. To address this limitation, this work presents the Mono-ViM framework, a CNN-Mamba hybrid architecture that enhances depth estimation accuracy through an innovative depth-first scanning mechanism. The proposed framework comprises a Depth Local Visual Mamba module employing depth-first scanning to extract rich structural features, and a cross-query layer, which reframes depth estimation as a soft classification problem to significantly enhance robustness and uncertainty handling in complex endoscopic environments. Experimental results on the SimCol Dataset and C3VD demonstrate that the proposed method achieves high depth estimation accuracy, with Abs Rel of 0.070 and 0.084, respectively. These results correspond to error reductions of 16.7% and 19.4% compared to existing methods, highlighting the efficacy of the proposed approach.

1. Introduction

Endoscopic technology, as a pivotal diagnostic tool in modern minimally invasive medicine, plays a critical role in clinical practice due to its minimally invasive access and real-time imaging capabilities [1]. With the increasing prevalence of gastrointestinal cancers and related diseases, precise intraoperative navigation and spatial awareness are essential for enhancing early lesion detection and ensuring surgical safety. However, in complex anatomical regions, conventional endoscopic systems with limited field of view often impede surgeons’ ability to precisely assess spatial distances between instrument tips and target tissues, posing operational risks from visual blind zones, such as tissue injury or perforation. Monocular depth estimation technology based on deep learning algorithms addresses this geometric perception deficiency by reconstructing 3D depth maps directly from single-frame endoscopic images. This approach effectively compensates for the inherent lack of geometric awareness in endoscopic visualization systems [2]. It provides a fundamental geometric perception basis for enabling safe automatic robotic intervention, accurate lesion measurement, and quantitative postoperative assessment. Supervised depth estimation methods rely on ground truth for model training. However, the acquisition of high-precision depth labels faces significant challenges due to the confined operational environments of endoscopes [3]. In contrast, self-supervised approaches utilizing sequential images have emerged as a research priority by achieving depth prediction without labeled data through multi-view geometric consistency constraints and Structure-from-Motion (SFM) optimization. Self-supervised methods are more applicable to real clinical data, because the natural geometric relationships between consecutive frames in endoscopic videos are more suitable for constructing unsupervised signals. In addition, the depth information learned by the model under unlabeled conditions has the ability to generalize and adapt to different organs and lighting conditions.

Several self-supervised paradigms have been explored for monocular depth estimation. Geometry and temporal-consistency methods [4,5] leverage multi-view reconstruction and Structure-from-Motion (SfM) constraints to predict depth, yet they are sensitive to non-rigid tissue deformation. Optical-flow-based approaches [6] both estimate motion and depth to enhance robustness in dynamic scenes, but their performance deteriorates when large occlusions occur. Generative reconstruction models [7] synthesizing target views as implicit supervision are efficient, but they struggle to preserve fine structural details in complex endoscopic scenes.

Recent advancements in model architectures [8] centered on convolutional neural networks (CNNs) and Vision Transformers (ViTs) [9] have demonstrated remarkable efficacy in monocular self-supervised depth estimation tasks. CNN-based and ViT-based models exhibit inherent limitations in depth estimation tasks. Convolutional Neural Networks (CNNs), a class of deep learning models that use convolutional operations to extract local image features such as edges and textures, demonstrate strong local feature perception, as shown in Figure 1a. However, their restricted receptive fields—the region of the image a model can analyze in a single operation—limit their ability to model geometric correlations between spatially distant regions. Vision Transformers (ViTs), which are deep learning models that process images by dividing them into non-overlapping patch sequences and applying self-attention mechanisms, partition input images and establish global long-range dependencies via multi-head self-attention, as illustrated in Figure 1b. The self-attention mechanism allows ViTs to capture relationships across the entire image, but its computation of attention weights incurs quadratic computational complexity relative to image size, resulting in significant overhead when processing high-resolution endoscopic images. The recently proposed Vision Mamba (ViM) architecture [10], based on Structured State Space Models (SSMs)—a framework for modeling dynamic systems that evolve over time—represents a breakthrough, as shown in Figure 1c. ViM captures positional information across all directions through a cross-scan strategy while maintaining linear computational complexity for long-range spatial relationship modeling. Nevertheless, its predefined fixed scanning paths may inadequately adapt to anisotropic feature distributions, where features vary unevenly across directions, in complex anatomical structures. For example, the rigid, geometry-driven scanning order often disrupts the continuity of semantically cohesive regions, thereby hindering effective learning of the structural priors essential for depth estimation.

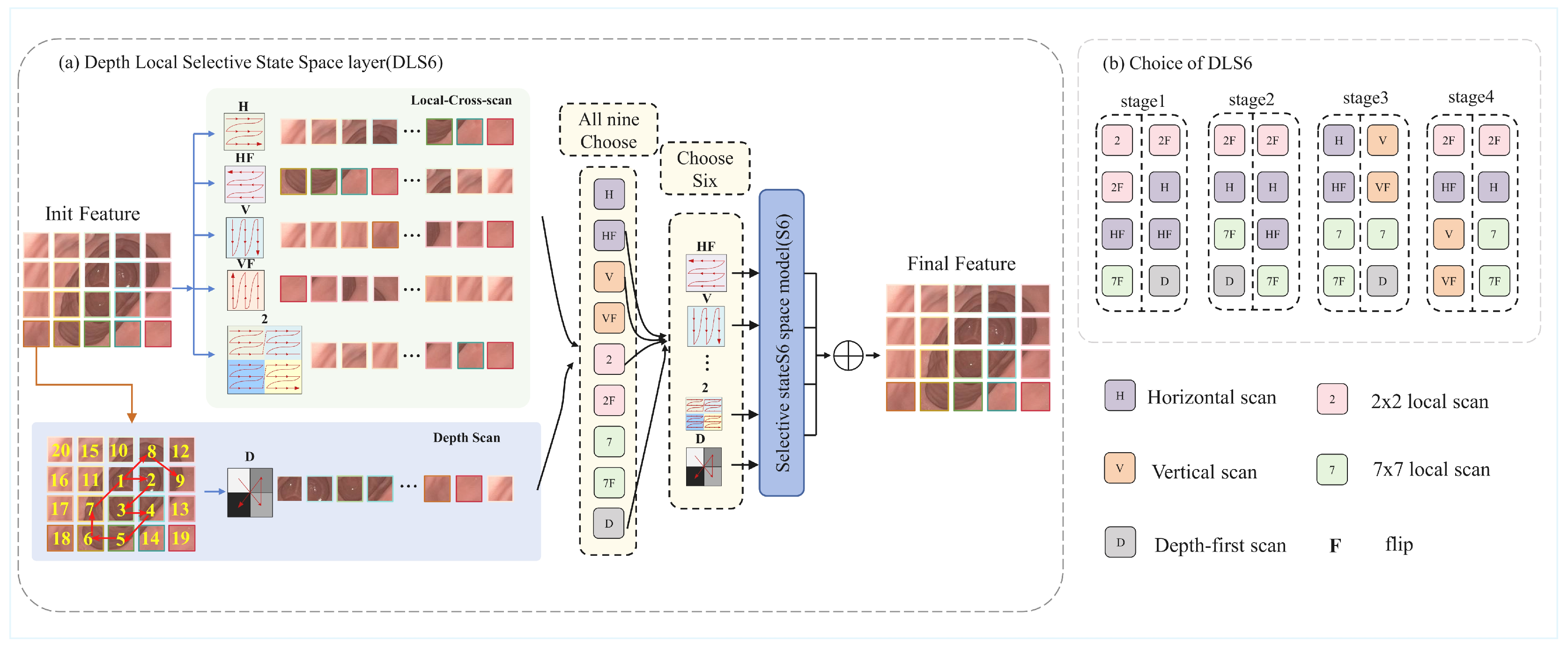
In order to obtain omnidirectional position information and adapt to complex environments while reducing the amount of calculation, this work proposes Mono-ViM, a lightweight and efficient self-supervised deep learning model based on the Mamba architecture. The proposed method uses the efficient sequence modeling of SSMs to achieve linear computational complexity. Compared to its based method ViM, we propose a depth-first scanning mechanism coupled with a cross-query interaction module. In detail, the Depth-Local Visual Mamba (DLViM) extends the ViM framework with adaptive depth-first scanning to model anatomical continuity, while the Cross-Query Layer (CQL), inspired by ViTs, employs query-based interaction to enhance global contextual understanding. Specifically, for endoscopic imaging where depth continuity induces distinct feature representations across varying tissue layers, we innovatively design the Depth Local Visual Mamba (DLViM) module. The core of DLViM is a depth-first scanning mechanism that prioritizes the serialized processing of image tokens originating from deeper anatomical structures before progressing to shallower ones. This scanning order is inherently aligned with the spatial configuration of endoscopic scenes, allowing the model to first establish a coherent representation of the underlying tissue geometry. As illustrated in Figure 1d, this sequential feature aggregation from deep to shallow enhances the correlation of features along the depth dimension, thereby effectively preserving the global spatial coherence of the environment. Furthermore, we designed an enhanced cross-query layer that utilizes ViT to extract encoded features as object queries, which interrogate the decoded depth map to derive depth binning and probability maps for high-precision depth prediction.

The main contributions of this work can be summarized as follows:

• Propose Mono-ViM, a lightweight Mamba-based model for monocular depth estimation in Endoscopic Images.
• Propose a novel depth-first scanning strategy to enhance local feature representation.
• Propose a Cross-Query Layer to boost fine-grained detail representation.
• Demonstrate that Mono-ViM achieves simplicity, effectiveness, and higher accuracy through comprehensive experiments on the SIMCOL Dataset, C3VD and KITTI.

2. Related Work

2.1. Monocular Depth Estimation

Estimating depth from a single image is an inherently ill-posed problem. Therefore, methods using deep learning enabled significant progress in the field.

Using ground-truth depth as supervision, the predictive model can exploit the relationship between color images and their corresponding depth values. Eigen et al. [11] first introduced a multi-scale convolutional framework combining global coarse prediction and local fine refinement, inaugurating the use of CNNs for depth regression. Subsequent studies enhanced accuracy through various architectural and loss-level innovations—such as Conditional Random Fields [12,13] for post-processing, the reverse Huber loss and improved up-sampling modules [14]. These networks demonstrated that deeper and better-designed CNNs could significantly improve pixel-wise depth prediction quality. Moreover, multi-scale ordinal regression strategies [15] are proposed by Fu et al. However, this is challenging to acquire in varied real-world settings. Recent work has shown that conventional structure-from-motion (SfM) pipelines [16] can generate sparse training signal for both camera pose and depth.

However, with the fully supervised methods advanced rapidly, the availability of precise depth labels in the real world became a major issue. Network architectures also play an important role in achieving good results in self-supervised depth estimation. Numerous studies explored monocular depth estimation through architectural refinements such as attention mechanisms [17], multi-scale feature modulation [18], and lightweight backbone designs [19]. These methods can capture local and global cues, yet they were limited by either computational complexity or restricted fields. With the evolution of deep vision models, self-supervised depth estimation based on CNNs and ViTs has achieved significant progress. Monodepth2 [20] substantially improves the accuracy and robustness of monocular video depth prediction through photometric consistency loss in multi-view synthesis and an automatic masking mechanism to handle dynamic objects and occlusions. SQLDepth [21] further captures fine-grained scene structures via self-query layers and self-cost convolution. SPIDepth [22] introduces a more robust pose network to enhance geometric understanding of scenes, thereby achieving more precise depth estimation. Lite-Mono [23] enables real-time and efficient inference on resource-constrained devices through depthwise separable convolutions and channel attention mechanisms. MonoViT [24] leverages vision transformers with multi-scale feature fusion and self-supervised learning to obtain high-precision depth predictions without paired annotations. However, CNNs are constrained by their limited local receptive fields, while ViTs suffer from quadratic computational complexity. To address these limitations, we propose a ViM-based depth estimation model that achieves a balanced integration of efficient computation and long-range dependency modeling.

2.2. State Space Models and Vision Mamba

Structured State Space Models (SSMs) have emerged as a powerful framework for long-range sequence modeling. S4 [25] leverages parameterized state transitions and convolutional kernels to achieve linear-complexity infinite-context modeling. However, its time-invariant design—with static system dynamics over time—limits adaptation to dynamic patterns. Mamba [26] overcomes this via selective SSMs (S6), where input-dependent gating dynamically adjusts state transitions, enabling feature-aware computation without sacrificing efficiency.

VMamba [27] adapts Mamba to vision via cross-scan patch partitioning, transforming 2D images into 1D sequences while preserving local context. LocalMamba [28] processes images through overlapping/non-overlapping windows with local selective scans and cross-window aggregation, balancing global-local modeling. However, medical images’ blurred boundaries challenge fixed scanning strategies. We propose a depth-first scanning approach to prioritize structurally similar regions, enhancing depth estimation accuracy in blurred medical images.

2.3. Architectural Comparison with Related Models

To clearly elucidate the architectural innovations of Mono-ViM, we first provide a systematic comparison with its most relevant counterparts, LocalMamba [28] and MonoViT [24], in

Table 1. Architectural comparison of Mono-ViM with related models.

Feature	Mono-ViM (Ours)	LocalMamba [28]	MonoViT [24]
2 Framework	Mamba,Transformer	Mamba	Transformer
Core Mechanism	Depth-first scan	Local selective scan	Self-attention
Complexity	Linear ($O\left(N\right)$)	Linear ($O\left(N\right)$)	Quadratic ($O\left(N^2\right)$)
Medical Adaptation	Excellent	Moderate	Limited

. While all three frameworks target enhanced visual representation learning, they diverge fundamentally in core architectural paradigms.

LocalMamba [28] processes images through overlapping/non-overlapping windows with local selective scans, emphasizing local feature extraction while maintaining computational efficiency through linear complexity. However, its window-based mechanism inherently limits global receptive fields, which may compromise the modeling of long-range dependencies in endoscopic scenes with continuous anatomical structures. MonoViT [24] leverages vision transformers with multi-scale feature fusion, achieving global context modeling through self-attention mechanisms. Nevertheless, the quadratic computational complexity of self-attention poses significant challenges when processing high-resolution endoscopic images, limiting its practical deployment in real-time applications.

In contrast, Mono-ViM introduces a novel depth-first scanning strategy within the Visual State Space Model (ViM) framework, enabling global receptive field coverage while maintaining linear computational complexity. The proposed Depth Local Visual Mamba (DLViM) module specifically addresses the challenges of endoscopic imaging by prioritizing structurally similar regions through adaptive scanning paths, effectively capturing both local details and global contextual information essential for accurate depth estimation in complex anatomical environments.

Beyond direct architectural comparisons, Mono-ViM’s Mamba-based design offers distinct advantages over other popular depth estimation paradigms. Compared to diffusion-based methods, which iteratively refine depth maps from noise through a multi-step denoising process, Mamba offers a significant advantage in inference speed by producing depth estimates in a single forward pass. However, diffusion models incur substantial computational overhead due to their iterative nature, hindering real-time application. In contrast, recurrent frameworks (e.g., based on LSTMs or GRUs) share Mamba’s sequential nature and are designed for efficient step-by-step processing. However, traditional RNNs often struggle with long-range dependencies due to vanishing gradients. Mamba’s selective state space mechanism fundamentally overcomes this limitation, enabling effective modeling of long-range contextual information—critical for understanding endoscopic scenes—while retaining high computational efficiency.

Thus, as summarized in Table 1, Mono-ViM occupies a unique niche: it integrates the global receptive field of Transformers, overcomes the quadratic complexity bottleneck through selective state spaces, and introduces a depth-first scanning strategy specifically optimized for the structural continuities and blurred boundaries characteristic of endoscopic imagery. This positions it as a highly suitable paradigm for real-time medical imaging applications where accuracy, efficiency, and contextual awareness are paramount.

3. Our Method

To overcome the incompatibility of fixed scanning paths with endoscopic anatomy, the Mono-ViM is proposed in this work (see Figure 2). The proposed framework utilizes the Depth Local Visual Mamba (DLViM) module for structured feature modeling, and the Cross-Query Layer (CQL) for high-precision depth decoding. This section introduces the basic principles of Mamba and detailed architecture of the Mono-ViM framework.

3.1. Preliminaries

We first introduce the basic principles of Mamba. Mamba is a highly efficient sequence modeling architecture based on SSM. Its core component, the S6 module, improves traditional SSM through selective state space mechanisms. The state equation is defined as:

$$\begin{array}{cc}\hfill h_t& ={\tilde{A}}_t{h}_{t-1}+{\tilde{B}}_t{x}_t\hfill \\ \hfill y_t& =C{h}_t\hfill \end{array}$$

(1)

where the dynamic parameter ${\tilde{A}}_t,$ ${\tilde{B}}_t$ are obtained from the continuous-time dynamic equations $\tilde{A}=exp(\Delta A)$ and $\tilde{B}={(\Delta A)}^{-1}(exp(\Delta A)-E)·\Delta B$. The step size parameter $\Delta$ is generated in real-time from the input parameter $x_t$ through a projection function, which constitutes the core of the selective mechanism.

This architecture is the key to achieving linear computational complexity. Unlike the self-attention mechanism in Transformers, which requires comparing every token to every other token (resulting in $O\left(N^2\right)$ complexity for a sequence of length $\left(N\right)$, the SSM processes the sequence recursively. As shown in Equation (1), the computation at each time step t depends only on the current input $x_t$ and the previous hidden state $h_{(t-1)}$. This recurrence means that processing an entire sequence of length N requires $O\left(N\right)$ operations. Furthermore, the selective mechanism (where $\Delta$, B, C are input-dependent) does not alter this linear scaling. Instead, it allows the model to dynamically focus on or ignore inputs based on the current context, significantly enhancing representation power without sacrificing computational efficiency. During training, hardware-optimized parallel scans are employed to exploit modern accelerators, while the inherent recurrent nature dominates during inference, ensuring high efficiency throughout the model’s life-cycle. This mechanism enables the S6 module to dynamically adjust the state transition process based on the input, thereby achieving linear complexity while maintaining strong performance.

3.2. Model Overall Framework

The overall framework of the proposed Mono-ViM framework is shown in Figure 2. The decoder plays a critical role in reconstructing the high-level semantic features extracted by the encoder into the original spatial resolution of the input image, producing depth maps with precise structural details and well-defined boundaries. This work introduces a lightweight decoder based on the Mamba architecture, specifically designed to efficiently recover encoded information. The framework comprises a DepthNet and a PoseNet. Given an input image $I_t$ for depth prediction, the DepthNet first estimates its inverse depth map $D_t$. For a source image and its reference image pair $(I_t,I_t^{\prime })$, the DepthNet computes the relative camera motion $T_{t^{\prime }\to t}$ between consecutive frames. The reference image can then be synthesized using the camera motion $T_{t^{\prime }\to t}$, intrinsic parameters K, and the estimated depth from the original image:

$$I_{t^{\prime }\to t}=I_{t^{\prime }}〈\mathrm{proj}\left(D_t,T_{t\to t^{\prime }},K\right)〉$$

(2)

where $\mathrm{proj}\left(\right)$ denotes a projection function that projects the 3D points obtained from $D_t$ onto the image plane of $I_{t^{\prime }}$, and $\langle ·\rangle$ represents the sampling operator. During training, DepthNet and PoseNet are jointly optimized through image reconstruction error.

3.2.1. Depth Encoder

In this work, Lite-Mono is adopted as the encoder, featuring an efficient hybrid design of lightweight CNN and Transformer components. It employs a continuous cavity convolution module with multi-rate convolutions to extract multi-scale local features, and a local–global feature interaction module to incorporate global context via lightweight self-attention. As shown in Figure 2, the size of the output three-stage feature map is $48\times {\displaystyle \frac{H}{4}}\times {\displaystyle \frac{W}{4}}$, $80\times {\displaystyle \frac{H}{8}}\times {\displaystyle \frac{W}{8}}$, $128\times {\displaystyle \frac{H}{16}}\times {\displaystyle \frac{W}{16}}$.

3.2.2. Depth Decoder

Mono-ViM employs four stages to aggregate the multi-scale features obtained from the encoder, and feeds the results into a Mamba-based decoder. In the decoder, global information is efficiently captured by DLViM and the feature maps are upsampled using Patch Expanding. The skip connection features are then concatenated, followed by further global integration using DLViM. Subsequently, $3\times 3$ convolutional blocks are applied to adjust channel dimensions and enhance inter-channel correlations. The input channels of the $3\times 3$ convolutional blocks are (144, 80, 24, 12), and the output channels are (6, 48, 24, 12). Finally, the CQL module refines the depth map by querying and integrating global contextual cues, enabling more accurate depth reconstruction.

3.2.3. PoseNet

We adopt the same PoseNet as Monodepth2 for pose estimation. Specifically, during the encoding stage, a pre-trained ResNet18 network extracts features from adjacent image pairs, while the decoding stage employs a 4-layer CNN to regress the 6-DoF relative pose parameters.

3.2.4. Depth Local Visual Mamba

The Depth Local Visual Mamba (DLViM), as depicted in Figure 2, serves as the central component of DLBlock, leveraging a dual-branch hierarchical architecture to enhance feature representation. Input features undergo layer normalization before parallel processing: The first branch employs linear projection to map features into the hidden state space of SSM, followed by non-linear activation to capture complex visual patterns such as edges, textures, and object shapes. The second branch sequentially undergoes linear transformation, depthwise separable convolution, and activation before being fed into the core module DLS6 for feature encoding. After layer normalization, the outputs of both branches are fused via element-wise multiplication. Finally, a linear layer projects the merged features back to the original input dimension, establishing a residual connection with the initial input to ensure stable gradient propagation.

The Depth Local Selective State Space Model (DLS6), as the core innovation of the DLViM module, builds upon the foundation of the S6 module. While the S6 module excels at processing 1D causal sequences through capturing sequential dependencies, images as 2D spatial data exhibit non-causal characteristics. Directly flattening them into 1D sequences disrupts local spatial correlations, making it challenging for models to effectively recognize 2D structural relationships. This dimensional discrepancy constitutes the fundamental challenge. Existing methods employ strategies like cross-scan to mitigate spatial information loss during serialization, yet their fixed scanning patterns remain inadequate for adapting to the complex anatomical features in endoscopic images. Our proposed hierarchical DLS6 architecture innovatively establishes a three-dimensional collaborative modeling paradigm: At the global level, a cross-scan strategy horizontally and vertically traverses flattened images to capture macro spatial correlations; Locally, a multi-scale window partitioning mechanism enhances neighborhood associations while preserving global awareness; The framework innovatively introduces a depth-first dynamic scanning algorithm that adaptively adjusts scanning paths based on depth correlations of anatomical structures, achieving fine-grained tissue modeling.

Following the approach introduced in [28], we employ a dynamic architecture search mechanism to determine the most suitable scanning directions for each layer. The method constructs the search space as an over-parameterized model, which enables simultaneous optimization of both the network parameters and architectural coefficients within a standard training paradigm. After training, we obtain the final directional configuration by selecting the four directions with the highest softmax confidence scores. A visualization of the selected directions is provided in Figure 3b.

3.2.5. Cross-Query Layer

The Cross-Query Layer (CQL) leverages relative distance information as a geometric cue to enhance depth estimation. Inspired by [21], it computes the dot product between pixel embeddings from the same image to capture intrinsic geometric relationships within the image. This approach approximates relative distances as dot products between pixels and image patches, effectively preserving geometric information while significantly reducing computational overhead.

The cross-cost volume represents the relative distances between pixels and local patches, but such distances inherently lack explicit physical meaning. To further capture more semantically meaningful geometric relationships between pixels and structural objects in the image, we introduce coarse-grained queries. First, incorporate positional encodings into the high-level semantic features extracted by the encoder and feed them into a Transformer to generate a set of query vectors Q representing the image’s structural patterns. These queries are then applied to the embedded feature maps from the decoder stage, and the final cost volume is obtained through dot-product computations:

$$V_{i,j,k}=Q_i^T·S_{j,k}$$

(3)

Then, use the potential depth of the cost volume to compute depth intervals to estimate depth bins b:

$$b=\mathrm{MLP}\left(\underset{i=1}{\overset{Q}{⨁}}\sum _{(j,k)=(1,1)}^{(h,w)}\mathrm{softmax}{\left(V_i\right)}_{j,k}·S_{j,k}\right)$$

(4)

Here, ⨁ denotes concatenation, MLP denotes multi-layer perceptron.

The cost volume is aligned with the depth bin dimensions using a convolution, followed by a planar softmax operation to obtain probability distributions. Pixel-level depth prediction is then achieved through a linearly weighted combination of the center values from all depth intervals, ultimately forming a high-precision depth map.

To address the potential performance degradation of depth estimation in complex scenarios caused by the limited number of query heads in CQL architecture, we propose two model variants: the full-featured Mono-ViM retaining CQL structures, and its lightweight counterpart Mono-ViM-small with CQL modules removed. This dual-model design is driven by the following considerations: For scenarios demanding high-precision depth estimation, Mono-ViM preserves complete feature representation capability through intact CQL components; while in computation-sensitive scenarios requiring lightweight solutions, Mono-ViM-small achieves operational efficiency through CQL elimination.

3.3. Loss Function

Self-supervised depth estimation problem can be regarded as a multi-view integration task. Specifically, DepthNet and PoseNet are used to predict the appearance of the current frame from the reference frame. The network is trained to minimize both the image reconstruction loss between the target image and the reconstructed current frame, and the edge-aware smoothness loss on the predicted depth map.

3.3.1. Image Reconstruction Loss

Following [23], we use the following formula with L1 and SSIM to construct the photometric error between two images.

$$pe(I_a,I_b)={\displaystyle \frac{\alpha }{2}}(1-SSIM(I_a,I_b))+(1-\alpha ){\parallel I_a-I_b\parallel }_1$$

(5)

where $\alpha =0.85$. To mitigate the effects of invisible pixels and occluded objects in the source images, the minimum photometric loss is computed across the sequence of frames:

$$L_p=\underset{f}{min}pe(I_t,I_{t\to t^{\prime }})$$

(6)

Additionally, a binary mask is applied to compute the training loss only on pixels that are reliably reconstructed after warping using depth and pose, thereby excluding uncertain or misleading pixels caused by static camera, dynamic objects moving in sync, or low-texture regions.

$$\mu =\left[\underset{t^{\prime }}{min}pe(I_t,I_{t\to t^{\prime }})<\underset{t^{\prime }}{min}pe(I_t,I_{t^{\prime }})\right]$$

(7)

Therefore, the final image reconstruction loss is defined as:

$$L_r=\mu ·L_p$$

(8)

3.3.2. Edge-Aware Smoothness Loss

To make the depth map smoother and more reasonable in the untextured region, we use edge-aware smoothing loss:

$$L_s=\left|{\partial }_x{d}_t^{\ast }\right|e^{-\left|{\partial }_x{I}_t\right|}+\left|{\partial }_y{d}_t^{\ast }\right|e^{-\left|{\partial }_y{I}_t\right|}$$

(9)

The total loss can be expressed as:

$$L=L_r+\lambda L_s$$

(10)

4. Experiments

In this section, we evaluate the proposed framework with effects on three public datasets.

4.1. Implementation Details

All models were implemented in the PyTorch 1.13.0 and CUDA 11.7 framework, and trained on an RTX 4090 GPU with a batch size of 12. We use AdamW as the optimizer with an initial learning rate of $1\times {10}^{-4}$, which decays to $1\times {10}^{-5}$ following a cosine schedule, and training is conducted for 25 epochs. Following the settings in [23], we apply color and flip augmentations to the images during training. To ensure fair comparison, each baseline model uses its own default learning rate settings.

The accuracy is evaluated using the seven metrics proposed in [23]: absolute relative error (Abs Rel), squared relative error (Sq Rel), root mean squared error (RMSE), root mean squared log error (RMSE log), and accuracy under threshold values ($\delta <1.25$, $\delta <1.{25}^2$, and $\delta <1.{25}^3$).

4.2. Datasets

To support intestinal surgical navigation, the C3VD dataset provides real clinical colonoscopy data for realistic evaluation, while the SimCol dataset offers high-precision synthetic data for quantitative validation. In addition, the KITTI dataset is included to assess the method’s generalization beyond medical scenes. The combination of these datasets allows comprehensive evaluation across synthetic, clinical, and outdoor domains.

The SimCol dataset: The SimCol Dataset [29] integrates three categories of anatomical structure data derived from real human CT scans, with each category containing multiple trajectory paths generated. Each trajectory contains synchronously captured RGB rendered images, corresponding camera intrinsic parameter matrices, high-precision depth field information, and camera extrinsic pose parameters. All available data maintains an original image resolution of The images are of size $475\times 475$ pixels, which is downsampled to $384\times 384$ to accommodate model requirements. The data partitioning scheme of the SimCol dataset is illustrated in

Table 2. Data splits used in the SIMCOL Dataset.

Split	Colonoscopy Videos	No. of Frames
Train	I_S1–S3, I_S6–S8, I_S11–S13, II_B1–B3, II_B6–B8, II_B11–B13	21,618
Val	I_S4, I_S9, I_S14, II_B4, II_B9, II_B14	7206
Test	I_S5, I_S10, I_S15, II_B5, II_B10, II_B15, III_O1–O3	9009

, with the triplet index set as $(-3,0,3)$. The ternary frame structure $(-3,0,3)$ means that the current frame is the center and the first 3 frames and the last 3 frames are used as reference frames for training. This choice can increase the parallax between adjacent frames while ensuring sufficient overlap between frames.

C3VD: Colonoscopy 3D Video Dataset (C3VD) [30] is an open source dataset designed to promote colonoscopy computer vision research, containing 22 high-definition clinical colonoscopy videos and their accurate 3D truth data. The dataset provides depth map, surface normal, optical flow, occlusion annotation, and 6-degree-of-freedom position, which effectively solves the bottleneck of missing truth data in colonoscopy vision tasks. All available data maintains an original image resolution of $1350\times 1080$ pixels, which is downsampled to $320\times 256$ to accommodate model requirements. The data partitioning scheme of the SimCol dataset is illustrated in

Table 3. Data splits used in C3VD.

Split	Colonoscopy Videos	No. of Frames
Train	c_1a, c_1b, c_2a, c_2b, c_2c, c_3a, d_4a, s_1a, s_2a, t_1a, t_1b, t_2a, t_2b, t_3a, t_3b	6849
Val	c_4a, s_3a, t_4a	1460
Test	c_4b, d_4a, s_3b, t_4b	1706

‘c’ refers to caecum, ‘s’ refers to sigmoid, ‘t’ refers to transverse and ‘d’ for descending colon.

, with the triplet index set as $(-20,0,20)$ due to the slow movement of the endoscope.

KiTTI: The KITTI dataset [31] is a widely adopted benchmark for stereo road scene understanding, encompassing multi-modal data from cameras, LiDAR, and an inertial measurement unit (IMU). Following the Eigen split [32], we partition the monocular sequences into 39,180 triplets for training, 4424 for validation, and 697 for testing. Notably, the test set employs refined ground truth depth maps generated through the method described in [33], ensuring enhanced measurement accuracy.

4.3. SimCol Dataset Results

We compare our model with previous representative methods, and the results are presented in

Table 4. Comparison of Mono-ViM with recent representative methods on the SimCol dataset.

Model	Depth Error (↓)				Depth Accuracy (↑)			Params
	Abs rel	Sq rel	RMSE	RMSE log	$\mathit{\delta }<\mathbf{1}.\mathbf{25}$	$\mathit{\delta }<\mathbf{1}.{\mathbf{25}}^{\mathbf{2}}$	$\mathit{\delta }<\mathbf{1}.{\mathbf{25}}^{\mathbf{3}}$
Monodepth2
(2019)	0.145	0.683	0.692	0.169	0.906	0.956	0.973	35.5 M
Lite-Mono
(2023)	0.187	1.474	0.803	0.179	0.907	0.947	0.963	3.1 M
MonoViT
(2022)	0.246	1.671	1.047	0.243	0.837	0.918	0.947	33.6 M
R-MSFM3
(2021)	0.084	0.070	0.393	0.113	0.948	0.983	0.992	3.5 M
R-MSFM6
(2021)	0.084	0.079	0.381	0.113	0.950	0.982	0.992	3.8 M
IID-SfmLearner
(2024)	0.302	2.619	1.197	0.271	0.822	0.921	0.953	14.3 M
Mono-ViM-
small (ours)	0.096	0.186	0.461	0.124	0.937	0.966	0.979	3.3 M
Mono-ViM (ours)	0.070	0.061	0.356	0.099	0.964	0.989	0.995	3.9 M
The best and the second best results are highlighted in bold and underlined. IID-SfmLearner [34] combines image intrinsic decomposition (IID) with unsupervised monocular depth estimation, specifically designed to improve depth prediction accuracy in endoscopic surgery.

. Mono-ViM outperforms all approaches while being the second smallest model. It achieves AbsRel (0.070), SqRel (0.061), RMSE (0.356), and RMSElog (0.099), demonstrating its accuracy in endoscopic image depth estimation.

Additionally, Mono-ViM exhibits significant performance improvements compared to Lite-mono, a prototype model that lays the groundwork for further development. In the self-supervised setting, Mono-ViM shows improvements of 16.7% in AbsRel, 14.8% in SqRel, 6.6% in RMSE, and 12.4% in RMSElog. These substantial improvements underscore the impact of strengthening the depth decoder network and its information flow in Mono-ViM.

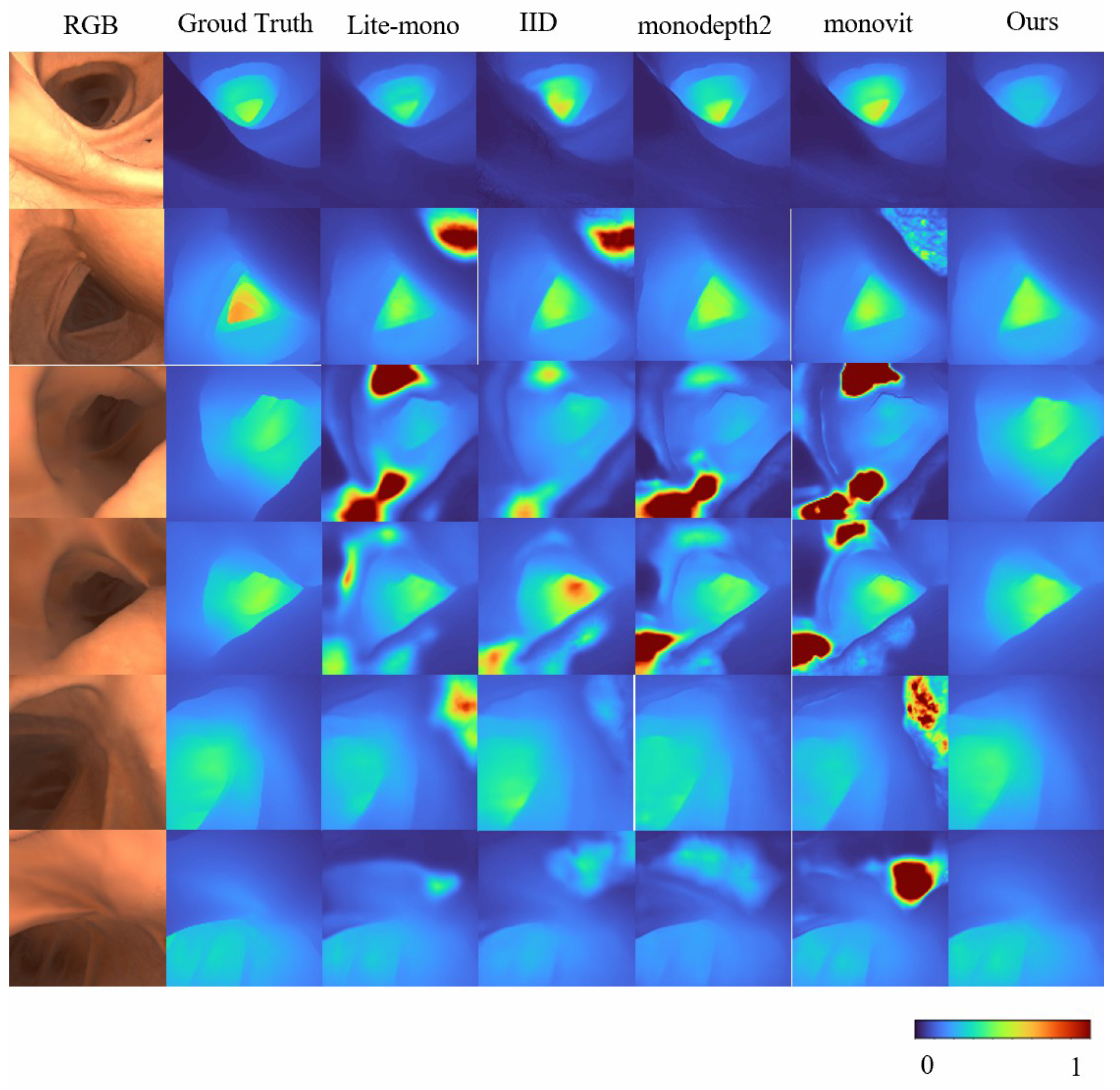
Overall, these results validate the effectiveness of Mono-ViM in self-supervised monocular depth estimation. The qualitative experiments in Figure 4 further demonstrate its superior performance by effectively reducing overestimated depth regions (e.g., diminished red high-depth areas) and generating depth maps that align closely with the ground truth, especially in challenging scenarios. Furthermore, compared to baseline models, our approach exhibits improved coherence characterized by smoother depth transitions and enhanced inter-region consistency. These improvements contribute to both higher reliability and superior visual quality of the depth estimation outputs.

4.4. C3VD Results

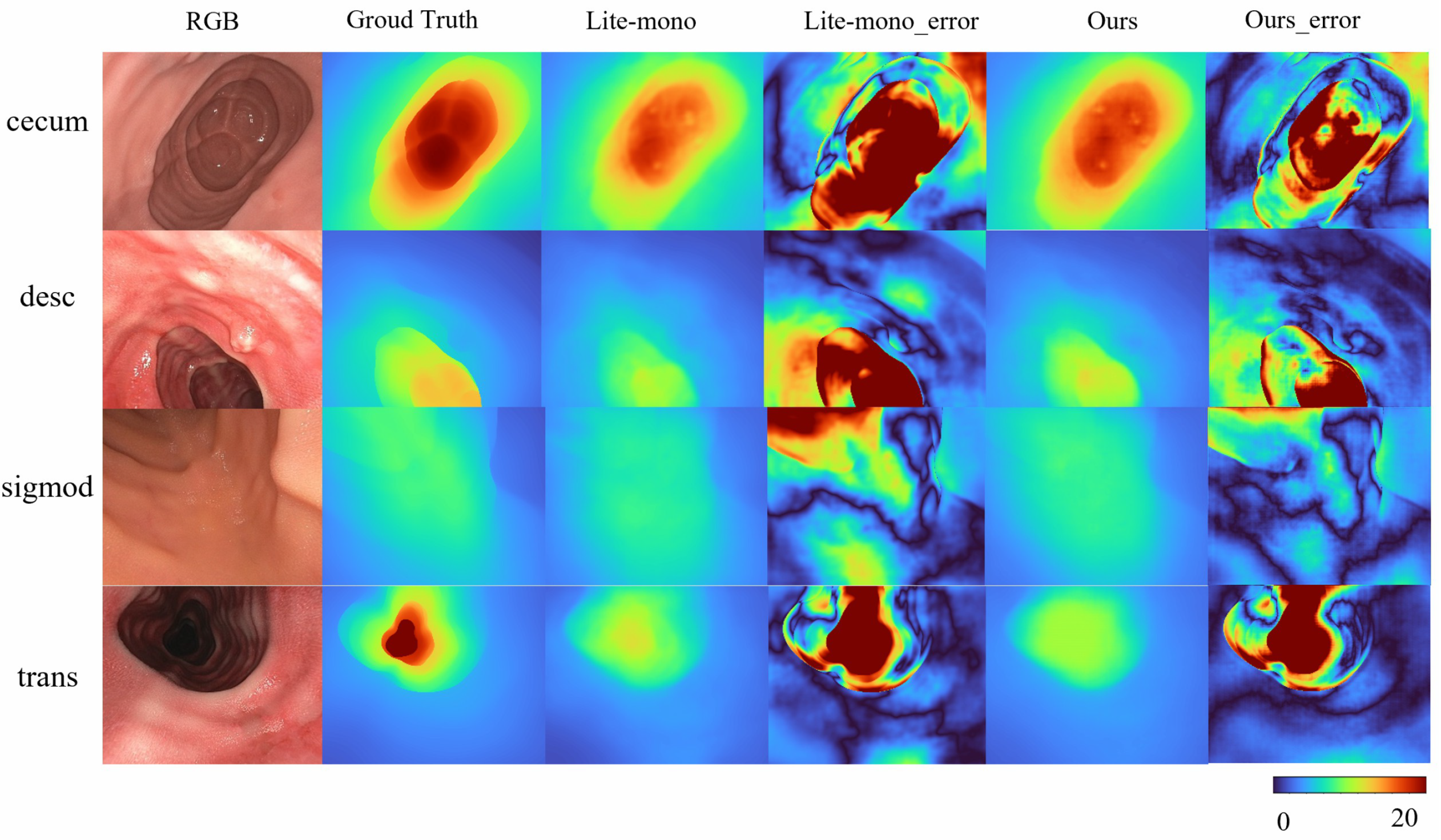
To address the domain gap in SimCol Dataset, we train our model on the real-world endoscopic dataset C3VD. As shown in

Table 5. Comparison of Mono-ViM with recent representative methods on C3VD.

Model	Depth Error (↓)				Depth Accuracy (↑)			Params
	Abs rel	Sq rel	RMSE	RMSE log	$\mathit{\delta }<\mathbf{1}.\mathbf{25}$	$\mathit{\delta }<\mathbf{1}.{\mathbf{25}}^{\mathbf{2}}$	$\mathit{\delta }<\mathbf{1}.{\mathbf{25}}^{\mathbf{3}}$
Monodepth2
(2019)	0.182	0.020	0.091	0.169	0.700	0.890	0.966	35.5 M
Lite-Mono
(2023)	0.103	0.007	0.062	0.179	0.907	0.987	0.998	3.1 M
MonoViT
(2022)	0.106	0.007	0.061	0.139	0.899	0.984	0.998	33.6 M
R-MSFM3
(2021)	0.199	0.026	0.109	0.282	0.670	0.894	0.947	3.5 M
R-MSFM6
(2021)	0.189	0.025	0.107	0.274	0.676	0.906	0.957	3.8 M
IID-SfmLearner
(2024)	0.202	0.022	0.099	0.261	0.635	0.907	0.967	14.3 M
Mono-ViM-
small (ours)	0.081	0.005	0.048	0.109	0.938	0.995	0.999	3.3 M
Mono-ViM (ours)	0.084	0.006	0.055	0.119	0.937	0.985	0.998	3.9 M
The best and the second best results are highlighted in bold and underlined.

Mono-ViM (small) achieves state-of-the-art performance on real-world benchmarks, with metrics of AbsRel (0.081), SqRel (0.005), RMSE (0.048), and RMSElog (0.109), demonstrating its robust adaptation to real endoscopic scenes. Qualitative comparisons in Figure 5 further highlight the framework’s superior capability in reconstructing fine-grained depth details from real endoscopic images.

4.5. Kitti Results

Furthermore, we evaluate our model on the outdoor KITTI dataset, conducting comparative experiments with lightweight baseline models (<10 M parameters). These baseline models are tested using their publicly available optimal configurations without additional fine-tuning, ensuring a fair comparison under identical training protocols.

As shown in

Table 6. Comparison of Mono-ViM with recent lightweight methods on KITTI.

Model	Abs rel	RMSE	$\mathit{\delta }<1.25$	Params
R-MSFM3 (2021)	0.088	3.767	0.916	3.5 M
R-MSFM6 (2021)	0.087	3.722	0.915	3.8 M
Lite-Mono (2023)	0.083	3.689	0.923	3.1 M
R-MSFM3-GC (2024)	0.088	3.763	0.915	5.0 M
R-MSFM6-GC (2024)	0.085	3.668	0.919	5.3 M
Mono-ViM-small (ours)	0.081	3.595	0.929	3.3 M

The best and the second best results are highlighted in bold and underlined. R-MSFM [35] focuses on efficient and accurate monocular depth estimation with a lightweight recurrent design, while R-MSFM-GC [36] enhances it with a mask geometry consistency loss to ensure cross-frame 3D alignment.

, the proposed Mono-ViM-small achieves the lowest absolute relative error (0.081) and the highest accuracy under the threshold $\delta <1.25$ (0.929) among all compared methods, while maintaining a compact model size of only 3.3 M parameters. Compared to other lightweight models such as Lite-mono (3.1 M), our method exhibits superior accuracy with marginal parameter overhead. Moreover, it surpasses heavier counterparts like R-MSFMX3-GC (5.0 M) and R-MSFMX6-GC (5.3 M), indicating a more efficient utilization of model capacity. These results demonstrate that Mono-ViM-small offers a favorable trade-off between accuracy and computational cost, making it well-suited for real-world applications with limited hardware resources.

4.6. Ablation Study on Model Architectures

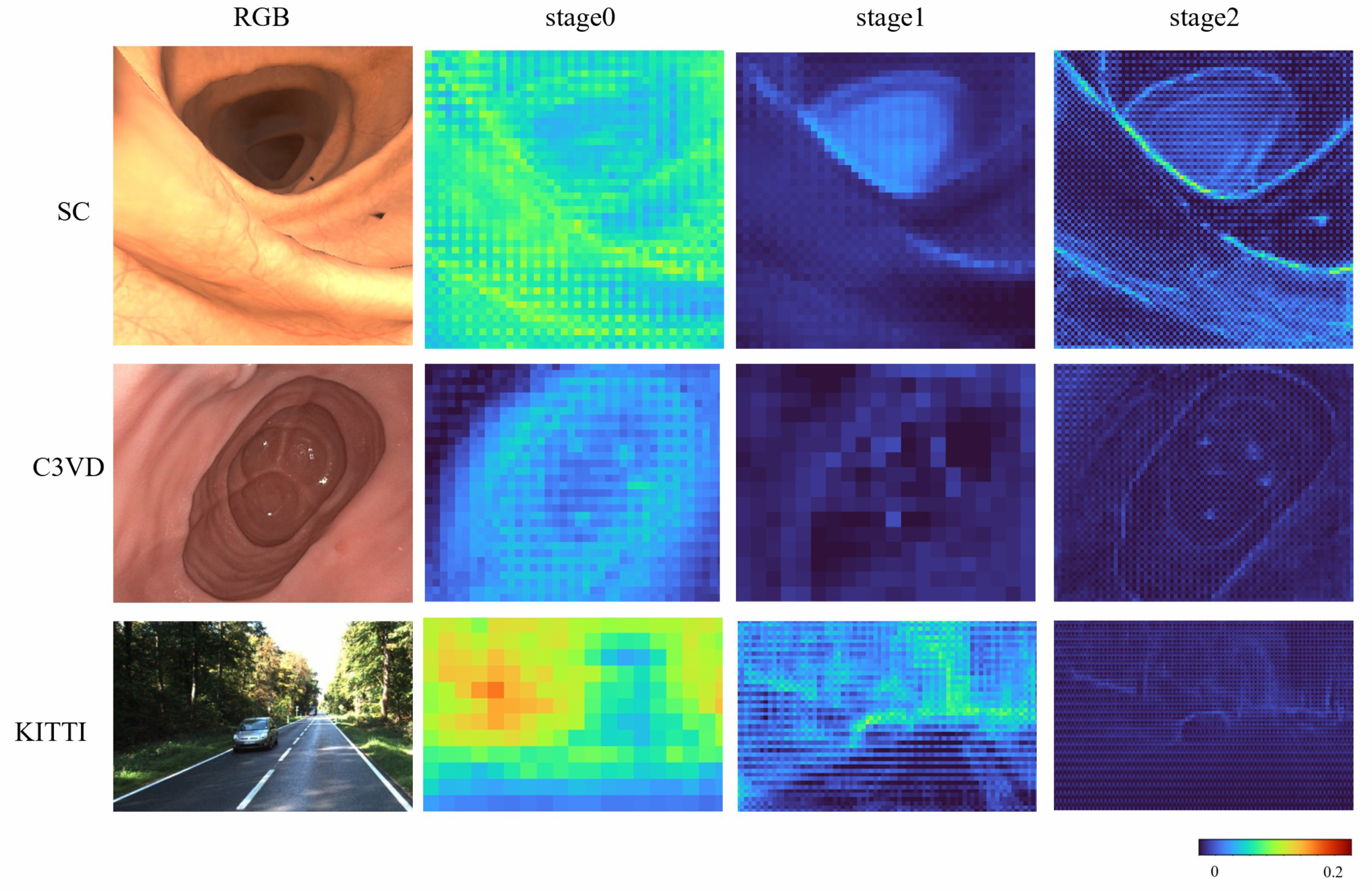
To more systematically evaluate the effectiveness of the proposed DLViM, we performed a qualitative analysis of the gating units across different stages. As illustrated in Figure 6, the activation weights are distributed relatively uniformly over the entire image at the early stage; however, as the network depth increases, these weights progressively concentrate on regions containing salient structural information, indicating that the model develops stronger spatial selectivity and structural awareness during the feature extraction process.

To further assess the effectiveness of the proposed model, we conducted a series of ablation studies to examine the contribution of individual components. All experiments were performed on the SimCol dataset, as illustrated in

Table 7. Ablation on the SimCol dataset.

Architecture	Abs rel	$\mathit{\delta }<1.25$	Params
Full model	0.070	0.964	3.90 M
Base model + CQL	0.116	0.919	3.63 M
Base model + LocalMamba	0.102	0.927	3.33 M
Base model + DLViM	0.096	0.937	3.33 M
Base model	0.187	0.907	3.07 M

The best and the second best results are highlighted in bold and underlined.

.

First, we evaluated the impact of removing the CQL module. This led to a reduction in model size by 0.3 M parameters; however, the RMSE increased by 12.5%, indicating a notable decline in accuracy. This highlights the importance of CQL in enhancing the model’s predictive performance. Next, we replaced the DLViM module with a standard CNN. While this replacement also reduces the model size by 0.3 M, it leads to a significant increase in prediction error. This suggests that DLViM is critical for capturing remote global context, a capability lacking in traditional CNNs limited to local feature extraction.

Furthermore, we examined the effect of substituting DLViM with the scanning strategy from LocalMamba. Although this modification did not significantly alter the number of model parameters, it led to a performance drop. This suggests that the proposed depth-first scan mechanism contributes to the model’s ability to understand structural information, reinforcing its role in maintaining global coherence in the learned representation.

5. Discussion and Conclusions

This work presents Mono-ViM, a novel self-supervised monocular depth estimation framework tailored for endoscopic imaging. The proposed architecture employs a hybrid design that seamlessly combines CNNs with Mamba to enhance global contextual understanding and refine semantic detail perception. Experiments on the SimCol and C3VD dataset both confirm that Mono-ViM comprehensively outperforms all state-of-the-art methods. In a self-supervised setting on the SimCol dataset, the proposed framework reduces errors by up to 16.7% in AbsRel, 14.8% in SqRel, 6.6% in RMSE, and 12.4% in RMSElog over current models. These results demonstrate the strength of incorporation of the DLViM module for capturing local–global feature dependencies and the CQL mechanism for improved fine-grained depth reconstruction. Furthermore, evaluations on the KITTI dataset confirm that the proposed framework maintains robust performance and exhibits strong generalization capability across varying environments.

The proposed Mono-ViM framework still presents several limitations. First, in endoscopic scenes, the presence of digestive fluids can produce strong specular reflections that disrupt the photometric consistency assumed in self-supervised learning. This will lead to local depth discontinuities. To address this, future work will incorporate reflection-aware photometric loss to enhance robustness under reflective conditions. Second, the proposed Mono-ViM assumes structural continuity between adjacent frames. However, periodic peristaltic motion introduces non-rigid deformation of tissues, which violates this assumption and affects depth stability. To mitigate this issue, optical-flow consistency constraints or temporal feature aggregation mechanisms can be adopted to explicitly model periodic deformation and reduce transient estimation errors.