Abstract
Diffusion in heterogeneous environments is usually governed by unusual dynamics, exhibiting sub- or superdiffusive scaling depending on the structural complexity and memory effects. In many systems, diffusing particles may alternate between periods of motion and rest, or may undergo stochastic resetting to a preferred position. While each of these mechanisms has been studied independently, their combined effect in a heterogeneous medium has been insufficiently investigated. We formulate and solve a coupled set of one dimension diffusion equations for the probability densities of moving and resting particles, accounting for space-dependent diffusivity and stochastic resetting. We obtain expressions for the probability distribution and show the behavior of the survival probability, mean-square displacement, and first-passage time. The results reveal a diverse range of behaviors with distinct diffusion regimes. One of them is obtained for small times, which can be connected to the heterogeneity present in the system, and another for intermediate times related to the intermittent process produced by the moving and pauses before the system reaches the stationary state.
MSC:
60J60; 60J65; 60J70
1. Introduction
One of the most fundamental phenomena in nature is diffusion, which can occur in various scenarios characterized by either usual [1,2] or anomalous [3,4,5]. For usual diffusion, we have the Markovian processes essentially characterized by a linear time dependence for the mean square displacement with the distribution of probabilities expressed in terms of a Gaussian distribution [1,2]. For anomalous diffusion, we have a nonlinear time dependence of the mean square displacement, e.g., , where and are connected with the sub- and superdiffusion, typical of non-Markovian processes [5,6]. Other dependencies for the mean square displacement are possible, such as , which characterizes an ultraslow diffusion [7,8]. We also have the Lévy distributions, which are asymptotically characterized by power laws, and the mean square displacement is not defined. These behaviors have been verified in many scenarios, such as electrical response [6], anomalous transport [9,10,11], ecology and movement patterns [12,13], and heterogeneous [14], bacterial motion in porous media [15], active particles in complex environments [16], and disordered [17,18] media. Another aspect of the diffusion processes concerns the feature that, in general, they can appear combined with others, such as reactions [19], adsorption–desorption [20,21,22], and stochastic resetting [23,24,25,26]. The interaction of particles with the substrate, where they are diffusing, can be represented by reactions or adsorption–desorption. This process promotes immobilization and, after a characteristic time, allows them to transition to motion, characterizing an intermittent process. These dynamics are observed in transport through porous media, molecular motors exhibiting pause phases, or random searchers alternating between relocation and inspection [27,28]. The stochastic resetting introduces processes in which particles in a diffusive system are periodically and randomly returned to a starting point, altering the system’s long-term behavior and creating non-equilibrium stationary states. This enables applications in areas such as search theory [29,30], biological processes [31], and economic modeling [32,33]. The interplay among these processes in a heterogeneous medium can provide insights into several physical and biological phenomena that involve complex structures and processes.
Here, we analyze intricate dynamics that arise from the combination of stochastic resetting and diffusion occurring within spatially heterogeneous environments with pauses for the one-dimensional case. For this, we consider the distribution , with and defined by the following set of equations:
where and represent the particles in the bulk, where represents the particles diffusing and represents the particles immobile (paused), and is the survival probability connected to the particles that are diffusing. The diffusion considered here is , which has been applied in several contexts such as diffusion on fractals [34], disordered media [18,35], and turbulent flux [36,37]. A different form of heterogeneity in the context of stochastic resetting has been explored in Refs. [38,39,40]. It is worth mentioning that for a space-dependent diffusivity , the Fokker–Planck equation corresponding to the stochastic process depends on the stochastic interpretation parameter (: Itô; : Stratonovich; : Hänggi–Klimontovich). The resulting FP operator includes an additional term , known as the spurious drift [41,42,43]. In our formulation, the diffusive term present in Equation (1) with spatial dependence corresponds to the Hänggi–Klimontovich convention. For Equation (1), we obtain the solution and the mean square displacement by considering the boundary conditions , , and the initial conditions and . To analyze the mean first passage time, we consider the system subjected to the boundary conditions with , which characterizes an absorbing surface in . These developments are performed in Section 2. In Section 3, we present our discussion and conclusions.
2. Diffusion and Stochastic Resetting
Let us start our analysis of Equation (1) by considering the eigenfunctions of the Sturm–Liouville problem related to the following differential equation:
with the condition , which results in
where the sub-indexes + and − refer to the even and odd solutions, , and is the Bessel function [44]. By using the eigenfunctions defined by Equations (3) and (4), it is possible to obtain the solution for Equation (1). To do this, we consider that the solution can be written as follows:
with
where is determined by Equation (1). By applying the previous equation in Equation (1), we find that
and
By using the Laplace transform and = and performing some additional calculations, it is possible to show that
with . By performing some calculations, it is possible to show that the
with defined as follows:
for , and
for , where and is the Bessel function of modified argument of second kind [44].
The survival probability can be determined from the set of Equation (1). For this, we can perform an integration on the spatial variable and obtain the following set of equations:
where and , which results in the following solutions for the survival probabilities:
and
Figure 1 shows the behavior of the distribution connected to the system for different values of to illustrate how the heterogeneity combined with the stochastic resetting and pauses modifies the time evolution of the system. This feature is more clearly illustrated in Figure 2 with the time behavior of the mean square displacement. The heterogeneous diffusivity introduces a non-trivial scaling of the mean square displacement, for small times (see Figure 2a), which interpolates between sub- and superdiffusive regimes depending on . The inclusion of pauses effectively tempers the transport exponent (see Figure 2b), while stochastic resetting establishes a nonequilibrium stationary state. Figure 3a,b show the behavior of the distribution for different times by considering and . It is worth mentioning that the distribution has different behaviors depending on the choices performed for , which is different from the standard case with stochastic resetting [24]. Particularly, it is possible to show that is given by
for the initial condition used in Figure 3, which implies that the parameters and influence only the time evolution of the system until it reaches the stationary state. This result also shows that the asymptotic behavior of mean square displacement, i.e., , in this scenario, for the system is independent of the and , yielding
For intermediate times, the influence of and is evident as show in Figure 2a,b.
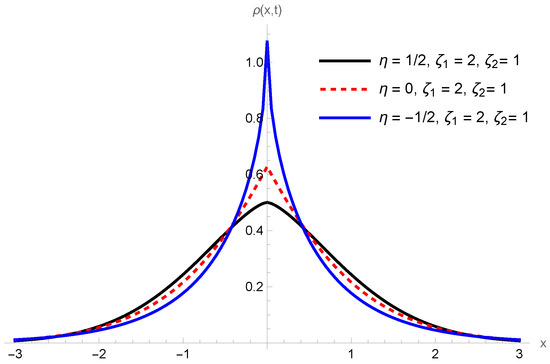
Figure 1.
Behavior of the distribution versus x for different values of by considering the diffusion process with pauses and stochastic resetting. We consider, for simplicity, , , , and the initial condition with .
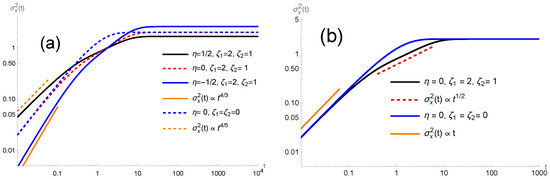
Figure 2.
(a) shows the behavior of the mean square displacement versus t for different values of by considering the diffusion process with pauses and stochastic resetting. (b) compares the behavior of the mean square displacement versus t for with pauses and without pauses to show the intermediate behavior introduced by the intermittent motion promoted by the pauses. We consider, for simplicity, , , , and the initial condition with .
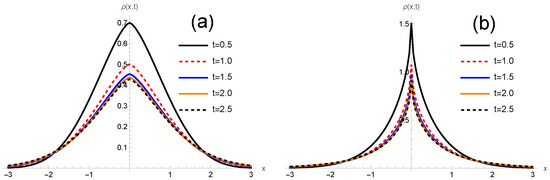
Figure 3.
(a,b) show the behavior of the distribution for different times by considering and . We consider, for simplicity, , , , , , , and the initial condition with .
Now, we consider the system subjected to the boundary conditions with , which characterizes an absorbing surface in . The system’s behavior in this context is analyzed to determine the mean first-passage time, accounting for stochastic resetting and pauses in diffusion processes within a heterogeneous medium. By using the considerations for the previous case, it is possible to show that the solution is given by
By performing some calculations, it is possible to show that the
with defined as follows:
for , and
for .
Figure 4 shows the behavior of the survival probability for the system when subjected to an absorbent surface for different values of , when subjected to the stochastic resetting and pauses. By using the previous equations, it is possible to obtain the mean first passage time, i.e.,
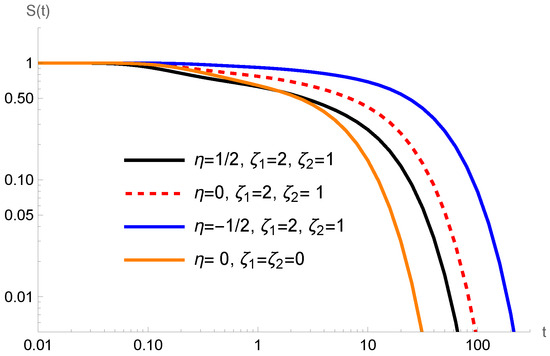
Figure 4.
Behavior of the survival probability versus t for different values of by considering the diffusion process with pauses and stochastic resetting. We consider, for simplicity, , , and the initial condition with .
Figure 5 shows the behavior of the mean first passage time for different scenarios. Figure 5a shows the behavior of the mean first passage time with the stochastic resetting rate r for different values of in the presence of pauses. This intermittent motion increases the first-passage time relative to the standard case. Figure 5b shows the behavior of the mean first passage time with the stochastic resetting rate r for different values of in the presence of pauses for different values of the resetting position.
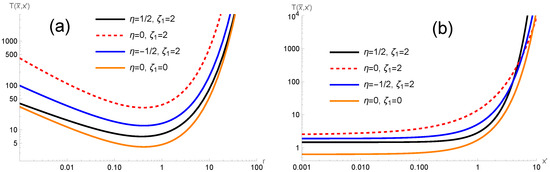
Figure 5.
Behavior of the mean first passage time for different values of by considering the diffusion process with pauses and stochastic resetting. (a) shows the behavior with the resetting rate r for and (b) shows the behavior with the resetting position for a given initial condition with . We consider, for simplicity, and the initial condition with .
3. Discussion and Conclusions
We have analyzed the combination of heterogeneous diffusion, pauses, and stochastic resetting. The results obtained here enable a rich dynamical behavior, governed by the interplay of spatial inhomogeneity and temporal intermittency. The heterogeneous diffusivity considered here modifies the local spreading rate. For , diffusion is hindered near the origin, generating an effective trapping potential, while favors outward propagation and superdiffusive trends. These features are connected to the behaviors observed for the mean square displacement, particularly for small times, which allows us to obtain . Introducing pauses during the process slows the growth of the mean-squared displacement, leading to a crossover between the active and immobilized regimes as the system responds to the intermittent process. The resetting process establishes a nonequilibrium stationary distribution whose shape depends sensitively on . The stochastic resetting also alters the first-passage statistics, producing a finite mean first-passage time as verified for the case of an absorbing surface. The results obtained for the mean first-passage time exhibit a familiar non-monotonic dependence on r, which for small resetting rates allows for long excursions, while very high r confines the dynamics excessively. This behavior yields an optimal resetting rate that minimizes search time, revealing how spatial heterogeneity with intermittent motion modifies the optimal search efficiency. This point can be verified by inspection in Figure 5. This interplay may explain, for example, adaptive strategies in active matter and living systems where movement intermittency and environmental inhomogeneity coexist. Finally, we hope that the results presented here will help to analyze diffusion in systems where the medium’s heterogeneity is combined with stochastic resetting and intermittent motion.
Author Contributions
Conceptualization, E.K.L., L.R.d.S. and M.K.L.; methodology, E.K.L., L.R.d.S. and M.K.L.; formal analysis, E.K.L., L.R.d.S. and M.K.L.; investigation, E.K.L., L.R.d.S. and M.K.L.; writing—original draft preparation, E.K.L., L.R.d.S. and M.K.L.; writing—review and editing, E.K.L., L.R.d.S. and M.K.L. All authors have read and agreed to the published version of the manuscript.
Funding
E.K.L. thanks the partial support of the CNPq (grant No. 301715/2022-0).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We thank the CNPq for the partial financial support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gardiner, C.W. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences (Springer Series in Synergetics); Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Risken, H. The Fokker-Planck Equation: Methods of Solution and Applications; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Pekalski, A.; Sznajd-Weron, K. Anomalous Diffusion from Basics to Applications; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Méndez, V.; Campos, D.; Bartumeus, F. Stochastic Foundations in Movement Ecology: Anomalous Diffusion, Front Propagation and Random Searches; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Havlin, S.; Weiss, G.H. A new class of long-tailed pausing time densities for the CTRW. J. Stat. Phys. 1990, 58, 1267–1273. [Google Scholar] [CrossRef]
- Bodrova, A.S.; Chechkin, A.V.; Cherstvy, A.G.; Metzler, R. Ultraslow scaled Brownian motion. New J. Phys. 2015, 17, 063038. [Google Scholar] [CrossRef]
- Höfling, F.; Franosch, T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 2013, 76, 046602. [Google Scholar] [CrossRef] [PubMed]
- Klages, R.; Radons, G.; Sokolov, I.M. Anomalous Transport; Wiley Online Library: Hoboken, NJ, USA, 2008. [Google Scholar]
- Zaslavsky, G.M. Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 2002, 371, 461–580. [Google Scholar] [CrossRef]
- Vilk, O.; Charter, M.; Toledo, S.; Barkai, E.; Nathan, R. Strong Anomalous Diffusion for Free-Ranging Birds. PRX Life 2025, 3, 033020. [Google Scholar] [CrossRef]
- Li, Y.; Suleiman, K.; Xu, Y. Anomalous diffusion, non-Gaussianity, nonergodicity, and confinement in stochastic-scaled Brownian motion with diffusing diffusivity dynamics. Phys. Rev. E 2024, 109, 014139. [Google Scholar] [CrossRef]
- Barletta, A.; Rees, D.; Celli, M.; Brandão, P. Open Boundaries, Anomalous Diffusion and the Darcy-Bénard Instability. Transp. Porous Media 2025, 152, 27. [Google Scholar] [CrossRef]
- Bhattacharjee, T.; Datta, S.S. Bacterial hopping and trapping in porous media. Nat. Commun. 2019, 10, 2075. [Google Scholar] [CrossRef]
- Bechinger, C.; Di Leonardo, R.; Löwen, H.; Reichhardt, C.; Volpe, G.; Volpe, G. Active particles in complex and crowded environments. Rev. Mod. Phys. 2016, 88, 045006. [Google Scholar] [CrossRef]
- Havlin, S.; Ben-Avraham, D. Diffusion in disordered media. Adv. Phys. 1987, 36, 695–798. [Google Scholar] [CrossRef]
- Ben-Avraham, D.; Havlin, S. Diffusion and Reactions in Fractals and Disordered Systems; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Méndez, V.; Fedotov, S.; Horsthemke, W. Reaction-Transport Systems: Mesoscopic Foundations, Fronts, and Spatial Instabilities; Springer Science & Business Media: Cham, Switzerland, 2010. [Google Scholar]
- Lenzi, E.K.; Yednak, C.A.R.; Evangelista, L.R. Non-Markovian diffusion and the adsorption-desorption process. Phys. Rev. E 2010, 81, 011116. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ledesma-Durán, A.; Hernández, S.; Santamaría-Holek, I. Effect of Surface Diffusion on Adsorption–Desorption and Catalytic Kinetics in Irregular Pores. I. Local Kinetics. J. Phys. Chem. C 2017, 121, 14544–14556. [Google Scholar] [CrossRef]
- Ledesma-Durán, A.; Hernández, S.I.; Santamaría-Holek, I. Effect of Surface Diffusion on Adsorption–Desorption and Catalytic Kinetics in Irregular Pores. II. Macro-Kinetics. J. Phys. Chem. C 2017, 121, 14557–14565. [Google Scholar] [CrossRef]
- Evans, M.R.; Majumdar, S.N. Diffusion with stochastic resetting. Phys. Rev. Lett. 2011, 106, 160601. [Google Scholar] [CrossRef]
- Evans, M.R.; Majumdar, S.N.; Schehr, G. Stochastic resetting and applications. J. Phys. A Math. Theor. 2020, 53, 193001. [Google Scholar] [CrossRef]
- Bressloff, P.C. Search processes with stochastic resetting and multiple targets. Phys. Rev. E 2020, 102, 022115. [Google Scholar] [CrossRef]
- Shkilev, V.P. Continuous-time random walk under time-dependent resetting. Phys. Rev. E 2017, 96, 012126. [Google Scholar] [CrossRef]
- Bénichou, O.; Loverdo, C.; Moreau, M.; Voituriez, R. Intermittent search strategies. Rev. Mod. Phys. 2011, 83, 81–130. [Google Scholar] [CrossRef]
- Fedotov, S. Subdiffusion, chemotaxis, and anomalous aggregation of self-attracting particles. Phys. Rev. E 2011, 83, 021110. [Google Scholar] [CrossRef]
- Belan, S. Restart could optimize the probability of success in a Bernoulli trial. Phys. Rev. Lett. 2018, 120, 080601. [Google Scholar] [CrossRef]
- Stanislavsky, A.; Weron, A. Optimal non-Gaussian search with stochastic resetting. Phys. Rev. E 2021, 104, 014125. [Google Scholar] [CrossRef] [PubMed]
- Roldán, É.; Lisica, A.; Sánchez-Taltavull, D.; Grill, S.W. Stochastic resetting in backtrack recovery by RNA polymerases. Phys. Rev. E 2016, 93, 062411. [Google Scholar] [CrossRef]
- Santra, I. Effect of tax dynamics on linearly growing processes under stochastic resetting: A possible economic model. Europhys. Lett. 2022, 137, 52001. [Google Scholar] [CrossRef]
- Jolakoski, P.; Pal, A.; Sandev, T.; Kocarev, L.; Metzler, R.; Stojkoski, V. A first passage under resetting approach to income dynamics. Chaos Solitons Fractals 2023, 175, 113921. [Google Scholar] [CrossRef]
- O’Shaughnessy, B.; Procaccia, I. Analytical solutions for diffusion on fractal objects. Phys. Rev. Lett. 1985, 54, 455. [Google Scholar] [CrossRef]
- O’Shaughnessy, B.; Procaccia, I. Diffusion on fractals. Phys. Rev. A 1985, 32, 3073. [Google Scholar] [CrossRef] [PubMed]
- Richardson, L.F. Atmospheric diffusion shown on a distance-neighbour graph. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1926, 110, 709–737. [Google Scholar]
- Salazar, J.P.; Collins, L.R. Two-particle dispersion in isotropic turbulent flows. Annu. Rev. Fluid Mech. 2009, 41, 405–432. [Google Scholar] [CrossRef]
- Sandev, T.; Kocarev, L.; Metzler, R.; Chechkin, A. Stochastic dynamics with multiplicative dichotomic noise: Heterogeneous telegrapher’s equation, anomalous crossovers and resetting. Chaos Solitons Fractals 2022, 165, 112878. [Google Scholar] [CrossRef]
- Sandev, T.; Domazetoski, V.; Kocarev, L.; Metzler, R.; Chechkin, A. Heterogeneous diffusion with stochastic resetting. J. Phys. A Math. Theor. 2022, 55, 074003. [Google Scholar] [CrossRef]
- Ray, S. Space-dependent diffusion with stochastic resetting: A first-passage study. J. Chem. Phys. 2020, 153. [Google Scholar] [CrossRef] [PubMed]
- Hanggi, P. Nonlinear fluctuations: The problem of deterministic limit and reconstruction of stochastic dynamics. Phys. Rev. A 1982, 25, 1130. [Google Scholar] [CrossRef][Green Version]
- Klimontovich, Y.L. Ito, Stratonovich and kinetic forms of stochastic equations. Physica A 1990, 163, 515–532. [Google Scholar] [CrossRef]
- Volpe, G.; Wehr, J. Effective drifts in dynamical systems with multiplicative noise: A review of recent progress. Rep. Prog. Phys. 2016, 79, 053901. [Google Scholar] [CrossRef]
- Wyld, H.W.; Powell, G. Mathematical Methods for Physics; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).