Abstract
The airline industry plays a vital role in global mobility and international trade, which makes the evaluation of its operational efficiency an important strategic task. This study evaluates and ranks the operational performance of passenger and freight air transport in Serbia over the period 2014–2023 by employing a fuzzy multi-criteria decision-making framework. Six key performance criteria were defined, with their weighting coefficients determined using the fuzzy MEREC method, while the ranking of alternatives was conducted using the fuzzy MARCOS method. The obtained results reveal noticeable variations in performance throughout the observed period and provide insights into efficiency trends in both passenger and freight segments of air transport. Furthermore, a sensitivity analysis confirmed the robustness and stability of the ranking outcomes. The findings of this research can support evidence-based decision-making and contribute to enhancing the operational efficiency and competitiveness of the air transport sector.
MSC:
90B06; 90B50; 90C70
1. Introduction
The efficient organization of air transportation is a key factor in strengthening airline competitiveness within the global transport system, particularly under conditions of increasing aviation globalization [1]. The development of aviation is recognized as a strategic priority in national transport policies, ensuring passenger safety, transparency, and adaptation to dynamic economic changes.
Air transport is characterized by short travel times but also by high operating costs, significant fuel consumption, and limited capacities. While passenger transport has historically dominated, the unreliability of freight carried on passenger aircraft led to the introduction of dedicated cargo carriers [2,3]. Passenger air transport fosters global connectivity, tourism, and international cooperation [4], whereas cargo transport supports global trade in high-value, perishable, and time-sensitive goods [5]. Effective cargo operations require multimodal integration, capacity planning, and storage efficiency.
In Serbia, air transport plays a vital role in international connectivity [6]. Investments in infrastructure and the privatization of Air Serbia have strengthened its regional position, with expanded routes achieved through global partnerships. Authorities enforce ICAO (International Civil Aviation Organization) and EASA (European Union Aviation Safety Agency) standards to ensure safety, protect passenger rights, and promote sustainability. However, the sector continues to face challenges from competition, economic pressures, and the need for further infrastructure investment.
Serbia’s future potential lies in expanding infrastructure, establishing new connections, and attracting international carriers [7]. Cargo air transport, though smaller in scale, has grown through targeted investments, particularly at Belgrade’s Nikola Tesla Airport, which benefits from a favorable geographical position. To enhance competitiveness, further development of cargo terminals, advanced technologies, and intermodal integration with road and rail is essential. Rising e-commerce and global logistics demands also create opportunities for specialized cargo services and stronger cooperation with international logistics firms [8].
The air transport system comprises interconnected carriers, airports, and air traffic control, supported by key stakeholders including airlines, navigation service providers, airport operators, and aircraft manufacturers [9].
Following the introductory section, which addresses the significance and operational performance of air transport within the framework of multi-criteria decision-making (MCDM), the Section 2 provides a comprehensive review of the literature concerning the application of various approaches and methodologies—particularly fuzzy extensions of MCDM—for evaluating the performance of both passenger and freight air transport (Figure 1). The integration of fuzzy logic into MCDM techniques has gained prominence due to its capacity to capture uncertainty, vagueness, and imprecision inherent in expert evaluations and operational data, thereby ensuring more robust and reliable assessment outcomes.
Figure 1.
Overview of the Paper Structure.
A broad spectrum of criteria can be taken into account when analyzing the operational performance of air transport systems, encompassing both passenger and cargo traffic. Accordingly, the Section 3 establishes the general framework for the application of MCDM methods, with particular emphasis on fuzzy extensions, together with the definition of evaluation criteria and the structure of the input dataset. The Section 4 provides a detailed exposition of the MEREC (Method based on the Removal Effects of Criteria) procedure, applied for the determination of the weighting coefficients of the evaluation criteria. These coefficients, expressed through fuzzy values to account for uncertainty and variability in the data, were subsequently incorporated into the MARCOS (Measurement of Alternatives and Ranking according to Compromise Solution) method in order to rank the operational performance of passenger and freight air transport in the Republic of Serbia for each year within the 2014–2023 periods. Each year was treated as a distinct alternative, and the analysis relied on relevant, officially available statistical data. In addition, in the Section 5 a sensitivity analysis was conducted to verify the robustness of the obtained weighting coefficients, thereby confirming the stability of the results. Finally, the Section 6 synthesizes the principal research findings and outlines recommendations and directions for future investigations.
Air transport represents a key component of modern logistics and transportation systems, and the operational efficiency of airlines significantly influences economic connectivity, competitiveness, and sustainable development. In conditions of fluctuating demand, rising operational costs, technological advancements, and global disruptions (e.g., the COVID-19 pandemic), it becomes essential to develop reliable methods for objectively measuring and comparing air transport performance over extended periods. However, existing literature and practice reveal a limited number of studies that jointly analyze the operational efficiency of both passenger and cargo air transport using fuzzy (MCDM) methodologies. This research gap constitutes the primary motivation for conducting this study.
The main novelties and contributions of this research can be summarized as follows:
- Simultaneous evaluation of passenger and freight air transport within a unified decision-making framework, which is rarely addressed in existing literature.
- Application of the fuzzy MEREC method to objectively determine criterion weights based on the influence of each criterion on the overall decision-making process.
- Use of the fuzzy MARCOS method for ranking performance across the observed time span, enabling the assessment of efficiency dynamics.
- Introduction of time as an alternative, where each year is treated as a unique alternative, allowing continuous monitoring of efficiency trends over a ten-year period.
- Implementation of sensitivity analysis to confirm the robustness and stability of the obtained results.
- Use of real operational data from the air transport sector of the Republic of Serbia (2014–2023), ensuring high practical relevance and providing a basis for strategic planning and decision-making.
2. Literature Review
In the contemporary interconnected environment, the airline industry assumes a pivotal role in facilitating the rapid and efficient global movement of both passengers and goods. Confronted with intensifying competition, airlines are compelled to continuously enhance their operations in order to secure a sustainable competitive advantage. The operational performance of the airline sector is shaped by a wide array of determinants, encompassing both short-term and long-term strategic planning, fleet and crew management, safety, reliability, cost efficiency, customer satisfaction, and environmental sustainability.
To stress the importance of the airline industry, different studies were conducted [10]. The causal relationship between air transport and economic growth in the ten countries with the highest air transport volumes from 1970 to 2021, employing bootstrap Toda–Yamamoto and Fourier Toda–Yamamoto causality tests, was a problem of interest [10]. The results reveal a unidirectional causal link from air transport to economic growth in most countries, except Russia and Brazil, while bidirectional relationships are observed between air freight and growth in Japan, and between registered departures and growth in China. The findings suggest that Fourier-based tests provide more consistent results and highlight the importance of considering multiple dimensions of air transport to capture its overall economic impact [10].
Airlines encounter numerous challenges related to optimization and decision-making, which necessitate the adoption of a comprehensive decision-making framework capable of integrating all relevant factors and providing effective solutions for performance improvement [11]. In recent years, the sector has increasingly embraced MCDM methodologies [12,13,14,15,16] as a means of addressing complex managerial problems characterized by multiple and often conflicting objectives. These approaches explicitly account for the interdependencies and trade-offs among diverse performance indicators, thereby enabling the evaluation and ranking of alternatives on the basis of a predefined set of criteria [17,18]. By embedding MCDM techniques within their strategic and operational processes, airlines are able to systematically assess performance outcomes and to identify targeted opportunities for operational enhancement [19,20].
The current state of the aviation industry and strategies for improving the organization of air transport within the broader economy is very interesting research topic [21]. Applying a dialectical-materialist approach and methods such as induction, deduction, and abstraction, the study draws on statistical data from both international and national sources. It identifies five key elements of global air transport, highlighting passenger traffic as the dominant activity and noting the pandemic’s significant impact on economic dynamics. The future of aviation is closely tied to innovation, including sustainable fuels, market expansion, and employment growth [22]. Operational efficiency is enhanced through precise scheduling, smart services, and improved safety protocols, all of which support the sustainable development of the industry.
A paradigm shift has emerged, emphasizing the alignment of outcomes with the preferences of the Decision Maker (DM), thereby prioritizing satisfactory solutions over strictly optimal ones. Decision problems are generally classified into four categories: selection, ranking, sorting, and elimination. Nevertheless, inaccuracies in both quantitative and qualitative data often undermine the reliability of MCDM applications, particularly in cases where linguistic assessments are transformed into numerical representations, which inevitably introduces uncertainty. Moreover, numerous methods are subject to the Rank Reversal Phenomenon (RRP), whereby the ranking of alternatives changes following the addition or removal of options, in contradiction to the principle of independence of alternatives.
A variety of problems in airline industry is being solved by applying MCDM techniques for analysis and improvement. The research [23] employs MCDM techniques to improve the ground operations of low-cost carriers (LCCs). Using fuzzy AHP and fuzzy TOPSIS, a case study of three Turkish airlines evaluates performance across five criteria and eighteen sub-criteria. The results indicate that the third airline performs best, providing insights into operational strategies and performance improvement in the LCC sector. The study also outlines limitations and offers directions for future research [23]. The Fuzzy TOPSIS methodology was used to prioritize risk mitigation strategies in air cargo operations, which face risks such as inefficiencies, cyber threats, regulatory challenges, and environmental concerns [24]. A structured framework combining expert judgment with fuzzy logic was developed to evaluate ten criteria, including cost-effectiveness, efficiency, and scalability. The results indicate that Enhanced Data Security Measures ranked highest, underscoring the importance of cyber security, while Resilience Building and Safety Protocols also proved critical. The study demonstrates the value of Fuzzy TOPSIS in addressing uncertainty in risk assessment and provides practical insights for improving risk management in air cargo, with future research directed toward dynamic assessment and complementary MCDM methods [24].
Service quality is recognized as a key corporate strategy for gaining a competitive advantage. With the growing demand for air transport, airports have become essential hubs, bringing airport service quality into focus. As gateways connecting cities to the world, the quality of service at airports is assessed based on how well it meets passenger expectations. This study [25] aims to evaluate service quality by analyzing 17 airports that were rated as five-star airports by Skytrax in 2021, using 11 criteria. The MEREC method was used to determine the significance of each criterion, while MARCOS and CoCoSo methods were applied to rank the airports based on service quality. The criteria used for evaluation include transportation services, security screenings, immigration services, signage, arrival services, departure services, transfer passenger services, terminal comfort, terminal facilities, shopping options, and food and beverage services. The analysis using the MEREC method identified immigration services as the most influential factor in determining airport service quality. Based on the combined results of MARCOS and CoCoSo methods, Chubu Centrair Airport ranked highest for service quality, while Tokyo Haneda Airport ranked lowest [25].
Classical approaches such as AHP (Analytic Hierarchy Process), TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution), PROMETHEE (Preference Ranking Organization METHod for Enrichment Evaluations), and ELECTRE (ELimination Et Choix Traduisant la REalité) remain widely employed, although they exhibit certain methodological limitations [26,27,28,29,30]. These shortcomings have stimulated the development of more advanced methodologies, including MARCOS, CoCoSo, and RAWEC, specifically designed to mitigate such challenges [31,32,33,34]. Among these, the MARCOS method has demonstrated considerable applicability across a variety of engineering and industrial contexts due to its conceptual simplicity and robustness. Furthermore, MARCOS is frequently combined with complementary techniques such as SWARA (Step-wise Weight Assessment Ratio Analysis) or AHP, thereby enhancing its methodological flexibility and practical relevance. The research [35] aims to analyze the factors that influence and determine the overall workload of transport operators (drivers and pilots) while comparing the key elements of both systems. To establish a general hierarchical model, the AHP is applied. In this study, the Saaty Scale is used for scoring, enabling the representation of missing data through matrices that can be calculated using a specific method [35].
In recent studies, fuzzy extensions of MARCOS have also been increasingly adopted, as they provide an effective means of addressing uncertainty, vagueness, and imprecision in expert evaluations, further strengthening the robustness of decision-making outcomes.
Numerous studies in the literature have examined the measurement of operational efficiency; however, this research area, particularly in the context of passenger and cargo air transport, remains insufficiently explored. The present study evaluates calendar years as alternatives against a defined set of criteria for the operational performance of passenger and cargo air transport in the Republic of Serbia by employing MCDM techniques. In order to account for uncertainty and imprecision in the data, fuzzy extensions of MCDM are integrated into the analysis, thereby enhancing the robustness and reliability of the obtained results.
3. Methods and Materials
Operational efficiency is one of the key indicators of success in the air transport sector. In light of modern challenges such as rising fuel costs, increased competition, strict environmental standards, and high user expectations, it is essential to continuously enhance the operational performance of airlines and airport operators. Operational efficiency is reflected in the system’s ability to optimally utilize available resources (human, material, technological) while minimizing costs, time, and negative impact on the environment, and ensuring a high level of service and security [36].
The process of improving operational efficiency therefore requires making numerous strategic, tactical, and operational decisions. Since such decisions are influenced by different criteria, including financial indicators, environmental standards, safety, user satisfaction, and regulatory requirements, harmonizing these often conflicting factors becomes a considerable challenge. Multi-criteria methods and DEA (Data Envelopment Analysis) [37] provide a structured framework for analyzing alternatives and selecting optimal strategies. Managing complex operations in air transport thus involves decision-making processes that encompass a wide range of interdependent factors. In this regard, MCDM emerges as an indispensable tool for managers and decision-makers. Moreover, given that decision-making environments are frequently characterized by uncertainty, subjectivity, and vagueness, fuzzy extensions of MCDM methods are increasingly applied [38,39,40]. By incorporating fuzzy numbers into the evaluation process, these methods allow for a more realistic representation of imprecise judgments and incomplete data, thereby enabling more robust and reliable assessments of alternatives [41,42].
3.1. Fuzzy MEREC Method
In MCDM tasks, the determination of criteria weights is of paramount importance, as they exert a considerable influence on the final outcomes. Consequently, a variety of techniques have been developed to evaluate these weights, which are generally classified as subjective, objective, or hybrid in nature. In this study, an objective weighting approach, namely MEREC, is employed [43]. This method introduces a novel concept by deriving weights from the impact of each criterion’s removal on the overall performance of the alternatives [44].
The originality of MEREC method lies in its focus on assessing how the exclusion of a given criterion alters the aggregate performance of alternatives, thereby distinguishing it from conventional techniques that rely predominantly on variations in magnitude. This perspective not only facilitates the assignment of more representative weights but also assists decision-makers in identifying criteria that may be redundant. By emphasizing causality and allowing for the incorporation of different aggregation functions, MEREC provides additional flexibility. In this research, fuzzy extensions are integrated into the MEREC framework to more effectively capture uncertainty, vagueness, and imprecision in the evaluation process [45,46]. The development of innovative MCDM methodologies from alternative viewpoints enhances the robustness of decision-making processes, particularly when such approaches are combined with other established methods. Although simulation results indicate that MEREC’s correlation with traditional weighting techniques diminishes with increasing problem complexity, this limitation is widely acknowledged in MCDM research and reinforces the need for methodological integration to ensure reliable and stable outcomes [47,48].
To account for uncertainty and imprecision in the evaluation process, triangular fuzzy numbers (TFNs) were employed to fuzzify the entries of the initial decision matrix [49,50]. Each TFN is expressed in the form xij = (lij, mij, uij), where lij denotes the lower bound, mij the most likely value, and uij the upper bound, with the condition lij ≤ mij ≤ uij), if its membership function is equal to:
Step 1: Creating a decision matrix
where xij is the value of alternative i according to criterion j.
Step 2: Decision matrix normalization
The values in the decision matrix are normalized depending on the type of criteria:
- maximizing criteria (beneficial criteria):
- minimizing criteria (non-beneficial criteria):
Step 3: The overall performance of the alternatives is assessed as follows:
Step 4: Evaluate the performance of the alternatives by excluding each criterion as follows:
Step 5: The summation of absolute deviations is computed in this step. Specifically, the impact of excluding the j-th criterion is evaluated based on the results obtained in Steps 3 and 4. Let Ej denote the removal effect associated with the j-th criterion. The corresponding values of Ej are determined using the following formula:
where values Si and are defuzzificated using the following expression:
Step 6: Calculate the final weights of the criteria. In this phase, the objective weight of each criterion is determined based on the removal effects Ej calculated in Step 5.
3.2. Fuzzy MARCOS Method
The MARCOS method evaluates the relationship between the performance scores of the examined alternatives and two predefined reference points, namely the ideal and anti-ideal solutions. Through this comparison, the method determines the extent to which each alternative approximates the optimal (ideal) outcome while simultaneously measuring its deviation from the least desirable (anti-ideal) scenario [51].
In its fuzzy extension, the MARCOS methodology computes the utility of each alternative in the fuzzy domain: criterion values and the two reference points are modeled as triangular fuzzy numbers (TFNs), the closeness to the (fuzzy) ideal and the remoteness from the (fuzzy) anti-ideal are obtained via fuzzy arithmetic, and the resulting fuzzy utilities are defuzzified (e.g., using the centroid method) to yield crisp utility values. On this basis, fuzzy MARCOS identifies the compromise solution—i.e., the alternative that most evenly balances multiple, potentially conflicting criteria while explicitly accounting for uncertainty and imprecision in measurements and expert judgments [52,53].
The MARCOS framework thus enables objective multi-criteria ranking while consistently incorporating both extreme reference points, ensuring that each alternative is assessed across the full spectrum of potential outcomes. By representing inputs and benchmarks fuzzily and resolving them to crisp scores only at the final stage, the approach enhances robustness to noise and vagueness and improves the interpretability of trade-offs among cost, efficiency, risk, and environmental impact.
Moreover, MARCOS-both in its classical and fuzzy variants-exhibits high adaptability across domains such as engineering design, logistics optimization, strategic resource management, and transport systems. Its clear structure supports rational and transparent decision-making in complex, dynamic settings where competing objectives must be carefully balanced to achieve operational excellence.
The MARCOS method follows a structured procedure that begins with the construction of the initial decision matrix, which incorporates n criteria and m alternatives [54,55]. Once the decision matrix is formed (Step 1), the ideal and anti-ideal solutions are determined for each criterion (Step 2) using Equations (10) and (11), representing the best and worst possible values depending on whether the criterion is beneficial or non-beneficial.
The third step involves the normalization of the decision matrix, where the values are adjusted according to the type of criterion. For maximizing (beneficial) criteria, normalization is carried out as in Equation (3), whereas for minimizing (non-beneficial) criteria, normalization is expressed as in Equation (4).
In the fourth step, the normalized values are multiplied by the corresponding weights to obtain the weighted normalized matrix:
The fifth step calculates the utility degrees and for each alternative, where
and Si denotes the sum of the weighted normalized values of the i-th alternative, while Sai and Saai represent the aggregate values of the ideal and anti-ideal alternatives, respectively.
In the sixth step, the utility functions relative to the ideal and anti-ideal solutions are computed:
The seventh step derives the overall utility function of each alternative:
where values f(Ki), and are defuzzificated using the following expression (7).
Since fuzzy numbers are applied in the earlier stages, these utility values are subsequently defuzzified to obtain crisp values suitable for ranking. The final step ranks the alternatives based on their utility scores, with higher values indicating closer proximity to the ideal solution. The alternative with the maximum utility value is identified as the compromise solution, representing the most suitable choice.
Through this structured sequence, the MARCOS method enables decision-makers to systematically balance multiple, and often conflicting, criteria. By incorporating fuzzy extensions, the method further enhances robustness by addressing uncertainty and imprecision in the input data. Its methodological flexibility and mathematical rigor make MARCOS particularly effective in domains such as transportation planning, logistics, and resource management, where decision-making must account for complex trade-offs under dynamic conditions.
3.3. Input Data
The MCDM represents a pivotal branch of Operations Research (OR) concerned with decisions that involve the simultaneous evaluation of multiple, often conflicting, criteria. The overarching aim of OR is to enhance decision-making processes by offering mathematical models and optimization tools that support rational and well-structured choices. The MCDM draws upon a wide range of disciplines, including engineering, economics, computer science, and mathematics. The use of multi-criteria techniques enables decision-makers—such as managers and policy-makers—to actively participate in the process, thereby improving their understanding of the complexity and uncertainty of the business environment. Their role extends beyond the application of pre-existing solutions to encompass the analysis, structuring, and modeling of problems, as well as the interpretation and implementation of results. The evolution of MCDM methodologies has been largely driven by advances in information technologies and computational systems, which have significantly contributed to their growing applicability. Owing to their practical relevance, multi-criteria methods have rapidly advanced, facilitating the resolution of complex decision problems. These methods differ in terms of the quantity and quality of available information, the approaches employed the degree of complexity, and their underlying mathematical properties.
Operational efficiency in air transport entails maximizing the utilization of available resources while minimizing costs and time. Effective flight planning, fleet management, ground service coordination, and timely adaptation to fluctuations in traffic and weather conditions are critical determinants of success. The integration of advanced information technologies, process automation, and data analytics can yield substantial improvements in operational performance. Decisions derived from MCDM analyses play a crucial role in strengthening operational efficiency, as they enable the attainment of an optimal balance among the frequently conflicting objectives of cost, quality, and safety. In this regard, the incorporation of fuzzy extensions into MCDM methods provides additional robustness, as they effectively capture uncertainty, vagueness, and imprecision inherent in expert judgments and operational data, thereby ensuring more reliable and resilient decision-making outcomes.
As part of the operational performance analysis of the passenger and freight air transport sectors in the Republic of Serbia over the period 2014–2023, the input data—defined as evaluation criteria (Table 1)—were derived from regular monthly, quarterly, and annual statistical reports, the aggregated results of which are presented in Table 2 and Table 3 [56].

Table 1.
Air transport criteria.

Table 2.
The initial matrix utilized for determining the performances of passenger air transport: C1, C3, C5, C6, C7 and C9 [56].

Table 3.
The initial matrix utilized for determining the performances of freight air transport: C2, C4, C5, C6, C8 and C9 [56].
These data are expressed through a set of criteria, including the number of passengers transported, passenger and tonne-kilometres achieved, the number of employees, fuel consumption, passenger and cargo traffic volume, and foreign currency receipts from transport services. These indicators enable a multi-criteria evaluation of air transport efficiency and performance, focusing on identifying the key factors contributing to operational effectiveness throughout the observed period.
4. Applied Methodology and Discussion of Findings
It should be emphasized that the solutions obtained through MCDM methods cannot be considered strictly optimal or the only acceptable outcomes. Instead, these approaches serve to provide a structured framework for analyzing complex decision problems, thereby assisting decision-makers in identifying high-quality and practically feasible solutions. Nevertheless, real-world decision-making environments are frequently characterized by uncertainty, vagueness, and incomplete information. Consequently, the application of fuzzy extensions of MCDM methods has become increasingly significant.
This approach promotes consensus-building by reducing unnecessary conflicts among stakeholders, including policymakers, the public and other interest groups. In this analysis, the alternatives—represented by the observed years—and the relevant evaluation criteria are organized within the initial decision matrices. The objective, determined based on whether each criterion has a positive or negative impact, focuses on assessing the operational performance of air transport in the Republic of Serbia.
4.1. Fuzzy MEREC Application
The subchapter formalizes and connects the entire fuzzy-MEREC procedure with the results reported in Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9. The starting point is the classical MEREC “removal-effect” logic, extended with triangular fuzzy numbers (TFNs) to capture measurement error and uncertainty. The TFNs were selected because this form of fuzzy representation is among the most widely used and computationally efficient in MCDM [57]. The TFN structure enables the expression of uncertainty using simple lower, middle, and upper bounds, which correspond to the real-world characteristics of transport and economic data that are frequently affected by fluctuations, measurement imprecision, reporting delays, or estimation error. In comparison with other fuzzy number types (e.g., trapezoidal or Gaussian), TFNs require fewer parameters, offer straightforward mathematical manipulation, and provide a clear interpretation of variability around the most likely value. Consequently, the use of TFNs offers an optimal balance between modeling accuracy and computational simplicity, making this representation suitable for evaluating operational efficiency in air transport under conditions of partial uncertainty [58,59]. Each raw entry xij (alternative i, criterion j) is fuzzified into a TFN (lij, mij, uij) with a ±5% tolerance, with the membership function μM(x) defined in Equation (1). The resulting fuzzy decision matrix X is given in Equation (2), and its entries (lower/middle/upper components for every criterion) are listed in Table 4.

Table 4.
Initial fuzzy decision matrix (TFNs, ±5%; L–M–U components) by alternatives and criteria.

Table 5.
Normalized fuzzy values by criterion.

Table 6.
Aggregated fuzzy performance Si of alternatives.

Table 7.
Criterion removal effects.

Table 8.
Final objective weight coefficients.

Table 9.
Obtain weight coefficients.
Step 1 (Fuzzification). Alternatives (observed years) and evaluation criteria are organized in X, where the goal—set by each criterion’s positive or negative impact—reflects the assessment of the operational performance of air transport in the Republic of Serbia.
Step 2 (Normalization). Fuzzy entries are normalized according to criterion type using the transformations in Equations (3) and (4) (separate forms for maximizing/beneficial and minimizing/non-beneficial criteria), yielding the normalized fuzzy values rij = (lij, mij, uij). These normalized TFNs are reported in Table 5.
Step 3 (Aggregation per alternative). The overall fuzzy performance of each alternative is obtained by the logarithmic aggregation given in Equation (5), which mitigates the influence of extremes and preserves the [0, 1] range. The resulting triplets Si are summarized in Table 6.
Step 4 (Leave-one-criterion-out aggregation). To quantify the “objective importance” of every criterion, we recompute the alternative scores when criterion j is excluded, producing Sij as in Equation (6). This provides a direct counterfactual for each criterion relative to the baseline Si.
Step 5 (Removal effects and defuzzification). For each criterion j, the removal effect Ej is the sum of absolute deviations across all alternatives Equation (7). The fuzzy effects are then defuzzified using the centroid method Equation (8) to obtain crisp impact measures Ej. The fuzzy triplets and their defuzzified values are presented in Table 7.
Step 6 (Final objective weights). The final weights follow by normalizing the defuzzified removal effects Equation (9). For completeness, the fuzzy weight intervals and the defuzzified weights wj are listed in Table 8, verifying .
For passenger air transport, integrating the initial decision matrix and applying fuzzy MEREC via Equations (1)–(9) yield the weight vector, while the corresponding freight weights are obtained by applying the same procedure to the freight matrix, both presented in Table 9.
The fuzzy MEREC–derived weights indicate distinct importance profiles for passenger and freight air transport. In the passenger case, the distribution is nearly balanced between benefit and cost criteria, with the largest emphasis falling on C5 and C7 (≈0.21 and ≈0.20), followed by moderate contributions from C1 and C3, while C6 and C9 are comparatively less influential. By contrast, the freight air transport is more cost-intensive at the criterion level—C6 is the single most influential factor (≈0.195)—yet, when aggregated by type, the overall structure leans toward benefits because C2 and C9 also carry substantial weight. On the common criteria, freight assigns markedly more importance than passenger to C6 and C9 (roughly +42% each relative to passenger), whereas passenger assigns more to C5 (about +11% relative to freight). These patterns imply that, for passenger air transport, performance gains are most effectively achieved by improving outcomes aligned with C7 while reducing costs associated with C5, whereas in freight air transport the greatest leverage arises from reducing C6 (and, secondarily, C5) alongside strengthening benefit-oriented dimensions such as C2 and C9 (Figure 2). Because the two segments are evaluated on partially different sets of criteria, direct cross-segment comparisons are meaningful only for the shared criteria (C5, C6, C9); otherwise, interpretations should remain segment-specific.
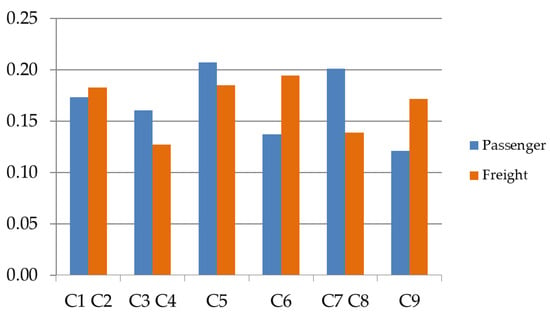
Figure 2.
The comparative view of weight coefficients.
4.2. Fuzzy MARCOS Application
When applying the fuzzy MARCOS method Equations (3)–(4) and (10)–(17) to rank operational performance based on selected indicators for passenger and freight air transport during the period from 2014 to 2023, the results show clear temporal patterns of efficiency. Table 10, Table 11 and Table 12 summarize the normalized decision matrices, weighted normalized values, and final fuzzy scores with corresponding rankings.

Table 10.
Normalization of the initial matrix.

Table 11.
The weighted normalized matrix.

Table 12.
Final defuzzified scores & ranking.
The structured procedure of the MARCOS method begins with the construction of the initial decision matrix, which incorporates n criteria and m alternatives. Once the decision matrix is formed (Step 1), the ideal and anti-ideal solutions are determined for each criterion (Step 2) using the following Equations (10) and (11). The third step involves normalizing the decision matrix according to the type of criterion Equations (3) and (4), as shown in Table 10, followed by the construction of the weighted normalized matrix (Equation (12)), as shown in Table 11.
Utility degrees relative to the ideal and anti-ideal solutions are then computed Equations (13) and (14), while Equations (15) and (16) yield partial utility functions. Finally, Equation (17) derives the overall utility function of each alternative, after which fuzzy results are defuzzified and used for ranking (Table 12). Since fuzzy numbers are applied in the earlier stages, these utility values are subsequently defuzzified to obtain crisp values suitable for ranking. The alternative with the maximum utility value is identified as the compromise solution.
Table 13 shows the annual results for both passenger and freight air transport. The findings indicate that the highest performance was achieved in 2023 for passenger air transport (f = 2.8379), whereas 2014 marked the weakest year for freight air transport (f = 1.1335). The results confirm that passenger air transport efficiency recovered more dynamically after the pandemic shock, while freight air transport demonstrated earlier peaks but greater instability during the 2019–2022 period.

Table 13.
Ranking results for passenger and freight air transport obtained by fuzzy MARCOS method.
Figure 3 illustrates the annual ranking of operational performance for air passenger and freight transport in the Republic of Serbia from 2014 to 2023. The y-axis represents the ranking positions (with 1 indicating the best performance and 10 the lowest), while the x-axis shows the corresponding years. The blue line with diamond markers denotes the performance ranking of passenger transport, while the orange line with square markers reflects the ranking of freight transport.
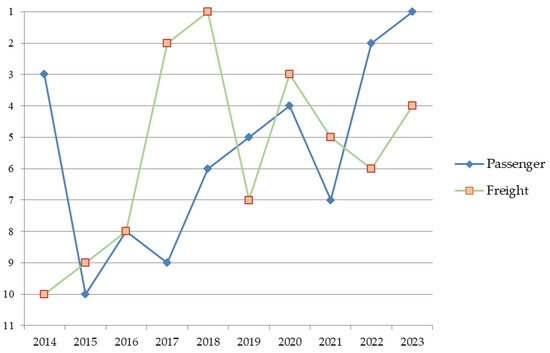
Figure 3.
Ranking Diagram of Annual Operational Efficiency of Passenger and Freight Air Transport in Serbia.
Segment by segment, freight exhibits a sustained pre-pandemic climb, improving from 2014 to its apex in 2018 (1st; fk = 3.66), followed by volatility and partial erosion in 2019–2022, and a modest recovery to 4th in 2023. Passenger performance shows early weakness with the nadir in 2015 (10th; fk = 1.43), steady improvement through 2020 (4th; fk = 1.76), a pandemic-related setback in 2021 (7th; fk = 1.51), and then a pronounced rebound to 2nd in 2022 (fk = 2.01) and 1st in 2023 (fk = 2.84).
Comparatively, freight air transport reached its peak earlier (2017–2018), whereas the passenger air transport segment lagged but delivered the strongest end-of-period acceleration (2022–2023). The crossings and divergent paths of the two series suggest distinct efficiency drivers—such as demand structure, network configuration, and operational constraints—implying differentiated policy levers: consolidate earlier gains in freight air transport while sustaining post-pandemic resilience and service quality in passenger air transport operations.
The diagram highlights not only the temporal dynamics of air transport efficiency but also the differing sensitivity of the passenger and freight sectors to external disruptions and recovery trends.
As an emerging player in the European air transport landscape, the Republic of Serbia must implement targeted strategies to support further growth. These strategies include the modernization of airport infrastructure, establishment of new air corridors, and upgrades to air traffic control systems, all aimed at improving both the quality and safety of air traffic management. Additional necessary actions involve expanding cargo terminals, enhancing fleet capabilities, and investing in sustainable technologies to improve air transport efficiency and meet the evolving needs of both passengers and freight operators. This would contribute to raising Serbia’s air transport quality standards, ensuring it can provide competitive services while addressing the demands of the sector’s stakeholders.
5. Sensitivity Analysis
Sensitivity analysis is included to confirm the stability of the weighting coefficients and the robustness of the resulting rankings. This analysis examines how small variations in criterion weights affect the ordering of alternatives, helping determine the degree to which the decision outcome depends on the weighting structure [60,61,62]. The approach evaluates the smallest change needed to alter relative ranking positions.
The initial ranking for passenger air transport was obtained using six criteria (C1, C3, C5, C6, C7, C9), where C1, C7, and C9 represent benefit-type criteria, and C3, C5, and C6 correspond to cost-type criteria. All indicators were normalized using standard monotone normalization [63], and aggregated through a weighted linear composite model with the weight vector w derived from the fuzzy MEREC procedure [64]. The baseline results are given in Table 14, where alternative A10 is identified as the dominant best-performing option.

Table 14.
Baseline results (normalized composite score and rank).
To evaluate how ranking positions change under local perturbations, one-at-a-time weight variations were applied following the Absolute-Any (AA), Percent-Any (PA), and Absolute-Top (AT) criteria [65,66]. The thresholds that produce the first rank reversals are presented in Table 15, while the minimal weight shifts that replace the top-ranked alternative are shown in Table 16. The earliest ranking changes occur for the cost criteria C3 and C6, where small increases in weight re-order closely ranked alternatives (A1 and A7). In contrast, much larger changes in the benefit criteria (C1 and C7) are required before the top alternative is affected, indicating strong dominance of A10 in the baseline decision setting.

Table 15.
AA/PA thresholds (minimal changes that alter the ranking).

Table 16.
AT thresholds (change of the top alternative).
To test robustness within a practically relevant range, a ± 10% variation was applied one criterion at a time, with renormalization to preserve ∑wj = 1 [67]. The resulting Spearman rank correlations remained high (ρ ≥ 0.964), and no rank reversals of the best-performing alternative were recorded, as shown in Table 17 [68,69]. The same procedure applied to freight air transport produced correlations equal to or very close to unity (Min ρ ≈ 0.988), confirming complete stability of the ranking within the examined variation interval.

Table 17.
Robustness under ±10% one-at-a-time weight changes (Spearman ρ).
These results show that the ranking of alternatives is highly robust, and the selection of the best-performing year remains unchanged under realistic adjustments of criterion weights. Therefore, the integrated fuzzy MEREC–fuzzy MARCOS framework demonstrates strong reliability and suitability for operational performance evaluation in air transport.
6. Conclusions
Based on the results presented and discussed in the previous sections, a final conclusion can be drawn regarding the operational performance of passenger and cargo air transport in the Republic of Serbia. Although this research provides valuable insights into the operational performance of passenger and cargo air transport in Serbia, several limitations should be noted. The analysis is based on available statistical data and does not include qualitative factors such as service quality or customer satisfaction. The selected set of criteria does not incorporate environmental, safety, or service-level indicators, which may also influence performance outcomes. Furthermore, the focus on the Serbian context limits the generalizability of the findings to other regions. Additionally, the results of the fuzzy MCDM methods depend on the chosen methodological assumptions. The evaluation results indicate that freight transport exhibited steady growth until 2018, experienced fluctuations during 2019–2022, and then showed moderate recovery in 2023. In contrast, passenger transport reached its lowest point in 2015, declined again in 2021 following the pandemic, and achieved its strongest recovery and highest performance in 2023. These findings highlight different efficiency drivers and sectoral sensitivities to external disruptions. Despite the outlined limitations, the conducted analysis offers valuable insights into the developmental trends and operational efficiency of air transport in Serbia, thus providing a reliable foundation for informed strategic decision-making and future sector improvement. Moreover, the study contributes to the scientific literature by demonstrating the effectiveness of the integrated fuzzy MEREC–fuzzy MARCOS framework in evaluating air transport performance, offering a methodological reference and practical decision-support tool for resource optimization, efficiency improvement, and long-term policy planning in the air sector.
Author Contributions
Conceptualization, N.P., D.M. and A.A.; methodology, N.P., N.K. and M.R.-R.; investigation, N.P., T.M.Q. and D.M.; writing—original draft preparation, N.P., N.K. and A.A.; software, N.P. and N.K.; validation, N.P., M.R.-R. and D.M.; formal analysis, D.M., N.K. and A.A.; writing—review and editing, N.P., D.M. and N.K.; supervision, N.P. and A.A.; project administration, T.M.Q. and M.R.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia (Contract No. 451-03-137/2025-03/200109).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Thangavel, K.; Safwat, N.E.-D.; Gardi, A.; Sabatini, R. Multi-Domain Traffic Management: Towards Integrated Air and Space Transport Operations. IEEE Aerosp. Electron. Syst. Mag. 2025, 40, 4–22. [Google Scholar] [CrossRef]
- Gurturk, M.; Celik, E. A Bibliometric Analysis of Air Cargo: Milestones, Trends, and Future Directions. Transp. J. 2025, 64, e70001. [Google Scholar] [CrossRef]
- Petrović, N.; Bojović, N.; Marinković, D.; Jovanović, V.; Milanović, S. A Two-Phase Model for the Evaluation of Urbanization Impacts on Carbon Dioxide Emissions from Transport in the European Union. Teh. Vjesn. 2023, 30, 514–520. [Google Scholar] [CrossRef]
- Kodanda, B.; Bhanumurthy, P.R. An Overview of Issues and Trends in Air Transport Demand Analysis and Modeling. J. Aerosp. Sci. Technol. 2025, 77, 1–37. [Google Scholar] [CrossRef]
- López-Escolano, C. A Geographical Approach to European Cargo Airports. In Key Challenges in Geography; Ruepert, G., Ilić, T., Eds.; Young Geographers; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Martin, V. Key performance indicators in green transition: The case of Serbia. Bankarstvo 2024, 53, 194–223. [Google Scholar] [CrossRef]
- Oliveira, A.; Couto, G.; Pimentel, P. Maximizing social welfare through air transport public service obligations in remote regions. Case Stud. Transp. Policy 2025, 20, 101407. [Google Scholar] [CrossRef]
- Lalošević, M.; Đerić, J. Urban plan as a precondition for continuous and directed development—The example of the Nikola Tesla Airport. Industrija 2022, 50, 7–20. [Google Scholar] [CrossRef]
- Naletina, D.; Petljak, K.; Sremac, M. Characteristics and the Overview of Air Traffic in the Republic of Croatia. Pomorstvo 2018, 32, 297–311. [Google Scholar] [CrossRef]
- Çelik, K.A.; Yalçınkaya, Ö.; Kutlu, M. The causal relationship between air transport and economic growth: Evidence from top ten countries with the largest air transport volume. Transp. Policy 2025, 162, 521–532. [Google Scholar] [CrossRef]
- Koma, Ş.; Kusakci, A.O.; Haji Amiri, M. A hybridized Pythagorean fuzzy AHP and WASPAS method for airline new route selection: Case study of Turkish Airline. J. Model. Manag. 2025; ahead-of-print. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Choudhury, B.B.; Dhal, P.R. A Bibliometric Analysis of Material Selection Using MCDM Methods: Trends and Insights. Spectr. Mech. Eng. Oper. Res. 2024, 1, 189–205. [Google Scholar] [CrossRef]
- Petrović, N.; Marković, S.; Nikolić, B.; Jovanović, V.; Petrović, M. Evaluating Alternative Propulsion Systems for Urban Public Transport in Niš: A Multicriteria Decision-Making Approach. J. Eng. Manag. Syst. Eng. 2024, 3, 72–81. [Google Scholar] [CrossRef]
- Kawecka, E.; Perec, A.; Radomska-Zalas, A. Use of the Simple Multicriteria Decision-Making (MCDM) Method for Optimization of the High-Alloy Steel Cutting Processby the Abrasive Water Jet. Spectr. Mech. Eng. Oper. Res. 2024, 1, 111–120. [Google Scholar] [CrossRef]
- Tadić, D.; Komatina, N. A Hybrid Interval Type-2 Fuzzy DEMATEL-MABAC Approach for Strategic Failure Management in Automotive Manufacturing. J. Eng. Manag. Syst. Eng. 2025, 4, 21–38. [Google Scholar] [CrossRef]
- Çilingir, D.; Öztürk, H.H.; Kaya, K. Invisible Walls to Green Mobility: Barriers to Sustainable Transportation in Izmir. Spectr. Decis. Mak. Appl. 2025, 3, 151–163. [Google Scholar] [CrossRef]
- Özekenci, E.K. A Multi-Criteria Framework for Economic Decision Support in Urban Sustainability: Comparative Insights from European Cities. Int. J. Econ. Sci. 2025, 14, 162–181. [Google Scholar] [CrossRef]
- Tarnanidis, T.; Papathanasiou, J.; Mareschal, B.; Vlachopoulou, M. MCDM Review in marketing and managerial decisions: Practical implications and Future research. Manag. Sci. Lett. 2025, 15, 45–54. [Google Scholar] [CrossRef]
- Dang, L.T.H.; Cheng, Z.H.; Wang, C.N.; Dang, T.T.; Nguyen, N.A.T. Evaluating the sustainable performance of international airlines: Application of Shannon entropy and CoCoSo methods. In Proceedings of the International Conference on “Green Solutions and Emerging Technologies for Sustainability” (GSETS 2025), Ho Chi Minh City, Vietnam, 10–11 April 2025. [Google Scholar]
- Farida, Y.; Laili, H.N.; Wibowo, A.T.; Desinaini, L.N.; Sari, S.K. Selecting the Best-Performing Low-Cost Carrier (LCC) Airlines Using Analytical Hierarchy Process (AHP) and Elimination et Choix Traduisant la Realite (ELECTRE). J. Inf. Syst. Eng. Bus. Intell. 2022, 8, 196–206. [Google Scholar] [CrossRef]
- Harazha, O.; Shevchuk, D. Air Transport Organization: Competitiveness, Globalization, and Innovation. Sci. Innov. 2024, 20, 79–90. [Google Scholar] [CrossRef]
- Nikolić, B.; Marković, S.; Petrović, N.; Marinković, D.; Jovanović, V. Biodiesel and feedstocks—Possibilities and characteristics: A review. Therm. Sci. 2025, 29, 3477–3490. [Google Scholar] [CrossRef]
- Kulakli, A.; Şahin, Y. A Combined Multi-Criteria Decision Making Approach for Improvement of Airlines’ Ground Operations Performance: A Case Study from Türkiye. Systems 2023, 11, 421. [Google Scholar] [CrossRef]
- Kütahya, C.K.; Kanmaz, U. Prioritizing Risk Mitigation Strategies in Air Cargo Freight Operations: A Fuzzy TOPSIS Approach. J. Aviat. 2025, 9, 181–195. [Google Scholar] [CrossRef]
- Sumerli Sarıgül, S.; Ünlü, M.; Yaşar, E. A New MCDM Approach in Evaluating Airport Service Quality: MEREC-Based MARCOS and CoCoSo Methods. Uluslararası Yönetim Akad. Derg. 2023, 6, 90–108. [Google Scholar] [CrossRef]
- Petrović, N.; Jovanović, V.; Petrović, M.; Nikolić, B.; Pavlović, J. Evaluating the operation performance of the Serbian transport freight system by using Multiple Criteria Decision-Making technique. Eng. Today 2023, 1, 33–40. [Google Scholar] [CrossRef]
- Petrović, N.; Jovanović, V.; Marković, S.; Marinković, D.; Nikolić, B. Multi-criteria decision-making approach for choising e-Bus for urban public transport in the city of Niš. Acta Tech. Jaurinensis 2025, 18, 1–8. [Google Scholar] [CrossRef]
- Wang, L.; Dong, M. An Entropy Weight-TOPSIS Based Method for e-Commerce Logistics Service Quality Evaluation. Teh. Vjesn. 2023, 30, 1253–1256. [Google Scholar] [CrossRef]
- Salvador, G.; Moura, M.; Campos, P.; Cardoso, P.; Espadinha-Cruz, P.; Godina, R. ELECTRE applied in supplier selection—A literature review. Procedia Comput. Sci. 2024, 232, 1759–1768. [Google Scholar] [CrossRef]
- Çilek, A.; Seyranlıoğlu, O. Portfolio Optimization with Entropy-CRITIC-IDDWS- PROMETHEE Model in BIST Retail Trade Sector. Int. J. Econ. Financ. Issues 2024, 14, 23–35. [Google Scholar] [CrossRef]
- Puska, A.; Stilic, A.; Pamucar, D.; Bozanic, D.; Nedeljkovic, M. Introducing a novel multicriteria ranking of alternatives with weights of criterion (RAWEC) model. MethodsX 2024, 12, 102628. [Google Scholar] [CrossRef]
- Radovanović, M.; Božanić, D.; Tešić, D.; Puška, A.; Hezam, I.M.; Jana, C. Application of hybrid DIBR-FUCOM-LMAW-BONFERRONI-GREY-EDAS model in multicriteria decision-making. Facta Univ. Ser. Mech. Eng. 2023, 21, 387–403. [Google Scholar] [CrossRef]
- Petrović, N.; Jovanović, V.; Marković, S.; Marinković, D.; Petrović, M. Multicriteria Sustainability Assessment of Transport Modes: A European Union Case Study for 2020. J. Green Econ. Low-Carbon Dev. 2024, 3, 36–44. [Google Scholar] [CrossRef]
- Ersoy, N. Normalization procedures for COCOSO method: A comparative analysis under different scenarios. Dokuz Eylül Üniversitesi İşletme Fakültesi Derg. 2022, 22, 217–234. [Google Scholar] [CrossRef]
- Alharasees, O.; Utku, K. Transport Operators Total Load Comparison by Analytical Hierarchy Process (AHP). In Emerging Trends in Electric Aviation; Karakoc, T.H., Letnik, T., Marksel, M., Ekmekci, I., Dalkiran, A., Ercan, A.H., Eds.; ISEAS 2022 Sustainable Aviation; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Petrović, N.; Mihajlović, J.; Jovanović, V.; Ćirić, D.; Živojinović, T. Evaluating annual operation performance of Serbian railway system by using multiple criteria decision-making technique. Acta Polytech. Hung. 2023, 20, 157–168. [Google Scholar] [CrossRef]
- Petrović, N.; Jovanović, V.; Marinković, D.; Marković, S.; Nikolić, B. Measuring the Efficiency of Rail FreightTransport—A Case Study. Acta Polytech. Hung. 2025, 22, 123–136. [Google Scholar] [CrossRef]
- Puška, A.; Nedeljković, M.; Božanić, D.; Štilić, A.; Muhsen, R.Y. Evaluation of agricultural drones based on the compromise ranking from alternative solutions (CORASO) methodology. Eng. Rev. 2024, 44, 77–90. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, B.; Yu, Y.; Ali, Z.; Almohsen, B. Complex intuitionistic fuzzy DOMBI prioritized aggregation operators and their application for resilient green supplier selection. Facta Univ. Ser. Mech. Eng. 2023, 21, 339–357. [Google Scholar] [CrossRef]
- Fu, H.; Du, Y.; Ding, Q.; Fu, M. Performance Evaluation of Port Enterprise Resource Integration Based on Fuzzy Comprehensive Evaluation Method. Teh. Vjesn. 2023, 30, 1185–1192. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Song, Y.F.; Meng, X.; Liu, Z.G. Optimizing Supply Chain Efficiency with Fuzzy CRITIC-EDAS. Int. J. Simul. Model. 2023, 22, 723–733. [Google Scholar] [CrossRef]
- Li, Q. Green Supply Chain Optimization with Fuzzy MCDM for Economic Growth. Int. J. Simul. Model. 2023, 22, 690–700. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Determination of Objective Weights Using a New Method Based on the Removal Effects of Criteria (MEREC). Symmetry 2021, 13, 525. [Google Scholar] [CrossRef]
- Dhal, R.P.; Choudhury, B.B.; Sahoo, K.S. Evaluating motor choices for a smart wheelchair prototype using an integrated TODIM-COCOSO approach with MEREC weighting. Eng. Rev. 2024, 44, 22–44. [Google Scholar] [CrossRef]
- Fan, J.; Lei, T.; Wu, M. MEREC-MABAC method based on cumulative prospect theory for picture fuzzy sets: Applications to wearable health technology devices. Expert Syst. Appl. 2024, 255, 124749. [Google Scholar] [CrossRef]
- Makki, A.A.; Abdulaal, R.M.S. A Hybrid MCDM Approach Based on Fuzzy MEREC-G and Fuzzy RATMI. Mathematics 2023, 11, 3773. [Google Scholar] [CrossRef]
- Narang, M.; Kumar, A.; Dhawan, R. A fuzzy extension of MEREC method using parabolic measure and its applications. J. Decis. Anal. Intell. Comput. 2023, 3, 33–46. [Google Scholar] [CrossRef]
- Popović, G.; Pucar, Đ.; Smarandache, F. MEREC-COBRA approach in e-commerce development strategy selection. J. Process Manag. New Technol. 2022, 10, 66–74. [Google Scholar] [CrossRef]
- Hasnan, Q.H.; Rodzi, Z.M.D.; Kamis, N.H.; Al-Sharqi, F.; Al-Quran, A.; Romdhini, M.U. Triangular fuzzy merec (TFMEREC) and its applications in multi criteria decision making. J. Fuzzy Ext. Appl. 2024, 5, 505–532. [Google Scholar] [CrossRef]
- Saidin, M.S.; Lee, L.S.; Marjugi, S.M.; Ahmad, M.Z.; Seow, H.-V. Fuzzy Method Based on the Removal Effects of Criteria (MEREC) for Determining Objective Weights in Multi-Criteria Decision-Making Problems. Mathematics 2023, 11, 1544. [Google Scholar] [CrossRef]
- Demir, G.; Chatterjee, P.; Kadry, S.; Abdelhadi, A.; Pamučar, D. Measurement of Alternatives and Ranking according to Compromise Solution (MARCOS) Method: A Comprehensive Bibliometric Analysis. Decis. Mak. Appl. Manag. Eng. 2024, 7, 313–336. [Google Scholar] [CrossRef]
- Tešić, D.Z.; Božanić, D.I.; Pamučar, D.S.; Din, J. DIBR—FUZZY MARCOS model for selecting a location for a heavy mechanized bridge. Vojnoteh. Glas. 2022, 70, 314–339. [Google Scholar] [CrossRef]
- Jana, S.; Giri, C.B.; Sarkar, A.; Asharaf, S.; Jana, C.; Pamučar, D.; Marinković, D. Selection of brokerage firms for e-services using fuzzy decision making process with AHP and MARCOS approaches. Eng. Rev. 2024, 44, 1–21. [Google Scholar] [CrossRef]
- El-Araby, A. The utilization of MARCOS method for different engineering applications: A comparative study. Int. J. Res. Ind. Eng. 2023, 12, 155–164. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Puška, A.; Chatterjee, P. Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of alternatives and ranking according to COmpromise solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Statistical Office of the Republic of Serbia, Statistical Yearbook of the Republic of Serbia. 2024. Available online: https://www.stat.gov.rs/en-us/publikacije/publication/?p=15984&tip=2 (accessed on 2 June 2025).
- Nayeb-Pashaei, K.; Vahabzadeh, S.; Hosseinian-Far, A.; Ghoushchi, S.J. Sustainable Urban Transportation: Key Criteria for a Greener Future. Spectr. Oper. Res. 2025, 3, 103–127. [Google Scholar] [CrossRef]
- Popa, L. Centroid-Induced Ranking of Triangular Picture Fuzzy Numbers and Applications in Decision-Making. Symmetry 2024, 16, 1492. [Google Scholar] [CrossRef]
- Giuclea, M.; Popescu, C.-C. An Approach to the Total Least Squares Method for Symmetric Triangular Fuzzy Numbers. Mathematics 2025, 13, 1224. [Google Scholar] [CrossRef]
- Więckowski, J.; Sałabun, W. Sensitivity analysis approaches in multi-criteria decision analysis: A systematic review. Appl. Soft Comput. 2023, 148, 110915. [Google Scholar] [CrossRef]
- Ecer, F.; Pamučar, D. MARCOS technique under intuitionistic fuzzy environment for determining the COVID-19 pandemic performance of insurance companies in terms of healthcare services. Appl. Soft Comput. 2021, 104, 107199. [Google Scholar] [CrossRef]
- Kamarul Zaman, M.M.; Rodzi, Z.M.; Andu, Y.; Shafie, N.A.; Sanusi, Z.M.; Ghazali, A.W.; Mahyideen, J.M. Adaptive Utility Ranking Algorithm for Evaluating Blockchain-Enabled Microfinance in Emerging—A New MCDM Perspective. Int. J. Econ. Sci. 2025, 14, 123–146. [Google Scholar] [CrossRef]
- Wang, Z.; Nabavi, S.R.; Rangaiah, G.P. Multi-criteria decision making in chemical and process engineering: Methods, progress, and potential. Processes 2024, 12, 2532. [Google Scholar] [CrossRef]
- Więckowski, J.; Sałabun, W. A new sensitivity analysis method for decision-making with multiple parameters modification (COMSAM). Inf. Sci. 2024, 678, 120902. [Google Scholar] [CrossRef]
- Meshref, A.N.; Elkasaby, E.A.A.; Ibrahim, A. Selecting key drivers for a successful lean construction implementation using Simos’ and WSM: The case of Egypt. Buildings 2022, 12, 673. [Google Scholar] [CrossRef]
- Dunke, F.; Nickel, S. Simulation-based multi-criteria decision making: An interactive method with a case study on infectious disease epidemics. In Annals of Operations Research; Springer: Berlin, Germany, 2021. [Google Scholar] [CrossRef]
- Więckowski, J.; Kizielewicz, B.; Sałabun, W. A multi-dimensional sensitivity analysis approach for evaluating the robustness of renewable energy sources in European countries. J. Clean. Prod. 2024, 469, 143225. [Google Scholar] [CrossRef]
- Kabassi, K. Comparing multi-criteria decision making models for evaluating environmental education programs. Sustainability 2021, 13, 11220. [Google Scholar] [CrossRef]
- Vassoney, E.; Mochet, A.M.; Desiderio, E.; Negro, G.; Pilloni, M.G.; Comoglio, C. Comparing multi-criteria decision-making methods for the assessment of flow release scenarios from small hydropower plants in the Alpine area. Front. Environ. Sci. 2021, 9, 635100. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).