Abstract
As technical discussions surrounding next-generation 6G networks are gaining momentum, dynamic and flexible network operation and management technologies remain essential for supporting services with diverse requirements. Specifically, the emergence and increasing generalization of new communication entities are driving structural changes that demand more dynamic environments and stricter constraints on network operation. These changes render conventional routing optimization significantly more complex, requiring consideration of intricate service characteristics and evolving network conditions. Meanwhile, genetic algorithms (GAs), a class of metaheuristic methods, have been effectively employed for routing optimization. However, the inherent randomness in the initialization of solution populations often leads to limitations in convergence stability and the quality of the final solutions. To address this issue, this paper proposes a routing optimization approach that evaluates the quality of initial solution populations by learning the network state using graph neural networks (GNNs). Based on this prediction, a high-quality initial population is constructed, which serves as the basis for the subsequent execution of the genetic algorithm. The proposed method jointly considers operational costs in both the communication and computational domains, enabling the derivation of optimal paths that satisfy service requirements under the given network conditions.
Keywords:
6G networks; routing optimization; genetic algorithm; graph neural network; metaheuristic algorithm MSC:
90B18
1. Introduction
With the rapid advancement of network technologies leading up to and beyond the era of 5G, the telecommunication foundation has been laid for enabling heterogeneous devices to interconnect and communicate through the network. Specifically, network softwarization technologies, epitomized by software-defined networking (SDN) and network function virtualization (NFV), have emerged as key enablers for dynamically building network environments capable of supporting services with diverse requirements [1]. In the upcoming era of next-generation communication networks, there will be a need to meet service performance requirements even stricter than those of 5G, while also supporting a broader range of service use cases. For example, the inclusion of communication relay entities such as low-Earth-orbit (LEO) satellites and aerial platforms is becoming commonplace beyond the conventional scope of terrestrial communications [2]. In parallel, the widespread adoption of artificial intelligence (AI) technologies is making the deployment of AI models and the provision of AI-based services a prerequisite for customized network configurations.
To construct tailored networks aligned with specific service characteristics under constrained communication and computational resources, flexible and dynamic network configurations must be realized in advance. This challenge can be formulated as a set of optimization problems aimed at the efficient operation and control of networks under limited resources to meet the complex requirements of various services. Among these challenges, the service traffic routing problem involves determining the optimal traffic paths that account for path cost, energy consumption, and the satisfaction of service performance requirements.
Achieving optimal routing under increasingly complex and heterogeneous network and service characteristics has become a more challenging task. Specifically, as network environments consist of multiple domains, recent routing problems must address a growing set of constraints, including end-to-end service optimization across domains and the placement of application services to meet stringent performance requirements. Accordingly, these requirements compel network operators to take routing optimization, along with the service placement problem, into account in a joint manner, thereby complicating the routing problem in networks. Although AI-based techniques have shown promise in solving such complex routing problems [3], challenges such as acquiring sufficient training data and the high computational cost of model training remain unresolved.
In addition to AI-based approaches, metaheuristic techniques have also been applied to routing problems to derive approximate optimal solutions. A representative example is the genetic algorithm (GA), a type of evolutionary algorithm that is often employed to solve combinatorial optimization problems in traffic routing under multiple constraints [4]. However, due to its exploratory nature, GA lacks a guarantee of convergence to the global optimum [5]. Moreover, as GAs rely on crossover and mutation operations across generations based on an initial solution population, the convergence time and final solution quality can vary depending on the quality of the initial population. Despite the importance of initial population design, most GA-based routing approaches still rely on randomly generated individuals for initialization [6,7], which undermines the efficiency and effectiveness of the algorithm.
To address this limitation, this paper proposes an initial population evaluation method to enhance GA-based routing optimization in a given network environment. Specifically, we employ a graph neural network (GNN) to learn the network topology and use it to predict the quality of an initial population composed of chromosomes representing candidate routing paths. The GA-based routing algorithm then selects initial populations with high predicted quality, as assessed by the GNN, to guide the path optimization process.
The remainder of this paper is organized as follows. Section 2 reviews related work on routing techniques for service traffic. Section 3 presents the system model for service traffic routing. Section 4 describes the proposed GNN-assisted GA-based routing method. Section 5 evaluates the performance of the implemented routing mechanism, and finally, Section 6 concludes the paper and discusses future research directions.
2. Related Work
2.1. AI-Assisted Traffic Routing
In the networking field, routing refers to the process of determining the path that traffic takes from its source to its destination. This path must satisfy the performance requirements of the traffic while minimizing operational costs [8]. Typically, the objective of traffic routing problems is to determine the shortest path that considers key network performance metrics such as bandwidth, latency, and availability [9,10].
AI technologies have recently emerged as a promising solution for achieving optimal routing, even in dynamically changing network environments [11]. For instance, Vinayakumar et al. [12] proposed a machine learning-based approach to predict future traffic patterns for use in routing decisions, while another study by Yuan et al. [13] demonstrated the classification of encrypted traffic using machine learning. Beyond such studies, Petro et al. [14] proposed an AI/ML framework for future networks, providing methods for network state prediction and dynamic optimal routing. Other research efforts have exploited the inherent graph-based structure of networks by applying graph neural networks (GNNs) to learn the current network state and integrating them with reinforcement learning to determine optimal routing paths [15].
2.2. Routing Optimization Approaches
To perform optimal routing based on graph representations of networks, it is essential to capture not only the static topology with predefined network conditions but also the dynamically changing states of the network. In this context, prior studies [16,17] proposed graph embedding techniques that consider traffic information and the types of network devices, and applied these embeddings in reinforcement learning frameworks. In addition, recent work by Sun et al. [18] explored the use of large language models (LLMs) to generate network graphs, which were employed as predictors, encoders, and aligners to address optimization challenges in dynamic networks.
As traffic routing can be formulated as an optimization problem, numerous studies have also employed metaheuristic approaches in addition to AI-based techniques. For example, Cavdar et al. [19] proposed a discrete particle swarm optimization method to determine traffic paths in an SDN environment with the goal of load balancing. Genetic algorithms (GAs) have also been utilized in various contexts, such as multipath routing [20] and energy-efficient traffic routing for improving network sustainability [21]. Additionally, a hybrid method combining different metaheuristic optimization techniques, such as GA and ant colony optimization (ACO), was proposed to improve network performance while addressing network failures [22].
More recently, routing has begun to incorporate environmental considerations in response to growing concerns about climate change. For instance, efforts have been made to reduce the carbon emissions generated by network operations through carbon-aware routing [23]. Given that carbon emissions are generally proportional to power consumption, some studies have also explored routing approaches that jointly consider both the energy usage of the network and the computational cost at the traffic’s destination [24]. Furthermore, in this context, energy efficiency is expected to be a major consideration for forthcoming 6G networks, where numerous sensor nodes are deployed and communicate with each other to enable various 6G use cases. To enhance energy efficiency in dynamic networks, Rakan et al. [25] proposed a machine learning-driven routing optimization method applicable to 6G-enabled wireless sensor networks. In addition to carbon-aware and energy-aware routing approaches, several studies have investigated service placement and auto-scaling for traffic destinations to jointly account for routing and service operations [26,27,28].
As demonstrated by these studies, the traffic routing problem in modern networks has evolved into a more complex form with additional constraints. Therefore, there is a growing need for efficient routing methods that can dynamically determine optimal paths tailored to the service requirements under varying network conditions. To this end, this paper proposes a routing approach that leverages the strengths of graph neural networks (GNNs) and genetic algorithms (GAs).
3. System Design
3.1. System Model
Software-defined networking (SDN) architecture enables dynamic network operations, including routing, load balancing, and task scheduling, by providing a centralized control plane that has a global view of the entire network state. Given that flexibility and dynamic reconfiguration are essential in next-generation communication networks, it is expected that routing decisions will similarly be managed via the control plane. Additionally, the control plane can be deployed in a hierarchical architecture, in which the entire network is managed by a set of control planes, each operating in different network domains or locations and interacting with a centralized control plane that acts as the end-to-end controller. Figure 1 illustrates the conceptual framework of service traffic routing conducted through the control plane.
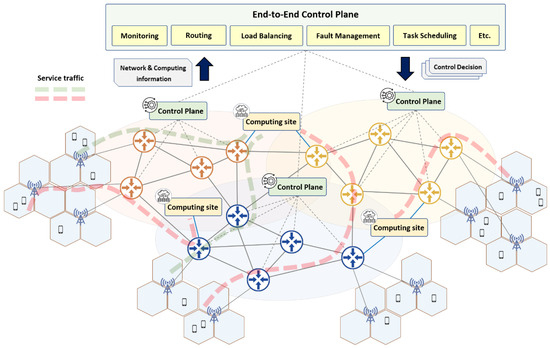
Figure 1.
System model of traffic routing in dynamic networks.
The service traffic routing problem addressed in this paper extends the formulation in [24] by considering not only the network domain responsible for forwarding traffic, but also the computational domain in which the traffic is processed. Specifically, the network is modeled as a graph , where N is the set of nodes comprising both network nodes and computational nodes, denoted by such that , and L is the set of links connecting these nodes. For a given service traffic demand with requirements denoted as , routing involves determining a path to a destination computational node via the control plane, such that the service requirements are satisfied.
3.2. Problem Formulation for Service Traffic Routing Optimization
The service traffic routing problem can be defined as the task of minimizing the operational cost incurred when traffic, generated in response to service demands, is routed to and processed at a computational node along the path determined by the routing algorithm. In this paper, we formulate the routing problem based on the optimization model defined in [24]. The optimization objective is to minimize the total operational cost, as expressed in Equation (1).
The objective function in (1) aims to minimize the total operational cost, which consists of the transmission cost for each link and the processing cost for each computation node included in the routing path of service traffic demand . The binary decision variables and indicate whether link l or computation node n is included in the routing path of service demand r. They are defined as follows:
In addition to the objective function, network-related Constraints (2)–(5) specify the conditions that must be satisfied in the routing process to ensure feasibility. Constraint (2) enforces the transmission capacity limit by requiring that the aggregate traffic volume of all service demands traversing a link l does not exceed its maximum capacity . Constraint (3) bounds the end-to-end propagation delay by ensuring that the sum of delays along the path of service traffic demand r remains within the maximum tolerable delay . Constraint (4) ensures reliability by requiring that the availability of links along the path meets or exceeds the minimum required availability . Finally, Constraint (5) restricts the maximum number of hops allowed in the routing path of each service traffic demand.
Subsequently, the model incorporates conditions related to the allocation of computation nodes where traffic is processed in addition to these network-level constraints. These constraints are expressed as follows:
Constraint (7) ensures that each service traffic demand r must be processed at exactly one computation node. Similarly, Constraint (8) specifies that service traffic must be processed at computation nodes rather than regular network nodes. Finally, Constraint (9) accounts for the resource requirements associated with processing the traffic of each service demand r at a computation node. Computation nodes provide multiple types of resources, such as CPU, GPU, and memory. Let the resource set be denoted as follows:
Accordingly, Constraint (9) requires that the total resource demand of all service demands r for resource j must not exceed the available capacity of resource j at computation node n. This ensures that sufficient resources are available to process the assigned traffic.
4. Proposed Approach
The aforementioned service traffic routing problem can be classified as a constrained shortest path (CSP) problem. As CSP is generally NP-Hard, finding an optimal solution within polynomial time is computationally intractable in most cases [29]. Therefore, in this paper, we employ a genetic algorithm (GA), a type of metaheuristic method, to perform optimal routing that jointly considers operational costs incurred at both network nodes and computational nodes.
4.1. Genetic Algorithm Framework for Routing Optimization
In the proposed GA-based routing approach, each chromosome in the solution population represents a candidate traffic path. Within a chromosome, the first gene always corresponds to the network node where the traffic originates, while the last gene represents the computational node where the traffic is processed. Due to the maximum hop constraint defined in Constraint (5), the length of each chromosome is also bounded. For instance, if the maximum number of hops is h, the maximum number of genes in a chromosome is .
To perform routing using the genetic algorithm, an initial population of chromosomes must be generated upon the arrival of each service traffic demand. In the proposed method, a breadth-first search (BFS) is employed to discover all feasible paths within the hop limit [30]. A subset of those paths is then randomly selected to construct the initial population of chromosomes, according to a predefined population size. In this procedure, the proposed approach can be used to evaluate the generated initial population, thereby selecting initial solutions that are predicted to be of high quality. Specifically, population quality refers to the best fitness value obtained from the genetic algorithm after the entire evolutionary process.
In each generation, tournament selection is used to choose pairs of parent chromosomes, which are then subjected to crossover and mutation operations with a predefined probability. To prevent the generation of infeasible paths, such as disconnected or loop routes, the crossover operator randomly selects one of the common nodes shared by both parents as the crossover point. For mutation, a node in the chromosome is altered by replacing it with one of the common neighbors shared between its preceding and succeeding nodes. These operators ensure the validity of the path after evolutionary operations. The genetic algorithm iterates this process until a termination condition is met, during which the fitness of each solution is evaluated to identify the optimal path. The termination condition is defined as either (i) no improvement in the best solution over a certain number of generations, represented by stagnation threshold, or (ii) reaching a predefined maximum number of generations. Figure 2 illustrates the overall flow of the GA-based routing process.
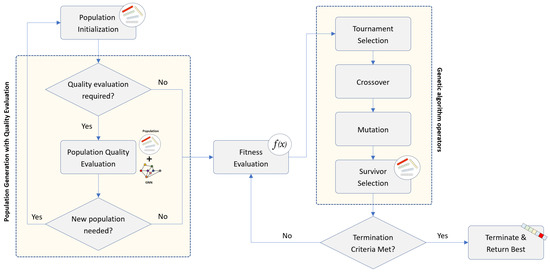
Figure 2.
Genetic algorithm-based routing employing evaluation for initial populations.
The objective of the proposed GA-based routing method is to identify a path that minimizes operational cost while satisfying service requirements. Therefore, for each candidate path corresponding to a service traffic demand, a fitness score must be computed. To this end, the fitness of a candidate path for a given service demand is evaluated using Equation (11), where a lower value indicates a better solution.
In this formulation, the fitness F incorporates not only the operational cost , defined in Equation (12) as the sum of the link cost and the computation node cost required for traffic processing, but also a penalty term , which depends on whether the service requirements are satisfied.
The penalty, as expressed in Equation (13), is computed as the sum of two components: the penalty imposed when a network-level performance metric is not satisfied, and the penalty incurred when the available resource of a computation node is insufficient.
Each penalty is calculated by multiplying the degree of violation against the requirement by a weighting factor w, which reflects its relative importance. Finally, Equation (14) provides an example of how the penalty is computed for a specific resource j. Here, the penalty value can be either 0 or a positive real number. However, the amount of required resources varies by resource type and is represented in different units, which introduces the risk of a specific resource penalty dominating the fitness value. To address this issue, the resource penalty is normalized using the sum of and , which represent the required resource size and a small constant to avoid division by zero, respectively.
4.2. Graph Neural Network Fundamentals for Topology Representation
The graph neural network (GNN) is a neural model that derives insights from data represented by a graph, which is a non-Euclidean structure. To capture these insights, a GNN employs the message-passing paradigm [31], which constructs hidden representations from an input graph, thereby enabling the discovery of structure-aware patterns and relationships [32]. Specifically, the message-passing method, which most GNN models adopt, refers to the process in which node features resulting from the embedding operation are propagated to neighboring nodes connected through edges, enabling each node to derive its own hidden state. Hence, the objective of a GNN is to learn node representations through state embedding and generate corresponding outputs [33]. The basic operations of a GNN are defined in Equations (15) and (16):
Let denote a graph, where V and E are the sets of nodes and edges, respectively. Note that the symbols used in this section are defined independently of those presented in the system model section. In Equation (15), x represents the features obtained from either a node or the set of edges connected to v, denoted by and , respectively. Furthermore, represents the features derived from the set of neighboring nodes of v, denoted by . In addition to these features, the transition function f takes the hidden states of neighboring nodes as input to generate the hidden state of node v, denoted by , which is considered the result of the state embedding. Subsequently, the output function g in Equation (16) is applied to produce the output corresponding to node v based on its representation and feature .
As a graph consists of multiple nodes and edges, all state embeddings, computed simultaneously at the node level, must be incorporated to derive a graph-level hidden representation. This leads to a stacking approach defined as follows:
In Equation (17), H represents the stacked hidden states of all nodes in the graph, resulting from the global transition function F, where X denotes the graph features. Additionally, O in Equation (18) refers to the outputs produced by the global output function G, considering the stacked node features represented by . These global functions F and G can be implemented as neural networks, including feedforward neural networks (FNNs), recurrent neural networks (RNNs), and convolutional neural networks (CNNs).
4.3. Gaussian Mixture Model Convolution for Performance-Aware Topology Embedding
Building upon the basic operations of GNNs, the message-passing paradigm, we employ GNN to support routing optimization in forthcoming 6G networks, which are characterized by strictly dynamic and heterogeneous conditions. In such environments, nodes are interconnected through edges associated with diverse and time-varying performance metrics including latency, bandwidth, and availability. Consequently, GNN-based approaches must incorporate edge attributes into their learning process in order to derive graph-level insights that can guide adaptive and efficient routing decisions.
To achieve this objective, we adopt the Gaussian mixture model convolutional network (GMMConv) [34,35], which extends the message-passing mechanism by introducing continuous, learnable edge-dependent kernels. In this model, messages from neighboring nodes are modulated by Gaussian mixture kernels parameterized by edge attributes, allowing the network to capture subtle structural variations and performance-related relationships in the underlying graph.
The Gaussian kernel for the k-th component is defined as follows:
where and denote the learnable mean vector and covariance matrix of the k-th Gaussian component, respectively.
The message aggregation process for node v is then expressed as follows:
where is the feature vector of a neighboring node u, is the learnable weight matrix associated with the k-th kernel, and is the mixture weight. The mixture weight can be computed either by softmax normalization or by uniform averaging, denoted by Equations (21) and (22), respectively.
Finally, the hidden representation of node v is updated as follows:
where is the weight matrix associated with the self-loop, b is a bias term, and denotes a nonlinear activation function.
This GMMConv formulation preserves the fundamental message-passing structure while enhancing it with continuous kernel-based weighting mechanisms. As a result, it enables the model to incorporate complex, performance-related edge information and derive hidden graph representations that are crucial for routing optimization in dynamic 6G network scenarios.
4.4. Embedding-Assisted Initial Population Evaluation for GA-Based Routing
In conventional GA-based routing, the random generation of path candidates for the initial population becomes increasingly computationally expensive as the network size grows. To mitigate this issue, a common alternative is to explore a subset of feasible paths within constrained conditions, such as a maximum hop count, and use those as the initial population. However, this approach still exhibits a notable limitation, as the convergence time and the quality of the final solution may vary depending on the composition of the initial population. Specifically, if the initial population is biased, the algorithm may converge prematurely to a local optimum or require a longer runtime to reach a satisfactory solution [36].
To overcome this limitation, the proposed GA-based routing method integrates a graph neural network (GNN) to evaluate the quality of candidate initial populations. By executing the genetic algorithm only on high-quality populations, identified through GNN-based evaluation, the method achieves improved convergence efficiency and solution quality. Figure 3 illustrates the overall architecture of the proposed quality evaluation mechanism for the initial population in GA-based routing using a GNN.
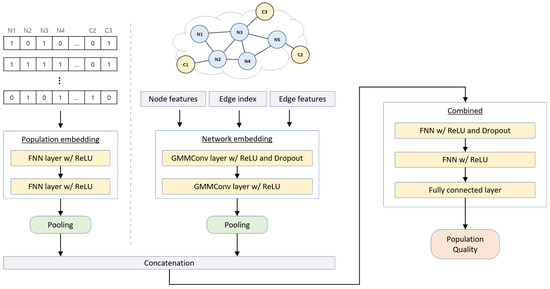
Figure 3.
Embedding-assisted initial population evaluation mechanism.
The proposed architecture combines a GNN that processes the network topology information with an FNN that processes initial population data from the genetic algorithm. The GNN module adopts the Gaussian mixture model convolutional network (GMMConv) architecture, which effectively learns structural and attribute-based relationships among nodes and links. Each node is represented with five features such as node type identifier (e.g., network node or computational node), operational cost, and available resources (CPU, memory, and GPU). Further, each link is represented with four attributes such as available bandwidth, latency, availability, and operational cost.
The FNN module processes the chromosomes that constitute the initial population. Each chromosome, representing a routing path, is encoded into a binary format where nodes included in the path are assigned a value of 1 and all others 0. This binary representation is fixed in length to accommodate all possible node IDs within the network, allowing for consistent dimensionality across different chromosomes. The features extracted from the GNN and the FNN are then aggregated through pooling operations and integrated in a joint embedding layer. The combined feature representation is used to predict the quality score of the given initial population within the context of the current network state.
Based on the predicted quality scores, the proposed routing method selectively executes the GA on high-quality initial populations. This enables the efficient determination of optimal traffic paths for each service, improving scalability and performance under diverse network conditions.
5. Evaluation
5.1. Experiment Environment
To demonstrate the effectiveness of the proposed GA-based routing method with embedding-assisted initial population evaluation, we evaluated it on four network topologies of varying sizes and structural characteristics obtained from SNDlib [37], as illustrated in Figure 4. Routing was performed from an arbitrary network node to a designated computational node. Accordingly, a subset of randomly selected nodes, shown in red, was assigned the role of computational nodes in each topology. Specifically, topology (a) represents a small-scale, sparsely connected network with limited path diversity, corresponding to the Abilene topology from SNDlib. Topology (b) is a moderately sized network with a denser interconnection pattern and additional routing alternatives, corresponding to GEANT. Topology (c) is a larger network with a broader range of routing options and more pronounced structural diversity, derived from Janos-US-CA. Finally, topology (d) is a large, densely connected mesh network, corresponding to Giul39.
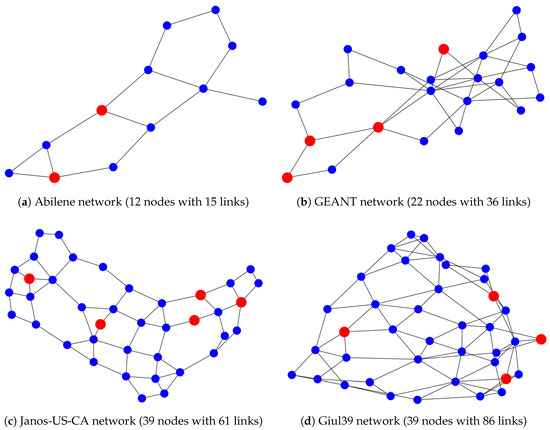
Figure 4.
Network topologies used in the performance evaluation.
For each topology, we generated 50, 75, 100, and 200 service demands. Each service demand requiring routing was randomly generated with requirements, including minimum transmission capacity, maximum allowable latency, minimum link availability, and computational resource requirements. Moreover, when service demands are generated for evaluation, network-related attributes, such as link capacity, link availability, and operating cost, are assigned random values within predefined ranges to introduce dynamic network conditions into the experimental environment. Based on these dynamic networks, routing decisions are required to establish end-to-end paths for the demands while minimizing the total operational cost.
To perform the evaluations, we compared the following three methods:
- Dijkstra-based routing: A deterministic shortest-path algorithm using operational cost as the edge weight
- Conventional GA (CGA): A genetic algorithm without an initial population evaluation mechanism.
- Embedding-assisted GA (EAGA): The proposed method using a GNN and a FNN to embed network topology and chromosomes, respectively, evaluating initial population in a given network topology.
5.2. Configuration and Tuning of GA-Based Routing Optimization
Parameters related to the GA-based methods include population size, number of generations, and weights for penalties in the fitness function. Additionally, as the EAGA method utilizes an evaluation model for initial populations, using neural networks, the model training must be conducted in advance. To this end, training was performed using mini-batch learning on a dataset comprising 10,000 samples, of which 80% were used for training and 20% for validation, over 250 epochs. Each dataset sample includes attributes related to the initial population of the GA and the network state. Specifically, the dataset features consist of a set of chromosomes representing the initial GA population, node features, an edge index, and edge features. The node features include five values: a node type identifier, operational cost, and available resources such as CPU, memory, and GPU. The edge index represents the connectivity between nodes, while the edge features include four attributes, including available bandwidth, latency, availability, and operational cost. Finally, each dataset sample contains a predicted population quality value, serving as a label, obtained from the GA procedure and representing the best fitness value derived from the given population.
We generated the dataset from a different topology, Germany50, in SNDlib, as illustrated in Figure 5, from those in the evaluation scenario to deal with model generalization. Detailed evaluation parameters are listed in Table 1.
Figure 5.
Germany50 network topology (50 nodes with 88 links) used for model training.

Table 1.
Simulation parameters.
5.3. Performance Analysis
Using this environment, each experiment was repeated 100 times, and the results are reported as averages. We evaluated performance based on four key metrics, such as operational cost, success rate, transmission capacity, and latency.
As the first performance metric, Figure 6 presents the total operational cost required to handle the given service demands across the four topologies. As expected, the total cost increases with the number of demands for all methods due to higher resource utilization. Among them, the Dijkstra method consistently yields the lowest total cost, reflecting its deterministic selection of minimum-cost paths. However, this per-path optimization does not consider network-wide resource utilization and may lead to resource fragmentation, particularly as the number of demands grows. The CGA exhibits significantly higher total costs, especially in the Janos-US-CA and Giul39 topologies. The absence of an evaluation mechanism for the initial population limits its ability to explore the large and complex solution space effectively, resulting in suboptimal path selection. On the other hand, the proposed method, EAGA, consistently reduces the total cost compared to CGA across all scenarios. This advantage becomes more pronounced in larger and more complex networks, such as the Giul39 topology, where the evaluation model based on embeddings provides richer structural context that enhances the evolutionary search process. Although EAGA’s total cost remains slightly above that of Dijkstra in most cases, it achieves this while maintaining more balanced network utilization.
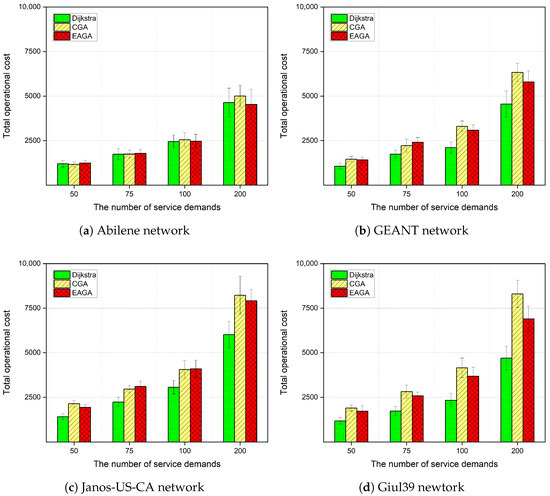
Figure 6.
Comparison of total operational cost.
In addition to the total operational cost, Figure 7 shows the average operational cost per demand. The Dijkstra-based routing achieves the lowest per-demand cost across all conditions, which is expected since it optimizes each individual path independently. However, its per-demand cost advantage narrows as network load increases, especially in larger topologies, suggesting that greedy path selection can degrade global efficiency under heavy traffic. The CGA presents both higher and more variable per-demand costs, particularly in larger networks, reflecting the instability of evolutionary search without evaluation model support. This variability becomes more pronounced as the number of demands increases, underscoring the difficulty of maintaining population diversity and convergence quality in a high-dimensional search space. In contrast, the proposed EAGA achieves lower and more stable per-demand costs than CGA. By leveraging learned representations of both the topology and chromosomes, EAGA explores more promising regions of the solution space, improving convergence and overall cost-efficiency.
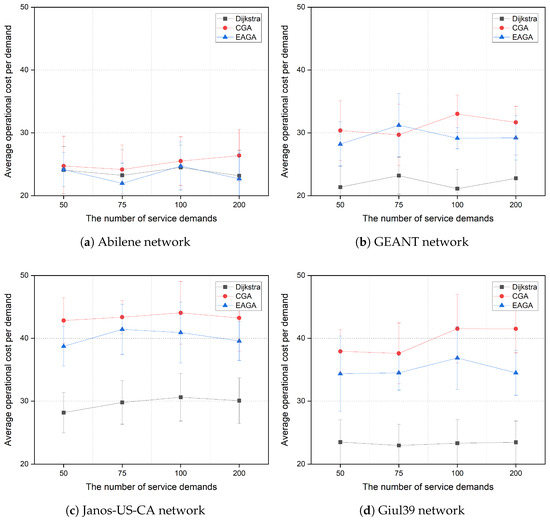
Figure 7.
Comparison of average operational cost per demand.
Next, Figure 8 illustrates the routing success rate, defined as the proportion of service demands that are successfully routed, where the service paths determined by the routing approaches meet all service requirements in terms of performance and capacity. Specifically, routing success is determined by whether the service path established for each demand satisfies Constraints (2)–(5). As expected, the success rate decreases for all methods as the number of demands increases due to intensified competition for network resources. The Dijkstra method performs well under light load but suffers significant degradation under heavy traffic. Its greedy nature results in uneven resource utilization, causing rapid exhaustion of available capacity and reducing the number of feasible routes. The CGA exhibits even lower success rates, particularly in larger topologies, due to its limited ability to capture and reason about network constraints in the chromosome representation. The proposed EAGA consistently achieves higher success rates than CGA across all topologies and often outperforms Dijkstra under medium-to-heavy load conditions. This improvement is most evident in Janos-US-CA and Giul39 topologies, where the search space is large and complex. It reveals that the use of GNN-based topology embeddings and FNN-based chromosome embeddings in the evaluation model enables EAGA to better capture global structural patterns and resource distribution, leading to more feasible routing solutions even under congestion.
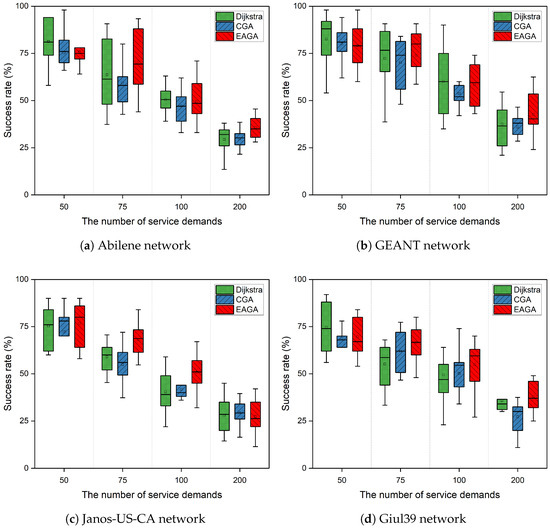
Figure 8.
Comparison of routing success rate.
As the next metric, Figure 9 illustrates the average transmission capacity (i.e., throughput) and the average latency per path. These values represent per-demand averages obtained from the corresponding service paths determined by each routing method within a given network topology, thereby reflecting both the quality of the selected routes and the efficiency of network resource utilization. The Dijkstra method achieves the highest throughput and lowest latency, as expected from its use of the shortest-path approach. However, its strong performance in these metrics comes at the expense of scalability and success rate under heavy load, limiting its practicality in large-scale or dynamic environments. The CGA produces lower throughput and higher latency, highlighting the inefficiency of heuristic search without structural guidance. This gap widens as network size and complexity increase. The proposed EAGA consistently improves upon CGA in both throughput and latency, offering a balanced trade-off between performance and scalability. Although its throughput and latency do not always match those of Dijkstra, EAGA delivers competitive results while maintaining significantly higher success rates and lower operational costs, as illustrated in previous results. Notably, EAGA exhibits more stable throughput and latency across varying load levels, demonstrating its ability to adapt to changing network conditions while preserving service quality.
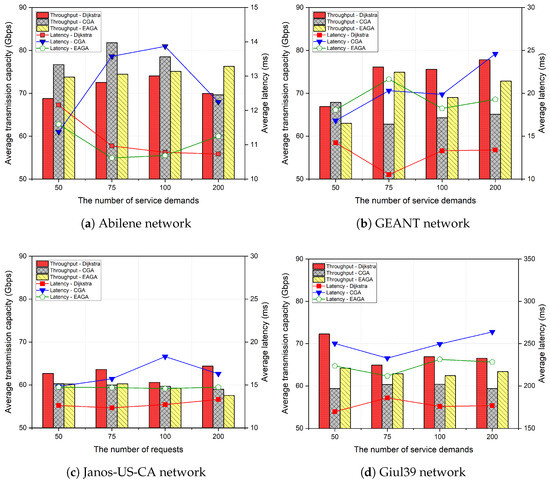
Figure 9.
Comparison of average transmission capacity and latency per path.
In addition to the performance metrics, Table 2 presents the computational time per demand required by the GA-based routing methods, CGA and EAGA, across four network topologies. Each value denotes the average execution time in seconds, along with the corresponding standard deviation (). Across all topologies, CGA consistently exhibits shorter computation times than EAGA, reflecting its simpler procedure without the initial population evaluation step. In contrast, EAGA requires slightly longer computation times due to its integration of neural network models, which perform inference for population evaluation before the evolutionary process. Despite this increased time, the standard deviations remain low, indicating stable performance and reproducibility for both algorithms. The time differences between CGA and EAGA become more pronounced as network size and complexity increase, demonstrating the scaling impact of neural-assisted adaptation mechanisms. Overall, while EAGA incurs a modest increase in computational time, this trade-off is compensated by its enhanced convergence efficiency and solution quality. Thus, EAGA achieves a balance between computational complexity and optimization robustness, highlighting the effectiveness of incorporating neural networks into evolutionary routing strategies.

Table 2.
Computational time (seconds) for routing optimization.
5.4. Discussion
The results across all four topologies and metrics clearly demonstrate the effectiveness of the proposed method, EAGA. While the Dijkstra method excels in minimizing path cost and latency, its greedy nature leads to rapid degradation in success rate and network utilization as traffic load increases. Additionally, the CGA lacks the representational richness required to handle complex routing problems efficiently, resulting in higher costs, lower success rates, and degraded throughput and latency performance.
In contrast, the EAGA achieves a more favorable balance across all performance dimensions. By incorporating GNN-based topology embeddings and FNN-based chromosome embeddings, EAGA enhances the evolutionary search process, enabling it to discover routing solutions that are cost-efficient, feasible under high load, and robust to network complexity. These results demonstrate that embedding-assisted evaluation for initial solutions in evolutionary algorithms offers a promising approach to scalable, adaptive, and cost-effective routing in future network environments.
However, although EAGA outperforms CGA in terms of performance metrics, several challenges remain and should be further investigated. First, the network topology used in the evaluation scenarios was static. We implemented dynamic network conditions by assigning random values to network attributes whenever routing decisions were required for the given service demands. Despite that, no topological changes were modeled, such as those caused by the addition or removal of network entities like satellites and vehicles. Since these entities are crucial components in 6G network scenarios, it is essential to consider connectivity changes in future routing optimization problems.
In addition, model training is a prerequisite for employing EAGA in the routing process, which introduces additional computational overhead. This represents a trade-off in the proposed approach: larger models typically yield higher accuracy in population quality prediction but also incur greater computational overhead and delay during both training and inference. Furthermore, model generalization must be considered to effectively address the dynamic network conditions in 6G routing scenarios.
6. Conclusions
In this paper, we proposed a routing optimization method that integrates a graph neural network (GNN) and feedforward neural network (FNN) for evaluating the quality of initial populations within a genetic algorithm (GA) to determine efficient routing paths that satisfy service requirements in dynamic network environments. Performance evaluations demonstrated that, compared to conventional GA-based routing with randomly generated initial populations, the proposed quality-prediction-assisted GA approach was able to reliably derive superior solutions by evaluating the quality of the initial search space and guiding the algorithm toward optimal routing paths.
For future work, we plan to extend the current optimization model to consider not only the minimization of operational cost but also the computational cost associated with executing the routing algorithm itself. Additionally, we plan to investigate an efficient model training method, as model preparation currently poses a burden that hinders the practical application of the proposed approach. Moreover, we will improve the integration between the GNN and GA components to support multi-objective optimization more effectively. From the perspective of performance validation, we aim to evaluate the proposed approach in large-scale and real-time network environments and to explore methods for enhancing its generalization and learning performance based on empirical findings, with particular consideration of model stability and convergence. In addition, we will investigate hybrid approaches that combine GA with other metaheuristic techniques and assess the applicability of our method in more variable network scenarios, such as multi-access edge computing (MEC) systems and satellite communication networks.
Author Contributions
Conceptualization, D.L.; methodology, D.L.; software, D.L.; validation, D.L.; formal analysis, D.L.; investigation, D.L.; resources, D.L.; data curation, D.L.; writing—original draft preparation, D.L.; writing—review and editing, T.K.; visualization, D.L.; supervision, T.K.; project administration, T.K.; funding acquisition, T.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Institute of Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (RS-2024-00392332, Development of 6G Network Integrated Intelligence Plane Technologies).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cerroni, W.; Galis, A.; Shiomoto, K.; Zhani, M.F. Network Softwarization and Management. IEEE Commun. Mag. 2020, 58, 14–15. [Google Scholar] [CrossRef]
- Reddy, Y.M.; Raj, V.H.; Thethi, H.P.; Gupta, S.; Maan, P.; Ghani, R.H. Low Earth Orbit (LEO) Satellite Networks: A New Era in Global Communication. In Proceedings of the 2023 10th IEEE Uttar Pradesh Section International Conference on Electrical, Electronics and Computer Engineering (UPCON), Gautam Buddha Nagar, India, 1–3 December 2023; Volume 10, pp. 1563–1568. [Google Scholar]
- Amin, R.; Rojas, E.; Aqdus, A.; Ramzan, S.; Casillas-Perez, D.; Arco, J.M. A survey on machine learning techniques for routing optimization in SDN. IEEE Access 2021, 9, 104582–104611. [Google Scholar] [CrossRef]
- Lambora, A.; Gupta, K.; Chopra, K. Genetic algorithm—A literature review. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; pp. 380–384. [Google Scholar]
- Maaranen, H.; Miettinen, K.; Penttinen, A. On initial populations of a genetic algorithm for continuous optimization problems. J. Glob. Optim. 2007, 37, 405–436. [Google Scholar] [CrossRef]
- Akhter, F.; Near, J.P. Energy Efficient Data Routing for IoT Networks Using Genetic Algorithm. In Proceedings of the 2024 International Conference on Smart Applications, Communications and Networking (SmartNets), Harrisonburg, VA, USA, 28–30 May 2024; pp. 1–8. [Google Scholar]
- Patel, J.; El-Ocla, H. Energy efficient routing protocol in sensor networks using genetic algorithm. Sensors 2021, 21, 7060. [Google Scholar] [CrossRef]
- Wang, N.; Ho, K.H.; Pavlou, G.; Howarth, M. An overview of routing optimization for internet traffic engineering. IEEE Commun. Surv. Tutor. 2008, 10, 36–56. [Google Scholar] [CrossRef]
- Ramasubramanian, V.; Malkhi, D.; Kuhn, F.; Balakrishnan, M.; Gupta, A.; Akella, A. On the treeness of internet latency and bandwidth. In Proceedings of the Eleventh International Joint Conference on Measurement and Modeling of Computer Systems, Seattle, WA, USA, 15–19 June 2009; pp. 61–72. [Google Scholar]
- Hogan, K.; Servan-Schreiber, S.; Newman, Z.; Weintraub, B.; Nita-Rotaru, C.; Devadas, S. Shortor: Improving tor network latency via multi-hop overlay routing. In Proceedings of the 2022 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 22–26 May 2022; pp. 1933–1952. [Google Scholar]
- Bouchmal, O.; Cimoli, B.; Stabile, R.; Vegas Olmos, J.J.; Tafur Monroy, I. From classical to quantum machine learning: Survey on routing optimization in 6G software defined networking. Front. Commun. Netw. 2023, 4, 1220227. [Google Scholar] [CrossRef]
- Vinayakumar, R.; Soman, K.; Poornachandran, P. Applying deep learning approaches for network traffic prediction. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 13–16 September 2017; pp. 2353–2358. [Google Scholar]
- Yuan, R.; Li, Z.; Guan, X.; Xu, L. An SVM-based machine learning method for accurate internet traffic classification. Inf. Syst. Front. 2010, 12, 149–156. [Google Scholar] [CrossRef]
- Tshakwanda, P.M.; Arzo, S.T.; Devetsikiotis, M. Advancing 6g network performance: Ai/ml framework for proactive management and dynamic optimal routing. IEEE Open J. Comput. Soc. 2024, 5, 303–314. [Google Scholar] [CrossRef]
- Almasan, P.; Xiao, S.; Cheng, X.; Shi, X.; Barlet-Ros, P.; Cabellos-Aparicio, A. ENERO: Efficient real-time WAN routing optimization with Deep Reinforcement Learning. Comput. Netw. 2022, 214, 109166. [Google Scholar] [CrossRef]
- Wei, W.; Gu, H.; Fu, L.; Li, B. Grace: Toward Routing in Dynamic Network Environments with Graph Embedding. IEEE Trans. Netw. 2025, 1–13. [Google Scholar] [CrossRef]
- Ding, M.; Guo, Y.; Huang, Z.; Lin, B.; Luo, H. GROM: A generalized routing optimization method with graph neural network and deep reinforcement learning. J. Netw. Comput. Appl. 2024, 229, 103927. [Google Scholar] [CrossRef]
- Sun, G.; Wang, Y.; Niyato, D.; Wang, J.; Wang, X.; Poor, H.V.; Letaief, K.B. Large language model (llm)-enabled graphs in dynamic networking. IEEE Netw. 2024, 39, 290–301. [Google Scholar] [CrossRef]
- Çavdar, T.; Aymaz, Ş. New approach to dynamic load balancing in software-defined network-based data centers. ETRI J. 2023, 45, 433–447. [Google Scholar] [CrossRef]
- Bhardwaj, A.; El-Ocla, H. Multipath routing protocol using genetic algorithm in mobile ad hoc networks. IEEE Access 2020, 8, 177534–177548. [Google Scholar] [CrossRef]
- Riveros-Rojas, G.J.; Cespedes-Sanchez, P.P.; Pinto-Roa, D.P.; Legal-Ayala, H. Energy-and-blocking-aware routing and device assignment in software-defined networking—A MILP and genetic algorithm approach. Math. Comput. Appl. 2024, 29, 18. [Google Scholar] [CrossRef]
- Agrawal, A.; Pal, A. Adaptive hybrid genetic-ant colony optimization for dynamic self-healing and network performance optimization in 5G/6G networks. Procedia Comput. Sci. 2025, 252, 404–413. [Google Scholar] [CrossRef]
- Tabaeiaghdaei, S.; Scherrer, S.; Kwon, J.; Perrig, A. Carbon-aware global routing in path-aware networks. In Proceedings of the 14th ACM International Conference on Future Energy Systems, Orlando, FL, USA, 20–23 June 2023; pp. 144–158. [Google Scholar]
- Ding, H.; He, F.; Zhang, P.; Zhang, L.; Zhang, X.; Qi, M. Optimal routing and heterogeneous resource allocation for computing-aware networks. ICT Express 2024, 10, 614–619. [Google Scholar] [CrossRef]
- Alanazi, R.; Obayya, M.; Alghamdi, A.M.; Nemri, N.; Alshahrani, S.; Alduaiji, N.; Hasanin, T.; Sorour, S. Machine learning-driven routing optimization for energy-efficient 6G-enabled wireless sensor networks. Alex. Eng. J. 2025, 129, 877–888. [Google Scholar] [CrossRef]
- Lee, D.; Shin, S.; Lee, C.; Na, T.; Kim, T. A Hybrid Auto-Scaling Method for Energy Efficiency of Network Services. In Proceedings of the 2024 15th International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 16–18 October 2024; pp. 1070–1075. [Google Scholar]
- Qi, S.; Moore, H.; Hogade, N.; Milojicic, D.; Bash, C.; Pasricha, S. CASA: A Framework for SLO-and Carbon-Aware Autoscaling and Scheduling in Serverless Cloud Computing. In Proceedings of the 2024 IEEE 15th International Green and Sustainable Computing Conference (IGSC), Austin, TX, USA, 2–3 November 2024; pp. 1–6. [Google Scholar]
- Chen, S.; Chen, J.; Li, H. Joint optimization of UPF placement and traffic routing for 5G core network user plane. Comput. Commun. 2024, 216, 86–94. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability; W. H. Freeman and Company: New York, NY, USA, 2002; Volume 29. [Google Scholar]
- Sihotang, J. Analysis of shortest path determination by utilizing breadth first search algorithm. J. Info Sains Inform. Dan Sains 2020, 10, 1–5. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1263–1272. [Google Scholar]
- Geerts, F.; Mazowiecki, F.; Perez, G. Let’s agree to degree: Comparing graph convolutional networks in the message-passing framework. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 3640–3649. [Google Scholar]
- Kim, H.G.; Park, S.; Lange, S.; Lee, D.; Heo, D.; Choi, H.; Yoo, J.H.; Hong, J.W.K. Graph neural network-based virtual network function deployment optimization. Int. J. Netw. Manag. 2021, 31, e2164. [Google Scholar] [CrossRef]
- Reynolds, D. Gaussian mixture models. In Encyclopedia of biometrics; Springer: Berlin/Heidelberg, Germany, 2015; pp. 827–832. [Google Scholar]
- Monti, F.; Boscaini, D.; Masci, J.; Rodola, E.; Svoboda, J.; Bronstein, M.M. Geometric deep learning on graphs and manifolds using mixture model CNNs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5115–5124. [Google Scholar]
- Abu-Lebdeh, G.; Benekohal, R.F. Convergence variability and population sizing in micro-genetic algorithms. Comput.-Aided Civ. Infrastruct. Eng. 1999, 14, 321–334. [Google Scholar] [CrossRef]
- Orlowski, S.; Wessäly, R.; Pióro, M.; Tomaszewski, A. SNDlib 1.0—Survivable network design library. Netw. Int. J. 2010, 55, 276–286. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).