Exploring the Application of Models of DNA Evolution to Normalized Compression Distance (NCD) Matrices

Abstract

Recent developments of Normalized Compressed Distance (NCD) matrices show potential to become a widely used method to develop phylogenetic trees among a group of organisms. However, such NCD matrices lack the biological and evolutionary context that is important to the development of phylogenetic trees. This study applied mathematical models of DNA evolution to NCD matrices with the goal of applying evolutionary context to improve the results of NCD methods and thus create better phylogenetic trees. Mammalian mitochondrial, Arabidopsis thaliana, and Tomato Solanum lycopersicum genomes were used in this study as benchmarks and underwent validation techniques to analyze whether the NCD matrix models were of better quality than their original NCD. The mathematical models applied were not sufficient in implementing a biological context towards NCD compression algorithms for phylogenetic trees, resulting in no successful improvement of them. However, this opens opportunities to explore ways to integrate biological context internally to NCD compression algorithms, rather than external methods of correcting NCD matrices after compression has been carried out.

1. Introduction

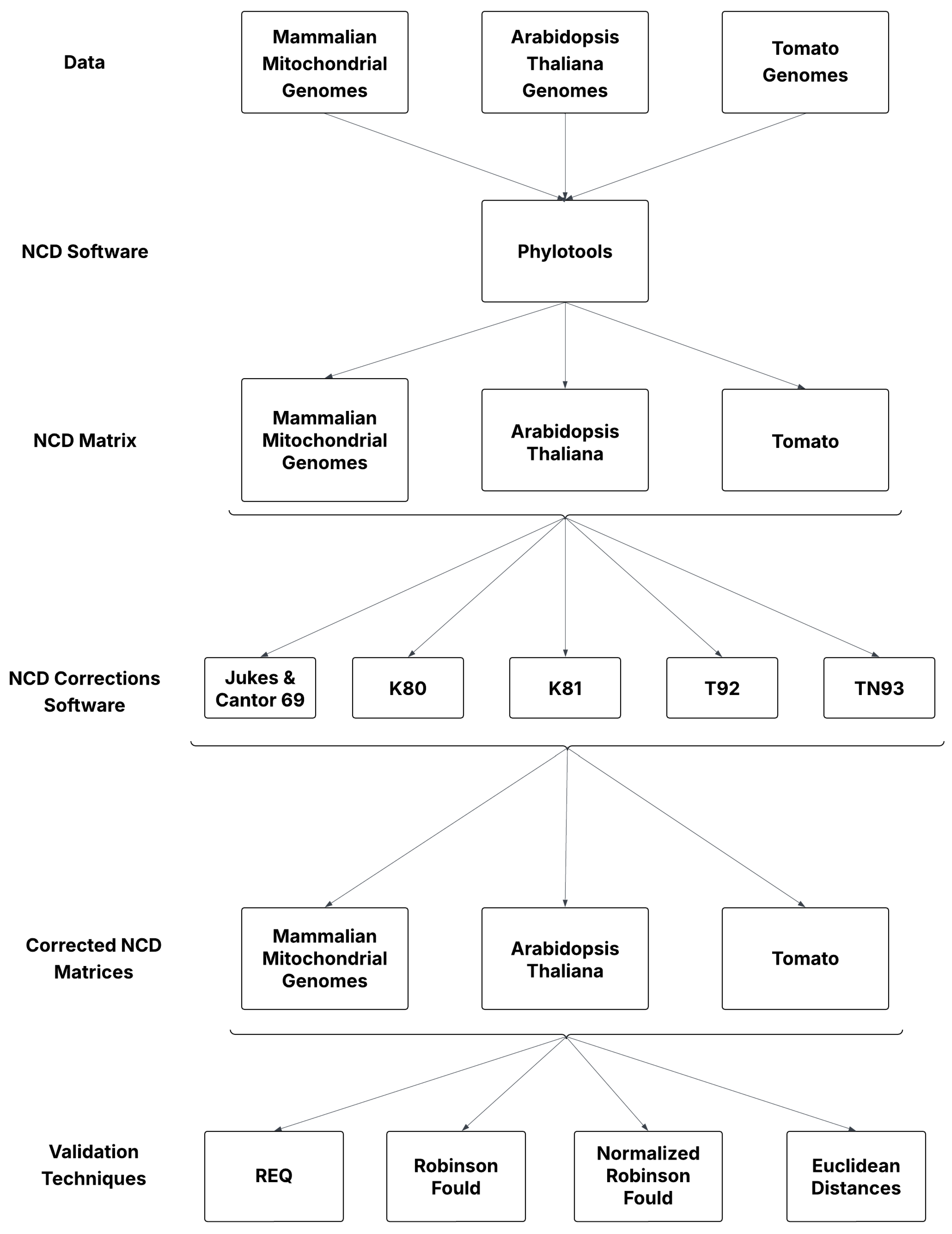
NCD Matrices and Their Significance

Phylogenomics utilizes genomic data from a group of organisms in order to describe the evolutionary relationships between all organisms in the group. These relationships are of significant importance, as they can be used to develop an understanding of the origin of diseases, to develop new crops and the tree of life, and to even classify organisms based on a common ancestor. Phylogenetic trees are the main source of analyzing such relationships and events. They are a visual diagram describing the evolutionary history of a group of organisms which must be computed via methods that utilize FASTA files [1,2].

Traditional methods of building phylogenetic trees involve the use of Multiple Sequence Alignment (MSA) methods [3]. These methods take a group of sequences such as mitochondrial DNA, rRNA sequences, and whole genomes in FASTA format, align every sequence to one another, and calculate their similarity to produce a phylogenetic tree [4]. These are often seen as the most reliable way to calculate phylogenetic trees. However, this makes aligning complex genomes and whole genomes impossible due to their very large size, the main limitation of using MSA-based methods [5,6]. One specific example of this is Eukaryotic genomes, which cannot be sequenced entirely due to their large size and complex genetic structure [7].

Due to this limitation being easily exploited by larger, more complex genomic datasets, there has been a movement of exploration towards alignment-free methods to compute phylogenomic trees.

Compression algorithms have risen towards the possibility of processing very large genomic datasets, such as whole genomes because they are computationally inexpensive when compared to other standard methods [8]. One of them is Normalized Compression Distance (NCD), a compression algorithm that is used to find the similarity between two pieces of texts such as emails and paragraphs [9]. When applied to FASTA files, they can find the similarity between two or more biological genomes and discover how similar they are through text pattern finding [9,10].

A recent study showed that Normalized Compression Distance (NCD) matrices allow for an alternative way to create phylogenetic trees. NCD matrices are produced via Phylotools (version 1.0.0), a software that uses the 7zip compression algorithm to find patterns in DNA sequences to produce a distance matrix that describes the pairwise differences among a group of organisms [9,10]. With promising results, NCD seems to be an effective and efficient approach to creating accurate phylogenetic trees without needing alignment.

However, NCD lacks evolutionary context when creating NCD matrices [9]. The 7zip compressor built into Phylotools has no knowledge of how likely certain nucleotides are to change over time within a species and how likely they are to change from organism to organism [9]. NCD and the 7zip compressor tool simply recognize patterns from different genomic sequences to generate a number describing how similar the sequences of the organisms are. This may create a bias in the creation of the NCD matrix, leading to results that may not capture the true relationship between a group of organisms.

In an attempt to contextualize the NCD, we applied models of DNA evolution to these NCD matrices produced by Phylotools. The goal of this study was to determine whether models of DNA evolution would produce more accurate NCD matrices and thus more accurate phylogenetic trees. This is a novel application of such mathematical models, since they were originally created to compute pairwise distances via alignment-based methods. However, in this study, the models were used as a way to integrate biological context into an NCD matrix to correct potentially inaccurate pairwise distance values and mitigate potential errors from the NCD algorithm.

2. Methods

2.1. Datasets

The genomic data used in this study consists of 3 different groups of organisms: 153 Mammalian mitochondrial sequences (

Table A1. Mammalian mitochondrial Genomes Accession IDs.

Species	NCBI Accession IDs
Ailuropoda_melanoleuca	EF196663.1
Ailurus_fulgens_styani	AB291074.1
Anoura_caudifer	NC_022420.1
Anourosorex_squamipes	NC_024563.1
Antilope_cervicapra	NC_012098.1
Artibeus_jamaicensis	AF061340.1
Artibeus_lituratus	NC_016871.1
Balaena_mysticetus	AP006472.1
Blarina_brevicauda	NC_027902.1
Bos_mutus	DQ124389.1
Bos_taurus	V00654.1
Bubalus_bubalis	AY488491.1
Camelus_bactrianus	AJ409393.1
Camelus_dromedarius	NC_009849.1
Canis_lupus_familiaris	U96639.2
Capra_hircus	GU295658.1
Castor_canadensis	FJ959094.1
Cavia_porcellus	AJ222767.1
Cebus_albifrons	NC_021952.1
Ceratotherium_simum	Y07726.1
Chinchilla_lanigera	EF567130.1
Cricetulus_griseus	NC_007936.1
Crocidura_tanakae	NC_035941.1
Cynopterus_sphinx	EU289411.1
Dasypus_novemcinctus	Y11832.1
Delphinapterus_leucas	NC_005279.1
Dipodomys_ordii	NC_005314.1
Elephas_maximus	DQ316068.1
Eptesicus_fuscus	NC_029342.1
Equus_asinus	NC_001788.1
Equus_caballus	NC_001640.1
Erinaceus_europaeus	X88898.1
Eubalaena_japonica	AP006472.1
Felis_catus	U20753.1
Gorilla_gorilla	D38114.1
Halichoerus_grypus	NC_001602.1
Hippopotamus_amphibius	AP003425.1
Homo_sapiens	NC_012920.1
Hylobates_lar	NC_002082.1
Loxodonta_africana	X56292.1
Macaca_fascicularis	X79547.1
Macaca_mulatta	AY612638.1
Microtus_arvalis	EF489115.1
Monodelphis_domestica	NC_006299.1
Mus_musculus	V00711.1
Mustela_putorius_furo	AJ544416.1
Myotis_lucifugus	NC_006897.1
Nomascus_leucogenys	NC_013993.1
Nycticebus_coucang	NC_002765.1
Ochotona_curzoniae	NC_011029.1
Odocoileus_virginianus	NC_008414.1
Orcinus_orca	Y13856.1
Oryctolagus_cuniculus	AJ001588.1
Ovis_aries	AF010406.1
Pan_troglodytes	D38116.1
Panthera_leo	NC_028302.1
Panthera_tigris	EF551002.1
Papio_hamadryas	Y18001.1
Phocoena_phocoena	NC_005280.1
Physeter_catodon	X72204.1
Pongo_pygmaeus	X97707.1
Pteropus_vampyrus	NC_009063.1
Rattus_norvegicus	X14848.1
Saimiri_sciureus	NC_025235.1
Sus_scrofa	AJ002189.1
Tarsius_syrichta	Y18001.1
Trichechus_manatus	NC_005279.1
Tursiops_truncatus	X72204.1
Ursus_arctos	AF303110.1
Ursus_maritimus	AJ428577.1
Vicugna_pacos	EF397824.1
Vulpes_vulpes_montana	KF387633.1

), 14 tomato (Solanum lycopersicum) sequences (refer to the Data Availability Statement Section to access tomato genomes used in this study), and 79 Arabidopsis thaliana sequences (

Table A2. Arabidopsis thaliana Genome Accession IDs.

Lines	NCBI Accession IDs
AUZE-A-5	GCA_946402385.1
FERR-A-8	GCA_946403025.1
BELC-C-10	GCA_946403525.1
ANGE-B-10	GCA_946404075.1
BARA-C-5	GCA_946404385.1
IP-San-9	GCA_946404515.1
BANI-C-1	GCA_946404995.1
IP-Met-6	GCA_946405265.1
FERR-A-12	GCA_946405525.1
IP-Evs-12	GCA_946405545.1
IP-Med-0	GCA_946405725.1
MONTM-B-16	GCA_946405905.1
IP-Alo-0.9506	GCA_946406325.1
Ler-0.7213	GCA_946406525.1
BANI-C-12	GCA_946406595.1
IP-Hom-4.9546	GCA_946406625.1
BARA-C-3	GCA_946406735.1
Rabacal-1.22005	GCA_946406895.1
CAMA-C-2	GCA_946406975.1
BARC-A-17	GCA_946407145.1
IP-Lor-16	GCA_946407795.1
SALE-A-10	GCA_946408365.1
CAMA-C-9	GCA_946408575.1
BELC-C-12	GCA_946408975.1
BROU-A-10	GCA_946409395.1
SALE-A-17	GCA_946409815.1
Tanz-1.10024	GCA_946409825.1
BARC-A-12	GCA_946410165.1
IP-Alo-19	GCA_946410485.1
IP-Cas-0.9831	GCA_946411375.1
IP-Hom-0	GCA_946411425.1
MERE-A-13	GCA_946411655.1
IP-Mos-9	GCA_946411805.1
IP-Mos-5	GCA_946411885.1
IP-Hum-4	GCA_946412005.1
GAIL-B-11	GCA_946412065.1
IP-Mdc-14	GCA_946412225.1
IP-Hum-2.9549	GCA_946413285.1
IP-Med-3	GCA_946413305.1
PREI-A-14	GCA_946413405.1
IP-Sln-22	GCA_946413935.1
Cvi-0.6911	GCA_946414125.1
IP-Cat-0.9832	GCA_946414305.1
ANGE-B-2	GCA_946415005.1
IP-Evs-0.9845	GCA_946415165.1
IP-Cas-6	GCA_946415445.1
MONTM-B-7	GCA_946415625.1
LACR-C-14	GCA_946415655.1
Ey15-2.9994	GCA_946499665.1
Col-0.6909	GCA_946499705.1
Pent-46.2212	GCA_964057255.1
LI-EF-011.685	GCA_964057265.1
14INRCT07	GCA_964057275.1
MONF-A-1.22045	GCA_965117475.1
RAYR-A-17.22055	GCA_965117485.1
LANT-B-1.22039	GCA_965117495.1
LUZE-A-14.22042	GCA_965117505.1
MONT-B-14.22048	GCA_965117515.1
NAUV-B-7.22052	GCA_965117525.1
LACR-C-4.22038	GCA_965117535.1
BELL-A-1.22021	GCA_965117545.1
PREI-A-9.22054	GCA_965117555.1
MERE-A-7.22044	GCA_965117565.1
LANT-B-10.22040	GCA_965117575.1
LUZE-A-12.22041	GCA_965117585.1
MONF-A-14.22046	GCA_965117595.1
RAYR-A-9.22056	GCA_965117605.1
JUZE-A-3.22036	GCA_965117615.1
BOULO-A-16.22024	GCA_965117625.1
BELL-A-7.22022	GCA_965117635.1
BROU-A-2.22026	GCA_965117645.1
NAUV-B-14.22051	GCA_965117655.1
JUZE-A-2.22035	GCA_965117665.1
BOULO-A-1.22023	GCA_965117675.1
CARL-A-16.22030	GCA_965117685.1
CARL-A-10.22029	GCA_965117695.1
MONT-B-12.22047	GCA_965117705.1
GAIL-B-9.22034	GCA_965117715.1
AUZE-A-11.22011	GCA_965117725.1

). All of the genomic data were in FASTA format, which were then later converted to non-aligned Normalized Compression Distance (NCD) matrices using Phylotools [11]. The datasets had the following GC%: mitochondria—38%, tomato—36%, Arabidopsis thaliana—36%. The justification for the datasets selected for this work was as follows: To evaluate the performance of the NCD method for phylogenetic inference, we selected three diverse genomic datasets spanning distinct evolutionary, structural, and biological contexts, 153 Mammalian mitochondrial genomes, 79 Arabidopsis thaliana genomes, and 14 tomato (Solanum lycopersicum) genomes. The Mammalian mitochondrial genomes dataset represents small circular genomes (16 to 20 kb) with well-established evolutionary relationships, providing a benchmark for assessing the NCD method. The A. thaliana dataset is characterized by a medium-sized nuclear genome (125–130 Mb) with high-quality chromosome-level assemblies and extensive population-level diversity data. This enables evaluation of NCD’s resolution in detecting intraspecific and subspecies-level variation. Lastly, in contrast, the tomato dataset, with a large and more complex nuclear genome (750–800 Mb), also completes chromosome-level assemblies. This dataset will help access NCD’s ability to handle higher genomic complexity and evolutionary distances. Collectively, these datasets span a continuum of genome sizes, complexities, and divergence scales, providing a comprehensive and representative framework to assess the robustness and adaptability of the NCD-based phylogenetic approach across biological domains.

2.2. NCD as an Alignment-Free Alternative

We measure the distance between two sequences using the Normalized Compression Distance (NCD) technique. NCD is an algorithmic approximation of the Normalized Information Distance (NID) measure. Informally, a measure of the similarity between two strings, over a finite alphabet, is how much their concatenation can be losslessly compressed relative to how much each string can be individually compressed. The idea is that if similar strings share a structure, a compressor can be used to minimize the number of bits needed to represent the concatenated strings.

The theoretical minimum compressed size of a string s is its Kolmogorov complexity [12], which is the length of the shortest program p such that, when run, produces s as output. We denote this size $K\left(s\right)$.

Based on this, Li et al. [13] defined the Normalized Information Distance (NID):

$$NID(s_0,s_1)={\displaystyle \frac{K\left(s_0{s}_1\right)-min(K\left(s_0\right),K\left(s_1\right))}{max(K\left(s_0\right),K\left(s_1\right))}}$$

Because the Kolmogorov complexity of a string is uncomputable [12], the NID cannot be computed exactly. But it can be approximated from above by selecting a compression algorithm A and replacing $K\left(s\right)$ by $C_A\left(s\right)$, which is the size of the bit string resulting from applying A to s. This new distance is called the Normalized Compression Distance (NCD):

$$NCD(s_0,s_1)={\displaystyle \frac{C\left(s_0{s}_1\right)-min(C\left(s_0\right),C\left(s_1\right))}{max(C\left(s_0\right),C\left(s_1\right))}}$$

Note that the NCD is always non-negative and, in general, less than or equal to 1 and greater than 0. A small NCD for two strings indicates that they are similar; values of less than 0.5 indicate greater similarity. We assume lossless compression, so, for example, one may use a compressor based on the Huffman algorithm, the various Lempel–Ziv algorithms, or a compressor designed specifically for a particular kind of data. One advantage is that a pair of sequences does not have to be aligned before determining their distance.

Wilson and Rogers [9] present a proof of concept for utilizing NCDs as an alternative approach to phylogeny estimation. In their study, they compare NCDs with traditional methods such as Maximum Likelihood (ML) and Bayesian inference using biological and simulated data. A key aspect of their analysis focuses on evaluating NCDs’ performance in the presence of incomplete lineage sorting (ILS), a common challenge in phylogenetic studies.

The results indicate that NCD performs comparably to traditional methods, particularly in scenarios with high levels of ILS, where methods such as ML and Bayesian inference often encounter difficulties. Wilson and Rogers highlight the computational efficiency of NCD, as it bypasses the need for sequence alignment, which can be computationally expensive with large datasets. This demonstrates the robustness of NCD in handling large and complex genomic data, offering a scalable and alignment-free alternative to traditional phylogeny estimation methods [9].

Phylotools utilized the 7zip compressor since it is an open-source command line tool that allowed for an effective compression ratio that is approximately 2–10% more effective than other compressors such as PKZip and WinZip [14]. Specifically, when applied to Phylogenetic data, 7zip outperformed other compressors such as MFC3 and PPMZ9 [9].

In this study, 153 Mammalian mitochondrial sequences, 14 Tomato (Solanum lycopersicum) genomes, and 79 Arabidopsis thaliana genomes were combined into one FASTA file, one for each species, for a total of three FASTA files as shown in Figure 1. Each FASTA file was used as input into Phylotools to compute a non-aligned NCD matrix representing the pairwise, evolutionary differences among all the species within the group of organisms mentioned earlier. NCD-based distances operate outside traditional model-based frameworks.

2.3. Models of DNA Evolution

The NCD matrix form Phylotools was then used as input for the NCD Corrections Program, a program that allowed for the application of five different models of DNA evolution to mathematically contextualize the evolutionary pairwise distances between each species [15]. Every model was programmed as a mathematical formula and applied to a NumPy matrix for faster and more efficient implementation of the models.

Most of the models used in this study are typically calculated via a rate matrix that allows for the representation of nucleotide rate changes between species. However, since the focus of this study was to apply these models without alignment methods, the models were applied to the NCD matrix produced by Phylotools. This was performed by taking derivations of the models that used pairwise distances instead of rate matrices. These models were chosen because they are time-continuous Markov Chain models, meaning that the next state of an environment is based on the current state [4]. This is the behavior that best mimics how genetic mutations occur throughout time.

2.4. MLE for Transition and Transversion Rates

In addition, there were some models that required the use of transition and transversion rates. Due to the lack of alignment utilization, transition and transversion rates were calculated via Maximum Likelihood Estimation (MLE) [16], which utilized the input of a very small initial arbitrary value to calculate optimal values in correspondence to transition and transversion rates. The initial arbitrary values that we used were 0.15 for transitions and 0.01 for transversions since transitions are approximately about 15 times more likely to occur than transversions [17]. MLE was programmed in the Scipy Python package using scipy.optimize.minimize and iteratively run until the sum of squared differences between the original distance matrix and the model-predicted distances was less than ${10}^{-6}$. This convergence criterion allowed for the parameter estimates to be as close as possible to the parameters that would likely be used to create the original matrix. Standard errors of the parameters were not computed since the focus of the study was to find the most optimal transition and transversion rates to use in the mathematical models of DNA evolution.

2.5. JC69 (Jukes and Cantor 1969)

Jukes and Cantor’s is known as the simplest model of DNA evolution due to having a single input parameter and several assumptions when computing evolutionary distances between species. These assumptions include equal base frequencies of 25% and equal mutation rates between base pairs [18]. The Jukes and Cantor model applied to the NCD matrix is denoted as

$$d=-{\displaystyle \frac{3}{4}}ln\left(1-{\displaystyle \frac{4}{3}}p\right).$$

(1)

where p is the proportion of sites that differ between sequence alignment and d is the evolutionary distance between each sequence. Due to the lack of alignment knowledge, this study replaced p with every value of the NCD matrix. This is because the proportion of sites that differ is analogous to the original NCD matrix value, and d is analogous to the model-predicted distance that is calculated after the model has been applied.

2.6. K80 (Kimura 1980)

Kimura 80 requires two parameters, one of which is the rate of transitions and the other being the rate of transversions. Similar to Jukes and Cantor’s model, however, it was also constructed with the idea that each base is equally frequent at 25%. The pairwise difference formula representing this model is denoted as

$$K=-{\displaystyle \frac{1}{2}}ln\left((1-2p-q)\sqrt{1-2q}\right).$$

(2)

where K is the output of the corrected NCD matrix, p is the rate of transitions, and q is the rate of transversions between all organisms in the dataset [19].

2.7. K81 (Kimura 1981)

K81 is similar to K80 in that it utilizes the rate of transitions and transversions in order to calculate pairwise distances, but differs in that there are two rates for transversions. Like all other previous models, each equilibrium base frequency is 25%. The pairwise difference formula has the following parameters and formulas:

$$\begin{array}{cc}\hfill {\lambda }_1& =-4(\alpha +\beta ).\hfill \\ \hfill {\lambda }_2& =-4(\alpha +\gamma ).\hfill \\ \hfill {\lambda }_3& =-4(\beta +\gamma ).\hfill \end{array}$$

$$\begin{array}{cc}\hfill P& =1-e^{{\lambda }_1}-e^{{\lambda }_2}-e^{{\lambda }_3}.\hfill \\ \hfill Q& =1-e^{{\lambda }_1}+e^{{\lambda }_2}-e^{{\lambda }_3}.\hfill \\ \hfill R& =1+e^{{\lambda }_1}-e^{{\lambda }_2}-e^{{\lambda }_3}.\hfill \end{array}$$

Ultimately,

$$K=-{\displaystyle \frac{1}{4}}ln\left((1-2P-2Q)(1-2P-2R)(1-2Q-2R)\right).$$

(3)

where K is the output of the corrected NCD matrix, $\alpha$ is the rate of transitions, $\beta$ is the first rate of transversions, and $\gamma$ is the second rate of transversions [20].

2.8. T92 (Tamura 1992)

T92 is well suited for sequences that have a strong G and C base content. It is an extension of K80, but with the addition of a parameter that describes the frequency of the content of G and C, which is denoted as $\theta$. Thus, T92 does not assume equal base pair frequencies among sequences.

$$\begin{array}{c}\hfill h=2\theta (1-\theta ).\end{array}$$

(4)

$$d=-hln(1-{\displaystyle \frac{p}{h}}-q)-{\displaystyle \frac{1}{2}}(1-h)ln(1-2q).$$

(5)

where d is the output to the NCD matrix, p is the rate of transitions, and q is the rate of transversions [21].

2.9. TN93 (Tamura and Nei 1993)

TN93 allows two different transition rates and two different transversion rates. In addition, this model does not assume any equal base frequencies. The derivation of this model that was used was the one that allowed the computation of the number of nucleotide substitutions between sequences, which we then used to apply to the NCD matrix [22]. In using this derivation of the model, we used the following parameters:

$$\begin{array}{cc}\hfill {\overline{P}}_1& ={\displaystyle \frac{2g_A{g}_G}{g_R}}\left\{g_R-{\left[{\displaystyle \frac{a}{a+2(g_R{\overline{\alpha }}_1+g_Y\overline{\beta })t}}\right]}^a+g_Y{\left({\displaystyle \frac{a}{a+2\overline{\beta }t}}\right)}^a\right\}.\hfill \\ \hfill {\overline{P}}_2& ={\displaystyle \frac{2g_T{g}_C}{g_Y}}\left\{g_Y-{\left[{\displaystyle \frac{a}{a+2(g_Y{\overline{\alpha }}_2+g_R\overline{\beta })t}}\right]}^a+g_R{\left({\displaystyle \frac{a}{a+2\overline{\beta }t}}\right)}^a\right\}.\hfill \\ \hfill \overline{Q}& =2g_R{g}_Y\left[1-{\left({\displaystyle \frac{a}{a+2\overline{\beta }t}}\right)}^a\right].\hfill \end{array}$$

where ${\overline{P}}_1$ is the number of transition differences between purines and ${\overline{P}}_2$ is the transition differences between pyrimidines. Furthermore, $\overline{Q}$ is the rate of transversion differences.

The underlying parameters of $g_A$, $g_T$, $g_C$, $g_G$ all represent base frequencies. The parameter a represents the index of dispersion, which tells how dispersed data points are relative to their mean. Specifically, it is expressed as

$$a=m^2-(s^2-m).$$

where m is the mean of nucleotide substitutions per site and p is the variance of nucleotide substitutions.

Additionally, $\overline{\beta }$ is considered to be the average transversion rate and $\overline{\alpha }$ is considered to be the average transition rate among all organisms. This is usually calculated before applying to the overlying parameters that they are in. The parameter t is considered to be a time parameter to take into account how much evolutionary time has passed before two sequences diverged. Due to the lack of this knowledge, we decided to keep $t=1$. MLE was used to optimize the parameters mentioned (besides t) as accurately as possible and then used in the formula below.

$$\begin{array}{cc}\hfill \widehat{d}& =2a[{\displaystyle \frac{g_A{g}_G}{g_R}}{(1-{\displaystyle \frac{g_R}{2g_A{g}_G}}{\widehat{P}}_1-{\displaystyle \frac{1}{2g_R}}\widehat{Q})}^{-1/a}\hfill \\ \hfill & +{\displaystyle \frac{g_T{g}_C}{g_Y}}{(1-{\displaystyle \frac{g_Y}{2g_T{g}_C}}{\widehat{P}}_2-{\displaystyle \frac{1}{2g_Y}}\widehat{Q})}^{-1/a}\hfill \\ \hfill & +(g_R{g}_Y-{\displaystyle \frac{g_A{g}_G{g}_Y}{g_R}}-{\displaystyle \frac{g_T{g}_C{g}_R}{g_Y}})\hfill \\ \hfill & \times {(1-{\displaystyle \frac{1}{2g_R{g}_Y}}\widehat{Q})}^{-1/a}\hfill \\ \hfill & -g_A{g}_G-g_T{g}_C-g_R{g}_Y].\hfill \end{array}$$

3. Results

3.1. Rate of Elementary Quartets (REQ)

For context, REQ is a distance-based approach for assessing branch support, which calculates the proportion of elementary quartets induced by each internal branch that align with the four-point condition applied to pairwise evolutionary distances [23]. Unlike bootstrap-based methods, REQ directly utilizes the dissimilarity matrix and provides branch confidence values ranging from 0 to 1, with higher values indicating stronger support for the branch.

Based on the results of

Table 1. Comparison of REQ values.

	Mammal		Tomato		Arabidopsis
	# Branches	Avg Req	# Branches	Avg Req	# Branches	Avg Req
NCD	150	0.79	11	0.62	76	0.56
JC69	150	0.53	11	0.57	76	0.51
K80	150	0.78	11	0.52	76	0.55
K81	150	0.78	11	0.45	76	0.55
T92	150	0.78	11	0.49	76	0.55
TN93	150	0.78	11	0.49	76	0.55

, most REQ values are uniform and have little to no differences between all tables, with the exception of tomatoes. They have the largest disparity of values among one group of species. This is worth noting, as tomato genomes are of the same lineage and are not very different from each other genetically.

For all REQ values in general, especially those of Arabidopsis thaliana and tomatoes, the values are less than 0.9 and typically fall in the range of 0.5–0.6. This means that the confidence level of the original vs. the NCD matrices is relatively low and shows only moderate similarity.

3.2. Robinson Fould and Normalized Robinson Fould (RF and nRF)

Structural similarity among these trees was quantified using the Robinson–Foulds (RF) distance [24]. The RF metric measures topological differences between trees, with lower values indicating greater similarity.

As shown in

Table 2. Comparison of Robinson Fould and Normalized Robinson Fould.

	Mammal		Tomato		Arabidopsis
	RF	RF-Norm	RF	RF-Norm	RF	RF-Norm
NCD vs. JC69	21.90	0.47	1.36	0.36	9.94	0.48
NCD vs. K80	8.41	0.12	1.46	0.42	5.87	0.19
NCD vs. K81	8.41	0.12	1.46	0.42	5.87	0.19
NCD vs. T92	8.41	0.12	1.46	0.42	5.87	0.19
NCD vs. TN93	8.41	0.12	1.46	0.42	5.87	0.19

all values with the exception of the Jukes and Cantor model had the same value. Similar to REQ, the Normalized RF shows moderate similarity, with some scores being 0.1–0.2. This is one tier below being very confident and shows that there were a large number of similarities, however, not enough to be considered very similar. However, most of the data points across the table are 0.3 and higher, indicating that there were a small number of similarities in the distance matrices between the original NCD and the model NCD.

3.3. Euclidean Distances

Euclidean Distance is a general way to compute the distance between two points in a space. In the context of this study, the goal was to utilize the Euclidean Distance to further establish how similar the original NCD matrix was to the corrected NCD matrices. The average Euclidean Distance was taken between each original matrix and a model matrix. The lower the values, generally the more similar to matrices are [25].

The values in

Table 3. Average Euclidean Distances.

	Mammals	Tomatos	Arabidopsis
NCD vs. JC69	0.0014	0.018	0.0017
NCD vs. K80	0.0011	0.020	0.0020
NCD vs. K81	0.0011	0.020	0.0020
NCD vs. T92	0.0011	0.020	0.0020
NCD vs. TN93	0.0011	0.020	0.0020

give a different indication of how similar each matrix is when compared to the other validation techniques. They show relatively small values, indicating that every original matrix is very similar to the model matrix. However, this is computed with values from matrices and is given no other context. It is possible that the overall values of the distance matrices are very similar since each matrix is normalized from 0 to 1 and thus gives a small value even if the matrices result in very different phylogenetic trees.

4. Discussion

As demonstrated by the results, the NCD correction models appear to give very similar results for the input matrix, with the exception of the Jukes and Cantor model. There are several possibilities as to why this may have occurred.

4.1. Maximum Likelihood Estimation

The goal of Maximum Likelihood Estimation (MLE) in the context of this study is to optimize a set of input parameters to minimize the difference between a new and original dataset. This makes MLE very accurate for predicting missing or unknown parameters of mathematical expressions and models that would change one dataset to another. This would indicate that every optimal parameter computed from MLE will attempt to create a matrix that is as close as possible to its original.

4.2. Models Are Non-Applicable to NCD Matrices

Another possibility of why the models are producing similar results is due to the applicability of the models to NCD matrices. As noted earlier, the study was adjusted to apply the models to the NCD matrices directly instead of creating rate matrices, which involve alignment. Since these models utilize alignments to count transition, transversion, and general point mutations, the modified versions of alignments are not accurate and lead to different results. Thus, the statistics provided in Table 1, Table 2 and Table 3 represent a lack of incompatibility with NCD matrices as the models do not provide sufficient biological context to NCD algorithms.

4.3. NCD Accuracy

It is also likely that the NCD matrices are accurate enough and do not need a correction model to be applied to. This would indicate that Phylotools computes accurate distance matrices and phylogenetic trees. Therefore, another method besides applying models of DNA evolution may correct the anomalies of NCD matrices.

4.4. Novel Evaluation Metrics

Due to the novelty of NCD distance matrices, it is possible that other metrics must be used in order to evaluate their results. Since compression algorithms are not typically used to create matrices, novel validation techniques may be needed to evaluate how well the matrices represent evolutionary change. Additionally, metrics that measure how much biological context is included within the compressor may be helpful.

5. Conclusions

Based on the results, applying mathematical models of DNA evolution to NCD matrices does not give a more accurate representation of phylogenomic trees.

This result supports the rationale that phylogenetic distance matrices produced based on NCD closely represent the evolutionary relationship among a group of organisms. We can confidently use these NCD matrices to look at Phylogeny from a whole-genome perspective rather than selecting representative sequences such as mitochondrial DNA or rRNA, which are well-suited for MSA-based methods.

Although NCD corrections did not show any improvements from our original NCD matrices, there is still potential to improve NCD matrices.

One future direction includes exploring different ways to take on even longer genomic sequences than the ones used in this study. Limitations such as compression window sizes can be addressed in order to improve the quality of NCD matrices. This would allow for sequences of any length to be compressed without applying any segmentation.

In addition, the exploration of existing techniques such as MFcompress [26] or developing other compression techniques that would specifically be designed to work with DNA sequences. This is so that no segmentation would be needed during the compression phase. This would allow for generating even more reliable NCD matrices.

Other methods besides compression such as Genome Language Processing [27] and Genome Large Language Models [27] may be used to continue exploration of non-alignment based methods. This allows for the fusion of Machine Learning and genomics to better study how nucleotides change over time. K-mer-based approaches are also gaining popularity due to their ability to take multiple short sequence alignment data from multiple genomes and analyze them for similarity [28]. This approach also utilizes distance matrices to compare the relationships among a group of organisms. Similarly, MinHash approaches, which fuse k-mers with hashing algorithms, have been shown to efficiently profile large eukaryotic genomes [29].

At the moment, Phylotools and compression-based methods seem to have a promising future, with the potential to be widely used for creating phylogenetic trees.