Some New Boole-Type Inequalities via Modified Convex Functions with Their Applications and Computational Analysis
Abstract
1. Introduction
- It provides a unified framework that includes the classical convex case as a special instance when ;
- The parameter s offers flexibility to obtain sharper and more refined inequality bounds;
- It allows the extension of classical results such as Hermite–Hadamard-, Simpson-, and Boole-type inequalities and other Newton–Cotes formulae-type inequalities to a broader class of functions;
- The derived inequalities often yield improved error bounds in numerical integration and approximation theory.
2. Boole-Type Inequality for Modified Convex Function
3. Applications
3.1. Application to Quadrature Formulas
3.2. Application to the Midpoint Formula
3.3. Application to Special Means
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gibb, D. A Course in Interpolation and Numerical Integration for the Mathematical Laboratory; G. Bell & Sons, Limited: London, UK, 1915. [Google Scholar]
- Leader, J.J. Numerical Analysis and Scientific Computation; Chapman and Hall/CRC: Boca Raton, FL, USA, 2022. [Google Scholar]
- Ali, M.A.; Kara, H.; Tariboon, J.; Asawasamrit, S.; Budak, H.; Hezenci, F. Some new Simpson’s-formula-type inequalities for twice-differentiable convex functions via generalized fractional operators. Symmetry 2021, 13, 2249. [Google Scholar] [CrossRef]
- Ali, M.A.; Fečkan, M.; Mateen, A. Study of quantum Ostrowski’s-type inequalities for differentiable convex functions. Ukr. Math. J. 2023, 75, 7–27. [Google Scholar] [CrossRef]
- Vivas-Cortez, M.J.; Ali, M.A.; Qaisar, S.; Sial, I.B.; Jansem, S.; Mateen, A. On some new Simpson’s formula type inequalities for convex functions in post-quantum calculus. Symmetry 2021, 13, 2419. [Google Scholar] [CrossRef]
- Mateen, A.; Zhang, Z.; Ali, M.A. Some Milne’s rule type inequalities for convex functions with their computational analysis on quantum calculus. Filomat 2024, 38, 3329–3345. [Google Scholar] [CrossRef]
- Dwilewicz, R.J. A short history of convexity. Differ.-Geom.-Dyn. Syst. 2009, 11, 112–129. [Google Scholar]
- Kirmaci, U.S. Inequalities for differentiable mappings and applications to special means of real numbers and to midpoint formula. Appl. Math. Comput. 2004, 147, 137–146. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Agarwal, R.P. Two inequalities for differentiable mappings and applications to special means of real numbers and to trapezoidal formula. Appl. Math. Lett. 1998, 11, 91–95. [Google Scholar] [CrossRef]
- Alomari, M.; Darus, M.; Dragomir, S.S. New inequalities of Simpson’s type for s-convex functions with applications. Res. Rep. Collect. 2009, 12, 50. [Google Scholar]
- Dragomir, S.S.; Agarwal, R.P.; Cerone, P. On Simpson’s inequality and applications. RGMIA Res. Rep. Collect. 2012, 2, 75. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Set, E.; Özdemir, M.E. On new inequalities of Simpson’s type for convex functions. RGMIA Res. Rep. Collect. 2010, 13, 25. [Google Scholar] [CrossRef]
- Özdemir, M.E.; Akdemir, A.O.; Kavurmaci, H.; Avci, M. On the Simpson’s inequality for co-ordinated convex functions. Turk. J. Math. Anal. Number Theory 2014, 2, 165–169. [Google Scholar] [CrossRef]
- Du, T.; Li, Y.; Yang, Z. A generalization of Simpson’s inequality via differentiable mappings using extended (s,m)-convex functions. Appl. Math. Comput. 2017, 293, 358–369. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Set, E.; Yaldiz, H.; Başak, N. Hermite–Hadamard’s inequalities for fractional integrals and related fractional inequalities. Math. Comput. Model. 2013, 57, 2403–2407. [Google Scholar] [CrossRef]
- İşcan, İ.; Wu, S. Hermite–Hadamard type inequalities for harmonically convex functions via fractional integrals. Appl. Math. Comput. 2014, 238, 237–244. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Yildirim, H. On Hermite-Hadamard type inequalities for Riemann-Liouville fractional integrals. Miskolc Math. Notes 2016, 17, 1049–1059. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Set, E.; Ozdemir, M.E. On new inequalities of Simpson’s type for s-convex functions. Comput. Math. Appl. 2010, 60, 2191–2199. [Google Scholar] [CrossRef]
- Chen, J.; Huang, X. Some new inequalities of Simpson’s type for s-convex functions via fractional integrals. Filomat 2017, 31, 4989–4997. [Google Scholar] [CrossRef]
- Budak, H.; Hezenci, F.; Kara, H. On parameterized inequalities of Ostrowski and Simpson type for convex functions via generalized fractional integrals. Math. Methods Appl. Sci. 2021, 44, 12522–12536. [Google Scholar] [CrossRef]
- Breckner, W.W. Stetigkeitsaussagen für eine klasse verallgemeinerter konvexer funktionen in topologischen linearen räumen. Publ. De L’Institut MathéMatique 1978, 23, 13–20. [Google Scholar]
- Hudzik, H.; Maligranda, L. Some remarks on s-convex functions. Aequationes Math. 1994, 48, 100–111. [Google Scholar] [CrossRef]
- Pycia, M. A direct proof of the s-Hölder continuity of Breckner s-convex functions. Aequationes Math. 2001, 61, 128–130. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Fitzpatrick, S. The Hadamard’s inequality for s-convex functions in the second sense. Demonstr. Math. 1999, 32, 687–696. [Google Scholar]
- Kirmaci, U.S.; Bakula, M.K.; Özdemir, M.E.; Pečarić, J. Hadamard-type inequalities for s-convex functions. Appl. Math. Comput. 2007, 193, 26–35. [Google Scholar] [CrossRef]
- Alomari, M.; Darus, M.; Dragomir, S.S. Inequalities of Hermite-Hadamard’s type for functions whose derivatives absolute values are quasi-convex. Res. Rep. Collect. 2009, 12, 1. [Google Scholar]
- Alomari, M.; Darus, M.; Kirmaci, U.S. Refinements of Hadamard-type inequalities for quasi-convex functions with applications to trapezoidal formula and to special means. Comput. Math. Appl. 2010, 59, 225–232. [Google Scholar] [CrossRef]
- Kashuri, A.; Liko, R. Fractional trapezium type inequalities for twice differentiable preinvex functions and their applications. Int. J. Optim. Control. Theor. Appl. 2020, 10, 226–236. [Google Scholar] [CrossRef]
- Yildiz, Ç.; Yergöz, B.; Yergöz, A. On new general inequalities for s-convex functions and their applications. J. Inequalities Appl. 2023, 2023, 11. [Google Scholar] [CrossRef]
- Sezer, S. The Hermite-Hadamard inequality for s-convex functions in the third sense. AIMS Math. 2021, 6, 7719–7732. [Google Scholar] [CrossRef]
- Barsam, H.; Ramezani, S.M.; Sayyari, Y. On the new Hermite–Hadamard type inequalities for s-convex functions. Afr. Mat. 2021, 32, 1355–1367. [Google Scholar] [CrossRef]
- Zhan, X.; Mateen, A.; Toseef, M.; Ali, M.A. Some Simpson- and Ostrowski-type integral inequalities for generalized convex functions in multiplicative calculus with their computational analysis. Mathematics 2024, 12, 1721. [Google Scholar] [CrossRef]
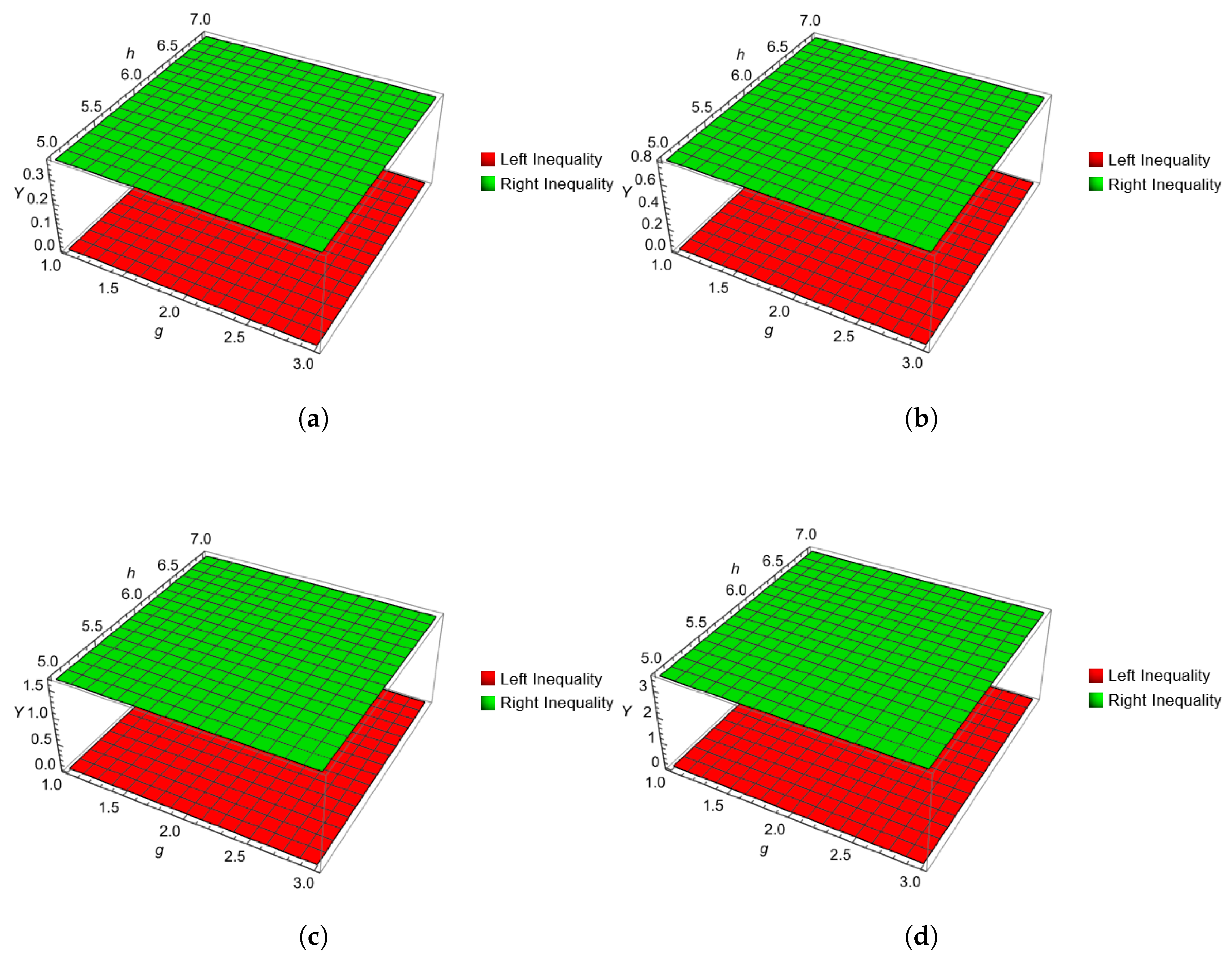
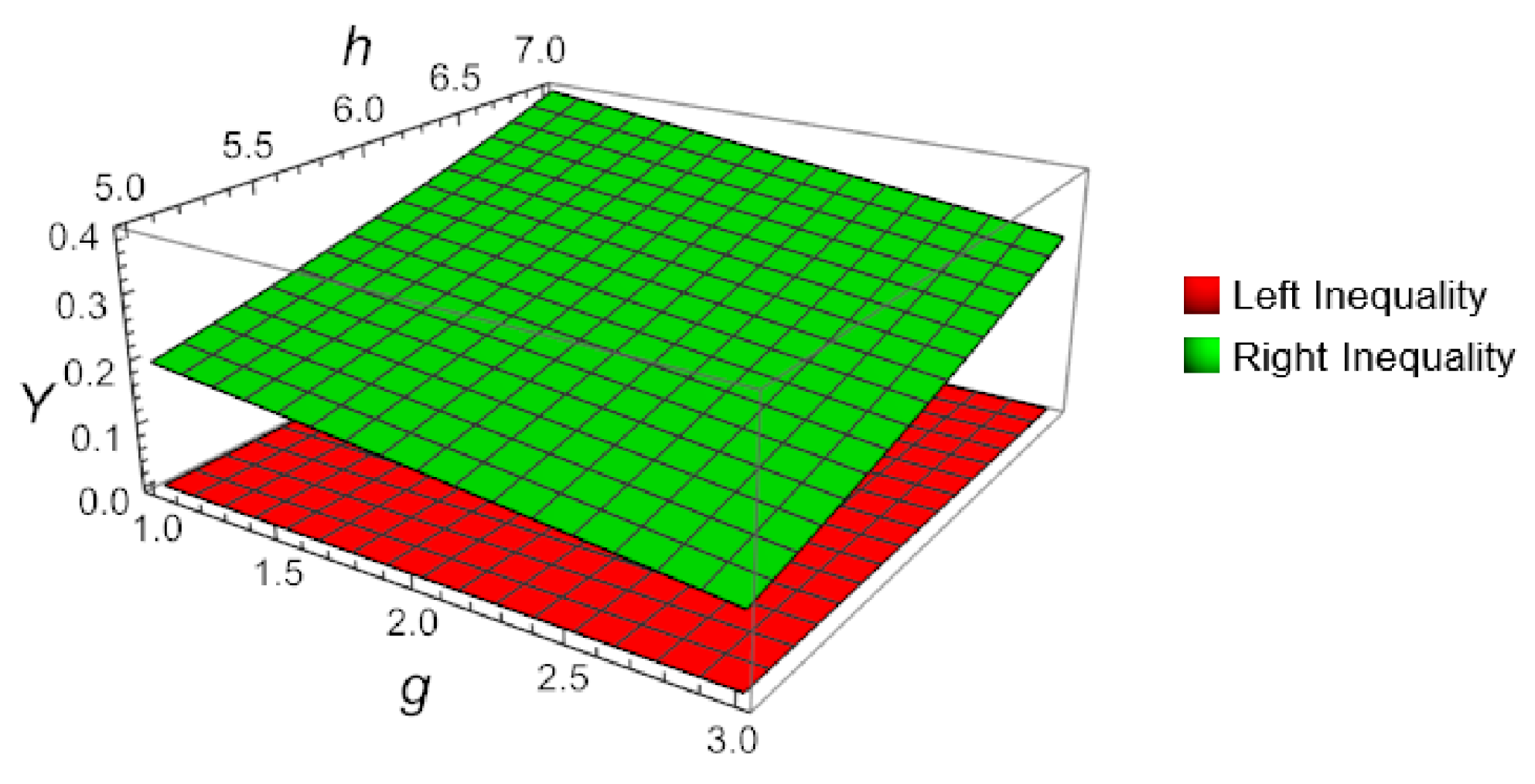
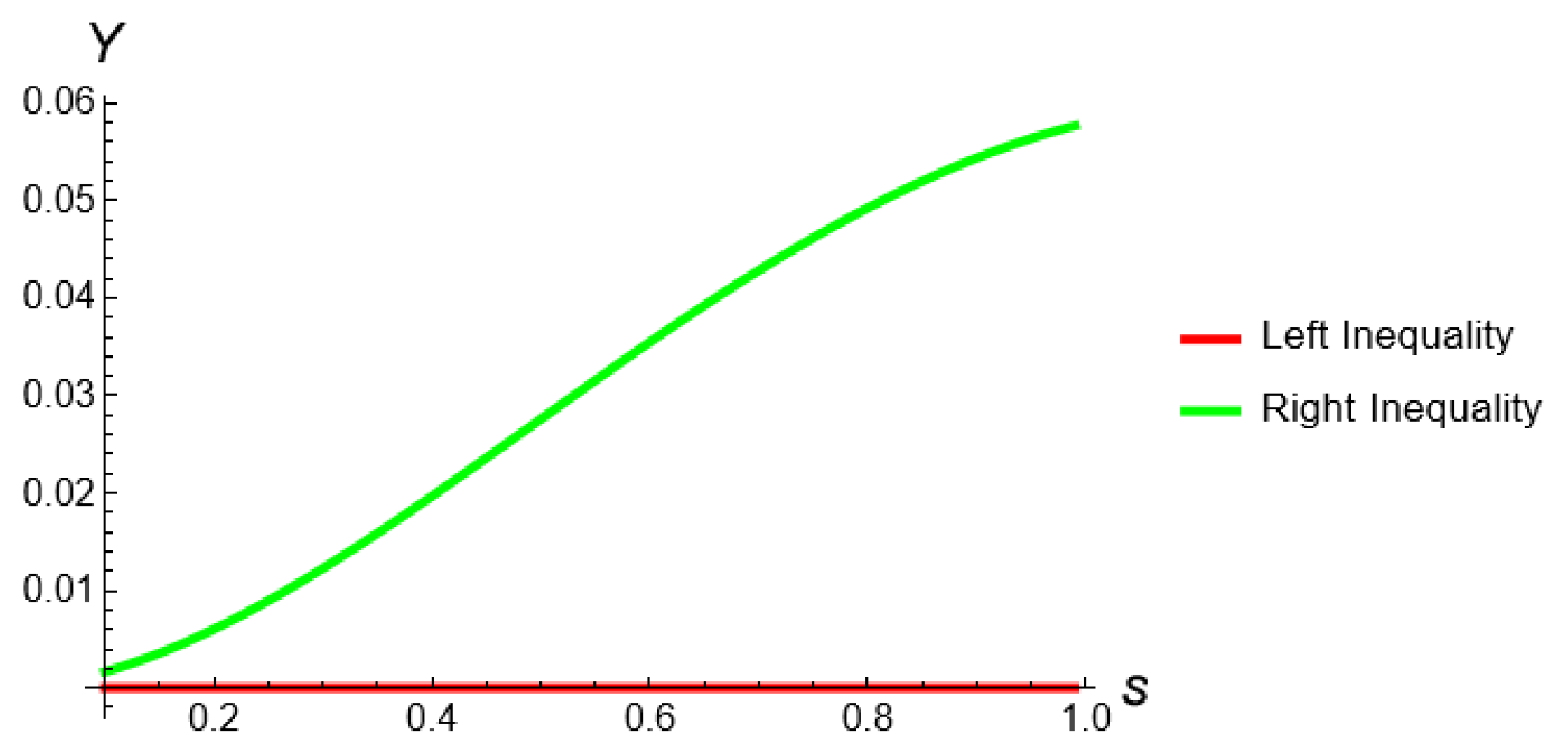
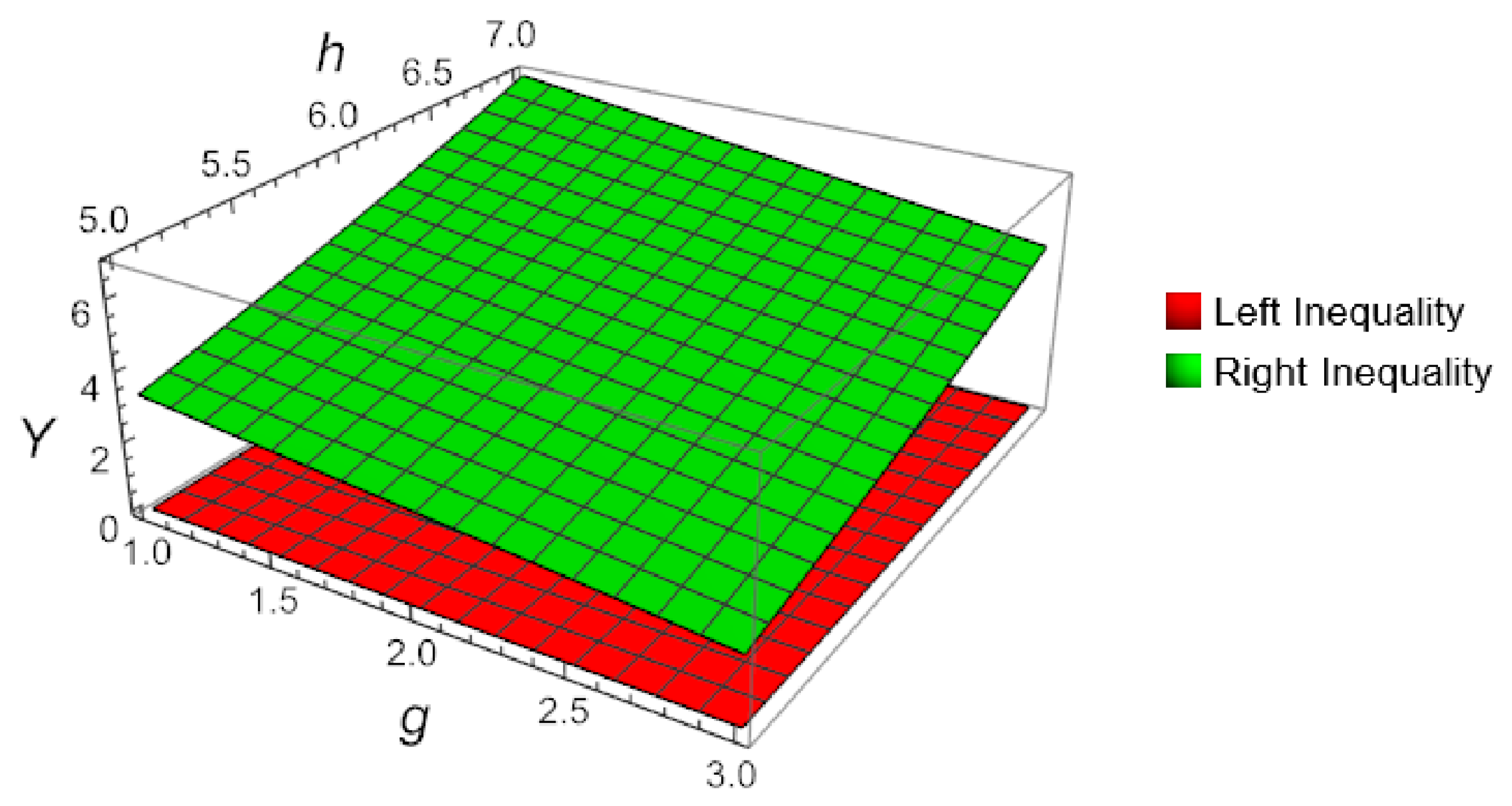
| s | Left Part | Right Part |
|---|---|---|
| 0.1 | 4.6039 | 0.2440 |
| 0.2 | 9.0000 | 0.3717 |
| 0.3 | 4.5617 | 0.5484 |
| 0.4 | 1.7000 | 0.7984 |
| 0.5 | 9.7969 | 1.1570 |
| 0.6 | 3.3000 | 1.6741 |
| 0.7 | 4.1696 | 2.4212 |
| 0.8 | 6.5000 | 3.5005 |
| 0.9 | 6.8820 | 5.0581 |
| 1 | 3.7200 | 7.3028 |
| s | Left Part | Right Part |
|---|---|---|
| 0.1 | 6.0151 | 0.01567 |
| 0.2 | 4.4653 | 0.03362 |
| 0.3 | 5.9121 | 0.05451 |
| 0.4 | 3.8618 | 0.07915 |
| 0.5 | 1.7129 | 0.10843 |
| 0.6 | 5.9483 | 0.14348 |
| 0.7 | 1.7446 | 0.18563 |
| 0.8 | 4.5226 | 0.23651 |
| 0.9 | 1.0668 | 0.29809 |
| 1 | 2.3363 | 0.37279 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anwar, T.; Mateen, A.; Elmannai, H.; Ali, M.A.; Ciurdariu, L. Some New Boole-Type Inequalities via Modified Convex Functions with Their Applications and Computational Analysis. Mathematics 2025, 13, 3517. https://doi.org/10.3390/math13213517
Anwar T, Mateen A, Elmannai H, Ali MA, Ciurdariu L. Some New Boole-Type Inequalities via Modified Convex Functions with Their Applications and Computational Analysis. Mathematics. 2025; 13(21):3517. https://doi.org/10.3390/math13213517
Chicago/Turabian StyleAnwar, Talha, Abdul Mateen, Hela Elmannai, Muhammad Aamir Ali, and Loredana Ciurdariu. 2025. "Some New Boole-Type Inequalities via Modified Convex Functions with Their Applications and Computational Analysis" Mathematics 13, no. 21: 3517. https://doi.org/10.3390/math13213517
APA StyleAnwar, T., Mateen, A., Elmannai, H., Ali, M. A., & Ciurdariu, L. (2025). Some New Boole-Type Inequalities via Modified Convex Functions with Their Applications and Computational Analysis. Mathematics, 13(21), 3517. https://doi.org/10.3390/math13213517







