Abstract
Against the backdrop of incomplete evaluation information prevalent in real-world decision-making scenarios and the limited application of Fermatean fuzzy numbers (FFNs) in the domain of two-sided matching (TSM) models, this paper proposes a Fermatean fuzzy two-sided matching model that integrates the regret aversion psychological behavior of agents and their matching willingness. Firstly, the TSM problem characterized by incomplete Fermatean fuzzy preference is described. Based on the incomplete Fermatean fuzzy evaluation information provided by bilateral agents, satisfaction matrices are constructed, and a fairness-aware matching willingness matrix is quantified. Moreover, a multi-objective TSM optimization model is established to maximize the satisfaction of agents on both sides, and the optimal TSM scheme is obtained by solving the model. Finally, the feasibility, effectiveness, and innovation of the proposed approach are validated by an example analysis of TSM on a data trading platform.
Keywords:
two-sided matching; Fermatean fuzzy number; matching willingness; fair matching; regret theory MSC:
03B52; 03E72; 94D05
1. Introduction
Two-sided matching (TSM) refers to the process of pairing agents from two distinct finite sets, with the objective of enabling each agent to be matched with a mutually satisfactory counterpart on the opposite side [1]. TSM problems have extensive practical backgrounds and exist widely in diverse two-sided markets. In the early stages of TSM research, scholarly attention primarily focused on traditional domains, including matches between men and women [2,3], buyers and sellers [4,5], students and colleges [6,7], and interns and hospitals [8,9]. With the evolution of economic and social systems, TSM problems in new contexts have emerged, particularly in scenarios involving intermediary platforms that connect supply and demand sides of products or services. Examples include financial institutions facilitating matching between creditors and debtors [10] or between venture capitalists and investment enterprises [11], data trading platforms linking data suppliers and demanders [12], ride-hailing platforms matching drivers with passengers [13], C2B crowdsourcing logistics platforms connecting merchants and drivers [14], O2O logistics information platforms bridging merchants and customers [15], and B2B export cross-border e-commerce platforms matching overseas demanders with domestic suppliers [16]. Depending on the matching structure, TSM problems can be categorized into one-to-one TSM [2,3], many-to-one TSM [17,18] and many-to-many TSM [19,20].
In the TSM process, agents on both sides express their preferences and matching objectives. From the perspective of agent preferences, existing TSM decision-making studies can be classified based on the type of preference information and the core objectives of matching, as detailed below.
Scholars have conducted extensive research on TSM decision-making based on diverse preference types, including ordinal preferences, fuzzy preferences, linguistic preferences, and multi-form preferences. In terms of ordinal preferences, Yue [21] proposed a satisfied TSM decision-making method under completely strict preference ordinals, uncertain preference ordinals, and incomplete preference ordinals. Liang et al. [22] developed a multi-objective satisfied and stable TSM decision-making method under strong preference ordinals, weak preference ordinals, indifference preference ordinals, and unknown preference ordinals. Due to the uncertainty and fuzziness of preferences, fuzzy set theory is introduced into TSM decision-making problems. The notion of fuzzy set was initially proposed by Zadeh [23] and was subsequently expanded into different forms, such as intuitionistic fuzzy sets (IFSs) [24], interval-valued intuitionistic fuzzy sets (IVIFSs) [25], Pythagorean fuzzy sets (PFSs) [26], Fermatean fuzzy sets (FFSs) [27], picture fuzzy sets (PFSs) [28], q-rung orthopair fuzzy sets (q-ROFSs) [29], etc. These extensions can mainly be divided into two classes: extensions with two independent membership parameters and extensions with three independent membership parameters [30]. In IFSs, membership degree and non-membership degree are employed to separately represent the degree of support and opposition toward a specific attribute. For example, an intuitionistic fuzzy number (IFN) means that “in a vote on a particular attribute, 6 out of 10 participants support it, 3 oppose it, and 1 abstains”. However, IFSs are constrained by the condition that the sum of membership and non-membership degrees must not exceed 1. PFSs relax this constraint to allow the sum of membership and non-membership degrees to exceed 1, provided that the sum of their squares is no greater than 1. In comparison to IFSs and PFSs, FFSs further expand the feasible domain by permitting the sum of the squares of membership and non-membership degrees to exceed 1 while requiring the sum of their cubes to be less than 1. This expanded constraint enables FFSs to capture higher levels of uncertainty and address stronger fuzziness in practical decision-making scenarios. Figure 1 illustrates the range of the Fermatean fuzzy number (FFN), Pythagorean fuzzy number (PFN), and intuitionistic fuzzy number (IFN).
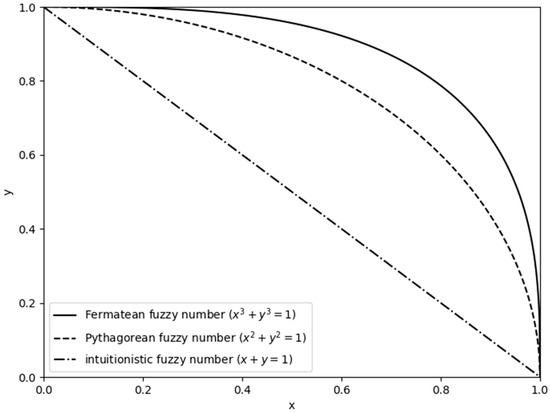
Figure 1.
The range of the Fermatean fuzzy number, Pythagorean fuzzy number, and intuitionistic fuzzy number.
Building on these fuzzy set extensions, Yu and Xu [31] put forward some novel intuitionistic fuzzy Choquet integral aggregation operators and applied them to personnel–position matching problems. Liang et al. [32] constructed an interval-valued intuitionistic fuzzy TSM model considering the level of automation and validated it using a personnel–position–machine (PPM) matching case in an intelligent production line. Yue and Deng [33] proposed a stable TSM method considering the matching intention of agents under a hesitant fuzzy environment. Hu and Yue [34] proposed a TSM method under a Pythagorean fuzzy environment targeting multiple decision-making psychological characteristics of decision-makers. Given their ability to enable bilateral agents to express evaluations across a broader spectrum, FFSs have garnered increasing scholarly attention and been introduced to the decision-making fields. Gul et al. [35] provided a Fermatean fuzzy technique for order preference by similarity to ideal solution (FF-TOPSIS) for evaluating occupational risks in the industry. Akram et al. [36] proposed an extended data envelopment analysis (DEA) method for a multi-objective transportation problem under a Fermatean fuzzy setting. Ali et al. [37] integrated Fermatean fuzzy logic and neutrosophic goal programming in multi-objective healthcare problems. Qin et al. [38] proposed a new multi-attribute decision-making (MADM) approach based on a new score function and hybrid weighted score measure under an interval-valued Fermatean fuzzy environment. Ruan et al. [39] proposed a novel MADM approach that integrates the distance measure and cross-entropy of Fermatean probabilistic hesitant fuzzy sets (FPHFSs) with the VlseKriterijuska Optimizacija I Komoromisno Resenje (VIKOR) method. Especially, in TSM decision-making problems, Yue et al. [40] proposed a Fermatean fuzzy multi-attribute group decision-making methodology for personnel–position matching with unknown attribute weights. Yue et al. [41] developed a two-stage one-to-two matching decision-making method under a Fermatean fuzzy environment and verified its practicality through a reviewer–paper matching case study. In terms of linguistic preferences, Jia et al. [42] proposed a TSM approach based on prospect theory under a probabilistic linguistic environment. Wang and Li [43] developed a TSM method that integrates the peer effect using multi-granularity probabilistic linguistic term sets. For TSM problems covering multi-form preferences, based on evaluation information including uncertain linguistic variables, uncertain preference ordinals, and incomplete complementary matrices, Zhang et al. [44] proposed a dynamic TSM method within the context of cloud manufacturing tasks and services with load balancing.
Satisfaction, stability, and fairness are the three core objectives in TSM decision-making. Satisfaction is the primary criterion used by scholars to evaluate the quality of TSM schemes [45,46]. Typically, satisfaction is calculated based on mutual evaluations between bilateral agents, and TSM models are formulated with the objective of maximizing satisfaction. Additionally, numerous studies on matching markets have focused on static and stable matching outcomes [20,46]. However, most TSM methods that prioritize satisfaction and stability tend to yield unilaterally optimal solutions, where only one side achieves satisfactory matching, thereby failing to ensure the fairness of TSM schemes. Fair matching plays a critical role in mitigating interest conflicts and psychological disparities between bilateral agents. However, fairness is a contested concept. Scholars have proposed different definitions and solutions to obtain a fair TSM scheme [47]. Zhang et al. [48] investigated supply chain channel mode fairness on e-platforms. Gui et al. [49] focused on the horizontal fairness concerns between cargo owners and cargo owners, as well as between vehicle owners and vehicle owners, on a freight platform. Zhang et al. [50] constructed a satisfied and fair TSM model that incorporates linguistic preferences while minimizing the deviation of preference values of two sides as the objective function. Liu et al. [51] integrated satisfaction, fairness degree, and risk attitude and proposed a hesitant fuzzy TSM method based on TODIM. Liu et al. [52] proposed a TSM method considering stability-based fairness based on TOPSIS and grey correlation degrees for graduate student–supervisor matching. Tozlu et al. [53] proposed an environment-based design approach to ensure unbiased criteria identification for TSM problems.
Most existing TSM studies assume that agents make decisions with complete rationality, prioritizing expected utility maximization. However, decision-makers are often bounded rational, with their choices influenced by psychological factors, leading to suboptimal outcomes in their choices [54]. To address this gap, scholars have integrated psychological characteristics such as reference dependence, disappointment avoidance, regret aversion, and loss aversion into TSM decision-making, drawing primarily on foundational behavioral theories such as prospect theory, disappointment theory, and regret theory. Based on prospect theory, Jia et.al [42] defined the Lance distance and proposed a TSM decision-making approach with probabilistic linguistic evaluations. Wang et al. [55] constructed a multi-attribute TSM model considering the psychological behavior of agents under Pythagorean fuzzy preferences. Based on disappointment theory, Fan et.al [56] put forward a satisfied TSM method considering the elation and disappointment of agents. Chen and Chen [57] examined the impact of psychological perceptions of disappointment and happiness on agent satisfaction and improved the predator search algorithm to solve the volunteer multi-person multi-task optimization dispatch TSM problem. Based on regret theory, Zhang et al. [58] proposed an intuitionistic fuzzy TSM model that considers regret aversion and matching aspirations. Li et al. [59] developed a novel TSM decision-making method for probabilistic linguistic term sets that accounts for the minimum acceptability threshold. Huang et al. [60] constructed a TSM model for hesitant fuzzy linguistic term sets (HFLTSs) and provided a viable solution to the two-way referral cooperation matching problem among hospitals. Zhao et al. [61] adopted a collaborative filtering algorithm to fill in incomplete information based on the probabilistic linguistic term set (PLTS) and constructed a dynamic stable TSM model. Chen et al. [62] proposed a cloud model-based TSM framework that integrates both prospect theory and regret theory, aiming to capture the complex psychological perceptions of decision-makers for task assignment problems. Beyond these core theories, to capture more nuanced decision-maker behaviors, scholars have also proposed decision-making methods based on diverse behavioral economics theories including risk attitude [51,63], self-confidence [64], and peer effect [43,65].
In addition, due to the complexity of practical environments and the limitations of individual cognition, it is difficult for agents to fully provide their preferences, resulting in incomplete evaluation or weight information. To address incomplete evaluation information, Liu et al. [66] proposed a multi-attribute TSM method under an incomplete intuitionistic fuzzy environment based on Dempster–Shafer (DS) evidence theory. Zhang et al. [67] developed a stable TSM decision-making method under incomplete fuzzy preference relations. Zhou et al. [63] developed a statistics-based approach for large-scale group decision-making under incomplete Pythagorean fuzzy information with risk attitude. Zhao et al. [68] proposed a TSM method with incomplete intuitionistic fuzzy preferences. Multi-attribute TSM problems require determining the weight of each attribute. For incomplete weight information in such TSM problems, Zhang et al. [39] constructed an optimization model based on deviation maximization to obtain attribute weights. Khan et.al [69] adopted gray relation analysis (GRA) method to solve the TSM group decision-making model with incomplete weight information under a Pythagorean fuzzy setting. Ullah et al. [70] extended the GRA method to construct a TSM model based on picture hesitant fuzzy sets for scenarios with incomplete or completely unknown attribute weights. Zhao et al. [71] developed a TSM decision-making approach with multi-attribute probability hesitant fuzzy sets and incomplete attribute weight information.
While existing studies have made significant contributions to addressing various TSM problems, three key gaps remain: (1) limited application of Fermatean fuzzy set theory in TSM decision-making; (2) insufficient research on TSM decision-making under incomplete evaluation information; (3) neglect of fairness considerations in most TSM decision-making frameworks. To fill in these gaps, this paper proposes a novel TSM decision-making approach that integrates regret aversion and matching willingness under an incomplete Fermatean fuzzy environment. The main contributions of this paper are outlined as follows: (1) development of an incomplete Fermatean fuzzy TSM decision-making framework; (2) design of a novel calculation method for fairness-aware matching willingness factors; (3) further exploration of the application of regret theory in TSM decision-making.
The remainder of this paper is structured as follows: In Section 2, four basic concepts, including Fermatean fuzzy sets (FFSs), two-sided matching (TSM), regret theory, and Fermatean fuzzy technique for order preference by similarity to ideal solution (FF-TOPSIS), are reviewed. In Section 3, the problem description of incomplete Fermatean fuzzy preference TSM decision-making is expressed. In Section 4, the proposed approach considering regret aversion psychological behavior and the matching willingness of the agents is developed. In Section 5, an example is introduced to verify the feasibility, effectiveness, and innovativeness of the proposed method. Finally, some conclusions are drawn in Section 6.
2. Preliminaries
2.1. Fermatean Fuzzy Set (FFS)
Definition 1
([27]). Assume X is a non-empty set. A Fermatean fuzzy set I on the universal X is an expression of the form
where
and
, respectively, indicate membership degree and non-membership degree of each element
in the set I, satisfying the condition . For all , is identified as the degree of indeterminacy of x to I, which represents the uncertainty and hesitancy.
In the interest of simplicity, for the components of the FFS, we define as the Fermatean fuzzy numbers (FFNs). Among the FFNs, the biggest is and the smallest is .
Definition 2
([27]). Let and be three FFNs and , then their operational laws are as follows:
- (1)
- (2)
- (3)
- (4)
- (5)
Definition 3
([72]). Let and be two FFNs, then the Fermatean fuzzy Euclidean distance between and is defined as
Further, the Fermatean fuzzy similarity (FFS) between and is defined as
2.2. Two-Sided Matching (TSM)
Let and be the set of agents on two sides, where is the i th agent on side M and is the j th agent on side W. Let , .
Definition 4
([54]). Let be a one-to-one mapping. If the following properties are established, then the mapping T is called a TSM: (1) , (2) , and (3) if and only if . Therefore, (a matching pair ) represents that and are matched, and (a non-matching pair ) represents that is not matched.
All agents on one side give their evaluation information to another side. If there is any missing evaluation information, the preference is considered incomplete. (a matching pair ) is compatible if and only if and give evaluation information to each other.
In conclusion, the mapping T can be denoted as , where is the set of matching pairs and is the set of non-matching pairs. If contains matching pairs, then we define the mapping T as a complete TSM.
2.3. Regret Theory
Regret theory was initially proposed by Bell [73] and Loomes and Sugden [74]. This theory describes the psychological behavior of bounded rational decision-makers, who evaluate the rationality of their chosen decisions by comparing the utility of the selected option with that of alternative unselected options. Compared to prospect theory, regret theory features a more parsimonious calculation framework while still maintaining the ability to explain all the violations of expected utility theory identified by Kahneman and Tversky [75].
In practical decision-making scenarios, if a decision-maker perceives that the utility of the currently adopted plan exceeds that of other available alternatives, they will experience a sense of “rejoice”; conversely, if the current plan’s utility is lower than that of alternatives, a sense of “regret” will arise. Given that decision-makers typically exhibit risk aversion toward both regret and rejoice, the regret–rejoice function can be defined as a non-decreasing concave function. This function satisfies the properties and , with the boundary condition . Let the regret–rejoice function be the following form:
In Equation (4), denotes the regret aversion coefficient: a larger indicates a stronger tendency of the decision-maker to avoid regret. represents the utility difference between two alternative options. When , quantifies the “rejoice value” derived from the current decision outperforming alternatives; when , measures the “regret value” resulting from the current decision underperforming alternatives. The image of the regret–rejoice function is shown in Figure 2. As illustrated in Figure 2, the comparison of regret–rejoice functions under different values shows that a larger leads to a steeper function curve.
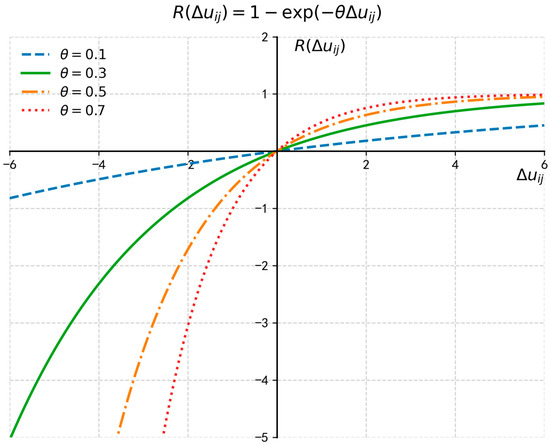
Figure 2.
The regret–rejoice function.
2.4. Fermatean Fuzzy Technique for Order Preference by Similarity to Ideal Solution (FF-TOPSIS)
In fuzzy-based multi-criteria decision-making (MCDM) problems, the Fermatean fuzzy technique for order preference by similarity to ideal solution (FF-TOPSIS) outperforms many conventional MCDM methods in extracting latent evaluation information [76]. A core advantage of FF-TOPSIS lies in its introduction of the “closeness coefficient”, a metric that quantifies the relative proximity of each evaluated alternative to both the positive ideal solution (PIS) and negative ideal solution (NIS) in the Fermatean fuzzy space. For FFN-based evaluation contexts, the closeness coefficient is formally defined to integrate the distance relationships between each evaluated subject and the two ideal solutions. Mathematically, it is expressed as
where denotes an FFN representing the evaluation value of a target alternative. The positive ideal solution (PIS), denoted as , corresponds to the maximum FFN. The negative ideal solution (NIS), denoted as , corresponds to the minimum FFN. refers to the Fermatean fuzzy distance metric that measures the spatial discrepancy between two FFNs. The closeness coefficient ranges within the interval : a larger indicates a closer proximity of to (and thus a more optimal alternative), while a smaller implies a closer proximity of to (and thus a less optimal alternative).
3. Problem Description of Incomplete Fermatean Fuzzy Preference TSM Decision-Making
With respect to the TSM decision-making problem in incomplete Fermatean fuzzy environments, let and be the set of agents on two sides, where is the i th agent on side M and is the j th agent on side W. Let , .
Agents on one side give their evaluation information to the other side in the form of FFNs. Let be the incomplete Fermatean fuzzy preference matrix of side M to side W, in which or denotes the evaluation information of to . Similarly, let be the incomplete Fermatean fuzzy preference matrix of side W to side M, in which or denotes the evaluation information of to . The main problem in this research is, based on the above stated incomplete Fermatean fuzzy evaluation information, how to construct a TSM model when considering the regret aversion behavior and matching willingness of agents on two sides.
4. Approach for Incomplete Fermatean Fuzzy Preference TSM Decision-Making
In this section, we propose an approach for incomplete Fermatean fuzzy preference TSM decision-making, in which the regret aversion psychological behavior and the matching willingness of bilateral agents are taken into account. The main procedures of this proposed approach are shown as follows. Firstly, based on the incomplete Fermatean fuzzy evaluation information, the incomplete overall regret–rejoice values on two sides are calculated. After standardization, the incomplete satisfaction degrees on two sides are further obtained. Secondly, a preliminary compatibility verification is conducted to confirm the existence of a complete TSM. When a complete TSM exists, the incomplete satisfaction degrees are transformed into the complete satisfaction degrees, and fairness-aware matching willingness factors are calculated. Thirdly, a TSM decision-making model considering the matching satisfaction and matching fairness is established. This model is solved by using the membership degree-based linear weighted method and the single-objective programming method, and the optimal TSM scheme can be derived.
4.1. Incomplete Satisfaction Degrees
This part firstly calculates the utility values of the agents by the FF-TOPSIS method, then obtains the regret–rejoice values according to the differences of the utility values of the agents’ options and further computes the satisfaction degrees of the agents of two matching sides.
4.1.1. Incomplete Utility Values
Let be the utility value obtained by of side M when matching with of side W under incomplete Fermatean fuzzy evaluation information. This utility value is computed using the FF-TOPSIS method, which measures the relative proximity of each Fermatean fuzzy evaluation to the positive/negative ideal solutions (PIS/NIS). Mathematically, is computed by
In Equation (6), and denote the PIS and NIS, respectively; refers to the Fermatean fuzzy Euclidean distance (Equation (2)) between two FFNs. When , : a larger indicates is closer to , while a smaller implies is closer to .
Likewise, let be the utility value obtained by of side W when matching with of side M under incomplete Fermatean fuzzy evaluation information, which can be calculated by
When , , with its value interpretation consistent with .
4.1.2. Incomplete Regret–Rejoice Values
Regret theory posits that agents evaluate decisions by comparing the utility of their chosen option with alternatives. Based on this, let represent the regret–rejoice value obtained by of side M when matched with comparative to of side W. This value is quantified using the regret–rejoice function (Equation (4)) and defined as
Then, the overall regret–rejoice value obtained by of side M when matched with comparative to all other agents of side W is
Similarly, let be the regret–rejoice value obtained by of side W when matched with comparative to of side M, which can be depicted as
Then, the overall regret–rejoice value obtained by of side W when matched with comparative to all other agents of side M is
Here, and are the regret aversion coefficients of and respectively. According to Zhang et al. [77], we assume . The regret aversion coefficient is commonly set to 0.3 in relevant studies to reflect a moderate level of regret avoidance that aligns with the bounded rationality of decision-makers.
4.1.3. Incomplete Standardized Overall Regret–Rejoice Values
A positive correlation exists between an agent’s overall regret–rejoice value and their satisfaction with the corresponding match: a larger (or ) implies higher satisfaction of (or ) with the match . Then, the overall regret–rejoice values of all agents can be standardized as their satisfaction degrees. Let and be the incomplete satisfaction matrices, where and are the incomplete satisfaction degrees of to and to . These values are computed via min–max normalization to map all non-empty regret–rejoice values to the interval :
4.2. Judgment of the Existence of Complete TSM
A matching pair is considered compatible if and only if both and . If either satisfaction value is missing (i.e., or ), the pair is deemed incompatible. According to the incomplete satisfaction matrices and , a comprehensive 0–1 matrix (i.e., TSM compatibility matrix) can be established, where represents a 0–1 variable indicating whether TSM compatibility exists:
To determine whether a complete TSM exists, an optimization model can be established based on the TSM compatibility matrix . Let be a 0–1 variable to denote whether to match:
The optimization model (M–1) for verifying complete TSM is as detailed follows:
A complete TSM exists if and only if the optimal objective value of model (16) is .
4.3. TSM Model Under the Condition of the Existence of Complete TSM
When a complete TSM is verified to exist, the first step is to convert the incomplete satisfaction matrices into complete ones to enable subsequent optimization. Further, to address fairness in TSM, a fairness-aware matching willingness factor is incorporated into the modeling process. This section first formulates a multi-objective TSM optimization model aimed at maximizing bilateral satisfaction, then introduces weight coefficients and for transforming the multi-objective model into a solvable single-objective one.
4.3.1. Multi-Objective TSM Model
Transform the incomplete satisfaction matrices and into the complete satisfaction matrices and , where and are the complete satisfaction degrees of to and to independently, which can be defined as
wherein K is a sufficiently large finite positive constant.
Then, the TSM 0–1 variable (consistent with the definition of ) is introduced. Grounded on the complete satisfaction matrices and , a multi-objective TSM model (M–2) to maximize the matching satisfaction of each side considering one-to-one matching constraint is developed as follows:
4.3.2. Matching Willingness Factors
While the linear weighting method enables the conversion of the multi-objective TSM model (M–2) into a single-objective optimization problem, a critical limitation arises: an objective function that solely maximizes the sum of bilateral satisfaction degrees often converges to unilaterally optimal solutions. Such solutions tend to induce unfair matching scenarios, where one side of agents achieves significantly higher satisfaction levels than the other, manifesting as substantial disparities in mutual matching satisfaction and undermining the sustainability of the matching outcome.
To address this issue, we first clarify the core principle underlying matching willingness: The mutual willingness of two agents from opposite sides to form a pair is positively correlated with two factors: (1) the joint satisfaction intensity (i.e., the sum of their mutual satisfaction degrees) and (2) the satisfaction equity (i.e., the smaller the absolute difference between their mutual satisfaction degrees). Additionally, since the overarching goal of the TSM model remains the maximization of bilateral satisfaction, the relative importance of joint satisfaction intensity and satisfaction equity in determining matching willingness can be flexibly adjusted via weight parameters. In existing studies on the fairness of TSM, scholars primarily adjust matching fairness by means such as incorporating the difference in satisfaction into the objective function [50,52], proposing novel matching algorithms [48,49], and defining calculation methods for fairness degree [51].
However, the adoption of novel fairness-oriented algorithms tends to be computationally complex, while the definition of fairness degree remains highly subjective. Among existing approaches, the most commonly used practice—treating the satisfaction difference and satisfaction sum as having equal priority when integrating them into the optimization objectives—may lead to compromised optimization efficiency. Specifically, the pursuit of a minimal satisfaction difference could excessively constrain the enhancement of total satisfaction, ultimately resulting in a suboptimal balance between the “fairness” of matching outcomes and the “overall utility” of the entire TSM system. Furthermore, this equal priority setting makes it difficult to flexibly adjust the trade-off between fairness and satisfaction maximization according to the actual scenario requirements. Such inflexibility limits the adaptability of the proposed methods to diverse TSM application contexts.
Therefore, this paper introduces a novel matching willingness factor that explicitly integrates both joint satisfaction intensity and satisfaction equity, with adjustable weights to reflect scenario-specific preferences. The matching willingness factor quantifies the propensity of agent of side M and agent of side W to form a matched pair, derived from two core dimensions: (1) joint satisfaction intensity is captured by , where and denote the mutual satisfaction degrees of agent towards and agent towards , respectively. A larger sum indicates a stronger combined willingness to match; (2) satisfaction equity is measured by , where a smaller absolute difference signifies a more balanced satisfaction distribution between the two agents, thus enhancing fairness.
The matching willingness factor optimization model (M–3) is formulated as
Here, h and v are weight parameters that quantify the relative importance of joint satisfaction intensity and satisfaction equity, respectively. The constraints and ensure that satisfaction equity is prioritized at least as much as joint intensity, which is a practical choice to avoid extreme unfairness, while still allowing flexibility to adjust their trade-off.
The solution of the above model is as follows:
Then, can be standardized as the following matching willingness factor :
Therefore, based on complete satisfaction matrices, this paper establishes a matching willingness matrix , where explicitly quantifies the mutual matching willingness between agent and agent , with its value determined by both joint satisfaction and satisfaction equity. is defined as
According to the matching willingness matrix , the multi-objective TSM optimization model (M–4) can be obtained:
4.3.3. Single-Objective TSM Model
Considering that there may be different dimension scales between objective functions, this paper adopts a membership degree-based weighted method proposed by Cohon [78].
First, we define the key extremal values of the objective functions to construct membership degrees: Let and represent the maximum possible values of and , respectively; let and represent the minimum possible values of and . Based on these extremal values, the membership degree functions and are expressed as
Next, we introduce weight coefficients and to reflect the relative importance of side M and side W in the matching process. These weights satisfy . To calculate and , and in the complete satisfaction matrices and should be
Here, K is still a sufficiently large finite positive constant.
Correspondingly, the mutual matching willingness factor should be
By integrating the membership degree functions and weight coefficients, the multi-objective TSM optimization model (M–4) is transformed into a single-objective TSM model (M–5):
Here, and () are weight coefficients, representing the priorities of the agents of each side. In accordance with multi-objective programming theory, the optimal solution of model (M–5) is the effective solution of model (M–4). This implies that no alternative matching scheme can improve the satisfaction of one side without reducing the satisfaction of the other, ensuring the optimality and fairness of the solution. Thus, solving the complete TSM problem is equivalent to finding the optimal solution of model (M–5).
4.4. Steps of Incomplete Fermatean Fuzzy Preference TSM Decision-Making
The specific steps of incomplete Fermatean fuzzy preference TSM decision-making are as follows:
Step 1. According to Equations (6) and (7), the incomplete utility values and on both sides are calculated based on the incomplete Fermatean fuzzy preference matrices and .
Step 2. According to Equations (8)–(11), the incomplete overall regret–rejoice values and on both sides are obtained based on the incomplete utility values and .
Step 3. According to Equations (12) and (13), the incomplete satisfaction matrices and on both sides are computed based on the incomplete overall regret–rejoice values and .
Step 4. Based on the incomplete satisfaction matrices and , the TSM compatibility matrix is established.
Step 5. Based on the TSM compatibility matrix , the optimization model (M–1) is developed.
Step 6. By solving the optimization model (M–1), whether complete TSM exists or not can be determined.
Step 7. If complete TSM exists, the incomplete satisfaction matrices and are converted into the complete satisfaction matrices and .
Step 8. Based on the complete satisfaction matrices and , the multi-objective TSM model (M–2) is developed.
Step 9. According to Equation (32), the matching willingness matrix is obtained based on the complete satisfaction matrices and .
Step 10. Considering the matching willingness matrix , the multi-objective TSM model (M–2) is transformed into the multi-objective TSM optimization model (M–4).
Step 11. By the membership degree-based linear weighting method, the multi-objective TSM optimization model (M–4) is transformed into the single-objective TSM model (M–5).
Step 12. The optimal TSM matrix is obtained by solving model (M–5).
In summary, the workflow of the proposed approach for solving TSM problems with incomplete Fermatean fuzzy preference is visualized in the flow chart presented in Figure 3.
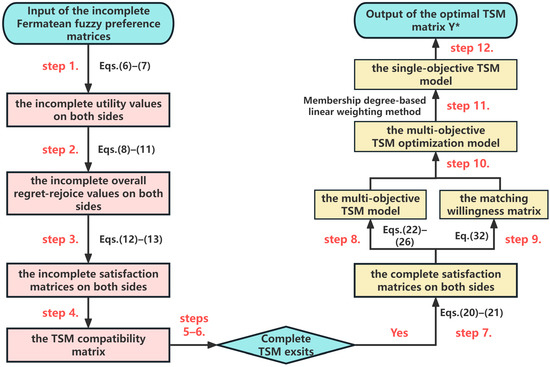
Figure 3.
Flow chart for solving incomplete Fermatean fuzzy preference TSM problems.
5. Example Analysis
To examine the applicability of the proposed TSM model in real-world decision-making, we applied it to an example analysis between data suppliers and demanders mediated by a data trading platform.
The Shanghai Data Exchange, established in Shanghai, China, in 2021, is committed to delivering efficient, compliant, and secure data trading services while constructing a global comprehensive big data trading platform. In recent years, by developing a new-generation data trading platform anchored in the core concepts of “precise product matching, precise demand docking, and precise service configuration”, it has rapidly evolved into a core infrastructure for China’s data element marketization and a pivotal hub in the global data circulation network, offering diverse data trading services to corporate members. This platform achieves precise matching and efficient transactions through real-time dynamic supply–demand relationships: it enables data suppliers to register and list data products, data demanders to post procurement requirements, and facilitates intelligent matching within a defined effective response period. Through these initiatives, the Shanghai Data Exchange continuously promotes the circulation and trading of data elements, thereby effectively propelling the development of the digital economy.
Currently, six data-demanding enterprises (denoted as ) have posted purchase demands for specific data types, while four data-supplying enterprises (denoted as ) are capable of providing such data. Drawing on the supply–demand multi-attribute evaluation system for the data trading TSM problem from Ref. [12], side M evaluates suppliers through attributes including enterprise scales, technical capabilities, platform credentials, and after-sales services, forming an incomplete Fermatean fuzzy preference matrix (as shown in Table 1). Moreover, side W assesses suppliers using criteria like enterprise scales, technical capabilities, platform credentials, and market reputations, creating an incomplete Fermatean fuzzy preference matrix (as shown in Table 2). Then, the data trading platform matches the two sides based on the incomplete Fermatean fuzzy evaluation information provided by them.

Table 1.
Incomplete Fermatean fuzzy preference matrix (given by side M).

Table 2.
Incomplete Fermatean fuzzy preference matrix (given by side M).
5.1. Solution Process
In order to solve the above case, the steps of incomplete Fermatean fuzzy preference TSM decision-making are given as follows:
Step 1. According to Equations (6) and (7), the incomplete utility values and of both sides are calculated based on the incomplete Fermatean fuzzy preference matrices and , as are shown in Table 3 and Table 4.

Table 3.
Incomplete utility value .

Table 4.
Incomplete utility value .
Step 2. According to Equations (8)–(11), the incomplete overall regret–rejoice values and of both sides are obtained based on the incomplete utility values and , as are shown in Table 5 and Table 6.

Table 5.
Incomplete overall regret–rejoice value .

Table 6.
Incomplete overall regret–rejoice value .
Step 3. According to Equations (12) and (13), the incomplete satisfaction matrices and of both sides are computed based on the incomplete overall regret–rejoice values and , as are shown in Table 7 and Table 8.

Table 7.
Incomplete satisfaction matrices .

Table 8.
Incomplete satisfaction matrices .
Step 4. Based on the incomplete satisfaction matrices and , the TSM compatibility matrix is established as follows:
Step 5. Based on the TSM compatibility matrix , the optimization model is developed as follows:
Step 6. By solving the optimization model, complete TSM exists, and the optimal objective function value is .
Step 7. When complete TSM exists, the incomplete satisfaction matrices and are converted into the complete satisfaction matrices and , as are represented as follows:
Step 8. Based on the complete satisfaction matrices and , the multi-objective TSM model is developed as follows:
Step 9. According to Equation (32), if the weights of joint satisfaction intensity and satisfaction equity are regarded as identical, i.e., , the matching willingness matrix is obtained based on the complete satisfaction matrices and , as follows:
Step 10. Considering the matching willingness matrix , the multi-objective TSM model is transformed into the following multi-objective TSM optimization model.
Step 11. Ordinarily, the priorities of the agents of each side are treated as the same, i.e., By the membership degree-based linear weighting method, the multi-objective TSM optimization model is transformed into the following single-objective TSM model.
Step 12. The optimal TSM matrix is obtained by solving the single-objective TSM model, as follows:
i.e., the matching pair set is .
5.2. Comparative Analysis
To validate the superiority of the proposed approach, three sets of comparative experiments are conducted: (1) a cross-method comparison with extended versions of the TSM frameworks proposed by Zhao et al. [68] and Jia et al. [42]; (2) a sensitivity analysis of key parameters in the matching willingness factor; (3) a sensitivity analysis of combined weight coefficients and matching willingness factors.
Zhao et al. [68] proposed a TSM decision-making method based on expected utility theory for incomplete intuitionistic fuzzy environments, while Jia et al. [42] put forward a TSM decision-making method based on prospect theory for probabilistic linguistic environments. To isolate the effects of fuzzy set type (intuitionistic vs. Fermatean vs. probabilistic linguistic) and psychological theory (expected utility vs. prospect theory vs. regret theory), these methods are extended to the Fermatean fuzzy domain, with three comparative scenarios designed.
The first scenario, Extended Method I, retains the expected utility theory of the original method by Zhao et al. [68] but adapts it to handle incomplete Fermatean fuzzy information without considering matching willingness. The second scenario, Extended Method II, incorporates the prospect theory from Jia et al.’s work [42], adapts it to the Fermatean fuzzy set, and also omits the matching willingness factor, aiming to discern the influence of psychological perception in gain–loss scenarios. The third scenario, Extended Method III, replaces expected utility theory with regret theory while still omitting the matching willingness factor to isolate the role of regret aversion psychological behavior rather than fairness consideration.
The proposed approach, along with Extended Method I, Extended Method II, and Extended Method III, is applied to the same data trading platform TSM case, with optimal schemes and performance metrics summarized in Table 9, while Figure 4 provides a visual comparison of these methods’ performance metrics from the perspectives of membership degrees. This comprehensive comparison enables a systematic evaluation of how different psychological theories, the integration of matching willingness, and their implementations in the Fermatean fuzzy context impact TSM performance.

Table 9.
Comparison results in different scenarios.
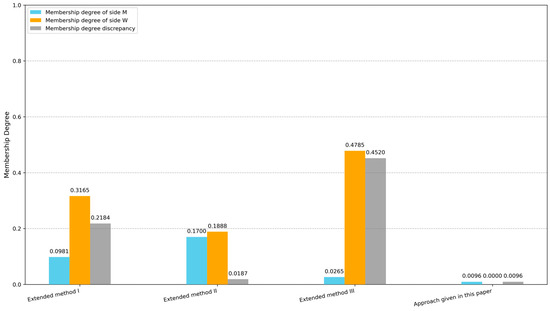
Figure 4.
Comparison of membership degrees and discrepancies across methods.
As illustrated in Table 9, four key insights emerge. Consistent with the membership function definitions in Equations (38) and (39), a membership degree approaching 0 signifies that the objective function value is closer to its maximum, whereas a value approaching 1 indicates a greater deviation from this maximum.
First, regarding the impact of the theoretical basis, Extended Method I, grounded in expected utility theory, fails to reach the single-objective optimal values for either side, with and . Extended Method II, based on prospect theory, yields membership degree function values and , which are not significantly better than those of methods incorporating regret theory. A plausible explanation lies in the fact that prospect theory overly relies on the selection of reference points, thus distorting TSM outcomes to an extent. As shown in Ref. [42], when one agent selects the average value of all evaluations from the other side as the reference evaluation value, if there is strong heterogeneity among the evaluating agents, the average value may fail to reflect the true expectations of individual decision-makers. At this point, the prospect value calculated based on this reference point will deviate from the decision-maker’s true psychological perception, which, in turn, makes it difficult to achieve the satisfaction goals of both sides simultaneously in the TSM process. In contrast, methods incorporating regret theory (Extended Method III and the proposed approach) exhibit superior satisfaction achievement: In Extended Method III, is close to its maximum ( is close to 0), while, in the approach proposed in this paper, achieves the optimal value (), confirming that regret theory better captures the bounded rationality of agents and thus improves satisfaction optimization. Second, the critical role of matching willingness is evident: Extended Method III, which adopts regret theory but disregards matching willingness, suffers from severe satisfaction inequality; its membership degree discrepancy (0.45199) is nearly 47 times that of the proposed approach (0.00957), indicating that neglecting fairness leads to unilaterally optimal outcomes (high but low ). Third, the proposed approach demonstrates superiority in balancing both satisfaction maximization and fairness: reaches the single-objective optimal value, is close to the optimal, and the bilateral membership degree discrepancy is minimized, validating the approach’s ability to avoid unfair matching while maintaining high satisfaction levels. To sum up, compared to expected utility theory and prospect theory, regret theory can capture the preference information of decision-makers relatively accurately and is more consistent with real-world cases. Therefore, the approach proposed in this paper is more feasible and effective in addressing the TSM case on a data trading platform.
Additionally, the matching willingness factor depends on two weights: h and v. h quantifies the weight of joint satisfaction intensity (i.e., ), and v quantifies the weight of satisfaction equity (i.e., ). To isolate the effect of v, a sensitivity analysis of different matching willingness factors is conducted by fixing and varying . The results, presented in Table 10 and visually illustrated in Figure 5, show the evolution of the optimal TSM scheme and overall satisfaction discrepancy with increasing v.

Table 10.
Sensitivity analysis of different matching willingness factors.
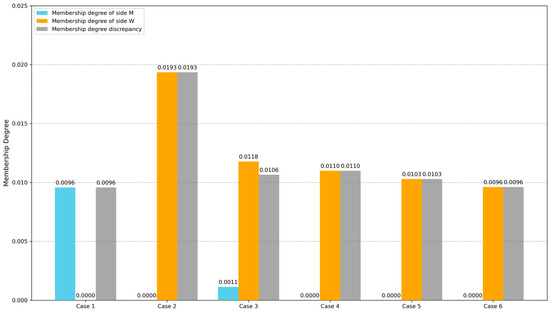
Figure 5.
Comparison of membership degrees and discrepancies across cases of different matching willingness factors.
For the optimal TSM scheme stabilization, as shown in Table 10, a clear pattern emerges with the increase of v: When and , the optimal TSM scheme changes (shifting from pairing to , then to ), but when , the optimal scheme stabilizes as and no longer changes. This indicates that, once v reaches a threshold (here, ), the emphasis on satisfaction equity at the individual pair level is sufficient to lock the optimal matching combination; any further increase in v no longer alters the selection of agent pairs.
However, even after the matching scheme stabilizes, the overall satisfaction discrepancy continues to evolve with v. For the membership degree function value, when , the discrepancy is 0.01065; when , it slightly rises to 0.01099; and when , it falls to 0.01029. When , it further decreases to 0.00960. This phenomenon arises because, even with the same set of matched pairs, a larger v further amplifies the weight of satisfaction equity in the matching willingness factor for each individual pair; this refinement of pair-level fairness adjusts the contribution of each pair to the overall objective functions, thereby leading to subtle changes in the overall satisfaction discrepancy.
Across all sensitivity analysis cases, the overall membership degree discrepancy remains relatively small, confirming that the proposed approach can effectively leverage v to balance pair-level fairness and overall satisfaction. Notably, the stabilization of the matching scheme at ensures solution robustness, while the continuous adjustability of the overall satisfaction discrepancy with further increases in v allows the approach to flexibly adapt to different fairness requirements in real-world TSM scenarios.
Finally, apart from matching willingness factors, weight coefficients and represent the priorities of the agents of each side, which will also affect the TSM results. Therefore, to investigate how the combined variation of agent priority weights ( and matching willingness factors ( influences the optimal TSM scheme and satisfaction discrepancy, a sensitivity analysis of different weight coefficients and matching willingness factors by varying , , and is conducted. The results are presented in Table 11, with visual comparisons provided in Figure 6 and Figure 7.

Table 11.
Sensitivity analysis of different weight coefficients and matching willingness factors.
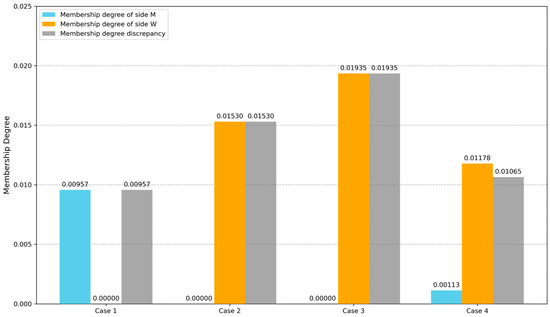
Figure 6.
Comparison of membership degrees and discrepancies across cases of different weight coefficients and matching willingness factors ().
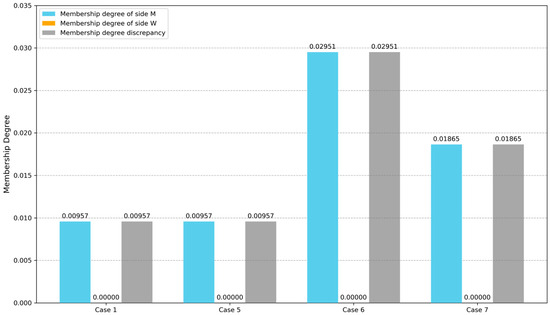
Figure 7.
Comparison of membership degrees and discrepancies across cases of different weight coefficients and matching willingness factors ().
As shown in Case 1, when the weight coefficients of two sides are equal ( and the satisfaction intensity parameter and satisfaction equity parameter in the matching willingness factor are set to the same value (), the optimal TSM scheme converges to . In this scenario, side W achieves the optimal value (), whereas side M fails to reach its single-objective optimum.
Notably, when side M holds a dominant weight coefficient (, the optimal matching scheme shifts, and side M’s satisfaction subsequently attains its single-objective optimal value. However, as the satisfaction equity parameter in the matching willingness factor increases incrementally, the dominant influence of side M’s weighted priority is gradually attenuated until it is fully neutralized. At this point, the resulting TSM scheme and satisfaction distribution become identical to those observed under the condition of equal weight coefficients ( with adjusted matching willingness factors. This evolutionary pattern vividly demonstrates the critical regulatory role of the proposed matching willingness factor in mediating fairness: it can effectively counterbalance the directional bias imposed by asymmetric weight coefficients, thereby enabling a more nuanced and equitable calibration of bilateral satisfaction in TSM scenarios.
Since side W in Case 1 has already attained its single-objective optimal value, further increments in (while reducing ) trigger adjustments in the matching scheme via modifications to the matching willingness factor. Notably, this regulatory mechanism yields a gradual improvement in side M’s satisfaction—evidenced by a declining membership degree—yet preserves side W’s absolute dominance, with its satisfaction remaining consistently at the optimal level (membership degree persisting at 0).
This indicates that the proposed matching willingness factor functions as a precision-tuning instrument in fairness calibration: when the priority gap between the two sides becomes excessively large, the factor can systematically elevate the satisfaction of the disadvantaged side through targeted adjustments to fairness parameters. Such behavior validates that the proposed method possesses a dual capacity to respect predefined priority hierarchies by sustaining the dominant side’s optimal status while mitigating extreme inequities by enhancing the disadvantaged side’s outcomes, thereby offering robust adaptability to real-world TSM scenarios characterized by asymmetric power dynamics.
The three analytical streams—cross-method comparison, sensitivity analysis of the matching willingness factor, and sensitivity analysis of combined weight coefficients and matching willingness factors—conducted on the TSM case of the data trading platform collectively validate the superiority of the proposed approach. By integrating regret theory to capture the bounded rationality of decision-makers and a matching willingness factor to balance satisfaction and fairness, the proposed method outperforms extended versions of the existing frameworks; it circumvents the suboptimal satisfaction outcomes associated with expected utility theory and prospect theory while addressing the severe equity imbalance that arises when regret theory is applied without incorporating fairness regulation. Notably, the satisfaction equity parameter within the matching willingness factor exhibits a threshold effect, which not only stabilizes the optimal TSM scheme once exceeded but also enables incremental refinements to overall fairness; further, this parameter can neutralize biases induced by asymmetric bilateral priorities and mitigate extreme equity gaps by elevating the satisfaction of disadvantaged agents, all without compromising the optimal satisfaction status of dominant agents. For managers of data trading platforms, these findings offer actionable guidance: (1) prioritize the integration of regret theory into TSM algorithms to align with real-world decision-making processes and avoid preference distortion in scenarios involving heterogeneous agent evaluations; (2) deploy the parameters of the matching willingness factor dynamically, leveraging the joint satisfaction intensity parameter to accelerate efficient matching in peak period data transaction scenarios and utilizing the satisfaction equity parameter as a precision “tuner” to mitigate asymmetric bargaining power; (3) preconfigure the satisfaction equity parameter above its identified threshold to ensure stable, equity-oriented matching outcomes. Collectively, these measures enhance the platform’s capacity to balance operational efficiency, bilateral agent satisfaction, and long-term ecosystem fairness in practical data trading contexts.
6. Conclusions
In this paper, a TSM decision-making approach based on the incomplete Fermatean fuzzy preference is proposed. Firstly, leveraging the incomplete Fermatean fuzzy evaluation matrices provided by bilateral agents, the satisfaction matrices are obtained according to regret theory. Furthermore, to address the fairness issue in unilateral optimization, a novel fairness-aware matching willingness factor is designed, which synthesizes both joint satisfaction intensity and satisfaction equity. Finally, a TSM decision-making model is developed, and the optimal TSM scheme is derived by solving the model. Compared to the existing extended TSM methods, the approach proposed in this paper possesses the following advantages: (1) It explicitly addresses TSM decision-making under incomplete Fermatean fuzzy evaluation information, filling the gap in handling high-uncertainty preferences in TSM research. (2) It extends the application of Fermatean fuzzy set theory to the TSM domain. (3) The proposed matching willingness factor calculation method directly targets satisfaction disparity reduction at the individual pair level, effectively avoiding unilaterally optimal outcomes and enhancing the fairness of the final matching scheme. (4) By integrating regret theory into satisfaction calculation, the approach incorporates agents’ regret aversion psychological characteristics, which aligns with the bounded rationality of decision-makers in practical scenarios and improves the realism of the decision model.
Despite these contributions, the limitations of this paper are as follows: (1) The preference information considered is limited to Fermatean fuzzy format, failing to accommodate multi-form heterogeneous preferences that are common in complex TSM scenarios. (2) Satisfaction calculation solely focuses on regret aversion, while other critical psychological characteristics of agents are not incorporated, which may restrict the model’s applicability to scenarios with diverse decision-making psychologies. (3) The current framework is only validated for cases where a complete TSM exists, and no corresponding approach has been developed for incomplete TSM scenarios.
Based on the above limitations, future research can be directed toward three directions: (1) The proposed framework should be extended to establish scenario-specific multi-attribute evaluation index systems for TSM agents and develop mechanisms to handle multi-form heterogeneous preferences. For example, index systems for data trading platforms should reflect data-specific attributes (demand-side: data quality, security, and usability; supply-side: economic benefits, transaction efficiency, and risk control), while those for ride-sharing platforms prioritize time-sensitive metrics (driver-side: service response time, route optimization, and passenger satisfaction; passenger-side: trip urgency, willingness-to-pay, and travel distance tolerance). For heterogeneous preferences (e.g., interval-valued numbers and probabilistic linguistic terms) within these indices, hybrid uncertain information integration mechanisms need to be developed to balance heterogeneous data contributions, thereby expanding the approach’s applicability to complex real-world TSM problems. (2) The model’s psychological foundation should be enriched by incorporating multiple bounded rationality characteristics into the satisfaction calculation. Specifically, regret theory could be integrated with other behavioral economics theories (e.g., prospect theory for loss aversion quantification and disappointment theory for measuring outcome expectation deviation impacts) to construct a holistic psychological utility framework. Supplementary behavioral constructs (e.g., risk attitude, decision-making confidence, and peer effect) may also be introduced to refine preference modeling, enabling the more precise characterization of bounded rational decision-makers’ psychological traits and enhancing the model’s practical relevance across diverse TSM contexts. (3) A generalized TSM decision-making approach applicable to both complete and incomplete TSM scenarios should be developed via two complementary strategies: (1) designing priority-based matching rules for incompatible pairs (constructing comprehensive priority indices via multi-criteria fusion and implementing sequential matching to maximize matched subset utility); (2) building multi-stage optimization models (screening feasible pairs via minimum satisfaction thresholds, optimizing subsets via mathematical programming, and designing supplementary mechanisms for unmatched agents) to balance matching completeness and satisfaction, thus expanding applicability to niche markets and large-scale systems.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/math13203321/s1.
Author Contributions
Conceptualization, C.R. and S.L.; Methodology, C.R. and S.L.; Validation, C.R. and S.L.; Visualization, C.R. and S.L.; Investigation, C.R. and S.L.; Writing—original draft, S.L.; Writing—review and editing, C.R. and S.L.; Project assessment, C.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Guangdong Provincial Philosophy and Social Science Planning Project (No GD23XGL012).
Data Availability Statement
The original contributions presented in this study are included in the Supplementary Materials. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xiang, N.; Dou, Y.J.; Xia, B.Y.; Yang, K.W.; Tan, Y.J. High-end equipment: An improved two-sided based S&M matching and a novel Pareto refining method considering consistency. Expert Syst. Appl. 2022, 202, 117175. [Google Scholar] [CrossRef]
- Cherchye, L.; Demuynck, T.; De Rock, B.; Vermeulen, F. Household consumption when the marriage is stable. Am. Econ. Review. 2017, 107, 1507–1534. [Google Scholar] [CrossRef]
- Gale, D.; Shapley, L.S. College admissions and the stability of marriage. Am. Math. Mon. 1962, 69, 9–15. [Google Scholar] [CrossRef]
- Sim, K.M.; Chan, R. A brokering protocol for agent-based e-commerce. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2000, 30, 474–484. [Google Scholar] [CrossRef]
- Shadkam, E.; Parvizi, M.; Rajabi, R. The study of multi-objective supplier selection problem by a novel hybrid method: COA/ε-constraint. Int. J. Res. Ind. Eng. 2021, 10, 223–237. [Google Scholar] [CrossRef]
- Pais, J. Random matching in the college admissions problem. Econ. Theory 2008, 35, 99–116. [Google Scholar] [CrossRef]
- Chakraborty, A.; Citanna, A.; Ostrovsky, M. Two-sided matching with interdependent values. J. Econ. Theory 2010, 145, 85–105. [Google Scholar] [CrossRef]
- Da Silva, I.R.; Gomes, J.A. Residency training: The role of neurocritical care in resident education. Neurology 2013, 80, e51–e53. [Google Scholar] [CrossRef]
- Ma, J.P. The singleton core in the college admissions problem and its application to the national resident matching program (NRMP). Games Econ. Behav. 2010, 69, 150–164. [Google Scholar] [CrossRef]
- Liang, D.C.; Zhang, Y.R.; Cao, W. q-Rung orthopair fuzzy Choquet integral aggregation and its application in heterogeneous multicriteria two-sided matching decision making. Int. J. Intell. Syst. 2019, 34, 3275–3301. [Google Scholar] [CrossRef]
- Wan, S.P.; Li, D.F. Decision-making method for multi-attribute two-sided matching problem between venture capitalists and investment enterprises with different kinds of information. Chin. J. Manag. Sci. 2014, 22, 40–47. [Google Scholar] [CrossRef]
- Li, X.Y.; Xiong, L.; Sun, W.C.; Wang, K. A fuzzy decision-making method with hybrid multi-attribute for two-sided matching of supply and demand in data trading. Sci. Technol. Prog. Policy 2018, 35, 23–30. [Google Scholar]
- Sühr, T.; Biega, A.J.; Zehlike, M.; Gummadi, K.P.; Chakraborty, A. Two-sided fairness for repeated matchings in two-sided markets: A case study of a ride-hailing platform. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD ‘19), New York, NY, USA, 4–8 August 2019. [Google Scholar] [CrossRef]
- Wang, S.Y.; Li, S.Q.; He, H.N.; Zhou, Q. Flexible supply-demand matching mechanism for C2B crowdsourcing logistics platforms with heterogeneous environment-inclined merchants. Ann. Oper. Res. 2024, 1–25. [Google Scholar] [CrossRef]
- Deng, Z.B.; Yuan, T.; Yue, Q.; Liu, X.H. One-to-many two-sided matching decision of logistics O2O platform considering the intermediary benefit. Knowl. Inf. Syst. 2025, 67, 689–725. [Google Scholar] [CrossRef]
- Miao, Y.M.; Du, R.; Li, J.; Christopher Westland, J. A two-sided matching model in the context of B2B export cross-border e-commerce. Electron. Commer. Res. 2019, 19, 841–861. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Z.W.; Zhang, W.Y. Research on guidance strategies for retired soldiers’ self-employment based on probabilistic hesitant fuzzy two-sided matching. Chin. J. Manag. Sci. 2023, 1–16. [Google Scholar] [CrossRef]
- He, Y.H.; Sinha, S.; Sun, X.T. Identification and estimation in many-to-one two-sided matching without transfers. Econometrica 2024, 92, 749–774. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Z.; Huang, Q.; Xia, W. Order allocation problem in many-to-many supply chain considering interdependence and capacity constraints. Control Decis. 2020, 35, 686–694. [Google Scholar] [CrossRef]
- Juárez, N.; Neme, P.; Oviedo, J. Lattice structure of the random stable set in many-to-many matching markets. Games Econ. Behav. 2022, 132, 255–273. [Google Scholar] [CrossRef]
- Yue, Q. Research on Decision Methods for the Satisfied Two-Sided Matching Based on Preference Ordinal Information. Ph.D. Thesis, Northeast University, Shenyang, China, 2011. [Google Scholar]
- Liang, H.M.; Jiang, Y.P.; Kong, D.C. Decision-making method on multiple targets of satisfied and stable two-sided matching considering the preference ordering. Syst. Eng.—Theory Pract. 2015, 35, 1535–1546. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers, and decision making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Senapati, T.; Yager, R.R. Fermatean fuzzy weighted averaging/geometric operators and its application in multi-criteria decision-making methods. Eng. Appl. Artif. Intell. 2019, 85, 112–121. [Google Scholar] [CrossRef]
- Cuong, B.C.; Kreinovich, V. Picture fuzzy sets—A new concept for computational intelligence problems. In Proceedings of the 2013 Third World Congress on Information and Communication Technologies (WICT 2013), Hanoi, Vietnam, 15–18 December 2013. [Google Scholar]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2016, 25, 1222–1230. [Google Scholar] [CrossRef]
- Kahraman, C.; Oztaysi, B.; Otay, I.; Onar, S.C. Extensions of Ordinary Fuzzy Sets: A Comparative Literature Review. In Intelligent and Fuzzy Techniques: Smart and Innovative Solutions (INFUS 2020), 1st ed.; Kahraman, C., Cevik Onar, S., Oztaysi, B., Sari, I., Cebi, S., Tolga, A., Eds.; Springer: Cham, Switzerland, 2021; Volume 1197. [Google Scholar]
- Yu, D.J.; Xu, Z.S. Intuitionistic fuzzy two-sided matching model and its application to personnel-position matching problems. J. Oper. Res. Soc. 2019, 71, 312–321. [Google Scholar] [CrossRef]
- Liang, Z.C.; Yang, Y.; Liao, S.G. Interval-valued intuitionistic fuzzy two-sided matching model considering level of automation. Appl. Soft Comput. 2022, 116, 108252. [Google Scholar] [CrossRef]
- Yue, Q.; Deng, Z.B. Two-sided stable matching decision-making method considering matching intention under a hesitant fuzzy environment. CMES-Comput. Model. Eng. Sci. 2022, 135, 1603–1623. [Google Scholar] [CrossRef]
- Hu, W.; Yue, Q. Two-sided matching decision method based on TODIM in the Pythagorean fuzzy environment. Oper. Res. Manag. Sci. 2024, 33, 35–40. [Google Scholar]
- Gul, M.; Lo, H.W.; Yucesan, M. Fermatean fuzzy TOPSIS-based approach for occupational risk assessment in manufacturing. Complex Intell. Syst. 2021, 7, 2635–2653. [Google Scholar] [CrossRef]
- Akram, M.; Shah, S.M.U.; Al-Shamiri, M.M.A.; Edalatpanah, S.A. Extended DEA method for solving multi-objective transportation problem with Fermatean fuzzy sets. AIMS Math. 2023, 8, 924–961. [Google Scholar] [CrossRef]
- Ali, W.; Khalid, M.; Khan, N.A.; Javaid, S. Integrating Fermatean fuzzy and neutrosophic goal programming for multi-objective healthcare optimization under uncertainty. Life Cycle Reliab. Saf. Eng. 2025, 1–21. [Google Scholar] [CrossRef]
- Qin, H.; Peng, Q.; Ma, X.; Zhan, J. A new multi-attribute decision making approach based on new score function and hybrid weighted score measure in interval-valued Fermatean fuzzy environment. Complex Intell. Syst. 2023, 9, 5359–5376. [Google Scholar] [CrossRef] [PubMed]
- Ruan, C.Y.; Yan, L.; Zeng, S.Z. Multi-attribute decision-making with extended VlseKriterijuska Optimizacija I Komoromisno Resenje method based on generalized Fermatean probabilistic hesitant fuzzy distance measure and cross-entropy. Eng. Appl. Artif. Intell. 2025, 159, 111684. [Google Scholar] [CrossRef]
- Yue, Q.; Ren, J.L.; Hu, B.; Tao, Y. Fermatean fuzzy multi-attribute personnel-position matching group decision-making with unknown weight information. Expert Syst. Appl. 2024, 237, 121451. [Google Scholar] [CrossRef]
- Yue, Q.; Zhai, K.L.; Hu, B.; Tao, Y. Two-stage multi-attribute reviewer-paper matching decision-making in a Fermatean fuzzy environment. Complex Intell. Syst. 2025, 11, 305. [Google Scholar] [CrossRef]
- Jia, X.; Wang, X.F.; Wang, Y.M.; Zhou, L. A two-sided matching decision-making approach based on prospect theory under the probabilistic linguistic environment. Soft Comput. 2022, 26, 3921–3938. [Google Scholar] [CrossRef]
- Wang, N.N.; Li, P. A new multi-granularity probabilistic linguistic two-sided matching method considering peer effect and its application in pension services. Int. J. Mach. Learn. Cybern. 2022, 13, 1907–1926. [Google Scholar] [CrossRef]
- Zhang, X.J.; Yang, Y.; Wang, J. Workload balance-based dynamic two-sided matching decision-making approach for cloud manufacturing tasks and services under uncertain preferences. Kybernetes 2022, 52, 5087–5118. [Google Scholar] [CrossRef]
- Han, J.; Li, B.; Liang, H.M.; Lai, K.K. A novel two-sided matching decision method for technological knowledge supplier and demander considering the network collaboration effect. Soft Comput. 2018, 22, 5439–5451. [Google Scholar] [CrossRef]
- Delorme, M.; García, S.; Gondzio, J.; Kalcsics, J.; Manlove, D.; Pettersson, W. Mathematical models for stable matching problems with ties and incomplete lists. Eur. J. Oper. Res. 2019, 277, 426–441. [Google Scholar] [CrossRef]
- Aird, A.; Farastu, P.; Sun, J.; Stefancová, E.; All, C.; Voida, A.; Mattei, N.; Burke, R. Dynamic fairness-aware recommendation through multi-agent social choice. ACM Trans. Recomm. Syst. 2025, 3, 21. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Xu, H.Y.; Chen, K.B.; Zhao, Y.X.; Liu, Z. Channel mode selection for an e-platform supply chain in the presence of a secondary marketplace. Eur. J. Oper. Res. 2023, 305, 1215–1235. [Google Scholar] [CrossRef]
- Gui, Y.M.; Tan, D.B.; Liu, Z.; Dong, F. Worry not rareness but disparity: Impact of fairness concerns on platforms’ pricing and matching decision in competitive two-sided markets. Expert Syst. Appl. 2024, 238, 121683. [Google Scholar] [CrossRef]
- Zhang, D.; Gong, Z.W.; Yan, S.L.; Chen, Z. Satisfied and fair two-sided matching method considering dual-reference with linguistic preference. Eng. Appl. Artif. Intell. 2024, 133, 108600. [Google Scholar] [CrossRef]
- Liu, L.Z.; Tao, Y.; Yue, Q. A hesitant fuzzy bilateral matching behavior decision-making method based on the satisfaction and fairness considering risk attitudes. J. Syst. Sci. Math. Sci. 2024, 44, 2013–2030. [Google Scholar] [CrossRef]
- Liu, X.; Yue, Q.; Hu, B.; Tao, Y. Graduate students and supervisors matching decision-making considering stability-based fairness based on TOPSIS and grey correlation degrees. Sci. Rep. 2025, 15, 22902. [Google Scholar] [CrossRef]
- Tozlu, B.; Akgunduz, A.; Zeng, Y. Unbiased criteria identification for two-sided matching: An environment-based design approach. Expert Syst. Appl. 2025, 277, 127233. [Google Scholar] [CrossRef]
- Ruan, C.Y.; Gong, S.C.; Chen, X.J. Multi-criteria group decision-making with extended ELECTRE III method and regret theory based on probabilistic interval-valued intuitionistic hesitant fuzzy information. Complex Intell. Syst. 2025, 11, 92. [Google Scholar] [CrossRef]
- Wang, L.; Sun, J.Q.; Gao, X.Y. Two-sided matching decision method with Pythagorean fuzzy and multi criteria considering agents’ psychological behavior. Fuzzy Syst. Math. 2022, 36, 100–111. Available online: https://link.cnki.net/urlid/43.1179.O1.20220921.0916.020 (accessed on 13 October 2025).
- Fan, Z.P.; Li, M.Y.; Zhang, X. Satisfied two-sided matching: A method considering elation and disappointment of agents. Soft Comput. 2018, 22, 7227–7241. [Google Scholar] [CrossRef]
- Chen, L.T.; Chen, S.Q. Volunteer multi-person multi-task optimization dispatch method considering two-sided matching. Soft Comput. 2022, 26, 3837–3861. [Google Scholar] [CrossRef]
- Zhang, D.; Dai, H.J.; Liu, X.R. Intuitionistic fuzzy two-sided matching method considering regret aversion and matching aspiration. Oper. Res. Manag. Sci. 2020, 29, 132–139. [Google Scholar]
- Li, P.; Wang, N.N.; Wei, C.P.; Zhang, N. A two-sided matching method considering the lowest value of acceptability with regret theory for probabilistic linguistic term sets. Int. J. Mach. Learn. Cybern. 2021, 12, 917–930. [Google Scholar] [CrossRef]
- Huang, R.L.; Wang, X.K.; Hou, W.H.; Chen, Z.Y.; Wang, Y.T.; Wang, J.Q. Two-way referral cooperative hospital selection with uncertain information: A two-sided matching decision-making approach. Comput. Ind. Eng. 2023, 183, 109430. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, Y.J.; Zhang, X.Y.; Xu, C. Online doctor-patient dynamic stable matching model based on regret theory under incomplete information. Socio-Econ. Plan. Sci. 2023, 87, 101615. [Google Scholar] [CrossRef]
- Chen, S.Q.; Zhang, L.; Shi, H.L.; Wang, Y.M. A two-sided matching model for assigning volunteer teams to relief tasks in the absence of sufficient information. Knowl.-Based Syst. 2021, 232, 107495. [Google Scholar] [CrossRef]
- Zhou, Y.Y.; Zheng, C.L.; Goh, M. Statistics-based approach for large-scale group decision-making under incomplete Pythagorean fuzzy information with risk attitude. Knowl.-Based Syst. 2022, 235, 107654. [Google Scholar] [CrossRef]
- Liu, W.Q.; Wu, Y.Z.; Chen, X.; Chiclana, F. Managing heterogeneous preferences and multiple consensus behaviors with self-confidence in large-scale group decision making. Inf. Fusion 2024, 107, 102289. [Google Scholar] [CrossRef]
- Han, T.J.; Lu, J.F.; Zhang, H. Two-sided matching model of service providers and demanders considering peer and synergy effects. Heliyon 2023, 9, e14732. [Google Scholar] [CrossRef]
- Liu, W.Q.; Wang, Y.M.; Lan, Y.X. intuitionistic fuzzy multi-attribute decision-making method based on evidential reasoning under incomplete information. Stat. Decis. 2018, 34, 42–45. [Google Scholar] [CrossRef]
- Zhang, Z.; Kou, X.Y.; Palomares, I.; Yu, W.Y.; Gao, J.L. Stable two-sided matching decision making with incomplete fuzzy preference relations: A disappointment theory based approach. Appl. Soft Comput. 2019, 84, 105730. [Google Scholar] [CrossRef]
- Zhao, P.C.; Yue, Q.; Hu, W. A two-sided matching decision method based on incomplete intuitionistic fuzzy information. J. Syst. Sci. Math. 2025, 45, 297–310. [Google Scholar] [CrossRef]
- Khan, M.S.; Abdullah, S.; Lui, P.D. Gray method for multiple attribute decision making with incomplete weight information under the Pythagorean fuzzy setting. J. Intell. Syst. 2020, 29, 858–876. [Google Scholar] [CrossRef]
- Ullah, W.; Ibrar, M.; Khan, A.; Khan, M. Multiple attribute decision making problem using GRA method with incomplete weight information based on picture hesitant fuzzy setting. Int. J. Intell. Syst. 2020, 36, 866–889. [Google Scholar] [CrossRef]
- Zhao, P.C.; Yue, Q.; Deng, Z.B. Two-sided matching decision making with multi-attribute probabilistic hesitant fuzzy sets. Intell. Autom. Soft Comput. 2023, 37, 849–873. [Google Scholar] [CrossRef]
- Senapati, T.; Yager, R.R. Fermatean fuzzy sets. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 663–674. [Google Scholar] [CrossRef]
- Bell, D.E. Regret in decision making under uncertainty. Oper. Res. 1982, 30, 961–981. [Google Scholar] [CrossRef]
- Loomes, G.; Sugden, R. Regret theory: An alternative theory of rational choice under uncertainty. Econ. J. 1982, 92, 805–824. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Akram, M.; Shahzadi, G.; Ahmadini, A.A. Decision-making framework for an effective sanitizer to reduce COVID-19 under Fermatean fuzzy environment. J. Math. 2020, 2020, 3263407. [Google Scholar] [CrossRef]
- Zhang, S.T.; Zhu, J.J.; Liu, X.D.; Chen, Y. Regret theory-based group decision-making with multidimensional preference and incomplete weight information. Inf. Fusion 2016, 31, 1–13. [Google Scholar] [CrossRef]
- Cohon, J.L. Multi Objective Programming and Planning; Academic Press: New York, NY, USA, 1978. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).