Black–Litterman Portfolio Optimization with Dynamic CAPM via ABC-MCMC
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Dynamic CAPM Model
2.3. ABC-MCMC Algorithm
| Algorithm 1 ABC-MCMC with initial validation and attempt limit for dynamic CAPM with Extreme |
| 1: Set , , counter , |
| 2: repeat |
| 3: Define |
| 4: Simulate |
| 5: |
| 6: counter |
| 7: until or counter = max_attempts |
| 8: if counter = max_attempts and then |
| 9: Terminate: asset rejected after max attempts |
| 10: else |
| 11: for to do |
| 12: Generate |
| 13: Simulate |
| 14: if then |
| 15: |
| 16: else |
| 17: |
| 18: end if |
| 19: end for |
| 20: end if |
| 21: return |
2.4. Black–Litterman Portfolio
3. Results
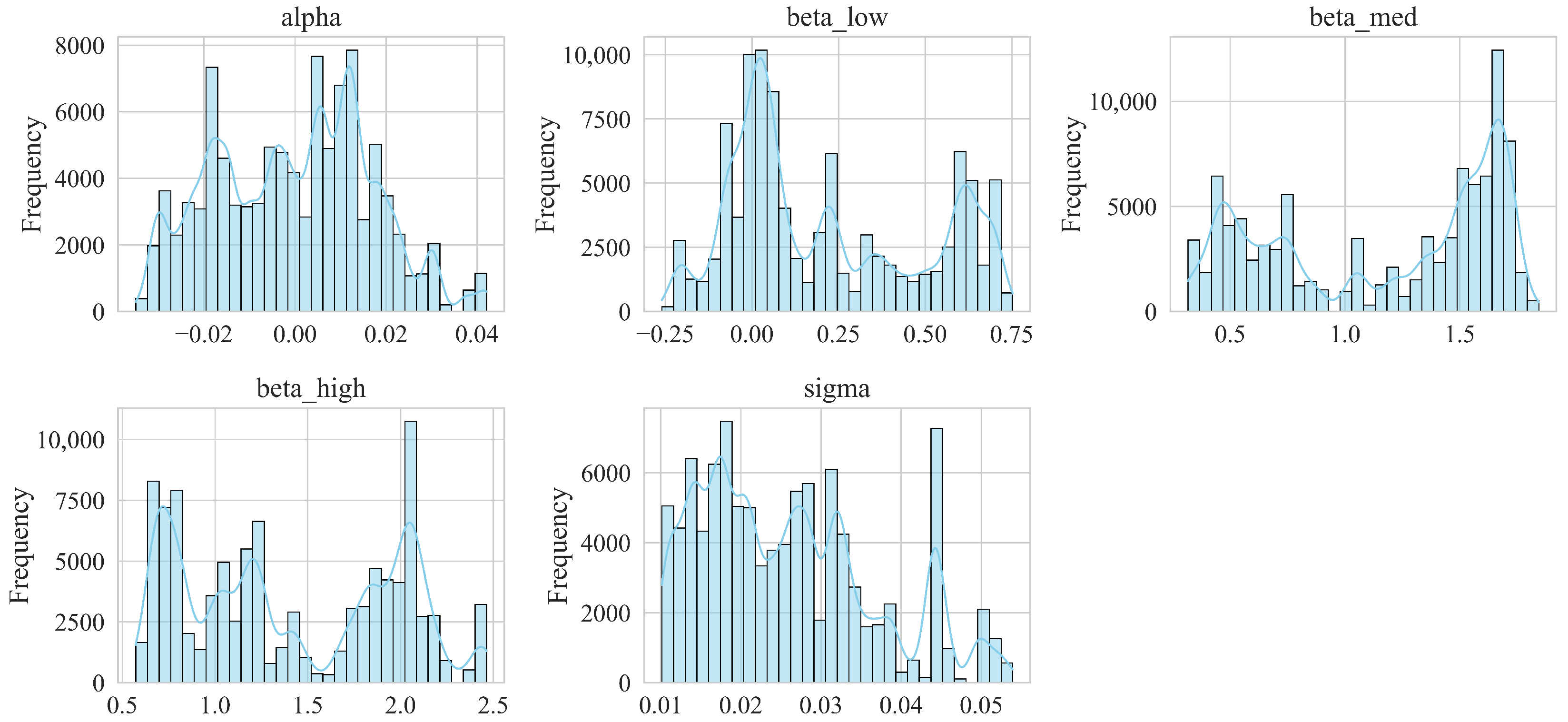
3.1. Estimation of Dynamic CAPM Parameters
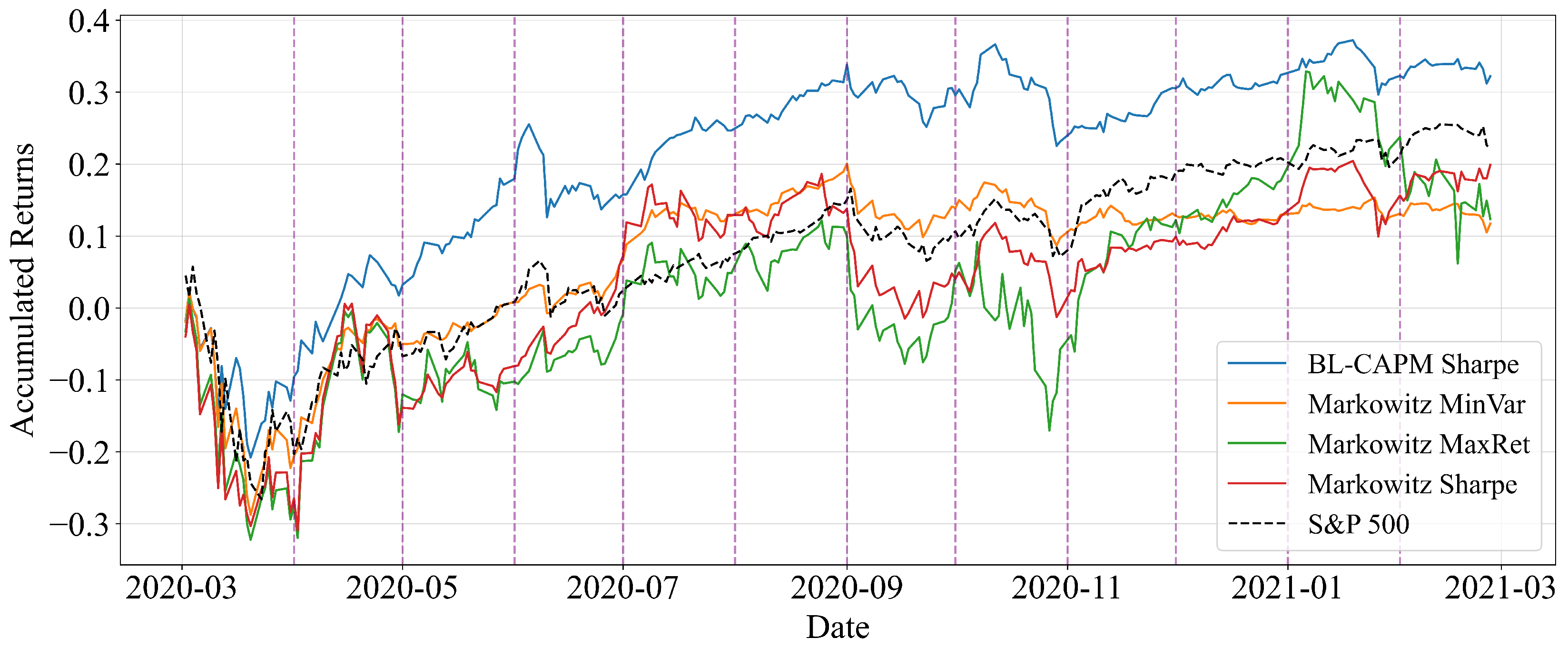
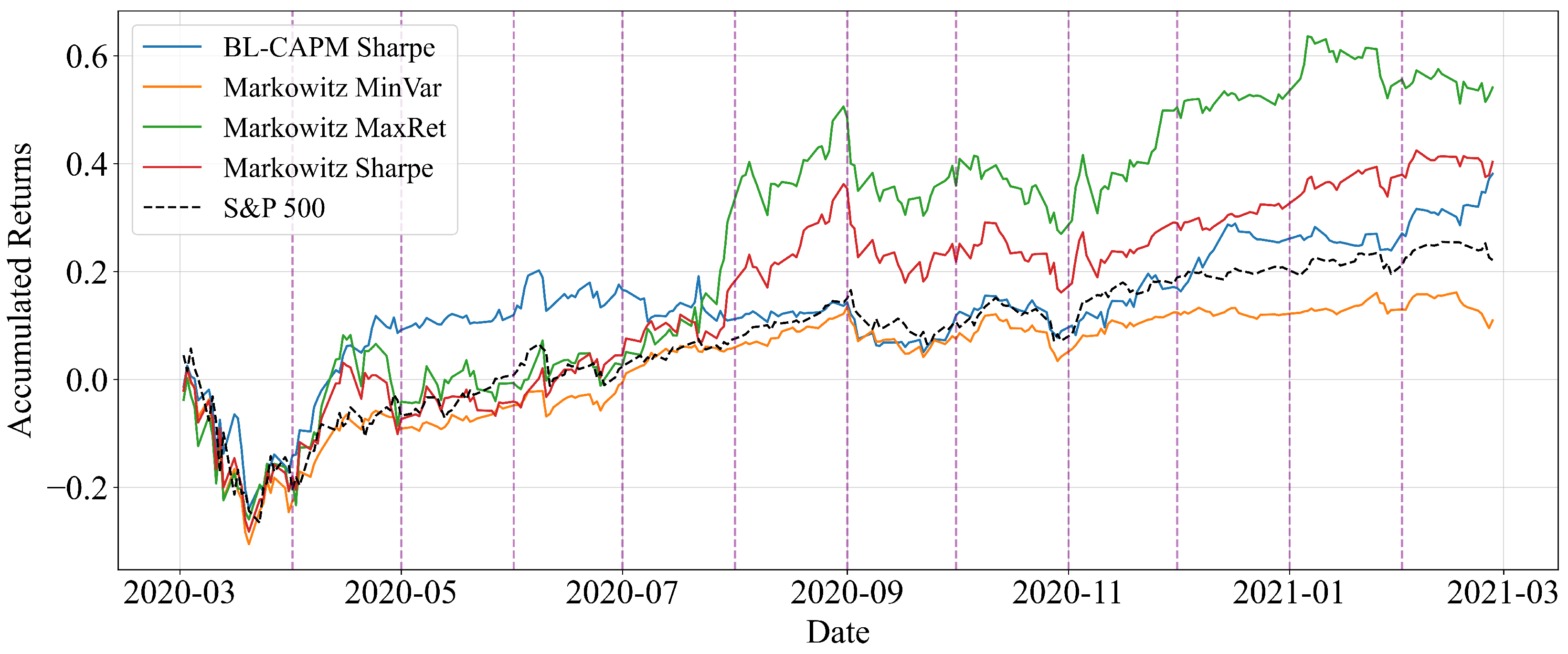
3.2. Performance During the Crisis Period (2020)
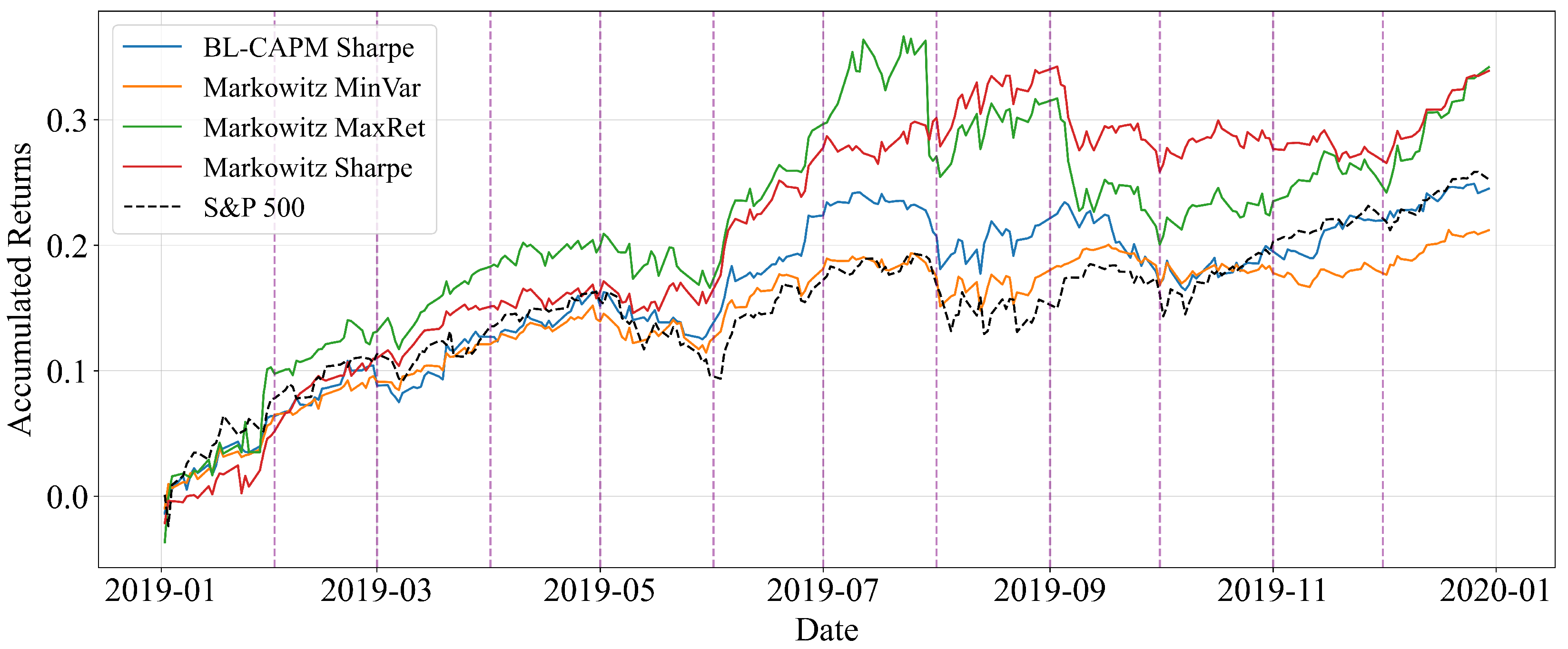
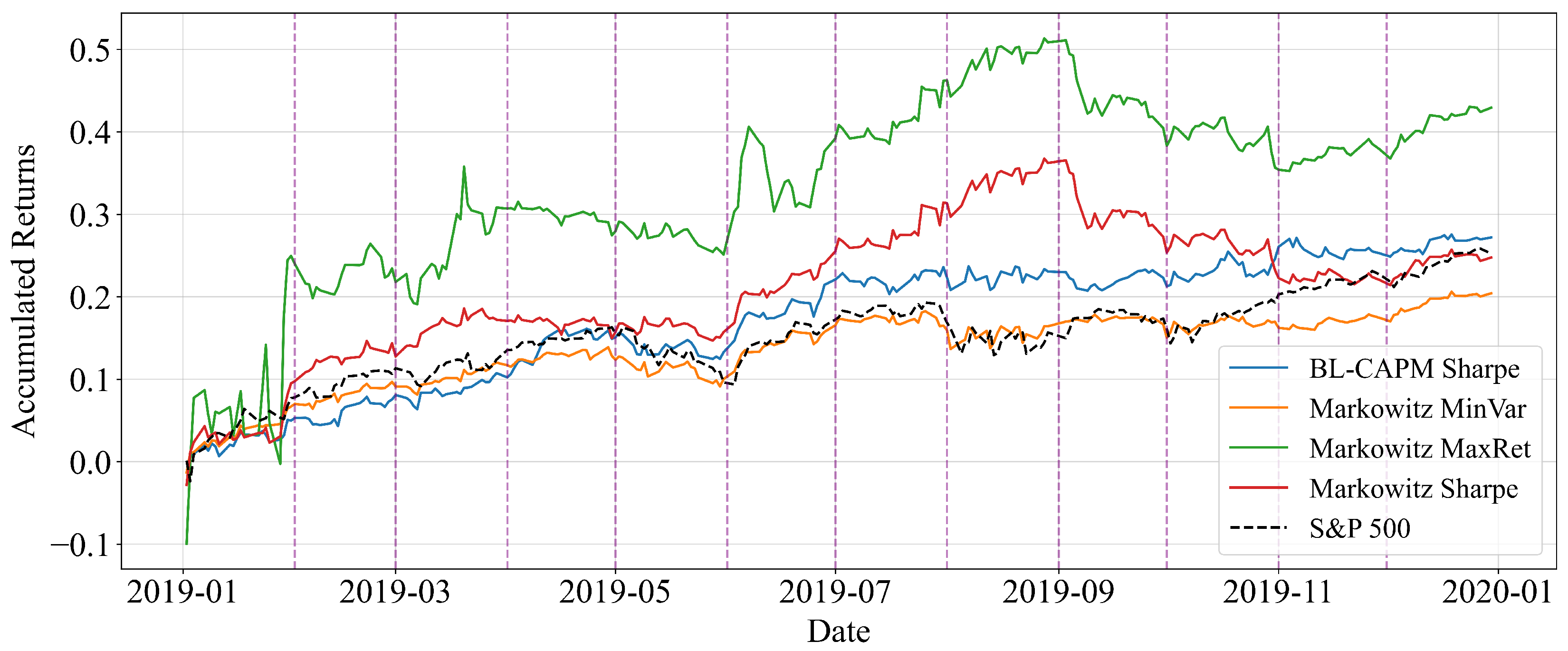
3.3. Performance During the Normal Growth Period (2019)
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Loayza, N.V.; Raddatz, C. The structural determinants of external vulnerability. World Bank Econ. Rev. 2007, 21, 359–387. [Google Scholar] [CrossRef]
- Black, F.; Litterman, R. Asset allocation: Combining investor views with market equilibrium. Goldman Sachs Fixed Income Res. 1990, 115, 7–18. [Google Scholar] [CrossRef]
- Black, F.; Litterman, R. Global portfolio optimization. Financ. Anal. J. 1992, 48, 28–43. [Google Scholar] [CrossRef]
- Gevorgyan, R.; Hovhannisyan, R. Text-mining approach with Black–Litterman model: A case study of Armenian pension funds. Invest. Anal. J. 2025, 1–10. [Google Scholar] [CrossRef]
- Deng, X.; Zhou, W.; Cao, Q. Portfolio with Copula-GARCH and Black-Litterman Model Using a Novel View Error Matrix. Comput. Econ. 2024, 66, 3197–3227. [Google Scholar] [CrossRef]
- Gao, J.; Wang, J.; Zhou, Y.; Lv, M.; Wei, D. Enhancing investment performance of Black-Litterman model with AI hybrid system: Can it be done? Expert Syst. Appl. 2024, 244, 122924. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, Y.; De, G. A novel black-litterman model with time-varying covariance for optimal asset allocation of pension funds. Mathematics 2023, 11, 1476. [Google Scholar] [CrossRef]
- Jisma, M.; Mohan, V.; Thomas, M.S. Risk-return optimised energy asset allocation in transmission-distribution system using tangency portfolio and Black–Litterman model. IET Energy Syst. Integr. 2023, 5, 290–306. [Google Scholar]
- Fuhrer, A.; Hock, T. Uncertainty in the Black–Litterman model: Empirical estimation of the equilibrium. J. Empir. Financ. 2023, 72, 251–275. [Google Scholar] [CrossRef]
- Yao, H.; Li, X.; Li, L. Asset allocation based on LSTM and the Black–Litterman model. Appl. Econ. Lett. 2024, 31, 1686–1691. [Google Scholar] [CrossRef]
- Ko, H.; Byun, J.; Lee, J. A privacy-preserving robo-advisory system with the Black-Litterman portfolio model: A new framework and insights into investor behavior. J. Int. Financ. Mark. Inst. Money 2023, 89, 101873. [Google Scholar] [CrossRef]
- Ko, H.; Son, B.; Lee, J. A novel integration of the Fama–French and Black–Litterman models to enhance portfolio management. J. Int. Financ. Mark. Inst. Money 2024, 91, 101949. [Google Scholar] [CrossRef]
- Yuan, J.; Jin, L.; Lan, F. A BL-MF fusion model for portfolio optimization: Incorporating the Black-Litterman solution into multi-factor model. Financ. Res. Lett. 2025, 80, 107464. [Google Scholar] [CrossRef]
- Han, Y.; Li, J. The impact of global economic policy uncertainty on portfolio optimization: A Black–Litterman approach. Int. Rev. Financ. Anal. 2023, 86, 102476. [Google Scholar] [CrossRef]
- Cho, P.; Lee, M. Dynamic Black–Litterman Portfolios Incorporating Asymmetric Fractal Uncertainty. Fractal Fract. 2024, 8, 642. [Google Scholar] [CrossRef]
- Stoilov, T.; Stoilova, K.; Vladimirov, M. Decision support for portfolio management by information system with black–litterman model. Int. J. Inf. Technol. Decis. Mak. 2022, 21, 643–664. [Google Scholar] [CrossRef]
- Unni, A.C.; Ongsakul, W.; Madhu, N. Fuzzy incorporated Black–Litterman model for renewable energy portfolio optimization. Electr. Eng. 2022, 104, 4279–4288. [Google Scholar] [CrossRef]
- Gómez, Y.A.F.; Trujillo, J.F.M.; Quimbayo, C.A.Z. Optimal Portfolio Selection Using the Black-Litterman Model with Fuzzy Views. Lect. Econ. 2022, 369–393. [Google Scholar] [CrossRef]
- Kara, M.; Ulucan, A.; Atici, K.B. A hybrid approach for generating investor views in Black–Litterman model. Expert Syst. Appl. 2019, 128, 256–270. [Google Scholar] [CrossRef]
- Bessler, W.; Opfer, H.; Wolff, D. Multi-asset portfolio optimization and out-of-sample performance: An evaluation of Black–Litterman, mean-variance, and naïve diversification approaches. Eur. J. Financ. 2017, 23, 1–30. [Google Scholar] [CrossRef]
- Kolm, P.; Ritter, G. On the bayesian interpretation of black–litterman. Eur. J. Oper. Res. 2017, 258, 564–572. [Google Scholar] [CrossRef]
- Tang, M.L.; Wu, F.Y.; Hung, M.C. Multi-asset allocation of exchange traded funds: Application of Black–Litterman model. Invest. Anal. J. 2021, 50, 273–293. [Google Scholar] [CrossRef]
- Palczewski, A.; Palczewski, J. Black–Litterman model for continuous distributions. Eur. J. Oper. Res. 2019, 273, 708–720. [Google Scholar] [CrossRef]
- Teplova, T.; Evgeniia, M.; Munir, Q.; Pivnitskaya, N. Black-Litterman model with copula-based views in mean-CVaR portfolio optimization framework with weight constraints. Econ. Change Restruct. 2023, 56, 515–535. [Google Scholar] [CrossRef]
- Pang, T.; Karan, C. A closed-form solution of the Black–Litterman model with conditional value at risk. Oper. Res. Lett. 2018, 46, 103–108. [Google Scholar] [CrossRef]
- Hasler, M.; Martineau, C. Explaining the Failure of the Unconditional CAPM with the Conditional CAPM. Manag. Sci. 2023, 69, 1835–1855. [Google Scholar] [CrossRef]
- Barua, R.; Sharma, A.K. Dynamic Black Litterman portfolios with views derived via CNN-BiLSTM predictions. Financ. Res. Lett. 2022, 49, 103111. [Google Scholar] [CrossRef]
- Su, X.; Lu, K.; Yen, J. Objective Black-Litterman views through deep learning: A novel hybrid model for enhanced portfolio returns. Expert Syst. Appl. 2025, 295, 128868. [Google Scholar] [CrossRef]
- Min, L.; Lin, D.; Wang, J.; Wang, B. Black-Litterman Portfolio Optimization Using Gaussian Mixture Model. Eng. Lett. 2025, 33, 1020. [Google Scholar]
- Li, C.; Chen, Y.; Yang, X.; Wang, Z.; Lu, Z.; Chi, X. Intelligent black–Litterman portfolio optimization using a decomposition-based multi-objective DIRECT algorithm. Appl. Sci. 2022, 12, 7089. [Google Scholar] [CrossRef]
- Ko, H.; Lee, J. Portfolio management transformed: An enhanced black–litterman approach integrating asset pricing theory and machine learning. Comput. Econ. 2025, 1–47. [Google Scholar] [CrossRef] [PubMed]
- Rubilar-Torrealba, R.; Chahuán-Jiménez, K.; de la Fuente-Mella, H. A stochastic analysis of the effect of trading parameters on the stability of the financial markets using a Bayesian approach. Mathematics 2023, 11, 2527. [Google Scholar] [CrossRef]
- Beaumont, M.A. Approximate bayesian computation. Annu. Rev. Stat. Its Appl. 2019, 6, 379–403. [Google Scholar] [CrossRef]
- Bernardo, R.C.; Grandón, D.; Said, J.L.; Cárdenas, V.H. Dark energy by natural evolution: Constraining dark energy using Approximate Bayesian Computation. Phys. Dark Universe 2023, 40, 101213. [Google Scholar] [CrossRef]
- Jin, H.; Du, W.; Yin, G. Approximate Bayesian computation design for phase I clinical trials. Stat. Methods Med. Res. 2022, 31, 2310–2322. [Google Scholar] [CrossRef] [PubMed]
- Chernikova, A.; Gozzi, N.; Perra, N.; Boboila, S.; Eliassi-Rad, T.; Oprea, A. Modeling self-propagating malware with epidemiological models. Appl. Netw. Sci. 2023, 8, 52. [Google Scholar] [CrossRef]
- Prangle, D. Lazy abc. Stat. Comput. 2016, 26, 171–185. [Google Scholar] [CrossRef]
- Breloer, B.; Lea Hühn, H.; Scholz, H. Jensen alpha and market climate. J. Asset Manag. 2016, 17, 195–214. [Google Scholar] [CrossRef]
- Jegadeesh, N.; Titman, S. Returns to Buying Winners and Selling Losers: Implications for Stock Market Efficiency. J. Financ. 1993, 48, 65–91. [Google Scholar] [CrossRef]
- Basu, D.; Stremme, A. CAPM and time-varying beta: The cross-section of expected returns. WBS Financ. Group Res. Pap. 2007. [Google Scholar] [CrossRef]
- Martin, G.M.; Frazier, D.T.; Maneesoonthorn, W.; Loaiza-Maya, R.; Huber, F.; Koop, G.; Maheu, J.; Nibbering, D.; Panagiotelis, A. Bayesian forecasting in economics and finance: A modern review. Int. J. Forecast. 2024, 40, 811–839. [Google Scholar] [CrossRef]
| Stock Symbol | Mean | Standard Deviation | Minimum | Maximum | Median |
|---|---|---|---|---|---|
| AAPL | 0.002218 | 0.015738 | −0.067602 | 0.032480 | 0.002749 |
| ABT | −0.000758 | 0.011996 | −0.042236 | 0.026701 | 0.000635 |
| JPM | 0.000562 | 0.012875 | −0.045670 | 0.029696 | 0.001151 |
| AES | 0.000826 | 0.014534 | −0.089151 | 0.028106 | 0.002338 |
| ALB | 0.002363 | 0.025202 | −0.088151 | 0.112723 | 0.001763 |
| MSFT | 0.001351 | 0.013946 | −0.073064 | 0.032387 | 0.001547 |
| AMD | 0.002975 | 0.024816 | −0.081295 | 0.076079 | 0.003701 |
| INTC | 0.001357 | 0.018183 | −0.066183 | 0.078194 | 0.000901 |
| HP | 0.000123 | 0.028573 | −0.073070 | 0.133893 | −0.000012 |
| XOM | −0.002096 | 0.014998 | −0.062064 | 0.044995 | −0.003482 |
| AZO | −0.000523 | 0.013298 | −0.045135 | 0.066995 | −0.000299 |
| AEE | 0.000296 | 0.009537 | −0.043657 | 0.022874 | 0.001318 |
| ALL | 0.000298 | 0.011180 | −0.051507 | 0.038595 | 0.002224 |
| MO | −0.000360 | 0.013485 | −0.046613 | 0.031875 | 0.001447 |
| AMGN | −0.000241 | 0.013087 | −0.052830 | 0.044657 | 0.000513 |
| MMM | −0.000505 | 0.015186 | −0.058925 | 0.042288 | −0.000650 |
| ANSS | 0.001283 | 0.016672 | −0.101343 | 0.030970 | 0.002670 |
| KO | −0.000112 | 0.009639 | −0.047463 | 0.031935 | 0.000928 |
| APA | 0.001317 | 0.041801 | −0.131225 | 0.237394 | 0.000032 |
| ADM | 0.000044 | 0.014057 | −0.058088 | 0.047394 | 0.000844 |
| AMZN | 0.000474 | 0.013820 | −0.049333 | 0.071196 | −0.000001 |
| T | 0.000280 | 0.011557 | −0.042000 | 0.041916 | 0.001024 |
| ADSK | 0.002339 | 0.017196 | −0.053983 | 0.055084 | 0.002362 |
| ATO | −0.000446 | 0.009728 | −0.044606 | 0.019619 | 0.000857 |
| AVY | 0.000001 | 0.015289 | −0.049899 | 0.063071 | 0.000000 |
| BALL | −0.001030 | 0.016855 | −0.055457 | 0.038048 | −0.001103 |
| COF | 0.000216 | 0.014184 | −0.057183 | 0.043749 | 0.000313 |
| CCL | −0.002037 | 0.023545 | −0.099011 | 0.073541 | 0.000000 |
| EBAY | −0.001150 | 0.017682 | −0.095770 | 0.084172 | −0.000564 |
| EFX | −0.000220 | 0.013696 | −0.055630 | 0.048876 | 0.000732 |
| IBM | −0.000148 | 0.013956 | −0.056823 | 0.049636 | 0.000140 |
| IRM | −0.000073 | 0.014304 | −0.057603 | 0.048206 | 0.001699 |
| JNJ | 0.000483 | 0.011178 | −0.064220 | 0.029938 | 0.000554 |
| JBL | 0.000892 | 0.019031 | −0.064404 | 0.075607 | 0.002168 |
| MCD | −0.000831 | 0.011236 | −0.051732 | 0.021926 | 0.000757 |
| DUK | 0.000074 | 0.009627 | −0.040742 | 0.031816 | 0.001318 |
| CTSH | −0.000010 | 0.014324 | −0.044586 | 0.094652 | 0.000240 |
| MSI | −0.000649 | 0.013980 | −0.051605 | 0.025364 | 0.001546 |
| CAG | −0.000375 | 0.022386 | −0.063458 | 0.147292 | 0.003026 |
| NKE | 0.000496 | 0.012751 | −0.044257 | 0.040794 | 0.000774 |
| PEP | −0.000170 | 0.009059 | −0.040314 | 0.029354 | 0.000295 |
| PFE | −0.000339 | 0.011342 | −0.051608 | 0.024640 | −0.001153 |
| DRI | −0.001615 | 0.015872 | −0.074733 | 0.033646 | −0.000043 |
| SBUX | −0.001599 | 0.012291 | −0.041304 | 0.027182 | −0.000512 |
| DE | 0.000153 | 0.015394 | −0.043917 | 0.067613 | 0.001396 |
| DTE | −0.001080 | 0.011089 | −0.055382 | 0.020766 | 0.001069 |
| WMT | −0.000442 | 0.008317 | −0.030156 | 0.015781 | 0.000377 |
| IPG | 0.000759 | 0.014699 | −0.053149 | 0.071770 | 0.002373 |
| XEL | −0.000138 | 0.010737 | −0.052565 | 0.024137 | 0.001630 |
| K | −0.000235 | 0.012483 | −0.088901 | 0.029212 | 0.001190 |
| S&P 500 | 0.000076 | 0.008544 | −0.045168 | 0.014869 | 0.000851 |
| Stock Symbol | BL-CAPM Sharpe | M. Max. Ret. | M. Min. Var. | M. Sharpe |
|---|---|---|---|---|
| EBAY | 100.0 | 0.0 | 18.44 | 0.00 |
| JNJ | 0.0 | 0.0 | 2.39 | 0.00 |
| K | 0.0 | 0.0 | 20.11 | 0.00 |
| KO | 0.0 | 0.0 | 2.02 | 0.00 |
| MCD | 0.0 | 0.0 | 2.72 | 0.00 |
| MMM | 0.0 | 0.0 | 4.25 | 0.00 |
| MO | 0.0 | 0.0 | 6.81 | 0.00 |
| PFE | 0.0 | 0.0 | 3.84 | 0.00 |
| WMT | 0.0 | 0.0 | 17.13 | 0.00 |
| AMZN | 0.0 | 0.0 | 22.29 | 73.96 |
| AMD | 0.0 | 100.0 | 0.00 | 26.04 |
| Stock Symbol | BL-CAPM Sharpe | M. Max. Ret. | M. Min. Var. | M. Sharpe |
|---|---|---|---|---|
| CAG | 49.2090 | 0.0000 | 2.9251 | 0.0000 |
| PFE | 33.2722 | 0.0000 | 1.2868 | 0.0000 |
| EBAY | 12.4321 | 0.0000 | 7.5622 | 7.6751 |
| SBUX | 2.6087 | 0.0000 | 0.0000 | 0.0000 |
| JBL | 2.4780 | 0.0000 | 0.0000 | 0.0000 |
| JNJ | 0.0000 | 0.0000 | 14.6766 | 0.0000 |
| K | 0.0000 | 0.0000 | 9.6348 | 0.0000 |
| MCD | 0.0000 | 0.0000 | 11.8623 | 0.0000 |
| EFX | 0.0000 | 0.0000 | 0.9029 | 0.0000 |
| NKE | 0.0000 | 0.0000 | 2.9119 | 10.4413 |
| PEP | 0.0000 | 0.0000 | 7.7470 | 0.0000 |
| T | 0.0000 | 0.0000 | 7.0734 | 0.0000 |
| XEL | 0.0000 | 0.0000 | 5.9676 | 0.0000 |
| AAPL | 0.0000 | 12.1778 | 0.0000 | 13.6823 |
| ABT | 0.0000 | 0.0000 | 0.5883 | 0.0000 |
| DUK | 0.0000 | 0.0000 | 6.1859 | 0.0000 |
| AEE | 0.0000 | 0.0000 | 3.3459 | 0.0000 |
| AES | 0.0000 | 21.2125 | 0.0000 | 4.9679 |
| ALB | 0.0000 | 31.4082 | 0.0000 | 0.0000 |
| AMD | 0.0000 | 0.0000 | 0.0000 | 4.4502 |
| AMGN | 0.0000 | 0.0000 | 5.4146 | 0.0000 |
| AMZN | 0.0000 | 0.0000 | 0.5418 | 0.0000 |
| AZO | 0.0000 | 0.0000 | 11.3731 | 0.0000 |
| BALL | 0.0000 | 0.0000 | 0.0000 | 22.8586 |
| DE | 0.0000 | 35.2015 | 0.0000 | 35.9245 |
| Train | and | and | and | |||
|---|---|---|---|---|---|---|
| Ret. | Vol. | Ret. | Vol. | Ret. | Vol. | |
| 1 year | 0.097507 | 0.091357 | 0.381154 | 0.069608 | 0.322843 | 0.067030 |
| 6 months | 0.386132 | 0.065647 | 0.322014 | 0.064647 | −0.021657 | 0.083106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flández, S.; Rubilar-Torrealba, R.; Chahuán-Jiménez, K.; de la Fuente-Mella, H.; Elórtegui-Gómez, C. Black–Litterman Portfolio Optimization with Dynamic CAPM via ABC-MCMC. Mathematics 2025, 13, 3265. https://doi.org/10.3390/math13203265
Flández S, Rubilar-Torrealba R, Chahuán-Jiménez K, de la Fuente-Mella H, Elórtegui-Gómez C. Black–Litterman Portfolio Optimization with Dynamic CAPM via ABC-MCMC. Mathematics. 2025; 13(20):3265. https://doi.org/10.3390/math13203265
Chicago/Turabian StyleFlández, Sebastián, Rolando Rubilar-Torrealba, Karime Chahuán-Jiménez, Hanns de la Fuente-Mella, and Claudio Elórtegui-Gómez. 2025. "Black–Litterman Portfolio Optimization with Dynamic CAPM via ABC-MCMC" Mathematics 13, no. 20: 3265. https://doi.org/10.3390/math13203265
APA StyleFlández, S., Rubilar-Torrealba, R., Chahuán-Jiménez, K., de la Fuente-Mella, H., & Elórtegui-Gómez, C. (2025). Black–Litterman Portfolio Optimization with Dynamic CAPM via ABC-MCMC. Mathematics, 13(20), 3265. https://doi.org/10.3390/math13203265







