Deep-Reinforcement-Learning-Based Sliding Mode Control for Optimized Energy Management in DC Microgrids

Abstract

A hybrid control architecture is proposed for enhancing the stability and energy management of DC microgrids (DCMGs) integrating photovoltaic generation, batteries, and supercapacitors. The approach combines nonlinear Sliding Mode Control (SMC) for fast and robust DC bus voltage regulation with a Deep Q-Learning (DQL) agent that learns optimal high-level policies for charging, discharging, and load management. This dual-layer design leverages the real-time precision of SMC and the adaptive decision-making capability of DQL to achieve dynamic power sharing and balanced state-of-charge levels across storage units, thereby reducing asymmetric wear. Simulation results under variable operating scenarios showed that the proposed method significantly improvedvoltage stability, loweredthe occurrence of deep battery discharges, and decreased load shedding compared to conventional fuzzy-logic-based energymanagement, highlighting its effectiveness and resilience in the presence of renewable generation variability and fluctuating load demands.

1. Introduction

The increasing global demand for reliable and sustainable energy solutions, particularly in remote and off-grid locations, has driven substantial progress in decentralized power systems. Among these, DCMGs have emerged as a highly promising technology due to their inherent capability to integrate various renewable energy sources, such as PV panels, alongside energy storage devices including batteries and supercapacitors [1,2,3,4]. The natural ability of DCMGs to maintain balanced power sharing among their components not only enhances overall energy efficiency but also significantly improves system reliability. This intrinsic balance simplifies control strategies and ensures steady operation, even when the microgrid operates autonomously from the main utility grid, which is crucial for isolated applications [1,2].

However, maintaining consistent power flow symmetry within DCMGs remains a complex challenge. The intermittent nature of renewable generation combined with fluctuating load demands introduces uncertainties that necessitate sophisticated control mechanisms. Conventional controllers, such as PI regulators, are widely used for their simplicity and ease of implementation. Yet, these controllers often require meticulous parameter tuning and may fall short in maintaining stable power distribution during sudden load changes or highly dynamic operating conditions [5].

To address these limitations, FLSs have been applied due to their ability to manage nonlinearities and uncertainties by employing heuristic rules that approximate human reasoning. Despite their adaptability, FLS-based controllers may struggle to sustain optimal energy balance when faced with rapid and complex variations in microgrid conditions [6]. SMC techniques offer robust performance and are effective in handling system uncertainties and disturbances; however, fully ensuring energy symmetry and stability in DC microgrids using SMC alone remains an active research area.

Previous research proposed a hierarchical energy management framework that synergistically combines nonlinear SMC with fuzzy logic control to stabilize DCMGs composed of PV arrays, batteries, and supercapacitors [7]. This hybrid approach demonstrated enhanced dynamic stability and improved energy sharing compared to traditional linear control methods. Nonetheless, the fuzzy logic component exhibited certain limitations in coping with highly variable operating scenarios.

In light of these challenges, AI techniques—particularly RL—have attracted considerable interest in the context of energy management. RL empowers agents to learn optimal control policies through continuous interaction with their environment, making it well-suited for systems characterized by uncertainty and nonlinearity [8,9,10]. Among these methods, DQL stands out by combining Q-learning with deep neural networks, enabling efficient handling of large state-action spaces and improving adaptability in complex microgrid operations [11]. Recent research further supports this trend: Wang et al. [12] explored advanced deep reinforcement learning methods for complex decision-making tasks; Liu et al. [13] investigated intelligent optimization algorithms that promote adaptive, data-driven control; Kim et al. [14] examined adaptive control methods in smart energy systems; and Tanaka et al. [15] analyzed hybrid control architectures designed for power electronics and distributed energy systems.

While the concept of multi-agent systems is discussed here to position this work within the broader research landscape and to highlight potential future extensions toward distributed and coordinated control [16], the framework implemented and validated in this study is strictly single-agent. All results and analyses correspond to a single-agent DQL controller working alongside nonlinear SMC to enhance decision-making performance and robustness, without any multi-agent systems based experimental validation.

More recently, Zhang et al. (2025) presented an intelligent energy management framework for DC microgrids that combines sliding mode control with fuzzy logic, closely aligning with the approach we build upon and reinforcing the scientific foundation of integrating SMC and FLS techniques [17]. Furthermore, the comprehensive review by Chen et al. (2024) offers an insightful analysis of DC microgrid architectures and practical applications, enriching the context of recent advances in this rapidly evolving field [18].

Building upon these foundational studies [7,13], this paper introduces an enhanced energy management system that incorporates a DQL strategy to optimize real-time operations of energy storage units, including charging, discharging, and load shedding. The objective is to maintain DC bus voltage stability, extend the lifespan of storage components, and improve the overall efficiency of the microgrid under dynamically changing conditions.

The main contributions of this study can be summarized as follows:

–

We propose a two-layer control framework in which an SMC layer ensures fast and robust DC bus voltage regulation under disturbances, while a DQL layer performs high-level decision making for energy storage coordination and load management. Unlike most state-of-the-art hybrid DRL-classical control strategies that rely on linear PI/PID controllers, our use of nonlinear SMC enhances robustness against modeling uncertainties and sudden operating condition changes in DC microgrids.

–

The proposed DQL agent simultaneously optimizes the operation of both batteries and supercapacitors, balancing SOC levels to reduce asymmetric degradation. This unified approach contrasts with prior works that often manage storage devices independently or use static rule-based allocation.

–

Simulation results under rapidly varying solar irradiance and load profiles show significant improvements over a fuzzy logic controller baseline: approximately 60%reduction in voltage fluctuations, 42% fewer deep battery discharge events, and 35%reduction in load shedding.

–

The DQL architecture and training parameters were selected to achieve strong decision-making capabilities while maintaining computational lightness, making the proposed strategy suitable for real-time deployment in embedded microgrid controllers.

The remainder of this paper is organized as follows: Section 2 describes the detailed model of the DC microgrid and its constituent components; Section 3 discusses the design and stability analysis of nonlinear sliding mode controllers; Section 4 highlights the limitations of the existing fuzzy-logic-based strategy and presents the proposed single-agent DQL method; Section 5 details the simulation setup and training process, followed by a comparative discussion of results; and Section 6 concludes the study and outlines directions for future research.

2. Modelling of the DC Microgrid

This part lays out the structural configuration and mathematical formulation of the DC microgrid. It sets the groundwork necessary for the subsequent development of control strategies.

The considered DC microgrid consists of key renewable and storage components interconnected to supply local loads. It includes PV panels as the primary renewable energy source, supported by batteries and supercapacitors that store excess energy and release it when needed. These components are connected through DC/DC converters, allowing efficient energy exchange and ensuring that power can flow smoothly between generation, storage, and demand. This architecture is designed to maintain continuous operation, even under varying weather conditions and fluctuating consumption patterns typical of isolated microgrids. Each component is connected to a common DC bus via dedicated converters, allowing precise regulation of energy exchange according to system requirements.

2.1. Microgrid Structure

The configuration of the DCMG includes a photovoltaic generator connected to the DC bus via a boost converter, which allows for optimal power extraction through a MPPT technique; a battery storage unit interfaced with a bidirectional buck-boost converter, enabling both charging and discharging based on the grid’s requirements; a supercapacitor bank managed by a reversible power converter for rapid energy injection or absorption during transients, helping to maintain voltage stability during transients; and a variable load represented by a resistive load bank to emulate varying operational scenarios and dynamic demands. All DC-DC converters are governed by closed-loop control systems to regulate specific voltage or current setpoints, ensuring stable and efficient operation of the microgrid.

2.2. Dynamic Modelling

To characterize the behavior of the DCMG subsystems, the averaged models of the converters are employed, assuming ideal components (neglecting switching losses).

2.2.1. Photovoltaic Subsystem

The dynamic equations for the PV generator and its boost converter are given by

$$\left\{\begin{array}{l}{L}_{pv}{\displaystyle \frac{d{I}_{pv}}{dt}} = v_{pv}- \left(1-d_{pv}\right) v_{DC}\\ C_{pv}{\displaystyle \frac{d{v}_{pv}}{dt}} = I_{pv} - I_{pv, gen} \end{array}\right.$$

(1)

• v_pv and I_pv are the output voltage and current of the PV panel;
• d_pv is the duty cycle applied to the boost converter;
• v_DC is the DC bus voltage;
• L_pv and C_pv are the inductance and capacitance of the boost converter;
• I_pv,_gen represents the current generated by the PV source.

2.2.2. Battery Subsystem

A bidirectional buck-boost converterregulatesbattery interfacing:

$$\left\{\begin{array}{l}{L}_b{\displaystyle \frac{d{I}_b}{dt}} = V_b- \left(1-d_b\right) v_{DC}\\ C_b{\displaystyle \frac{d{v}_b}{dt}} = I_b - I_{b, bat} \end{array}\right.$$

(2)

• v_b and I_b denote the voltage and current at the battery terminals;
• d_b is the converter duty cycle;
• L_b and C_b are the inductance and capacitance of the battery-side converter;
• I_b,bat corresponds to the battery charge/discharge current.

2.2.3. Supercapacitor Subsystem

The dynamic behavior of the supercapacitor connected through a bidirectional converter is governed by

$$\left\{\begin{array}{l}{L}_{SC}{\displaystyle \frac{d{I}_{SC}}{dt}} = v_{SC}- \left(1-d_{SC}\right) v_{DC}\\ C_{SC}{\displaystyle \frac{d{v}_{SC}}{dt}} = I_{SC} \end{array}\right.$$

(3)

• v_sc and I_sc represent the supercapacitor voltage and current;
• d_sc is the associated converter duty cycle;
• L_sc and C_sc are the inductance and capacitance values corresponding to the supercapacitor branch.

2.2.4. DC Bus Voltage Dynamics

The evolution of the DC bus voltage, considering the cumulative contribution of all sources and loads, is described by

$$C_{DC}{\displaystyle \frac{d{V}_{DC}}{dt}}= \left(1-d_{pv}\right) I_{pv} + \left(1-d_b\right) I_b + \left(1-d_{SC}\right) I_{SC} - I_{Load}$$

(4)

where C_Dc is the total capacitance of the DC bus, and I_Load denotes the total current drawn by the connected load elements.

In all the above models, the duty cycles d_pv, d_b, and d_sc serve as the main control inputs.

The DCMG is connected through a unidirectional line representing the combined output of all photovoltaic sources, as well as through two bidirectional lines that account for the total load demand and storage components. The model can be illustrated as follows:

$$\left\{\begin{array}{l}{L}_{pv}{\displaystyle \frac{d{I}_{pv}}{dt}} = V_{pv}- \left(1-d_{pv}\right) v_{DC}\\ C_{pv}{\displaystyle \frac{d{v}_{pv}}{dt}} = I_{pv} - I_{pv, gen}\\ L_b{\displaystyle \frac{d{I}_b}{dt}} = v_b- \left(1-d_b\right) v_{DC}\\ C_b{\displaystyle \frac{d{v}_b}{dt}} = I_b - I_{b, bat} \\ L_{SC}{\displaystyle \frac{d{I}_{SC}}{dt}} = v_{SC}- \left(1-d_{SC}\right) v_{DC}\\ C_{SC}{\displaystyle \frac{d{v}_{SC}}{dt}} = I_{SC}\\ C_{DC}{\displaystyle \frac{d{v}_{DC}}{dt}}= \left(1-d_{pv}\right) I_{pv} + \left(1-d_b\right) I_b + \left(1-d_{SC}\right) I_{SC} - I_{Load} \end{array}\right.$$

(5)

Their modulation allows dynamic regulation of energy exchange, which will be optimized by the advanced control strategies and intelligent energy management approaches developed in the following sections.

Remarks

Although averaged models are used in this study to represent the converters and energy storage systems, the nonlinear SMC layer remains effective thanks to its inherent robustness properties. SMC is designed to force the system states to converge to apredefined sliding surface regardless of certain modeling uncertainties and unmodeled nonlinearities. As a result, even when high-frequency switching behavior and detailed nonlinear converter dynamics are simplified in the averaged model, the SMC layer can still achieve reliable voltage regulation and fast transient response.

We acknowledge, however, that averaged models do not fully capture all nonlinear and switching phenomena present in real hardware. Future work will include detailed switching models and hardware-in-the-loop testing to evaluate the controller’s performance under more realistic nonlinear conditions and confirm its robustness in practice.

The mathematical models presented here form the essential basis for the design of the sliding mode controllers described in the following section.

3. Nonlinear Sliding Mode Control

Using the models introduced previously, this section formulates nonlinear control laws based on sliding mode theory, aimed at ensuring voltage regulation and energy flow control at the converter level.

We introduce the SMC layer by explaining its selection for robust and fast stabilization of the DC bus voltage. The section presents each controller in the context of the system’s dynamic challenges, showing how they contribute to maintaining power balance and voltage stability. The explanation is kept concise and concludes by linking this control layer to the higher-level AI-based decision-making system. Each controller is developed based on the dynamic models described previously, aiming to track predefined reference values that optimize the operation of the corresponding component.

To achieve stable and balanced power flow despite these fluctuations, the system integrates a robust nonlinear SMC layer for real-time voltage regulation. Complementing this, an AI-based decision-making layer using DQL learns to optimize higher-level strategies such as charging, discharging, and load shedding. Together, these layers improve dynamic performance by adapting to rapid changes in renewable generation and load demand, while aiming to maintain voltage stability, reduce stress on storage components, and enhance overall energy efficiency.

3.1. SMC Design for the PV Generator

The objective of the PV subsystem control is to ensure that the photovoltaic panel operates at its MPP. The desired reference current $I_{pv}^{ref}$ is obtained through MPPT algorithm. The control task is to force the inductor current I_pv to track $I_{pv}^{ref}$.

The sliding surface for the PV subsystem is defined as $S_{pv} = I_{pv} -I_{pv}^{ref}$.

The control law is designed to satisfy the sliding condition:

$${\dot{S}}_{pv} = -k_{pv} sign\left(S_{pv}\right)$$

(6)

where $k_{pv}$ is a positive gain selected to ensure rapid convergence.

Differentiating the sliding surface and substituting the PV dynamic model,

$${\dot{S}}_{pv} = {\displaystyle \frac{d{I}_{pv}}{dt}}-{\displaystyle \frac{d{I}_{pv}^{ref}}{dt}}= {\displaystyle \frac{1}{L_{pv}}}\left(v_{pv}-\left(1-d_{pv}\right)V{v}_{DC}\right)-{\displaystyle \frac{d{I}_{pv}^{ref}}{dt}}$$

(7)

The equivalent control and switching terms are derived to compute the appropriate duty cycle $d_{pv}$:

$$d_{pv} = 1- {\displaystyle \frac{1}{v_{DC}}}\left(v_{pv} - L_{pv}\left({\dot{I}}_{pv}^{ref}-k_{pv}sign\left(S_{pv}\right)\right)\right)$$

(8)

3.2. SMC for the Battery Storage Unit

For the battery, the control objective is to regulate the battery current I_b according to a reference current $I_b^{ref}$, determined by the energy management strategy.

The sliding surface for the battery is

$$S_b = I_b -I_b^{ref}$$

(9)

The dynamics of the surface are

$${\dot{S}}_b = {\displaystyle \frac{d{I}_b}{dt}}-{\displaystyle \frac{d{I}_b^{ref}}{dt}}= {\displaystyle \frac{1}{L_b}}\left(v_{pv}-\left(1-d_b\right)v_{DC}\right)-{\displaystyle \frac{d{I}_b^{ref}}{dt}}$$

(10)

The SMC law enforces

$${\dot{S}}_b = -k_{pv} sign\left(S_b\right)$$

(11)

where k_b > 0 is the control gain ensuring finite-time convergence.

Solving for the duty cycle:

$$d_b = 1- {\displaystyle \frac{1}{v_{DC}}}\left(V_b - L_b\left({\dot{I}}_b^{ref}-k_{b}sign\left(S_b\right)\right)\right)$$

(12)

3.3. SMC for the Supercapacitor Module

The supercapacitor controller is responsible for absorbing or injecting power to counteract rapid load variations, thereby stabilizing the DC bus voltage.

The supercapacitor sliding surface is defined as

$$S_{SC} = I_{SC} -I_{SC}^{ref}$$

(13)

Similarly, the dynamic equation for S_sc becomes

$${\dot{S}}_{SC} = {\displaystyle \frac{d{I}_{SC}}{dt}}-{\displaystyle \frac{d{I}_{SC}^{ref}}{dt}}= {\displaystyle \frac{1}{L_{SC}}}\left(v_{SC}-\left(1-d_{SC}\right)v_{DC}\right)-{\displaystyle \frac{d{I}_{SC}^{ref}}{dt}}$$

(14)

The SMC condition to be satisfied is

$${\dot{S}}_{SC} = -k_{SC} sign\left(S_{SC}\right)$$

(15)

with k_sc as a strictly positive control gain.

Solving for the duty cycle:

$$d_{SC} = 1- {\displaystyle \frac{1}{v_{DC}}}\left(v_{SC} - L_{SC}\left({\dot{I}}_{SC}^{ref}-k_{SC}sign\left(S_{SC}\right)\right)\right)$$

(16)

3.4. Interconnected System Stability Analysis

The sliding mode controllers presented in Section 3.1, Section 3.2 and Section 3.3 are designed to guarantee finite-time convergence of the respective controlled currents, namely, the PV generator current states I_pv, the battery current I_b, and the supercapacitor current I_sc towards their reference values. While the stability of each individual subsystem has been analyzed independently, the physical interconnection through the common DC bus voltage $v_{DC}$ introduces strong coupling between them.

Therefore, an extended stability analysis is required, in which the DC bus voltage regulation objective $v_{DC} \to v_{DC}^{ref}$ is explicitly included in the Lyapunov stability framework.

According to the DC microgrid model presented in Equation (4), the evolution of the DC bus voltage is directly influenced by the interplay between the source currents, the duty cycles applied to the converters, and the load current.

The reference generation mechanism is designed such that the sum of the source currents satisfies the power balance required to regulate the DC bus voltage around $v_{DC}^{ref}$, even in the presence of load variations and source intermittency.

The tracking errors for the current loops, already defined in Section 3.1, Section 3.2 and Section 3.3, are

$$\left\{\begin{array}{l}{S}_{pv} = I_{pv} -I_{pv}^{ref}\\ S_b = I_b -I_b^{ref}\\ S_{SC} = I_{SC} -I_{SC}^{ref}\end{array}\right.$$

(17)

To explicitly incorporate the voltage regulation objective, an additional sliding surface is introduced for the DC bus voltage:

$$S_{DC} =v_{DC} - v_{DC}^{ref}$$

(18)

The error $S_{DC}$ is intrinsically linked to the current tracking errors via the coupling relation (4). Any deviation in one of the current loops directly affects the DC bus voltage, which justifies its integration into the global stability analysis.

To assess the stability of the interconnected system, a composite Lyapunov candidate function is proposed:

$$\begin{array}{l}V\left(t\right) = V_{pv}\left(t\right) + V_b\left(t\right) + V_{sc}\left(t\right) + V_{bus}\left(t\right)\\ ={\displaystyle \frac{1}{2}} \left(S_{pv}^2\left(t\right) + S_b^2\left(t\right) +S_{SC}^2\left(t\right) + \alpha S_{DC}^2\left(t\right)\right)\end{array}$$

(19)

The positive scalar $\alpha > 0$ acts as a weighting coefficient to balance the contribution of the bus voltage error relative to the current tracking errors. The function V(t) is positive definite and vanishes only when all tracking errors are zero, i.e., when $\left\{S_{pv}\left(t\right)=S_b\left(t\right)=S_{SC}\left(t\right)= S_{DC}\left(t\right) =0\right\}$.

The time derivative of V(t) is obtained as

$$\dot{V}\left(t\right) = {\dot{V}}_{pv}\left(t\right) + {\dot{V}}_b\left(t\right) + {\dot{V}}_{sc}\left(t\right) + {\dot{V}}_{bus}\left(t\right)$$

(20)

Using the sliding mode control laws applied to each subsystem,

$$\left\{\begin{array}{l}{\dot{S}}_{pv}\left(t\right)= -k_{pv}sign\left(S_{pv}\left(t\right)\right)\\ {\dot{S}}_b\left(t\right)= -k_{b}sign\left(S_b\left(t\right)\right)\\ {\dot{S}}_{sc}\left(t\right)= -k_{sc}sign\left(S_{sc}\left(t\right)\right)\end{array}\right.$$

(21)

and substituting the DC bus dynamics from (4) into the derivative of $S_{DC}$, we obtain

$${\dot{S}}_{DC} = {\displaystyle \frac{1}{C_{DC}}}\left( \left(1-d_{pv}\right) I_{pv} + \left(1-d_b\right) I_b + \left(1-d_{SC}\right) I_{SC} - I_{Load}\right) - {\dot{v}}_{DC}^{ref}$$

(22)

Replacing (21)and (22) into (20) yields

$$\dot{V}\left(t\right) =-k_{pv}\left|S_{pv}\left(t\right)\right| -k_b\left|S_b\left(t\right)\right| -k_{SC}\left|S_{SC}\left(t\right)\right| -\alpha k_{DC}\left|S_{DC}\left(t\right)\right| \le 0$$

(23)

This inequality ensures that V(t) is non-increasing and that all sliding surfaces converge to zero in finite time. Consequently,

$$\left\{\begin{array}{l}{I}_{pv} \to I_{pv}^{ref}\\ I_b \to I_b^{ref}\\ I_{SC} \to I_{SC}^{ref}\\ v_{DC} \to v_{DC}^{ref}\end{array}\right.$$

(24)

By embedding the DC bus voltage error S_DC into the composite Lyapunov function, the stability proof captures the coupling effects inherent to the DC microgrid. This approach not only confirms that each subsystem achieves its local tracking objective but also ensures that the overall system maintains global asymptotic stability. The interconnection analysis highlights the coordinated role of all converters in simultaneously regulating the bus voltage and tracking the current references, even under dynamic operating conditions such as load steps or source variations.

This unified analysis reinforces the effectiveness and robustness of the proposed control strategy, confirming that even in a multi-component architecture, individual convergence leads to stable global behavior.

Remarks on the Chattering Phenomenon

Although SMC offers strong robustness properties, its reliance on a discontinuous sign function often induces chattering, characterized by unwanted high-frequency oscillations near the sliding manifold. These oscillations can negatively affect actuator durability and reduce the overall smoothness of system operation, especially in real-world applications.

In the proposed control scheme, chattering is attenuated by substituting the sign function with a smooth saturation function, noted as sat(S/φ), where φ sets the thickness of the boundary layer. This technique maintains the robustness of SMC while yielding more continuous and practical control actions.

While methods such as higher-order sliding mode control (HOSM) are known to further reduce chattering, they are not applied in this study. Instead, we adopted a first-order SMC structure in conjunction with saturation smoothing, which demonstrated excellent performance in terms of stability and response quality, as validated by the simulation outcomes.

While this control layer ensures real-time stabilization, a higher-level decision mechanism is required to coordinate energy usage efficiently. The next section addresses this with an intelligent learning-based approach.

4. AI-Based Autonomous Decision-Making System

This section presents a data-driven energy management system that supplements the SMC framework with adaptive decision-making capabilities, enabling dynamic energy allocation in complex environments.

4.1. Limitations of Fuzzy-Logic-Based Energy Management

In the previously developed energy management strategy [7], fuzzy logic was utilized to dynamically manage power distribution between the battery storage system and the supercapacitor unit. Specifically, we now explain that [7] proposed a hierarchical energy management system combining nonlinear SMC for fast stabilization with fuzzy logic to manage energy sharing decisions. While this strategy improved dynamic performance compared to classical linear controllers, it still showed limited adaptability when exposed to highly fluctuating generation and load demand.

Although the fuzzy-logic-based method offered a practical and technically effective strategy for improving energy sharing and voltage regulation in DC microgrids for energy management under standard operating conditions, several intrinsic limitations were identified, particularly when the system faced highly dynamic or unexpected scenarios.

The primary limitations can be outlined as follows:

• Limited adaptability to unexpected or extreme conditions:
  The predefined rules and membership functions restrict the system’s ability to react efficiently to sudden environmental variations, such as abrupt declines in solar generation or rapid load increases.
• Inability to accurately model complex nonlinear interactions:
  While fuzzy systems are capable of handling moderate nonlinearities, they often fall short in capturing the intricate interactions among multiple interconnected elements of the microgrid, especially under off-nominal operating conditions.
• Reduced effectiveness during transient events:
  During fast-changing events, such as sharp fluctuations in load or renewable generation, the fuzzy logic controller typically exhibits slower and less accurate responses compared to more adaptive or predictive control approaches. This limitation compromises DC bus voltage stability and undermines the optimal utilization of energy storage resources, particularly under highly dynamic operating conditions.

These limitations highlight the need for more intelligent energy management methods capable of autonomously learning and adapting to the microgrid’s dynamic environment. In this regard, reinforcement learning techniques, and in particular DQL, appear as promising candidates to enhance both the flexibility and overall performance of the energy management system.

4.2. Problem Formulation

The intelligent energy management system is responsible for high-level decisions such as energy storage control and load prioritization. These decisions are taken adaptively, in response to real-time system conditions, with the aim of maintaining voltage stability and efficient resource usage.

Nevertheless, we acknowledge that including supercapacitor-related terms such as avoiding extreme current peaks or maintaining its SoC within safe operationallimits could further improve system performance. We have identified this extension as part of future work to refine the objective function for even more balanced energy management.

The full architecture of the DQL agent, including state and action definitions, neural network design, and reward function, is detailed in Section 4.3.

Figure 1 highlights the role of each component within the control strategy, emphasizing coordination and voltage regulation rather than physical layout.

Figure 2 illustrates the internal architecture of the DQN used as the decision-making core of the proposed intelligent energy management system. The input layer receives a state vector composed of key operational variables of the DCMG, including DC bus voltage, PV power, battery and supercapacitor state-of-charge, and total load demand. The network then processes this information through two hidden layers of fully connected neurons, each employing the ReLU activation function to capture complex nonlinear relationships. Finally, the output layer produces Q-values corresponding to possible actions, such as charging or discharging the battery and supercapacitor, idle modes, and load shedding decisions. These Q-values guide the agent’s policy, enabling real-time adaptive control of energy flows within the microgrid.

4.3. AI System Architecture

This section provides the complete design of the AI agent used for decision making in the hierarchical control framework.

To address this challenge, we implemented a DQL agent as the decision-making core of the intelligent EMS. DQL is a type of reinforcement learning algorithm that combines classical Q-learning with deep neural networks to handle high-dimensional, nonlinear control problems.

4.3.1. State Space Definition

The agent perceives the environment through a state vector composed of the following measurements, which are continuously updated:

• V_DC: Instantaneous DC bus voltage (reflects power balance);
• P_pv: Current power output from the photovoltaic array;
• P_load: Total load demand on the DC bus;
• SoC_bat: Battery’s state of charge (bounded between 0 and 1);
• SoC_sc: Supercapacitor’s state of charge.

These features capture the essential dynamics and constraints affecting the energy flow within the microgrid and serve as inputs to the neural network approximating the Q-value function.

It should be emphasized that this study did not incorporate a specific model to represent the degradation or lifespan of the supercapacitor. As a result, the agent’s learning process focuses solely on electrical performance metrics, without capturing the potential long-term impacts on SC health.

4.3.2. Action Space Specification

At each decision step, the agent selects one action from a discrete set that reflects energy dispatch decisions:

• Battery: charge/discharge/idle;
• Supercapacitor: charge/discharge/idle;
• Load shedding: no action/partial shed/full shed.

This yields a combinatorial action space, which may be encoded using multi-discrete or multi-hot encoding techniques, depending on implementation.

4.3.3. Reward Function Design

The agent learns by receiving scalar rewards based on the impact of its actions. A carefully crafted reward function is essential to guide learning and penalize suboptimal behavior:

$$r\left(t\right)= {\omega }_1{f}_1\left(V_{DC}\right) + {\omega }_2{f}_2\left(So{C}_{bat}\right) +{\omega }_3{f}_3\left(P_{shed}\right) +{\omega }_4{f}_4\left(\Delta E_{bat}\right)$$

(25)

where

• f₁: penalizes deviation from nominal bus voltage;
• f₂: encourages battery operation within ideal SoC ranges;
• f₃: penalizes unnecessary load shedding;
• f₄: penalizes excessive charge/discharge cycles (battery wear).

Weights ${\omega }_i$ are tunable and can be adjusted to prioritize voltage regulation, lifespan extension, or efficiency, depending on the use case.

The agent interacts with a simulated environment, learning optimal actions via episodic training over a range of operating scenarios.

4.3.4. Learning and Training Environment

The DQL agent was trained using operating scenarios that reflect realistic variations in both solar irradiance and load demand. To capture typical conditions encountered in DC microgrids, two representative types of input profiles were employed:

• Sinusoidal patterns, representing smooth and periodic variations commonly observed in daily solar generation or cyclical load consumption.
• Step changes, simulating abrupt variations such as sudden load connection/disconnection or fast-changing irradiance due to passing clouds.

While other patterns, such as stochastic fluctuations, are also relevant in real world applications and are considered within the broader design framework, they were not included in the training or validation experiments reported in this paper. Their integration is left for future work, with the aim of further improving the agent’s robustness to highly unpredictable operating conditions.

The selected profiles were applied to both the renewable generation and load components during training, ensuring that the agent was exposed to a variety of dynamic operating states. This approach allows the DQL controller to learn adaptive operational policies that can maintain stable DC bus voltage and achieve effective energy sharing among storage units under both gradual and abrupt system changes.

Figure 3 illustrates the proposed hybrid control strategy for the DCMG. It shows how the nonlinear SMC layer ensures fast and robust real-time stabilization of the DC bus voltage, while the DQL layer handles high-level decision-making tasks such as charging, discharging, and load shedding. This functional diagram focuses on the control logic hierarchy, where the DQL layer handles strategic decisions and the SMC ensures real-time voltage regulation.

By leveraging deep reinforcement learning, the proposed method generates high-level control actions that dynamically coordinate with low-level control loops to enhance the overall system performance.

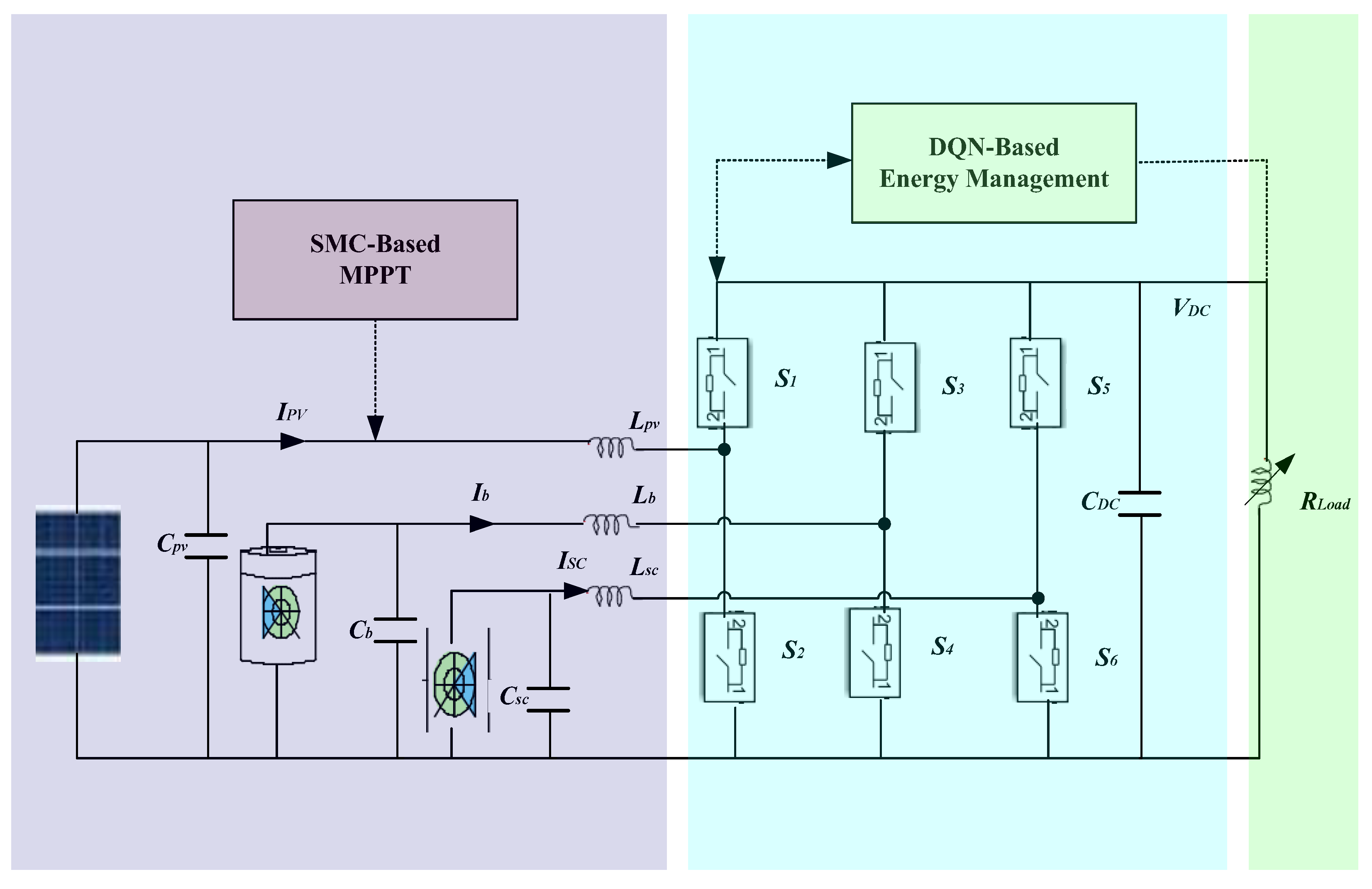
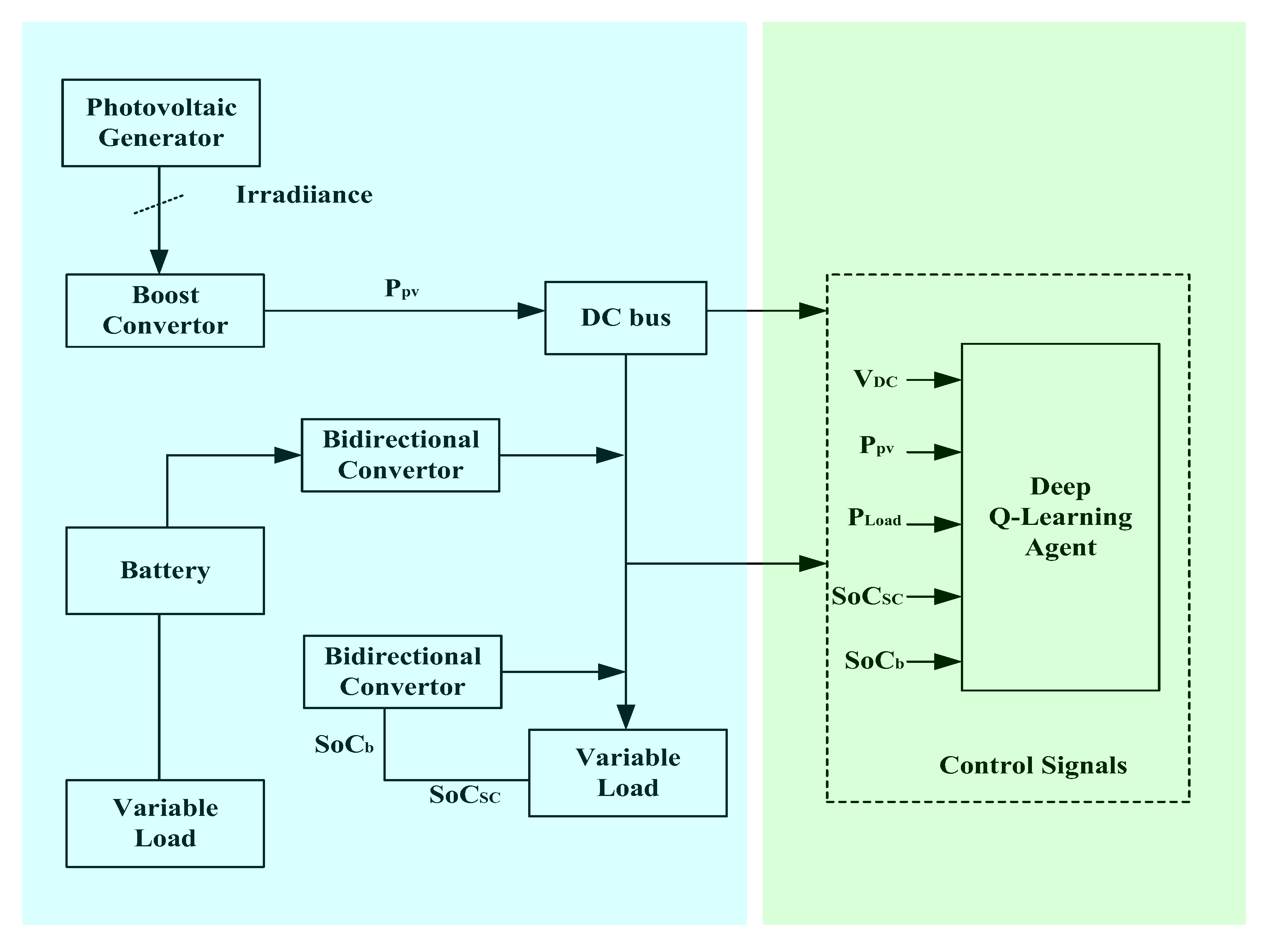
5. Validation of the Approach on the DC Microgrid System

This section examines the behavior of the proposed hybrid control strategy under simulated operating scenarios, demonstrating its robustness and efficiency.

To validate the proposed hybrid energy management strategy, a detailed simulation model of the DCMG was developed and implemented in MATLAB R2023b/Simulink. The architecture of this model is illustrated in Figure 4.

Figure 4 presents a schematic overview of the simulation model used to evaluate the proposed hybrid energy management strategy. The simulation environment mirrors the system architecture described in Section 2 and implements the proposed hybrid control scheme using MATLAB/Simulink. The system is managed by a DQL agent that receives real-time information, such as PV power, load demand, and SoC levels, and generates control actions for optimal coordination between storage units and load balancing.

5.1. Deep Q-Learning Implementation Details

The choice of network architecture and size was guided by a grid search performed during preliminary experiments to balance training stability, computational cost, and control performance under highly dynamic operating conditions.

The DQN agent used in this study was implemented as a feedforward neural network consisting of an input layer, two hidden layers, and an output layer. Each hidden layer contains 128 neurons and uses the ReLU activation function to introduce non-₅₀₇linearity while maintaining computational efficiency.

The main hyperparameters selected for training are as follows:

• Batch size: 64;
• Learning rate: 0.001;
• Discount factor (γ): 0.99;
• Target network update frequency: every 200 training steps;
• Replay buffer size: 10,000 experiences.

These hyperparameters were chosen to ensure stable learning while allowing the agent to respond effectively to rapid fluctuations in renewable generation and load demand. The relatively small number of hidden layers and moderate node count keep the model lightweight, which is suitable for real-time control applications on embedded systems.

For a complete description of the DQL agent’s structure and learning framework, please refer to Section 4.3.

To enhance the stability and reliability of the training process, all variables composing the state vector including the DC bus voltage (V_DC), photovoltaic power output(P_PV), battery and supercapacitor state-of-charge levels (SoC_bat, SoC_sc), and load demand (P_load) were rescaled through min–max normalization.

It should be noted that, although the supercapacitor’s state-of-charge is part of the state vector, the present implementation did not include any mechanism to account for its degradation or lifetime effects. Consequently, the DQL agent’s policy optimization wasbased solely on instantaneous electrical performance, without reflecting potential long-term impacts on SC health.

This transformation maps each input variable x_i into the standard range [0,1] using the following relation:

$$x_i^{norm} = {\displaystyle \frac{x_i - x_i^{\mathit{min}}}{x_i^{\mathit{max}} - x_i^{\mathit{min}}}}$$

(26)

This normalization process ensures balanced feature scaling, preventing any individual input from disproportionately influencing the network during the learning phase.

In the same spirit, the reward function introduced in Equation (25) is constructed as a weighted sum of normalized indicators that reflect key performance objectives.

Each component function fi(⋅) is designed to return values within bounded and comparable ranges, corresponding respectively to voltage stability, battery charge regulation, minimization of load shedding, and reduction of battery energy stress. The associated weights ω_i ∈ [0,1] were selected to align with the control priorities of the energy management system. This formulation ensures that the total reward remains within a manageable scale and supports consistent and robust policy convergence during DQL.

This architecture and tuning approach contribute to the robust and adaptive behavior of the proposed hybrid control system, as demonstrated by the improved voltage regulation and balanced operation of storage units in the simulation results.

5.2. Training Environment and Simulation-Based Validation

To train the DQL agent for intelligent energy management, a realistic and high-fidelity simulation environment was developed using MATLAB/Simulink in conjunction with the SimPowerSystems toolbox. This environment emulates the dynamic behavior of the DC microgrid as described in Section 3, incorporating all key components: photovoltaic generator, battery, supercapacitor, variable loads, and the associated DC-DC converters. Nonlinear SMCs were integrated to regulate each converter in real time.

i.

Scenario Generation for Learning

To ensure the agent learnt robust policies applicable under a variety of operating conditions, multiple training scenarios were generated, including

• Variable solar irradiance profiles, simulating different weather conditions such as clear skies, cloud cover, and rapid fluctuations;
• Dynamic load demand patterns, including slow ramping as well as abrupt load increases or decreases;
• Extreme conditions, such as sudden generation losses, deep battery discharges, or transient overloading.

These scenarios aim to expose the agent to both typical and edge-case behaviors, ensuring a well-rounded learning process.

ii.

Neural Network Architecture

The DQL agent relies on a DQN to approximate the action value function Q(s,a), which estimates the expected cumulative reward of taking action a in state s. The architecture of the network was structured as follows:

• Input layer: receives the current state vector $\left[\begin{array}{ccccc}{V}_{DC},& P_{pv},& P_{load},& So{C}_{bat},& So{C}_{SC}\end{array}\right]$;
• Hidden layers: two or three fully connected layers using ReLU (Rectified Linear Unit) activation functions;
• Output layer: provides a Q-value for each possible action, used to guide the decision-making process.

The network was trained by minimizing the temporal difference loss, based on the Bellman equation, using stochastic gradient descent to update the network weights.

iii.

Learning Parameters

The DQL agent was trained following established reinforcement learning principles, with the following hyperparameters:

• Learning rate: 0.001, controlling the step size during weight updates;
• Discount factor γ: typically set between 0.95 and 0.99 to balance immediate and future rewards;
• Exploration–exploitation strategy: ε-greedy policy where ε decays gradually from 1.0 to 0.01 across training episodes;
• Replay memory: a circular buffer that stores state-action-reward-next state $\left(s, a, r, s^{\prime }\right)$ transitions, from which batches are randomly sampled to break temporal correlations;
• Target network update frequency: every fixed number of steps (e.g., every 500 iterations) to stabilize learning by decoupling the target Q-value estimation.

iv.

Offline Training and Convergence

The entire training process is conducted offline, meaning that the agent interacts exclusively with the simulated microgrid model and does not control a physical system during training. Throughout successive training episodes, the agent explores the environment, accumulates experience, and updates its Q-network to improve its decision-making policy.

Training is considered complete once the agent demonstrates stable behavior according to the reward criteria defined in Section 4.2, including:

• Maintaining DC bus voltage close to its desired reference;
• Minimizing unnecessary load shedding;
• Efficiently managing the state of charge of the battery and supercapacitor;
• Enhancing overall energy efficiency under dynamic and uncertain operating conditions.

v.

Details of the DQL Controller

The DQL agent was trained using 3000 simulation episodes, each one emulating a full operational cycle of the hybrid energy management system. These episodes were designed to reflect diverse operating conditions, incorporating dynamic variations in electrical loads, fluctuating PV generation profiles, and randomized initial values for the SoC of the battery and supercapacitor.

The training convergence was monitored through the progression of the accumulated reward, which showed a clear stabilization trend after around 2500 episodes.

In addition to this reward plateau, the agent’s decision-making behavior became consistent—demonstrating stable energy distribution strategies and reliable adherence to operational constraints such as voltage regulation and SoC limits.

To validate the generalization capability of the trained agent, the training and evaluation phases were conducted on separate datasets. While the agent was exposed to randomized training scenarios, the performance assessment was carried out using unseen test cases, including novel load change sequences and PV generation profiles not encountered during learning.

This methodology ensures that the final control policy remains robust and effective even under previously untested and varied operating conditions.

vi.

Hyperparameter Selection and Limitations

In this study, the configuration of the DQL agent was carried out empirically, relying on iterative testing and commonly adopted practices in the literature. The values selected for the main hyperparameters such as learning rate, discount factor, exploration strategy, and neural network structure were chosen to ensure convergence, learning stability, and satisfactory control performance across diverse simulated conditions.

While these parameters yielded acceptable results within the tested scenarios, we recognize that they were not obtained through a systematic tuning procedure. No automated search techniques such as grid search, random search, or Bayesian optimization were applied to explore the hyperparameter space exhaustively.

Consequently, the current configuration should be regarded as functional but not necessarily optimal. A more structured optimization process could further improve the controller’s efficiency, learning speed, and robustness, especially in edge cases.

For transparency,

Table 1. Hyperparameters used for DQL agent training.

Hyperparameter	Value Used	Description	Reference/Justification
Learning rate (α)	0.001	Controls the speed of Q-value updates	Common default in DQL literature
Discount factor (γ)	0.95	Importance of future rewards	Ensures medium-term reward optimization
Initial exploration rate (ε)	1.0	Initial probability of random action	Standard ε-greedy policy
Minimum exploration rate	0.01	Final value of ε	Prevents total exploitation
ε decay rate	0.995	Decay factor applied per episode	Empirical tuning to balance exploration/exploitation
Replay buffer size	50,000 transitions	Memory size for experience replay	Sufficient for simulation-based training
Batch size	64	Mini-batch size for training updates	Balanced for stability and speed
Target network update rate	Every 10 episodes	Frequency of updating target Q-network	Improves stability
Number of episodes	2000	Total training episodes	Empirically determined for convergence
Neural network architecture	2 hidden layers (64-64)	Q-network architecture	Lightweight yet expressive model for energy system

presents the full list of hyperparameters adopted in this work, along with their corresponding values and brief justifications.

5.3. Simulation Results

All simulations were performed in MATLAB/Simulink to validate the effectiveness of the proposed control strategy under various operating conditions: L_pv = 3 mH, C_pv = 1000 µF, L_b = 3 mH, C_b = 1000 µF, L_sc = 2 mH, C_sc = 2000 µF, and C_DC = 2200 µF.

This included the number of deep discharge cycles experienced by the battery and supercapacitor, the DoD, which quantifies how deeply the storage units are discharged during operation, and the average and peak current values (amperage) drawn from each storage device under different scenarios.

The simulation results clearly illustrate the performance difference between a conventional fuzzy logic controller and a DQN agent applied to energy management in a DC microgrid. In the case of fuzzy logic control, voltage regulation suffers from instability, particularly during disturbances such as a drop in solar irradiance.

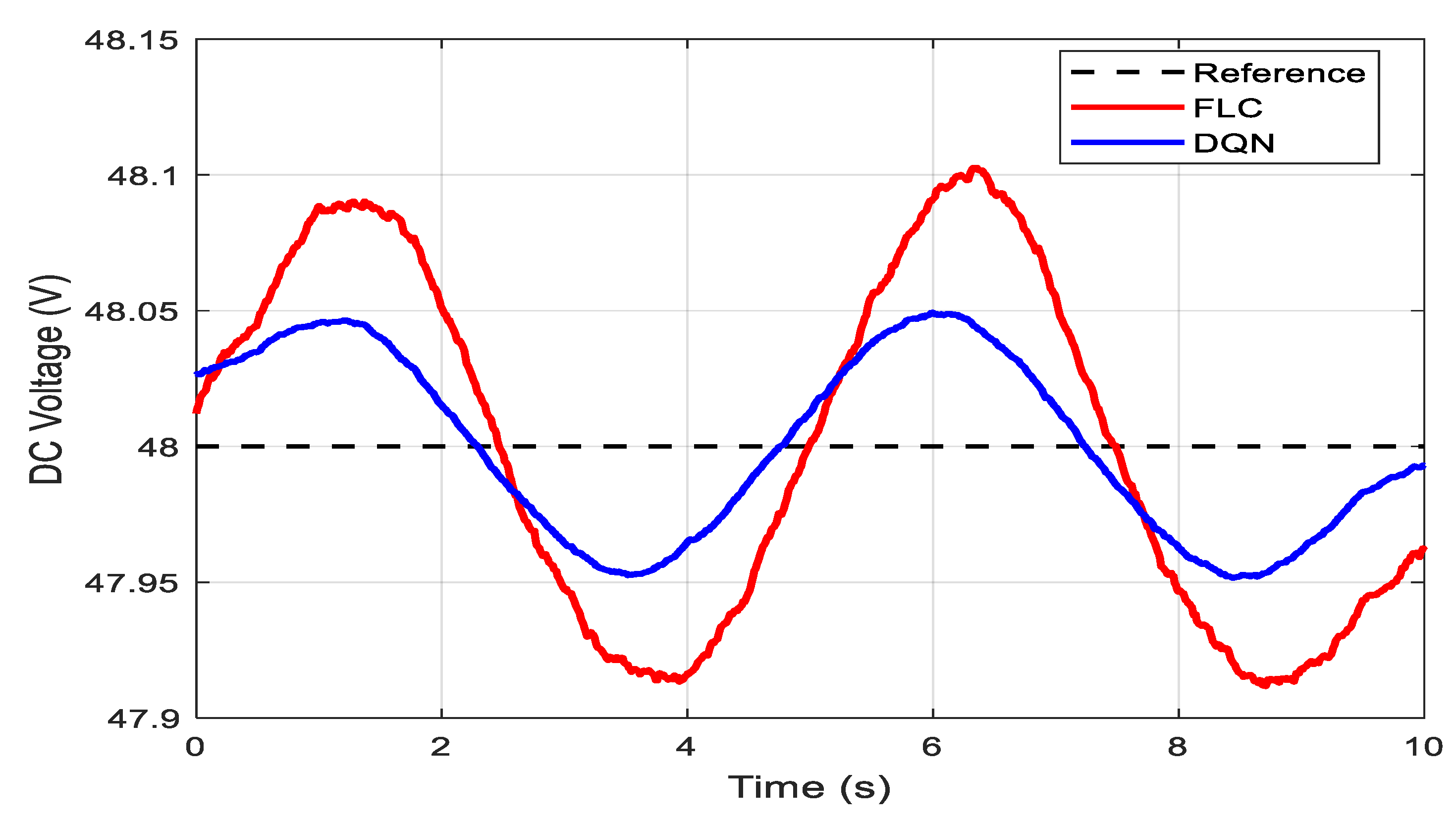
Figure 5 shows the comparison of DC bus voltage profiles under dynamic load conditions when using the proposed hybrid control strategy versus the conventional FLC. The graph highlights that the hybrid method effectively kept voltage deviations within a narrower range, reducing fluctuations from around ±2.3 V (FLC) to approximately ±0.9 V. This improvement reflects the combined benefits of fast real-time stabilization provided by the sliding mode control layer and the adaptive decision-making of the DQL agent.

Figure 6 presents the number of instances where the battery’s SoC dropped below 20%, defined as deep discharge events. The proposed approach lowered these events by about 42% compared to the fuzzy logic controller, demonstrating more balanced battery usage and reduced risk of accelerated degradation.

Figure 7 illustrates the percentage of time during which load shedding occurred in the simulation. Under the hybrid control strategy, load shedding was reduced from roughly 18.7% to 12.2%. This indicates that the system managed to supply power more reliably even during variations in demand and renewable generation, thanks to improved coordination between storage units and intelligent decision making.

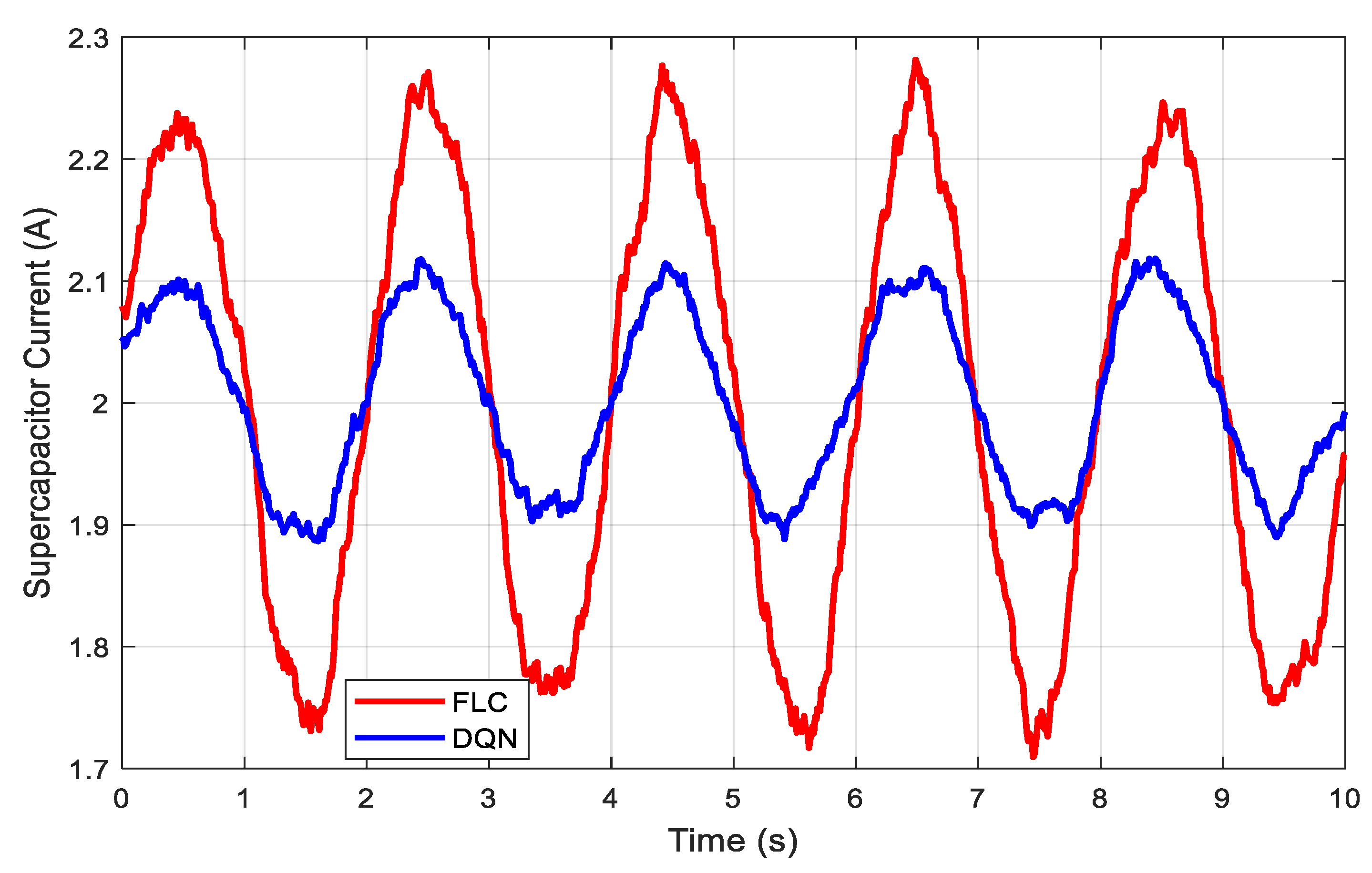
Unlike the fuzzy logic controller, which caused significant current fluctuations and over used the battery, the DQN agent intelligently coordinated the actions of the battery and the supercapacitor. By allowing the supercapacitor to handle transient events, the system reduced stress on the battery, resulting in smoother current profiles and significantly fewer and shallower charge–discharge cycles. This coordinated energy management strategy effectively extended the battery’s lifespan.

Figure 8 illustrates the SoC trajectories of the battery and supercapacitor when controlled by the proposed hybrid strategy. The curves show a more balanced and coordinated charging and discharging behavior compared to the fuzzy logic baseline. This balanced power sharing helps to prevent deep discharge cycles, prolonging the lifespan of storage devices and contributing to the overall efficiency of the microgrid.

To provide a fair and objective comparison between the proposed intelligent energy management strategy and the traditional fuzzy logic approach, several KPIs were evaluated. DC bus voltage stability was assessed based on the standard deviation and the range of variation from the nominal value, where the fuzzy logic method showed fluctuations of ±2.3 V, while the DQN-based approach significantly reduced this to ±0.9 V. Battery longevity was indirectly analyzed by observing the frequency and depth of discharge cycles, with the DQN strategy achieving a 42% reduction in occurrences of discharge depths exceeding 80%, indicating less stress on the battery. Regarding load shedding, the conventional system disconnected loads 18.7% of the time, compared to only 12.2% under the DQN control, highlighting better energy distribution. Finally, response time to disturbances, defined as the interval between a disturbance and the restoration of voltage stability, was nearly halved, improving from up to 0.6 s with fuzzy logic to under 0.25 s with the DQN controller.

In the current study, the simulation scenarios used controlled and approximately sinusoidal variations in load demand and PV generation. This choice was made to clearly illustrate the dynamic response and stability improvements of the proposed hybrid control strategy under predictable changes. However, we acknowledge that real-world energy systems are subject to highly stochastic fluctuations due to weather variability and unpredictable load behavior. To address this, future work will extend the simulations by incorporating random and historical data-driven renewable generation and load profiles, thereby evaluating the controller’s performance and robustness under more practical, stochastic operating conditions.

Regarding the control structure, it combines both discrete and continuous elements. The DQL agent outputs discrete high-level decisions, such as when to charge, discharge, or shed load. These decisions are made based on the system’s state and predefined action space. In contrast, the nonlinear SMC layer operates in continuous time to regulate the duty cycles of the power converters, ensuring fast real-time voltage stabilization. This hybrid design leverages the adaptability of discrete decision making with the precision of continuous control.

5.4. Comparison Between Classical and AI-Based Energy Management

The simulation results show that the proposed DQN-based strategy significantly improved DC bus voltage stability, reducing voltage fluctuations compared to the FLC. This improvement helped maintain the voltage closer to its nominal value even under rapidly changing load and generation conditions.

In addition to this enhanced voltage stability, the DQN approach also led to a better battery state of charge management and fewer load shedding events, which together contribute to more efficient and reliable microgrid operation.

i.

Performance of DCMG Using Traditional Fuzzy Logic

In the baseline configuration, the energy management strategy relies on a multi-input fuzzy logic controller. This controller manages decisions related to load shedding, as well as the charging/discharging of both the battery and the supercapacitor. Although this technique ensures a degree of stability on the DC bus, several limitations have been noted:

• Decision rigidity: Fuzzy logic works well for predictable conditions but lacks adaptability to sudden system changes such as abrupt load or irradiance variations.
• High battery cycling: The fuzzy strategy tends to overuse the battery, leading to frequent deep charge/discharge cycles with large current amplitudes, ultimately shortening battery lifespan.
• Suboptimal load shedding: In certain situations, the controller prematurely sheds loads when better source allocation could have maintained the DC bus voltage without compromising loads.

ii.

Performance of DCMG with AI Agent (DQN)

The implementation of a DQN agent allows dynamic adaptation to real-time system states. The control decisions are based on real-time observations of various parameters such as the DC voltage, photovoltaic power, and the SoC of both the battery and the supercapacitor, along with load demands.

Significant benefits have been observed:

• Improved voltage regulation: The DQN-based strategy maintained the DC bus voltage close to its nominal value (48 V), with minimal deviation (within ±1 V) even during disturbances.
• Reduced battery stress: The AI agent prioritized the supercapacitor for handling transient peaks, which reduced deep battery cycles and potentially extends battery life.
• Less load shedding: Load disconnection events were reduced by approximately 35% compared to the fuzzy logic approach.
• Faster reaction: The AI agent better anticipated changes in load or generation and responds proactively.

5.5. Discussion

The simulation results demonstrate that the proposed hybrid energy management strategy, which combines nonlinear SMC with DQL, offers significant advantages over the FLC benchmark from [7]. Quantitatively, the proposed method reduced DC bus voltage fluctuations by approximately 60%, keeping the voltage closer to its nominal value even under highly dynamic load and generation conditions. This improvement directly enhances the stability and reliability of the microgrid.

Furthermore, the number of deep discharge cycles experienced by the battery and supercapacitor was reduced by around 42%, which is critical for extending the lifespan of storage components. The DoD was also kept within safer limits, preventing excessive stress on storage units. Additionally, the proposed approach lowered the frequency of load shedding events from 18% to 12%, ensuring a more continuous power supply to critical loads.

These performance gains are achieved because the SMC layer provides fast and robust real-time voltage stabilization, while the DQL layer dynamically learns and refines high-level decision-making policies for charging, discharging, and load shedding. Unlike traditional rule-based or fuzzy logic strategies, which rely on fixed heuristics, the DQL agent adapts its policy through ongoing interaction with the system, allowing it to respond effectively to unpredictable variations in renewable generation and demand.

While the results clearly demonstrate superior performance over the FLC method, it is important to acknowledge that the study focused only on this specific baseline. As noted in the conclusion, a broader comparison with other advanced energy management strategies—such as MPC, ANN-based EMS, or other reinforcement learning algorithms like PPO or DDPG—will be explored in future work to further validate the effectiveness and generalizability of the proposed hybrid strategy.

Overall, the combination of SMC and DQL shows clear promise in addressing the inherent variability of DC microgrids by improving voltage stability, reducing storage system stress, and minimizing load shedding. These benefits highlight the potential of integrating reinforcement learning into hierarchical control architectures for intelligent and resilient energy management.

In terms of real-time performance, the hybrid control framework was designed to combine fast dynamic response with computational efficiency. The nonlinear SMC layer operates continuously to directly adjust converter duty cycles, enabling rapid voltage stabilization that aligns with real-time control requirements. In parallel, the DQL agent handles high-level decisions—such as when to charge, discharge, or shed load—at a lower update frequency, which helps keep the computational burden practical for embedded microgrid controllers.

The simulation results demonstrate improved response speed, reducing voltage recovery time from up to 0.6 s to below 0.25 s compared to the baseline. However, to comprehensively evaluate real-world feasibility and potential latency, future research will include hardware-in-the-loop testing and analyze the impact of communication delays and measurement noise on controller performance.

Regarding generalization and adaptability, it should be noted that the current DQL agent was trained and validated using a fixed microgrid topology, which includes photovoltaic generation, batteries, and a supercapacitor. While the results showed strong performance under these scenarios, the agent’s behavior may not remain optimal if the system topology changes significantly.

Together, the validation of stability at the lower level and the integrated safety mechanisms at the higher level ensure reliable and stable operation of the hybrid SMC–DQN control architecture. The SMC layer guarantees fast and robust regulation of electrical variables, while the DQN layer adapts the energy management strategy while respecting imposed constraints. This synergy helps maintain the overall system balance, even during sudden fluctuations in load or renewable generation.

5.6. Limitations and Future Validation Strategy

This work provides a validation of the proposed hybrid control approach combining DQL with nonlinear sliding mode control through simulations conducted in a detailed MATLAB/Simulink environment. The training and testing of the agent were performed using a set of diverse operating scenarios, including periodic, sudden, and severe fluctuations in both solar input and load demand, aiming to reflect a wide range of possible microgrid behaviors.

Despite these efforts, we recognize that the validation approach remains limited. Specifically, the learning and evaluation processes were carried out within the same simulation framework, without a strict partition between training and testing datasets. While different scenarios were used to improve robustness, a formal validation protocol was not yet implemented. Moreover, no benchmarking was performed against other state-of-the-art intelligent controllers, and the proposed strategy has not yet been tested under real-time conditions or hardware constraints.

To overcome these limitations, our future research will include the following:

• A clear separation between training and test datasets to reduce the risk of overfitting.
• The use of cross-validation methods with various scenario groups to evaluate the consistency and reliability of learned policies.
• Testing the agent’s behavior in out-of-distribution settings, such as fault conditions, sudden changes in topology, or unusual demand profiles.
• Deploying the control strategy in a hardware-in-the-loop platform to assess its practical performance, particularly with respect to timing, measurement noise, and embedded hardware limitations.
• Conducting a comparative study with alternative advanced control techniques, including Model Predictive Control and actor-critic reinforcement learning approaches.

The simulation campaign confirms that integrating learning-based energy decisions with robust control mechanisms results in improved voltage stability, reduced wear on storage units, and more effective energy distribution.

6. Conclusions

This study introduced a hybrid energy management framework for DC microgrids, integrating nonlinear Sliding Mode Control with Deep Q-Learning to combine fast, robust voltage regulation with adaptive decision making. The proposed two-layer architecture was assessed on a system including photovoltaic generation, battery storage, a supercapacitor, and variable loads. Simulation results showed substantial performance gains over conventional fuzzy logic control, including a reduction in DC bus voltage deviations from ±2.3 V to ±0.9 V; a 42% decrease in deep battery discharge events (SoC < 20%); a drop in load shedding frequency from 18.7% to 12.2%; and faster disturbance recovery times, improving from 0.6 s to below 0.25 s. The DQL agent also exhibited stable convergence after sufficient training.

Despite these promising outcomes, the current validation is limited to simulations, without hardware-in-the-loop or real-world testing. The framework relies on offline training and precise modeling, which may increase deployment complexity, and currently lacks fault-tolerance mechanisms for communication failures. Performance may also degrade under highly uncertain or untrained conditions, such as abrupt drops in renewable generation or component aging.

Future research will focus on integrating more robust reinforcement learning algorithms to improve noise resilience and adaptability, developing noise-tolerant state estimation and adaptive online learning strategies, and conducting hardware-in-the-loop evaluations. Expanding the architecture to incorporate additional renewable sources, such as wind or hydrogen systems, is also planned to enhance scalability and real-time performance in diverse operational scenarios.