Overcurrent Limiting Strategy for Grid-Forming Inverters Based on Current-Controlled VSG
Abstract
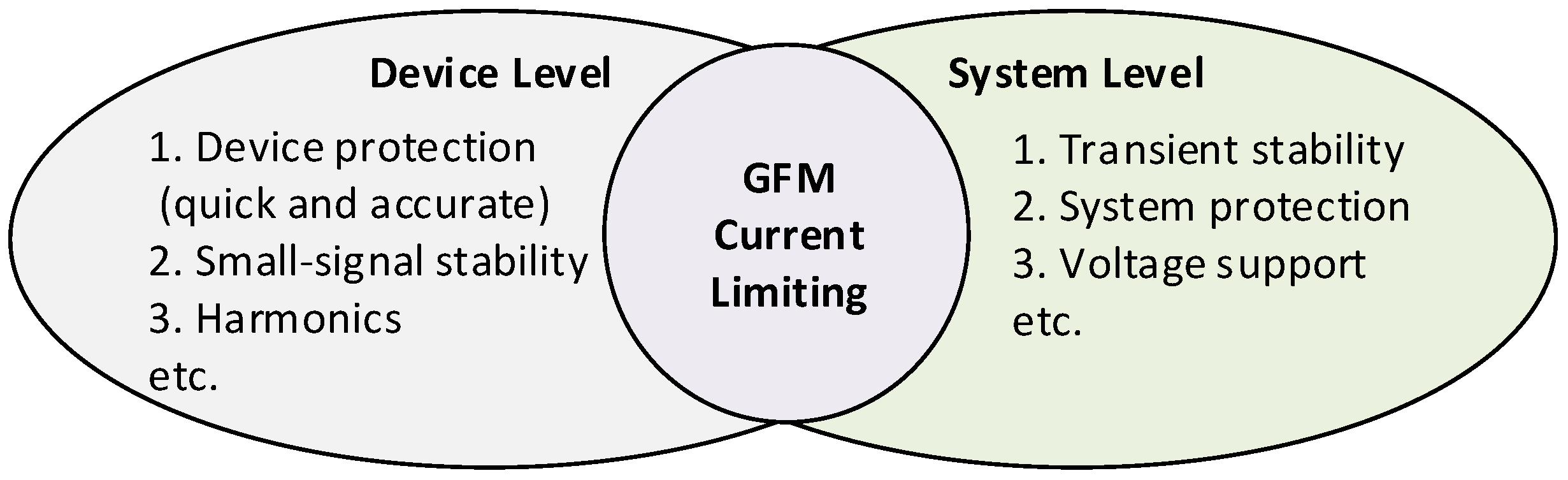
1. Introduction
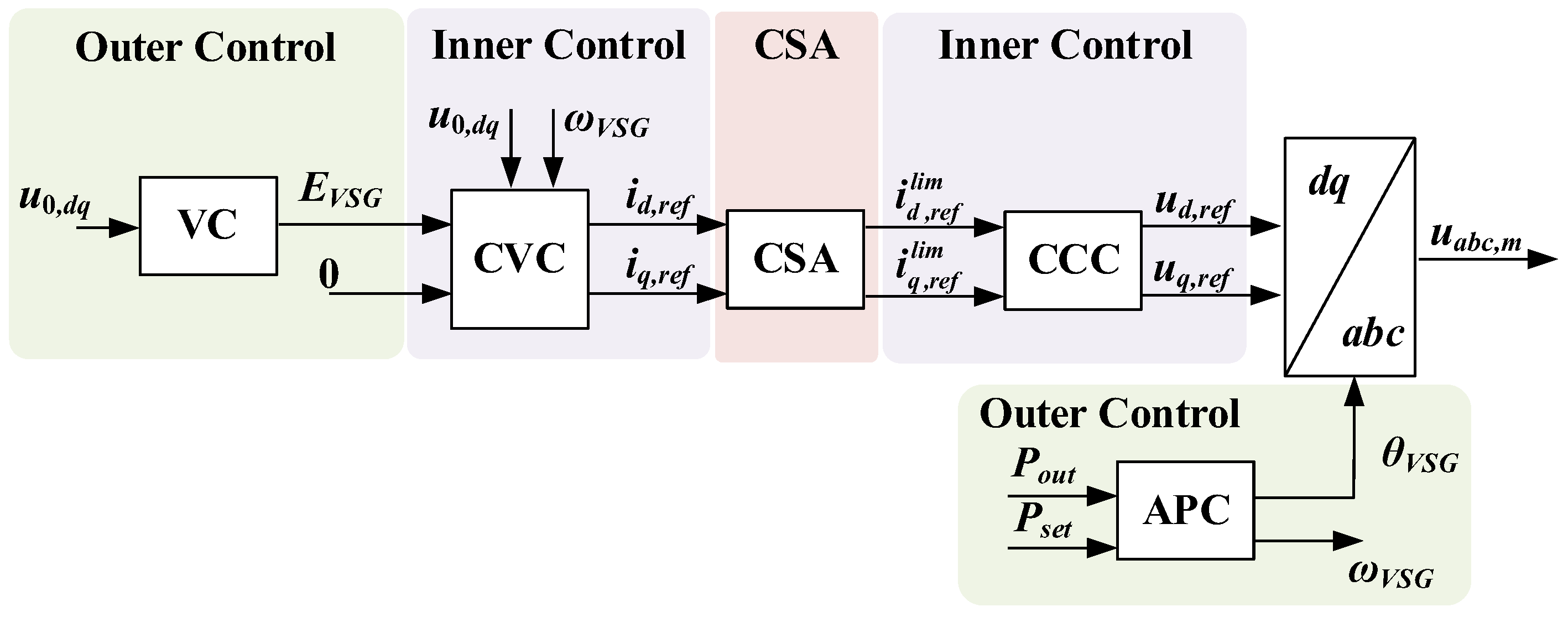
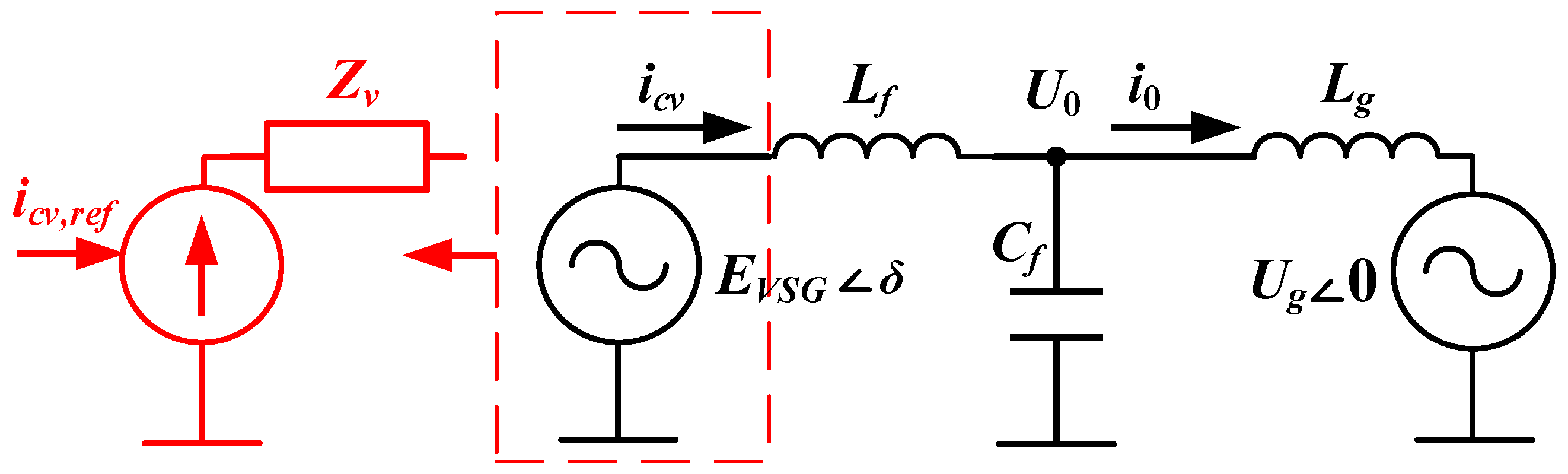
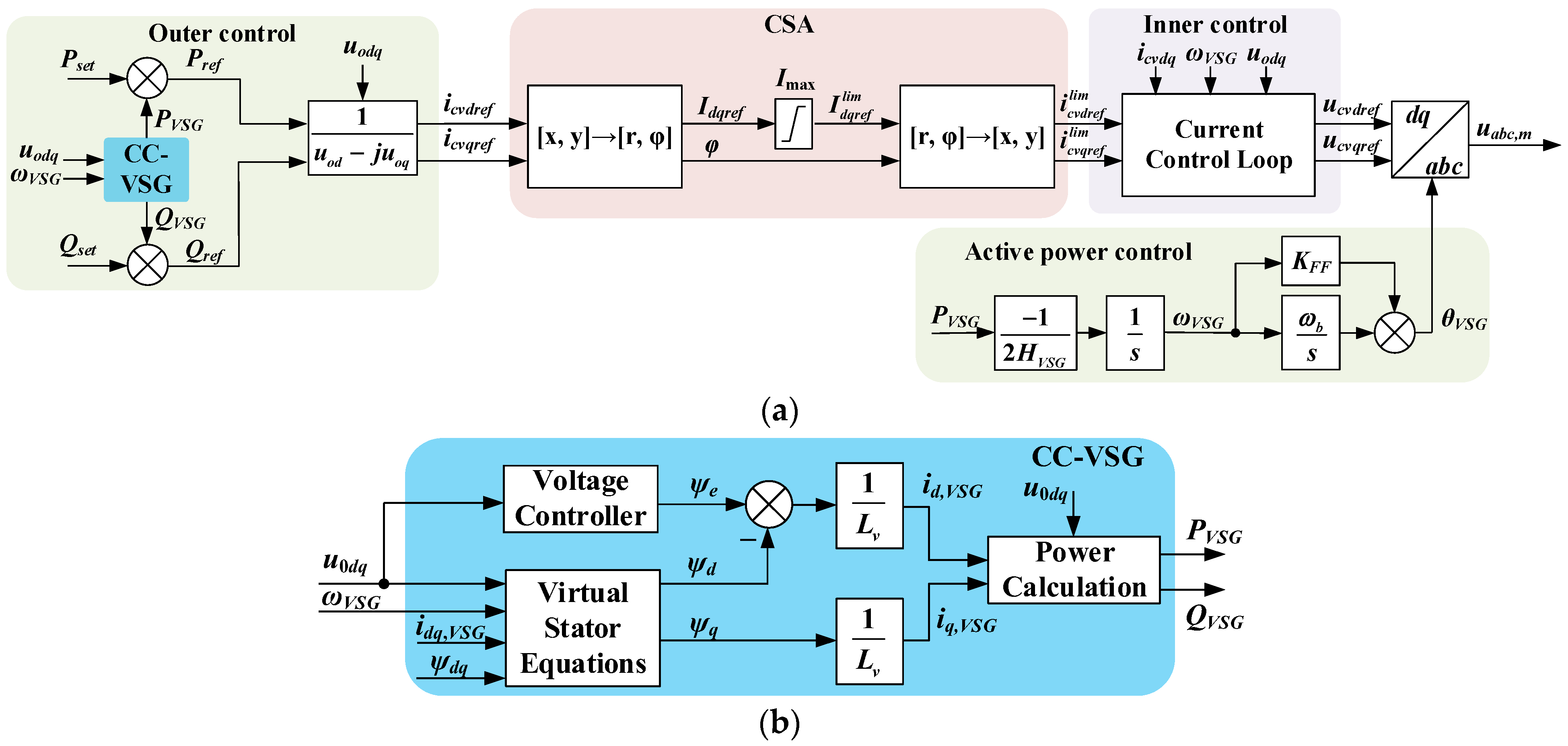
- A novel structure of the current-controlled VSG (CC-VSG) with feedforward control has been proposed, which is a current source with virtual impedance. In this case, the reference signal for the inner current control loop is formed taking into account the dynamics of the virtual synchronous machine, which has no current limiting. Due to the presence of the inner current control loop in the CC-VSG, only the amplitude of the reference current vector is directly limited. The phase of the output current remains regulated due to the continuous formation of virtual currents based on the known equations of the synchronous machine. Thus, the properties of the grid-forming source (power synchronization without the PLL, voltage, and frequency control) are preserved.
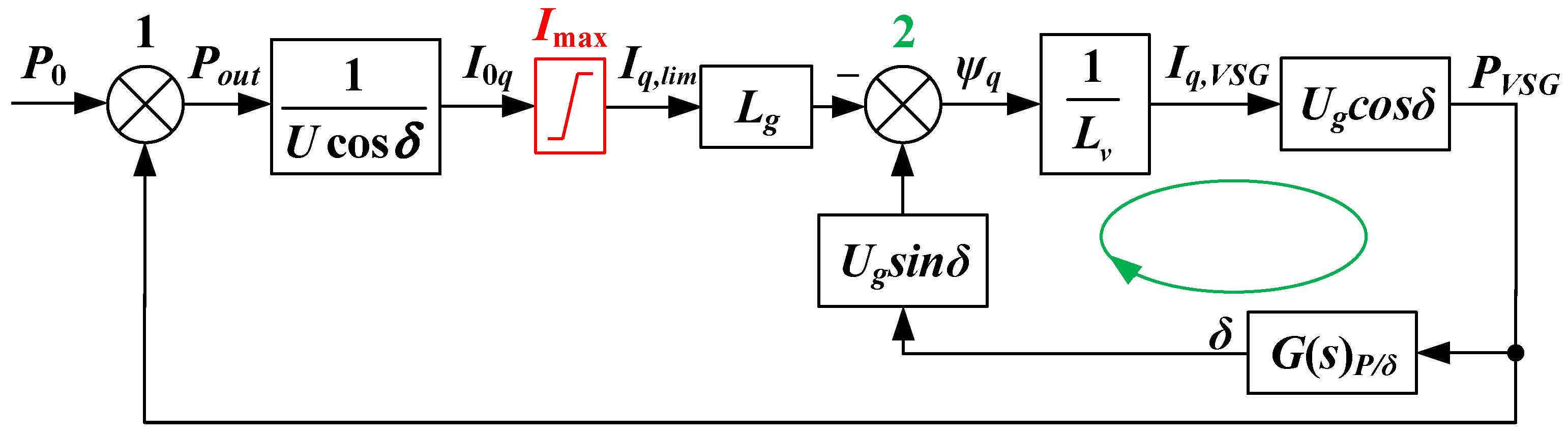
- To avoid saturation of the voltage controller, a blocking algorithm is proposed, which is activated by a signal from the current limiter. The resetting of the blocking signal and exit from the limiting mode occur naturally due to continuous regulation of the output current phase (demonstrated by saving the voltage feedback). In this way, an extremely simple and reliable way to prevent saturation and lock-up of the control system in the current-limiting mode is implemented.
2. Challenges of VSG Current Limiting
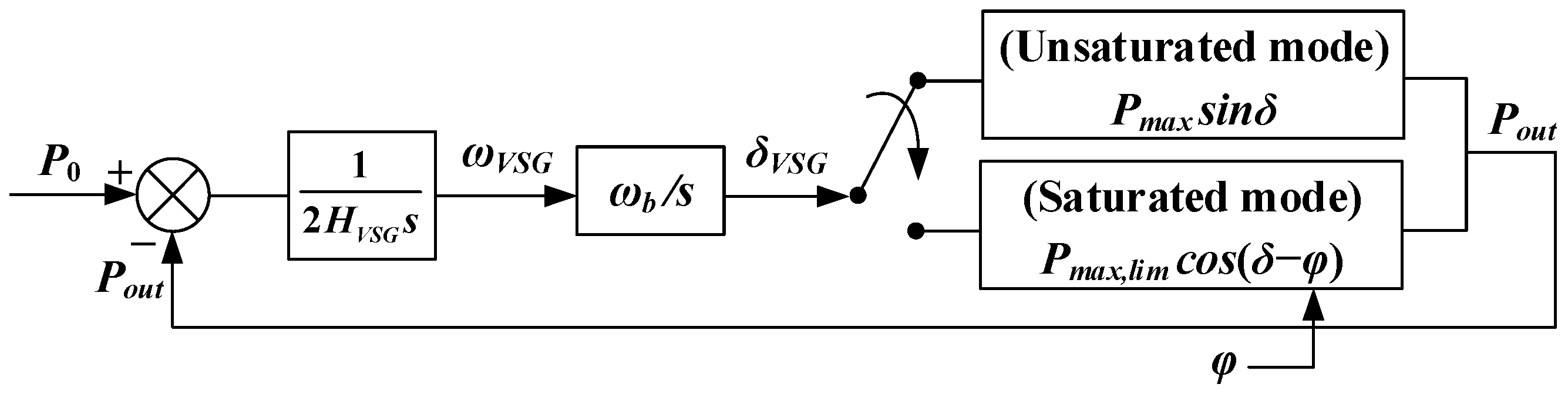
2.1. Traditional VC-VSG with Current Reference Saturation and Fixed Angle
2.2. Proposed CC-VSG with Current Saturation Algorithm
3. Comparative Analysis of Traditional VC-VSG and Proposed CC-VSG During Overcurrent Limiting
3.1. Simulation Test #1: A Voltage Sag During Grid-Connected Operation for the Traditional VC-VSG
3.2. Simulation Test #2: A Voltage Sag During Grid-Connected Operation for the Proposed CC-VSG with the CSA
3.3. Simulation Test #3: A Change in the Active Power Reference During Grid-Connected Operation for the Proposed CC-VSG with the CSA
3.4. Simulation Test #4: A Step Change in Load During Stand-Alone Mode for the Proposed CC-VSG with the CSA
3.5. Simulation Test #5: A Gradual Change in Load During Stand-Alone Mode for the Proposed CC-VSG with the CSA
3.6. Simulation Test #6: Different Approaches to VC Blocking Within CC-VSG Structure Under Gradual Change in C-Load and Stand-Alone Mode
4. Experimental Verification
4.1. Experimental Test #1: A Voltage Sag During Grid-Connected Operation for the Proposed CC-VSG with the CSA
4.2. Experimental Test #2: A Voltage Sag During Grid-Connected Operation and Specified Active Power Reference for the Proposed CC-VSG with the CSA
4.3. Experimental Test #3: Synchronization and Transition to Stand-Alone Mode for the CC-VSG Prototype and the Hybrid Inverter
4.4. Experimental Test #4: Change in R-Load During Stand-Alone Mode for the Proposed CC-VSG with the CSA and the Hybrid Inverter
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Uac,b | 380 V | Rg | 0.06 pu | KFF | 10 pu |
| Udc,b | 700 V | Lg | 0.2 pu | Uset | 1 pu |
| Sb | 6 kW | Lv | 0.2 pu | KU | 1 pu |
| fb | 50 Hz | Rv | 0.1 pu | fsw | 4 kHz |
| Lf | 0.16 pu | Kw | 25 pu | Imax | 0.9 pu |
| Cf | 0.2268 pu | HVSG | 2 s | Rload | 30.723 Ohm |
References
- Kroposki, B.; Johnson, B.; Zhang, Y.; Gevorgian, V.; Denholm, P.; Hodge, B.-M.; Hannegan, B. Achieving a 100% Renewable Grid: Operating Electric Power Systems with Extremely High Levels of Variable Renewable Energy. IEEE Power Energy Mag. 2017, 15, 61–73. [Google Scholar] [CrossRef]
- Baier, C.R.; Melin, P.E.; Torres, M.A.; Ramirez, R.O.; Muñoz, C.; Quinteros, A. Developing and Evaluating the Operating Region of a Grid-Connected Current Source Inverter from Its Mathematical Model. Mathematics 2024, 12, 1775. [Google Scholar] [CrossRef]
- Ilyushin, P.V.; Shepovalova, O.V.; Filippov, S.P.; Nekrasov, A.A. Calculating the Sequence of Stationary Modes in Power Distribution Networks of Russia for Wide-Scale Integration of Renewable Energy Based Installations. Energy Rep. 2021, 7, 308–327. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C.; Ajjarapu, V.; Canizares, C.; Erlich, I.; Hill, D.; Hiskens, I.; Kamwa, I.; Pal, B.; et al. Definition and Classification of Power System Stability—Revisited & Extended. IEEE Trans. Power Syst. 2021, 36, 3271–3281. [Google Scholar] [CrossRef]
- Wang, J.; Ganguly, S.; Kroposki, B. Performance Evaluation of Multi-Vendor Grid-Forming Inverters for Grid-Connected Operation Through Hardware Experimentation. In Proceedings of the 2024 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Anaheim, CA, USA, 6–9 May 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Tozak, M.; Taskin, S.; Sengor, I.; Hayes, B.P. Modeling and Control of Grid Forming Converters: A Systematic Review. IEEE Access 2024, 12, 107818–107843. [Google Scholar] [CrossRef]
- Wang, Y.; Ji, H.; Luo, R.; Liu, B.; Wu, Y. Energy Optimization Strategy for Wind–Solar–Storage Systems with a Storage Battery Configuration. Mathematics 2025, 13, 1755. [Google Scholar] [CrossRef]
- Milano, F.; Dörfler, F.; Hug, G.; Hill, D.J.; Verbič, G. Foundations and Challenges of Low-Inertia Systems (Invited Paper). In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–25. [Google Scholar] [CrossRef]
- Suvorov, A.; Askarov, A.; Kievets, A. A Freely Configurable Structure of Virtual Synchronous Generator for Grid-Forming Converters. Electr. Eng. 2023, 105, 1331–1345. [Google Scholar] [CrossRef]
- Rathnayake, D.B.; Akrami, M.; Phurailatpam, C.; Me, S.P.; Hadavi, S.; Jayasinghe, G.; Zabihi, S.; Bahrani, B. Grid Forming Inverter Modeling, Control, and Applications. IEEE Access 2021, 9, 114781–114807. [Google Scholar] [CrossRef]
- Baeckeland, N.; Chatterjee, D.; Lu, M.; Johnson, B.; Seo, G.-S. Overcurrent Limiting in Grid-Forming Inverters: A Comprehensive Review and Discussion. IEEE Trans. Power Electron. 2024, 39, 14493–14517. [Google Scholar] [CrossRef]
- Fan, B.; Liu, T.; Zhao, F.; Wu, H.; Wang, X. A Review of Current-Limiting Control of Grid-Forming Inverters Under Symmetrical Disturbances. IEEE Open J. Power Electron. 2022, 3, 955–969. [Google Scholar] [CrossRef]
- Lu, M.; Mallik, R.; Johnson, B.; Dhople, S. Dispatchable Virtual-Oscillator-Controlled Inverters with Current-Limiting and MPPT Capabilities. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 3316–3323. [Google Scholar] [CrossRef]
- Du, W.; Nguyen, Q.; Liu, Y.; Mohiuddin, S.M. A Current Limiting Control Strategy for Single-Loop Droop-Controlled Grid-Forming Inverters Under Balanced and Unbalanced Faults. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Du, W.; Mohiuddin, S.M. A Two-Stage Current Limiting Control Strategy for Improved Low-Voltage Ride-Through Capability of Direct-Droop-Controlled, Grid-Forming Inverters. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 2886–2890. [Google Scholar] [CrossRef]
- Bottrell, N.; Green, T.C. Comparison of Current-Limiting Strategies During Fault Ride-Through of Inverters to Prevent Latch-Up and Wind-Up. IEEE Trans. Power Electron. 2014, 29, 3786–3797. [Google Scholar] [CrossRef]
- Brucoli, M.; Green, T.C.; McDonald, J.D.F. Modelling and Analysis of Fault Behaviour of Inverter Microgrids to Aid Future Fault Detection. In Proceedings of the 2007 IEEE International Conference on System of Systems Engineering, San Antonio, TX, USA, 16–18 April 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Talebi, H.A. A New Current Limiting Strategy and Fault Model to Improve Fault Ride-through Capability of Inverter Interfaced DERs in Autonomous Microgrids. Sustain. Energy Technol. Assess. 2017, 24, 71–81. [Google Scholar] [CrossRef]
- Sadeghkhani, I.; Hamedani Golshan, M.E.; Guerrero, J.M.; Mehrizi-Sani, A. A Current Limiting Strategy to Improve Fault Ride-Through of Inverter Interfaced Autonomous Microgrids. IEEE Trans. Smart Grid 2017, 8, 2138–2148. [Google Scholar] [CrossRef]
- Zhang, L.; Harnefors, L.; Nee, H.-P. Power-Synchronization Control of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
- Khayat, Y.; Chen, P.; Bongiorno, M.; Johansson, B.; Majumder, R. FRT Capability of Grid-Forming Power Converters: An Antiwindup Scheme. IEEE Trans. Power Electron. 2024, 39, 12842–12855. [Google Scholar] [CrossRef]
- Barsali, S.; Ceraolo, M.; Pelacchi, P.; Poli, D. Control Techniques of Dispersed Generators to Improve the Continuity of Electricity Supply. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting, New York, NY, USA, 27–31 January 2002; Volume 2, pp. 789–794. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.; Wang, Z.; Wu, K.; Wang, H.; Hu, J.; Lu, C. A Virtual Synchronous Control for Voltage-Source Converters Utilizing Dynamics of DC-Link Capacitor to Realize Self-Synchronization. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1565–1577. [Google Scholar] [CrossRef]
- Saffar, K.G.; Driss, S.; Ajaei, F.B. Impacts of Current Limiting on the Transient Stability of the Virtual Synchronous Generator. IEEE Trans. Power Electron. 2023, 38, 1509–1521. [Google Scholar] [CrossRef]
- Rokrok, E.; Qoria, T.; Bruyere, A.; Francois, B.; Guillaud, X. Transient Stability Assessment and Enhancement of Grid-Forming Converters Embedding Current Reference Saturation as Current Limiting Strategy. IEEE Trans. Power Syst. 2022, 37, 1519–1531. [Google Scholar] [CrossRef]
- Zhao, X.; Flynn, D. Freezing Grid-Forming Converter Virtual Angular Speed to Enhance Transient Stability Under Current Reference Limiting. In Proceedings of the 2020 IEEE 21st Workshop on Control and Modeling for Power Electronics (COMPEL), Aalborg, Denmark, 9–12 November 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Chen, J.; Prystupczuk, F.; O’Donnell, T. Use of Voltage Limits for Current Limitations in Grid-Forming Converters. CSEE J. Power Energy Syst. 2020, 6, 259–269. [Google Scholar] [CrossRef]
- Zhou, J.Z.; Ding, H.; Fan, S.; Zhang, Y.; Gole, A.M. Impact of Short-Circuit Ratio and Phase-Locked-Loop Parameters on the Small-Signal Behavior of a VSC-HVDC Converter. IEEE Trans. Power Deliv. 2014, 29, 2287–2296. [Google Scholar] [CrossRef]
- Askarov, A.; Bay, Y.; Ufa, R.; Radko, P.; Ilyushin, P.; Suvorov, A. Signatures and Mechanism Analysis of Converter-Grid Subsynchronous Oscillations. Mathematics 2024, 12, 3884. [Google Scholar] [CrossRef]
- Li, Z.; Hu, J.; Chan, K.W. A New Current Limiting and Overload Protection Scheme for Distributed Inverters in Microgrids Under Grid Faults. IEEE Trans. Ind. Appl. 2021, 57, 6362–6374. [Google Scholar] [CrossRef]
- Lu, X.; Wang, J.; Guerrero, J.M.; Zhao, D. Virtual-Impedance-Based Fault Current Limiters for Inverter Dominated AC Microgrids. IEEE Trans. Smart Grid 2018, 9, 1599–1612. [Google Scholar] [CrossRef]
- Erdocia, J.; Urtasun, A.; Marroyo, L. Dual Voltage–Current Control to Provide Grid-Forming Inverters With Current Limiting Capability. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 3950–3962. [Google Scholar] [CrossRef]
- Baeckeland, N.; Seo, G.-S. Novel Hybrid Current Limiter for Grid-Forming Inverter Control During Unbalanced Faults. In Proceedings of the 2023 11th International Conference on Power Electronics and ECCE Asia (ICPE 2023—ECCE Asia), Jeju Island, Republic of Korea, 22–25 May 2023; pp. 1517–1522. [Google Scholar] [CrossRef]
- Rosso, R.; Engelken, S.; Liserre, M. On The Implementation of an FRT Strategy for Grid-Forming Converters Under Symmetrical and Asymmetrical Grid Faults. IEEE Trans. Ind. Appl. 2021, 57, 4385–4397. [Google Scholar] [CrossRef]
- Qoria, T.; Gruson, F.; Colas, F.; Kestelyn, X.; Guillaud, X. Current Limiting Algorithms and Transient Stability Analysis of Grid-Forming VSCs. Electr. Power Syst. Res. 2020, 189, 106726. [Google Scholar] [CrossRef]
- Lyu, X.; Du, W.; Mohiuddin, S.M.; Nandanoori, S.P.; Elizondo, M. Criteria for Grid-Forming Inverters Transitioning Between Current Limiting Mode and Normal Operation. IEEE Trans. Power Syst. 2024, 39, 6107–6110. [Google Scholar] [CrossRef]
- Ghoshal, A.; John, V. Anti-windup schemes for proportional integral and proportional resonant controller. In Proceedings of the National Power Electronic Conference, Roorkee, India, 10–13 June 2010; pp. 1–6. [Google Scholar]
- Teodorescu, R.; Blaabjerg, F.; Borup, U.; Liserre, M. A New Control Structure for Grid-Connected LCL PV Inverters with Zero Steady-State Error and Selective Harmonic Compensation. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, APEC’04, Anaheim, CA, USA, 22–26 February 2004; Volume 1, pp. 580–586. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A.; Fosso, O.B. Control System Tuning and Stability Analysis of Virtual Synchronous Machines. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 2664–2671. [Google Scholar] [CrossRef]
- Yuan, H.; Yuan, X.; Hu, J. Modeling of Grid-Connected VSCs for Power System Small-Signal Stability Analysis in DC-Link Voltage Control Timescale. IEEE Trans. Power Syst. 2017, 32, 3981–3991. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Design-Oriented Transient Stability Analysis of Grid-Connected Converters With Power Synchronization Control. IEEE Trans. Ind. Electron. 2019, 66, 6473–6482. [Google Scholar] [CrossRef]
- Kkuni, K.V.; Yang, G. Effects of Current Limit for Grid Forming Converters on Transient Stability: Analysis and Solution. Int. J. Electr. Power Energy Syst. 2024, 158, 109919. [Google Scholar] [CrossRef]
- Xin, H.; Huang, L.; Zhang, L.; Wang, Z.; Hu, J. Synchronous Instability Mechanism of P-f Droop-Controlled Voltage Source Converter Caused by Current Saturation. IEEE Trans. Power Syst. 2016, 31, 5206–5207. [Google Scholar] [CrossRef]
- Orihara, D.; Taoka, H.; Kikusato, H.; Hashimoto, J.; Otani, K.; Khaliqur, R.; Ustun, T.S. Theoretical Comparison of Current Limiting Algorithms in Grid-Forming Inverter in Terms of Transient Stability. IEEE Open J. Power Electron. 2025, 6, 109–119. [Google Scholar] [CrossRef]
- Askarov, A.; Rudnik, V.; Ruban, N.; Radko, P.; Ilyushin, P.; Suvorov, A. Enhanced Virtual Synchronous Generator with Angular Frequency Deviation Feedforward and Energy Recovery Control for Energy Storage System. Mathematics 2024, 12, 2691. [Google Scholar] [CrossRef]
- Mallemaci, V.; Mandrile, F.; Carpaneto, E.; Bojoi, R. Simplified Virtual Synchronous Compensator With Grid–Forming Capability. IEEE Trans. Ind. Appl. 2023, 59, 6203–6219. [Google Scholar] [CrossRef]
- Askarov, A.; Ruban, N.; Bay, Y.; Ufa, R.; Malkova, Y.; Suvorov, A. A Feedforward Control for Increasing the Damping Effect of Enhanced Current-Controlled Virtual Synchronous Generator. Electr. Power Syst. Res. 2024, 234, 110659. [Google Scholar] [CrossRef]
- Gkountaras, A.; Dieckerhoff, S.; Sezi, T. Evaluation of Current Limiting Methods for Grid Forming Inverters in Medium Voltage Microgrids. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 1223–1230. [Google Scholar] [CrossRef]
- He, X.; Desai, M.A.; Huang, L.; Dörfler, F. Cross-Forming Control and Fault Current Limiting for Grid-Forming Inverters. IEEE Trans. Power Electron. 2025, 40, 3980–4007. [Google Scholar] [CrossRef]
- Akagi, H.; Watanabe, E.H.; Aredes, M. Instantaneous Power Theory and Applications to Power Conditioning; Wiley IEEE Press: Hoboken, NJ, USA, 2007. [Google Scholar]
- Suvorov, A.; Askarov, A.; Ruban, N.; Rudnik, V.; Radko, P.; Achitaev, A.; Suslov, K. An Adaptive Inertia and Damping Control Strategy Based on Enhanced Virtual Synchronous Generator Model. Mathematics 2023, 11, 3938. [Google Scholar] [CrossRef]
- Aragon, D.; Unamuno, E.; Ceballos, S.; Barrena, J. Comparative small-signal evaluation of advanced grid-forming control techniques. Electr. Power Syst. Res. 2022, 211, 108154. [Google Scholar] [CrossRef]
- Ilyushin, P.V.; Shepovalova, O.V.; Filippov, S.P.; Nekrasov, A.A. The Effect of Complex Load on the Reliable Operation of Solar Photovoltaic and Wind Power Stations Integrated into Energy Systems and into Off-Grid Energy Areas. Energy Rep. 2022, 8, 1515–1529. [Google Scholar] [CrossRef]
- Yuan, M.; Chen, L.; Min, Y.; Gao, P.; Tan, B.; Wang, M. Lock-Up Problem in the Current-Limiting Mode of the Grid-Forming Converter with Priority-Based Limiter and Its Solution. IET Gener. Transm. Distrib. 2025, 19, e70052. [Google Scholar] [CrossRef]

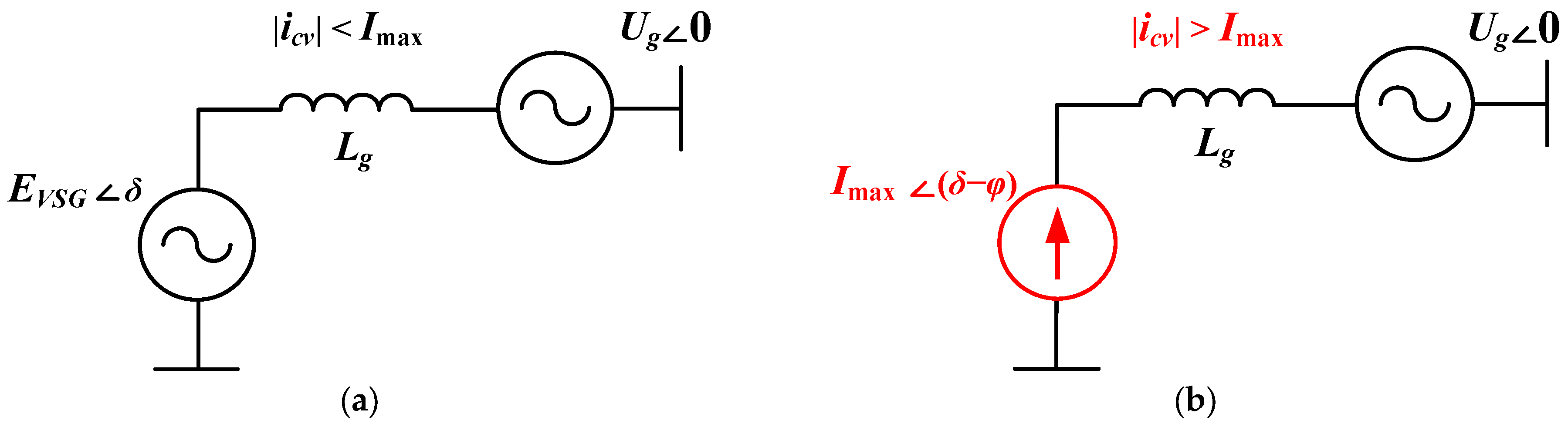

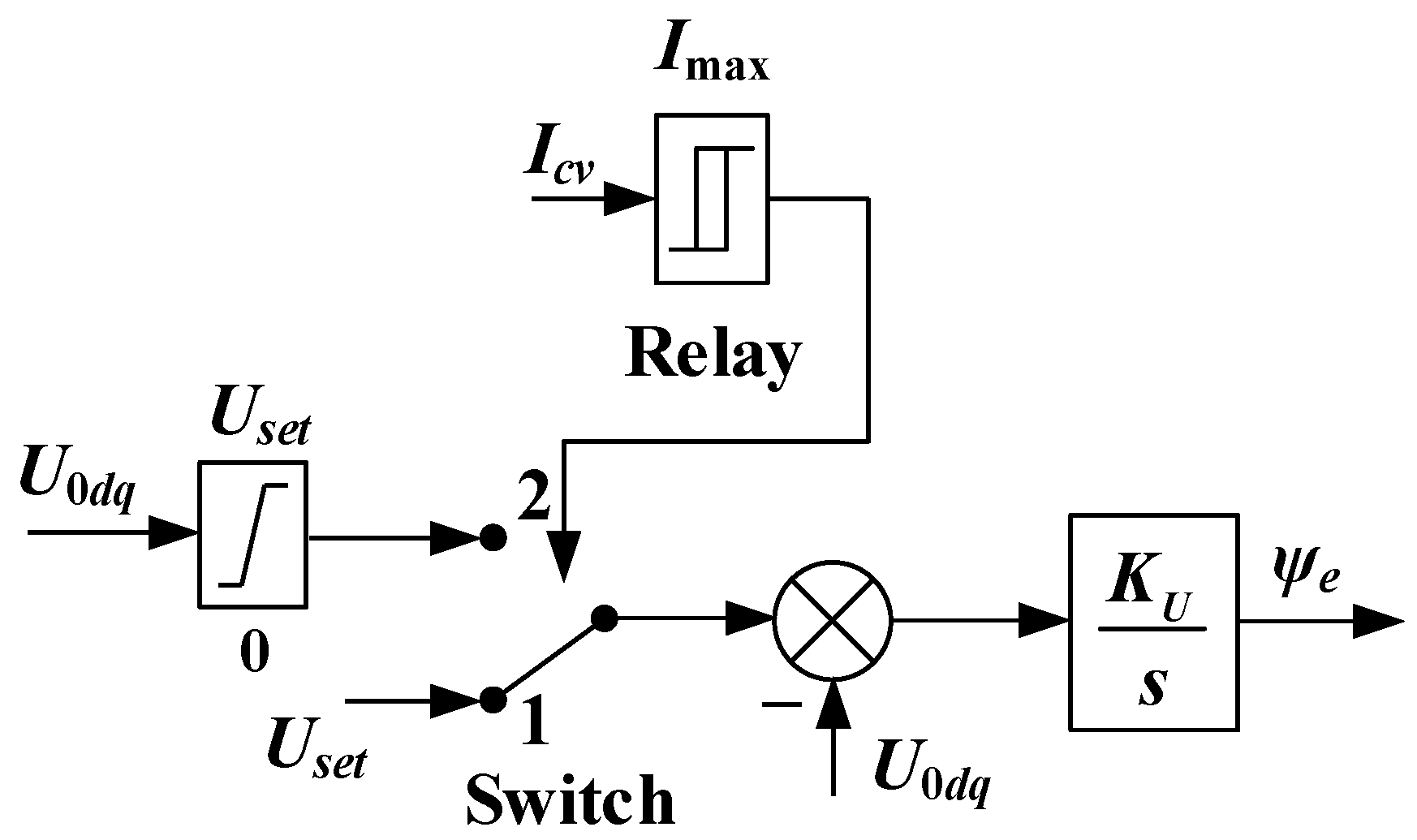
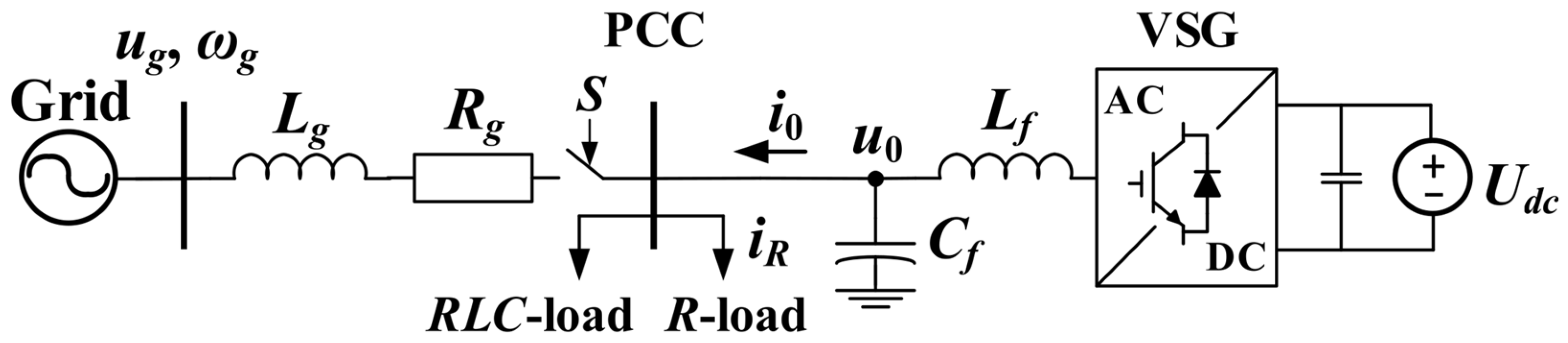
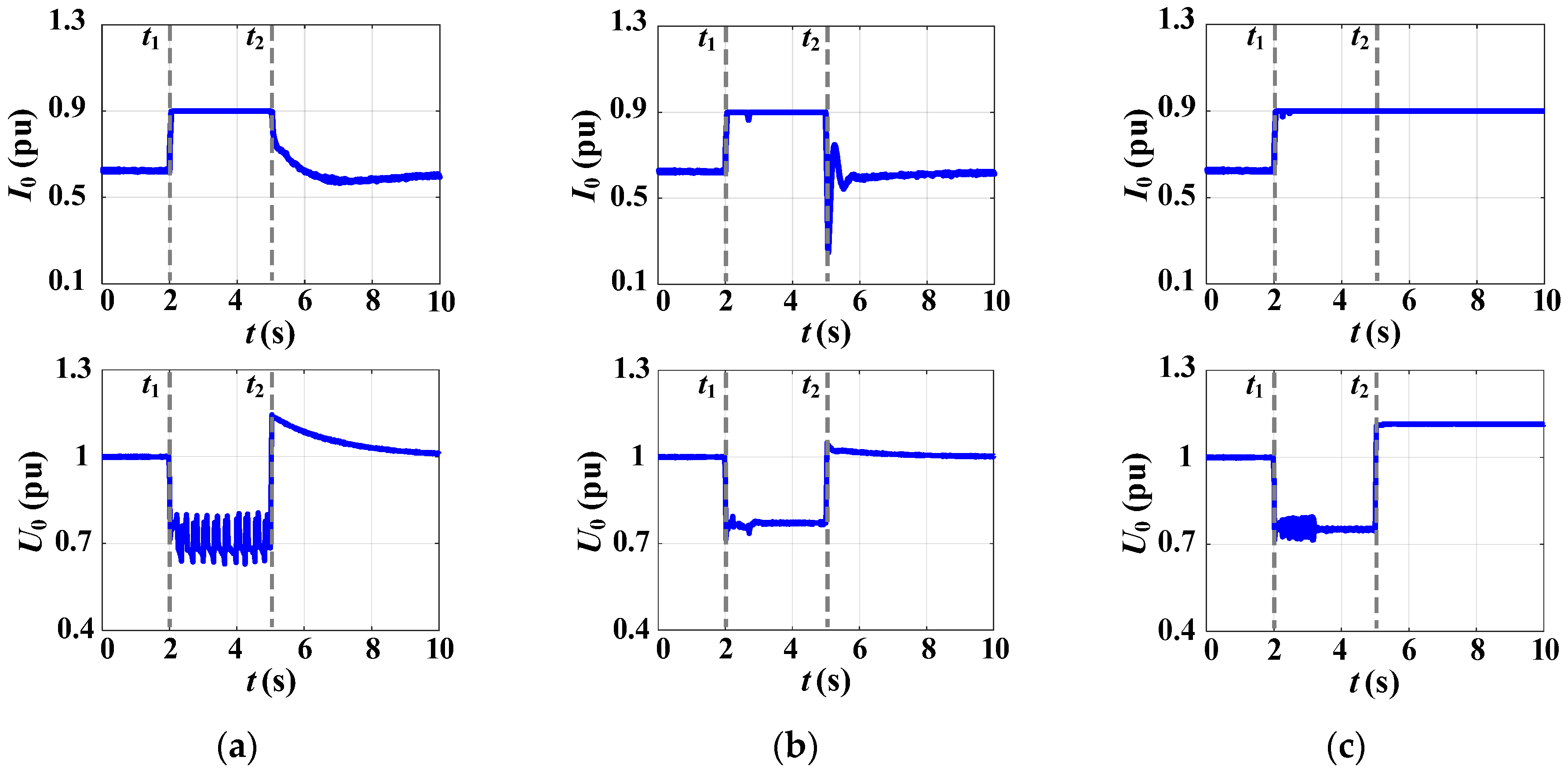
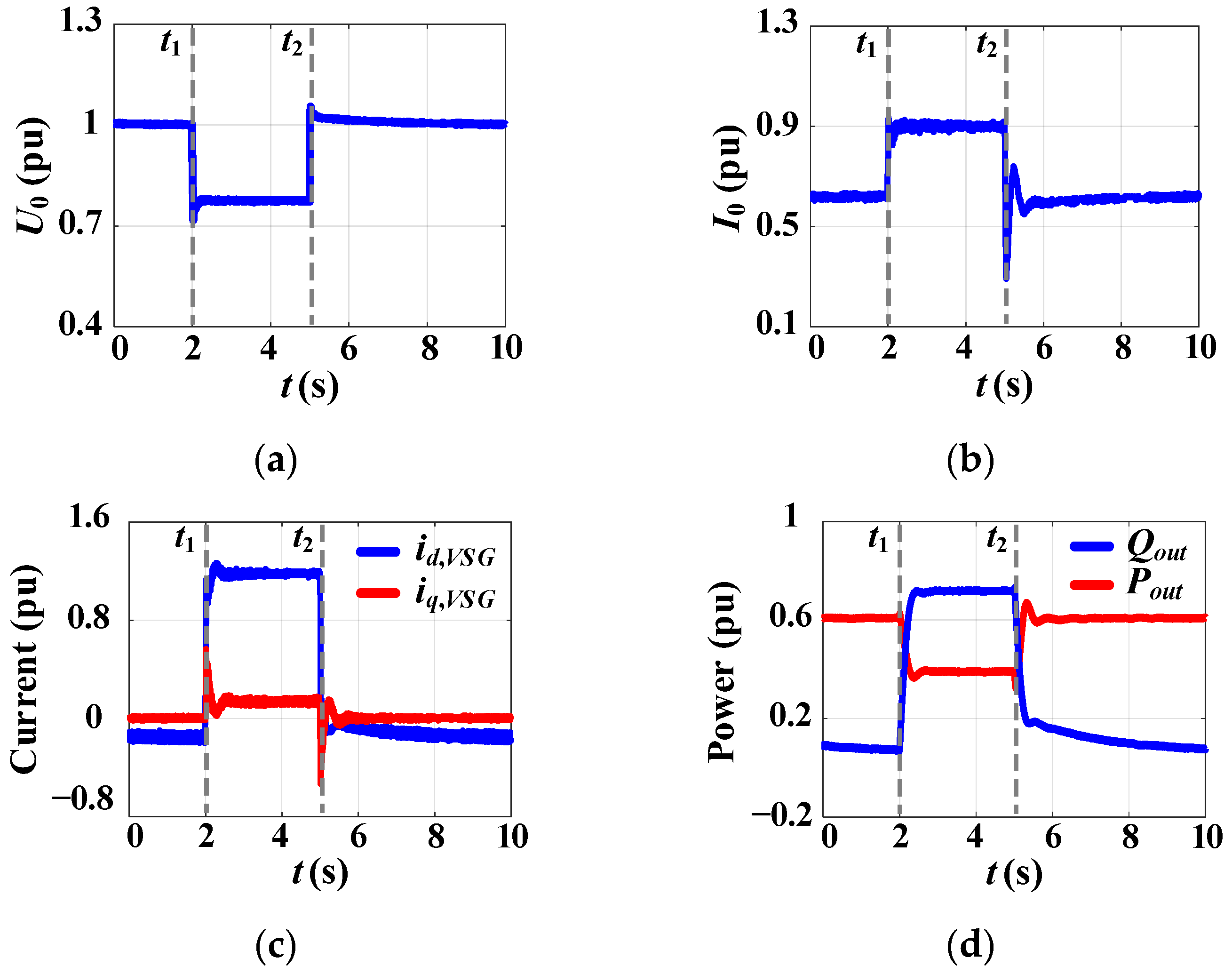
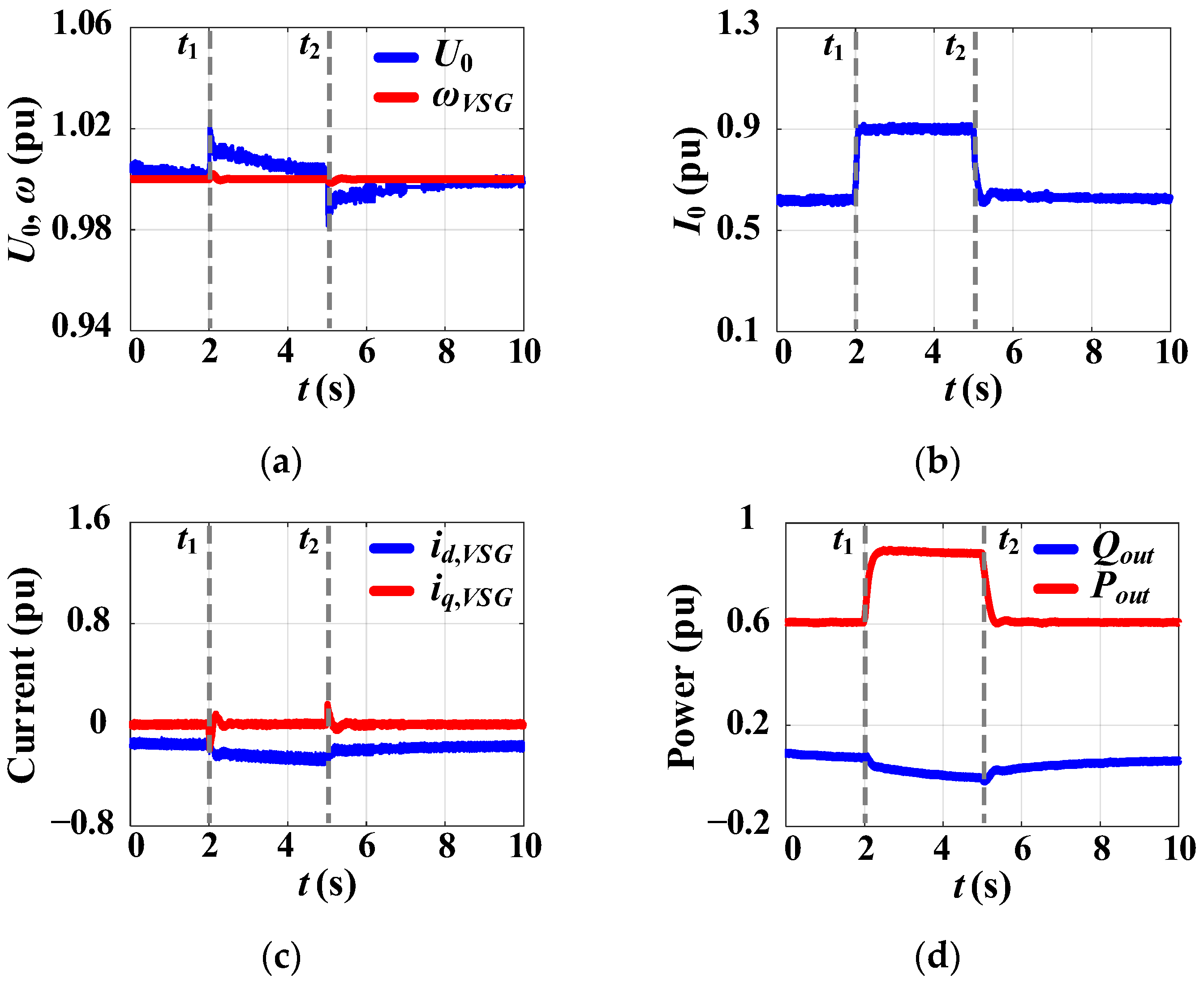
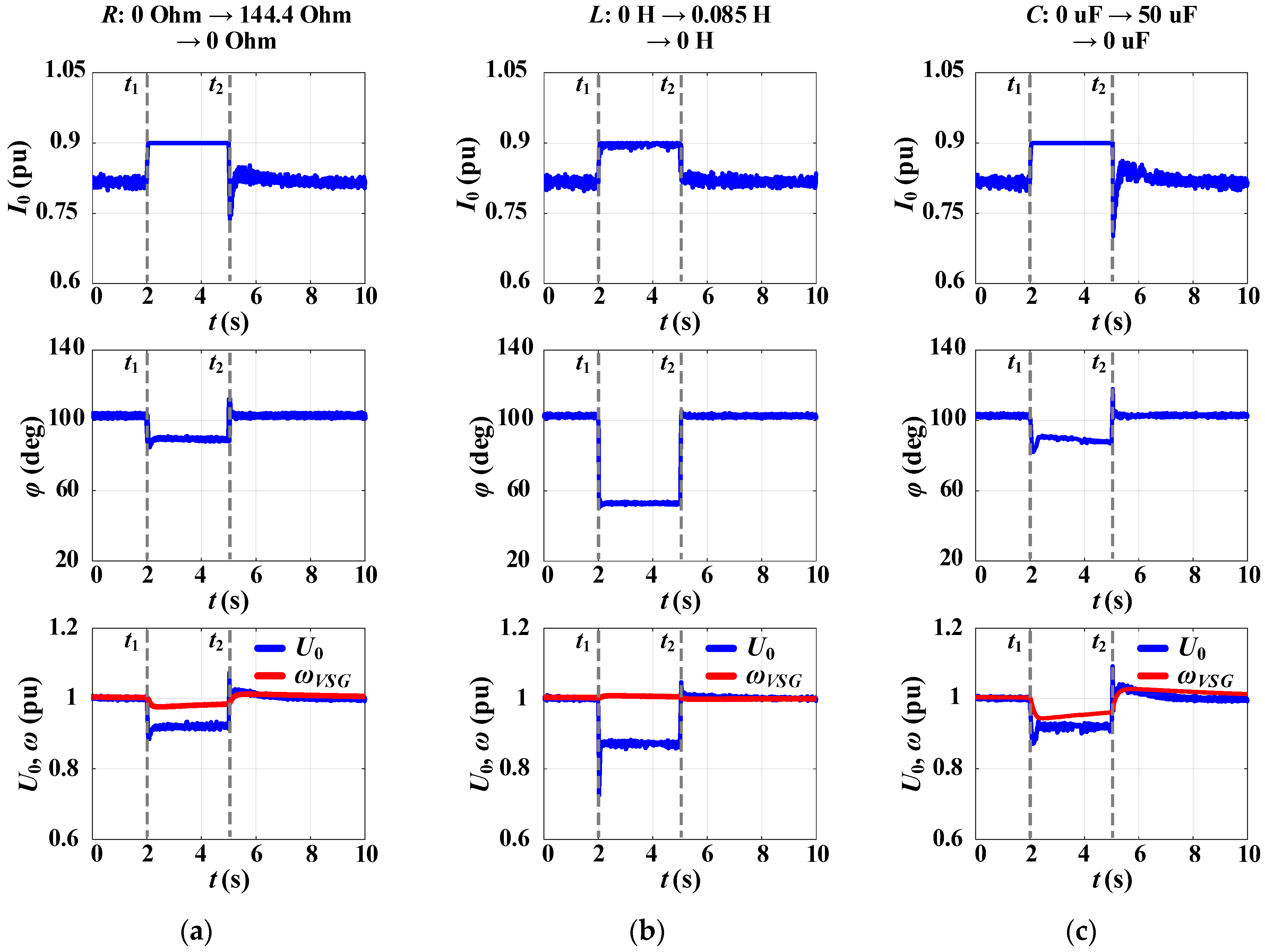
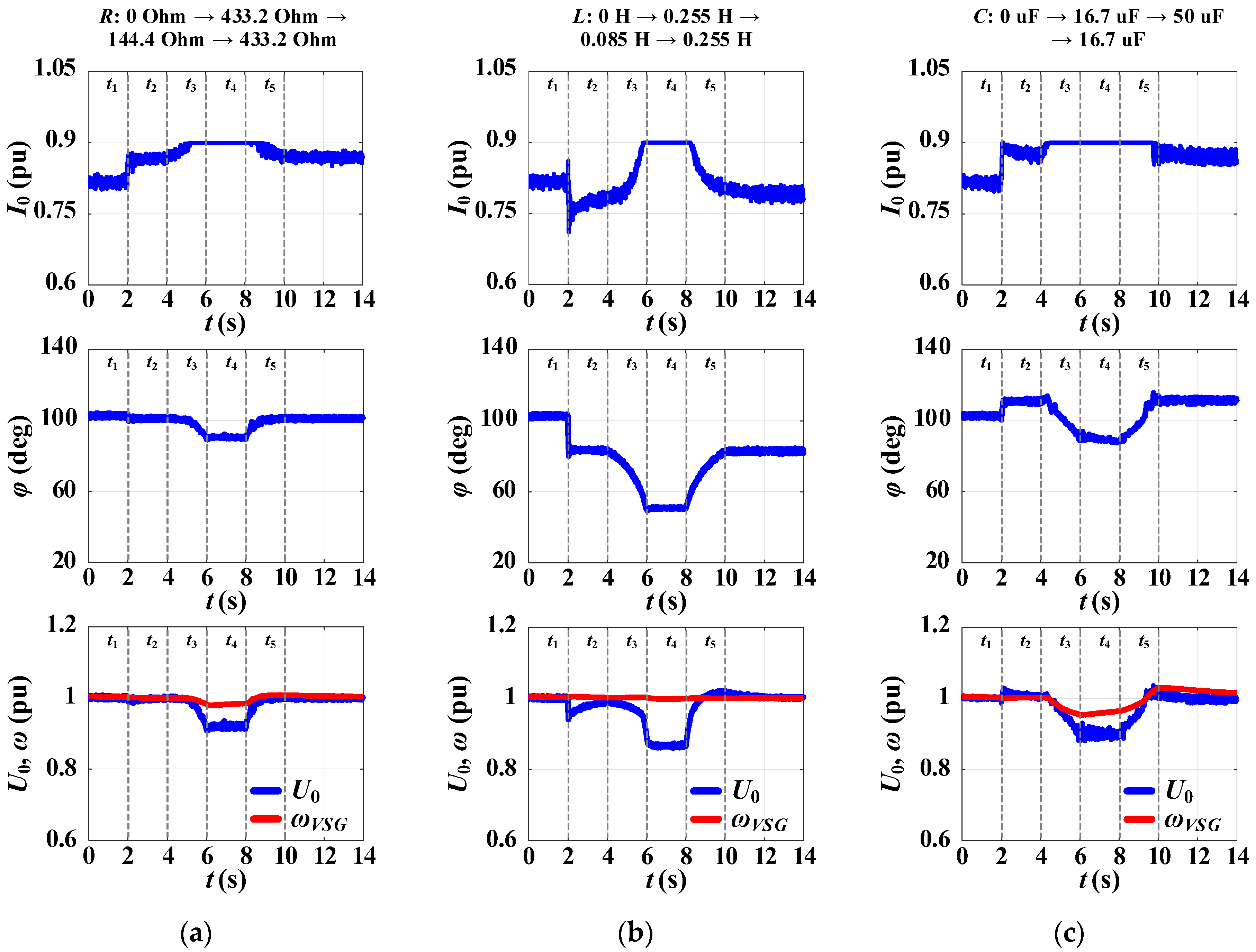
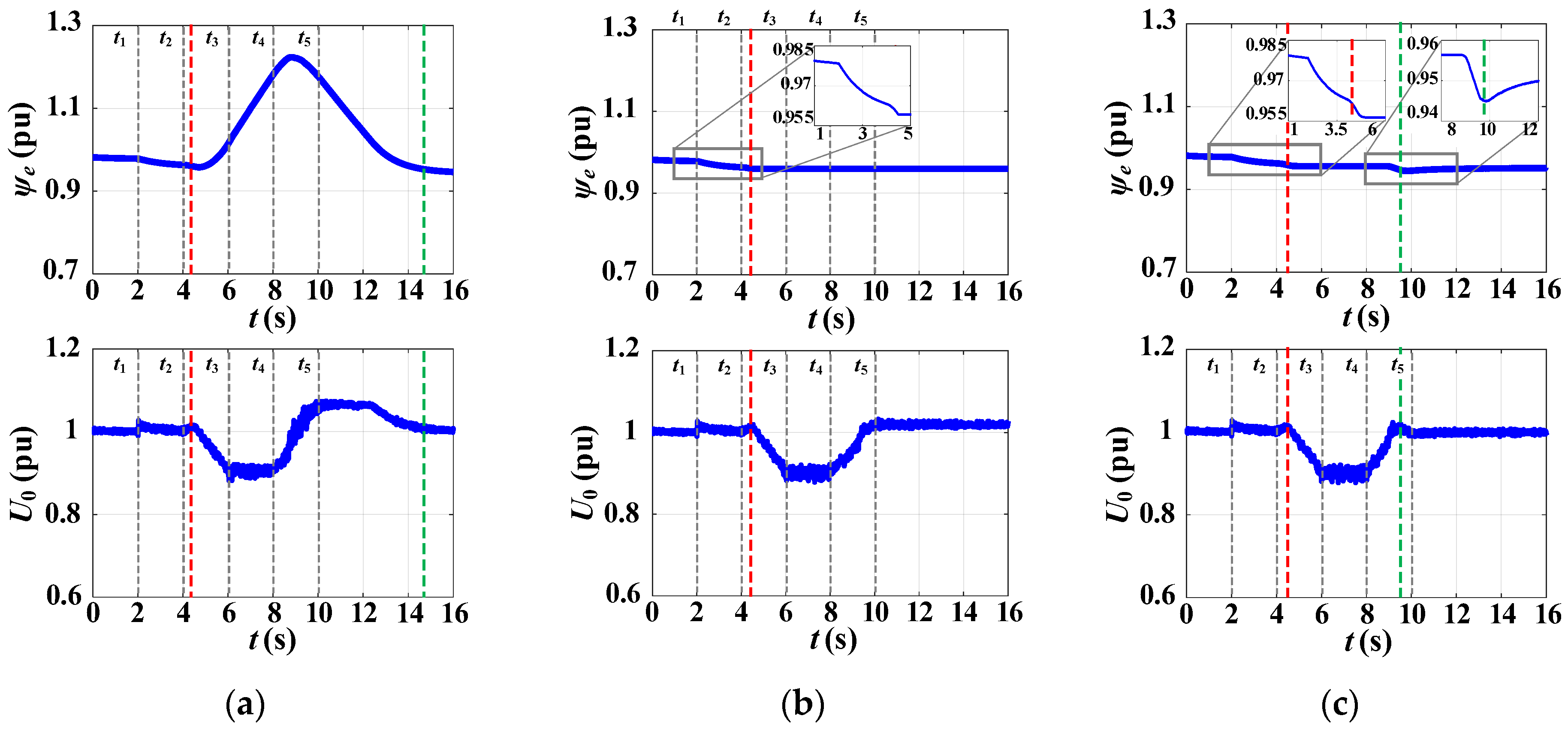


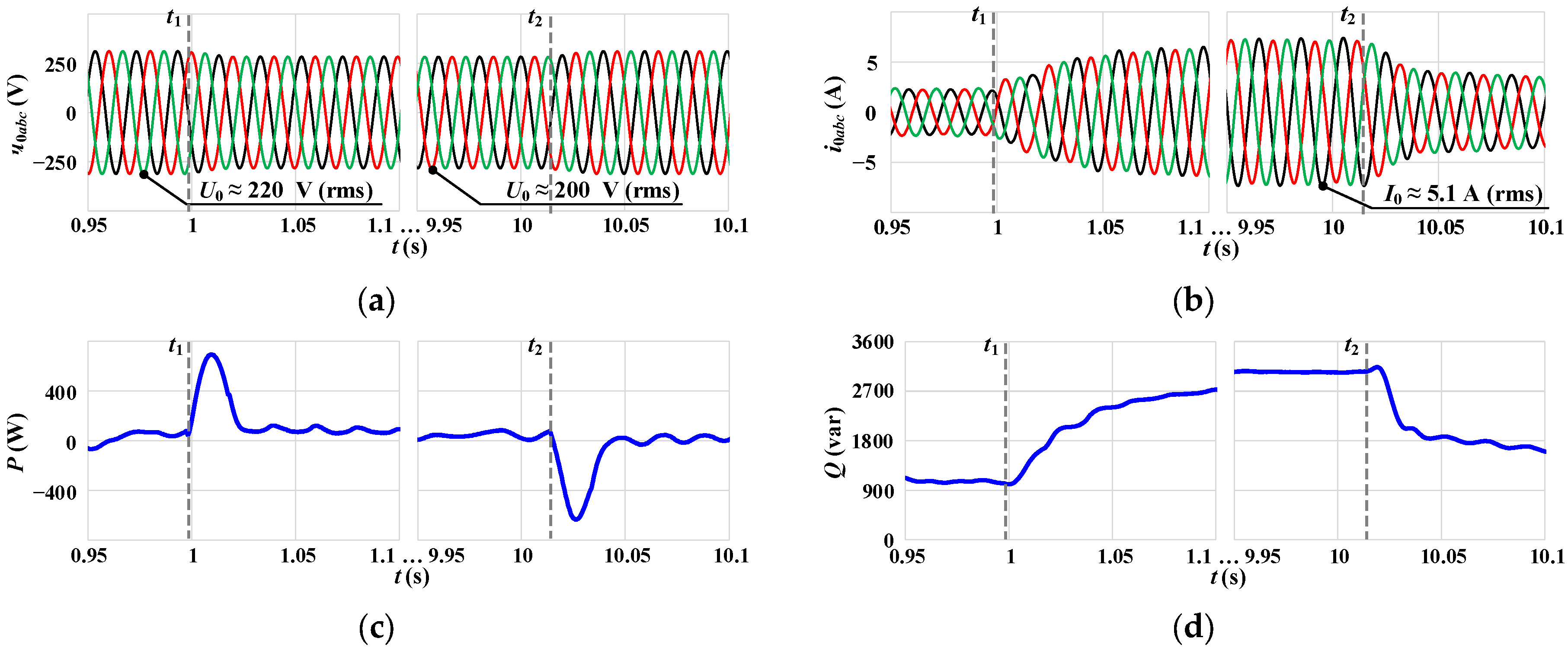
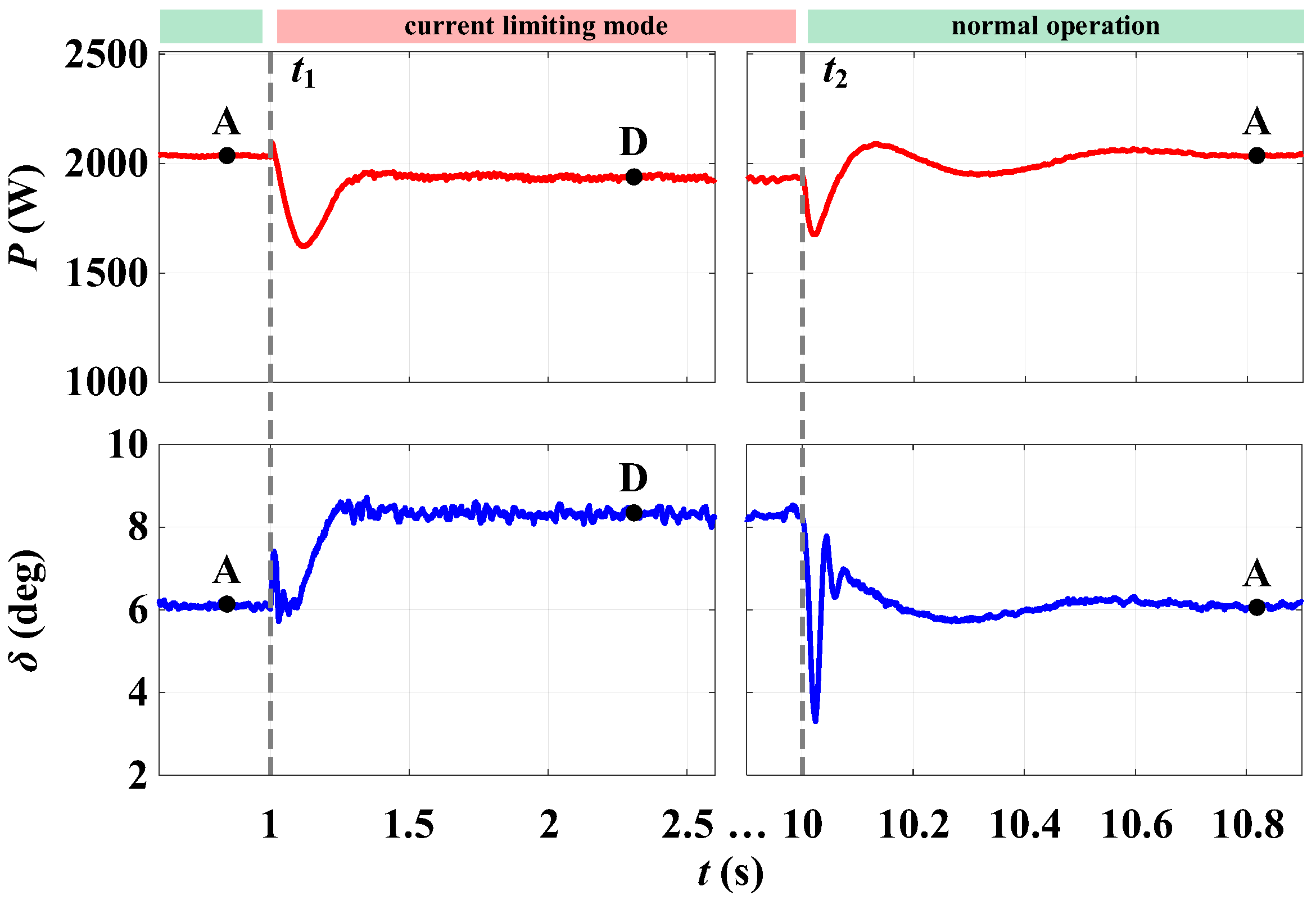
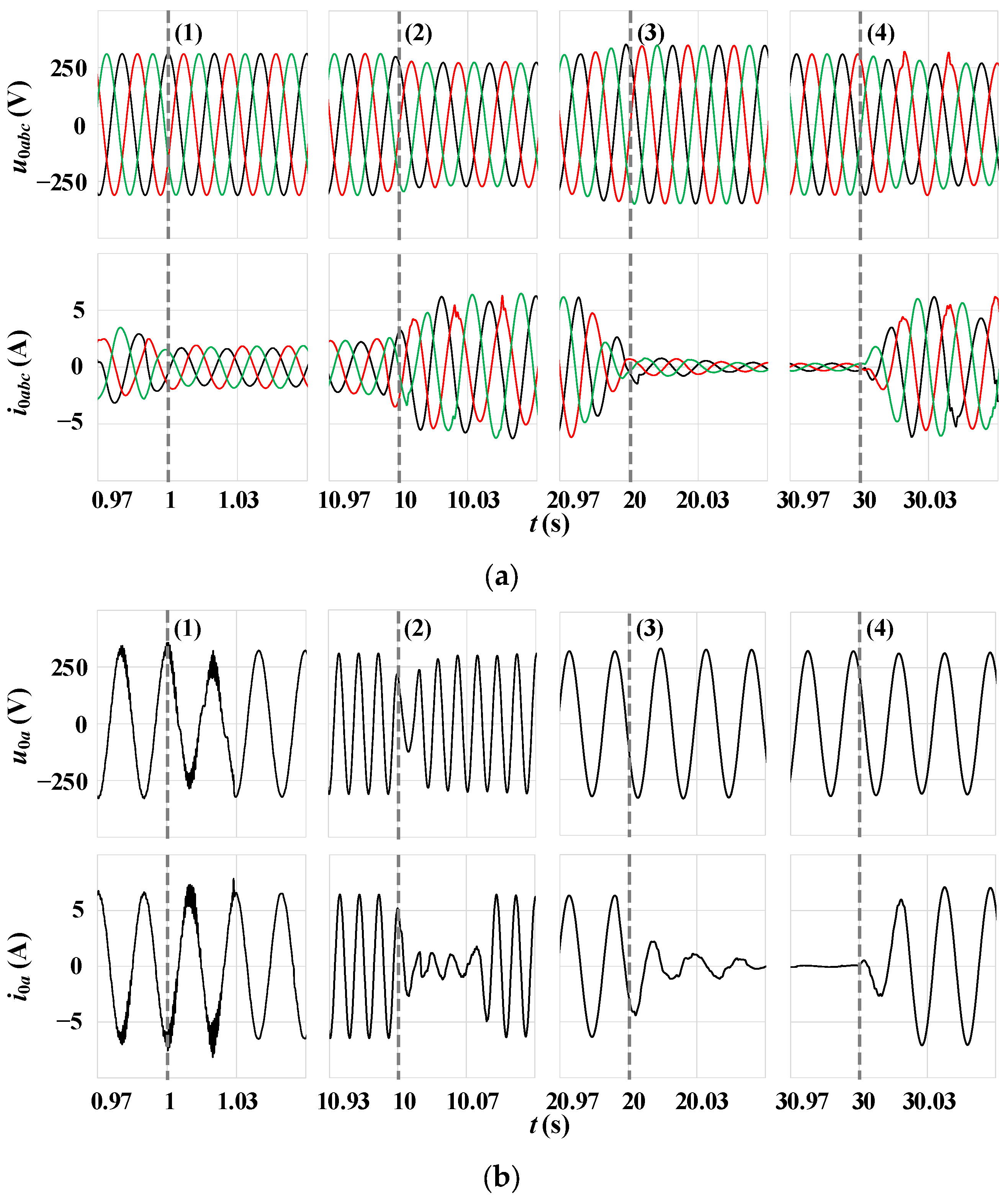
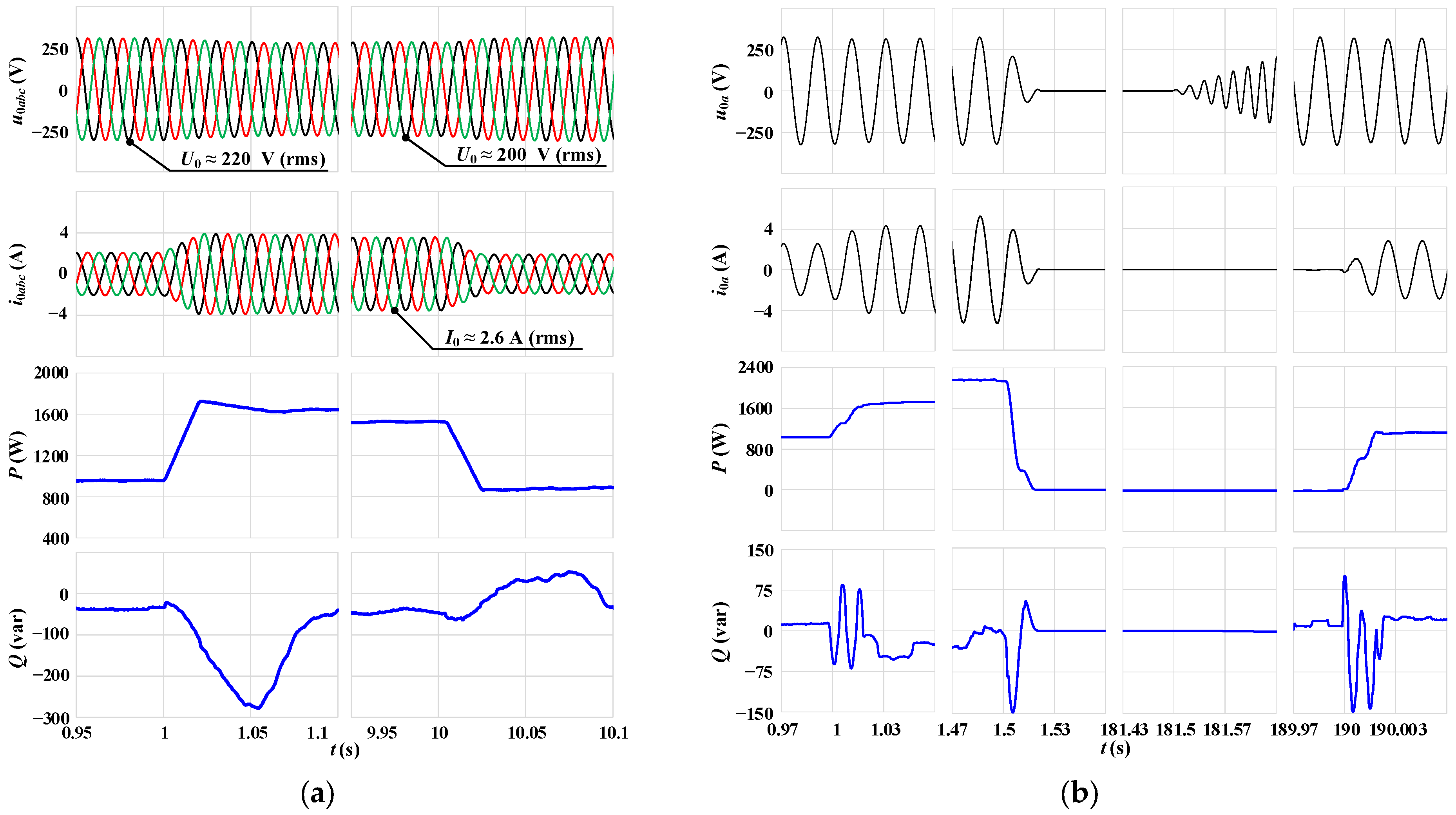
| Current-Limiting Method | Ref. | Key Features |
|---|---|---|
| Direct | [13,14,15,16,17,18,19,20,22,23,27] | Forms a reference signal for the inner current control loop based on instantaneous current values, only current amplitude, or current vector. Operates as a current-controlled source. In this regard, loss of grid-forming capabilities is possible. Fast-operating |
| Indirect | [30,31,32,33] | Based on the use of virtual impedance or voltage controller settings. Operates as a voltage-controlled source. The output current range is limited. To increase efficiency, settings must be changed during the process |
| Hybrid | [34,35,36] | Represent various combinations of direct and indirect methods. Complication of algorithms to prevent integrator saturation and exclude lock-up in current-limiting mode |
| Method | Current Limiter | Virtual Impedance | Voltage Limiter | Developed Algorithm | |
|---|---|---|---|---|---|
| Performance | |||||
| Group of CSAs | Direct | Indirect | Indirect | Hybrid | |
| Variable limited | I | E | E | I | |
| Phase regulation during limiting | No | Yes | Yes | Yes | |
| Wind-up strategy | Yes | Yes | Yes | Yes | |
| Latch-up strategy | No | No | No | Yes | |
| Grid-forming preservation | No | Yes | Yes | Yes | |
| Implementation burden | Small | Medium | Medium | High | |
| Output current range | Not reduced | Reduced | Reduced | Not reduced | |
| Applicability to other VSG structures | Yes | Yes | Yes | Yes | |
| Conditions and Features in the Current-Limiting Mode | Control Algorithm | |
|---|---|---|
| Traditional VC-VSG | Proposed CC-VSG | |
| Preserving the properties of a grid-forming source | No, only with additional control loops | Yes |
| Settling time of the output current I0 | <100 ms | <100 ms |
| Exceeding the Imax reference | <2% | <2% |
| Operation during RLC-load changes | Possible lock-up in the current-limiting mode, especially during C-load changes | Any type of load |
| Maximum permissible voltage sag until instability in the stand-alone mode (for overload case, w/o LVRT consideration) | Up to 0.75 pu | Up to 0.75 pu |
| Current phase regulation | No, only with additional control loops | Yes |
| Permissible value of the current phase φ | Limited range (determined by operating conditions, Equation (3)) | Wide range (up to 0÷180°) |
| VC blocking to prevent its saturation | No, only with additional control loops | Yes |
| Parameter | Value | ||
|---|---|---|---|
| Analytical | Experimental | ||
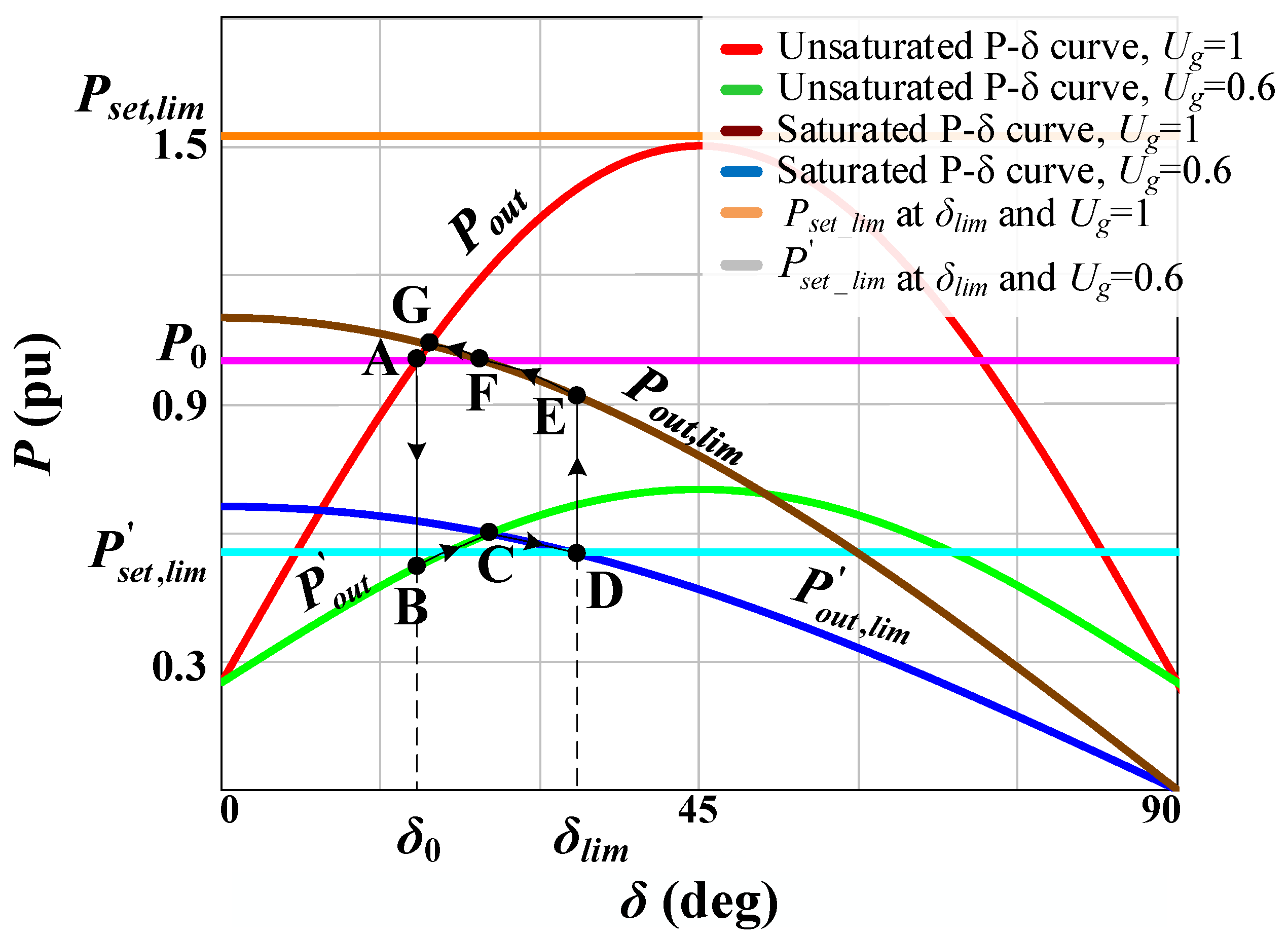
| Normal operation (point A) | Pout | 0.34 pu | 0.339 pu |
| δ0 | 7.09° | 6.13° | |
| Current-limiting mode (point D) | P′out,lim | 0.294 pu | 0.323 pu |
| δlim | 8.525° | 8.39° | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Askarov, A.; Radko, P.; Bay, Y.; Gusarov, I.; Kabirov, V.; Ilyushin, P.; Suvorov, A. Overcurrent Limiting Strategy for Grid-Forming Inverters Based on Current-Controlled VSG. Mathematics 2025, 13, 3207. https://doi.org/10.3390/math13193207
Askarov A, Radko P, Bay Y, Gusarov I, Kabirov V, Ilyushin P, Suvorov A. Overcurrent Limiting Strategy for Grid-Forming Inverters Based on Current-Controlled VSG. Mathematics. 2025; 13(19):3207. https://doi.org/10.3390/math13193207
Chicago/Turabian StyleAskarov, Alisher, Pavel Radko, Yuly Bay, Ivan Gusarov, Vagiz Kabirov, Pavel Ilyushin, and Aleksey Suvorov. 2025. "Overcurrent Limiting Strategy for Grid-Forming Inverters Based on Current-Controlled VSG" Mathematics 13, no. 19: 3207. https://doi.org/10.3390/math13193207
APA StyleAskarov, A., Radko, P., Bay, Y., Gusarov, I., Kabirov, V., Ilyushin, P., & Suvorov, A. (2025). Overcurrent Limiting Strategy for Grid-Forming Inverters Based on Current-Controlled VSG. Mathematics, 13(19), 3207. https://doi.org/10.3390/math13193207








