Abstract
In recent years, numerous constrained multi-objective evolutionary algorithms (CMOEAs) have been proposed to tackle constrained multi-objective optimization problems (CMOPs). However, most of them still struggle to achieve a good balance among convergence, diversity, and feasibility. To address this issue, we develop an adaptive constraint-boundary learning-based two-stage dual-population evolutionary algorithm for CMOPs, referred to as CL-TDEA. The evolutionary process of CL-TDEA is divided into two stages. In the first stage, two populations cooperate weakly through environmental selection to enhance the exploration ability of CL-TDEA under constraints. In particular, the auxiliary population employs an adaptive constraint-boundary learning mechanism to learn the constraint boundary, which in turn enables the main population to more effectively explore the constrained search space and cross infeasible regions. In the second stage, the cooperation between the two populations drives the search toward the complete constrained Pareto front (CPF) through mating selection. Here, the auxiliary population provides additional guidance to the main population, helping it escape locally feasible but suboptimal regions by means of the proposed cascaded multi-criteria hierarchical ranking strategy. Extensive experiments on 54 test problems from four benchmark suites and three real-world applications demonstrate that the proposed CL-TDEA exhibits superior performance and stronger competitiveness compared with several state-of-the-art methods.
Keywords:
evolutionary algorithm; constraint boundary learning; two-stage; dual-population; cascading multi-criteria hierarchical ranking MSC:
68W50; 65K10; 49K30
1. Introduction
In practice, many optimization problems must balance multiple competing objectives while meeting various constraints, such as water resource management [1,2], robust analog circuit design [3], and so on. Such problems are called CMOPs [4,5]. Their mathematical formulation is given by:
where presents a solution in the D-dimensional decision space and m represents the number of objectives. and refer to i-th inequality and j-th equality constraint, respectively. In the constrained evolutionary optimization, the constraint violation degree of x on the j-th constraint is defined as follows:
where is a small positive tolerance parameter, converting the equality constraints into inequality constraints. In this work, the is set to . According to Equation (2), the total constraint violation of x is computed as:
when , solution x is called a feasible solution. Otherwise, solution x is called an infeasible solution.
Due to the existence of constraints, the objective space in constrained multi-objective optimization problems (CMOPs) may be divided into challenging shapes, such as long and discontinuous feasible regions, discrete feasible regions, or even disjoint feasible regions [6,7]. These characteristics make it difficult for common multi-objective evolutionary algorithms (MOEAs) to effectively solve CMOPs. To overcome these difficulties, early studies incorporated constraint-handling techniques (CHTs) into MOEAs. The most widely used CHTs include the constraint dominance principle (CDP) [8], the -constraint method [9,10,11], penalty functions [12], and stochastic ranking [13]. Although effective to some extent, these methods often rely heavily on feasible solutions and may underutilize valuable information from infeasible solutions. More recent works have emphasized that properly exploiting infeasible solutions can significantly enhance the search process [14,15].
Based on these insights, a large number of constrained MOEAs (CMOEAs) have been proposed, which can be broadly classified into two categories. The first category is multi-stage algorithms [7,10,16,17], where the evolutionary process is divided into multiple phases, each employing a different CHT. Representative methods include PPS [10], ToP [18], CMOEA-MS [19], and MSCMO [20]. The second category is multi-population algorithms [11,21], which leverage the cooperation among populations to enhance the search capability and promote convergence toward the constrained Pareto front (CPF). Typical representatives are C-TAEA [22], ACREA [23], and CMOEA-PP [24].
While these approaches have demonstrated certain effectiveness, most still struggle to simultaneously balance convergence, diversity, and feasibility, often failing to obtain well-converged and well-distributed feasible solutions [25,26]. To address this gap, this work proposes a novel adaptive constraint-boundary learning-based two-stage dual-population evolutionary algorithm (CL-TDEA) for CMOPs. The key contributions of this work are summarized as follows:
- (1)
- This paper adopts a novel two-stage and dual-population evolutionary algorithm for CMOPs. The first stage aims at making the auxiliary population approach the Unconstrained Pareto Front (UPF) and assisting the main population to cross the infeasible regions. The second stage aims at making the main population and auxiliary population converge to the CPF from the feasible side and infeasible side, respectively.
- (2)
- A constraint boundary learning mechanism is designed that adaptively adjusts according to the proportion of feasible solutions, which can help the main population of the first stage fully explore the constraint space and further improve the exploration ability of the main population. Moreover, it can drive the main population to cross the infeasible regions as well.
- (3)
- A cascaded multi-criteria hierarchical ranking-based environment selection is proposed to update the auxiliary population of the second stage, including non-dominated sorting, reverse objective sorting, convergence sorting, and diversity sorting. Thus, this mechanism can discover different types of promising infeasible solutions and further assist the population to find the complete CPF.
In summary, the key novelty of the proposed algorithm lies in three aspects. First, it introduces a two-stage and dual-population evolutionary framework for CMOPs, which fundamentally differentiates it from recent algorithms of a similar class. Second, the algorithm achieves a more effective balance between exploration and exploitation by employing a constraint boundary learning mechanism that adaptively adjusts according to the proportion of feasible solutions. Third, our method provides a cascaded multi-criteria hierarchical ranking-based environmental selection for updating the auxiliary population. These features collectively make the proposed algorithm a distinct and promising contribution to the field of CMOPs.
2. Related Work and Motivation
2.1. Related Work
In recent years, researchers have developed numerous CMOEAs for CMOPs. The existing CMOEAs can be broadly categorized into the following three groups.
- (1)
- Multi-population-based CMOEAs: The main idea of this category is to utilize the cooperation of multiple populations to guide solutions to converge toward the CPFs. For instance, Li et al. [22] developed a two-archive algorithm C-TAEA, where these two archives evolve feasible solutions and infeasible solutions, respectively. Ming et al. [27] proposed a concept of collaborative multi-population assistance (CMOEMT), with the main algorithmic innovation being the enhancement of mating pools and environmental selection capabilities. Liu et al. [28] developed a bidirectional co-evolution algorithm with two populations for CMOPs (BiCO), where two populations can approach the CPFs from feasible sides and infeasible sides, respectively. In [24], a cooperative algorithm with two populations (CMOEA-PP) was designed. In CMOEA-PP, the propulsive population only searched corner and center solutions, while the normal population searched solutions in all feasible regions. Moreover, Yang et al. [29] developed a new dual-population algorithm (dp-ACS), where the main population is optimized by the designed adaptive constraint strength function.
- (2)
- Multi-stage-based CMOEAs: This category divides the evolution process into multiple stages, and each stage utilizes different strategies to deal with constraints. A typical example is PPS including push and pull search stages [10]. In the push stage, PPS ignores constraints and aims at making the population approach the UPFs. In the pull stage, an improved constraint method was designed to deal with constraints. In [18], a two-phase framework (ToP) was proposed. The first phase aims to search for promising feasible regions, while the second phase applies a CMOEA to obtain the final solutions. Similarly, Tian et al. [19] designed a two-stage algorithm (CMOEA-MS) that is capable of dynamically adjusting the priority relationships between objectives and constraints. In [30], a three indicator-based two-stage CMOEA (TSTI) was developed. Moreover, Ma et al. [11] proposed a multi-stage CMOEA (MSCMO) for CMOPs, in which constraints were added one after the other handled in different stages of evolution.
- (3)
- Multi-stage and multi-population-based CMOEAs: In order to maintain the balance between population diversity and convergence, some researchers have proposed the theoretical idea of two-stage two-population framework. In [31], a co-evolution framework for dual populations, called CCMO, is proposed. In simple terms, in two different stages, one population deals with CMOP, and the other population solves CMOP in the unconstrained case to further maintain the diversity of the algorithm. Ming et al. [7] proposed a two-population two-stage evolutionary algorithm (CTSEA). In phase 1, the algorithm ignores the constraints, finds feasible solutions, and then obtains a good PF. In stage 2, the CPF is obtained considering the constraints.
- (4)
- Multi-ranking-based CMOEAs: Recently, some researchers developed the multi-ranking technique to balance convergence, diversity, and feasibility. Ma et al. [32] utilized two rankings to design a fitness function and embedded them into NSGA-II [8], where one ranking is based on the CDP and the other ranking is based on the Pareto dominance. Zhou et al. [33] applied the multi-ranking technique to integrate the convergence, diversity, and feasibility indicators. Cheng et al. [34] proposed a method of using infeasible solutions to handle subpopulations, thereby identifying narrow feasible regions.
2.2. Motivations of This Work
In recent years, although numerous CMOEAs have been developed, many existing methods still face challenges in obtaining well-distributed and convergent non-dominated feasible solution sets under complex constraints. This is mainly because such constraints can divide the objective space into narrow, discrete, or even disconnected feasible regions, which greatly increases the difficulty of the search process. In such a way, the non-dominated feasible solutions are distributed in different feasible regions. Under such circumstances, CMOEAs have difficulty finding the entire Pareto optimal solutions. Additionally, sometimes the Pareto optimal solutions are distributed on the constraint boundaries, which are challenging to obtain as well. This is because once CMOEAs emphasize the objective optimization, CMOEAs will obtain solutions far away from the CPF. The common idea of CMOEAs in solving CMOPs is to make the population searches feasible regions. Unfortunately, such an idea easily makes the population fall into partial feasible regions. For this problem, researchers attempt to use the infeasible solutions to relieve the problem. This is because infeasible solutions can make CMOEAs search more broadly and further make CMOEAs find more feasible regions. Although such CMOEAs are beneficial to find the entire CPF, the solutions have poor distributions on the CPF. In order to visually present the above two findings, we plot the distributions of solutions obtained by four representative CMOEAs (i.e., C-TAEA, PPS, MSCMO, and TiGE2) on DC1-DTLZ1 and LIRCMOP11 in Figure 1. The gray area represents the feasible region, the purple line represents the Pareto Front (PF), and the blue dots represent the feasible solutions. Note that four CMOEAs belong to four categories of CMOEAs, respectively. From this figure, we can intuitively see that all CMOEAs fail to obtain solutions that evenly distribute on the CPF. Based on this, the validity of the two findings mentioned above is confirmed.
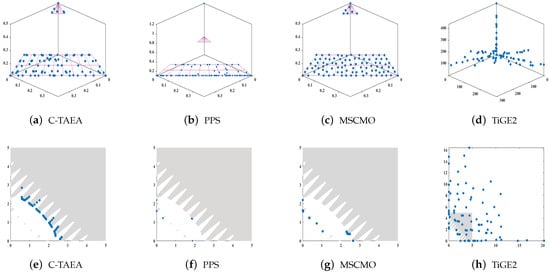
Figure 1.
Distributions of final solutions obtained by four representative CMOEAs on 3-objective DC1-DTLZ1 and 2-objective LIRCMOP11.
According to the above figure, we know that utilizing infeasible solutions can improve the exploration and further prevents the solutions from falling into partial feasible regions. However, utilizing infeasible solutions will bring a problem as well: the feasibility of final solutions is difficult to guarantee. As a result, how to guarantee the feasibility of final solutions in utilizing infeasible solutions is important. This is because when the solutions are feasible, convergence and diversity only make sense.
Based on the aforementioned observations and considerations, in this work, we propose an adaptive constraint-boundary learning-based two-stage dual-population evolutionary algorithm for CMOPs.
3. The Proposed CL-TDEA
In this section, we elaborate on the proposed TDEA. To be specific, the framework of CL-TDEA is given, and then the details of TDEA are presented.
3.1. Framework of CL-TDEA
The overall framework of CL-TDEA is outlined in Algorithm 1. Specifically, two populations—the main population () and the auxiliary population (), each consisting of N solutions—are randomly initialized in the decision space. The constraint violation (CV) value of each solution in the auxiliary population is then computed using Equation (3). After initialization, CL-TDEA proceeds into an iterative process, where each iteration consists of two stages. In the first stage, the dynamic constraint boundary for is calculated. At the same time, the fitness estimation values of all solutions in and are computed and ranked. Here, we adopt the fitness estimation scheme from SPEA2 [35], which is mathematically described as follows:
where C denotes the set of all solutions in the current population and is its size. The constant 2 is used as an offset to avoid division by zero. Here, measures the convergence of solution x, while the second term corresponds to the density estimation. Specifically, is defined as:
where
Here, means that solution y constraint-dominates solution x under the constraint dominance principle (CDP). The density estimation evaluates the crowding degree of solution x as:
where denotes the distance from solution x to its i-th nearest neighbor and is a small positive constant.
| Algorithm 1 Framework of CL-TDEA. |
Input: N (population size) Output: P (final population)
|
Where represents the i-th reference point, representing an ideal solution and d(x, ) denotes the distance from an individual x to its i-th reference point, with k set to . denotes the total distance from x to all reference points, indicating its overall spread. z serves as a placeholder for any solution in C when identifying the set’s minimum or maximum and may include x itself. denotes a small positive offset added to avoid division by zero and maintain numerical stability.
Then, based on the ranking values of solutions in and , binary tournament selection is carried out to construct the mating pool. Subsequently, genetic operators are applied to generate offspring, which are then combined with and , respectively. Finally, the environmental selection procedure of SPEA2 [35] is applied to the two combined populations (, ) to select N solutions for the next generation.
In the second stage, elite mating selection together with genetic operators is first applied to generate offspring, which are then combined with and . The combined population is subsequently divided into the feasible population and the infeasible population . Finally, NSGA-II’s environmental selection [8] is applied to to select parents for the next generation while the proposed cascaded sorting-based environmental selection is applied to for the same purpose. Table 1 provides explanations of all the notations.

Table 1.
Notation used in this paper.
3.2. The Adaptive Constraint Boundary Learning Mechanism
The mechanism aims at making the auxiliary population able to continuously learn the constraint boundary and further provide the main population useful information. More details of the mechanism are as follows: First, the constrained boundary is constructed as follows:
where is the constrained boundary, t is the current generations, and T is the predefined maximum generations. Here, is designed to dynamically adjust with the current generation t. The motivation for this design is as follows: (1) in the early stage, since most feasible solutions lack quality, the auxiliary population should explore unexplored regions, requiring a larger constraint boundary; (2) in the later stage, with many infeasible solutions introduced and the feasible region expanded, the auxiliary population should move closer to the constraint boundary, which should therefore be smaller. Based on the above motivation, the is calculated by the following formula:
where is the constraint violation of the i solution, t is the current generations, T is the predefined maximum generations, is the initial values of main population and auxiliary population, and is the parameter controlling the descent rate . Here, denotes the indicator function, returning 1 when the condition holds and 0 otherwise.
3.3. The Elite Mating Selection
The elite mating selection Algorithm 2 aims at fully utilizing the information of and to select high-quality parents for variation in the second stage. If or contains fewer than N feasible solutions, two solutions are randomly selected from their combined population, and then the solution having the smaller value is retained to enter the mating pool. Otherwise, parents are selected from and . When the random number is less than 0.5, a parent is selected from . On the contrary, a parent is selected from . During the selection process, two solutions are randomly selected. Then, the solution with good convergence and diversity is selected to enter the mating pool, where the convergence and diversity are respectively measured by the constraint dominance principle (i.e., Equation (5)) and diversity measure (i.e., Equation (7)) in SPEA2 [35]. The above process is repeated until the size of the mating pool is N.
| Algorithm 2 The elite mating selection. |
Input: (main population), (auxiliary population), N (population size) Output: (mating pool)
|
During the elite mating pool selection process, the choice of high-quality parents not only enhances the population’s diversity but also drives the population towards UPF, effectively eliminating interference from redundant solutions to high-quality ones and significantly reducing computational costs. By implementing an equal probability mechanism for selecting parents from both the main and auxiliary populations, an effective trade-off between diversity and convergence is attained. When selecting solutions from the main population (), the elite mating pool evaluates both feasibility and convergence potential, promoting faster movement toward the CPF. For the auxiliary population (), it prioritizes diversity, boosting exploration and reducing the likelihood of local optima. Therefore, this elite mating strategy ensures the feasibility of solutions while fostering rapid convergence without sacrificing diversity, thereby optimizing the overall solution quality and computational efficiency of the algorithm.
3.4. The Cascading Multi-Criteria Hierarchical Ranking Environment Selection
The cascaded multi-criteria hierarchical ranking-based environmental selection Algorithm 3 focuses on updating in the second stage. Initially, non-dominated sorting is applied in the -objective space to divide the combined population of , , and offspring into different fronts. The objectives consist of m objectives and the objective. Infeasible solutions from the first front are then selected to help maintain the diversity of . If the size of > N, reverse objective (Equation (11)), convergence sorting (Equation (5)), and diversity sorting (Equation (7)) are used to truncate , with the reverse objective defined as follows:
where the reverse objective sorting aims at improving the exploration ability of CL-TDEA by providing the force to jump out of the locally feasible regions. The diversity sorting from small to large is implemented based on Formula (7). Conversely, if < N, sort () non-dominantly by objective and fitness values (Equation (4)) and fill with the highest-ranked solutions until it reaches N members.
| Algorithm 3 Cascading multi-criteria hierarchical ranking environment selection. |
Input: U (combined population), N (population size) Output: (auxiliary population)
|
The process for implementing reverse objective sorting, convergence sorting, and diversity sorting is as follows: First, non-dominated sorting from NSGA-II [8] is applied to the reverse objective (i.e., Formula (10)) to partition the solutions of the front into multiple fronts (e.g., , , etc.). Then, solutions from to are selected to form the next generation, with l determined by . Finally, the remaining solutions are chosen from the front based on convergence and diversity sorting.
3.5. Exploration–Exploitation Balance
One of the key challenges in constrained multi-objective optimization is to maintain a proper balance between exploration and exploitation. The proposed CL-TDEA addresses this challenge through its two-stage design. In the first stage, the auxiliary population approaches the unconstrained Pareto front (UPF) and assists the main population in crossing infeasible regions, which enhances the exploration ability of the algorithm. At the same time, the constraint boundary learning mechanism adaptively adjusts according to the proportion of feasible solutions, further improving the search capability across different problem dimensions. In the second stage, the main and auxiliary populations converge to the constrained Pareto front (CPF) from feasible and infeasible sides, respectively. Moreover, the cascaded multi-criteria hierarchical ranking-based environmental selection emphasizes convergence and diversity, thereby strengthening the exploitation ability. This design ensures broad exploration in the early stage and effective exploitation in the later stage, resulting in a well-balanced search process for solving CMOPs.
4. Experimental Studies
In this section, we conduct a series of experiments to verify the effectiveness of CL-TDEA. First, CL-TDEA is compared with eight state-of-the-art CMOEAs on four test suites. Then, the performance effectiveness of CL-TDEA is verified. Note that all experiments are conducted on the PlatEMO [36].
4.1. Experimental Settings
(1) Test problems
In this work, four test suites (i.e., MW [37], LIRCMOP [38], ZXH_CF [39], and C_DTLZ [40]) are selected to test the performance of algorithms. In comparative experiments, the numbers of objective functions (m) and decision spaces (D) of all algorithms are kept in accordance with the platform’s default settings, ensuring fairness in the comparative experiments.
(2) Performance indicator
To further validate the performance of CL-TDEA and the competing algorithms, the performance indicators (i.e., inverted generational distance, IGD [41] and the hypervolume, HV [42]) are adopted to evaluate the performance of each algorithm. IGD denotes the average distance between solutions obtained by an algorithm and solutions sampled on the true PF. When an algorithm obtains a smaller IGD value, this means that the algorithm has the better performance. HV quantifies the volume of the space covered by the solutions obtained by the algorithm in the objective space. A higher HV value indicates higher solution quality, representing excellent diversity of the algorithm.
(3) Compared algorithms
In this study, nine state-of-the-art methods (i.e., C-TAEA [22], ToP [18], TIGE2 [33], MSCMO [20], POCEA [34], CMOEA-MS [19], CMOEMT [27], and IMTCMO [43]) are selected as compared methods. Some of them represent the methods of multiple evolution stages, such as PPS, CMOEA-MS, MSCMO; and some of them include two populations, such as , such as C-TAEA and CMOEMT. The parameter settings of these algorithms are summarized as follows:
- (1)
- Population size: The population size N is fixed at 100 for all test instances across all compared algorithms.
- (2)
- Genetic operators: All methods except for ToP, IMTCMO, and POCEA adopt the simulated binary crossover (SBX) [44] and polynomial mutation (PM) [45] to generate the offspring. The crossover and mutation probability, respectively, are set as 1 and 1/D, and the corresponding distribution indexes both are set to 20. For ToP, IMTCMO, and POCEA, they adopt the differential evolution to reproduce the offspring, whose relevant settings follow their original papers.
- (3)
- Run times and terminal conditions: All methods on each test instance independently run 20 times. The terminal condition of each run is the maximum fitness evaluations () that is set to 100,000.
- (4)
- Parameters in compared algorithms: The parameters in these compared methods are the same as in their original papers. For our TDEA, the parameter , determining the computational resource cost of different stages, is set to 0.4.
- (5)
- Statistical test method: The Wilcoxon test at a 0.05 significant level is adopted to analyze the significant difference between CL-TDEA and its competitors [46].
(4) Comparative Methods
To evaluate the performance of the proposed CL-TDEA, we compared it with several representative and widely used algorithms that have been frequently adopted as baselines in constrained multi-objective optimization (CMOP) studies, including C-TAEA, POCEA, and CMOEA-MS. These algorithms span different design philosophies, such as constraint-handling techniques, evolutionary frameworks, and decomposition-based strategies, thereby ensuring a fair and comprehensive comparison.
It is worth mentioning that several very recent state-of-the-art optimizers (e.g., CMOEMT [27] and IMTCMO [43]) have also demonstrated promising results in the literature. Nevertheless, due to the lack of publicly available implementations or the substantial computational resources required, these methods were not included in the present experimental study. A more extensive benchmarking that incorporates such recent optimizers will be considered as an important direction for future research.
4.2. Comparison on MW Test Suite
Table 2 and Table 3 provide a summary of the statistical results for IGD and HV values, respectively. At first glance, the proposed CL-TDEA can perform best on most test problems in terms of IGD and HV values. To validate this finding, the Friedman test is used to rank the IGD and HV values of each CMOEA on every test suite, with smaller ranks indicating better performance. As shown in Figure 2 and Figure 3, CL-TDEA consistently achieves the lowest ranks across all test suites. In short, the proposed CL-TDEA has the best comprehensive performance. In all the tables, the data highlighted in gray indicate the best values obtained. In the table, the plus sign indicates better than, the minus sign indicates worse than, and ≈ indicates similar to.

Table 2.
IGD values (avg ± std) obtained by nine algorithms on MW test problems.

Table 3.
HV values (avg ± std) obtained by nine algorithms on MW test problems.
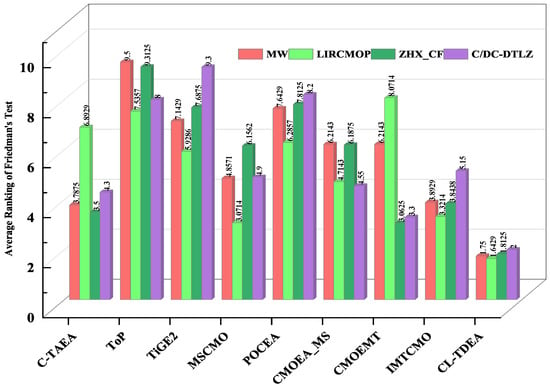
Figure 2.
The IGD rankings of eight methods were determined using the Friedman test across various test suites.
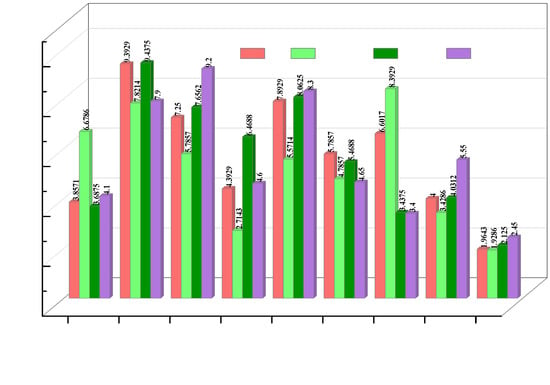
Figure 3.
The HV rankings of eight methods were determined using the Friedman test across various test suites.
To be specific, it can be seen from Table 2 that CL-TDEA achieves the best performance on ten test problems, IMTCMO performs similarly to CL-TDEA on five test problems, and only C-TAEA outperforms CL-TDEA on the MW6 test problem. ToP fails to find feasible solutions on MW1 and MW10. CL-TDEA outperforms C-TAEA, ToP, TIGE2, MSCMO, POCEA, CMOEA_MS, and IMTCMO on 10, 9, 14, 10, 14, 14, 14, and 9 test problems, respectively. For the HV results in Table 2, CL-TDEA achieves the best performance on eight test problems. IMTCMO outperforms CL-TDEA on MW3 and MW14 test problems. C-TAEA outperforms CL-TDEA on the MW6 test problem. C-TAEA, ToP, TIGE2, MSCMO, POCEA, CMOEA_MS, and IMTCMO perform worse than TDEA on 10, 9, 14, 9, 14, 14, 14, and 10 problems, respectively. To intuitively present the significant difference of TDEA and its competitors, the Wilcoxon rank-sum test is conducted on the IGD and HV results achieved by CL-TDEA and its competitors, and the corresponding results are presented in Table 4. From this table, we can clearly see that (1) values of CL-TDEA vs. each competitor are much greater; (2) From the results of the Wilcoxon signed-rank test, it can be observed that CL-TDEA is significantly superior to most compared algorithms in terms of both IGD and HV. The p-values are generally smaller than 0.05, indicating that the differences are statistically significant. (3) From the results of the Nemenyi post hoc test, the average ranks of CL-TDEA are 1.25 for IGD and 1.33 for HV, both of which are substantially lower than those of the other methods. In the table, algorithms that exhibit a significant difference in average rank from CL-TDEA are marked with * (CD = 5.2583). It can be observed that the differences in average rank between CL-TDEA and ToP, TiGE2, POCEA, CMOEA-MS, and CMOEMT all exceed the CD value, indicating that CL-TDEA has a statistically significant overall performance advantage. Thus, CL-TDEA demonstrates statistically significant overall superiority on the MW test suite: the Wilcoxon signed-rank test confirms that its improvements in IGD and HV are statistically significant, while the Nemenyi post hoc test shows that CL-TDEA’s average ranks are substantially lower than those of most competitors. It should be noted that the Wilcoxon signed-rank test and the Nemenyi rank test are commonly used statistical methods to verify the reliability of performance comparisons, and their use in this study ensures that the observed improvements are statistically meaningful.

Table 4.
Comparison of CL-TDEA with other CMOEAs on the MW test suite. Wilcoxon values and p-values are shown for IGD and HV. Average ranks are reported with * indicating significant difference from CL-TDEA according to the Nemenyi test (CD = 5.2583).
For these test problems (i.e., MW1-2, MW4-6, and MW8), the CPFs of them are the same as or a part of UPFs. Therefore, the difficulties in solving them are how to make algorithms have the extensive search. According to the results in Table 2 and Table 3, we can know that the proposed CL-TDEA is significantly superior to or at least comparable with its competitors on MW1-2, MW4-5, and MW8, while C-TAEA performs best on MW6. This indicates that TDEA is suitable to solve these problems since the constraint boundary learning mechanism and the cascading sorting strategy can make CL-TDEA have an extensive search ability. For the remaining problems, some of their CPFs are partially located on the constrained boundary and others’ CPFs are all located on the constrained boundary. Therefore, the ability of algorithms to explore promising feasible regions is important to solve such problems. From Table 2 and Table 3, it is still evident that CL-TDEA performs better than its competitors on the majority of test problems. This is because CL-TDEA with the help of the constraint boundary learning can find the promising feasible regions.
In order to intuitively present the performance of nine CMOEAs, we plot the distributions of final non-dominated feasible solutions achieved by nine CMOEAs on MW4 in Figure 4. In Figure 4, the purple line represents the Pareto Front (PF), and the blue dots represent the feasible solutions.
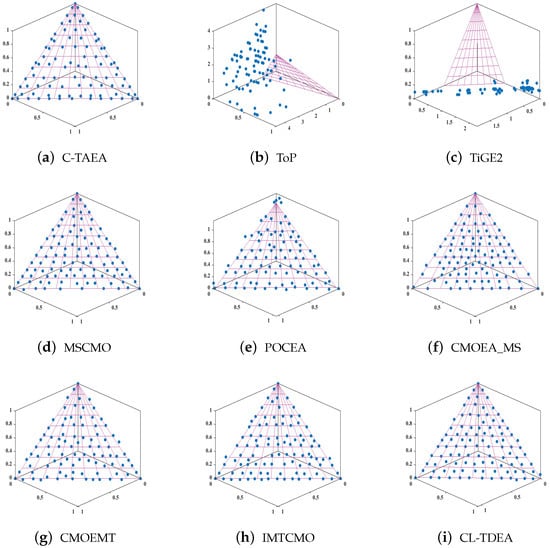
Figure 4.
Distributions of final solutions obtained by nine CMOEAs on MW4.
As shown in this figure, CL-TDEA is significantly superior to its eight competitors since solutions evenly distribute on the CPF. This is because high-quality infeasible solutions have a chance to be chosen, which can assist CL-TDEA to explore more promising feasible regions.
4.3. Comparison on LIRCMOP Test Suite
Due to the presence of large infeasible regions in LIRCMOP problems, they present a significant challenge for CMOEAs. Moreover, some of them have the disconnected PFs, and some have narrow feasible regions. Therefore, when solving these problems, it is important for CMOEAs to properly utilize the infeasible solution to cross the large infeasible regions and arrive at the narrow the feasible regions.
Table 5 and Table 6 present the IGD and HV results achieved by CL-TDEA and its competitors. From these two tables, it can be observed that IMTCMO and CL-TDEA are two top algorithms. For verifying the truth of this finding, the Friedman test is applied to rank the IGD and HV values of each CMOEA on every test suite, with smaller ranks indicating better performance. The results are presented in Figure 2 and Figure 3. According these two figures, we can clearly know that our CL-TDEA has the smallest ranking values on this test suite. That is to say, the proposed CL-TDEA has the best comprehensive performance.

Table 5.
IGD values (avg ± std) obtained by nine algorithms on LIRCMOP test problems.

Table 6.
HV values (avg ± std) obtained by nine algorithms on LIRCMOP test problems.
To be specific, for the IGD results, CL-TDEA is slightly inferior to IMTCMO on LIRCMOP1, LIRCMOP3, and LIRCMOP7-11. However, compared to other algorithms, CL-TDEA has a significant advantage. TDEA outperforms C-TAEA, ToP, TIGE2, MSCMO, POCEA, CMOEA_MS, and IMTCMO on the 14, 13, 14, 5, 10, 10, 14, and 5 test problems, respectively. For the HV results, TDEA is only superior to or similar to IMTCMO on LIRCMOP5, LIRCMOP11-12, and LIRCMOP14. However, CL-TDEA is significantly ahead of the other eight competitors. For intuitively presenting the significant difference of CL-TDEA and its competitors, the Wilcoxon rank-sum test is conducted on the IGD and HV results achieved by CL-TDEA and its competitors, and the corresponding results are presented in Table 7. From this table, we can clearly see that (1) values of CL-TDEA vs. each competitor are much greater; (2) From the results of the Wilcoxon signed-rank test, it can be observed that CL-TDEA is significantly superior to most compared algorithms in terms of both IGD and HV. The p-values are generally smaller than 0.05, indicating that the differences are statistically significant; (3) From the results of the Nemenyi post hoc test, the average ranks of CL-TDEA are 1.64 for both IGD and HV, which are substantially lower than those of the other methods. In the table, algorithms that exhibit a significant difference in average rank from CL-TDEA are marked with * (CD = 3.43). The differences in average rank between CL-TDEA and C-TAEA, ToP, TiGE2, POCEA, and CMOEMT all exceed the CD value, indicating statistically significant superiority. Thus, CL-TDEA demonstrates statistically significant overall superiority on the LIRCMOP test suite: the Wilcoxon signed-rank test confirms that its improvements in IGD and HV are statistically significant, while the Nemenyi post hoc test shows that CL-TDEA’s average ranks are substantially lower than those of most competitors. It should be noted that the Wilcoxon signed-rank test and the Nemenyi rank test are commonly used statistical methods to verify the reliability of performance comparisons, and their use in this study ensures that the observed improvements are statistically meaningful.

Table 7.
Comparison of CL-TDEA with other CMOEAs on the LIRCMOP test suite. Wilcoxon values and p-values are shown for IGD and HV. Average ranks are reported with * indicating significant difference from CL-TDEA according to the Nemenyi test (CD = 3.43).
The reasons for the superiority of IMTCMO and CL-TDEA are as follows: (1) they are capable of learning the constraint boundary via adaptive relaxation constraints; (2) they properly utilize the infeasible solutions to improve their exploration ability and further cross the large infeasible regions.
For visually showing the performance of nine CMOEAs in solving CMOPs with the large infeasible regions, we give the distributions of non-dominated feasible solutions achieved by nine CMOEAs on LIRCMOP11 in Figure 5. In the Figure 5, the gray area represents the feasible region, and the blue represents the feasible solutions. From this figure, we can see that C-TAEA, ToP, TiGE2, MSCMO, POEA, and IMECMO fail to make individuals converge to the true CPF. This is because all of them fail to reasonably utilize infeasible solutions to cross the infeasible regions. For CMOEA_MS and CL-TDEA, they are capable of converging to the CPF. However, CMOEA_MS does not evenly distribute solutions across the CPF, while CL-TDEA achieves even distribution of solutions on the CPF. The reason for this is that CL-TDEA can reasonably utilize infeasible solutions to explore some promising infeasible regions via the constraint boundary learning and cascading sorting.
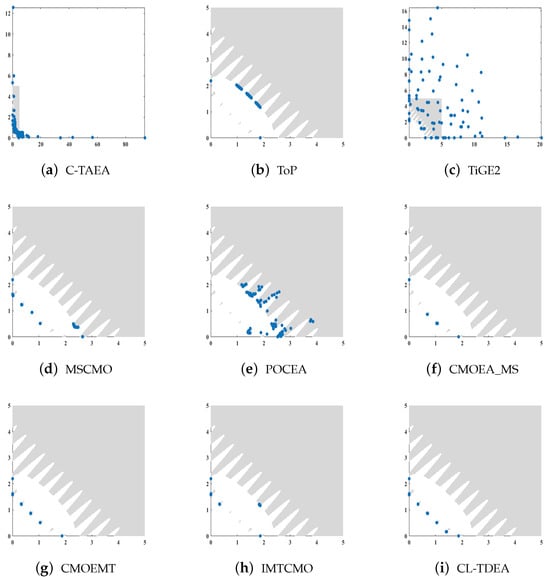
Figure 5.
Distributions of final solutions obtained by nine CMOEAs on 2-objective LIRCMOP11.
4.4. Comparison on ZXH_CF Test Suite
The ZXH_CF test problems have irregular PF shapes, and the variable relations are complicated. Therefore, it is difficult for CMOEAs to solve them. Table 8 and Table 9 give the IGD and HV results of CL-TDEA and its competitors on the test suite. From these two tables, we can observe that CL-TDEA performs best on most test problems of the test suite. To validate this finding, the Friedman test is conducted to rank the IGD and HV values of each CMOEA on every test suite, with smaller ranks indicating better performance. As shown in Figure 2 and Figure 3, CL-TDEA achieves the lowest ranks on this test suite. In conclusion, the proposed CL-TDEA has the best comprehensive performance on this test suite.

Table 8.
IGD values (avg ± std) obtained by nine algorithms on ZXH_CF test problems.

Table 9.
HV values (avg ± std) obtained by nine algorithms on ZXH_CF test problems.
To be specific, for the IGD results in Table 8, TDEA defeats its competitors on ZXH_CF3, ZXH_CF6, ZXH_CF8-11, ZXH_CF14, and ZXH_CF16. The remaining optimal results are achieved by IMTCMO. As for the HV results in Table 9, it can be seen that C-TAEA, ToP, TIGE2, MSCMO, POCEA, CMOEA_MS, and IMTCMO outperform CL-TDEA on 2, 0, 0, 0, 0, 1, 3, and 4 test problems, respectively. CL-TDEA is significantly superior to or at least comparable to its competitors on 11 test problems. For intuitively presenting the significant difference of CL-TDEA and its competitors, the Wilcoxon rank-sum test is conducted on the IGD and HV results achieved by CL-TDEA and its competitors, and the corresponding results are presented in Table 10. From this table, we can clearly see that (1) values of CL-TDEA vs. each competitor are much greater; (2) From the results of the Wilcoxon signed-rank test, it can be observed that CL-TDEA is significantly superior to most compared algorithms in terms of both IGD and HV. Most p-values are smaller than 0.05, indicating that the differences are statistically significant; (3) From the results of the Nemenyi post hoc test, the average ranks of CL-TDEA are 1.50 for IGD and 1.44 for HV, which are substantially lower than those of the other methods. In the table, algorithms that exhibit a significant difference in average rank from CL-TDEA are marked with * (CD = 3.21). The differences in average rank between CL-TDEA and C-TAEA, ToP, TiGE2, MSCMO, POCEA, and CMOEA-MS all exceed the CD value, indicating statistically significant superiority. Therefore, CL-TDEA demonstrates statistically significant overall superiority on the ZXH_CF test suite, with the Wilcoxon signed-rank test confirming improvements in IGD and HV and the Nemenyi post hoc test showing substantially lower average ranks than most competitors. It should be noted that the Wilcoxon signed-rank test and the Nemenyi rank test are commonly used statistical methods to verify the reliability of performance comparisons, and their use in this study ensures that the observed improvements are statistically meaningful.

Table 10.
Comparison of CL-TDEA with other CMOEAs on the ZXH_CF test suite. Wilcoxon values and p-values are shown for IGD and HV. Average ranks are reported with * indicating significant difference from CL-TDEA according to the Nemenyi test (CD = 3.21).
4.5. Comparison on C-DTLZ and DC_DTLZ Test Suite
Table 11 and Table 12 summarize the statistical results of IGD and HV values obtained by nine CMOEAs on the C-DTLZ and DC_DTLZ test suites, respectively. At a glance, CL-TDEA is capable of achieving better comprehensive performance on most of the test instances. To confirm this finding, the Friedman test is used to rank the IGD and HV values of each CMOEA on the C-DTLZ and DC_DTLZ test suites, with smaller ranks indicating better performance. As shown in Figure 2 and Figure 3, CL-TDEA achieves the lowest ranks on both suites, demonstrating its superior overall performance.

Table 11.
IGD values (avg ± std) obtained by nine algorithms on C_DTLZ test problems.

Table 12.
HV values (avg ± std) obtained by nine algorithms on C_DTLZ test problems.
From Table 11, we can see that CL-TDEA obtains seven best results out of ten test problems in terms of IGD values, while the remaining optimal HV results are mainly achieved by CMOEMT. For the HV results in Table 12, CL-TDEA obtains four best results, while MSCMO, and CMOEMT obtain one and three best results, respectively. To visually present the superiority of TDEA, Figure 6 gives the distributions of non-dominated feasible solutions achieved by nine CMOEAs on DC1-DTLZ1. In the Figure 6, the gray area represents the feasible region, and the blue represents the feasible solutions. As shown in the figure, CL-TDEA distributes solutions evenly across the CPF, whereas other algorithms cover only part of it. Furthermore, the Wilcoxon rank-sum test is performed on the IGD and HV results of CL-TDEA and its competitors, with the outcomes summarized in Table 13. From this table, we can see that (1) values of CL-TDEA vs. each competitor are much greater; (2) From the results of the Wilcoxon signed-rank test, it can be observed that CL-TDEA is significantly superior to most compared algorithms in terms of both IGD and HV. The p-values against ToP, TiGE2, MSCMO, POCEA, and CMOEA-MS are all smaller than 0.05, indicating that the differences are statistically significant; (3) From the results of the Nemenyi post hoc test, the average ranks of CL-TDEA are 1.00 for both IGD and HV, which are substantially lower than those of the other methods. In the table, algorithms that exhibit a significant difference in average rank from CL-TDEA are marked with * (CD = 3.70). The differences in average rank between CL-TDEA and ToP, TiGE2, MSCMO, POCEA, and CMOEA-MS all exceed the CD value, indicating statistically significant superiority. Thus, CL-TDEA demonstrates statistically significant overall superiority on the C/DC-DTLZ test suite, with the Wilcoxon signed-rank test confirming improvements in IGD and HV and the Nemenyi post hoc test showing substantially lower average ranks than most competitors. It should be noted that the Wilcoxon signed-rank test and the Nemenyi rank test are commonly used statistical methods to verify the reliability of performance comparisons, and their use in this study ensures that the observed improvements are statistically meaningful.
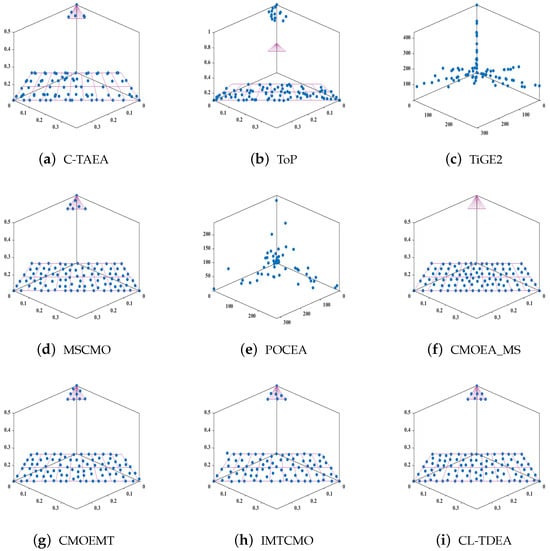
Figure 6.
Distributions of final solutions obtained by nine CMOEAs on 3-objective DC1-DTLZ1.

Table 13.
Comparison of CL-TDEA with other CMOEAs on the C/DC-DTLZ test suite. Wilcoxon values and p-values are shown for IGD and HV. Average ranks are reported with * indicating significant difference from CL-TDEA according to the Nemenyi test (CD = 3.70).
C-DTLZ has various CPF shapes. Nonetheless, TDEA still shows promising performance on most test instances in terms of both IGD and HV values. This can be attributed to the fact that the constraint boundary learning mechanism and the cascading sorting-based environmental selection can make CL-TDEA have strong exploration ability. As for DC-DTLZ, the feasible regions of the test suite include inner–outer layers and their CPFs are disconnected. Such characteristics easily make CMOEAs fall into local optima. Even so, the proposed CL-TDEA obtains the best results on most test problems in terms of both IGD and HV values. The underlying reason is that the constraint boundary learning mechanism in the first stage and the cascading sorting-based environmental selection in the second stage can make the CL-TDEA effectively utilize the infeasible solutions and further improve the exploration ability of CL-TDEA.
4.6. Comparison on SDC Test Suite
To further validate the performance of CL-TDEA on large-scale high-dimensional test sets, Table 14 illustrates its results on the 50-dimensional SDC test problems. It is evident that CL-TDEA achieves the best or near-best IGD values in most instances, highlighting its significant advantages in high-dimensional constrained multi-objective optimization. In particular, on problems such as SDC1, SDC3, and SDC6, CL-TDEA markedly outperforms other algorithms (e.g., POCEA, CMOEA-MS, and IMCMO), whose IGD values are generally an order of magnitude higher. Furthermore, the standard deviations of CL-TDEA are generally smaller, indicating that it offers more stable performance across multiple independent runs compared with both traditional algorithms and other newly developed methods. In our experiments on the 50-dimensional SDC problems, the runtime of CL-TDEA was observed to be comparable to that of state-of-the-art algorithms such as POCEA and CMOEA-MS. Although CL-TDEA introduces additional computations due to its adaptive learning and constraint-handling mechanisms, the overhead remains moderate and does not lead to prohibitive computational costs. More importantly, the significant improvements in convergence accuracy and solution stability clearly justify this computational investment.

Table 14.
IGD values (avg ± std) obtained by nine algorithms on SDC test problems.
In comparison, traditional approaches (such as ToP and C-TAEA) suffer a clear performance degradation in high-dimensional scenarios, as reflected by significantly larger IGD values, suggesting their limitations in maintaining convergence and diversity under complex constraints. IMTCMO achieves acceptable results on some problems but still falls short of CL-TDEA in terms of overall stability and convergence accuracy. By contrast, CL-TDEA not only ranks highest in the win/tie/loss statistics but also consistently maintains its superiority across SDC problems with varying constraint difficulties.
In summary, on high-dimensional (D = 50) constrained multi-objective optimization problems, CL-TDEA demonstrates stronger convergence, stability, and robustness than existing algorithms, thereby confirming its effectiveness in tackling large-scale complex optimization problems.
4.7. Validation of Main Components in CL-TDEA
In this subsection, we aim at investigating the influence of the main components in CL-TDEA on the performance of CL-TDEA. For this purpose, five variants (i.e., CL-TDEA1–5) are designed to compare with CL-TDEA, whose details are as follows:
(1) In CL-TDEA1, the designed adaptive constraint-boundary learning mechanism is deleted.
(2) In CL-TDEA2, the elite mating selection has been substituted with random mating selection.
(3) In CL-TDEA3, the designed cascading multi-criteria hierarchical ranking mechanism is deleted. As an alternative, the fitness estimation in SPEA2 [35] is adopted to select promising infeasible solutions.
(4) In CL-TDEA4, the first stage is deleted, and only the second stage is retained.
(5) In CL-TDEA5, the second stage is deleted, and only the first stage is retained.
Table 15 and Table 16 give the IGD and HV results achieved by five variants of CL-TDEA and itself on LIRCMOP problems, respectively. Compared with CL-TDEA1, CL-TDEA is is better than or similar to CL-TDEA1 on most test problems in terms of IGD and HV values. This validates the importance of the constraint boundary learning mechanism in CL-TDEA. Compared with CL-TDEA2, TDEA is superior to or at least comparable with CL-TDEA2 on all test problems as well. Thus, the effectiveness of the elite mating selection is validated. Compared with CL-TDEA3, CL-TDEA3 fails to find feasible solutions in the five test problems and performs worse than CL-TDEA on the six test problems. This further illustrates the importance of the cascading multi-criteria hierarchical ranking in CL-TDEA. This is because the cascading multi-criteria hierarchical ranking can make CL-TDEA properly utilize the infeasible solutions and further improve the exploration ability of CL-TDEA. Compared with CL-TDEA4 and CL-TDEA5, CL-TDEA is still significantly better than or similar to CL-TDEA4 on almost all test problems. This validates the importance of two-stage evolution in CL-TDEA. In summary, each main component in CL-TDEA is important to CL-TDEA, and their mutual cooperation makes CL-TDEA have higher competitiveness.

Table 15.
IGD values (avg ± std) obtained by CL-TDEA and its variants on LIRCMOP test problems.

Table 16.
HV values (avg ± std) obtained by CL-TDEA and its variants on LIRCMOP test problems.
4.8. Applications of CL-TDEA on Three Real-World Problems
This section aims at investigating the capacity of CL-TDEA in solving the practical engineering problem. Therefore, we compare CL-TDEA with its eight competitors on three engineering problems. The first problem concerns the disc brake design (DBD), focused on minimizing braking time, brake disc thickness, and brake temperature rise. The second problem is the water resources management (WRM) problem, including five objective functions and seven constraints. More details about it can be found in [2]. The third problem is the car side impact (CSI) problem that includes three objectives and ten constraints, whose details can be found in [47]. For a fair comparison, the experimental settings follow Section 4.1. Note that for the real-world problems, since their true PFs are unknown, we can only select the HV metric to evaluate the algorithm performance.
Table 17 presents the statistical HV results obtained by the nine CMOEAs. From this Table 17, we can see that CL-TDEA is significantly superior to all its competitors on the DBD and WRM problems. For the CSI problem, CL-TDEA is comparable with C-TAEA and IMTCMO. In summary, CL-TDEA has the ability to solve the practical engineering problem to some extent.

Table 17.
HV values (mean and standard deviation) obtained by nine algorithms on three real-world test problems.
4.9. Discussion on Exploration–Exploitation Balance
In CMOPs, exploration refers to the ability to cover diverse regions of the search space, while exploitation in the standard sense denotes the ability to intensively search promising regions, which do not necessarily lie close to the PF [8]. In this work, we specifically emphasize useful exploitation, i.e., exploitation occurring near the PF that directly contributes to convergence. Although these properties are not directly measured via attraction basin-based methods, they can be indirectly assessed through population diversity and solution distribution.
In our experiments, CL-TDEA maintains high population diversity, as indicated by the spread metric [35] (measuring boundary coverage and uniformity of spacing between solutions; e.g., the solution distributions in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6), while simultaneously achieving superior convergence performance (low IGD and high HV). This is achieved through a combination of a two-archive mechanism, learning strategies, and a cascaded multi-criteria hierarchical ranking selection, which together promote the discovery of new regions (exploration) and refinement of solutions near the PF (useful exploitation).
For instance, in comparative experiments, some algorithms, such as TiGE2 (Figure 6c,e), tend to exploit feasible regions far from the PF, which often leads to stagnation in local areas of the search space. While such behavior qualifies as exploitation under the standard definition, it contributes little to convergence. In contrast, algorithms shown in Figure 6a,g–i, including our proposed CL-TDEA (Figure 6i), focus exploitation near the CPF. Specifically, CL-TDEA leverages a two-stage population mechanism and adaptive learning strategies to guide the population across infeasible regions and concentrate exploitation around the CPF. This results in more effective convergence and higher-quality solution sets.
Based on the above analysis, we conclude that CL-TDEA achieves a well-balanced trade-off between exploration and exploitation, thereby producing uniformly distributed solution sets and delivering superior IGD and HV performance across benchmark problems.
5. Conclusions
This work proposes a new constrained multi-objective evolutionary algorithm (CMOEA), termed CL-TDEA, for solving constrained multi-objective optimization problems (CMOPs). The main innovations of CL-TDEA lie in three aspects: (i) a two-stage dual-population framework that guides the search from both feasible and infeasible sides, (ii) an adaptive constraint-boundary learning mechanism that improves exploration and facilitates crossing infeasible regions, and (iii) a cascaded multi-criteria hierarchical ranking strategy that discovers diverse promising solutions and enhances the approximation of the constrained Pareto front (CPF). These mechanisms collectively enable CL-TDEA to achieve a better balance among convergence, diversity, and feasibility.
Extensive experiments on four test suites (MW, LIRCMOP, ZXH_CF, and C_DTLZ) and three real-world applications confirm that CL-TDEA is competitive against several state-of-the-art CMOEAs, demonstrating its effectiveness and robustness. Future work will focus on extending the benchmarking with more recent state-of-the-art optimizers and investigating the scalability of CL-TDEA. In addition, we plan to apply the algorithm to real-world engineering problems, such as logistics vehicle dispatching and wireless sensor placement.
Author Contributions
Conceptualization, X.X. and Y.S.; Methodology, Y.S.; Software, Y.S.; Validation, Y.S. and X.X.; Formal analysis, Y.S.; Investigation, Y.S.; Resources, X.X.; Data curation, X.X. and Y.S.; Writing—original draft preparation, X.X., Y.S., H.W., and F.Y.; Writing—review and editing, X.X., Y.S., H.W., and F.Y.; Visualization, Y.S.; Supervision, X.X. and Y.S.; Project administration, X.X.; Funding acquisition, X.X. All authors have read and agreed to the published version of the manuscript.
Funding
China Postdoctoral Science Foundation (grant number: 2024M761587).
Data Availability Statement
Data available in a publicly accessible repository. All experimental data used in this study were obtained from the PlatEMO 4.6 platform, which provides publicly available benchmark test sets (MW, LIRCMOP, ZXH_CF, C_DTLZ/DC_DTLZ and RWMOP). The data can be accessed at https://github.com/BIMK/PlatEMO (accessed on 4 November 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hao, L.; Peng, W.; Liu, J.; Zhang, W.; Li, Y.; Qin, K. Competition-based two-stage evolutionary algorithm for constrained multi-objective optimization. Math. Comput. Simul. 2025, 230, 207–226. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Y.; Fan, N.; Wei, S.; Tong, W. A convergence-diversity balanced fitness evaluation mechanism for decomposition-based many-objective optimization algorithm. Integr. Comput.-Aided Eng. 2019, 26, 159–184. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, F.; Yan, C.; Zhou, D.; Zeng, X. An efficient batch-constrained bayesian optimization approach for analog circuit synthesis via multiobjective acquisition ensemble. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2021, 41, 1–14. [Google Scholar] [CrossRef]
- Liang, J.; Ban, X.; Yu, K.; Qu, B.; Qiao, K.; Yue, C.; Chen, K.; Tan, K.C. A survey on evolutionary constrained multiobjective optimization. IEEE Trans. Evol. Comput. 2022, 27, 201–221. [Google Scholar] [CrossRef]
- Long, W.; Dong, H.; Wang, P.; Huang, Y.; Li, J.; Yang, X.; Fu, C. A constrained multi-objective optimization algorithm using an efficient global diversity strategy. Complex Intell. Syst. 2023, 9, 1455–1478. [Google Scholar] [CrossRef]
- Qiao, K.; Liang, J.; Yu, K.; Wang, M.; Qu, B.; Yue, C.; Guo, Y. A Self-Adaptive Evolutionary Multi-Task Based Constrained Multi-Objective Evolutionary Algorithm. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 1098–1112. [Google Scholar] [CrossRef]
- Ming, F.; Gong, W.; Zhen, H.; Li, S.; Wang, L.; Liao, Z. A simple two-stage evolutionary algorithm for constrained multi-objective optimization. Knowl.-Based Syst. 2021, 228, 107263. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Fan, Z.; Li, W.; Cai, X.; Huang, H.; Fang, Y.; You, Y.; Mo, J.; Wei, C.; Goodman, E. An improved epsilon constraint-handling method in MOEA/D for CMOPs with large infeasible regions. Soft Comput. 2019, 23, 12491–12510. [Google Scholar] [CrossRef]
- Fan, Z.; Li, W.; Cai, X.; Li, H.; Wei, C.; Zhang, Q.; Deb, K.; Goodman, E. Push and pull search for solving constrained multi-objective optimization problems. Swarm Evol. Comput. 2019, 44, 665–679. [Google Scholar] [CrossRef]
- Qin, C.; Ming, F.; Gong, W.; Gu, Q. Constrained multi-objective optimization via two archives assisted push–pull evolutionary algorithm. Swarm Evol. Comput. 2022, 75, 101178. [Google Scholar] [CrossRef]
- Coello, C.A.C. Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: A survey of the state of the art. Comput. Methods Appl. Mech. Eng. 2002, 191, 1245–1287. [Google Scholar] [CrossRef]
- Runarsson, T.P.; Yao, X. Stochastic ranking for constrained evolutionary optimization. IEEE Trans. Evol. Comput. 2000, 4, 284–294. [Google Scholar] [CrossRef]
- Bao, Q.; Wang, M.; Dai, G.; Chen, X.; Song, Z.; Li, S. An archive-based two-stage evolutionary algorithm for constrained multi-objective optimization problems. Swarm Evol. Comput. 2022, 75, 101161. [Google Scholar] [CrossRef]
- Ming, M.; Wang, R.; Ishibuchi, H.; Zhang, T. A Novel Dual-Stage Dual-Population Evolutionary Algorithm for Constrained Multiobjective Optimization. IEEE Trans. Evol. Comput. 2021, 26, 1129–1143. [Google Scholar] [CrossRef]
- Lai, Y.; Chen, J.; Chen, Y.; Zeng, H.; Cai, J. Feedback Tracking Constraint Relaxation Algorithm for Constrained Multi-Objective Optimization. Mathematics 2025, 13, 629. [Google Scholar] [CrossRef]
- Zhang, K.; Zhao, S.; Zeng, H.; Chen, J. Two-Stage Archive Evolutionary Algorithm for Constrained Multi-Objective Optimization. Mathematics 2025, 13, 470. [Google Scholar] [CrossRef]
- Liu, Z.Z.; Wang, Y. Handling constrained multiobjective optimization problems with constraints in both the decision and objective spaces. IEEE Trans. Evol. Comput. 2019, 23, 870–884. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, Y.; Su, Y.; Zhang, X.; Tan, K.C.; Jin, Y. Balancing objective optimization and constraint satisfaction in constrained evolutionary multiobjective optimization. IEEE Trans. Cybern. 2021, 52, 9559–9572. [Google Scholar] [CrossRef]
- Ma, H.; Wei, H.; Tian, Y.; Cheng, R.; Zhang, X. A multi-stage evolutionary algorithm for multi-objective optimization with complex constraints. Inf. Sci. 2021, 560, 68–91. [Google Scholar] [CrossRef]
- Liang, J.; Chen, Z.; Wang, Y.; Ban, X.; Qiao, K.; Yu, K. A dual-population constrained multi-objective evolutionary algorithm with variable auxiliary population size. Complex Intell. Syst. 2023, 9, 5907–5922. [Google Scholar] [CrossRef]
- Li, K.; Chen, R.; Fu, G.; Yao, X. Two-archive evolutionary algorithm for constrained multiobjective optimization. IEEE Trans. Evol. Comput. 2018, 23, 303–315. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, K.; Zeng, H.; Yan, J.; Dai, J.; Dai, Z. Adaptive Constraint Relaxation-Based Evolutionary Algorithm for Constrained Multi-Objective Optimization. Mathematics 2024, 12, 3075. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Zhang, Q.; Zhang, Z.; Gao, S. Cooperative multiobjective evolutionary algorithm with propulsive population for constrained multiobjective optimization. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 3476–3491. [Google Scholar] [CrossRef]
- Cao, J.; Yan, Z.; Chen, Z.; Zhang, J. A Pareto front estimation-based constrained multi-objective evolutionary algorithm. Appl. Intell. 2023, 53, 10380–10416. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, J.; Tan, S. A constrained multi-objective evolutionary algorithm based on decomposition and dynamic constraint-handling mechanism. Appl. Soft Comput. 2020, 89, 106104. [Google Scholar] [CrossRef]
- Ming, F.; Gong, W.; Wang, L.; Gao, L. Constrained multi-objective optimization via multitasking and knowledge transfer. IEEE Trans. Evol. Comput. 2022, 28, 77–89. [Google Scholar] [CrossRef]
- Liu, Z.Z.; Wang, B.C.; Tang, K. Handling constrained multiobjective optimization problems via bidirectional coevolution. IEEE Trans. Cybern. 2021, 52, 10163–10176. [Google Scholar] [CrossRef]
- Yang, K.; Zheng, J.; Zou, J.; Yu, F.; Yang, S. A dual-population evolutionary algorithm based on adaptive constraint strength for constrained multi-objective optimization. Swarm Evol. Comput. 2023, 77, 101247. [Google Scholar] [CrossRef]
- Dong, J.; Gong, W.; Ming, F.; Wang, L. A two-stage evolutionary algorithm based on three indicators for constrained multi-objective optimization. Expert Syst. Appl. 2022, 195, 116499. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, T.; Xiao, J.; Zhang, X.; Jin, Y. A coevolutionary framework for constrained multiobjective optimization problems. IEEE Trans. Evol. Comput. 2020, 25, 102–116. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Y.; Song, W. A new fitness function with two rankings for evolutionary constrained multiobjective optimization. IEEE Trans. Syst. Man, Cybern. Syst. 2019, 51, 5005–5016. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhu, M.; Wang, J.; Zhang, Z.; Xiang, Y.; Zhang, J. Tri-goal evolution framework for constrained many-objective optimization. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 3086–3099. [Google Scholar] [CrossRef]
- He, C.; Cheng, R.; Tian, Y.; Zhang, X.; Tan, K.C.; Jin, Y. Paired offspring generation for constrained large-scale multiobjective optimization. IEEE Trans. Evol. Comput. 2020, 25, 448–462. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm. TIK Rep. 2001, 103, 1–21. [Google Scholar]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [educational forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, J.; Zhang, Y. A multi-constraint handling techniquebased niching evolutionary algorithm for constrained multi-objective optimization problems. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Zhang, L.; Yu, R.; Liu, J.; Xu, Y.; Jiang, H.; Xu, P.; Lin, P.; Luo, Y. A constrained multi-objective evolutionary algorithm based on weak cooperation framework and multi-chaotic operators. In Proceedings of the 2022 Global Conference on Robotics, Artificial Intelligence and Information Technology (GCRAIT), Chicago, IL, USA, 30–31 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 102–106. [Google Scholar]
- Zhang, H.; Yue, D.; Dou, C.; Hancke, G.P. PBI based multi-objective optimization via deep reinforcement elite learning strategy for micro-grid dispatch with frequency dynamics. IEEE Trans. Power Syst. 2022, 38, 488–498. [Google Scholar] [CrossRef]
- Wen, X.; Guo, X.; Wang, S.; Lu, Z.; Zhang, Y. Breast cancer diagnosis: A systematic review. Biocybern. Biomed. Eng. 2024, 44, 119–148. [Google Scholar] [CrossRef]
- Sun, Y.; Yen, G.G.; Yi, Z. IGD indicator-based evolutionary algorithm for many-objective optimization problems. IEEE Trans. Evol. Comput. 2018, 23, 173–187. [Google Scholar] [CrossRef]
- Xie, Y.; Li, J.; Li, Y.; Zhu, W.; Dai, C. Two-stage evolutionary algorithm with fuzzy preference indicator for multimodal multi-objective optimization. Swarm Evol. Comput. 2024, 85, 101480. [Google Scholar] [CrossRef]
- Qiao, K.; Liang, J.; Yu, K.; Yue, C.; Lin, H.; Zhang, D.; Qu, B. Evolutionary constrained multiobjective optimization: Scalable high-dimensional constraint benchmarks and algorithm. IEEE Trans. Evol. Comput. 2023, 28, 965–979. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, R.B. Simulated binary crossover for continuous search space. Complex Syst. 1995, 9, 115–148. [Google Scholar]
- Deb, K.; Goyal, M. A combined genetic adaptive search (GeneAS) for engineering design. Comput. Sci. Inform. 1996, 26, 30–45. [Google Scholar]
- Wilcoxon, F. Some rapid approximate statistical procedures. Ann. N. Y. Acad. Sci. 1950, 52, 808–814. [Google Scholar] [CrossRef]
- Kumar, A.; Wu, G.; Ali, M.Z.; Mallipeddi, R.; Suganthan, P.N.; Das, S. A test-suite of non-convex constrained optimization problems from the real-world and some baseline results. Swarm Evol. Comput. 2020, 56, 100693. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).