A Deep Reinforcement Learning Model to Solve the Stochastic Capacitated Vehicle Routing Problem with Service Times and Deadlines

Abstract

Vehicle Routing Problems are central to logistics and operational research, arising in diverse contexts such as transportation planning, manufacturing systems, and military operations. While Deep Reinforcement Learning has been successfully applied to both deterministic and stochastic variants of Vehicle Routing Problems, existing approaches often neglect critical time-sensitive conditions. This work addresses the Stochastic Capacitated Vehicle Routing Problem with Service Times and Deadlines, a challenging formulation that is suited to model time routing conditions. The proposal, POMO-DC, integrates a novel dynamic context mechanism. At each decision step, this mechanism incorporates the vehicle’s cumulative travel time and delays—features absent in prior models—enabling the policy to adapt to changing conditions and avoid time violations. The model is evaluated on stochastic instances with 20, 30, and 50 customers and benchmarked against Google OR-Tools using multiple metaheuristics. Results show that POMO-DC reduces average delays by up to 88% (from 169.63 to 20.35 min for instances of 30 customers) and 75% (from 4352.43 to 1098.97 min for instances of 50 customers), while maintaining competitive travel times. These outcomes highlight the potential of Deep Reinforcement Learning-based frameworks to learn patterns from stochastic data and effectively manage time uncertainty in Vehicle Routing Problems.

1. Introduction

Vehicle Routing Problems (VRPs) are a class of combinatorial optimization formulations of significant importance due to their computational complexity [1] and broad practical applications [2]. Generally, VRPs are employed to model and optimize transportation and delivery systems, leading to an extensive taxonomy of problem variants. These include applications in goods distribution [3], service operations [4], navigation [5], passenger transportation [6], and food delivery [7]. It is crucial to note that these domains incorporate diverse constraints and operational conditions. The comprehensive review conducted by Rios et al. [8] provides an in-depth analysis of this diversification.

Many different computational methods have been proposed to tackle routing formulations, including exact algorithms [9], heuristics [10], and metaheuristics [11]. Exact algorithms guarantee optimality but are often computationally prohibitive for large-scale or online problems. Heuristics and metaheuristics, while significantly more efficient, rely on empirically designed rules and human-crafted logic, which may result in suboptimal solutions and limited adaptability to problem variants. Although many heuristic approaches are fast and scalable, their solution quality tends to degrade with increasing problem complexity, additional constraints, or changing instance distributions.

Alternatively, Deep Learning (DL) frameworks offer standardized structures capable of identifying patterns across different instances of a problem and their corresponding solutions [12]. This ability helps address the challenges posed by the lack of generalization and aims to automatically learn effective policies from data, reducing the reliance on handcrafted rules. Supervised Learning (SL) and Reinforcement Learning (RL) have been employed as training paradigms to ensure the effectiveness of these frameworks, as demonstrated by Vynials et al. [13] and Bello et al. [14], respectively. SL relies on optimal labels, which are computationally expensive to obtain; however, the approach proposed by Luo et al. [15] leverages partial labels, highlighting the potential advantages of this paradigm in the VRPs context. In contrast, RL has become the dominant paradigm in the research community, relying solely on reward signals to optimize model parameters. This trend has enabled the wide development of Deep Reinforcement Learning (DRL) frameworks for VRPs, including contributions for static and deterministic variants [14,15,16,17,18].

Significant extensions of DRL algorithms for stochastic and dynamic VRP variants—an active and growing area of research—have been proposed by Bono et al. [19] and Gama et al. [20]. However, these methods do not leverage the algorithmic innovations and structural insights achieved in state-of-the-art approaches for static VRP variants, most notably POMO (Policy Optimization with Multiple Optima) [16]. POMO is specifically tailored to exploit the combinatorial structure of routing problems through multi-trajectory generation and stands as the culmination of a series of advances in policy-based DRL for combinatorial optimization.

A more recent study by Pan et al. [21] proposes a DRL framework for dynamic routing under uncertain customer demands using a Partially Observable Markov Decision Process and a type of dynamic attention. However, it does not account for time-sensitive constraints, focusing primarily on adaptability and demand fulfillment.

For non-learning approaches—such as those based on stochastic programming [22] or hybrid metaheuristics [23]—solutions to Stochastic VRPs (SVRPs) often depend on scenario sampling or rule-based evaluation. While these methods can produce high-quality routes in specific settings, they require full re-optimization whenever input conditions change, such as variations in customer demand or travel times, and cannot generalize across different problem instances. This limits their overall efficiency, scalability, and robustness.

This work addresses a challenging stochastic variant of the VRP, termed the Stochastic Capacitated Vehicle Routing Problem with Service Times and Deadlines (SCVRPSTD). The problem can be viewed as a simplified version of the SCVRP with Soft Time Windows (SCVRPSTW), in which travel times and/or service times are modeled as random variables. In the literature, some works have addressed this more general formulation, e.g., Li et al. [24] and Taş et al. [25]; however, their solution strategies rely on conventional methods—exact, heuristic, or metaheuristic—which suffer from the limitations discussed earlier.

The proposed formulation models a delivery system in which a single vehicle with a fixed capacity must execute a sequence of geographically distributed deliveries, returning to a central depot as necessary. Each customer is characterized not only by location and demand but also by temporal features, including service times and delivery deadlines (i.e., latest allowable service start times). Three constraints are addressed: (1) every route must start and end at the depot, (2) the total load per route must not exceed the vehicle’s capacity, and (3) all deliveries must be completed before their respective deadlines. The objective is to minimize the total travel time while also reducing cumulative delays caused by late deliveries.

The solution pipeline for this problem is based on the DRL approach proposed by Kwon et al. [16]. Hence, this study aims to:

• Solve the SCVRPSTD through POMO with Dynamic Context (POMO-DC), which is based on the POMO framework. The proposal incorporates a time-aware dynamic context, enriched state representations, and modified state-transition and reward functions that explicitly capture cumulative travel time and delivery delays.
• Design adaptive state-update mechanisms that ensure feasibility under stochastic travel and service times, enforcing time, and operational constraints throughout the decision-making process.
• Evaluate the solution model against state-of-the-art metaheuristics implemented in Google OR-Tools, including Guided Local Search, Tabu Search, Simulated Annealing, and Greedy Tabu Search, enabling a robust cross-paradigm comparison.

The remainder of this paper is organized as follows. Section 2 reviews related work, with emphasis on DRL-based approaches to VRPs. Section 3 details the problem formulation, proposed model architecture, and training algorithm. Section 4 presents the experimental setup and discusses the results in comparison with the baselines. Finally, Section 5 and Section 6 discuss limitations, outline promising avenues for future research, and summarize the key findings.

2. Literature Review

This section outlines the key literature underpinning this research. The discussion begins with studies addressing VRPs and SVRPs, and then turns to approaches that incorporate DL and DRL as solutions techniques into these class of formulations. Finally, a description of recent and closer research to our proposal is presented. While the discussion is organized along a general chronological trajectory, it emphasizes critical analysis, identifies limitations in existing approaches, and highlights the research gap that this work aims to address.

2.1. VRPs and the Evolution of Strategies for SVRPs

The seminal work on VRPs [26] aimed to optimize fuel delivery to service stations using Linear Programming techniques—an example of exact algorithms. Subsequent research expanded this foundation to a variety of transportation systems through diverse computational approaches. For a more comprehensive review, refer to Toth & Vigo [2]. More recently, Rios et al. [8] summarized seven years of research on Dynamic VRP variants—where customer requests change over time. Notably, this work categorizes the reviewed literature according to the solution methods employed.

SVRPs extend the classical VRP by introducing uncertainty into problem parameters such as travel times, service times, or customer demands [2]. This uncertainty reflects the inherent variability of real-world operations, where exact parameter values are unknown at the planning stage. The VRP with stochastic travel and service times was first formally introduced by Laporte et al. [27] under an a priori framework, where routes are planned before the realization of uncertain values. Their penalty-based formulation, which excluded capacity constraints, incurred costs when route durations exceeded predefined deadlines. Although methodologically rigorous—employing chance constraints, recourse models, and a branch-and-cut algorithm—the approach was evaluated only on small-scale instances (up to 20 customers) with limited scenario sets, constraining its practical applicability. Later, Lei et al. [28] incorporated capacity constraints, stochastic service times, and maximum route duration limits into the formulation, proposing a generalized variable neighborhood search heuristic as solution method.

More complex variants have since been explored. For example, Li et al. [24] studied the SCVRPSTW, modeling travel and service times as independent normally distributed random variables. Their approach incorporates penalties on time windows or route duration violations, evaluated within a two-stage recourse framework using Monte Carlo simulation. Similarly, Taş et al. [25] considered stochastic travel times modeled via a gamma distribution, balancing operational costs against customer inconvenience, and later extended their work with an exact branch-and-price algorithm [29]. While these contributions represent important advances in integrating temporal features with stochasticity, they rely on scenario-based evaluation and either heuristics or exact optimization methods. This reliance limits scalability, adaptability, and robustness. Additionally, most early SVRP models focused on a single source of uncertainty—such as travel times or service times—ignoring the joint effects of multiple stochastic parameters. Realistic extensions should account for the simultaneous presence of uncertainty in several attributes. Furthermore, the assumption of independent random variables is often unrealistic. In practice, external factors such as adverse weather or traffic incidents induce spatial and temporal correlations across multiple route segments [2].

Currently, the methodological landscape for SVRPs remains explored by conventional approaches, including rollout policies, scenario-based metaheuristics, and stochastic programming. For example, Fachini et al.  [22] proposed a metaheuristic combining column generation and granular local search for a VRP with stochastic travel times. Although effective, their approach required scenario sampling and repeated re-optimization. Similarly, Xia et al. [23] introduced a discrete spider monkey optimization algorithm for a VRP formulation with stochastic demands; however, its performance degraded as problem size increased, and it lacked generalization across instance distributions. While often effective for the specific settings they target, these disadvantages limit scalability and real-time applicability.

The emergence of decision-making frameworks, such as the proposal by Ulmer et al. [30], formalized SVRPs as sequential decision processes. This was achieved using RL and dynamic programming principles. Likewise, Soeffker et al. [31] promoted decision-making-based formulations and provided a functional taxonomy of VRP dimensions. These works establish a conceptual bridge between classical optimization and data-driven approaches by clearly defining the core components of the solution pipeline and identifying opportunities for integrating Neural Network Models (NNMs). Within this domain, NNMs became particularly relevant due to their capacity to learn adaptive policies directly from interaction with the environment, enabling solvers that generalize across a wider range of stochastic scenarios without explicit re-optimization. Before the mid-2010s, NNMs in VRPs were primarily employed as auxiliary components within heuristics or metaheuristics, serving as function approximators for tasks such as value estimation or operator selection, rather than generating solutions end-to-end. Representative examples include the works by Ulmer et al. [32], Shi et al. [6], and Chandomí et al. [33], where NNMs assist decision-making under uncertainty but do not benefit from their complete generalization potential.

2.2. End-to-End Learning-Based Models for VRPs

The first end-to-end DL model for combinatorial optimization, including the CVRP, was introduced by Vynials et al. [13]. This work represents a pivotal milestone in the research area. Their Pointer Network (PN) architecture, inspired by sequence-to-sequence models in natural language processing, directly outputs solution sequences without resorting to handcrafted heuristics or metaheuristics. However, training relied on the SL paradigm, requiring optimal solution labels generated via exact solvers—an approach that significantly limits scalability and generalization to larger or stochastic instances.

To address this limitation, Bello et al. [14] replace SL with RL as the training paradigm, introducing the Neural Combinatorial Optimization (NCO) framework. NCO has since become a foundational approach for policy-based DRL methods that construct solutions autoregressively, i.e., sequentially generating solution components from scratch, guided by a neural network that models the underlying probability distribution. The policy is trained using variants of, or directly applying, the REINFORCE algorithm [34]. In particular, actor–critic methods [35] extend REINFORCE by introducing a learned value function (critic) that serves as a baseline, substantially reducing variance and providing more stable and efficient guidance for updating the actor’s policy.

Subsequent works extended NCO by modifying the PN architecture [18] or adapting the framework to other routing problem variants [36]. Nevertheless, a key limitation of these approaches—shared with many Recurrent Neural Network (RNN)-based models—is their reliance on compressed hidden states to carry information across decoding steps, which can lead to the loss of fine-grained input details. Additionally, their training is often slow due to the inherently sequential nature. Furthermore, when applied to VRPs, these models struggle with long routes, as they are prone to vanishing gradient issues—even though the PN utilizes architectures such as LSTMs or GRUs.

The advent of the Transformer model [37] led to a surge of studies redesigning the NCO approach for VRPs. One of the most influential was the Attention Model (AM) proposed by Kool et al. [17], which achieved competitive performance on CVRP instances with up to 100 customers, comparable to heuristic solvers such as LKH3 [10]. One relevant subsequent study based on the AM was the POMO algorithm [16], which proposed a method for generating multiple solutions for a single instance in a single pass. This strategy helps avoid getting trapped in local optima and reduces biases caused by the initial decision-making. Moreover, it provides a stable and simple baseline for estimating the reference reward during the training of NNMs. The algorithm was applied to both the Traveling Salesman Problem (TSP) and the CVRP. Empirical results show that models trained with this approach for problem instances with 20, 50, and 100 customers outperform those using the original AM, as well as learning-to-improve strategies—a kind of hybrid approach that selects classic heuristic operators to improve a feasible solution based on a trained NNM, such as those proposed by Chen et al. [38] and Lu et al. [39].

Despite its success, most of the works discussed in this section were originally designed for static and fully deterministic environments, and their effectiveness in handling stochasticity and time constraints remains fairly unexplored. Indeed, the AM is the most extended approach; the following section demonstrates this statement.

2.3. Recent DRL Advances for Variants of the VRP

From a broad perspective, Zhou et al. [40] provides a comprehensive survey of learning-based approaches for VRPs, proposing a classification into construction-based and improvement-based frameworks. Their work highlights emerging trends, identifies key challenges, and emphasizes the need for standardized benchmarking, while also aligning future research directions with sustainability objectives. However, despite its stated scope encompassing Machine Learning (ML), the review primarily focuses on DRL and NNMs, offering limited coverage of classical ML techniques such as support vector machines and ensemble methods.

Building on the AM [17], Zhang et al. [41] adapted such an architecture to address the VRP with Soft Time Windows (VRPSTW) and multiple capacitated vehicles. In their formulation, each vehicle is modeled as an agent that perceives the state of both the environment and other vehicles. The context vector is extended by concatenating the embeddings of the last customer visited by each vehicle, enabling inter-vehicle coordination. Temporal information—specifically the service time window—is incorporated as an additional real-valued feature for each node, alongside the standard coordinates and demands. The model outputs both the next customer to visit and the vehicle assigned to perform the delivery. Their approach was benchmarked against a genetic algorithm, iterative local search, and OR-Tools [42], showing superior performance in several synthetic settings.

The work by Bono et al. [19] is particularly relevant to the present study, as it constitutes one of the closest research efforts to ours in terms of problem scope. They proposed the Multi-Agent Routing Deep Attention Mechanism (MARDAM), an AM-based framework designed to handle multiple VRP variants, including the CVRP, CVRP with time windows, SCVRP with time windows (with uncertainty in travel times and demands), and a Dynamic-SCVRP with Time Windows (DSCVRPTW) where part of the requests are revealed online. All formulations assume a homogeneous fleet of capacitated vehicles. The problem is modeled using an extended Multi-Agent Markov Decision Process (MAMDP), where an aggregated control variable determines which vehicle updates its route at each decision step, ensuring sequential decision-making across agents. MARDAM introduces an additional embedding module to encode both the fleet state and the currently active vehicle, thereby enhancing the model’s ability to reason over multiple agents in dynamic and stochastic environments. Experimental results against OR-Tools [42] show strong performance in the addressed scenarios. However, their study applies hard time windows through masking processes rather than using penalizations. Additionally, the absence of detailed mathematical formulations in the paper makes direct reproducibility and extension challenging.

The analysis of the revised literature highlights that although DRL approaches have advanced significantly in solving static and deterministic VRPs, their extensions to realistic stochastic and time-sensitive variants remain limited. Notably, even state-of-the-art models such as those by Zhang et al. [41] and Bono et al.[19], which address multi-vehicle and stochastic settings, do not incorporate algorithmic innovations from leading static VRP solvers like POMO [16]. In particular, they lack mechanisms for multi-solution rollout, inductive biases for the problem addressed and more stable reward estimation—features that enhance exploration and training stability. This work bridges these gaps by extending the POMO framework to the SCVRPSTD, a variant that integrates stochastic travel times, uncertain service durations, and delivery deadlines. The proposed POMO-DC model introduces a time-aware dynamic context that explicitly tracks cumulative travel time and delivery delays, enabling adaptive decision-making under uncertainty. By embedding these temporal dynamics into the state, policy and reward structure, the approach advances the robustness and practical applicability of DRL-based routing solvers in urban logistics.

To summarize,

Table 1. Comparison of DRL approaches for VRPs, focusing on problem type, model architecture, training method, and handling of stochastic and time-sensitive elements. A cross indicates the feature is absent from the model, whereas a check mark indicates its inclusion.

Study	Problem Type	NNM Architecture	Training	Stochastic Inputs		Delay Tracking
				Travel	Service
[13]	CVRP	PN	SL	×	×	×
[14]	CVRP	PN	Actor-critic	×	×	×
[18]	CVRP	PN-based	Actor-critic	×	×	×
[17]	CVRP	Transformer-based	REINFOCE with greedy rollout	×	×	×
[16]	CVRP	AM-based	REINFOCE with shared baseline	×	×	×
[41]	Capacitated VRPSTW	Multi-Agent AM	REINFOCE with greedy rollout	×	×	×
[19]	DSCVRPTW	MARDAM	Actor-critic	✓	×	×
[21]	Dynamic and Uncertain VRP	RNN-based	Actor-critic	×	✓	×
This work	SCVRPSTD	POMO-DC	REINFORCE with shared baseline	✓	×	✓

classifies key DRL approaches by problem type, model architecture, training method, and support for stochastic and time-sensitive elements.

3. Materials and Methods

This section presents the qualitative and formal modeling of the delivery system under study, referred to as the SCVRPSTD. To contextualize this variant, it is first necessary to revisit the foundational CVRP and its most closely related extension to the proposed formulation, the SCVRPSTW.

The CVRP extends the TSP by incorporating vehicle capacity constraints [2]. In this formulation, a fleet of vehicles with limited load capacity is tasked with serving a set of geographically distributed customers, each associated with a known demand. All vehicle routes begin and end at a central depot, and each route must respect the vehicle’s capacity limit, ensuring that the total demand served does not exceed its carrying capacity. The objective is to construct a set of feasible tours that collectively fulfill all customer demands while minimizing the total travel cost.

Similarly, the SCVRPSTW builds upon the CVRP, but integrates temporal features with uncertainty and relaxes strict temporal requirements. Hence, travel times and/or service times are modeled as random variables—typically with known probability distributions—to capture real-world variability arising from both predictable factors (e.g., traffic patterns) and unpredictable disruptions (e.g., accidents, adverse weather). Customers are assigned time windows representing preferred service intervals; however, these are treated as “soft” constraints, allowing early or late arrivals at the cost of penalties proportional to the deviation. The formulation thus aims to balance cost efficiency with service quality under stochastic operating conditions.

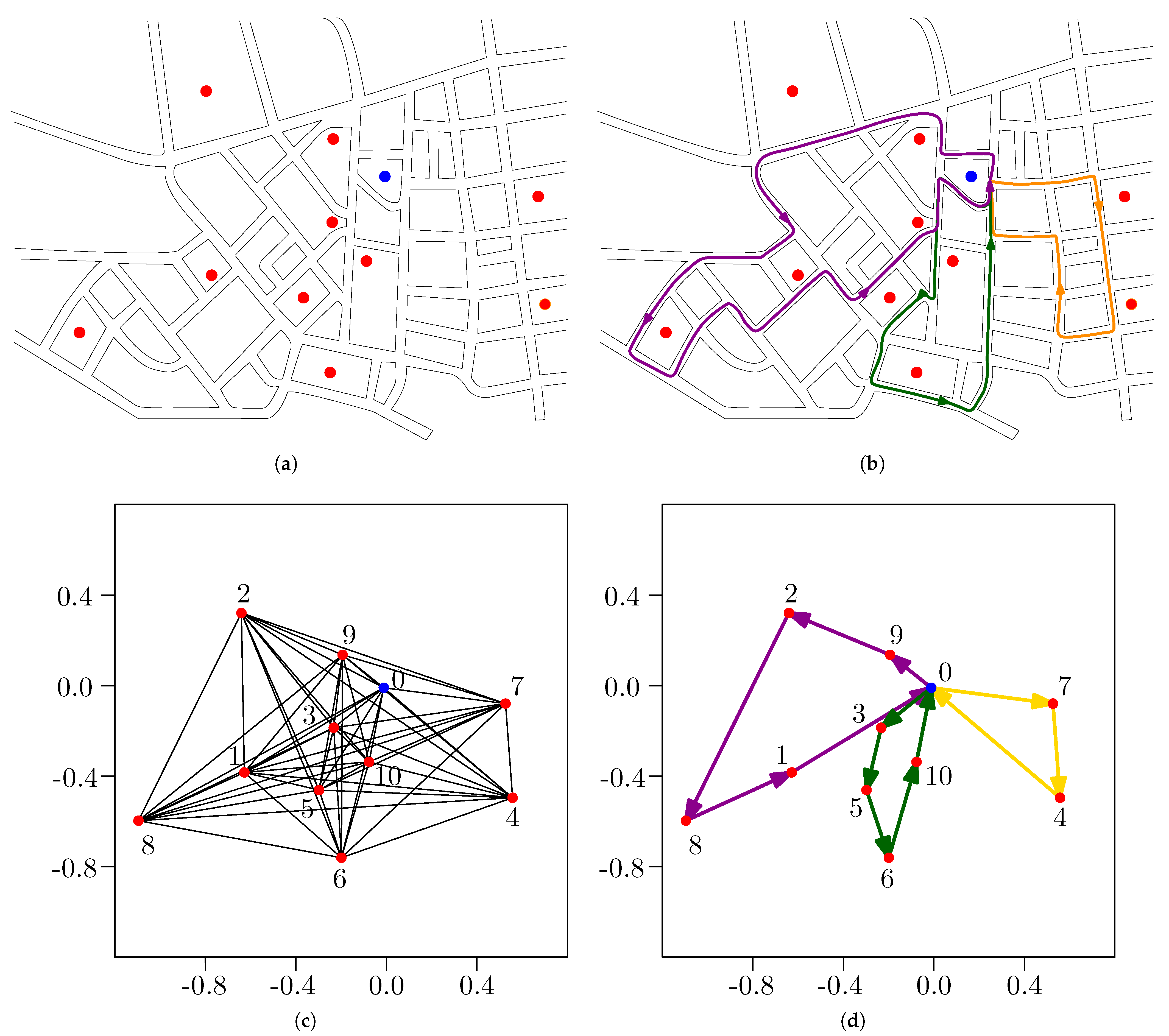
In the specific variant examined in this study—consistent with the single-vehicle framework employed by Kwon et al. [16] and Kool et al. [17]—a single vehicle is responsible for serving all customer requests. Given the vehicle’s limited capacity, multiple returns to the depot are permitted to reload, effectively decomposing the global tour into a sequence of sub-tours, as illustrated in Figure 1. This structure guarantees satisfaction of customer demands even when the aggregate exceeds the vehicle’s carrying capacity in a single trip. The resulting solution can thus be interpreted as a single route that revisits the depot, forming a series of Hamiltonian circuits over disjoint subsets of customers. Nevertheless, in cases where the travel time of a single vehicle becomes infeasible (e.g., exceeding an 8-hour work shift), these Hamiltonian circuits or sub-routes may be reassigned across multiple vehicles, thereby maintaining operational feasibility.

Additionally, to more faithfully capture real-world operational complexities, the formulation preserves the classical CVRP setting—each customer specified by a location and demand—while incorporating three additional features:

• Stochastic travel times: Travel durations between locations are represented as random variables, accounting for variability induced by factors such as traffic congestion, weather, or road conditions. These realizations become known only upon route completion or during traversal.
• Uncertain service times: The service duration at each customer is drawn from a known distribution, reflecting variability in customer availability, unloading procedures, or accessibility constraints.
• Delivery deadlines: Each customer is associated with a latest admissible service start time; arrivals beyond this deadline incur penalties in the reward function, discouraging excessive delays and promoting service reliability.

The objective is to minimize the expected total travel time while simultaneously reducing deadline violations, all within the bounds of strict capacity constraints. By integrating these elements, the SCVRPSTD formulation explicitly addresses the dual challenges of uncertainty and time sensitivity that characterize urban delivery systems.

3.1. Markov Decision Process Formulation

The problem introduced above is formally represented as a Markov Decision Process (MDP), characterized by the tuple $\mathcal{E}=\langle \mathcal{S},\mathcal{A},\mathcal{T},\mathcal{R}\rangle$, where $\mathcal{S}$ denotes the state space, $\mathcal{A}$ the action space, $\mathcal{T}$ the transition function, and $\mathcal{R}$ the reward function. The precise definition of each component is provided in the following subsections.

3.1.1. State Space

A state $s_t\in \mathcal{S}$ at decision epoch t contains all information required to make a decision [30]. In the proposed formulation, the state is composed of both static and dynamic elements:

• Static elements

  -

  Vehicle capacity $L_{\max }$. An integer specifying the maximum number of items the vehicle can carry. Its value depends on the instance size, defined by the number of delivery requests n.

  -

  Depot features $x_0\in {\mathbb{R}}^{b\times 1\times 3}$. A tensor with three attributes for the depot in each of the b problem instances (batch dimension): 2D coordinates and the service time for reloading, $t_{\mathrm{reload}}$.

  -

  Delivery features $x_c\in {\mathbb{R}}^{b\times n\times 5}$. A tensor with five attributes for each of the n customer locations across the b instances: 2D coordinates, demand (number of items to deliver), service time (delivery duration), and deadline (latest possible time for fulfilling the request).

• Dynamic elements

  -

  Current actions $a_t\in {\{0,\dots ,n\}}^{b\times \Gamma }$. The set of locations selected at decision epoch t, representing feasible next locations or nodes that respect problem constraints. The symbol $\Gamma$ is the number of parallel solutions or trajectories computed per instance [16].

  -

  Current vehicle load $L_t\in {\mathbb{R}}^{b\times \Gamma }$. The load carried by the vehicle at epoch t, updated according to the cumulative demands of visited customers.

  -

  Accumulated travel time $t_{\mathrm{travel}}^{\left(t\right)}\in {\mathbb{R}}^{b\times \Gamma }$. The elapsed travel time up to epoch t, computed from stochastic travel durations and service times. This feature informs both state transitions and the reward signal.

  -

  Accumulated delay $t_{\mathrm{out}}^{\left(t\right)}\in {\mathbb{R}}^{b\times \Gamma }$. The total penalty time incurred when customer deadlines are violated, dynamically updated throughout the route.

  -

  Feasibility mask ${\xi }_t\in {\{0,1\}}^{b\times \Gamma \times (n+1)}$. A binary tensor that excludes invalid actions by masking locations already visited or infeasible due to load constraints at epoch t.

  -

  Trajectory completion mask ${\xi }_{\mathrm{trajectory}}^{\left(t\right)}\in {\{0,1\}}^{b\times \Gamma }$. A binary tensor indicating whether a trajectory has been fully constructed, thereby disabling further action selection for that trajectory.

It is important to note that most of the temporal features and tensors defined above were not part of the original CVRP formulation addressed in [16]. Consequently, the state transition and reward functions have been consistently adapted to the extended problem structure.

3.1.2. Action Space

The action space $\mathcal{A}$ consists of all valid action tensors $a_t\in {\{0,1,\dots ,n\}}^{b\times \Gamma }$ for the b instances in the batch and the $\Gamma$ trajectories at the current decision epoch t. These tensors are generated sequentially by the NNM based on the current state $s_t$.

After T decision epochs, the solution tensor $\mathcal{H}\in {\{0,1,\dots ,n\}}^{b\times \Gamma \times T}$ is constructed by concatenating the sequence of actions along the last dimension, as described in Equation (1).

$$\mathcal{H}=\left[a_0;a_1;\dots ;a_T\right]$$

(1)

To ensure feasibility concerning problem constraints, such as vehicle capacity and unvisited nodes, action masking is applied during inference using ${\xi }_t$. A detailed description of the action generation mechanism and masking process is provided in Section 3.2.2, where the NNM’s decoding procedure is discussed.

3.1.3. Transitions

Transitions capture the effects of actions on the environment, manifesting as changes in the states.

Given the action tensor $a_t={\{0,1,\dots ,n\}}^{b\times \Gamma }$, the type of each selected location is evaluated. If the selected location corresponds to the depot (i.e., ${\left[a_t\right]}_{ij}=0$), the vehicle’s available load is reset to its maximum capacity: ${\left[L_t\right]}_{ij}=L_{\max }$. Additionally, the corresponding travel time ${[t_{\mathrm{travel}}^{(t+1)}]}_{ij}$ is updated to include the time required to reload the vehicle, as defined in Equation (2).

$${[t_{\mathrm{travel}}^{(t+1)}]}_{ij}={[t_{\mathrm{travel}}^{\left(t\right)}]}_{ij}+t_{\mathrm{reload}}$$

(2)

On the other hand, for entries in $a_t$ corresponding to delivery requests, the delivery delays, available supplies, and travel times are updated according to Equations (3), (4) and (5), respectively. Where $d\in {\mathbb{R}}^{b\times n}$ denotes the demand tensor, and $t_{\mathrm{service}}\in {\mathbb{R}}^{b\times n}$ is the tensor of service times—features included in $x_c$.

$$\begin{array}{cc}\hfill {[t_{\mathrm{out}}^{(t+1)}]}_{ij}& ={[t_{\mathrm{out}}^{\left(t\right)}]}_{ij}+max({[t_{\mathrm{travel}}^{\left(t\right)}]}_{ij}-{[t_{\mathrm{deadline}}]}_{i{\left[a_t\right]}_{ij}},0)\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill [L_{t+1}{]}_{ij}& ={\left[L_t\right]}_{ij}-{\left[d\right]}_{i{\left[a_t\right]}_{ij}}\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill [t_{\mathrm{travel}}^{(t+1)}{]}_{ij}& ={[t_{\mathrm{travel}}^{\left(t\right)}]}_{ij}+{[t_{\mathrm{service}}]}_{i{\left[a_t\right]}_{ij}}\hfill \end{array}$$

(5)

Following these updates, the next set of requests to be delivered is determined and gathered into the action tensor $a_{t+1}$. The edge travel time between consecutive locations is computed based on Euclidean distance, scaled by a stochastic multiplier $\omega$. Specifically, the distance between locations j and k, with coordinates $({\left[x\right]}_{ij},{\left[y\right]}_{ij})$ and $({\left[x\right]}_{ik},{\left[y\right]}_{ik})$, respectively, is given by $d_{\mathrm{edge}}=\sqrt{{({\left[x\right]}_{ij}-{\left[x\right]}_{ik})}^2+{({\left[y\right]}_{ij}-{\left[y\right]}_{ik})}^2}$. The corresponding travel time is proportional to this distance: $t_{\mathrm{edge}}=\omega d_{\mathrm{edge}}$, where $\omega$ is sampled independently for each edge, introducing the main stochastic component of the formulation. These values are accumulated into the global travel time tensor $t_{\mathrm{travel}}^{\left(t\right)}$, in a similar way as expressed by Equation (5).

This transition mechanism ensures that the state evolves dynamically in response to agent actions, incorporating both the constraints and stochastic factors of the formulation.

3.1.4. Reward Function

The objective of this formulation is to jointly minimize the total travel time $t_{\mathrm{travel}}^{\left(T\right)}$ and the accumulated delivery delays $t_{\mathrm{out}}^{\left(T\right)}$, given the solution tensor $\mathcal{H}$. The reward is computed by simply summing the expected values of these two terms, as shown in Equation (6).

$$\mathcal{R}=-\mathbb{E}\left[t_{\mathrm{travel}}^{\left(T\right)}+t_{\mathrm{out}}^{\left(T\right)}\right]$$

(6)

In addition to this direct formulation, a normalized weighted sum was also explored for computing the reward. This is a common approach used in multiobjective formulations; refer to Lin et al. [43] for a detailed explanation of this and other schemes. While this approach allows for explicit control over the trade-off between objectives, the empirical results indicate that the simpler additive form in Equation (6) consistently leads to better performance. Comments that argue this behavior are discussed in Section 5.

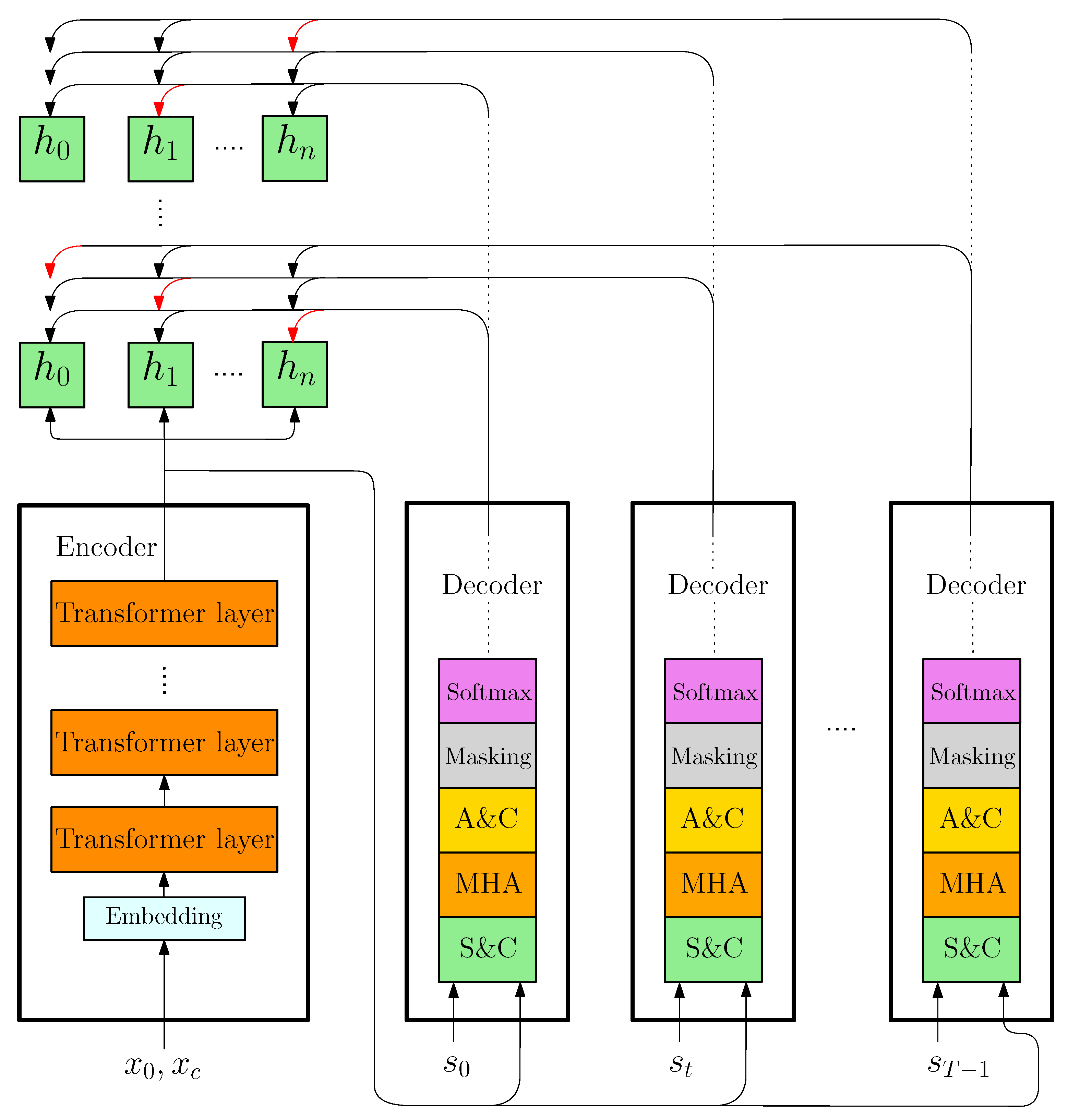
3.2. Solution Model

Figure 2 presents a schematic representation of the computational pipeline executed by the proposed NNM. The architecture builds upon the AM framework introduced by Kool et al. [17] and follows the implementation principles of POMO [16], while incorporating key adaptations and contributions developed in this work. As discussed in Section 2, Transformer-based architectures offer superior modeling capabilities compared to RNNs, particularly through their ability to process input sequences in parallel and capture long-range dependencies. These attributes, combined with their capacity to exploit structural symmetries in graph-structured problems make them especially well-suited for combinatorial optimization tasks, specifically VRPs. The mentioned features provide a strong rationale for adopting this type of architecture in the context addressed and argue for the design of the proposed model.

The architecture follows an encoder–decoder structure. The encoder maps the input problem instance into a set of vector representations using the standard Transformer architecture [37]. The decoder, on the other hand, generates multiple solution trajectories in parallel for each instance by leveraging both the encoder outputs and a dynamic context vector that evolves over decision epochs. This process is carried out in an autoregressive manner, enabling sequential decision-making conditioned on the current state. The following sections formally describe the design and functionality of each component in the proposed architecture.

3.2.1. Encoder

The encoder transforms raw input features into high-dimensional representations through a series of learned embeddings and Transformer layers [37]. This process enables the model to capture both local node characteristics and global structural dependencies within the routing instance.

To facilitate unified processing of heterogeneous node types, the depot and customer features are projected into a shared latent space of dimension $d_h$. This ensures that all nodes—despite differing input dimensions—are represented in a common “semantic” or “functional” space, enabling the attention mechanism to reason over them coherently. In Figure 2, such a process is depicted within the encoder under the “Embedding” block.

The transformation of depot features into this latent space is defined in Equation (7). Specifically, the normalized depot tensor ${\widehat{x}}_0\in {\mathbb{R}}^{b\times 1\times 3}$ is linearly mapped using a learnable weight matrix $W_0\in {\mathbb{R}}^{3\times d_h}$ and bias vector $u_0\in {\mathbb{R}}^{d_h}$, resulting in the embedded representation $X_0$.

$$\begin{array}{cc}\hfill X_0& =W_0{\widehat{x}}_0+u_0\hfill \end{array}$$

(7)

Customer features, which include coordinates, demand, service time, and deadline, are processed through a separate but analogous transformation, as given in Equation (8). The normalized tensor ${\widehat{x}}_c\in {\mathbb{R}}^{b\times n\times 5}$ is projected using learnable parameters $W_c\in {\mathbb{R}}^{5\times d_h}$ and $u_c\in {\mathbb{R}}^{d_h}$.

$$\begin{array}{cc}\hfill X_c& =W_c{\widehat{x}}_c+u_c\hfill \end{array}$$

(8)

This separation preserves the distinct semantics of depot and customer nodes while mapping them into the same latent space.

Once computed, the individual embeddings are combined to form a global node representation. As expressed in Equation (9), $X_0$ and $X_c$ are concatenated along the second dimension to yield a unified feature tensor $X\in {\mathbb{R}}^{b\times (n+1)\times d_h}$.

$$\begin{array}{cc}\hfill X& =[X_0;X_c]\hfill \end{array}$$

(9)

This tensor serves as the input to a stack of L Transformer layers, where relational reasoning among all nodes is performed.

Each Transformer layer applies Multi-Head Attention (MHA) to refine the node representations. For the m-th attention head in layer l, the key, query, and value projections are computed according to Equations (10), (11) and (12), respectively.

$$\begin{array}{cc}\hfill K_m^{\left(l\right)}& =H^{(l-1)}{W}_{K,m}^{\left(l\right)}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill Q_m^{\left(l\right)}& =H^{(l-1)}{W}_{Q,m}^{\left(l\right)}\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill V_m^{\left(l\right)}& =H^{(l-1)}{W}_{V,m}^{\left(l\right)}\hfill \end{array}$$

(12)

where $H^{\left(0\right)}=X$, and the projection matrices $W_{K,m}^{\left(l\right)}$, $W_{Q,m}^{\left(l\right)}\in {\mathbb{R}}^{d_h\times d_k}$, $W_{V,m}^{\left(l\right)}\in {\mathbb{R}}^{d_h\times d_v}$ are learned to extract relevant features for attention computation.

The attention scores are derived from the dot products of queries and keys, scaled by $\sqrt{d_k}$ to prevent vanishing gradients and stabilize training. This operation is formalized in Equation (13).

$$\begin{array}{cc}\hfill C_m^{\left(l\right)}& ={\displaystyle \frac{1}{\sqrt{d_k}}}{Q}_m^{\left(l\right)}{\left(K_m^{\left(l\right)}\right)}^{\top }\hfill \end{array}$$

(13)

The resulting scores are normalized via softmax and used to weight the value vectors, producing the output of the attention head. Such a transformation is specified in Equation (14).

$$\begin{array}{cc}\hfill {\alpha }_m^{\left(l\right)}& =\mathrm{softmax}\left(C_m^{\left(l\right)}\right)V_m^{\left(l\right)}\hfill \end{array}$$

(14)

Each ${\alpha }_m^{\left(l\right)}\in {\mathbb{R}}^{b\times (n+1)\times d_v}$ thus represents an instance-aware summary, where attention is focused on the most relevant locations.

The outputs from all M heads are concatenated and linearly transformed to restore the original dimensionality. This step, shown in Equation (15), integrates information from multiple attention subspaces.

$$\begin{array}{cc}\hfill O^{\left(l\right)}& =[{\alpha }_1^{\left(l\right)};\dots ;{\alpha }_M^{\left(l\right)}]W_O\hfill \end{array}$$

(15)

The matrix $W_O\in {\mathbb{R}}^{M{d}_v\times d_h}$ projects the concatenated output back into ${\mathbb{R}}^{d_h}$, ensuring compatibility with the residual connection [44].

A residual connection is then applied, followed by instance normalization, as defined in Equation (16). This promotes stable gradient propagation and accelerates convergence [44].

$$\begin{array}{cc}\hfill O_n^{\left(l\right)}& =\mathrm{InstanceNormalization}\left(H^{(l-1)}+O^{\left(l\right)}\right)\hfill \end{array}$$

(16)

Subsequently, a Feed-Forward Network (FFN) further processes the normalized output. This transformation, detailed in Equation (17), consists of a linear projection, ReLU activation, and a second linear layer.

$$\begin{array}{cc}\hfill O_f^{\left(l\right)}& =\mathrm{ReLU}\left(O_n^{\left(l\right)}{W}_{f_1}\right)W_{f_2}\hfill \end{array}$$

(17)

Finally, a second residual connection and normalization yield the output of the l-th layer, as given in Equation (18).

$$\begin{array}{cc}\hfill H^{\left(l\right)}& =\mathrm{InstanceNormalization}\left(O_n^{\left(l\right)}+O_f^{\left(l\right)}\right)\hfill \end{array}$$

(18)

This two-sublayer structure—attention followed by FFN—constitutes one Transformer block, as depicted in Figure 2 by the orange boxes, and is repeated L times to progressively refine the node embeddings. After L layers, the final output $H^{\left(L\right)}\in {\mathbb{R}}^{b\times (n+1)\times d_h}$ contains enriched, instance-sensitive representations for all nodes. Specifically, it consists of $n+1$ feature vectors of dimension $d_h$ for each of the b instances in the batch. Such embeddings are used by the decoder to guide the sequential construction of vehicle routes.

3.2.2. Decoder

While Kool et al. [17] introduced dynamic context in attention-based models by incorporating the vehicle’s remaining load and the representation of the last visited node during decoding, the proposed decoder extends this concept by explicitly integrating a broader set of dynamic, time-varying features. In addition to these, it accounts for variables such as elapsed travel time and cumulative delay (or time-outs), which evolve as the route progresses. This enriched dynamic context enables more accurate modeling of realistic routing scenarios, where decisions must adapt continuously to changing environmental conditions.

At every decision point t, the decoder processes the current dynamic state and uses it to construct a context-aware query that guides attention toward the most promising next node (as depicted in Figure 2 by the arrows). Specifically, the first step is to “Scale and Concatenate (S&C)” the relevant dynamic quantities, forming the dynamic context vector. These quantities include the embedding of the last visited location $h^{(t-1)}$, the current vehicle load $L_t$, the cumulative travel time $t_{\mathrm{travel}}^{\left(t\right)}$, and the accumulated delay $t_{\mathrm{out}}^{\left(t\right)}$, each normalized by its respective maximum possible value (the result of this operation is denoted by the hat symbol). The resulting context vector is defined in Equation (19).

$$c_t=[h^{(t-1)};{\widehat{L}}_t,{\widehat{t}}_{\mathrm{travel}}^{\left(t\right)},{\widehat{t}}_{\mathrm{out}}^{\left(t\right)}]$$

(19)

where the concatenation is applied along the second dimension. As a result, the dynamic context tensor satisfies $c_t\in {\mathbb{R}}^{b\times \Gamma \times (d_h+3)}$.

This context vector serves as the query input to the MHA mechanism in the decoder. The key and value projections are derived from the encoder’s final output $H^{\left(L\right)}$ using linear transformations, as specified in Equations (20) and (21), respectively.

$$\begin{array}{cc}\hfill K_m& =H^{\left(L\right)}{W}_{K,m},W_{K,m}\in {\mathbb{R}}^{d_h\times d_k},K_m\in {\mathbb{R}}^{b\times (n+1)\times d_k}\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill V_m& =H^{\left(L\right)}{W}_{V,m},W_{V,m}\in {\mathbb{R}}^{d_h\times d_v},V_m\in {\mathbb{R}}^{b\times (n+1)\times d_v}\hfill \end{array}$$

(21)

The query is obtained by projecting the dynamic context $c_t$, as defined in Equation (22).

$$\begin{array}{cc}\hfill q_m& =c_t{W}_{Q,m},W_{Q,m}\in {\mathbb{R}}^{(d_h+3)\times d_k},q_m\in {\mathbb{R}}^{b\times \Gamma \times d_k}\hfill \end{array}$$

(22)

Attention scores are computed using scaled dot products between the query and key matrices. To ensure feasibility, inadmissible actions are masked out during this computation. The masked attention scores are given in Equation (23).

$$\begin{array}{cc}\hfill C_m& =\left\{\begin{array}{cc}-\infty \hfill & \mathrm{if}{\left[{\xi }_t\right]}_{ijk}=1\hfill \\ {\displaystyle \frac{1}{\sqrt{d_k}}}{q}_m{K}_m^{\top }\hfill & \mathrm{otherwise}\hfill \end{array}\right.,C_m\in {\mathbb{R}}^{b\times \Gamma \times (n+1)}\hfill \end{array}$$

(23)

In Equation (23), ${\xi }_t\in {\{0,1\}}^{b\times \Gamma \times (n+1)}$ is the dynamic feasibility mask that disables invalid actions at the current decision or time step. For the depot, the mask is activated if it has already been visited in a previous iteration. For customer locations, a mask is applied if the location has either already been visited (i.e., its demand is zero) or if its current demand exceeds the available load in the vehicle. These constraints are mathematically defined in Equations (24)–(27). In this context, $d_t$ represents an expanded tensor that indicates the demands for all $n+1$ locations (with the depot having zero demand) across all $\Gamma$ trajectories and b samples in the current batch.

$$\begin{array}{cc}\hfill {\left[{\xi }_{\mathrm{visit}}\right]}_{ij0}& =\left\{\begin{array}{cc}1\hfill & \mathrm{if}{\left[a_{t-1}\right]}_{ij}=0\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.,{\xi }_{\mathrm{visit}}\in {\mathbb{R}}^{b\times \Gamma \times (n+1)}\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill [{\xi }_{\mathrm{visit}}{]}_{ijk}& =\left\{\begin{array}{cc}1\hfill & \mathrm{if}{\left[d_t\right]}_{ijk}=0\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.,k\ne 0\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill [{\xi }_{\mathrm{demand}}{]}_{ijk}& =\left\{\begin{array}{cc}1\hfill & \mathrm{if}{\left[d_t\right]}_{ijk}>{\left[L_t\right]}_{ij}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.,\forall k=1,\dots ,n+1,{\xi }_{\mathrm{demand}}\in {\mathbb{R}}^{b\times \Gamma \times (n+1)}\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill {\xi }_t& =\mathrm{OR}({\xi }_{\mathrm{visit}},{\xi }_{\mathrm{demand}})\hfill \end{array}$$

(27)

The masked scores are passed through a softmax function and used to compute a weighted sum of the value vectors, as shown in Equation (28).

$$\begin{array}{cc}\hfill {\alpha }_m& =\mathrm{softmax}\left(C_m\right)V_m,{\alpha }_m\in {\mathbb{R}}^{b\times \Gamma \times d_v}\hfill \end{array}$$

(28)

The outputs from all M attention heads are concatenated and linearly transformed to restore the original embedding dimension. This operation, defined in Equation (29), produces the refined context vector $c_t^{\prime }$.

$$\begin{array}{cc}\hfill c_t^{\prime }& =[{\alpha }_1;\dots ;{\alpha }_M]W_O,W_O\in {\mathbb{R}}^{M{d}_v\times d_h},c_t^{\prime }\in {\mathbb{R}}^{b\times \Gamma \times d_h}\hfill \end{array}$$

(29)

Such an output integrates information from multiple attention subspaces and serves as input to the final attention layer. In this layer, compatibility scores between $c_t^{\prime }$ and the encoded node features $H^{\left(L\right)}$ are computed via scaled dot product attention. The resulting score tensor $\widehat{S}$ is defined in Equation (30).

$$\begin{array}{cc}\hfill \widehat{S}& ={\displaystyle \frac{1}{\sqrt{d_h}}}{c}_t^{\prime }{\left(H^{\left(L\right)}\right)}^{\top },\widehat{S}\in {\mathbb{R}}^{b\times \Gamma \times (n+1)}\hfill \end{array}$$

(30)

A second masking operation (Note that the first masking operation is performed within the MHA block) is applied to enforce feasibility constraints based on the dynamic mask ${\xi }_t$. As described in Equation (31), if a location is deemed infeasible (i.e., ${\left[{\xi }_t\right]}_{ijk}=1$), its corresponding score is set to $-\infty$ to eliminate it from further consideration during the softmax operation effectively, while valid scores are clipped using a hyperbolic tangent function scaled by a constant $\kappa$, ensuring that extreme values are smoothly controlled.

$$\begin{array}{cc}\hfill {\left[{\widehat{S}}_c\right]}_{ijk}& =\left\{\begin{array}{cc}-\infty \hfill & \mathrm{if}{\left[{\xi }_t\right]}_{ijk}=1\hfill \\ \kappa tanh\left({\left[\widehat{S}\right]}_{ijk}\right)\hfill & \mathrm{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(31)

Finally, the policy’s output distribution over feasible actions is obtained by applying a softmax function to the masked and clipped scores, as given in Equation (32).

$$\begin{array}{cc}\hfill p_t& =\mathrm{softmax}\left({\widehat{S}}_c\right),p_t\in {\mathbb{R}}^{b\times \Gamma \times (n+1)}\hfill \end{array}$$

(32)

The tensor $p_t$ represents the probability of selecting each node at step t, or it is understood a realization of the policy ${\pi }_{\theta }$ (i.e., the NNM). During training, actions $a_t$ are sampled from $p_t$ to enable exploration; during inference, a greedy selection is typically used. Additionally, $p_t$ is appended to a global tensor $\mathcal{P}=[p_1;\dots ;p_T]$, which is used in policy gradient updates.

The decoding process continues until all trajectories are complete. The trajectory completion mask ${\xi }_{\mathrm{trajectory}}^{\left(t\right)}\in {\{0,1\}}^{b\times \Gamma }$ is updated at each step based on whether all customer demands have been satisfied. This condition is evaluated using the visit mask ${\xi }_{\mathrm{visit}}$ (if all their elements in the last dimension are set to 1, then the computation is finished).

3.3. Training Scheme

The NNM introduced in the preceding section is trained using a variant of the REINFORCE algorithm [34] that uses a shared baseline [16] to reduce the variance of the gradient estimates. For a given sample i in a batch of size b, the shared baseline is computed as the average reward across all $\Gamma$ trajectories:

$$B_i={\displaystyle \frac{1}{\Gamma }}\sum _{j=1}^{\Gamma }{\left[\mathcal{R}\right]}_{ij}$$

(33)

This tensor should be expanded to match the shape of the full reward tensor, yielding $B\in {\mathbb{R}}^{b\times \Gamma }$.

The complete training procedure, detailing the computational steps performed at each epoch, is outlined in Algorithm 1. POMO-DC refers to the proposed DRL model trained using a POMO-based pipeline and enhanced with the dynamic context-aware decoder. The whole process involves encoding the batch of problem instances, executing rollouts to collect rewards and log-probabilities of actions, and updating the model parameters using policy gradient updates. The learning rate is dynamically adjusted according to a predefined schedule, and model checkpoints are periodically saved to facilitate evaluation and ensure fault-tolerant training.

In this form, the objective function to be minimized is approximated by:

$$\mathcal{L}\left(\theta \right)=-{\displaystyle \frac{1}{b\Gamma }}\sum _{i=1}^b\sum _{j=1}^{\Gamma }\left({\mathcal{R}}_{ij}-B_{ij}\right)log{\mathcal{P}}_{ij}$$

(34)

This loss encourages the model to assign a higher probability to trajectories that outperform the average solution for the same instance.

Algorithm 1 Overview of the POMO-DC training procedure for the SCVRPSTD

1: Input: Environment hyperparameters $\varphi$, model hyperparameters $\psi$, train hyperparameters $\eta$, and optimizer hyperparameters $\Omega$ 2: Output: Trained model parameters $\theta$ 3: Initialize environment $\mathcal{E}\leftarrow \mathrm{CVRPEnv}\left(\varphi \right)$ 4: Initialize model ${\pi }_{\theta }\leftarrow \mathrm{CVRPModel}\left(\psi \right)$ 5: Initialize optimizer $\mathcal{O}\leftarrow \mathrm{Optimizer}(\Omega )$ 6: Initialize learning rate scheduler $lr\leftarrow \mathrm{Scheduler}(\Omega )$ 7: for epoch $e=1$ to $E\in \eta$ do 8:    Reset loss: $\mathcal{L}\leftarrow 0$ 9:    for episode $k=1$ to $K\in \eta$ with step size $b\in \eta$ do 10:      Sample batch instances: $X\leftarrow \mathcal{E}$ 11:      Encode instances: $H^{\left(L\right)}\leftarrow \mathrm{Encoder}\left(X\right)$ 12:      Initialize rollout: $s_0\leftarrow \mathrm{Reset}\left(X\right)$ 13:      repeat 14:         Select actions and probabilities: $a_t,p_t\leftarrow {\pi }_{\theta }\left(s_t\right)$ 15:         Apply actions: $s_{t+1},r_t\leftarrow \mathcal{E}(s_t,a_t)$ 16:         Accumulate log-probabilities: $log\mathcal{P}\leftarrow \sum log{p}_t$ 17:      until termination 18:      Compute reward: $\mathcal{R}\leftarrow {\sum }_t{r}_t$ 19:      Compute advantage: $A\leftarrow \mathcal{R}-B$ 20:      Compute loss: $\mathcal{L}\leftarrow -A·log\mathcal{P}$ 21:      Update mode parameters: $\theta \leftarrow \mathcal{O}=\theta -\alpha {\nabla }_{\theta }\mathcal{L}$ 22:    end for 23:    Step learning rate scheduler: $\alpha \leftarrow lr$ 24: end for

4. Experiments and Results

4.1. Experimental Setup

Table 2. Environment, model, training and testing parameters.

Parameter	Symbol	Value, Range or Distribution
Number of customers	n	20, 30 or 50
Loading capacity	$L_{\max }$	30, 35 or 40
Time to reload the vehicle	$t_{\mathrm{reload}}$	15
Coordinates	$x_c$	$\mathcal{U}(0,12)$ *
Demands		$\mathcal{U}\{3,4,5\}$
Service times		$\mathcal{U}(3,5)$
Deadlines		$\mathcal{U}(60,480)$
Random proportionality constant	$\omega$	$\mathcal{U}(1,2)$
Number of generated trajectories	$\Gamma$	20, 30 or 50
Hidden or embedding dimension	$d_h$	128
Transformer layers in the encoder	L	6
Attention heads	M	8
Key, value dimension	$d_k$/$d_v$	16
Feed forward hidden dimension	$d_{ff}$	512
Clipping constant	$\kappa$	10
Batch dimension	b	64
Number of training samples	-	1,280,000
Number of testing samples	-	100
Epochs	E	50
Learning rate	$\alpha$	${10}^{-4}$
Optimizer	$\mathcal{O}$	Adam [45]

* This range is also used for the depot coordinate generation.

summarizes the parameters used for the environment setup, model architecture, and training configuration. The symbol $\mathcal{U}$ denotes a uniform distribution, with braces indicating discrete sets and parentheses representing continuous intervals. These settings are based on prior work in the literature—such as [17,19]—as well as operational conditions observed in local logistics companies. Particularly, the stochastic multiplier $\omega$ is calibrated to produce a maximum velocity of 61 km/h when traversing an edge. The environment setup (first part of Table 2) can be adapted to specific real-world scenarios or delivery system requirements using historical data. Three instance sizes were considered, corresponding to 20, 30, and 50 customers. Vehicle capacity was scaled accordingly, with maximum loads of 30, 35, and 40 units, respectively. The NNM model was trained for 50 epochs using over 1.28 million synthetic samples, in batches of 64. During evaluation, a separate set of 100 independent test instances was considered.

Concerning hardware, all experiments were conducted on a workstation equipped with an Intel(R) Core(TM) i7-4790 CPU (3.60 GHz) and an NVIDIA GeForce RTX 3080 Ti GPU.

The remainder of this section presents a detailed analysis of the results obtained by the proposed method, referred to as POMO-DC, and its performance in comparison with state-of-the-art metaheuristic approaches. Direct comparisons with other learning-based methods are challenging to establish, as existing architectures typically require significant adaptations to align with the specific formulation addressed. Such modifications often result in models that differ substantially from the original and may be considered entirely new proposals.

4.2. General Results

To evaluate the performance of the proposed approach against the considered classical metaheuristic methods, a benchmarking framework is implemented using the Google OR-Tools library [42], an open-source toolkit designed for solving a wide range of combinatorial optimization problems. OR-Tools has been widely adopted in both academic and industrial research, e.g., Zhang et al. [41] and Bono et al. [19], serving as a standard baseline for VRPs and scheduling applications. This software enables the use of different algorithms to obtain solutions for a particular problem once the features of the formulation have been established.

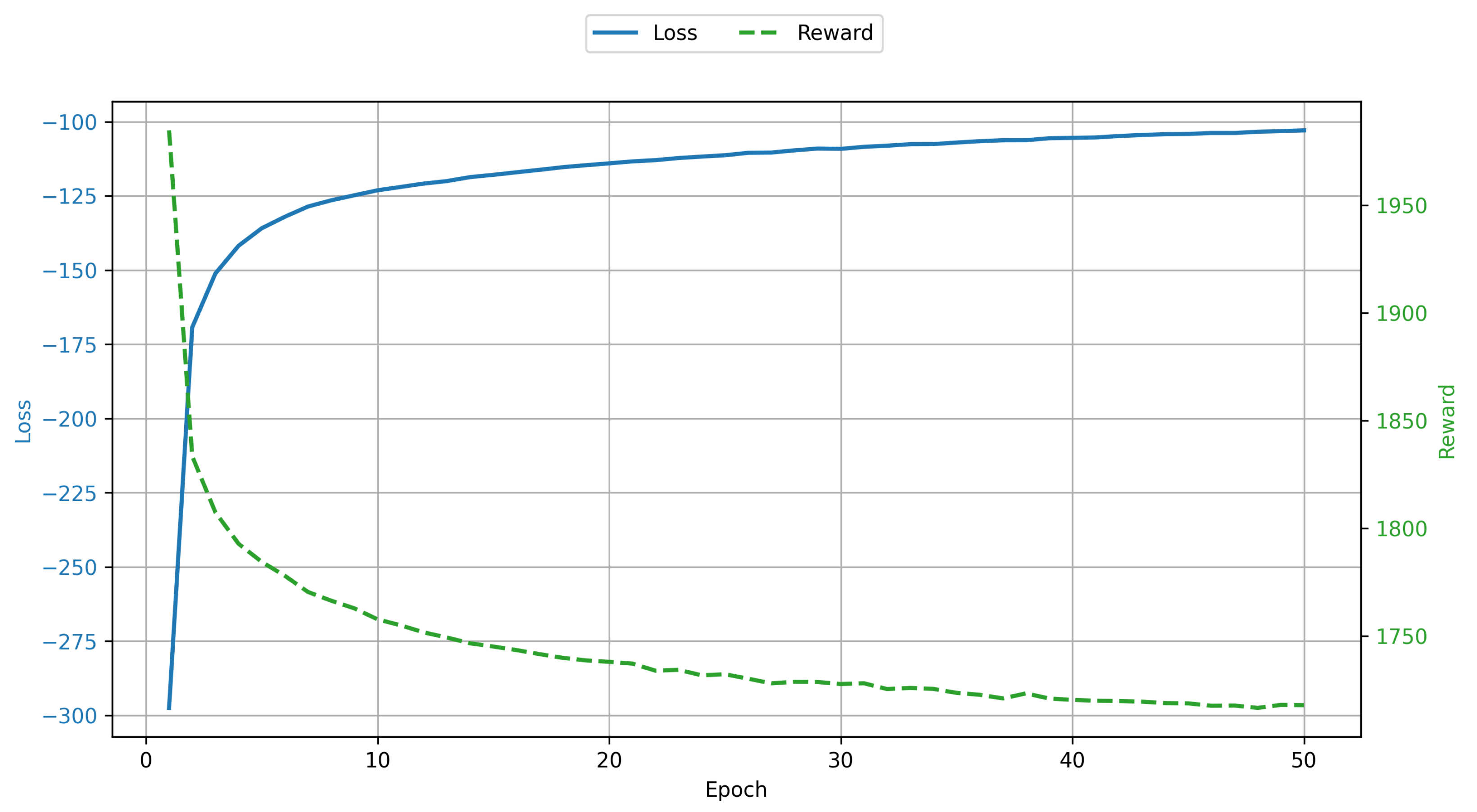
Three NNM using the POMO-DC approach (see Algorithm 1) were trained using different instance sizes ($n=20,30,50$). Figure 3 shows the evolution of the training loss and reward across epochs for the proposed POMO-DC model using instances of $n=50$ customers; for the other instance sizes, the behavior is similar. As expected, the loss decreases steadily, indicating that the policy network is effectively learning the direction in which its parameters should be changed to maximize expected return, in line with the principles of policy-based RL. Concurrently, the reward curve exhibits a consistent upward trend (to simplify training visualization, a minus sign is applied to this value, making the reward positive), demonstrating that the model progressively improves its routing performance as training proceeds.

After training, the models are evaluated on 100 previously unseen instances and benchmarked against OR-Tools configurations employing Guided Local Search (GLS), Tabu Search (TS), Simulated Annealing (SA), and Greedy Tabu Search (GTS).

Table 3. Performance comparison metrics on instances with $n=20$ customers.

Model	Travel Times (min)		Delays (min)
	Mean	Std. Dev.	Mean	Std. Dev.
POMO-DC	258.44	±18.47	0.30	±1.55
GLS	246.46	±19.78	0.49	±2.62
TS	252.22	±19.46	1.06	±8.16
SA	255.34	±21.85	0.55	±2.58
GTS	260.46	±22.25	2.20	±10.03

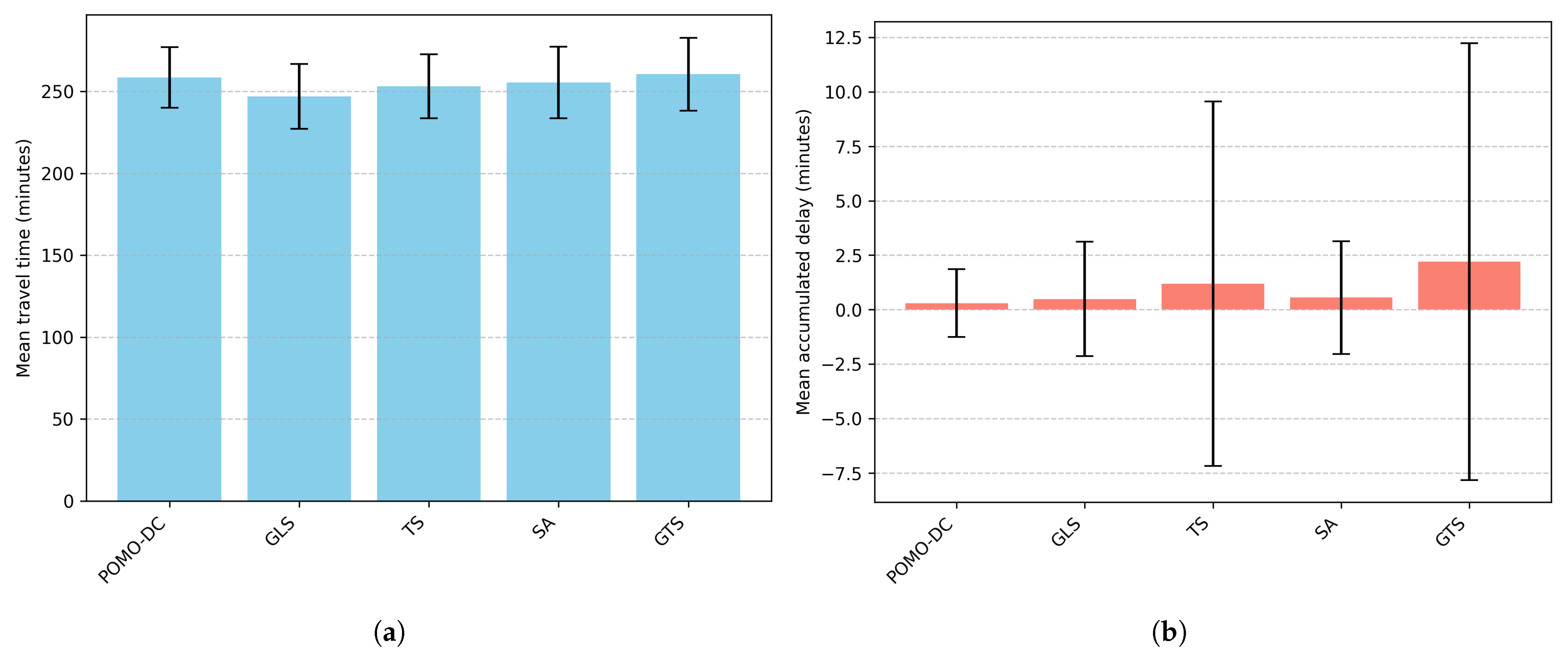
and Figure 4 present the numerical and graphical results for $n=20$. In terms of travel time, GLS obtains the best average performance (246.46 min), followed closely by TS (252.22 min) and SA (255.34 min). The proposed method, POMO-DC, achieves a mean travel time of 258.44 min—slightly above metaheuristics—but with the lowest variability (±18.47 min). These outcomes highlight the model’s ability to generate efficient and reliable solutions for small-scale instances, despite relying on a learning-based approach rather than a deterministic optimization procedure.

When considering delivery delays, POMO-DC outperforms all baselines in instances with 20 customers. It reports the lowest mean delay accumulation (0.30 min) and the lowest variance (±1.55 min), indicating consistent schedule adherence across problem instances. Although GLS achieves a low mean delay as well (0.49 min), its variability is nearly double that of POMO-DC. The other metaheuristics, TS, SA, and GTS, incur larger and more variable delays, with GTS reaching a mean delay accumulation of 2.20 min and a relatively high standard deviation of 10.03 min. This reflects signs of unstable performance under scheduling constraints.

For $n=30$,

Table 4. Performance comparison metrics on instances with $n=30$ customers.

Model	Travel Times (min)		Delays (min)
	Mean	Std. Dev.	Mean	Std. Dev.
POMO-DC	366.28	±26.74	20.35	±65.27
GLS	391.70	±30.95	172.72	±256.77
TS	391.83	±28.35	171.57	±248.30
SA	393.15	±27.93	169.63	±251.98
GTS	394.37	±26.40	188.83	±264.77

and Figure 5 report the performance of POMO-DC and the four benchmarks (GLS, TS, SA, and GTS). The reported mean travel time for our proposal is not only the lowest among all methods but also comes with a relatively tight spread (±26.74 min), reflecting consistent performance across instances. The metaheuristics, while still within a comparable range of travel times (approximately 391–394 min), incur substantially higher penalties from out-of-schedule deliveries. As the problem size increases, the advantage of POMO-DC in terms of delay control becomes more pronounced. It achieves a mean delay of only 20.35 min, compared to well over 170 min for all metaheuristic methods. Furthermore, the standard deviation of delays for POMO-DC (65.27 min) is nearly four times lower than that of its closest metaheuristic counterpart, underscoring the model’s robustness and stability in maintaining schedule feasibility.

Finally,

Table 5. Performance comparison metrics on instances with $n=50$ customers.

Model	Travel Times (min)		Delays (min)
	Mean	Std. Dev.	Mean	Std. Dev.
POMO-DC	537.62	±27.75	1098.97	±508.58
GLS	602.18	±34.98	4370.15	±864.83
TS	602.29	±36.64	4352.43	±933.20
SA	602.80	±34.35	4377.05	±905.23
GTS	602.19	±36.04	4354.73	±939.24

and Figure 6 summarize the performance of the proposal and the mentioned metaheuristic approaches for $n=50$. POMO-DC continues to demonstrate strong generalization capabilities. It achieves the lowest travel time (537.62 min) among all methods, outperforming the metaheuristic baselines by more than 60 units on average. Additionally, its travel time variation (±27.75 min) remains tightly controlled, reinforcing the model’s consistency across complex instances.

The most significant advantage of POMO-DC for this setting ($n=50$), as in the case for $n=30$, lies in the accumulation of delays. While the NNM records an average delay of 1098.97 min, the metaheuristic methods exhibit massive delay values exceeding 4300 min. This indicates that, although the benchmarks can find reasonably short routes, they struggle to maintain feasibility concerning delivery deadlines. Moreover, the variance in delays for the metaheuristics remains high (the standard deviations are above 900 min), revealing unstable performance in time-sensitive scenarios.

5. Discussion

Overall, POMO-DC demonstrates competitive performance within the proposed comparative framework. As shown in Table 3, the model achieves travel time values higher than the best metaheuristic but remains competitive across instances with 20 customers. It is important to note that the proposed method relies on learned policies, which approximate optimal behavior through pattern recognition rather than exhaustive combinatorial search. Therefore, these models can produce a high-quality but slightly suboptimal route simply because they learn statistical patterns using average performance as a reference.

In contrast, for the second optimization objective—delay accumulation—the mean values achieved by POMO-DC are comparable for $n=20$ and significantly superior for $n=30$ and $n=50$. These outcomes confirm that DRL-based models are capable of effectively managing soft time constraints, mitigating infeasibility through the incorporation of penalty terms in the reward function. The proposed framework is also generalizable to other problem formulations, objectives, and constraints. For instance, in a customer inconvenience minimization scheme, such as that of Taş et al. [25], service quality ratings could be accumulated over a route and incorporated into the reward function and the dynamic context to promote higher service levels. Future work could also extend the approach to additional operational constraints, including, but not limited to, energy consumption, route duration limits, and pickup-and-delivery requirements.

The values reported in Table 5 for delay accumulation are impractical in real-world operations. This limitation stems from the computational setup, which assumes that a single vehicle is responsible for serving all requests—a scenario that diverges from typical delivery systems, where a fleet of vehicles is usually deployed. An alternative interpretation is to consider that multiple vehicles are available but constrained to begin their routes sequentially, with each departing only after the previous one has completed its journey. A short-term mitigation strategy would be to assign a vehicle to each route identified in the solution and dispatch them simultaneously; however, this may still yield suboptimal outcomes due to the time constraints embedded in the training process. A more effective and sustainable approach is to integrate multi-vehicle scheduling directly into the model’s training pipeline, ensuring that routing decisions are optimized jointly with vehicle assignment. The inductive biases proposed by Zhang et al. [41] offer valuable insights for pursuing this research direction.

Some conjectures may explain why the simplest additive form of the reward computation, Equation (6), outperforms a normalized weighted sum. In RL—particularly in policy gradient methods such as REINFORCE and its variants—reward design plays a crucial role in training stability. The weighted sum introduces additional hyperparameters (weights, normalization constants) that must be tuned carefully; suboptimal settings could amplify variance or bias in the policy gradient estimates, leading to slower convergence or unstable learning. Moreover, simpler reward structures could produce more stable gradients, especially in stochastic environments such as the proposed formulation. Nevertheless, these statements must be supported by quantitative results based on experimentation. To the best of our knowledge, no research has developed a comprehensive survey on reward functions for VRPs, particularly addressing their design choices, stability implications, and impact on policy generalization. Such a study could provide valuable guidelines for selecting or tuning reward structures in DRL-based VRP solvers.

It is also important to acknowledge the limitations of this work regarding comparability. In particular, comparisons with other DRL approaches are inherently constrained, as existing methods often address different VRP variants with distinct constraints and operational conditions, making direct benchmarking non-trivial. A systematic head-to-head evaluation across DRL models under standardized conditions remains an open and valuable direction for future research, though it would require substantial effort to adapt and train different NNMs on a common test formulation. In the case of the CVRP, for example, such cross-model evaluations have been pursued by Nazari et al. [18] Kool et al. [17] and Kwon et al. [16]. Bono et al. [19] also claim to perform this type of comparison between their proposal and the AM; however, details regarding the adaptation process are not provided in the manuscript, which limits reproducibility and interpretability of their results.

Other immediate extensions of this proposal include evaluating the model on real-world instances. In this context, publicly available benchmarks derived from historical data—such as TSPLib [46] or CVRPLib [47]—provide valuable resources for standardized testing. Alternatively, constructing a custom dataset tailored to a specific operational context would allow direct assessment of the model’s impact on real transportation system performance. Furthermore, the stochastic components used in instance generation can be refined by aligning their distributions with empirical studies focused on dataset design. Fachini et al. [22] offer a dataset based on several previous contributions, combining them effectively.

Summarizing, the results demonstrate that the POMO-DC algorithm can effectively address stochastic variants of the VRP—a significant advancement given the strong inductive biases embedded in its design. In particular, the integration of a richer context within the decoding process provides a simple and adaptable mechanism for incorporating dynamic aspects of the environment. This design enables the model to track cumulative metrics such as travel time and delays, which can be directly leveraged in the reward function.

6. Conclusions

This work addresses the SCVRPSTD. The formulation is solved using an attention-based DL model trained through RL. The proposed model, POMO-DC, is a novel extension of the POMO approach, which integrates a dynamic context mechanism to capture travel times and delivery delays. By enriching the state representation and modifying the transition and reward dynamics, the model effectively handles uncertainty and enforces time constraints in a stochastic environment.

Empirical results show that POMO-DC achieves competitive travel times while significantly outperforming classical metaheuristics in delay management. This demonstrates the potential of DRL models to balance efficiency and schedule adherence in complex routing scenarios. Nevertheless, the high delay values observed in large single-vehicle instances highlight the need for multi-vehicle coordination. The study also suggests that simpler reward formulations can yield more stable learning in stochastic VRP settings, though systematic experimentation is required to validate this hypothesis.

Several directions emerge for future research. First, incorporating multi-vehicle coordination within the training framework would address the limitations of single-vehicle assumptions and improve real-world applicability. Second, exploring additional operational constraints—such as energy use, duration limits, or pickup-and-delivery—could broaden the scope of the proposed model. Third, systematic studies on reward design are needed to assess its role in stability and generalization across VRP variants. Finally, standardized cross-model evaluations and testing on real-world or empirically grounded datasets would enhance comparability, reproducibility, and practical impact.