Synchronization of Singular Perturbation Complex Networks with an Event-Triggered Delayed Impulsive Control
Abstract
1. Introduction
2. Preliminaries
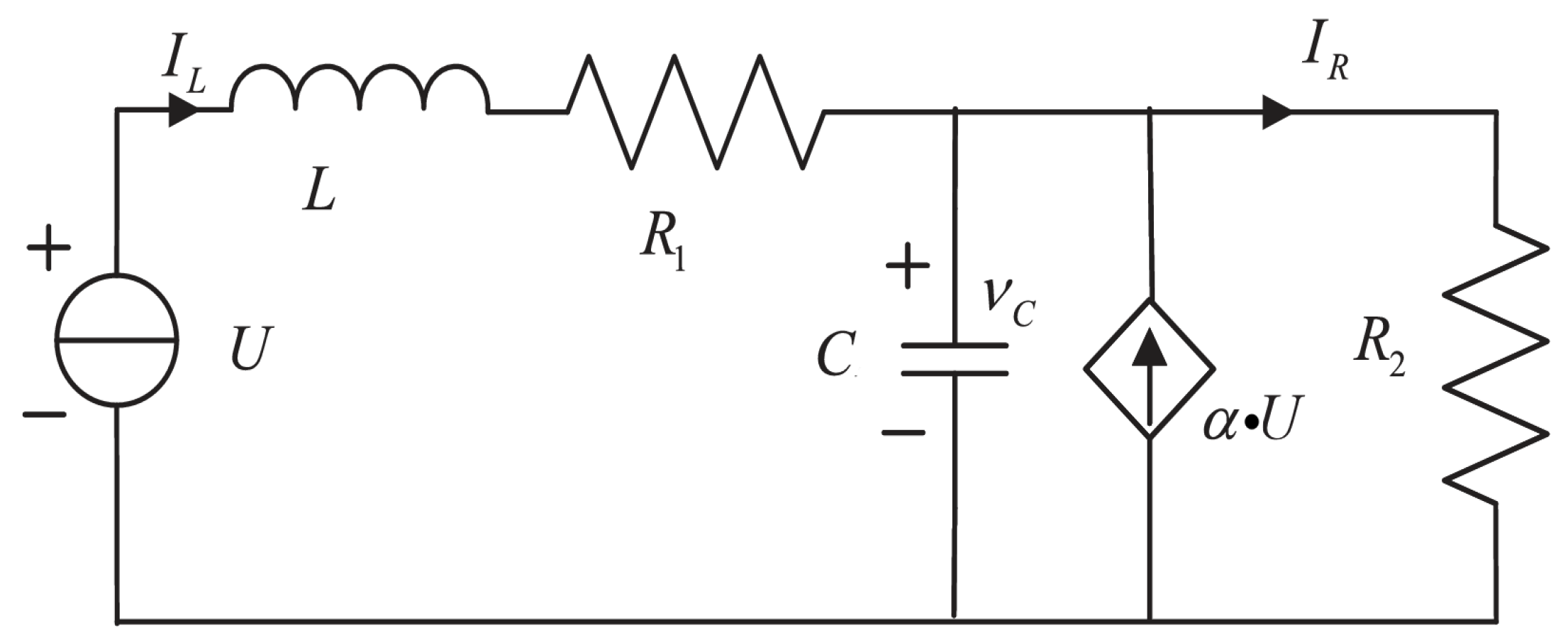
2.1. Problem Formulation
2.2. -Dependent Impulsive Controller
2.3. -Dependent Impulsive Event-Triggered Mechanism
3. Main Results
| Algorithm 1 Event-Triggered Delayed Impulsive Control for Synchronization of SPCN |
|
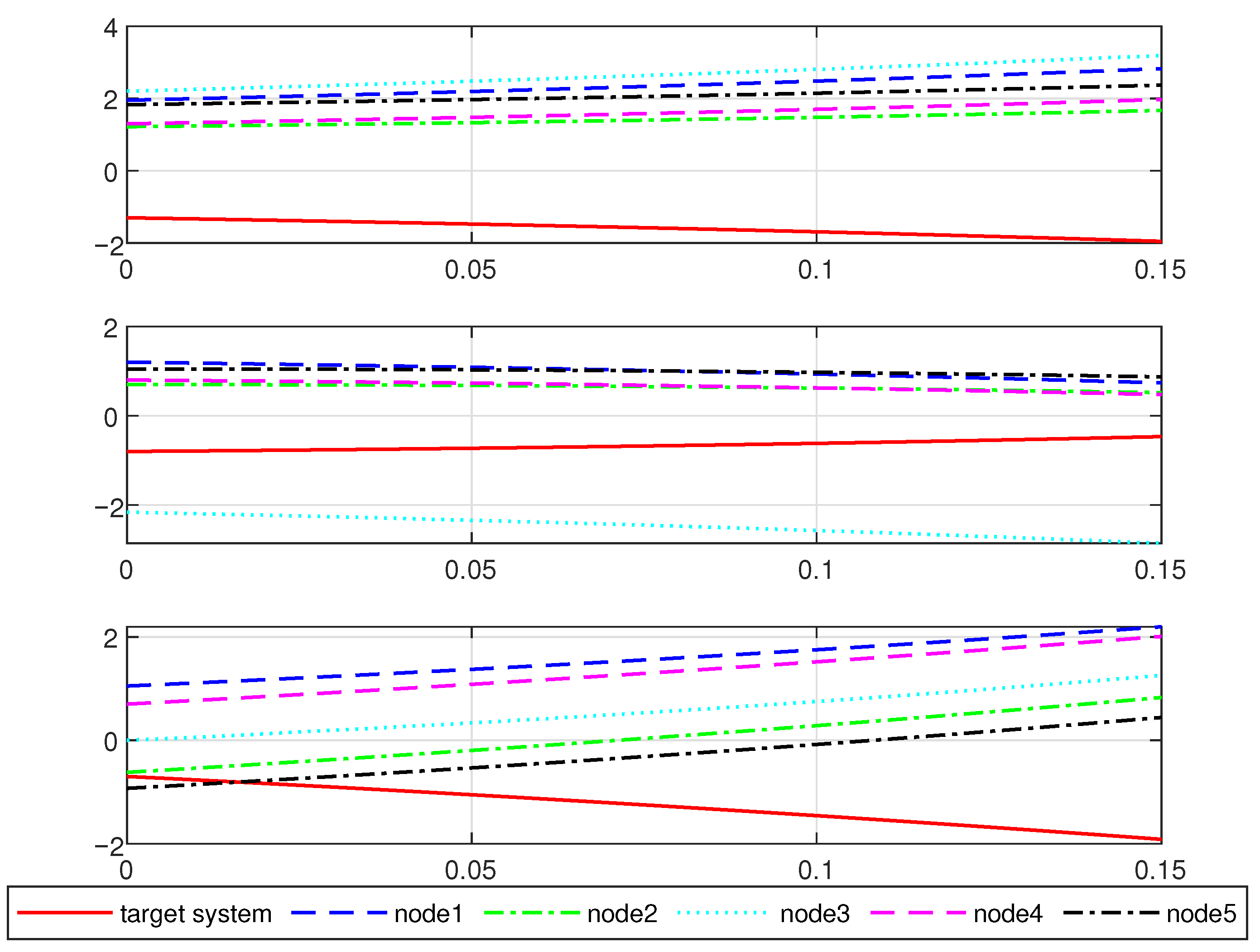
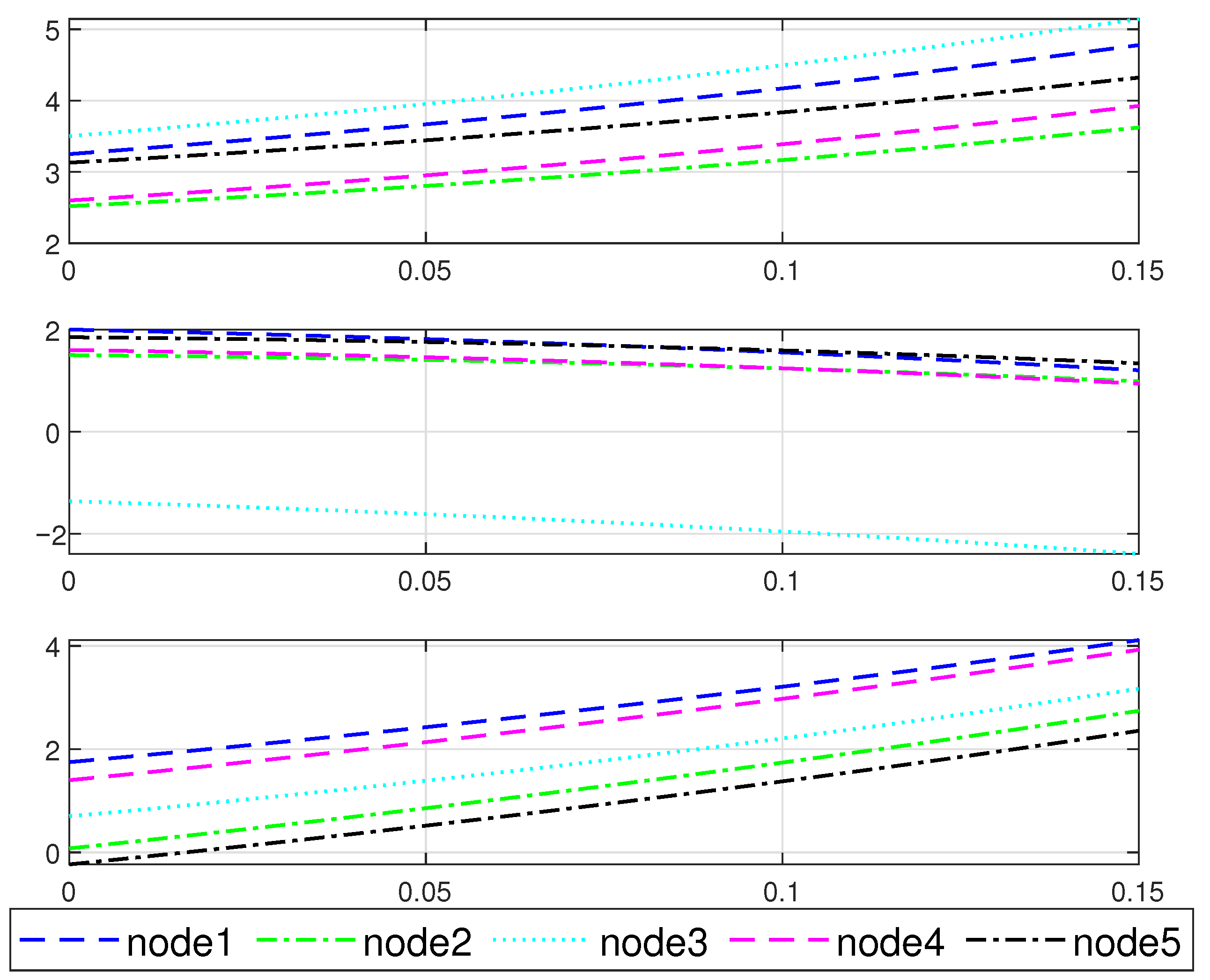
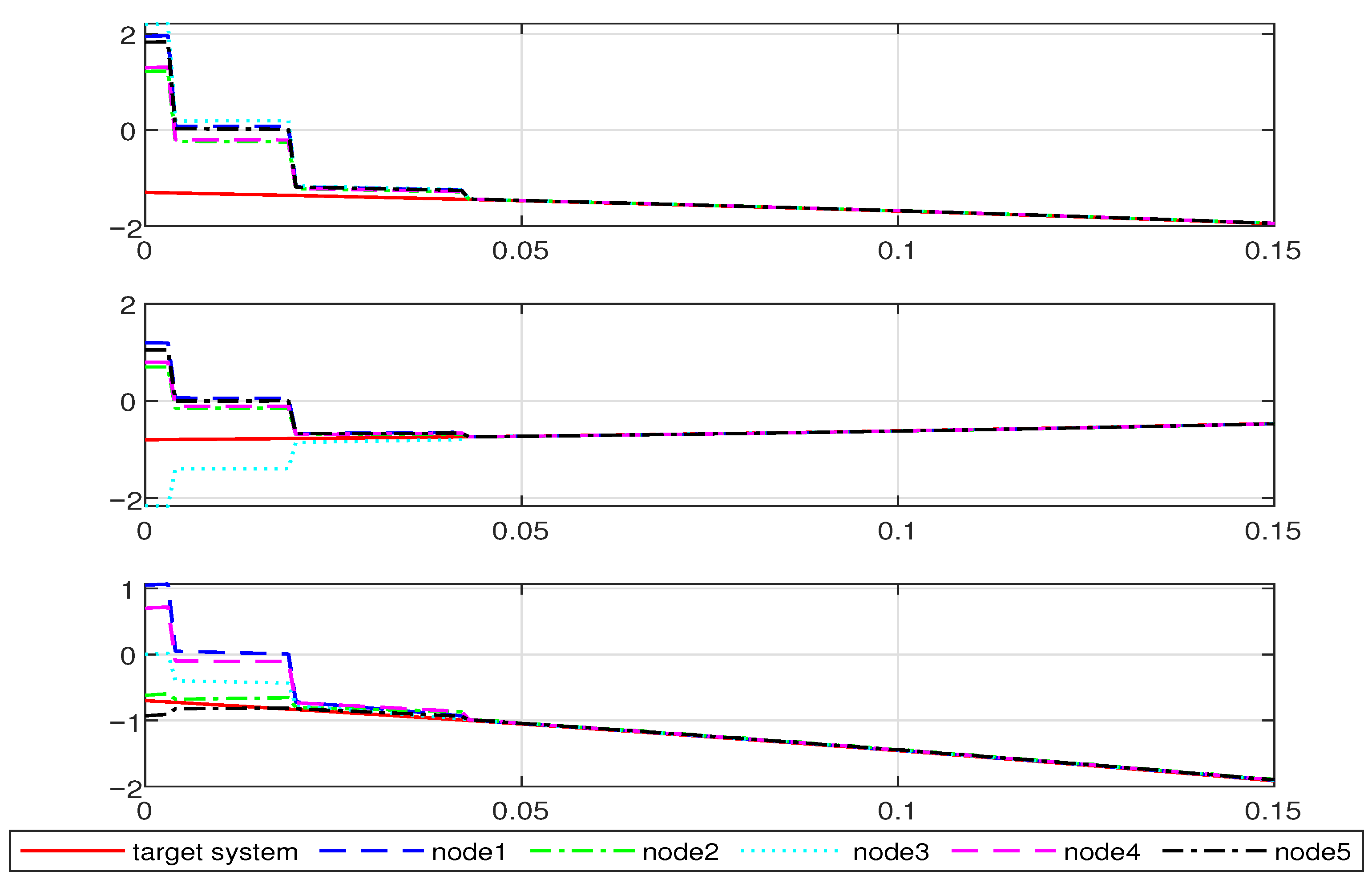
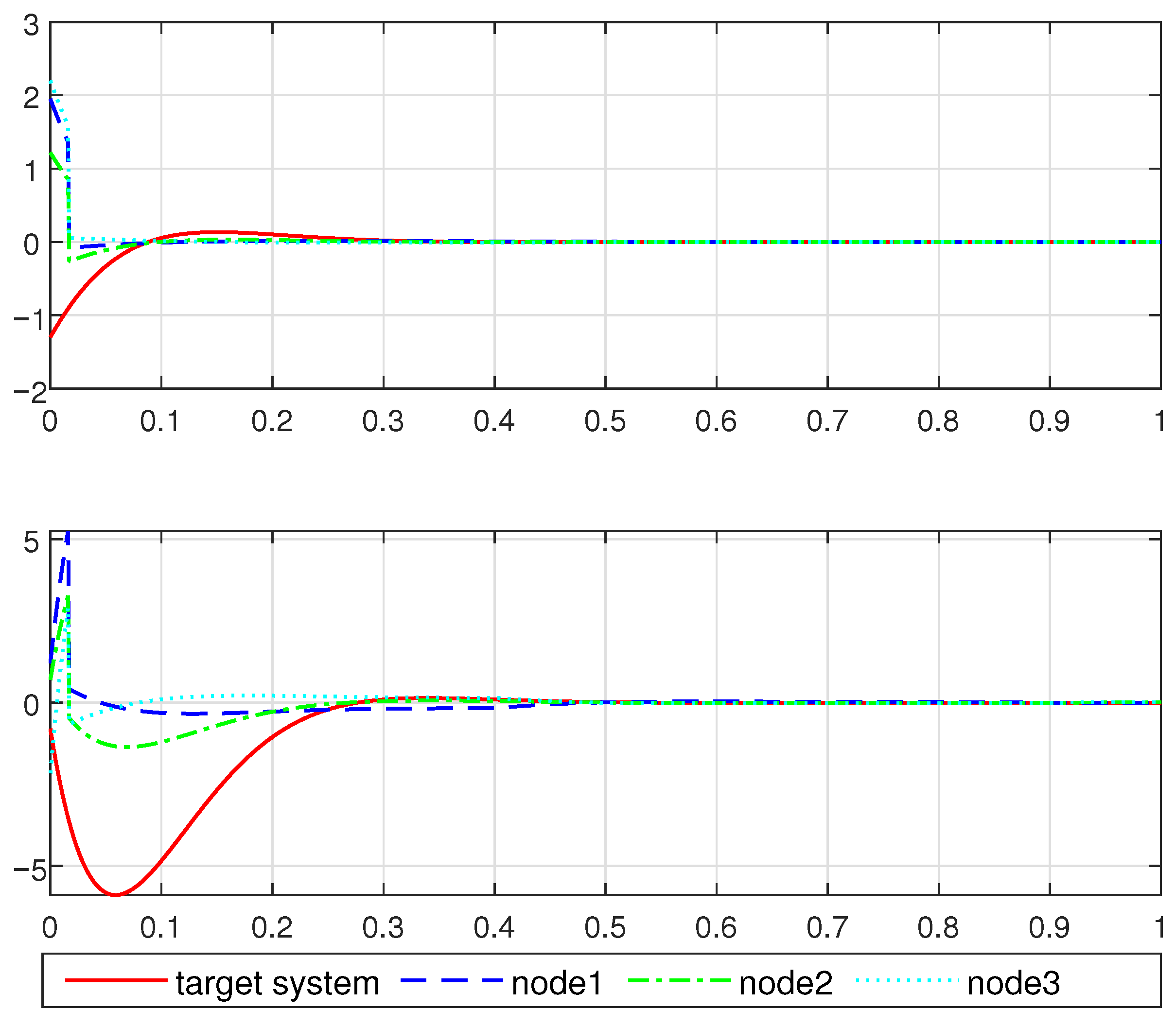
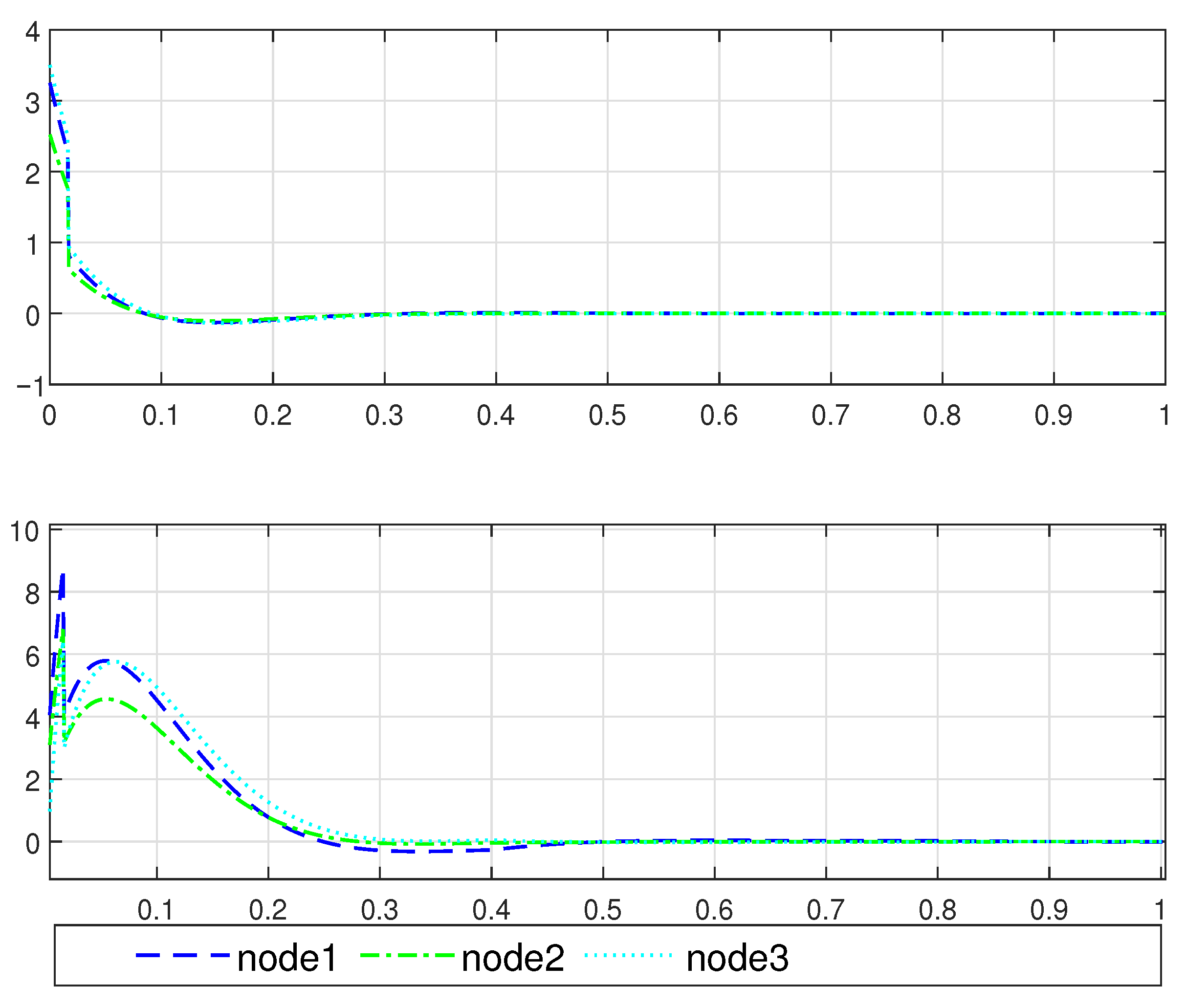
4. Simulation Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kong, Z.; Zhang, Y.; Wang, H.; Yang, L. Robust outage-constrained secrecy rate of hybrid power line and wireless communication with artificial noise-aided beamforming for smart grid. IEEE Trans. Commun. 2025, 73, 3940–3955. [Google Scholar] [CrossRef]
- Jiang, B.; Lou, J.; Lu, J.; Shi, K. Synchronization of chaotic neural networks: Average-delay impulsive control. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6007–6012. [Google Scholar] [CrossRef]
- Fan, J.; Jin, L.; Li, P.; Liu, J.; Wu, Z.; Chen, W. Coevolutionary Neural Dynamics Considering Multiple Strategies for Nonconvex Optimization. Tsinghua Sci. Technol. 2025. [Google Scholar] [CrossRef]
- Jin, L.; Wei, L.; Li, S. Gradient-Based Differential Neural-Solution to Time-Dependent Nonlinear Optimization. IEEE Trans. Autom. Control 2023, 68, 620–627. [Google Scholar] [CrossRef]
- Chen, W.-H.; Chen, Y.; Zheng, W.X. Variable gain impulsive synchronization for discrete-time delayed neural networks and its application in digital secure communication. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 18674–18686. [Google Scholar] [CrossRef] [PubMed]
- Zeng, L.; Chen, X.; Shi, X.; Shen, X. Feature noise boosts DNN generalization under label noise. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 7711–7724. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.; Li, H.; Cao, Z. Synchronization of uncertain coupled neural networks with time-varying delay of unknown bound via distributed delayed impulsive control. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 3624–3635. [Google Scholar] [CrossRef]
- He, W.; Liang, K.; Qian, F.; Chen, G. Designing distributed impulsive controller for networked singularly perturbed systems. IEEE Trans. Autom. Control 2023, 68, 3680–3686. [Google Scholar] [CrossRef]
- Wu, X.; Zheng, W.X.; Tang, Y.; Jin, X. Stability analysis for impulsive stochastic time-varying systems. IEEE Trans. Autom. Control 2023, 68, 2584–2591. [Google Scholar] [CrossRef]
- Cai, C.; Wang, Z.; Hu, J. Synchronization of a linear singularly perturbed complex network with potential application in electric power systems. In Proceedings of the 18th International Conference on Automation and Computing (ICAC), Loughborough, UK, 7–8 September 2012. [Google Scholar]
- Liang, K.; He, W.; Xu, J.; Qian, F. Impulsive effects on synchronization of singularly perturbed complex networks with semi-Markov jump topologies. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3163–3173. [Google Scholar] [CrossRef]
- Li, Y.; Gao, M.; Zha, L.; Liu, J.; Tian, E.; Peng, C. Secure observer-based H∞ synchronization for singularly perturbed multiweighted complex networks with stochastic communication protocol. IEEE Trans. Signal Inf. Process. Netw. 2025, 11, 767–779. [Google Scholar] [CrossRef]
- Li, X.; Li, P. Input-to-state stability of nonlinear systems: Event-triggered impulsive control. IEEE Trans. Autom. Control 2022, 67, 1460–1465. [Google Scholar] [CrossRef]
- Yang, T. Impulsive Control Theory; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2001; Volume 272. [Google Scholar]
- Gilbert, E.; Harasty, G. A class of fixed-time fuel-optimal impulsive control problems and an efficient algorithm for their solution. IEEE Trans. Autom. Control 1971, 16, 1–11. [Google Scholar] [CrossRef]
- He, X.; Li, X.; Song, S. Prescribed-time stabilization of nonlinear systems via impulsive regulation. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 981–985. [Google Scholar] [CrossRef]
- Liu, Q.; He, Y. A robust fully arctangent adaptive interpolated Volterra filtering algorithm against impulsive noise. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2742–2746. [Google Scholar] [CrossRef]
- Ning, D.; Wu, X.; Han, J. Guaranteed cost impulsive synchronization of uncertain multiplex networks. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1757–1761. [Google Scholar] [CrossRef]
- Lv, X.; Cao, J.; Li, X.; Abdel-Aty, M.; Al-Juboori, U.A. Synchronization analysis for complex dynamical networks with coupling delay via event-triggered delayed impulsive control. IEEE Trans. Cybern. 2021, 51, 5269–5278. [Google Scholar] [CrossRef]
- Li, X.; Song, S. Stabilization of delay systems: Delay-dependent impulsive control. IEEE Trans. Autom. Control 2017, 62, 406–411. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.; Huang, T.; He, X. Synchronization of memristor-based coupling recurrent neural networks with time-varying delays and impulses. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 3308–3313. [Google Scholar] [CrossRef]
- He, W.; Han, Q.-L.; Peng, C. Network-based leader-following consensus of nonlinear multi-agent systems via distributed impulsive control. Inf. Sci. 2017, 380, 145–158. [Google Scholar] [CrossRef]
- Dong, H.; Cao, J.; Li, W.; Wang, H. Observers-based event-triggered adaptive fuzzy backstepping synchronization of uncertain fractional order chaotic systems. Chaos Solitons Fractals 2023, 166, 112957. [Google Scholar] [CrossRef]
- He, W.; Xu, B.; Han, Q.-L.; Qian, F. Adaptive consensus control of linear multiagent systems with dynamic event-triggered strategies. IEEE Trans. Cybern. 2020, 50, 2996–3008. [Google Scholar] [CrossRef]
- Xing, M.; Deng, F.; Li, P.; Feng, Z. Event-triggered tracking control for multi-agent systems with measurement noises. Int. J. Syst. Sci. 2021, 52, 1022–1037. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, D.; Han, Q.-L. Event-based leader-following consensus of multi-agent systems with input time delay. IEEE Trans. Autom. Control 2015, 60, 2482–2487. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, D.; Cao, J. Event-based impulsive control of continuous-time dynamic systems and its application to synchronization of memristive neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3651–3661. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Peng, D.; Cao, J. Lyapunov stability for impulsive systems via event-triggered impulsive control. IEEE Trans. Autom. Control 2020, 65, 4928–4935. [Google Scholar] [CrossRef]
- Xu, J.; Liu, Y.; Qiu, J.; Shen, H. Event-triggered impulsive control for nonlinear stochastic delayed systems and complex networks. Commun. Nonlinear Sci. Numer. Simul. 2025, 132, 107912. [Google Scholar] [CrossRef]
- Tu, Y.; Zhang, L.; Lu, J.; Alsaadi, F.E. Event-triggered impulsive control for input-to-state stability of nonlinear time-delay system with delayed impulse. Math. Biosci. Eng. 2025, 22, 876–896. [Google Scholar] [CrossRef]
- Wang, X.; Park, J.H.; Shen, H.; Zhang, G. Multiple mismatched synchronization for coupled memristive neural networks with topology-based probability impulsive mechanism on time scales. IEEE Trans. Cybern. 2023, 53, 1485–1498. [Google Scholar] [CrossRef]
- Li, X.; Zhang, T.; Wu, J. Input-to-state stability of impulsive systems via event-triggered impulsive control. IEEE Trans. Cybern. 2022, 52, 7187–7195. [Google Scholar] [CrossRef]
- Tan, X.; Xiang, C.; Cao, J.; Xu, W.; Wen, G.; Rutkowski, L. Synchronization of neural networks via periodic self-triggered impulsive control and its application in image encryption. IEEE Trans. Cybern. 2022, 52, 8246–8257. [Google Scholar] [CrossRef] [PubMed]
- Doostmohammadian, M.; Meskin, N. Finite-time stability under denial of service. IEEE Syst. J. 2020, 15, 1048–1055. [Google Scholar] [CrossRef]
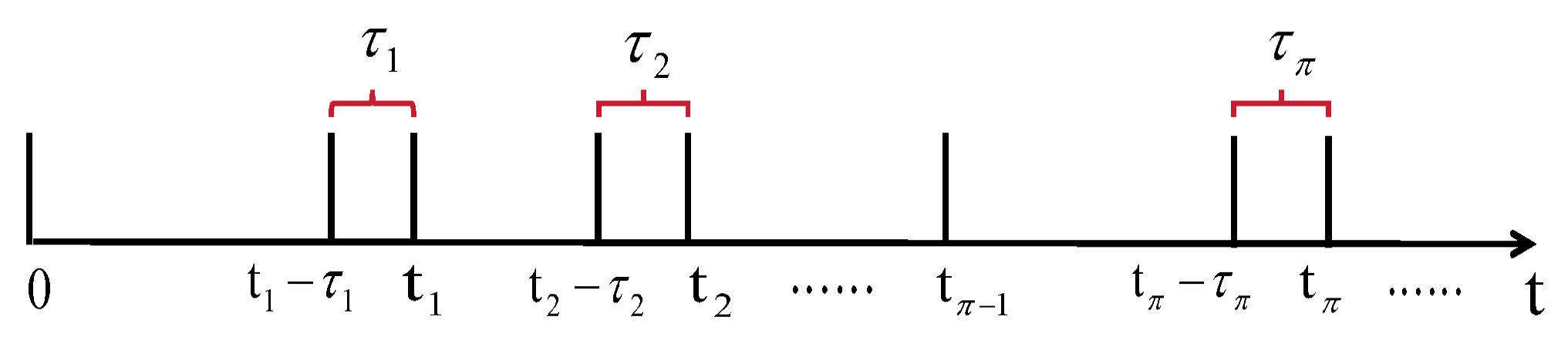
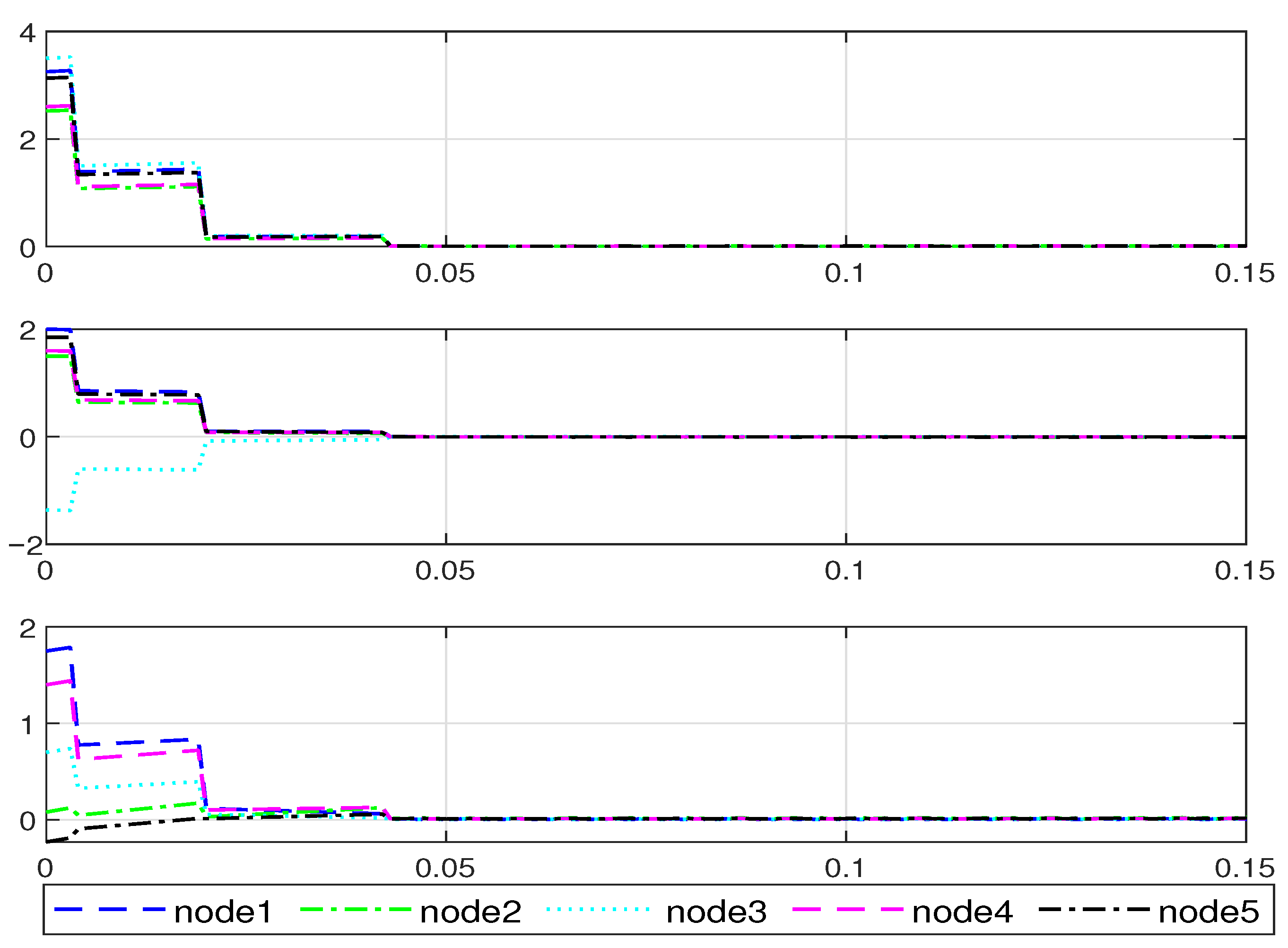
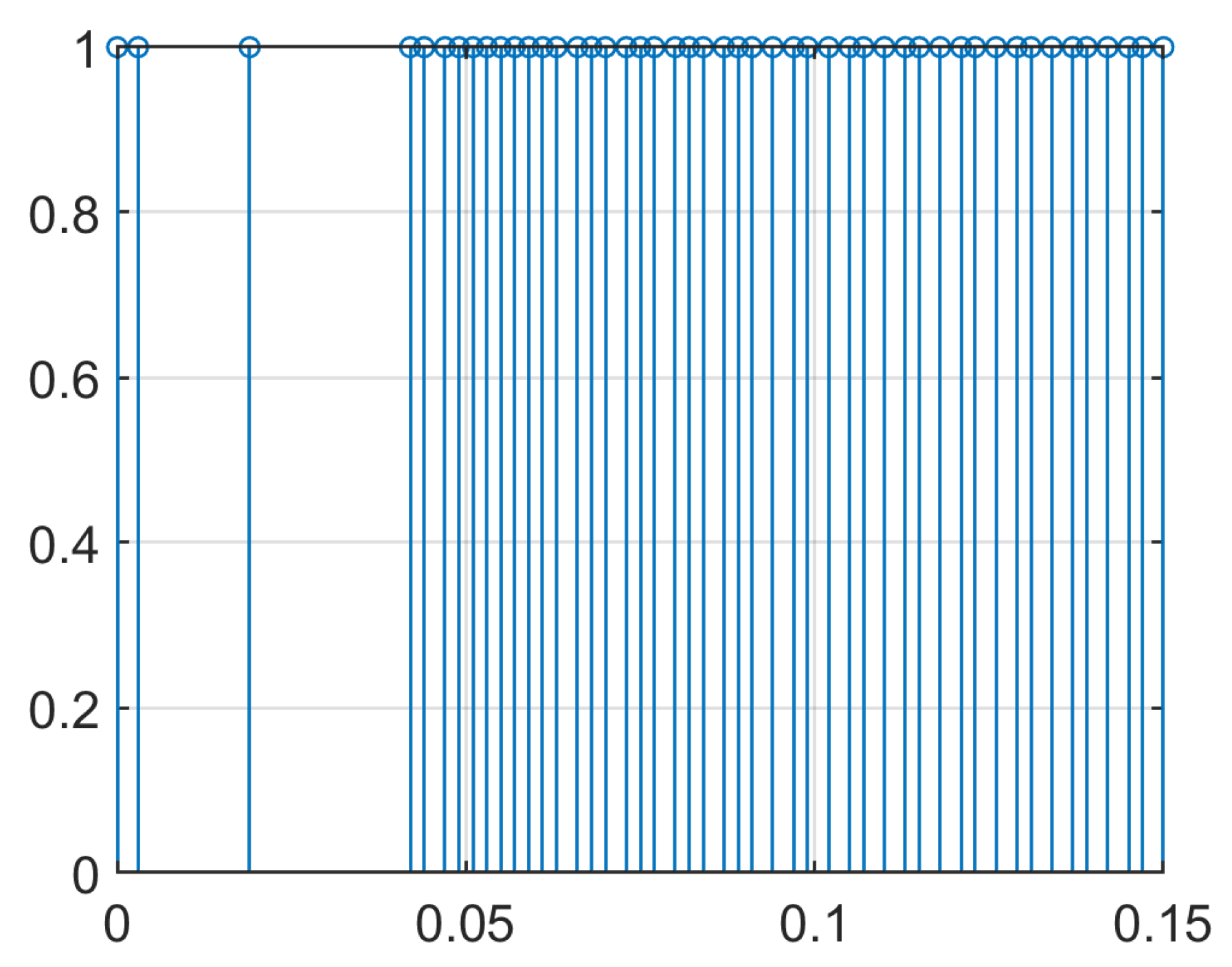
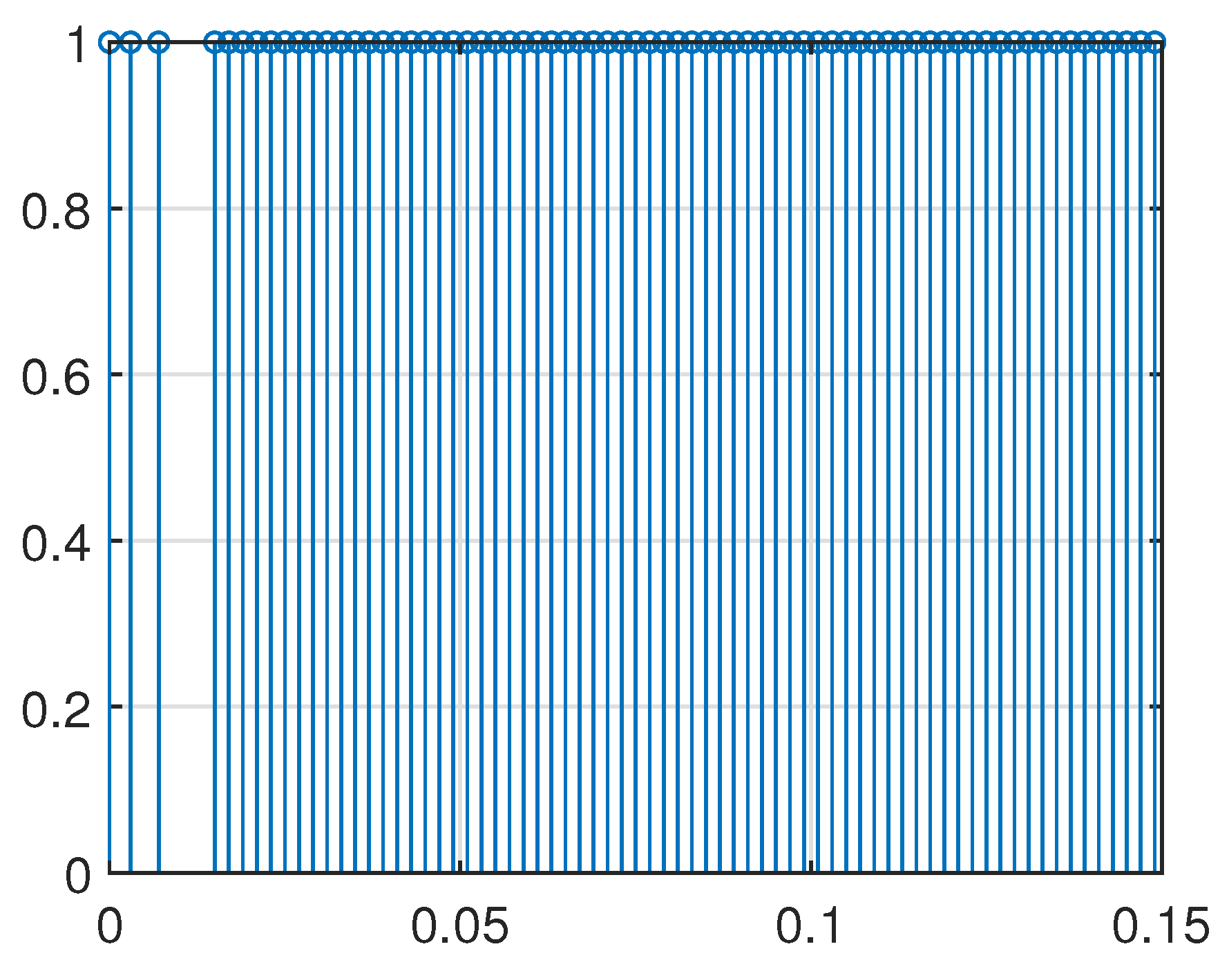
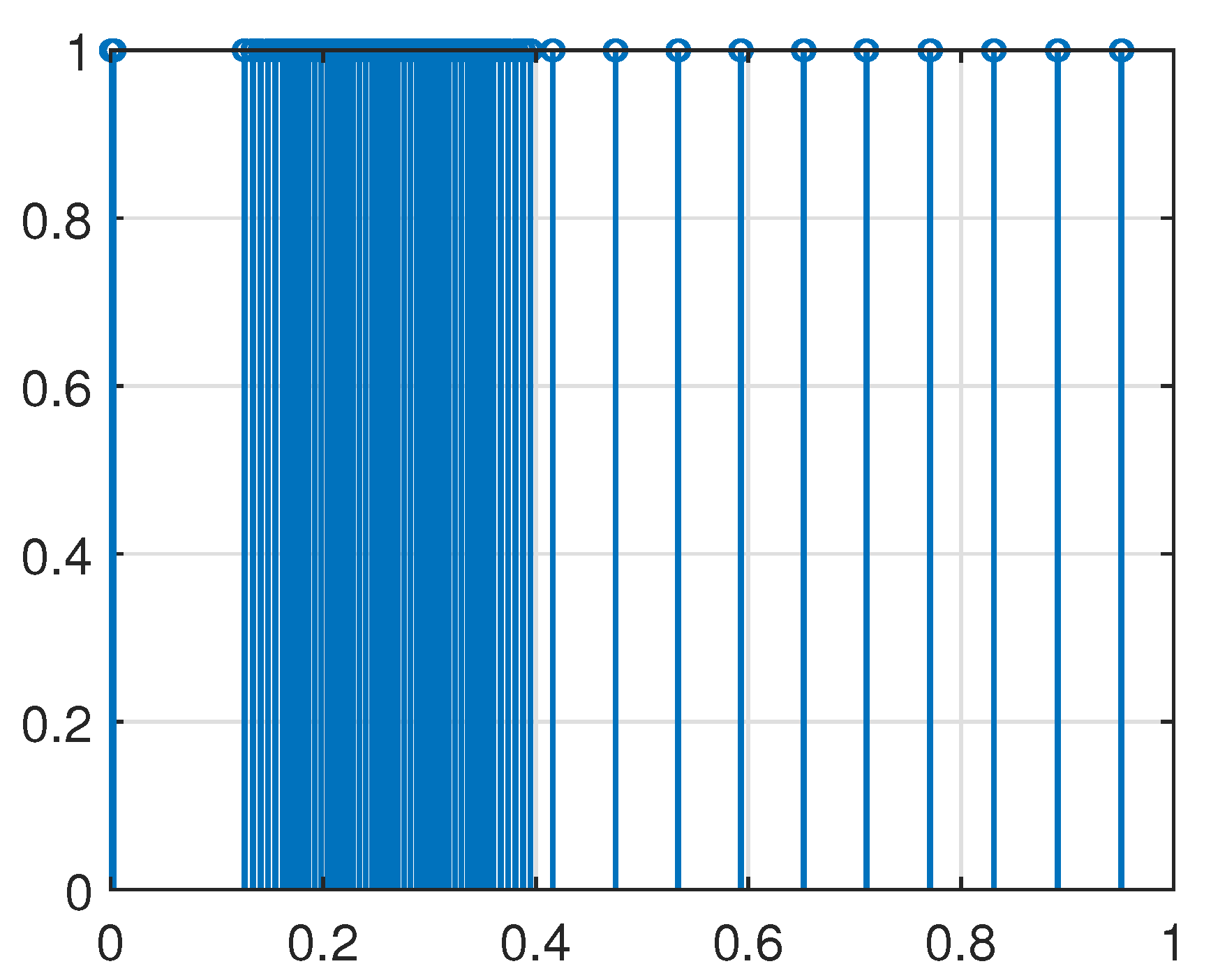
| Proposed ETDIC | Static Event-Triggered Mechanism | |
|---|---|---|
| Data transmission rate | 32% | 47.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, K.; Zheng, K.; Chen, M.; Wang, X. Synchronization of Singular Perturbation Complex Networks with an Event-Triggered Delayed Impulsive Control. Mathematics 2025, 13, 3033. https://doi.org/10.3390/math13183033
Liang K, Zheng K, Chen M, Wang X. Synchronization of Singular Perturbation Complex Networks with an Event-Triggered Delayed Impulsive Control. Mathematics. 2025; 13(18):3033. https://doi.org/10.3390/math13183033
Chicago/Turabian StyleLiang, Kun, Kaiwen Zheng, Mengshen Chen, and Xin Wang. 2025. "Synchronization of Singular Perturbation Complex Networks with an Event-Triggered Delayed Impulsive Control" Mathematics 13, no. 18: 3033. https://doi.org/10.3390/math13183033
APA StyleLiang, K., Zheng, K., Chen, M., & Wang, X. (2025). Synchronization of Singular Perturbation Complex Networks with an Event-Triggered Delayed Impulsive Control. Mathematics, 13(18), 3033. https://doi.org/10.3390/math13183033





