Balanced Hoeffding Tree Forest (BHTF): A Novel Multi-Label Classification with Oversampling and Undersampling Techniques for Failure Mode Diagnosis in Predictive Maintenance
Abstract
1. Introduction
- (i).
- Three learning paradigms integration: The proposed Balanced Hoeffding Tree Forest (BHTF) uniquely combines Multi-Label Learning (MLL), Incremental Learning (IL), and Ensemble Learning (EL), within a single framework. This integration allows BHTF to simultaneously handle multiple co-occurring failure modes, continuously update with streaming data, and leverage ensemble strategies for robust predictive performance.
- (ii).
- Introduction of BHTF for predictive maintenance: BHTF is a novel artificial intelligence-based method that applies both oversampling and undersampling techniques for multi-label classification in manufacturing environments, addressing challenges of data imbalance and real-world complexity for the first time.
- (iii).
- Multi-label failure mode diagnosis: BHTF predicts multiple failure types simultaneously using the binary relevance strategy, enabling detection of co-occurrence patterns and providing more detailed diagnostic insights for targeted maintenance actions.
- (iv).
- Hybrid class balancing: The method incorporates a hybrid data preprocessing strategy by proposing a novel undersampling technique, named Proximity-Driven Undersampling (PDU), and combining it with the Synthetic Minority Oversampling Technique (SMOTE), effectively mitigating class imbalance in highly skewed datasets.
- (v).
- Outperformance of existing methods: BHTF achieved an average accuracy of 97.44% to simultaneously predict failure modes with 11% improvement over state-of-the-art approaches. This result underscores its high potential for deployment in industrial predictive maintenance systems, particularly within manufacturing sectors.
2. Related Works
3. Materials and Methods
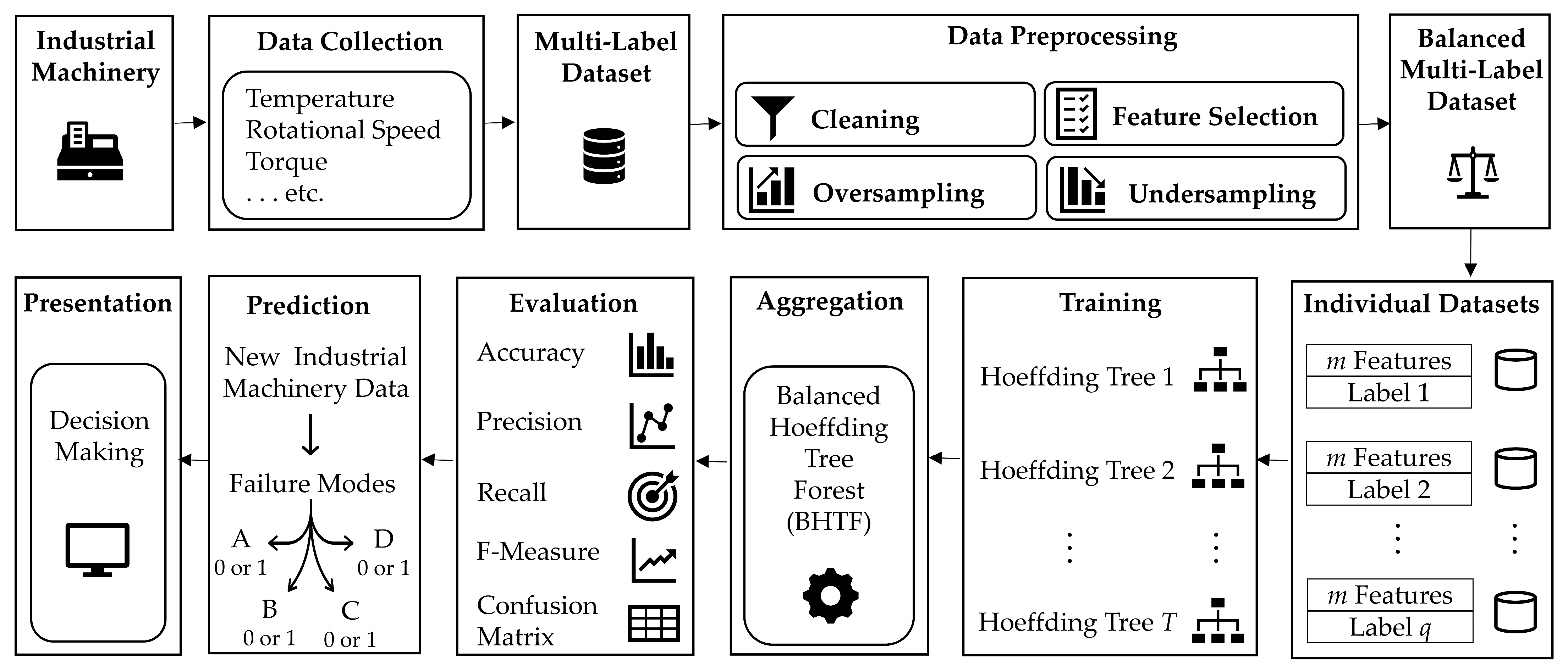
3.1. Proposed Method
- Data collection: The predictive maintenance dataset usually contains sensor-based data collected from industrial machinery operating under various conditions. The dataset can include input features such as temperature, rotational speed, and torque related to machinery to reflect real-time machine behavior. These data are typically gathered in manufacturing environments, where operational precision is critical.
- Multi-label dataset construction: The dataset includes several target variables, each representing a different failure type that may occur concurrently. This setup naturally forms a multi-label learning problem, where each machine instance can be associated with multiple failure types. To address this, the classification task is modeled using the binary relevance (BR) [43] strategy, which decomposes the multi-label problem into independent binary classification tasks—one for each failure. For each label, the value is 1 if the corresponding failure occurs, and 0 otherwise.
- Data preprocessing: To improve data quality and prepare it for modeling, the following preprocessing steps can be performed:
- –
- Cleaning: It involves detecting and removing errors, duplicates, and inconsistencies in the data to ensure that the model is trained on high-quality and reliable input. In addition, it also includes the removal of unique identifiers since they do not contribute predictive value. Some data cleaning techniques can also be applied to handle any missing values in the features.
- –
- Feature selection: The redundant or irrelevant features were removed to reduce overfitting, improve accuracy, and decrease computational cost.
- –
- Oversampling and undersampling (hybrid resampling): Due to the inherent data imbalance in the PdM dataset—where failure cases are considerably underrepresented compared to the healthy class—a hybrid resampling strategy was employed after identifying the minority and majority classes dynamically based on their frequencies.
- ○
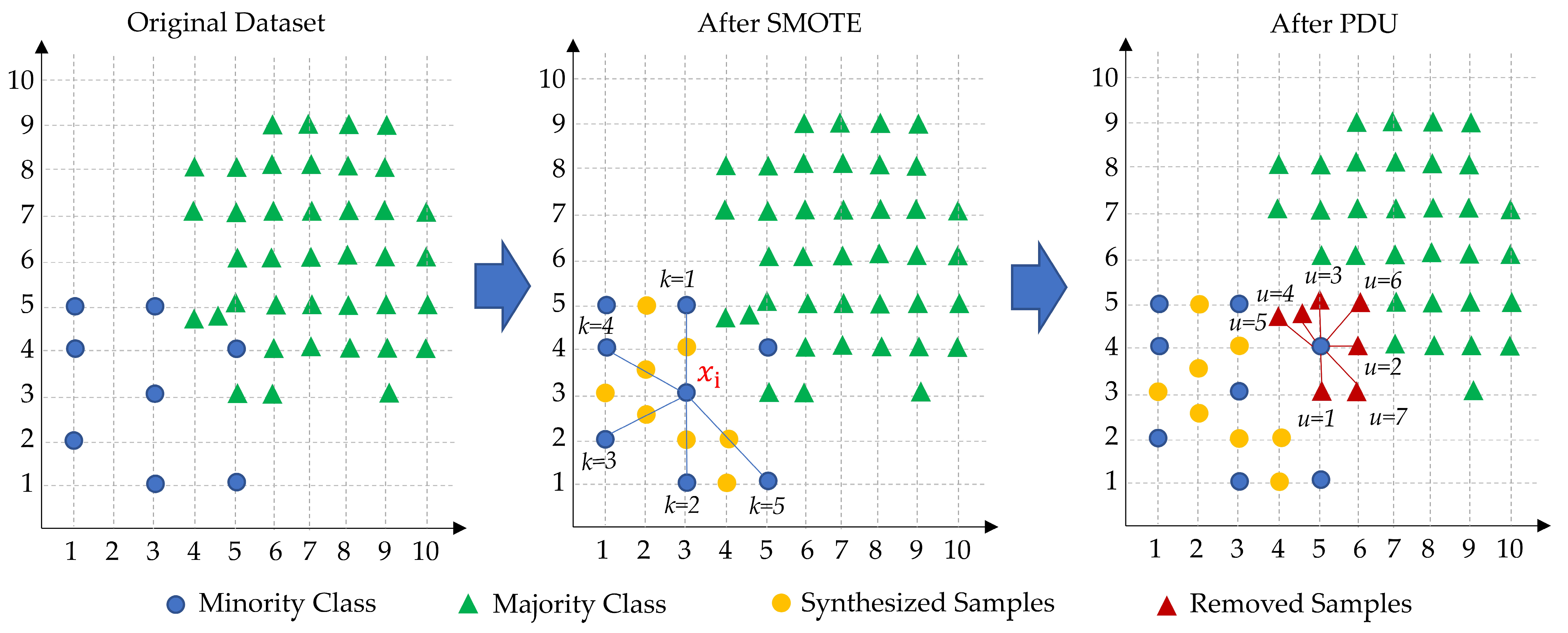
- First, the synthetic minority over-sampling technique (SMOTE) [44] was applied to generate synthetic samples for minority failure classes. It is a widely used method for mitigating class imbalance by generating synthetic samples for minority classes rather than merely duplicating existing ones. Unlike basic oversampling methods such as random oversampling, which risk overfitting by repeating identical instances, SMOTE generates diverse new samples through interpolation between similar minority class instances in the feature space.
- ○
- Then, our proposed PDU method was used to reduce the number of healthy (non-failure) instances, resulting in a more balanced and learnable dataset. These steps are essential to prevent model bias toward the majority class and enhance the model’s ability to identify rare failure types, thereby contributing to more effective fault detection.
- Label-wise dataset separation: Following data balancing, the multi-label dataset was decomposed into multiple binary datasets, one for each of the four selected failure types. Each dataset contains the same feature set but is independently labeled according to whether the corresponding failure occurred. This decomposition aligns with the binary relevance framework and enables independent model training for each failure mode.
- Model training—Hoeffding Tree forest construction: Each balanced dataset was used to train several Hoeffding Trees, which are well-suited for efficiently processing large-scale scenarios. Hoeffding Trees inherently support incremental learning, allowing the model to adapt continuously to streaming or sequential data without retraining from scratch. The result in a collection of Hoeffding Tree models, each focused on detecting a specific failure mode. This process leverages the speed, adaptability, and online learning capabilities of lightweight artificial intelligence algorithms in dynamic industrial environments.
- Model aggregation—BHTF: The individually trained Hoeffding Trees for each failure mode were combined to form BHTF. This ensemble learning structure utilizes the efficiency and scalability of Hoeffding Trees while enabling multi-label predictions across multiple failure types simultaneously. Although each tree is trained independently, the ensemble facilitates an integrated diagnosis of probable co-occurring failures within a single inference step.
- Prediction and evaluation: The BHTF model is applied to new, unseen data to predict possible failure types. The performance of the model is evaluated using standard classification metrics, including accuracy, precision, recall, F-measure and confusion matrix, measured for each label as well as overall. This mathematical evaluation framework ensures a comprehensive understanding of the model’s ability to correctly diagnose failure modes in manufacturing systems.
- Presentation: It involves effective visualization of model outputs and integration with business rules. It includes decision making, where predictions inform or directly drive actions—ranging from automated responses to human-guided choices.
3.2. Multi-Label Learning
3.3. Hybrid Resampling Strategy
3.3.1. Oversampling with SMOTE
3.3.2. Undersampling with PDU
- Consider the dataset for a given target class label as an input.
- Compute the Euclidean distance according to Equation (2) between (i.e., label = 1) and all other instances.
- Identify its nearest neighbor, denoted by .
- If belongs to the majority class (i.e., label = 0), remove it from the training set.
- Repeat the steps 3 and 4 until a user-specified number of iterations, denoted by
- Return to the step 2 to repeat the same process for all minority instances in the dataset.
3.4. Hoeffding Tree Classifier
3.5. Hoeffding Tree Forest
3.6. Algorithm
| Algorithm 1: Balanced Hoeffding Tree Forest (BHTF) |
| Inputs: : multi-label dataset : label set : number of Hoeffding Trees per label : oversampling rate : number of nearest neighbors : undersampling threshold : new instance to be predicted Outputs: : the ensemble of models, i.e., models for the jth label : predicted label set for input instance |
| // Step 1—Binary Relevance Decomposition // Multi-label learning: Decompose the problem intobinary tasks to capture co-occurring failures. for // Initialize binary dataset for label for each in if .Add // Assign positive label for presence of else .Add // Assign negative label for absence of end if end for each end for |
| // Step 2—Hybrid Resampling // Hybrid imbalance handling: Integrate SMOTE-based oversampling with proximity-driven undersampling (PDU). for // Step 2.1—Oversampling // Identify minority class for each where class == // Find k-nearest neighbors for // Generate synthetic samples for each // Synthetic instance, .Add // Add synthetic minority sample to dataset end for each end for end for each // Step 2.2—Undersampling // Identify minority class // Identify majority class // Initialize removal set for each where class for // Find nearest neighbor if classthen // Flag majority neighbor for removal else break; end if end for end for each .Remove // Remove flagged majority instances end for |
| // Step 3—Model Training // Ensemble learning: Construct multiple Hoeffding Trees per label to improve robustness. // Initialize ensemble of models for // Initialize ensemble for label for = Bootstrapping() // Train Hoeffding Tree on resampled data // Add trained tree to ensemble end for end for |
| // Step 4—Model Testing // Prediction across multiple labels through majority voting within each ensemble. // Initialize predicted label set for // Collect predictions from ensemble mode() // Compute majority vote for label // Add to predicted label set if voted as present end for End Algorithm |
4. Experimental Setup
4.1. Dataset Description
4.2. Evaluation Metrics
4.2.1. Standard Per-Label Metrics
- TP refers to the number of correctly predicted positive instances,
- TN to the correctly predicted negatives,
- FP to the negative instances incorrectly classified as positive, and
- FN to the positive instances that were missed by the classifier.
4.2.2. Weighted Metrics
4.2.3. Multi-Label Metrics
4.3. Hyperparameters
- SMOTE oversampling: To address class imbalance within each binary decomposition, SMOTE was applied. The number of nearest neighbors for generating synthetic samples was set to k = 5, and an aggressive oversampling ratio of R = 4000% was chosen. This configuration confirmed that sufficient synthetic instances were generated for underrepresented failure classes to prevent classifier bias.
- PDU undersampling: For balancing the overrepresented majority class, a proximity-based dynamic undersampling strategy was adopted. This method removes the majority instances located close to each minority instance in the feature space. Mainly, for each minority instance, up to u = 7 nearest majority neighbors were identified using a LinearNNSearch with k = 1, a brute-force search algorithm that computes Euclidean distances linearly to find the closest neighbor. This step helped refine class boundaries and reduce overlap between majority and minority classes.
- Ensemble configuration: The multi-label learning approach in BHTF utilized an ensemble of Hoeffding Trees for each label. Specifically, for each binary classification task related to a distinct failure mode, an ensemble of T = 10 trees was trained using a bagging meta-classifier. This strategy was implemented to improve prediction robustness, and configured with the following main parameters:
- –
- numIterations = 10 (number of Hoeffding Trees in each ensemble);
- –
- bagSizePercent = 100 (100% of the training data in each bootstrap sample);
- –
- batchSize = 100 (the batch size for model updates);
- –
- seed = 1 (reproducibility of randomized processes);
- –
- numExecutionSlots = 1 (sequential performance of model training);
- –
- representCopiesUsingWeights = false (explicitly sampling of each instance without relying on weighting schemes).
- Hoeffding Tree settings: Each base classifier in the ensemble was configured using the Hoeffding Tree implementation. The following parameters were set to control tree growth and splitting behavior:
- –
- gracePeriod = 200 (minimum number of instances seen between split attempts);
- –
- hoeffdingTieThreshold = 0.05 (threshold to break ties for close information gains);
- –
- leafPredictionStrategy = Naive Bayes adaptive (Naive Bayes prediction in leaf nodes when beneficial);
- –
- minimumFractionOfWeightInfoGain = 0.01 (minimum fraction of total weight required to consider a split);
- –
- naiveBayesPredictionThreshold = 0.0 (threshold below which Naive Bayes predictions are used);
- –
- splitConfidence = 1.0 × 10−7 (confidence level used for splitting decisions);
- –
- splitCriterion = Info gain split (uses information gain as the splitting metric).
- Feature selection: We employed the Pearson correlation technique [47] as a filter-based supervised attribute selection approach. It was combined with the Ranker search method to measure the predictive relevance of each feature. Multiple configurations were empirically tested, including heuristic strategies based on logarithmic and square root formulas for determining the number of features to retain (e.g., , , where is the number of original features). Among these, selecting all six features provided the most favorable balance between model accuracy and complexity. This optimal configuration (numToSelect = 6) was identified through extensive experimentation and justified further in the results section.
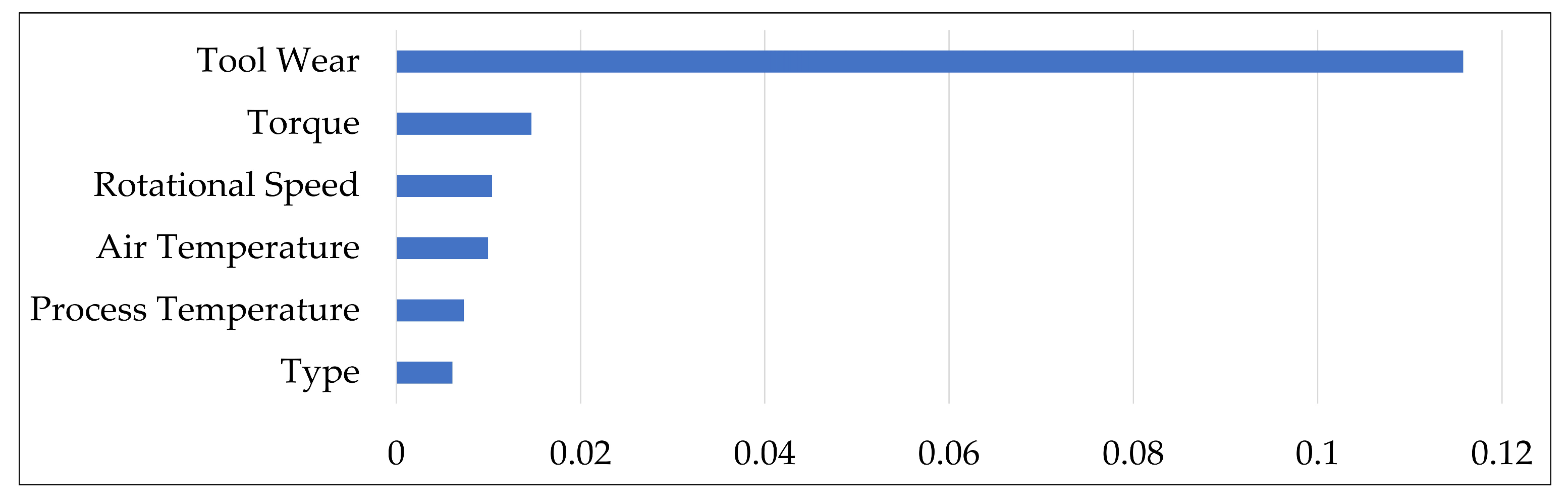
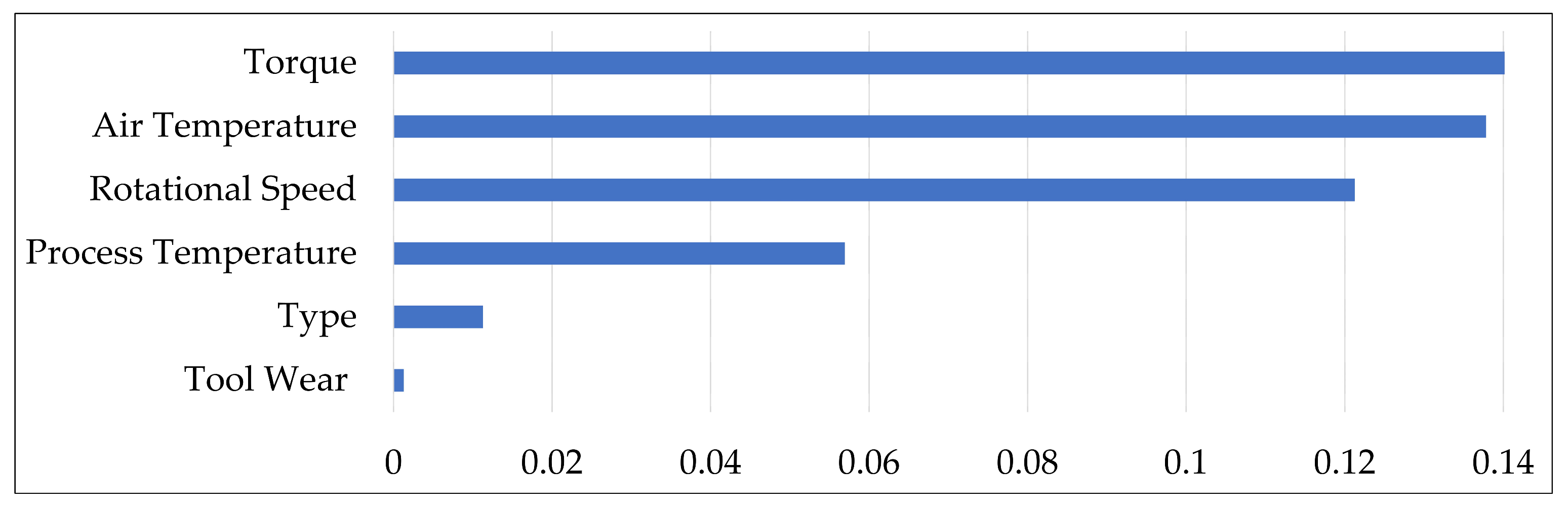
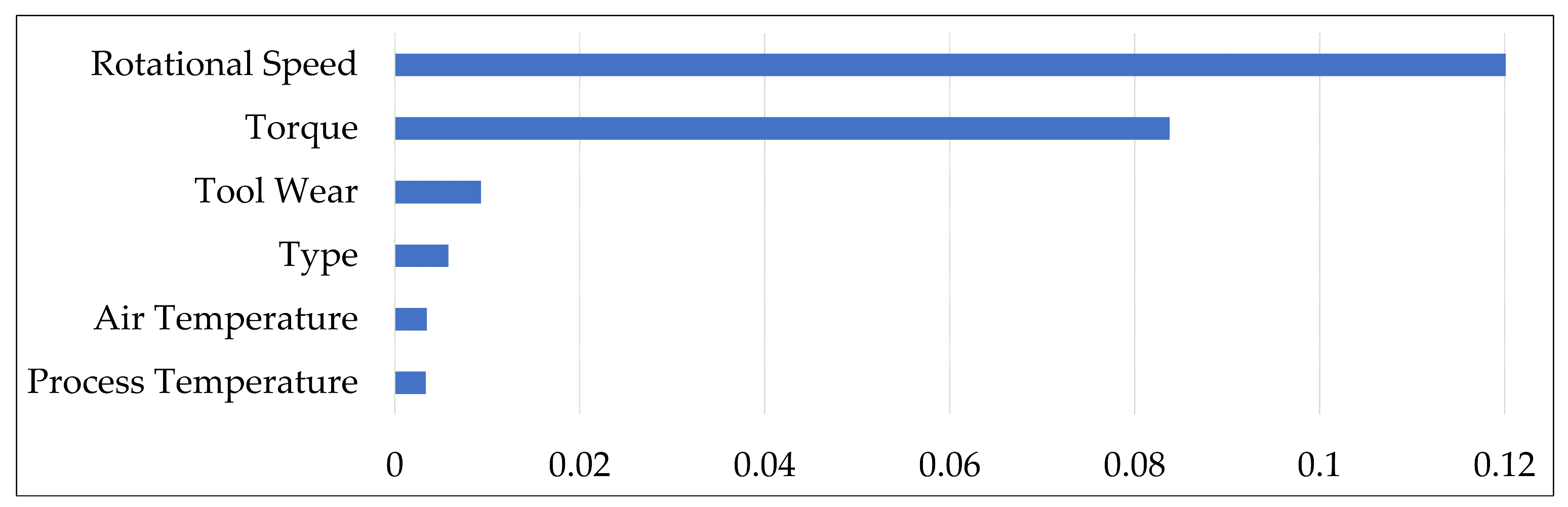
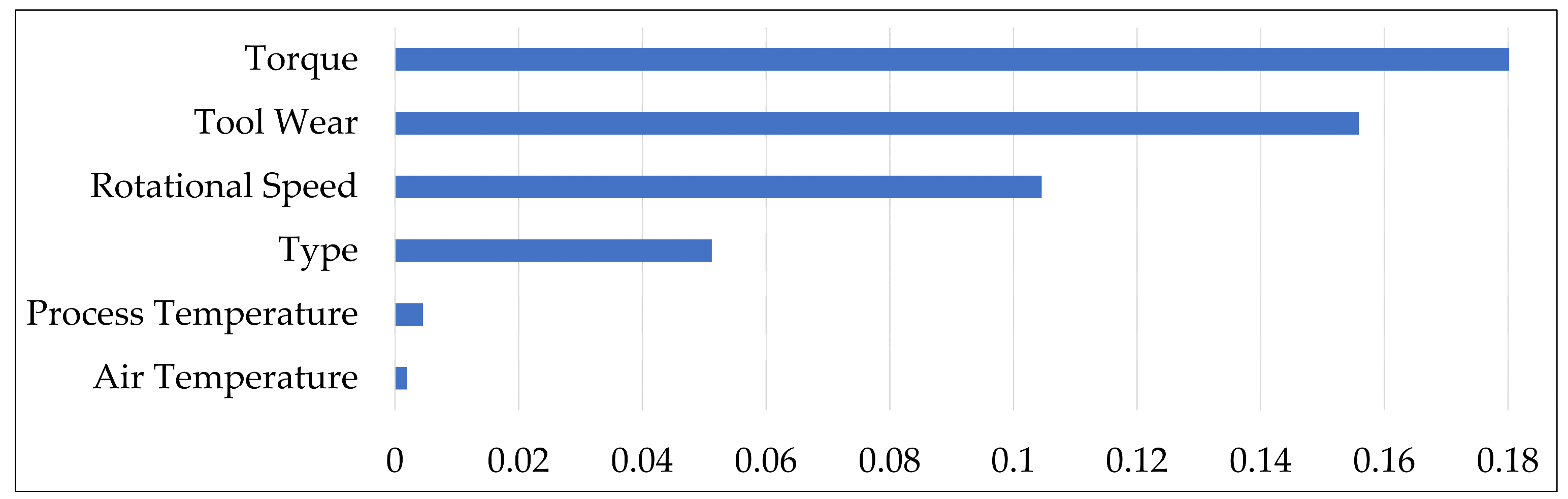
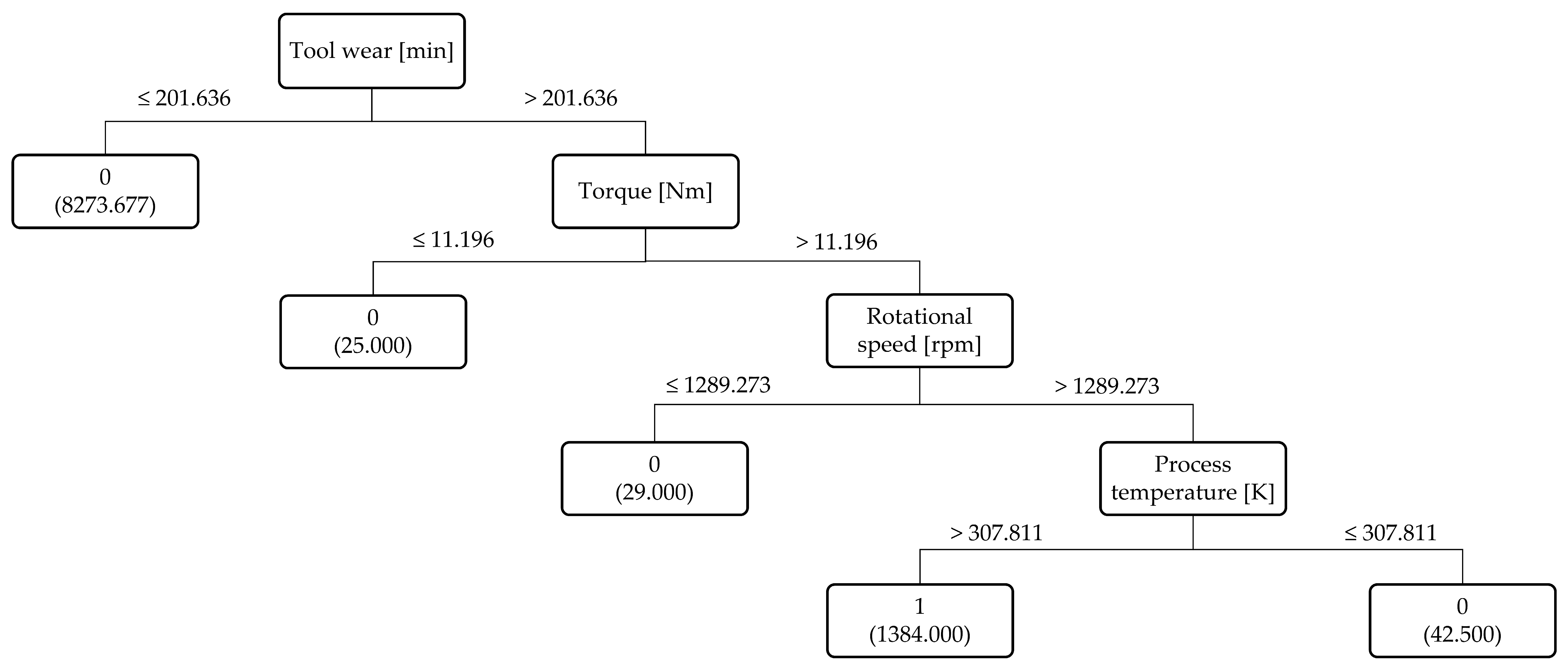
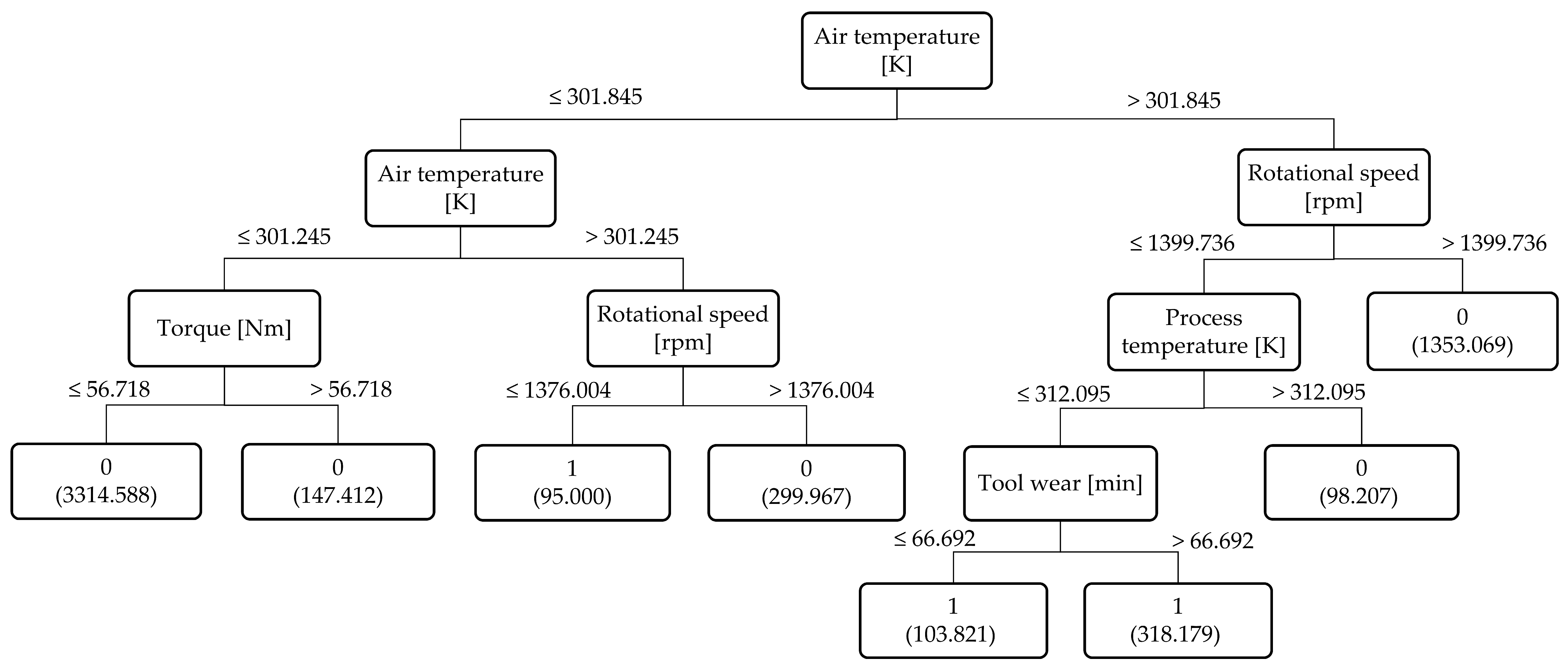
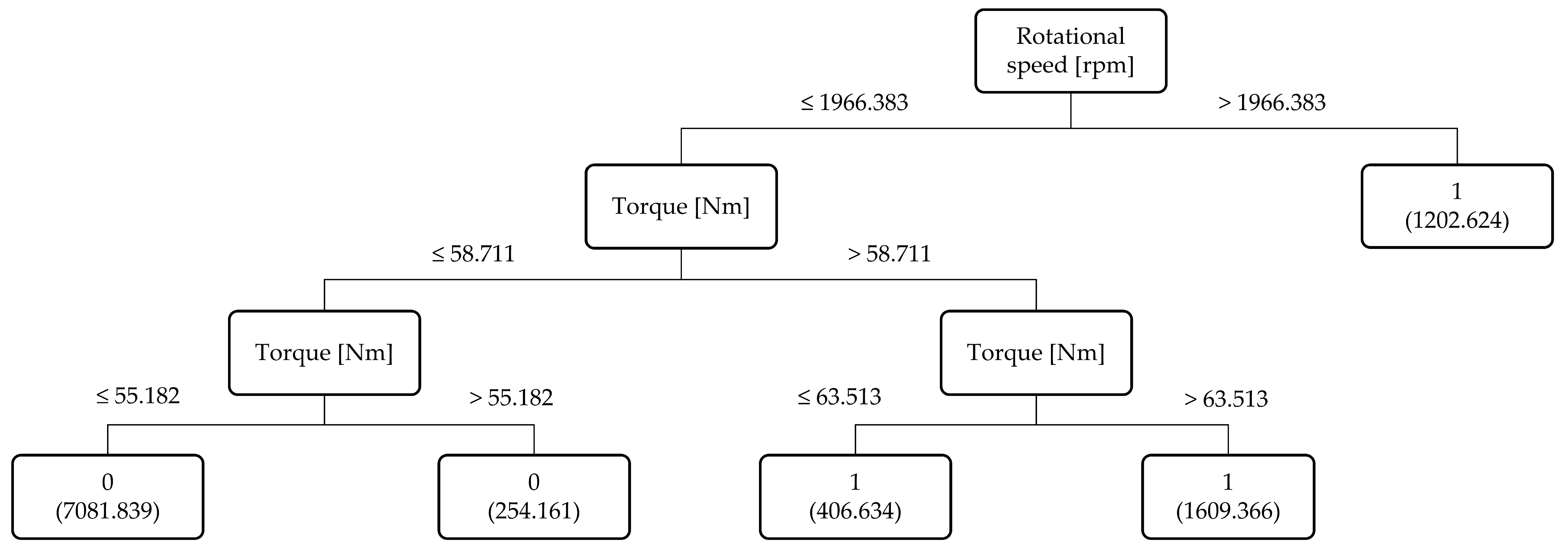
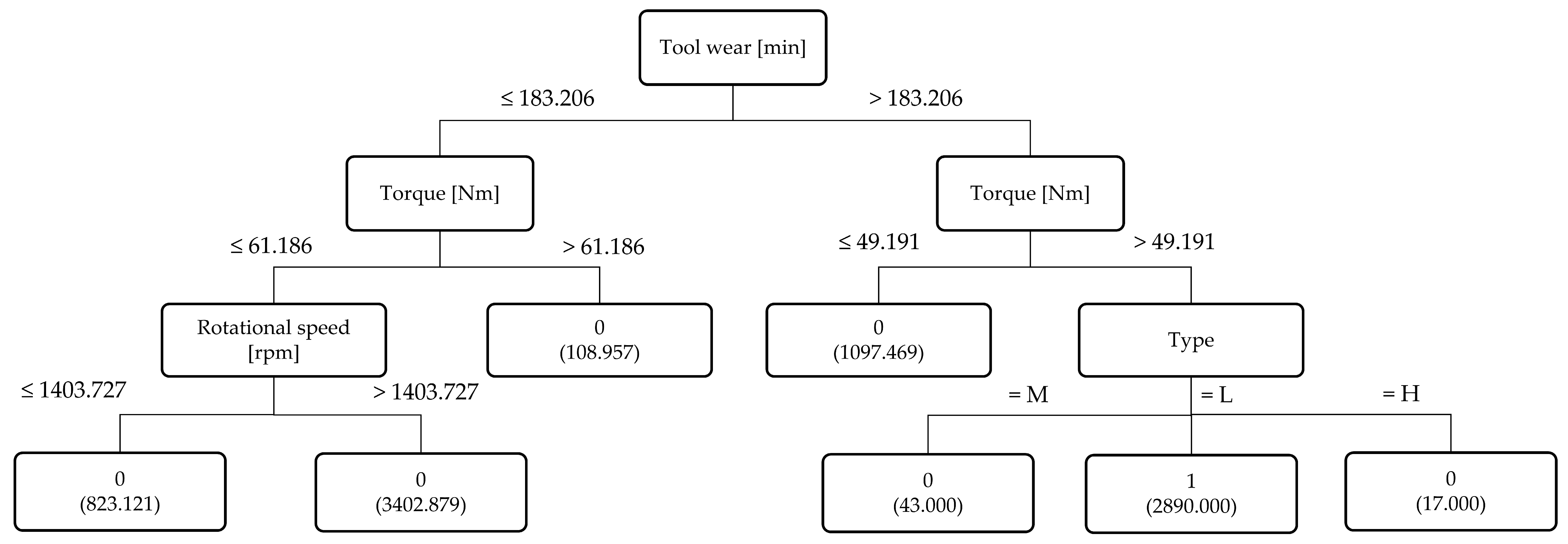
- Feature importance: To further enhance interpretability and provide visual analysis, we examined the contribution of individual features to each failure mode using Pearson correlation scores. The results are presented in Figure 3, Figure 4, Figure 5 and Figure 6, where features are ranked for each of the four failure modes: TWF, HDF, PWF, and OSF. For instance, torque and tool wear emerge as dominant indicators for OSF and TWF, respectively, while air temperature and rotational speed strongly influence HDF and PWF. These findings not only validate our decision to retain six features during preprocessing but also provide explicit evidence of how different sensors contribute to specific failures. Importantly, these visualizations offer an intuitive understanding of the data characteristics prior to modeling, thereby complementing the performance-driven results of BHTF.
5. Results
5.1. Overall BHTF Performance
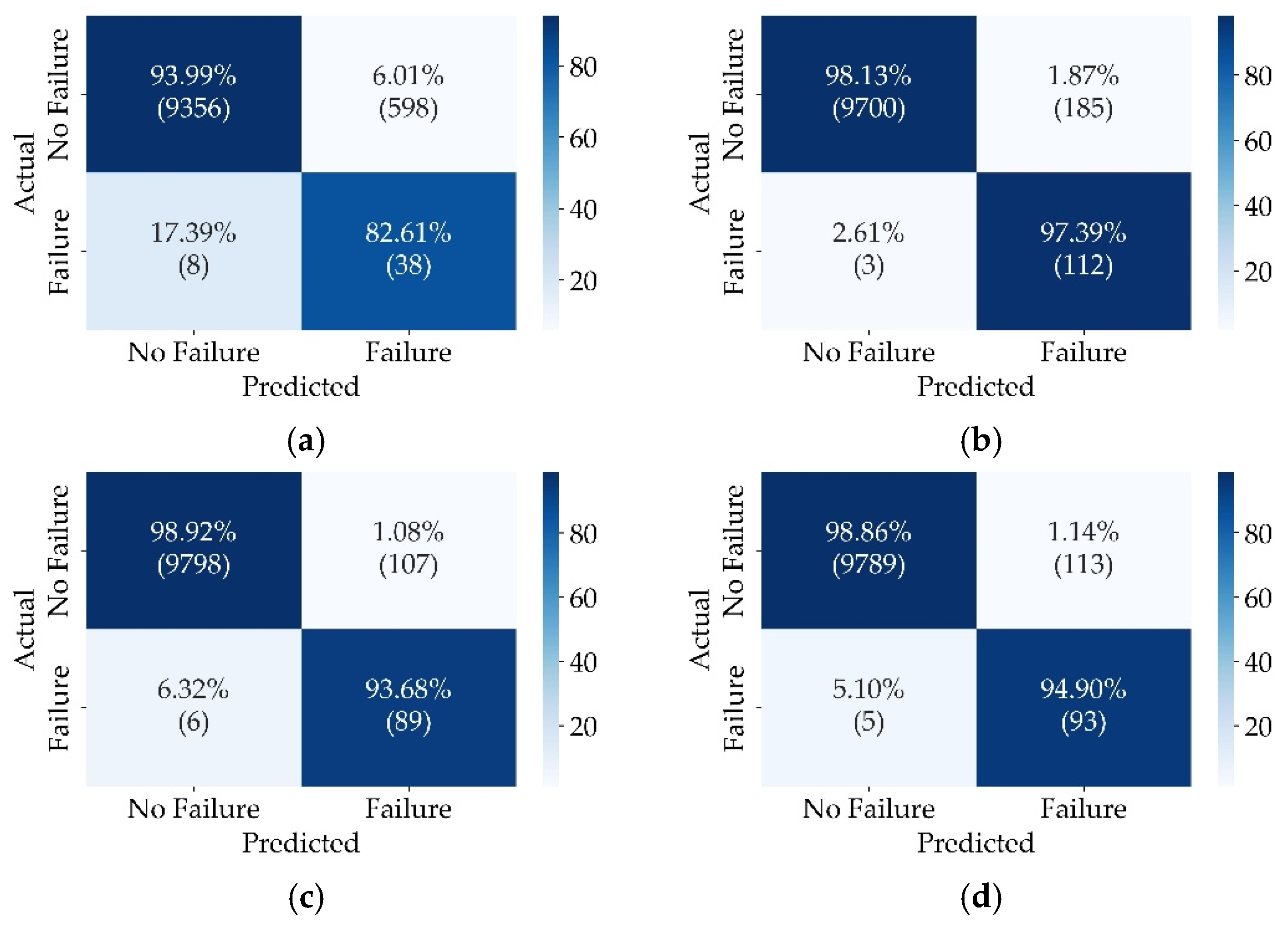
5.2. Confusion Matrix
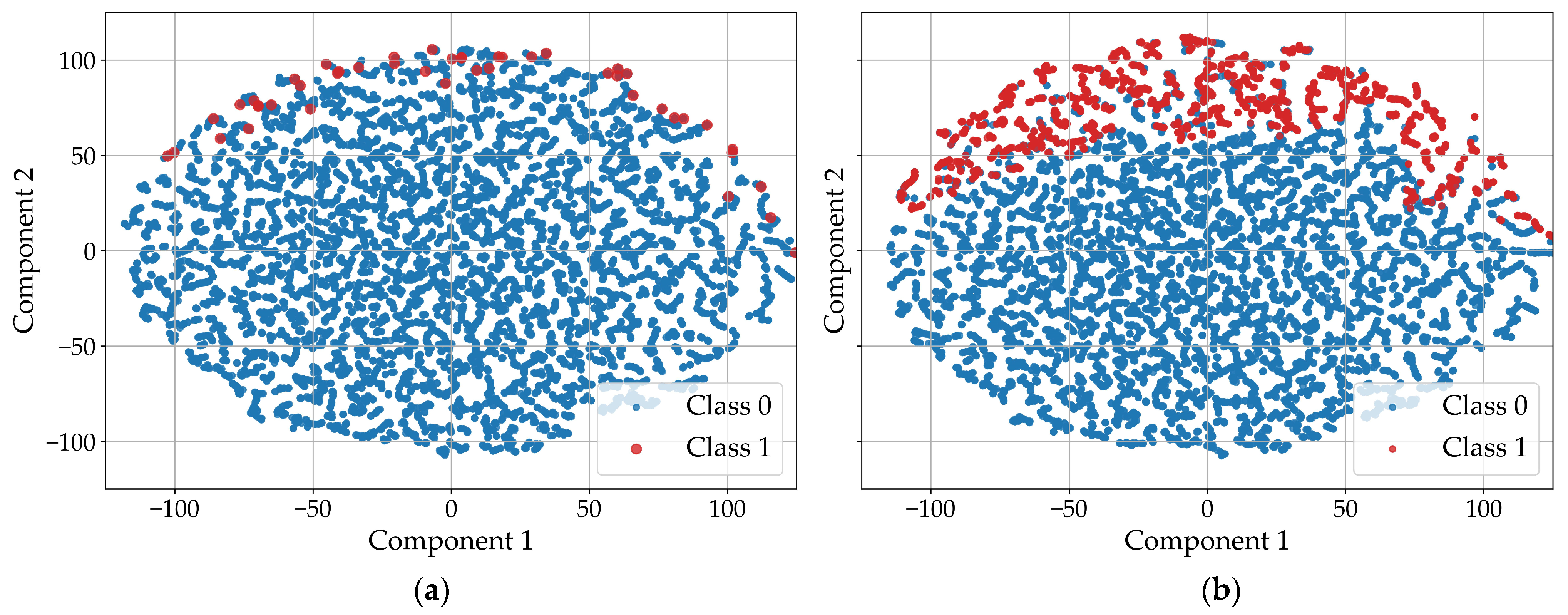
5.3. Resampling Performance Across Folds
5.4. Sensitivity Analysis
5.4.1. Effect of SMOTE Ratio
| Failure | R = 4000 | R = 5000 | R = 6000 |
|---|---|---|---|
| TWF | 93.94 | 93.08 | 92.77 |
| HDF | 98.12 | 98.15 | 98.28 |
| PWF | 98.87 | 98.84 | 98.80 |
| OSF | 98.82 | 99.07 | 99.07 |
| Average | 97.44 | 97.29 | 97.23 |
5.4.2. Effect of Number of Neighbors in PDU
| Failure | u = 1 | u = 3 | u = 5 | u = 7 | u = 9 |
|---|---|---|---|---|---|
| TWF | 93.96 | 93.75 | 93.76 | 93.94 | 93.80 |
| HDF | 98.13 | 98.05 | 98.03 | 98.12 | 98.19 |
| PWF | 98.92 | 98.91 | 99.01 | 98.87 | 98.94 |
| OSF | 98.72 | 98.84 | 98.75 | 98.82 | 98.81 |
| Average | 97.43 | 97.39 | 97.39 | 97.44 | 97.44 |
5.4.3. Effect of Number of Hoeffding Trees
| Failure | T = 10 | T = 50 | T = 100 |
|---|---|---|---|
| TWF | 93.94 | 93.85 | 93.77 |
| HDF | 98.12 | 98.11 | 98.09 |
| PWF | 98.87 | 98.91 | 98.95 |
| OSF | 98.82 | 98.80 | 98.80 |
| Average | 97.44 | 97.42 | 97.40 |
5.4.4. Effect of Number of Selected Features
| Failure | f = 2 | f = 3 | f = 4 | f = 5 | f = 6 |
|---|---|---|---|---|---|
| TWF | 93.46 | 93.69 | 93.83 | 93.80 | 93.94 |
| HDF | 93.87 | 97.29 | 98.02 | 98.11 | 98.12 |
| PWF | 98.86 | 98.95 | 98.93 | 98.90 | 98.87 |
| OSF | 98.78 | 98.76 | 98.75 | 98.79 | 98.82 |
| Average | 96.24 | 97.17 | 97.38 | 97.40 | 97.44 |
5.5. Computational Cost Analysis
5.6. Hoeffding Tree Structure Analysis
6. Discussion
- : the total number of non-zero matched differences used in the analysis;
- : the rank given to each positive difference between matched pairs to represent the contribution of that pair to the overall test statistic;
- : the Wilcoxon signed-rank statistic, determined by summing the ranks of all positive differences observed in the paired data.
7. External Validation Across Diverse Datasets
8. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AdaBoost | Adaptive boosting |
| ADASYN | Adaptive synthetic sampling |
| AI | Artificial Intelligence |
| ANN | Artificial neural network |
| AUC-ROC | Area under the receiver operating characteristic curve |
| BFT | Byzantine fault tolerant |
| BGRU | Bidirectional gated recurrent unit |
| BHTF | Balanced Hoeffding Tree forest |
| BLR | Binary logistic regression |
| BR | Binary relevance |
| CART | Classification and regression trees |
| CAST | Channel-spatial attention-base temporal |
| CatBoost | Categorical boosting |
| CC | Classifier chain |
| CNN | Convolutional neural network |
| ctGAN | Conditional tabular generative adversarial network |
| DFPAIS | Data filling approach based on probability analysis in incomplete soft sets |
| DNN | Deep neural network |
| DT | Decision tree |
| EFNC-Exp | Evolving fuzzy neural classifier with expert rules |
| EL | Ensemble learning |
| ELM | Extreme learning machine |
| FD | Fault detection |
| FPR | False-positive rate |
| GB | Gradient boosting |
| HDF | Heat dissipation failure |
| IL | Incremental learning |
| KNN | K-nearest neighbors |
| LDA | Linear discriminant analysis |
| LightGBM | Light gradient boosting machin |
| LIME | Local interpretable model-agnostic explanations |
| LOF | Local outlier factor |
| LP | Label powerset |
| LR | Logistic regression |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| MCC | Matthews correlation coefficient |
| ML | Machine learning |
| MLL | Multi-label learning |
| MLP | Multi-layer perceptron |
| MRMR | Minimum redundancy maximum relevance |
| MSE | Mean squared error |
| NB | Naive Bayes |
| NN | Neural network |
| OSF | Overstrain failure |
| PART | Partial decision tree |
| PCA | Principal component analysis |
| PdM | Predictive maintenance |
| PDU | Proximity-driven undersampling |
| PLSCO | Polar lights salp cooperative optimizer |
| PWF | Power failure |
| QDA | Quadratic discriminant analysis |
| RAKEL D | random k-labelsets D |
| RAKEL O | random k-labelsets O |
| ResNet | Residual neural network |
| RF | Random forest |
| RMSE | Root mean squared error |
| RNF | Random failures |
| RUL | Remaining useful life |
| RUS | Random under sampling |
| RUSBoost | Random undersampling boosting |
| SA | Simulated annealing |
| SDFIS | Simplified approach for data filling in incomplete soft sets |
| Self-ONN | Self-organized operational neural network |
| SHAP | Shapley additive explanations |
| SMOTE | Synthetic minority over-sampling technique |
| SMOTENC | Synthetic minority over-sampling technique for nominal and continuous |
| SODA | Self-organized direction-aware data partitioning |
| SVM | Support vector machine |
| TPR | True-positive rate |
| TTML | Tensor trains-based machine learning |
| TWF | Tool wear failure |
| t-SNE | t-distributed stochastic neighbor embedding |
| XAI | Explainable artificial intelligence |
| XGBoost | Extreme gradient boosting |
References
- Tsallis, C.; Papageorgas, P.; Piromalis, D.; Munteanu, R.A. Application-Wise Review of Machine Learning-Based Predictive Maintenance: Trends, Challenges, and Future Directions. Appl. Sci. 2025, 15, 4898. [Google Scholar] [CrossRef]
- Khattach, O.; Moussaoui, O.; Hassine, M. End-to-End Architecture for Real-Time IoT Analytics and Predictive Maintenance Using Stream Processing and ML Pipelines. Sensors 2025, 25, 2945. [Google Scholar] [CrossRef] [PubMed]
- Ucar, A.; Karakose, M.; Kırımça, N. Artificial Intelligence for Predictive Maintenance Applications: Key Components, Trustworthiness, and Future Trends. Appl. Sci. 2024, 14, 898. [Google Scholar] [CrossRef]
- Esteban, A.; Zafra, A.; Ventura, S. Data Mining in Predictive Maintenance Systems: A Taxonomy and Systematic Review. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2022, 12, e1471. [Google Scholar] [CrossRef]
- Altalhan, M.; Algarni, A.; Alouane, M.T.-H. Imbalanced Data Problem in Machine Learning: A Review. IEEE Access 2025, 13, 13686–13699. [Google Scholar] [CrossRef]
- Sajid, N.A.; Rahman, A.; Ahmad, M.; Musleh, D.; Basheer Ahmed, M.I.; Alassaf, R.; Chabani, S.; Ahmed, M.S.; Salam, A.A.; AlKhulaifi, D. Single vs. Multi-Label: The Issues, Challenges and Insights of Contemporary Classification Schemes. Appl. Sci. 2023, 13, 6804. [Google Scholar] [CrossRef]
- Hulten, G.; Spencer, L.; Domingos, P. Mining Time-Changing Data Streams. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 26–29 August 2001; pp. 97–106. [Google Scholar] [CrossRef]
- Lins, R.G.; Nascimento de Freitas, T.; Gaspar, R. Methodology for Commercial Vehicle Mechanical Systems Maintenance: Data-Driven and Deep-Learning-Based Prediction. IEEE Access 2025, 13, 33799–33812. [Google Scholar] [CrossRef]
- Lin, K.Y.; Hong, Y.H.; Li, M.H.; Shi, Y.; Matsuno, K. Predictive maintenance in industrial systems: An XGBoost-based approach for failure time estimation and resource optimization. J. Ind. Prod. Eng. 2025, 1–24. [Google Scholar] [CrossRef]
- Aydın, C.; Evrentuğ, B. Evaluation of Predictive Maintenance Efficiency with the Comparison of Machine Learning Models in Machining Production Process in Brake Industry. PeerJ Comput. Sci. 2025, 11, e2999. [Google Scholar] [CrossRef]
- Yıldırım, Ş.; Yücekaya, A.D.; Hekimoğlu, M.; Ucal, M.; Aydin, M.N.; Kalafat, İ. AI-Driven Predictive Maintenance for Workforce and Service Optimization in the Automotive Sector. Appl. Sci. 2025, 15, 6282. [Google Scholar] [CrossRef]
- Gunckel, P.; Lobos, G.; Rodríguez, F.; Bustos, R.; Godoy, D. Methodology proposal for the development of failure prediction models applied to conveyor belts of mining material using machine learning. Reliab. Eng. Syst. Saf. 2025, 256, 110709. [Google Scholar] [CrossRef]
- Aminzadeh, A.; Sattarpanah Karganroudi, S.; Majidi, S.; Dabompre, C.; Azaiez, K.; Mitride, C.; Sénéchal, E. A Machine Learning Implementation to Predictive Maintenance and Monitoring of Industrial Compressors. Sensors 2025, 25, 1006. [Google Scholar] [CrossRef]
- Hu, H.; Xu, K.; Zhang, X.; Li, F.; Zhu, L.; Xu, R.; Li, D. Research on Predictive Maintenance Methods for Current Transformers with Iron Core Structures. Electronics 2025, 14, 625. [Google Scholar] [CrossRef]
- Wu, M.; Goh, K.W.; Chaw, K.H.; Koh, Y.S.; Dares, M.; Yeong, C.F.; Zhang, Y. An Intelligent Predictive Maintenance System Based on Random Forest for Addressing Industrial Conveyor Belt Challenges. Front. Mech. Eng. 2024, 10, 1383202. [Google Scholar] [CrossRef]
- Shah, S.S.; Daoliang, T.; Kumar, S.C.H. RUL forecasting for wind turbine predictive maintenance based on deep learning. Heliyon 2024, 10, e39268. [Google Scholar] [CrossRef]
- Yu, B.; Kim, Y.; Lee, T.; Cho, Y.; Park, J.; Lee, J.; Park, J. Study on Methods Using Multi-Label Learning for the Classification of Compound Faults in Auxiliary Equipment Pumps of Marine Engine Systems. Processes 2024, 12, 2161. [Google Scholar] [CrossRef]
- Qureshi, U.R.; Rashid, A.; Altini, N.; Bevilacqua, V.; La Scala, M. Radiometric Infrared Thermography of Solar Photovoltaic Systems: An Explainable Predictive Maintenance Approach for Remote Aerial Diagnostic Monitoring. Smart Cities 2024, 7, 1261–1288. [Google Scholar] [CrossRef]
- Maldonado-Correa, J.; Valdiviezo-Condolo, M.; Artigao, E.; Martín-Martínez, S.; Gómez-Lázaro, E. Classification of Highly Imbalanced Supervisory Control and Data Acquisition Data for Fault Detection of Wind Turbine Generators. Energies 2024, 17, 1590. [Google Scholar] [CrossRef]
- Khalil, A.F.; Rostam, S. Machine Learning-Based Predictive Maintenance for Fault Detection in Rotating Machinery: A Case Study. Eng. Technol. Appl. Sci. Res. 2024, 14, 13181–13189. [Google Scholar] [CrossRef]
- Hadi, R.H.; Hady, H.N.; Hasan, A.M.; Al-Jodah, A.; Humaidi, A.J. Improved Fault Classification for Predictive Maintenance in Industrial IoT Based on AutoML: A Case Study of Ball-Bearing Faults. Processes 2023, 11, 1507. [Google Scholar] [CrossRef]
- Fordal, J.M.; Schjølberg, P.; Helgetun, H.; Skjermo, T.Ø.; Wang, Y.; Wang, C. Application of Sensor Data Based Predictive Maintenance and Artificial Neural Networks to Enable Industry 4.0. Adv. Manuf. 2023, 11, 248–263. [Google Scholar] [CrossRef]
- Muideen, A.A.; Lee, C.K.M.; Chan, J.; Pang, B.; Alaka, H. Broad Embedded Logistic Regression Classifier for Prediction of Air Pressure Systems Failure. Mathematics 2023, 11, 1014. [Google Scholar] [CrossRef]
- Berghout, T.; Bentrcia, T.; Lim, W.H.; Benbouzid, M. A Neural Network Weights Initialization Approach for Diagnosing Real Aircraft Engine Inter-Shaft Bearing Faults. Machines 2023, 11, 1089. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, B.; Wang, C. A Fault Diagnosis Method for Electrical Equipment With Imbalanced SCADA Data Based on SMOTE Oversampling and Domain Adaptation. In Proceedings of the 2023 8th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 22–25 September 2023; IEEE: New York, NY, USA, 2023; pp. 195–202. [Google Scholar] [CrossRef]
- Dangut, M.D.; Jennions, I.K.; King, S.; Skaf, Z. A Rare Failure Detection Model for Aircraft Predictive Maintenance Using a Deep Hybrid Learning Approach. Neural Comput. Appl. 2023, 35, 2991–3009. [Google Scholar] [CrossRef]
- Hung, Y.-H. Developing an Improved Ensemble Learning Approach for Predictive Maintenance in the Textile Manufacturing Process. Sensors 2022, 22, 9065. [Google Scholar] [CrossRef] [PubMed]
- Mihigo, I.N.; Zennaro, M.; Uwitonze, A.; Rwigema, J.; Rovai, M. On-Device IoT-Based Predictive Maintenance Analytics Model: Comparing TinyLSTM and TinyModel from Edge Impulse. Sensors 2022, 22, 5174. [Google Scholar] [CrossRef]
- Abdalla, R.; Samara, H.; Perozo, N.; Carvajal, C.P.; Jaeger, P. Machine learning approach for predictive maintenance of the electrical submersible pumps (ESPs). ACS Omega 2022, 7, 17641–17651. [Google Scholar] [CrossRef]
- Ouadah, A.; Zemmouchi-Ghomari, L.; Salhi, N. Selecting an appropriate supervised machine learning algorithm for predictive maintenance. Int. J. Adv. Manuf. Technol. 2022, 119, 4277–4301. [Google Scholar] [CrossRef]
- Chen, H.; Hsu, J.Y.; Hsieh, J.Y.; Hsu, H.Y.; Chang, C.H.; Lin, Y.J. Predictive maintenance of abnormal wind turbine events by using machine learning based on condition monitoring for anomaly detection. J. Mech. Sci. Technol. 2021, 35, 5323–5333. [Google Scholar] [CrossRef]
- Ince, T.; Malik, J.; Devecioglu, O.C.; Kiranyaz, S.; Avci, O.; Eren, L.; Gabbouj, M. Early Bearing Fault Diagnosis of Rotating Machinery by 1D Self-Organized Operational Neural Networks. arXiv 2021, arXiv:2109.14873. [Google Scholar] [CrossRef]
- Arora, A.; Tsigelny, I.F.; Kouznetsova, V.L. Laryngeal cancer diagnosis via miRNA-based decision tree model. Eur. Arch. Oto-Rhino-Laryngol. 2024, 281, 1391–1399. [Google Scholar] [CrossRef]
- Iqbal, N.; Kumar, P. Coronavirus Disease Predictor: An RNA-Seq Based Pipeline for Dimension Reduction and Prediction of COVID-19. J. Phys. Conf. Ser. 2021, 2089, 012025. [Google Scholar] [CrossRef]
- Mercaldo, F.; Nardone, V.; Santone, A. Diabetes Mellitus Affected Patients Classification and Diagnosis through Machine Learning Techniques. Procedia Comput. Sci. 2017, 112, 2519–2528. [Google Scholar] [CrossRef]
- Thaiparnit, S.; Kritsanasung, S.; Chumuang, N. A Classification for Patients with Heart Disease Based on Hoeffding Tree. In Proceedings of the International Joint Conference on Computer Science and Software Engineering, Chonburi, Thailand, 10–12 July 2019; pp. 352–357. [Google Scholar] [CrossRef]
- Pramkeaw, P.; Chumuang, N.; Ketcham, M.; Ganokratanaa, T.; Yimyam, W.; Kwansomkid, K.; Makararpong, D. A Machine Learning Framework for Diabetes Detection Using Hoeffding Tree. In Proceedings of the 2025 IEEE International Conference on Cybernetics and Innovations (ICCI), Chonburi, Thailand, 2–4 April 2025; pp. 1–6. [Google Scholar] [CrossRef]
- Mohammad, M.A.; Kolahkaj, M. Detecting Network Anomalies Using the Rain Optimization Algorithm and Hoeffding Tree-Based Autoencoder. In Proceedings of the 2024 10th International Conference on Web Research (ICWR), Tehran, Iran, 24–25 April 2024; pp. 137–141. [Google Scholar] [CrossRef]
- Rezki, D.; Mouss, L.-H.; Baaziz, A.; Bentrcia, T. Adaptive Prediction of Rate of Penetration While Oil-Well Drilling: A Hoeffding Tree Based Approach. Eng. Appl. Artif. Intell. 2025, 159, 111465. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S. GIS-based comparative study of Bayes network, Hoeffding tree and logistic model tree for landslide susceptibility modeling. Catena 2021, 203, 105344. [Google Scholar] [CrossRef]
- de Araújo Josephik, J.G.A.; Siqueira, Y.; Machado, K.G.; Terada, R.; dos Santos, A.L.; Nogueira, M.; Batista, D.M. Applying Hoeffding Tree Algorithms for Effective Stream Learning in IoT DDoS Detection. In Proceedings of the Latin-American Conference on Communications (LATINCOM), Panama City, Panama, 15–17 November 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Soares, D.; Dewan, M.A.A.; Lin, O. A Hoeffding Decision Tree Based Approach for Soil Classification. In Proceedings of the 35th Canadian Conference on Artificial Intelligence, Toronto, Ontario, Canada, 30 May–3 June 2022; pp. 1–12. [Google Scholar] [CrossRef]
- Zhang, M.L.; Li, Y.K.; Liu, X.Y.; Geng, X. Binary relevance for multi-label learning: An overview. Front. Comput. Sci. 2018, 12, 191–202. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority oversampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- AI4I 2020 Predictive Maintenance Dataset; UCI Machine Learning Repository: Irvine, CA, USA, 2020. [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques, 4th ed.; Morgan Kaufmann: Cambridge, MA, USA, 2016; pp. 1–664. Available online: https://ml.cms.waikato.ac.nz/weka (accessed on 22 May 2025).
- Pearson, K. Notes on regression and inheritance in the case of two parents. In Proceedings of the Royal Society of London, London, UK, 20 June 1895; Volume 58, pp. 240–242. [Google Scholar]
- Chandu, H.S. A Study of Machine Learning Techniques for Predicting Equipment Failures in Industrial Maintenance. In Proceedings of the 2025 IEEE International Conference on Emerging Technologies and Applications (MPSec ICETA), Gwalior, India, 21–23 February 2025; pp. 1–6. [Google Scholar] [CrossRef]
- Besha, A.R.M.A.; Ojekemi, O.S.; Oz, T.; Adegboye, O. PLSCO: An Optimization-Driven Approach for Enhancing Predictive Maintenance Accuracy in Intelligent Manufacturing. Processes 2025, 13, 2707. [Google Scholar] [CrossRef]
- Jahani, K.; Moshiri, B.; Hossein Khalaj, B. Secure PDM: A Novel Byzantine Fault Tolerant Federated Learning Framework Using a Robust PCA-Based Anomaly Detection Approach. Int. J. Ind. Electron. Control Optim. 2025. [Google Scholar] [CrossRef]
- Araujo, S.A.d.; Bomfim, S.L.; Boukouvalas, D.T.; Lourenço, S.R.; Ibusuki, U.; Oliveira Neto, G.C.d. Integration of Data Analytics and Data Mining for Machine Failure Mitigation and Decision Support in Metal–Mechanical Industry. Logistics 2025, 9, 109. [Google Scholar] [CrossRef]
- Prashanth, B.S.; Manoj Kumar, M.V.; Almuraqab, N.; Puneetha, B.H. Leveraging Safe and Secure AI for Predictive Maintenance of Mechanical Devices Using Incremental Learning and Drift Detection. Comput. Mater. Contin. 2025, 83, 4979–4998. [Google Scholar] [CrossRef]
- Özdemir, K.; Işık, G. Üretim Süreçlerinde Yapay Zekâ Destekli Hatalı Parça Tahminine Yönelik Bir Uygulama. In Proceedings of the 1. Bilsel Uluslararası Anı Bilimsel Araştırmalar Kongresi, Kars, Turkey, 28–29 June 2025; pp. 175–182. [Google Scholar]
- Kumar, S.; Panchal, A.; Rawat, U.; Bhattacharya, P.; Kumar, K. Optimizing Grid Equipment Maintenance through Robust Machine Learning. In Proceedings of the 2025 International Conference on Next Generation Communication & Information Processing (INCIP), Bangalore, India, 23–24 January 2025; pp. 194–199. [Google Scholar] [CrossRef]
- Misaii, H.; Fouladirad, M.; Ponchet-Durupt, A.; Askari, B. Predictive Degradation Modelling Using Artificial Intelligence: Milling Machine Case Study. In Proceedings of the European Safety and Reliability Conference ESREL 2024, Cracow, Poland, 23–27 June 2024; Jagiellonian University: Cracow, Poland, 2024; pp. 193–200. Available online: https://hal.science/hal-04564828v1 (accessed on 22 May 2025).
- Presciuttini, A.; Cantini, A.; Portioli-Staudacher, A. From Explanations to Actions: Leveraging SHAP, LIME, and Counterfactual Analysis for Operational Excellence in Maintenance Decisions. In Proceedings of the 4th International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Male, Maldives, 4–6 November 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Hung, Y.-H.; Huang, M.-L.; Wang, W.-P.; Chen, G.-L. Hybrid Approach Combining Simulated Annealing and Deep Neural Network Models for Diagnosing and Predicting Potential Failures in Smart Manufacturing. Sens. Mater. 2024, 36, 49–65. [Google Scholar] [CrossRef]
- Liu, C.-L.; Su, H.-C. Temporal learning in predictive health management using channel-spatial attention-based deep neural networks. Adv. Eng. Inform. 2024, 62, 102604. [Google Scholar] [CrossRef]
- Ghadekar, P.; Manakshe, A.; Madhikar, S.; Patil, S.; Mukadam, M.; Gambhir, T. Predictive Maintenance for Industrial Equipment: Using XGBoost and Local Outlier Factor with Explainable AI for Analysis. In Proceedings of the 2024 14th International Conference on Cloud Computing, Data Science & Engineering (Confluence), Noida, India, 18–19 January 2024; pp. 25–30. [Google Scholar] [CrossRef]
- Kong, Z.; Lu, Q.; Wang, L.; Guo, G. A Simplified Approach for Data Filling in Incomplete Soft Sets. Expert Syst. Appl. 2023, 213, 119248. [Google Scholar] [CrossRef]
- Souza, P.V.C.; Lughofer, E. EFNC-Exp: An evolving fuzzy neural classifier integrating expert rules and uncertainty. Fuzzy Sets Syst. 2023, 466, 108438. [Google Scholar] [CrossRef]
- Chen, C.-H.; Tsung, C.-K.; Yu, S.-S. Designing a Hybrid Equipment-Failure Diagnosis Mechanism under Mixed-Type Data with Limited Failure Samples. Appl. Sci. 2022, 12, 9286. [Google Scholar] [CrossRef]
- Vandereycken, B.; Voorhaar, R. TTML: Tensor trains for general supervised machine learning. arXiv 2016, arXiv:2203.04352. [Google Scholar] [CrossRef]
- Falla, B.F.; Ortega, D.A. Evaluación De Algoritmos De Inteligencia Artificial Aplicados Al Mantenimiento Predictivo. Ph.D. Thesis, Corporación Universitaria Autónoma de Nariño (AUNAR), Nariño, Colombia, 3 June 2022. Available online: http://repositorio.aunar.edu.co:8080/xmlui/handle/20.500.12276/1258 (accessed on 22 May 2025).
- Iantovics, L.B.; Enachescu, C. Method for Data Quality Assessment of Synthetic Industrial Data. Sensors 2022, 22, 1608. [Google Scholar] [CrossRef] [PubMed]
- Vuttipittayamongkol, P.; Arreeras, T. Data-driven Industrial Machine Failure Detection in Imbalanced Environments. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Kuala Lumpur, Malaysia, 7–10 December 2022; pp. 1224–1227. [Google Scholar] [CrossRef]
- Mota, B.; Faria, P.; Ramos, C. Predictive Maintenance for Maintenance-Effective Manufacturing Using Machine Learning Approaches. In Lecture Notes in Networks and Systems, Proceedings of 17th International Conference on Soft Computing Models in Industrial and Environmental Applications, Salamanca, Spain, 5–7 September 2022; Springer International Publishing AG: Cham, Switzerland, 2022; Volume 531, pp. 13–22. [Google Scholar] [CrossRef]
- Diao, L.; Deng, M.; Gao, J. Clustering by Constructing Hyper-Planes. IEEE Access 2021, 9, 70167–70181. [Google Scholar] [CrossRef]
- Torcianti, A.; Matzka, S. Explainable Artificial Intelligence for Predictive Maintenance Applications using a Local Surrogate Model. In Proceedings of the 4th International Conference on Artificial Intelligence for Industries, Laguna Hills, CA, USA, 20–22 September 2021; pp. 86–88. [Google Scholar] [CrossRef]
- Pastorino, J.; Biswas, A.K. Data-Blind ML: Building privacy-aware machine learning models without direct data access. In Proceedings of the IEEE Fourth International Conference on Artificial Intelligence and Knowledge Engineering, Laguna Hills, CA, USA, 1–3 December 2021; pp. 95–98. [Google Scholar] [CrossRef]
- Zimmerman, D.W.; Zumbo, B.D. Relative Power of the Wilcoxon Test, the Friedman Test, and Repeated-Measures ANOVA on Ranks. J. Exp. Educ. 1993, 62, 75–86. [Google Scholar] [CrossRef]
- Jakubowski, J.; Bobek, S.; Nalepa, G.J. TCM: Benchmark Datasets for Predictive Maintenance in Steel Manufacturing; Zenodo: Geneva, Switzerland, 2024. [Google Scholar] [CrossRef]
| Ref | Year | Method | Machine | C | R | Label | Sampling | Purpose |
|---|---|---|---|---|---|---|---|---|
| [8] | 2025 | LSTM | Vehicle | √ | - | S | O | Failure prediction |
| [9] | 2025 | XGBoost, RF, LSTM | Aircraft engine | √ | √ | S | - | RUL prediction |
| [10] | 2025 | DT, NB, KNN, SVM, AdaBoost, RF, CatBoost, XGBoost, LightGBM, MLP | Braking component | √ | - | S | U | Failure classification |
| [11] | 2025 | DT, RF, LightGBM, XGBoost | Vehicle | √ | - | S | - | Service prediction |
| [12] | 2025 | ARIMA, LR, ANN, SVM, PCA, DT, LDA, QDA | Conveyor belt | √ | - | S | - | Failure prediction |
| [13] | 2025 | LR | Compressor | - | √ | S | - | Monitoring of equipment health |
| [14] | 2025 | RF | Current transformers | √ | - | S | O | Fault classification |
| [15] | 2024 | RF, LR, ANN, DT, GB | Conveyor belt | √ | - | S | - | Fault classification |
| [16] | 2024 | CNN, LSTM, ResNet | Wind turbine | - | √ | S | - | RUL prediction |
| [17] | 2024 | CNN, BR, CC, LP, RAKEL D, RAKEL O, Multi-label KNN | Pump | √ | - | M | - | Fault detection |
| [18] | 2024 | CNN | Solar panels | √ | - | S | O | Diagnostic monitoring |
| [19] | 2024 | RF, DT, MLP | Wind turbine | √ | - | S | O | Fault detection |
| [20] | 2024 | SVM, AdaBoost, Bagging, MLP | Rotating machinery | √ | - | S | - | Fault detection |
| [21] | 2023 | RF, XGBoost, LightGBM, Auto DNN | Ball bearing | √ | - | S | U | Failure classification |
| [22] | 2023 | ANN | Lumber machinery | √ | - | S | - | Failure prediction |
| [23] | 2023 | LR | Air pressure system | √ | - | S | O | Failure prediction |
| [24] | 2023 | LSTM | Aircraft engine | √ | - | S | O | Fault diagnosis |
| [25] | 2023 | ResNet, CNN | Hydraulic system, generator bearing, gearbox | √ | - | S | O | Fault diagnosis |
| [26] | 2022 | Autoencoder, BGRU, CNN | Aircraft | √ | - | S | - | Rare failure prediction |
| [27] | 2022 | LightGBM, XGBoost, RF | Textile machinery | √ | - | S | O | Defect classification |
| [28] | 2022 | TinyLSTM, DNN | Autoclave sterilizer | - | √ | S | - | RUL prediction |
| [29] | 2022 | XGBoost | Pump | √ | - | S | - | Failure classification |
| [30] | 2022 | RF, DT, KNN | Oil consumption system | √ | √ | S | - | Fault diagnosis |
| [31] | 2021 | DNN, RF, SMOTE, PCA | Wind turbine | √ | - | S | O | Failure prediction |
| [32] | 2021 | Self-ONN | Rotating machinery | √ | - | S | - | Fault diagnosis |
| Proposed | BHTF | Industrial machinery | √ | - | M | O, U | Failure diagnosis | |
| Sample | X | Y | |||
|---|---|---|---|---|---|
| … | |||||
| … | |||||
| … | … | … | … | … | … |
| … | |||||
| X | Y | X | Y | X | Y | X | Y | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| … | … | … | … | … | … | … | … | … | … | … | … |
| Feature | SMOTE | PDU |
|---|---|---|
| Type | Oversampling | Undersampling |
| Add samples? | Yes | No |
| Remove samples? | No | Yes |
| Which Class is Affected? | Minority class (Adds to it) | Majority class (Removes some if noisy or misclassified) |
| Scenario | When the minority class is underrepresented | When data has noise or overlapping classes |
| Uses k-Nearest Neighbors? | Yes (to generate data) | Yes (to remove misclassified points) |
| Risk | Overfitting if overused | Underfitting if too aggressive |
| Goal | Balance the dataset by adding more representative samples | Clean and balance the dataset by removing noisy or borderline samples |
| Sensitivity to Noise | High—may synthesize noisy or borderline instances | Low—helps eliminate noisy or ambiguous instances |
| Effect on Decision Boundary | Expands the decision region of the minority class | Sharpens or clarifies the decision boundary by removing overlapping samples |
| Computational Cost | Moderate—needs distance computations and synthetic generation | Moderate—distance computations for each minority instance |
| Main Technique | Feature-space interpolation | Disagreement with the classes of neighbors |
| Dataset Type | Attribute Types | Learning Tasks | #Instances | #Variables | Missing Values | Subject Area | Release Year | View Counts |
|---|---|---|---|---|---|---|---|---|
| Time Series, Multivariate | Real, Boolean | Regression, Classification, Causal Discovery | 10,000 | 14 | None | Computer Science | 2020 | 77,511 |
| Variable Name | Category | Type | Description | Unit |
|---|---|---|---|---|
| UID | Identifier | Integer | Unique identifier | – |
| Product ID | Identifier | Categorical | Product variant identifier | – |
| Type | Feature | Categorical | Product quality level (low, medium, high) | – |
| Air temperature | Feature | Continuous | Air temperature | K |
| Process temperature | Feature | Continuous | Process temperature | K |
| Rotational speed | Feature | Integer | Rotational speed | rpm |
| Torque | Feature | Continuous | Torque | Nm |
| Tool wear | Feature | Integer | Tool wear | min |
| Machine failure | Target | Boolean | Indicates any failure occurrence | – |
| RNF | Target | Boolean | Random failures | – |
| TWF | Target | Boolean | Tool wear failure | – |
| HDF | Target | Boolean | Heat dissipation failure | – |
| PWF | Target | Boolean | Power failure | – |
| OSF | Target | Boolean | Overstrain failure | – |
| Variable Name | Min | Max | Mean | Standard Deviation |
|---|---|---|---|---|
| Air temperature | 295.3 | 304.5 | 300.0 | 2.000 |
| Process temperature | 305.7 | 313.8 | 310.0 | 1.484 |
| Rotational speed | 1168 | 2886 | 1538.8 | 179.284 |
| Torque | 3.8 | 76.6 | 39.9 | 9.969 |
| Tool wear | 0 | 253 | 107.9 | 63.654 |
| Failure Type | Accuracy | Precision | Recall | F-Measure |
|---|---|---|---|---|
| TWF | 93.94% | 0.9948 | 0.9394 | 0.9663 |
| HDF | 98.12% | 0.9925 | 0.9812 | 0.9868 |
| PWF | 98.87% | 0.9942 | 0.9887 | 0.9914 |
| OSF | 98.82% | 0.9941 | 0.9882 | 0.9911 |
| Average | 97.44% | 0.9939 | 0.9744 | 0.9839 |
| Fold | Before SMOTE | After SMOTE Before PDU | After PDU |
|---|---|---|---|
| 1 | 8958/42 | 8958/1722 | 8827/1722 |
| 2 | 8958/42 | 8958/1722 | 8826/1722 |
| 3 | 8958/42 | 8958/1722 | 8835/1722 |
| 4 | 8958/42 | 8958/1722 | 8822/1722 |
| 5 | 8959/41 | 8959/1681 | 8839/1681 |
| 6 | 8959/41 | 8959/1681 | 8815/1681 |
| 7 | 8959/41 | 8959/1681 | 8833/1681 |
| 8 | 8959/41 | 8959/1681 | 8864/1681 |
| 9 | 8959/41 | 8959/1681 | 8831/1681 |
| 10 | 8959/41 | 8959/1681 | 8830/1681 |
| Average | 8959/41 | 8959/1697 | 8832/1697 |
| Fold | Before SMOTE | After SMOTE Before PDU | After PDU |
|---|---|---|---|
| 1 | 8896/104 | 8896/4264 | 8843/4264 |
| 2 | 8896/104 | 8896/4264 | 8851/4264 |
| 3 | 8896/104 | 8896/4264 | 8842/4264 |
| 4 | 8896/104 | 8896/4264 | 8841/4264 |
| 5 | 8896/104 | 8896/4264 | 8839/4264 |
| 6 | 8897/103 | 8897/4223 | 8838/4223 |
| 7 | 8897/103 | 8897/4223 | 8851/4223 |
| 8 | 8897/103 | 8897/4223 | 8841/4223 |
| 9 | 8897/103 | 8897/4223 | 8838/4223 |
| 10 | 8897/103 | 8897/4223 | 8842/4223 |
| Average | 8897/104 | 8897/4244 | 8843/4244 |
| Fold | Before SMOTE | After SMOTE Before PDU | After PDU |
|---|---|---|---|
| 1 | 8914/86 | 8914/3526 | 8856/3526 |
| 2 | 8914/86 | 8914/3526 | 8849/3526 |
| 3 | 8914/86 | 8914/3526 | 8851/3526 |
| 4 | 8914/86 | 8914/3526 | 8850/3526 |
| 5 | 8914/86 | 8914/3526 | 8854/3526 |
| 6 | 8915/85 | 8915/3485 | 8857/3485 |
| 7 | 8915/85 | 8915/3485 | 8865/3485 |
| 8 | 8915/85 | 8915/3485 | 8854/3485 |
| 9 | 8915/85 | 8915/3485 | 8859/3485 |
| 10 | 8915/85 | 8915/3485 | 8843/3485 |
| Average | 8915/86 | 8915/3506 | 8854/3506 |
| Fold | Before SMOTE | After SMOTE Before PDU | After PDU |
|---|---|---|---|
| 1 | 8911/89 | 8911/3649 | 8884/3649 |
| 2 | 8911/89 | 8911/3649 | 8885/3649 |
| 3 | 8912/88 | 8912/3608 | 8882/3608 |
| 4 | 8912/88 | 8912/3608 | 8879/3608 |
| 5 | 8912/88 | 8912/3608 | 8886/3608 |
| 6 | 8912/88 | 8912/3608 | 8873/3608 |
| 7 | 8912/88 | 8912/3608 | 8888/3608 |
| 8 | 8912/88 | 8912/3608 | 8887/3608 |
| 9 | 8912/88 | 8912/3608 | 8885/3608 |
| 10 | 8912/88 | 8912/3608 | 8883/3608 |
| Average | 8912/88 | 8912/3616 | 8883/3616 |
| Fold | TWF | HDF | PWF | OSF |
|---|---|---|---|---|
| 1 | 0.547 | 0.225 | 0.185 | 0.209 |
| 2 | 0.235 | 0.215 | 0.184 | 0.195 |
| 3 | 0.164 | 0.204 | 0.183 | 0.193 |
| 4 | 0.203 | 0.210 | 0.188 | 0.194 |
| 5 | 0.145 | 0.202 | 0.183 | 0.193 |
| 6 | 0.150 | 0.209 | 0.186 | 0.195 |
| 7 | 0.148 | 0.201 | 0.182 | 0.193 |
| 8 | 0.148 | 0.201 | 0.180 | 0.192 |
| 9 | 0.148 | 0.196 | 0.179 | 0.191 |
| 10 | 0.145 | 0.202 | 0.179 | 0.190 |
| Average | 0.203 | 0.207 | 0.183 | 0.195 |
| Reference | Year | Method | Training Protocol | Dataset Split | Hyperparameters Settings | Accuracy (%) | Precision | Recall | F-Measure |
|---|---|---|---|---|---|---|---|---|---|
| Chandu [48] | 2025 | GB | Feature selection; SMOTE; min–max normalization; outlier removal | Train/test (not specified ratios) | N/A | 90.00 | 0.9200 | 0.9000 | 0.8569 |
| MLP | 61.00 | 0.7300 | 0.6100 | 0.6000 | |||||
| KNN | 71.68 | 0.6709 | 0.6831 | 0.6769 | |||||
| Besha et al. [49] | 2025 | ELM + PLSCO | Optimization-driven training with metaheuristic hybrid (PLO + CSO + SSA) | 70–30% | m = 100, a = [1,1.5], c1 = [2/e,2] | 95.47 | 0.8679 | 0.8659 | 0.8669 |
| Jahani et al. [50] | 2025 | BFT + PCA (Byzantine = 0.2) | Federated learning | N/A | N/A | 89.90 | - | - | - |
| BFT + PCA (Byzantine = 0.4) | 89.83 | - | - | - | |||||
| BFT + PCA (Byzantine = 0.6) | 89.00 | - | - | - | |||||
| Araujo et al. [51] | 2025 | CART | SMOTE; categorical encoding; MRMR feature selection | Five-fold-cross-validation | criterion = entropy, splitter = best, max_depth = 5, min_samples_split = 2, min_samples_leaf = 1, num_features_split = none, max_leaf_nodes = none, random_state = 42 | 82.10 | - | - | - |
| Prashanth et al. [52] | 2025 | DNN | Incremental and dynamic learning | Hold-out validation | 3 layers (64,32, 1), ReLU, sigmoid | 84.00 | - | - | - |
| SVM | N/A | N/A | N/A | 89.00 | - | - | - | ||
| Özdemir et al. [53] | 2025 | LR | SMOTE; categorical encoding; supervised learning | N/A | N/A | 88.00 | 0.4200 | 0.6100 | 0.5000 |
| RF | 94.00 | 0.4500 | 0.6800 | 0.5400 | |||||
| XGBoost | 97.00 | 0.4700 | 0.7400 | 0.5800 | |||||
| Kumar1 et al. [54] | 2025 | KNN | Nearest-neighbor voting | Train/validation/test (not specified ratios) | k = 1, Euclidean distance | 94.00 | - | - | 0.9400 |
| SVM | Kernel-based supervised learning | C = 100, gamma = 1, kernel = RBF | 95.00 | - | - | 0.9500 | |||
| RF | Ensemble learning | Max depth = 10, number of trees = 500 | 96.00 | - | - | 0.9600 | |||
| XGBoost | Gradient boosting | learning rate = 0.1, max depth = 5, n_estimators = 500 | 97.00 | - | - | 0.9700 | |||
| Misaii et al. [55] | 2024 | LSTM | Sequential deep learning; SMOTE; binary cross-entropy loss function | 80–20% | N/A | 80.00 | 0.96 | 0.83 | 0.89 |
| Presciuttini et al. [56] | 2024 | RF + XAI (SHAP, LIME, counterfactual) | Supervised learning | 80–20% | number of trees = 100, random_state = 42 | 95.00 | - | - | - |
| Hung et al. [57] | 2024 | DNN+Adam SingleHL Model I | Models trained for 100 epochs; batch size 400; single- and double-hidden-layer architectures | 90–10% | number of neurons per hidden layer = 100, activation function (hidden layers) = ReLU, activation function (output layer) = Softmax, output classes = 6, input neurons = 5 | 93.58 | - | 0.9400 | 0.9300 |
| DNN+Adam SingleHL Model II | 95.37 | - | 0.9600 | 0.9600 | |||||
| DNN+SA DoubleHL Model III | 96.54 | - | 0.9500 | 0.9500 | |||||
| DNN+SA DoubleHL Model IV | 97.09 | - | 0.9700 | 0.9700 | |||||
| Liu and Su [58] | 2024 | CAST | Early stopping if validation loss does not improve for 3 iterations | Five-fold-cross-validation | Epochs = 100, batch size = 64, learning rate = 0.001, hidden size = 512, optimizer = AdamW | - | - | - | 0.8800 |
| SE-ResNet 18 | - | - | - | 0.8400 | |||||
| GE-ResNet 18 | - | - | - | 0.8100 | |||||
| SE-SCNet 18 | - | - | - | 0.8600 | |||||
| Ghadekar et al. [59] | 2024 | XGBoost | SMOTE | N/A | N/A | 96.00 | 0.9800 | 0.9600 | 0.9690 |
| RF | 95.50 | 0.9760 | 0.9550 | 0.9640 | |||||
| LOF | 91.70 | 0.9510 | 0.9170 | 0.9330 | |||||
| One-class SVM | 91.20 | 0.9530 | 0.9120 | 0.9300 | |||||
| Kong et al. [60] | 2023 | DFPAIS | Iterative data filling | N/A | N/A | 83.74 | - | - | - |
| SDFIS | Simplified data filling | 82.03 | - | - | - | ||||
| Souza and Lughofer [61] | 2023 | EFNC-Exp | Sequential stream-based updating; fuzzification; expert rules | 70–30% | γ for DA plane (single hyperparameter) | 97.30 | - | - | - |
| SODA | Incremental clustering; dynamically updating clouds and feature weights | No separate hyperparameters beyond γ | 96.80 | - | - | - | |||
| Chen et al. [62] | 2022 | CatBoost | Ordered boosting and gradient descent | Three-fold cross-validation | Hyperparameters optimized using Optuna | 64.23 | - | 0.2868 | - |
| SMOTENC + CatBoost | SMOTE | 88.09 | - | 0.7881 | - | ||||
| ctGAN + CatBoost | Data normalization; learning distribution; oversampling | 87.08 | - | 0.8305 | - | ||||
| SMOTENC + ctGAN + CatBoost | SMOTE, GAN | 88.83 | - | 0.9068 | - | ||||
| Vandereycken and Voorhaar [63] | 2022 | XGBoost | Training with different TT initializations | 70% train/ 15% validation/ 15% test | Optimized via validation set | 95.74 | - | - | - |
| RF | 95.10 | - | - | - | |||||
| TTML + XGBoost | 77.00 | - | - | - | |||||
| TTML + RF | 78.00 | - | - | - | |||||
| TTML + MLP 1 | 76.20 | - | - | - | |||||
| TTML + MLP 2 | 65.00 | - | - | - | |||||
| Falla and Ortega [64] | 2022 | RF | Supervised learning, oversampling | 70–30% | Sklearn default parameters; random seed = 42 | 96.81 | 0.9740 | 0.7639 | 0.8563 |
| Neural Networks | Hidden layers = 10, max iterations = 500, penalty = 0.001, random seed = 21, other defaults | 91.50 | 0.9166 | 0.8611 | 0.8880 | ||||
| Iantovics and Enachescu [65] | 2022 | BLR | Mathematical modeling for data quality assessment | N/A | Standard β coefficients | 97.10 | 0.9950 | 0.2830 | 0.4407 |
| Vuttipittayamongkol and Arreeras [66] | 2022 | SVM | Standard supervised learning | 70–30% | Default caret parameters | - | 0.7229 | 0.5941 | 0.6522 |
| DT | - | 0.8391 | 0.7228 | 0.7766 | |||||
| KNN | - | 0.8108 | 0.2970 | 0.4348 | |||||
| RF | - | 0.8267 | 0.6139 | 0.7045 | |||||
| NN | - | 0.7333 | 0.2178 | 0.3359 | |||||
| Mota et al. [67] | 2022 | GB, SVM | Batch training; preprocessing with data aggregation, min–max normalization, imputation, feature engineering, oversampling, and undersampling | 80–20% | Automatic hyperparameter tuning using five-fold cross-validation | 94.55 | - | 0.9200 | - |
| Diao et al. [68] | 2021 | Constructing Hyper-Planes | Unsupervised learning; mean-shift and min–max normalization | N/A | H = TL (set of hyper-planes); δ determined automatically | - | - | - | 0.6200 |
| Torcianti and Matzka [69] | 2021 | RUSBoost Trees | Decision tree-based learning | 20 dataset points | Kernel width σ = 0.05, iteratively decreased by 0.01 down to 0.01; feature importance threshold ≥ 25% | 92.74 | 0.3071 | 0.9085 | 0.4590 |
| Pastorino and Biswas [70] | 2021 | Data-Blind Machine Learning | Simple NN training for tabular datasets, CNN training for MNIST | Train/test (not specified ratios) | CTGAN settings for generative model; no special tuning for MNIST | 97.30 | - | - | - |
| Average | 88.94 | 0.7845 | 0.7492 | 0.7793 | |||||
| Proposed Method | Balanced Hoeffding Tree Forest (BHTF) | Multi-label learning (MLL); incremental learning (IL); ensemble learning (EL); oversampling; undersampling | 10-fold-cross-validation | SMOTE: k = 5, R = 4000%; PDU: u = 7; numIterations = 10 | 97.44 | 0.9939 | 0.9744 | 0.9839 | |
| Dataset | Observations | Anomalies | Features | Anomaly Types | Products | Data Drift |
|---|---|---|---|---|---|---|
| tcm5_dataset_3 | 20003 | 981 | 51 | 4 (16) | 4 | False |
| tcm5_dataset_4 | 20001 | 925 | 51 | 4 (16) | 20 | False |
| tcm5_dataset_5 | 20005 | 1031 | 51 | 4 (16) | 5 | True |
| tcm5_dataset_6 | 20008 | 954 | 51 | 4 (16) | 25 | True |
| Variable Name | Category | Type | Description | Unit |
|---|---|---|---|---|
| thickness_entry | Feature | Continuous | Steel entry thickness before rolling | mm |
| thickness_exit | Feature | Continuous | Steel exit thickness after rolling | mm |
| width | Feature | Continuous | Steel width | mm |
| ys_entry | Feature | Continuous | Steel yield strength at entry | MPa |
| ys_exit | Feature | Continuous | Steel yield strength at exit | MPa |
| work_roll_diam | Feature | Continuous | Work roll diameter for stands 1–5 | mm |
| work_roll_mileage | Feature | Continuous | Work roll mileage for stands 1–5 | km |
| reduction | Feature | Continuous | Thickness reduction per stand (1–5) | – |
| tension | Feature | Continuous | Interstand tension (0: before stand 1, 1–5: after stands 1–5) | N |
| roll_speed | Feature | Continuous | Linear work roll speed for stands 1–5 | NaN |
| force | Feature | Continuous | Rolling force for stands 1–5 | N |
| torque | Feature | Continuous | Rolling torque for stands 1–5 | Nm |
| gap | Feature | Continuous | Stand gap for stands 1–5 | mm |
| motor_power | Feature | Continuous | Electric motor power for stands 1–5 | kW |
| Anomaly_Reduction | Target | Boolean | Label for anomaly in reduction scheme | – |
| Anomaly_Electric | Target | Boolean | Label for anomaly in electric motor per stand | – |
| Anomaly_Bearing | Target | Boolean | Label for anomaly in stand bearings | – |
| Anomaly_WorkRoll | Target | Boolean | Label for anomaly in work roll friction per stand | – |
| Label | Failure Type | tcm5_dataset_3 | tcm5_dataset_4 | tcm5_dataset_5 | tcm5_dataset_6 |
|---|---|---|---|---|---|
| 1 | Anomaly Reduction | 93.24 | 90.81 | 98.05 | 86.15 |
| 2 | Anomaly Electric 1 | 97.63 | 99.55 | 97.93 | 95.96 |
| 3 | Anomaly Bearing 1 | 99.66 | 99.46 | 99.75 | 98.08 |
| 4 | Anomaly WorkRoll 1 | 98.50 | 97.41 | 99.34 | 95.94 |
| 5 | Anomaly Electric 2 | 96.48 | 99.07 | 97.22 | 99.14 |
| 6 | Anomaly Bearing 2 | 99.28 | 98.04 | 99.86 | 99.62 |
| 7 | Anomaly WorkRoll 2 | 98.29 | 96.69 | 97.93 | 95.14 |
| 8 | Anomaly Electric 3 | 99.32 | 99.18 | 98.32 | 98.21 |
| 9 | Anomaly Bearing 3 | 99.61 | 99.75 | 99.69 | 96.33 |
| 10 | Anomaly WorkRoll 3 | 99.08 | 94.83 | 95.52 | 96.35 |
| 11 | Anomaly Electric 4 | 99.95 | 99.84 | 98.27 | 97.90 |
| 12 | Anomaly Bearing 4 | 99.73 | 99.35 | 99.73 | 99.36 |
| 13 | Anomaly WorkRoll 4 | 96.80 | 97.58 | 95.66 | 93.80 |
| 14 | Anomaly Electric 5 | 99.89 | 99.80 | 99.75 | 98.66 |
| 15 | Anomaly Bearing 5 | 99.26 | 98.52 | 99.61 | 99.72 |
| 16 | Anomaly WorkRoll 5 | 98.84 | 94.95 | 96.73 | 92.10 |
| Average | 98.47 | 97.80 | 98.34 | 96.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghasemkhani, B.; Kut, R.A.; Birant, D.; Yilmaz, R. Balanced Hoeffding Tree Forest (BHTF): A Novel Multi-Label Classification with Oversampling and Undersampling Techniques for Failure Mode Diagnosis in Predictive Maintenance. Mathematics 2025, 13, 3019. https://doi.org/10.3390/math13183019
Ghasemkhani B, Kut RA, Birant D, Yilmaz R. Balanced Hoeffding Tree Forest (BHTF): A Novel Multi-Label Classification with Oversampling and Undersampling Techniques for Failure Mode Diagnosis in Predictive Maintenance. Mathematics. 2025; 13(18):3019. https://doi.org/10.3390/math13183019
Chicago/Turabian StyleGhasemkhani, Bita, Recep Alp Kut, Derya Birant, and Reyat Yilmaz. 2025. "Balanced Hoeffding Tree Forest (BHTF): A Novel Multi-Label Classification with Oversampling and Undersampling Techniques for Failure Mode Diagnosis in Predictive Maintenance" Mathematics 13, no. 18: 3019. https://doi.org/10.3390/math13183019
APA StyleGhasemkhani, B., Kut, R. A., Birant, D., & Yilmaz, R. (2025). Balanced Hoeffding Tree Forest (BHTF): A Novel Multi-Label Classification with Oversampling and Undersampling Techniques for Failure Mode Diagnosis in Predictive Maintenance. Mathematics, 13(18), 3019. https://doi.org/10.3390/math13183019








