Abstract
Let objects be arranged in n rows with objects and one last row with m objects. The Janjić–Petković counting function denotes the number of -insets, defined as subsets containing objects such that at least one object is chosen from each of the first n rows, generalizing the binomial coefficient that is recovered for = … = = 1, as then only the last row matters. Here, we discuss two explicit forms, combinatorial interpretations, recursion relations, an integral representation, generating functions, convolutions, special cases, and inverse pairs of summation formulas. Based on one of the generating functions, we show that the Janjić–Petković counting function, like the binomial coefficients that it generalizes, may be regarded as a Riordan array, leading to additional identities. As an application to a physical system, we calculate the heat capacity of a many-body system for which the configurations are constrained as described by the Janjić–Petković counting function, resulting in a modified Schottky anomaly.
MSC:
05A10; 11B65
1. Introduction
Suppose that objects are arranged in n rows with objects and one last row with m objects. The Janjić–Petković counting function denotes the number of -insets, defined in this context as subsets containing objects such that at least one object is chosen from each of the first n rows, as in Figure 1. This function was introduced by Janjić in Ref. [1] and developed further in Refs. [2,3]. It reduces to the binomial coefficient for = … = = 1, as then k objects are chosen only from the m objects in the last row. Note that the order of the numbers does not matter in . By convention, = 0 for k < 0 or > . From the many properties and applications of presented in Refs. [1,2,3], we will start from the special case n = 1 (see (3) in [1], (6) in [2]),
and, for , the recursion relation (see (13) in [2])
Combinatorially, (1) means that, for n = 1, one chooses = out of a total of objects, of which the choices only from the last row do not count and are therefore subtracted. The combinatorial meaning of (2) was given in Ref. [2] and may be paraphrased as follows: in row n, let (1 ≤ ≤ ) be the index of the selected object with the highest index; then, objects remain to be selected, namely at least one object each from the first rows, as well as objects from the last row and the rest of row n, for which there are choices. Summing this over = = yields .
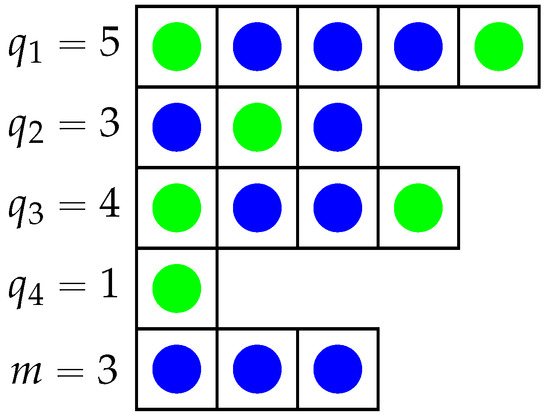
Figure 1.
Suppose that n + k objects are chosen from n = 4 rows with 5, 3, 4, 1 objects (from which at least one per row must be chosen) and from a last row with m = 3 objects—for example, for k = 2, we choose those in green but not those in blue. The number of choices is given by , which, for k = 0 … − n = 12, takes the values (see Section 6).
Below, we use (1) and (2) to establish several properties and applications related to . In Section 2, two explicit forms and an integral representation are obtained and checked against the recursion relations of Refs. [1,2]. In Section 3, a generating function appearing in [3] is obtained, leading to several convolution identities involving the number of partitions of m into parts from . In [2], the special set = was related to Euler’s pentagonal number theorem, which we extend in Section 4 to the case where this set contains gaps. Using the generating function from Section 3, in Section 5, further relations for are obtained by regarding it as a Riordan array. In Section 6, we obtain another type of generating function and use it to obtain inverse relations for a set of linear equations. Finally, in Section 7, the thermodynamic properties of a many-body system with restricted configurations as in are discussed, leading to a generalized Schottky anomaly in the heat capacity.
For brevity, similarly to [3], we write
Note also that, if a list Q has more than n elements, then, by convention, = , where are the first n elements of Q.
2. Explicit Forms, Row Extension, and Integral Representation
Proposition 1
(Explicit form). For integers , ,
Proof.
Combinatorially, the explicit form (4) can be understood in a similar fashion as (2): in each of the rows j = , let (1 ≤ ≤ ) be the index of the selected object with the highest index; then, k objects remain to be selected from the objects in the last row and the rest of the rows , for which there are choices. Summing this over all = = yields .
As mentioned at the beginning, is nonzero if ≥ . However, it should be noted that, if, as in (1) or (4), is expressed in terms of binomial coefficients, then some of them may not contribute because their upper argument is smaller than the lower one. For example, for n = 1, is nonzero if ≥ , but the second binomial coefficient in (1) is zero for k > m, which can happen for q > 1, e.g.,
From (4) follow several properties of that are known from Refs. [1,2], such as the special cases (see Section 1 in [2])
The recursion relation for the binomial coefficients,
when inserted in (4), leads to a similar relation for the generalized coefficients (see (9) in [2]):
Further recursion relations are obtained from (4) by exchanging the order of summations, such as (see (4) in [1], (10) in [2])
where the inner sum in the first line is a Chu–Vandermonde sum. For , we also have (see (16) in [1], (13) in [2])
where the inner sum in the first line is a Chu–Vandermonde sum with the first term missing, while (5) and (4) are used in the third line.
On the other hand, a different type of recursion relation is obtained from (4) if we add r objects to row n, i.e., if we increase by r.
Proposition 2
(Row extension). For integers , ,
Proof.
The combinatorial meaning of (14) is the following. One can first ignore the r additional objects in the extended row, which gives choices, and then select -insets considering only the r additional objects in row n (but grouping the other objects in this row with the m unrestricted objects in the last row), which gives an additional choices. In (15), the roles of and r are interchanged.
Proposition 3
(Integral representation). For integers , ,
Proof.
We use an integral representation of the binomial coefficients in (4),
and perform n geometric sums (setting = x ≠ 0),
which results in (18) after replacing x = . □
The integral representation (18) reduces to (19) for = … = = 1, in agreement with (8). Next, we use it to obtain a different type of explicit form of the counting function.
Proposition 4
(Alternative explicit form). For integers , ,
Proof.
We start from (18), abbreviate = x for the moment, and expand the binomials in the product,
after which we replace x = , integrate over t using (19), and arrive at (22). □
The combinatorial interpretation of (22) is straightforward: set = + 1 ≥ 1; for j = , select elements from the elements in row j; then, select the remaining (= ≥ 0) elements from the m elements in the last row.
3. Generating Function for a Fixed Number of Selected Objects and Convolutions with Partition Counts
The following generating function for a fixed number of selected objects appears as Theorem 1 in [3] with a proof by induction. Here, we provide a short alternative proof using the explicit representation (4).
Proposition 5
(Janjić: Generating functions for fixed number of selected objects ). For < 1 and integers , k ≥ ,
with the abbreviation s = ≥ 0.
Proof.
We use (4), omitting the initial terms in the sum for which the binomial coefficient vanishes,
where = , and
arriving at (24). □
As discussed in [3], the generating function (24) implies the connection of to , the number of partitions of the integer m into parts taken from [4]; by definition, = 0 for m < 0. These partitions are generated by the generating function ,
in the denominator of which the product appears, which characterizes the rows and appears in the numerator of . This relation suggests that we should eliminate this product from the two generating functions, providing convolutions of and .
Proposition 6
(Convolutions). For integers , k ≥ , and integer r ≥ 0,
Here, (29) is equivalent to [3] (Theorem 2).
Proof.
From (24) and (27), we have
and, taking the coefficients of in each of these, respectively, gives (28), which becomes (29) for r = 0, and (30), which becomes (31) for r = . □
4. Linearly Increasing Number of Objects per Row with Gaps and Connection to Pentagonal and Related Numbers
In this section, special sets of will be considered, namely the first n = entries (for integer N ≥ 1) of one of the following lists:
i.e., for integer r ≥ 4, there are repeating gaps in of missing entries on the list of consecutive integers (namely , …, ), while, for r = 2, each of the odd entries is once repeated. In other words, is a lacunary list of triples centered around multiples of r. For this set = , the first and last entries are thus = 1 and = , and the sum of all entries is
The reason for choosing from these lists is that their entries occur precisely in the power series exponents in a lacunary product identity (see (42) below) that generalizes Euler’s pentagonal number theorem, the connection of which to was already discussed in [3]. To derive this identity, we follow [5] and start from Jacobi’s triple product identity [4], which reads, for < 1 and v ≠ 0,
It reduces to the pentagonal number theorem for u = , v = , < 1,
which is well known for the cancellation of powers of x in the series and the fact it involves only coefficients . It may be regarded as the special case (r = 3) of the identity that follows from letting instead u = and v = in (40), with integer r ≥ 2,
For r ≥ 4, the factors with exponents , …, are absent in (42), resulting in a lacunary product, while, for r = 2, factors with odd powers occur twice,
and even more powers of x are cancelled in the series than in (41).
The cancellation of summands in the pentagonal number theorem requires an infinite product. If, instead, the product in (41) is finite, i.e., terminating with , then the expansion into a polynomial only agrees with the power series in (41) up to order , while, for exponents in the range to other than pentagonal numbers and coefficients other than , we have, e.g.,
and similar cases occur for truncated lacunary products (42).
However, the generating function (24) for our (i.e., by the first n = elements of ) gives us
provided that k ≥ = = . Before taking coefficients of for 0 ≤ i ≤ n, we replace the product on the right-hand side with (42), as the extra factors result in a difference only for higher exponents.
Proposition 7
(Linearly increasing number of objects per row with gaps). For the set = ⊂ with integers r ≥ 2, N ≥ 1, n = , k ≥ − n (see (39)), 0 ≤ i ≤ n,
Proof.
Equate the coefficients of on the left-hand side of (45) and right-hand side of (42). □
5. The Janjić–Petković Counting Function as a Riordan Array
As discussed above, the counting function is a generalization of the binomial coefficients . As shown in this section, the former may be regarded as a Riordan array, like the latter, which is also suggested the by the Pascal triangle analog (11) discussed in [2], as well as by the generating functions occurring in the previous two sections.
Let us first recall the essential properties of Riordan arrays [6,7,8], using slightly unconventional lettering (i.e., N, K, x instead of the usual n, k, t) for better compatibility with the notation used here for and its generating functions. An infinite lower triangular matrix with entries = and generating function
is called a Riordan array and denoted as , referring either to the matrix or the pair of formal power series. They form the Riordan group, so called because the matrix multiplication = of two Riordan arrays and gives again a Riordan array,
with the identity element given by unit array with ones on the diagonal as the only nonzero entries. A useful case corresponds to the matrix times vector, i.e., for a Riordan array ,
Furthermore, the matrix inverse is also a Riordan array,
where is the compositional inverse of , defined by x = = . The binomial coefficients are a well-known example of a Riordan array:
Let us now return to the counting function , which is found to fit within the Riordan array framework.
Proposition 8
(Janjić–Petković counting function as Riordan array). For integers ≥ 0, , we have the Riordan arrays
for fixed n and , with = = 0 if K > N. Furthermore,
Proof.
Setting N = and K = k in (24), we obtain a generating function of the form (47),
where we use the fact that = 0 for < to start the second summation at N = 0. This establishes (55) and (57). Then, (56) follows by applying (53), using the fact that the compositional inverse of = is = . Then, from (56), together with the generating functions (27) and (54), we have
and taking the coefficients yields (58). Then, (59) and (60) follow from (53),
upon inserting (57) and (58). □
The Riordan array property also entails the following inverse pair of summation formulas involving the counting function .
Proposition 9
(Inverse relations I). For fixed integers , the following sets of linear equations for two sequences and (for all N ≥ 0) are equivalent:
Proof.
The claim corresponds to = ⇔ = , which corresponds to (63). □
6. Generating Function for Fixed Number of Rows, Inverse Pair of Summation Formulas, and Restricted Power Set
The representation (4) also provides a generating function for a fixed number of rows.
Proposition 10
(Generating functions for fixed number of rows m). For integers , m ,
where the sum in fact terminates, i.e., 0 ≤ k ≤ .
Proof.
For x = 0, Equation (66) is trivially true (because n ≥ 1). Hence, we assume that x ≠ 0 and find from (4), using the summation (21),
establishing (66) for all x. □
For the example in Figure 1, we find from (66) that
the coefficients of which are listed in the figure caption.
The product appearing in (66) is reminiscent of the denominator of in (27). This is expressed in the following pair of summation formulas.
Proposition 11
(Inverse relations II). For fixed integers , the following sets of linear equations for two sequences and (for all k ≥ 0) are equivalent:
Proof.
In terms of the generating functions = and = , we have from (66)
Replacing x with , this is equivalent to
and the claim follows by taking the coefficients of . □
Note that, for = , the equivalence (69) reduces to the standard binomial inversion formula [9]
As a simple application, the total number of -insets, setting x = 1 in (66), is
Combinatorially, this means that, in each row, each object can either be selected or not, but zero objects must not be selected from any of the first n rows. Therefore, this restricted power set has fewer than the elements of the unrestricted power set.
7. Thermodynamic Properties of a Many-Body System with Janjić–Petković Interaction: A Generalized Schottky Anomaly
Statistical mechanics describes the macroscopic properties of many-body systems in thermodynamic equilibrium [10]. One of the simplest such systems is given by L noninteracting quantum particles, each of which may be in a state 0 or 1 with respective energies and , e.g., a collection of spins- with Zeeman coupling to a magnetic field. The Hamiltonian for such a system reads
where each number operator has eigenvalues 0 and 1. The canonical partition function at temperature T for this system, with the abbreviation = and the Boltzmann constant , is
where the trace is over all microstates. Here, the two types of summations correspond to either choosing each of the L particles to be in state 0 or 1 or alternatively choosing ℓ particles to be in state 0 and the remaining particles to be in state 0, for which there are possibilities. Although this is one of the most elementary thermodynamic model systems, it nevertheless has observable consequences, e.g., for the heat capacity , given by the derivative with respect to T of the average internal energy ,
which are both extensive in L. Here, and are the energy and heat capacity contributions of a single particle, respectively,
with the energy gap = . The specific heat = is shown in Figure 2. The maximum of as a function of T is known as the Schottky anomaly [10], a feature that is qualitatively different from the monotonous increase typical for continuum systems. It is due to the limited number of available states and is observed, e.g., in paramagnetic materials or materials with paramagnetic impurities.
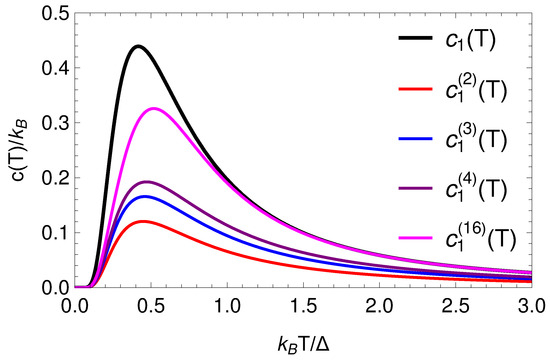
Figure 2.
Specific heat contributions and several of (79) and (85) as a function of T, each featuring a Schottky-like maximum, with approaching for large q.
Let us now consider a slightly different setting that will require use of the Janjić–Petković counting function. Suppose that we cannot freely choose ℓ out of L particles to have energy as before. Rather, the L particles are arranged into n groups (e.g., magnetic domains), each with size , and at least one particle must be in state 1 in each of these domains, e.g., because the particles are strongly (magnetically) interacting. We also suppose that there is a nonmagnetic domain of m = L− ≥ 0 particles that are not constrained in this way. The canonical partition function for a system with this Janjić–Petković interaction is then
which corresponds to a generating function for a fixed number of rows (66),
The average internal energy in this case can be written as
where the unconstrained magnetic domain of size m = contributes energy , while the constrained magnetic domains for each contribute energy , written in terms of an auxiliary function ; note that = 1. We then obtain, for the heat capacity of the constrained system,
where m = unconstrained contributions are supplemented by contributions for each . The functions are shown in Figure 2 for several q ≥ 2. They increase with q, with each featuring a Schottky-like maximum as a function of temperature T, expressing the restricted availability of states. Note that = 0, i.e., magnetic domains with = 1 must be in state 1 and thus cannot contribute to the heat capacity. On the other hand, we have = 1, as its argument lies in the interval 0 < x < 1 for T > 0; hence, approaches the unrestricted case , because the constraint becomes irrelevant in this limit.
Finally, let us illustrate the physical meaning of the generalized Schottky anomaly due to the terms in (84). Suppose, for this purpose, that there is no nonmagetic domain, m = L− = 0, and all = q are equal, so that L = with n ≥ 1 and q ≥ 2. In this case, = equals the specific heat of the system, i.e., we may regard as replacing if the system consists of n interacting domains of equal size .
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Janjić, M. An Enumerative Function. arXiv 2008, arXiv:0801.1976. [Google Scholar] [CrossRef]
- Janjic, M.; Petkovic, B. A Counting Function Generalizing Binomial Coefficients and Some Other Classes of Integers. J. Int. Seq. 2014, 17, 14.3.5. [Google Scholar]
- Janjić, M. A Generating Function for Numbers of Insets. J. Int. Seq. 2014, 17, 14.9.7. [Google Scholar]
- Andrews, G.E. The Theory of Partitions; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Generalizations of the Pentagonal Number Theorem, Mathematics Stack Exchange. 2017. Available online: https://math.stackexchange.com/questions/1477145/generalizations-of-the-pentagonal-number-theorem (accessed on 21 May 2025).
- Shapiro, L.W.; Getu, S.; Woan, W.J.; Woodson, L.C. The Riordan group. Discret. Appl. Math. 1991, 34, 229. [Google Scholar] [CrossRef]
- Sprugnoli, R. Riordan arrays and combinatorial sums. Discret. Math. 1994, 132, 267. [Google Scholar] [CrossRef]
- Merlini, D.; Rogers, D.G.; Sprugnoli, R.; Verri, M.C. On some alternative characterizations of Riordan arrays. Can. J. Math. 1997, 49, 301. [Google Scholar] [CrossRef]
- Riordan, J. Inverse Relations and Combinatorial Identities. Am. Math. Mon. 1964, 71, 485. [Google Scholar] [CrossRef]
- Kittel, C.; Kroemer, H. Thermal Physics, 2nd ed.; Bedford: New York, NY, USA, 1980. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).