Abstract
This paper investigates the use of Riordan arrays in the enumeration and transformation of lattice paths through a combinatorial framework of promotion. We demonstrate how Dyck paths can be promoted to generalised Motzkin and Schröder paths via two key transformations: the Binomial and Chebyshev transforms, each associated with specific Riordan arrays. These promotions yield classical integer sequences and continued fraction representations that enumerate weighted lattice paths. The framework is further extended to analyse grand paths, which are permitted to cross below the x-axis. We develop constructive bijections establishing explicit correspondences between promoted path families. The promotion framework offers new insights into known integer sequences and enables a unified approach to the generalisation and classification of lattice paths.
MSC:
05A15; 05A19
1. Introduction
Riordan arrays and lattice paths provide a unifying framework for studying and counting combinatorial structures. Riordan arrays, formally introduced in 1991 by Shapiro et al., are infinite, lower-triangular matrices defined by pairs of generating functions, originally used to generalise properties of Pascal’s triangle [1]. Lattice paths have played a central role in combinatorics since the 1960’s [2], where they have been approached through analytical techniques (e.g., the kernel method), probabilistic methods, and algebraic tools such as Riordan arrays, where many connections have been established. Here the aim is to further deepen these connections by using Riordan array theory to enable the enumeration of broader path families, particularly focusing on the framework of promotion. In this paper, the term promotion refers to the action of a Riordan array on lattice paths, whereby the array systematically alters the step set and weights of the paths. This approach provides a structured way to derive new enumerative results and uncover hidden bijections between seemingly unrelated path families. A key tool in this study is the use of Riordan transforms, particularly the Binomial transform [3], which corresponds to the action of the Riordan array known as the Binomial matrix on a generating function. Similarly, we refer to the Riordan matrix as the Chebyshev transform. These transformations enable the systematic “promotion” of simple paths (e.g., Dyck paths) to more complex ones (e.g., Motzkin or Schröder paths), and they play a central role in the framework developed here.
The key contributions of this paper are as follows:
- 1.
- Developing a generalised framework that extends classical paths to broader families using Riordan arrays.
- 2.
- Deriving new enumerative results for these path families, including explicit generating functions and recurrence relations.
- 3.
- Uncovering bijections between paths with different step sets and boundary conditions, revealing previously unnoticed combinatorial correspondences.
This expanded framework enriches our understanding of Riordan arrays and lattice paths. The promotion of simpler paths, such as Dyck paths, to Motzkin or Schröder paths via Riordan arrays is motivated by both theoretical and practical considerations. Riordan array transformations enable the derivation of new enumerative results. Practically, such paths appear in diverse areas such as coding theory, computational biology (e.g., RNA secondary structures) and, more recently, solutions to a variety of polymer models of absorption.
1.1. Preliminaries
1.1.1. Riordan Arrays
Riordan arrays [1,4,5] are defined by a pair of power series, drawn from two relevant subsets of the set of power series. These power series can be over a suitable ring that allows for the operations that are particular to the context of the problem at hand. In analytic contexts the coefficient ring is often taken as . In combinatorial settings, the ring of integers is often sufficient. Thus, we let
be the set of power series with a non-zero constant term. Elements are thus invertible, that is, we can talk about the reciprocal . We also define
Elements then possess a compositional inverse , which satisfies and . Thus is the solution of the equation that satisfies . Note that as a formal power series, in this case just means that the constant term of the power series is zero. Elements in are composable. Thus, if , we can talk about the power series . By a Riordan array, we mean a pair . Each such pair has a matrix representation given by
where is the functional that extracts the coefficient of in a power series. The set of Riordan arrays forms a group for the operations
and
In the matrix representation, these expressions correspond to matrix multiplication and the matrix inverse. The identity element is since, with that, we have .
As seen in the group product above, the operation of a Riordan array on a power series is given by
We call this the fundamental theorem of Riordan arrays. In the matrix representation, it corresponds to multiplying the vector whose elements are by the matrix .
A subgroup of interest in this paper is the Bell subgroup. The Bell subgroup of the Riordan group is composed of elements of the form .
Example 1.
The Binomial matrix is given by the element of the Bell subgroup as
We refer to the effect of the Riordan array on a power series as the Binomial transform of the series. Note that . A second element of interest of the Bell subgroup is . We calculate that general term of the second array . We obtain
Now this gives the matrix with first few entries
We let be the generating function of the sequence . Then, the generating function
expands to give the sequence with the general term
The Chebyshev polynomials of the second kind can be expressed as . The coefficient structure in this expansion closely mirrors that generated by the Riordan array For this reason, throughout this paper, we refer to the action of this array on a sequence as the Chebyshev transform, emphasising the connection with the combinatorial structure underlying the Chebyshev polynomials. Note that
1.1.2. Lattice Paths
In what follows are the definitions and notations that can be found in [6,7]. Meanwhile, known sequences of integers in this note will be referred to by their On-Line Encyclopedia of Integer Sequences (OEIS) numbers [8]. A step set is a finite set of vectors . An n-step lattice path or walk is a sequence of vectors such that is in S. Geometrically, it is a set of points , where and for . The elements of S are called steps or jumps. The length of a lattice path is its number of jumps. Here we introduce the paths we will meet throughout this paper and present their enumerations using Riordan arrays. Motzkin paths with step set that begin at , end at and remain in the first quadrant are enumerated by the well known Motzkin numbers, (OEIS A001006), and satisfy the recurrence
The Motzkin numbers can also be expressed in closed form as , where is the n-th Catalan number. This expression translates the fact that the Motzkin numbers are the Binomial transform of the aerated Catalan numbers (i.e., recall that the aerated sequence is formed by inserting a zero between each pair of Catalan numbers: ). Now, using Riordan arrays, we can express the result as follows:
which is the generating function of the Motzkin numbers, and is the generating function of the Catalan numbers. Thus, the above binomial expression suggests that Dyck paths are “promoted” to full Motzkin paths by the Binomial matrix. Note that Dyck paths with step set that begin at , end at and remain in the first quadrant are enumerated by the Catalan numbers (OEIS A000108) and satisfy the recurrence
The Catalan numbers can also be expressed in closed form as
Motzkin paths with step set that begin at , end at and are not constrained to the first quadrant are known as grand Motzkin paths and are enumerated by the central trinomial numbers (OEIS A002426), with
That is, is given by the Binomial transform of the aerated central binomial coefficients. In terms of generating functions and Riordan arrays, we have
which is the generating function of the trinomial numbers. Note that Dyck paths with step set that begin at , end at and do not have to remain in the first quadrant are enumerated by the aerated central binomial numbers and are known as grand Dyck paths, so, again, we have the notion of promotion by the Binomial matrix. Schröder paths with step set that begin at , end at and remain in the first quadrant are enumerated by the large Schröder numbers (OEIS A006318) governed by the recurrence
A closed form expression for the large Schröder numbers is , where Paths with step set that begin at , end at and remain in the first quadrant are known as Motzkin–Schröder paths [9]. Note that these paths have also been referred to in the literature as 2-Motzkin paths, but this term has been also used to describe Motzkin paths with two types of horizontal steps [10,11]. These paths have also been called 2-generalised Motzkin paths [12]. To avoid confusion, the term Motzkin–Schröder path is used in this paper. Removing the restriction to remain in the first quadrant gives grand Motzkin–Schröder paths. The notion of weighted Motzkin paths was first introduced by P. Flajolet in [13] and has been widely used in the literature related to Motzkin paths. In particular, the study of lattice path colourings is viewed as an assignment of weights on each step of a path; such a connection can be seen in some papers in enumerative and bijective combinatorics [9,11,14,15]. The following fundamental result shows the connection between weighted Motzkin paths and continued fractions.
Theorem 1
([13,16]). Let
where the sum is over the set of Motzkin paths of length n. Here, is the level after the step and the valuation of a path is the product of valuations of its steps , where
Then, the generating function
has the Jacobi type continued fraction (J-fraction) expansion (see [17]).
Consequently, the above theorem can be extended to Schröder paths. The proof of this corollary follows from the symbolic method [18] applied to the step set .
Corollary 1.
Suppose that
where is the collection of Schröder paths of semilength n and having the valuation , defined as follows:
Then, the generating function
has the Thron type continued fraction (T-fraction) expansion.
In the generating function above, we can change and into and x, respectively, without ill effect.
We end this section by introducing a result concerning coloured (or weighted) Motzkin–Schröder paths.
Proposition 1
([9]). The number of Motzkin–Schröder paths of length n, where the horizontal steps can be of r colours, the horizontal steps can be of s colours and the up steps can be of t colours, is given by the following recurrence:
2. Promotion of Lattice Paths
2.1. Promotion of a Family of Paths Restricted to the First Quadrant
We motivate this section first with the following example.
Example 2.
The Motzkin–Schröder paths are enumerated by the sequence (OEIS A128720) which begins
Expressing the related generating function using Riordan arrays, we have
The sequence OEIS A128720 has its general term given by . From a path construction perspective, the Chebyshev transform is inducing the ‘Schröder’ step in the paths. The first few rows of the matrices expand as follows:
We note that these paths can also be constructed from a double promotion of the aerated Catalan numbers as we have the following expression for the generating function.
Here we see two stages of promotion: Dyck paths to Motzkin, the promotion via the Binomial transform inducing a level step, and Motzkin to Motzkin–Schröder, the Chebyshev transform inducing a ‘Schröder’ step.
We introduced two promotion-based Riordan arrays above. In the following sections, we generalise these promotions to a broader class of generating functions and examine the resulting bijections between associated lattice path families.
2.1.1. Binomial Transform Promotions
The following proposition establishes the connection between promotion via the Binomial transform and generalised Motzkin paths.
Proposition 2.
The -Binomial transform of the generating function that enumerates Dyck paths with α-weighted steps enumerates Motzkin paths with β-weighted steps and α-weighted steps.
Proof.
The generating function for Dyck paths with -weighted steps is Applying the -Binomial transform gives
The Binomial transform adds -weighted steps, promoting Dyck paths to Motzkin paths. The generating function has continued fraction expansion.
□
The J-fraction in Theorem 1, Equation (1) has a well-known connection to lattice paths. The resulting sequences for various and are listed below, with OEIS references where available.
Example 3.
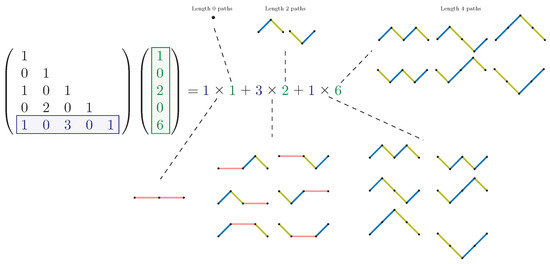
For and , the promotion construction is expanded below. The matrix shows the first few entries of the Binomial transform Riordan array .
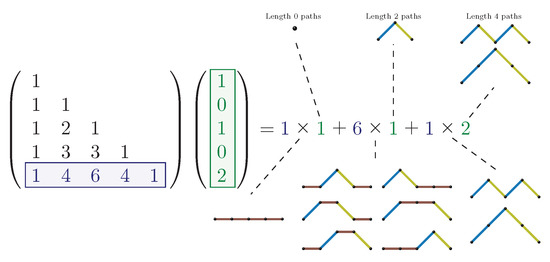
The entry of the vector represents the number of Dyck paths of length n. These paths are promoted to Motzkin paths via the Binomial transform. The coloured lattice paths on the right illustrate the construction of the nine Motzkin paths of length 4 through the promotion of Dyck paths via the Binomial transform.
- 1.
- The one Dyck path of length 0 is promoted to Motzkin by adding four horizontal steps.
- 2.
- The one Dyck path of length 2 is promoted to Motzkin by adding two horizontal steps that are uniquely placed to make six distinct Motzkin paths.
- 3.
- The two Dyck paths of length 4 remain unchanged.
2.1.2. Bijections Arising from the Path Classifications in Table 1
We consider three types of walks confined to the first quadrant of , all starting at . In the case where and in Table 1, the sequence expansion corresponds to the aerated Schröder numbers. In this subsection, we introduce three distinct families of lattice paths that are enumerated by this generating function. We then present explicit, constructive bijections between these path classes.
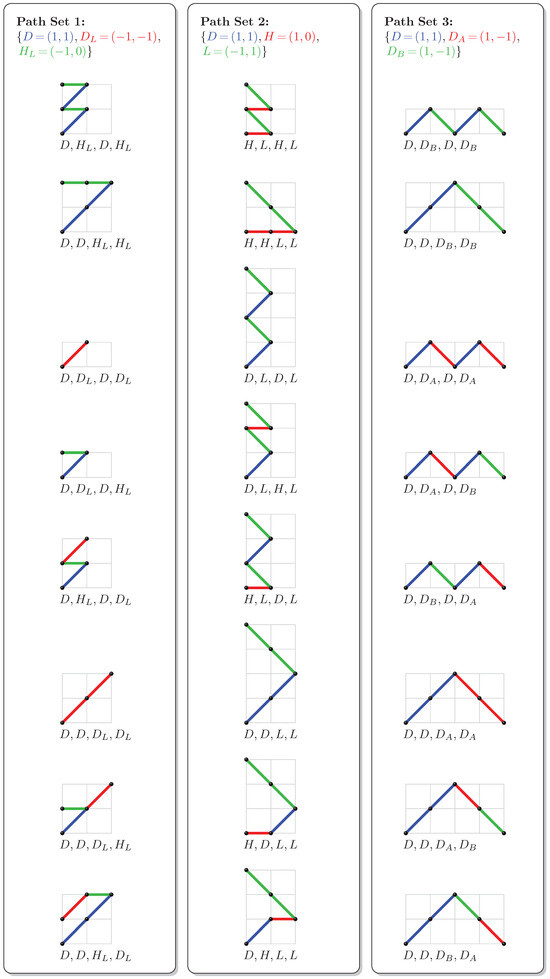
- 1.
- Path 1: Starts at ; ends on the y-axis. Step set: . There are two choices , for returning to the y-axis and one step for leaving the y-axis.
- 2.
- Path 2: Starts at ; ends on the y-axis. Step set: . There are two steps , for leaving the y-axis and one step for returning to the y-axis.
- 3.
- Path 3: Starts at ; ends on the x-axis. Step set: . There are two coloured steps for returning to the x-axis and one step for leaving the x-axis.

Table 1.
Sequences indexed by parameters and of the generating function in Equation (4).
Table 1.
Sequences indexed by parameters and of the generating function in Equation (4).
| Sequence Expansion | OEIS ID | Note | ||
|---|---|---|---|---|
| 1 | 0 | A000108 | Aerated (zeros between terms) | |
| 1 | 1 | A001006 | ||
| 1 | 2 | A000108 | Excludes the initial term | |
| 2 | 0 | A151374 | Aerated | |
| 2 | 1 | A025235 | ||
| 2 | 2 | A071356 |
Example 4.
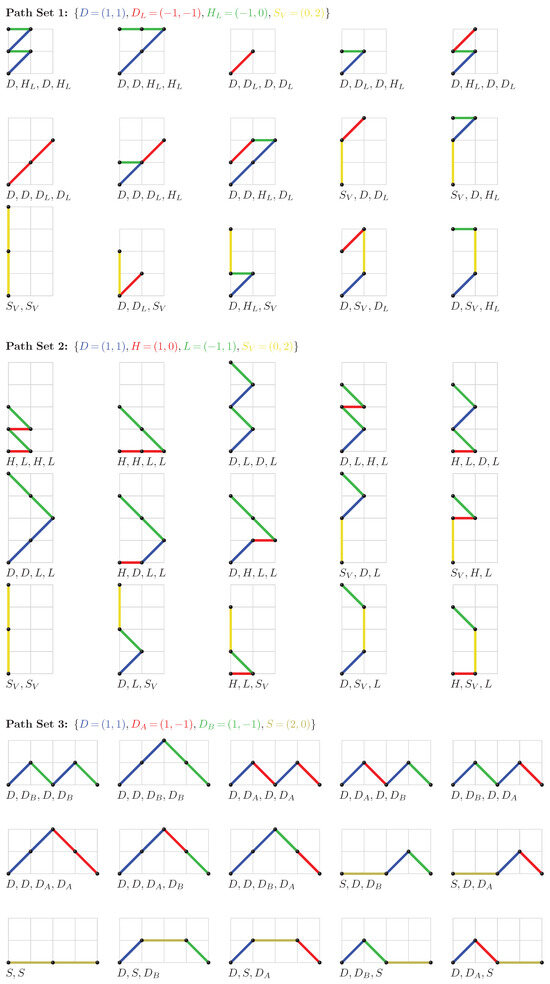
For , the eight paths for paths 1, 2 and 3 as defined above are drawn below.
2.1.3. Constructive Bijection Between Paths 1, 2 and 3
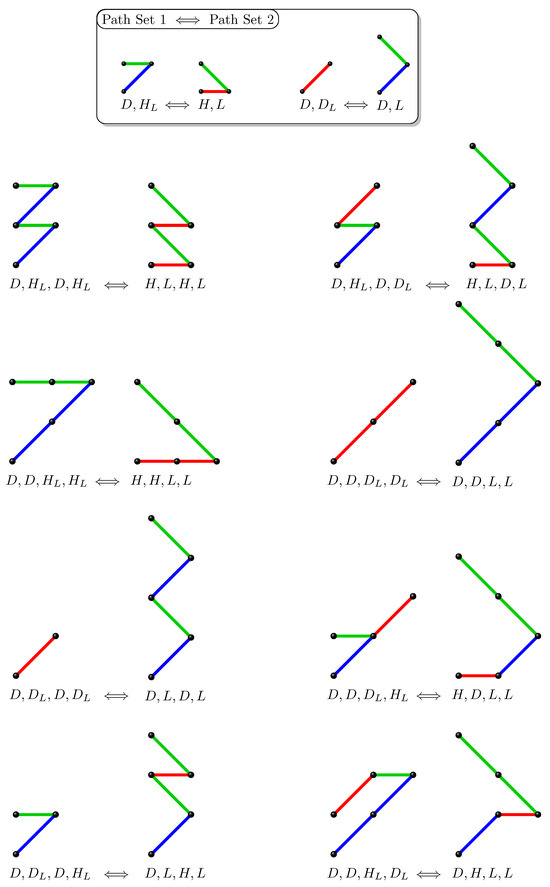
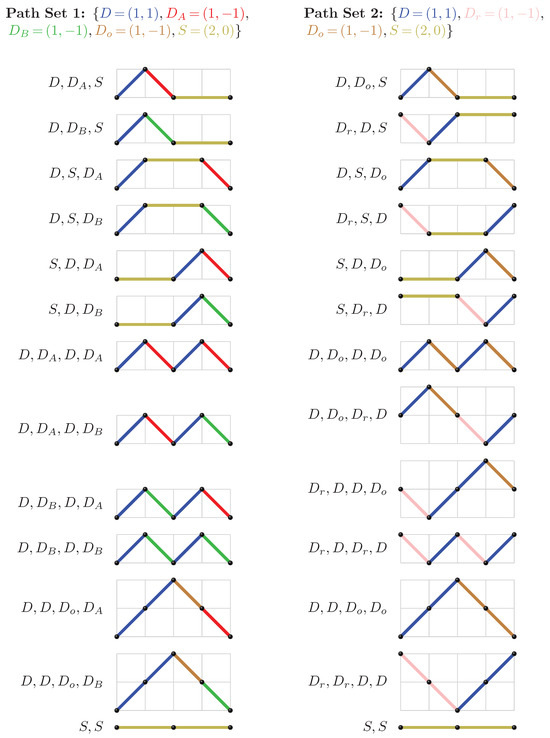
We define a bijection between paths 1 and 2 by reinterpreting their step types as follows.
- In path 1 the steps are defined as , and .
- In path 2 the steps are defined as , and .
The mapping between these step types defines the bijection. Bijective steps are shown below, accompanied by an illustrative example for .
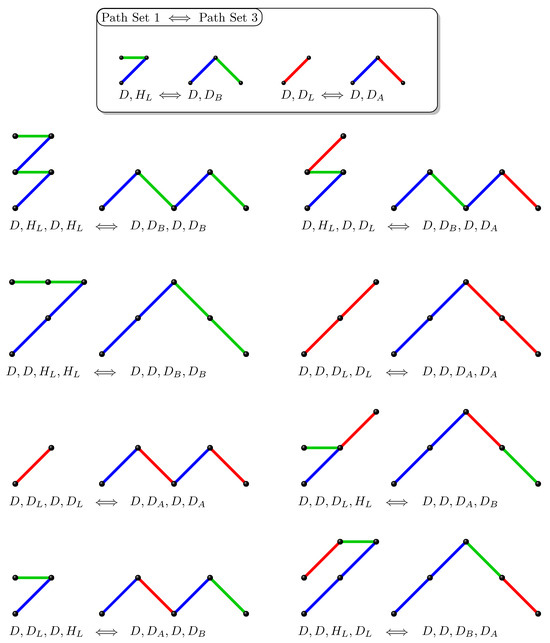
We also define a bijection between paths 1 and 3, again by reinterpreting their step types as follows:
- In path 1 the steps are defined as , and .
- In Path 3 the steps are defined as and , where and are two differently coloured steps representing a weighting of 2.
Once again, the mapping between these step types defines the bijection. Bijective steps are again shown below, accompanied by an illustrative example for .
Both substitutions preserve the overall step count and establish a one-to-one correspondence, mapping Path 1 to Path 2 and Path 1 to Path 3. To complete the triangle of bijections, we leave it to the reader to construct an analogous bijection between Paths 2 and 3.
2.1.4. Promotion and Extended Bijections
The notion of promotion can be now applied to the bijective framework as described above to extend the step set of paths 1, 2 and 3.
Under the Binomial transform promotion, paths 1 and 2 are extended by the inclusion of a vertical step. The resulting promoted step sets are
- 1.
- Path 1: ;
- 2.
- Path 2: .
This now yields a bijection between the promoted path 1 and path 2 families and the family of Motzkin paths featuring two types of weighted steps. The explicit construction of this bijection is omitted, as it follows naturally from the earlier bijections. We now generalise this construction in the following corollary:
Corollary 2.
Let the paths start at , end on the y-axis and use either of the following step sets:
where the vertical step occurs with weight β. Then, the generating function for the paths is given by
This generating function also enumerates Motzkin paths of length n starting at and ending on the x-axis, with step set , where each step is weighted (or 2-coloured) with weight 2 and each step is weighted with weight β (or β-coloured).
Note that for , path 2 corresponds to the class of paths studied in [19], as they generalise the Delannoy paths. OEIS references for the generating function with values are listed in Table 1.
2.1.5. Chebyshev Transform Promotions
The following proposition establishes the connection between promotion via the Chebyshev transform and generalised Schröder paths.
Proposition 3.
The Chebyshev transform of the generating function that enumerates Dyck paths with α-weighted steps enumerates Schröder paths with β-weighted steps and α-weighted steps.
Proof.
The generating function for Dyck paths with -weighted steps is Applying the -Chebyshev transform gives
The Chebyshev transform adds -weighted steps, promoting Dyck paths to Schröder paths. The generating function has continued fraction expansion.
□
The generalised Chebyshev transform introduces a -weighted Schröder step to Dyck paths with -weighted steps. Here we see the T-fraction with a well known connection to lattice paths. The continued fraction above precisely coincides with that in Corollary 1, Equation (2). Some of the sequences are tabulated below for various values of and , with the OEIS reference of the sequence listed.
Example 5.
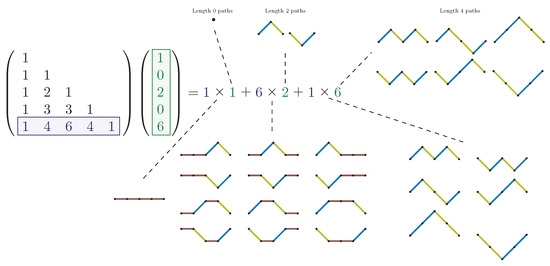
For and (as shown in Table 2), the promotion construction is expanded below. The matrix below shows the first few entries of the Chebyshev transform Riordan array .
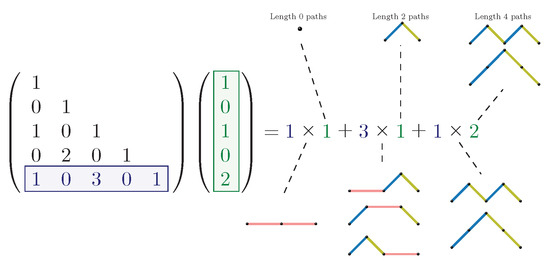

Table 2.
Sequences indexed by parameters and of the generating function in Equation (5).
Table 2.
Sequences indexed by parameters and of the generating function in Equation (5).
| Sequence Expansion | OEIS ID | Note | ||
|---|---|---|---|---|
| 1 | 0 | A000108 | Aerated Catalan numbers | |
| 1 | 1 | A006318 | Aerated Schröder numbers | |
| 1 | 2 | A047891 | Aerated | |
| 2 | 0 | A151374 | Aerated | |
| 2 | 1 | A103210 | Aerated | |
| 2 | 2 | A156017 | Aerated |
The entry of the vector represents the number of Dyck paths of length n. These paths are promoted to Schröder paths via the Chebyshev transform. The coloured lattice paths on the right illustrate the construction of the six Schröder paths of length 4 through the promotion of Dyck paths via the Chebyshev transform.
- 1.
- The one Dyck path of length 0 is promoted to Schröder by adding two horizontal steps.
- 2.
- The one Dyck path of length 2 is promoted to Motzkin by adding one horizontal step that is uniquely placed to make three distinct Schröder paths.
- 3.
- The two Dyck paths of length 4 remain unchanged.
Previously, we observed that the Binomial transform promotion introduces level steps of length 1. Here we see the Chebyshev transform promotion inducing Schröder steps or level steps of length 2. Importantly, the bijections established under the Binomial transform promotion remain valid under the Chebyshev transform also. This observation leads to the following result.
Corollary 3.
Let the paths start at , end on the y-axis and use either of the following step sets:
where the vertical step occurs with weight β. Then, the generating function for the paths is given by
This generating function also enumerates Schröder paths of length , starting at and ending on the x-axis, with step set , where each step is weighted (or 2-coloured) with weight 2 and each step is weighted with weight β (or β-coloured).
Before proceeding, we illustrate each of the path types with an example of length .
Example 6.
For , we have the following paths:
2.2. Promotion of a Family of Paths Unrestricted When Crossing the X-Axis
In this section, we extend our study to include paths that are permitted to cross below the x-axis. By relaxing this constraint, we observe new types of promotions and structural behaviour in the resulting path families. As before, we begin with a motivating example to illustrate the key ideas and once again introduce the two promotion Riordan matrices.
Example 7.
The grand Motzkin–Schröder paths are enumerated by the sequence (OEIS A059345) which begins
The generating function of the grand Motzkin–Schröder paths can be expressed as follows.
The sequence OEIS A059345 has its general term given by . As seen in the last section, the Chebyshev matrix induces the ‘Schröder’ step in the paths. The first few rows of the matrices expand as follows. These are known generating functions of OEIS A059345.
Once again we can decompose into the promotion matrices as follows:
In particular, we see that the general term of the sequence OEIS A059345 may be expressed as .
2.2.1. Binomial Transform Promotions
The following proposition establishes the connection between the Binomial transform and generalised grand Motzkin paths.
Proposition 4.
The -Binomial transform of the generating function that enumerates grand Dyck paths with α-weighted steps enumerates grand Motzkin paths with β-weighted steps and α-weighted steps.
Proof.
The generating function for grand Dyck paths with -weighted steps is Applying the -Binomial transform gives
The Binomial transform adds -weighted steps, promoting grand Dyck paths to grand Motzkin paths. □
Sequences are tabulated in Table 3 for various values of and , with the OEIS reference of the sequence listed.

Table 3.
Sequences indexed by parameters and of the generating function in Equation (6).
Example 8.
For for ; the promotion construction is expanded below.
The matrix above shows the first few entries of the Binomial transform seen previously in Example (3) in Section 2.1.1. The entry of the vector represents the number of grand Dyck paths of length n. These paths are promoted to grand Motzkin paths via the Binomial transform. The coloured lattice paths on the right illustrate the construction of the 19 grand Motzkin paths of length 4 through the promotion of grand Dyck paths via the Binomial transform.
- 1.
- The one grand Dyck path of length 0 is promoted to grand Motzkin by adding four horizontal steps.
- 2.
- The two grand Dyck paths of length 2 are promoted to grand Motzkin by adding two horizontal steps. For each of these grand Dyck paths, adding two horizontal steps gives six different choices of paths.
- 3.
- The six Dyck paths of length 4 remain unchanged.
2.2.2. Bijections Arising from the Path Classifications in Table 3
Note that the table above reveals a bijection between grand Motzkin paths with weighted steps and , and Motzkin paths constrained to remain above the x-axis, where all steps are weighted by and , except for the steps that return to the x-axis, which are assigned a weight of . We begin with the continued fraction corresponding to paths where each return to the x-axis via a step is given weight , while all other steps are given weight .
From Proposition 2, we have the generating function for Motzkin-type paths with uniform weight on down steps and on horizontal steps.
Substituting (8) into (7), we obtain
This corresponds to the generating function of grand Motzkin paths with uniform weights and , as shown in Proposition 4.
2.2.3. Constructive Bijection Between Restricted and Unrestricted Motzkin Paths
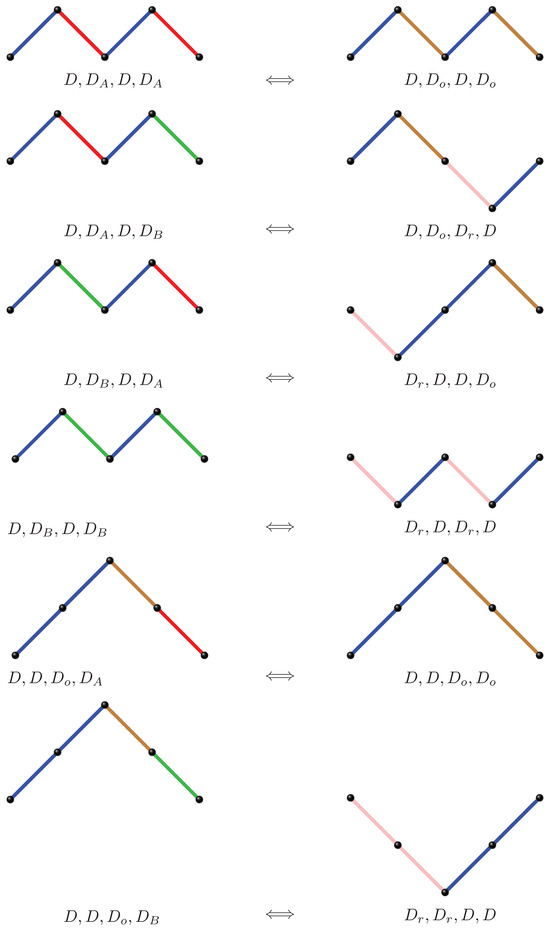
Let a path start at with step set , where every step returning to the x-axis has a weight of , while all other steps have weight . We construct a bijection between this set of weighted paths and a family of reflected paths using the same step set, where all steps returning to the x-axis are uniformly weighted by .
- 1.
- Single return to the x-axis.A path that returns to the x-axis exactly once has a single, nontrivial reflection: its mirror image across the x-axis. If the return step is weighted , both the original and the reflected path contribute weight , assigning weight to this step in the restricted paths.
- 2.
- Multiple returns to the x-axis.If the path returns to the x-axis n times, it naturally decomposes into n excursions. Each excursion can be independently reflected about the x-axis, producing distinct path variants corresponding to the weighting for the steps returning to the x-axis in the restricted paths.
Example 9.
For , we illustrate the bijection between the six paths of length 4 shown below.
2.2.4. Chebyshev Transform Promotions
The following proposition establishes the connection between promotion via the Chebyshev transform and generalised grand Schröder paths.
Proposition 5.
The Chebyshev transform of the generating function that enumerates grand Dyck paths with α-weighted steps enumerates grand Schröder paths with β-weighted steps and α-weighted steps.
Proof.
The generating function for grand Dyck paths with -weighted steps is Applying the -Chebyshev transform gives
The Chebyshev transform adds -weighted steps, promoting grand Dyck paths to grand Schröder paths. □
Table 4 highlights some of the sequences on the OEIS for values of and

Table 4.
Sequences indexed by parameters and of the generating function in Equation (10).
Note that many of the OEIS references listed in Table 4 pertain to Delannoy numbers or paths. In particular, the central Delannoy paths are lattice paths from to using the step set . These paths are structurally equivalent to grand Schröder paths, differing only in their terminal point: central Delannoy paths end at , whereas grand Schröder paths typically return to the x-axis.
Example 10.
For and , the promotion construction is expanded below. The
- 1.
- The one grand Dyck path of length 0 is promoted to grand Schröder by adding two horizontal steps.
- 2.
- The two grand Dyck paths of length 2 are promoted to grand Schröder by adding one horizontal step. For each of these grand Dyck paths, the horizontal step is uniquely placed to make three distinct grand Schröder paths.
- 3.
- The six Dyck paths of length 4 remain unchanged.
Similarly to the promotion of generalised grand Dyck paths under the Binomial transform promotion, here, we have a bijection between grand Schröder paths with weighted steps and and Schröder paths constrained to remain above the x-axis, where all steps are weighted by and , except for the steps that return to the x-axis, which are assigned a weight of . We begin with the continued fraction corresponding to paths where each return to the x-axis via a step given weight , while all other steps are given weight .
From Proposition 3, we have the generating function for generalised Schröder paths with uniform weight on down-steps and on horizontal steps.
Substituting (12) into (11), we obtain
This corresponds to the generating function of grand Schröder paths, i.e., Schröder paths allowed to cross below the x-axis, with uniform weights and as shown in Proposition 5. We illustrate each of the path types with an example of length .
Example 11.
For , and , the 13 paths for restricted and unrestricted Schröder paths are drawn below.
3. Discussion
The results presented in this paper highlight the role of Riordan arrays in the enumeration of lattice paths. By applying the Binomial and Chebyshev transforms as forms of promotion, we are able to reinterpret classical lattice path families such as Dyck, Motzkin and Schröder paths within a coherent framework. The notion of promotion introduced in this work builds upon earlier studies in enumerative combinatorics, particularly those involving weighted paths, continued fractions (e.g., Flajolet [13]), and Riordan group theory (e.g., Shapiro et al. [1,4]). The main contributions are as follows:
- Formalisation of promotion as the action of Riordan arrays on generating functions for restricted paths.
- Demonstration that the Binomial transform promotes Dyck paths to Motzkin paths and the Chebyshev transform promotes Dyck paths to Schröder paths.
- Derivation of generalised generating functions for these promoted paths.
- Introduction of bijective constructions linking promoted paths to other path sets found in the literature.
- Extension of the framework to unrestricted path families and construction of a bijection between restricted and unrestricted paths.
These findings demonstrate that Riordan arrays offer a unifying framework for deriving and interpreting families of lattice paths. This suggests that Riordan array promotions can serve as a foundation for further exploration, particularly in discovering new transforms applicable to a broader range of path families.
Author Contributions
Conceptualization, A.H. and P.B.; methodology, A.H.; formal analysis, A.H.; writing—original draft preparation, A.H.; writing—review and editing, A.H., K.M. and N.G.; visualization, K.M.; student support, N.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shapiro, L.W.; Getu, S.; Woan, W.J.; Woodson, L.C. The Riordan group. Discr. Appl. Math. 1991, 34, 229–239. [Google Scholar] [CrossRef]
- Humphreys, K. A history and a survey of lattice path enumeration. J. Stat. Plan. Inference 2010, 140, 2237–2254. [Google Scholar] [CrossRef]
- Barry, P. Riordan Arrays, the A-Matrix, and Somos 4 Sequences. arXiv 2019, arXiv:1912.01126. [Google Scholar]
- Shapiro, L.W.; Sprugnoli, R.; Barry, P.; Cheon, G.-S.; He, T.-X.; Merlini, D.; Wang, W. The Riordan Group and Applications; Springer: Cham, Switzerland, 2022; pp. 47–57. [Google Scholar]
- Barry, P. Riordan Arrays: A Primer, 2nd ed.; Logic Press: Kildare, Ireland, 2022; pp. 95–117. [Google Scholar]
- Lackner, M.-L.; Wallner, L. An Invitation to Analytic Combinatorics and Lattice Path Counting; Lecture Notes of a Mini-Course Held at the ALEA in Europe Young Researchers’ Workshop; University of Bath: Bath, UK, 2015; Available online: https://dmg.tuwien.ac.at/mwallner/files/lpintro.pdf (accessed on 4 February 2025).
- Stanley, R.P. Enumerative Combinatorics, Volume 1, 2nd ed.; Cambridge University Press: New York, NY, USA, 2012; p. 21. [Google Scholar]
- Sloane, N.J.A. The On-Line Encyclopedia of Integer Sequences. Available online: http://oeis.org (accessed on 14 April 2025).
- Barry, P. On Motzkin-Schröder paths, Riordan arrays, and Somos-4 Sequences. J. Integer Seq. 2023, 26, 23.4.7. [Google Scholar]
- Chen, W.Y.C.; Yan, S.H.F.; Yang, L.L.M. Weighted 2-Motzkin paths. arXiv 2004, arXiv:math/0410200. [Google Scholar]
- Deutsch, E.; Shapiro, L.W. A bijection between ordered trees and 2-Motzkin paths and its many consequences. Discret. Math. 2002, 256, 655–770. [Google Scholar] [CrossRef]
- Ramirez, J.L. The Pascal rhombus and the generalised grand Motzkin paths. J. Fibonacci Quart. 2015, 54, 99–104. [Google Scholar] [CrossRef]
- Flajolet, P. Combinatorial aspects of continued fractions. Discret. Math. 1980, 32, 125–161. [Google Scholar] [CrossRef]
- Merlini, D.; Sprugnoli, R. The relevant prefixes of coloured Motzkin walks: An average case analysis. Theor. Comput. Sci. 2010, 411, 148–163. [Google Scholar] [CrossRef][Green Version]
- Yang, L.; Yang, S.-L. Riordan arrays, Łukasiewicz paths and Narayana polynomials. Linear Algebra Appl. 2021, 622, 1–18. [Google Scholar] [CrossRef]
- Viennot, X.G. Introduction to Chapter 3 on Continued Fractions; Version 6; LaBRI, CNRS, Université de Bordeaux. 2013. Available online: https://www.viennot.org/abjc4-ch3.html (accessed on 20 November 2024).
- Wall, H.S. Analytic Theory of Continued Fractions; AMS Chelsea Publishing: New York, NY, USA, 2000; pp. 192–213. [Google Scholar]
- Flajolet, P.; Sedgewick, R. Analytic Combinatorics; Cambridge University Press: Cambridge, UK, 2009; pp. 15–94. [Google Scholar]
- Dziemiańczuk, M. Counting lattice paths with four types of steps. Graphs Comb. 2014, 30, 1427–1452. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).