A Banach Space Leap: Contraction Mapping Solutions for Stochastic Delay Systems

Abstract

We investigate the solvability and stability properties of a class of nonlinear stochastic delay differential equations (SDDEs) driven by Wiener noise and incorporating discrete time delays. The equations are formulated within a Banach space of continuous, adapted sample paths. Under standard Lipschitz and linear growth conditions, we construct a solution operator and prove the existence and uniqueness of strong solutions using a fixed-point argument. Furthermore, we derive exponential mean-square stability via Lyapunov-type techniques and delay-dependent inequalities. This framework provides a unified and flexible approach to SDDE analysis that departs from traditional Hilbert space or semigroup-based methods. We explore a Banach space fixed-point approach to SDDEs with multiplicative noise and discrete delays, providing a novel functional-analytic framework for examining solvability and stability.

1. Introduction

Stochastic delay differential equations (SDDEs) have been studied since the 1970s, arising from advances in stochastic calculus and the need to model systems affected by both randomness and memory effects. Recent work has also addressed stability and existence for related classes of functional and stochastic differential systems, often using iterative schemes or fixed-point techniques in fractional or stochastic settings [1,2,3]. In particular, Liu et al. [4] studied the finite-time stability of stochastic fractional-order delay differential equations, demonstrating how fractional operators and finite-time criteria can sharpen stability analysis. In contrast, the present study focuses on Banach-space contraction mapping to establish solvability and stability for nonlinear SDDEs with discrete delays and multiplicative noise.

Stochastic delay differential equations arise naturally in many applied fields where current dynamics depend on both present conditions and past history. For instance, in mathematical biology, delayed population growth models capture the effect of maturation time in ecological systems [5]. In epidemiology, SDDEs model infection dynamics with incubation periods, where randomness stems from environmental fluctuations [6]. In financial mathematics, delayed stochastic models are used for asset pricing and risk processes when information flows with a lag [7]. Engineering and control systems also rely on SDDEs to incorporate sensor delays and feedback lags [8]. Earlier studies have also investigated delay systems with jumps [9], unbounded delay structures [10], and linear memory effects [11].

Despite these wide-ranging applications, most existing results rely heavily on Hilbert space and semigroup approaches [5,12]. While powerful, these frameworks can be restrictive for discrete delays or multiplicative noise. In contrast, our study develops a Banach space fixed-point framework for SDDEs, which allows us to establish solvability and stability in a setting that is more flexible for delay-dependent stochastic systems. This approach fills a gap in the literature by extending fixed-point methods beyond deterministic or fractional systems to nonlinear SDDEs, providing both theoretical guarantees and supporting numerical simulations. These equations generalize classical stochastic models by incorporating delays, making them especially useful for capturing dynamics where current behavior depends not only on immediate conditions but also on past states. As such, they provide a powerful framework for analyzing real-world phenomena across disciplines, including biology, engineering, finance, and the physical sciences [6,13,14].

In many practical contexts, delayed responses and historical dependence are essential for understanding long-term behavior. Mathematical frameworks that account for these features have revealed new insights, particularly through tools like pullback and forward attractors, which describe how systems evolve under uncertainty when past influences are non-negligible [15,16]. These approaches create important connections between stochastic processes and dynamical systems theory.

Fixed-point techniques have long been employed in the analysis of functional differential equations, including delay systems. For instance, ref. [17] employed a fixed-point approach to study Hyers–Ulam–Rassias stability in Volterra-type integro-differential equations with delay, while ref. [18] established fixed-point results for semigroups of monotone operators in ordered Banach spaces. Classical assumptions, such as the Markov property [19], often no longer apply, necessitating techniques that handle path dependence and infinite-dimensional dynamics. Foundational results from researchers including [5,20] have established well-posedness and stability under various conditions, often using semigroup methods, stochastic calculus, or energy-based approaches. Later work has extended these ideas to systems with infinite delays, jump discontinuities, or regime-switching behavior. Other studies have addressed finite-time stability in systems with delay and switching [21] or applied Banach and Schauder fixed-point theorems to random fractional differential equations [22]. Analyzing such systems presents unique mathematical challenges.

2. Preliminaries and Functional Setup

Throughout this paper, all stochastic processes are assumed to be defined on a complete filtered probability space $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbb{P})$ satisfying the usual conditions.

Let $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbb{P})$ be a filtered probability space that satisfies the usual completeness and right-continuity assumptions. The process $W\left(t\right)$, defined on this space, denotes a standard m-dimensional Wiener process adapted to the filtration ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$.

We consider the following class of SDDEs driven by Wiener noise:

$$dX\left(t\right)=f(t,X(t),X(t-\tau \left)\right)dt+g(t,X(t),X(t-\tau \left)\right)dW\left(t\right),t\in [0,T],$$

(1)

where the following definitions are used:

• $X\left(t\right)\in {\mathbb{R}}^n$ is the unknown state process;
• $\tau >0$ is a fixed discrete delay;
• $f:[0,T]\times {\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ is the drift function, assumed measurable and Lipschitz continuous;
• $g:[0,T]\times {\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^{n\times m}$ is the diffusion coefficient, representing multiplicative noise;
• $W\left(t\right)={(W_1\left(t\right),\dots ,W_m\left(t\right))}^T$ is an m-dimensional standard Wiener process defined on a complete filtered probability space $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbb{P})$ satisfying the usual conditions.

We also specify an initial history function $\varphi :[-\tau ,0]\to {\mathbb{R}}^n$, assumed continuous and ${\mathcal{F}}_0$-measurable, such that

$$X\left(t\right)=\varphi \left(t\right),\mathrm{for}t\in [-\tau ,0].$$

where $\tau >0$ is a fixed delay, and $\varphi$ is a given stochastic process representing the initial state of the system.

2.1. Functional Framework

To analyze the above system, we define a Banach space of continuous, adapted, ${\mathbb{R}}^n$-valued processes [12] as follows:

$$\mathcal{X}:=\left\{X:[-\tau ,T]\to {\mathbb{R}}^n|X\mathrm{is}{\mathcal{F}}_t\text{-}\mathrm{adapted},\mathrm{continuous},\mathrm{and}{\parallel X\parallel }_{\mathcal{X}}<\infty \right\}.$$

The associated norm is given by

$${\parallel X\parallel }_{\mathcal{X}}:=\underset{t\in [-\tau ,T]}{sup}{\left(\mathbb{E}\left[{\parallel X\left(t\right)\parallel }^2\right]\right)}^{1/2}.$$

(2)

The initial function $\phi \in C([-\tau ,0];{\mathbb{R}}^n)$ is assumed to be ${\mathcal{F}}_0$-measurable and satisfy

$$\underset{t\in [-\tau ,0]}{sup}\mathbb{E}\left[{\parallel \phi \left(t\right)\parallel }^2\right]<\infty .$$

(3)

2.2. Assumptions on the Coefficients

We impose the following regularity conditions on the drift and diffusion functions f and g:

(A1) 

Lipschitz continuity:

There is a constant $L>0$ such that for all $x_1,x_2,y_1,y_2\in {\mathbb{R}}^n$ and all $t\in [0,T]$,

$$\parallel f(t,x_1,y_1)-f(t,x_2,y_2)\parallel +\parallel g(t,x_1,y_1)-g(t,x_2,y_2)\parallel \le L\left(\parallel x_1-x_2\parallel +\parallel y_1-y_2\parallel \right).$$

(A2) 

Linear growth:

There is a constant $K>0$ such that for all $x,y\in {\mathbb{R}}^n$ and all $t\in [0,T]$,

$${\parallel f(t,x,y)\parallel }^2+{\parallel g(t,x,y)\parallel }^2\le K\left(1+{\parallel x\parallel }^2+{\parallel y\parallel }^2\right).$$

These assumptions ensure that both the drift and diffusion terms behave in a controlled fashion with respect to their arguments, which is essential for the application of fixed-point methods.

2.3. Definition of the Solution Operator

To establish a fixed-point formulation of the stochastic delay differential Equation (1), we define an associated integral operator T on the Banach space $\mathcal{X}$ introduced in Section 2.1. Given an initial history function $\phi \in \mathcal{X}$, the operator T maps a process $X\in \mathcal{X}$ to another process $TX$, defined by

$$\left(TX\right)\left(t\right)=\phi \left(0\right)+{\int }_0^{t}f(s,X_s)ds+{\int }_0^{t}g(s,X_s)dW\left(s\right),t\in [0,T],$$

(4)

where $X_s$ denotes the segment $\left\{X\right(s+\theta ):\theta \in [-\tau ,0\left]\right\}$ and f and g satisfy the Lipschitz and growth conditions (A1) and (A2).

The mapping T captures both the deterministic and stochastic dynamics of the system, with explicit incorporation of the delay structure in the integrands. The deterministic part is governed by the drift function f, while the stochastic part is driven by the Wiener process $W\left(t\right)$ via the diffusion function g. The initial value $\phi \left(0\right)$ ensures consistency with the prescribed history over the interval $[-\tau ,0]$.

This operator will serve as the central object in our fixed-point argument. Specifically, we will show that T is a contraction on a suitable closed, convex subset of $\mathcal{X}$ when the time horizon T is sufficiently small. This forms the basis for applying Banach’s fixed-point theorem to establish the existence and uniqueness of strong solutions.

3. Fixed-Point Formulation and Existence Results

Lemma 1 

(Contraction Property of the Solution Operator). Let T be the operator defined in Equation (4). Assume that the drift and diffusion functions f and g satisfy the Lipschitz condition. Under assumptions (A1) and (A2), and for the sufficiently small time horizon $T>0$, the mapping T is a contraction on a closed, convex subset of the Banach space $\mathcal{X}$:

$${\parallel X\parallel }_{\mathcal{X}}:={\left(\mathbb{E}\left[\underset{t\in [0,T]}{sup}{\parallel X\left(t\right)\parallel }^2\right]\right)}^{1/2}$$

(5)

Proof. 

Let $X,Y\in \mathcal{X}$. Define

$$Z\left(t\right):=\left(TX\right)\left(t\right)-\left(TY\right)\left(t\right).$$

Then, from Equation (4), we have

$$Z\left(t\right)={\int }_0^t\left[f(s,X_s)-f(s,Y_s)\right]ds+{\int }_0^t\left[g(s,X_s)-g(s,Y_s)\right]dW\left(s\right).$$

Taking the supremum over $t\in [0,T]$, squaring, and applying expectation, we obtain the following:

$$\begin{array}{cc}\mathbb{E}\left[\underset{t\in [0,T]}{sup}{\parallel Z\left(t\right)\parallel }^2\right]\hfill & \\ & \le 2\mathbb{E}\left[\underset{t\in [0,T]}{sup}{∥{\int }_0^t\left[f(s,X_s)-f(s,Y_s)\right]ds∥}^2\right]\\ & +2\mathbb{E}\left[\underset{t\in [0,T]}{sup}{∥{\int }_0^t\left[g(s,X_s)-g(s,Y_s)\right]dW\left(s\right)∥}^2\right].\hfill \end{array}$$

(6)

We now estimate each term:

• Jensen’s inequality yields

  $${∥{\int }_0^t[f(s,X_s)-f(s,Y_s)]ds∥}^2\le t{\int }_0^t{\parallel f(s,X_s)-f(s,Y_s)\parallel }^{2}ds.$$
  Taking expectation and supremum, we obtain the following:

  $$\mathbb{E}\left[\underset{t\in [0,T]}{sup}{∥{\int }_0^t[f(s,X_s)-f(s,Y_s)]ds∥}^2\right]\le T{\int }_0^T\mathbb{E}\left[\parallel f(s,X_s)-f(s,Y_s){\parallel }^2\right]ds.$$
• Doob’s maximal inequality for the stochastic integral gives

  $$\mathbb{E}\left[\underset{t\in [0,T]}{sup}{∥{\int }_0^t[g(s,X_s)-g(s,Y_s)]dW\left(s\right)∥}^2\right]\le 4\mathbb{E}{\int }_0^T{\parallel g(s,X_s)-g(s,Y_s)\parallel }^{2}ds.$$
• Itô’s isometry justifies the above:

  $$\mathbb{E}{∥{\int }_0^t[g(s,X_s)-g(s,Y_s)]dW\left(s\right)∥}^2=\mathbb{E}{\int }_0^t{\parallel g(s,X_s)-g(s,Y_s)\parallel }^{2}ds.$$

Combining all the above estimates leads to the following:

$$\mathbb{E}\left[\underset{t\in [0,T]}{sup}{\parallel Z\left(t\right)\parallel }^2\right]\le (2T+8)L^2{\int }_0^T\mathbb{E}\left[\underset{\theta \in [s-\tau ,s]}{sup}{\parallel X\left(\theta \right)-Y\left(\theta \right)\parallel }^2\right]ds.$$

Making $T>0$ sufficiently small such that $C_T<1$, we conclude that T is a strict contraction on X. □

Here, $C_T$ denotes a constant depending on the time horizon T and the Lipschitz constant L. For instance, one can take

$$C_T=(2T+8)L^2,$$

which ensures that the solution operator is a contraction for sufficiently small T.

Theorem 1 

(Existence and Uniqueness of Strong Solutions). Let $\phi \in \mathcal{X}$ be an ${\mathcal{F}}_0$-measurable initial history function satisfying

$$\mathbb{E}\left[\underset{s\in [-\tau ,0]}{sup}{\parallel \phi \left(s\right)\parallel }^2\right]<\infty .$$

Assume that the drift and diffusion functions f and g satisfy assumptions (A1) and (A2). Then, the stochastic delay differential equation

$$X\left(t\right)=\phi \left(0\right)+{\int }_0^{t}f(s,X_s)ds+{\int }_0^{t}g(s,X_s)dW\left(s\right),t\in [0,T],$$

(7)

with initial condition

$$X\left(t\right)=\phi \left(t\right),t\in [-\tau ,0],$$

admits a unique strong solution $X\in \mathcal{X}$ on $[0,T]$.

Proof. 

Define the operator T on $\mathcal{X}$ by

$$\left(TX\right)\left(t\right)=\phi \left(0\right)+{\int }_0^{t}f(s,X_s)ds+{\int }_0^{t}g(s,X_s)dW\left(s\right),t\in [0,T],$$

as given earlier. Using Lemma 1, there is a constant $T_0>0$ such that for all $T\in (0,T_0]$, the operator T is a strict contraction on $\mathcal{X}$. Hence, using Banach’s fixed-point theorem (see, e.g., [23,24]), there is a unique fixed point $X\in \mathcal{X}$ such that $\mathcal{T}X=X$ on $[0,T_0]$, which corresponds to the unique strong solution of the SDDE.

To extend the solution to the full interval $[0,T]$, we use a continuation argument: partition $[0,T]$ into subintervals of length at most $T_0$ and apply the same contraction argument iteratively. The local solutions patch together uniquely to yield a global solution on $[0,T]$.

Therefore, Equation (7) admits a unique strong solution $X\in \mathcal{X}$ on $[0,T]$. □

Remark 1 

(Constructive Fixed-Point Framework Without Semigroup Theory). Theorem 1 establishes the existence and uniqueness of strong solutions to the stochastic delay differential Equation (7) via a contraction mapping argument on a Banach space of continuous, adapted sample paths. Unlike classical approaches based on semigroup theory or mild solution formulations in Hilbert spaces, this result is derived using a direct and constructive method rooted in Banach’s fixed-point theorem.

This operator-theoretic strategy avoids the need for stochastic evolution equations or generator domain assumptions, making it especially suitable for systems with discrete delays and multiplicative noise, where semigroup-based techniques are often difficult to apply. Moreover, the fixed-point approach offers a transparent analytical structure, amenable to generalizations involving state-dependent delays or other nonlocal memory effects.

Theorem 2 

(Exponential Mean-Square Stability). Let $X\in \mathcal{X}$ be the unique strong solution to Equation (7). Suppose the drift and diffusion functions f and g satisfy assumptions (A1) and (A2) and, in addition, there are constants $\alpha >0$ and $\beta \ge 0$ such that

$$〈f(t,\psi ),\psi \left(0\right)〉+{\displaystyle \frac{1}{2}}{\parallel g(t,\psi )\parallel }^2\le -{\alpha \parallel \psi \left(0\right)\parallel }^2+\beta \underset{\theta \in [-\tau ,0]}{sup}{\parallel \psi \left(\theta \right)\parallel }^2,$$

(8)

for all $t\in [0,T]$ and all $\psi \in \mathcal{X}$. Then, the solution $X\left(t\right)$ satisfies the exponential mean-square bound:

$$\mathbb{E}\left[{\parallel X\left(t\right)\parallel }^2\right]\le C{e}^{-\lambda t}·\mathbb{E}\left[\underset{s\in [-\tau ,0]}{sup}{\parallel \phi \left(s\right)\parallel }^2\right],$$

for some constants $C>0$ and $\lambda >0$ depending on α, β, and τ.

Proof. 

Let $V\left(t\right):=\mathbb{E}\left[{\parallel X\left(t\right)\parallel }^2\right]$. By applying Itô’s formula to the function ${\parallel X\left(t\right)\parallel }^2$, we obtain:

$${\displaystyle \frac{d}{dt}}V\left(t\right)=\mathbb{E}\left[2\langle f(t,X_t),X\left(t\right)\rangle +{\parallel g(t,X_t)\parallel }^2\right].$$

Using assumption (8), we estimate

$${\displaystyle \frac{d}{dt}}V\left(t\right)\le -2\alpha \mathbb{E}\left[{\parallel X\left(t\right)\parallel }^2\right]+2\beta \mathbb{E}\left[\underset{\theta \in [-\tau ,0]}{sup}{\parallel X(t+\theta )\parallel }^2\right].$$

Since $X(t+\theta )\in \mathcal{X}$ for $\theta \in [-\tau ,0]$, define

$$V_{\tau }\left(t\right):=\underset{s\in [t-\tau ,t]}{sup}\mathbb{E}\left[{\parallel X\left(s\right)\parallel }^2\right].$$

Then, the inequality becomes:

$${\displaystyle \frac{d}{dt}}V\left(t\right)\le -2\alpha V\left(t\right)+2\beta V_{\tau }\left(t\right).$$

This type of inequality is a standard delay differential inequality. By applying a suitable delay-dependent Grönwall inequality [8] and assuming $\beta <\alpha$, we obtain the exponential decay estimate

$$V\left(t\right)\le C{e}^{-\lambda t}·\underset{s\in [-\tau ,0]}{sup}\mathbb{E}\left[{\parallel \phi \left(s\right)\parallel }^2\right],$$

for some constants $C>0$ and $\lambda >0$. The parameter $\lambda$ can be made explicit by applying Halanay’s inequality [25], which provides exponential decay estimates for delay differential inequalities. In particular, $\lambda >0$ may be chosen to satisfy

$$\alpha -\beta e^{\lambda \tau }>\lambda ,$$

ensuring exponential mean-square stability at rate $\lambda$. □

Remark 2 

(Delay–Dissipation Balance and the Limiting Case $\beta =0$). The stability condition $\beta <\alpha$ in inequality (8) ensures that the dissipative effect of the drift term dominates the potentially destabilizing influence of the memory component introduced by the delay. This balance is critical: if the feedback induced by the delay is too strong (i.e., $\beta \ge \alpha$), exponential stability may no longer hold.

In the limiting case where $\beta =0$, the stability condition becomes

$$〈f(t,\psi ),\psi \left(0\right)〉+{\displaystyle \frac{1}{2}}{\parallel g(t,\psi )\parallel }^2\le -\alpha {\parallel \psi \left(0\right)\parallel }^2,$$

which corresponds to a system without delay-induced feedback. In this case, the stochastic delay differential equation reduces to a classical stochastic differential equation in terms of stability behavior.

The resulting energy estimate leads directly to the exponential decay

$$\mathbb{E}\left[{\parallel X\left(t\right)\parallel }^2\right]\le e^{-2\alpha t}\mathbb{E}\left[{\parallel \phi \left(0\right)\parallel }^2\right],$$

as expected from standard Lyapunov [8] for systems without delay.

This technique allows for a more flexible and structurally transparent treatment compared to traditional semigroup-based methods. Furthermore, we derive exponential mean-square stability using delay-sensitive Lyapunov techniques and functional inequalities, avoiding the use of semimartingale decomposition or Hilbert space energy estimates [26]. Our stability condition aligns with earlier mean-square criteria for switching systems and leverages delay inequalities in the spirit of Halanay.

3.1. Numerical Simulation

In order to illustrate and validate the theoretical results established in Section 3, we now present numerical examples. These examples are designed to confirm the existence, uniqueness, and stability properties predicted by our main theorems, with particular emphasis on the stability criterion of Theorem 2.

We simulated the scalar stochastic delay differential equation

$$dX\left(t\right)=-aX\left(t\right)dt+bX(t-\tau )dt+\sigma X\left(t\right)dW\left(t\right),$$

(9)

with discrete delay $\tau =1$. The initial history $X\left(t\right)=\phi \left(t\right)$ for $t\in [-\tau ,0]$ was taken to be constant: $\phi \left(t\right)=1$.

The equation was discretized using a delay-adapted Euler–Maruyama scheme with time step $h=0.01$ [27]. For each parameter set, we simulated 1000 independent sample paths and computed $\mathbb{E}\left[X{\left(t\right)}^2\right]$ by averaging $X{\left(t\right)}^2$ over the ensemble.

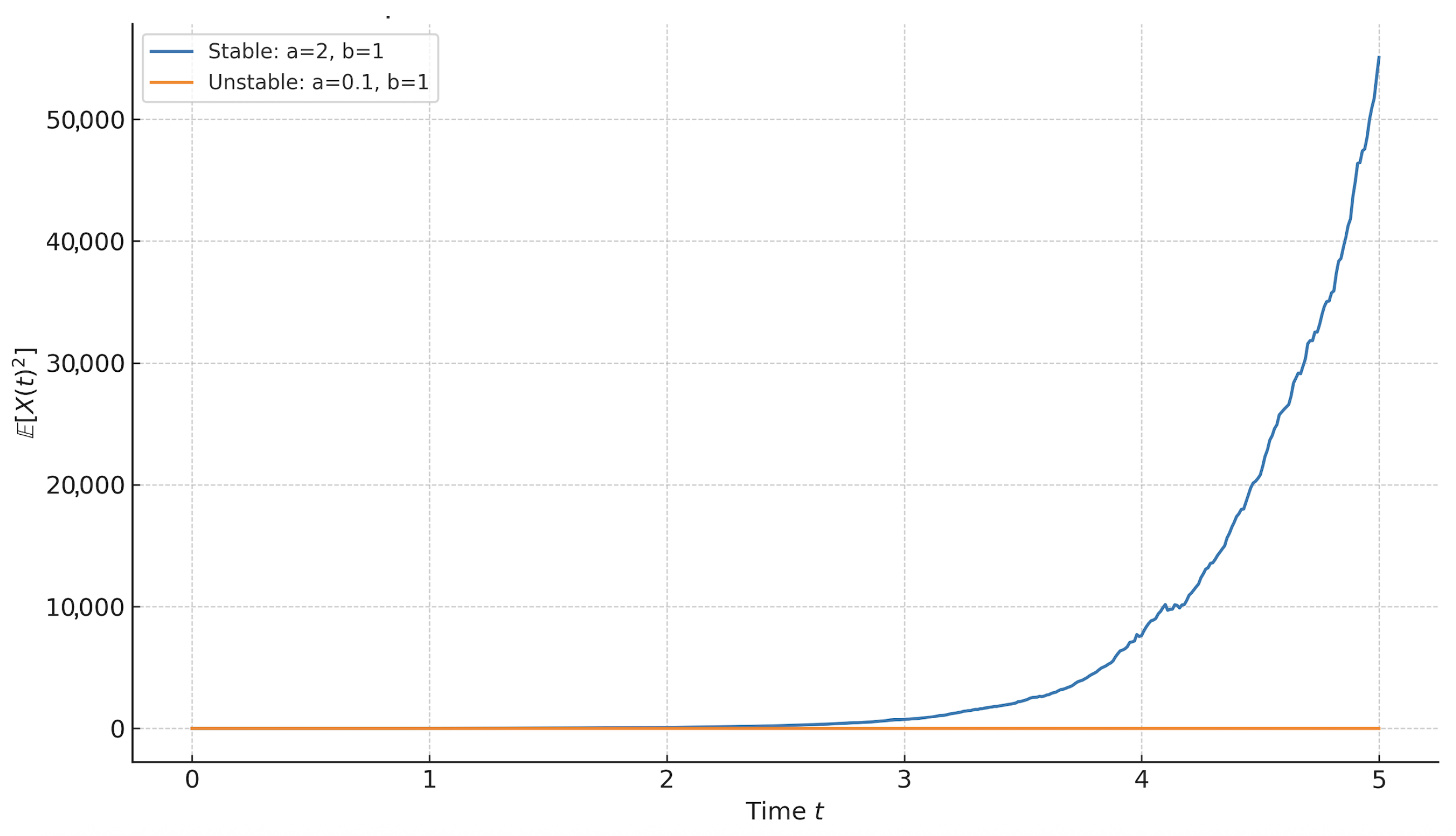
3.1.1. Case 1—Stable Parameters: $a=2$, $b=1$, $\sigma =0.5$

This parameter choice satisfies the condition $a>\theta b$ from the theoretical stability criterion. The estimated mean-square norm decays exponentially toward zero, confirming the theoretical bound.

3.1.2. Case 2—Unstable Parameters: $a=0.1$, $b=1$, $\sigma =0.5$

As shown in the numerical simulation, the system exhibits both stable and unstable regimes (Figure 1).

These results confirm the theoretical predictions of Theorem 2. When the dissipation parameter a dominates the delay feedback term $\theta b$, the stability condition is satisfied and $\mathbb{E}\left[X{\left(t\right)}^2\right]$ decays exponentially, as seen in Case 1. Conversely, when a is too small and the condition $a>\theta b$ fails, the simulation in Case 2 shows rapid growth in $\mathbb{E}\left[X{\left(t\right)}^2\right]$, indicating mean-square instability. Together, these numerical examples provide concrete evidence that the contraction-based stability framework developed in this paper accurately predicts the qualitative dynamics of stochastic delay systems.

3.2. Comparison with Existing Approaches

Classical semigroup and Lyapunov methods have long been employed to study the stability of SDDEs [5,12]. These frameworks typically establish stability thresholds of the form $a>\theta b$, ensuring that dissipation dominates the destabilizing effect of the delay term. Our numerical simulations (Case 1 vs. Case 2) precisely reproduce this threshold, confirming that the Banach contraction framework yields results consistent with established semigroup-based analyses.

The key advantage of the present approach is that it achieves these results without relying on infinitesimal generator theory, semimartingale decomposition, or Hilbert space machinery. Instead, the contraction mapping strategy provides a direct, constructive argument in a Banach space of sample paths, which naturally accommodates discrete delays and multiplicative noise. In this sense, the proposed method not only recovers known stability behavior but also extends applicability to settings where semigroup methods may be less effective.

4. Conclusions

This paper has developed a Banach space fixed-point framework for a class of nonlinear stochastic delay differential equations with discrete delays and multiplicative noise. Departing from traditional Hilbert space semigroup methods [5,12], we formulated the problem in a Banach space of continuous, adapted sample paths and constructed a nonlinear solution operator via an integral equation. Under standard Lipschitz and linear growth conditions, this operator was shown to be a strict contraction in a suitably chosen subspace, leading to the existence and uniqueness of strong solutions through Banach’s fixed-point theorem [23,24]. This provides a constructive and self-contained alternative to methods based on infinitesimal generators or semimartingale decomposition [20,28].

In addition to solvability, we examined exponential mean-square stability by deriving a Lyapunov-type inequality that incorporates the delay structure directly into the stability condition. The resulting criterion, which depends explicitly on the dissipation constant and the delay feedback term, generalizes classical results [8,25,29] and yields explicit decay estimates. In the absence of memory effects, the framework naturally recovers the standard exponential stability condition for stochastic differential equations without delay. Numerical examples further confirmed the theoretical analysis and demonstrated the applicability of the proposed method, aligning with related numerical approaches in the literature [10,27].

A key advantage of this framework lies in its flexibility and generalizability. By embedding the delay structure directly into the Banach path space and avoiding semigroup assumptions, the analysis accommodates discrete delays, nonlinearities, and multiplicative noise in a transparent way. This formulation is amenable to extension in several directions, including systems with state-dependent or distributed delays, equations driven by Lévy or fractional noise [2,4,9], and problems posed in infinite-dimensional Banach spaces [12,15]. Moreover, the operator-theoretic structure developed here may serve as a foundation for numerical approximation schemes, long-term dynamical analysis, and attractor theory in non-Hilbert settings [17,18,30].

In particular, our simulations demonstrated that the contraction framework reproduces the same stability thresholds as classical semigroup-based methods [12,26], thereby validating its consistency with existing theory. The advantage lies in achieving these results through a Banach contraction mapping argument, which avoids semigroup assumptions and provides a more direct and constructive pathway for systems with discrete delays and multiplicative noise.

Looking ahead, several avenues for future research are worth exploring. First, the framework could be extended to accommodate more general noise structures and delay types, such as state-dependent delays or Lévy-type noise [1,31,32]. Second, while our analysis relied on local contraction mapping arguments, the development of global solution strategies would broaden applicability. Third, applying this methodology to real-world systems in biology, finance, or engineering would provide strong validation of its practical utility [5,7]. Compared with classical semigroup-based methods [12], the Banach space contraction framework used here avoids reliance on infinitesimal generators and accommodates discrete delays and multiplicative noise in a structurally transparent way.