Development of a Global Maximum Power Point Tracker for Photovoltaic Module Arrays Based on the Idols Algorithm
Abstract
1. Introduction
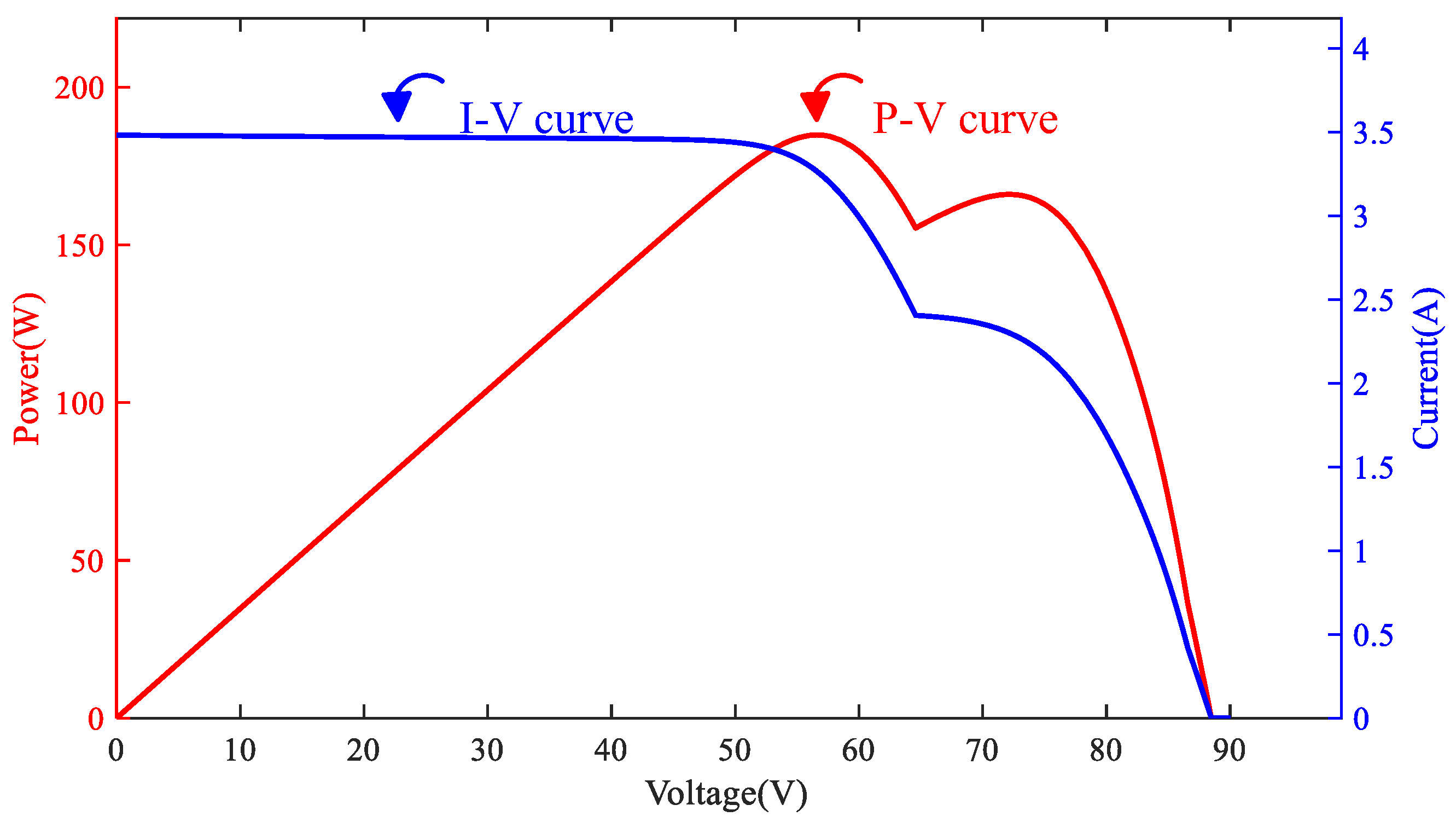
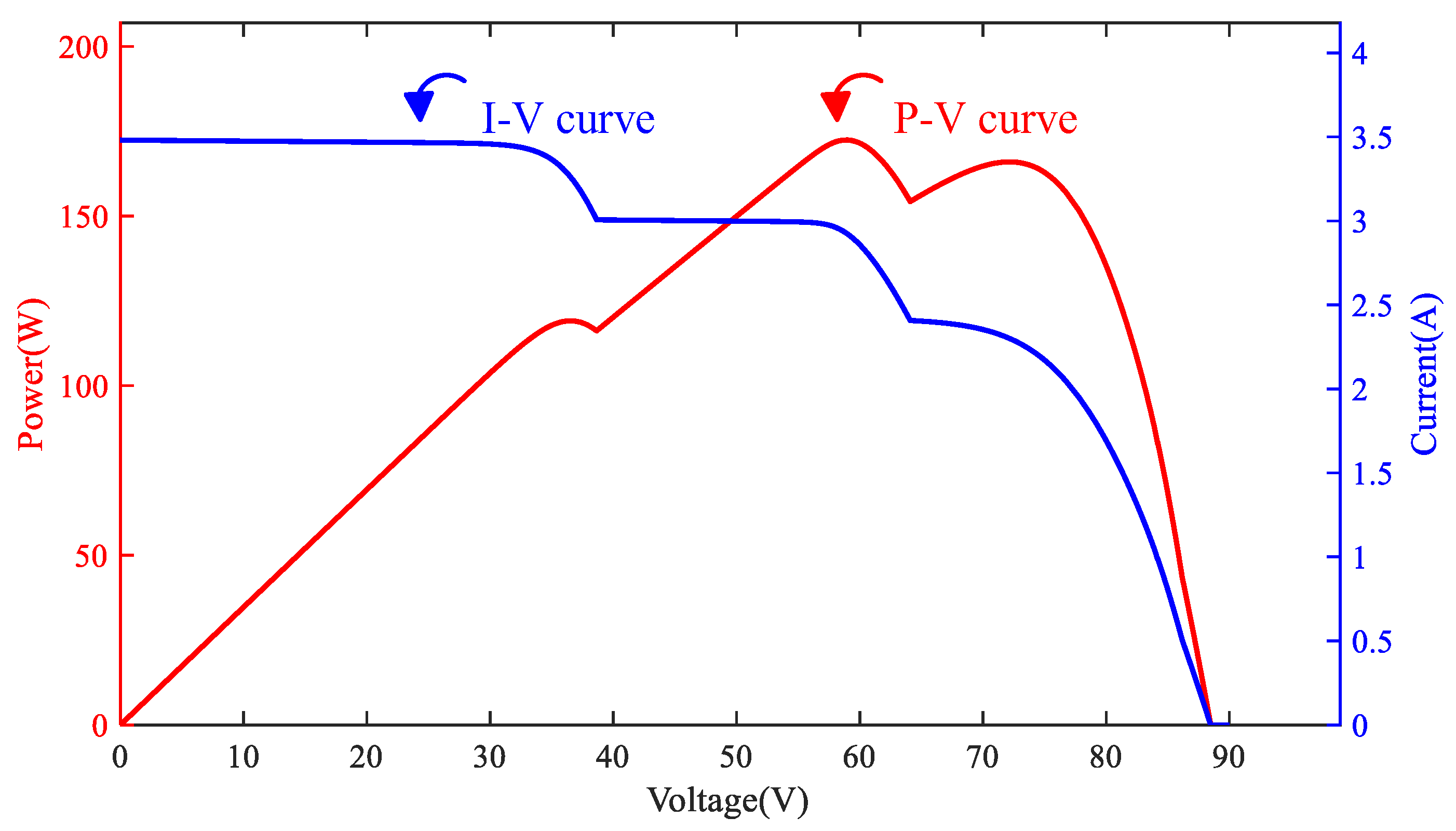
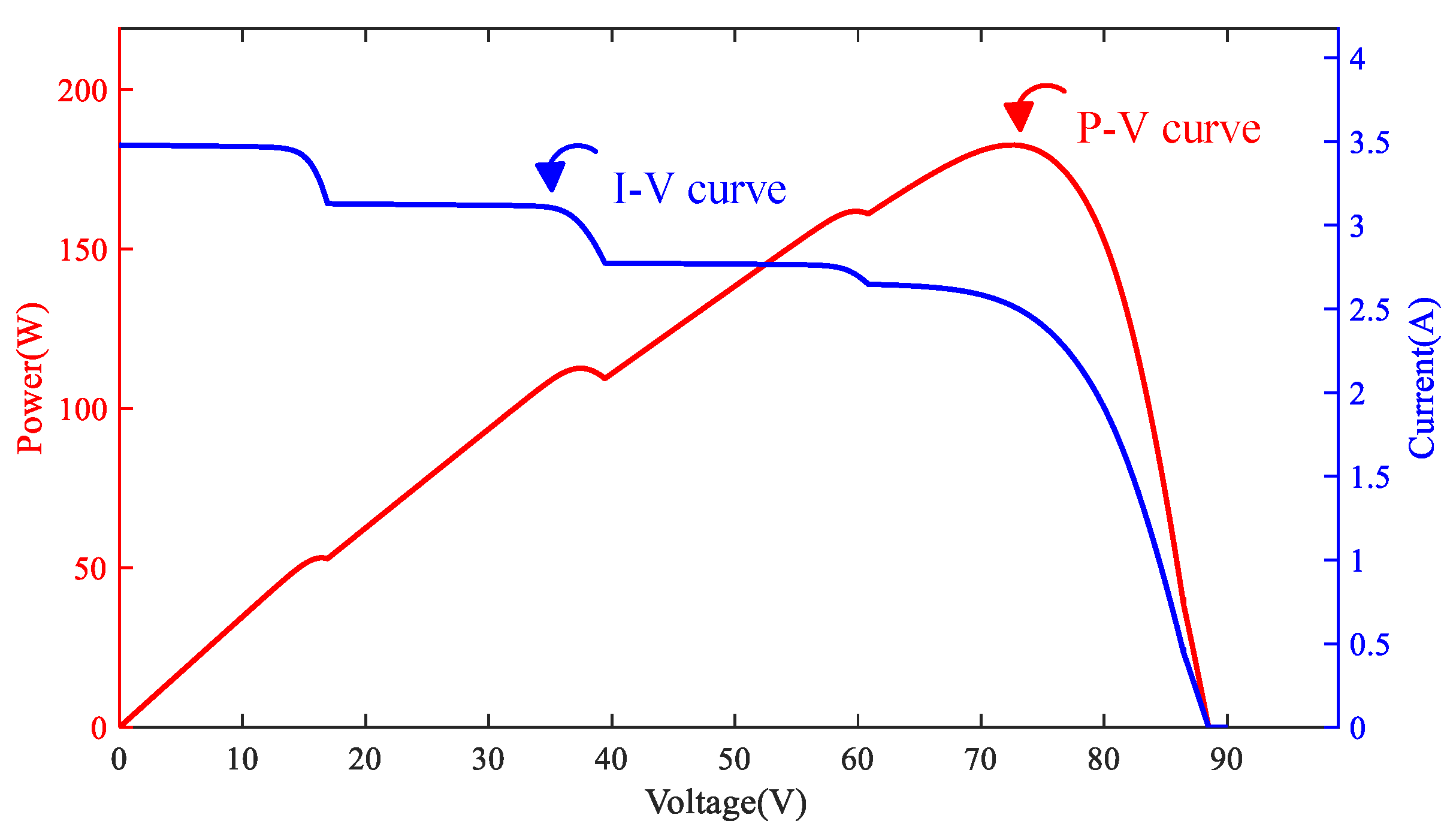
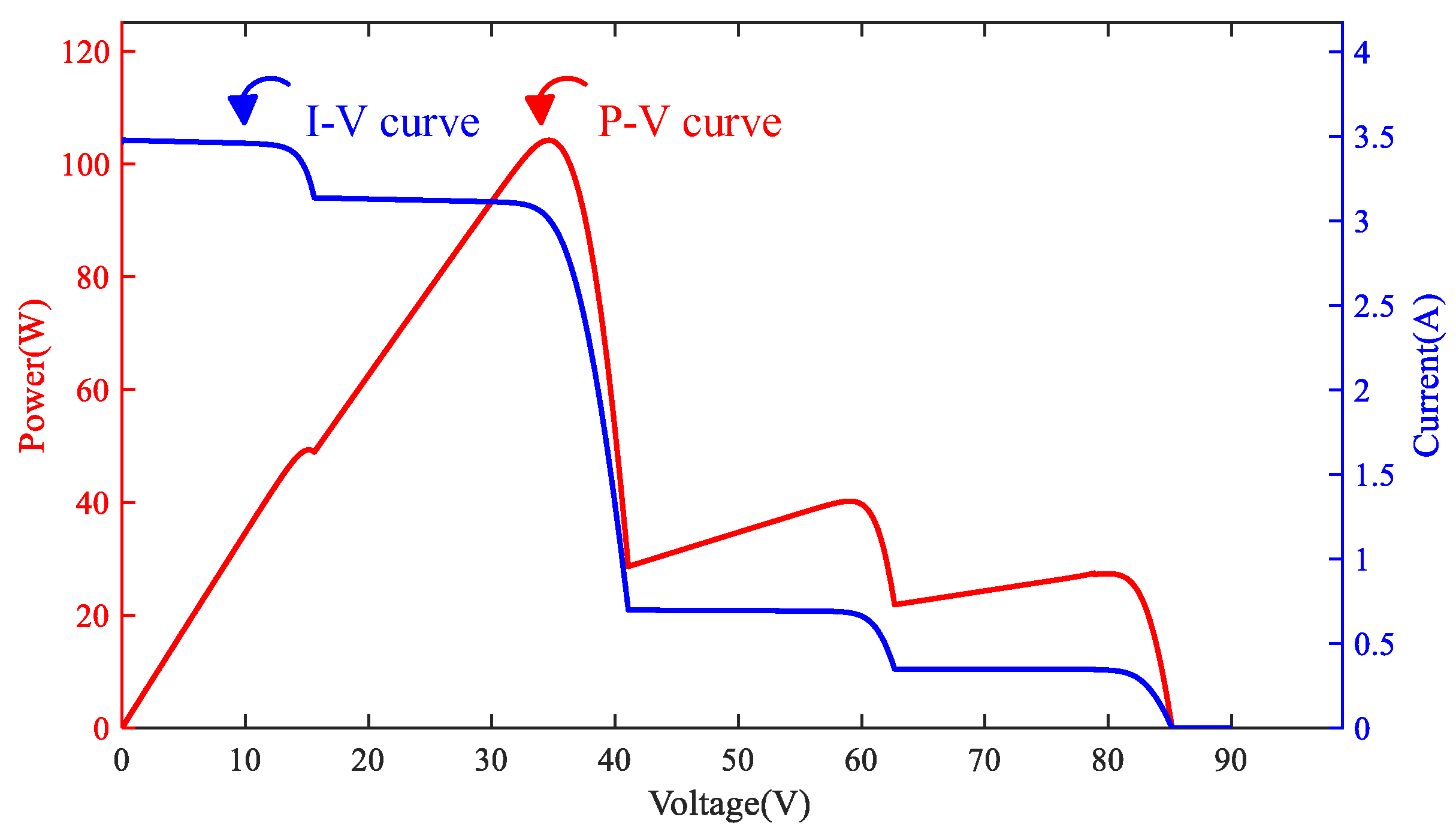
2. Output Characteristics of the PVMAs Under Different Shading Conditions
3. Idols Algorithm
3.1. Inspiration and Introduction
3.2. IA Execution Steps
- (1)
- Initialize all parameters of the IA, defining the total number of trainees (TNt) as the search scale. The duty ratio of the boost converter is represented as “trainee,” while the output power of the PVMAs is represented as “online celebrity.” Each trainee has a corresponding online celebrity.
- (2)
- Through the establishment of a “company system”, each TN is assigned a corresponding BOC, which is then ranked accordingly.
- (3)
- Each trainee has a corresponding promotion value (PM), which is determined by three main factors: basic online celebrity, public performance, and solo performance. BOC refers to the talent showcased to fans before considering solo performances and public appearances. Each trainee must increase their popularity (likes) by managing their self-media platforms (including Facebook, Instagram, TikTok, YouTube, or Twitter), thereby attracting online celebrity. Trainees can only gain fan affection based on their appearance. The appearance factor is represented by a physical attribute factor, which is determined by facialA, body fat percentage (BFP), and Aw. The mathematical model for this is shown in Equation (5). Since every individual possesses innate features and acquired body shape, the BOC is determined by the body factor (BF). Let represent the promotion value of the current i trainee, and its mathematical model is shown in Equation (6). The initial PM for each TN is calculated using Equations (5) and (6), incorporating facialA and BF to compute the BOC.
- (4)
- During the elimination round, the current fans count (fans) and the fandom are used to calculate the fan ratio (fr), as shown in Equation (7). This ratio is then used for adjustment. The current fans count represents the number of iterations, while the fandom represents the total number of iterations.
- (5)
- Each trainee’s individual best online celebrity is calculated through solo performances (SL). In solo performances, trainees are required to improve their singing abilities (e.g., vocal) and dance skills (e.g., hip-hop, breaking, locking, popping, krump) to enhance their performance and gain more popularity with the audience. After each solo performance, the OC of all trainees is compared. Trainees whose OC decreases will see their rankings drop, while those whose OC increases will replace the ones with lower rankings. Eventually, the trainee with the highest OC during the solo performance will be identified. Let represent the current trainee at position , represent the highest individual OC of the trainee during the solo performance, represent the solo performance coefficient, and represent a random number for the solo performance, with a range of 0 to 1. Therefore, the mathematical model can be expressed as Equation (14).
- (6)
- The public performance (PBP) is used to compare the online celebrity of all trainees, identifying the trainee with the highest online celebrity. In public performances, each trainee is required to engage in group life, enhance their teamwork skills, and foster a spirit of collaboration. This involves participating in various public events (such as concerts, fan meetings, variety shows, talent shows, company year-end parties, and school celebrations), which helps trainees increase their exposure by showcasing themselves in the public eye. After each public performance, the OC of all trainees is compared. The trainee with the highest OC is rewarded accordingly, and this information is made public to all trainees. This motivates the trainees to compete and learn from one another to achieve a higher OC. Let represent the trainee with the highest OC during the public performance, represent the public performance coefficient, and represent a random number for the public performance, with a range of 0 to 1. Therefore, the mathematical model can be expressed as Equation (15).
- (7)
- The new promotion value for the next iteration is calculated based on the BOC, public performance, and solo performance OC. Let represent the new promotion value, and the mathematical model can be expressed as Equation (16).
- (8)
- Entering the “annual KPI review” stage, the OC of all trainees is updated based on their current number of fans, afw, and the changes in OC from the current year and previous year. The annual KPI review is a process where entertainment companies track, record, and evaluate each trainee’s number of fans at the end of each year. If the current number of fans is less than the total number of fans in the fandom, the process returns to Step (3) to continue nurturing the trainee to achieve better OC. On the other hand, if the current number of fans is equal to the total number of fans in the fandom, it means that the trainee has gained full attention and support from all the fans, with no more anti-fans. At this point, the trainee can debut in the C position (where “C” stands for “center”, originally meaning the central or most important position, later implying a strong, central figure in the group who has more screen time and is more memorable to the audience). Let represent the new trainee, the trainee with the highest OC during public performance, the anti-fans rate, and the new promotion value. The mathematical model is given in Equation (17).
4. Design of Converter for Maximum Power Point Tracking Control
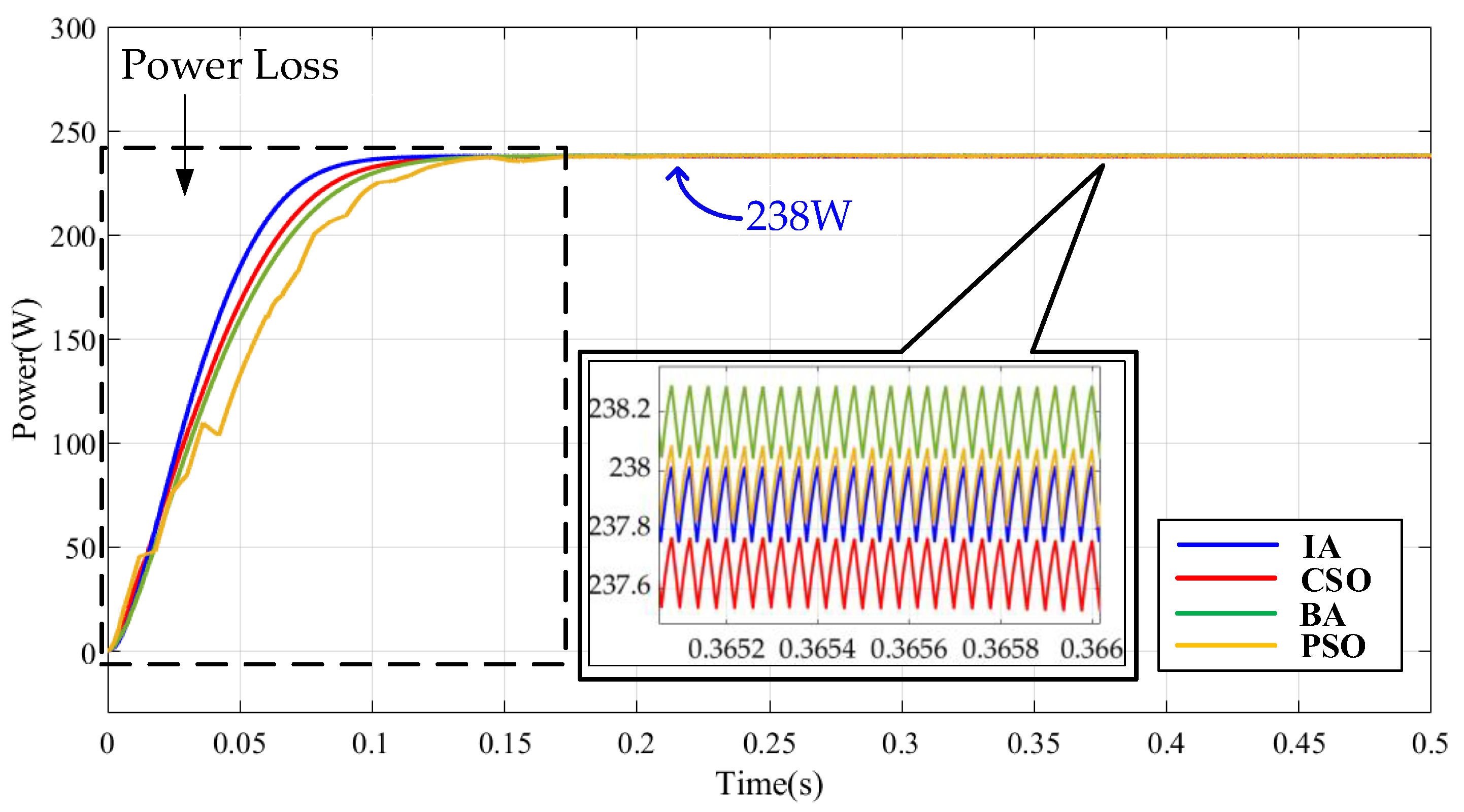
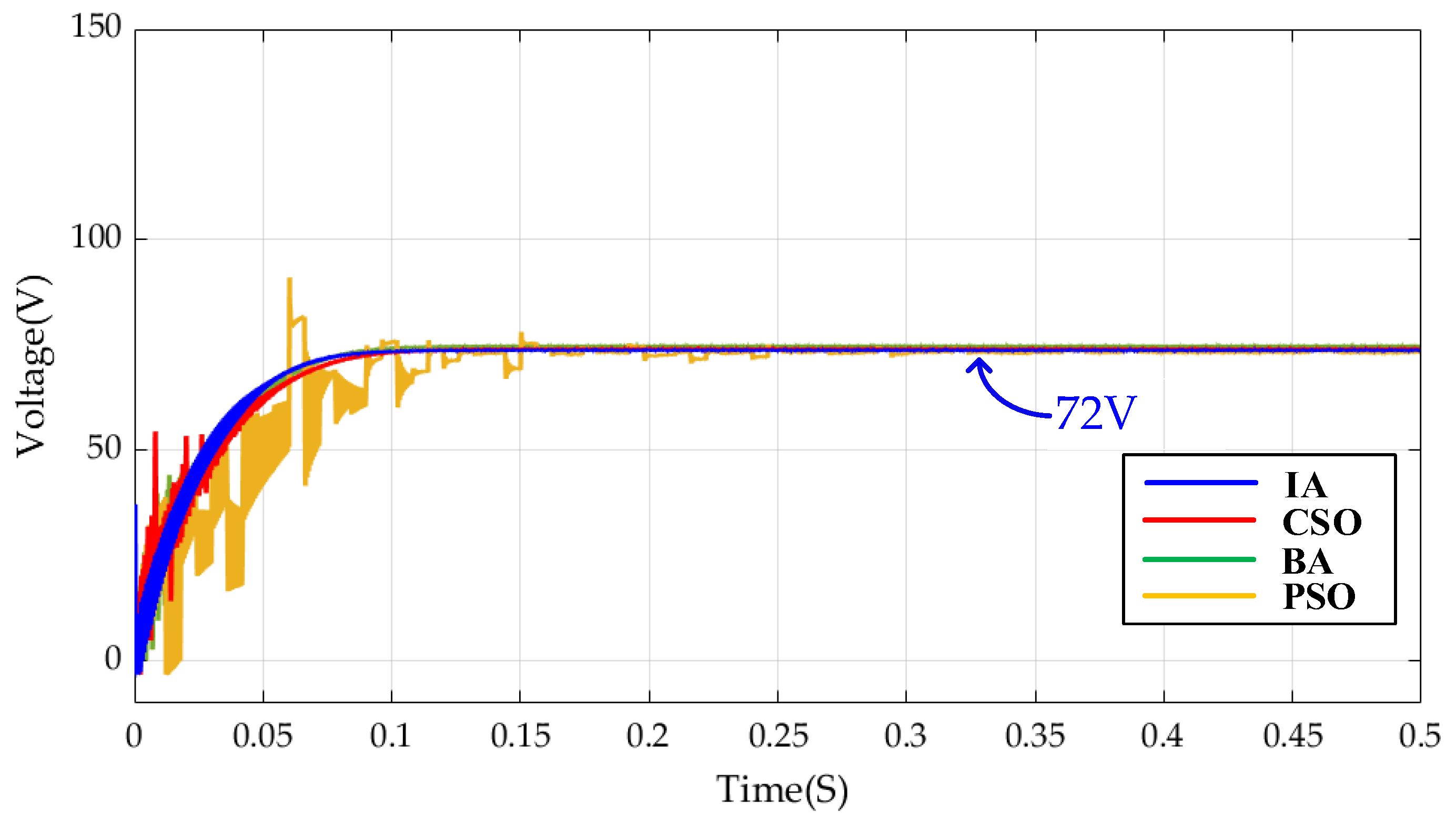
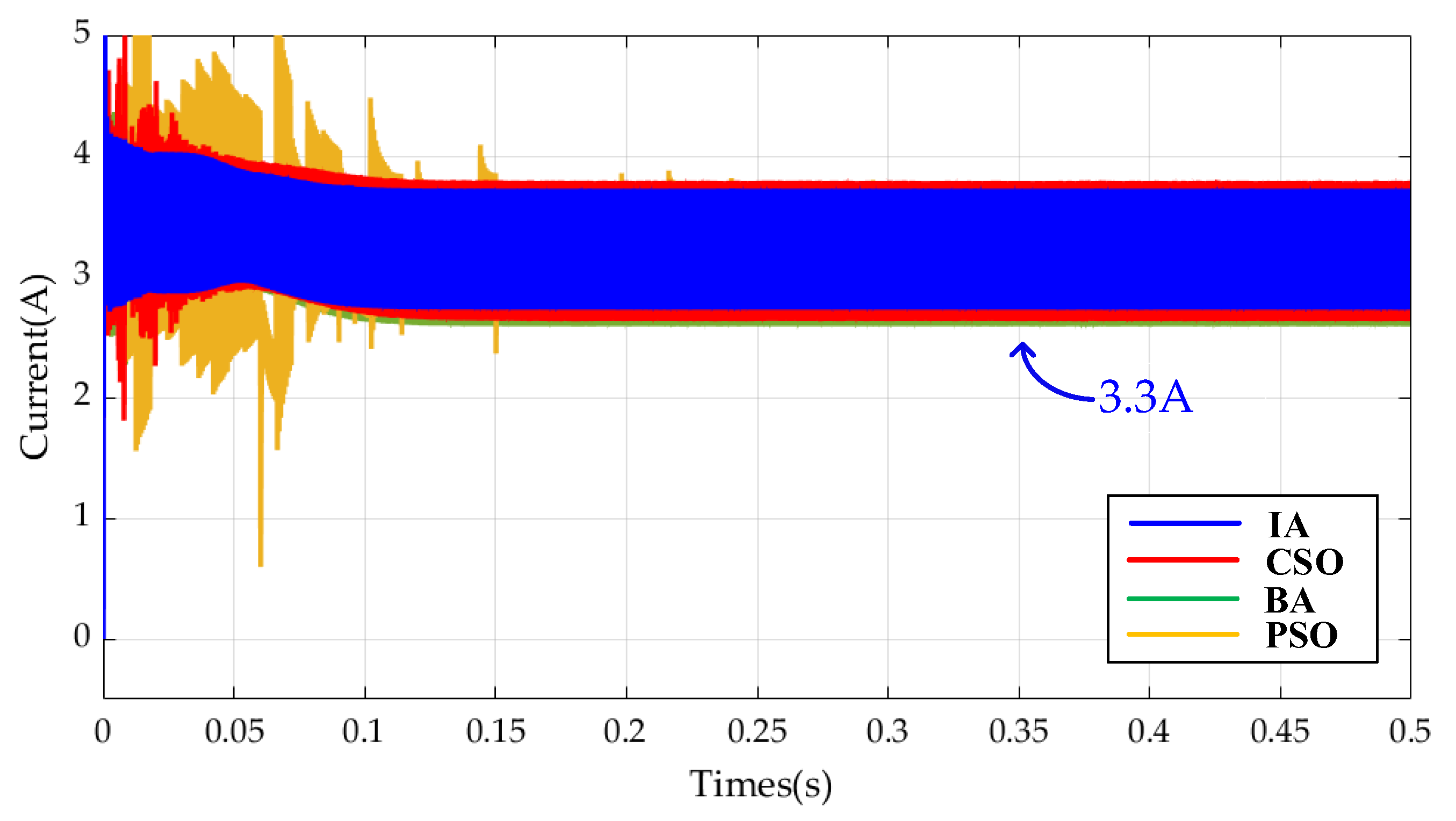
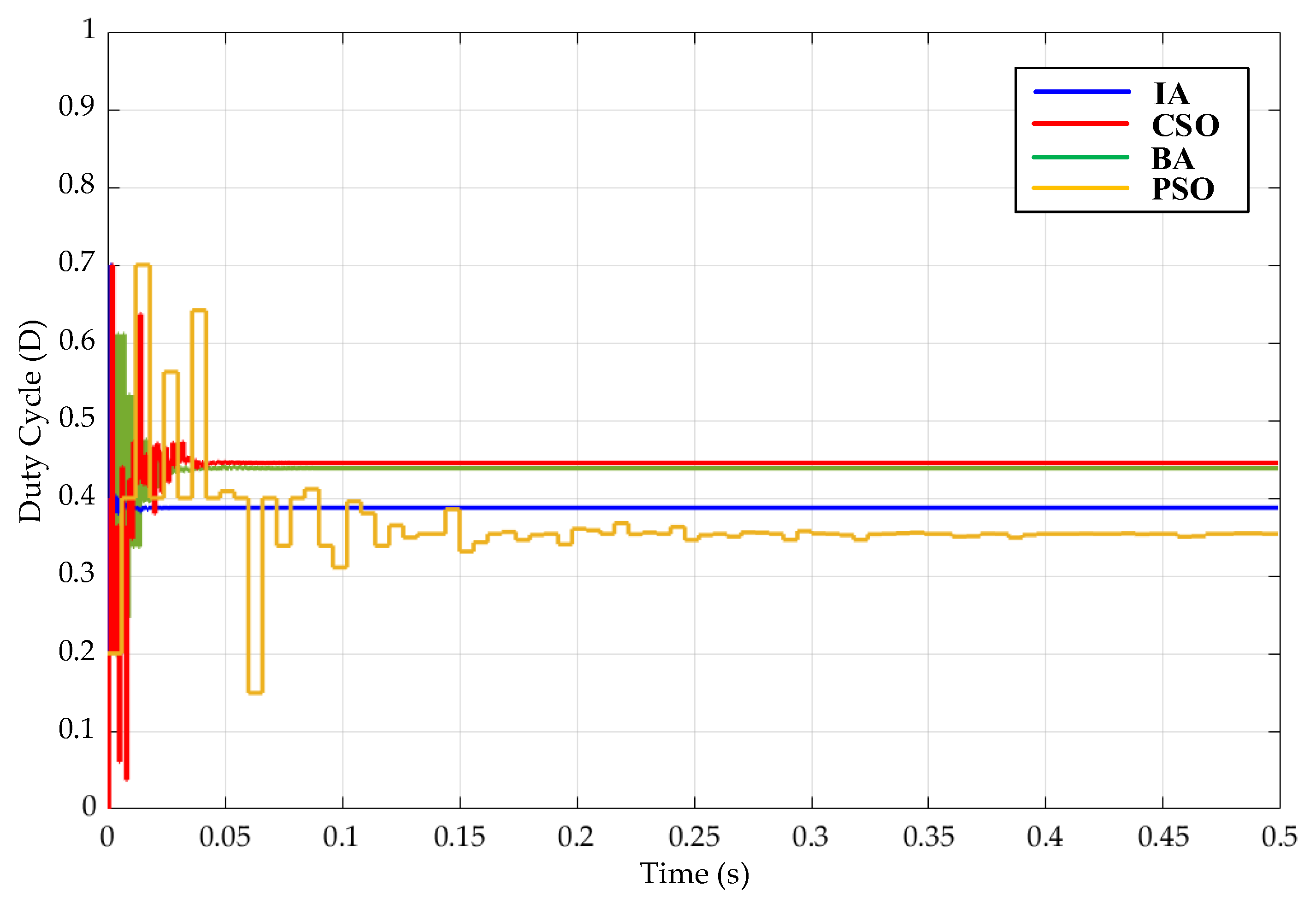
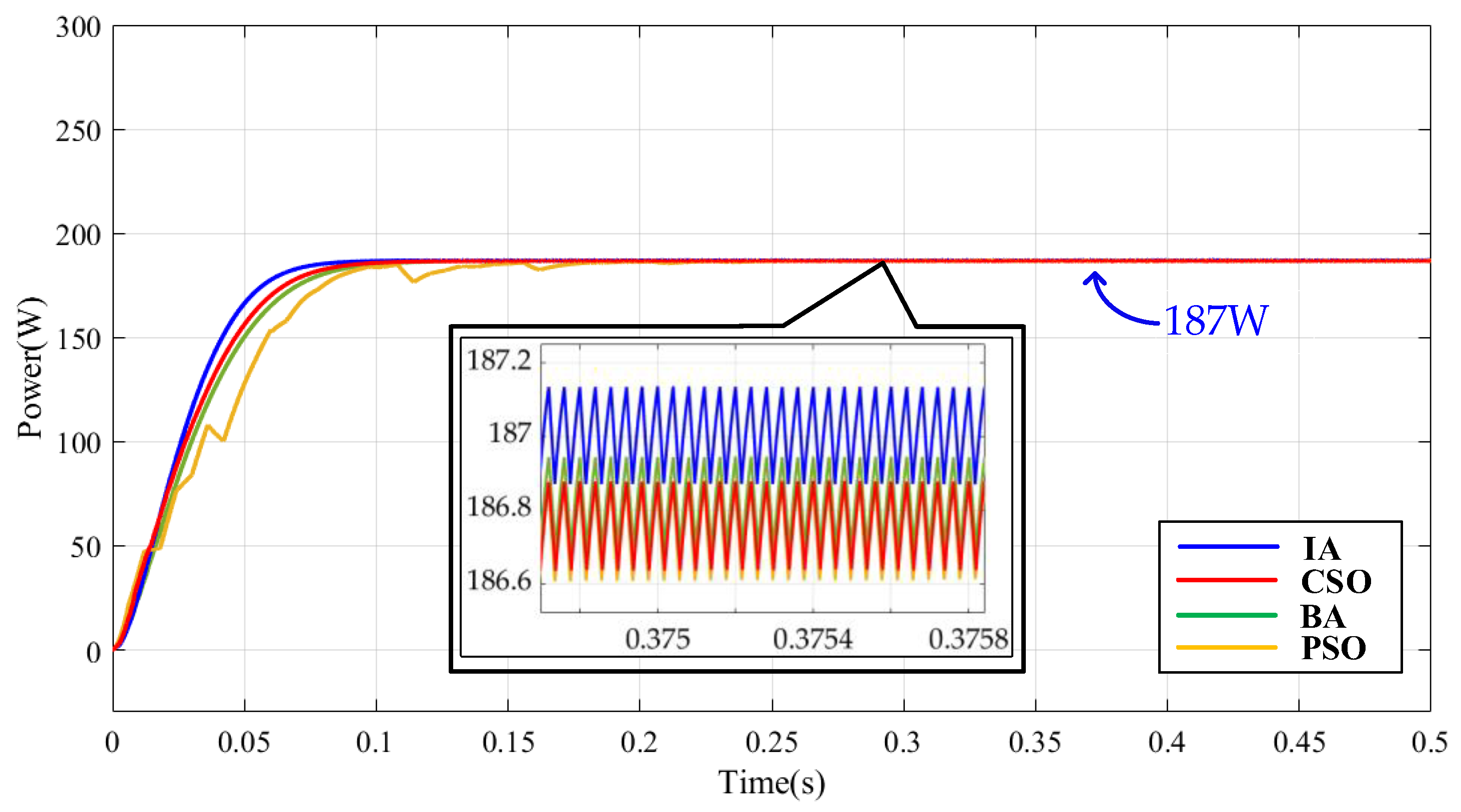
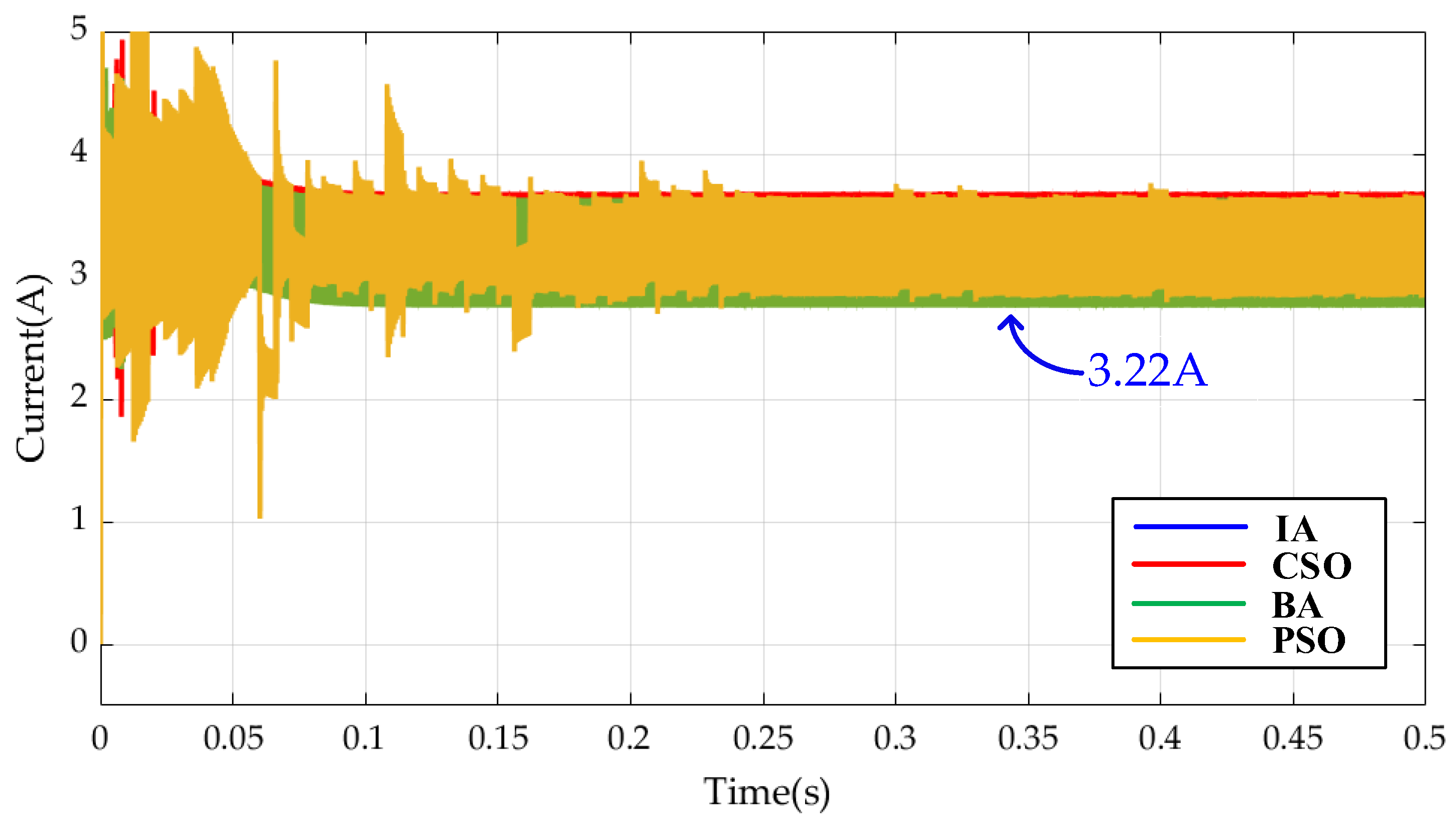
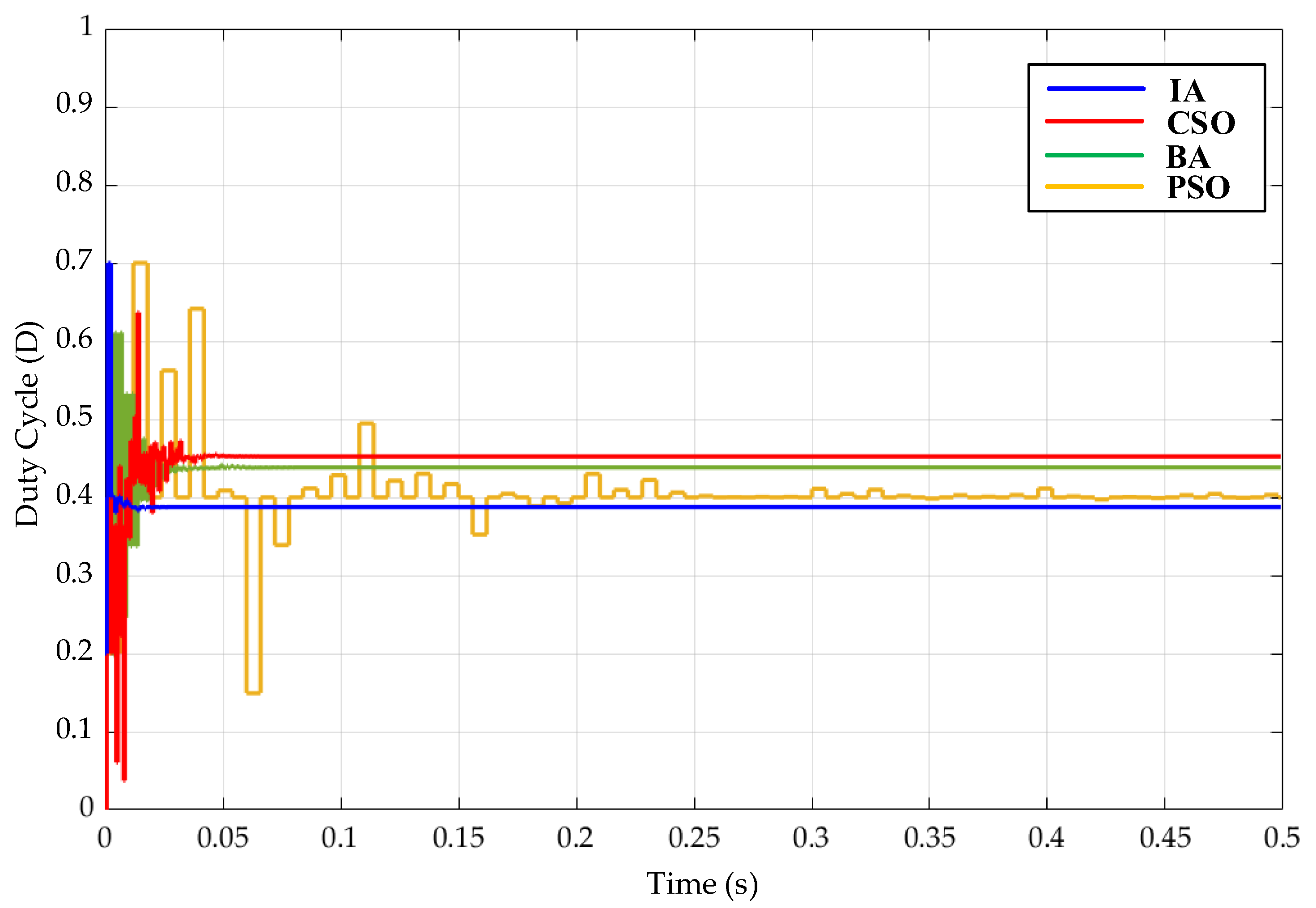
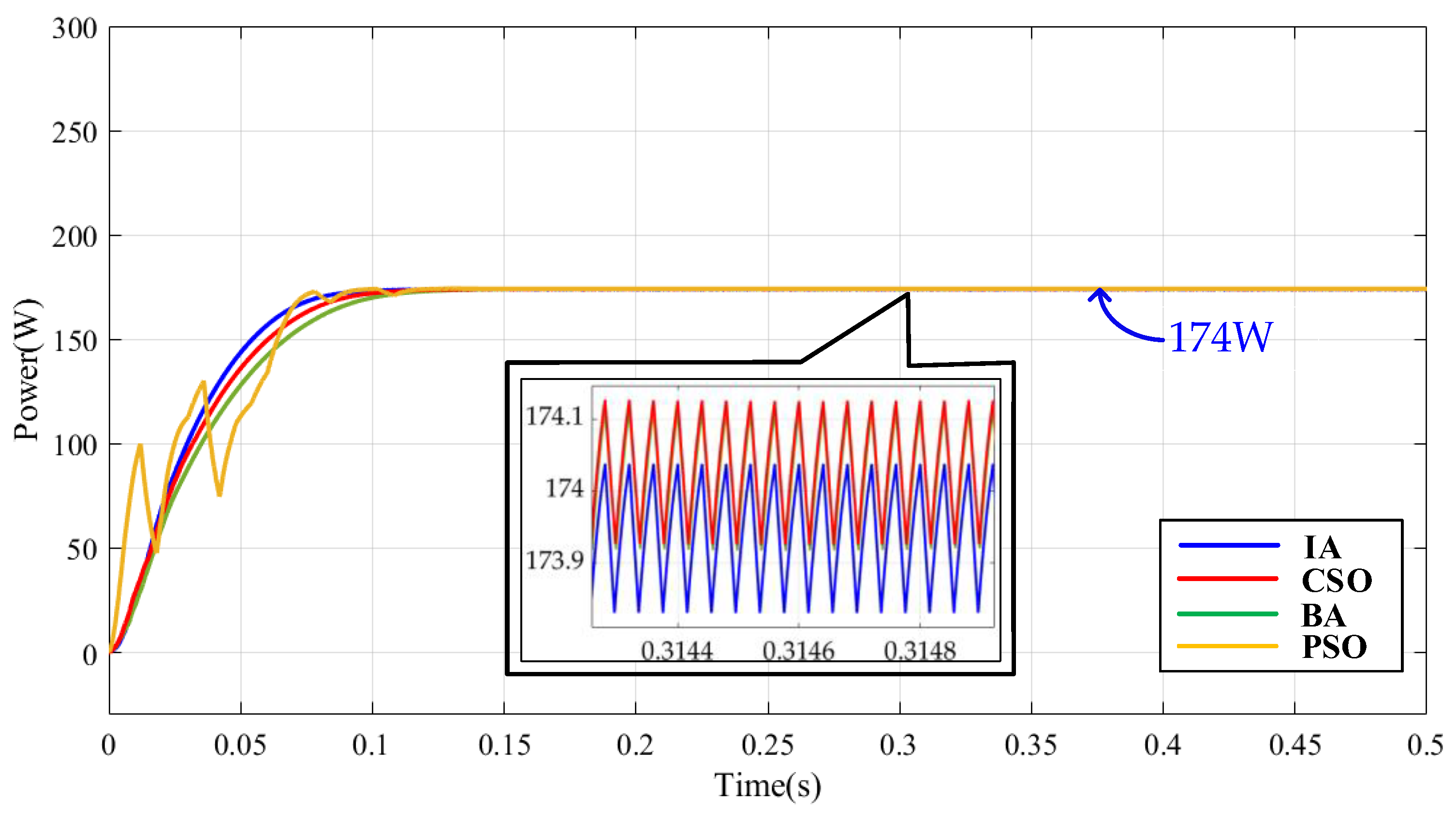
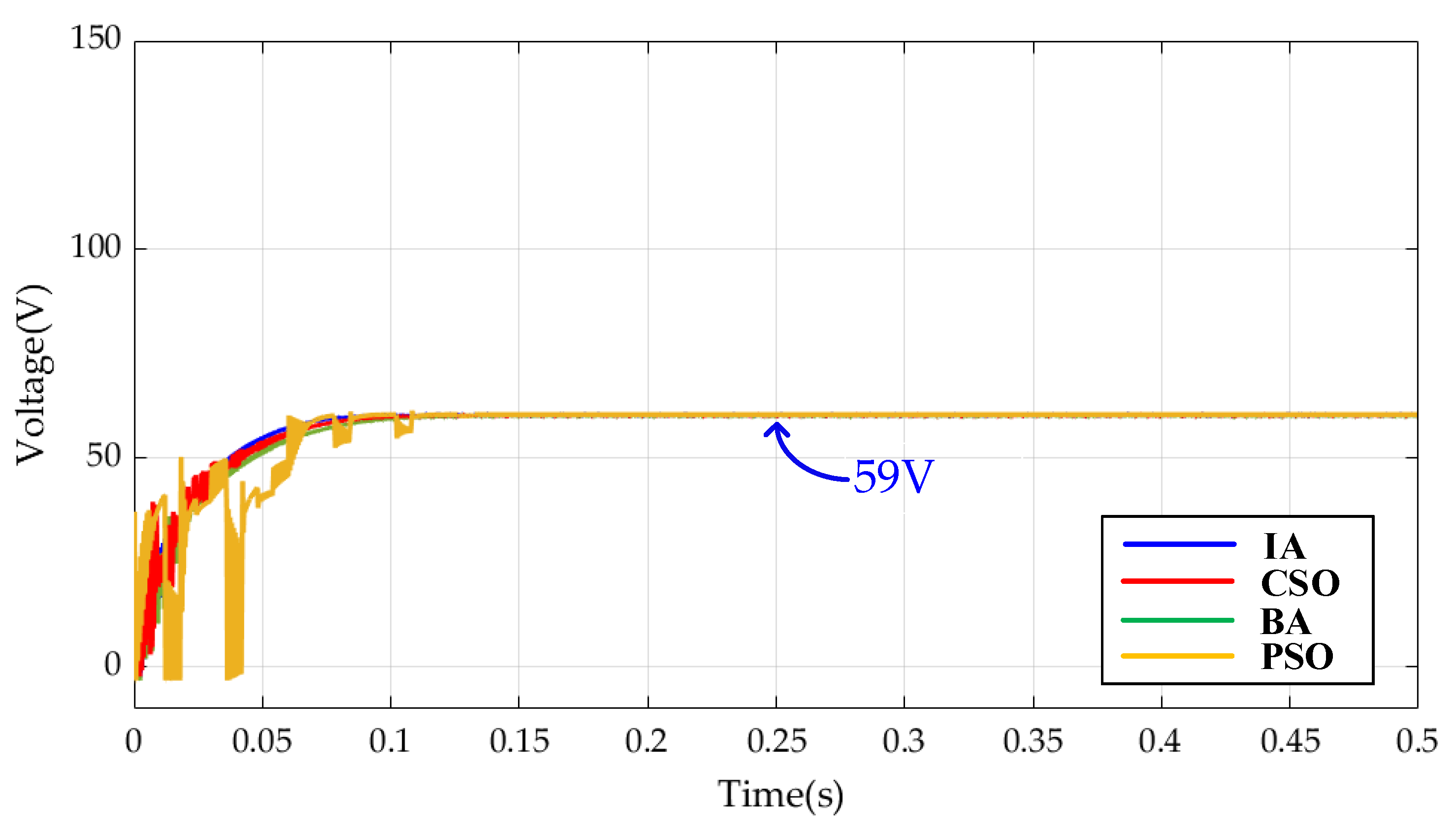
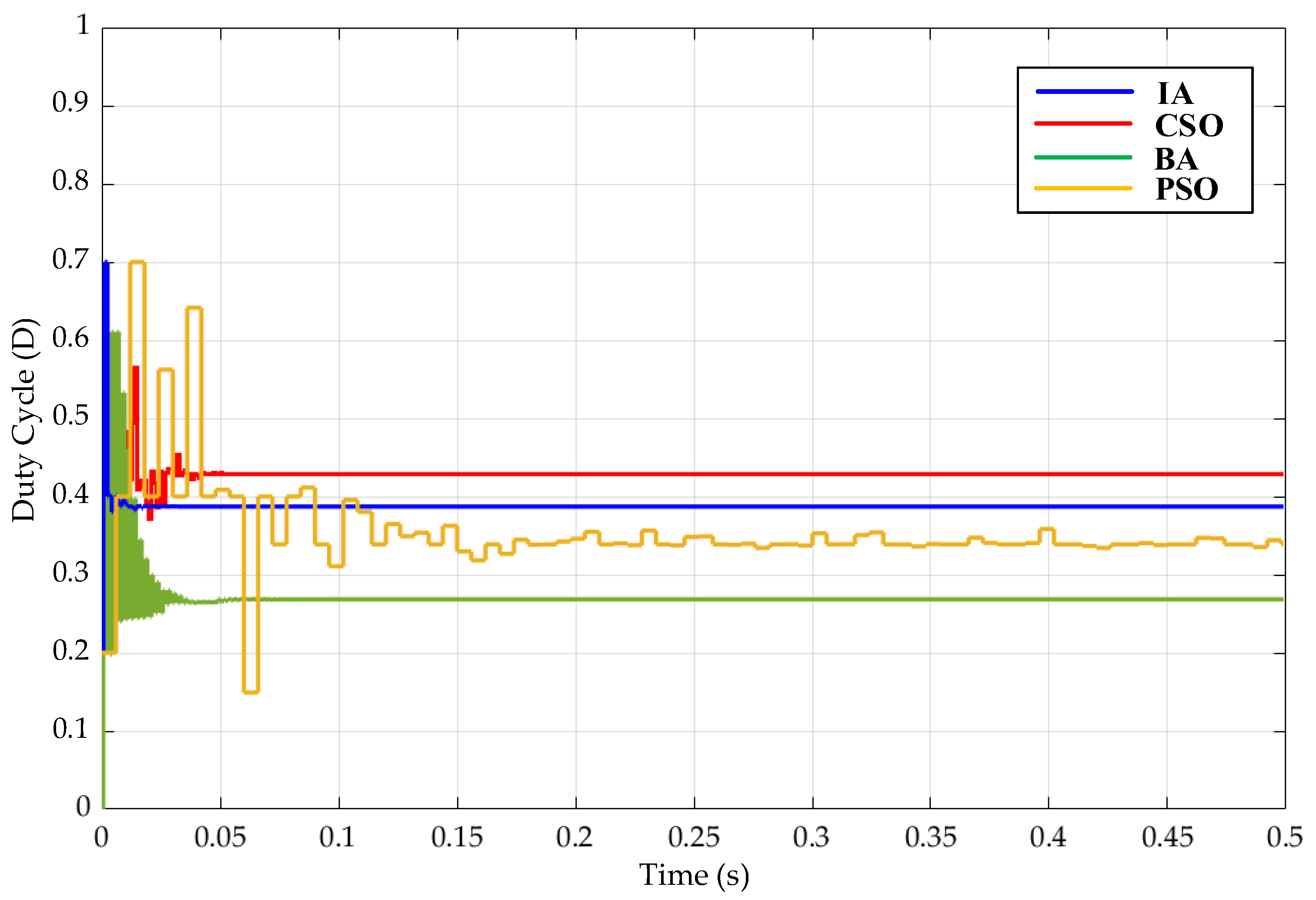
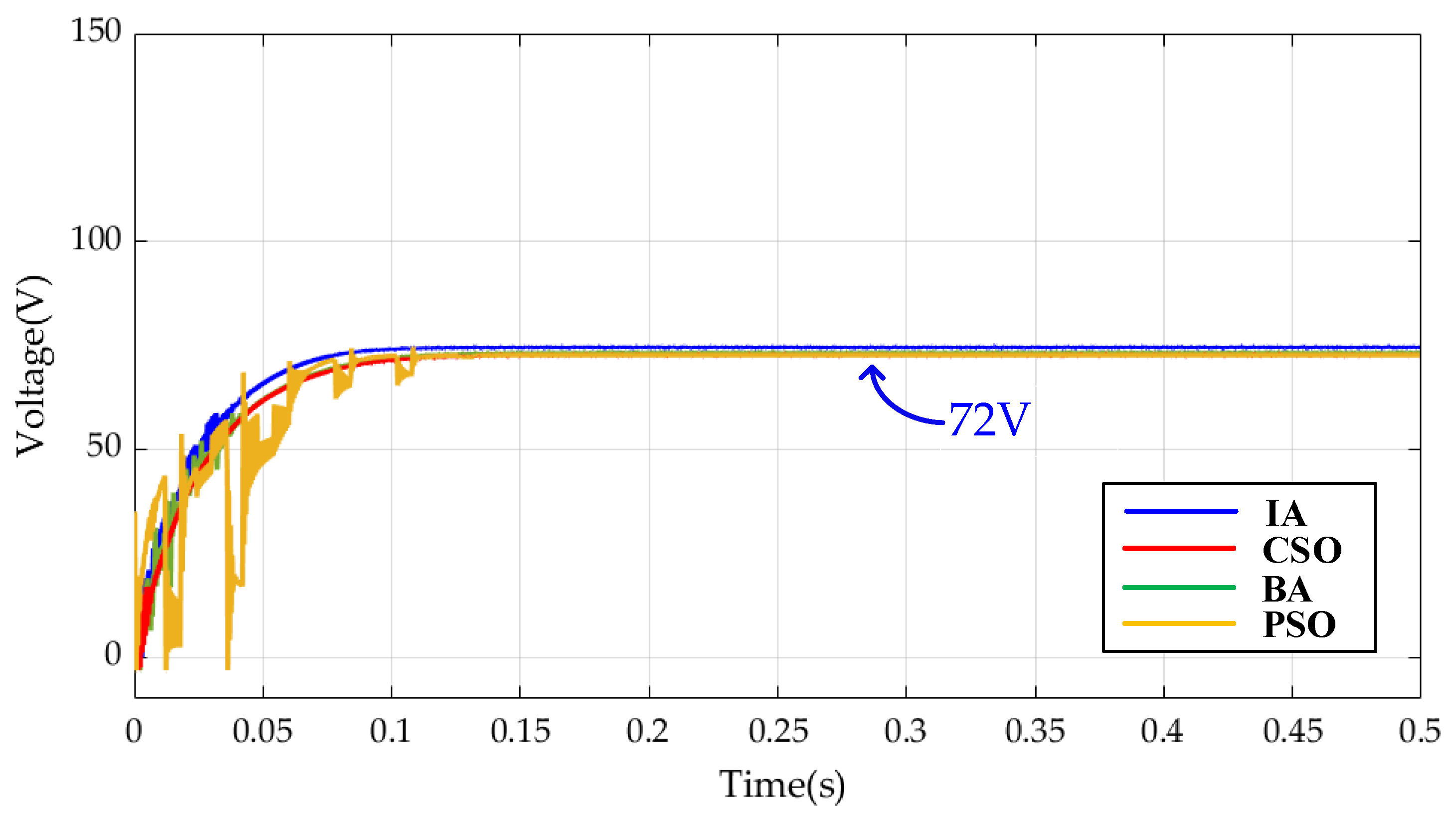
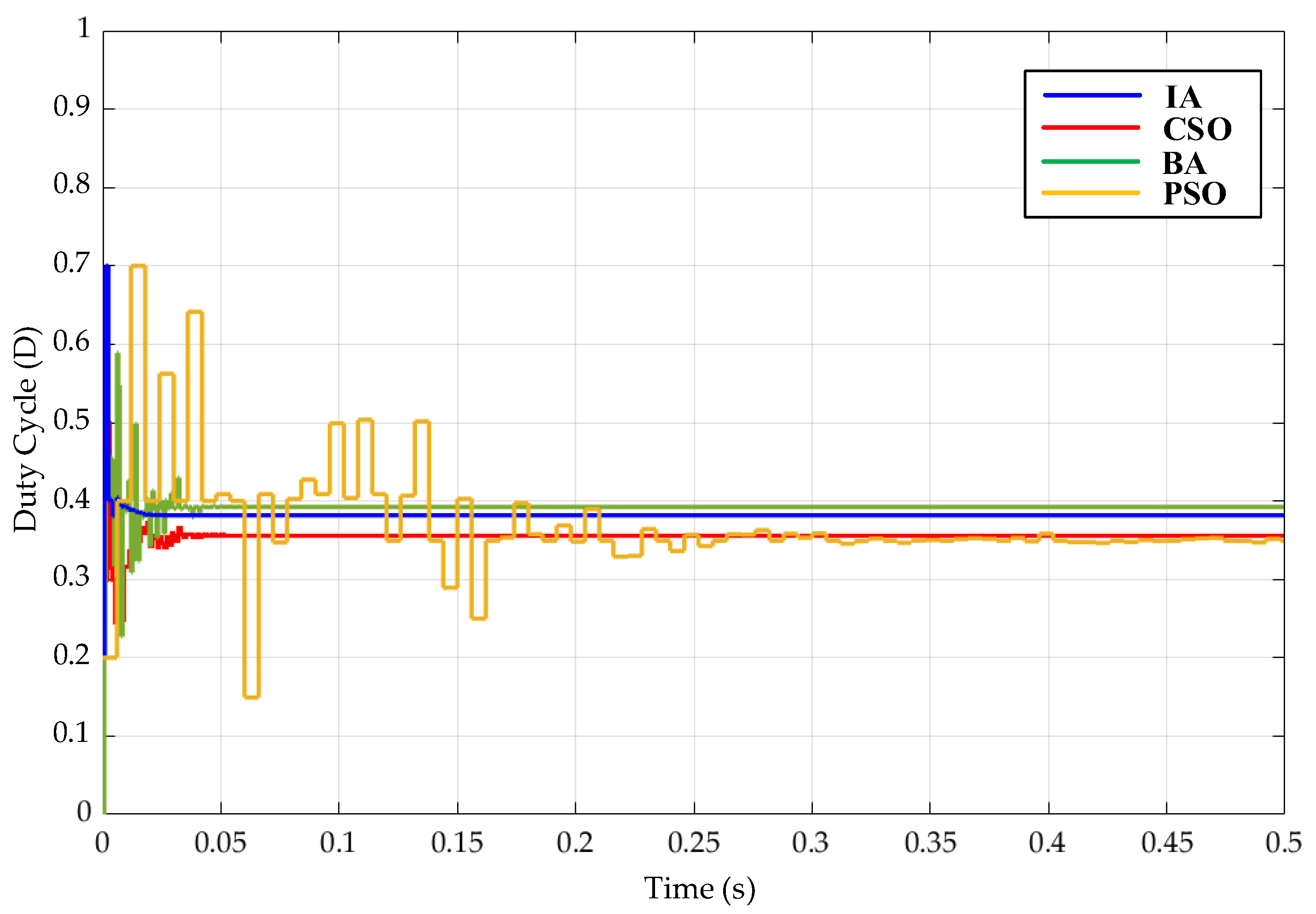
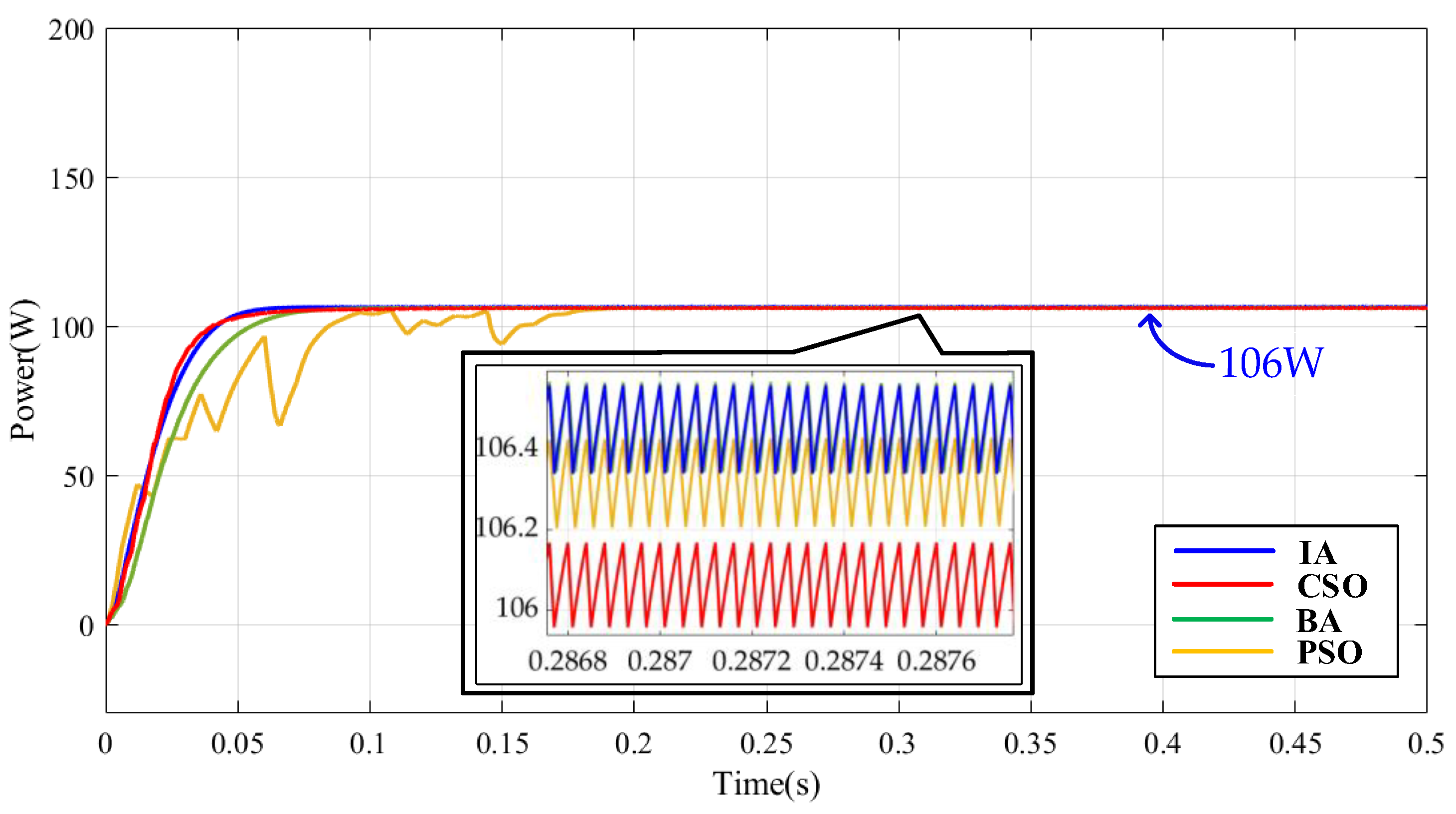
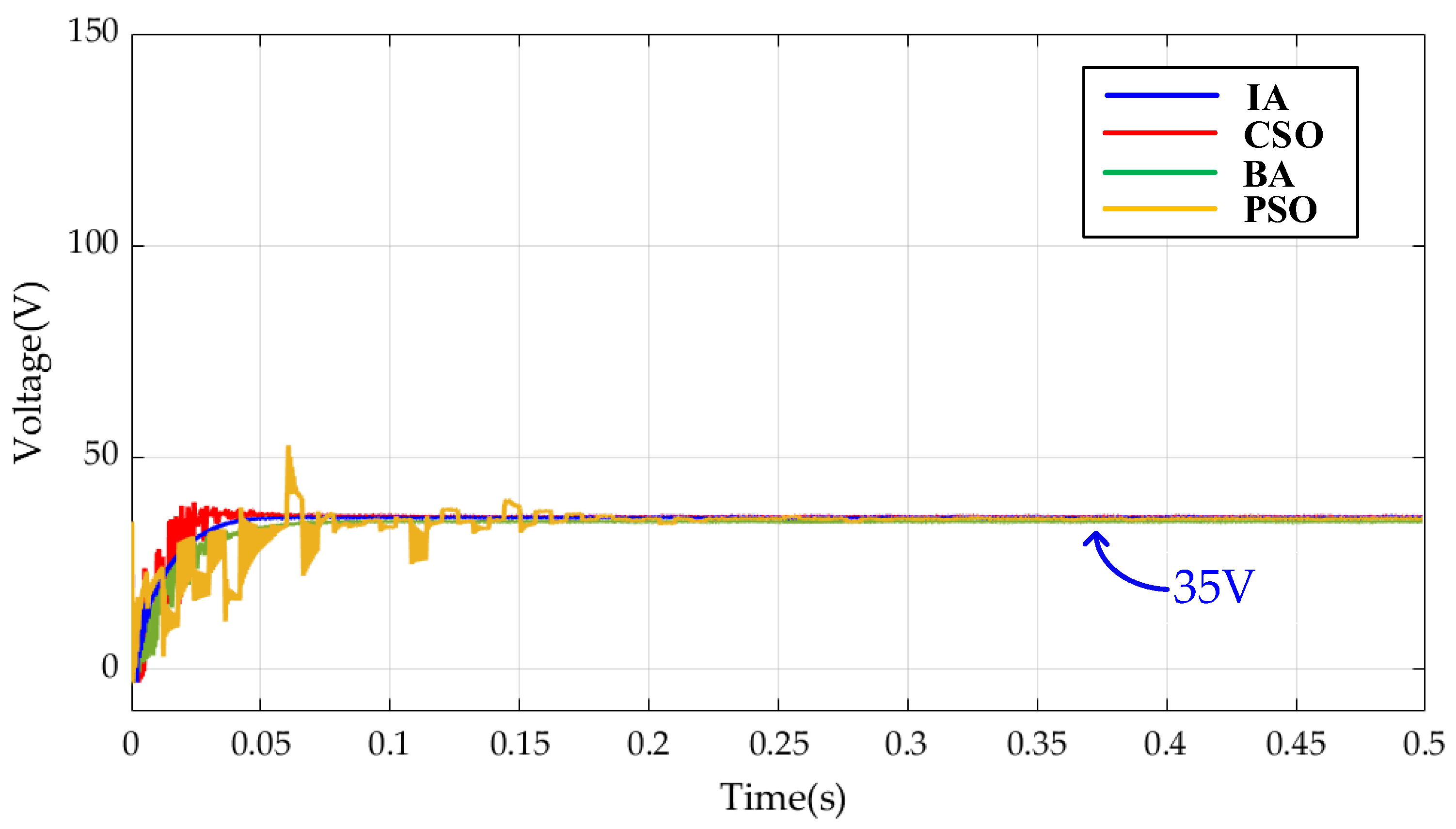
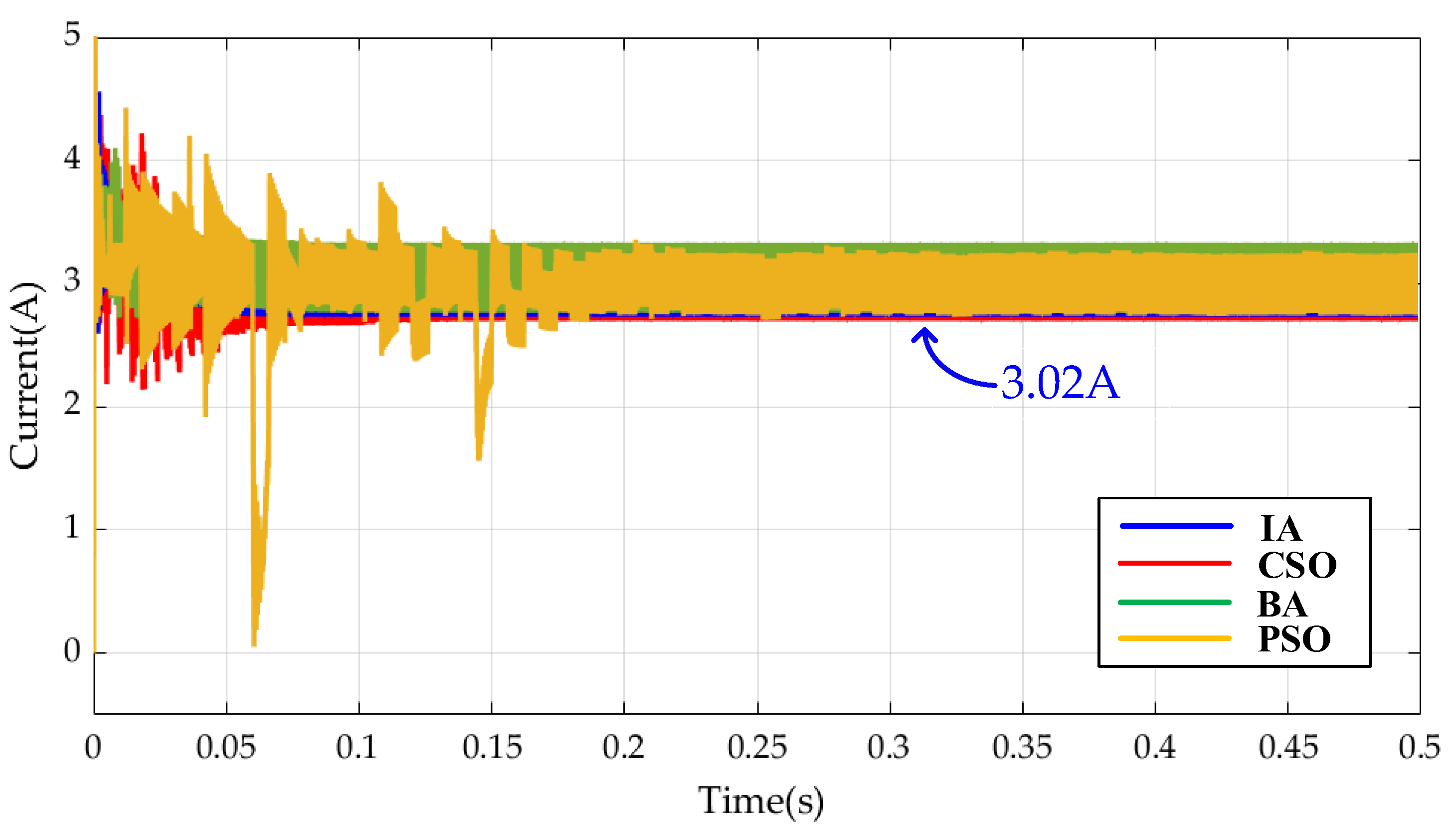
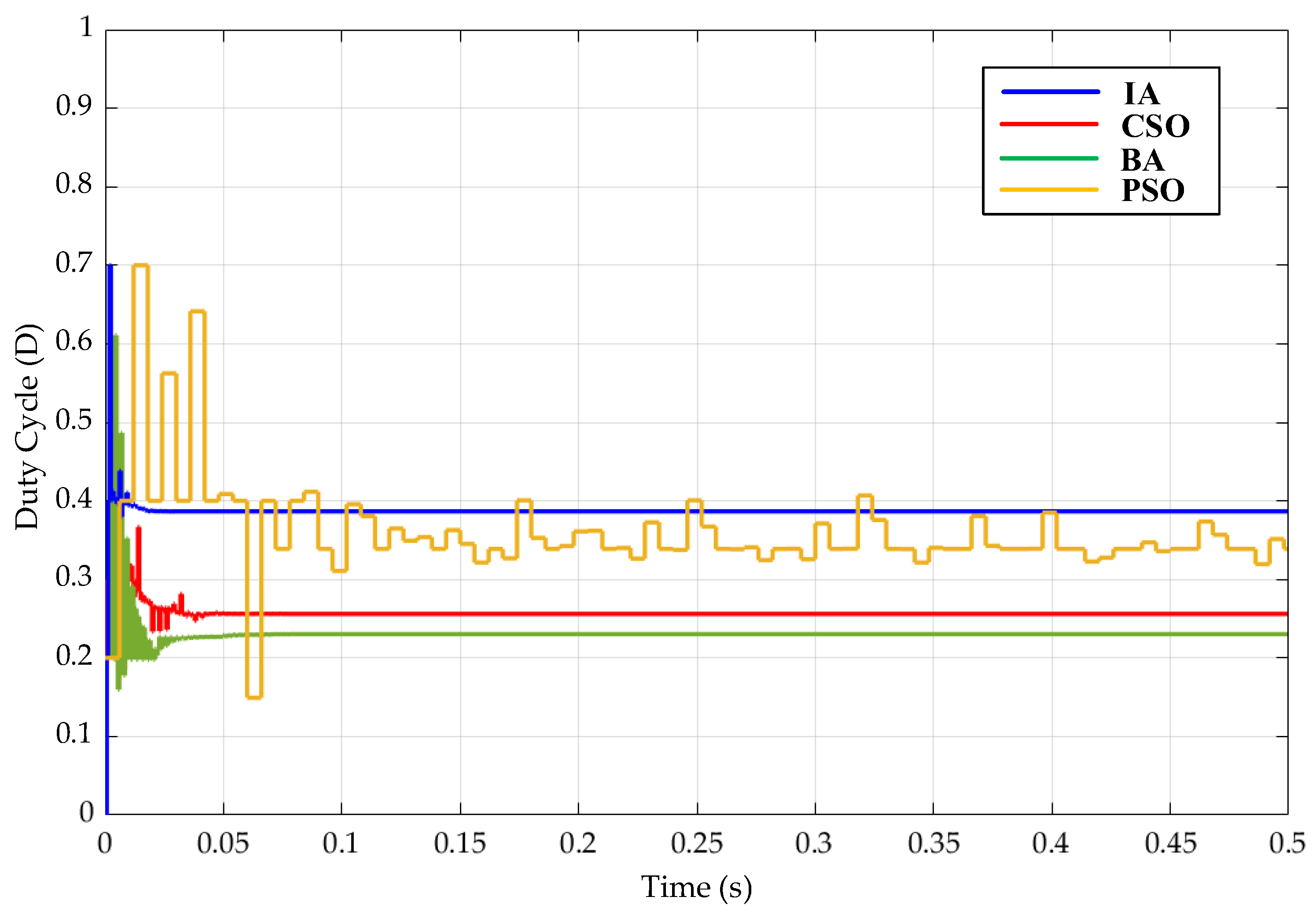
5. Simulation Results
- (1)
- Case 1 Test
- (2)
- Case 2 Test
- (3)
- Case 3 Test
- (4)
- Case 4 Test
- (5)
- Case 5 Test
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, X.; Huang, B.; Ye, Y.; Fang, Y.; Wang, Z.; He, X. Optimizing Grid-connected Photovoltaic Systems through Reactive Power Control Strategy. In Proceedings of the 2023 Panda Forum on Power and Energy (PandaFPE), Chengdu, China, 27–30 April 2023; pp. 119–124. [Google Scholar]
- Lu, K.C.; Lin, F.J.; Yang, B.H. Profit Optimization-based Power Compensation Control Strategy for Grid-Connected PV System. IEEE Syst. J. 2018, 12, 2878–2881. [Google Scholar] [CrossRef]
- Routray, D.; Rout, P.K.; Sahu, B.K. A Brief Review and Comparative Analysis of Two Classical MPPT Techniques. In Proceedings of the 2021 International Conference in Advances in Power, Signal, and Information Technology (APSIT), Bhubaneswar, India, 8–10 October 2021; pp. 1–6. [Google Scholar]
- Masoum, M.A.S.; Dehbonei, H.; Fuchs, E.F. Theoretical and Experimental Analyses of Photovoltaic Systems with Voltage and Current-based Maximum Power-point Tracking. IEEE Trans. Energy Convers. 2002, 17, 514–522. [Google Scholar] [CrossRef]
- Shams, I.; Mekhilef, S.; Tey, K.S. Improved Social Ski Driver-based MPPT for Partial Shading Conditions Hybridized with Constant Voltage Method for Fast Response to Load Variations. IEEE Trans. Sustain. Energy 2021, 12, 2255–2267. [Google Scholar] [CrossRef]
- Femia, N.; Granozio, D.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Predictive & Adaptive MPPT Perturb and Observe Method. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 934–950. [Google Scholar] [CrossRef]
- Killi, M.; Samanta, S. Modified Perturb and Observe MPPT Algorithm for Drift Avoidance in Photovoltaic Systems. IEEE Trans. Ind. Electron. 2015, 62, 5549–5559. [Google Scholar] [CrossRef]
- Tsai, Z.M.; Sun, K.J.; Vendelin, G.D.; Wang, H. A New Feedback Method for Power Amplifier with Unilateralization and Improved Output Return Loss. IEEE Trans. Microw. Theory Tech. 2006, 54, 1590–1597. [Google Scholar] [CrossRef]
- Verma, P.; Katal, N.; Jain, G.; Jayaswal, K. Global Maximum Power Point Tracking Methods for Multi-Peak Power Versus Voltage Curve of Photovoltaics: A Review. In Proceedings of the 6th IEEE International Conference on Recent Advances and Innovations in Engineering (ICRAIE), Kedah, Malaysia, 1–3 December 2021; pp. 1–5. [Google Scholar]
- Ma, Y.; Zhou, X.; Gao, Z.; Bai, T. Summary of the Novel MPPT (Maximum Power Point Tracking) Algorithm Based on Few Intelligent Algorithms Specialized on Tracking the GMPP (Global Maximum Power Point) for Photovoltaic Systems under Partially Shaded Conditions. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 6–9 August 2017; pp. 311–315. [Google Scholar]
- Huang, Y.P.; Huang, M.Y.; Ye, C.E. A Fusion Firefly Algorithm with Simplified Propagation for Photovoltaic MPPT under Partial Shading Conditions. IEEE Trans. Sustain. Energy 2020, 11, 2641–2652. [Google Scholar] [CrossRef]
- Chao, K.H.; Zhang, S.W. An Maximum Power Point Tracker of Photovoltaic Module Arrays Based on Improved Firefly Algorithm. Sustainability 2023, 15, 8550. [Google Scholar] [CrossRef]
- Pragallapati, N.; Sen, T.; Agarwal, V. Adaptive Velocity PSO for Global Maximum Power Control of a PV Array under Nonuniform Irradiation Conditions. IEEE J. Photovolt. 2017, 7, 624–639. [Google Scholar] [CrossRef]
- Tey, K.S.; Mekhilef, S.; Seyedmahmoudian, M. Implementation of Bat Algorithm as Maximum Power Point Tracking Technique for Photovoltaic System under Partial Shading Conditions. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 2531–2535. [Google Scholar]
- Eltamaly, A.M.; AI-Saud, M.S.; Abokhalil, A.G. A Novel Bat Algorithm Strategy for Maximum Power Point Tracker of Photovoltaic Energy Systems Under Dynamic Partial Shading. IEEE Access 2020, 8, 10048–10060. [Google Scholar] [CrossRef]
- Chao, K.H.; Bau, T.T.T. Global Maximum Power Point Tracking of Photovoltaic Module Arrays Based on an Improved Intelligent Bat Algorithm. Electronics 2024, 13, 1207. [Google Scholar] [CrossRef]
- Chao, K.H.; Nguyen, T.B.N. Global Maximum Power Point Tracking of a Photovoltaic Module Array Based On Modified Cat Swarm Optimization. Appl. Sci. 2024, 14, 2853. [Google Scholar] [CrossRef]
- Thangam, T.; Mythuvel, K. Hybrid Algorithm Based PFoPID Control Design of a Grid-connected PV Inverter for MPPT. In Proceedings of the IEEE Second International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 15–17 July 2020; pp. 992–998. [Google Scholar]
- Guo, X.C.; Xu, D. Application of Improved Cat Swarm Optimization in MPPT Control of Photovoltaic Arrays. IOP Conf. Ser. Earth Environ. Sci. 2018, 153, 032024. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Kang, J.W.; Park, H.J.; Ro, J.; Jung, H.K. A Strategy-selecting Hybrid Optimization Algorithm to Overcome the Problems of the No Free Lunch Theorem. IEEE Trans. Magn. 2018, 54, 8201904. [Google Scholar] [CrossRef]
- SunWorld Datasheet. Available online: http://www.ecosolarpanel.com/ecosovhu/products/18569387_0_0_1.html (accessed on 1 April 2025).
- Chao, K.H.; Chang, L.Y.; Xu, F.Q. Smart Fault-tolerant Control System Based on Chaos Theory and Extension Theory for Locating Faults in a Three-level T-type Inverter. Appl. Sci. 2019, 9, 3071. [Google Scholar] [CrossRef]
- Luo, J.; Zhou, J.; Jiang, X. A Modification of The Imperialist Competitive Algorithm with Hybrid Methods for Constrained Optimization Problems. IEEE Access 2021, 9, 161745–161760. [Google Scholar] [CrossRef]
- International Society of Aesthetic Plastic Surgeons (ISAPS). Global Survey 2015. Available online: https://www.isaps.org/discover/about-isaps/global-statistics/reports-and-press-releases/global-survey-2015-full-report-and-press-releases-english/ (accessed on 2 June 2025).
- Azer, P.; Emadi, A. Generalized State Space Average Model for Multi-Phase Interleaved Buck, Boost and Buck-Boost DC-DC Converters: Transient, Steady-State and Switching Dynamics. IEEE Access 2020, 8, 77735–77745. [Google Scholar] [CrossRef]
- Veerachary, M.; Kumar, P. Analysis and Design of Quasi-Z-Source Equivalent DC–DC Boost Converters. IEEE Trans. Ind. Appl. 2020, 56, 6642–6656. [Google Scholar] [CrossRef]
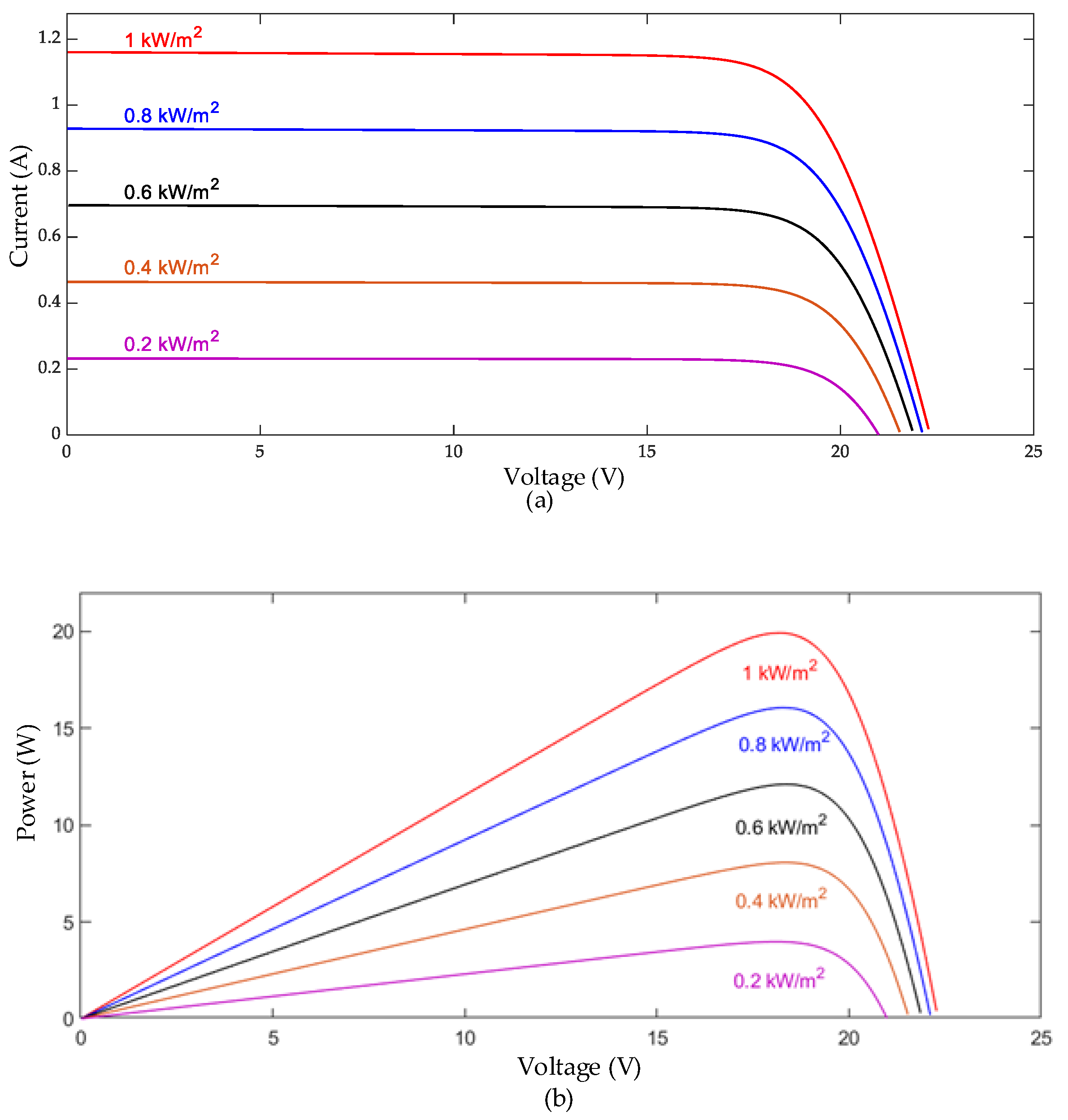

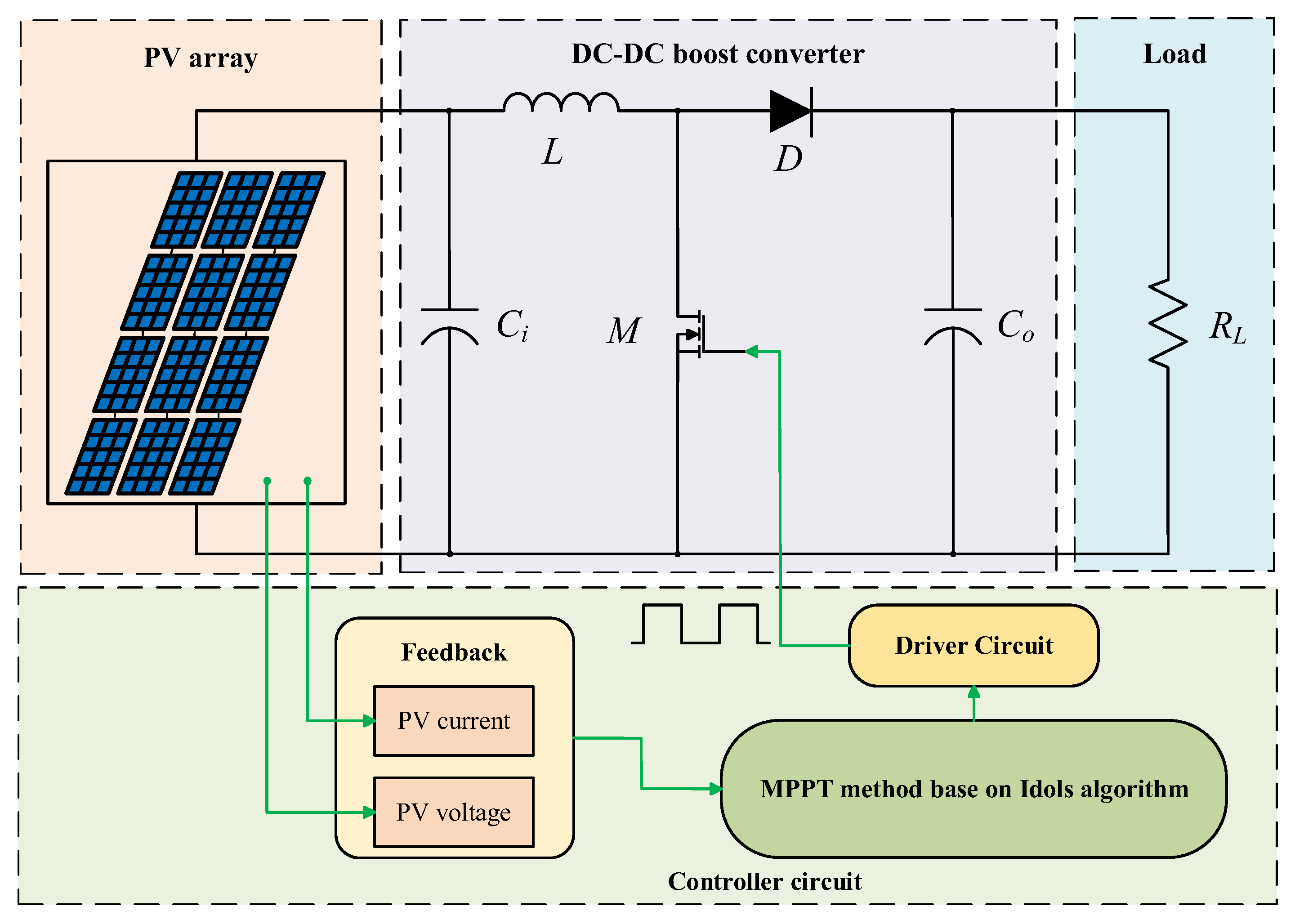
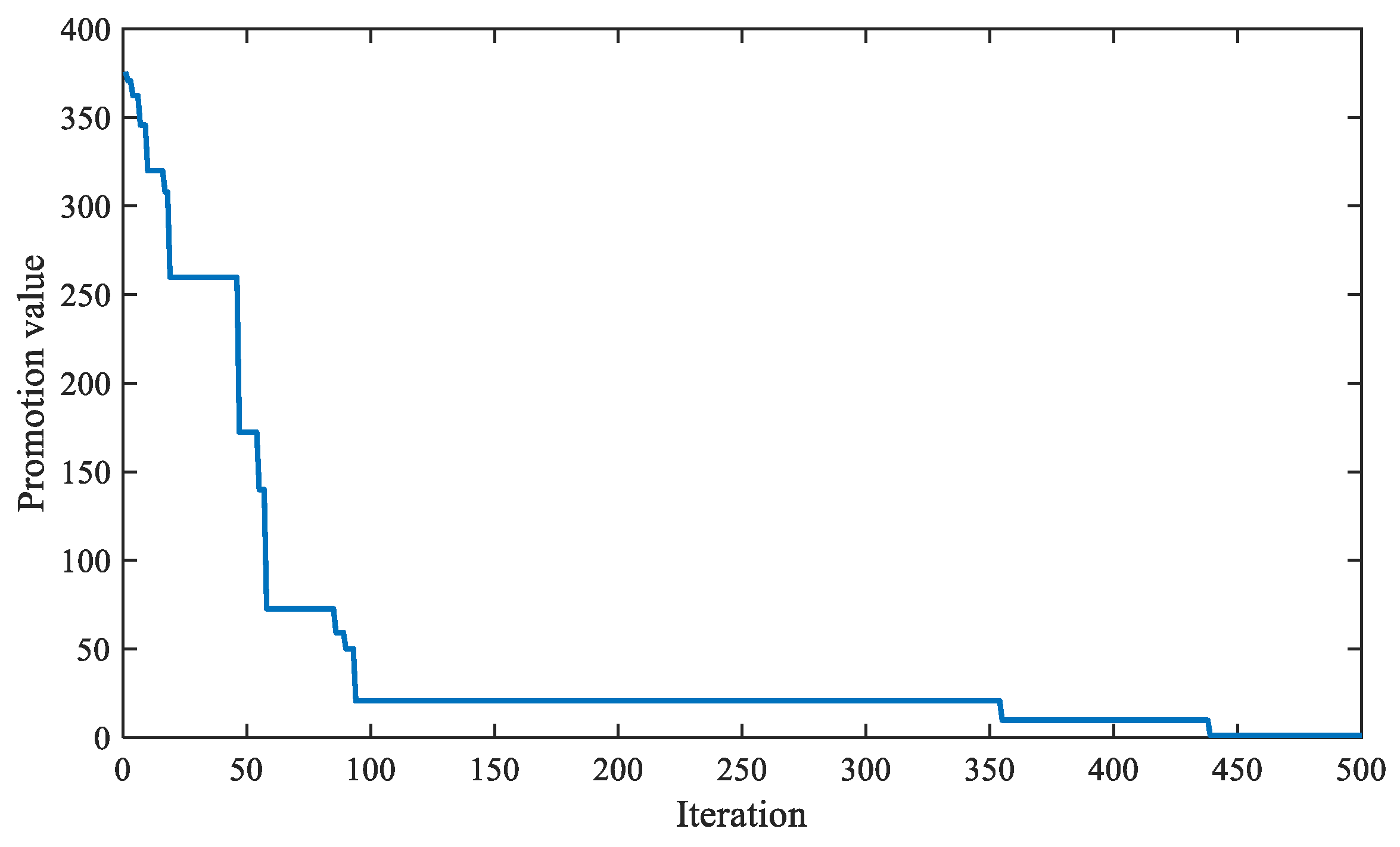
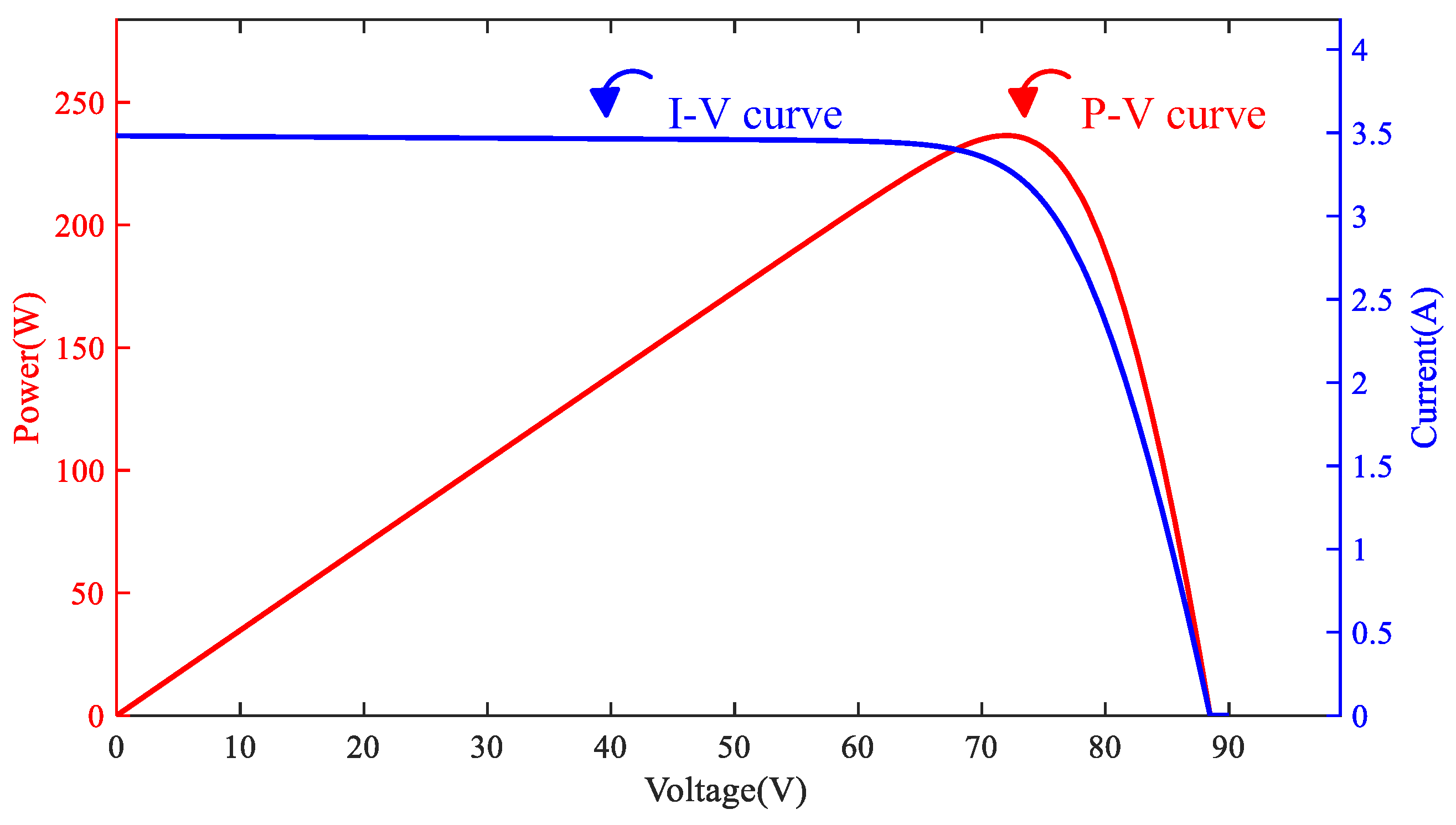




| Parameter | Value |
|---|---|
| Maximum output power (Pmax) | 20 W |
| Maximum power point current (Impp) | 1.1 A |
| Maximum power point voltage (Vmpp) | 18.18 V |
| Short-circuit current (Isc) | 1.15 A |
| Open-circuit voltage (Voc) | 22.32 V |
| Overall dimensions of a single module | 395 × 345 × 17 mm |
| TNt | Total number of trainees planned for cultivation by the entertainment company (trainee total). |
| OC | Originally referring to “online celebrity,” which originally meant internet celebrities. Over time, it has come to refer to “traffic stars,” so it is defined here as the online celebrity of each trainee. |
| PM | Promotion value, which is proportional to the change in online celebrity (ΔOC). |
| BOC | Basic online celebrity, which is proportional to individual physique and promotion value. |
| BF | Body fat percentage. |
| facialA | Originally referring to “facial attractiveness,” it is commonly referred to as “facial value” in modern internet slang. |
| Aw | Average weight. |
| SL | “Solo,” commonly used in dance clubs, the entertainment industry, rap, and modern internet slang, generally referring to solo singing, solo playing, solo dancing, and other types of solo performances. |
| Sc | Solo coefficient. |
| PBP | Public performance, commonly referred to as a group performance. |
| Pc | Public performance coefficient. |
| fandom | Originally referring to “fan culture,” it later came to refer to the internet slang “fandom culture,” where “fandom” refers to the group or community of fans. Note: Fandom culture is a cultural term referring to an organization or group formed by a group of fans. |
| AFR | Anti-fan rate, where anti-fans generally refer to people who oppose certain celebrities, commonly known as “haters.” |
| afw | Anti-fan weight. |
| fans | Current number of fans. |
| fr | Fans ratio. |
| Component | Specification |
|---|---|
| Input capacitor | 220 uF/450 V |
| Output capacitor | 470 uF/450 V |
| Energy storage inductor | 1.68 mH |
| Fast diode (IQBD30E60A1) | 600 V/60 A |
| Switching transistor (IRFP460) | 500 V/20 A |
| Parameter Name | Setting Value |
|---|---|
| Fandom | 50 |
| Random value (r) | [0~1] |
| Solo performance coefficient (Sc) | 1.2 |
| Public performance coefficient (Pc) | 2 |
| Anti-fan weight (afw) | 0.4 |
| Facial attractiveness (facialA) | 100 |
| Average weight (Aw) | 50 kg |
| Body fat percentage (BFP) | 20% |
| Case | P-V Characteristic Curve Peak Numbers | Shading Ratio for 4s3p Configuration |
|---|---|---|
| 1 | Single peak | (0% shading + 0% shading + 0% shading + 0% shading)// |
| (0% shading + 0% shading + 0% shading + 0% shading)// | ||
| (0% shading + 0% shading + 0% shading + 0% shading) | ||
| 2 | Dual peak (the maximum power point is on the left side) | (0% shading + 0% shading + 0% shading + 90% shading)// |
| (0% shading + 0% shading + 0% shading + 0% shading)// | ||
| (0% shading + 0% shading + 0% shading + 0% shading) | ||
| 3 | Triple peak (the maximum power point is in the middle) | (0% shading + 0% shading + 40% shading + 90% shading)// |
| (0% shading + 0% shading + 0% shading + 0% shading)// | ||
| (0% shading + 0% shading + 0% shading + 0% shading) | ||
| 4 | Quadruple peak (the maximum power point is at the first peak) | (0% shading + 30% shading + 60% shading + 70% shading)// |
| (0% shading + 0% shading + 0% shading + 0% shading)// | ||
| (0% shading + 0% shading + 0% shading + 0% shading) | ||
| 5 | Quadruple peak (the maximum power point is at the third peak) | (0% shading + 10% shading + 80% shading + 90% shading)// |
| (0% shading + 10% shading + 80% shading + 90% shading)// | ||
| (0% shading + 10% shading + 80% shading + 90% shading) |
| Case | Number of Peaks on the P-V Curve | Tracking Efficiency (%) | |||
|---|---|---|---|---|---|
| PSO | BA | CSO | IA | ||
| 1 | Single peak | 78.41% | 83.92% | 84.62% | 85.63% |
| 2 | Dual peak (MPP on the left side) | 81.26% | 85.55% | 85.69% | 86.71% |
| 3 | Triple peak (MPP is in the middle) | 83.41% | 85.59% | 85.90% | 86.93% |
| 4 | Quadruple peak (MPP is at the first peak) | 74.4% | 84.95% | 84.73% | 85.86% |
| 5 | Quadruple peak (MPP is at the third peak) | 75.34% | 82.68% | 85.94% | 86.47% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chao, K.-H.; Kuo, Y.-C. Development of a Global Maximum Power Point Tracker for Photovoltaic Module Arrays Based on the Idols Algorithm. Mathematics 2025, 13, 2999. https://doi.org/10.3390/math13182999
Chao K-H, Kuo Y-C. Development of a Global Maximum Power Point Tracker for Photovoltaic Module Arrays Based on the Idols Algorithm. Mathematics. 2025; 13(18):2999. https://doi.org/10.3390/math13182999
Chicago/Turabian StyleChao, Kuei-Hsiang, and Yi-Chan Kuo. 2025. "Development of a Global Maximum Power Point Tracker for Photovoltaic Module Arrays Based on the Idols Algorithm" Mathematics 13, no. 18: 2999. https://doi.org/10.3390/math13182999
APA StyleChao, K.-H., & Kuo, Y.-C. (2025). Development of a Global Maximum Power Point Tracker for Photovoltaic Module Arrays Based on the Idols Algorithm. Mathematics, 13(18), 2999. https://doi.org/10.3390/math13182999







