Abstract
Network reliability refers to a probabilistic measure of a network system’s ability to maintain its intended service functionality within a specified time interval and under given operating conditions. Let be the set of all simple two-terminal networks on n vertices and m edges. If each edge operates independently with the same fixed probability , then the two-terminal reliability, denoted by , is the probability that there exists a path between two target vertices s and t. For a given number of vertices n and edges m, there are some graphs within that have higher reliability than others, and these are known as extremely optimal graphs. In this work, we determine the sets of extremely optimal graphs in two classes of two-terminal network with sizes and , consisting of 2 and 5 networks, respectively. Moreover, we identify one class of graphs obtained by deleting some edges among non-target vertices in the complete two-terminal graph, and we count the number of graphs of this class with size by applying the Pólya counting principle.
Keywords:
two-terminal network; two-terminal reliability; extremely optimal graph; reliability polynomial MSC:
05C82
1. Introduction
Network reliability refers to the probability that a network system maintains connectivity between specified nodes under given conditions, typically modeled using probabilistic graph theory that accounts for random failures of edges or nodes [1]. Primary evaluation approaches include exact analytical methods based on minimal path/cut sets, Monte Carlo simulation for large-scale networks, and graph-theoretical methods that identify optimal network configurations through extremal theory. This research provides a theoretical foundation for fault-tolerant network design and has significant application value in fields such as communication networks and distributed systems.
In the study of an optimal network based on extremal theory, the exploration of extremely optimal graphs holds significant theoretical value and application prospects. These graph structures can achieve the theoretical limits of network reliability under given constraints, providing benchmark references for the performance upper bounds in network design. Currently, research in this field remains in its infancy, having extremely limited existing results. The available literature focuses primarily on all-terminal reliability scenarios, which investigate the properties of extremal graphs that ensure connectivity among all the nodes in a network. However, there is a notable lack of systematic research on two-terminal reliability scenarios, which is a more practically valuable context in engineering applications. By advancing the study of extremely optimal graphs in two-terminal networks, this research will propel the expansion of network reliability theory from all-connected scenarios to more targeted point-to-point connectivity scenarios, carrying substantial academic innovation value and engineering application significance.
Let be a two-terminal graph, where is the vertex set and is the edge set. An -path set in the two terminal graph G is a set of edges in that contains a path from the vertices s to t. In this work, we are only concerned with simple graphs. In fact, determining exact values for the size of an -path set is a difficult problem [2,3].
The above model—a two-terminal graph—can be applied to observe the two-terminal reliability of a network. If each edge of such a graph operates independently with the same fixed probability , the two-terminal reliability, denoted by , is the probability that there exists a path between the target vertices. Much of the work in this field focuses on identifying bounds on the coefficients of two-terminal reliability polynomials [4,5,6]. A two-terminal graph is said to be uniformly most reliable or uniformly optimal in , if for all and all H in . However, a uniformly optimal graph does not always exist [7]. The problem of graph reliability is then considered from another perspective [8] by asking whether we can find an extremely optimal graph set in which the reliability of any other graph is less than that of each graph in this set for all . We must consider the existence of a uniformly optimal graph and the determination of an extremely optimal graph set. If such a graph exists, then it is clearly the only graph contained in the corresponding extremely optimal graph set. Much similar research has been performed [9,10,11,12,13].
For all-terminal graphs, Zhao [8] proved that when was even, the cardinalities of the extremely optimal graph set for the graph family and were 2 and 6, respectively, and when was odd, the cardinality of the extremely optimal graph set for the graph family was 4. In the case of two-terminal graphs, their extremely optimal graphs are different from those of all-terminal graphs. Two-terminal graphs have been used in real-world applications such as transportation networks [14,15,16,17], but there are few results on this topic.
In [18], the authors determined the uniformly optimal graph of the two-terminal network and proved that, when , there was no uniformly optimal graph in the corresponding network. In this work, we expand the study to extremely optimal graphs with the same conditions as above. In other words, utilizing the related theory of two-terminal graphs, extremely optimal graph sets are found for the cases of and . Moreover, we determine a type of graph obtained by deleting some edges among non-target vertices in the complete two-terminal graph, and we apply the Pólya counting principle to count the number of graphs in this class with size .
This study of extremely optimal networks provides novel theoretical perspectives and optimization pathways for the analysis of network reliability. These graph structures exhibit optimal reliability characteristics under specific constraints, enabling researchers to circumvent the challenge of seeking “universally optimal solutions”. By analyzing the topological properties of extremely optimal graphs, we can not only uncover the intrinsic principles of highly reliable networks but also develop actionable optimization frameworks for practical network design. Through rigorous mathematical proofs and extensive numerical experiments, this research systematically establishes the evaluation criteria and construction methods for extremely optimal graphs. The findings have significant guiding value for engineering practices such as survivability design in communication networks and redundancy configuration in power systems, particularly to improve the resilience of critical infrastructure against random failures and targeted attacks.
2. Existence of the Extremely Optimal Network
For any simple graph G with n vertices and m edges, the two-terminal reliability polynomial can be defined as
where is the number of -path sets with size i in G for each , and is the probability that its edges operate independently.
Definition 1
([8]). Let n and m be positive integers. If there are graphs , such that , for each and all G in , then is an extremely optimal graph set of .
For simplicity, if the graphs satisfy , then denote this by .
Definition 2
([18]). Let and be positive integers.
- 1
- Define as the two-terminal graph on n vertices and m edges with vertex set , and edge set ;
- 2
- Define as the two-terminal graph on n vertices and m edges with vertex set , and edge set ;
- 3
- Define as the two-terminal graph on n vertices and m edges with vertex set , and edge set .
The above three graphs are shown in Figure 1, where the red edges represent the deleted edges, and the blue edges represent the independently operable edges, and the Figure 2, Figure 3, Figure A1 and Figure A2 in the following text represent the same meaning. Furthermore, the pseudo-code for the algorithm of network two-terminal reliability is provided in Appendix A.
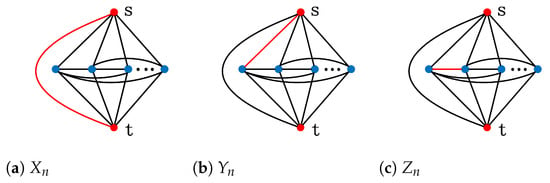
Figure 1.
Graphs , , and .
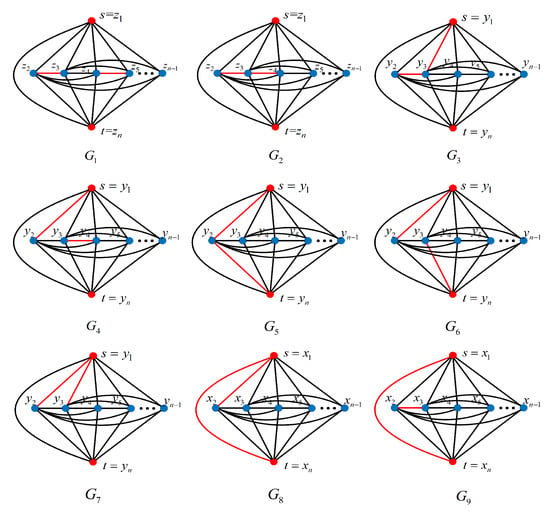
Figure 2.
All cases of graph family .
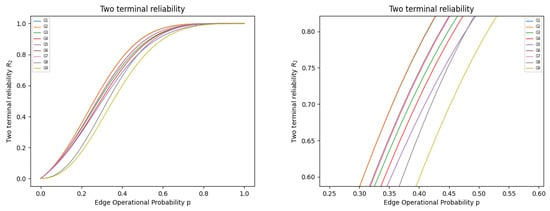
Figure 3.
In the figure, the one on the left shows Two-terminal reliabilities for graphs in the case of ; the one on the right represents its partial enlargement of the left one.
As previously noted, when removing two or three edges from a complete graph, there is no uniformly optimal graph in the graph family [5]. Based on the above case, the existence of the extremely optimal graphs and the determination of the minimal extremely optimal graph set will be considered as follows.
Theorem 1
([18]). Let and be positive integers. If , then there is no uniformly most reliable two-terminal graph in .
To determine the existence of an extremely optimal graph in a graph family is mainly to analyze the reliability of graphs globally on the interval . The reliability of each graph in the extremely optimal graph set is greater than that of any other graph in the same graph family. Later, we analyze the extremely optimal graph sets of two graph families with and .
Now, we classify all graphs into according to three types:
- In an -type graph, the edge and the other edges are deleted;
- In a -type graph, the r edges between the target vertex and non-target vertices are deleted;
- In a -type graph, the r edges between the non-target vertices are deleted.
Theorem 2.
Let be a positive integer and . Then there are two extremely optimal graphs in .
Proof of Theorem 2.
We can construct all the non-isomorphic subgraphs obtained by removing two edges from an n-order complete two-terminal graph, as shown in Figure 2. Based on the above classification, we have the following: -type graphs contain and ; -type graphs contain , , , , and ; -type graphs contain and .
To prove that a -type graph is more reliable than any one of the -type and -type graphs, we show that there are more -path sets with size in -type graphs than in -type graphs and -type graphs by constructing an injection from the -path sets of size k in -type and -type graphs to the -path sets of size k in a -type graph. Thus, we consider the following two cases.
Case 1. A -type graph is more reliable than an -type graph. Without loss of generality, we prove that .
Let , , , and . Now construct an injection from the -path sets of size k in to the -path sets of size k in . Let P be the -path sets of size k in . The following two sub-cases are considered.
Subcase 1.1. Suppose P does not contain an edge . Then set . Note that the image is an -path set in with the same size as P that does not contain edge .
Subcase 1.2. Suppose P contains edge . Then define . Note that the image is an -path set in with the same size as P that contains edge , which is distinct from that in subcase 1.1.
Then is an injection and there are at least as many -path sets in as in . Thus is uniformly more reliable than , i.e., . Similarly, , and .
Case 2. A -type graphs is more reliable than a -type graph. Without loss of generality, we can prove that .
Let , , and . We construct a mapping from an -path sets of k in to an -path sets of k in . Let P be an -path sets of size in . We discuss four sub-cases.
Subcase 2.1. Suppose does not contain edge . Then let . The image is an -path sets in with the same size as P, which does not contain edge .
Subcase 2.2. Suppose P contains edge and is still an -path sets. Then define . The image is an -path sets in with the same size as P which contains edge . We can see that is still an -path sets.
Subcase 2.3. Suppose P contains edge and is not an -path sets but it is a -path-set. Then define . Note that the image is an -path sets in with the same size as P, which contains the edge . Evidently, is not an -path sets which is distinct from any one of the images in subcase 2.2.
Subcase 2.4. Now suppose P contains edge , is not an -path sets and it is also not a -path-set. Then define
.
Note that has the same size as P, which is completely disjoint from the image described in subcase 2.3. Since the mapping defined in both of these two cases yields disjoint -path sets of , it is an injection. Then, there are at least as many -path sets of size k in as in , and is uniformly more reliable than . That is, .
Similarly, , and .
Thus, we find that graphs and are uniformly more reliable than other graphs in , which are just the -type graphs. □
In Figure 3, we plot the two-terminal reliabilities for graphs in the case of .
In Figure 3, we clearly see that the curves corresponding to and are at the top. Furthermore, we consider the case of removing three edges from a complete two-terminal graph, which will appear as more non-isomorphic subgraphs. However, the extremely optimal graphs can still be found in the same way. Therefore, we obtain Theorem 3.
Theorem 3.
Let be a positive integer and . Then there are five extremely optimal graphs in .
Proof of Theorem 3.
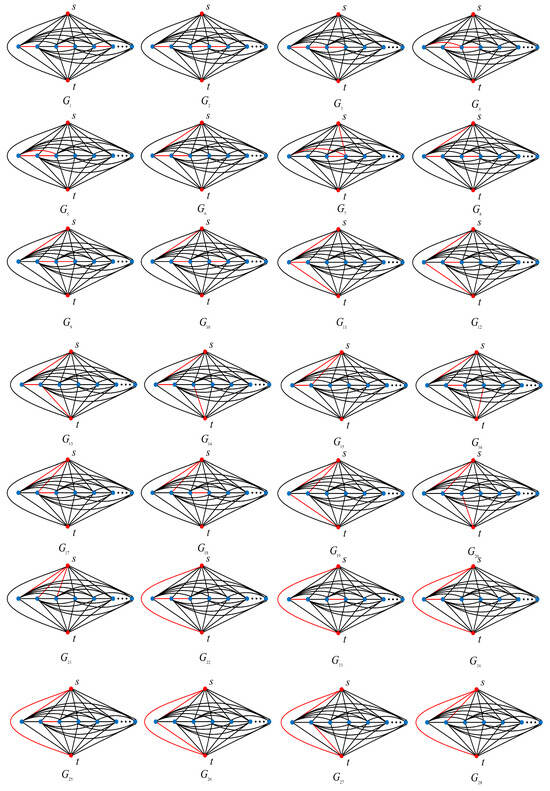
All the non-isomorphic graphs obtained by removing three edges from an n-order complete two-terminal graph can be constructed, as shown in Figure 4. We have:

Figure 4.
All cases of graph family .
-type graphs containing , , , ,;
-type graphs containing –;
-type graphs containing –.
We can also construct two injections from the -path sets of size k in -type and -type graphs to -path sets of size k in -type graphs.
Case 1. A -type graph is more reliable than an -type graph. Without loss of generality, we prove that .
Let , , and . We construct an injection from an -path sets of size k in to the -path sets of size k in . Let Q be the -path sets of size k in . We consider two subcases.
Subcase 1.1. Suppose Q does not contain edge . Then let . Note that the image is an -path sets in with the same size as Q, which does not contain edge .
Subcase 1.2. Suppose Q contains edge . Then define . The image is an -path sets in with the same size as Q, which contains the edge . Thus, the image is distinct from those in subcase 1.1.
Then is an injection and there are at least as many -path sets in as in . Thus, is uniformly more reliable than , i.e., . We can prove the following results analogous to the proof of Theorem 2. It holds that , and .
Case 2. A -type graph is more reliable than a -type graph. In this case, without loss of generality, we prove that .
Let , , , and . We construct a mapping from an -path set of k in to an -path set of k in . Let Q be the -path set of size in . We discuss four sub-cases.
Subcase 2.1. Suppose Q does not contain edge . Then let . Note that the image is the -path set in with the same size as Q, which does not contain edge .
Subcase 2.2. Suppose Q contains edge , and is still an -path set. Then define . The corresponding image is the -path set in with the same size as Q, which contains edge . We can see that is still an -path set.
Subcase 2.3. Suppose Q contains edge and that is not an -path set, but it is a -path-set. Then define . Note that the image consists of the -path sets in , with the same size as Q, which contain the edge , but is not an -path set, which is distinct from the image in subcase 2.2.
Subcase 2.4. Now suppose Q contains edge , and is not an -path set and it is not a -path-set. Then define
.
Note that has the same size as Q, and it is completely disjoint from the image described in subcase 2.3.
In each of the above four subcases, yields disjoint -path sets of . Then the mapping is an injection. There are at least as many -path sets of size k in as in , and hence is uniformly more reliable than , i.e., . We can similarly prove that , , and .
In summary, we can find that graphs , , , , and are uniformly more reliable than other graphs, constitute the minimum extremely optimal graph set in the graph family , and are exactly the -type graphs. □
For better visualization, in Figure 5 we plot two-terminal reliabilities for the graphs in the case of .
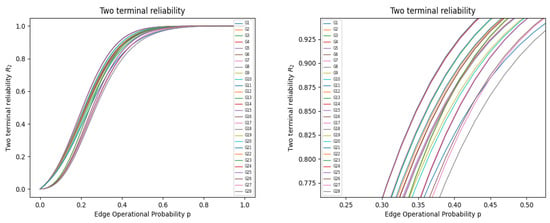
Figure 5.
The left figure shows the two-terminal reliability curve for graphs in the case of , , while the right figure represents its partial enlargement.
Referring to Theorems 2 and 3, it is evident that -type graphs exhibit higher uniform reliability than the other two types of graph in , as more edges are deleted. Moreover, we can find that the number of extremely optimal graphs in their corresponding graph classes is constant as n keeps increasing.
3. The Number of Extremely Optimal Networks
It is easy to see that a -type graph is formed by deleting r() edges among non-target vertices for the complete two-terminal graph , which is equivalent to the simple graph obtained by deleting any r edges in the complete graph with non-target vertices.
Let N be the number of non-isomorphic subgraphs of the complete two-terminal graph . We can visualize the relationship between r and N in logarithmic coordinates and fit the corresponding curves, as shown in Figure 6. Then we can see that, as the parameter r increases, the number of non-isomorphic subgraphs N grows exponentially. This work aims to reduce the search range for more reliable graphs. Then it is sufficient to count the number of a specific type of graphs, i.e., -type graphs. In the following, we apply the Pólya counting principle to count the parameter N by deleting the edges of .
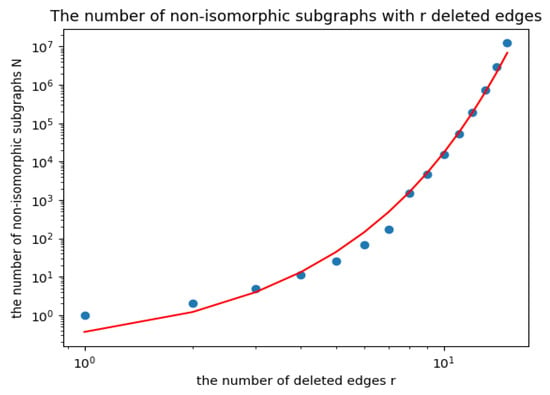
Figure 6.
The relationship between r and N in logarithmic coordinates and their curve fitting.
Lemma 1.
(Pólya theorem for generating function type) Let n objects be colored with m colors and n objects to form a permutation group , where and denotes the number of rotations of j order in the permutation . Then the Pólya theorem for generating function type is as follows.
where the coefficients of indicate the numbers of coloring schemes in which there are objects with color , .
If the edges of are colored by two colors and , then the number of different schemes is the number of its spanning subgraphs, which is equivalent to enumeration polynomials in the Pólya theorem in the case of .
Next, we calculate the number of -type graphs as deleting 2 and 3 edges and take complete two-terminal graphs of order 8 as an example. Clearly, we only need to calculate the number of spanning subgraphs of (See Figure 7 and Table 1).
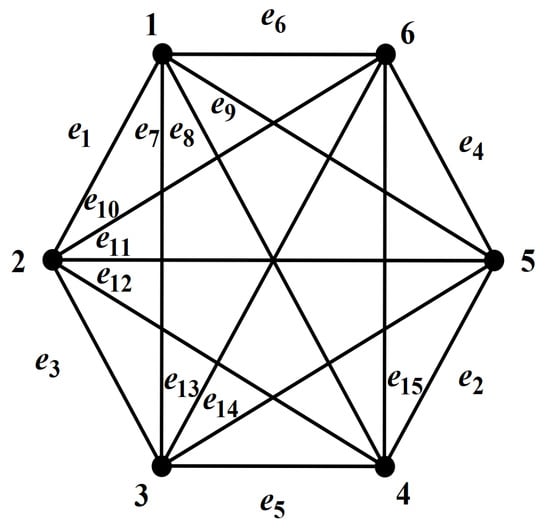
Figure 7.
.

Table 1.
Enumeration of non-isomorphic subgraphs of .
As , if , then
Similarly, we have
We see that the coefficients of the terms with exponents 2 and 3 are 2 and 5, respectively, which is consistent with Theorems 2 and 3. Table 2 gives the number of -type graphs for . Additionally, we provide pseudo-code for Pólya’s counting principle in Appendix A (See Algorithm A2).

Table 2.
The number of the -type graphs for .
From the above, the determination of extremely optimal graphs is useful to find consistently more reliable graphs in the same graph family. From Table 2, we see that the number of -type graphs shows exponential growth as r increases.
However, for any r, there is a minimal subset of extremely optimal graphs, which is included in the set of the corresponding -type graphs.
4. Conclusions
The study of extremely optimal networks holds unique value for network reliability optimization. These special network structures reveal the theoretical upper bounds of reliability under resource constraints, providing benchmark references for practical network design. By analyzing the topological characteristics of extremal graphs, critical vulnerability points in networks can be identified to guide targeted reinforcement. This research avoids the computational complexity challenges inherent in traditional reliability analysis, offering new perspectives for evaluating reliability in large-scale network systems, with significant application potential in data center networks and IoT scenarios, etc.
In this paper, we studied the locally most reliable graphs in two special two-terminal graph families in which there are no uniformly optimal graphs. In particular, -type graphs are uniformly more reliable than - and -type graphs under the same conditions. By classifying and comparing graphs, we proved the existence of an extremely optimal graph set, which plays an important role in constructing the most reliable graphs. Furthermore, the Pólya counting theorem was used to enumerate the number of -type graphs, which provided quantifiable design principles and optimization pathways for building highly robust networks. Its value extends beyond improving communication efficiency and resource utilization.
Author Contributions
Z.W.: conceptualization, methodology, validation, formal analysis, writing—review and editing; Z.Y.: writing—original draft. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (2020YFC1523300), the Key R&D and Transformation Program of Qinghai Province (2025-QY-215), and the Major Research Program of National Natural Science Foundation of China (92470202).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors are very grateful to anonymous referees and editors for their constructive suggestions and insightful comments, which have considerably improved the presentation of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. The Pseudo-Codes of Two Algorithms
| Algorithm A1 An algorithm computing the reliable polynomial coefficients for two-terminal networks |
| Require: The incidence matrix I of the two-terminal network |
| Ensure: All coefficients of the two-terminal reliable polynomial |
|
| Algorithm A2 Pólya’s counting principle |
| Require: the number of vertices n |
| Ensure: coefficient of |
|
Appendix B. The Extremely Optimal Graph Sets in Ω(6,13) and Ω(8,25)
For the graph family , its extremely optimal graph set contains two graph structures, as shown in Figure A1.
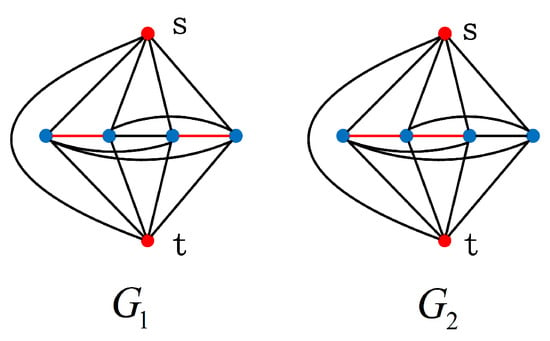
Figure A1.
The extremely optimal graph set in .
The coefficient sequences of the two terminal reliable polynomials in are, respectively,
;
.
For the graph family , its extremely optimal graph set contains two graph structures, as shown in Figure A2.
The coefficient sequences of the two terminal reliable polynomials in are, respectively,
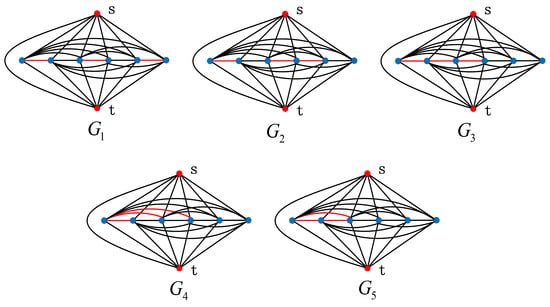
Figure A2.
The extremely optimal graph set in .
References
- Colbourn, C.J. The Combinatorics of Network Reliability; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Brown, J.; Cox, D. Nonexistence of optimal graphs for all terminal reliability. Networks 2013, 63, 146–153. [Google Scholar] [CrossRef]
- Kelmans, A.K. On graphs with randomly deleted edges. Acta. Math. Acad. Sci. Hung. 1981, 37, 77–88. [Google Scholar] [CrossRef]
- Brecht, T.B.; Colbourn, C.J. Lower bounds on the two-terminal network reliability. Discrete Appl. Math. 1998, 21, 185–198. [Google Scholar] [CrossRef]
- Harms, D.D.; Colbourn, C.J. Renormalization of two-terminal reliability. Networks 1993, 23, 289–297. [Google Scholar] [CrossRef]
- Van Slyke, R.M.; Frank, H. Network reliability analysis: Part I. Networks 1972, 1, 279–290. [Google Scholar] [CrossRef]
- Myrvold, W.; Cheung, K.H.; Page, L.B.; Perry, J.E. Uniformly-most reliable networks do not always exist. Networks 1991, 21, 417–429. [Google Scholar] [CrossRef]
- Zhao, H.X. Research on Subgraph Polynomials and Reliability of Networks. Doctoral Dissertation, Northwestern Polytechnical University, Xi’an, China, 2004. [Google Scholar]
- Bauer, D.; Boesch, F.; Suffel, C.; Tindell, R. Combinatorial optimization problems in the analysis and design of probabilistic networks. Networks 1985, 15, 257–271. [Google Scholar] [CrossRef]
- Boesch, F.T.; Li, X.; Suffel, C. On the existence of uniformly optimal networks. Networks 1991, 21, 181–194. [Google Scholar] [CrossRef]
- Byer, O.D. Two path extremal graphs and an application to a Ramsey-type problem. Discrete Math. 1999, 196, 51–64. [Google Scholar] [CrossRef][Green Version]
- Romero, P. Uniformly optimally reliable graphs: A survey. Networks 2021, 80, 466–481. [Google Scholar] [CrossRef]
- Gross, D.; Saccoman, J.T. Uniformly optimal graphs. Networks 1998, 31, 217–225. [Google Scholar] [CrossRef]
- Shao, F.M.; Zhao, L.C. Optimal design improving a communication networks reliability. Microelectron Reliab. 1997, 37, 591–595. [Google Scholar] [CrossRef]
- Bobylev, D.A.; Borovskikh, L.P. A universal converter for the parameters of multicomponent two-terminal networks. Autom. Remote Control 2016, 77, 1649–1655. [Google Scholar] [CrossRef]
- Bai, G.; Zuo, M.J.; Tian, Z. Search for all d-MPs for all d levels in multistate two-terminal networks. Reliab. Eng. Syst. Saf. 2015, 142, 300–309. [Google Scholar] [CrossRef]
- Ibe, A.O.; Cory, B.J. Traveling Wave-based Fault Locator for Two and Three Terminal Networks. IEEE Trans. Power Syst. 1986, 1, 283–288. [Google Scholar] [CrossRef]
- Bertrand, H.; Goff, O.; Graves, G.; Sun, M. On uniformly most reliable two-terminal graphs. Networks 2018, 72, 200–216. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).