Modeling of Soliton Behavior in Nonlinear Transmission Line Systems

Abstract

This study focuses on the nonlinear partial differential equation known as the Lonngren wave equation, which plays a significant role in plasma physics, nonlinear wave propagation, and astrophysical research. By applying a suitable wave transformation, the nonlinear model is reduced to an ordinary differential equation. Analytical wave solutions of the Lonngren wave equation are then derived using the extended direct algebraic method. The physical behavior of these solutions is illustrated through 2D, 3D, and contour plots generated in Mathematica. Finally, the stability analysis of the Lonngren wave equation is discussed.

1. Introduction

In recent years, nonlinear partial differential equations (NLPDEs) [1,2] have been widely employed to construct mathematical models across diverse disciplines, including physics, chemistry, biology, engineering, and finance [3,4,5]. For instance, in biology, NLPDE-based models are used to describe tumor growth, while in finance, they provide effective tools for modeling and pricing financial derivatives such as options and warrants. In physics, their applications are particularly extensive, spanning areas such as fluid dynamics, quantum mechanics, and plasma physics [6,7]. Moreover, NLPDEs have been instrumental in simulating nonlinear phenomena in various scientific and technological domains. Prominent examples include the extended KP hierarchy-type equation [8], the fractional omicron mathematical model [9], the Fractional Magneto-Electro-Elastic System [10], the Kraenkel–Manna–Merle system [11], and the fractional stochastic Fokas–Lenells equation [12].

Analytical wave solutions of NPDEs have significance in the sense that they give precise accounts of the way disturbances, vibrations, or signals travel in space and time. They are a basis of the fundamental behavior of physical systems, quite generally, sound waves, water waves, electromagnetic waves, and seismic waves [13,14]. The solutions are commonly used in physics and in engineering to estimate the speed, shape, and stability of waves, and serve as tests of numerical or approximate algorithms. In addition, analytical wave solutions also expose richer mathematical tools such as symmetries and conservation laws, and are fundamental to both theoretical and practical use in fields such as communication, materials science, and geophysics [15,16]. Researchers have focused extensively on nonlinear systems, developing and applying a variety of mathematical approaches to obtain new analytical solutions for nonlinear differential equations. Among these approaches are the extended direct algebraic method (EDAM) [17], the extended hyperbolic function method [18], the generalized exponential rational function [19,20], the logistic equation approach [21], the neural network-based method [8], and the multivariate generalized exponential rational integral function method [22].

The transmission line used here is similar to that in earlier solitary wave studies. Figure 1 shows part of the 50-section line, where each section consists of a parallel resonant circuit resonance frequency $v_0/\left(2m\right)\sim 30$ MHz in the series branch and a reverse-biased p–m junction diode in the shunt branch, whose capacitance depends on bias and signal voltages. The full line length is 100 cm. The voltage variable V is defined by transmission line equations [23]:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial G}{\partial \varpi }}+{\displaystyle \frac{\partial \left[V{D}_n\left(V\right)\right]}{\partial \tau }}=0,\hfill \\ {\displaystyle \frac{\partial V}{\partial \varpi }}+Q{\displaystyle \frac{\partial G^{\prime }}{\partial \tau }}=0,\hfill \\ {\displaystyle \frac{{\partial }^{2}V}{\partial \varpi \partial \tau }}+{\displaystyle \frac{1}{Z}}(G-G^{\prime })=0.\hfill \end{array}\right.$$

(1)

The units for the numbers Q and $1/P$ are, respectively, henries per unit length and $\left({\displaystyle \frac{1}{farads}}\right)$ per unit length. $M=D_n\left(V\right)$ represents the nonlinear diode. Using the information provided, we can describe the voltage V as a wave equation and create Equation (1):

$${\displaystyle \frac{{\partial }^{4}V}{\partial {\omega }^2\partial {\tau }^2}}+{\displaystyle \frac{1}{Q{D}_z}}{\displaystyle \frac{{\partial }^{2}V}{\partial {\omega }^2}}-{\displaystyle \frac{1}{D_z}}{\displaystyle \frac{{\partial }^2\left(VM\right)}{\partial {\tau }^2}}=0.$$

(2)

We can declare with confidence that $D_n\left(V\right)$ equals $D_{n_0}{\left({\displaystyle \frac{V}{\overline{V}}}\right)}^{-n}$. In this case, n is a numerical number and $\overline{V}$ is a normalizing constant. Our research will show that $0<n<1$, which includes a range of possible experimental values (n = ${\displaystyle \frac{1}{3}}$ in our studies). Equation (2) becomes the following fourth-order NPDE after introducing dimensionless variables. Applying the spiral group yields the Lonngren wave equation (LWE) [24]:

$${\displaystyle \frac{{\partial }^{4}B}{\partial {\tau }^2\partial {\omega }^2}}-a{\displaystyle \frac{{\partial }^{2}B}{\partial {\tau }^2}}+{\displaystyle \frac{{\partial }^{2}B}{\partial {\omega }^2}}+2b\left[{\left({\displaystyle \frac{\partial B}{\partial \tau }}\right)}^2+B{\displaystyle \frac{{\partial }^{2}B}{\partial {\tau }^2}}\right]=0.$$

(3)

Equation (3) represents a well-established mathematical model that is widely regarded as significant and influential because of its diverse and extensive applications in the domain of electrical science. The present investigation relies on the LWE as the foundation, since it offers a powerful analytical and numerical framework for simulating the electrical responses of tunnel diodes. Originally designed to describe wave propagation phenomena in shallow water environments, the equation has since been adapted for additional purposes, such as explaining electrical pulses in telegraphic systems through the behavior of tunnel diodes. This versatility allows the equation to serve not only as a research tool but also as a subject of theoretical inquiry. In this work, special attention is given to the involvement of the arbitrary constants a and b, together with the spatial parameter $\omega$ and the temporal parameter $\tau$, in shaping the wave function $B(\omega ,\tau )$. The interconnections between B and these elements will be examined in detail. In particular, the constant b plays an essential role as a coefficient that determines the degree of nonlinearity expressed in Equation (3). From a mathematical standpoint, the equation highlights the dynamics of electrical impulses in Sony’s tunnel diode, a well-known type of semiconductor diode [25]. Furthermore, Equation (3) can also shed light on how energy is accumulated in electric circuits through charge storage, as well as how electrical signals are propagated across different media that exhibit semiconductor characteristics [24].

In earlier works, Lonngren et al. [26] investigated the mathematical modeling of a specific physical phenomenon. Lonngren et al. [26] applied the $\left(\frac{G^{\prime }}{G}\right)$ expansion method with the modified extended tanh method to explore its solutions. Jhangeer et al. [24] conducted a dynamical analysis of Equation (3) using bifurcation and chaos analysis. Furthermore, Durur [27] identified hyperbolic traveling wave solutions of Equation (3) by employing the $\left(\frac{1}{G^{\prime }}\right)$ expansion method. This study addresses the solution of Equation (3) via the extended direct algebraic method (EDAM), which is valued for its simplicity, efficiency, and ability to construct exact analytical solutions. The stability of the model is also examined. We selected this method because it is a systematic approach for obtaining exact solutions of nonlinear partial differential equations. The advantages of the extended direct algebraic method are as follows:

• It can be applied to a wide range of nonlinear evolution equations.
• It reduces complex nonlinear equations into simpler algebraic forms.
• It provides exact solutions in an efficient and straightforward manner.
• It yields diverse types of solutions, such as solitons and periodic waves.
• It offers closed-form expressions that facilitate qualitative analysis and comparison with numerical results.

According to Drazin and Johnson [28], the notion of a soliton is defined by three fundamental properties. The first is that a soliton represents a type of wave that propagates in a stable manner without experiencing any modification in its form or behavior during motion. The second essential characteristic is the capacity of solitons to interact with one another. Furthermore, solitons are typically localized within specific regions, and in modern times, optical soliton technology has proven to be a crucial tool in enabling the reliable and efficient transmission of information. The presence of numerous electronic communication platforms today, such as social media networks, Facebook posts, and Twitter interactions, can in part be attributed to advancements in soliton-based technologies. In the context of our study, the phenomenon under consideration is a pulse that preserves its structural profile while continuing to move at a uniform velocity.

This paper is organized as follows: Section 2 derives soliton solutions using the extended algebraic method. Section 3 presents the graphical representations. Section 4 discusses the stability analysis. Section 5 compares the results with the existing literature. Finally, Section 6 provides the conclusion.

2. Analytical Wave Solutions of Equation (3)

In this section, we will find the soliton solution of LWE (3) using a direct algebraic method. As a first step in resolving the issue, we will simplify the situation by introducing the wave transformation below:

$$B(\omega ,\tau )=U\left(\lambda \right),\lambda =s(c\tau -\omega ).$$

(4)

Here, c is the phase speed and s is the wave number in Equation (4). We obtain the nonlinear ODE:

$$k^4{c}^2\left({\displaystyle \frac{d^{2}U}{d{\lambda }^2}}\right)+k^4{c}^2\left({\displaystyle \frac{b{U}^2}{k^2}}-{\displaystyle \frac{aU}{k^2}}+{\displaystyle \frac{U}{k^2{c}^2}}\right)=0.$$

(5)

In the subsequent analysis, the EDAM approach (see Appendix A) is applied to derive a soliton solution of the LWE, which is formulated in terms of the ODE:

$$U\left(\lambda \right)=h_0+\sum _{i_1=1}^B{h}_{i_1}{\left(R\left(\lambda \right)\right)}^{i_1},h_B\ne 0.$$

(6)

Comparing the highest-order linear term $U^{″}$ with the nonlinear term $U^2$ gives the index $B=2$. Thus, the equation becomes

$$U^{\prime }\left(\lambda \right)=h_0+h_{1}R\left(\lambda \right)+h_2{\left(R\left(\lambda \right)\right)}^2,h_2\ne 0.$$

(7)

By converting Equation (7) into Equation (5), we obtain an equation in powers of $R\left(\lambda \right)$. Arranging coefficients of like powers yields a system of algebraic equations:

$$\left\{\begin{array}{c}{R}^1\left(\lambda \right):k^2{c}^{2}b{h}_0^2-k^2{c}^{2}a{h}_0+k^4{c}^2{h}_{1}ln{\left(\eta \right)}^2\mathrm{{\rm Y}}+2k^4{c}^2{h}_{2}ln{\left(\eta \right)}^2{\mathrm{{\rm Y}}}^2+k^2{h}_0=0,\hfill \\ R^2\left(\lambda \right):k^2{h}_1+k^4{c}^2{h}_{1}ln{\left(\eta \right)}^2{\mathrm{\Phi }}^2+2k^2{c}^{2}b{h}_0{h}_1+2k^4{c}^2{h}_{1}ln{\left(\eta \right)}^2\zeta \mathrm{{\rm Y}}+6k^4{c}^2{h}_{2}ln{\left(\eta \right)}^2\mathrm{\Phi }\mathrm{{\rm Y}}\hfill \\ -k^2{c}^{2}a{h}_1=0,\hfill \\ R^3\left(\lambda \right):k^2{h}_2+4k^4{c}^2{h}_{2}ln{\left(\eta \right)}^2{\mathrm{\Phi }}^2+2k^2{c}^{2}b{h}_0{h}_2+8k^4{c}^2{h}_{2}ln{\left(\eta \right)}^2\mathrm{{\rm Y}}\zeta +3k^4{c}^2{h}_{1}ln{\left(\eta \right)}^2\mathrm{\Phi }\zeta \hfill \\ +k^2{c}^{2}b{h}_1^2-k^2{c}^{2}a{h}_2=0,\hfill \\ R^4\left(\lambda \right):2k^4{c}^2{h}_{1}ln{\left(\eta \right)}^2{\zeta }^2+2k^2{c}^{2}b{h}_1{h}_2+10k^4{c}^2{h}_{2}ln{\left(\eta \right)}^2\mathrm{\Phi }\zeta =0,\hfill \\ R^5\left(\lambda \right):6k^4{c}^2{h}_{2}ln{\left(\eta \right)}^2{\zeta }^2+k^2{c}^{2}b{h}_2^2=0.\hfill \end{array}\right.$$

(8)

After solving the above algebraic system, we obtain the resulting solutions by computation using Maple:

$$\left\{\begin{array}{c}a=-{\displaystyle \frac{4ln{\left(\eta \right)}^2\zeta c^2{k}^2\mathrm{{\rm Y}}-ln{\left(\eta \right)}^2{c}^2{k}^2{\mathrm{\Phi }}^2-1}{c^2}},h_0={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}},\hfill \\ h_1=-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}},h_2=-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}.\hfill \end{array}\right.$$

(9)

$$\left\{\begin{array}{c}a=-{\displaystyle \frac{4ln{\left(\eta \right)}^2\zeta c^2{k}^2\mathrm{{\rm Y}}-ln{\left(\eta \right)}^2{c}^2{k}^2{\mathrm{\Phi }}^2-1}{c^2}},h_0={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}},\hfill \\ h_1=-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}},h_2=-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}.\hfill \end{array}\right.$$

(10)

• Case 1: If $\Delta <0$ and $b,\zeta \ne 0$, then

$$\begin{array}{cc}\hfill & B_1(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}+{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^3{k}^2}{2b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2{\mathrm{\Phi }}^2{k}^2\sqrt{-\Delta }}{2b}}{tan}_{\eta }\left({\displaystyle \frac{\sqrt{-\Delta }}{2}}(sc\tau -s\omega )\right)\hfill \\ & -{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}+{\displaystyle \frac{\sqrt{-\Delta }}{2\zeta }}{tan}_{\eta }\left({\displaystyle \frac{\sqrt{-\Delta }}{2}}(sc\tau -s\omega )\right)\right)}^2.\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & B_2(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}+{\displaystyle \frac{6ln{\left(\eta \right)}^2{\mathrm{\Phi }}^3{k}^2}{2b}}+{\displaystyle \frac{6ln{\left(\eta \right)}^2{\mathrm{\Phi }}^2{k}^2\sqrt{-\Delta }}{2b}}{cot}_{\eta }\left({\displaystyle \frac{\sqrt{-\Delta }}{2}}(sc\tau -s\omega )\right)\hfill \\ & -{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}-{\displaystyle \frac{\sqrt{-\Delta }}{2\zeta }}{cot}_{\eta }\left({\displaystyle \frac{\sqrt{-\Delta }}{2}}(sc\tau -s\omega )\right)\right)}^2.\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & B_3(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}+{\displaystyle \frac{\sqrt{-\Delta }}{2\zeta }}({tan}_{\eta }\left(\sqrt{-\Delta }(sc\tau -s\omega )\right)\hfill \\ & \pm \sqrt{mn}{sec}_{\eta }\left(\sqrt{-\Delta }(sc\tau -s\omega )\right)\left)\right)-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}+{\displaystyle \frac{\sqrt{-\Delta }}{2\zeta }}({tan}_{\eta }\left(\sqrt{-\Delta }(sc\tau -s\omega )\right)\hfill \\ & \pm \sqrt{mn}{sec}_{\eta }\left(\sqrt{-\Delta }(sc\tau -s\omega )\right)){)}^2.\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & B_4(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}+{\displaystyle \frac{\sqrt{-\Delta }}{2\zeta }}({cot}_{\eta }\left(\sqrt{-\Delta }(sc\tau -s\omega )\right)\hfill \\ & \pm \sqrt{mn}{csc}_{\eta }\left(\sqrt{-\Delta }(sc\tau -s\omega )\right)\left)\right)-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}+{\displaystyle \frac{\sqrt{-\Delta }}{2\zeta }}({cot}_{\eta }\left(\sqrt{-\Delta }(sc\tau -s\omega )\right)\hfill \\ & \pm \sqrt{mn}{csc}_{\eta }\left(\sqrt{-\Delta }(sc\tau -s\omega )\right)){)}^2.\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & B_5(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}+{\displaystyle \frac{\sqrt{-\Delta }}{4\zeta }}({tan}_{\eta }\left({\displaystyle \frac{\sqrt{-\Delta }}{4}}(sc\tau -s\omega )\right)\hfill \\ & -{cot}_{\eta }\left({\displaystyle \frac{\sqrt{-\Delta }}{4}}(sc\tau -s\omega )\right)\left)\right)-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}+{\displaystyle \frac{\sqrt{-\Delta }}{4\zeta }}({tan}_{\eta }\left({\displaystyle \frac{\sqrt{-\Delta }}{4}}(sc\tau -s\omega )\right)\hfill \\ & -{cot}_{\eta }\left({\displaystyle \frac{\sqrt{-\Delta }}{4}}(sc\tau -s\omega )\right)){)}^2.\hfill \end{array}$$

(15)

• Case 2: If $\Delta >0$ and $b,\zeta \ne 0$, then

$$\begin{array}{cc}\hfill & B_6(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}\left(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}-{\displaystyle \frac{\sqrt{\Delta }}{2\zeta }}{tanh}_{\eta }\left({\displaystyle \frac{\sqrt{\Delta }}{2}}(sc\tau -s\omega )\right)\right)\hfill \\ & -{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}-{\displaystyle \frac{\sqrt{\Delta }}{2\zeta }}{tanh}_{\eta }\left({\displaystyle \frac{\sqrt{\Delta }}{2}}(sc\tau -s\omega )\right)\right)}^2.\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & B_7(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}\left(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}-{\displaystyle \frac{\sqrt{\Delta }}{2\zeta }}{coth}_{\eta }\left({\displaystyle \frac{\sqrt{\Delta }}{2}}(sc\tau -s\omega )\right)\right)\hfill \\ & -{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}-{\displaystyle \frac{\sqrt{\Delta }}{2\zeta }}{coth}_{\eta }\left({\displaystyle \frac{\sqrt{\Delta }}{2}}(sc\tau -s\omega )\right)\right)}^2.\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & B_8(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}+{\displaystyle \frac{\sqrt{\Delta }}{2\zeta }}(-{tanh}_{\eta }\left(\sqrt{\Delta }(sc\tau -s\omega )\right)\hfill \\ & \pm \tau \sqrt{mn}sec{h}_{\eta }\left(\sqrt{\Delta }(sc\tau -s\omega )\right)\left)\right)-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}+{\displaystyle \frac{\sqrt{\Delta }}{2\zeta }}(-{tanh}_{\eta }\left(\sqrt{\Delta }(sc\tau -s\omega )\right)\hfill \\ & \pm \tau \sqrt{mn}sec{h}_{\eta }\left(\sqrt{\Delta }(sc\tau -s\omega )\right)){)}^2.\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & B_9(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}+{\displaystyle \frac{\sqrt{\Delta }}{2\zeta }}(-{coth}_{\eta }\left(\sqrt{\Delta }(sc\tau -s\omega )\right)\hfill \\ & \pm \sqrt{mn}csc{h}_{\eta }\left(\sqrt{\Delta }(sc\tau -s\omega )\right)\left)\right)-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}+{\displaystyle \frac{\sqrt{\Delta }}{2\zeta }}(-{coth}_{\eta }\left(\sqrt{\Delta }(sc\tau -s\omega )\right)\hfill \\ & \pm \sqrt{mn}csc{h}_{\eta }\left(\sqrt{\Delta }(sc\tau -s\omega )\right)){)}^2.\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & B_{10}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}-{\displaystyle \frac{\sqrt{\Delta }}{4\zeta }}({tanh}_{\eta }\left({\displaystyle \frac{\sqrt{\Delta }}{4}}(sc\tau -s\omega )\right)+\hfill \\ & {coth}_{\eta }\left({\displaystyle \frac{\sqrt{\Delta }}{4}}(sc\tau -s\omega )\right)\left)\right)-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}(-{\displaystyle \frac{\mathrm{\Phi }}{2\zeta }}-{\displaystyle \frac{\sqrt{\Delta }}{4\zeta }}({tanh}_{\eta }\left({\displaystyle \frac{\sqrt{\Delta }}{4}}(sc\tau -s\omega )\right)+\hfill \\ & {coth}_{\eta }\left({\displaystyle \frac{\sqrt{\Delta }}{4}}(sc\tau -s\omega )\right)){)}^2.\hfill \end{array}$$

(20)

• Case 3: If $\zeta \mathrm{{\rm Y}}>0$, $b\ne 0,$ and $\mathrm{\Phi }=0$, then

$$\begin{array}{cc}\hfill & B_{11}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}\left(\sqrt{{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}{tan}_{\eta }\left(\sqrt{\mathrm{{\rm Y}}\zeta }(sc\tau -s\omega )\right)\right)\hfill \\ & -{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(\sqrt{{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}{tan}_{\eta }\left(\sqrt{\mathrm{{\rm Y}}\zeta }(sc\tau -s\omega )\right)\right)}^2.\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & B_{12}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}\left(-\sqrt{{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}{cot}_{\eta }\left(\sqrt{\zeta \mathrm{{\rm Y}}}(sc\tau -s\omega )\right)\right)\hfill \\ & -{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(-\sqrt{{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}{cot}_{\eta }\left(\sqrt{\zeta \mathrm{{\rm Y}}}(sc\tau -s\omega )\right)\right)}^2.\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & B_{13}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}(\sqrt{{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}({tan}_{\eta }\left(2\sqrt{\zeta \mathrm{{\rm Y}}}(sc\tau -s\omega )\right)\hfill \\ & \pm \sqrt{mn}{sec}_{\eta }\left(2\sqrt{\zeta \mathrm{{\rm Y}}}(sc\tau -s\omega )\right)\left)\right)-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}\left(\sqrt{{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}\right({tan}_{\eta }\left(2\sqrt{\zeta \mathrm{{\rm Y}}}(sc\tau -s\omega )\right)\hfill \\ & \pm \sqrt{mn}{sec}_{\eta }\left(2\sqrt{\zeta \mathrm{{\rm Y}}}(sc\tau -s\omega )\right)){)}^2.\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & B_{14}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}\left(\sqrt{{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}\right(-{cot}_{\eta }\left(2\sqrt{\zeta \mathrm{{\rm Y}}}(sc\tau -s\omega )\right)\hfill \\ & \pm \sqrt{mn}{csc}_{\eta }\left(2\sqrt{\zeta \mathrm{{\rm Y}}}(sc\tau -s\omega )\right)\left)\right)-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}\left(\sqrt{{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}\right(-{cot}_{\eta }(2\sqrt{\zeta \mathrm{{\rm Y}}}(sc\tau -s\omega )\hfill \\ & \pm \sqrt{mn}{csc}_{\eta }\left(2\sqrt{\zeta \mathrm{{\rm Y}}}(sc\tau -s\omega )\right)){)}^2.\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & B_{15}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}({\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}({tan}_{\eta }\left({\displaystyle \frac{\sqrt{\zeta \mathrm{{\rm Y}}}}{2}}(sc\tau -s\omega )\right)-\hfill \\ & {cot}_{\eta }\left({\displaystyle \frac{\sqrt{\zeta \mathrm{{\rm Y}}}}{2}}(sc\tau -s\omega )\right)\left)\right)-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}\left({\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}\right({tan}_{\eta }\left({\displaystyle \frac{\sqrt{\zeta \mathrm{{\rm Y}}}}{2}}(sc\tau -s\omega )\right)-\hfill \\ & {cot}_{\eta }\left({\displaystyle \frac{\sqrt{\zeta \mathrm{{\rm Y}}}}{2}}(sc\tau -s\omega )\right)){)}^2.\hfill \end{array}$$

(25)

• Case 4: If $\zeta \mathrm{{\rm Y}}<0$, $b\ne 0,$ and $\mathrm{\Phi }=0$, then

$$\begin{array}{cc}\hfill & B_{16}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}\left(-\sqrt{-{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}{tanh}_{\eta }\left(\sqrt{-\mathrm{{\rm Y}}\zeta }(sc\tau -s\omega )\right)\right)\hfill \\ & -{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(-\sqrt{-{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}{tanh}_{\eta }\left(\sqrt{-\mathrm{{\rm Y}}\zeta }(sc\tau -s\omega )\right)\right)}^2.\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & B_{17}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}\left(-\sqrt{-{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}{coth}_{\eta }\left(\sqrt{-\mathrm{{\rm Y}}\zeta }(sc\tau -s\omega )\right)\right)\hfill \\ & -{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(-\sqrt{-{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}{coth}_{\eta }\left(\sqrt{-\mathrm{{\rm Y}}\zeta }(sc\tau -s\omega )\right)\right)}^2.\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & B_{18}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}(\sqrt{-{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}(-{tanh}_{\eta }\left(2\sqrt{-\mathrm{{\rm Y}}\zeta }(sc\tau -s\omega )\right)\hfill \\ & \pm \tau \sqrt{mn}{sech}_{\eta }\left(2\sqrt{-\mathrm{{\rm Y}}\zeta }(sc\tau -s\omega )\right)\left)\right)-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}\left(\sqrt{-{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}\right(-{tanh}_{\eta }\left(2\sqrt{-\mathrm{{\rm Y}}\zeta }(sc\tau -s\omega )\right)\hfill \\ & \pm \tau \sqrt{mn}{sech}_{\eta }\left(2\sqrt{-\mathrm{{\rm Y}}\zeta }(sc\tau -s\omega )\right)){)}^2.\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & B_{19}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}(\sqrt{-{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}(-{coth}_{\eta }\left(2\sqrt{-\mathrm{{\rm Y}}\zeta }(sc\tau -s\omega )\right)\hfill \\ & \pm \sqrt{mn}{csch}_{\eta }\left(2\sqrt{-\mathrm{{\rm Y}}\zeta }(sc\tau -s\omega )\right)\left)\right)-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}\left(\sqrt{-{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}\right(-{coth}_{\eta }\left(2\sqrt{-\mathrm{{\rm Y}}\zeta }(sc\tau -s\omega )\right)\hfill \\ & \pm \sqrt{mn}{csch}_{\eta }\left(2\sqrt{-\mathrm{{\rm Y}}\zeta }(sc\tau -s\omega )\right)){)}^2.\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & B_{20}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}(-{\displaystyle \frac{1}{2}}\sqrt{-{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}({tanh}_{\eta }\left({\displaystyle \frac{\sqrt{-\mathrm{{\rm Y}}\zeta }}{2}}(sc\tau -s\omega )\right)+\hfill \\ & {coth}_{\eta }\left({\displaystyle \frac{\sqrt{-\mathrm{{\rm Y}}\zeta }}{2}}(sc\tau -s\omega )\right)\left)\right)-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}(-{\displaystyle \frac{1}{2}}\sqrt{-{\displaystyle \frac{\mathrm{{\rm Y}}}{\zeta }}}({tanh}_{\eta }\left({\displaystyle \frac{\sqrt{-\mathrm{{\rm Y}}\zeta }}{2}}(sc\tau -s\omega )\right)+\hfill \\ & {coth}_{\eta }\left({\displaystyle \frac{\sqrt{-\mathrm{{\rm Y}}\zeta }}{2}}(sc\tau -s\omega )\right)){)}^2.\hfill \end{array}$$

(30)

• Case 5: If $\mathrm{\Phi }=0$, $b\ne 0$, and $\mathrm{{\rm Y}}=\zeta$, then

$$\begin{array}{cc}\hfill & B_{21}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}\left({tan}_{\eta }\left(\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\right)\hfill \\ & -{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left({tan}_{\eta }\left(\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\right)}^2.\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & B_{22}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}\left(-{cot}_{\eta }\left(\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\right)\hfill \\ & -{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(-{cot}_{\eta }\left(\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\right)}^2.\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & B_{23}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}({tan}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\pm \hfill \\ & \sqrt{mn}{sec}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right))-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}({tan}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\hfill \\ & \pm \sqrt{mn}{sec}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right){)}^2,mn>0.\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & B_{24}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}(-{cot}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\pm \sqrt{mn}{csc}_{\eta }\hfill \\ & \left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right))-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(-{cot}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\pm \sqrt{mn}{csc}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\right)}^2,\hfill \\ & mn>0\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & B_{25}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}({\displaystyle \frac{1}{2}}({tan}_{\eta }\left({\displaystyle \frac{\mathrm{{\rm Y}}}{2}}(sc\tau -s\omega )\right)-\hfill \\ & {cot}_{\eta }\left({\displaystyle \frac{\mathrm{{\rm Y}}}{2}}(sc\tau -s\omega )\right)\left)\right)-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left({\displaystyle \frac{1}{2}}({tan}_{\eta }\left({\displaystyle \frac{\mathrm{{\rm Y}}}{2}}(sc\tau -s\omega )\right)-{cot}_{\eta }\left({\displaystyle \frac{\mathrm{{\rm Y}}}{2}}(sc\tau -s\omega )\right))\right)}^2.\hfill \end{array}$$

(35)

• Case 6: If $\mathrm{\Phi }=0$, $b\ne 0$, and $\zeta =-\mathrm{{\rm Y}}$, then

$$\begin{array}{cc}\hfill & B_{26}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}\left(-{tanh}_{\eta }\left(\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\right)\hfill \\ & -{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(-{tanh}_{\eta }\left(\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\right)}^2.\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & B_{27}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}\left(-{coth}_{\eta }\left(\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\right)\hfill \\ & -{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(-{coth}_{\eta }\left(\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\right)}^2.\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill & B_{28}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}(-{tanh}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\hfill \\ & \pm \tau \sqrt{mn}{sech}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right))-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}(-{tanh}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\hfill \\ & \pm \tau \sqrt{mn}{sech}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right){)}^2,mn>0.\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & B_{29}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}(-{coth}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\pm \hfill \\ & \sqrt{mn}{csch}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right))-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}(-{coth}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right)\pm \hfill \\ & \sqrt{mn}{csch}_{\eta }\left(2\mathrm{{\rm Y}}(sc\tau -s\omega )\right){)}^2,mn>0.\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & B_{30}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta {\mathrm{\Phi }}^2{k}^2}{b}}(-{\displaystyle \frac{1}{2}}({tanh}_{\eta }\left({\displaystyle \frac{\mathrm{{\rm Y}}}{2}}(sc\tau -s\omega )\right)+\hfill \\ & {coth}_{\eta }\left({\displaystyle \frac{\mathrm{{\rm Y}}}{2}}(sc\tau -s\omega )\right)\left)\right)-{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(-{\displaystyle \frac{1}{2}}({tanh}_{\eta }\left({\displaystyle \frac{\mathrm{{\rm Y}}}{2}}(sc\tau -s\omega )\right)+{coth}_{\eta }\left({\displaystyle \frac{\mathrm{{\rm Y}}}{2}}(sc\tau -s\omega )\right))\right)}^2.\hfill \end{array}$$

(40)

• Case 7: If ${\mathrm{\Phi }}^2=4\mathrm{{\rm Y}}\zeta$ and $\mathrm{\Phi },b\ne 0$, then

$$\begin{array}{cc}& B_{31}(\omega ,\tau )={\displaystyle \frac{-6\zeta k^2\mathrm{{\rm Y}}ln{\left(\eta \right)}^2}{b}}+\left({\displaystyle \frac{126ln\left(\eta \right)\zeta 4\mathrm{{\rm Y}}\zeta k^2\mathrm{{\rm Y}}(\mathrm{\Phi }(sc\tau -s\omega )ln\left(\eta \right)+2)}{b{\mathrm{\Phi }}^2(sc\tau -s\omega )}}\right)\hfill \\ & -{\left({\displaystyle \frac{3k^2{(\mathrm{\Phi }(sc\tau -s\omega )ln\left(\eta \right)+2)}^2}{b(sc\tau -s\omega )}}\right)}^2.\hfill \end{array}$$

(41)

• Case 10: If $\mathrm{\Phi }=\rho$, $\zeta =p\rho (b,p\ne 0)$ and $\mathrm{{\rm Y}}=0$, then

$$\begin{array}{cc}& B_{34}(\omega ,\tau )=-{\displaystyle \frac{6k^2}{b\zeta {(sc\tau -s\omega )}^2}}.\hfill \end{array}$$

(42)

• Case 11: If $\mathrm{{\rm Y}}=0$ and $\mathrm{\Phi },b,\zeta \ne 0$, then

$$\begin{array}{cc}& B_{35}(\omega ,\tau )=-{\displaystyle \frac{6m\mathrm{\Phi }ln{\left(\eta \right)}^2{\mathrm{\Phi }}^2{k}^2}{b({cosh}_{\eta }\left(\mathrm{\Phi }(sc\tau -s\omega )\right)-{sinh}_{\eta }\left(\mathrm{\Phi }(sc\tau -s\omega )\right)+m)}}\hfill \\ & -{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(-{\displaystyle \frac{m\mathrm{\Phi }}{\zeta ({cosh}_{\eta }\left(\mathrm{\Phi }(sc\tau -s\omega )\right)-{sinh}_{\eta }\left(\mathrm{\Phi }(sc\tau -s\omega )\right)+m)}}\right)}^2.\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill & B_{36}(\omega ,\tau )=-{\displaystyle \frac{6ln{\left(\eta \right)}^2{\mathrm{\Phi }}^2{k}^2}{b}}\left(-{\displaystyle \frac{\mathrm{\Phi }({sinh}_{\eta }\left(\mathrm{\Phi }(sc\tau -s\omega )\right)+{cosh}_{\eta }\left(\mathrm{\Phi }(sc\tau -s\omega )\right))}{({sinh}_{\eta }\left(\mathrm{\Phi }(sc\tau -s\omega )\right)+{cosh}_{\eta }\left(\mathrm{\Phi }(sc\tau -s\omega )\right)+n)}}\right)\hfill \\ & -{\displaystyle \frac{6ln{\left(\eta \right)}^2\zeta k^2}{b}}{\left(-{\displaystyle \frac{\mathrm{\Phi }({sinh}_{\eta }\left(\mathrm{\Phi }(sc\tau -s\omega )\right)+{cosh}_{\eta }\left(\mathrm{\Phi }(sc\tau -s\omega )\right))}{\zeta ({sinh}_{\eta }\left(\mathrm{\Phi }(sc\tau -s\omega )\right)+{cosh}_{\eta }\left(\mathrm{\Phi }(sc\tau -s\omega )\right)+n)}}\right)}^2.\hfill \end{array}$$

(44)

• Case 12: If $\mathrm{\Phi }=\rho$, $b\ne 0$, $\zeta =p_0\rho (p\ne 0)$ and $\mathrm{{\rm Y}}=0$, then

$$\begin{array}{cc}& B_{37}(\omega ,\tau )=-{\displaystyle \frac{6mln{\left(\eta \right)}^2{p}_0{\rho }^3{k}^2{\eta }^{\rho (sc\tau -s\omega )}}{b(n-p_1{\eta }^{\rho (sc\tau -s\omega )})}}-{\displaystyle \frac{6ln{\left(\eta \right)}^2{p}_0\rho k^2}{b}}{\left({\displaystyle \frac{m{\eta }^{\rho (sc\tau -s\omega )}}{n-p_1{\eta }^{\rho (sc\tau -s\omega )}}}\right)}^2.\hfill \end{array}$$

(45)

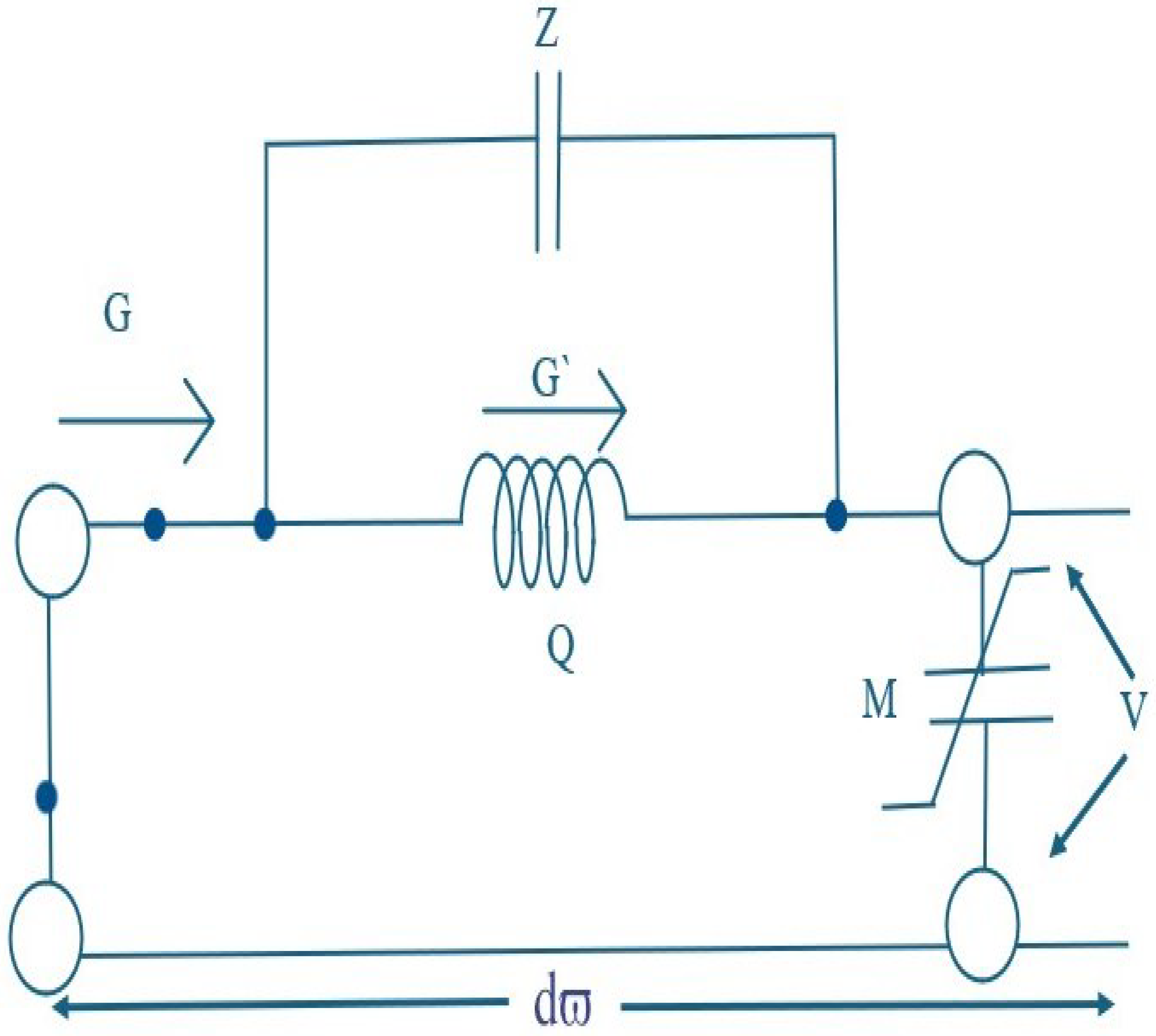
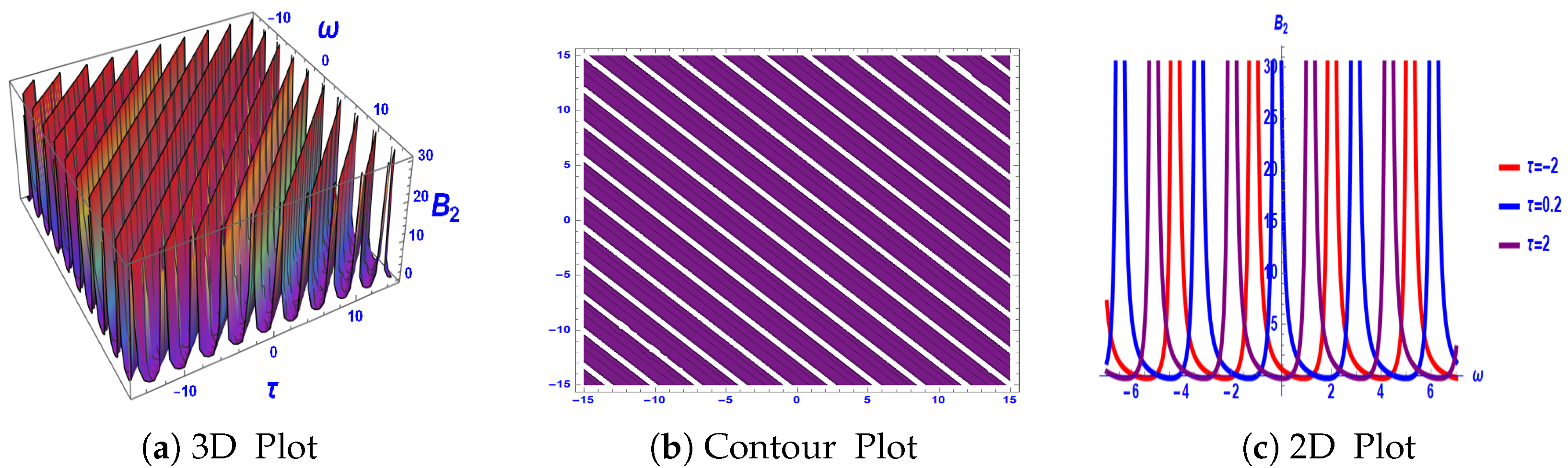
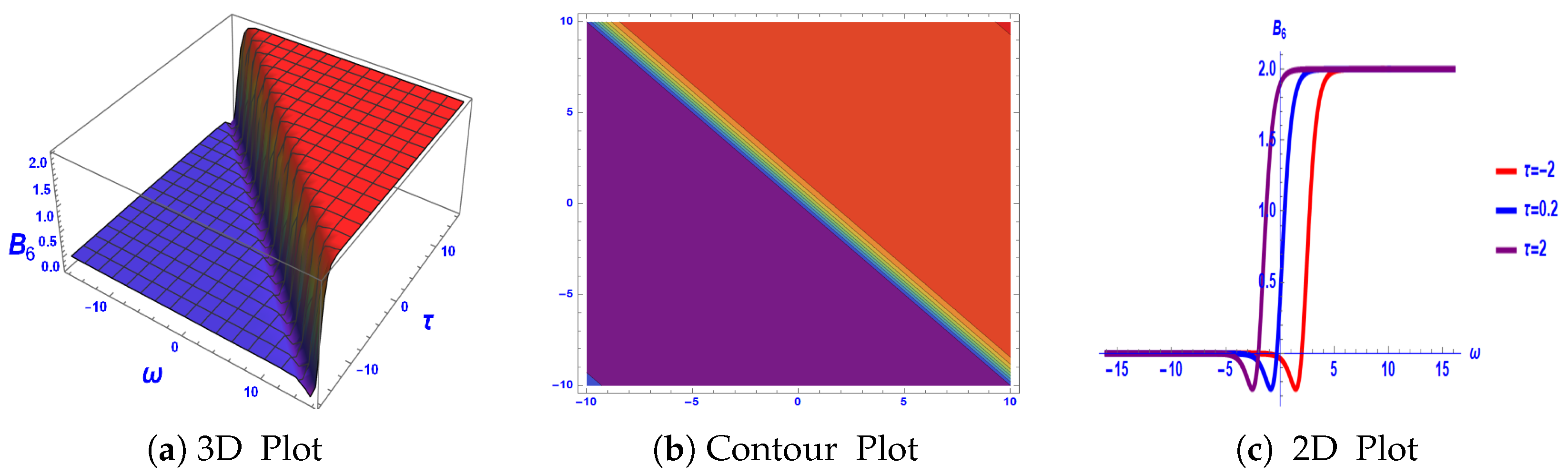
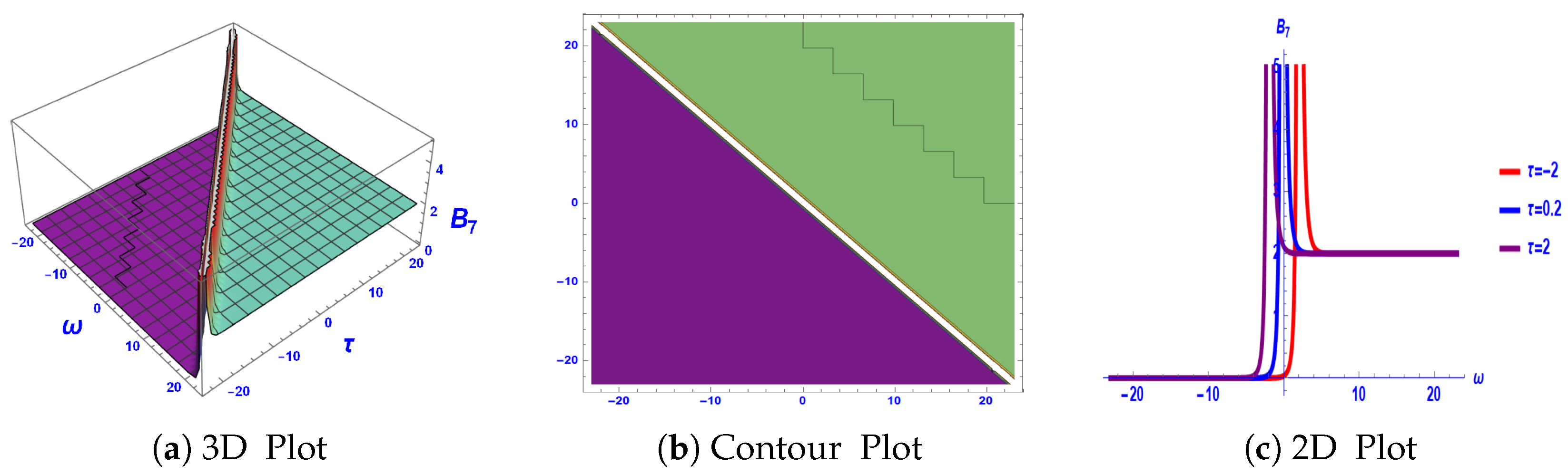
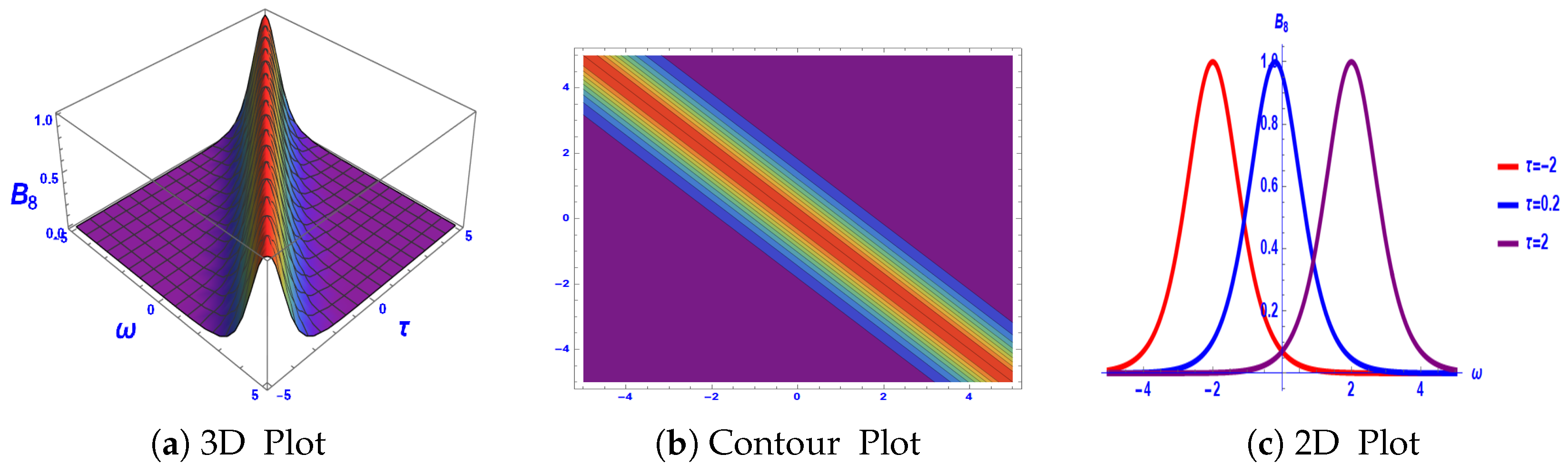
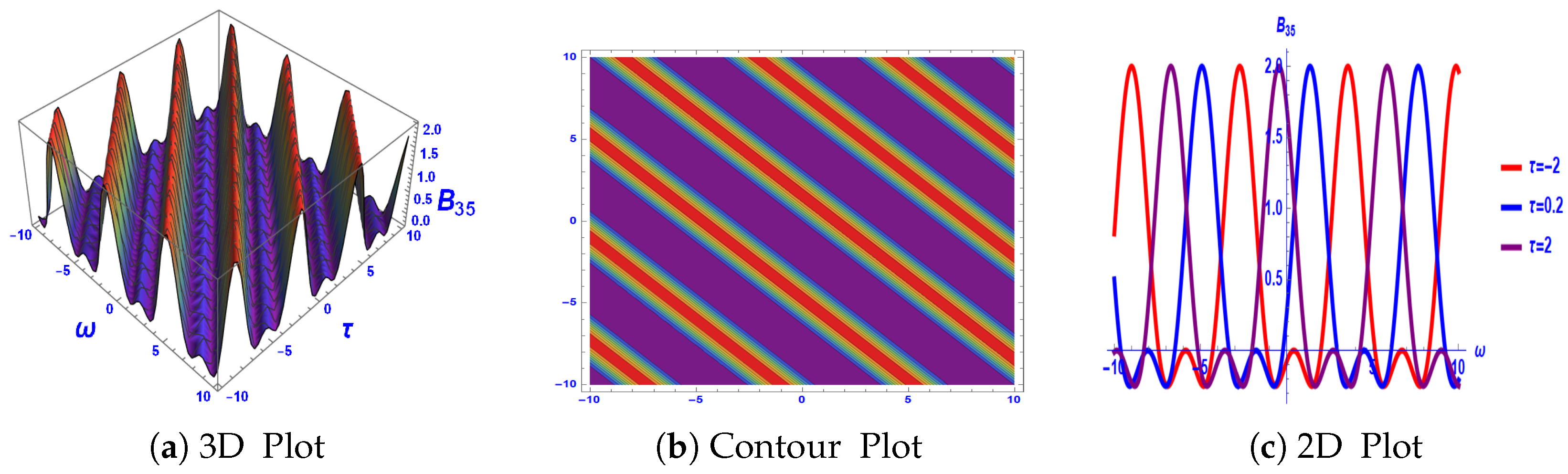
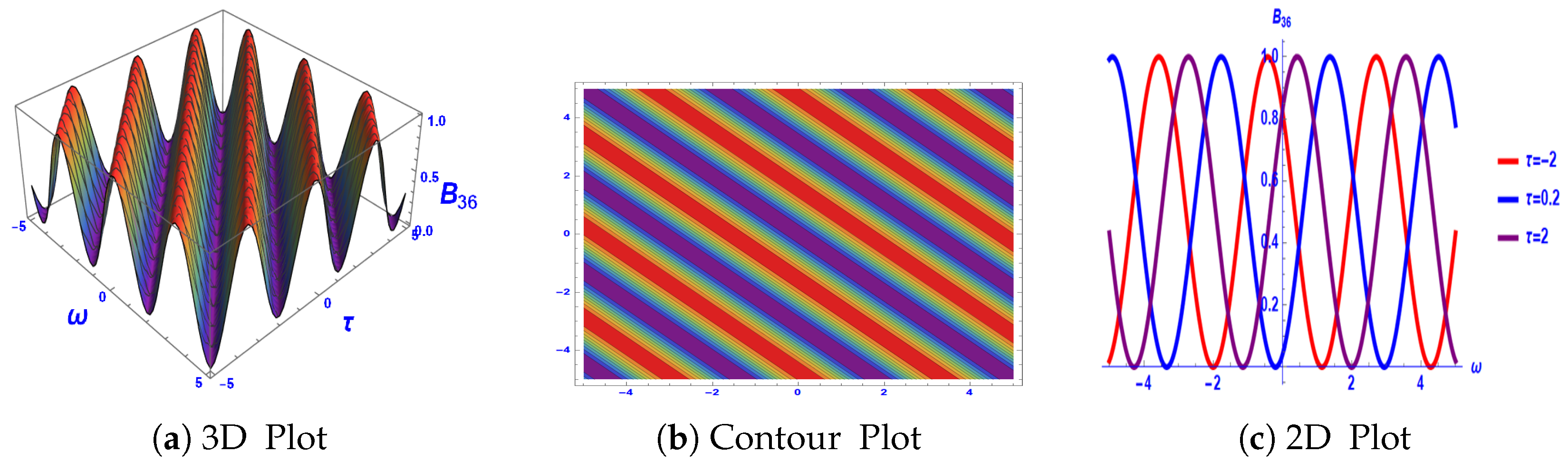
3. Graphical Explanation

The obtained solutions to the LWE will be graphically described in this section. Trigonometric, hyperbolic, and rational function solutions will be the results obtained. We will obtain contour, two-dimensional, and three-dimensional graphical representations of Equation (3) by selecting appropriate parameter values. In Figure 2, we plot the solution $B_2(\omega ,\tau )$ under the condition $\Delta <0,b,\zeta \ne 0$. We choose the values $\mathrm{\Phi }=0.78,\gamma =0.34,\zeta =0.76,k=0.25,b=3.25,\eta =e,s=1.56,c=1.19$, which yield the family of singular soliton solutions. Singular soliton solutions are important for modeling extreme nonlinear phenomena with sharp peaks or singularities, applied in optics, plasma, and fluid dynamics. In Figure 3, we plot the solution $B_6(\omega ,\tau )$ under the condition $\Delta >0,b,\zeta \ne 0$. We choose the values $\mathrm{\Phi }=1.89,\gamma =0.34,\zeta =0.76,k=1.34,b=2.55,\eta =e,s=3.56,c=1.29$, which yield the kink soliton solutions. Kink soliton solutions represent smooth topological transitions between two states, with applications in nonlinear optics, condensed matter, and biophysics [29,30,31].

In Figure 4, we plot the solution $B_7(\omega ,\tau )$ under the condition $\Delta >0,b,\zeta \ne 0$. We choose the values $\mathrm{\Phi }=1.23,\gamma =0.34,\zeta =0.76,k=0.34,b=0.35,\eta =e,s=0.56,c=0.29$, which yield the singular wave soliton solution. Singular soliton solutions play a key role in describing intense nonlinear behaviors characterized by sharp peaks or singular structures, with applications in optics, plasma physics, and fluid dynamics. In Figure 5, we plot the solution $B_8(\omega ,\tau )$ under the condition $\Delta >0,b,\zeta \ne 0$. We choose the values $\mathrm{\Phi }=1.23,\gamma =0.40,\zeta =0.76,k=0.14,b=0.05,\eta =e,s=0.26,c=0.69$, which yield the bright wave soliton solution. A bright soliton wave is a self-reinforcing, extremely stable solitary wave that travels without changing shape because dispersion and nonlinear effects are perfectly balanced. Its mathematical form frequently uses the sech function as a representation of its sharply peaked, localized structure, and it is essential in fluid dynamics, optics, and plasma physics [32,33,34].

In Figure 6, we plot the solution $B_{35}(\omega ,\tau )$ under the condition $\mathrm{{\rm Y}}=0$. We choose the values $\mathrm{\Phi }=1.23,\gamma =0.40,\zeta =0.76,k=0.14,b=0.05,\eta =e,s=0.23,c=0.99$, which yield the periodic wave soliton solution. In Figure 7, we plot the solution $B_{36}(\omega ,\tau )$ under the condition $\mathrm{{\rm Y}}=0,\mathrm{\Phi },b,z$. We choose the values $\mathrm{\Phi }=1.23,\gamma =0.40,\zeta =0.36,k=0.04,b=0.12,\eta =e,s=0.29,c=0.59$, which yield the periodic wave soliton solution. Periodic wave soliton solutions characterize stable, repeating nonlinear waveforms, widely applied in optical communications, plasma dynamics, and fluid systems [35,36,37,38].

4. Stability Analysis

We analyze the disturbed solution corresponding to a particular configuration [39]:

$$B(\omega ,\tau )=Q_2+\mu S(\omega ,\tau ).$$

(46)

Every constant value of $Q_2$ corresponds to an equilibrium solution of Equation (3). Substituting Equation (46) into Equation (3) yields the following result:

$$\mu {\displaystyle \frac{{\partial }^{4}S}{\partial {\omega }^2\partial {\tau }^2}}-a\mu {\displaystyle \frac{{\partial }^{2}S}{\partial {\tau }^2}}+\mu {\displaystyle \frac{{\partial }^{2}S}{\partial {\omega }^2}}+2b{\mu }^2{\left({\displaystyle \frac{\partial S}{\partial \tau }}\right)}^2+2b\left(Q_2+\mu S\right)\mu \left({\displaystyle \frac{{\partial }^{2}S}{\partial t^2}}\right)=0.$$

(47)

Using linearization Equation (47), we yield:

$$\mu {\displaystyle \frac{{\partial }^{4}S}{\partial {\omega }^2\partial {\tau }^2}}+\mu {\displaystyle \frac{{\partial }^{2}S}{\partial {\omega }^2}}+\mu (2b{Q}_2-a){\displaystyle \frac{{\partial }^{2}S}{\partial {\tau }^2}}=0.$$

(48)

Suppose Equation (48) admits a solution of the form:

$$S(\omega ,\tau )=e^{i\mathrm{\Pi }\omega +\vartheta \tau }·$$

(49)

Letting $\mathrm{\Pi }$ denote the normalized wave number, the substitution of Equation (49) into Equation (48) yields:

$$-\mu e^{i\omega \mathrm{\Pi }+\tau \vartheta }{\mathrm{\Pi }}^2{\vartheta }^2-a\mu e^{i\omega \mathrm{\Pi }+\tau \vartheta }{\vartheta }^2-\mu e^{i\omega \mathrm{\Pi }+\tau \vartheta }{\mathrm{\Pi }}^2+2b{Q}_2\mu e^{i\omega \mathrm{\Pi }+\tau \vartheta }{\vartheta }^2=0.$$

(50)

Isolating $\vartheta$, the growth rate is obtained as:

$$\vartheta \left(\mathrm{\Pi }\right)={\displaystyle \frac{\mp i\mathrm{\Pi }}{\sqrt{a-2b{Q}_2+\mathrm{\Pi }}}}·$$

(51)

Let $D\left(\mathrm{\Pi }\right)=a-2b{Q}_2+\mathrm{\Pi }$. The stability of the equilibrium solution depends on the sign of $D\left(\mathrm{\Pi }\right)$:

• If $D\left(\mathrm{\Pi }\right)>0$, the denominator is real and $\vartheta$ is purely imaginary. In this case, the perturbation is oscillatory in time, corresponding to marginal (neutral) stability.
• If $D\left(\mathrm{\Pi }\right)=0$, the expression becomes singular, indicating a threshold or bifurcation point.
• If $D\left(\mathrm{\Pi }\right)<0$, the denominator is imaginary and $\vartheta$ is real. One of the roots is positive, leading to exponential growth. Hence, the system is unstable.

For stability against all perturbations ($\mathrm{\Pi }\ge 0$), the minimum of $D\left(\mathrm{\Pi }\right)$ occurs at $\mathrm{\Pi }=0$. Therefore, the global stability condition is

$$Q_2\le {\displaystyle \frac{a}{2b}}.$$

(52)

The equilibrium is stable when $Q_2>{\displaystyle \frac{a}{2b}}$, marginally stable at the threshold $Q_2=a/\left(2b\right)$, and unstable when $Q_2>{\displaystyle \frac{a}{2b}}$.

5. Comparison of Results

This section compares prior studies in

Table 1. Comparative evaluation with existing work.

Reference	Work
[26]	The authors work on soliton solutions using the $\left({\displaystyle \frac{G^{\prime }}{G}}\right)$ method and the modified extended tanh method, but without providing any graphical explanation, which is a limitation of this study.
[24]	The authors work on soliton solutions using the tanh method. They obtain only two types of solitons: kink and anti-kink. Moreover, the soliton solution is derived solely in the tanh form. In addition, they study the dynamical behavior of the model.
Current study	In this study, the extended algebraic method is applied to obtain soliton solutions. Unlike other approaches, this method provides all types of solutions and allows a detailed discussion of their graphical behavior. An additional advantage of the extended algebraic method is its simplicity, effectiveness, and ability to generate diverse solution structures that highlight the physical characteristics of the model.

, highlighting this work’s unique contributions.

6. Conclusions

In this study, we investigated the analytical wave solutions and stability properties of the LWE, a nonlinear model that describes electric signals in telegraph lines incorporating tunnel diode effects. Owing to its strong physical background, the LWE has also been shown to be an effective mathematical framework for modeling nonlinear wave propagation and heat transfer phenomena, especially in systems involving nonlinearity, viscosity, and inter-phase interactions, such as rising gas bubbles in a liquid medium.

To obtain analytical wave solutions, the EDAM was employed, which enabled us to derive a wide variety of wave structures in exact analytical form. The solutions obtained include trigonometric, hyperbolic, exponential, irrational, and rational types, thereby demonstrating the versatility of the method. The symbolic computations were carried out using Maple software to ensure the accuracy and completeness of the derived solutions. In addition, graphical representations were presented to illustrate the physical behavior of the obtained solutions. A comprehensive set of 2D, 3D, and contour plots, generated with Mathematica, were used to analyze the dynamical evolution of different solution profiles over time. These visualizations reveal diverse nonlinear wave structures, including bright, dark, kink, anti-kink, singular, mixed-type, and periodic waves, which provide deeper insights into the physical interpretation of the mathematical results.

Finally, the stability analysis of the LWE was carried out by considering perturbations around the equilibrium state. The results show that the stability of the equilibrium depends sensitively on the system parameter $Q_2$. The threshold condition $Q_2=\frac{a}{2b}$ was identified as a critical bifurcation point, marking the transition between stability, marginal stability, and instability. This finding highlights the delicate balance between nonlinear effects and system parameters that governs the onset of oscillatory, marginal, or unstable behaviors in the model. Overall, the combination of analytical solutions, graphical illustrations, and stability analysis provides a comprehensive understanding of the LWE. These results not only enrich the theoretical framework of nonlinear wave equations but also serve as a useful reference for practical applications in nonlinear electrical circuits, fluid dynamics, and wave propagation phenomena in complex media.

Directions for Future Research: The present work opens up several promising directions for future research. One potential extension is the application of chaos analysis to investigate the irregular and complex behaviors of the LWE using modern nonlinear dynamical tools. Furthermore, the development of numerical methods such as the variational iteration method, adomian decomposition method, perturbation techniques, and finite element methods can provide approximate solutions and validate the analytical results. Another promising avenue is the integration of machine learning approaches, such as Artificial Neural Networks and Physics-Informed Neural Networks, which can offer efficient and accurate frameworks for solving high-dimensional and nonlinear problems. These approaches not only improve computational efficiency but also allow the exploration of solution behaviors in regimes where analytical methods may not be feasible. By combining analytical, numerical, and computational intelligence approaches, future studies can further enhance our understanding of the LWE and its wide-ranging applications across physics, engineering, and applied mathematics [40,41,42,43,44].