On Comparing Analytical and Numerical Solutions of Time Caputo Fractional Kawahara Equations via Some Techniques

Abstract

One of the important techniques for solving several partial differential equations is the residual power series method, which provides the approximate solutions of differential equations in power series form.In this work, we use Aboodh transform in the analogical structure of the residual power series method to obtain a new method called the Aboodh residual power series method (ARPSM). By using this technique, we calculate the coefficients of some power series solutions of time Caputo fractional Kawahara equations. To obtain analytical and numerical solutions for the TCFKEs, we use ARPSM, first with the approximate initial condition and then with the exact initial condition. We present ARPSM’s reliability, efficiency, and capability by graphically describing the numerical results for analytical solutions and by comparing our solutions with other solutions for the TCFKEs obtained using two alternative methods, namely, the residual power series method and the natural transform decomposition method.

1. Introduction

The partial fractional differential equations are considered good descriptions for many models in sciences such as groundwater science, electrical networks, physics, medicine, fluid mechanics, polymer science, and engineering [1,2]. For the wave motions, there are many partial differential equations represented, which are considered to be among the most important equations in physics, mathematics, and fluid theory. One of theses equations, called the Kawahara equation, was introduced by Kawahara in 1970 [3] to characterize solitary-wave propagation in media [4,5,6], which is given by

$${\displaystyle \frac{\partial \mu ({\vartheta }_1,{\vartheta }_2)}{\partial {\vartheta }_2}}+\mu ({\vartheta }_1,{\vartheta }_2){\displaystyle \frac{\partial \mu ({\vartheta }_1,{\vartheta }_2)}{\partial {\vartheta }_1}}+{\displaystyle \frac{{\partial }^3\mu ({\vartheta }_1,{\vartheta }_2)}{\partial {\vartheta }_1^3}}-{\displaystyle \frac{{\partial }^5\mu ({\vartheta }_1,{\vartheta }_2)}{\partial {\vartheta }_1^5}}.$$

(1)

Concerning the theory of shallow water waves with magnetoacoustic waves, the generalization conservation and symmetry laws that concern the Kawahara equation were introduced in [7]. For capillary–gravity water waves and plasma waves, there are many applications of the Kawahara equations [8,9,10,11]. In plasma physics, the Kawahara equation can describe wave propagation in magnetized plasmas, where nonlinear effects play a significant role in wave dynamics. In engineering, the Kawahara equation can be used to analyze stability in structures subjected to dynamic loading, especially in materials science, where wave propagation is significant.

To support mathematical modeling in fractional calculus, many fractional operators and studies that describe the various materials and hereditary properties of the processes have been introduced. Concerning the theory behind various biological equations and physical systems, many mathematical researchers have examined the exact and approximate solutions of the partial differential equations involved in the fractional order using mathematical methods. Several techniques and efficient methods have been introduced to provide approximate solutions to biological and physical fractional partial differential equations, such as the fractional Newton method [12], the sine-Gordon expansion technique for solving Wu-Zhang system models [13], a modified Adams–Bashforth method [14], a modified expansion map technique for solving the non-linear Schrodinger equation [15], the homotopy perturbation technique [16], the Laplace transform technique [1], the expansion technique [17], the variational iteration technique [18], a monotone iterative method for solving the reaction diffusion equation [19], an extended direct algebraic mapping technique [20], and the reproducing kernel Hilbert space method with three equations, namely, the Fornberg–Whitham-type equation [21], the telegraph equation [22] and the non-local fractional equation [23]. Also, one of these methods is the ARPSM, which is used in the solving of some fractional differential equations, such as in Yasmin and Almuqrin [24], who used the ARPSM to obtain some solutions. Yang et al. [25] developed a full-stage creep constitutive model by integrating fractional calculus theory with statistical damage mechanics and, in [26], introduced some results concerning the fractional order analysis of the creep characteristics of sandstone. Damag et al. [27] used the Laplace residual power series method to solve modified time Caputo fractional Kawahara equations. Liaqat et al. [28] developed an analytic technique, i.e., the ARPSM, to obtain some solutions for the Caputo time-fractional partial differential equations. Edalatpanah and Abdolmaleki [29] provided some results for the N–Wh–S equation using the ARPSM. Noor et al. [30] identified some approximate solutions for a number of equations with one-dimensional nonlinear shock waves using ARPSM. Liaqat et al. [31] used ARPSM to solve the Black–Scholes differential equations.

Consider the following TCFKE:

$$\left\{\begin{array}{c}{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)+\mu ({\vartheta }_1,{\vartheta }_2){\mathcal{D}}_{{\vartheta }_1}\mu ({\vartheta }_1,{\vartheta }_2)+{\mathcal{D}}_{{\vartheta }_1}^3\mu ({\vartheta }_1,{\vartheta }_2)-{\mathcal{D}}_{{\vartheta }_1}^5\mu ({\vartheta }_1,{\vartheta }_2)=0,0<\rho \le 1\hfill \\ \mu ({\vartheta }_1,0)={\displaystyle \frac{105}{169}}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\hfill \end{array}\right.$$

(2)

where ${\mathcal{D}}_{{\vartheta }_1}:={\displaystyle \frac{\partial }{\partial {\vartheta }_1}}$ and ${}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }$ is the Caputo differential operator of order $\rho$. A number of techniques have been used to solve the TCFKE (2), such as the residual power series method (RPSM) [32], the natural transform method (NTDM) [33], the homotopy analysis method [34], an iterative Laplace transform method [35], the Laplace Adomian decomposition method [36], the homotopy analysis transform technique [37], and the septic collocation B-spline technique [38].

In this work, we introduce and investigate the analytical scheme and efficiency of the ARPSM in finding analytical and numerical solutions for the TCFKE (2). Section 2 presents some definitions and facts concerning Aboodh transform with Caputo fractional differential operators. Section 3 presents the basic steps of the ARPSM. In Section 4, we use the ARPSM to find the analytical solutions for the TCFKE (2), first with the approximate initial condition and then with the exact initial condition. In Section 5, we present our numerical results graphically and compare them with the solutions obtained for the TCFKE (2) using the NTDM [33] and RPSM [32]. Some discussion and our conclusions are presented in Section 6.

2. Aboodh Transform of Caputo Operator

Definition 1

([39]). Let I be any interval in $\mathbb{R}$ and μ be any map on $I\times [0,\infty )$. The R-L fractional derivative of $\mu ({\vartheta }_1,{\vartheta }_2)$ of order $\rho >0$ is given by

$${\mathcal{D}}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)={\mathcal{D}}_{{\vartheta }_2}^n{\mathcal{I}}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)n-1<\rho <n,$$

(3)

where $n=1,2,3,\dots$ and ${\mathcal{I}}_{0,{\vartheta }_2}^{\rho }$ is the R-L integral operator [39]. That of $\mu ({\vartheta }_1,{\vartheta }_2)$ of order ρ is given by

$${\mathcal{I}}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)=\left\{\begin{array}{c}{\displaystyle \frac{1}{\mathrm{\Gamma }\left(\rho \right)}}{\int }_0^{{\vartheta }_2}{({\vartheta }_2-s)}^{\rho -1}\mu ({\vartheta }_1,s)ds,\rho >0\hfill \\ \mu ({\vartheta }_1,{\vartheta }_2),\rho =0.\hfill \end{array}\right.$$

(4)

Definition 2

([40]). The Caputo fractional derivative for $\mu ({\vartheta }_1,{\vartheta }_2)$ of order ρ is given by

$${}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)=\left\{\begin{array}{c}{\mathcal{I}}_{0,{\vartheta }_2}^{n-\rho }\left[{\displaystyle \frac{{\partial }^n\mu ({\vartheta }_1,{\vartheta }_2)}{\partial {\vartheta }_2^n}}\right],n-1<\rho <n\hfill \\ {\displaystyle \frac{{\partial }^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)}{\partial {\vartheta }_2^{\rho }}},\rho \in \mathbb{N},\hfill \end{array}\right.$$

(5)

Remark 1

([40]). For ${\vartheta }_2\ge 0$ and for $n-1<\rho <n$, we have ${}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }{\mathcal{I}}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)=\mu ({\vartheta }_1,{\vartheta }_2)$, ${}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }{\vartheta }_2^{\gamma }={\displaystyle \frac{\mathrm{\Gamma }(\rho +2)}{\mathrm{\Gamma }(\gamma -\rho +2)}}{\vartheta }_2^{\gamma -\rho }$, and

$${\mathcal{I}}_{0,{\vartheta }_2}^{\rho }{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)=\mu ({\vartheta }_1,{\vartheta }_2)+\sum _{k=0}^{n-1}{\displaystyle \frac{{\vartheta }_2^k}{k!}}{\displaystyle \frac{{\partial }^k\mu ({\vartheta }_1,{\vartheta }_2)}{\partial {\vartheta }_2^k}}{|}_{{\vartheta }_2=0},$$

where $\gamma >-1$, $c\in \mathbb{R}$ and $n\in \mathbb{N}$.

Definition 3

([30]). Let $\mu ({\vartheta }_1,{\vartheta }_2)$ be of exponential order α and map on $I\times [0,\infty )$. The Aboodh transform $A_{{\vartheta }_2\sigma }$ of $\mu ({\vartheta }_1,{\vartheta }_2)$ w.r.t ${\vartheta }_2$ is given by

$${\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma ):=A_{{\vartheta }_2\sigma }\mu ({\vartheta }_1,{\vartheta }_2)={\displaystyle \frac{1}{\sigma }}{\int }_0^{\infty }{e}^{-{\vartheta }_2\sigma }\mu ({\vartheta }_1,\sigma )d\sigma {\alpha }_1\le \sigma \le {\alpha }_2.$$

(6)

The inverse Aboodh transform $A_{{\vartheta }_2\sigma }^{-1}$ of ${\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )$ w.r.t σ is given by

$$\mu ({\vartheta }_1,{\vartheta }_2):=A_{{\vartheta }_2\sigma }^{-1}{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )={\displaystyle \frac{1}{2\pi i}}{\int }_{d-i\infty }^{d+i\infty }\sigma e^{{\vartheta }_2\sigma }\mu ({\vartheta }_1,\sigma )d\sigma .$$

(7)

Lemma 1

([31]). Let $\mu , \lambda :I\times [0, \infty )\to \mathbb{R}$ be any map on $I\times [0,\infty )$. Then,

1.

$A_{{\vartheta }_2\sigma }[c_1\mu ({\vartheta }_1,{\vartheta }_2)+c_2\lambda ({\vartheta }_1,{\vartheta }_2)]=c_1{A}_{{\vartheta }_2\sigma }\mu ({\vartheta }_1,{\vartheta }_2)+c_2{A}_{{\vartheta }_2\sigma }\lambda ({\vartheta }_1,{\vartheta }_2)$, where $c_1$ and $c_2$ are constants;

2.

$A_{{\vartheta }_2\sigma }^{-1}[c_1{A}_{{\vartheta }_2\sigma }\mu ({\vartheta }_1,{\vartheta }_2)+c_2{A}_{{\vartheta }_2\sigma }\lambda ({\vartheta }_1,{\vartheta }_2)]=c_1\mu ({\vartheta }_1,{\vartheta }_2)+c_2\lambda ({\vartheta }_1,{\vartheta }_2)$, where $c_1$ and $c_2$ are constants;

3.

$A_{{\vartheta }_2\sigma }{\mathcal{I}}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)={\sigma }^{-\rho }{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )$;

4.

$A_{{\vartheta }_2\sigma }\left[{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)\right]={\sigma }^{\rho }{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-{\sum }_{j=0}^{n-1}{\sigma }^{\rho -j-2}{\partial }_{{\vartheta }_2}^j\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}$ $(n-1<\rho <n)$.

From [24], it is clear that the power series form is given by

$$\sum _{j=0}^{\infty }{\mu }_j\left({\vartheta }_1\right){({\vartheta }_2-{\vartheta }^{\prime })}^{jn}={\mu }_0\left({\vartheta }_1\right){({\vartheta }_2-{\vartheta }^{\prime })}^0+{\mu }_1\left({\vartheta }_1\right){({\vartheta }_2-{\vartheta }^{\prime })}^n+{\mu }_2\left({\vartheta }_1\right){({\vartheta }_2-{\vartheta }^{\prime })}^{2n}+\dots$$

(8)

The multiple fractional power series (MFPS) means that the series concerning ${\vartheta }^{\prime }$ with ${\vartheta }_2$ is a variable, along with the series coefficients ${\mu }_j\left({\vartheta }_1\right)$.

Lemma 2.

Let $\mu :I\times [0,\infty )\to \mathbb{R}$ be continuous on $I\times [0,\infty )$. Then,

$$A_{{\vartheta }_2\sigma }\left[{}^c\mathcal{D}_{0,{\vartheta }_2}^{k\rho }\mu ({\vartheta }_1,{\vartheta }_2)\right]={\sigma }^{k\rho }{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-\sum _{j=0}^{k-1}{\sigma }^{(k-j)\rho -2}{}^c\mathcal{D}_{0,{\vartheta }_2}^{j\rho }\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}(0<\rho \le 1).$$

(9)

Proof. 

We use the induction to prove the relation (9). At $k=1$, since $0<\rho \le 1$ in (9), $n=0$ in the part (4) of Lemma above. Hence,

$$A_{{\vartheta }_2\sigma }\left[{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)\right]={\sigma }^{\rho }{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-{\sigma }^{\rho -2}\mu ({\vartheta }_1,0).$$

(10)

That is, (9) holds at $k=1$. At $k=2$, let $\lambda ({\vartheta }_1,{\vartheta }_2)={}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)$. By (10) above we have

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\left[{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\lambda ({\vartheta }_1,{\vartheta }_2)\right]={\sigma }^{\rho }{\lambda }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-{\sigma }^{\rho -2}\lambda ({\vartheta }_1,0)\hfill \\ \hfill & ={\sigma }^{\rho }{A}_{{\vartheta }_2\sigma }{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)-{\sigma }^{\rho -2}{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}\hfill \\ \hfill & ={\sigma }^{\rho }\left[{\sigma }^{\rho }{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-{\sigma }^{\rho -2}\mu ({\vartheta }_1,0)\right]-{\sigma }^{\rho -2}{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}\hfill \\ \hfill & ={\sigma }^{2\rho }{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-{\sigma }^{2\rho -2}\mu ({\vartheta }_1,0)-{\sigma }^{\rho -2}{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}.\hfill \end{array}$$

(11)

That is, (9) holds at $k=2$. Let (9) be true at $k=m$; that is,

$$A_{{\vartheta }_2\sigma }\left[{}^c\mathcal{D}_{0,{\vartheta }_2}^{m\rho }\mu ({\vartheta }_1,{\vartheta }_2)\right]={\sigma }^{m\rho }{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-\sum _{j=0}^{m-1}{\sigma }^{(m-j)\rho -2}{}^c\mathcal{D}_{0,{\vartheta }_2}^{j\rho }\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}.$$

(12)

We will prove (9) holds at $k=m+1$. Let $\lambda ({\vartheta }_1,{\vartheta }_2)={}^c\mathcal{D}_{0,{\vartheta }_2}^{m\rho }\mu ({\vartheta }_1,{\vartheta }_2)$. By (10) and (12), we have

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\left[{}^c\mathcal{D}_{0,{\vartheta }_2}^{k\rho }\lambda ({\vartheta }_1,{\vartheta }_2)\right]=A_{{\vartheta }_2\sigma }\left[{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\lambda ({\vartheta }_1,{\vartheta }_2)\right]={\sigma }^{\rho }{\lambda }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-{\sigma }^{\rho -2}\lambda ({\vartheta }_1,0)\hfill \\ \hfill & ={\sigma }^{\rho }{A}_{{\vartheta }_2\sigma }{}^c\mathcal{D}_{0,{\vartheta }_2}^{m\rho }\mu ({\vartheta }_1,{\vartheta }_2)-{\sigma }^{\rho -2}{}^c\mathcal{D}_{0,{\vartheta }_2}^{m\rho }\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}\hfill \\ \hfill & ={\sigma }^{\rho }\left[{\sigma }^{m\rho }{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-\sum _{j=0}^{m-1}{\sigma }^{(m-j)\rho -2}{}^c\mathcal{D}_{0,{\vartheta }_2}^{j\rho }\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}\right]\hfill \\ & -{\sigma }^{\rho -2}{}^c\mathcal{D}_{0,{\vartheta }_2}^{m\rho }\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}\hfill \\ \hfill & ={\sigma }^{(m+1)\rho }{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-\sum _{j=0}^{m-1}{\sigma }^{(m+1-j)\rho -2}{}^c\mathcal{D}_{0,{\vartheta }_2}^{j\rho }\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}\hfill \\ & -{\sigma }^{\rho -2}{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}\hfill \\ \hfill & ={\sigma }^{(m+1)\rho }{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-\sum _{j=0}^m{\sigma }^{(m+1-j)\rho -2}{}^c\mathcal{D}_{0,{\vartheta }_2}^{j\rho }\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}\hfill \\ \hfill & ={\sigma }^{k\rho }{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-\sum _{j=0}^{k-1}{\sigma }^{(k-j)\rho -2}{}^c\mathcal{D}_{0,{\vartheta }_2}^{j\rho }\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}\hfill \end{array}$$

(13)

Hence, the relation (9) is true for all $k\in \mathbb{N}.$ □

Lemma 3.

Let $\mu :{\mathbb{R}}^n\times [0,\infty )\to \mathbb{R}$ be an exponential order function. The MFPS notation for the Aboodh transform is given by

$${\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )=\sum _{j=0}^{\infty }{\displaystyle \frac{{\gamma }_j\left({\vartheta }_1\right)}{{\sigma }^{jn+2}}}\sigma >0,$$

(14)

where ${\vartheta }_1=({\vartheta }_{11},{\vartheta }_{12},\dots ,{\vartheta }_{1n})\in {\mathbb{R}}^n,n\in \mathbb{N}$.

Proof. 

By Taylor series, we have

$$\mu ({\vartheta }_1,{\vartheta }_2)={\gamma }_0\left({\vartheta }_1\right)+{\gamma }_1\left({\vartheta }_1\right){\displaystyle \frac{{\vartheta }_2^n}{\mathrm{\Gamma }(n+1)}}+{\gamma }_2\left({\vartheta }_1\right){\displaystyle \frac{{\vartheta }_2^{2n}}{\mathrm{\Gamma }(2n+1)}}+\dots$$

(15)

Take the Aboodh transform for (14):

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mu ({\vartheta }_1,{\vartheta }_2)=A_{{\vartheta }_2\sigma }{\gamma }_0\left({\vartheta }_1\right)+{\gamma }_1\left({\vartheta }_1\right){\displaystyle \frac{A_{{\vartheta }_2\sigma }{\vartheta }_2^n}{\mathrm{\Gamma }(n+1)}}+{\gamma }_2\left({\vartheta }_1\right){\displaystyle \frac{A_{{\vartheta }_2\sigma }{\vartheta }_2^{2n}}{\mathrm{\Gamma }(2n+1)}}+\dots \hfill \\ \hfill & ={\displaystyle \frac{{\gamma }_0\left({\vartheta }_1\right)}{{\sigma }^2}}+{\gamma }_1\left({\vartheta }_1\right){\displaystyle \frac{\mathrm{\Gamma }(n+1)}{{\sigma }^{n+2}\mathrm{\Gamma }(n+1)}}+{\gamma }_2\left({\vartheta }_1\right){\displaystyle \frac{\mathrm{\Gamma }(n+2)}{{\sigma }^{2n+2}\mathrm{\Gamma }(n+2)}}+\dots \hfill \\ & =\sum _{j=0}^{\infty }{\displaystyle \frac{{\gamma }_j\left({\vartheta }_1\right)}{{\sigma }^{jn+2}}}.\hfill \end{array}$$

(16)

This is the desired result. □

Lemma 4.

Let $\mu :{\mathbb{R}}^n\times [0,\infty )\to \mathbb{R}$ be a map with exponential order. Then, ${lim}_{\sigma \to \infty }{\sigma }^2{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )=\mu ({\vartheta }_1,0)$ for all ${\vartheta }_1\in {\mathbb{R}}^n$.

Proof. 

From the Equation (16), we have

$$\begin{array}{cc}\hfill & \underset{\sigma \to \infty }{lim}{\sigma }^2{A}_{{\vartheta }_2\sigma }\mu ({\vartheta }_1,{\vartheta }_2)={\gamma }_0\left({\vartheta }_1\right)+\underset{\sigma \to \infty }{lim}{\gamma }_1\left({\vartheta }_1\right){\displaystyle \frac{\mathrm{\Gamma }(n+1)}{{\sigma }^n\mathrm{\Gamma }(n+1)}}\hfill \\ \hfill & +\underset{\sigma \to \infty }{lim}{\gamma }_2\left({\vartheta }_1\right){\displaystyle \frac{\mathrm{\Gamma }(n+2)}{{\sigma }^{2n}\mathrm{\Gamma }(n+2)}}+\dots ={\gamma }_0\left({\vartheta }_1\right)=\mu ({\vartheta }_1,0).\hfill \end{array}$$

(17)

□

Theorem 1.

Let $\mu :{\mathbb{R}}^n\times [0,\infty )\to \mathbb{R}$ be a map with exponential order. Then,

$${\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )=\sum _{j=0}^{\infty }{\displaystyle \frac{{\gamma }_j\left({\vartheta }_1\right)}{{\sigma }^{jn+2}}}(0<\rho \le 1)$$

(18)

for all ${\vartheta }_1\in {\mathbb{R}}^n$ and $\sigma >0$, where ${\gamma }_j\left({\vartheta }_1\right)={\partial }_{{\vartheta }_2}^{jn}\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}$.

Proof. 

The new form of Taylor’s series will be

$${\gamma }_1\left({\vartheta }_1\right)={\sigma }^{n+2}{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-{\sigma }^n{\gamma }_0\left({\vartheta }_1\right)-{\displaystyle \frac{1}{{\sigma }^n}}{\gamma }_2\left({\vartheta }_1\right)-{\displaystyle \frac{1}{{\sigma }^{2n}}}{\gamma }_3\left({\vartheta }_1\right)-\dots$$

(19)

Take the limit of (19) when $\sigma \to \infty$ to obtain

$${\gamma }_1\left({\vartheta }_1\right)=\underset{\sigma \to \infty }{lim}\left[{\sigma }^{n+2}{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-{\sigma }^n{\gamma }_0\left({\vartheta }_1\right)\right].$$

(20)

By Lemma 2,

$${\gamma }_1\left({\vartheta }_1\right)=\underset{\sigma \to \infty }{lim}{\sigma }^2{A}_{{\vartheta }_2\sigma }\left[{\partial }_{{\vartheta }_2}^n\mu ({\vartheta }_1,{\vartheta }_2)\right].$$

(21)

By Lemma 4, we have ${\gamma }_1\left({\vartheta }_1\right)={\partial }_{{\vartheta }_2}^n\mu ({\vartheta }_1,0).$

Similarly, the new form of Taylor’s series of ${\gamma }_2$ will be

$${\gamma }_2\left({\vartheta }_1\right)={\sigma }^{2n+2}{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-{\sigma }^{2n}{\gamma }_0\left({\vartheta }_1\right)-{\sigma }^n{\gamma }_1\left({\vartheta }_1\right)-{\displaystyle \frac{1}{{\sigma }^n}}{\gamma }_3\left({\vartheta }_1\right)-{\displaystyle \frac{1}{{\sigma }^{2n}}}{\gamma }_4\left({\vartheta }_1\right)-\dots$$

(22)

By taking the limit of two sides of Equation (22) when $\sigma \to \infty$, we obtain

$${\gamma }_2\left({\vartheta }_1\right)=\underset{\sigma \to \infty }{lim}\left[{\sigma }^{2n+2}{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-{\sigma }^{2n}{\gamma }_0\left({\vartheta }_1\right)-{\sigma }^n{\gamma }_1\left({\vartheta }_1\right)\right].$$

(23)

By Lemmas 2 and 4, we have ${\gamma }_2\left({\vartheta }_1\right)={\partial }_{{\vartheta }_2}^{2n}\mu ({\vartheta }_1,0).$ By this continuity, we determine that ${\gamma }_j\left({\vartheta }_1\right)={\partial }_{{\vartheta }_2}^{jn}\mu ({\vartheta }_1,0).$ □

By Theorem 1, we have

$$A_{{\vartheta }_2\sigma }\left[{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)\right]=\sum _{j=0}^{\infty }{\displaystyle \frac{1}{{\sigma }^{j\rho +2}}}{}^c\mathcal{D}_{0,{\vartheta }_2}^{j\rho }\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}(0<\rho \le 1)$$

for all ${\vartheta }_1\in {\mathbb{R}}^n$, $\sigma >0$, and the inverse Aboodh transform will be

$$\mu ({\vartheta }_1,{\vartheta }_2)=\sum _{j=0}^{\infty }{\displaystyle \frac{{}^c\mathcal{D}_{0,{\vartheta }_2}^{j\rho }\mu ({\vartheta }_1,{\vartheta }_2){|}_{{\vartheta }_2=0}}{\Gamma (j\rho +2)}}{\vartheta }_2^{j\rho }(0<\rho \le 1)$$

for all ${\vartheta }_1\in {\mathbb{R}}^n$ and ${\vartheta }_2>0$.

Theorem 2.

Let $\mu :{\mathbb{R}}^n\times [0,\infty )\to \mathbb{R}$ be a map with exponential order. If $\left|{\sigma }^r{A}_{{\vartheta }_2\sigma }\left[{}^c\mathcal{D}_{0,{\vartheta }_2}^{(n+1)\rho }\mu ({\vartheta }_1,{\vartheta }_2)\right]\right|\le M$ for all $0<\sigma \le q$ and $0<\rho \le 1$, then the residual $\mathcal{R}e{s}_n({\vartheta }_1,\sigma )$ of MFPS satisfies $\parallel \mathcal{R}e{s}_n({\vartheta }_1,\sigma )\parallel \le {\displaystyle \frac{M}{{\sigma }^{(n+1)\rho }}}$.

Proof. 

We use the new form of Taylor’s series by

$$\mathcal{R}e{s}_n({\vartheta }_1,\sigma )={\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )+\sum _{j=0}^n{\displaystyle \frac{{\gamma }_j\left({\vartheta }_1\right)}{{\sigma }^{j\rho +2}}}.$$

(24)

By Theorem 1, we have

$$\mathcal{R}e{s}_n({\vartheta }_1,\sigma )={\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )+\sum _{j=0}^n{\displaystyle \frac{{}^c\mathcal{D}_{0,{\vartheta }_2}^{j\rho }\mu ({\vartheta }_1,0)}{{\sigma }^{j\rho +2}}}.$$

(25)

We multiply (25) by ${\sigma }^{(n+1)\rho +2}$ to obtain

$${\sigma }^{(n+1)\rho +2}\mathcal{R}e{s}_n({\vartheta }_1,\sigma )={\sigma }^2\left[{\sigma }^{(n+1)\rho }{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )+\sum _{j=0}^n{\sigma }^{(n+1-j)\rho -2}{}^c\mathcal{D}_{0,{\vartheta }_2}^{j\rho }\mu ({\vartheta }_1,0)\right].$$

(26)

By Lemma 2, we have

$${\sigma }^{(n+1)\rho +2}\mathcal{R}e{s}_n({\vartheta }_1,\sigma )=A_{{\vartheta }_2\sigma }\left[{}^c\mathcal{D}_{0,{\vartheta }_2}^{(n+1)\rho }\mu ({\vartheta }_1,{\vartheta }_2)\right].$$

(27)

Hence,

$$\left|{\sigma }^{(n+1)\rho +2}\mathcal{R}e{s}_n({\vartheta }_1,\sigma )\right|=\left|A_{{\vartheta }_2\sigma }\left[{}^c\mathcal{D}_{0,{\vartheta }_2}^{(n+1)\rho }\mu ({\vartheta }_1,{\vartheta }_2)\right]\right|.$$

That is, $|\mathcal{R}e{s}_n({\vartheta }_1,\sigma )|\le {\displaystyle \frac{M}{{\sigma }^{(n+1)\rho }}}$. □

3. The ARPSM Steps

Consider the following TCFKE:

$$\left\{\begin{array}{c}{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)=-\mu ({\vartheta }_1,{\vartheta }_2){\mathcal{D}}_{{\vartheta }_1}\mu ({\vartheta }_1,{\vartheta }_2)-{\mathcal{D}}_{{\vartheta }_1}^3\mu ({\vartheta }_1,{\vartheta }_2)+{\mathcal{D}}_{{\vartheta }_1}^5\mu ({\vartheta }_1,{\vartheta }_2),0<\rho \le 1\hfill \\ \mu ({\vartheta }_1,0)={\beta }_0\left({\vartheta }_1\right).\hfill \end{array}\right.$$

(28)

Take the Aboodh transform $A_{{\vartheta }_2\sigma }$ of (28):

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\left[{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\left[\mu ({\vartheta }_1,{\vartheta }_2)\right]\right]=-A_{{\vartheta }_2\sigma }\left[\mu ({\vartheta }_1,{\vartheta }_2){\mathcal{D}}_{{\vartheta }_1}\mu ({\vartheta }_1,{\vartheta }_2)\right]-A_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3\mu ({\vartheta }_1,{\vartheta }_2)\right]\hfill \\ \hfill & +A_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5\mu ({\vartheta }_1,{\vartheta }_2)\right].\hfill \end{array}$$

(29)

By Lemma 1, $A_{{\vartheta }_2\sigma }$ for the left side of (29) will be

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\left[{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)\right]={\sigma }^{\rho }{\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-{\sigma }^{\rho -2}{\beta }_0\left({\vartheta }_1\right).\hfill \end{array}$$

(30)

Then, from (29) and (30), we obtain

$$\begin{array}{cc}\hfill & {\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )={\displaystyle \frac{1}{{\sigma }^2}}{\beta }_0({\vartheta }_1)-{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )){\mathcal{D}}_{{\vartheta }_1}{A}_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma ))\right]\hfill \\ \hfill & -{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3{A}_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma ))\right]+{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5{A}_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma ))\right].\hfill \end{array}$$

(31)

The analytical solution ${\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )$ for (29) is given by

$${\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )={\displaystyle \frac{1}{{\sigma }^2}}{\beta }_0\left({\vartheta }_1\right)+\sum _{j=1}^{\infty }{\displaystyle \frac{{\beta }_j\left({\vartheta }_1\right)}{{\sigma }^{j\rho +2}}}.$$

(32)

By using the initial condition in (28) and Lemma 1, we provide the following sequence as a partial sums sequence ${⟨{\mu }_{{\vartheta }_{2}n}^A⟩}_{n\in {\mathbb{N}}_0}$ of (32) as

$${\mu }_{{\vartheta }_{2}n}^A({\vartheta }_1,\sigma )={\displaystyle \frac{1}{{\sigma }^2}}{\beta }_0\left({\vartheta }_1\right)+\sum _{j=1}^n{\displaystyle \frac{{\beta }_j\left({\vartheta }_1\right)}{{\sigma }^{j\rho +2}}},$$

(33)

where ${\mathbb{N}}_0:=\{0,1,2,\dots \}$. Now, we structure the residual function of the Aboodh transform, $A_{{\vartheta }_2\sigma }\mathcal{R}es{\mu }_{{\vartheta }_1{\vartheta }_2}$, for (31) as follows:

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mathcal{R}es{\mu }_{{\vartheta }_1{\vartheta }_2}={\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-{\displaystyle \frac{1}{{\sigma }^2}}{\beta }_0({\vartheta }_1)\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )){\mathcal{D}}_{{\vartheta }_1}{A}_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma ))\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3{A}_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma ))\right]-{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5{A}_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma ))\right]\hfill \end{array}$$

(34)

and the nth Aboodh residual function $A_{{\vartheta }_2\sigma }\mathcal{R}e{s}_n{\mu }_{{\vartheta }_1{\vartheta }_2}$ is

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mathcal{R}e{s}_n{\mu }_{{\vartheta }_1{\vartheta }_2}={\mu }_{{\vartheta }_{2}n}^A({\vartheta }_1,\sigma )-{\displaystyle \frac{1}{{\sigma }^2}}{\beta }_0({\vartheta }_1)\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_{2}n}^A({\vartheta }_1,\sigma )){\mathcal{D}}_{{\vartheta }_1}{A}_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_{2}n}^A({\vartheta }_1,\sigma ))\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3{A}_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_{2}n}^A({\vartheta }_1,\sigma ))\right]-{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5{A}_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_{2}n}^A({\vartheta }_1,\sigma ))\right]\hfill \end{array}$$

(35)

We have $A_{{\vartheta }_2\sigma }\mathcal{R}es{\mu }_{{\vartheta }_1{\vartheta }_2}=0$ and ${lim}_{n\to \infty }{A}_{{\vartheta }_2\sigma }\mathcal{R}e{s}_n{\mu }_{{\vartheta }_1{\vartheta }_2}=A_{{\vartheta }_2\sigma }\mathcal{R}es{\mu }_{{\vartheta }_1{\vartheta }_2}$ for all $\sigma >0$. If ${lim}_{\sigma \to \infty }{\sigma }^2{A}_{{\vartheta }_2\sigma }\mathcal{R}es{\mu }_{{\vartheta }_1{\vartheta }_2}=0$, then ${lim}_{\sigma \to \infty }{\sigma }^2{A}_{{\vartheta }_2\sigma }\mathcal{R}e{s}_n{\mu }_{{\vartheta }_1{\vartheta }_2}=0.$ In general, if

$$\underset{\sigma \to \infty }{lim}{\sigma }^{n\rho +2}{A}_{{\vartheta }_2\sigma }\mathcal{R}es{\mu }_{{\vartheta }_1{\vartheta }_2}=0$$

then

$$\underset{\sigma \to \infty }{lim}{\sigma }^{n\rho +2}{A}_{{\vartheta }_2\sigma }\mathcal{R}e{s}_n{\mu }_{{\vartheta }_1{\vartheta }_2}=0$$

for every $n\in \mathbb{N}$ and $0<\rho \le 1$. We will use the iterative method to obtain the coefficients ${\beta }_n\left({\vartheta }_1\right)$ in solving the following:

$$\underset{\sigma \to \infty }{lim}{\sigma }^{n\rho +2}{A}_{{\vartheta }_2\sigma }\mathcal{R}e{s}_n{\mu }_{{\vartheta }_1{\vartheta }_2}=0$$

(36)

for all $n=1,2,3,\dots$. Next, we introduce the coefficients ${\beta }_n\left({\vartheta }_1\right)$ into (33) to obtain the nth proximate solutions ${\mu }_{{\vartheta }_{2}n}^A({\vartheta }_1,\sigma )$ of (31). Finally, we use the inverse Aboodh transform of the nth proximate solutions ${\mu }_{{\vartheta }_{2}n}^A({\vartheta }_1,\sigma )$ to obtain the nth proximate solutions ${\mu }_{{\vartheta }_2}^n({\vartheta }_1,{\vartheta }_2)$ of (28).

4. Some Applications

Here, we use the ARPSM set out above to obtain analytical solutions of the TCFKE (2), first with the approximate initial condition obtained using the Taylor series on the exact initial condition of the TCFKE (2) for the 7th order. Consider the following TCFKE:

$$\left\{\begin{array}{c}{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)+\mu ({\vartheta }_1,{\vartheta }_2){\mathcal{D}}_{{\vartheta }_1}\mu ({\vartheta }_1,{\vartheta }_2)+{\mathcal{D}}_{{\vartheta }_1}^3\mu ({\vartheta }_1,{\vartheta }_2)-{\mathcal{D}}_{{\vartheta }_1}^5\mu ({\vartheta }_1,{\vartheta }_2)=0,0<\rho \le 1\hfill \\ \mu ({\vartheta }_1,0)=0.6213-0.0249{\vartheta }_1^2+5.106\times {10}^{-6}{\vartheta }_1^4-8.79\times {10}^{-8}{\vartheta }_1^6.\hfill \end{array}\right.$$

(37)

Take the Aboodh transform on (37) to obtain

$$\begin{array}{cc}\hfill & {\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )={\displaystyle \frac{1}{{\sigma }^2}}[0.6213-0.0249{\vartheta }_1^2+5.106\times {10}^{-6}{\vartheta }_1^4-8.79\times {10}^{-8}{\vartheta }_1^6]\hfill \\ \hfill & -{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )){\mathcal{D}}_{{\vartheta }_1}[A_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma ))]\right]\hfill \\ \hfill & -{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3[A_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma ))]\right]+{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5[A_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma ))]\right]\hfill \end{array}$$

(38)

and ${⟨{\mu }_{{\vartheta }_{2n}}^A⟩}_{n\in {\mathbb{N}}_0}$ as

$${\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )={\displaystyle \frac{1}{{\sigma }^2}}[0.6213-0.0249{\vartheta }_1^2+5.106\times {10}^{-6}{\vartheta }_1^4-8.79\times {10}^{-8}{\vartheta }_1^6]+\sum _{j=1}^n{\displaystyle \frac{{\beta }_j\left({\vartheta }_1\right)}{{\sigma }^{j\rho +2}}}.$$

(39)

The nth construction of (38) is given by

$$\begin{array}{cc}\hfill & {\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )={\displaystyle \frac{1}{{\sigma }^2}}[0.6213-0.0249{\vartheta }_1^2+5.106\times {10}^{-6}{\vartheta }_1^4-8.79\times {10}^{-8}{\vartheta }_1^6]\hfill \\ \hfill & -{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )){\mathcal{D}}_{{\vartheta }_1}[A_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma ))]\right]\hfill \\ \hfill & -{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3[A_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma ))]\right]+{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5[A_{{\vartheta }_2\sigma }^{-1}({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma ))]\right]\hfill \end{array}$$

(40)

for $n\in \mathbb{N}$. The Aboodh eesidual map, $A_{{\vartheta }_2\sigma }\mathcal{R}es\mu ({\vartheta }_1,\sigma )$, for (38) will be

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mathcal{R}es\mu ({\vartheta }_1,\sigma )={\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-{\displaystyle \frac{1}{{\sigma }^2}}[0.6213-0.0249{\vartheta }_1^2+5.106\times {10}^{-6}{\vartheta }_1^4\hfill \\ \hfill & -8.79\times {10}^{-8}{\vartheta }_1^6]+{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )\right){\mathcal{D}}_{{\vartheta }_1}\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )\right)\right]\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )\right)\right]\right]-{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )\right)\right]\right]\hfill \end{array}$$

(41)

with the nth Aboodh Residual function

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mathcal{R}e{s}_n\mu ({\vartheta }_1,\sigma )={\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )-{\displaystyle \frac{1}{{\sigma }^2}}[0.6213-0.0249{\vartheta }_1^2+5.106\times {10}^{-6}{\vartheta }_1^4\hfill \\ \hfill & -8.79\times {10}^{-8}{\vartheta }_1^6]+{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )\right){\mathcal{D}}_{{\vartheta }_1}\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )\right)\right]\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )\right)\right]\right]-{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )\right)\right]\right]\hfill \end{array}$$

(42)

for $n\in \mathbb{N}$. Next, we find the terms of ${⟨{\beta }_n⟩}_{n\in {\mathbb{N}}_0}$ by using the relation

$$\underset{\sigma \to \infty }{lim}{\sigma }^{n\rho +2}{A}_{{\vartheta }_2\sigma }\mathcal{R}e{s}_n\mu ({\vartheta }_1,\sigma )=0n=1,2,3,\dots$$

(43)

At $n=1$, by using (39), we have

$${\mu }_{{\vartheta }_2}^{A1}({\vartheta }_1,\sigma )={\displaystyle \frac{1}{{\sigma }^2}}[0.6213-0.0249{\vartheta }_1^2+5.106\times {10}^{-6}{\vartheta }_1^4-8.79\times {10}^{-8}{\vartheta }_1^6]+{\displaystyle \frac{{\beta }_1\left({\vartheta }_1\right)}{{\sigma }^{\rho +2}}}$$

and (42) becomes

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mathcal{R}e{s}_1\mu ({\vartheta }_1,\sigma )={\displaystyle \frac{{\beta }_1\left({\vartheta }_1\right)}{{\sigma }^{\rho +2}}}+{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A1}({\vartheta }_1,\sigma )\right){\mathcal{D}}_{{\vartheta }_1}\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A1}({\vartheta }_1,\sigma )\right)\right]\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A1}({\vartheta }_1,\sigma )\right)\right]\right]-{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A2}({\vartheta }_1,\sigma )\right)\right]\right].\hfill \end{array}$$

This implies

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mathcal{R}e{s}_1\mu ({\vartheta }_1,\sigma )={\displaystyle \frac{1}{{\sigma }^{\rho +2}}}\left[{\beta }_1\left({\vartheta }_1\right)+\mathcal{M}\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}\mathcal{M}\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^3\mathcal{M}\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^5\mathcal{M}\left({\vartheta }_1\right)\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{2\rho +2}}}\left[\mathcal{M}\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_1\left({\vartheta }_1\right)+{\beta }_1\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}\mathcal{M}\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^3\mathcal{M}\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^5\mathcal{M}\left({\vartheta }_1\right)\right]\hfill \\ \hfill & +{\displaystyle \frac{\Gamma (2\rho +2)}{{(\Gamma (\rho +2))}^2{\sigma }^{3\rho +2}}}{\beta }_1\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_1\left({\vartheta }_1\right)\hfill \end{array}$$

(44)

where $\mathcal{M}\left({\vartheta }_1\right)=0.6213-0.0249{\vartheta }_1^2+5.106\times {10}^{-6}{\vartheta }_1^4-8.79\times {10}^{-8}{\vartheta }_1^6$. By multiplying both sides of (44) by ${\sigma }^{\rho +2}$ and by (43), we have

$$\begin{array}{cc}\hfill & {\beta }_1\left({\vartheta }_1\right)=-3.86321\times {10}^{-14}{\vartheta }_1^{11}+3.59054\times {10}^{-12}{\vartheta }_1^9-6.64434\times {10}^{-9}{\vartheta }_1^7\hfill \\ \hfill & +4.00201\times {10}^{-7}{\vartheta }_1^5+0.00123{\vartheta }_1^3-0.03097991{\vartheta }_1.\hfill \end{array}$$

(45)

At $n=2$, by (39), we have

$${\mu }_{{\vartheta }_2}^{A2}({\vartheta }_1,\sigma )={\displaystyle \frac{1}{{\sigma }^2}}[0.6213-0.0249{\vartheta }_1^2+5.106\times {10}^{-6}{\vartheta }_1^4-8.79\times {10}^{-8}{\vartheta }_1^6]+{\displaystyle \frac{{\beta }_1\left({\vartheta }_1\right)}{{\sigma }^{\rho +2}}}+{\displaystyle \frac{{\beta }_2\left({\vartheta }_1\right)}{{\sigma }^{2\rho +2}}}$$

and (42) becomes

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mathcal{R}e{s}_2\mu ({\vartheta }_1,\sigma )={\displaystyle \frac{{\beta }_1\left({\vartheta }_1\right)}{{\sigma }^{\rho +2}}}+{\displaystyle \frac{{\beta }_2\left({\vartheta }_1\right)}{{\sigma }^{2\rho +2}}}+{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A2}({\vartheta }_1,\sigma )\right){\mathcal{D}}_{{\vartheta }_1}\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A2}({\vartheta }_1,\sigma )\right)\right]\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A2}({\vartheta }_1,\sigma )\right)\right]\right]-{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A2}({\vartheta }_1,\sigma )\right)\right]\right].\hfill \end{array}$$

This implies

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mathcal{R}e{s}_2\mu ({\vartheta }_1,\sigma )={\displaystyle \frac{1}{{\sigma }^{2\rho +2}}}[{\beta }_2\left({\vartheta }_1\right)+\mathcal{M}\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_1\left({\vartheta }_1\right)+{\beta }_1\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}\mathcal{M}\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^3{\beta }_1\left({\vartheta }_1\right)\hfill \\ \hfill & +{\mathcal{D}}_{{\vartheta }_1}^5{\beta }_1\left({\vartheta }_1\right)]+{\displaystyle \frac{1}{{\sigma }^{3\rho +2}}}[\mathcal{M}\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_2\left({\vartheta }_1\right)+{\beta }_2\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}\mathcal{M}\left({\vartheta }_1\right)\hfill \\ & +{\displaystyle \frac{\Gamma (2\rho +2)}{{(\Gamma (\rho +2))}^2}}{\beta }_1\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_1\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^3{\beta }_2\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^5{\beta }_2\left({\vartheta }_1\right)]\hfill \\ \hfill & +{\displaystyle \frac{\Gamma (3\rho +2)}{\Gamma (\rho +2)\Gamma (2\rho +2){\sigma }^{4\rho +2}}}\left[{\beta }_1\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_2\left({\vartheta }_1\right)+{\beta }_2\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_1\left({\vartheta }_1\right)\right]\hfill \\ \hfill & +{\displaystyle \frac{\Gamma (4\rho +2)}{{(\Gamma (\rho +2))}^2{\sigma }^{5\rho +2}}}\left[{\beta }_2\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_2\left({\vartheta }_1\right)\right].\hfill \end{array}$$

(46)

By multiplying both sides of (46) by ${\sigma }^{\rho +2}$ and by (43), we have

$$\begin{array}{cc}\hfill & {\beta }_2\left({\vartheta }_1\right)=4.815\times {10}^{-18}{\vartheta }_1^{16}+3.7141\times {10}^{-15}{\vartheta }_1^{14}+7.26878\times {10}^{-12}{\vartheta }_1^{12}\hfill \\ \hfill & +5.35202\times {10}^{-10}{\vartheta }_1^{10}-1.27589\times {10}^{-7}{\vartheta }_1^8-8.92491\times {10}^{-6}{\vartheta }_1^6\hfill \\ \hfill & -0.005354902{\vartheta }_1^4-0.00221268{\vartheta }_1^2+0.011039.\hfill \end{array}$$

(47)

Next, we input the values of ${⟨{\beta }_n⟩}_{n\in {\mathbb{N}}_0}$ in (32) to obtain

$$\begin{array}{cc}\hfill & {\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )=\sum _{j=0}^{\infty }{\displaystyle \frac{{\beta }_j\left({\vartheta }_1\right)}{{\sigma }^{j\rho +2}}}={\displaystyle \frac{1}{{\sigma }^2}}{\beta }_0\left({\vartheta }_1\right)+{\displaystyle \frac{1}{{\sigma }^{\rho +2}}}{\beta }_1\left({\vartheta }_1\right)+{\displaystyle \frac{1}{{\sigma }^{2\rho +2}}}{\beta }_2\left({\vartheta }_1\right)+\dots \hfill \\ \hfill & ={\displaystyle \frac{1}{{\sigma }^2}}[0.6213-0.0249{\vartheta }_1^2+5.106\times {10}^{-6}{\vartheta }_1^4-8.79\times {10}^{-8}{\vartheta }_1^6]\hfill \\ & +{\displaystyle \frac{1}{{\sigma }^{\rho +2}}}\{-3.86321\times {10}^{-14}{\vartheta }_1^{11}+3.59054\times {10}^{-12}{\vartheta }_1^9-6.64434\times {10}^{-9}{\vartheta }_1^7\hfill \\ \hfill & +4.00201\times {10}^{-7}{\vartheta }_1^5+0.00123{\vartheta }_1^3-0.03097991{\vartheta }_1\}\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{2\rho +2}}}[4.815\times {10}^{-18}{\vartheta }_1^{16}+3.7141\times {10}^{-15}{\vartheta }_1^{14}+7.26878\times {10}^{-12}{\vartheta }_1^{12}\hfill \\ \hfill & +5.35202\times {10}^{-10}{\vartheta }_1^{10}-1.27589\times {10}^{-7}{\vartheta }_1^8-8.92491\times {10}^{-6}{\vartheta }_1^6\hfill \\ \hfill & -0.005354902{\vartheta }_1^4-0.00221268{\vartheta }_1^2+0.011039]+\dots \hfill \end{array}$$

(48)

We take the inverse Aboodh transform of (48):

$$\begin{array}{cc}\hfill & \mu ({\vartheta }_1,{\vartheta }_2)=0.6213-0.0249{\vartheta }_1^2+5.106\times {10}^{-6}{\vartheta }_1^4-8.79\times {10}^{-8}{\vartheta }_1^6\hfill \\ & +{\displaystyle \frac{{\vartheta }_2^{\rho }}{\Gamma (\rho +1)}}\{-3.86321\times {10}^{-14}{\vartheta }_1^{11}+3.59054\times {10}^{-12}{\vartheta }_1^9-6.64434\times {10}^{-9}{\vartheta }_1^7\hfill \\ \hfill & +4.00201\times {10}^{-7}{\vartheta }_1^5+0.00123{\vartheta }_1^3-0.03097991{\vartheta }_1\}\hfill \\ \hfill & +{\displaystyle \frac{{\vartheta }_2^{2\rho }}{\Gamma (2\rho +1)}}[4.815\times {10}^{-18}{\vartheta }_1^{16}+3.7141\times {10}^{-15}{\vartheta }_1^{14}+7.26878\times {10}^{-12}{\vartheta }_1^{12}\hfill \\ \hfill & +5.35202\times {10}^{-10}{\vartheta }_1^{10}-1.27589\times {10}^{-7}{\vartheta }_1^8-8.92491\times {10}^{-6}{\vartheta }_1^6\hfill \\ \hfill & -0.005354902{\vartheta }_1^4-0.00221268{\vartheta }_1^2+0.011039]+\dots \hfill \end{array}$$

(49)

Now, we find the analytical solution of the TCFKE (2) by using the exact initial condition. Consider the TCFKE:

$$\left\{\begin{array}{c}{}^c\mathcal{D}_{0,{\vartheta }_2}^{\rho }\mu ({\vartheta }_1,{\vartheta }_2)+\mu ({\vartheta }_1,{\vartheta }_2){\mathcal{D}}_{{\vartheta }_1}\mu ({\vartheta }_1,{\vartheta }_2)+{\mathcal{D}}_{{\vartheta }_1}^3\mu ({\vartheta }_1,{\vartheta }_2)-{\mathcal{D}}_{{\vartheta }_1}^5\mu ({\vartheta }_1,{\vartheta }_2)=0,0<\rho \le 1\hfill \\ \mu ({\vartheta }_1,0)={\displaystyle \frac{105}{169}}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right).\hfill \end{array}\right.$$

(50)

It is clear that by [34], if $\rho =1$, then the exact solution of (50) is given by

$$\mu ({\vartheta }_1,{\vartheta }_2)={\displaystyle \frac{105}{169}}{\mathrm{sech}}^4\left[{\displaystyle \frac{1}{2\sqrt{13}}}\left({\vartheta }_1-{\displaystyle \frac{36}{169}}{\vartheta }_2\right)\right].$$

(51)

We take the Aboodh transforms on (50) to obtain

$$\begin{array}{cc}\hfill & {\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )={\displaystyle \frac{105}{169\sigma }}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)-{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )\right){\mathcal{D}}_{{\vartheta }_1}\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )\right)\right]\right]\hfill \\ \hfill & -{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )\right)\right]\right]+{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )\right)\right]\right]\hfill \end{array}$$

(52)

with the sequence ${⟨{\mu }_{{\vartheta }_2}^{An}⟩}_{n\in {\mathbb{N}}_0}$

$${\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )={\displaystyle \frac{105}{169\sigma }}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)+\sum _{j=1}^n{\displaystyle \frac{{\beta }_j\left({\vartheta }_1\right)}{{\sigma }^{j\rho +2}}}.$$

(53)

The nth construction of (52) is given by

$$\begin{array}{cc}\hfill & {\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )={\displaystyle \frac{105}{169\sigma }}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)-{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )\right){\mathcal{D}}_{{\vartheta }_1}\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )\right)\right]\right]\hfill \\ \hfill & -{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )\right)\right]\right]+{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )\right)\right]\right]\hfill \end{array}$$

(54)

for $n\in \mathbb{N}$. The Aboodh residual map, $A_{{\vartheta }_2\sigma }\mathcal{R}es\mu ({\vartheta }_1,\sigma )$, for (52) will be

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mathcal{R}es\mu ({\vartheta }_1,\sigma )={\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )-{\displaystyle \frac{105}{169\sigma }}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )\right){\mathcal{D}}_{{\vartheta }_1}\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )\right)\right]\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )\right)\right]\right]-{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )\right)\right]\right]\hfill \end{array}$$

(55)

with the nth Aboodh residual map:

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mathcal{R}e{s}_n\mu ({\vartheta }_1,\sigma )={\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )-{\displaystyle \frac{105}{169\sigma }}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )\right){\mathcal{D}}_{{\vartheta }_1}\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )\right)\right]\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )\right)\right]\right]-{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{An}({\vartheta }_1,\sigma )\right)\right]\right]\hfill \end{array}$$

(56)

for $n\in \mathbb{N}$. The terms of ${⟨{\beta }_n⟩}_{n\in {\mathbb{N}}_0}$, using the following relation, are

$$\underset{\sigma \to \infty }{lim}{\sigma }^{n\rho +2}{A}_{{\vartheta }_2\sigma }\mathcal{R}e{s}_n\mu ({\vartheta }_1,\sigma )=0n=1,2,3,\dots$$

(57)

At $n=1$, by using (53), we have ${\mu }_{{\vartheta }_2}^{A1}({\vartheta }_1,\sigma )={\displaystyle \frac{105}{169\sigma }}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)+{\displaystyle \frac{{\beta }_1\left({\vartheta }_1\right)}{{\sigma }^{\rho +2}}}$, and (56) becomes

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mathcal{R}e{s}_1\mu ({\vartheta }_1,\sigma )={\displaystyle \frac{{\beta }_1\left({\vartheta }_1\right)}{{\sigma }^{\rho +2}}}+{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A1}({\vartheta }_1,\sigma )\right){\mathcal{D}}_{{\vartheta }_1}\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A1}({\vartheta }_1,\sigma )\right)\right]\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A1}({\vartheta }_1,\sigma )\right)\right]\right]-{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A1}({\vartheta }_1,\sigma )\right)\right]\right].2\hfill \end{array}$$

This implies

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mathcal{R}e{s}_1\mu ({\vartheta }_1,\sigma )={\displaystyle \frac{1}{{\sigma }^{\rho +2}}}\left[{\beta }_1\left({\vartheta }_1\right)+\mathcal{A}\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}\mathcal{A}\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^3\mathcal{A}\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^5\mathcal{A}\left({\vartheta }_1\right)\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{2\rho +2}}}\left[\mathcal{A}\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_1\left({\vartheta }_1\right)+{\beta }_1\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}\mathcal{A}\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^3{\beta }_1\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^5{\beta }_1\left({\vartheta }_1\right)\right]\hfill \\ \hfill & +{\displaystyle \frac{\Gamma (2\rho +2)}{{(\Gamma (\rho +2))}^2{\sigma }^{3\rho +2}}}{\beta }_1\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_1\left({\vartheta }_1\right)\hfill \end{array}$$

(58)

where $\mathcal{A}\left({\vartheta }_1\right)={\displaystyle \frac{105}{169}}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)$. By multiplying both sides of (58) by ${\sigma }^{\rho +2}$ and by (57), we have

$$\begin{array}{cc}\hfill & {\beta }_1\left({\vartheta }_1\right)={\displaystyle \frac{22050}{28561\sqrt{13}}}{\mathrm{sech}}^8\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\tanh \left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\hfill \\ \hfill & +{\displaystyle \frac{210}{169\sqrt{13}}}\left[{\displaystyle \frac{4}{13}}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right){\tanh }^3\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)-{\displaystyle \frac{7}{26}}{\mathrm{sech}}^6\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\tanh \left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\right]\hfill \\ \hfill & +{\displaystyle \frac{105}{57122}}[{\displaystyle \frac{94}{\sqrt{13}}}{\mathrm{sech}}^8\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\tanh \left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)+{\displaystyle \frac{64}{\sqrt{13}}}{\tanh }^5\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right){\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\hfill \\ \hfill & -{\displaystyle \frac{262}{\sqrt{13}}}{\mathrm{sech}}^6\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right){\tanh }^3\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)].\hfill \end{array}$$

(59)

At $n=2$, by (53) we have

$${\mu }_{{\vartheta }_2}^{A2}({\vartheta }_1,\sigma )={\displaystyle \frac{105}{169\sigma }}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)+{\displaystyle \frac{{\beta }_1\left({\vartheta }_1\right)}{{\sigma }^{\rho +2}}}+{\displaystyle \frac{{\beta }_2\left({\vartheta }_1\right)}{{\sigma }^{2\rho +2}}}$$

and (56) becomes

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mathcal{R}e{s}_2\mu ({\vartheta }_1,\sigma )={\displaystyle \frac{{\beta }_1\left({\vartheta }_1\right)}{{\sigma }^{\rho +2}}}+{\displaystyle \frac{{\beta }_2\left({\vartheta }_1\right)}{{\sigma }^{2\rho +2}}}+{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A2}({\vartheta }_1,\sigma )\right){\mathcal{D}}_{{\vartheta }_1}\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A2}({\vartheta }_1,\sigma )\right)\right]\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^3\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A2}({\vartheta }_1,\sigma )\right)\right]\right]-{\displaystyle \frac{1}{{\sigma }^{\rho }}}{A}_{{\vartheta }_2\sigma }\left[{\mathcal{D}}_{{\vartheta }_1}^5\left[A_{{\vartheta }_2\sigma }^{-1}\left({\mu }_{{\vartheta }_2}^{A2}({\vartheta }_1,\sigma )\right)\right]\right].\hfill \end{array}$$

This implies

$$\begin{array}{cc}\hfill & A_{{\vartheta }_2\sigma }\mathcal{R}e{s}_2\mu ({\vartheta }_1,\sigma )={\displaystyle \frac{1}{{\sigma }^{2\rho +2}}}[{\beta }_2\left({\vartheta }_1\right)+\mathcal{A}\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_1\left({\vartheta }_1\right)+{\beta }_1\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}\mathcal{A}\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^3{\beta }_1\left({\vartheta }_1\right)\hfill \\ \hfill & +{\mathcal{D}}_{{\vartheta }_1}^5{\beta }_1\left({\vartheta }_1\right)]+{\displaystyle \frac{1}{{\sigma }^{3\rho +2}}}[\mathcal{A}\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_2\left({\vartheta }_1\right)+{\beta }_2\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}\mathcal{A}\left({\vartheta }_1\right)\hfill \\ & +{\displaystyle \frac{\Gamma (2\rho +2)}{{(\Gamma (\rho +2))}^2}}{\beta }_1\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_1\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^3{\beta }_2\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^5{\beta }_2\left({\vartheta }_1\right)]\hfill \\ \hfill & +{\displaystyle \frac{\Gamma (3\rho +2)}{\Gamma (\rho +2)\Gamma (2\rho +2){\sigma }^{4\rho +2}}}\left[{\beta }_1\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_2\left({\vartheta }_1\right)+{\beta }_2\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_1\left({\vartheta }_1\right)\right]\hfill \\ \hfill & +{\displaystyle \frac{\Gamma (4\rho +2)}{{(\Gamma (\rho +2))}^2{\sigma }^{5\rho +2}}}\left[{\beta }_2\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_2\left({\vartheta }_1\right)\right].\hfill \end{array}$$

(60)

By multiplying both sides of (60) by ${\sigma }^{\rho +2}$ and by (57), we have

$$\begin{array}{c}\hfill {\beta }_2\left({\vartheta }_1\right)=-\mathcal{A}\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_1\left({\vartheta }_1\right)-{\beta }_1\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}\mathcal{A}\left({\vartheta }_1\right)-{\mathcal{D}}_{{\vartheta }_1}^3{\beta }_1\left({\vartheta }_1\right)-{\mathcal{D}}_{{\vartheta }_1}^5{\beta }_1\left({\vartheta }_1\right).\end{array}$$

(61)

Next, we input the terms of ${⟨{\beta }_n⟩}_{n\in {\mathbb{N}}_0}$ in (32) to obtain

$$\begin{array}{cc}\hfill & {\mu }_{{\vartheta }_2}^A({\vartheta }_1,\sigma )=\sum _{j=0}^{\infty }{\displaystyle \frac{{\beta }_j\left({\vartheta }_1\right)}{{\sigma }^{j\rho +2}}}={\displaystyle \frac{1}{{\sigma }^2}}{\beta }_0\left({\vartheta }_1\right)+{\displaystyle \frac{1}{{\sigma }^{\rho +2}}}{\beta }_1\left({\vartheta }_1\right)+{\displaystyle \frac{1}{{\sigma }^{2\rho +2}}}{\beta }_2\left({\vartheta }_1\right)+\dots \hfill \\ \hfill & ={\displaystyle \frac{105}{169\sigma }}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)+{\displaystyle \frac{1}{{\sigma }^{\rho +2}}}\{{\displaystyle \frac{22050}{28561\sqrt{13}}}{\mathrm{sech}}^8\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\tanh \left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\hfill \\ \hfill & +{\displaystyle \frac{210}{169\sqrt{13}}}\left[{\displaystyle \frac{4}{13}}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right){\tanh }^3\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)-{\displaystyle \frac{7}{26}}{\mathrm{sech}}^6\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\tanh \left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\right]\hfill \\ \hfill & +{\displaystyle \frac{105}{57122}}[{\displaystyle \frac{94}{\sqrt{13}}}{\mathrm{sech}}^8\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\tanh \left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)+{\displaystyle \frac{64}{\sqrt{13}}}{\tanh }^5\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right){\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\hfill \\ \hfill & -{\displaystyle \frac{262}{\sqrt{13}}}{\mathrm{sech}}^6\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right){\tanh }^3\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\left]\right\}-{\displaystyle \frac{1}{{\sigma }^{2\rho +2}}}(\mathcal{A}\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_1\left({\vartheta }_1\right)+{\beta }_1\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}\mathcal{A}\left({\vartheta }_1\right)\hfill \\ \hfill & +{\mathcal{D}}_{{\vartheta }_1}^3{\beta }_1\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^5{\beta }_1\left({\vartheta }_1\right))+\dots \hfill \end{array}$$

(62)

We use the inverse Aboodh transform of (62),

$$\begin{array}{cc}\hfill & \mu ({\vartheta }_1,{\vartheta }_2)={\displaystyle \frac{105}{169}}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)+{\displaystyle \frac{{\vartheta }_2^{\rho }}{\Gamma (\rho +1)}}\{{\displaystyle \frac{22050}{28561\sqrt{13}}}{\mathrm{sech}}^8\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\tanh \left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\hfill \\ \hfill & +{\displaystyle \frac{210}{169\sqrt{13}}}\left[{\displaystyle \frac{4}{13}}{\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right){\tanh }^3\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)-{\displaystyle \frac{7}{26}}{\mathrm{sech}}^6\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\tanh \left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\right]\hfill \\ \hfill & +{\displaystyle \frac{105}{57122}}[{\displaystyle \frac{94}{\sqrt{13}}}{\mathrm{sech}}^8\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\tanh \left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)+{\displaystyle \frac{64}{\sqrt{13}}}{\tanh }^5\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right){\mathrm{sech}}^4\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\hfill \\ \hfill & -{\displaystyle \frac{262}{\sqrt{13}}}{\mathrm{sech}}^6\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right){\tanh }^3\left({\displaystyle \frac{{\vartheta }_1}{2\sqrt{13}}}\right)\left]\right\}-{\displaystyle \frac{{\vartheta }_2^{2\rho }}{\Gamma (2\rho +1)}}(\mathcal{A}\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}{\beta }_1\left({\vartheta }_1\right)\hfill \\ & +{\beta }_1\left({\vartheta }_1\right){\mathcal{D}}_{{\vartheta }_1}\mathcal{A}\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^3{\beta }_1\left({\vartheta }_1\right)+{\mathcal{D}}_{{\vartheta }_1}^5{\beta }_1\left({\vartheta }_1\right))+\dots \hfill \end{array}$$

(63)

5. Numerical Discussion

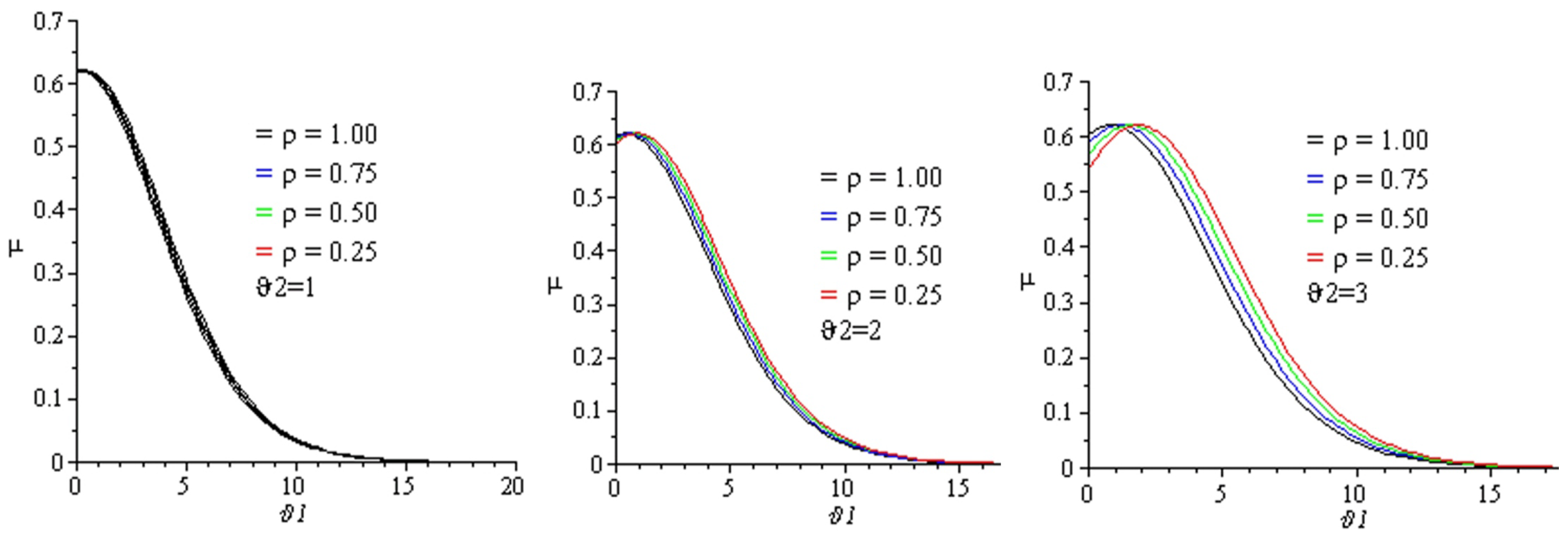
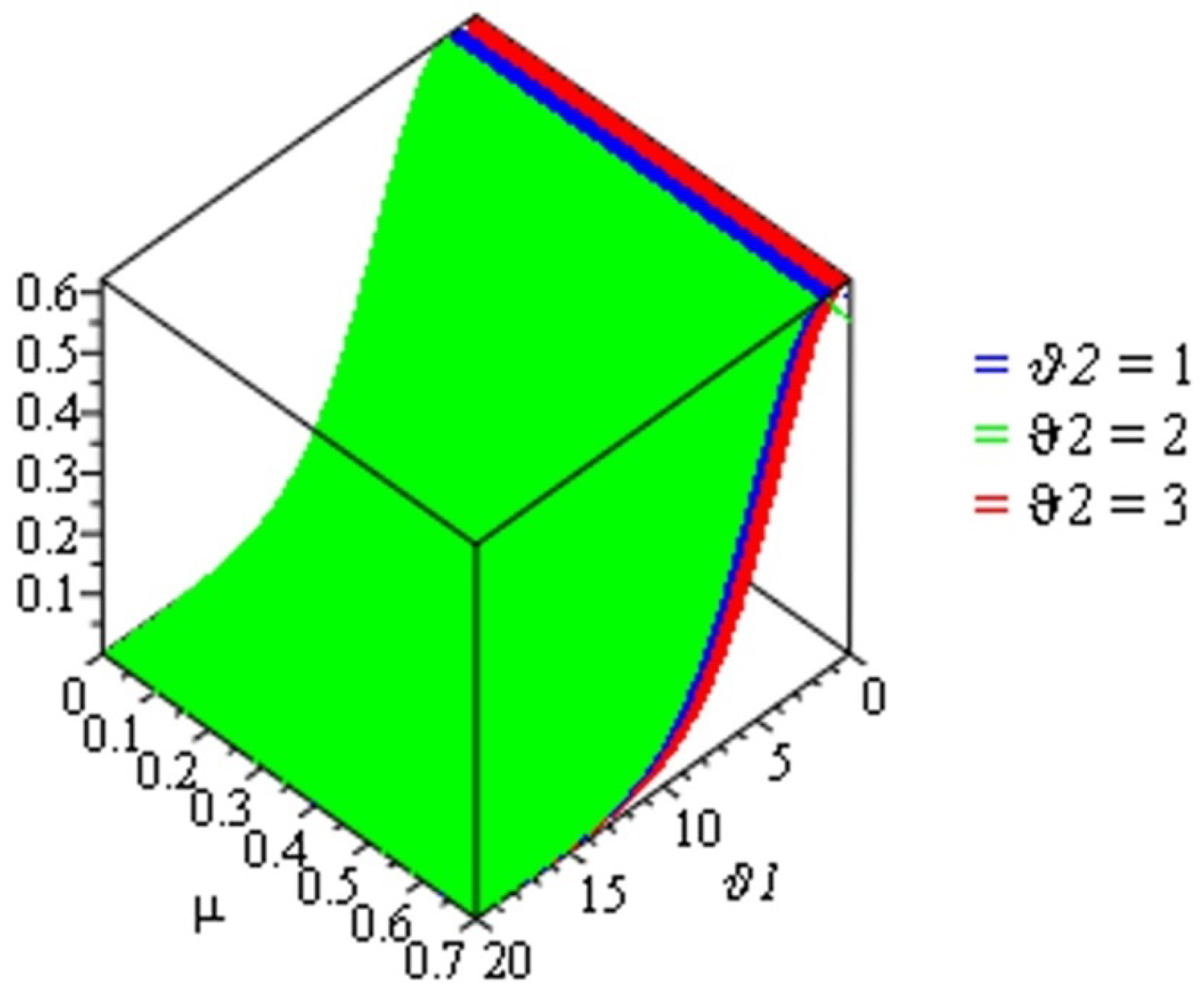
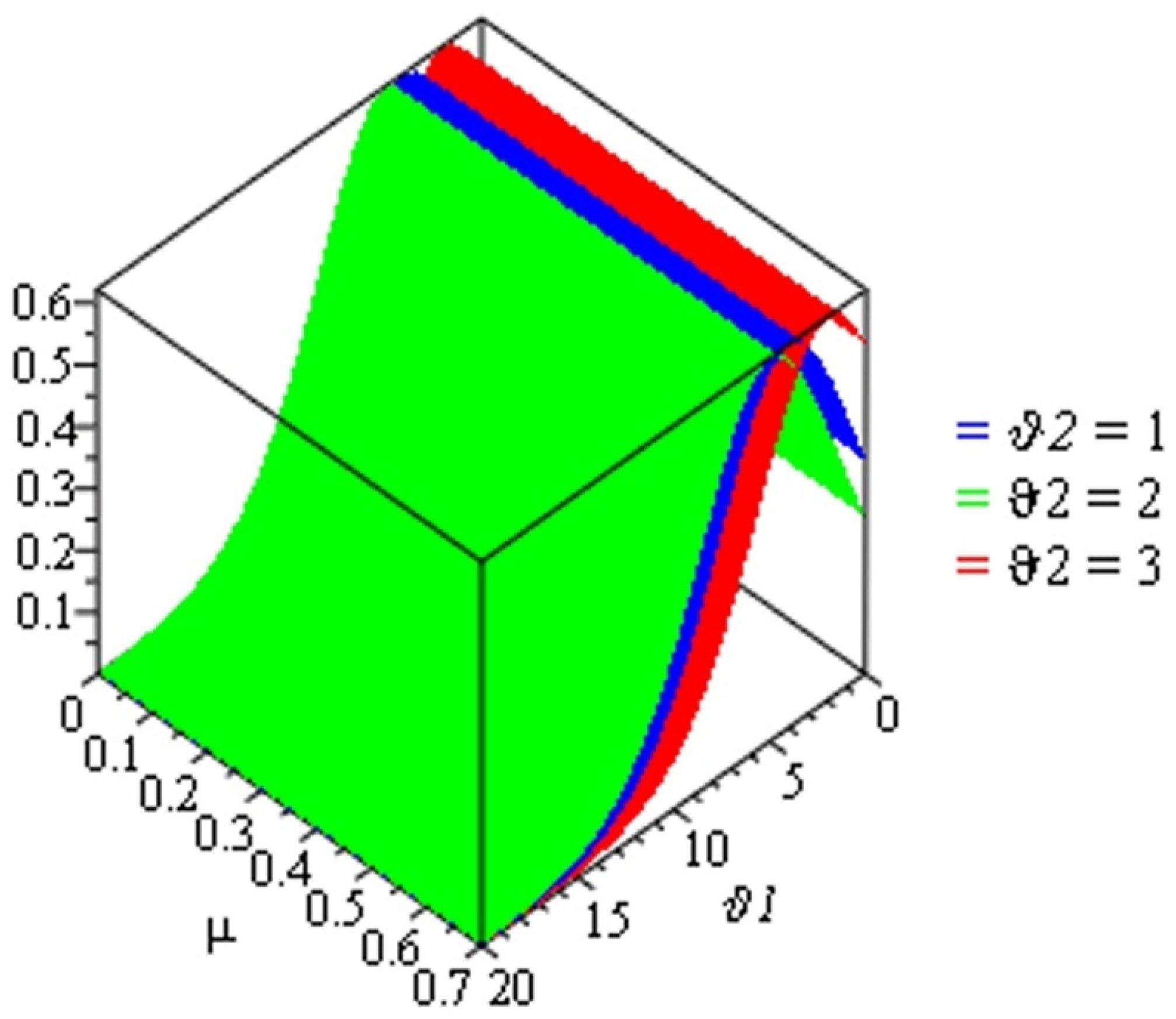
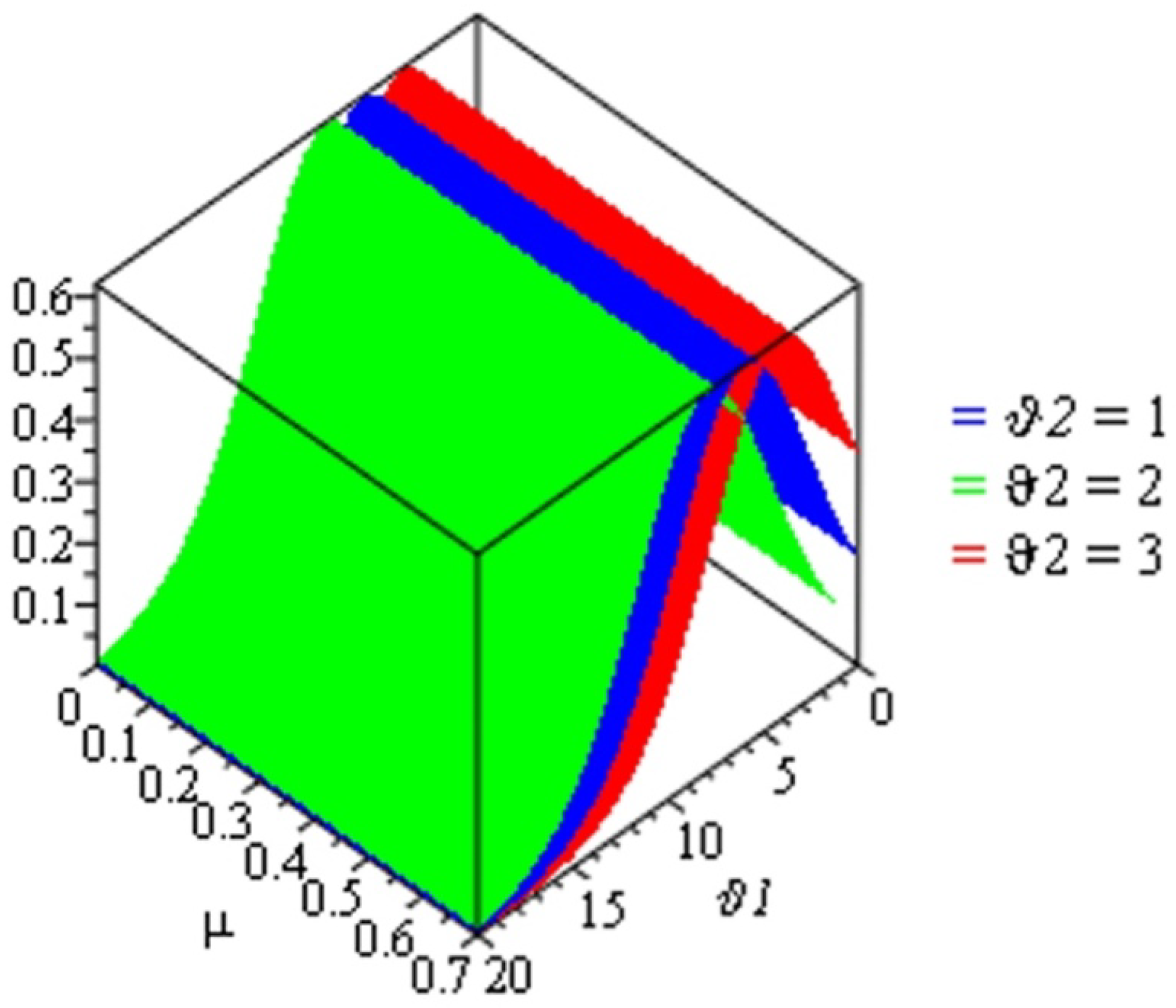
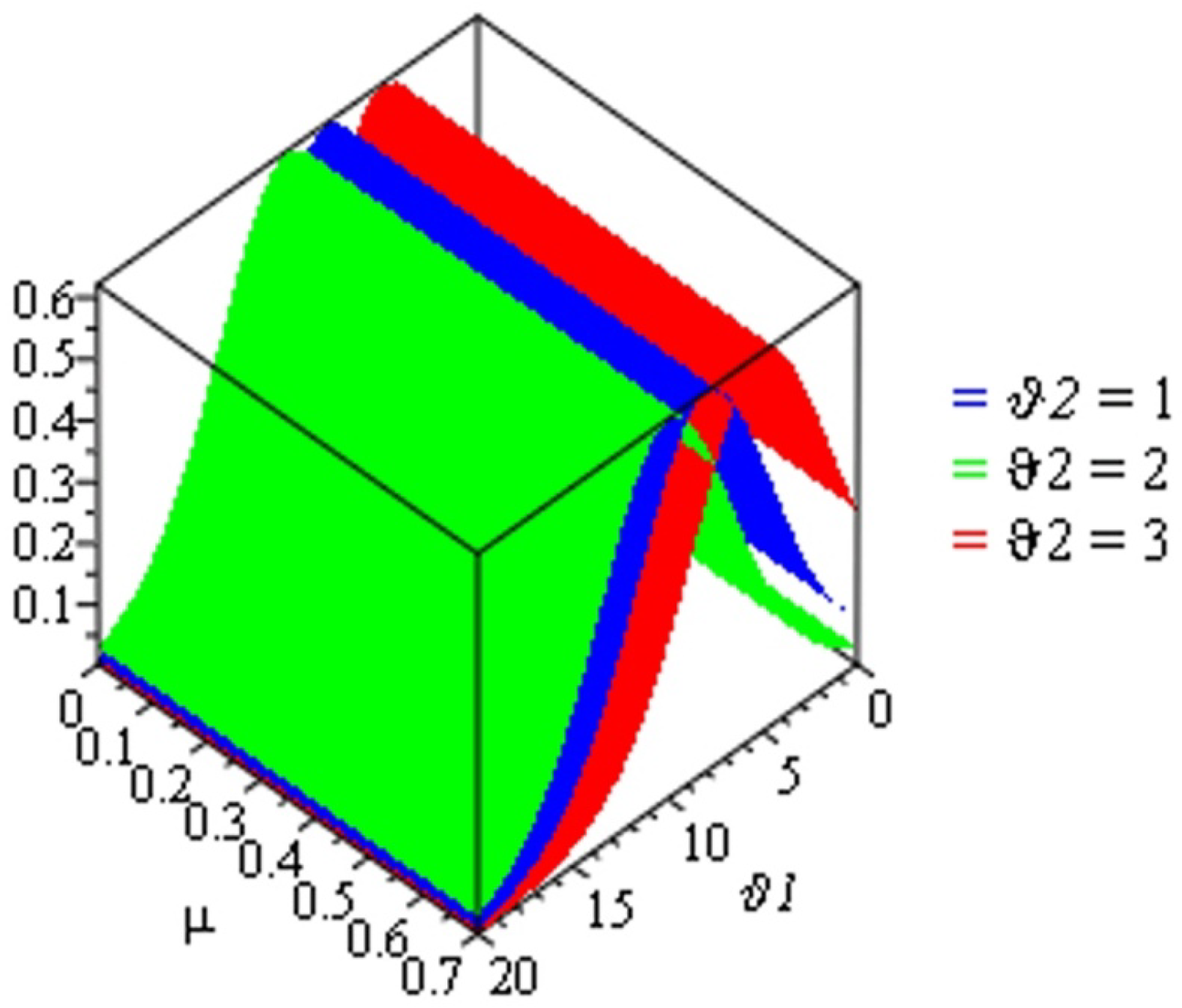
This section illustrates and presents the approximate solutions of the TCFKE (37) by giving some different values of fractional-order $\rho$ in Table 1 and Table 2 and by using numerical imitation in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5. We demonstrate the dynamical behavior of the approximate solutions of the TCFKE (37). Table 1 includes some comparison studies concerning the absolute error (AE) for the exact solutions of the TCFKE (37) at $\rho =1$ and ${\vartheta }_1=10$, with the obtained solutions of TCFKE (37) given by the RPSM [32] and NTDM [33]. Table 2 presents the numerical solution of (37) at ${\vartheta }_1=10$ and several values of $\rho$ and ${\vartheta }_2$ obtained via the ARPSM. We compare our solutions and other solutions that were obtained by the RPSM [32] and NTDM [33] techniques. In Figure 1, we present a number of curves for the numerical solutions for (37), with ${\vartheta }_2=1$, ${\vartheta }_2=2$, ${\vartheta }_2=3$, and certain values of $\rho$. Figure 2 presents some surface plots of ARPSM solutions for the TCFKE (37), with $\rho =1.0$, ${\vartheta }_2=1$, ${\vartheta }_2=2$, ${\vartheta }_2=2$, and different values of ${\vartheta }_1$. Figure 3 presents some surface plots of ARPSM solutions for the TCFKE (37), with $\rho =0.75$, ${\vartheta }_2=1$, ${\vartheta }_2=2$, ${\vartheta }_2=2$, and different values of ${\vartheta }_1$. Figure 4 presents some surface plots of ARPSM solutions for the TCFKE (37), with $\rho =0.50$, ${\vartheta }_2=1$, ${\vartheta }_2=2$, ${\vartheta }_2=2$, and different values of ${\vartheta }_1$. Figure 5 presents some surface plots of ARPSM solutions for TCFKE (37), with $\rho =0.025$, ${\vartheta }_2=1$, ${\vartheta }_2=2$, ${\vartheta }_2=2$, and different values of ${\vartheta }_1$. The graphs and tables explain the ARPSM’s accuracy and applicability; that is, the tables show the accuracy of the proposed method compared to existing techniques, with various fractional-order values, and the figures present the similarity and symmetricality of three derivative graphical patterns.

Table 1. Comparison of absolute errors of the ARPSM at $\rho =1$ and ${\vartheta }_1=10$ and several values of ${\vartheta }_2$ in TCFKE (37).

${\mathit{\vartheta }}_2$	AE (ARPSM)	AE (NTDM) [33]	AE (RPSM) [32]
$0.1$	$1.41551\times {10}^{-15}$	$1.41552\times {10}^{-15}$	$1.41553\times {10}^{-15}$
$0.2$	$4.68062\times {10}^{-14}$	$4.68063\times {10}^{-14}$	$4.68063\times {10}^{-14}$
$0.3$	$3.63910\times {10}^{-13}$	$3.63910\times {10}^{-13}$	$3.63910\times {10}^{-13}$
$0.4$	$1.56883\times {10}^{-12}$	$1.56886\times {10}^{-12}$	$1.56886\times {10}^{-12}$
$0.5$	$4.89614\times {10}^{-12}$	$4.89617\times {10}^{-12}$	$4.89617\times {10}^{-12}$
$0.6$	$1.24541\times {10}^{-11}$	$1.24542\times {10}^{-11}$	$1.24542\times {10}^{-11}$
$0.7$	$2.75067\times {10}^{-11}$	$2.75069\times {10}^{-11}$	$2.75069\times {10}^{-11}$
$0.8$	$5.47828\times {10}^{-11}$	$5.47829\times {10}^{-11}$	$5.47829\times {10}^{-11}$
$0.9$	$1.00810\times {10}^{-10}$	$1.00810\times {10}^{-10}$	$1.00810\times {10}^{-10}$
$1.0$	$1.74279\times {10}^{-10}$	$1.74280\times {10}^{-10}$	$1.74280\times {10}^{-10}$

Table 2. Numerical solutions of TCFKE (37) at ${\vartheta }_1=10$ with several values of ${\vartheta }_2$ and $\rho$.

$\mathit{\rho }$	${\mathit{\vartheta }}_2$	ARPSM	NTDM [33]	RPSM [32]
$0.25$	$0.2$	$3.29233\times {10}^{-2}$	$3.29225\times {10}^{-2}$	$3.29247\times {10}^{-2}$
	$0.4$	$3.34354\times {10}^{-2}$	$3.34339\times {10}^{-2}$	$3.34378\times {10}^{-2}$
	$0.6$	$3.37861\times {10}^{-2}$	$3.37839\times {10}^{-2}$	$3.37893\times {10}^{-2}$
	$0.8$	$3.40620\times {10}^{-2}$	$3.40585\times {10}^{-2}$	$3.40655\times {10}^{-2}$
	$1.0$	$3.42922\times {10}^{-2}$	$3.42882\times {10}^{-2}$	$3.42966\times {10}^{-2}$
$0.5$	$0.2$	$3.20843\times {10}^{-2}$	$3.20842\times {10}^{-2}$	$3.20845\times {10}^{-2}$
	$0.4$	$3.28117\times {10}^{-2}$	$3.28114\times {10}^{-2}$	$3.28122\times {10}^{-2}$
	$0.6$	$3.33858\times {10}^{-2}$	$3.33850\times {10}^{-2}$	$3.33867\times {10}^{-2}$
	$0.8$	$3.38815\times {10}^{-2}$	$3.38794\times {10}^{-2}$	$3.38822\times {10}^{-2}$
	$1.0$	$3.43252\times {10}^{-2}$	$3.43233\times {10}^{-2}$	$3.43273\times {10}^{-2}$
$0.75$	$0.2$	$3.14736\times {10}^{-2}$	$3.14737\times {10}^{-2}$	$3.14737\times {10}^{-2}$
	$0.4$	$3.22161\times {10}^{-2}$	$3.22162\times {10}^{-2}$	$3.22163\times {10}^{-2}$
	$0.6$	$3.28841\times {10}^{-2}$	$3.28839\times {10}^{-2}$	$3.28842\times {10}^{-2}$
	$0.8$	$3.35113\times {10}^{-2}$	$3.35111\times {10}^{-2}$	$3.35117\times {10}^{-2}$
	$1.0$	$3.41132\times {10}^{-2}$	$3.41124\times {10}^{-2}$	$3.41135\times {10}^{-2}$
1	$0.2$	$3.10613\times {10}^{-2}$	$3.10612\times {10}^{-2}$	$3.10612\times {10}^{-2}$
	$0.4$	$3.17142\times {10}^{-2}$	$3.17143\times {10}^{-2}$	$3.17143\times {10}^{-2}$
	$0.6$	$3.23801\times {10}^{-2}$	$3.23800\times {10}^{-2}$	$3.23800\times {10}^{-2}$
	$0.8$	$3.30587\times {10}^{-2}$	$3.30588\times {10}^{-2}$	$3.30588\times {10}^{-2}$
	$1.0$	$3.37505\times {10}^{-2}$	$3.37506\times {10}^{-2}$	$3.37506\times {10}^{-2}$

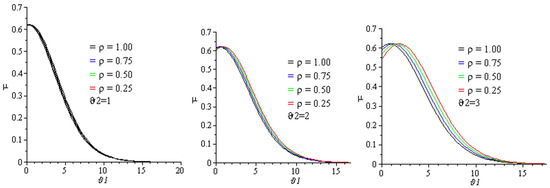
Figure 1. ARPSM graphs for solution (63) with ${\vartheta }_2=1$, ${\vartheta }_2=2$, ${\vartheta }_2=3$, and some values of $\rho$.

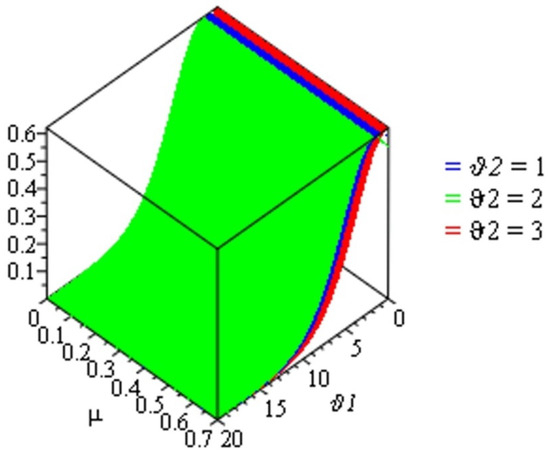
Figure 2. Surface plot of solution (63) with $\rho =1.00$ and some values of ${\vartheta }_2$.

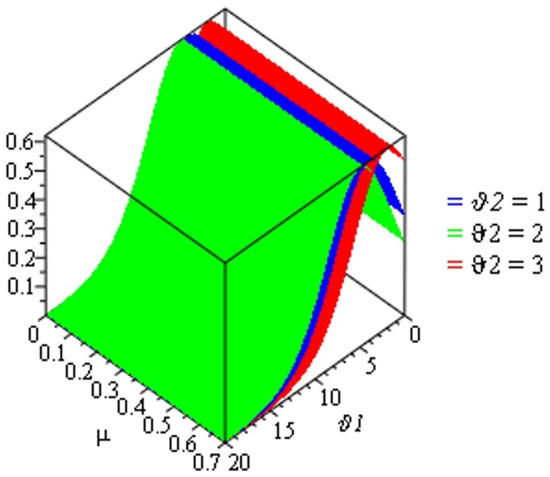
Figure 3. Surface plot of solution (63) with $\rho =0.75$ and some values of ${\vartheta }_2$.

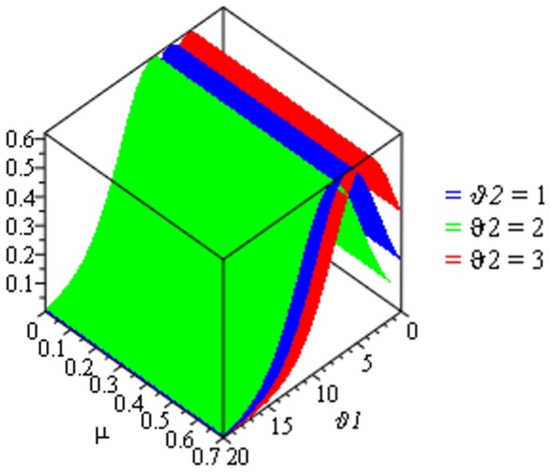
Figure 4. Surface plot of solution (63) with $\rho =0.50$ and some values of ${\vartheta }_2$.

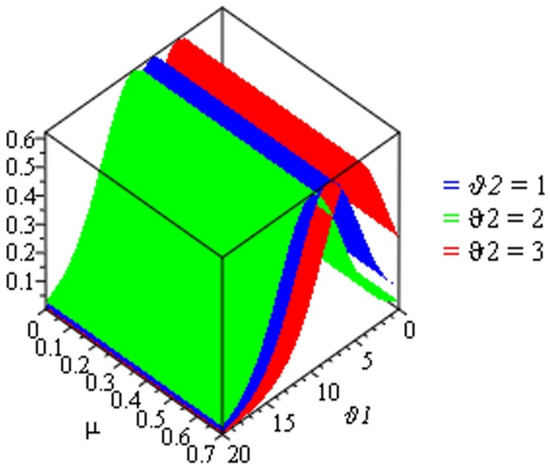
Figure 5. Surface plot of solution (63) with $\rho =0.25$ and some values of ${\vartheta }_2$.

6. Conclusions

The residual power series method using Aboodh transforms was efficient in examining the numerical solutions of the TCFKE. The ARPSM revealed the analytical solutions for the TCFKE as the sum of the terms of the convergent sequence ${⟨{\beta }_n⟩}_{n\in {\mathbb{N}}_0}$. The efficiency and systematic approach of the ARPSM provide approximate solutions that align well with numerical simulations. The comparisons in the tables above show the efficacy and reliability of our method, where it can be seen that the obtained solutions emphasize the method’s suitability for biological and mathematical–physical systems of equations, as well as those of other fields.