Free Vibration Analysis of Porous FGM Plates on Elastic Foundations with Temperature-Dependent Material Properties

Abstract

This study investigates the free vibration behaviors of functionally graded (FGM) plates with a porous structure, resting on a Kerr-type elastic foundation, while accounting for thermal effects and complex material property distributions. Within the framework of higher-order shear deformation theory (HSDT), two novel shape functions are introduced to accurately model transverse shear deformation across the plate thickness without employing shear correction factors. These functions are constructed to satisfy shear stress boundary conditions and capture nonlinear effects induced by material gradation and porosity. A variational formulation is developed to describe the dynamic response of FGM plates in a thermo-mechanical environment, incorporating temperature-dependent material properties and three porosity distributions: uniform, linear, and trigonometric. Numerical solutions are obtained using in-house MATLAB codes, allowing complete control over the formulation and interpretation of the results. The model is validated through detailed comparisons with existing literature, demonstrating high accuracy. The findings reveal that the porosity distribution pattern and gradient intensity significantly influence natural frequencies and mode shapes. The trigonometric porosity distribution exhibits favorable dynamic performance due to preserved stiffness in the surface regions. Additionally, the Kerr-type elastic foundation enables fine tuning of the dynamic response, depending on its specific parameters. The proposed approach provides a reliable and efficient tool for analyzing FGM structures under complex loading conditions and lays the groundwork for future extensions involving nonlinear, time-dependent, and multiphysics analyses.

1. Introduction

In modern engineering applications, especially under extreme thermo-mechanical conditions, functionally graded materials (FGMs) offer an exceptionally effective solution due to their ability to combine high thermal resistance with excellent mechanical strength. FGMs were developed in Japan during the 1980s in response to the aerospace industry’s demand for advanced thermal protection systems. They were designed to eliminate discontinuities and mechanical weaknesses typical of conventional multilayer composites by employing a continuous gradation of composition and functional properties throughout the material volume [1]. Their initial application as thermal insulators in spacecraft highlighted the fundamental advantage of FGMs: the ability to reduce thermally induced deformations without the delamination issues commonly observed in traditional laminated composites.

Unlike multilayered structures, where interfacial regions often represent potential zones of weakness, functionally graded materials enable a smooth and continuous transition of properties between different constituent phases—typically from ceramic to metal. This gradation encompasses not only the material composition but also functional characteristics, ensuring a uniform distribution of thermo-mechanical properties throughout the entire volume. As a result, FGMs combine the excellent high-temperature resistance typical of ceramics with the load-bearing capacity characteristic of metals. This unique combination of properties makes them ideal for use in systems exposed to pronounced temperature gradients, such as thermal barriers, aircraft engine components, nuclear reactor elements, and other high-tech systems where reliability under extreme conditions is of critical importance.

One of the most prominent contemporary directions in this field is the development of functionally graded structures with controlled porosity, which enable spatial variation in porosity within the material to optimize both mechanical and thermal performance [2,3]. Such structures allow for precise control of density and porosity levels, which is crucial for applications in civil engineering, the automotive and aerospace industries and energy technologies [4]. In this context, FGMs represent a key solution for enhancing the performance of components operating under extreme conditions [5]. Owing to the continuous variation in their microstructural and macroscopic properties throughout the volume, FGMs enable optimized stress and temperature distributions, minimizing local concentrations and enhancing structural integrity. These characteristics make them particularly suitable for use in absorbers, supports, and other thermally loaded components of solar thermal systems, where efficient heat transfer and mechanical stability are essential. As such, FGMs are positioned as next-generation materials with significant potential to contribute to more efficient and reliable utilization of solar energy in the energy infrastructure of the future.

In today’s energy landscape, renewable energy sources have become a critical component of sustainable development strategies, primarily due to the urgent need to reduce greenhouse gas emissions and gradually phase out fossil fuels in favor of cleaner alternatives, in line with the 2015 Paris Agreement on climate change. Among the various renewable options, solar energy stands out as a promising resource with the potential to significantly contribute to the global energy balance. Technological platforms for harnessing solar radiation are evolving along multiple lines, including photovoltaic systems for direct conversion of sunlight into electricity, solar thermal systems for heat utilization in heating and industrial processes, and concentrated solar power systems that focus solar radiation to generate steam and electricity. In thermal applications involving high operating temperatures, structural materials are subjected to extreme thermal and mechanical conditions, necessitating materials with superior resistance, stability, and long-term operational performance.

Due to their geometric simplicity and large surface area for radiation absorption, plate configurations are the most common structural form used in solar thermal collectors [6]. Consequently, a significant number of studies have focused on analyzing the behavior of plates made from functionally graded materials under thermal loading conditions, employing various theoretical modelling approaches. Different plate theories have been applied, ranging from classical to higher-order shear deformation theories.

The classical plate theory served as the basis in the work of Chakraverty and Pradhan [7], where the dynamics of FGM plates with exponentially graded properties in a thermal environment were analyzed using the Rayleigh–Ritz method.

Mokhtar et al. [8] applied the first-order shear deformation theory (FSDT) to investigate the thermoelastic response of FGM plates under various temperature profiles, including uniform, linear, and sinusoidal distributions. Trabelsi et al. [9] modified the FSDT to analyze the post-buckling behavior of FGM structures under thermal conditions. From the perspective of the second-order shear deformation theory (SSDT), Shahrjerdi et al. [10] examined the natural frequencies of solar FGM plates subjected to different thermal conditions, including nonlinear distributions, constant temperature, heat flux, and sinusoidal variations. Unlike FSDT, which requires the introduction of a correction factor to compensate for the simplified shear stress assumptions, higher-order shear deformation theories (HSDT) provide a significantly more accurate representation of deformation through the plate thickness without the need for such corrections. One key advantage of HSDT is its ability to account for the curvature and displacement of normal fibers, which are considered incompressible and inflexible through the thickness in classical theories, by modelling them with higher-order nonlinear displacement functions [11]. Based on this feature, HSDT has emerged as a robust approach for analyzing complex thermo-mechanical responses of FGMs, especially under conditions of large thermal gradients and complex boundary constraints.

Numerous researchers have developed variants of higher-order shear deformation theory (HSDT) employing different functional forms, including third-order, sinusoidal, hyperbolic, and exponential models, in order to achieve an optimal balance between modeling accuracy and computational efficiency [12,13]. Over the past decade, an increasing number of studies have introduced quasi-3D theories as generalizations of classical higher-order formulations, among which polynomial [14], sinusoidal [15], exponential [16], and hyperbolic [17] models stand out. For example, Kenanda et al. [17] proposed a quasi-3D hyperbolic theory combined with the Navier method for analyzing the free vibration of porous FGM plates, demonstrating that this approach yields significantly more accurate results compared to traditional third-order theories and other HSDT variants.

On the other hand, theories incorporating nonlocal elasticity effects, such as the model presented by Daikha and Zenkour [18], offer valuable insights into material behavior at the micro- and nano-scale, which is particularly relevant in the context of thin functional layers used in solar applications [19]. Novel approaches such as the polynomial quasi-3D HSDT developed by Ghumare and Sayyad [14], although more computationally intensive due to an increased number of degrees of freedom, provide superior results in modelling the static response of FGM plates. These concepts have further been applied in finite element method (FEM) analyses of bending, buckling, and vibrational behavior of porous FGM structures [20,21].

Despite the theoretical and numerical advancements, the practical implementation of FGM plates in real engineering systems, such as solar thermal collectors, faces challenges in the domain of manufacturing, particularly in controlling the microstructure and material homogeneity. In practice, porosity often forms during fabrication, significantly affecting the mechanical stiffness, structural stability, and overall reliability of components. These porosities may result from non-uniform sintering, thermal fluctuations during processing, or inadequate control of the material gradient [22,23]. In response to this challenge, an increasing number of studies have focused on investigating the influence of porosity on the thermo-mechanical behavior of FGM structures. While some works have addressed mechanical behavior without thermal effects [24,25,26,27,28,29], others have considered scenarios involving significant thermal gradients, which are typical of operational conditions in solar applications [30,31,32,33,34,35]. These studies highlight the need for sophisticated modelling approaches.

Despite substantial progress in understanding the fundamental mechanisms governing the behavior of porous functionally graded structures, further research is required to enhance the predictive accuracy of existing models and to ensure their reliable application in industrial practice. Khatir and Filali [36] investigated the free vibration characteristics of a novel functionally graded porous microplate using isogeometric analysis (IGA). They developed a numerical model for computing natural frequencies and analyzed the effects of size parameters, porosity, aspect ratio, and plate thickness on its macromechanical properties.

Wang and Zu [37] conducted a vibration analysis of rectangular FG plates with porosities in a thermal environment. They employed the von Kármán nonlinear plate theory and the harmonic balance method to investigate the effects of porosity distribution, moving speed, and temperature variations on natural frequencies and the system’s nonlinear response.

Analyses of free vibrations of porous FGM plates on elastic foundations, including Winkler, Pasternak, and Kerr models, enable a detailed understanding of dynamic response under realistic operating conditions, particularly in thermo-mechanical environments. Hoang and Thanh [38] developed a new theoretical model for analyzing the free and transient vibrations of FG plates resting on Kerr-type elastic foundations under thermal loading. They applied Reddy’s third-order shear deformation theory and the Galerkin method, with a comprehensive investigation of the effects of foundation stiffness, thermal profiles, and material parameters on the plate’s dynamic behavior. Kumar et al. [39] examined the free vibration behavior of conically shaped porous FG plates on an elastic foundation using FSDT. Their study evaluated the influence of material gradation laws, porosity, geometry, boundary conditions, and Winkler–Pasternak foundation parameters on vibrational characteristics. Similar problems have also been addressed in studies [28,29,40].

As highlighted in recent studies [41,42], the dynamic behavior of porous FGM structures remains challenging due to the complex combined effects of porosity and material gradation. These findings further underline the significance and timeliness of the present study and emphasize the need for continued development of advanced theoretical models.

Higher-order shear deformation theories (HSDT) provide a solid foundation for such analyses due to their accurate modelling of transverse shear deformation without the need for correction factors.

The present work focuses on a detailed investigation of the mechanical performance of functionally graded porous structures, with special emphasis on the analysis of free vibrations. Within this study, two new shape functions (Present 1 and Present 2) are proposed to enable accurate modelling of nonlinear shear strain distributions and optimization of the vibrational response of porous FGM plates resting on elastic foundations.

2. Shape Functions and Kinematic Formulation in Higher-Order Models

Higher-order shear deformation theories (HSDT) represent an advanced theoretical framework for modelling the behavior of layered and functionally graded materials (FGMs). In the context of dynamic analysis, particularly in the study of free vibrations, HSDT enables a detailed representation of displacement and strain distributions across the thickness of the composite. Unlike classical bending theories, which require empirical shear correction factors, HSDT offers accurate modelling of shear effects, thus providing enhanced precision and reliability in the analysis of complex structural systems.

FGMs, characterized by a continuous variation in mechanical properties through the thickness, pose specific challenges in analysis, especially in the accurate modelling of shear deformation. In such structures, no material discontinuities are present, making simplified approaches used in homogeneously laminated composites inapplicable. In this context, HSDT allows for the integration of higher-order functions dependent on the thickness coordinate, thereby enabling precise modelling of property variation and its influence on plate behavior. This approach facilitates the detailed tracking of changes induced by thermal and other external effects, making it particularly suitable for thermo-mechanical analyses.

The application of HSDT to FGM plates ensures an accurate representation of shear deformation, especially in cases where the material exhibits functional gradation through the thickness. This framework enables analyses that consider all relevant behavioral variations in materials under different thermal and mechanical loads, offering a robust modelling platform for the design and evaluation of advanced structural components.

The displacement fields within the framework of HSDT are assumed in the following form:

$$\begin{array}{c}u(x,y,z)=u_0(x,y)+z{\varphi }_z(x,y)+f(z){\psi }_x(x,y),\\ v(x,y,z)=v_0(x,y)+z{\varphi }_y(x,y)+f(z){\psi }_y(x,y),\\ w(x,y,z)=w_0(x,y),\end{array}$$

(1)

where

• u₀(x,y), v₀(x,y), w₀(x,y)—displacements of the mid-surface in the x, y, and z directions, respectively;
• ϕ_x(x,y), ϕ_y(x,y)—rotations of transverse cross-sections about the y and x axes, respectively;
• ψ_x(x,y), ψ_y(x,y)—higher-order terms which, in combination with the shape function f(z), enable the interpolation of shear deformation across the plate thickness.

The shape function f(z) plays a pivotal role in the accuracy and reliability of the proposed model. It must satisfy the boundary conditions of zero transverse shear stress at the free surfaces, allow for a flexible and realistic representation of the nonlinear distribution of shear strains consistent with the material property variation through the thickness, and be suitable for mathematical manipulation within energy-based methods and numerical implementation.

Within this work, two new shape functions along the thickness coordinate z are proposed, denoted as f₁(z) and f₂(z), which are used in the formulation of the macromechanical model for the analysis of free vibrations of functionally graded materials:

$$f_1\left(z\right)=z\cdot \left(\cosh \left({\displaystyle \frac{z}{h}}\right)-1.388\right)\hspace{1em}\hspace{1em}\mathrm{and}\hspace{1em}\hspace{1em}{f}_2\left(z\right)=-\left({\displaystyle \frac{z^2\cdot \sinh \left(\frac{z}{h}\right)}{h}}-0.8z\right).$$

(2)

Unlike the existing functions traditionally used in higher-order shear deformation theories, the proposed functions enable a more precise description of nonlinear deformations through the thickness, which is crucial for accurate frequency analysis of FGM plates.

The proposed shape functions $f_1\left(z\right)$ and $f_2\left(z\right)$ are introduced because they naturally satisfy the conditions of zero shear stresses at the top and bottom surfaces. The hyperbolic character provides a more realistic distribution of deformations through the thickness, while the linear and quadratic multipliers allow greater flexibility in describing higher-order displacement gradients. In this way, a better balance between mathematical simplicity and physical consistency is achieved compared with existing HSDT approaches.

The function f₁(z) is constructed as a product of a linear dependence on z and a hyperbolic component that introduces and generates a nonlinear distribution of transverse deformations. This form satisfies the zero tangential stress condition on the free surfaces, which is particularly important in vibration problems where an accurate definition of boundary conditions significantly influences the natural frequencies and mode shapes.

The second shape function, denoted as f₂(z), is formulated as a combination of a quadratic dependence on the thickness coordinate z and the hyperbolic function sinh(z/h). Compared to f₁(z), this function provides an enhanced ability to capture higher-order nonlinear effects of transverse shear deformation through the plate thickness. Such a formulation makes f₂(z) particularly suitable for porous FGM plates with strong gradients of elastic modulus and density, ensuring a more refined description of their vibration modes.

Unlike conventional shape functions (such as sinusoidal, exponential and rational forms) that are often mathematically simple but physically limited, the proposed shape functions possess a deeper physical foundation and better adaptability to complex deformation fields. Application in the formulation of vibration problems leads to improved accuracy in the calculation of natural frequencies, especially in the case of multilayer composite laminates and FGM structures.

Another important advantage of the proposed functions is their suitability for numerical implementation, they can be easily differentiated and integrated, making them convenient for use in analytical and numerical methods such as the Ritz method, finite element method, and other variational approaches. Thus, the contribution of these functions is reflected not only in more accurate physical modelling but also in enhancing the efficiency and stability of numerical solutions for free vibrations of FGM structures. Their mathematical form eliminates the need for additional correction functions or numerical stabilization procedures, improving the robustness and accuracy of the results. Therefore, these functions are recommended as a valid alternative to existing models in the context of higher-order deformation theories.

Using such a kinematic model, the strain–displacement relations are derived in accordance with linear elasticity theory for small displacements:

$${\epsilon }_{ij}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\mathsf{\partial }{u}_i}{\mathsf{\partial }{x}_j}}+{\displaystyle \frac{\mathsf{\partial }{u}_j}{\mathsf{\partial }{x}_i}}\right),$$

(3)

with the inclusion of higher-order terms along the thickness coordinate, which enables detailed consideration of local effects. This ensures accurate determination of thermal stresses, shear forces, and bending moments in FG plates supported on a Kerr elastic foundation, considering the additional response of the foundation in interaction with the plate.

3. Formulation of Temperature-Dependent Constitutive Models for Functionally Graded Materials with Porous Structure

Constitutive models of functionally graded materials are formulated based on locally defined effective properties that vary along the thickness coordinate z. The fundamental approach is based on the power-law distribution, which describes the continuous variation in elastic, thermal, and thermally induced characteristics along the thickness direction of the component. Within this model, the effective material properties, excluding porosity effects, are defined as

$$\eta (z,T)=[{\eta }_c(T)-{\eta }_m(T)]{\left({\displaystyle \frac{z}{h}}+{\displaystyle \frac{1}{2}}\right)}^N+{\eta }_m(T),$$

(4)

where

• η ∈ {ρ, E, α}—denotes the generic symbol for density, Young’s modulus, and coefficient of thermal expansion;
• η_c(T) and η_m(T)—represent the temperature-dependent properties of the ceramic and metal constituents, respectively;
• N is the power-law exponent defining the gradient variation in the properties,
• z is the local coordinate through the thickness;
• h is the total thickness of the plate.

Temperature dependence of the properties is modelled by an analytical function in the form of a third-degree polynomial [41]:

$$\eta (T)=P_0(P_{-1}{T}^{-1}+1+P_{1}T+P_2{T}^2+P_3{T}^3),$$

(5)

where P₋₁, P₀, P₁, P₂, P₃ are experimentally determined coefficients for specific materials (e.g., Si33N44 and SUS304).

To more accurately represent the microstructure, models incorporating the effect of porosity as a corrective factor on the effective material properties have been introduced. In this context, three different porosity distributions [19,42] have been developed, which complement the basic power-law function:

• Uniform porosity (Type I):

$$\eta (z,T)=[{\eta }_c(T)-{\eta }_m(T)]{\left({\displaystyle \frac{z}{h}}+{\displaystyle \frac{1}{2}}\right)}^N+{\eta }_m(T)-{\displaystyle \frac{\beta }{2}}[{\eta }_c(T)+{\eta }_m(T)],$$

(6)

• Linearly non-uniform porosity (Type II):

$$\eta (z,T)=[{\eta }_c(T)-{\eta }_m(T)]{\left({\displaystyle \frac{z}{h}}+{\displaystyle \frac{1}{2}}\right)}^N+{\eta }_m(T)-{\displaystyle \frac{\beta }{2}}[{\eta }_c(T)+{\eta }_m(T)]\left(1-{\displaystyle \frac{2\left|z\right|}{h}}\right),$$

(7)

• Trigonometric porosity (Type III):

$$\eta (z,T)=[{\eta }_c(T)-{\eta }_m(T)]{\left({\displaystyle \frac{z}{h}}+{\displaystyle \frac{1}{2}}\right)}^N+{\eta }_m(T)-{\displaystyle \frac{\beta }{2}}[{\eta }_c(T)+{\eta }_m(T)]{\cos }^5\left({\displaystyle \frac{\pi z}{h}}\right),$$

(8)

where β ∈ [0, 1] is a parameter describing the porosity intensity.

This approach models the reduction in porosity near the surface layers of the material, which is especially important in the design of functionally graded materials used in solar thermal collectors and other applications with high efficiency requirements. Uniform porosity implies a constant porosity effect through the thickness of the material, except for the variation defined by the power-law function. Linearly non-uniform porosity decreases linearly toward the surface, thereby modeling lower porosity in the surface layers, while trigonometric porosity allows for a smoother, wave-like decrease in porosity toward the surface, more accurately reflecting the actual microstructure of the material.

In this study, the temperature-dependent material properties are represented using polynomial approximations, which is a common and convenient practice in the analysis of functionally graded materials. Such representations ensure smooth variation in the effective properties with temperature and allow for closed-form evaluation of integrals in the variational formulation, thus simplifying the mathematical treatment. However, the accuracy of these approximations inherently depends on the quality of the experimental data used for their calibration, and deviations may occur in extreme temperature ranges. The adopted approximations were verified against tabulated reference data reported in the literature, confirming satisfactory accuracy within the temperature intervals relevant for the engineering applications considered here. For applications involving broader or more extreme thermal environments, further refinement of the coefficients through direct experimental characterization would be recommended.

4. Variational Formulation of the Dynamic Behavior of a Porous FGM Plate

This approach utilizes Hooke’s law for anisotropic materials:

$${\sigma }_{ij}=C_{ijkl}{\epsilon }_{kl},$$

(9)

where

• σ_ij are the stress components in different directions;
• C_ijkl is the material elasticity tensor;
• ε_kl are the strain components.

This law is applied locally at each point through the thickness, taking into account the corresponding variations in elastic moduli and thermal expansion coefficients. Using Equations (1) and (9) and grouping terms, the components of the resultant force vector and resultant moment vector are obtained.

The total external load, consisting of components of in-plane resultant forces N_x, N_y, N_xy, bending moment components M_x, M_y, M_xy, moments associated with the transverse shear deformation function P_x, P_y, P_xy, and components of the resultant transverse shear forces R_x, R_y, can be calculated as follows:

$$\begin{gathered} \left\{\begin{array}{c}{N}_x\\ N_y\\ N_{xy}\end{array}\right\}=\left[\begin{array}{ccc}{A}_{11}& A_{12}& 0\\ A_{12}& A_{22}& 0\\ 0& 0& A_{66}\end{array}\right]\left\{\begin{array}{c}{\displaystyle \frac{\mathsf{\partial }{u}_0}{\mathsf{\partial }x}}\\ {\displaystyle \frac{\mathsf{\partial }{v}_0}{\mathsf{\partial }y}}\\ {\displaystyle \frac{\mathsf{\partial }{u}_0}{\mathsf{\partial }y}}+{\displaystyle \frac{\mathsf{\partial }{v}_0}{\mathsf{\partial }x}}\end{array}\right\}+\left[\begin{array}{ccc}{B}_{11}& B_{12}& 0\\ B_{12}& B_{22}& 0\\ 0& 0& B_{66}\end{array}\right]\left\{\begin{array}{c}{\displaystyle \frac{{\mathsf{\partial }}^2{w}_0}{\mathsf{\partial }{x}^2}}\\ {\displaystyle \frac{{\mathsf{\partial }}^2{w}_0}{\mathsf{\partial }{y}^2}}\\ 2{\displaystyle \frac{{\mathsf{\partial }}^2{w}_0}{\mathsf{\partial }x\mathsf{\partial }y}}\end{array}\right\}+\left[\begin{array}{ccc}{C}_{11}& C_{12}& 0\\ C_{12}& C_{22}& 0\\ 0& 0& C_{66}\end{array}\right]\left\{\begin{array}{c}{\displaystyle \frac{\mathsf{\partial }{\psi }_x}{\mathsf{\partial }x}}\\ {\displaystyle \frac{\mathsf{\partial }{\psi }_y}{\mathsf{\partial }y}}\\ {\displaystyle \frac{\mathsf{\partial }{\psi }_x}{\mathsf{\partial }y}}+{\displaystyle \frac{\mathsf{\partial }{\psi }_y}{\mathsf{\partial }x}}\end{array}\right\}, \\ \left\{\begin{array}{c}{M}_x\\ M_y\\ M_{xy}\end{array}\right\}=\left[\begin{array}{ccc}{B}_{11}& B_{12}& 0\\ B_{12}& B_{22}& 0\\ 0& 0& B_{66}\end{array}\right]\left\{\begin{array}{c}{\displaystyle \frac{\mathsf{\partial }{u}_0}{\mathsf{\partial }x}}\\ {\displaystyle \frac{\mathsf{\partial }{v}_0}{\mathsf{\partial }y}}\\ {\displaystyle \frac{\mathsf{\partial }{u}_0}{\mathsf{\partial }y}}+{\displaystyle \frac{\mathsf{\partial }{v}_0}{\mathsf{\partial }x}}\end{array}\right\}+\left[\begin{array}{ccc}{D}_{11}& D_{12}& 0\\ D_{12}& D_{22}& 0\\ 0& 0& D_{66}\end{array}\right]\left\{\begin{array}{c}{\displaystyle \frac{{\mathsf{\partial }}^2{w}_0}{\mathsf{\partial }{x}^2}}\\ {\displaystyle \frac{{\mathsf{\partial }}^2{w}_0}{\mathsf{\partial }{y}^2}}\\ 2{\displaystyle \frac{{\mathsf{\partial }}^2{w}_0}{\mathsf{\partial }x\mathsf{\partial }y}}\end{array}\right\}+\left[\begin{array}{ccc}{T}_{11}& T_{12}& 0\\ T_{12}& T_{22}& 0\\ 0& 0& T_{66}\end{array}\right]\left\{\begin{array}{c}{\displaystyle \frac{\mathsf{\partial }{\psi }_x}{\mathsf{\partial }x}}\\ {\displaystyle \frac{\mathsf{\partial }{\psi }_y}{\mathsf{\partial }y}}\\ {\displaystyle \frac{\mathsf{\partial }{\psi }_x}{\mathsf{\partial }y}}+{\displaystyle \frac{\mathsf{\partial }{\psi }_y}{\mathsf{\partial }x}}\end{array}\right\}, \\ \left\{\begin{array}{c}{P}_x\\ P_y\\ P_{xy}\end{array}\right\}=\left[\begin{array}{ccc}{C}_{11}& C_{12}& 0\\ C_{12}& C_{22}& 0\\ 0& 0& C_{66}\end{array}\right]\left\{\begin{array}{c}{\displaystyle \frac{\mathsf{\partial }{u}_0}{\mathsf{\partial }x}}\\ {\displaystyle \frac{\mathsf{\partial }{v}_0}{\mathsf{\partial }y}}\\ {\displaystyle \frac{\mathsf{\partial }{u}_0}{\mathsf{\partial }y}}+{\displaystyle \frac{\mathsf{\partial }{v}_0}{\mathsf{\partial }x}}\end{array}\right\}+\left[\begin{array}{ccc}{T}_{11}& T_{12}& 0\\ T_{12}& T_{22}& 0\\ 0& 0& T_{66}\end{array}\right]\left\{\begin{array}{c}{\displaystyle \frac{{\mathsf{\partial }}^2{w}_0}{\mathsf{\partial }{x}^2}}\\ {\displaystyle \frac{{\mathsf{\partial }}^2{w}_0}{\mathsf{\partial }{y}^2}}\\ 2{\displaystyle \frac{{\mathsf{\partial }}^2{w}_0}{\mathsf{\partial }x\mathsf{\partial }y}}\end{array}\right\}+\left[\begin{array}{ccc}{G}_{11}& G_{12}& 0\\ G_{12}& G_{22}& 0\\ 0& 0& G_{66}\end{array}\right]\left\{\begin{array}{c}{\displaystyle \frac{\mathsf{\partial }{\psi }_x}{\mathsf{\partial }x}}\\ {\displaystyle \frac{\mathsf{\partial }{\psi }_y}{\mathsf{\partial }y}}\\ {\displaystyle \frac{\mathsf{\partial }{\psi }_x}{\mathsf{\partial }y}}+{\displaystyle \frac{\mathsf{\partial }{\psi }_y}{\mathsf{\partial }x}}\end{array}\right\}, \\ \left\{\begin{array}{c}{R}_x\\ R_y\end{array}\right\}=\left[\begin{array}{cc}{F}_{44}& 0\\ 0& F_{55}\end{array}\right]\left\{\begin{array}{c}{\psi }_x\\ {\psi }_y\end{array}\right\} \end{gathered}$$

(10)

where

$$\begin{array}{l}\left\{A_{ij},B_{ij},C_{ij},D_{ij},T_{ij},G_{ij}\right\}={\displaystyle \underset{-h(x,y)/2}{\overset{h(x,y)/2}{\int }}\left\{1,z,f(x,y,z),z^2,zf(x,y,z),{[f(x,y,z)]}^2\right\}{Q}_{ij}dz},\\ (i,j=1,2,6),\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left\{F_{ij}\right\}=\underset{-h(x,y)/2}{\overset{h(x,y)/2}{\int }}{\left[\frac{\mathsf{\partial }f(x,y,z)}{\mathsf{\partial }z}\right]}^2{Q}_{ij}dz,\hspace{1em}\hspace{1em}(i,j=4,5)\end{array}$$

(11)

The next step involves deriving the energy expressions using Hamilton’s principle, through which the variational form of the problem is formulated:

$$\delta {\displaystyle \underset{t_1}{\overset{t_2}{\int }}\left(T-U-U_e\right)dt}=0,$$

(12)

where

• T—kinetic energy of the system (due to oscillatory motion);
• U—strain energy of the plate (including bending, stretching, and other forms of deformation);
• U_e—potential energy of the elastic foundation (reaction of the foundation to the plate displacement).

In the analysis of free vibrations of functionally graded (FG) plates resting on an elastic foundation, the contribution of the elastic foundation is expressed through the variation in potential energy, defined as

$$\delta U_e={\displaystyle \underset{A}{\int }{f}_e}\delta w_{0}dA,$$

(13)

where

• A is the plate surface area;
• w₀ is the displacement of the mid-surface of the plate in the vertical direction;
• f_e is the reaction force of the elastic foundation per unit area, whose specific form depends on the type of foundation.

The foundation reaction f_e can be modelled in various ways depending on the physical model of the foundation employed:

• Winkler Foundation (Figure 1)—models the foundation as a series of independent elastic springs (linear and local response without interaction between foundation points):

$$f_e^{\mathrm{Winkler}}=q_{\mathrm{Winkler}}=k_w{w}_0,$$

(14)

where

• k_w—Winkler foundation modulus (stiffness coefficient).

Figure 1. FGM plate on a Winkler foundation.

Figure 1. FGM plate on a Winkler foundation.

2.

Pasternak foundation (Figure 2)—includes shear interaction between adjacent points of the foundation (enables the distribution of force through the foundation and a better approximation of real conditions):

$$f_e^{\mathrm{Pasternak}}=q_{\mathrm{Pasternak}}=k_w{w}_0-G_p{\nabla }^2{w}_0,$$

(15)

where

• $G_p$ —shear modulus (stiffness) of the foundation;
• ${\nabla }^2{w}_0$ —Laplacian operator (second derivative with respect to spatial coordinates).

Figure 2. FGM plate on a Pasternak elastic foundation.

Figure 2. FGM plate on a Pasternak elastic foundation.

3.

Kerr Foundation (Figure 3)—a more complex model that accounts for surface and internal layers of the foundation with mutual interactions (includes both local and nonlinear interaction through the thickness of the foundation):

$$f_e^{\mathrm{Kerr}}=q_{\mathrm{Kerr}}=\left({\displaystyle \frac{k_l{k}_u}{k_l+k_u}}\right)w_0-\left({\displaystyle \frac{k_s{k}_u}{k_s+k_u}}\right){\nabla }^2{w}_0,$$

(16)

where

• k_l, k_u—elastic moduli of the lower and upper layers of the foundation;
• k_s—shear stiffness of the layer between them.

Figure 3. FGM plate on Kerr elastic foundation.

Figure 3. FGM plate on Kerr elastic foundation.

If the expressions for kinetic and potential energy defined as follows are substituted into the Hamilton’s principal Equation (12):

$$\begin{array}{l}T={\displaystyle \frac{1}{2}}{\displaystyle \underset{A}{\iint }{\displaystyle {\int }_{-h/2}^{h/2}\rho (z)\left[{\left({\dot{u}}_0+z{\dot{\varphi }}_x+f(z){\dot{\psi }}_x\right)}^2+{\left({\dot{v}}_0+z{\dot{\varphi }}_y+f(z){\dot{\psi }}_y\right)}^2+{\dot{w}}_0^2\right]dzdA}},\\ U={\displaystyle \frac{1}{2}}{\displaystyle \underset{V}{\iiint }\left[{\sigma }_{xx}{\epsilon }_{xx}+{\sigma }_{yy}{\epsilon }_{yy}+{\sigma }_{zz}{\epsilon }_{zz}+2{\sigma }_{xy}{\epsilon }_{xy}+2{\sigma }_{xz}{\epsilon }_{xz}+2{\sigma }_{yz}{\epsilon }_{yz}\right]dV}.\end{array}$$

(17)

The differential equations of free vibrations of the plate are obtained in the form

$$\begin{array}{l}{\displaystyle \frac{\mathsf{\partial }{N}_x}{\mathsf{\partial }x}}+{\displaystyle \frac{\mathsf{\partial }{N}_{xy}}{\mathsf{\partial }y}}=I_1{\displaystyle \frac{{\mathsf{\partial }}^2{u}_0}{\mathsf{\partial }{t}^2}}-I_2{\displaystyle \frac{{\mathsf{\partial }}^3{w}_0}{\mathsf{\partial }{t}^2\mathsf{\partial }x}}+I_4{\displaystyle \frac{{\mathsf{\partial }}^2{\theta }_x}{\mathsf{\partial }{t}^2}},\\ {\displaystyle \frac{\mathsf{\partial }{N}_{xy}}{\mathsf{\partial }x}}+{\displaystyle \frac{\mathsf{\partial }{N}_y}{\mathsf{\partial }y}}=I_1{\displaystyle \frac{{\mathsf{\partial }}^2{v}_0}{\mathsf{\partial }{t}^2}}-I_2{\displaystyle \frac{{\mathsf{\partial }}^3{w}_0}{\mathsf{\partial }{t}^2\mathsf{\partial }y}}+I_4{\displaystyle \frac{{\mathsf{\partial }}^2{\theta }_y}{\mathsf{\partial }{t}^2}},\\ {\displaystyle \frac{{\mathsf{\partial }}^2{M}_x}{\mathsf{\partial }{x}^2}}+2{\displaystyle \frac{{\mathsf{\partial }}^2{M}_{xy}}{\mathsf{\partial }x\mathsf{\partial }y}}+{\displaystyle \frac{{\mathsf{\partial }}^2{M}_y}{\mathsf{\partial }{x}^2}}=I_1{\displaystyle \frac{{\mathsf{\partial }}^2{w}_0}{\mathsf{\partial }{t}^2}}+I_2\left({\displaystyle \frac{{\mathsf{\partial }}^3{u}_0}{\mathsf{\partial }{t}^2\mathsf{\partial }x}}+{\displaystyle \frac{{\mathsf{\partial }}^3{v}_0}{\mathsf{\partial }{t}^2\mathsf{\partial }x}}\right)\\ -I_3\left({\displaystyle \frac{{\mathsf{\partial }}^4{w}_0}{\mathsf{\partial }{t}^2\mathsf{\partial }{x}^2}}+{\displaystyle \frac{{\mathsf{\partial }}^4{w}_0}{\mathsf{\partial }{t}^2\mathsf{\partial }{y}^2}}\right)+I_5\left({\displaystyle \frac{{\mathsf{\partial }}^3{\theta }_x}{\mathsf{\partial }{t}^2\mathsf{\partial }x}}+{\displaystyle \frac{{\mathsf{\partial }}^3{\theta }_y}{\mathsf{\partial }{t}^2\mathsf{\partial }y}}\right)-f_e , \\ {\displaystyle \frac{\mathsf{\partial }{P}_x}{\mathsf{\partial }x}}+{\displaystyle \frac{\mathsf{\partial }{P}_{xy}}{\mathsf{\partial }y}}-R_x=I_4{\displaystyle \frac{{\mathsf{\partial }}^2{u}_0}{\mathsf{\partial }{t}^2}}-I_5{\displaystyle \frac{{\mathsf{\partial }}^3{w}_0}{\mathsf{\partial }{t}^2\mathsf{\partial }x}}+I_6{\displaystyle \frac{{\mathsf{\partial }}^2{\theta }_x}{\mathsf{\partial }{t}^2}},\\ {\displaystyle \frac{\mathsf{\partial }{P}_{xy}}{\mathsf{\partial }x}}+{\displaystyle \frac{\mathsf{\partial }{P}_y}{\mathsf{\partial }y}}-R_y=I_4{\displaystyle \frac{{\mathsf{\partial }}^2{v}_0}{\mathsf{\partial }{t}^2}}-I_5{\displaystyle \frac{{\mathsf{\partial }}^3{w}_0}{\mathsf{\partial }{t}^2\mathsf{\partial }y}}+I_6{\displaystyle \frac{{\mathsf{\partial }}^2{\theta }_y}{\mathsf{\partial }{t}^2}}.\end{array}$$

(18)

The mass inertia term I_i (i = 1, 2, …, 6) is defined as

$$\left\{I_1,I_2,I_3,I_4,I_5,I_6\right\}={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}\left\{1,z,f(x,y,z),z^2,zf(x,y,z),{[f(x,y,z)]}^2\right\}\rho (x,y,z)dz.}$$

(19)

The proposed shape functions are constructed in such a way that all required integrals can be evaluated in closed form. In this manner, the need for numerical integration is eliminated, which simplifies the formulation process and ensures the stability of the resulting expressions. This approach avoids the usual issues related to numerical convergence and significantly enhances computational efficiency, since the results can be obtained directly from analytical formulations without additional approximations.

5. Analytical Solution of Natural Frequencies of an FGM Plate

For obtaining numerical results in the analysis of laminated plates, both analytical and numerical methods can be employed. The application of an analytical approach, based on assumed solution forms, enables efficient examination of the influence of various parameters, especially for plates with complex functional gradients and elastic supports. An additional advantage of analytical methods lies in their suitability for testing and validating new shape functions and deformation theories, making them particularly valuable in the early stages of model development and verification of numerical solutions. In this work, the Navier method is used to solve the free vibration problem of a functionally graded plate with the following boundary conditions:

$$\begin{array}{c}{v}_0=w_0={\theta }_x=N_x=M_x=P_x=0 (\mathrm{at} x=0,\hspace{0.33em}a),\\ u_0=w_0={\theta }_y=N_y=M_y=P_y=0 (\mathrm{at} y=0,\hspace{0.33em}b).\end{array}$$

(20)

The assumed solution forms, consistent with the boundary conditions for a simply supported (SSSS) rectangular plate with dimensions a × b, are given by:

$$\begin{array}{l}{u}_0(x,y,t)={\displaystyle \sum _{m=1}^{\infty }}{\displaystyle \sum _{n=1}^{\infty }}{U}_{mn}\sin {\displaystyle \frac{m\pi x}{a}}\cos {\displaystyle \frac{n\pi y}{b}}{e}^{i\omega t},\\ v_0(x,y,t)={\displaystyle \sum _{m=1}^{\infty }}{\displaystyle \sum _{n=1}^{\infty }}{V}_{mn}\cos {\displaystyle \frac{m\pi x}{a}}\sin {\displaystyle \frac{n\pi y}{b}}{e}^{i\omega t},\\ w_0(x,y,t)={\displaystyle \sum _{m=1}^{\infty }}{\displaystyle \sum _{n=1}^{\infty }}{W}_{mn}\sin {\displaystyle \frac{m\pi x}{a}}\sin {\displaystyle \frac{n\pi y}{b}}{e}^{i\omega t}, \\ \begin{array}{c}{\theta }_x(x,y,t)={\displaystyle \sum _{m=1}^{\infty }}{\displaystyle \sum _{n=1}^{\infty }}{T}_{xmn}\cos {\displaystyle \frac{m\pi x}{a}}\sin {\displaystyle \frac{n\pi y}{b}}{e}^{i\omega t},\\ {\theta }_y(x,y,t)={\displaystyle \sum _{m=1}^{\infty }}{\displaystyle \sum _{n=1}^{\infty }}{T}_{ymn}\sin {\displaystyle \frac{m\pi x}{a}}\cos {\displaystyle \frac{n\pi y}{b}}{e}^{i\omega t}.\end{array}\end{array}$$

(21)

where ω denotes the natural frequency associated with frequency mode numbers m and n.

In the dynamic extension adopted here, the spatial dependence of the displacement field is represented by double trigonometric series that identically satisfy the simply supported boundary conditions, while the corresponding modal amplitudes are time-dependent functions. Substitution of these forms into the potential and kinetic energy expressions, including the contribution of the elastic foundation, and application of Hamilton’s principle reduce the governing PDEs to a system of ODEs in the modal coordinates. Assuming a sinusoidal time dependence of the modal amplitudes, the ODE system is further transformed into the generalized eigenvalue problem of the following form:

$$(K+K_f)q={\omega }^{2}Iq,$$

(22)

where

• K—bending stiffness matrix of the functionally graded plate;
• K_f—stiffness contribution from the elastic foundation (Winkler, Pasternak, or Kerr model);
• I—mass matrix;
• q—vector of unknown vibration amplitudes.

The eigenvalue problem is solved using standard methods:

$$\det (K+K_f-{\omega }^{2}I)=0,$$

(23)

To ensure brevity and clarity, the following compact notation is adopted:

$$L=K+K_f,$$

(24)

i.e.,

$$\left|L-{\omega }^{2}I\right|=0$$

(25)

$$\underset{L}{\underbrace{\left[\begin{array}{ccccc}{L}_{11}& L_{12}& L_{13}& L_{14}& L_{15}\\ L_{12}& L_{22}& L_{23}& L_{24}& L_{25}\\ L_{13}& L_{23}& L_{33}& L_{34}& L_{35}\\ L_{14}& L_{24}& L_{34}& L_{44}& L_{45}\\ L_{15}& L_{25}& L_{35}& L_{45}& L_{55}\end{array}\right]}}-{\omega }^2\underset{I}{\underbrace{\left[\begin{array}{ccccc}{I}_1& 0& -\alpha I_2& I_4& 0\\ 0& I_4& -\beta I_2& 0& I_4\\ -\alpha I_2& -\beta I_2& I_3\left({\alpha }^2+{\beta }^2\right)+I_1& -\alpha I_5& -\beta I_5\\ I_4& 0& -\alpha I_5& I_6& 0\\ 0& I_4& -\beta I_5& 0& I_6\end{array}\right]}}=0$$

(26)

where the coefficients $L_{ij}, \left(i,j=1÷5\right)$ are functions of the parameters and the coefficients specified in Equation (11) and parameters $\alpha ={\displaystyle \frac{m\pi }{a}}, \beta ={\displaystyle \frac{n\pi }{b}}$.

6. Numerical Results

To obtain numerical results based on the developed theoretical formulation, custom MATLAB R2024a codes were implemented for the analysis of free vibrations of a simply supported FGM plate resting on an elastic foundation. This type of boundary condition was selected as it represents the most commonly used benchmark case in the literature and allows for clear comparison with existing results while also serving as a fundamental test for the validation of new models. Nevertheless, different boundary conditions can significantly affect the dynamic behavior of plates: clamped edges are expected to increase the natural frequencies due to stronger kinematic constraints, whereas free edges generally lead to lower frequencies and more pronounced local deformations. Extending the analysis to other combinations of boundary conditions is envisaged as part of future research. In the numerical study, three different materials are considered, with their properties summarized in

Table 1. Material properties of Alumina and Aluminum [12].

Alumina (Al2O3)	Aluminum (Al)
Ec = 380 GPa	Em = 70 GPa
ρc = 3800 kg/m3	ρm = 2707 kg/m3
νc = 0.3	νm = 0.3
αc = 7 × 10−6 1/°C	αm = 23 × 10−6 1/°C

and

Table 2. Material properties of porous ceramic and metal for two types of FGMs [19].

	Material	P−1	P0	P1	P2	P3
E (Pa)	Si3N4	0	348.43 × 10−4	3.070 × 10−4	2.160 × 10−7	−8.946 × 10−11
	SUS304	0	201.04 × 109	3.079 × 10−4	−6.534 × 10−7	0
ρ (kg/m3)	Si3N4	0	2370	0	0	0
	SUS304	0	8166	0	0	0
α (1/K)	Si3N4	0	5.8723 × 10−6	9.095 × 10−4	0	0
	SUS304	0	12.330 × 10−6	8.086 × 10−4	0	0

.

To present and verify the results, dimensionless parameters are employed, enabling standardization and comparison across different materials and geometric configurations. This approach simplifies the mathematical model and facilitates more efficient computation of vibration and dynamic characteristics. The formulas for the dimensionless parameters used in the analysis are defined as follows:

$$\begin{array}{l}\overline{\omega }=\omega \left({\displaystyle \frac{a^2}{h}}\right){\left({\displaystyle \frac{{\rho }_m(1-v^2)}{E_{m{T}_0}}}\right)}^{{\displaystyle \frac{1}{2}}};\hspace{1em}\hspace{0.17em}\widehat{\omega }=\omega h\sqrt{{\displaystyle \frac{{\rho }_m}{E_{m{T}_0}}}}; \tilde{\omega }=\omega h\sqrt{{\displaystyle \frac{{\rho }_C}{G}}};\hspace{1em}\hspace{0.17em}G={\displaystyle \frac{E_C}{2(1+v)}};\hspace{1em}\hspace{0.17em}\stackrel{0}{\omega }=\omega h\sqrt{{\displaystyle \frac{{\rho }_c}{E_c}}};\hspace{1em}\\ \hspace{0.17em}{}^{\prime }\omega =\omega h\sqrt{{\displaystyle \frac{{\rho }_m}{E_m}}},\overline{k_0}={\displaystyle \frac{k_0{a}^4}{D_{11}}};\hspace{1em}\hspace{0.17em}\overline{k_s}={\displaystyle \frac{k_s{a}^2}{D_{11}}};\hspace{1em}\hspace{0.17em}\overline{k_1}={\displaystyle \frac{k_1{a}^4}{D_{11}}};\hspace{1em}\hspace{0.17em}{D}_{11}={\displaystyle \frac{E_{m{T}_0}{h}^3}{12\left(1-v^2\right)}}\end{array}$$

(27)

The elastic modulus of metal $E_{m{T}_0}$ is evaluated at room temperature $\left(T_0=300 \mathrm{K}\right)$.

6.1. Validation of Material Modeling and Input Functions

Figure 4 and Figure 5 illustrate the variation in the effective Young’s modulus E(z) along the nondimensional thickness coordinate z/h for different porosity distribution models (uniform, linear non-uniform, and trigonometric), considering variations in the porosity parameter β and the power-law exponent N.

In the case of homogeneously distributed constituent materials (N = 0, Figure 4), the variations in elastic properties arise solely from the porosity distribution. Uniform porosity results in a constant Young’s modulus throughout the thickness. In contrast, linear and trigonometric porosity profiles induce more pronounced variations, exhibiting a minimum at the mid-plane for Type II and low values in the interior with higher values near the surfaces for Type III. For functionally graded material distribution (N = 2, Figure 4), the elastic modulus increases toward the top surface due to the dominance of the ceramic phase. The trigonometric porosity distribution further amplifies this effect by eliminating porosity in the surface layers.

This behavior clearly confirms the significant influence of the combined effects of porosity and material gradation on the stiffness distribution, which is crucial for accurate calculations and optimization of functionally graded structures under thermomechanical loading conditions.

Table 3 presents the nondimensional fundamental frequencies of a square FGM plate under conditions without a temperature gradient, at room temperature, and for a geometric ratio of a/h = 8. The comparison includes various theoretical approaches from the literature, as well as two new formulations labeled Present 1 and Present 2. Both versions implement modified shape functions along the thickness coordinate within the framework of a higher-order shear deformation theory, with particular emphasis on physically consistent satisfaction of the natural boundary conditions for shear deformation.

The results obtained using the proposed models closely match those from the reference HSDT formulation, confirming their high accuracy and consistency. The minimal discrepancies between Present 1 and Present 2 models, as well as relative to established references (e.g., Refs. [18,22,24,43]), further attest to the numerical stability of the implementation. Deviations compared to other approaches, especially for larger values of the power-law exponent N, indicate differences in assumptions regarding the distribution of deformation through the thickness, which is particularly noticeable in works such as Refs. [44,45].

Table 3. Non-dimensional fundamental frequencies $\left(\overline{\omega }\right)$ of a square $S{I}_3{N}_4-SUS304$ FGM solar plate for varying power-law parameters at ΔT = 0 °C and T₀ = 300 K, with aspect ratio a/h = 8.

Source	N = 0	N = 0.5	N = 1	N = 2
Present 1	12.5068	8.60908	7.54435	6.77066
Present 2	12.5068	8.60908	7.54436	6.77069
Ref. [19]	12.508	8.610	7.545	6.771
Refs. [18,22]	12.507	8.609	7.544	6.771
Ref. [7]	12.506	8.652	7.584	6.811
Refs. [18,23]	12.507	8.609	7.544	6.770
Ref. [18]	12.507	8.609	7.544	6.770
Refs. [18,24]	12.509	8.611	7.546	6.772
Ref. [46]	12.506	8.616	7.552	6.777
Ref. [47]	12.495	8.675	7.555	6.777
Ref. [44]	12.508	8.717	7.608	6.737
Ref. [45]	12.528	8.622	7.557	6.786
Ref. [21]	12.463	8.592	7.565	6.763
Ref. [43]	12.508	8.610	7.545	6.771

Table 3. Non-dimensional fundamental frequencies $\left(\overline{\omega }\right)$ of a square $S{I}_3{N}_4-SUS304$ FGM solar plate for varying power-law parameters at ΔT = 0 °C and T₀ = 300 K, with aspect ratio a/h = 8.

Source	N = 0	N = 0.5	N = 1	N = 2
Present 1	12.5068	8.60908	7.54435	6.77066
Present 2	12.5068	8.60908	7.54436	6.77069
Ref. [19]	12.508	8.610	7.545	6.771
Refs. [18,22]	12.507	8.609	7.544	6.771
Ref. [7]	12.506	8.652	7.584	6.811
Refs. [18,23]	12.507	8.609	7.544	6.770
Ref. [18]	12.507	8.609	7.544	6.770
Refs. [18,24]	12.509	8.611	7.546	6.772
Ref. [46]	12.506	8.616	7.552	6.777
Ref. [47]	12.495	8.675	7.555	6.777
Ref. [44]	12.508	8.717	7.608	6.737
Ref. [45]	12.528	8.622	7.557	6.786
Ref. [21]	12.463	8.592	7.565	6.763
Ref. [43]	12.508	8.610	7.545	6.771

6.2. Effect of Gradient Index, Geometric Ratios, and Temperature

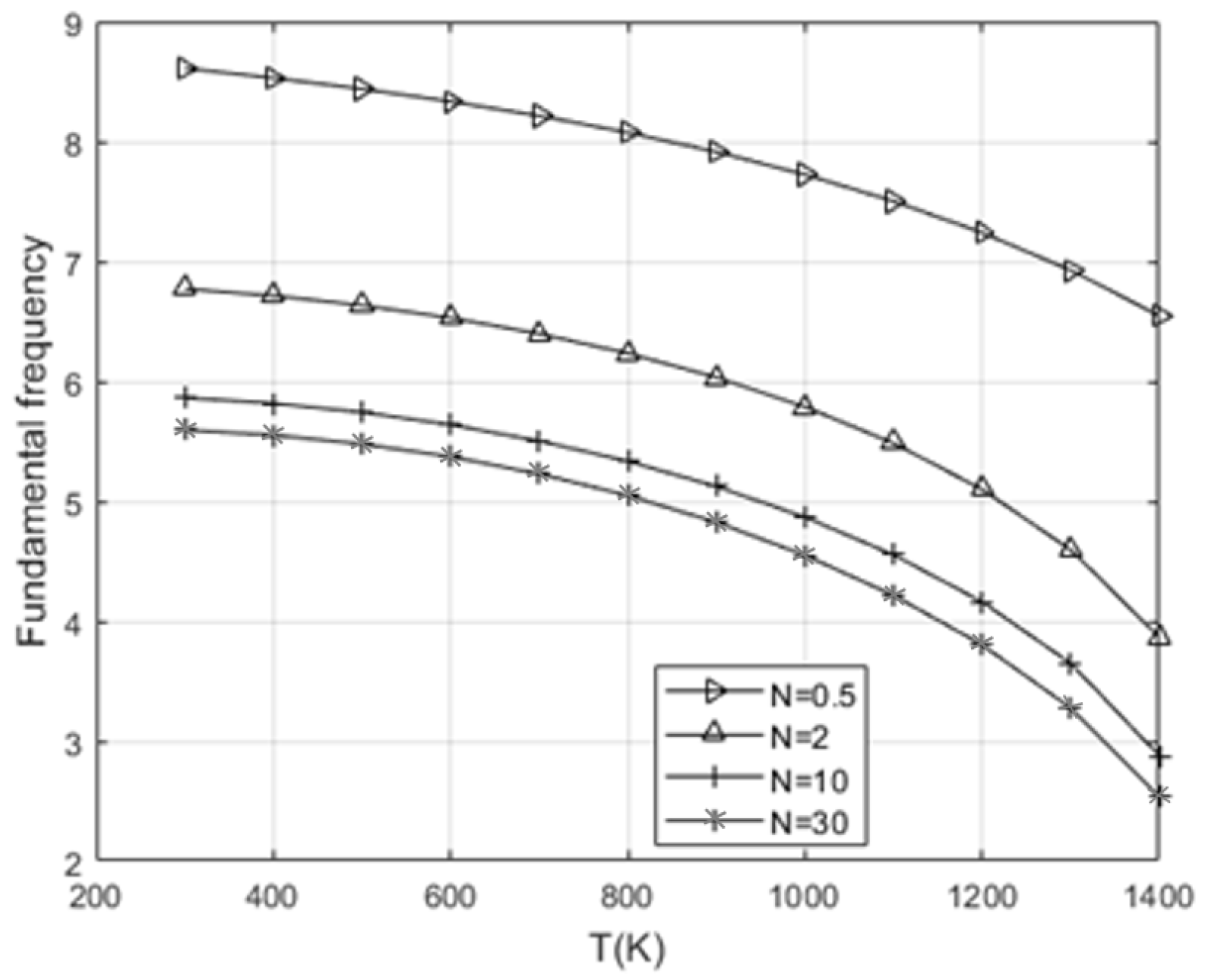
The systematic decrease in natural frequencies with increasing N clearly reflects the transition in material distribution from ceramic to metal composition, aligning with the known mechanical behavior of FGM structures. This confirms that the proposed shape functions not only provide accurate results but also enable physically consistent modelling of gradient effects without the need for additional correction parameters, making them well-suited for vibration analysis of composite systems.

Based on the results shown in Figure 6 and Figure 7, a pronounced influence of temperature effects, as well as the material gradient exponent, on the fundamental nondimensional frequency of square $S{I}_3{N}_4-SUS304$ FGM plates is observed. An increase in temperature leads to a systematic reduction in the fundamental frequency, which is a direct consequence of the degradation of the material’s mechanical properties due to thermal softening. This effect is more pronounced for higher values of the gradient exponent N, indicating that structures with more pronounced heterogeneity, i.e., with a higher metal content, are more susceptible to thermal loading.

On the other hand, the analysis of the frequency dependence on the gradient exponent N, which characterizes the distribution of material properties, shows an initial sharp decrease in frequency at low values of N, followed by stabilization. This saturation suggests that within a certain range of N values, the effect of the gradient on the dynamic response practically saturates, especially pronounced in thicker plates (with smaller a/h ratios).

Such behavior confirms that by proper selection of the material property distribution, the dynamic response of FGM structures under thermal loading can be effectively controlled, representing a key prerequisite for the optimization of these systems in engineering applications.

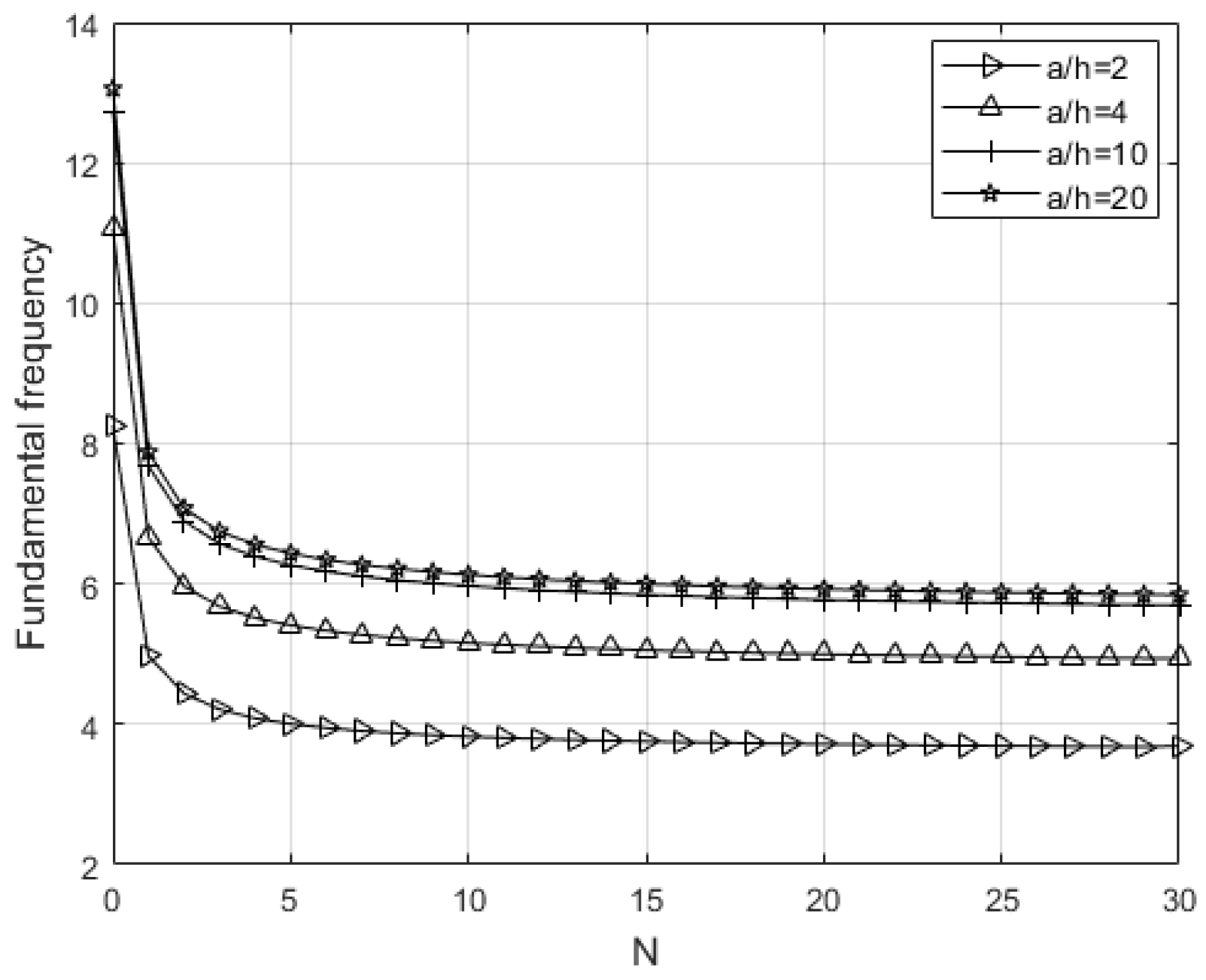
The influence of geometrical aspect ratios on the fundamental frequencies of $S{I}_3{N}_4-SUS304$ FGM plates is illustrated in Figure 8 and Figure 9. The shape function labelled Present 1 was used in the analysis. Figure 8 shows the variation in the nondimensional fundamental frequency as a function of the a/h ratio at a constant temperature of T = 300 K, for different values of the material gradient exponent N. A clear increase in frequency is observed with increasing a/h ratio, which is physically expected, as a reduction in relative thickness (i.e., an increase in width aa relative to height h) results in greater stiffness per unit mass.

However, the rate of this increase depends on the value of the parameter N, higher values of N (indicating a greater concentration of material with weaker mechanical properties in the lower region of the plate) are associated with lower values of fundamental frequency. This highlights the significant effect of material distribution on the dynamic response of the plate, further confirming the importance of incorporating functionally graded materials in engineering applications.

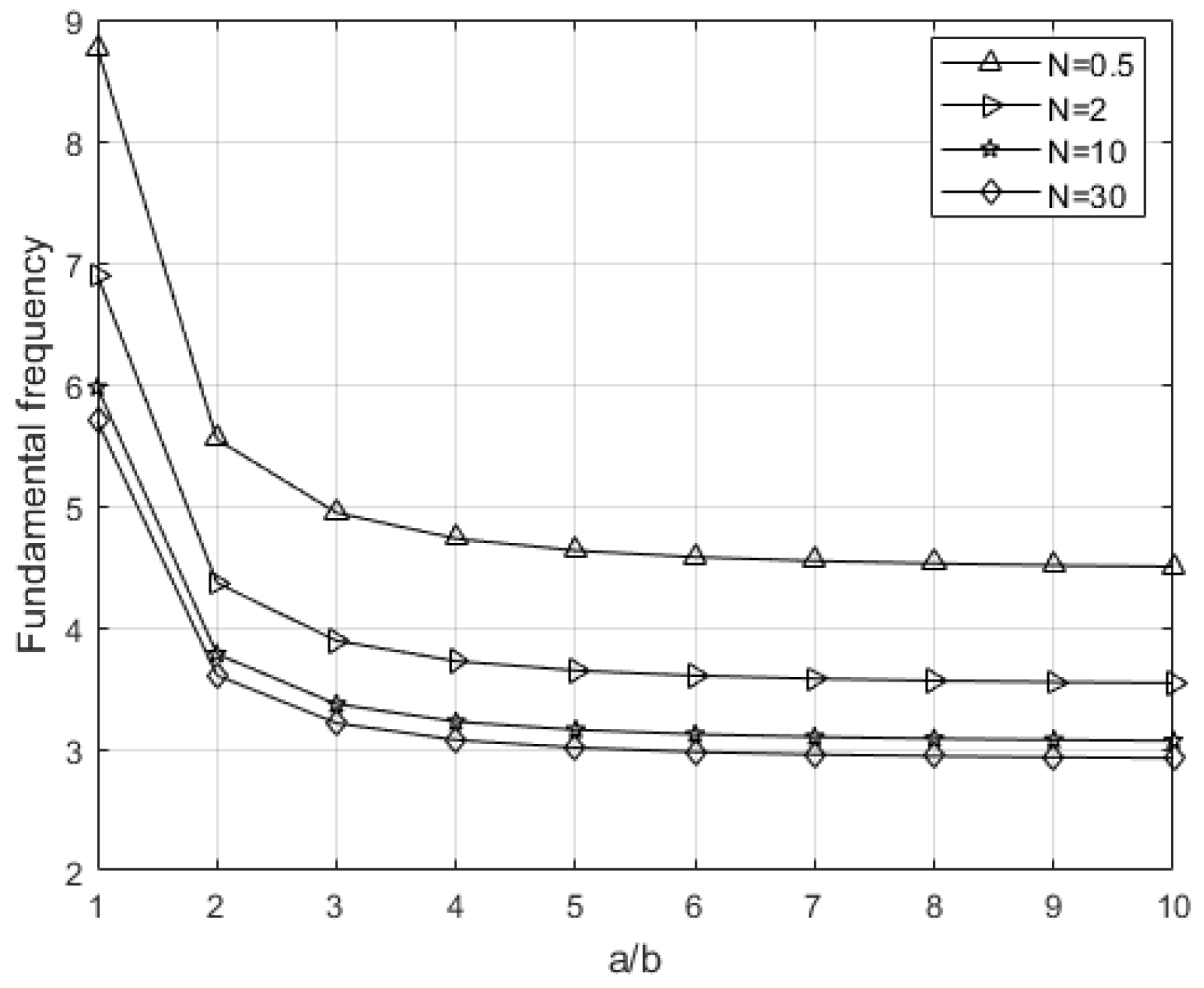
Figure 9 shows the effect of the a/b ratio (length-to-width ratio of the plate) on the fundamental frequencies at the same temperature and for different values of the gradient exponent N. A significant drop in frequency is observed at low a/b values, followed by stabilization or saturation at higher a/b ratios. This phenomenon results from a shift in the plate’s mode shape, were for more elongated geometries, the dominant vibration modes transition from two-dimensional to nearly one-dimensional.

The values of the exponent N continue to exert influence, higher N values reduce the overall structural stiffness and thus lower the frequency, but this effect becomes less pronounced as the geometry approaches the saturation region.

Overall, these results confirm that both geometric parameters and the material gradient exponent are key factors defining the dynamic behavior of FGM plates. Such dependencies provide an important basis for optimizing structural design in terms of mass, stiffness, and resonant response, thereby justifying the need for accurate modelling of functional gradation in analysis and engineering design.

6.3. Effect of Elastic Foundation and Porosity Distributions

Table 4. Effect of Kerr-type elastic foundation on the non-dimensional frequency $\widehat{\omega }$ of Al-Al₂O₃ FGM plates for different values of the gradient exponent N, with fixed parameters a/b = 1 and a/h = 20.

(kl, ku, ks)	Source	N = 0	N = 0.5	N = 1	N = 5
(100, 0, 100)	Ref. [19]	0.0294	0.0251	0.0227	0.0198
	Ref. [40]	0.0294	0.0253	0.0231	0.0202
	Ref. [48]	0.0294	0.0253	0.0231	0.0202
	Present1	0.0294	0.0251	0.0227	0.0198
	Present2	0.02942	0.0251	0.02274	0.01978
(100, 100, 100)	Ref. [19]	0.0356	0.0328	0.0314	0.0303
	Ref. [40]	0.0356	0.0329	0.0316	0.0305
	Ref. [48]	0.0356	0.0329	0.0316	0.0305
	Present1	0.03558	0.03275	0.03138	0.0303
	Present2	0.03558	0.03275	0.03138	0.0303
(100, 100, 200)	Ref. [19]	0.0375	0.035	0.0339	0.0332
	Ref. [40]	0.0375	0.0351	0.0341	0.0334
	Ref. [48]	0.0375	0.0351	0.0341	0.0334
	Present1	0.0375	0.03504	0.03389	0.0332
	Present2	0.0375	0.03504	0.03389	0.0332
(100, 200, 200)	Ref. [19]	0.044	0.0426	0.0421	0.0425
	Ref. [40]	0.044	0.0427	0.0423	0.0426
	Ref. [48]	0.044	0.0427	0.0422	0.0426
	Present1	0.04404	0.04264	0.04209	0.04248
	Present2	0.04404	0.04264	0.04209	0.04248

presents the non-dimensional fundamental frequencies of an aluminium functionally graded (FGM) plate for different values of the gradient parameter N, and four sets of Kerr-type elastic foundation parameters: (100, 0, 100), (100, 100, 100), (100, 100, 200), and (100, 200, 200). All results correspond to a geometric ratio of a/h = 20, which represents a typical case of a thin plate subjected to bending and shear deformations.

The objective of this analysis is to verify the numerical results obtained using the newly proposed shape functions (Present1 and Present2) by comparing them with data from the literature (Refs. [19,40,48]).

In all analyzed cases, the results obtained using the Present1 and Present2 models perfectly match the values from Ref. [19], which was used as the primary benchmark example. Deviations from the results reported in Refs. [40,48] are less than 0.3%, confirming the exceptional accuracy of the proposed models.

For the foundation configuration (100, 0, 100), the Present1 and Present2 results for the gradient parameter N in the range of 0 to 5 precisely reproduce the reference values from Ref. [19], with virtually negligible numerical error. Deviations from Refs. [40,48] for N = 1 and N = 5 are in the range of 0.002 to 0.004.

A similar level of accuracy is observed for more complex Kerr foundation configurations: for (100, 100, 100) and (100, 100, 200), the Present1 and Present2 models achieve exact agreement with Ref. [19] up to the third decimal place, while the differences compared to Refs. [40,48] remain below 0.2%.

In the most demanding case, (100, 200, 200), the proposed models maintain high precision and consistency across all three references, with the maximum recorded deviation being 0.002 for N = 1.

In addition to their high accuracy, the results exhibit a consistent trend of decreasing nondimensional fundamental frequencies with increasing values of the gradient parameter N, which corresponds to a higher content of the metallic component in the FGM structure and reflects the overall reduction in system stiffness due to the lower elastic modulus of the metal. This outcome fully aligns with physical expectations and further confirms the validity of the proposed model.

The observed trends in gradient exponent, metallic content, and porosity distribution also carry important implications for engineering design. The systematic reduction in fundamental frequencies with increasing gradient exponent and metallic content highlights the need for careful control of these parameters in applications where dynamic stability is critical. At the same time, tailoring the porosity distribution provides opportunities for structural weight optimization. This allows for a compromise between mass reduction and preservation of vibration performance. The present findings therefore offer guidelines that can serve as a basis for preliminary optimization strategies in future studies.

It is important to emphasize that the shape functions in the Present1 and Present2 models are carefully constructed to satisfy physically realistic shear deformation distributions through the thickness without the need for shear correction factors. Their mathematical structure enables efficient integration into the Navier method while maintaining numerical stability under variations in substrate and material parameters.

Based on the data presented in Table 4, it can be confidently confirmed that the proposed shape functions enable a high level of accuracy and predictability of results across a wide range of mechanical and geometrical conditions. This consistency with renowned results from the literature serves as clear evidence of the validity and scientific relevance of the proposed model in the analysis of free vibrations of FGM plates resting on elastic foundations.

Table 5. Values of the non-dimensional frequency of a square $S{I}_3{N}_4-SUS304$ FGM solar plate resting on a Kerr-type elastic foundation for different geometric ratios a/h and various values of the power-law exponent N.

(kl, ku, ks)	a/h	Source	N = 0	N = 0.5	N = 2	N = 10
(50, 50, 50)	2	Ref. [19]	12.3247	8.5891	6.6386	5.6486
		Present1	12.3247	8.2849	6.40381	5.61505
		Present2	12.3247	8.28482	6.40388	5.61501
	4	Ref. [19]	16.2081	11.5922	9.4233	8.3917
		Present1	16.2047	11.5904	9.42176	8.3899
		Present2	16.2047	11.5904	9.42177	8.38987
	10	Ref. [19]	17.5734	12.5496	10.1637	9.0126
		Present1	17.5728	12.5492	10.1635	9.01226
		Present2	17.5728	12.5492	10.1635	9.01227
(100, 100, 100)	2	Ref. [19]	12.3247	8.5891	6.6386	5.6486
		Present1	12.3247	8.28489	6.40381	5.61505
		Present2	12.3247	8.28489	6.40388	5.61501
	4	Ref. [19]	20.067	14.5002	11.896	10.6767
		Present1	20.0647	14.4993	11.8949	10.6754
		Present2	20.0647	14.4993	11.8949	10.6754
	10	Ref. [19]	21.3429	15.432	12.611	11.2598
		Present1	21.3424	15.4317	12.6108	11.2595
		Present2	21.3424	15.4317	12.6109	11.2595
(200, 200, 200)	2	Ref. [19]	12.3247	8.5891	6.6386	5.6486
		Present1	12.3247	8.28489	6.40381	5.61505
		Present2	12.3247	8.28482	6.40388	5.61505
	4	Ref. [19]	24.6493	17.1782	13.2772	11.2972
		Present1	24.6495	17.0131	13.1459	11.2796
		Present2	24.6495	17.0131	13.1459	11.2796
	10	Ref. [19]	27.366	19.9856	16.4466	14.761
		Present1	27.3656	19.9854	16.4464	14.7608
		Present2	27.3656	19.9854	16.4464	14.7608

presents the fundamental dimensionless frequencies $\overline{\omega }$ of square $S{I}_3{N}_4-SUS304$ FGM solar plates resting on elastic Kerr-type foundations with parameters (50, 50, 50), (100, 100, 100), and (200, 200, 200), for various geometric ratios a/h = 2, 4, 10 and power-law index values N = 0, 0.5, 2, 10. The results obtained using the newly proposed shape functions, Present1 and Present2, are compared with the reference values reported in the literature (Ref. [19]).

The analysis indicates that the frequencies computed using the Present1 and Present2 models exhibit near-perfect agreement, yielding results that closely match the reference values with minimal deviations. Specifically, for all three Kerr foundation configurations and all examined geometric ratios, the Present models consistently reproduce the reference frequencies for N = 0, thereby confirming the accurate implementation of the initial boundary conditions.

As the parameter N increases, representing a higher proportion of the metallic phase within the FGM structure, a clear trend of decreasing fundamental frequencies is observed. This behavior is attributed to the reduction in overall stiffness due to the lower elastic modulus of the metallic component. This trend is evident across all investigated cases, and the results from the Present models follow it with a high degree of accuracy.

More specifically, for a/h = 2, the differences between the Present models and Ref. [19] are negligible, particularly for higher values of N, where the deviations are on the order of 10⁻³. For larger geometric ratios, a/h = 4 and a/h = 10, the agreement remains exceptionally high, with differences that are virtually imperceptible and do not exceed a few thousandths. This indicates the stability and robustness of the proposed shape functions across different deformation regimes and foundation configurations.

Furthermore, the Present1 and Present2 models produce practically identical results, which further confirms the consistency and reliability of their mathematical formulations. Such alignment demonstrates the successful integration of the shape functions into the numerical methods used for analyzing the free vibration behavior of FGM plates resting on elastic foundations.

In conclusion, based on the results presented in Table 5, it can be affirmed that the proposed Present1 and Present2 models offer a high level of accuracy and reliability in predicting the fundamental frequencies of FGM plates with varying Kerr foundation parameters and geometric ratios. This analysis further strengthens confidence in the applicability of these shape functions for comprehensive dynamic analyses of functionally graded materials.

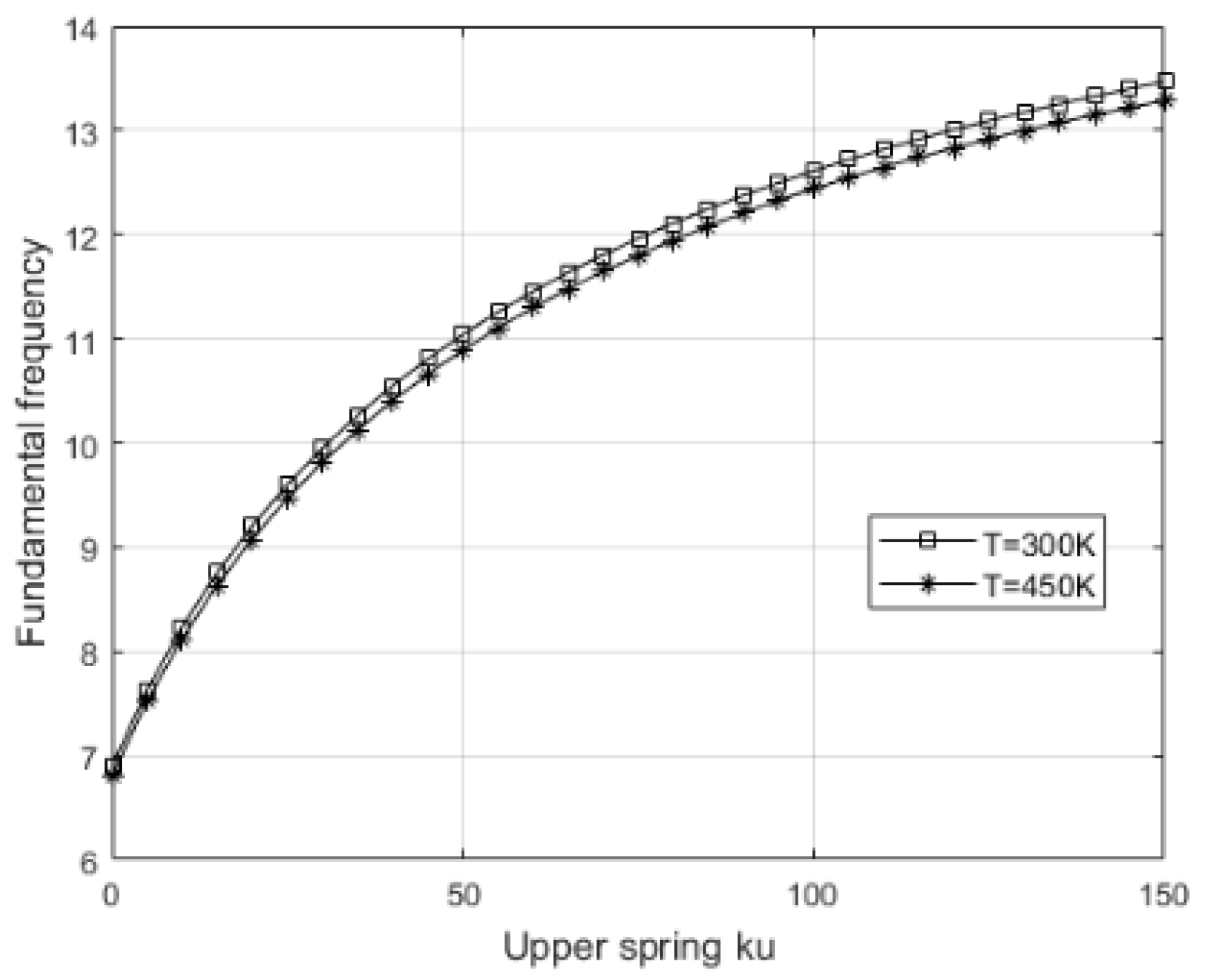
The study of the influence of the elastic foundation modelled according to the Kerr approach reveals a pronounced dependence of the fundamental nondimensional frequency $\overline{\omega }$ on the individual foundation components: the upper spring stiffness k_u, the lower spring stiffness k_l, and the shear layer stiffness k_s. An increase in k_u (Figure 10) results in a systematic rise in $\overline{\omega }$, which can be attributed to the additional support provided in the upper zone of the plate. This component acts as an active constraint against bending, increasing the effective flexural stiffness and reducing amplitudes in the fundamental vibration mode. Such behavior highlights the importance of introducing vertical reactive forces at the surface layer of the foundation, especially in thin FGM plates with a pronounced gradient in material properties.

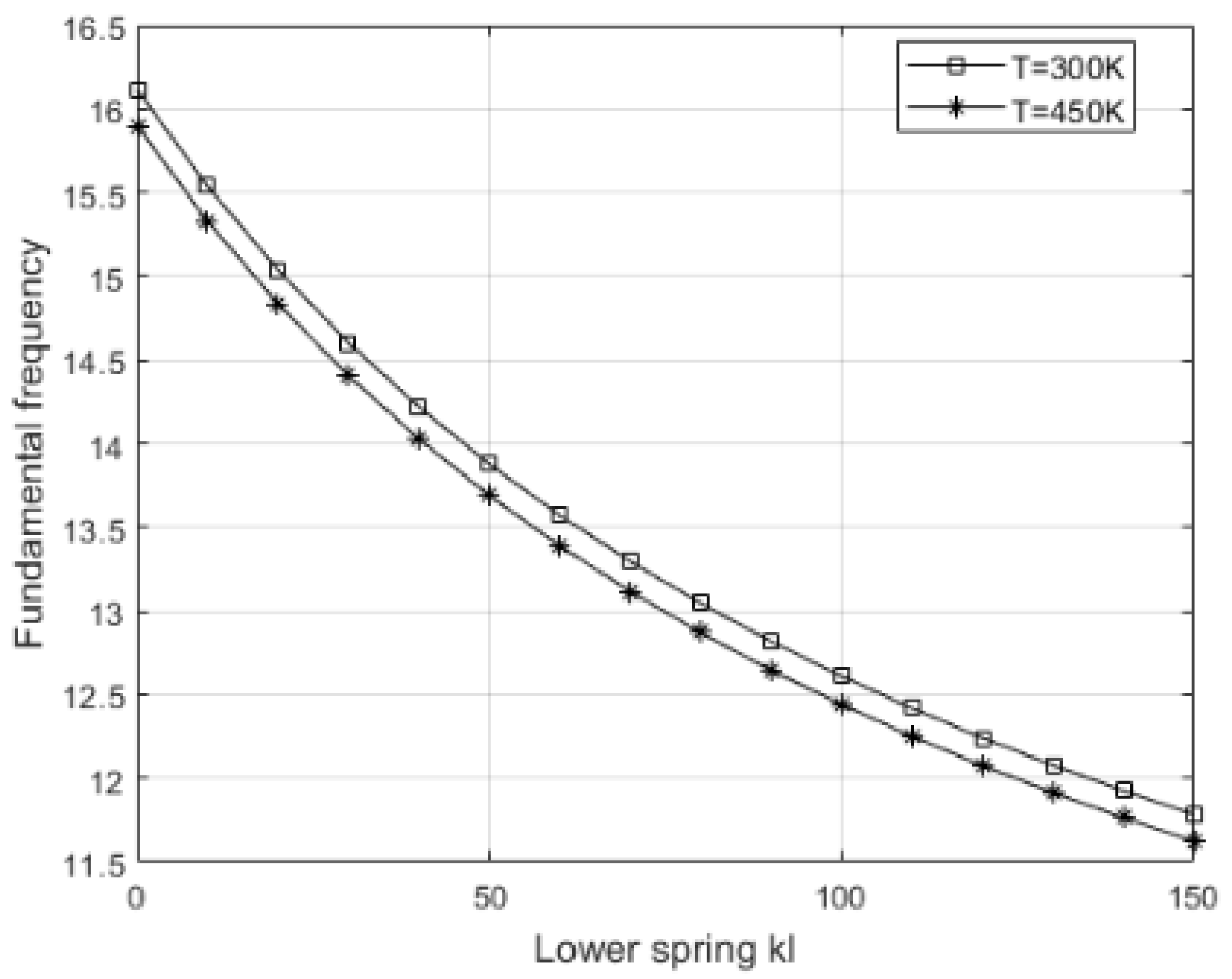
In contrast, an increase in k_l (Figure 11) leads to a reduction in $\overline{\omega }$, indicating a redistribution of deformations and energy dissipation in the lower zone. Rather than enhancing stability, a high lower spring stiffness creates localized system behavior and limits the efficient transfer of energy, thereby reducing the global dynamic stiffness. This result reveals the delicate balance between support and deformability, where the lower layer may exert a destabilizing effect if not properly coordinated with the rest of the system.

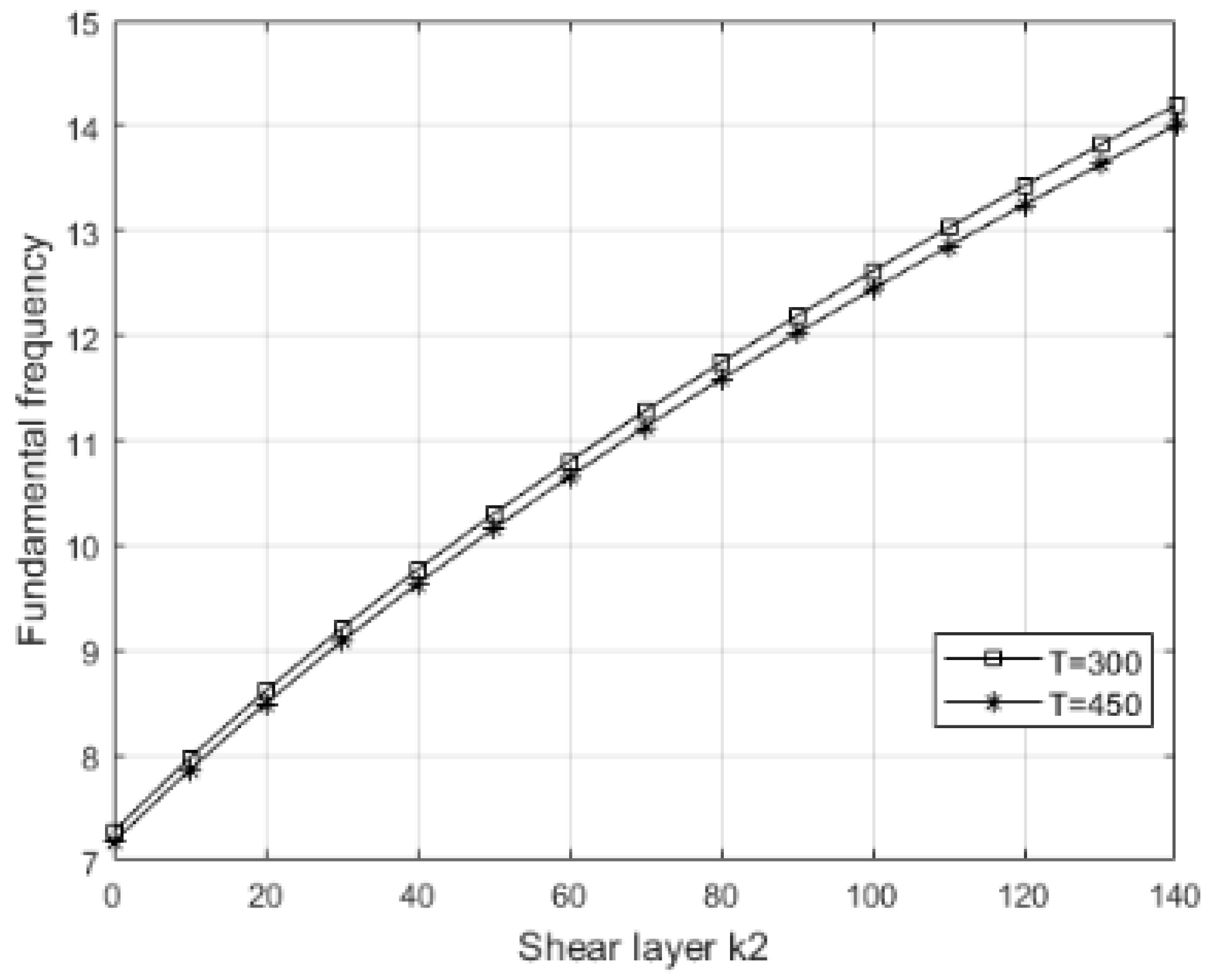
Finally, an increase in k_s (Figure 12) consistently has a positive effect on $\overline{\omega }$, underscoring the importance of shear rigidity in limiting relative displacements between layers. This parameter further homogenizes the dynamic response of the system, particularly in the presence of thermal variations and material gradation. Comparative analysis shows that k_u is the most effective in increasing frequency, k_l can be potentially counterproductive, while k_s acts as a stabilizing factor across a wide range of configurations.

These findings emphasize the need for an integrated design approach to elastic foundations in FGM structures, where the optimization of individual parameters must be aligned with the goals of vibration control and mechanical stability.

Table 6. Effect of porosity distributions and temperature rise on the non-dimensional fundamental frequencies $\bar{\omega }$ of the square $S{I}_3{N}_4-SUS304$ FGM plate at a/h = 5 and ΔT = 0 K.

Porosity Distributions	β	Source	N = 0	N = 0.5	N = 1	N = 2	N = 5
Type I	0	Ref. [19]	11.6778	8.0369	7.0405	6.3109	5.726
		Present1	11.6737	8.0342	7.0381	6.3092	5.7246
		Present2	11.6737	8.0342	7.0381	6.3092	5.7247
	0.1	Ref. [19]	12.6857	8.1528	7.0258	6.2248	5.5976
		Present1	12.6812	8.1501	7.0234	6.2231	5.5964
		Present2	12.6812	8.1501	7.0234	6.2232	5.5965
	0.2	Ref. [19]	14.3225	8.302	7.0052	6.1171	5.4418
		Present1	14.3175	8.2993	7.0028	6.1156	5.4408
		Present2	14.3175	8.2993	7.0028	6.1157	5.4409
	0.3	Ref. [19]	17.5594	8.5016	6.975	5.9787	5.248
		Present1	17.553	8.4989	6.9727	5.9773	5.2473
		Present2	17.5533	8.4989	6.9727	5.9774	5.2474
	0.4	Ref. [19]	28.7275	8.783	6.9284	5.7934	4.9992
		Present1	28.7175	8.7803	6.9262	5.7922	4.9989
		Present2	28.7175	8.7803	6.9262	5.792	4.999
Type II	0	Ref. [19]	11.6778	8.0369	7.0405	6.3109	5.726
		Present1	11.6737	8.0342	7.0381	6.3092	5.7246
		Present2	11.6737	8.0342	7.0381	6.3092	5.7247
	0.1	Ref. [19]	12.2057	8.1601	7.098	6.329	5.7188
		Present1	12.203	8.1584	7.097	6.3285	5.7188
		Present2	12.2031	8.1585	7.0967	6.329	5.719
	0.2	Ref. [19]	12.8464	8.2955	7.1586	6.3456	5.7073
		Present1	12.8455	8.2952	7.1586	6.3467	5.7092
		Present2	12.8457	8.2953	7.1587	6.3469	5.7095
	0.3	Ref. [19]	13.6445	8.445	7.2222	6.3596	5.6897
		Present1	13.6463	8.4464	7.224	6.3628	5.6943
		Present2	13.6467	8.4467	7.2243	6.3632	5.6948
	0.4	Ref. [19]	14.6746	8.611	7.2886	6.3695	5.6635
		Present1	14.68	8.6147	7.2928	6.3757	5.672
		Present2	14.6808	8.6152	7.2932	6.3763	5.6727
Type III	0	Ref. [19]	11.6778	8.0369	7.0405	6.3109	5.726
		Present1	11.6737	8.0342	7.0381	6.3092	5.7246
		Present2	11.674	8.0342	7.04	6.3092	5.7247
	0.1	Ref. [19]	12.0516	8.1431	7.1013	6.3433	5.7394
		Present1	12.0502	8.1424	7.101	6.3438	5.7405
		Present2	12.0504	8.1426	7.1011	6.344	5.7407
	0.2	Ref. [19]	12.4718	8.2541	7.1628	6.3738	5.7492
		Present1	12.474	8.256	7.165	6.3772	5.7535
		Present2	12.4744	8.2563	7.1653	6.3776	5.754
	0.3	Ref. [19]	12.9492	8.3702	7.2245	6.4017	5.7541
		Present1	12.9558	8.3754	7.2299	6.4087	5.7628
		Present2	12.9566	8.3759	7.2304	6.4094	5.7635
	0.4	Ref. [19]	13.4981	8.4916	7.2858	6.4258	5.7525
		Present1	13.5106	8.5008	7.2954	6.4376	5.767
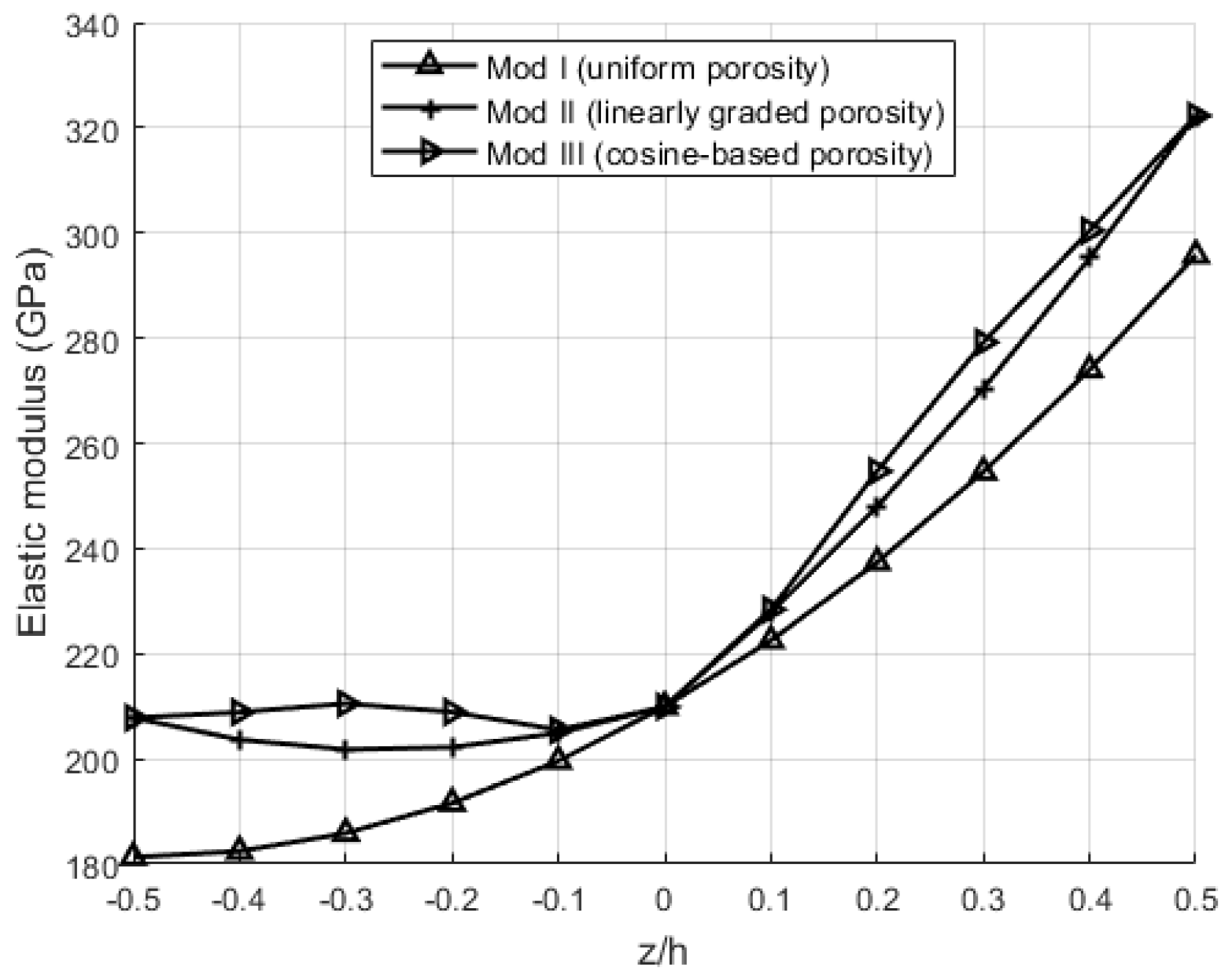
		Present2	13.5117	8.5016	7.2962	6.4385	5.7681

presents the influence of different porosity distributions (Types I, II, and III), the porosity coefficient β, and the material gradient exponent N on the dimensionless fundamental frequencies $\bar{\omega }$ of a square FGM plate with a side-to-thickness ratio a/h = 5, evaluated at room temperature (ΔT = 0 K). Special emphasis is placed on comparing the reference results from the literature [19] with those obtained using the newly proposed porosity functions Present1 and Present 2.

By introducing these new functions, a quantitatively almost identical response is achieved compared to the reference models for all parameter combinations, with frequency deviations ranging from 10⁻⁴ to 10⁻². This consistency confirms the accuracy and reliability of the new models, along with the added flexibility and improved numerical stability they offer for subsequent implementation in higher-dimensional simulations.

The contribution of the Present1 and Present2 shape functions is primarily reflected in their ability to accurately approximate complex porosity distributions with minimal error, making them suitable for application in nonlinear analyses and optimization tasks, where traditional models often exhibit limitations.

An analysis of the results clearly shows that an increase in the porosity parameter β leads to a reduction in the fundamental frequencies for all porosity distribution types, which can be attributed to the decrease in the material’s effective stiffness due to increased porosity. Conversely, increasing the material gradient exponent N results in a continuous decline in frequencies, because of the redistribution of mass and elastic modulus across the plate thickness.

It is noteworthy that Present1 and Present2 yield virtually identical values in most cases, indicating the numerical consistency of both formulations. The minor deviations observed at higher values of β, and N further confirm the robustness of the proposed models under more demanding engineering conditions.

In conclusion, the proposed porosity models represent a valid alternative to existing approaches, exhibiting extremely small deviations and strong potential for improving analytical and numerical models in engineering applications involving functionally graded materials with porous structures.

The influence of the porosity volume fraction β and porosity distribution on the fundamental dimensionless natural frequency of a square FGM plate is presented in Figure 13, while Figure 14 illustrates the effect of the gradient exponent N for different porosity distributions.

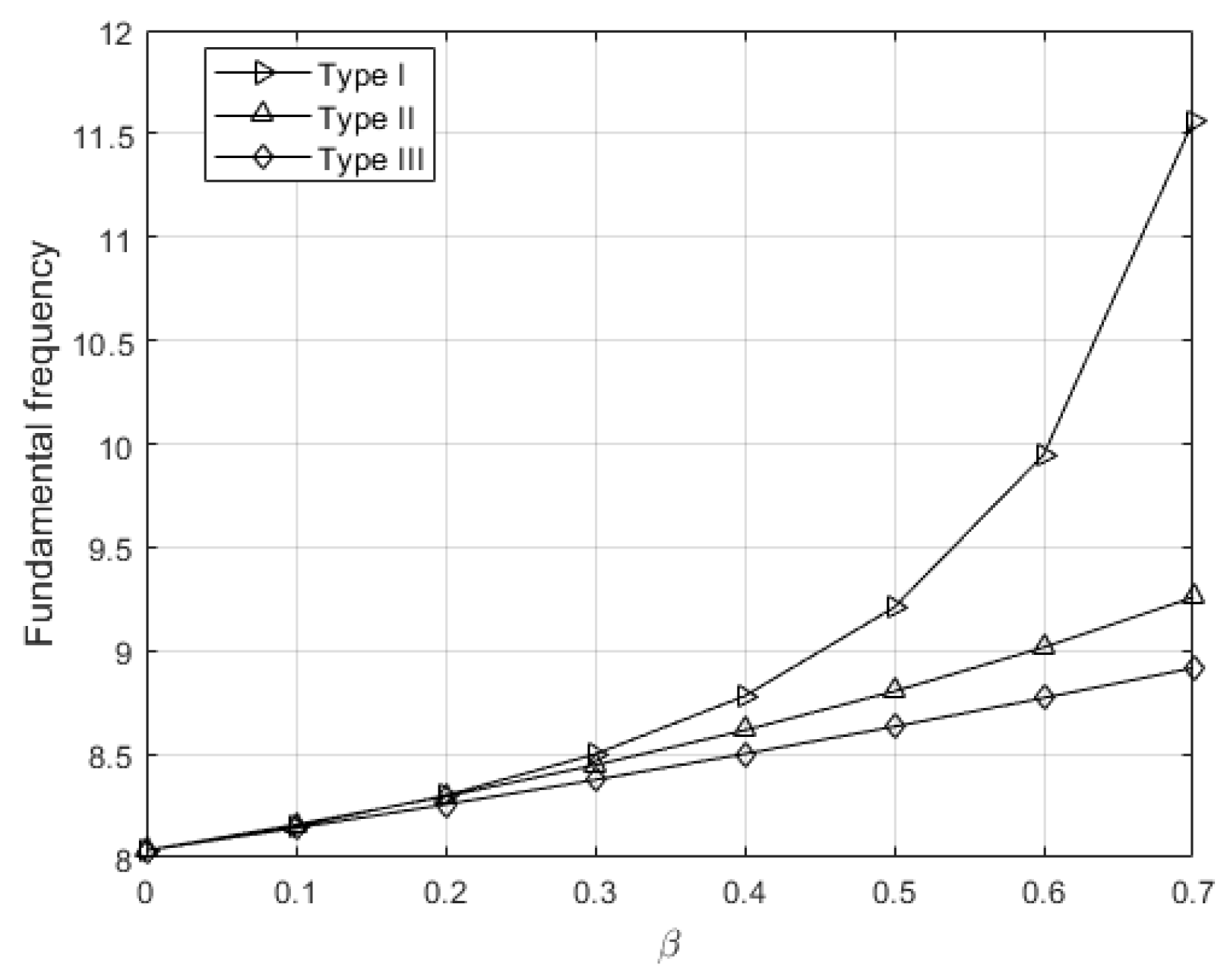
In Figure 13, the dependence of the frequency ω on the porosity β is analyzed at a fixed N = 0.5. Three different functional porosity distributions are considered: uniform (Type I), linear (Type II), and trigonometric (Type III). The results show that an increase in β leads to a rise in the natural frequency for all distributions, with the most pronounced effect observed in the Type III distribution.

This behavior can be explained by the fact that the trigonometric distribution concentrates a larger amount of the solid (ceramic) component near the plate surfaces, contributing to greater bending stiffness. The increase in $\overline{\omega }$ despite higher porosity is a result of the nonuniform distribution of stiff and porous zones, where the effective mass decreases while stiffness is maintained or even locally enhanced in critical bending regions. It should be emphasized, however, that this trend is not universal; for different porosity models or boundary conditions, stiffness degradation may dominate over mass reduction, leading to decreasing frequencies with increasing β.

Figure 14 shows the dependence of ω on the gradient exponent N at a constant porosity β = 0.2. An increase in frequency is observed with the rise in N, which is explained by the greater presence of the ceramic component in the upper region of the plate as N increases. However, at higher values of N (e.g., N > 1.2), the curves reach a plateau, indicating saturation of the effect of mass and stiffness redistribution. The trigonometric distribution (Type III) consistently results in the highest frequency values across the entire range of N, confirming its efficiency in localizing stiffness in regions of dominant deformation. In contrast, uniform porosity (Type I) produces the lowest ω values because the evenly distributed porosity degrades stiffness throughout the plate thickness without local optimization of bending resistance.

Overall, the results show that besides the porosity value β itself, the distribution of the porous material has a dominant influence on the dynamic behavior. An appropriate distribution (especially Type III), combined with a higher exponent N, enables achieving an optimal balance between mass reduction and increased dynamic stability. These findings can directly contribute to the development of FGM structures with improved vibration performance in high-precision engineering applications.

Table 7. Non-dimensional fundamental frequencies $\tilde{\omega }$ of the square solar isotropic plate for several mode numbers at a/h = 10 and ν = 0.3.

Source	Theories	Mode (n, m)
		$\left(\mathrm{1,1}\right)$	$\left(\mathrm{2,2}\right)$	$\left(\mathrm{1,3}\right)$	$\left(\mathrm{3,3}\right)$	$\left(\mathrm{2,4}\right)$
Present 1	HSDT	0.0930	0.3406	0.4151	0.6840	0.7453
Present 2	HSDT	0.0930	0.3406	0.4151	0.6839	0.7453
Reddy and Phan [49]	FSDT	0.0930	0.3406	0.4149	0.6834	0.7446
Akavci and Tanrikulu [50]	HSDT	0.0930	0.3407	0.4151	0.6841	0.7455
Srinivas et al. [51]	3D-Exact	0.0932	0.3421	0.4171	0.6889	0.7511
Mechab et al. [47]	HSDT	0.0930	0.3406	0.4151	0.6839	0.7454
Kenada [19]	LLHSDT	0.0930	0.3408	0.4153	0.6845	0.7460

clearly demonstrates the high level of accuracy of the proposed shape functions Present1 and Present2 within the HSDT formulation. The obtained non-dimensional frequencies for higher modes show an almost perfect agreement with the reference 3D exact solutions and existing HSDT models, with deviations consistently below 0.3% and practically negligible.

Importantly, both functions yield identical results, confirming their numerical stability and robustness. Compared to classical HSDT approaches, the Present functions provide an accurate description of transverse shear deformation without the need for additional correction factors, while retaining a simple expression structure. This makes them well-suited for further analytical and numerical applications.

Their use is therefore not only justified but also highly desirable, as they enhance the accuracy of the model without increasing computational complexity.

Table 8. Non-dimensional fundamental frequencies of the square FGM plate Al-Al₂O₃ for several power-law parameters at a/h = 5.

Source	Theories	N = 0.5	N = 1	N = 4	N = 10
Present 1	HSDT	0.1807	0.1631	0.1378	0.1301
Present 2	HSDT	0.1807	0.1631	0.1379	0.1301
Ref. [19]	LLHSDT	0.1808	0.1632	0.1377	0.1300
Ref. [49]	FSDT	0.1805	0.1631	0.1397	0.1324
Ref. [50]	TOSDT	0.1807	0.16321	0.1378	0.1301
Ref. [47]	HSDT	0.1807	0.1631	0.1378	0.1301
Ref. [52]	HSDT	0.1807	0.1632	0.1375	0.1303
Ref. [53]	HSDT	0.1811	–	0.1389	0.1305

presents the non-dimensional fundamental frequencies of a square FGM plate for various values of the material distribution parameter N. The results obtained using the shape functions Present1 and Present2 show complete agreement. For all analyzed values of N, these results closely match the existing HSDT models available in the literature.

A stable performance of the proposed functions is observed with increasing nonlinearity in the material gradient, which becomes especially evident at higher values of N, where the ceramic component is more significantly concentrated toward the surfaces. The deviation from the FSDT model increases with rising N, indicating the limitations of simplified theories in capturing the more complex transverse response. In contrast, the results based on the Present functions remain within expected bounds when compared with higher-order theories.

This consistency suggests that the proposed shape functions enable an accurate representation of the influence of variable material property distributions within the analytical model.

Table 9. Effect of porosity distributions on the non-dimensional fundamental frequencies of the square FGM plate Al-Al₂O₃ for several power-law parameters at a/h = 10.

β	Source	Porosity Distributions	N = 0.1	N = 0.5	N = 1
0.2	Present 1	Type I	0.1120	0.0959	0.0823
	Present 2		0.1120	0.0959	0.0823
	FSDT [54]		0.1123	0.0951	0.0824
	Ref. [19]		0.1120	0.0959	0.0823
	Present 1	Type II	0.1122	0.0984	0.0876
	Present 2		0.1122	0.0984	0.0876
	FSDT [54]		0.1126	0.0986	0.0879
	Ref. [19]		0.1122	0.0984	0.0876
	Present 1	Type III	0.1118	0.0985	0.0883
	Present 2		0.1118	0.0985	0.0883
	Ref. [19]		0.1118	0.0985	0.0880
0.4	Present 1	Type I	0.1163	0.0947	0.0713
	Present 2		0.1163	0.0947	0.0713
	FSDT [54]		0.1166	0.0949	0.0714
	Ref. [19]		0.1163	0.0947	0.0713
	Present 1	Type II	0.1157	0.1008	0.0883
	Present 2		0.1157	0.1008	0.0883
	FSDT [54]		0.1162	0.1011	0.0887
	Ref. [19]		0.1157	0.1007	0.0883
	Present 1	Type III	0.1148	0.1009	0.0900
	Present 2		0.1148	0.1009	0.0900
	Ref. [19]		0.1147	0.1009	0.0899
0.6	Present 1	Type I	0.1234	0.0908	0.0102
	Present 2		0.1234	0.0908	0.0102
	Present 1	Type II	0.1200	0.1036	0.0887
	Present 2		0.1200	0.1036	0.0888
	Present 1	Type III	0.1180	0.1036	0.0916
	Present 2		0.118	0.1036	0.0917

presents the influence of different porosity distributions on the non-dimensional fundamental frequencies of an FGM plate, considering three values of the power-law exponent N and three levels of total porosity, represented by the parameter β. The results across all porosity types (Type I—uniform, Type II—linear, and Type III—cosine) demonstrate that the Present1 and Present2 shape functions yield solutions in full agreement with the reference values, maintaining consistency regardless of porosity level or distribution profile.

Notably, with increasing β, the frequency values for Type I distribution exhibit a more pronounced decline compared to Type II and Type III, indicating a higher sensitivity of uniform porosity to reductions in the system’s mechanical stiffness. In the domain of higher N values, where the ceramic component is more concentrated near the surface, the distinctions between the porosity types become more significant.

The presence of more complex porosity distributions (Type II and Type III) is clearly reflected in the frequency behavior due to the mass and stiffness redistribution, with the Present functions accurately capturing these effects. This confirms the validated applicability of the proposed model even in scenarios where porosity effects are nonlinearly distributed through the plate thickness.

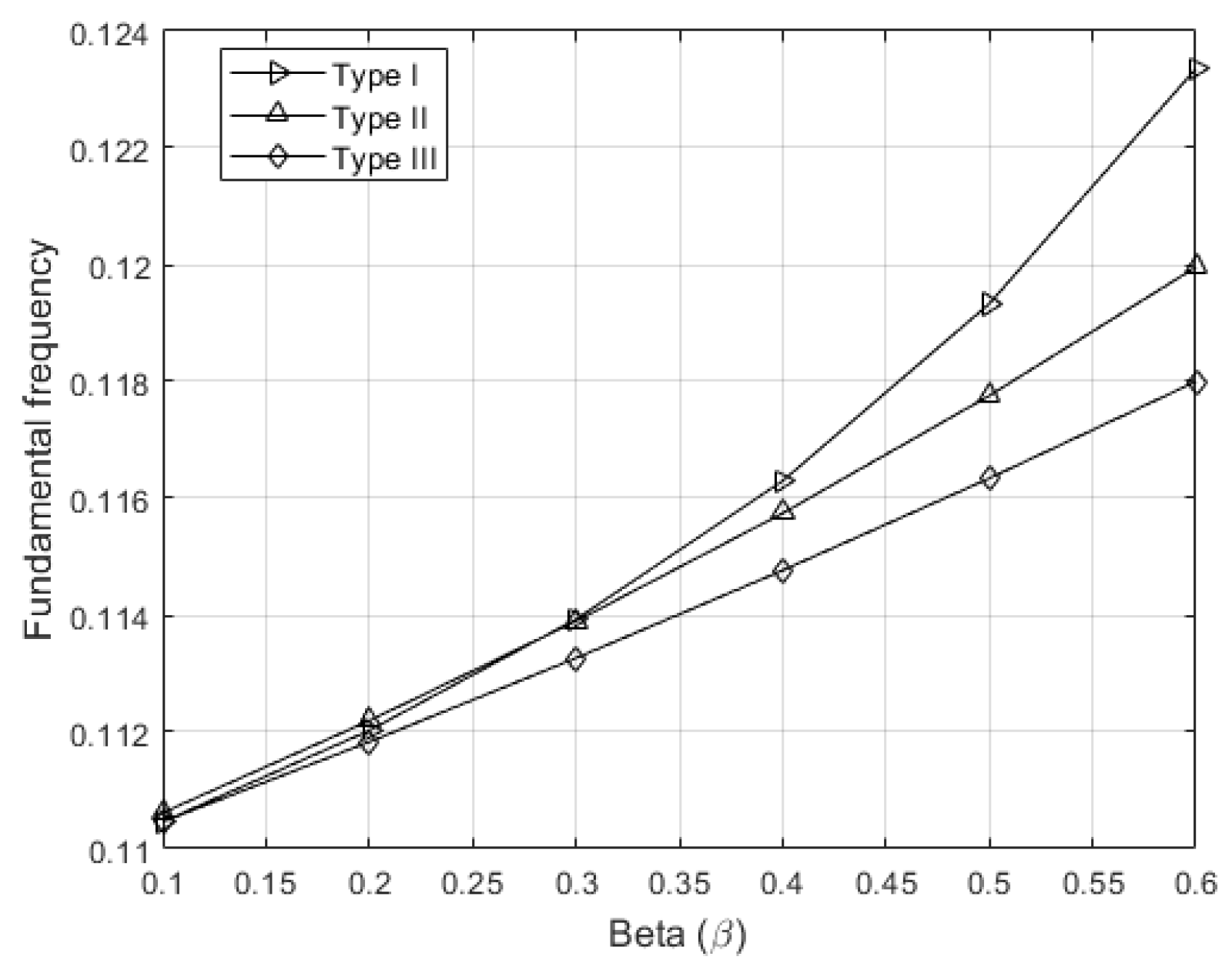
Figure 15 illustrates the dependence of the non-dimensional fundamental frequency on the porosity volume fraction β for three different porosity distributions (Type I, II, and III), at a constant aspect ratio of a/h = 10 and a fixed power-law index of N = 0.1. The diagram clearly confirms that the frequency increases with rising β for all distribution types, which is a direct consequence of the reduction in effective material mass due to porosity, while the stiffness remains the dominant factor. The differences among the distributions become more pronounced at higher β values, with Type II and Type III showing higher frequencies compared to Type I, implying a more favorable pore arrangement in terms of dynamic response. This behavior should be interpreted in the context of the present modeling assumptions; under different porosity patterns or boundary conditions, the reduction in stiffness may become more dominant, in which case the natural frequencies could decrease with increasing β.

This diagram not only validates the mechanical sensitivity of FGM plates to the porosity distribution profile but also highlights the potential for design optimization through controlled pore allocation, thereby enabling the development of structures with tailored dynamic characteristics.

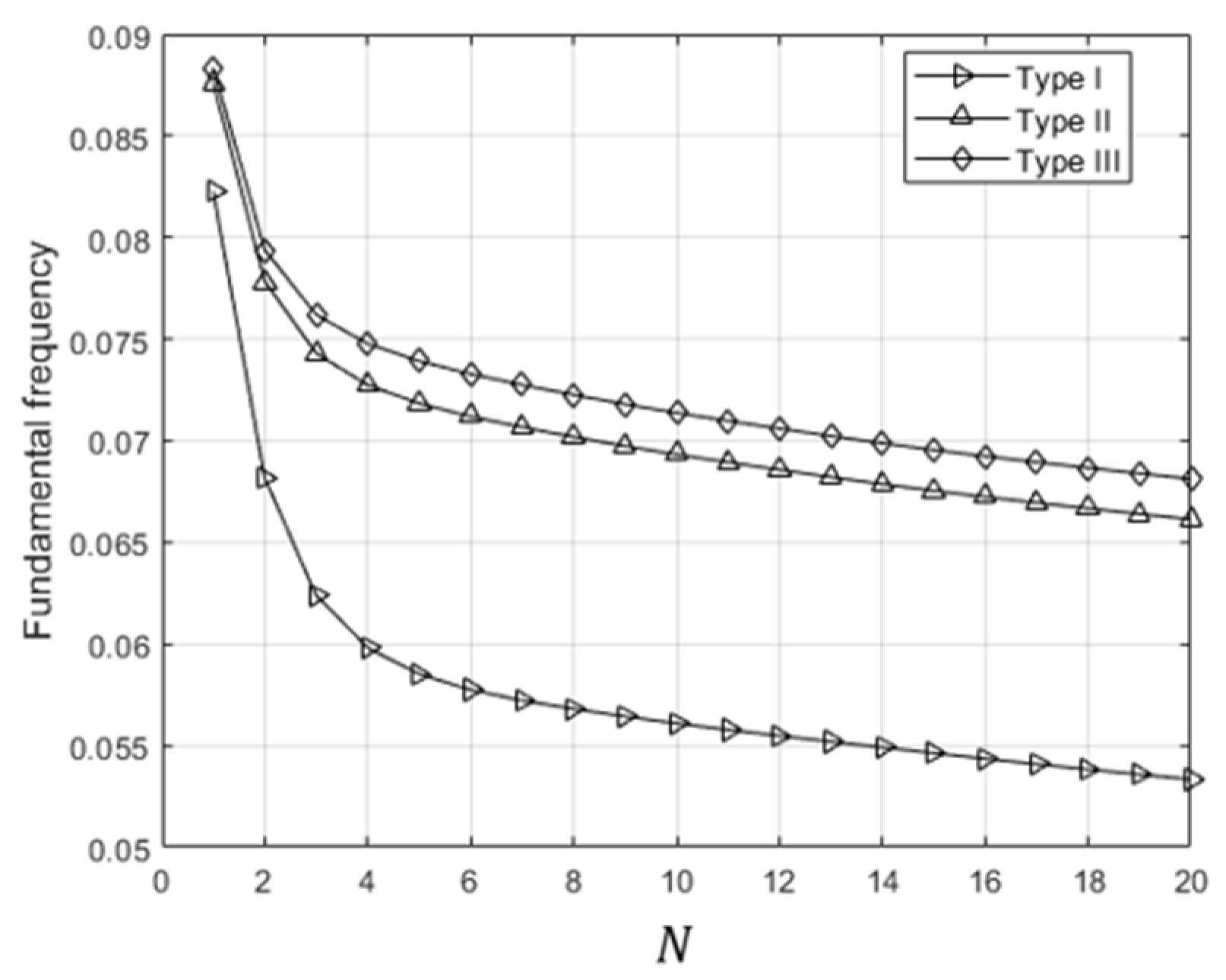
Figure 16 analyses the influence of the power-law index N on the fundamental frequency under a fixed porosity volume fraction of β = 0.2. For all porosity types, a distinct nonlinear decrease in frequency is observed as the material transitions from a homogeneous to a highly graded distribution (from low to high N values), which gradually stabilizes beyond N > 10. This effect can be attributed to the redistribution of mass and stiffness within the FGM plate: higher N values lead to a dominant metallic phase (Al) toward the mid-thickness, reducing overall stiffness and thus lowering the resonant frequency.

Type III distribution exhibits slightly elevated frequency values across the entire N range, indicating that a specific porosity profile can mitigate the adverse effect of stiffness degradation at high gradient levels. The diagram provides a quantitative insight into the interrelationship between material gradient index and porosity distribution, which is of critical importance for the design of advanced FGM systems subjected to dynamic loading.

The bar chart shown in Figure 17 illustrates the influence of different porosity distributions (Type I, II, and III) on the non-dimensional fundamental frequency of a functionally graded Al-Al₂O₃ plate, for a fixed aspect ratio of a/h = 10, a constant porosity volume fraction β = 0.4, and three characteristic material gradient indices (N = 0.1, 0.5, 1). It is clear that an increase in the gradient parameter N, which models a progressive transition from the ceramic to the metallic component through the thickness of the plate, leads to a systematic decrease in the natural frequency for all porosity distribution types.

The most significant frequency reduction is observed for Type I distribution, suggesting that a uniform distribution of porous defects through the thickness further amplifies the degradation of the effective stiffness as the metallic phase becomes more dominant. In contrast, Type II and especially Type III distributions, which introduce linear and trigonometric non-uniformity in the porosity profile, respectively, demonstrate a more stable frequency response with changes in N. Type III exhibits the smallest frequency reduction gradient with increasing N, indicating potentially more favorable mechanical performance in terms of vibrational stability. This behavior can be attributed to the redistribution of mass and stiffness that mitigates localized zones of reduced rigidity.

Such analysis provides both quantitative and qualitative insight into the complex interdependence between porosity distribution, material gradient profile, and vibrational characteristics of FGM structures. Consequently, it can serve as a foundation for design optimization in engineering applications where dynamic performance is of critical importance.

The present study has been restricted to linear free vibration analysis, which is appropriate for small amplitude oscillations where linear kinematics provide accurate predictions. However, in applications involving large deflections, high mechanical loads, or severe thermal environments, nonlinear effects such as geometric nonlinearity and material plasticity may become significant. A systematic extension of the present formulation to nonlinear vibration analysis, including amplitude-dependent frequency shifts and stability considerations, represents a natural direction for future research.

7. Conclusions

In this study, a theoretical model is developed for the free vibration analysis of functionally graded material (FGM) plates resting on elastic foundations, introducing two novel shape functions within the framework of the higher-order shear deformation theory (HSDT). The proposed functions are carefully constructed to satisfy physically consistent conditions of zero transverse shear stress on free surfaces, enabling accurate modelling of transverse deformations without resorting to shear correction factors. Their form encompasses combined nonlinear effects of property gradation and porosity, thereby enhancing the description of complex deformation fields in FGM plates.

Based on these functions, a complete variational formulation of the dynamic problem is derived, incorporating temperature effects, porosity, and elastic foundation models including Winkler, Pasternak, and Kerr foundations. Numerical computations are performed using original MATLAB codes developed specifically for this work, ensuring full control over formulation, discretization, and eigenvalue problem solving.

The obtained results confirm the accuracy and stability of the proposed shape functions through detailed comparisons with existing theories, showing a high degree of agreement across all tested configurations. Notably, the influence of porosity distribution shape on the effective stiffness distribution is observed, where the trigonometric porosity model allows stiffness localization near the surfaces, thereby improving the dynamic response.

Analyses demonstrate that increasing porosity and gradient exponent systematically decreases the fundamental frequencies, while saturation effects are noted at higher values of these parameters, an insight important for engineering optimization. The impact of elastic foundation parameters is examined in detail, revealing that variations in layer stiffness and shear interaction allow precise control over the plate’s dynamic behavior.

The model is successfully validated for various material combinations, including porous ceramic–metal FGM structures, under different thermal conditions and geometries. Based on these findings, the proposed model with new shape functions provides a reliable foundation for vibration analysis of functionally graded structures, especially in applications involving complex thermomechanical loading such as solar absorbers, thermal insulation barriers, and support components in high-energy systems.

Although the proposed model provides accurate predictions of vibration characteristics, it is necessary to emphasize its limitations. The formulation is based on linear kinematic assumptions and does not account for large deformation effects or material plasticity, while porosity is represented by idealized distributions (uniform, linear, and trigonometric). In addition, damping effects and interactions with the surrounding fluid medium are not considered, which defines the scope of applicability of the model and indicates directions for future research.

Future research may extend to nonlinear vibration analysis, damping effects, multiphysics coupling, and experimental validation of numerical predictions, aiming to further confirm the model’s practical applicability.